Turbulence statistics from optical whole-field measurements in particle-laden turbulence

Abstract

Obtaining turbulence statistics in particle-laden flows using optical whole-field measurements is complicated due to the inevitable data loss. The effects of this data loss are first studied using synthetic data and it is shown that the interpolation of missing data leads to biased results for the turbulence spectrum and its derived quantities. It is also shown that the use of overlapping interrogation regions in images with a low image density can lead to biased results due to oversampling. The slotting method is introduced for the processing of particle image velocimetry (PIV) data fields with missing data. Next to this, it is extended to handle unstructured data. Using experimental data obtained by a dual-camera PIV/PTV (particle tracking velocimetry) system in particle-laden grid turbulence, the performance of the new approach is studied. Some preliminary two-phase results are presented to indicate the significant improvement in the statistics, as well as to demonstrate the unique capabilities of the system.

1 Introduction

Dispersed two-phase flows occur abundantly in both nature and industry, yet little is known about the fundamentals of particle–fluid interaction and its effects on the turbulence characteristics. This lack of understanding, despite significant research efforts, can be attributed to one major cause: there is not enough consistent experimental data to validate theoretical models. Although numerical investigations advance very rapidly, it cannot yield the data required for this validation at the moment. Therefore, most models are validated using rather fragmentary data. For a review of work on turbulent two-phase flows, one is referred to the paper by Poelma and Ooms (2005), while an overview of applications and modeling approaches can be found in the book by Sommerfeld et al. (1997).

In this paper, an approach to obtain turbulence statistics in two-phase flows is presented that consists of a measurement system, in combination with a novel processing algorithm. The measurement system consists of a dual-camera particle image velocimetry/particle tracking velocimetry (PIV/PTV) system (described in Sect. 3.2). Since the data obtained by this optical method inevitably have some amount of signal drop-out, the processing of this data needs special care. The effects of data loss on the resulting turbulence statistics are first studied using synthetic data in Sect. 2. An alternative to the conventional interpolation-based processing technique, the slotting method, is presented and extended in the same section. In Sects. 3 and 4, the developed method is applied to real experimental data obtained in single- and two-phase turbulent flows, respectively.

1.1 Background

To study the interaction between the particles and fluid in a turbulent flow, a number of metrics can be used. Earlier studies, predominantly in particle-laden grid turbulence, have relied on single-point statistics, obtained with either laser Doppler anemometry (LDA, Schreck and Kleis 1993; Hussainov et al. 2000) or Hot Film Anemometry (Rensen 2003). These techniques yield information on the change in turbulence level, length scales, dissipation rate, etc. While this approach is very useful, recent work has identified certain aspects of the so-called ‘two-way coupling’ that cannot be studied easily using single-point measurements; for example, Eaton and Fessler (1994) found experimental evidence that certain particles exhibited ‘preferential concentration’ effects, accumulating in low-vorticity regions in the flow. Ferrante and Elghobashi (2003) showed in their numerical work that particles preferentially accumulate in the ‘down-sweeping’ side of vortices. In a DNS study using small bubbles, Mazzitelli et al. (2003) found that these clustering effects play a crucial role in two-way coupling.

It is thus desirable that simultaneous, whole-field measurements of the fluid and particle velocities can be obtained. The most obvious candidate to achieve this is PIV. Earlier work in which PIV has been applied to particle-laden flows is described by, for example, Kiger and Pan (2000) and Khalitov and Longmire (2002). Both captured the images of fluid tracer particles and the larger dispersed phase particles on one camera. By means of image processing, the two phases are separated and processed using conventional cross-correlation algorithms and PTV algorithms, respectively.

It is difficult to image both phases properly using only one camera: the small tracer particles and the bigger dispersed phase particles often have a huge difference in scattering intensity (roughly determined by the squared ratio of the dispersed and tracer particle sizes), exceeding the dynamic range of the CCD sensor. This leads to a compromise in the optimization of the imaging parameters (i.e., lens aperture, exposure time, laser power), which negatively influences the quality of the tracer and dispersed phase particle images. The image quality suffers due to the ‘blocking’ of the dispersed phase too. This decrease in image quality obviously has a negative effect on the phase separation accuracy and displacement estimations. In some cases, this may also lead to ‘cross-talk’: the contamination of the fluid phase data with particle phase data or vice versa.

To reduce the chances of cross-talk, an additional camera can be introduced, in combination with fluorescent tracer particles and color filtering can be used (see Sect. 3.2 for more details). The color filters ensure that each camera captures one phase only so that any cross-talk is unlikely. Additionally, it allows an optimization of imaging parameters for each camera separately. Studies in bubbly flow using this technique can be found in the work by Philip et al. (1995), Lindken and Merzkirch (2002) and Deen et al. (2000).

The use of PIV has two drawbacks: first, it is often more associated with qualitative flow analysis than as a tool to extract e.g., turbulence power spectra. Work by, for example, Westerweel et al. (1997), and more recently Donnely et al. (2002) and Uijttewaal and Jirka (2003) showed that PIV can be used to study second-order statistics too. Nevertheless, the resolution can currently not match that of the well-established single-point methods.

The second drawback is that there will be data loss due to non-ideal PIV images. There are two main reasons for the latter. First, the dispersed phase particles take up space in an image so that there may not be enough tracer particles in an interrogation area surrounding a dispersed particle. In this work, this effect is negligible, since the volume load is so low that the fraction of ‘excluded’ pixels in an image is always smaller than 1%. Furthermore, the interrogation areas are (slightly) larger than a particle so that only half of an interrogation area will be covered at most. The second reason for the reduced image quality is the presence of particles in the line of sight between the field-of-view and the sensor. They partially block scattered light of the tracers, which results in a significant drop in the signal-to-noise ratio of the tracer images. It is difficult to quantify this effect beforehand without resorting to complex ray-tracing techniques. Preliminary PIV experiments in a thermal convection cell with comparable characteristics to the flow geometry that will be used later on (i.e., laser path length, viewing depth) indicated that even at a modest volume load of 0.5%, at least 10–15% of the data is missing in a PIV result (Rotteveel 2004). In a publication by Deen (2001), an approach is described to estimate the data drop-out based on the gas fraction in a bubbly flow. Using this approach, results are predicted similar to our experimental findings. As will be shown in the next section, this unavoidable data drop-out necessitates an elaborate data analysis to avoid systematic errors.

It is a priori not known to what extent the coupling effect between the phases affect the fluid phase statistics, especially since conflicting results have been reported in the literature [see Poelma and Ooms (2005) for a review]. For instance, reports on the change in turbulent kinetic energy range from a few percent to as much as 50% (both positive and negative!). An additional metric to study the interaction is the shape of the power spectrum; Boivin et al. (2000) used the slope of the spectrum to model the ‘energy-sink behavior’ of particles in an LES study of particle-laden flows and find a slightly higher slope compared to the single-phase case. In a detailed DNS study, Mazzitelli et al. (2003) finds an increase in the slope from −5/3 for single-phase flows to −8/3 for a turbulent flow laden with small air bubbles. Others have found a ‘pivoting’ or ‘cross-over’ of the spectrum, where the large scales are suppressed, while energy at higher wave numbers is augmented, see e.g., Ten Cate et al. (2004). This is associated with a lower slope. Since all these changes are relatively subtle, the extraction of turbulence statistics (such as the power spectrum) from the ‘incomplete’ experimental data sets has to be done with special care and any systematic errors should be minimized.

2 Data processing

Most of the relevant turbulence quantities can be derived from the power spectrum or autocorrelation function, which contain the same information (Pope 2000). Conventionally, the spatial spectrum is determined by taking the Fourier transform of a row (or column) of vectors of the PIV result. Assuming the flow is homogeneous within the field-of-view, a smooth estimate can be obtained by averaging over all rows for a number of realizations. The problem with this method here is that any missing data (mainly resulting from the deteriorated image quality due to the presence of dispersed phase) have to be interpolated in order to use the Fourier transform. However, interpolation can have a significant effect on the outcome of the result, since it introduces a systematic error to the data.

2.1 Synthetic data

To illustrate the effect of interpolation of missing data on the power spectrum, synthetic data are generated with a known spectrum. To simplify the analysis, one-dimensional records are generated, instead of two-dimensional vector fields as obtained by PIV. Subsequent rows in real vector fields are obviously not statistically independent. The data sets generated here can be considered to represent parts of real vector fields, each time skipping a number of rows (the number of rows skipped representing a separation larger than the integral length scale of the flow). The synthetic data will therefore capture the relevant phenomena of real data.

The data are generated using a technique similar to kinematic simulations (Fung et al. 1992); a model power spectrum is assumed, the square root of which is inverse Fourier transformed. This yields a signal with the specified power spectrum. Note that the ‘power’ is first distributed over a real and imaginary component for each wave number so that the contributions of different frequencies have different phase information. The process is shown schematically in Fig. 1. The spectrum is assumed to have a constant energy level to a certain wave number k ₀, after which it decreases as k ^−5/3 until some cut-off frequency k ₁, above which no energy is present. This shape can be considered as a crude approximation of a longitudinal one-dimensional turbulence spectrum of homogeneous isotropic turbulence (Pope 2000). Records are generated of 256 data points each, with an ‘inertial sub-range’ between k ₀=8 and k ₁=48 ¹. Explicit ‘zero-padding’ is not necessary, since no energy is present above k ₁. Note that all wave numbers mentioned actually represent Fourier modes and can be assumed to be made dimensionless (with respect to the arbitrary units used for the signal) by dividing by k ₀.

Fig. 1

The generation of synthetic data by inverse Fourier transformation of a known spectrum

Data are removed using a simple algorithm: for each record, a random number between 0 and 1 is generated. If this number is below a specified threshold, the record is removed and its location marked. Subsequently, linear interpolation is performed to fill up these marked locations. The power spectrum is obtained by taking the Fourier transform of these interpolated data records and plotting the absolute squared value. In Fig. 2, the results for the data losses of 10 and 20% are shown, together with the original (‘input’) spectrum. The dashed lines indicate k ₀ and k ₁, respectively.

Fig. 2

The effect of different levels of data loss on the resulting power spectrum as obtained from synthetic data. The missing data were interpolated using a linear interpolation. The dashed lines indicate k ₀ and k ₁, respectively (see text)

As can be seen in Fig. 2, the slope is affected increasingly when more data are lost. For the 20% data loss case, the slope approaches −2 versus the original −5/3, which would make a physical interpretation as mentioned in Sect. 1.1 difficult. These levels of data loss have negligible effect on the variance (i.e., the integral of the spectrum). This is obvious, since this quantity is dominated by low wave number energy, while data loss affects the small-scale structure. Nevertheless, small-scale behavior can affect the calculation of the variance; for instance, in the process of the removal of uncorrelated noise, as described in the next section.

2.2 Noise removal

Obviously, any real signal will have some level of noise. To demonstrate the effect of data loss and interpolation in a signal contaminated with noise, the same analysis as above is performed, yet this time uncorrelated, Gaussian noise is added to the signal. Noise removal is commonly done in the processing of LDA data by fitting a parabola to the first few points of the autocovariance function, while ignoring the value at r=0, i.e., the total signal variance (Benedict and Gould 1998). This autocovariance function can be obtained by taking the Fourier transform of the power spectrum. The abscissa of the fitted parabolic function with the ordinate axis gives a corrected estimate of the variance, while the second derivative at this location is related to the Taylor microscale and dissipation rate (Pope 2000). Examples of this approach can be found in the aforementioned work of Benedict and Gould (1998) and also in the work of Romano et al. (1999). If the first point of the covariance function is replaced with the value obtained from the fit, the corrected power spectrum can be obtained subsequently by an inverse Fourier transform. Note that this procedure is similar to subtracting a constant (i.e., contribution from uncorrelated noise) from the spectrum. This constant can be determined by the ‘plateau’ of white noise at high wave numbers (most evident in Fig. 5).

In Fig. 3, the results are shown for increasing data loss in a noisy signal. The noise represented 20% of the variance of the total signal. Again, parts of the data were removed using the same algorithm as described earlier. The figure shows three cases: no data loss, 10 and 20% data losses. Additionally, the reference (‘input’) spectrum is shown, as well as the uncorrected, noisy spectrum. The missing data were replaced using linear interpolation. It should be noted that the choice of interpolation scheme slightly affected the outcome of the result, and for an extensive analysis one is referred to Poelma (2004). Linear interpolation is the most commonly used technique, and it was chosen here as a representative example. After interpolation, the spectrum is again calculated by means of Fourier transforms. Subsequently, the uncorrelated noise was removed as described above.

Fig. 3

The effect of different levels of data loss on the resulting power spectrum as obtained from noisy synthetic data. The missing data were interpolated using a linear interpolation, and the uncorrelated noise was removed using the method described in the text

As can be seen in Fig. 3, with increasing data loss, the slope of the spectrum increases due to the redistribution of energy from the uncorrelated noise over the spectrum. Therefore, the uncorrelated noise cannot be removed completely anymore; in the covariance function, not only the point at zero separation (i.e., the variance) is overestimated, but also the neighboring points. Therefore, the parabolic fit will overestimate the variance. For 10 and 20% data loss, the variance is overestimated by 8.3 and 13.5%, respectively, as compared to the noise-free spectrum (the uncorrected spectrum obviously is overestimated by 20%). Needless to say, also the Taylor microscale, dissipation rate and other derived quantities are increasingly biased with increasing data loss.

2.3 Slotting

In order to overcome the problems associated with the interpolation of missing data, the slotting method is introduced for the estimation of the power spectrum from PIV data. Originally, the slotting method was developed to process non-equidistant data as produced by LDA (Mayo et al. 1974). The rows in the PIV vector fields with missing data can be assumed to be a non-equidistant-sampled signal (albeit mostly at equidistant instances), so the slotting method should be useful in this context too. Here, the principles are described only briefly; for a detailed description, one is referred to, for example, work by Tummers and Passchier (1996).

In the slotting method, the autocovariance function of a signal is reconstructed by calculating, for all possible combinations, the product of a velocity pair and sorting this result in an appropriate slot (or ‘bin’) according to the temporal or spatial differences between the realizations. For a continuous signal, the autocovariance function of a time-invariant stochastic process is defined as:

$$\Gamma (\delta t) = \overline{u(t) u(t + \delta t)}. $$

(1)

An equivalent expression can be given for a discrete signal and/or function:

$$\Gamma (\delta t_{k}) = \frac{1}{N_{k}}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n} u(t_{i}) u(t_{j}) \quad \forall \; |t_{j} - t_{i} - \delta t_{k}| \leq \Delta/2 $$

(2)

with

$$ N_{k} = \sum_{i=1}^{n} \sum_{j=1}^{n} 1 \quad \forall \;|t_{j} - t_{i} - \delta t_{k} | \leq \Delta/2. $$

(3)

In these equations, N _k is the number of realizations for the k-th slot and Δ the slot width. To simplify the notation, we set r ≡ δt _k . It should be noted that the number of realizations for each slot (N _k ) is not a constant. For an equidistant data set, N _k will linearly decrease from the number of samples n to 1 at the spacing corresponding to the length of the data set. Instead of dividing the sum of realizations per slot by the number of realizations, a better result for the autocorrelation function is obtained using the so-called ‘local normalization’: per slot, the data are normalized by the variance of only the data actually used for that slot (Tummers and Passchier 1996). This results in a smoother function and avoids problems with ‘negative energy’ in the power spectrum.

When processing LDA data, the choice of the slot size is a compromise between resolution and noise level (since with decreasing slot size, there is less data available per slot). For PIV data, it is obvious to choose the slotting size equal to the vector spacing. The vector data are then processed row by row and for all measurements available, ignoring any missing data. This ensemble averaging results in a covariance function—and thus power spectrum—without the need for interpolation, as long as there is at least one realization for each separation distance available in the entire the data set. Obviously, a limited number of realizations for a separation distance will lead to a high uncertainty.

The exercise with the one-dimensional synthetic data as mentioned above is repeated, this time using the slotting method. For the case without noise, the results are given in Fig. 4. As can be seen, the results for both the 10 and 20% data loss cases collapse on the reference spectrum. In principle, the data loss percentage can be arbitrarily high, as long as enough realizations are available to yield a converged result.

Fig. 4

The effect of different levels of data loss on the resulting power spectrum as obtained from synthetic data. The missing data are NOT interpolated and the spectrum was obtained using the slotting method

When uncorrelated noise is added (again, 20% of the total variance), the input spectrum can still be retrieved after noise correction for the three cases of data loss, as can be seen in Fig. 5: all three spectra collapse on the reference spectrum. The variance for the three cases is within 1% from the reference variance and can be explained by the limited number of records used.

Fig. 5

The effect of different levels of data loss on the resulting power spectrum as obtained from noisy synthetic data. The missing data are NOT interpolated and the spectrum was obtained using the slotting method. The results for 0, 10 and 20% data loss collapse on the reference spectrum

Based on these results, it can be concluded that the slotting method is a better alternative to the conventional method of obtaining spectra: regardless of noise level and amount of data loss, an unbiased estimate for the power spectrum can be obtained. Obviously, practical limitations for the data size apply: the total amount of vectors used for input should be at least equal for the conventional and slotting methods. This means that if there is a data loss of 50%, twice as many image pairs should be recorded. As interpolation redistributes the uncorrelated noise, spectra obtained this way tend to be smoother than their counterparts obtained using the slotting method. For the 20% noise case used in this section, eight times more data were needed to get a converged result.

A minor drawback of the slotting method is the relatively long processing time needed, because all multiplications are done explicitly, in contrast to the use of Fast Fourier transforms with the interpolated data. This means that for longer data series the processing time rapidly increases: O(n ²) versus O(n  log  n) for one-dimensional data. Since PIV data have only a limited number of data recordings per row (typically n<100), in practice the optimized implementation of the algorithm in Matlab is currently approximately only five times slower than the Fourier-based method.

2.4 Effect of overlapping interrogation areas

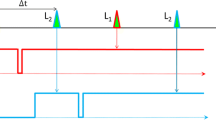
It is a common practice to use overlapping interrogation areas in the cross-correlation analysis of PIV images (Raffel et al. 1998). Overlapping areas, usually with 50% overlap between adjacent areas, will lead to a smaller data spacing, while maintaining a low correlation of the error between neighboring data points. However, if the number of tracer particles per interrogation area (N _I) becomes too low, overlapping windows can lead to oversampling. To illustrate this, we assume an average, homogeneous tracer particle distribution. The probability of finding no or a maximum of one particle per half interrogation area as a function of N _I can be calculated fairly easily and is shown in Fig. 6. The case for just half of the area is considered, because if no (or only one) particle is in this half, it will not or hardly contribute to the cross-correlation result of the total interrogation window. Hence, two very similar velocity estimates will likely be obtained (equivalent to ‘sample-and-hold’), based on the same tracer pattern displacement (see Fig. 7).

Fig. 6

Probability of finding zero or a single tracer particle in one half of an interrogation area with average image density N _I

Fig. 7

A simple schematic representation of oversampling: overlapping interrogation areas use the same tracer pair in the absence of other tracer particles, leading to a duplication of the vector result

As can be seen in Fig. 6, the probability of finding ‘empty’ interrogation area halves drops quickly: for an average density of 13 tracer particles or more, on average less than one percent of the interrogation halves would be empty. In this case, overlapping areas can be used without problems. For images with a reduced tracer density (e.g., 4–8 particles per interrogation area), oversampling may introduce a systematic error in the turbulence statistics.

To study the effect of oversampling, again synthetic data are used; yet instead of removing a certain percentage or records, they are replaced with their neighboring value. The results for a ‘duplication’ percentage of 10 and 20% are shown in Fig. 8. The effect of duplication is not as significant as the artifacts due to interpolation: the slope increases by 10% from −5/3 to approximately −1.8. Only with very low tracer particle densities (i.e., <4 particles per interrogation area), oversampling will have a more significant effect on the turbulence statistics.

Fig. 8

The effect of oversampling (10 and 20%) on the resulting power spectrum

2.5 Unstructured data processing

The principle of the slotting method can also be extended to handle completely unstructured data, such as is obtained by, e.g., particle tracking velocimetry or super-resolution PIV (Keane et al. 1995). In most work reported in the literature, this kind of data are interpolated back onto a regular grid, so the conventional techniques can be used (Agui and Jimenez 1987; Stuër and Blaser 2000). As was shown earlier, interpolation introduces errors that may diminish the specific strength of unstructured data: improved spatial resolution. Therefore, two new alternatives are introduced here:

2.5.1 Vector decomposition

In this method, for each possible vector pair v _i and v _j in the vector field, the separation vector r is determined. Next, the vectors v _i and v _j are decomposed in the transversal and longitudinal components with respect to the separation vector (see Fig. 9). By multiplying these longitudinal and transverse components of both vectors, both corresponding autocovariance functions can be reconstructed. A similar approach has been used successfully by Paris and Eaton (1999) to obtain dispersed phase correlation functions.

Fig. 9

The pairwise decomposition of two vectors (u ₁ and u ₂), either on a grid or unstructured. The vectors are projected along the separation vector r, at angle Θ. This results in the transverse and longitudinal components; u _1,l , u _1,t , u _2,l and u _2,t , which are used as input for the slotting method

A disadvantage of this method is that it assumes isotropic data, since all directional information is lost in the averaging. This can be overcome by reconstructing the autocovariance functions for each angle, e.g., by also slotting the orientation of the separation vector (θ). In practice, it appears to be sufficient to reconstruct only two-directional slots (i.e., |θ|<π/4 ‘horizontal’ and |θ|>π/4 ‘vertical’). The ‘true’ horizontal and vertical autocovariance function can be reconstructed by extrapolation from these averaged results. An important disadvantage of this method is the computational effort needed to do the decomposition for each vector pair, as discussed in Sect. 2.3.

2.5.2 Fine-grid redistribution

This method is closely related to the original PIV slotting method as introduced above, except that a fine-grid discretization step is applied before using the slotting method: each vector is relocated to the nearest grid point of a sufficiently high resolution grid. This results in a large, sparse matrix containing the original data. This matrix is now used as input for the slotting method, again ignoring all the ‘empty’ entries. In Fig. 10 the method is illustrated schematically. The choice for the grid size is again a compromise between spatial resolution and noise level. Obviously, the error due to displacing the vector to the nearest grid point should be smaller than the expected error due to interpolation of the sparse field. On the other hand, with a too fine grid, no vector combinations will be found at all.

Fig. 10

Extension of the slotting method to two-dimensional, unstructured data; first, the data are discretized on a fine grid. The resulting sparse (regularly spaced) vector field is then processed row by row to obtain the autocovariance function

In practice, the fine-grid distribution method works fine for relatively large vectors fields (e.g., over 1,000 vectors, for instance obtained using super-resolution PIV). For less dense fields (up to 100–200 vector per field, e.g., from the tracking of individual dispersed-phase particles), the decomposition method appears to be more appropriate.

3 Grid turbulence experiments

To test the measurement system and processing techniques using real data, experiments are performed in grid-generated turbulent flow. First, the single-phase will be studied to verify the performance of the new measurement system by comparing it with results from a different measurement technique and with literature results. Subsequently, the two-phase case will be considered.

The flow geometry was chosen because it is the most ‘simple’ turbulent flow available, since the (single-phase) flow is nearly homogeneous and isotropic. A vast amount of experimental and theoretical work is available for single-phase grid turbulence (Comte-Bellot and Corrsin 1971; Batchelor 1953). These data, such as dissipation rates, the development of length scales, shape of the spectrum, etc., serve as a validation for the measurement system and facility itself. Obviously, a real validation of the new measurement set-up can only be achieved by comparison with a separate measurement technique in the same flow (in this case laser Doppler anemometry). However, further supporting evidence can be obtained by checking the consistency of the obtained turbulence statistics with the well-established theories for decaying, homogeneous turbulence. Naturally, the data can also serve as a reference case for the two-phase experiments.

The flow is only moderately turbulent compared to, e.g., flows encountered in nature, but it still exhibits many interesting two-way coupling phenomena for the particle-laden case (Poelma et al. 2004). Also, the turbulent level and separation of scales are comparable to the values at the centerline of a fully developed turbulent pipe flow at moderate Reynolds number, see e.g., the often-cited work by Tsuji et al. (1984).

An advantage of having a relatively low Reynolds number is that all length scales can be captured in the PIV measurements so that a ‘complete’ view of the flow becomes available. Additionally, it reduces the likelihood of artifacts due to, e.g., the finite window size or aliasing, which may complicate the analysis.

3.1 Description of the flow facility

Turbulence is generated in a vertical water channel by directing the fluid through a grid before it enters the test section. The grid consists of a perforated plate with 7.5×7.5 mm² holes, with a solidity of 0.44. As grid-generated turbulence is not completely isotropic in the initial stage, a 1:1.11 contraction is placed between the grid and the test section (Comte-Bellot and Corrsin 1966). A schematic drawing of the facility is shown in Fig. 11, while some key parameters are summarized in Table 1. The test section consists of an 80-cm-long glass round pipe with a diameter of 10 cm enclosed in a water-filled square box to minimize optical distortion due to the curved pipe wall (3 mm thick). The flow rate was fixed at a mean axial velocity of 0.5 m/s, leading to a grid-based Reynolds (UM/ν) number of 3,750. More details on the flow facility can be found in Poelma (2004).

Fig. 11

A schematic representation of the grid turbulence facility

Table 1 Summary of the key parameters of the grid turbulence facility

3.2 Description of the measurement set-up

In Fig. 12, a schematic drawing of the combined two-camera set-up is given. A light sheet is generated with a frequency-doubled, double pulse Nd:YAG laser (15 mJ/pulse at 532 nm; Mini Lase II, New Wave research) and a pair of lenses (f=−40 and 100 mm, respectively). Two 2,048×2,048 pixels, 12-bit double-frame CCD cameras (ES4.0, Roper Scientific) are used to record the images. The cameras are both equipped with a 105 mm focal length lens (Micro Nikkor), which give a typical field of view of approximately 4×4 cm². The camera and laser triggering and the data acquisition are done using a LaVision Flowmaster system running DaVis 6.2. Initial analysis and calibration is also done using this software, while the PIV and PTV image processings were done using in-house developed software (Westerweel 1993; Poelma 2004).

Fig. 12

A schematic drawing of the combined particle image velocimetry/particle tracking velocimetry (PIV/PTV) set-up

As tracer particles we use polystyrene particles of 20 μm containing Rhodamine 6G and dichlorofluorescein (supplied by the Laboratory for Experimental Fluid Dynamics at the Johns Hopkins University, Baltimore, MD, USA). In Fig. 13, details about the wavelength-based separation are given (for Rhodamine 6G); the fluorescent dye absorbs the original laser light at 532 nm and emits in a broad band at longer wavelengths. One camera is equipped with a cut-off filter at 550 nm, hereby effectively blocking the original laser light and allowing most (>95% above 575 nm) of the fluorescent light to pass. The second camera is equipped with a neutral density filter (effectively blocking light by six ‘stops’, equivalent to an optical density of 1.8). This filter ensures that the tracer particle image intensity is reduced below the detection threshold of the CCD camera, while the dispersed phase particles are still clearly visible.

Fig. 13

The absorption and emission spectrum for Rhodamine 6G (data from Molecular Probes, Inc.). Also indicated are the emission wavelength of the frequency-doubled Nd:YAG laser and the cut-off wavelength of the filter

The cameras are focused on the same field of view using a combination of a beam splitter plate (i.e., a semi-transparent mirror) and a standard mirror. The overlap of the two fields of view is optimized by imaging a calibration plate mounted at the second focal plane. This way, no calibration plate had to be put inside the test section and the calibration could easily be checked in between measurements. Using a local cross-correlation (similar to a PIV analysis), the local difference between the two images can be estimated (Willert 1997). The camera position adjustment and error calculation are iterated a few times until the maximum local deviation between the images (‘disparity’) is less than 15 pixels (corresponding to 0.32 mm at the used magnification); see Fig. 14. The remaining differences between the two camera images are compensated by using a simple second-order polynomial fit of the local differences. The correction using this fit will be applied to the obtained vector fields (as opposed to the images), and the total error (viz. displacement) was found to be less than 4 pixels on average. This error is small compared to the data spacing of the PIV result, which typically is equivalent to 16 or 32 pixels. As a conventional calibration plate could not be placed inside the test section easily, the pixel-to-millimeter calibration of each camera is performed by an accurate translation of the camera with respect to a horizontal laser beam in the field of view (estimated error <0.5%).

Fig. 14

Example of the camera overlap optimization: left: zoom of overlapped calibration images, right: resulting local error (‘disparity map’) from local cross-correlation. In this example, the disparity map is dominated by a relative rotation of the cameras of approximately 0.5°

3.3 Single-phase experiments

The turbulent flow inside the facility was first characterized using LDA. The LDA system is a Dantec two-component system, based on a 5 W Spectra Physics Argon-ion laser and two Dantec Burst Signal Analyzers. The LDA measurements are mainly performed to check the homogeneity of the flow in the transverse, i.e., horizontal, direction. Furthermore, an initial estimation of the turbulence characteristics (length, time and velocity scales) is obtained, which was used in the design of the PIV system (e.g., choice of field of view). At five downstream locations (z/M = 42.9, 56.3, 70, 86.3 and 100.1, with z/M the dimensionless downstream distance using the mesh spacing M) time series of both streamwise and transverse velocities are obtained at the center of the measurement section. Since the turbulence level is small compared to the mean fluid velocity (u′/U≈2%), the time series can be converted to spatial series using Taylor’s hypothesis. These series are subsequently processed using the slotting method, as described earlier.

The single-phase turbulence statistics are subsequently obtained using the new PIV system. Though there is no need to use the fluorescent tracer particles and color-filtering techniques for the single-phase flow, they are used nevertheless. This serves as a test to see if they give an unbiased estimate of the fluid behavior and eliminates any possible effects due to different tracer particles used in the single- and two-phase experiments. At each downstream location 100 image pairs are recorded. Before obtaining turbulence statistics, the mean flow is determined and subtracted to avoid any mean spatial gradients in the velocity fields. These mean gradients are found to be well below 1% of the mean velocity. The PIV data are processed using a standard two-pass cross-correlation algorithm (Westerweel 1993) using 32×32 interrogation areas and no overlap. The interrogation area size is chosen to get optimal resolution, but retain sufficiently high percentage good vectors (>95%). The initial shift between the interrogation areas is set to 60 pixels, equivalent to the mean fluid flow displacement at the specified laser pulse delay time (see next paragraph). The data are validated using a median test, with a threshold of 1.25 times the standard deviation of the neighboring vectors (Westerweel 1994).

The optimal laser pulse time delay, ΔT, is chosen by determining the root-mean-square values of the fluid velocities (u′) using different delay times. Some typical results of this exercise can be found in Fig. 15. For small delay times, the root-mean-square value is significantly overestimated due to the fact that the pixel displacement is overshadowed by the error in the sub-pixel displacement. The latter error is fixed for a given image quality and interrogation algorithm and is here estimated to be of the order of 0.1 pixel. The ‘real’ displacement—and dynamic range—increases proportional to ΔT, so the observed sub-pixel error in the velocity r.m.s. decreases with 1/ΔT as can be observed in the graph. At a certain ΔT, the sub-pixel error is lower than the fluctuations (here this typically occurs at ΔT=1,000–2,000 μs) and the obtained r.m.s. value becomes independent of the delay time (the plateau in Fig. 15). At even higher ΔT, the signal drop-out due to out-of-plane motion starts to dominate and the signal-to-noise ratio of the cross-correlation result decreases: errors due to loss-of-pairs start to dominate and the observed r.m.s. dramatically increases. The optimal delay time is a compromise between the highest dynamic range and acceptable loss-of-pairs. Note that the delay times considered here are still an order of magnitude smaller than the Kolmogorov time scale (as obtained by LDA), so the flow can still be considered to be frozen during the measurement. Here, a ΔT at roughly three-quarters of the plateau is chosen, ΔT=2,000 μs. This yielded a mean displacement of 60 pixels, with a fluctuating component (r.m.s.) of 1.5 pixel. For a more detailed discussion of this procedure, the reader is referred to Poelma (2004). It should be noted that our value for ΔT corresponds closely to the value obtained from the commonly used ‘one-quarter’ rule (Keane and Adrian 1992).

Fig. 15

The influence of the laser pulse delay (ΔT) on the resulting root-mean-square value of the measured fluid velocity for three pump settings (respectively corresponding to centerline velocities of 0.16, 0.24 and 0.33 m/s)

The PIV results for the turbulence statistics are summarized in Table 2, together with the LDA results at the first measurement location. The mean data rate of the LDA system was approximately 750 Hz. At a mean fluid velocity of 0.5 m/s, this corresponds to a sample spacing of 0.65 mm. This is very similar to the PIV data spacing, which is 0.63 mm (equivalent to 32 pixels). As can be seen in the table, the agreement between the PIV and LDA results is within the estimated experimental error; the 95% confidence intervals are shown for the PIV results at the first location (column 4). These intervals were estimated by dividing the total series of images in smaller groups and calculating the standard error of the mean of the obtained results for these sub-series. The intervals correspond to twice the standard error. The integral length scale (Λ) was obtained by integrating the longitudinal autocorrelation function. The decay of the turbulent kinetic energy was used to determine the dissipation rate. The Kolmogorov scales were subsequently derived from the dissipation rate. This may explain their relatively large discrepancy compared to the other quantities.

Table 2 Summary of single-phase particle image velocimetry (PIV) results at the five measurement locations, laser Doppler anemometry (LDA) results at r0 shown for reference in the third column. In the fourth column, the PIV results at the first location are shown with the 95% confidence interval

The dissipation rate was also determined from the Taylor microscale, using the following relationship, which is valid for homogeneous, isotropic turbulence (Pope 2000):

$$\epsilon = 15 \nu \frac{{u'}^{2}}{\lambda_{g}^{2}}. $$

(4)

The results using Eq. 4 were in reasonably good agreement with the results based on the decay of the turbulent kinetic energy (see Table 2). This consistency suggests that the PIV results are reliable. Additional evidence for this is, e.g., the fact that the Reynolds number based on the turbulence length scales does not vary significantly over the test section.

An important parameter is the decay of the turbulent kinetic energy over time (viz. space), which is plotted in Fig. 16. Note that the reciprocal values are plotted, normalized with the square of the mean fluid velocity, i.e., (U/u′)², as is conventional in representing grid-generated turbulence data. As can be seen in the graph, the decay shows a clear power-law behavior over the measurement region, as predicted by theory (Batchelor 1953). Note that in this graph the 95% confidence intervals at the first location correspond approximately to the marker height.

Fig. 16

The decay of the horizontal and vertical variances of the fluid velocity (u′ u′ and v′ v′) as a function of distance to the grid. Symbols denote experiments, while the lines indicate the fitted results

As an additional characterization, the (longitudinal) power spectrum is considered; see Fig. 17. The results obtained by PIV and LDA are both plotted, together with previous data of grid-generated turbulence obtained by Comte-Bellot and Corrsin (1971). The latter data have been found to collapse on a large body of other experiments, when appropriately scaled (Pope 2000). This scaling is done using the Kolmogorov scales so that the data should collapse for wave numbers in the inertial sub-range and higher. The present Reynolds number is too low for the flow to exhibit a true inertial sub-range in the spectrum (with slope ‘−5/3’ as indicated in the graph for reference). Since the Reynolds number of the current experiment and the two experiments by Comte-Bellot and Corrsin (1971) are different (Re _λ=72 and 49, vs. 30 for the current experiment), the data are expected to deviate for low wave numbers. For higher wave numbers, the data collapse, except for the final part. Here, the LDA data noise level starts to dominate. The PIV systematically underestimates the power, which is most likely caused by the fact that a parabolic fit of the autocovariance function requires sufficiently spatially resolved data. Here, the vector spacing is three times larger than the estimated Kolmogorov scale, so the data are slightly under-resolved. Therefore, the noise correction filters out some high-frequency energy. An extensive study of the spatial filtering behavior of PIV measurements can be found in work by Foucaut et al. (2004).

Fig. 17

The longitudinal spectrum obtained by laser Doppler anemometry (LDA) and PIV, compared with classic data by Comte-Bellot and Corrsin (1971). The data are plotted using Kolmogorov scaling. The LDA and PIV results are corrected using the noise-removal method described in Sect. 2.2

No significant differences can be found between the data processed using the conventional FFT-based method and the new slotting method. This can be explained by the fact that for the single-phase flow there is hardly any signal loss (typically 2–3%) and the noise level is low: the variance of the original signal and the result from the parabolic fit are always within a few percent.

In conclusion, it can be stated that all major statistics obtained with PIV and LDA are in close agreement with each other, so the quantitative capabilities of the PIV system are here equal to that of the LDA system. Furthermore, the results are consistent with classic turbulence theory and experiments; for a detailed comparison of the turbulence statistics with earlier experimental and theoretical work, one is referred to Poelma (2004).

4 Two-phase grid turbulence experiments

The true test of the system is obviously the application in real dispersed two-phase grid turbulence. In this experiment, particles of several different materials (glass, ceramic and polystyrene) and diameter (100–500 μm) are used. The particles are introduced at the top of the facility, after which they are recirculated in the facility. The mean volume load is determined by measuring the increased pressure drop over the test section due to the effective density of the suspension (Poelma 2004). Experiments are performed using different volume loads, with a maximum of 0.5%. Most results discussed here are obtained in measurements with (approximately) spherical ceramic particles with a mean diameter 280 μm and a density of 3,800 kg/m³. These particles have a measured terminal velocity of approximately 6 cm/s, a Reynolds number (based on this velocity and the particle diameter) of 17 and a Stokes number (defined as the ratio of particle response time scale and the Kolmogorov scale of the fluid) of 0.23.

When particles are added to the flow, it is found that the laser pulse delay time has to be decreased from 2,000 to 1,500 μs to get acceptable results (the percentage of good vectors increased from 70% to 80–85%). Most likely, tracer loss-of-pair increases due to obscuration: the cumulative, contrast-reducing effect of the (out of focus) dispersed-phase particles between the light sheet and camera. In terms of Fig. 15, increased loss-of-pair infers that the ‘plateau’ of acceptable laser pulse delay times is shortened. Despite the loss in dynamic range due to the change in ΔT, the new value still lies on the plateau, so sub-pixel errors most likely do not dominate the results.

Examples of details of the obtained images for the dispersed and fluid phase are shown in Figs. 18 and 19, respectively. The images of the dispersed phase (Fig. 18) are relatively straightforward to process, since they are devoid of any fluid tracer particles. The images are processed using the so-called particle mask correlation technique (Kiger and Pan 2000; Takehara et al. 1999). Here, particles are detected using the cross-correlation of the image with a model particle image or ‘mask’. This also discards some of the particles with weaker intensities that can be observed in Fig. 18. Since the separation between the particles is large compared to the displacement (after subtracting the mean shift), a simple nearest-neighbor scheme can be used to match the particle locations in both frames.

Fig. 18

A close-up of a typical dispersed-phase image (superposition of both exposures, colors inverted for clarity, first 256 gray values only). The vectors are obtained by particle tracking velocimetry

Fig. 19

A close-up of a typical fluid-phase image obtained in a two-phase flow (single exposure, colors inverted for clarity, first 256 gray values only)

The PIV images (see Fig. 19) are far from ideal; the tracer concentration is relatively low and the image is contaminated with larger ‘donut’-shaped structures. The first problem is caused by the obscuration due to the out-of-plane dispersed-phase particles. As the tracer concentration is relatively low (visual inspection suggests a maximum of eight particles per 32×32 interrogation area), it is decided not to use the overlapping interrogation areas, to avoid any possible oversampling effects as mentioned in Sect. 2.4.

The presence of larger structures in Fig. 19 may on first sight be explained as dispersed phase particles: fluorescent light emitted by the tracer particles might illuminate the dispersed phase so that cross-talk occurs. To verify this hypothesis, a particle tracking algorithm is applied to these images. This algorithm yielded the velocity as well as the size of each object in the image. It is found that the large structures had the same mean velocity as the small tracer particles. Since a significant slip velocity is expected for these particles (6 cm/s, equivalent to a displacement of six pixels), it is thus not likely that these structures are dispersed phase particles. An alternative explanation is that the structures are out-of-focus tracer particles. The light sheet thickness increases due to scattering from the dispersed phase, from approximately 0.5 to 1 mm. Therefore, tracer particles outside of the focal depth region of the camera may be imaged, since the depth of field was estimated at 0.4 mm (Adrian 1997). Out-of-focus particles will move at approximately the same velocity as the in-focus particles. To avoid any possible influence of the structures during processing, the raw images are first high-pass filtered by subtracting a smoothened version of the image. This smoothing is done using a 5×5 uniform kernel. Visual inspection shows that the structures, which already have a lower intensity than the tracer particles, are significantly reduced. Further processing of these images is done similar to the single-phase PIV analysis.

The results from both cameras are combined using the disparity function which is determined from the calibration. An example of a typical result is given in Fig. 20; a fluid vector field of 64×64 vectors on a regular grid, together with typically 100 particle locations and velocities. For each location and experimental condition (particle load, size, etc.), 128 image pairs are collected. It was found that 128 image pairs were enough for statistical convergence of the variance. The data are acquired with a frequency of approximately 1.5 Hz. This frequency is lower than the lowest time scale of the turbulence (the eddy turn-over time, see Table 2), so they are assumed to be statistically independent. The data as shown in Fig. 20 serve as the starting point for all further analyses.

Fig. 20

A typical snapshot of the combined PIV/PTV results. The regularly spaced vectors represent fluid vectors, discs indicate particles and bold vectors indicate the particle velocities. The mean components have been subtracted from both phases separately for clarity

4.1 Fluid phase results

As mentioned in Sect. 2, the power spectrum is used to derive the turbulence characteristics. In Fig. 21, an example of the longitudinal spectrum of the fluid, obtained at the first downstream location (z/M=43), is given. The spectrum has been calculated by means of the ‘conventional’ method and the slotting method. For reference, the single-phase spectrum is also shown. As can be seen in the graph, the slotting method results in a slightly steeper spectrum. These differences are significant compared to the statistical fluctuations in the data, which start to dominate at 200 m⁻¹; to give an indication of the latter, the 95% confidence interval of the slotting result is shown as the shaded envelope. Based on the results obtained using synthetic data in Sect. 2, it is assumed here that the result of the slotting method is the closest to the real result. When the variance is calculated, it appears to be overestimated by 5–10% if the interpolation-based method is used. This is significant, since changes in the variance due to particles are reported in the literature in the range of 10–50% (Hussainov et al. 2000; Schreck and Kleis 1993; Poelma and Ooms 2005). Note that due to alignment changes, flow conditions, etc. the number of outliers, and thus systematic error can change. This makes a correction of interpolation-based results difficult.

Fig. 21

The longitudinal fluid spectrum obtained in two-phase grid turbulence. The data were processed by both using interpolation of the missing data and the slotting method. For the latter, also the 95% confidence interval is shown as the shaded envelope. The single-phase case is shown as reference

When the variance is calculated at different downstream locations for the horizontal and vertical velocity components, the decay rate of the particle-laden turbulence can be studied. Figure 22 shows the case for a particle-laden flow with a mass load of 0.38% (equivalent to 0.1% volume load) of the aforementioned ceramic particles. Note that both the results obtained using interpolation (open symbols) and using the slotting method (closed symbols) are shown, together with the reference (single-phase) case; as can be seen in the figure, the interpolation method systematically overestimates the variance, compared to the slotting result.

Fig. 22

The decay of the reciprocal, non-dimensional horizontal (open triangle) and vertical (open circle) variance for grid turbulence with a particle mass load of Φ_m=0.38 (particle size 280 μm, relative density 3.8). Open symbols refer to results using interpolation, closed symbols refer to results using slotting. Single-phase results for the horizontal and vertical components are shown as continuous and dashed lines, respectively

The addition of particles has a significant effect on the decay characteristics: first of all, there is considerably less (≈25%) energy overall initially (i.e., the data lie higher in the graph, note that the reciprocal value is plotted). Second, the decay of the horizontal component is faster, while the streamwise (vertical) component is slightly slower. These results are consistent with recent experimental work by Geiss et al. (2004).

The spectra calculated using the horizontal velocity component (i.e., the longitudinal spectra) are very similar to the single-phase spectra at all downstream locations (see e.g., Fig. 21 for the result at the first location). However, the transverse spectra—using the vertical velocity component—change compared to the single-phase case, as is shown in Fig. 23. At z/M=42, the particle-laden fluid spectrum indicates that less energy is present at large scales compared to the single-phase spectrum, while at higher wave numbers more energy can be found. This leads to a slightly lower slope, which is referred to as ‘crossover’ in the previous studies. Note that these spectra have been normalized by the total power for each case; the particle-laden spectrum has less energy than the single-phase at all wave numbers.

Fig. 23

The downstream development of the transverse power spectrum (same measurement conditions as previous figure)

As the flow develops, a relative increase in energy at the highest wave numbers (k<40 m⁻¹) can be seen. This energy is responsible for the observed slower decay in the vertical component in Fig. 22 and thus the increasing anisotropy of the flow. The physical explanation of the growth at these large scales (on the order of the measurement region dimensions) is the occurrence of column-like structures, as described also by, for example, Nishino et al. (2003). These structures, resulting from the two-way coupling of the particles and fluid, only occur (or become apparent) when the initial turbulence from the grid has decayed sufficiently.

4.2 Particle phase results

If the slotting method is applied to the unstructured particle velocity data, the spectrum of the particle phase can be calculated. This also allows an estimation of the error in these measurements (cf. the noise removal in Sect. 2.2). In this case, the decomposition method was used, due to the relatively low number of particles in the images (<100). In Fig. 24, the corrected power spectra of the fluid and particle phase at z/M=42 are shown. Here, neutrally buoyant particles with a diameter of 250 μm were added to the flow, with a volume load of 0.3%. As can be seen, the spectra collapse up to a wave number of 200 m⁻¹. From there on, the scattering in the data of the particle phase starts increases rapidly. This scatter can be attributed to the low total number of particles available (note the confidence intervals), in combination with the inherent relatively large uncertainty in the displacement (Poelma 2004). From the autocovariance function, it can be estimated that approximately 25% of the variance in the signal can be contributed to measurement noise. As the Stokes number of these particles is significantly smaller than unity, it is expected that the particles follow most of the fluid fluctuations and the two spectra should collapse.

Fig. 24

The longitudinal spectrum obtained in two-phase grid turbulence at z/M=42 for the fluid phase (line) and the particle phase (symbols); volume load of 0.3%, 250 μm neutrally buoyant particles

5 Conclusion

In this study, the possibility of obtaining turbulence statistics from optical whole-field measurements in particle-laden flows is investigated. Any optical method will inevitably have some percentage of signal drop-out. Using synthetic one-dimensional data, the effect of this data loss is studied. It is found that the conventional method of obtaining the power spectrum (and derived quantities) yields an unreliable result with increasing data drop-out and noise level. Using the slotting method, a better, unbiased result can be obtained. The slotting method can also be generalized to handle completely unstructured data.

The new processing method is tested using data obtained in particle-laden grid turbulence. Measurements are performed using a combined PIV/PTV system, with a dedicated camera for both the fluid and particle phases. Separation of the phases is achieved by using fluorescent tracer particles in combination with color filtering. The system was validated first in the single-phase flow by comparing the obtained statistics with literature results and statistics obtained with a second measurement technique (LDA). The new system was found to be capable of accurately predicting all relevant turbulence statistics.

When particles were added to the flow, data loss of 15–20% occurred at volume loads as low as 0.5%. The statistics obtained for the fluid phase using the slotting method here deviated from the conventional method, most notably in the higher wave numbers of the power spectrum. It is shown that despite the data loss, the slotting method can yield useful turbulence statistics such as the turbulence power spectrum. The unstructured data obtained from the PTV measurements were processed using a vector decomposition variant of the slotting method so that the power spectrum of the particle phase could be obtained too. This allows a far more accurate assessment of, for example, the energy contained in the particle phase.

These unique possibilities make the new measurement system and processing algorithm a very powerful tool for the future studies of particle-laden flows. Here, it is demonstrated that using a moderately turbulent grid flow, it can readily be applied to other flows. Naturally, the turbulence statistics obtained in this way are only meaningful if the majority of the (length) scales is captured in the field of view of the measurement. Apart from the improved accuracy in single-point statistics, the whole-field character of the measurement technique opens up new ways to study these flows experimentally (e.g., through the use of conditional averaging of fluid properties around particles).