1 Introduction

Nanotechnology has enormous potential to develop new devices applied to pharmaceuticals, life sciences, electronics, and energy technologies [1,2,3]. Among a wide class of commercially interest nanomaterials, kesterite copper zinc tin sulfide (Cu2ZnSnS4 or CZTS) is considered as a potential direct band gap semiconductor for solar energy harvesting due to its suitable energy gap in the range of 1.0–1.5 eV through cation/anion substitution, high absorption coefficient (~ 104 cm−1), and intrinsic p-type conductivity [4,5,6]. Besides, it is made of earth abundant and nontoxic elements that make CZTS a good candidate to be used as active layer in thin film solar cells, as alternative to CIGS and CdTe [7, 8]. The synthesis of nanocrystals with controlled physical properties is highly desired for the application in the field of optoelectronics devices such as solar cells [9,10,11], photodetectors [12], thermoelectricity [13], sensors [14], photocatalysts for hydrogen production [15], and so on.

For CZTS mineral, two types of crystalline structure are found, namely kesterite and the stannite type. Kesterite CZTS adopts tetragonal structure, while stannite is found in wurtz-stannite- and wurtz-kesterite-type structures which crystallize in orthorhombic and monoclinic phases, respectively [16, 17]. In literature, we frequently encounter the synthesis of CZTS nanocrystals and its cation substituted alloys by hot injection and solvothermal methods [5, 18,19,20,21,22,23]. In particular, solvothermal method is particularly malleable, leading to the formation of product with high yield and good crystallinity. By tuning the solvothermal temperature, aging time, and use of complexing agent, one can obtain either kesterite or wurtzite structure [5, 21,22,23]. In crystallography, the crystal is any solid material where the atoms are spatially arranged in a repetitive three-dimensional structure to display a long-range order. A perfect crystal maintains its periodicity in x and y directions up to infinity and the peaks in X-ray diffraction pattern should appear as very sharp and narrow. However, in reality, no crystal of finite size can be perfect at any temperature greater than 0 K as different types of intrinsic lattice defects start to form within the crystal lattice of any pure material, resulting in X-ray peak broadening [24]. Therefore, the principal origin of peak broadening in XRD is crystallite size as well as strain. Lattice strain in nanomaterials may arise from the grain boundary, coherency stresses, contact or sinter stresses, stacking faults, etc. [25]. Therefore, using XRD peak profile analysis, we can estimate the crystallite size, energy density and lattice strain. In general, the particle or grain size can be obtained by direct methods such as scanning electron microscopy (SEM), transmission electron microscopy (TEM) or atomic force microscopy (AFM). The indirect methods may include XRD or Raman spectroscopy. However, it is frequently observed that the size estimated from indirect methods do not coincide well with that obtained from direct methods. There are several methods reported in the literature to estimate the crystallite size and lattice strain such as Scherrer method, Williamson–Hall method and Warren–Averbach method, based on the full width at half maximum (FWHM) of the diffraction peak and the Stokes–Fourier deconvolution, respectively.

In the present work, we have performed a comparative study of the crystallite size and intrinsic lattice strain of our experimentally prepared Cu2ZnSnS4 NCs based on the XRD peak broadening. Here, we considered the well-known Scherrer equation, Williamson–Hall (W–H), size–strain plot (SSP), Halder–Wagner (H–W), and Warren–Averbach methods. On the basis of Williamson–Hall (W–H) analysis, other modified models have been analyzed such as uniform deformation model (UDM), uniform stress deformation model (USDM), and uniform deformation energy density model (UDEDM) to calculate the crystallite size and elastic parameters such as strain, stress and energy density. The average particle size determined from different methods was compared with the transmission electron microscopy (TEM) image. The band gap of CZTS NCs was estimated using optical absorption spectrum in diffuse reflectance mode by applying the Kubelka–Munk (K–M) function which is found to be 1.37 eV. An Urbach tail is observed in the absorption spectrum, suggesting the presence of overall disorder in the system. The optical properties of CZTS was further evaluated using the Kramers–Kronig relations on reflectivity curves to obtain energy gap and other important optical constants such as complex refractive index, extinction coefficient, and dielectric constant. A good agreement was observed in the band gap values estimated by these two methods. The present research will give important guideline to select the suitable model which will reduce errors in data fit and provide the accurate information about elastic properties including stress, strain, energy density along with particle size of CZTS NCs for their application in solar cell and other solid state devices.

2 Experimental methods

2.1 Materials

The chemicals used were copper(I) chloride (CuCl, Aldrich, > 99%), zinc acetate dihydrate (Zn(CH3COO)2•2H2O, J.T. Baker, 99%), tin(IV) chloride pentahydrate (SnCl4•5H2O, Aldrich, 98%), elemental sulfur powder (S, Alfa-Aeser, 99.5%), and ethylenediamine (C2H8N2, J.T. Baker > 98%). All chemicals were used without any additional purification.

2.2 Nanocrystal synthesis

The CZTS nanocrystals were synthetized by solvothermal method (Fig. 1). In a typical synthesis, 1.85 mmol of CuCl, 1.2 mmol of Zn(CH3COO)2•2H2O, 1.02 mmol of SnCl4•5H2O and 8 mmol of elemental sulfur powder were added into 25 mL of ethylenediamine (EDA). The mixture was stirred vigorously until a homogeneous green solution was obtained. This solution was transferred into a Teflon lined stainless steel autoclave which was sealed and maintained at 180 °C for 24 h in an electric oven. After the autoclave was cooled down naturally to room temperature, the black precipitate was recovered by centrifugation and washed thoroughly by ethanol at 9000 rpm for 15 min at 18 °C. Finally, the sample was dried at ambient temperature. In each batch, we obtained 700 mg of CZTS nanoparticles. To induce the desired phase, the sample was thermally treated in the presence of 5 mg of elemental sulfur powder inside a tubular furnace under N2 atmosphere at 500 °C for 30 min (under a pressure of 5.97 × 102 Torr) using a heating ramp of 3–5 °C increment/min, as reported in our previous research [5].

Fig. 1
figure 1

Schematic representation of the solvothermal process to obtain CZTS nanocrystals

Full size image

3 Characterization techniques

The structural, compositional, morphological, and optical properties of the CZTS nanocrystals were studied using appropriate analytical tools. X-ray diffraction pattern of the nanoparticles was obtained on a Panalytical-Empyrean X-ray Diffractometer operating at 40 kV and 40 mA using CuKα radiation with the wavelength of 1.5406 Å. The data were collected in the 2θ range 20–75° with a scan rate of 0.02°/sec. The correct phase and crystal structure were investigated in detail using Raman spectroscopy (Jobin Yvon LabRAM HR800) with an excitation wavelength of 632.8 nm. The morphological analyses and crystalline property of the CZTS NCs were studied by field emission scanning electron microscopy (FESEM; JEOL JSM-7800F), conventional transmission electron microscopy (TEM) and high-resolution TEM (HRTEM) using a JEOL JEM 2200FS transmission electron microscope operated at an accelerating voltage of 200 kV. The sample dispersed in ethanol was drop-casted onto lacey carbon-coated nickel grids. The stoichiometry of CZTS NCs was analyzed using an Oxford Instrument X-Max energy-dispersive X-ray spectroscopy (EDS) detector attached to the field emission scanning electron microscope (JEOL JSM-7800F) at an acceleration voltage of 15 kV. The detection limit of EDS analysis was ≤ 0.4 wt %, all mapping was done with 500 s of acquisition time. Optical properties of the powder CZTS nanocrystals were evaluated on a Varian (Agilent) Cary 5000 UV–vis spectrophotometer with diffuse Reflectance Accessory (DRA-CA-30I). The reflectance of the sample was measured with respect to the reflectance of a standard (Teflon) in the wavelength range of 250–2000 nm.

4 Results and discussion

4.1 X-Ray diffraction analysis and morphological study

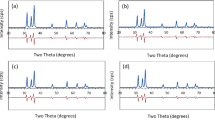
The XRD patterns of CZTS kesterite in the 2θ range of 20–75° is shown in Fig. 2. The diffraction patterns of the sample exhibit acute and well-defined Bragg diffraction peaks which coincides with the JCPDS standard of CZTS with card number 26-0575. All the peaks were indexed to tetragonal structure with \(I\overline{4 }\) space group; no additional impurity peak was detected. To determine the correct structure such as lattice parameters and unit cell volume, Rietveld refinement of the experimental XRD data was performed by employing EdPCR routine of FullProf Suite software. A numerical convolution of pseudo-Voigt function with the axial divergence asymmetry function was used to fit the peak shape. The reliability of the Rietveld profile fitting of experimental powder XRD patterns was checked by R-factors: Rwp (weighed residue profile factor, %), Rexp (expected profile factor, %) and the ratio between these two, which is known as goodness of fitting (GoF) and corresponds to the most elegant fit with experimental data. These fitting factors confirm the successful formation of single phase of CZTS kesterite. All parameters obtained are summarized in the Table 1 along with other important data such as the ratio of lattice parameters (η = c/2a). Here, this value is found to be less than one for our CZTS nanocrystals. The first-principle calculations claim that the parameter η has different value with symmetry, i.e., η < 1 for kesterite structure and η > 1 for stannite structure [26]. This further confirms the formation of single phase tetragonal structure of kesterite CZTS in the prepared sample.

Fig. 2
figure 2

a Rietveld refinement of the powder XRD pattern of CZTS nanocrystals. The black circles, red lines, blue lines and magenta ticks represent experimental data, calculated data, difference between experimental and calculated data and positions of Bragg reflections, respectively. b Representation of kesterite CZTS structure using FullProf Suite software

Full size image
Table 1 Structural parameters obtained after Rietveld refinement
Full size table

4.1.1 Scherrer method

It is well known that the broadening of XRD peaks in the nanocrystals is attributed to both crystallite size and intrinsic strain effects. Therefore, it is essential to consider the instrumental factor since depending on the instrumental configuration used in the measurement, the contribution to the width and shape of the peaks may change. Here, the observed broadening of X-ray diffraction peaks is attributed to the contribution of sample defects as well as instrumental factor. The instrumental broadening can be corrected using different relations depending on the peak shape and distribution functions such as Cauchy (Lorentzian), Gaussian, Pseudo-function, and so on [24, 25]. The instrumental broadening in this case is corrected using the Eq. (1):

$$\beta_{hkl} = \left( {(\beta_{m} - \beta_{i} } \right)\left( {\beta_{m}^{2} - \beta_{i}^{2} } \right)^{1/2} )^{1/2} ,$$
(1)

where βhkl is the corrected broadening, βm is the measurement broadening and βi is the instrumental broadening. In this study, we used the standard lanthanum hexaboride as reference material (LaB6) for position and instrumental broadening calculation. After correction of instrumental broadening and ignoring the contribution of the strain, we calculated the average (Scherrer equation) crystallite size with the help of Eq. (2):

$$D = \frac{k\lambda }{{\beta_{hkl } cos\theta }} \to cos\theta = \frac{k\lambda }{D} \frac{1}{{\beta_{hkl} }} ,$$
(2)

where k is the morphological parameter or shape factor for spherical particles (equal to 0.9), λ is the wavelength, θ is Bragg diffraction angle and D is the average particle size. Figure 3a shows the plot of cosθ vs. 1/βhkl for CZTS nanocrystals using each XRD peak of the diffractogram. It is observed that the linear fit of these scattered points is not a good fitted line as the linear regression coefficient of R2 is 0.71. The average crystallite size has been determined from its slope, corresponding to 38.1 nm. For the accuracy, it is suggested that the Scherrer equation is appropriate when the average NP size is around 100 nm [25]. However, in Scherrer method, we consider the broadening of the diffraction peaks to obtain the crystallite size but the broadening is also related to the lattice strain. To reduce the errors, Monshi et al. introduced some modifications in Eq. (2), which involves the consideration of all diffraction peaks to determine the crystallite size. The sum of absolute values of errors is given by Eq. 3 [25]:

$$errors = \sum \left( { \mp \Delta ln\beta_{hkl} } \right)^{2} .$$
(3)
Fig. 3
figure 3

a Scherrer plot and b Monshi–Scherrer plot for CZTS

Full size image

Therefore, the modified Scherrer equation takes the form of Eq. (4), which gives more accurate value of D by reducing the errors:

$$ln\beta_{hkl} = ln\left( {\frac{k\lambda }{D}} \right) + ln\left( {\frac{1}{cos\theta }} \right).$$
(4)

Now, the linear plot of ln(β) vs. ln(1/cosθ) (Fig. 3(b)) using this modification yields an improved linear regression value (R2) of 0.86 compared to 0.71 using Scherrer method. The intercept of the linear plot gives the value of ln(kλ/D) from which a single value of average crystallite size is obtained. According to Monshi–Scherrer equation, the value of crystal size is 21.9 nm.

4.1.2 Williamson–Hall study (W–H)

Scherrer equation only considers the effect of crystallite size on the diffraction peak broadening but does not consider the effect of intrinsic strain on the peak broadening. Williamson–Hall (W–H) method takes into account the strain-induced peak broadening which is originated in the nanocrystals through point defects, grain boundaries, interstitial defects and stacking faults. This is one of the most used methods and part of the Scherrer equation that inversely relates the width of the diffraction peaks to the apparent size of the nanoparticle. By considering that the broadening of the diffraction profiles βhkl is a combination of grain size and intrinsic strain, and both factors are additive phenomena, the line broadening can be expressed by the Eq. (5):

$$\beta_{hkl} = \beta_{size} + \beta_{strain} .$$
(5)

For accuracy, we analyzed the crystallite size and micro-strain using modified W–H equation and models involving Uniform Deformation (UDM), Uniform Stress Deformation (USDM) and Uniform Deformation Energy Density Model (UDEDM) [27, 28].

The UDM model considers uniform strain along all crystallographic directions (isotropic). As the intrinsic deformation affects the physical broadening of the XRD profile, the effective strain can be written as (6):

$$\beta_{strain} = 4\varepsilon tan\theta .$$
(6)

Therefore, the broadening due to the strain (βstrain) and the size (βsize) can be expressed according to the Eq. (7):

$${\beta }_{hkl}=\frac{k\lambda }{Dcos\theta }+4\varepsilon tan\theta .$$
(7)

Rearranging Eq. (7), we get the following relation which is known as UDM (8):

$${\beta }_{hkl}cos\theta =\frac{k\lambda }{D}+4\varepsilon sin\theta .$$
(8)

By plotting βhkl cosθ vs. 4sinθ, the particle size can be estimated from linear fit where the slope and intercept of the fitted line correspond to the micro-strain ε and crystalline size (D), respectively (Fig. 4). In this case, we obtained the crystallite size and intrinsic strain of around 26.36 nm and 1.36 × 10–3, respectively. The slope of the linear plot (corresponding to intrinsic strain) is positive, which is related to the tensile strain or lattice expansion.

Fig. 4
figure 4

UDM plot for CZTS nanocrystals

Full size image

The assumption in UDM that strain is isotropic in all crystallographic directions is not justified in a real crystal system. A more realistic approach considered in USDM is the generalized Hooke´s law, where strain (ε) is proportional to the stress (σ) and the proportionality constant is the Young modulus as expressed by Eq. 9:

$$\sigma ={\varepsilon Y}_{hkl}\leftrightarrow \varepsilon =\frac{\sigma }{{Y}_{hkl}}.$$
(9)

Here, Yhkl is the Young’s modulus or modulus of elasticity and is valid for a significantly small strain. Now, substituting this expression of σ in Eq. (8), we get a new expression for USDM (Eq. 10):

$${\beta }_{hkl}cos\theta =\frac{k\lambda }{D}+4\frac{\sigma }{{Y}_{hkl}} sin\theta .$$
(10)

This expression considers the uniform stress in every crystallographic direction. The Yhkl depends on the crystallographic direction perpendicular to the set of planes (hkl) of the Miller indices. For a given tetragonal crystal, Young’s modulus is related to their elastic compliances Sij given by the following relation (11) [29, 30]:

$$\frac{1}{{Y}_{hkl}}=\frac{{S}_{11}\left({h}^{4}+{k}^{4}\right)+\left(2{S}_{12}+{S}_{66}\right){h}^{2}{k}^{2}+\left(2{S}_{13}+{S}_{44}\right)\left({h}^{2}+{k}^{2}\right){l}^{2}+{S}_{33}{l}^{4}}{{\left({h}^{2}+{k}^{2}+{l}^{2}\right)}^{2}},$$
(11)

where, S11, S12, S13, S33, S44 and S66 are the elastic compliances of tetragonal structure for kesterite CZTS, and their theoretical values are 21.3 × 10–12, -8.7 × 10–12, -7.6 × 10–12, 20.1 × 10–12, 24.7 × 10–12 and 23.6 × 10–12, respectively [31, 32]. Using these values, the Young’s modulus has been calculated for (110), (112), (200), (220), (312), (224) and (008) planes as 82, 80.6, 46.9, 82, 78.3, 80.6 and 49.8 GPa, respectively, and an average Young’s modulus for tetragonal CZTS nanoparticles was estimated as ~ 71.5 GPa. By plotting βhklcosθ as a function of 4sinθ/Yhkl (Fig. 5), the uniform deformation stress σ can be estimated from the slope of the linear fit, while y-intercept gives the crystallite size. The strain ε can be obtained from the Young’s modulus. The average particle size and strain calculated from USDM are 22.81 nm and 0.66 × 10–3, respectively. (Fig. 6)

Fig. 5
figure 5

USDM plot for CZTS nanocrystals

Full size image
Fig. 6
figure 6

UDEDM plot for CZTS nanocrystals

Full size image

Another model that can be used to determine the lattice energy density of a crystal is the UDEDM. As we have seen earlier, UDM model assumes the isotropic nature of the crystal, while USDM model considers a linear relationship between stress–strain described by Hooke’s law. However, due to different defects formed in the crystal, neither the isotropic nature of lattice strain is correct, nor the constants in stress–strain relation are independent when strain energy density (U) is considered. UDEDM model considers the uniform anisotropic deformation of the lattice in all crystallographic directions. Then, according to Hooke’s law, energy density U is related to strain by the following Eq. (12):

$$U={\varepsilon }^{2}\frac{{Y}_{hkl}}{2}.$$
(12)

By substituting the value of ε extracted from the above relation, Eq. (8) can be rewritten as follows:

$${\beta }_{hkl}cos\theta =\frac{k\lambda }{D}+4{ sin\theta \left(\frac{2U}{{Y}_{hkl}}\right)}^{1/2}.$$
(13)

By plotting βhkl cosθ vs. 4sinθ(2/Yhkl) and applying linear fitting through the points (corresponding to each diffraction peak), we can obtain the energy density from the slope and the average crystallite size (D) from the intercept of the straight line. Using this model, we have obtained the average size of 24.70 nm, the energy density of 42.64 kJ/m3 and the strain of 1.02 × 10–3.

4.1.3 Size–strain plot (SSP)

The W–H plots describe that the line broadening is basically isotropic and broadening occurs due to the contributions of grain size and strain. However, at higher angles, the reflections are of poor quality and the data are not as reliable as those resulting from reflections at lower angles. SSP method considers the XRD peak profile as a combination of the Cauchy (Lorentzian) and Gaussian functions. The strain profile is expressed by the Gaussian function and the crystallite size by Cauchy (Lorentzian) function, so that the total broadening can be written as Eq. (14) [33]:

$${\beta }_{hkl}={\beta }_{G}+{\beta }_{L,}$$
(14)

where βG and βL are the peak broadening due to Gaussian and Lorentzian functions, respectively.

Therefore, SSP method is governed by the following Eq. (15):

$${\left({d}_{hkl}{\beta }_{hkl}cos\theta \right)}^{2}=\frac{k\lambda }{D}\left({d}_{hkl}^{2}{\beta }_{hkl}cos\theta \right)+\frac{{\varepsilon }^{2}}{4},$$
(15)

where dhkl is the lattice distance between the (hkl) planes, which can be expressed by Eq. (16) for the tetragonal unit cell:

$${d}_{hkl}=\frac{1}{\sqrt{\frac{{h}^{2}+{k}^{2}}{{a}^{2}}+\frac{{l}^{2}}{{c}^{2}}}}.$$
(16)

Figure 7 displays a plot of (dhklβhklcosθ)2 vs. (dhkl2βhklcosθ) corresponding to each diffraction peak. The slope of the straight line provides the average size as 21.3 nm, whereas the intercept gives the intrinsic strain of the CZTS nanocrystals as 6.8 × 10–3, which is about six times higher than the strain value obtained from others models as discussed in previous sections. This happens because less importance is given to data from reflections at higher angles where the precision is usually lower. In this regard, the SSP method provides a reliable result for isotropic broadening as it prioritizes low angle reflections over peaks at higher diffraction angles. It is worth to note that the value of R2 in SSP plot is 0.95 indicating that the data are closely fitted to the regression line.

Fig. 7
figure 7

SSP plot for CZTS nanocrystals

Full size image

4.1.4 Halder–Wagner study (H–W)

In SSP method, the peak profile has been assumed as a Lorentzian and Gaussian functions, but in some region of our X-ray diffractogram, XRD peak is neither Lorentzian nor Gaussian function. To overcome this problem, the Halder–Wagner (H–W) method is employed, which is based on the assumption that the peak broadening is a symmetric Voigt function. The Voigt function is the convolution of a Gaussian function with a Lorentz function. According to Voigt function, the full width at half maximum of the physical profile can be written as Eq. (17) [33, 34]:

$${\beta }_{hkl}^{2}={{\beta }_{L}\beta }_{hkl}+{\beta }_{G,}^{2}$$
(17)

where βL and βG are the full width at half maximum of the Lorentzian and Gaussian function. The relation between the size of the crystallite and the lattice strain as per this method is given by the Eq. (18):

$${\left(\frac{{\beta }_{hkl}^{*}}{{d}_{hkl}^{*}}\right)}^{2}=\frac{1}{D}\frac{{\beta }_{hkl}^{*}}{{d}_{hkl}^{* 2}}+{\left(\frac{\varepsilon }{2}\right)}^{2},$$
(18)

where \({\beta }_{hkl}^{*}=\frac{{\beta }_{hkl}cos\theta }{\lambda }\) and \({d}_{hkl}^{* 2}=\frac{2{d}_{hkl}sin\theta }{\lambda }\); \({d}_{hkl}^{*}\) is the interplanar distance between hkl planes.

Figure 8 shows the plot of \(\frac{{\beta }_{hkl}^{*}}{{d}_{hkl}^{* 2}}\) term along x-axis and the term of \({\left(\frac{{\beta }_{hkl}^{*}}{{d}_{hkl}^{*}}\right)}^{2}\) along y-axis. The slope of the plotted straight lines provides the average crystallite size and the intercept gives the intrinsic strain of the CZTS nanocrystals. The average crystallite size obtained from H–W method is 24.62 nm, and the strain is found to be 7.2 × 10–3, which is very close to the value obtained from SSP method. The accuracy of measuring lattice strain by this method is considerably high (R2 = 0.99) as it gives more importance to the XRD peaks at low and mid angle, where the overlapping of diffraction peaks is less.

Fig. 8
figure 8

H–W plot for CZTS NCs

Full size image

4.1.5 Warren–Averbach study (W–A)

The Warren–Averbach method provides an alternative analysis for the separation of size and strain contributions to the diffraction peak broadening and is based on the deconvolution of Fourier transforms for the determination of line profile of the diffraction peak [35, 36]. If A(L) is the Fourier transform of the intrinsic peak profile, then it can be expressed as the product of the size coefficient and the stress coefficient according to the Eq. (19):

$$A\left(L\right)={A}^{size}\left(L\right){A}^{strain}\left(s,L\right),$$
(19)

where Asize(L) and Astrain(L) are the size Fourier transform and strain coefficient, respectively. Both the Fourier transform and the deconvolution have been made through the Matlab program. The reason for determining the real part of Fourier transform of the diffraction peaks is to separate the size and strain contributions using the Eq. (20):

$$\mathrm{lnA}\left(s,L\right)=ln{A}^{size}\left(L\right)-2{\pi }^{2}{s}^{2}{L}^{2}\langle {\varepsilon }^{2}\left(L\right)\rangle ,$$
(20)

where \(L=\frac{n\lambda }{2(sin{\theta }_{2}-sin{\theta }_{1})}\), n is the harmonic number of the Fourier transform, θ1 and θ2 correspond to the angle range of the measured diffraction, \(s=\frac{2sin\theta }{\lambda }\) represents the variable in reciprocal space and \(\langle {\varepsilon }^{2}\left(L\right)\rangle\) is the mean-square strain for the correlation distance (L).

The size coefficient plotted as a function of L for the CZTS nanocrystals is illustrated in Fig. 9a. The area-weighted mean length < L > area is obtained from the tangent of small L value of A(L) extrapolated to the x-axis. On the other hand, the volume-weighted column length < L > vol is obtained from the area under the curve of A(L) against L, as reported by Krill and Birringer [37], following the relations (21) and (22)

Fig. 9
figure 9

a Plot of Fourier size coefficient versus distance L and b RMSS distribution of CZTS nanocrystals

Full size image
$${\left(\frac{d{A}^{size}\left(L\right)}{dL}\right)}_{L\to 0}=-\frac{1}{{\langle L\rangle }_{area}},$$
(21)
$${\langle L\rangle }_{vol}=2{\int }_{0}^{\infty }{A}^{size}\left(L\right)dL.$$
(22)

From the above equations, the area and volume-weighted average grain sizes are given by (23):

$${\langle D\rangle }_{area}=\frac{3}{2}{\langle L\rangle }_{area} ; {\langle D\rangle }_{vol}=\frac{4}{3}{\langle L\rangle }_{vol.}$$
(23)

Herein, the area-weighted average grain size < D > area and volume-weighted average grain size < D > vol were estimated, as 25.05 nm and 22.6 nm, respectively. Figure 9b displays the root-mean-square strain (RMSS), where we can observe that the RMSS decreases with increasing column length L, being the maximum value of 2.3 × 10–3 with an average micro-strain of 1.5 × 10–3. Depending on the number of points to define the linear part of Asize(L), different values of the < L > area are obtained.

4.1.6 Morphological study and chemical composition analysis: FE-SEM, TEM, and EDS

The direct and basic methods to examine the size and shape of the nanocrystals is picture image analysis using SEM and TEM techniques. Figure 10a displays the SEM micrograph of CZTS nanoparticles. It can be clearly seen that the particles are almost uniform in size and round-shaped with well-defined grain boundary. The size distribution histogram was plotted by measuring the diameter of around 200 individual particles in the SEM image (Fig. 10b). The average particle size is estimated as 22.7 ± 0.6 with a narrow size distribution, which is close to the crystalline domain size determined from the XRD peak broadening.

Fig. 10
figure 10

a FE-SEM image of and b the size distribution of CZTS nanocrystals

Full size image

Figure 11a shows the EDS spectrum and elemental mapping performed on CZTS nanocrystals. In the EDS spectrum, we could observe the emission peaks of the constituent elements, indicating the compositional purity of CZTS nanoparticles. To verify the homogeneous distribution of Cu, Zn, Sn and S in CZTS nanocrystals, EDS elemental mapping was carried out and the results are shown in Fig. 11b. The SEM–EDS analysis indicates that the metals and sulfur are evenly distributed within the nanoparticles.

Fig. 11
figure 11

a EDS spectrum and b elemental maps of Cu, Zn, Sn and S of CZTS nanocrystals.

Full size image

The chemical composition has been investigated using energy-dispersive X-ray spectroscopy (EDS) and the results are shown in Table 2. The sample is found to be slightly Cu-poor and Zn-rich with Cu/(Zn + Sn) ratio of 0.88 and Zn/Sn ratio of 1.06. According to previous studies, the non-stoichiometric CZTS having Cu/(Zn + Sn) between 0.75 and 1, and Zn/Sn ratio between 1 and 1.25 are known to deliver high conversion efficiency over 8% when integrated as absorber layer in a solar cell [38, 39]. From EDS analysis, the molecular formula is estimated as Cu1.93Zn1.12Sn1.04S3.88 which fulfills the criteria of a good absorber.

Table 2 The elemental stoichiometry of CZTS nanocrystals obtained through EDS analysis
Full size table

Figure 12a displays the bright field TEM micrograph of the prepared nanocrystals, showing that most of the particles are nearly spherical in shape with minimal aggregation. The mean size and standard deviation of the nanoparticles were estimated from size distribution histogram (Fig. 12b) by measuring a population of ~ 150 individual particles from TEM images. The results reveal that the nanocrystals are almost uniform in size with the average diameter of 23.2 ± 0.4 nm.

Fig. 12
figure 12

a Low magnification TEM images of CZTS nanocrystals and b the corresponding size distribution histogram

Full size image

High resolution TEM (HRTEM) image of CZTS NCs (Fig. 13a) reveals the continuous lattice fringes of individual CZTS nanocrystals, suggesting the good crystallinity. The Fast Fourier Transform (FFT) image (Fig. 13b) shows the periodicity of different d-spacing values, which can be indexed as (112), (220) and (312) diffraction planes of tetragonal CZTS (JCPDS# PDF 26–0575). The distance between adjacent planes measured directly on the HRTEM image reveals that the interplanar distances are 3.34, 1.97 and 1.65 Å, which are in accordance with (112), (220) and (312) planes of tetragonal CZTS [5], as shown in Fig. 13c, d, e.

Fig. 13
figure 13

a HRTEM image showing excellent crystallinity, b the FFT pattern with the most intense peaks and c–e interplanar distances corresponding the (112), (220) and (312) planes, respectively, of CZTS nanocrystals

Full size image

Figure 14 exhibits the values of average crystallite size estimated from direct and indirect methods. As observed in the figure, the majority of the methods give the particle size value in the interval of 22–28 nm except Scherer formula where the value is almost double with 38.1 nm. After careful inspection, we came to the conclusion that the average size calculated from H–W and W–A method coincides closely (R2 tends to 1) with the average particle size observed in SEM and low resolution TEM images. The inset table compares the strain determined by different methods. All methods provide the same tendency, except SSP and W–H, which give a very high value of strain, because both methods consider the contribution of low and mid angle XRD data, attributed by the lattice dislocations. Table 3 summarizes the crystalline size and lattice strain of CZTS nanocrystals obtained by different models. Based on the above results, it is clear that out of different available methods to estimate the crystallite size and lattice strain, the W–H analysis, H–W method, Rietveld refinement, and W–A analysis are the most common. All these methods can be applied to other semiconductor nanocrystals regardless of either the material is in powder form or supported on a substrate.

Fig. 14
figure 14

Average particle size calculated from XRD peak broadening and morphological studies

Full size image
Table 3 The crystallite size and intrinsic strain of CZTS nanocrystals obtained by different models based on XRD pattern
Full size table

4.2 Raman analysis

Group theory analysis predicts the following irreducible representation for the \(I\overline{4 }\) symmetry of tetragonal kesterite at the Γ point of the Brillouin zone: Γ = (1B \(\oplus\) 1E) \(\oplus\) (3A \(\oplus\) 6B \(\oplus\) 6E), where 1B and 1E modes are acoustic, 3A, 6B and 6E are Raman-active modes, and only 6B and 6E are infrared-active modes. Raman spectra presents a superposition of multiple vibrational modes, which can be modeled by Lorentzian deconvolution of the asymmetric peaks. The Raman spectrum of CZTS nanocrystals is displayed in Fig. 15. In this case, the intensive scattering peak at 330 cm−1 is accompanied by two shoulder peaks, which were deconvoluted into two weaker peaks at 284 and 365 cm1. Different deconvolution parameters are listed in the inset of the Raman spectrum. The intensive scattering at 330 and week peaks at 284 and 365 cm−1 are representative of CZTS and close to the literature values. The peaks at 284 and 330 cm−1 correspond to the A vibrational mode and are originated from the vibrations of sulfur atoms in CZTS lattice, while rest of the atoms remain stationary. On the other hand, the peak at 365 cm−1 is related to E symmetry mode of phase pure kesterite. No other peaks for any impurity phases were detected which confirms the phase purity of the as synthetized CZTS nanocrystals. The full width at half maximum (FWHM) value for the most intense peak is a good indicator of size and crystallinity of the material under study. In this case, the FWHM for the 330 cm−1 peak was calculated to be 19.6 cm−1 which is narrowest of the three peaks. Such narrow widths suggest that the phonon confinement effect does not contribute to the line width broadening and indicate good crystallinity of the sample. The average phonon lifetime (τ) in the CZTS nanocrystals can be determined from the energy time uncertainty relation, \(\frac{1}{\tau }=\frac{2\pi \Delta E}{h}=2\pi c\Gamma\), where, τ is the mean phonon lifetime, ΔE is the uncertainty in the phonon energy state, h is Planck’s constant (6.626 \(\times\) 10–34 Js), c is the velocity of light (2.998 \(\times\) 10–10 cm/s) and Γ is the FWHM of the most intense Raman peak in cm−1. With this relation the average phonon lifetime of the CZTS nanocrystals was calculated to be 0.27 \(\times\) 10–12 s, which is consistent with the theoretical predictions [40]. The observed peak broadening in Raman peaks is commonly observed for nanostructures because of the finite grain size as well as defect states.

Fig. 15
figure 15

Raman spectrum of CZTS nanocrystals with deconvoluted spectra (Lorentzian curves)

Full size image

4.3 Optical properties

The diffuse reflectance spectrum (DRS) of CZTS nanocrystals is shown in Fig. 16a. The absorption edge is found to lie in the near infrared region which can be associated with the band gap of CZTS. The optical band gap of CZTS nanocrystals was estimated from the DRS spectrum using Kubelka–Munk (KM) formalism converting the reflectance data into equivalent absorption coefficient (αKM) (Fig. 16b) with the help of Eq. (24):

$${\alpha }_{KM}=F\left({R}_{\infty }\right)=\frac{{\left(1-{R}_{\infty }\right)}^{2}}{2{R}_{\infty }}=\frac{k}{s},$$
(24)

where k is the effective absorption coefficient, s is the effective dispersion coefficient of the sample and R∞ is defined as: \({R}_{\infty }=\frac{R(\%)}{{R}_{ref}(\%)}\), being Rref is the diffuse reflectance of the reference (here, it is Teflon).

Fig. 16
figure 16

a Diffuse reflectance spectrum and b the equivalent absorption coefficient using the Kubelka–Munk relation, showing the optical band gap of CZTS NCs (inset)

Full size image

Hence, to estimate the optical band gap of CZTS nanocrystals, a plot of (αKM hν)2 vs. photon energy was drawn using the Tauc relation associated with the direct transition: (αKM hν) = A(hν-Eg)1/2; where h is the Planck’s constant, ν is the frequency and Eg the optical band gap. By extrapolating the linear portion of the plot to photon energy axis, we estimated the optical band gap of 1.37 eV, as displayed in the inset of Fig. 16b. Similar value of Eg for CZTS nanoparticles was observed by Kannan et al., where the nanoparticles were synthesized by solvothermal method in five different solvents (water, ethylene glycol, diethylene glycol, ethylene diamine, and ethanol) and the band gap of CZTS was found to vary from 1.39 eV to 1.53 eV for the particle sizes varying between 14 and 7 nm [41].

The Urbach energy (EU) is governed by the overall disorder present in the material. Any structural disorder in the lattice creates localized states close to the band edge, leading to the Urbach tail at energies below the main absorption edge and can be expressed by the Eq. (25):

$${\alpha }_{KM}\left(h\nu \right)={\alpha }_{0}{e}^{\frac{h\nu }{{E}_{U}}},$$
(25)

where α0 is a constant. Due to the occurrence of Urbach tail states, a transition occurs between the defects states to the energy band. The value of EU was calculated by taking the inverse of the slope from the linear portion of Ln(αKM) vs. hν plot as displayed in Fig. 17. The Urbach energy value for CZTS nanocrystals was 234 meV. Regularly, the reported values for CZTS nanostructures vary from 30 to 125 meV [42, 43]. As can be noticed, the estimated Eg of 1.37 eV for our CZTS nanocrystals is relatively smaller than the reported values [44]. This can be due to the sub-band states formed in between the valence band and conduction bands, leading to the narrowing of the band gap. As a multinary semiconductor, these defect states are frequently formed in bulk CZTS due to site vacancies (VCu, VZn, VSn, Vs), interstitial (Cui, Zni, Sni) and antisite (CuZn, ZnSn) defects [38]. In this case, the high Urbach energy of 234 meV further supports the increased number of defect levels within the forbidden energy gap, thereby reducing the effective band gap of CZTS.

Fig. 17
figure 17

Relation between Ln(αKM) vs. hν to determine the Urbach energy of CZTS particles

Full size image

The application of Kramers–Kronig (KK) dispersion relations to reflectance data at normal incidence allows us to determine optical and dielectric parameters of a material as described by the following relation: \(\widehat{n}\left(\omega \right)=n\left(\omega \right)+i\kappa (\omega )\), where n(ω) is the refractive index and κ(ω) is extinction coefficient. Experimental diffuse reflectance spectra are always measured in bounded frequency region, while the KK relations include integration over all frequencies, with a singularity. The KK relations is simpler, accurate and the optical parameters can be calculated using the reflectance data without a detailed requirement of boundary conditions, i.e., the KK relations do not require any assumption or extrapolations of the reflectance experimental data which is beyond the measured range.

One of the standard forms of the KK transform is given by (26) [45]:

$$KK\left\{{\mathbb{O}}\right\}\left(\omega \right)=\frac{2}{\pi }\boldsymbol{\rm P}{\int }_{0}^{\infty }\frac{{\omega }^{^{\prime}}{\mathbb{O}}\left({\omega }^{^{\prime}}\right)}{{\omega }^{2}-{\omega }^{\boldsymbol{^{\prime}}2}}d{\omega }^{^{\prime}},$$
(26)

where P is the Cauchy principal value, \({\mathbb{O}}(\omega )\) denotes an optical property and KK can be regarded as the Kramers–Kronig operator.

The reflectance data as the input parameter in determining the n(ω) and κ(ω) are [45]:

$$n\left(\omega \right)=\frac{1-R\left(\omega \right)}{1+R\left(\omega \right)-2\sqrt{R\left(\omega \right)}cos\theta (\omega )},$$
(27)
$$\kappa \left(\omega \right)=\frac{2\sqrt{R\left(\omega \right)}sin\theta (\omega )}{1+R\left(\omega \right)-2\sqrt{R\left(\omega \right)}cos\theta \left(\omega \right)},$$
(28)

where θ(ω) is the phase change or shift on reflection after the photon travel inside the material. This phase change can be derived from KK dispersion relation (29) [45]:

$$\theta \left( \omega \right) = - \frac{\omega }{\pi }\mathop \smallint \limits_{0}^{\infty } \frac{{\ln R\left( {\omega^{\prime}} \right) - lnR\left( \omega \right)}}{{\omega^{^{\prime}2} - \omega^{2} }}d\omega^{\prime}.$$
(29)

Several integration methods have been proposed, in this case, we used the Maclaurin’s method and this integration method features higher calculation accuracy, but it usually takes a longer time for calculation. We may consider a new form for a relatively simple computation (30) [45]:

$$\theta \left({\omega }_{j}\right)=\frac{4{\omega }_{j}}{\pi }\Delta \omega \sum_{i}\frac{\mathrm{ln}\left(\sqrt{R({\omega }_{i})}\right)}{{\omega }_{i}^{2}-{\omega }_{j}^{2}},$$
(30)

where \(\Delta \omega ={\omega }_{i+1}-{\omega }_{i}\) and if j is an odd number then i = 2, 4, 6, …, j-1, j + 1. On the other hand, if j is an even number i = 1, 3, 5, …, j-1, j + 1 and it allows to avoid direct calculation of the point at i = j.

Figure 18a, b shows the plots of n(ω) and κ(ω) versus photon energy, which are calculated by KK method. For CZTS nanocrystals, the refractive index changed from 4.3 to 2 when the photon energy is varied from 1 to 2.5 eV and remains steady for higher photon energies (Fig. 18a). The high refractive index is attributed to the good crystallinity and probably the Cu-poor/Zn-rich stoichiometry because the velocity of light into the material decreases with an increment in the refractive index. Figure 18b displays the extinction coefficient of CZTS nanocrystals, which increases from 1 to 1.25 eV photon energy range followed by a slight decrease near the band gap energy and then it again increases steadily in the range of 1.5–4.5 eV photon energy. The lower value of extinction coefficient is probably due to the weak absorption in the CZTS nanocrystals since this optical constant has direct relation to the absorption coefficient. The complex dielectric constant is the basic intrinsic property of materials and it has two parts: the real part of the dielectric constant represents how much it will slow down the velocity of light in the material, whereas the imaginary part of dielectric constant describes the interaction of a dielectric material with an electric field due to polarization. The real (εr) and imaginary (εi) parts of the dielectric constant have been evaluated through the relation (31) [46, 47]:

Fig. 18
figure 18

Optical constants in terms of a refractive index, b extinction coefficient, c real and d imaginary parts of the dielectric function of CZTS NCs calculated by KK method

Full size image
$$\widehat{n}\left(\omega \right)=n\left(\omega \right)+i\kappa \left(\omega \right)\to {\widehat{n}\left(\omega \right)}^{2}={\left[n\left(\omega \right)+i\kappa \left(\omega \right)\right]}^{2}={n\left(\omega \right)}^{2}+2in\left(\omega \right)\kappa \left(\omega \right)-{\kappa \left(\omega \right)}^{2}={\varepsilon }_{r}+i{\varepsilon }_{i}.$$
(31)

The variation of the real and imaginary parts of the dielectric function with photon energy is shown in Fig. 18c, d, where the plots show the similar trends as the plots of refractive index and extinction coefficient (Fig. 18a, b). The real part of dielectric constant decreases from 17.8 to 4.6, while the imaginary part of the dielectric constant decreases gradually from 2.25 to 0.75 × 10–4 in the photon energy range of 1.0 to 1.5 eV followed by an increase over this energy The values of optical constants reported here are well matched with previous experimental data observed for CZTS nanocrystals [48].

We calculated the absorption coefficient using the equation: \({\alpha }_{KK}=\frac{4\pi \kappa }{\lambda }\). Figure 19a illustrates the absorption coefficient of the CZTS nanocrystals obtained by KK method. The band gap of CZTS NCs associated with direct transition was determined by Tauc method: (αKK hν) = A(hν-Eg)1/2 (Fig. 19b). The αKK plot has similar shape as the plot obtained by Kubelka–Munk relation except a less steep slope. The band gap estimated by KK method is found to be 1.28 eV compared with 1.37 eV obtained with the Kubelka–Munk relation, confirming that the KK method is another useful way to determine the optical band gap.

Fig. 19
figure 19

a Absorption coefficient and b the optical band gap of CZTS nanocrystals using the Kramers–Kronig relations (KK)

Full size image

5 Conclusions

In this work, an exhaustive analysis of XRD data for kesterite CZTS NCs is presented using peak broadening analysis to calculate various microstructural properties, such as, crystallite size, stress, strain, and energy density using Scherrer method, different models of Williamson–Hall plot including UDM, USDM, and UDEDM. Besides, Size–Strain Plot (SSP), Halder–Wagner (H–W) and Warren–Averbach (W–A) are also explored. SEM and TEM image analysis revealed that the average particle size of CZTS NCs are 22.7 ± 0.6 and 23.2 ± 0.4 nm, respectively. After comparing all the methods based on experimental diffraction line profiles, we came to the conclusion that the average size calculated from Warren–Averbach (W–A) and Halder–Wagner (H–W) methods coincide closely with the average particle size observed in SEM and TEM images. The estimated band gap from UV–vis diffuse reflectance spectrum is 1.37 eV, which is similar to the value obtained from Kramers–Kronig relations. Normal incidence reflectance measurement has been further used for the determination of optical constants using KK analysis. The knowledge of the wavelength-dependent complex refractive index, dielectric constant, and optical band gap of this material is important from scientific and technological point of view as well as for the design and theoretical modeling of optoelectronic devices.