1 Introduction

In the polycrystalline ceramics, the electrical properties are mainly affected by the existence of crystal grains and grain boundaries. The complex impedance spectroscopy (CIS) analysis is a powerful study to differentiate the microstructure of any ceramic system [1, 2]. This investigation allows one to determine the contributions of various processes, such as volume effects in the frequency domain, grain boundary and electrode interface effects [3, 4]. This research can be extended to a wide range of temperatures and frequencies.

Usually, the data in the complex representation can be expressed in basic forms, namely, complex impedance Z∗, complex admittance Y∗, complex permittivity ε∗ and complex modulus M∗ [5].

The Complex Electric Modulus (CEM) characterization is relevant only when the relaxation times of various processes are different due to different capacitance components [5]. Complex impedance spectroscopy (CIS) is a functional tool to determine the main contribution of resistance, and it is not sensitive to the smaller capacitance values in the material. However, CEM spectroscopy can be used to determine the smallest contribution of capacitance in a material [6].

Additionally, the CEM is a powerful appliance to reveal the phenomena of dielectric relaxation and charge transport in materials [7]. It can distinguish between grain boundary conduction processes and electrode polarization. A CEM diagram can also be used to distinguish components with similar resistance but different capacitance values [8, 9].

CIS is considered to be a dynamic non-destructive method for studying the microstructure and electrical properties of solids, where electrical properties are usually expressed by some complex parameters, for example the impedance [Z*(w) = Z′ − jZ″ = Rs − j/wCs], permittivity [ε*(w) = ε′ − j ε″], electric modulus [M*(w) = M′ + jM″] and admittance [Y*(w) = Y′ + jY″ = 1/Rp + jwCp]. They are related to each other as: M* = 1/ε* = jwC0 Z* = jwC0 (1/Y*) and the dielectric loss, tan (δ) = ε″/ε′ = Z′/Z″ = M″/M′, where Rs, Cs are the series resistance and capacitance; Rp, Cp are the parallel resistance and capacitance [10].

There are two methods are usually used in CIS data analysis. The first one is a visual inspection based on the data (usually impedance (Z*) complex representation (Z″ vs Z′) plots), assuming an equivalent circuit, and extracting the resistance and capacitance values based on the quality of the agreement between the experimental data and the simulated data. However, the main difficulty in the interpretation of the impedance spectroscopy data is that it is usually possible to fit many reasonable equivalent circuits into a given data set. Obviously, a rigorous evaluation is required to determine the most suitable circuit, but there are a few complete guidelines that can help to evaluate it. Thus, a great deal of attention is desired in this direction. In this work, herein, we track the investigation of the electrical properties of Ca0.85Er0.1Ti(1−x)Co4x/3O3 (x = 0.15 and 0.20) using the complex impedance spectroscopy. The complex electric modulus (CEM) is used to investigate the process of dielectric relaxation and to study the electric phenomena of samples.

2 Sample preparation and experimental details

Ca0.85Er0.1Ti(1−x)Co4x/3O3 (0.15 ≤ x ≤ 0.20) ceramics were prepared by sol–gel method. Mix high-purity of CaCO3, TiO2, Er2O3 and Co Cl2·6H2O powders in a stoichiometric ratio are dissolved in distilled water with some drops of acid. This solution was heated at 120 °C, under magnetic agitation. After that, we added an adequate amount of citric acid and ethylene glycol. The citric acid is used as a complexing agent and the ethylene glycol as a polymerization agent for different metal cations. Subsequently, an amount of ammonia has been added to adjust the pH value of the solution around 7. After approximately 3 h, we observed the formation of a viscous gel. Then, this gel was dried for 6 h at 300 °C and ground in an agate mortar to obtain a fine powder. The obtained mixture has undergone a cycle of grinding, pelting and sintering. During during the experience the powder was calcined at 600 °C and at 800 °C for 12 h in air. Then, it was sintered at 1000 °C for 24 h.

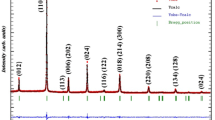
The X-Ray diffraction analysis with Cukα radiation (λCukα = 1.540598 Å) was used to identify phase purity, crystallinity and homogeneity. Use Rietveld structure refinement program FULLPROF software to fit the experimental data of X-ray diffraction. The XRD patterns of the samples showed a perovskite single-phase having an orthorhombic structure with a Pbnm space group. After sputtering the gold electrode on the circular electrode, the dielectric properties are extracted from the ceramic disks. To measure the impedance, we use the “Agilent 4294 A impedance analyzer” to measure the conductance ‘G’ and capacitance ‘C’ over a wide range of temperatures and frequencies.

3 Results and discussion

3.1 Structural investigation

The structural characterization has been carried out from powder XRD analysis. The XRD patterns obtained at room temperature of Ca0.85Er0.1Ti(1−x)Co4x/3O3 for (x = 0.15 and 0.20) are characteristic of an orthorhombic symmetry with a Pbnm space group [11, 12]. Figure 1 shows the X-ray diffraction pattern for both samples. The structural characterization is more detailed in the previous work [12].

Fig. 1
figure 1

X-ray diffraction pattern of Ca0.85Er0.1Ti(1−x)Co4x/3O3 for (0.15 ≤ x ≤ 0.20)

Full size image

3.2 Complex impedance spectroscopy

The complex impedance study is a useful characterization technique for investigation of electrical properties of the ferroelectric, ionic conductors, and other ceramics in materials research. It provides essential information on the microstructure of polycrystalline materials, such as grains, grain boundaries and electrode interfaces [13].

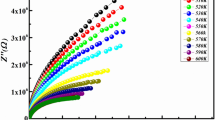
Figure 2a, b shows the complex impedance plots of Ca0.85Er0.1Ti(1−x)Co4x/3O3 (x = 0.15 and 0.20). We note from the spectra the appearance of one wide semicircle arc, which corresponds to the merging of two semicircles, at high and medium frequencies, which is attributed to the contribution of grains and grain boundaries. The merging into a single arc, indicating a major change in the electrical properties of the material. This effect can be related to changes in microstructure determined by the thermal state of the material [13]. At low frequency, we note the existence of a small semicircle arc, which is attributed to the contribution of electrodes. With increasing temperature, the diameters of semicircles decrease. Such behavior indicates that the conduction process is thermally activated and confirms the semiconducting characteristic of both samples. The diameter of these semicircles changes with the increase of temperature, and their center is recessed below the real axis, which indicates the decrease of the bulk resistance of the material and the non-Debye type relaxation process [14,15,16].

Fig. 2
figure 2

a, b The Nyquist plots of Ca0.85Er0.1Ti(1−x)Co4x/3O3 for (0.15 ≤ x ≤ 0.20) ceramics at different temperature. c Z* plot of samples and the solid line is fitting line based on the equivalent circuit. The inset is the electrical equivalent circuits for x = 0.15 and 0.2

Full size image

Taking into account the response of the electrode-material interface, each of the phenomena occurring in the grains, grain boundaries and electrodes is modeled by a parallel R-CPE circuit (Fig. 2c) with a characteristic pulsation W0 which is specific to it and the impedance spectrum of a material has, therefore, generally three semicircles or arcs of a circle.

These spectra can be modeled by an equivalent circuit containing three parallel resistance—constant phase element (CPE) (inset Fig. 2c). The modeled circuit for the studied compound consists of a series array of three sub circuits: one corresponds to the grain contribution while others correspond to the effect of grain boundaries and electrode processes. Each sub circuit contains a parallel combination of a resistance and a constant phase element. Where (R1, R2, R3) and (CPE1, CPE2, CPE3) are the resistances and constant phase elements of grains, grain boundaries and electrodes, respectively. The values of resistances for different media are given in Table 1. It is observed that as the temperature increases, the resistance provided by the grain boundary and electrode processes decreases (Fig. 3, Table 1), indicating that the barrier of charge carriers decreases, thus contributing to the increase at higher temperatures Conductivity. In addition, as the temperature increases, the crystal grains, grain boundaries, and electrode phenomena seem to merge into an arc, indicating that the overall electrical properties of the material have undergone substantial changes. This effect may be related to changes in the microstructure determined by the thermal state of the material [13].

Table 1 The R1, R2 and R3 resistance of Ca0.85Er0.1Ti(1−x)Co4x/3O3 for (0.15 ≤ x ≤ 0.20)
Full size table
Fig. 3
figure 3

Grains, grain boundaries and electrode resistances plot for both samples

Full size image

Figure 4a–d shows the variation of real part (Z′) and the imaginary part (Z″) of impedance as a function of frequency in a wide temperature range [460–620 K] for Ca0.85Er0.1Ti1−xCo4x/3O3 (x = 0.15 and 0.2) samples, respectively.

Fig. 4
figure 4

a, b The variation of real part of impedance with frequency at different temperature. c, d The variation of imaginary part of impedance with frequency at different temperature

Full size image

In a low frequencies region, the real part of impedance Z′ (Fig. 4a, b) presents a higher value, which decreases simultaneously with increasing frequency.

Furthermore, Z′ value weakens with growing temperature, which denotes an increase in the electrical conductivity (ac conductivity), which means that the material becomes more conducting [17]. The merging of Z′ spectra in the higher frequency region may be due to the release of space charge, which is the result of the decrease in the barrier properties of the material with increasing temperature, and can be explained by the presence of space charge polarization [18]. The process of Z′ observed for the compounds at all frequency ranges is in a good agreement with literature [19].

One can also notice from Fig. 4a, b that Z′ values for x = 0.15 sample are lower in comparison with the second sample. This is in good agreement with the reported results of electrical conductivity in the previous work [12].

Additionally, we represent the evolution of the imaginary part of impedance (Z″ = Im[Z]) with frequency for a wide temperature range in Fig. 4c, d. Initially, Z″ value rises to attain the maxima Z″max, after that it decreases at higher frequencies. In addition, the peak observed shifts to the higher frequencies with increasing temperatures. The decreased magnificence of Z″max with the increase of temperature indicates a diminution in resistive property [20]. The broadening of the peaks with increasing temperature is another feature, which proves the presence of an electrical relaxation process, depending on temperature, of non-Debye nature in the compound [21].

The relaxation process is the result of the existence of vacancies/defects at higher temperatures and immobile species at lower temperatures [22]. Similar behavior has been reported for other manganites and different perovskite systems [23,24,25] and it has been attributed to localized hopping of polarons between lattice sites with a characteristic timescale [26].

3.3 Electrical modulus studies

When the electric induction ‘D’ is remains constant, the complex dielectric modulus ‘M*’ corresponds to the relaxation of the electric field in the compounds [27, 28]. Studying the form M* is another way to explore electrical characteristics of our polycrystalline samples. By interpreting the formalism of electrical modulus, it is possible to better understand the overall view of conductivity relaxation and electrical transmission mechanisms (such as carrier hopping frequency).This investigation can also clarify many other effects existent in the material because of the different relaxation time constants. The complex electric modulus plot is more efficacious than the Nyquist plot of impedance in separating components with different capacitances despite their having same electrical resistance and it also suppresses the electrode effects, i.e., the complex electric modulus is used to explain the resistance and capacitive effect present in the compound. The capacitance contributed by the grains (Cg) is obtained from the left intercept between the semicircle and M′ axis, while the right intercept indicates the total capacitance value (C) contributed by grains (Cg) and grain boundaries (Cgb) where C = Cg + Cgb.

The values of real (M′) and imaginary (M″) part of the modulus were obtained using the impedance data [29,30,31,32,33]:

$$ M^{\prime} = w\mathop c\nolimits_{0} Z^{\prime\prime}, \;\;\; M^{\prime\prime} = w\mathop c\nolimits_{0} Z^{\prime} .$$

Figure 5 shows the complex electric modulus plots (M″ vs. M′) (at temperatures [460–620 K] and in the frequency range [1 to 107 Hz] for Ca0.85Er0.1Ti1−xCo4x/3O3 (x = 0.15 and 0.2) samples. It clearly shows the presence of a non-completed semicircular arc, which gradually increases with the increase of the temperature. We can deduce also from the plots that the total capacitance (C) of our compounds decreased with increasing temperature from 460 to 620 K, which can be attributed to the release of space charges at the grain boundaries [34].

Fig. 5
figure 5

Cole–Cole (M″ vs. M′) plot of Ca0.85Er0.1Ti(1−x)Co4x/3O3 for (0.15 ≤ x ≤ 0.20) ceramics at different temperature

Full size image

That is mean due the accumulation of defects (non-stoichiometric oxygen distribution) at the grain boundary (the component has a larger capacitance Cgb), the contribution of the grain is reduced [35], and in the conductive mechanism, the role of the grain boundary More important than the role of grains [36, 37].

Figure 6a, b depicts the variation of the real part of modulus (M′) as a function of frequency at various temperatures respectively for x = 0.15 and 0.2. This graph is used to understand the dynamic of mobility. It is observed from the spectra that the value of M′ is almost zero at lower frequencies, suggesting that the interface effect tends to be eliminated in the modulus representation [38].

Fig. 6
figure 6

a, b Frequency dependencies of M′ at different temperatures respectively for x = 0.15 and 0.20. The inset represent the M′max versus temperatures at different frequencies. c, d Frequency dependencies of M″ at different temperatures respectively for x = 0.15 and 0.20. The inset represent the M″max versus temperatures at different frequencies

Full size image

The M′ value continuously increases with increasing frequency and presents a tendency toward saturation when it reaches the maximum asymptotic value at all temperatures. The maximum value of M′ (M′max) obtained at high frequency can be attributed to the conduction phenomenon caused by the migration of carriers in a small distance [33].

The evolution of M′max as a function of temperatures is shown in the insets of Fig. 6a, b the graph indicating a gradual decrease with increasing temperatures, which can be associated with the release of space charges at the grain boundaries [39].

The plots in Fig. 6c, d (M″) are characterized by the presence of a relaxation peak. It is observed that the peak value (M″max) shifts towards higher frequency with increasing temperature. This indicates sharp dependence of M″ on temperature and frequency correlating the motion of mobile charge carriers [38]. At lower frequencies, charge carriers can move freely over longer distances, up to a certain frequency (peak maximum). A further increase in frequency, i.e., the frequency above maximum (the region on the right of the peak), confines carriers to potential wells. Therefore, the region where the peak occurs indicates the transition from long-range to short-range mobility with increasing frequency [40].

The changes in the peak positions of the real and imaginary parts of the complex electronic modulus of Ca0.85Er0.1Ti(1−x)Co4x/3O3 (x = 0.15and 0.20) are related to the changes in the cation distribution and microstructure with temperatures. In addition, the asymmetric broadening of the imaginary peak indicates that the conduction process is related to the non-Debye type [41, 42].

The imaginary parts M″ (f) can be fitted using the Kohlrausch, Williams and Watts (KWW) formula expressed as follow:

$$M^{{\prime\prime}} = \frac{{M_{{_{1\max } }} }}{{\left( {\left( {1 - \beta_{1} } \right) + \left( {\frac{{\beta_{1} }}{{1 + \beta_{1} }}} \right)} \right)\left[ {\left( {\frac{{f_{1\max } }}{f}} \right) + \left( {\frac{f}{{f_{1\max } }}} \right)^{\beta 1} } \right]}} + \frac{{M_{2\max } }}{{\left( {\left( {1 - \beta_{2} } \right) + \left( {\frac{{\beta_{2} }}{{1 + \beta_{2} }}} \right)} \right)\left[ {\left( {\frac{{f_{2\max } }}{f}} \right) + \left( {\frac{f}{{f_{2\max } }}} \right)^{\beta 2} } \right]}} $$

where \(M_{\max }^{{\prime\prime}}\) is the peak maxima and \(f_{\max }\) his corresponding frequency. β1 and β2 are called the stretching factors which are less than 1 [43]. Using the last Equation, we applied the fit on M″ plots. It is clear that the fitting plot is reasonable and in good agreement with the experimental one. The obtained values of \({\beta }_{1}\) are found less than 1 in the range of 0.79 to 0.52 for x = 0.15 as an example (Fig. 7). These results confirm the non-Debye relaxation process of our compound.

Fig. 7
figure 7

Example of fitting line using the KWW relation of x = 0.15

Full size image

To identify the relaxation process, i.e., there is a long-range or short-range motion of charge carriers. For the long-range movement of charge carriers, the peaks of Z″ and M″ occur at the same frequency (fM″ = fZ″). However, for the short-range motion, the peaks occurs at different frequencies (fM″ # fZ″) [44, 45].

Figure 8 shows the evolution of Z″ and M″ as a function of frequency at 500 K (the other temperatures exhibits the same behavior) for Ca0.85Er0.1Ti(1−x)Co4x/3O3 (0.15 ≤ x ≤ 0.20). It is noticed from these plots, the peak of Z″ and M″ versus frequency occurs at different frequencies, which suggests the presence of short-range mobility. The peak frequency fM″ shifted to a higher frequency region as compared to fZ″ curve (fM″ > fZ″). From these representations, we can observe the change in the apparent polarization by checking the magnitude of mismatch between the peaks of both parameters (Z″ and M″) [46, 47]. The Comparison of the modulus and impedance data allows us to identify the overall response based on ionic conductivity (delocalization relaxation process) and dielectric relaxation (local relaxation process) [48].

Fig. 8
figure 8

Z″ and M″ vs. frequency plots

Full size image

The variation of normalized parameter Z′′/Z″max and M′′/M″max as a function of normalized frequency (f/fmax) at various temperatures [460–620 K] is shown in Fig. 9, where fmax corresponds to the frequency for Z″max and M″max. As it is seen in the figure, the scaled impedance and the scaled modulus resemble the same nature. Where we note that,regardless of the temperature, different curves are merged on one peak. This overlap of the curves corresponding to different Z″/Z″max and M″/M″max values indicates that the distribution of relaxation time is independent of temperature. This further demonstrates that the same relaxation process occurs at different temperatures [20]. The overlap of the peaks indicates that both long-distance and local relaxation exist in the system. The superposition of curves confirms the fact that the mechanism is non-Debye type [13, 49, 50].

Fig. 9
figure 9

Normalized parameters (Z″/Z″max) and M″/M″max versus f/fmax) plots at various temperatures Ca0.85Er0.1Ti(1−x) Co4x/3O3 for (0.15 ≤ x ≤ 0.20)

Full size image

4 Conclusion

In this study, we investigate and develop the complex impedance and electrical modulus analysis of Ca0.85Er0.1Ti(1−x)Co4x/3O3 (x = 0.15 and 0.20). The electrical properties of the compound derived from CIS analysis shows a strong dependence on frequency. The Nyquist study proved the appearance of a decentered semicircle modeled as an equivalent circuit consisting of three parallel resistance—constant phase element (CPE). The results obtained from the real part of impedance are in good agreement with the interpretation of electrical conductance results in the previous work. Due to the short-range mobility of charge carriers, the electrical properties of the compound derived from the complex electronic modulus show a process of conduction. The imaginary part of the modulus proves that the relaxation is related to temperature, and the charge carrier jumps.