1 Introduction

Polarization is an important characteristic of electromagnetic (EM) wave, it is essential to manipulate the polarization state of an EM wave for various EM applications, such as radio communication, antenna design, radar technology and radar stealth technology [1,2,3]. Conventional methods of controlling polarization are usually realized using the birefringence effect and optical activity of natural materials, which usually suffer from bulky volume, high loss, and narrow bandwidth in practical applications [4, 5]. Over the past decade, it has been found that metasurface can provide a convenient way to control the polarization state of a EM waves, now many different types of polarization converters have been proposed based on various anisotropic or chiral metasurfaces, which can realize linear [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20], linear-to-circular [21,22,23,24,25,26,27,28], and transmission-type circular polarization conversion [29, 30], respectively, at linear polarized (LP) or circular polarized (CP) incidences. In addition, in common cases, a right-handed and left-handed CP (RCP and LCP) wave will be converted to a LCP(−) and RCP(+) wave, respectively, after reflection on a conducting surface, however, based on a proper anisotropic or chiral metasurface, the polarization state of the reflected wave can remain the same as that of the CP incident wave, which is very similar to a transmission-type circular polarization conversion and can be regarded as a reflection-type circular polarization conversion, this kind of anisotropic or chiral metasurfaces has been considered as a reflective circular polarization converter [31]. As this kind of reflective circular polarization converters can be used to design phase gradient metasurface using Pancharatnam–Berry (PB) phase, they have drawn much attention in recent years, and several different designs and applications have been proposed effectively [32,33,34,35].

In this work, we propose an ultra-wideband and high-efficiency reflective polarization converter based on an orthotropic anisotropic metasurface, which can realize not only ultra-wideband linear polarization conversion at x- and y-polarized incidences, but also reflection-type ultra-wideband circular polarization conversion at CP incidence in the same band. We have carried out simulation and experiment to verify the polarization converter, and presented the root cause of these polarization conversions.

2 Design, simulation and experiment

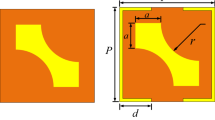
The unit cell of the proposed polarization converter is shown in Fig. 1, which consists of one layer of patterned metal film printed on a grounded dielectric substrate. The geometric pattern of the patterned metal film is a square ring with two splits at a pair of opposite corners and four open stubs attached to the inner sides. The geometrical parameters of the unit cell are shown in Fig. 1a. After appropriate selection, these parameters are chosen as follows: P = 9.20 mm, l = 6.80 mm, w = 0.65 mm, t = 1.15 mm, g = 0.80 mm and h = 3.00 mm; in addition, the metallic layer, together with the grounded plane, is modeled as a 0.017 mm copper film with an electric conductivity \(\sigma =5.8 \times {10^7}\) S/m, and the dielectric substrate is selected as a polytetrafluoroethylene (PTFE) one with a relative permittivity of 1.8 and a dielectric loss tangent of 0.0013.

Fig. 1
figure 1

Proposed polarization converter: a top view of unit cell, b side view of unit cell, c fabricated sample

Full size image

To verify the polarization conversion performance of our design, we have carried out numerical simulation and experimental measurement successively on the proposed polarization converter. The numerical simulations were carried out using the CST MICROWAVE STUDIO. In the simulations, the unit-cell boundary conditions were applied in the x- and y-axis directions, the open (add space) was employed in the z-axis direction, and several different LP and CP incident waves were successively defined as the excitation sources. In the experimental process, an experimental sample was fabricated by the conventional printed circuit board (PCB) process, which contains 35 × 35 unit cells, covering an area of about 322 mm × 322 mm, as shown in Fig. 1c. First, we have measured its reflection coefficients at LP incidence, which was measured in a microwave anechoic chamber using an Agilent E8363B network analyzer together with a pair of identical standard-gain LP horn antennas. The two horn antennas were used to transmit and receive a LP wave, the sample was irradiated, and the distance between the antennas and the sample was set as 1.0 m; to carry out the measurement at normal incidence, the separation angle between the orientations of the two antennas should ideally be close to 0°, it was set as 5° for the finite sizes of the fabricated sample. The co- and cross-polarization LP reflections were measured when the receiving horn antenna rotated by 0° and 90°, respectively. Second, to measure the reflection coefficients at CP incidence, the pair of LP horn antennas was replaced by CP horn antennas. In the measuring of the co-polarization reflection, the emitter and receiver were both RCP antennas, three pairs of RCP horn antennas with a continuous frequency doubling in working band (4–8 GHz, 8–18 GHz, 18–40 GHz) were used; however, to measure the cross-polarization reflection, the three RCP receiving antennas were replaced by three similar LCP ones.

As the polarization converter is an anisotropic structure, when a LP or CP wave is incident on it, the reflected wave would consist of both cross- and co-polarized components in most cases. At LP and CP incidences, the reflection matrix R, which is used to describe the relationships between the incident and reflected electric fields, can be expressed as:

$$\left( {\begin{array}{*{20}{c}} {E_{x}^{r}} \\ {E_{y}^{r}} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {{r_{xx}}{r_{yy}}} \\ {{r_{yx}}{r_{yy}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {E_{x}^{i}} \\ {E_{y}^{i}} \end{array}} \right)={\mathbf{R}_{{\text{lin}}}}\left( {\begin{array}{*{20}{c}} {E_{x}^{i}} \\ {E_{y}^{i}} \end{array}} \right),$$
(1)

and

$$\left( {\begin{array}{ll} {E_{+}^{r}} \\ {E_{ - }^{r}} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {{r_{++}}{r_{ - - }}} \\ {{r_{ - +}}{r_{ - - }}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {E_{+}^{i}} \\ {E_{+}^{i}} \end{array}} \right)={{\mathbf{R}}_{{\text{cir}}}}\left( {\begin{array}{*{20}{c}} {E_{+}^{i}} \\ {E_{+}^{i}} \end{array}} \right),$$
(2)

respectively, wherein \(r_{{ij}}^{{}}=E_{i}^{r}/E_{j}^{i}\), the first and the second subscripts i and j correspond to the polarized states of the reflected and incident waves, respectively. In addition, the polarization conversion ratio (PCR) at y- or x-polarized incidence can be calculated by:

$$\begin{gathered} {\text{PCR}}={{{{\left| {{r_{xy}}} \right|}^2}} \mathord{\left/ {\vphantom {{{{\left| {{r_{xy}}} \right|}^2}} {\left( {{{\left| {{r_{xy}}} \right|}^2}+{{\left| {{r_{yy}}} \right|}^2}} \right)}}} \right. \kern-0pt} {\left( {{{\left| {{r_{xy}}} \right|}^2}+{{\left| {{r_{yy}}} \right|}^2}} \right)}} \hfill \\ {\text{or}} \hfill \\ {\text{PCR}}={{{{\left| {{r_{yx}}} \right|}^2}} \mathord{\left/ {\vphantom {{{{\left| {{r_{yx}}} \right|}^2}} {\left( {{{\left| {{r_{yx}}} \right|}^2}+{{\left| {{r_{xx}}} \right|}^2}} \right)}}} \right. \kern-0pt} {\left( {{{\left| {{r_{yx}}} \right|}^2}+{{\left| {{r_{xx}}} \right|}^2}} \right)}}. \hfill \\ \end{gathered}$$
(3)

However, at RCP or LCP incidence, the PCR must be altered as:

$$\begin{gathered} {\text{PCR}}={{{{\left| {{r_{++}}} \right|}^2}} \mathord{\left/ {\vphantom {{{{\left| {{r_{++}}} \right|}^2}} {\left( {{{\left| {{r_{++}}} \right|}^2}+{{\left| {{r_{ - +}}} \right|}^2}} \right)}}} \right. \kern-0pt} {\left( {{{\left| {{r_{++}}} \right|}^2}+{{\left| {{r_{ - +}}} \right|}^2}} \right)}} \hfill \\ {\text{or}} \hfill \\ {\text{PCR}}={{{{\left| {{r_{ - - }}} \right|}^2}} \mathord{\left/ {\vphantom {{{{\left| {{r_{ - - }}} \right|}^2}} {\left( {{{\left| {{r_{+ - }}} \right|}^2}+{{\left| {{r_{ - - }}} \right|}^2}} \right)}}} \right. \kern-0pt} {\left( {{{\left| {{r_{+ - }}} \right|}^2}+{{\left| {{r_{ - - }}} \right|}^2}} \right)}}. \hfill \\ \end{gathered}$$
(4)

First, we assumed the incident wave is a LP one, simulated and measured the polarization converter at y-polarized incidence. The simulated and measured results, the cross- and co-polarized reflection coefficients, together with the PCR, are shown in Fig. 2. From the simulated results, we can see that the co-polarized reflection ryy is less than − 10 dB in the frequency range from 8.77 to 24.71 GHz, which means that an ultra-wideband linear polarization conversion is realized in this band, and the relative bandwidth of the polarization converter is up to 95.2%. Compared to the previous two ultra-broadband polarization converter proposed in Reference [13, 14], whose relative bandwidth were only 78.6% and 73%, respectively, the polarization converter has a much wider bandwidth. In addition, in Fig. 2b, it is shown that the PCR is higher than 95% between 11.91 and 24.58 GHz, and it can realize high-efficiency polarization conversion. Moreover, Fig. 2 shows that the measured results are in good agreement with the simulated ones, however, a slight discrepancy of frequency and magnitude between them still exists due to unexpected fabrication tolerance and measurement error.

Fig. 2
figure 2

Simulated and measured results of the proposed polarization converter at y-polarized incidence: a the magnitudes of ryy and rxy, b the polarization-conversion ratio (PCR)

Full size image

The above results are obtained at y-polarized incidence, which have clearly demonstrated its performance at LP incidence. In fact, in the simulation at y-polarized incidence, we have obtained the reflection coefficients at x-polarized incidence at the same time, it is shown that ryy = rxx and rxy = ryx. This is just because the polarization converter is a symmetric structure, and the x- and y-axis are completely symmetric to each other in the polarization converter structure. In addition, in the experiment, when the transmitting and receiving antennas rotate 90° at the same time, there is basically no change in the received wave, which just verifies that ryy = rxx and rxy = ryx.

Next, the polarization converter is simulated and measured at CP incidence, and the obtained simulated results, shown in Fig. 3, show that the magnitudes of the co-polarized reflection coefficients, together with PCRs, at RCP and LCP incidences are almost equal to those at y-polarized incidence, and it is indicated that an ultra-wideband reflection-type circular polarization conversion is realized in the same band, moreover, if we ignore the little simulation errors between them, we can know that \(\left| {{r_{++}}} \right|=\left| {{r_{ - - }}} \right|=\left| {{r_{xy}}} \right|\) according to these simulated results. In addition, the measured values at RCP incidence basically agreed with the simulated results, which further prove that \(\left| {{r_{++}}} \right|=\left| {{r_{ - - }}} \right|=\left| {{r_{xy}}} \right|\) though there is a little difference between the measured and simulated results for the RCP incident waves radiated by these RCP horn antennas which have no ideal axial ratios.

Fig. 3
figure 3

Simulated and measured results of the proposed polarization converter at CP incidence: a the magnitudes of \({r_{++}}\) and \({r_{ - - }}\), b the polarization-conversion ratio (PCR)

Full size image

3 Theory analysis

To gain insight into the cause of these polarization conversions for the proposed polarization converter, we present a detailed analysis in succession. First, we present the root cause of the linear polarization conversion. As the polarization converter is an orthotropic anisotropic structure with a pair of mutually perpendicular symmetric axes u and v, no cross-polarized reflected components will exist at u- and v-polarized incidences, moreover, the reflection coefficients ruu and rvv will be mutually independent, but the magnitudes of ruu and rvv will both be close to 1.0 because of the small dielectric loss, thus if we neglect the dielectric loss, one formula can be established as follows:

$${r_{vv}}={r_{uu}}{{\text{e}}^{ - j\Delta \varphi }},$$
(5)

wherein \(\Delta \varphi\) denotes the phase difference between ruu and rvv. In fact, in Reference [11], it has been illustrated that this kind of anisotropic polarization converters can realize linear polarization conversion at both x- and y-polarized incidences, and the root cause is the orthotropic anisotropy of the unit cell structures, which results in multiple different eigenmodes being excited by v- and u-polarized incidences and a large phase difference \(\Delta \varphi\) between ruu and rvv that maybe be generated in a large frequency range. At x- and y-polarized incidences, the incident and reflected waves can both be regarded as a composite wave composed of equal amounts of u- and v-polarized components, the two components in the incident wave are in phase, however, in the reflected wave, a large phase difference \(\Delta \varphi\) maybe be generated between the two components, so the anticipated polarization conversion maybe be realized. In addition, in Ref. [11], the following equation has been established after detailed derivation:

$${r_{yx}}={r_{xy}}=\sqrt {(1 - \cos \Delta \varphi )/2} ,$$
(6a)
$${r_{xx}}={r_{yy}}=\sqrt {(1+\cos \Delta \varphi )/2} ,$$
(6b)

it is illustrated that the cross- and co-polarized reflection coefficients at x- and y-polarized incidences can be completely determined by \(\Delta \varphi\), and the PCR will increase along with the increase of \(\left| {\Delta \varphi } \right|\), and when \(\left| {\Delta \varphi } \right|\) reaches a maximum value of 180°, a perfect linear polarization conversion \(({r_{xx}}={r_{yy}}=0,\quad {r_{yx}}={r_{xy}}=1)\) will be realized.

According to the above conclusion, to make clear the root cause of the linear polarization conversion for the proposed polarization converter, we have carried out numerical simulations at u- and v-polarized incidences, respectively. The simulated results in Fig. 4a indicate that the magnitudes of ruu and rvv are both close to 1.0, however, through detailed observation, it is found that the data curves of ruu and rvv both have two minimum values at the frequencies 15.01 GHz, 25.07 GHz and 8.59 GHz, 22.54 GHz, respectively, and it is implied that two pairs of eigenmodes are excited by u- and v-polarized incidences, respectively, which cause several maximums of the dielectric loss existing at the four eigenfrequencies.

Fig. 4
figure 4

a The magnitudes of ruu and rvv, b the phase difference between ruu and rvv, c the phase variations of ruu and rvv caused by the eigenmodes and d the comparison between the simulated and calculated ryy

Full size image

To know the effect of these eigenmodes on the generation of the linear polarization conversion, after several simulations, we presented the surface current on the square split ring at each eigenfrequency in Fig. 5, and it is shown that the square split ring can be regarded as a two-level fractal structure due to the four open stubs attached to its inner side, and the first eigenmodes excited by u- and v-polarized incidences are both generated on the first level of the fractal structure, however, the two second eigenmodes excited by u- and v-polarized incidences are both generated on the second level of the fractal structure; moreover, the surface currents in these eigenmodes excited by u- and v-polarized incidence are completely symmetrical with respect to u and v-axis, respectively, due to the symmetry of the polarization converter structure, thus these surface currents can all be equivalent to a resonant current in the direction of v- or u-axis, which is the same with the polarization direction of the incident wave, so no cross-polarized reflection is generated at u- and v-polarized incidence. In Fig. 5a, it is indicated that the current distribution pattern in the first eigenmode occurring at 15.01 GHz is completely symmetrical with respect to u-axis for it is excited by u-polarized incidence, and two identical local resonances occur at the upper-left and lower-right edges of the square split ring, respectively, however, at point A and point B, which are just the intersection points between the square split ring and u-axis, the electric currents will always remain 0, and the current oscillating regions of the two local resonances are between point A and point B, thus the two local resonances can both be equivalent to a LC series resonance, in which the equivalent inductance L results from the electric current on the edge of the square split ring and the equivalent capacitance C results from the electric charge accumulation between the split, and their quality factor Q will be proportional to \(\sqrt {L/C}\). In the two local resonances, the electric currents on two edges are cut off by the splits at the corner, the equivalent inductance L is very small, but in contrast to the equivalent inductance L, the equivalent capacitance C is still large for much of the electric charge accumulation will be caused between the split by the cut-off current, so the quality factor Q of the eigenmode at 15.01 GHz is low. In addition, Fig. 5b shows that two identical local resonances occur at the upper-right and lower-left edges in the first eigenmode occurring at 8.59 GHz and excited by v-polarized incidence, which are very similar to the two in the first eigenmode occurring at 15.01 GHz and excited by u-polarized incidence, however, the electric currents on two adjacent edges are connected in the two local resonances, and the two splits are just at A and B two points, thus the equivalent inductance L is large, but the equivalent capacitance C is small for the electric currents near the splits that are close to zero and the electric charge accumulations between the splits will be very little, in this way, we can know the quality factors Q of the eigenmode at 8.59 GHz are high. Furthermore, in Fig. 5c, d, it is indicated that there are two identical local resonances excited on second-level square split rings in each second eigenmode excited by u- or v-polarized incidence, which can be equivalent to a LC parallel resonance for the electric current directions are uniform on these second-level square split rings, thus their quality factors Q will be proportional to \(\sqrt {C/L}\). In the second eigenmode occurring at 25.09 GHz and excited by u-polarized incidence, the two local resonances are generated on the second-level square split ring with two splits, so the quality factor Q of this eigenmode is high as the resonant currents in the two local resonances have been cut off by two splits successively, whose equivalent inductance L is very small. However, in the second eigenmode occurring at 22.54 GHz and excited by v-polarized incidence, the two local resonances are generated on the second-level square split ring with one wide split, the quality factor Q is low as the equivalent capacitance C in each local resonance is very small. In fact, in Fig. 4a, it is indicated that the data curves of rvv and ruu vary rapidly near the eigenfrequencies of 8.59 and 25.07 GHz, respectively, however, near the other two eigenfrequencies 15.01 and 22.54 GHz, the data curves of rvv and ruu vary very slowly, which just shows that the quality factors Q of the two eigenmodes occurring at 8.59 and 25.09 GHz are high, but those of the two eigenmodes at 15.01 and 22.09 GHz are very low.

Fig. 5
figure 5

The surface current distributions at each eigenfrequency: a the first eigenmode excited by u-polarized incidence, b the first eigenmode excited by v-polarized incidence, c the second eigenmode excited by u-polarized incidence and d the second eigenmode excited by v-polarized incidence

Full size image

In addition, in Fig. 4b, it is shown that \(\Delta \varphi\) is increased first and then decreased rapidly when the frequency increased from 8.5 to 25.0 GHz, and it stays close to 180° between 9.0 and 24.5 GHz, which implies that the anticipated linear polarization conversion will be realized in the frequency band. Furthermore, to explain the effect of the eigenmodes excited by u- and v-polarized incidences on the occurrence of the linear polarization conversion, the phase variations of ruu and rvv are shown in Fig. 4c, in which the effect of the wavepath has been eliminated, and they are obtained by the following equation:

$${\varphi _{uu}}={\text{Arg}}({r_{uu}})+2{k_0}d,$$
(7a)
$${\varphi _{vv}}={\text{Arg}}({r_{vv}})+2{k_0}d,$$
(7b)

wherein d denotes the distance between Floquet Port and the polarization converter in the simulation structure. In Fig. 4c, it is shown that the slopes of the data curves of \({\varphi _{vv}}\) and \({\varphi _{uu}}\) are the largest near the eigenfrequencies 8.59 and 25.07 GHz, respectively, which indicates that the linear polarization conversion is caused and ended by the two eigenmodes, respectively, and it is just because the quality factors of the two eigenmodes are high. However, the quality factors of the other two eigenmodes are both very low, and the slope of the data curve of \({\varphi _{vv}}\) near the eigenfrequency 15.01 GHz, together with that of \({\varphi _{uu}}\) near the eigenfrequency 22.54 GHz, is very small, so the two eigenmodes have little effect on the phase difference \(\Delta \varphi\), which can stay close to 180° between 9.0 and 24.5 GHz. Finally, we calculate the magnitudes of rxy and ryy using Eq. (6a), (6b) according to the phase differences \(\Delta \varphi\) in Fig. 4b, and the calculated results are shown in Fig. 4d, and it is shown that the calculated results are essentially in agreement with the simulated results at y-polarized incidence in Fig. 2a. According to the above results, we can conclude that the root cause of the linear polarization conversion is the appropriate anisotropy of the unit cell in the polarization converter structure, which results in different eigenmodes excited by v- and u-polarized incidences, thus the phase differences \(\Delta \varphi\) between ruu and rvv is close to 180° in a large frequency range, and the anticipated linear polarization conversion is realized in this frequency band.

According to the root cause of the linear polarization conversion presented above, we have analyzed the root cause of the circular polarization conversion in succession. Because a CP wave consists of two perpendicular LP waves with equal amplitude and ± 90° phase difference, the reflection matrix Rcir at CP incidence in Eq. (2) can be derived from Rlin at LP incidence in Eq. (1). In Fig. 1a, it is shown the incident wave is in the −Z axis direction, and the reflected wave is in + Z axis direction, so the incident RCP unit wave, together with the reflected LCP unit wave, can be expressed as:

$$e={\hat {e}_x}+i{\hat {e}_y},$$
(8)

and the reflected RCP and incident LCP unit wave can both be expressed as:

$$\hat {e}={\hat {e}_x} - i{\hat {e}_y}.$$
(9)

We assume the polarization converter is under a RCP and LCP unit wave incidences in succession and regard the RCP and LCP unit waves as a composite LP wave consisting of both x- and y-polarized components. For the expression of their cross- and co-polarized reflected wave can be deduced using Eq. (1), in this way, we have obtained the reflection matrix Rcir for CP wave as follows:

$$\begin{aligned} {{\mathbf{R}}_{{\text{cir}}}} & =\left( {\begin{array}{*{20}{c}} {{r_{{\text{++}}}}}&{{r_{{\text{+}} - }}} \\ {{r_{ - +}}}&{{r_{ - - }}} \end{array}} \right) \\ & =\frac{1}{2}\left( {\begin{array}{*{20}{c}} {{r_{xx}} - {r_{yy}}+i({r_{xy}}+{r_{yx}})}&{{r_{xx}}+{r_{yy}}+i({r_{yx}} - {r_{xy}})} \\ {{r_{xx}}+{r_{yy}}+i({r_{xy}} - {r_{yx}})}&{{r_{xx}} - {r_{yy}} - i({r_{xy}}+{r_{yx}})} \end{array}} \right). \\ \end{aligned}$$
(10)

For the proposed polarization converter, the cross- and co-polarization reflection coefficients at x- and y-polarized incidences are equal, respectively, because of the symmetry of the polarization converter structure, ryy = rxx, rxy = ryx, thus Eq. (10) can be simplified as:

$${{\mathbf{R}}_{{\text{cir}}}}=\left( {\begin{array}{*{20}{c}} {{r_{{\text{++}}}}}&{{r_{{\text{+}} - }}} \\ {{r_{ - +}}}&{{r_{ - - }}} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {i{r_{xy}}}&{{r_{yy}}} \\ {{r_{yy}}}&{ - i{r_{xy}}} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {i{r_{yx}}}&{{r_{xx}}} \\ {{r_{xx}}}&{ - i{r_{yx}}} \end{array}} \right),$$
(11)

it is shown that \({r_{ - +}}\) and \({r_{+ - }}\) are completely equal to \({r_{yy}}\) and \({r_{xx}}\), and the magnitudes of \({r_{++}}\) and \({r_{ - - }}\) are equal to those of \({r_{xy}}\) and\({r_{yx}}\); in addition, compared with \({r_{xy}}\) and\({r_{yx}}\), \({r_{++}}\) has a phase lead of 90°, but \({r_{ - - }}\) has a phase lag of 90°.

Why does the polarization converter have this anomalous reflection performance? We provided a detailed explanation in succession. Now we regard both RCP and LCP incident wave as a composite LP incident wave consisting of both x- and y-polarized components, thus due to the linear polarization conversions at x- and y-polarized incidences, together with rxy = ryx, according to Eqs. (1), (8) and (9), the cross-polarized electric field components in the two composite LP reflected wave can be expressed as:

$${\left. {E_{{\operatorname{cros} }}^{r}} \right|_{\operatorname{RCP} }}={E_0}\left( {i{r_{xy}}{{\hat {e}}_x}+{r_{yx}}{{\hat {e}}_y}} \right)=i{r_{xy}}{E_0}\left( {{{\hat {e}}_x} - i{{\hat {e}}_y}} \right),$$
(12a)

and

$${\left. {E_{{\operatorname{cros} }}^{r}} \right|_{\text{RCP}}}={E_0}\left( { - i{r_{xy}}{{\hat {e}}_x}+{r_{yx}}{{\hat {e}}_y}} \right)= - i{r_{xy}}{E_0}\left( {{{\hat {e}}_x}+i{{\hat {e}}_y}} \right).$$
(12b)

In addition, for ryy = rxx, the co-polarized electric field components in the composite LP reflected wave can be written as:

$${\left. {E_{{\operatorname{co} }}^{r}} \right|_{\operatorname{RCP} }}={E_0}\left( {{r_{xx}}{{\hat {e}}_x}+i{r_{yy}}{{\hat {e}}_y}} \right)={r_{yy}}{E_0}\left( {{{\hat {e}}_x}+i{{\hat {e}}_y}} \right),$$
(13a)

and

$${\left. {E_{{\operatorname{co} }}^{r}} \right|_{LCP}}={E_0}\left( {{r_{xx}}{{\hat {e}}_x} - i{r_{yy}}{{\hat {e}}_y}} \right)={r_{yy}}{E_0}\left( {{{\hat {e}}_x} - i{{\hat {e}}_y}} \right).$$
(13b)

For the reflected wave is in + Z axis direction, \(\hat {e}={\hat {e}_x} - i{\hat {e}_y}\) and \(\hat {e}={\hat {e}_x}+i{\hat {e}_y}\) are the expressions of the RCP and LCP unit wave, respectively, Eq. (12a), (12b) shows that the cross-polarized electric field components in the two composite LP reflected waves will both form a CP reflected wave with the same handedness as the CP incident wave, which is just a co-polarized reflected wave; moreover, at RCP incidence, the co-polarized reflection coefficient \({r_{++}}\) is just equal to \(i{r_{xy}}\), and at LCP incidence, \({r_{ - - }}\)is equal to \(- i{r_{xy}}\). In addition, Eq. (13a), (13b) expresses that the co-polarized electric field components will form a CP reflected wave with handedness opposite to the CP incident wave, which is just a cross-polarized reflected wave, and the cross-polarized reflection coefficients \({r_{ - +}}\) and \({r_{+ - }}\) are both equal to \({r_{yy}}\) and \({r_{xx}}\). Now we can know that the root cause of the circular polarization conversion is the anisotropy and symmetry of the polarization converter structure, and an appropriate anisotropy leads to \(\left| {{r_{xy}}} \right|=1\), and the symmetry ensures that \({r_{++}}=i{r_{xy}}\) and \({r_{ - - }}= - i{r_{xy}}\). If an orthogonal anisotropic polarization converter can realize linear polarization conversion at LP incidence, it can realize reflection-type circular polarization conversion at CP incidence at the same time. In fact, based on various orthotropic anisotropic metasurfaces, a series of ultra-wideband and high-efficiency reflective polarization converters have been proposed in recent years, but they were only regarded as a linear polarization converter in a number of previous literatures [6,7,8,9,10,11,12,13,14,15,16]. Now we can announce that this kind of polarization converters can all be regarded as a reflective circular polarization converter at the same time.

4 Conclusions

In this work, a high-efficiency and ultra-wideband reflective polarization converter was proposed based on an orthotropic anisotropic metasurface. Both the simulated and measured results show that the polarization converter can realize linear polarization conversion at x- and y-polarized incidences in the frequency range from 8.77 to 24.71 GHz, and keep the handedness of the reflected wave the same as that of the incident wave in this band, moreover, \({r_{++}}=i{r_{xy}}\) and \({r_{ - - }}= - i{r_{xy}}\). We have explained the root cause of these polarization conversions in detail. Due to the anisotropy of the polarization converter structure, a phase difference between the two reflection coefficients ruu and rvv was generated, when the phase difference was close to 180°, the anticipated linear polarization conversion was realized at y- and x-polarized incidences; in addition, the reflection coefficients at y- and x-polarized incidences were completely equal for the symmetry of the polarization converter structure, and the reflection-type circular polarization conversion was realized at the same time. Finally, an effective conclusion has been obtained, and it is shown that the previously proposed various reflective linear polarization converters based on orthotropic anisotropic metasurfaces can all be used as a reflective circular polarization converter at the same time.