1 Introduction

Plasmonics have emerged as an inevitable field in nanophotonics because of its unique property of overcoming the limitation of conventional optics to confine light at nanoscale dimensions due to diffraction limit. The ability of subwavelength confinement of light by plasmonic devices results from the strong localization of surface plasmon polaritons (SPPs) at the interface of a metal and a dielectric [1]. Surface plasmon polaritons are quantized surface waves propagating along a metal–dielectric interface and result from coherent oscillation of the free electrons of a metal on being excited by an electromagnetic field [2]. Among the SPP-guided systems, metal–dielectric–metal (MDM) waveguide-coupled structure has emerged to be one of the promising candidates because of its wide range of applications in integrated photonic devices such as optical switches [3, 4], power splitters [5], waveguide couplers [6, 7], optical filters [8, 9], impedance matching elements [10], tunable filters, sensors [11] and many others. Cavity-coupled MDM waveguide systems resulting in asymmetric resonances have also attracted considerable attention for very efficient sensing as well as switching applications [12, 13]. Because of the compact sizes and capability to sustain subwavelength optical modes, these components are emerging as efficient devices for nanoscale integrated optics.

A MDM waveguide side coupled to one or more nanostubs [14–17] is the most promising candidate among the other waveguide cavity-coupled systems because of certain advantages which include its small size, simple structure, easy fabrication and its insensitivity to surface roughness of the metal other than supporting deep subwavelength modes and their wide range of applications in nanophotonics. The transmission characteristics of these types of nanostructured photonic systems can be investigated using different powerful simulation tools which are implemented by full-wave simulation methods in time and frequency domain (finite difference time domain [18, 19] and finite difference frequency domain method, respectively), or finite element method (FEM) at the expense of computational time and cost. Scattering matrix theory is still another approach of solving such systems, but it also requires the use of full-wave methods for extracting the coefficients at the waveguide junctions. Another method of analysis is the application of transmission line theory which involves the analogy of MDM waveguide structures with microwave transmission lines [20–22]. Though the transmission line theory was previously developed for lossless plasmonic waveguides, a revised model of transmission line theory incorporating plasmonic dissipation has been reported by Pannipitiya et al. [23, 24], yielding fairly accurate results and eliminating all computational complexities.

In this paper, the properties of a subwavelength plasmonic nanostub side coupled to a MDM waveguide are investigated using transmission line theory applicable for dissipative plasmonic waveguides and its performance as an optical switch is explored in detail. The organization of the paper is as follows. Structure description, dispersion characteristics of MDM structures and mode propagation through a subwavelength MDM waveguide are demonstrated in Sect. 2. Section 3 deals with the numerical approach considered for theoretical analysis of our device. In Sect. 4, field transmission through the structure in wavelength regime is analyzed and further explanation of the device response is provided using complex plane and phase analysis and by using the concept of impedance matching. Also, influence of the stub geometry on spectral response is analyzed in detail, for obtaining correct device parameters for various nanophotonic applications. Finally, the operation of the device as an optical switch and its performance evaluation is illustrated in Sect. 5.

2 Device description and dispersion characteristics

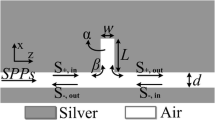
Our device is simply a T-shaped dielectric waveguide embedded within suitable metal. Precisely, it comprises of a subwavelength stub located perpendicularly to a plasmonic waveguide which is a simple MDM structure. The dielectric core of the waveguide is also of subwavelength dimension, surrounded by semi-infinite metallic cladding. The nanostub can be described as a finite branch of the MDM structure. The device in consideration is depicted in Fig. 1. The stub S of length d and width w s is coupled normally to the waveguide of width w wg. Our analysis is independent of the dimension along z-axis. When the plasmonic waveguide is excited by an electromagnetic (EM) field, localized transverse magnetic surface plasmon polariton (TM-SPP) mode will be generated at both the metal–dielectric interfaces of the waveguide. This mode will propagate through the waveguide along the x-direction. If the thickness of the dielectric layer is less than the skin depth of the SPPs in the dielectric, then the localized TM-SPP modes of each metal–dielectric interfaces will couple with each other [25].

Fig. 1
figure 1

3D schematic representation of a nanostub coupled to a metal–dielectric–metal waveguide

Full size image

The propagation of the TM-SPP mode along the waveguide is governed by the complex propagation constant \( \beta = k \times n_{\text{eff}} \), where n eff is the effective refractive index of the MDM waveguide and \( k = \frac{2\pi }{\lambda } \) where λ is the wavelength of the incident photons. The effective refractive index of the MDM waveguide as expressed in Eq. (1) is strongly dependent on frequency or wavelength and can be obtained by coupled mode approximation [26, 27]:

$$ n_{\text{eff}} = \sqrt {\varepsilon_{\text{d}} } \left( {1 + \frac{\lambda }{{\pi w_{\text{wg}} \sqrt { - \varepsilon_{\text{m}} } }}\sqrt {1 + \frac{{\varepsilon_{\text{d}} }}{{\varepsilon_{\text{m}} }}} } \right) $$
(1)

where ε m and ε d are the permittivity of the metal and dielectric, respectively. The complex and frequency-dependent metal permittivity can be obtained using the Drude–Lorentz model [28], which yields fairly accurate results in the wavelength range of 0.2–2 μm, and is given by:

$$ \varepsilon_{\text{m}} (\omega ) = 1 - \frac{{f_{0} \omega_{\text{p}}^{2} }}{{\omega^{2} + i\omega\Gamma _{0} }} + \sum\limits_{j = 1}^{\text{m}} {\frac{{f_{j} \omega_{\text{p}}^{2} }}{{\omega_{j}^{2} - \omega^{2} - i\omega\Gamma _{j} }}} $$
(2)

Here the first two terms collectively describe the well-known Drude model contributing to the free-electron effects (intraband transition), and the final term in summation represents the bound-electron effects (interband transition) accounting for the Lorentz oscillations. ω p denotes the plasma frequency, m is the number of interband transitions with oscillator strength f j , frequency ω j and damping constant Г j . f 0 and Г0 represent the oscillator strength and damping constant associated with the intraband transition.

Wavelength dependency of the complex parts of the metal permittivity of three noble metals, silver (Ag), gold (Au) and aluminum (Al), commonly used for surface plasmon generation, is shown in Fig. 2. The value of plasma frequency, damping constants and oscillator strengths for various metals has been obtained from [29]. The real part of the metal permittivity which describes the frequency-dependent behavior of the metal with electromagnetic field is shown in Fig. 2a, and the imaginary part accounting for the absorption of the EM energy within the metal is depicted in Fig. 2b. Aluminum is seen to exhibit a distinct absorption peak due to interband transition (Lorentz oscillation) at 0.81 μm approximately (1.53 eV). The absorption peak is generated as a result of the superposition of bound-electron absorption over the intraband absorption. Silver and gold depict almost identical behavior, silver exhibiting higher negative values of real part of the metal permittivity, which is a desirable feature for surface plasmon excitation. In view of this, silver has been considered as the metallic substrate for further analysis of the device in present work.

Fig. 2
figure 2

Spectral dispersion of a real and b imaginary parts of metal permittivity using Drude–Lorentz model

Full size image

A silver–air–silver plasmonic waveguide is considered in Fig. 3a, and the real part of the effective refractive index is plotted as a function of wavelength in Fig. 3b for varying waveguide core thickness. As the real part of the effective refractive index determines the guided wavelength through a MDM waveguide, the guided wavelength is seen to be higher at very low wavelengths and then decreases monotonously at higher wavelengths. Moreover, a strong increase in the guided wavelength for very narrow waveguides is observed, resulting from the enhanced coupling of the SPPs at both metal–dielectric interfaces. The propagation length of the SPPs can be determined through the imaginary part of the effective refractive index through the relation:

Fig. 3
figure 3

a Schematic of a MDM waveguide. Contour plot of b real part of the effective refractive index of the MDM waveguide and c propagation length of the SPP mode with variation in wavelength and waveguide width. d Longitudinal (E x ) and e transverse (E y ) electric field profile of the fundamental SPP mode calculated by considering waveguide width of 50 nm using FDTD software

Full size image
$$ L_{\text{spp}} = \frac{\lambda }{4\pi }\left( {\frac{1}{{\text{Im} (n_{\text{eff}} )}}} \right) $$
(3)

The propagation length (L spp) is plotted for varying subwavelength dimensions of the waveguide core thickness in Fig. 3c as a function of wavelength. Stronger localization of SPPs leading to higher values of propagation depth at higher wavelengths is observed. Greater confinement of SPPs within the dielectric for larger dimensions of waveguide core thickness is evident because of the reduction in energy buildup within the metal.

MDM waveguide supports two types of SPP modes: the symmetric mode and the antisymmetric mode. In the subwavelength regime (w wg ≪ λ), the symmetric mode is cutoff and only a single antisymmetric mode is supported by the MDM waveguide [30–32]. For this fundamental antisymmetric SPP mode of the single-mode MDM plasmonic waveguide, the longitudinal and transverse components of the electric field are simulated as shown in Fig. 3d, e, respectively. The longitudinal mode (E x ) is seen to be strongly localized at the interface, with almost symmetric field penetration at each metal–dielectric interfaces, while the transverse electric field component (E y ) is concentrated within the dielectric layer owing to the negligible field penetration into the metal.

3 Numerical approach

The properties of MDM waveguide coupled to a single stub resonator have been investigated using transmission line theory developed and revised by Pannipitiya et al. [23, 24]. For simplification of the model, the fringing field effects and higher-order decaying modes near the waveguide stub junction have been neglected. The concept of transmission line theory applied for investigating systems consisting of deep subwavelength MDM waveguides is built on the analogy between subwavelength MDM structures and microwave transmission lines. Also, the electric and magnetic fields of the plasmon mode are analogous to the voltage and current in transmission line, respectively. Employing the above analogies, the MDM waveguide can be represented by an infinite transmission line with characteristic impedance [33]:

$$ Z_{\text{wg}} = \frac{{E_{{y\;{\text{dielectric}}}} w_{\text{wg}} }}{{H_{{Z\;{\text{dielectric}}}} }} = \frac{{\beta_{\text{wg}} w_{\text{wg}} \eta }}{{k\varepsilon_{\text{d}} }} $$
(4)

where η is the wave impedance in vacuum (377 Ω). Here β wg is the propagation constant within the waveguide with thickness w wg. The stub that is a finite branch of MDM waveguide can also be represented by a finite transmission line of length equal to the stub height and characteristic impedance \( Z_{\text{s}} = \frac{{\beta_{\text{s}} w_{\text{s}} \eta }}{{k\varepsilon_{\text{d}} }} \), β s being the constant of propagation in the stub. These representations are valid as long as w wg and w s are much less than the order of wavelength. Phase shift at the stub end induced by SPP reflection is included by terminating Z s with a load impedance Z L given by \( Z_{\text{L}} = \sqrt {\frac{{\varepsilon_{\text{d}} }}{{\varepsilon_{\text{m}} }}} Z_{\text{s}} \). This equation had been derived by equating reflection coefficient using circuit theory analysis and Fresnels complex amplitude reflection coefficient and under the consideration that the stub end is represented by a short-circuited line [34–36]. An equivalent transmission line network diagram employing series connection of Z wg and Z s and its simplified circuit model using the concept of effective impedance given by Eq. (5) [37] is well explained and illustrated in [24].

$$ Z_{\text{stub}} = Z_{\text{s}} \frac{{Z_{\text{L}} - iZ_{\text{s}} \tan \left( {\beta_{\text{s}} d} \right)}}{{Z_{\text{s}} - iZ_{\text{L}} \tan \left( {\beta_{\text{s}} d} \right)}} $$
(5)

where β s d constitutes the phase shift of the surface plasmon wave with propagation constant β s.

Finally, the transmittance of the MDM waveguide coupled to a single nanostub can be evaluated using transfer matrix method and is expressed as:

$$ T = \left| t \right|^{2} = \left| {1 + \frac{{Z_{\text{stub}} }}{{2Z_{\text{wg}} }}} \right|^{ - 2} \exp \left( { - \frac{L}{{L_{\text{spp}} }}} \right) $$
(6)

where t denotes the complex transmission coefficient and L spp is the propagation length of SPP wave. The term within the modulus contributes to the interference of the incident field and the EM field reflected from the stub. The exponential term accounts for the SPP damping. The phase associated with the transmitted wave can be determined as:

$$ \theta = \tan^{ - 1} \left[ {\frac{{\text{Im} (t)}}{{\text{Re} (t)}}} \right] $$
(7)

4 Investigation of spectral response in MDM waveguide-coupled nanostub

4.1 Resonance response analysis

Light transmission through the device is demonstrated in Fig. 4a with device parameters w wg = w s = 50 nm, d = 300 nm, L = 400 nm, air as the dielectric and silver as the metal. Two dips are observed in the transmittance spectrum at wavelengths of 0.62 and 1.78 μm for the chosen device parameters. The occurrence of these dips is attributed to the fact that at these particular wavelengths light energy from the waveguide gets coupled to the stub and forms standing waves within the stub thereby trapping the EM energy and hence restricting light at the output. However, different amount of energy coupling takes place for these two different wavelengths. Maximum energy is coupled at the resonant wavelength. But exact resonant wavelength cannot be determined directly from the spectral characteristics owing to the asymmetric nature of the lineshape. The asymmetric response is confirmed by the spiral nature of the complex amplitude transmission Argand diagram (CATAD) shown in the inset as against circular CATAD for symmetric lineshapes. In case of these asymmetric responses, the resonant wavelength is determined to be the one for which the relative intensity for two dielectric media is maximum. Here, relative intensity has been defined as \( \left| {{\text{d}}I/I} \right| \) where dI is the difference of the intensities for two different dielectric medium and I is the intensity of the reference dielectric. This relative intensity is plotted in Fig. 4a considering air and water as two dielectric media, and the maximum intensity is obtained at 1.78 μm. Moreover, from Fig. 4b, the effective impedance of the stub is seen to play an important role in the spectral lineshape response of the device. The effective impedance is observed to have finite values only at the wavelengths in the vicinity of transmittance dips and possesses a maximum value at the resonant wavelength (1.78 μm). Thus, resonance condition of the device occurs through impedance matching phenomenon. The Argand diagram for the effective impedance of the stub is plotted in the inset of Fig. 4b. The inner circle of smaller diameter corresponds to the narrower dip at 0.62 μm (low effective impedance value), while the outer circle of larger diameter accounts for the broader transmission dip (high impedance value). The phase of the transmitted wave is also plotted in Fig. 4b. The phase depicts sharp transition at wavelengths of 0.62 and 1.78 μm (wavelengths of transmission minima), transition at 0.62 μm being sharper.

Fig. 4
figure 4

a Transmission spectrum of the structure and relative intensity plot considering two dielectric media; complex amplitude transmission Argand diagram is shown in the inset. b Spectral behavior of the effective impedance of the stub and phase of the transmitted wave; Argand diagram for the effective impedance is shown in the inset

Full size image

4.2 Influence of structural parameters: cavity width and cavity height

The spectral response for the waveguide-coupled nanostub structure can be engineered by alteration of the stub geometry. The alteration of system response due to variation of the stub width (w s) investigated is shown in Fig. 5. The transmission spectrum is plotted for different stub widths in Fig. 5a varying from 30 to 130 nm by a step of 10 nm, with other parameters unaltered as in Fig. 4. The spectrum is observed to become narrower with simultaneous increment in the value of the transmission peak with increase in the stub width for the range of the values of w s considered in the simulation. Change in stub width causes alteration in the number of stationary waves formed within the stub leading to modified energy trapping which finally results in the shift of the transmission dips in the spectrum. The full width half maxima (FWHM) of the spectral response calculated from the transmittance plots of Fig. 5a and depicted graphically in the inset of Fig. 5b reveal obvious reduction in FWHM with increase in stub width. Since the spectral width can be tuned by alteration of the stub width, the device may be looked upon as a structural-dependent tunable filter. A contour plot showing the transmittance for variation of stub width and wavelength band is shown in Fig. 5b. The contour confirms the narrowing down of the spectrum with increment in stub width. The contour also reveals occurrence of very high value of transmittance approximately in the wavelength range of 700–1000 nm. Two arbitrary wavelengths 760 and 880 nm are chosen from this wavelength band, and the variation of transmittance with stub width at these two wavelengths is simulated in Fig. 5c. At both the wavelengths, the transmission initially increases with stub width and then monotonically decreases at higher values of stub width. The intersection of the two curves corresponding to stub width of 86.6 nm reveals identical transmission at both the wavelengths. For this fixed value of w s = 86.6 nm, the transmittance spectrum is plotted for the wavelength range of 760–880 nm and is shown in the inset of Fig. 5c. Almost flat transmission spectrum reveals the application of the device as band-pass filter within this particular spectral range for this particular choice of stub width. This procedure of achieving band-pass performance is equally applicable for any other value of stub width over a different wavelength band.

Fig. 5
figure 5

a Transmission characteristics for different stub widths. b Contour plot of transmission for varying stub width and varying wavelength. FWHM for varying stub width is plotted in the inset. c Transmittance versus stub width plots for two fixed wavelengths. Almost flat transmission response (band-pass behavior) is shown in the inset

Full size image

The variation of transmittance with stub height and wavelength is also simulated as shown in the contour plot of Fig. 6a. The plot depicts that at any particular wavelength, the transmission switches alternatively between maximum and minimum values. This oscillatory behavior of transmittance between high and low values can be explained as follows. The phase shift of the reflected wave is affected by the phase change as the wave traverses the length of the stub (d) and phase shift at the stub end. Hence, by changing the stub height, the phase of the reflected wave changes. The total phase shift between this reflected and transmitted wave causes constructive or destructive interference resulting in alternate occurrence of maxima and minima. The density of this occurrence of maxima and minima is seen to be higher at lower wavelengths in the wavelength range considered. Two fixed wavelengths, visible wavelength 633 nm and zero dispersion wavelength 1550 nm, are considered, and 2D plots of transmittance versus stub height are plotted for these two wavelengths as shown in Fig. 6b, c, respectively. At both these wavelengths, the amplitude of oscillation between maxima and minima gradually decreases at higher values of stub height. The frequency of switching between low and high transmission values with increasing stub height decreases at higher wavelengths. Repetitive nature of dips and peaks in the transmission spectrum allows us to choose a proper stub height as per requirement of maximum and minimum transmission for a predefined wavelength value. Moreover, reverse engineering, i.e., selecting a wavelength for predefined stub height, is also possible with the help of the contour plot depicted in Fig. 6a.

Fig. 6
figure 6

a Transmission contour plot for varying stub height and wavelength. 2D plots of transmission characteristics for varying stub heights for b 633 nm and c 1550 nm wavelength, respectively

Full size image

5 Switching application

Incorporation of a semiconductor material in the cavity of a cavity-coupled plasmonic waveguide leads the device to act as an on–off switch [4], as tuning the absorption coefficient of semiconductor material results in optical gain which is utilized for on–off switching application. Tuning the absorption coefficient of certain semiconductor quantum dots by optical excitation also leads to active control of optical signals [38, 39].

CdSe quantum dot (QD)-doped silicon dioxide has been used as a filling material within the cavity for switching application [40], where absorption of the optical energy by CdSe QD-doped silica in the presence of optical pumping provides the switching mechanism. Though II–VI semiconductor quantum dots like CdSe and ZnSe provide stronger exciton–photon interaction and higher exciton binding energies compared to IV and III–V semiconductors, CdSe is difficult to be tuned in UV and is toxic and hence not preferable for medical applications and ZnSe shows considerable degradation [41]. ZnO having direct wide bandgap energy of 3.37 eV at room temperature and having the advantage of large exciton binding (60 meV), long-term stability, high defect resistance, biocompatibility, environmental friendliness and low material cost is preferable over CdSe and ZnSe for practical applications [41]. In view of these advantages, ZnO QDs have been considered as the active material for switching application in present analysis.

5.1 Principle of switching and performance evaluation of the optical switch

For switching operation with our device, we consider the nanostub to be filled with ZnO QDs, whose absorption coefficient (imaginary part of the refractive index) is intensity dependent and thus can be tuned by optical pump excitation. Numerically, the refractive index of the active material can be represented as n + iκ, κ being the absorption coefficient whose zero and nonzero values, respectively, determine the ‘off’ and ‘on’ switching states.

At resonant wavelength, transmission is almost zero as seen from the transmission characteristics of Fig. 4a. The wavelength corresponding to transmission minima (i.e., resonant wavelength) can be tuned to the desired value by optimizing the stub geometry. By proper choice of the stub parameters, the resonant wavelengths of 1.55 and 1.3 μm (minimum dispersion windows) have been obtained and transmission spectrum in both the presence and absence of optical pumping has been plotted for these two resonant wavelengths in Fig. 7. In the absence of optical pumping (corresponding to κ = 0), the transmission is significantly low, whereas in the presence of pumping (corresponding to κ ≠ 0), the on-resonance transmission increases owing to absorption of photons by the active material. The transmission enhancement due to absorption in the cavity can be explained as follows. The bandgap of different semiconductor materials (ZnO QD in this case) is dependent on its refractive index (r.i.) [42]. Modulation of its absorption coefficient (κ) through optical pump excitation results in alteration of refractive index (since r.i. = n + iκ) and consequent modulation in the bandgap of the material. Thus, in the presence of pumping, the bandgap energy is so modified that the photons are absorbed by an intraband transition process in the QDs, unlike in the absence of pumping where the energy of the photons is smaller than that of the QDs for absorption to take place [40]. Moreover, from [40], the on-resonance transmission can be deduced from: \( T = \left[ {{{Q_{e} } \mathord{\left/ {\vphantom {{Q_{e} } {(Q_{e} + Q_{o} )}}} \right. \kern-0pt} {(Q_{e} + Q_{o} )}}} \right]^{2} \), where Q e and Q o are the quality factors associated with power escape through the waveguide and internal loss of the cavity, respectively. When the material absorbs photon energy in the presence of pumping, more energy builds up within the cavity causing an increase in Q e and hence finally enhances the transmittance. Thus, the presence and absence of optical pump in the presence of the active material within the stub provide the on–off switching mechanism of the device.

Fig. 7
figure 7

Transmission characteristics for κ = 0 (without pumping) and κ = 0.1 (with pumping) for resonant wavelength a 1.55 and 1.3 μm. For both figures, the device parameters are chosen to be L = 400 nm and w wg = w s = 50 nm and d = 147 nm in (a) and 120 nm in (b)

Full size image

The transmission characteristics during both ‘on’ state and ‘off’ state are plotted for two communication wavelengths 1.55 and 1.3 μm in Fig. 7a, b, respectively. The stub parameters chosen for obtaining resonant wavelength of 1.55 and 1.3 μm are w s = 50 nm, d = 147 nm and w s = 50 nm, d = 120 nm, respectively. The value of the absorption coefficient for ‘off’ and ‘on’ state is taken as κ = 0 and κ = 0.1, respectively. If T on-res and T off-res be defined to be the transmittance values during the ‘on’ and ‘off’ states, respectively, at the resonant wavelength (λ res), then difference of transmittance value between these two states (∆T) at λ res can be represented as

$$ \Delta T = T_{\text{on - res}} - T_{\text{off - res}} $$
(8)

which has been calculated to be 25 dB and 24 dB from Fig. 8a, b, respectively. High value of ∆T reveals efficient switching operation provided by the device.

Fig. 8
figure 8

a “On–off” ratio (T on/T off) is plotted against absorption coefficient (κ) with device parameters L = 400 nm and w wg = w s = 50 nm and d = 147 nm (solid curve) and 120 nm (dotted curve) corresponding to two chosen wavelengths. Plot of transmittance (T) versus wavelength (λ) for κ = 0 and κ on-max = 0.22 and 0.19 in (b) and (c), respectively

Full size image

The variation of “on–off” ratio [(η = T on/T off), T on and T off being the transmission values during on and off states] with absorption coefficient (κ) is plotted in Fig. 8a for two values of λ res 1.3 and 1.55 μm. Maximum value of “on–off” ratio (η max) has been obtained at κ = 0.19 and κ = 0.22 for 1.3 and 1.55 μm resonant wavelength, respectively. Let κ on-max be the value of κ at η max when η is evaluated for transmission response plotted at the resonant wavelength. η max has been determined to be 16.62 (28.11 dB) and 14.28 (26.59 dB) at values of κ on-max = 0.22 and 0.19, respectively. Transmittance (T) versus wavelength (λ) for κ = 0 (representing the off state) and κ = κ on-max (representing the on state) is plotted in Fig. 8b, c, respectively. Values of κ on-max taken to simulate these two plots are 0.22 and 0.19 as obtained from Fig. 8a. Moreover, ∆T max (value of ∆T at λ res for κ on-max) have been evaluated to be 28 and 27 dB at two resonant wavelengths 1.55 and 1.3 μm, respectively.

As already discussed earlier, ∆T is an important factor in realizing the switching efficiency of the device. The performance of the optical switch can also be expressed in terms of η res and ∆T through the relation:

$$ \eta_{\text{res}} = 1 + \frac{{\Delta T}}{{T_{{{\text{off}} - {\text{res}}}} }} $$
(9)

where (T on-res/T off-res) defines the parameter η res. This equation confirms that a high value of ∆T would yield a higher on–off ratio at the resonant wavelength, for a fixed value of T off-res. Thus, appreciable values of ∆T as obtained from the plots of Fig. 8b, c manifest efficient switching efficiency of the device. However, for different resonant wavelengths, different sets of optimized structural parameters would lead to different values of T off-res and hence η res would no longer retain proportional relation with ∆T as in Eq. (9). Moreover, lower value of T off along with higher ∆T, resulting in a higher value of η res, would provide enhanced switching performance of the device.

5.2 Switching performance for different resonant wavelengths in the infrared (IR) spectral range

Different physical quantities, namely κ on-max, η, η max, η res, ∆T and ∆T max, are defined in Sect. 5.1 to evaluate the performance of the optical switch. All these values have been determined at two fixed telecommunication wavelengths for the corresponding set of optimized device parameters. In order to gain an insight into the nature of variation of these parameters with change in resonant wavelength, κ on-max, η max, ∆T max and η res-max (value of η res for κ on-max) are calculated and tabulated in Table 1 for different infrared resonant wavelengths (λ res) considered in the range 1–1.9 μm. Values of stub height (d) which has been varied in order to achieve the corresponding values of λ res are also provided in the table, other device dimensions being the same as that in Figs. 7 and 8.

Table 1 Optimized parameters for efficient switching at different infrared wavelengths
Full size table

The calculated data in Table 1 reveal a proportional relation of κ on-max with resonant wavelength. Also, ∆T max increases at higher values of λ res. Since ∆T max is a measure of switching efficiency, the device performance as an optical switch enhances with red shift of the resonant wavelength.

The more or less oscillating nature of η max with change in λ res may be accounted to the oscillating nature of transmittance with variation in d (Fig. 6), since d had to be varied for obtaining the corresponding value of λ res. Though the value of ∆T max increases with increase in resonant wavelength, η res-max decreases with λ res due to the simultaneous increment of T off-res along with ∆T max.

6 Conclusions

To summarize, we have thoroughly investigated the optical field transmission through a subwavelength MDM waveguide coupled to a nanocavity, where the transmission characteristics can be tailored by tuning the stub dimensions. We have also shown that by varying the stub width we can tune the spectral bandwidth, leading the device to be used as a tunable band-pass filter. On the other hand, alteration of the stub height causes the transmission to shift between maxima and minima, and this phenomenon has been used to select the desired resonant wavelength for switching operation. If the stub is filled with an active semiconductor medium like ZnO quantum dots accompanied by excitation through an optical pump, present theoretical simulations are found to support enhancement of transmission at the resonant wavelength (on state) compared to a lower value of transmission in the absence of pumping (off state). It is to be noted that the light launching within the waveguide is challenging due to the subwavelength dimension in the present scheme. However, overcoming this limitation, novel coupling schemes have been recently reported [43, 44]. In conclusion, present simulation-based quantitative analysis provides the optimized parameters for efficient switching at different resonant wavelengths which will definitely benefit the future research community interested in further exploring this field theoretically as well as experimentally.