1 Introduction

Dielectric elastomer (DE) has emerged as one of the appealing soft active materials for diverse applications, ranging from soft actuators [1–7], bio-electronics [8], flexible sensors [9, 10], and adaptive optics [11, 12], to energy generators [13]. A variety of configurations of DE transducers have been developed, including tube-shaped, stacked, rolled, diaphragm-like, and actuators with interconnected chambers [14–19].

Carpi et al. [14, 15] firstly developed such DE actuators with interconnected chambers, called hydrostatically coupled or granularly coupled actuators. These actuators comprise an active chamber and a passive chamber, where fluid or granular materials are mediators with which to connect the active and the passive parts. Wang et al. [16] presented a computational model to analyze such type of actuators. Rudykh et al. [17] investigated the electromechanical actuation of a single thick-wall DE balloon. They showed that the abrupt changes in the balloon sizes, i.e., the so-called snap-through instability, can be triggered based on the Ogden model. This snap-through instability was also harnessed by Keplinger et al. [18, 19] by connecting a DE balloon with a reservoir with pretty large volume and achieved a record of 1,692 % areal expansion. They also analyzed the actuation and instability of this giant voltage-actuated deformation [18, 19].

Such actuators with interconnected chambers are also adopted in other fields, particularly those microfluidic devices. Piyasena et al. [20] used soft lithography technique to fabricate voltage-driven microfluidic actuators from poly (dimethylsiloxane) (PDMS), which consists of a passive supply balloon and an active expansion balloon. The electroactive polymer actuator utilizes electroosmosis to create hydraulic pressure. Figallo et al. [21] designed and fabricated twelve interconnected micro-bioreactor wells as controllable cellular microenvironment. Interconnected microfluidic network can also be used to develop a lab-on-chip platform for continuous monitoring of gene expression in living cells [22]. The monograph by Müller and Strehlow [23] presents comprehensive results on thermodynamics of rubber balloons.

We theoretically study the actuation and instability of two interconnected DE balloons. The two balloons may have the same volume or finite volume ratio. The interconnected balloons have the same inflated pressure, and the air inside the balloons is governed by ideal gas equation. We probe the actuating behaviors of the balloons under various inflated pressure and different environment pressure.

2 Model and formulation of interconnected DE balloons

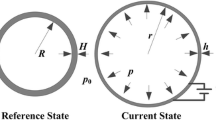
Figure 1 shows schematically the analysis model and various states of two interconnected DE balloons. The system consists of an active balloon and a passive balloon, which are interconnected via a channel with negligible volume. In Fig. 1a, two balloons are stress-free and the interior and the ambient environment of balloons shares the same pressure in this reference state. The initial radii of these two sphere balloons are R 1 and R 2, respectively.

Fig. 1
figure 1

Schematic of three states of two interconnected balloons, one active and the other passive. a Reference state. The initial radii of the two balloons are R 1 and R 2, respectively. In this state, the difference between pressure inside and outside of balloons is zero. The environment pressure outside balloons is denoted by P env; b Inflated state. The interconnected balloons are inflated by a pressure difference ΔP = P 0. The radii of the two balloons expand to r 1p and r 2p, respectively; c Actuated state. The inflated active balloon is subject to a voltage, Φ; the radius of the active balloon increases to r 1 while the radius of the passive balloon shrinks to r 2. The pressure difference between the inside and outside of balloons drops to P

Full size image

The excess pressure inside the two balloons is increased until it reaches the value P 0. This initial inflation process is pressure-controlled. The radii of balloons are inflated, respectively, to r 1p and r 2p in this state, and λ ip = r ip/R i (i = 1, 2) are the two corresponding stretches. The physically stable triples of P 0, λ 1p, and λ 2p are uniquely determined by the ideal gas law and the thermodynamic model describing the elastomers [23] and the fact that the balloons are inflated until the pressure reaches P 0. Note that upon decreasing the pressure, different triples are stable due to the nonmonotonic pressure-deformation characteristics. Adopting the commonly used Gent model to describe the hyperelasticity of the elastomer, the elastic free energy is expressed as [24]

$$ W\left( \lambda \right) = - \frac{{\mu J_{\lim } }}{2}\log \left( {1 - \frac{{2\lambda^{2} + \lambda^{ - 4} - 3}}{{J_{\lim } }}} \right), $$
(1)

where J lim denotes the extension limit of the polymer network and is assigned as a material constant herein; μ is the shear modulus. True stress in the inflated state, σ, is calculated from Eq. (1) as σ = λ/2∂W/∂λ. A coefficient 1/2 appears because two hoop stretches are identical for a spherically symmetrical system concerned here, and the balloon is in a state of equal biaxial stress. Draw the free-body diagram of a half balloon in the current state and balance the forces: \( 2\pi {\kern 1pt} r_{\rm p} h\sigma = \pi {\kern 1pt} r_{\rm p}^{2} P_{0} \). One has

$$ P_{0} = \frac{2h}{{r_{\rm p} }}\sigma , $$
(2)

where h = H/λ 2p is the thickness of the membrane in current state, while H is the thickness in the reference state. Substituting expression of σ into Eq. (2) and after algebraic manipulation, Eq. (2) can be rewritten as

$$ f\left( {\lambda_{\rm ip} } \right) - \frac{{P_{0} R_{\rm i} }}{\mu H}\lambda_{\rm ip}^{2} = 0\quad \left( {i = 1,\;2} \right), $$
(3)

where f(λ) = 2J lim (λ − λ −5)/[J lim − (2λ 2 + λ −4 − 3)].

Plotting the P 0 versus volume or equivalently P 0 versus λ p exhibits the typical N-shaped curve as shown in Fig. 2. For small or large P 0, such as states A and C in Fig. 2, one P 0 corresponds to only one stretch. For intermediate value of P 0 designated by state B, there are three values of stretches corresponding. The smallest of these three stretches (marked state B) is reached when a process increases the pressure starting from very small values of stretch. The other possible stable stretches corresponding to P 0 can only be reached if the pressure previously exceeded the critical pressure at the local maximum or the system is not pressure-controlled, a situation which we exclude, to uniquely identify the starting conditions of actuation. After reaching the starting pressure P 0, the system is sealed containing Nk B T = 4π/3(P0 + P env)(R 31 λ 31p  + R 32 λ 32p ) particles, assuming an ideal gas law for the filling medium with N the total particle number.

Fig. 2
figure 2

Inflation curve of the interconnected balloons. The inflated pressure is normalized to \( \frac{{P_{0} R_{2} }}{\mu H} \), where μ and H are shear modulus and thickness of the balloons; R 2 is the radius of the passive balloon. Three representative points, corresponding, respectively, to \( \frac{{P_{0} R_{2} }}{\mu H} = 0.6,\;1.2\;{\text{and}}\;1.3 \), are marked by A, B, and C in the figure. The peak of the inflation curve determines the critical snap-through pressure, \( \frac{{P_{\text{snap}} R_{2} }}{\mu H} = 1.254 \) and λ snap = 1.4. When the inflated pressure is greater than this critical value, the balloon undergoes mechanical snap-through and jumps to a large deformation state as indicated by the dashed line

Full size image

Then, balloon one is connected with an external battery to supply a voltage, Φ, and is called “active balloon,” while balloon two is not and called “passive balloon” in the following discussion. The radius of the active balloon increases from r 1p to r 1 as shown in Fig. 1c, and an amount of charge is accumulated on the surface of the balloon. Denoting λ 1 = r 1/R 1 the stretch of the balloon in this current state and D the true electric displacement, an additional electrical free energy is added to Eq. (1) to prescribe the total free energy of the balloon, which reads

$$ W\left( {\lambda_{1} ,D} \right) = - \frac{{\mu J_{\lim } }}{2}\log \left( {1 - \frac{{2\lambda_{1}^{2} + \lambda_{1}^{ - 4} - 3}}{{J_{\lim } }}} \right) + \frac{{D^{2} }}{2\varepsilon }. $$
(4)

Here, the ideal dielectric model [25–27] is adopted to approximate the electrostatic energy, and ε is the dielectric permittivity of the elastomer. Replacing Eq. (1) by Eq. (4), results in a modified equilibrium equation for the active balloon

$$ f\left( {\lambda_{1} } \right) - \frac{{PR_{1} }}{\mu H}\lambda_{1}^{2} - 2\frac{{\varepsilon \varPhi^{2} }}{{\mu H^{2} }}\lambda_{1}^{3} = 0. $$
(5)

The force balance equation of the passive balloon remains the same form as Eq. (3) except replacing P 0 by P and λ 2P by λ 2, i.e.,

$$ f\left( {\lambda_{2} } \right) - \frac{{PR_{2} }}{\mu H}\lambda_{2}^{2} = 0. $$
(6)

Note that, in Eqs. (5) and (6), the pressure difference between inside and outside of the balloons is varied to P due to the volume change caused by electrostatic deformation. Actuating and harnessing the snap-through instability of the active balloon is possible because the second passive balloon can sustain the variation of pressure as the active balloon expands or deflates. Given a specific inflation pressure, P 0, the pressure P in Eq. (5) and Eq. (6) is not an independent variable. Assuming the process from inflated state to the current actuation state is an isothermal process, the gas inside the balloons behaves like an ideal gas, which dictates that

$$ \left( {P_{0} + P_{\text{env}} } \right)\left( {\frac{4\pi }{3}r_{1\rm p}^{3} + \frac{4\pi }{3}r_{2\rm p}^{3} } \right) = \left( {P + P_{\text{env}} } \right)\left( {\frac{4\pi }{3}r_{1}^{3} + \frac{4\pi }{3}r_{2}^{3} } \right). $$
(7)

Equation (7) can be recast into

$$ \left( {P_{0} + P_{\text{env}} } \right)\left( {m^{3} \lambda_{1\rm p}^{3} + \lambda_{2\rm p}^{3} } \right) = \left( {P + P_{\text{env}} } \right)\left( {m^{3} \lambda_{1}^{3} + \lambda_{2}^{3} } \right), $$
(8)

with m = R 1/R 2 being the radius ratio of the two balloons in the reference state. Thus far, Eqs. (3), (5), (6), and (8) constitute the governing equations of the interconnected DE balloons.

3 Results and discussions

Figure 2 plots the inflation curve of the balloons as normalized pressure versus hoop stretch of the passive balloon. The deformation of the two balloons is assumed to be homogeneous and spherically symmetric. Two hoop stretches are assumed to be identical as λ θ = λ φ = λ = r/R, and the radial stretch is defined as λ r = 1/(λ θ λ φ) = λ −2 due to incompressibility. The pressure is normalized by shear modulus of polymer, μ, initial thickness of balloon, H, and initial radius of the passive balloon, R 2, and given as \( \frac{{P_{0} R_{2} }}{\mu H} \). Solving the nonlinear equation for a typical value of J lim = 100, Eq. (2), and plotting λ 2 versus \( \frac{{P_{0} R_{2} }}{\mu H} \), Fig. 2 is obtained readily. The inflation curve of the active balloon is identical to the passive balloon, except a radius ratio defined above, m, would enter, and this is shown in Fig. 3a. In this paper, only Figs. 2, 3a are pressure-controlled inflation curves where gas particle number is varying, while for all other figures, the gas particle number is fixed and the system is in an isolated environment. The N-shaped curve of Fig. 2—going up, going down, and then going up—indicates that mechanical snap-through occurs at \( \frac{{P_{\text{snap}} R_{2} }}{\mu H} = 1.254 \) and λ snap = 1.4. This mechanical snap-through instability is well understood for inflating a rubber balloon [28]. Three representative points, designated by A, B, and C, are marked in Fig. 2. They correspond to a state far below snap-through, at the verge near the snap-through, and a state beyond the snap-through instability. We carefully classify three different states and probe in details the actuation and instability of the active balloon under three different inflation conditions.

Fig. 3
figure 3

Actuation curves of interconnected balloons with same radii under various environmental and inflated pressure. The points marked by stars are the critical points for electromechanical instability, while the points marked by crosses are the critical points for loss of tension. Normalized environmental pressure, \( \frac{{P_{\text{env}} R_{2} }}{\mu H} \), is varied to 1, 0.2, and 0.015. The dashed line in Fig. 3c represents the path of snap-through induced by voltage

Full size image

Introducing a dimensionless voltage, \( \frac{\varPhi }{H}\sqrt {\varepsilon /\mu } \), Fig. 3 plots the actuation curves of two interconnected DE balloons with the same radius. Actuation curves of the active balloon for varied normalized environment pressure, \( \frac{{P_{\text{env}} R_{2} }}{\mu H} = 1.0,\;0.2,\;{\text{and}}\;0.015 \), are plotted in Figs. 3a, b, c, respectively, for comparison. The curves in Fig. 3 with three different inflation pressure are differentiated by various colors, corresponding to the processes that actuate the balloons from three inflated states marked by A, B, and C in Fig. 2. Actuating the balloons under a large ambient pressure, e.g., \( \frac{{P_{\text{env}} R_{2} }}{\mu H} = 1.0 \) in Fig. 3a, the stretch of the active balloon increases with increasing voltage but the pressure inside the balloon decreases. Starting from inflation states below mechanical snap-through, i.e., states A and B, the voltage-induced deformation goes up monotonically until terminates at the points marked by crosses, where the pressure difference between inside and outside the balloon vanishes and loss of tension instability occurs. Starting from inflation state beyond mechanical snap-through marked by C, however, balloons undergoes a very steep stretch–voltage curve where the stretch approaches the limit approximately seven for the parameters considered here. Loss of tension is not an issue for this case but the system would fail to work due to electrical breakdown for such a large deformation. Electrical breakdown would destroy actuators. So far four mechanisms are identified that are responsible for electrical breakdown: electrical, electromechanical, thermal, and partial discharge [29]. Among these, the thermal effect of destroying dielectric elastomer due to the heat generated by current leakage, as well as the weakening of dielectrics due to partial discharge, is recognized as two main reasons [29].

Decreasing the environment pressure to 0.2, the stretch–voltage curves for states A and B are not monotonic anymore, and they firstly go up, reach a peak, and then go down. The peaks represent an instability called electromechanical instability (EMI) or an electrical snap-through [30]. The curves terminate at crosspoints where loss of tension occurs. In reality, upon ramping up the voltage, the actuation process is limited by EMI and can not reach loss of tension. Loss of tension can only be reached if the voltage is at some point decreased again. Decreasing the ambient pressure further to a state approaches vacuum, say \( \frac{{P_{\text{env}} R_{2} }}{\mu H} = 0.015 \), actuation curves from states A and B. For the blue line in Fig. 3c, the actuation is limited by the EMI point marked by star as in Fig. 3b: The balloon undergoes electrical snap-through to an unstable state, and eventually it ruptures or breaks down electrically; the path from the EMI point to the loss of tension point is unstable, and it can not be realized in practice. If actuation starts from state B as given by the red line in Fig. 3c, ramping up voltage reaches the EMI point, snaps through suddenly as indicated by the dashed line to a stable state, and then continues to deform before the loss of tension occurs. In other words, actuating the balloon from a state near the verge of mechanical snap-through can trigger electrical snap-through that can be harnessed to obtain giant deformation, which is stable and achievable in physics. This was firstly proposed and implemented both theoretically and experimentally by Keplinger et al. [18, 19], where a balloon was connected with a chamber with pretty large volume to produce a giant areal expansion.

To probe in details the underlying physics behind the snap-through phenomenon shown in Fig. 3c, we fix m = 1, P env R 2/μH = 0.015, P 0 R 2/μH = 1.2 (exactly the parameters of the red line in Fig. 3c), and plot the actuation curve in Fig. 4. Figure 4a gives the pressure–stretch curve of the active balloon at various voltages. The dashed line is the pressure–stretch curve of the air derived from the ideal gas equation, Eq. (8). The dashed line intersects with the pressure–stretch curve of the membrane, defining different equilibrium states. As voltage ramping up, the active balloon expands and pressure drops; thus, the pressure–stretch curve lowers. When the applied voltage reaches the critical value, 0.36, the dashed line tangents to the solid line, defining two stable states O and O’ as in Fig. 4a. Figure 4b plots the voltage-stretch curve of the active balloon and indicates the snapping-through from O to O’. Figure 4c presents the pressure–stretch curve of the passive balloon. The arrows in Fig. 4b, c indicate the discontinuous jump path when voltage is ramped up—active balloon snaps and expands suddenly while the passive balloon deflates rapidly to accommodate this deep pressure drop and volume variation.

Fig. 4
figure 4

Actuation curve of two interconnected balloons with identical radii under the conditions P env R 2/μH = 0.015 and P 0 R 2/μH = 1.2. a pressure–stretch curve of the active balloon at various voltages. The dashed line is the pressure–stretch curve of the air deduced from the ideal gas equation. b voltage-stretch curve of the active balloon. The dashed line indicates snap-through from point O to point O’. c The pressure–stretch curve of the passive balloon. When the active balloon snaps and expands suddenly, the passive balloon deflates from O to point O’ as indicated by the arrow

Full size image

Figure 5 depicts the actuation curves for two balloons with different radii, m = R 1/R 2 = 0.5, for example. Note that, if a small active balloon is connected with a larger passive balloon, and is activated from a state near the edge of mechanical snap-through, snap-through can be realized to produce stable large deformation regardless the ambient pressure. In Fig. 5b for \( \frac{{P_{\text{env}} R_{2} }}{\mu H} = 1.0 \), only the actuation starting from state B can snap through to a stable state, while for \( \frac{{P_{\text{env}} R_{2} }}{\mu H} = 0.05 \) in Fig. 5c, snap-through can be realized and harnessed either for states A or B. In all these figures, the actuation curves for state C change little. Also note that for the discontinuous snap-through actuation curve from state B, when the voltage is turned off from a snapped state, the active balloon can not restore its initial inflated state but retain a stable state with pretty large deformation, ~6 as determined by the intersection of the red line with the horizontal axis.

Fig. 5
figure 5

Actuation curves of interconnected balloons with different radii under various environmental and inflated pressure. The radius of the active balloon is half of that of the passive balloon, i.e., R 1/R 2 = 0.5. Normalized environment pressure, \( \frac{{P_{\text{env}} R_{2} }}{\mu H} \), is varied to 1 and 0.05. The dashed lines represent the path of snap-through induced by voltage

Full size image

4 Concluding remarks

We present a theoretical analysis of the actuating performance of two interconnected balloons, one active and the other passive. The assembly can work as an actuator, in the sense that applying a voltage to the active balloon can produce deformation, and the passive balloon supplies gas to compensate the pressure drop inside the active balloon due to deformation. Radius ratio, environment pressure, as well as the inflation state from which the electrical activation sets in, affect the electromechanical performance of the system. Letting the system work in nearly vacuum condition, or actuating the balloon near the verge of mechanical snap-through, may induce discontinuous voltage-actuated deformation, which is physically achievable and can be utilized to produce large actuation stroke.