1 Introduction

The industrialized world requires new and sophisticated technologies, for example, from bio-science to aerospace. As other breakthroughs in science, these new technologies desire new devices constructed from novel materials. Due to some of their outstanding properties, these structures are quite crucial to industry. Carbon nanotubes (CNTs) are hollow cylinders, built by hexagonal unit cells, shaped by carbon atoms which were found by Iijima in 1991 [1]. Their important mechanical, electrical and thermal properties made these nanostructures distinctive and consequently made them very interesting for a large number of advanced applications as either stand-alone nanomaterials or reinforced composite materials. An increasing attention in the scientific and industrial community has been drawn because of the special mechanical and physical properties of CNTs such as lightness, strength, and their wide potential application in nano-engineering. Several investigations have been applied on finding and improving the properties of CNTs. Prediction of Young’s modulus (of about 1 TPa) and tensile strength (of up to 63 GPa) for CNTs were of the most important objectives of these studies [2]. These investigations can be divided into two groups of experimental and computational approaches. Molecular dynamics (MD) and continuum mechanics procedures such as the finite element method (FEM) have been the most prevalent and predominant computational approaches to evaluate the behavior of CNTs [3, 4]. The investigation on buckling behavior of CNTs is crucially important due to their plentiful application in various mechanical aspects for which several related studies are presented in the following.

In 2003, Wang et al. [5] conducted the simulation of the compression deformation of single-walled carbon nanotubes (SWCNTs) applying the Tersoff–Brenner potential to depict the interactions of atoms in CNTs. Their investigations revealed that by increasing the radius of CNTs, the Young’s modulus of CNTs decreases. Moreover, there is a considerable difference between the Young’s modulus of zigzag CNT and the armchair type. Their results also showed that there are two different buckling modes for SWCNTs. Studying the differences between the buckling behavior at microscopic scale and that at nano-scale was another aspect of their investigations. Then in 2004, Tserpes and Papanikos [6] proposed a three-dimensional finite element (FE) model for armchair, zigzag and chiral SWCNTs. In their suggested models, nodes are placed at the location of carbon atoms and the bonds between them are modeled using three-dimensional elastic beam elements. Their results obtained the dependence of elastic moduli on diameter and chirality of the nanotubes. Moreover, it was proven that the elastic moduli of the SWCNTs increase while the tube diameter is increased. Finally, they showed that the Young’s modulus of chiral SWCNTs is found to be larger than that of the armchair and zigzag SWCNTs. In 2004, Xiao et al. [7] developed a model for the prediction of mechanical properties of defect-free CNTs, applying the modified Morse potential with an analytical molecular structural model. Their results indicated that the tube diameter and helicity are two factors correlated with Young’s modulus of CNTs. In addition, Young’s moduli of both armchair and zigzag CNTs increase monotonically and approach Young’s modulus of graphite when the tube diameter is increased. Afterwards, Chang et al. [8] obtained the analytical solution for the critical buckling strain of single-walled achiral CNTs under axial compression based on a mechanic molecular model. Their results revealed the fact that zigzag tubes are more stable than the armchair tubes with the same diameter. Moreover, they found that the van der Waals interaction has little effect on the critical buckling strain for double-walled carbon nanotubes (DWCNTs). Yao et al. [9] investigated the bending buckling behavior of SWCNTs, DWCNTs, and multi-walled carbon nanotubes (MWCNTs) in 2007. They applied a modified FE method, at which the simulations were performed to examine the buckling behavior of CNTs under bending deformation. The simulation results proved that a clear relationship between the critical bending curvature and the diameter of CNTs can be established. Parvaneh et al. [10] conducted a study on the impact of various vacancy defects on the critical buckling loads and strains in CNTs under axial compression in 2008. They performed their investigation by applying a new structural model in a commercial FE code (Abaqus). The model used in their research was a combination of other structural models designed to eliminate the deficiencies inherent in individual approaches. Their results indicated that vacancy defects in the CNTs can most likely be modeled as cut-outs of the shells. They finally compared their results of the structural model with those from MD simulations in which the outputs got along well with the present model. In 2010, Kang et al. [11] investigated the buckling behavior of intramolecular junctions (IMJs) under axial compression by conducting FE analysis and MD simulations. After studying the strain rate effects in the MD simulation, they concluded that there was no sensitive connection between the critical compressive strain and the strain rate of relatively low range. Nevertheless, the critical compressive strain is highly dependent upon the strain rate under high speed compression. Consequently, the results revealed that despite chirality of the IMJs, the critical compressive strain is dependent upon the length and radial dimension of the IMJs. Then in 2011, Wong and Vijayaraghavan [12] studied the buckling characteristics of several SWCNTs with curved axes (imperfectly straight) performing MD simulations. They concluded that the load-carrying capacity of curved CNTs is significantly lower compared to their perfectly straight counterparts. Recently in 2012, Fakhrabadi et al. [13] investigated the buckling behavior of CNTs with different dimensions. In order to study the mentioned properties of these nanostructures, they applied a molecular mechanics based FE method. They finally came to the conclusion that there is an opposite correlation between the length and apex angle of CNTs and the elastic and critical compressive force. The effect of defects on the buckling behavior of SWCNTs and MWCNTs was investigated by Ghavamian and Öchsner [14] in 2012 as well. Their study was as well based on the FE method. In detail, they constructed two fundamental CNTs in their perfect form; then the buckling behavior of CNTs was evaluated by comparing their critical loads obtained from the simulation and analytical calculations. As a result, their findings indicated that the existence of any curvature in the structure of nanotube decreases their buckling strength. Li et al. [15] continued the study on the MD simulation performed to inspect the compressive behavior of IMJs. Their findings showed that there is a direct correlation between increasing the critical strain and loading rate. Moreover, with increasing the tune length, the instability mode of the IMJ transfers from shell buckling to column buckling.

Although the mentioned reviews on previous investigations have been comprehensive and substantial progress in the study of the mechanical properties of CNTs has been obtained, the investigation of hetero-junction CNTs is only rarely addressed. Hetero-junction CNTs are connections of two dissimilar tubes where pentagon-heptagon pair defects play an important role in the transition region. The basic shape of hetero-junction CNTs is constructed when a pair of heptagon and pentagon is introduced to the perfect hexagonal graphite lattice after connecting two nanotubes with different chiralities. These specific CNTs are crucially important based on their significant characteristics. Although extensive investigations have been done to study the atomic structure as well as electrical properties of IMJs and great achievements have been accomplished, mechanical responses of IMJs, buckling behavior in particular, which could be effective on developing their electronic properties and electric conductance, are still not fully explored [11, 16]. The aim of the actual research is to continue and broaden the previous investigations, and to study the buckling behavior of CNTs, straight hetero-junctions in particular. Moreover, comparison between the mechanical properties (especially the buckling behavior) of homogeneous CNTs and straight hetero-junctions has been taken under special consideration. Within this work, buckling is understood as a structural instability which results in the sudden failure of a mechanical component. This instability is characterized by the loss of structural stiffness and is susceptible for slender and thin-walled structures as in the case of the considered CNTs.

2 Methodology

2.1 Geometric definition

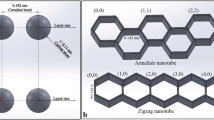
Carbon nanotubes are presumed to be a hollow cylinder shaped structure based on the major similarity between a CNT and graphene atomic structure. Such a CNT can be imagined by rolling a graphene sheet into a cylinder with diameters ranging from 1 to 50 nm and lengths over 10μm. The atomic geometry of CNTs is defined by the chiral or roll-up vector \(\vec{C}_{h}\) and the chiral angle θ. The chiral vector is introduced by two unit vectors, \(\vec{a}_{1}\) and \(\vec{a}_{2}\), and two integers, m and n (steps along the unit vectors), as it is presented by the following equation [17]:

$$ \vec{C}_{h} =\ \vec{a}_{1} +\ \vec{a}_{2}. $$
(1)

The basic configuration of CNTs can be defined according to the chiral vector or angle by which the sheet is rolled into a cylinder, and categorized as armchair, zigzag, or chiral. An armchair CNT is constructed in terms of chiral vector (m=n) or in terms of chiral angle (θ=30∘). In the case of (θ=0∘) or (m=0) the zigzag CNT is obtained, and finally a chiral CNT is formed if (0∘<θ<30∘) or (m≠n≠0) [3].

Based on the following equation, the diameter of the CNT can be calculated:

$$ d_{\mathrm{CNT}} = a_{0} \sqrt{m^{2} +mn+ n^{2}} /\pi, $$
(2)

where \(a_{0} = \sqrt{3} b\) and b=0.142 nm is the length of the C–C bond [17].

A homogeneous CNT can be viewed as a rolled graphene sheet with specified width, as shown in Fig. 1, while a hetero-junction CNT, treated as a wrapped graphene sheet with specific geometry, is constructed by connecting two CNTs through the introduction of a Stone–Wales defect (pentagon and heptagon defect) into the connecting region, as illustrated in Fig. 2.

Fig. 1
figure 1

(a) Schematic of a graphene sheet and definition of geometrical parameters for describing a CNT. (b) Side view of the (6,6) CNT

Full size image
Fig. 2
figure 2

Pentagon–heptagon pair defects of (5,5)–(7,7) hetero-junction carbon nanotube

Full size image

Hetero-junction CNTs are categorized based on the configurations of their two fundamental CNTs. For instance, a hetero-junction CNT constructed by connecting a (5,5) armchair CNT and a (7,7) armchair CNT is referred to as a (5,5)–(7,7) hetero-junction CNT [15]. When investigating the mechanical properties, for example the buckling behavior, of straight hetero-junction CNTs, we also compare them with those of their constituent CNTs. The geometry of a hetero-junction CNT is more sophisticated as compared with that of a CNT owing to the irregular structure of the connecting region. The axis of the wider CNT is defined as the reference axis of the junction due to the fact that the two constituent CNTs of a hetero-junction are able to align on a planar surface. The overall length of a hetero-junction is defined as (see Fig. 3):

$$ l= l_{\mathrm{thin}} + l_{\mathrm{connecting}} + l_{\mathrm{wide}} $$
(3)

where l thin, l connecting, and l wide are the lengths of the thinner tube, the connecting region and the wider tube, respectively. By the geometries of the connected CNTs, the length of the connecting region can be approximately obtained based on the simplified geometry of a right-angled triangle as [18]:

$$ l_{\mathrm{connecting}} = \frac{\sqrt{3}}{2} \pi( d_{\mathrm{wide}} - d_{\mathrm{thin}} ) $$
(4)

where d wide and d thin are the diameters of the wider and thinner tubes, respectively (see Figs. 3 and 4).

Fig. 3
figure 3

Simulation of an SWCNT as a space-frame structure, adapted from [6]

Full size image
Fig. 4
figure 4

Different types of straight hetero-junctions: (a) (3,3)–(5,5); (b) (5,5)–(7,7); (c) (5,5)–(10,10); (d) (9,0)–(12,0); (e) (7,7)–(9,9); (f) (12,0)–(16,0); (g) (11,0)–(12,0); (h) (9,9)–(11,11); (i) (14,14)–(16,16)

Full size image

As the junction may consist of two homogeneous CNTs with different diameters, we define the diameter of junction as the average diameter of both CNTs, i.e.,

$$ \overline{d} = \frac{1}{2} ( d_{\mathrm{wide}} + d_{\mathrm{thin}}). $$
(5)

The aspect ratio of the junction is defined as [15]

$$ \eta= \frac{l}{\overline{d}}. $$
(6)

Another way to characterize a hetero-junction can be based on the difference in carbon atoms per cross section. This difference is calculated by subtracting the number of carbon atoms of the thinner tube’s cross section from those of the wider tube’s cross section.

Our modeling approach follows the idea first proposed in [19] where the theory of classical structural mechanics was extended into the modeling of carbon nanotubes: In a carbon nanotube, carbon atoms are bonded together by covalent bonds which have their characteristic lengths and angles in a three-dimensional space. It was then assumed that carbon nanotubes, when subjected to loading, behave like space-frame structures. Thus, the bonds between carbon atoms are considered as connecting load-carrying generalized beam members, while the carbon atoms act as joints of the members. This idea is illustrated in Fig. 3.

In this study, the models of hetero-junction CNTs were constructed by the CoNTub software [20, 21], a computer program for determining the coordinates of hetero-junctions between two arbitrary carbon nanotubes. Defining the chirality and the length of the tubes, the spatial coordinates of the C-atoms and the corresponding connectivities (i.e. the primary bonds between two nearest-neighboring atoms) were calculated. Then the gathered data was transferred to a commercial finite element package, where C–C bonds were modeled as circular beam elements [11]. These elements are based on Timoshenko’s beam theory with shear deformation effects included and the ability of torsional deformations around the longitudinal axis. Afterwards the FE analyses were conducted and buckling behavior of different straight hetero-junction CNTs was taken under special investigation. In order to have a precise and plausible conclusion, we examined various types of straight hetero-junctions with different chirality as illustrated in Fig. 4.

The phenomenon of buckling is in its simplest form a specific kind of elastic instability in a slender structure that occurs under certain compressive loads. In the basic theory of elasticity, the critical buckling load of a structure, as presented in Eq. (7), i.e. the famous Euler formula of buckling load, depends on its shape and geometry, as well as its boundary conditions [22]:

$$ P_{\mathrm{cr}} = \frac{n^{2} \pi^{2} EI}{(KL)^{2}} $$
(7)

where P cr is the critical buckling load, K is the effective length constant, E is the Young’s modulus of the material, and L is the length of the tube. In the above equation, n represents the buckling mode and I is the structure’s second moment of area. As the classical structure of CNTs is mostly presented by a hollow cylinder, Eq. (8) can be used to obtain analytical results for straight CNTs as:

$$ I=\pi \bigl[ ( d+t )^{4} - ( d-t )^{4} \bigr]/64, $$
(8)

in which t is the thickness of the tube’s shell and d represents the diameter of the pertaining tube [22]. It should be noted that different assumptions for the shell thickness t can be found in literature, see for example [19, 23] and a detailed discussion of this problem in [24]. We assign here the same value as in [19, 23] where the thickness of a single-walled carbon nanotube was assumed to be the same as the interlayer spacing of graphite (0.34 nm).

2.2 Material parameters and boundary conditions

In this paper, we investigate buckling properties of hetero-junction CNTs under cantilevered boundary conditions in which one end is fully fixed and the other end is completely free and exposed to a compressive axial load. Figure 5 illustrates hetero-junction CNTs under two different types of cantilevered boundary conditions. For one case, the wider tube is completed fixed at one side and for the other case, the thinner tube is completely fixed. Considering these two different cases, we are able to obtain a wider spectrum of results.

Fig. 5
figure 5

(5,5)–(7,7) straight hetero-junction CNT’s first mode under buckling load in original and buckled form with two different types of cantilevered boundary conditions: (a) wider tube fixed, and (b) thinner tube fixed

Full size image

For macroscopic space frame structures in the scope of classical structural mechanics, the material properties (e.g. Young’s and shear moduli) and element sectional parameters (e.g. second moment of area) can be easily obtained from basic material tests and calculated based on the given dimensions of the cross-sectional area. However, for the carbon–carbon bonds of carbon nanotubes, no such classical tests or geometric derivations are available to define the properties of the equivalent beam elements. Therefore, we assume the same values for the equivalent beam elements as in the approach proposed in [19, 23, 25]. These effective material and geometrical properties were obtained in the mentioned references based on a molecular mechanics approach where carbon nanotubes were regarded as a large molecule consisting of carbon atoms with atomic nuclei treated as material points. Their motions are regulated by a force field, which is generated by electron–nucleus interactions and nucleus–nucleus interactions, and usually expressed in the form of steric potential energy. This steric potential energy is in general the sum of contributions from bond stretch interaction, bond angle bending, dihedral angle torsion, improper (out-of-plane) torsion, and a non-bonded van der Waals interaction in the case of multi-walled tubes, see Fig. 6. Li et al. applied in [19] the harmonic approximation and used further simplification to derive the energy expressions. These remaining energy expressions were equated with the corresponding energy expressions for a beam obtained from classical structural mechanics, see Fig. 6. As a result, the stiffness parameters of the beam for elongation, bending and torsion were obtained as function of three force field constants (available in literature) for stretching, bond angle bending and torsional resistance [26].

Fig. 6
figure 6

Equivalence of molecular mechanics and structural mechanics for covalent and non-covalent interactions between carbon atoms. Molecular mechanics model (left) and structural mechanics model (right), adapted from [25]

Full size image

These introduced constants and the element properties are listed in Table 1.

Table 1 Material and geometric properties of C–C covalent bonds [27]
Full size table

3 Results and discussion

We investigated the buckling properties of straight hetero-junctions and their constituent homogeneous CNTs, by obtaining their critical load (to be more precise, the first positive buckling mode since this is in practical applications the most critical one) analytically and computationally applying an FE approach. Afterwards, both methods were compared in the case of the homogeneous CNTs in order to have some kind of validation of the FE approach. For the FE method, first, homogeneous zigzag and armchair CNTs with lengths of 15 and 15.4 nm, respectively, were simulated by a commercial finite element package (MSC.Marc). Then, by introducing arbitrary compressive point loads to one of the CNT’s end, the buckling behavior of the CNTs was investigated for two types of cantilevered boundary condition (one end fixed and the other end free). Finally, the computations yielded the critical buckling loads of the CNTs. In the second approach, the homogeneous CNTs were presumed to be hollow cylinders, so that by using Eq. (7) their critical loads were evaluated as an analytical solution. In this equation we considered K=2 for the cantilevered case. The simulated homogeneous CNTs and their characteristics are presented in Table 2.

Table 2 Characteristic of simulated homogeneous CNTs
Full size table

The next stage was to simulate the hetero-junction CNTs, and then compare their FE results with those of constituent homogeneous CNTs. We believe that the critical buckling load of hetero-junction CNTs was supposed to be something between the critical buckling loads of their fundamental homogeneous CNTs. Figure 7 illustrates three different CNTs (two homogeneous and one hetero-junction CNT) which were compared with respect to their buckling loads. The buckling behavior of the middle hetero-junction CNT is evaluated for two types of boundary conditions. For the first condition, the wider tube is fixed, and for the second type the thinner tube is fixed.

Fig. 7
figure 7

Homogeneous (left- and right-hand side) and straight hetero-junction (middle) CNTs under buckling load

Full size image

The investigated straight hetero-junctions and their characteristics are listed in Table 3.

Table 3 Investigated straight hetero-junctions and their characteristics
Full size table

The relative difference between the analytical solution and FEM result is defined by the following equation:

$$\begin{aligned} &{\mathrm{Relative}\ \mathrm{difference}\ \mbox{in }\%} \\ &{\quad = \bigg\vert \frac{\mathrm{FEM}\ \mathrm{result}-\mathrm{analytical}\ \mathrm{solution}}{\mathrm{analytical}\ \mathrm{solution}} \bigg\vert \times100.} \end{aligned}$$
(9)

This difference is listed in Table 2 for each homogeneous CNT. Based on the results, it can be concluded that the analytical solutions are in good agreement with the computational outcomes. Hence, the assumption of considering hollow cylinders with the same length and wall thickness as homogeneous CNTs is a plausible approach so that the buckling behavior of CNTs could be well approximated. Having a closer look on the results, it can be also concluded that the buckling strength of hetero-junctions and their constituent CNTs increases by increasing the chiral number of both armchair and zigzag CNTs. Figure 8 supports that this claim is also applicable for hetero-junction CNTs.

Fig. 8
figure 8

(a) Change in critical buckling load (P cr) for armchair hetero-junctions with wider tube fixed. (b) Change in critical buckling load (P cr) for armchair hetero-junctions with thinner tube fixed. (c) Change in critical buckling load (P cr) for zigzag hetero-junctions with wider tube fixed. (d) Change in critical buckling load (P cr) for zigzag hetero-junctions with thinner tube fixed

Full size image

The comparison of the computational results of the critical buckling loads of straight hetero-junctions to their constituent CNTs under different boundary conditions is illustrated in Fig. 9. As it was already predicted, the critical buckling load of hetero-junction CNTs lies between the critical buckling loads of their homogeneous CNTs.

Fig. 9
figure 9

Computational results of critical buckling load of CNTs with (a) wider tube fixed, and (b) thinner tube fixed

Full size image

4 Outlook

In this research, several straight hetero-junction carbon nanotubes and their constituent homogeneous CNTs were simulated by an FE approach, and their mechanical properties, buckling behavior in particular, were evaluated through performing several computational tests with different boundary conditions. According to our investigations, the behavior of homogeneous CNTs under cantilevered boundary conditions follows the assumption of the classical Euler equation and the analytical solutions are in good agreement with the FE results. Towards achieving the most accurate results, the buckling behavior of straight hetero-junction CNTs was compared with those of their constituent homogeneous CNTs. It was shown that the critical buckling load of straight hetero-junction CNTs lies within the range of critical buckling load of their fundamental CNTs. Moreover, it can be also concluded that the buckling strength of straight hetero-junctions and their fundamental CNTs increases by increasing the chiral number of both armchair and zigzag CNTs. The findings of this research may have significant effects on further investigations of straight hetero-junction CNTs. In addition, it should be noted that other physical properties of hetero-junction CNTs should be investigated in the future works, as the investigation of buckling behavior in the presented paper was only the first step and more investigations in this direction are required to complete the characterization of hetero-junctions. There are other specific configurations of hetero-junction CNTs, for example, kink hetero-junctions, which we recommend for future research as well.