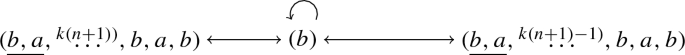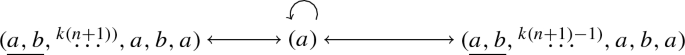Ejection–Collision Orbits in Two Degrees of Freedom Problems in Celestial Mechanics

Abstract

In a general setting of a Hamiltonian system with two degrees of freedom and assuming some properties for the undergoing potential, we study the dynamics close and tending to a singularity of the system which in models of N-body problems corresponds to total collision. We restrict to potentials that exhibit two more singularities that can be regarded as two kind of partial collisions when not all the bodies are involved. Regularizing the singularities, the total collision transforms into a 2-dimensional invariant manifold. The goal of this paper is to prove the existence of different types of ejection–collision orbits, that is, orbits that start and end at total collision. Such orbits are regarded as heteroclinic connections between two equilibrium points and are mainly characterized by the partial collisions that the trajectories find on their way. The proof of their existence is based on the transversality of 2-dimensional invariant manifolds and on the behavior of the dynamics on the total collision manifold; both of them are thoroughly described.

1 Introduction

In Celestial Mechanics, the aim is to understand the dynamical behavior of N particles which interact under their mutual Newtonian gravitational attraction. The dynamics of the problem turns out to be tremendously rich and, although all the studies devoted to this problem, it is still far from being completely well understood. A particular critical point is to identify the behavior near the total collision. The work of McGehee in 1974, (McGehee 1974), on the triple-collision behavior in the collinear three-body problem was essential to tackle this problem. He introduced a change of coordinates plus a scaling of time that allow to blow up the singularity due to triple collision and to obtain a two-dimensional invariant manifold, the total collision manifold, which is boundary for all of the energy surfaces. The flow extends smoothly over the total collision manifold, and the study of the dynamics on it allows to describe the bearings of the solutions passing close by. A later work of great relevance is due to Devaney in 1980, (Devaney 1980), where he used the McGehee’s coordinates plus a Sundman’s type regularization of the binary collisions as main tools to describe the dynamics on the collision manifold in the planar isosceles three-body problem. Since then, McGehee’s coordinates have been widely used to blow up the total collision in different three or four-body problems, see, for example, Simó (1981), isosceles three-body problem), Moeckel (1981, 1989), three-body problem), Simó and Lacomba (1982), Lacomba (1983), trapezoidal four-body problem), Kaplan (1999), collinear three-body problem), etc. In particular, Lacomba and Simó (1982) explore the same idea to introduce a blow-up of the infinity to study the total collision and infinity manifolds associated with several problems. A general reference for collisions in N-body problems is due to Saari (2005).

An intriguing question that becomes the purpose of this paper concerns with the so called ejection–collision orbits (ECO), that is, trajectories where all the bodies eject from a common point and after some time collide at the same point. ECO orbits have been studied in some of the three and four-body problems mentioned above, which can be written as a Hamiltonian dynamical system of two degrees of freedom. Here, we shall consider a general setting of Hamiltonian systems of two degrees of freedom that include all such problems that exhibit a common feature: the total collision manifolds have the same geometry and dynamical properties. In this general context, we will prove the existence of large sets of ECO and characterize them in terms of partial collisions. One way to obtain orbits tending to a total collision is starting with a central configuration, in which all the acceleration vectors are proportional (with the same constant) to the position vectors with respect the center of mass. If the bodies in a central configuration are released with zero initial velocity, each one follows a straight line until collision occurs. That is, the configuration goes homothetically to a total collision. The first nontrivial case was given by Euler in 1767, where three bodies are arranged in a line such that the spacing between them chosen in a suitable way (depending on the ordering of the masses and on the ratios of such masses). Lagrange, in 1772, found out that the same occurs if the particles are arranged in an equilateral triangle on a plane (regardless the values of the masses). Taking into account the possible orderings of the bodies, there are five central configurations of the three-body problem. It is worth mentioning that, in the context of the N-body problem, central configurations play an important role: on the one hand, from each planar central configuration a family of periodic solutions of the N-body problem (nonzero angular momentum solutions) is born; on the other hand, they influence the topology of the integral manifolds and govern the dynamics near collisions.

The problem of the existence of ECO has been tackled in different problems. Therefore, in order to frame the problem from a general setting and to review the state of art, we include here a summary of some relevant works.

We initiate our revision with the collinear three-body problem [see (McGehee 1974)] where McGehee introduces the coordinates that allow to transform the singularity of the total collision into a two-dimensional invariant manifold. The crucial point is the existence of two hyperbolic equilibrium points and the behavior of their invariant manifolds, as well as the existence of heteroclinic connections between them. Kaplan (1999) introduced a symbolic dynamics to describe orbits near triple collision (in such orbits the three bodies have close passages to triple collision without reaching it) that also allows to derive the existence of oscillatory motions. Tanikawa and Mikkola (2000a, 2000b), in the case of equal masses, include a regularization of the binary collisions to explore numerically the problem, computing large sets of solutions exhibiting certain sequences of binary collisions and ECO orbits.

The rectangular and the symmetric collinear four-body problems are Hamiltonian problems with two degrees of freedom that exhibit a total collision manifold with the same geometry and dynamics as the collinear three-body problem when applying the blow-up. Simó and Lacomba (1982), Lacomba (1983) use the McGehee’s coordinates to deal with the quadruple collision and to describe on the total collision manifold the heteroclinic connections between the equilibrium points (in terms of the mass parameter in the case of the collinear problem) and the dynamical consequences near the total collision. Later, Lacomba and Medina (2004) give proof of the existence of some specific ECO in this problem. Extensive numerical explorations can be found in Sekiguchi and Tanikawa (2004), Alvarez-Ramírez et al. (2019). Similar problems where analytical and numerical methods are used to study near total collision orbits are the trapezoidal four-body problem (Lacomba 1983; Alvarez-Ramírez et al. 2015; Alvarez-Ramírez and Medina 2020) and the rhomboidal four-body problem (Delgado Fernández and Pérez-Chavela 1991; Lacomba and Pérez-Chavela 1993).

A natural question that arises is to extend the previous results to the general three-body problem. As an intermediate problem, some authors considered the planar isosceles three-body problem in which two equal masses have symmetric positions with respect to the y axis, whereas the third body moves along this axis. A major difference with the collinear problem is that for the isosceles problem the triple collision manifold turns out to have three pairs of equilibria, two of them correspond to Lagrange equilateral configurations (which are saddles for all values of the masses) and the third pair to an Euler’s collinear one (which can be a sink or a source). Therefore, any orbit beginning or ending in triple collision must follow one of these configurations when approaching the singularity. Devaney (1980) analyzes the behavior of the invariant manifolds associated with the equilibrium points on the collision manifold. These points have associated complex eigenvalues and their invariant manifolds spiral on the total collision manifold. This allows him to prove analytically the existence of ECO in which the third mass goes through the center of mass of the other two exactly k times when the third mass is relatively small. Broucke (1979) previously had given numerical evidence of such type of orbits. Moeckel (1987) takes the study a step further, generalizing this fact to higher dimensional systems. He defines multidimensional spiraling manifolds and develops a criterion to decide when two spirals must intersect. Then, he proves that spirals of this type are created when an invariant manifold passes through a neighborhood of a hyperbolic equilibrium point with complex eigenvalues and that spiraling can work as a mechanism for producing intersections of invariant manifolds in high dimensions. In particular, Moeckel exploits this mechanism to prove the existence of infinitely many ECO of the isosceles three-body problem for a particular range of the mass ratios. We stress that Simó (1981) numerically showed the existence of such connections for large mass ratios as well.

It is well known that total collapse is only possible when the angular momentum vanishes. Moeckel in Moeckel (1984) considers the nonzero angular momentum case for the isosceles problem. He constructs an invariant set containing a variety of periodic orbits which exhibit close approaches to triple collision and startling changes of configuration. He describes this invariant set using symbolic dynamics and analyzes the case of small but nonzero angular momentum as a perturbation of the zero angular momentum case.

Concerning the general planar three-body problem and the qualitative behavior of orbits that pass close to the triple collision singularity, Sundman showed that orbits which experience triple collision tend asymptotically to one of the five central configurations, while Siegel proved that the set of orbits tending to a given central configuration is an analytic manifold. In a series of papers, Moeckel studies this problem widely. In Moeckel (1981), he shows the existence of orbits of the system whose $\alpha$- and $\omega$-limit sets are ECO homothetic orbits of Euler type configuration. This is done giving a fully rigorous discussion of the ultimate behavior of the stable and unstable manifolds in the triple collision manifold. Moreover, in Moeckel (1983), he analyzes the differences and implications considering the zero angular momentum case and the nonzero one and recovers some classical results due to Sundman and Siegel. In particular, Moeckel describes how these five manifolds fit together and how orbits which do not actually collide exhibit amazing changes of configuration when the three bodies are precisely close to triple collision. It is worth noting that in Moeckel (1987, 1989), he also proved the existence of ECO in the general planar three-body problem.

As a continuation of such series of papers, Moeckel in Moeckel (2007) proves, using symbolic dynamics, the existence of a chaotic invariant set for the general three-body problem which contains (among others) an infinite number of periodic orbits that show close approaches to triple collision and homoclinic and heteroclinic orbits connecting these periodic orbits, as well as escape, capture and oscillating solutions which are heteroclinic connections between infinity and any of the bounded near-collision orbits in the invariant set. The reader is addressed to the section entitled Some history (Moeckel 2007) for a discussion of the historical aspects of the planar three-body problem regarding orbits that exhibit close approaches to triple collision and also excursions near infinity.

In this paper, we focus on ECO and we want to remark that essential tools are the McGeehe’s coordinates, the total collision manifold (eventually in a Sundman’s type of regularized coordinates) and the dynamics on it governed by the behavior of the invariant manifolds associated with suitable hyperbolic equilibrium points and their intersections. In Simó and Llibre (1981), Llibre and Simó consider the N-body problem in $\mathbb {R}^d$ (being d any dimension) and characterize the transversality between these stable and unstable manifolds.

We present here a unified approach to prove analytically the existence of ECO in a general context including some of the problems from Celestial Mechanics mentioned above, which share several common properties that we generalize. More precisely, we consider the general system of ODE with two degrees of freedom:

$$\begin{aligned} \left\{ \begin{array}{rcl} {\dot{\mathbf{q}}} &{}=&{} A^{-1} \mathbf{p}, \\ {\dot{\mathbf{p}}} &{}=&{} \nabla U(\mathbf{q}), \end{array} \right. \end{aligned}$$

(1)

where $\mathbf{q}\in \mathbb {R}^2 \setminus \Delta$, $\mathbf{p}\in \mathbb {R}^2$, A is a diagonal constant matrix, $A=\mathop \mathrm{diag}\nolimits (a_1,a_2)$, $a_1$, $a_2>0$, and U is an homogeneous function of degree -1 on $\mathbb {R}^2\setminus \Delta$ singular in $\Delta$ that corresponds to all the possible collisions between the bodies in the context of an N-body problem. In particular, $\mathbf{q}=0\in \Delta$ corresponds to the total collision of all the bodies. In fact, we will refer to these singularities as partial or total collisions. The main goal of this paper is, under certain conditions of the potential U (that will appear later on), to prove the existence of an specific and large set of ECO which can be fully characterized by the sequence of partial collisions. More concretely, our main objectives are two: First, in a general setting of a Hamiltonian system of two degrees of freedom as in Eq. (1) with a potential with specific properties, to describe the main characteristics of its dynamics in which the collision manifold plays a key role. Second, to prove the existence and to give a classification of the ECO that can be obtained depending on the specific behavior of the 1D-invariant manifolds on the total collision manifold. The main results are given in Theorems 1–4.

As we have said, we will follow the ideas and methodologies briefly explained in the historical background due to McGehee, Devaney, Kaplan and Moeckel. In order to accomplish our aims, and for completeness of the work, we recover and prove in our more general setting some results already known in several of the three- and four-body problems mentioned above. This is done in Sects. 2 and 3, where we also introduce the necessary nomenclature for the proofs of the main theorems. In Sect. 4, we give proof of the existence and characterization of the type of ECO that the problem can exhibit.

2 General Setting

In this section, we give the conditions for the undergoing potential, U in (1), recall some particular examples, derive the regularized equations of the model and present the main features (we consider a suitable Poincaré section and define the collision manifold) that will play an essential role along the paper.

2.1 Statement of the Problem

We consider the problem defined by a Hamiltonian system with two degrees of freedom and Hamiltonian function

$$\begin{aligned} H(\mathbf{q},\mathbf{p}) = \dfrac{1}{2} \mathbf{p}^T A^{-1}\mathbf{p}- U(\mathbf{q}), \end{aligned}$$

(2)

$\mathbf{q}\in \mathbb {R}^2 \setminus \Delta \subset \mathbb {R}^2$, $\mathbf{p}\in \mathbb {R}^2$, A is a diagonal constant matrix, $A=\mathop \mathrm{diag}\nolimits (a_1,a_2)$, $a_1$, $a_2>0$, and U is an homogeneous function of degree $-1$ with some properties to be specified later. We can think of an N-body problem with the Newtonian potential (we will show some of these problems later), where $\mathbf{q}=0$ is a singularity that corresponds to the total collision of the bodies. The model was also considered, for example, by Martínez (2012, 2013) to study the existence of Shubart-like orbits. Here, we recall some known features of the model. For more details, see the aforementioned articles.

It is well known that the Hamiltonian H is a constant of motion for the N-body problem. We confine our attention to a fixed negative level of energy $H=h<0$. Thus, we have the following classical result.

Proposition 1

Consider the Hamiltonian system given by (2). Then, bounded motion can only occur for $h<0$.

The proof of this result is based on the Lagrange–Jacobi equation ${\ddot{I}}=U+2h$, where $I=\frac{1}{2} (\mathbf{q}^T A \mathbf{q})$ is the moment of inertia, and the fact that U is a homogeneous function of degree $-1$. See, for instance, Proposition 4.1 in Saari (2005).

Our goal is to study the existence of ejection–collision orbits (ECO from now on). Roughly speaking, an ejection orbit is an orbit that “starts” at $\mathbf{q}=0$, and a collision orbit is an orbit that “ends” at $\mathbf{q}=0$ (we give the precise definition later on). Therefore, it is mandatory to regularize the singularity $\mathbf{q}=0$. Regularization theory is a tool that allows us to transform a singular differential equation into a regular one, in such a way that we can analyze, under the regularized equations, the behavior of solutions leading to collisions.

We use McGehee’s coordinates (McGehee 1974) that not only regularize but perform a blow-up of the total collision $\mathbf{q}=0$. First, the following change to a polar-like set of coordinates r, $\theta$, is introduced:

$$\begin{aligned} r^2 = \mathbf{q}^T A\mathbf{q}, \qquad \mathbf{q} =r \mathbf{w}=r (A^{-1})^{1/2}(\cos \theta \; \sin \theta )^T. \end{aligned}$$

where $\mathbf{w}^T A \mathbf{w}=1$. Differentiating with respect to the usual time denoted by ${\tilde{\tau }}$, ${\dot{\mathbf{q}}}$ can be written as

$$\begin{aligned} {\dot{\mathbf{q}}} = \dot{r} \; \mathbf{w} + r\dot{\theta }\; \mathbf{u}, \end{aligned}$$

where $\mathbf{u}=(A^{-1})^{1/2}(-\sin \theta \; \cos \theta )^T$, so that $\mathbf{u}^T A \mathbf{u}=1$, $\mathbf{w}^T A \mathbf{u}=0$, and the radial component of the velocity is given by ${\dot{r}}=\mathbf{w}^T\mathbf{p}$. Next, variables v, u are defined as

$$\begin{aligned} v=r^{1/2}{\dot{r}}, \qquad u=r^{3/2}{\dot{\theta }}, \end{aligned}$$

so that $\mathbf{p}= r^{-1/2} A (v\;\mathbf{w} + u\; \mathbf{u})$.

Introducing the new coordinates $(r,v,\theta ,u)$ together with the scaling in time given by $d\tau = r^{-3/2} d{\tilde{\tau }}$, $\tau$ being the new time, the equations of motion become

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{\mathrm{d}r}{\mathrm{d}\tau } &{}=&{} rv, \\ \dfrac{\mathrm{d}v}{\mathrm{d}\tau } &{}=&{} \dfrac{v^2}{2}+u^2-V(\theta ), \\ \dfrac{\mathrm{d}\theta }{\mathrm{d}\tau } &{}=&{} u, \\ \dfrac{\mathrm{d}u}{\mathrm{d}\tau } &{}=&{} \dfrac{-vu}{2}+V'(\theta ), \end{array} \right. \end{aligned}$$

(3)

where $V(\theta )=r U(\mathbf{q})$ and $V'=dV/d\theta$. Clearly, the system of Eq. (3) can be extended to $r=0$, which is an invariant manifold of the system.

The energy relation $h=H$ in these new variables is written as

$$\begin{aligned} hr = \dfrac{1}{2} (v^2+u^2)-V(\theta ). \end{aligned}$$

(4)

Notice that for any fixed energy level $h<0$,

$$\begin{aligned} V(\theta ) + hr =0 \end{aligned}$$

(5)

is the zero velocity curve which limits the region in configuration space where the motion is admissible (see Fig. 1).

We want to prove the existence of ECO under certain conditions for the potential $V(\theta )$. As it is common in this kind of problems, the leading actors in the dynamics of the problem are the invariant manifold $r=0$, the existence of unstable equilibrium points and the behavior of the invariant manifolds associated with them. Next result states the hypotheses on the potential $V(\theta )$ to ensure the existence of the key ingredients.

Proposition 2

Assume that $V(\theta )$ is such that

$$\begin{aligned} V(\theta ) = \dfrac{c_b}{\sin (\theta _b-\theta )}+\dfrac{c_a}{\sin (\theta -\theta _a)} + {\widetilde{V}}(\theta ), \end{aligned}$$

where $\theta \in (\theta _a,\theta _b)$ for fixed values $\theta _a$, $\theta _b$ such that $0 < \theta _b-\theta _a \le \pi$, and

• $c_a>0$, $c_b\ge 0$ are constants, and $c_b=0$ if and only if $\theta _b-\theta _a =\pi$;

• ${\widetilde{V}}(\theta )>0$ is a smooth bounded function in $[\theta _a,\theta _b]$;

• $V(\theta )$ has only one non-degenerate critical value at $\theta =\theta _c\in (\theta _a,\theta _b)$, which is a minimum.

Then, the system of Eq. (3) has two equilibrium points, denoted by $E^{\pm }$, given by $r=0$, $v=\pm v_c$, $\theta = \theta _c$, $u=0$, where $v_c^2=2V(\theta _c)$. Both equilibrium points $E^{\pm }$ are saddle points, and there exist invariant unstable and stable manifolds $W^{u/s}(E^{\pm })$. Restricted to a fixed energy level $H=h$, $\dim (W^u(E^-))=1$, $\dim (W^s(E^-))=2$ and $\dim (W^u(E^+))=2$, $\dim (W^s(E^+))=1$.

See Martínez (2012) for the proof of the last proposition, and a discussion about the linear approximation of the invariant manifolds depending on $\theta _c$. Simó and Llibre (1981) give a condition on the potential at the critical point to prove the existence of transversal intersection of the invariant manifolds associated with total collision and total ejection in a general n-body problem of dimension d. In our case, the condition is fulfilled by the fact that $\theta _c$ is a non-degenerate critical value.

In Fig. 1, we show the configuration space $(q_1,q_2)$, which is a subset of the half-cone $\theta \in (\theta _a,\theta _b)$ limited by the zero velocity curve (5).

Fig. 1

Left: qualitative picture of the configuration space of the system (3), where the zero velocity curve (5) is also shown. Right: example of an ejection trajectory in the configuration space in the model SC4BP for $\alpha =1$ (see Sect. 2.2)

In the models of N-body problems, when a collision between two or more bodies occurs, the distance between them becomes zero and the velocity of the colliding particles is infinite. This corresponds to a singularity for Newton’s equations. As we mentioned, one kind of collision occurs when all particles of the system collide simultaneously, and corresponds to $r=0$. In fact, the manifold defined as

$$\begin{aligned} {{\mathcal {C}}}:= \{ (r,\theta ,v,u) | \, r=0, \, \theta _a< \theta < \theta _b, \, u^2+v^2=2V(\theta ) \}, \end{aligned}$$

(6)

is invariant under the flow given by Eq. (3), and it is called the total collision manifold. By Proposition 2, the equilibrium points $E^{\pm } \in {{\mathcal {C}}}$.

It is relevant that the flow on ${\mathcal {C}}$ is almost-gradient with respect to v, see McGehee (1974). That is, introducing the energy relation (4) in the second equation of system (3), $dv/d\tau = hr+u^2/2$, so when $r=0$, $dv/d\tau \ge 0$. Later on, we will strongly use this property of the flow on the total collision manifold ${\mathcal {C}}$.

Other singularities appear when “partial” collisions occur, that is, collisions when not all of the bodies are involved. The simplest one, a binary collision, arises when two bodies occupy the same point. Also there can be collisions of more than two bodies or simultaneous collisions of different clusters of particles. Under the hypotheses of Proposition 2, these additional singularities occur at $\theta =\theta _{a,b}$. Therefore, we will say that we have a collision of type a or b depending on whether $\theta =\theta _a$ or $\theta =\theta _b$.

Next we define ejection and collision orbits. These are orbits that tend, backwards and forwards, respectively, to $r=0$, so they belong to the invariant manifolds of the equilibrium points $W^{u/s}(E^{\pm })$. As we will see, the one-dimensional invariant manifolds are embedded in the collision manifold ${\mathcal {C}}$, so we only consider the trajectories on the two dimensional invariant manifolds for their definition.

Definition 1

We say that an orbit is a collision orbit if it is contained in $W^s(E^-)$ and an ejection orbit if it is contained in $W^u(E^+).$ An orbit is an ejection–collision orbit if it is contained in $W^s(E^-)\cap W^u(E^+).$

Therefore, an ejection–collision orbit (ECO) satisfies $\displaystyle {\lim _{\tau \rightarrow \pm \infty }r(\tau )=0}.$

From now on, we consider that we are under the hypotheses of Proposition 2 and the energy is fixed at a value $h<0$.

2.2 Examples from Celestial Mechanics

Next, we provide a few examples of problems from Celestial Mechanics that match the general model presented.

• The rectangular four-body problem (Rec4BP). In this problem, four equal masses lie at the vertices of a rectangle, so that their positions and velocities are symmetric with respect to two axes, vertical and horizontal, passing through their center of mass, placed at the origin. Its potential can be written as

  $$\begin{aligned} V(\theta )=2+\frac{2}{\cos \theta }+\frac{2}{\sin \theta }, \end{aligned}$$

  for $\theta \in (0,\pi /2)$. The two singularities correspond to two double collisions. See, for example, (Simó and Lacomba 1982; Lacomba and Medina 2008).

• The rhomboidal four-body problem (Rh4BP). In this problem, there are two different pairs of equal mass particles, $m_1=m_3$ and $m_2=m_4$ and $\alpha$ is the mass ratio between them. The bodies are placed at the vertices of a rhombus with initial positions and velocities symmetric with respect to the diagonals of the rhombus. The potential is given by

  $$\begin{aligned} V(\theta )=\frac{1}{\sqrt{2}\cos \theta }+\frac{\alpha ^{5/2}}{\sqrt{2}\sin \theta }+\frac{4\sqrt{2}\alpha ^{3/2}}{\sqrt{\alpha \cos ^2\theta +\sin ^2\theta }}, \end{aligned}$$

  for $\theta \in (0,\pi /2)$. As in the previous example, the two singularities correspond to two double collisions. See, for example, (Delgado Fernández and Pérez-Chavela 1991; Lacomba and Pérez-Chavela 1993).

• The symmetric collinear four-body problem (SC4BP). In this problem, four bodies of masses, $m_4=\alpha$, $m_2=1$, $m_1=1$, and $m_3=\alpha$, $\alpha >0$, are collinear, ordered from left to right and moving symmetrically by pairs about their center of mass. In this case, the potential writes

  $$\begin{aligned} V(\theta )= & {} \frac{1}{\sqrt{2}} \left( \frac{1}{\cos \theta }+\frac{\alpha ^{5/2}}{\sin \theta }\right) \\&\quad + \frac{2\sqrt{2}\alpha ^{3/2}}{\sin \theta -\sqrt{\alpha }\cos \theta } +\frac{2\sqrt{2}\alpha ^{3/2}}{\sin \theta +\sqrt{\alpha }\cos \theta } \end{aligned}$$

  for $\theta _{\alpha } \le \theta \le \pi /2$, where $\theta _\alpha =\arctan (\sqrt{\alpha } \,)$. The singularity $\theta =\theta _{{\alpha }}$ corresponds to double binary collisions between $m_4$ and $m_2$, and $m_1$ and $m_3$, and the singularity $\theta =\theta _{{\pi /2}}$ corresponds to single binary collisions between $m_1$ and $m_2$. See, for example, (Lacomba and Medina 2004; Alvarez-Ramírez et al. 2015, 2019).

• The collinear three-body problem (C3BP), where three masses $m_1,m_2$ and $m_3$ form a collinear configuration, labeled from left to right. The potential is given by

  $$\begin{aligned} V(\xi )=\sin (2\lambda ) \left( \frac{m_1m_2}{(b_2-b_1)\sin \left( \lambda (\xi +1)\right) }+\frac{m_2m_3}{(a_3-a_2)\sin \left( \lambda (1-\xi )\right) } \right. \\ \left. +\frac{m_1m_3}{(b_2-b_1)\sin (\lambda (\xi +1))+(a_3-a_2)\sin (\lambda (1-\xi ))}\right) , \end{aligned}$$

  where $\xi \in (-1,1)$ and $\lambda$ is a constant depending on the masses of the system. The singularities correspond to collisions of the left binaries, $\xi =-1$, or collisions of the right binaries, $\xi =1$. See McGehee (1974); Kaplan (1999).

• A symmetric planar 2N body problem. Consider 2N equal masses located in a configuration in which the mass $m_j$ is symmetric to $m_{j+1}$ with respect the line $\theta =j\pi /N$, $j=1,\ldots ,N$. Due to the symmetries of the problem, it reduces to a two degrees of freedom system with potential

  $$\begin{aligned} V(\theta ) = \dfrac{1}{\sin (\pi /n-\theta )}+\dfrac{1}{\sin (\pi /n+\theta )} + {\widetilde{V}}(\theta ), \end{aligned}$$

  for $-\pi /N \le \theta \le \pi /N$, and ${\widetilde{V}}(\theta )$ analytic. See, for example, (Martínez 2013).

2.3 Regularization of Non-total Collisions

In the present model, the system of Eq. (3) has singularities at $\theta =\theta _a$ and $\theta =\theta _b$. These singularities correspond to distinct partial collisions for the different N-body problems. For instance, for the Rec4BP, both singularities correspond to double binary collisions between two different pairs of bodies, whereas for the SC4BP, $\theta =\theta _{\alpha }$ corresponds to a double binary collision of the two particles on the left and the two particles on the right, and $\theta =\pi /2$ corresponds to a single binary collision of the two particles at the center.

The two singularities at $\theta =\theta _a,\theta _b$ can be removed simultaneously through a Sundman type regularization. See Martínez (2012) and the references therein for more details. Consider the functions

$$\begin{aligned} W(\theta )=f(\theta )V(\theta ) \quad \hbox {and} \quad F(\theta )=\dfrac{f(\theta )}{\sqrt{W(\theta )}}, \end{aligned}$$

where $f(\theta )=\sin (\theta -\theta _a)\sin (\theta _b-\theta )$ if $\theta _b-\theta _a\ne \pi$, and $f(\theta )=\sin (\theta _b-\theta )$ otherwise. Notice that $W(\theta )$ is a positive and bounded smooth function in $[\theta _a,\theta _b]$. Then, introducing a new variable and the change of time

$$\begin{aligned} w=F(\theta )u, \qquad d\tau = F(\theta ) dt, \end{aligned}$$

t being the new time, the system of Eq. (3) transforms into

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\mathrm{d}r}{\mathrm{d}t} = rvF(\theta ), \\ \dfrac{\mathrm{d}v}{\mathrm{d}t} = F(\theta ) \left( 2hr - \dfrac{v^2}{2}\right) +\sqrt{W(\theta )}, \\ \dfrac{\mathrm{d}\theta }{\mathrm{d}t} = w, \\ \dfrac{\mathrm{d}w}{\mathrm{d}t} = -F(\theta )\dfrac{vw}{2}+\dfrac{W'(\theta )}{W(\theta )}\left( f(\theta )-\dfrac{w^2}{2}\right) +f'(\theta ) \left( 1 + \dfrac{f(\theta )}{W(\theta )}(2hr-v^2) \right) , \end{array} \right. \end{aligned}$$

(7)

where $W'=dW/d\theta$.

The energy relation $H=h$ (4), in these new variables, writes

$$\begin{aligned} W(\theta ) w^2 + f(\theta )^2 v^2 = 2f(\theta )^2rh+2W(\theta )f(\theta ). \end{aligned}$$

(8)

Notice that if $(r,v,\theta ,w)$ is a solution with energy h, then $(\lambda r,v,\theta ,w)$ is also a solution with energy $\lambda h$, with $\lambda >0$. Therefore, it is enough to fix any negative value for h.

We will study the system of differential Eq. (7) in the regularized and reduced McGehee coordinates $(r,v,\theta ,w)$ on the phase space ${\mathcal {F}}=[0,\infty )\times \mathbb {R}\times I \times \mathbb {R}$, $I=[\theta _a,\theta _b]$. A solution of the above set of ordinary differential equations, also called orbit, will be denoted by $\Gamma =\left\{ \gamma (t,\xi )\right\} _{t}$ (or just by $\gamma (t)$), where $\gamma (0,\xi )=\xi$.

Notice that system (7) exhibits the symmetry

$$\begin{aligned} \; (r,v,\theta ,w,t) \rightarrow (r,-v,\theta ,-w,-t). \end{aligned}$$

(9)

This can be phrased in terms of solutions as follows: if $\gamma (t)=(r(t),v(t),\theta (t),w(t))$ is a solution, then ${\overline{\Gamma }}$ defined as:

$$\begin{aligned} {{\overline{\gamma }}}(t)=(r(-t),-v(-t),\theta (-t),-w(-t)) \end{aligned}$$

(10)

is also a solution.

The claim of Proposition 2 persists in the new variables, so system (7) has two hyperbolic equilibrium points $E^{\pm }$, with coordinates $(r,v,\theta ,w)=(0,\pm v_c,\theta _{c},0)$. Next result states the existence of an orbit that connects both equilibrium points (see Martínez (2012)). It is called the homothetic solution because the configuration maintains the same shape along its evolution for all the time, only changing its size.

Proposition 3

For every fixed level of energy $H=h<0$, there exists a solution of the system of Eq. (7) of the form

$$\begin{aligned} \gamma _h(t) = (r(t), \theta =\theta _c, v(t), w=0), \end{aligned}$$

such that $r(t) \underset{t\rightarrow \pm \infty }{\longrightarrow }0$.

Notice that this is an ejection–collision orbit since it starts and ends at $r=0$.

2.4 Poincaré Section and Map

In this section, we introduce a convenient Poincaré section, which shall be a keystone to show the existence of ECO. We consider as a Poincaré section the set where partial collisions occur, that is, where $\theta =\theta _{a,b}$. Notice that, from the energy relation (8), any point on $\Sigma$ also must satisfy $w=0$.

Definition 2

We denote by $\Sigma$ is the union of two half planes $\Sigma _{a,b}$:

$$\begin{aligned} \Sigma= & {} \Sigma _a \cup \Sigma _b = \left\{ (r,v,\theta ,w)\; |\; r\ge 0,\,w=0,\,\theta =\theta _a\right\} \cup \\&\quad \left\{ (r,v,\theta ,w)\; | \; r\ge 0,\,w=0,\, \theta =\theta _b\right\} . \end{aligned}$$

Next, we present a property which shows that if a solution is such that the variable $\theta (t)$ is on the right side of $\theta _c$ increasingly, or on the left side but decreasingly, then the orbit must reach the section $\Sigma$. It has been proved useful in the context of different N-body problems, as shown in Kaplan (1999); Tanikawa and Mikkola (2000a) for the C3BP or Sekiguchi and Tanikawa (2004); Lacomba and Medina (2004); Alvarez-Ramírez et al. (2019) for the SC4BP.

Proposition 4

Let $\gamma (t)$ be a solution of the system given by (7) such that a certain time $t_0$, either $\theta (t_0) >\theta _c$ and $w(t_0)>0$ or $\theta (t_0) <\theta _c$ and $w(t_0)<0$. Then, the trajectory must reach the section $\Sigma$ at least once.

Proof

We may assume that $\theta (t_0) >\theta _c$ and $w(t_0)>0$, and we will see that the orbit must reach the section $\Sigma _b$. In the other scenario, the orbit must reach $\Sigma _a$, and it can be proved using the same arguments.

First, let us prove that $\theta (t)$ cannot reach a maximum at $\theta < \theta _b$ and $t>t_0$. Indeed, assume there exists $t^*$ such that, $\theta (t^*)\ne \theta _b$, $w(t^*)=0$ and $w(t)>0$ for $t\in (t_0,t^*)$. From the properties of function V, we have that $V(\theta (t^*))>0$, $V'(\theta (t^*))>0$, and using Eq. (7) and (8), we obtain

$$\begin{aligned} \dfrac{\mathrm{d}w}{\mathrm{d}t}(t^*) = f(\theta (t^*)) \dfrac{V'(\theta (t^*))}{V(\theta (t^*))}>0, \end{aligned}$$

so $\theta (t)$ has a minimum in $t^*$, but this is impossible since $\theta (t)$ increases in $(t_0,t^*)$.

Since $\theta (t)$ is bounded between $\theta _a$ and $\theta _b$, then either

• (i) $\theta (t)$ reaches $\Sigma _b$ and the proposition is proved;

• (ii) or $\theta (t)$ tends asymptotically to $\theta _b$. Let us prove that this situation is not possible. The corresponding solution would satisfy that

  $$\begin{aligned} \lim _{t\rightarrow +\infty } \theta (t)=\theta _b, \quad \quad \lim _{t\rightarrow +\infty } w (t)=0 \quad \hbox {and} \quad \lim _{t\rightarrow +\infty } \frac{\mathrm{d}w}{\mathrm{d}t}(t)=0. \end{aligned}$$

  However, using Eq. (7), if $\theta =\theta _b$ and $w=0$, then $\dfrac{dw}{dt} (\theta _b)=-\sin (\theta _b-\theta _a)\ne 0$, which is a contradiction. $\square$

In Fig. 1 right, we show an orbit of the SC4BP exhibiting different partial collisions (when $\theta =\theta _{a,b}$) and crossings with the section $\theta =\theta _c$. Actually, in Sekiguchi and Tanikawa (2004), the authors use this later section to construct a Poincaré map in order to describe the dynamics for this problem. However, in general, a trajectory experiences a sequence (maybe finite) of partial collisions, where the solution reaches $\Sigma _{a,b}$. This idea has been exploited by different authors when studied the three and four-body problems mentioned in Sect. 2.2, by introducing symbolic dynamics and characterizing the orbits by the sequence of partial collisions that they suffer. See, for example, (Kaplan 1999; Tanikawa and Mikkola 2000a; Lacomba and Medina 2004; Sekiguchi and Tanikawa 2004; Alvarez-Ramírez et al. 2019), and references therein. In Kaplan (1999), Lacomba and Medina (2004), Alvarez-Ramírez et al. (2019) the authors show that, in order to deal with ejection–collision orbits, the use of $\Sigma$ is quite more appropriate.

We will follow the same idea. We consider the Poincaré map (in forward time) defined on $\Sigma$

$$\begin{aligned} {{\mathcal {P}}}:\Sigma \longrightarrow \Sigma , \end{aligned}$$

(11)

as ${{\mathcal {P}}}(\mathbf{Z}) = \Phi _t(\mathbf{Z})$, where $\Phi _t$ is the flow associated with the system (7), and t is the first positive time needed to reach the section $\Sigma$ starting at $\mathbf{Z}$. In a similar way, we define ${{\mathcal {P}}}^{-1}$, the Poincaré map in backward time.

2.5 Collision Manifold

We have already defined the total collision manifold ${\mathcal {C}}$ in (6), and for simplicity, in the new variables the total collision manifold is also denoted by ${\mathcal {C}}$. It corresponds to Eq. (8) for $r=0$, and it is a 2-dimensional manifold, topologically equivalent to a sphere minus four points, independent of the total energy h, see Fig. 2. It is invariant under the flow (7), which is gradient-like with respect the variable v, that is, $dv/dt \ge 0$. It is also the boundary of the energy constant manifold $H=h$, for every fixed level of energy h. We can think the space as a book of infinite sheets where a fixed level of energy corresponds to a sheet of the book, and the spine corresponds to the zero level of energy, which is precisely the total collision manifold.

Fig. 2

Qualitative scheme of the total collision manifold ${\mathcal {C}}$. The two equilibrium points $E^{\pm }$ are also shown

Next results provide us with useful information about the solutions on the total collision manifold ${\mathcal {C}}$, information that later will be meaningful to describe the dynamics of the invariant manifolds of $E^{+,-}$.

Lemma 1

Consider the system given by (7) on the manifold ${{\mathcal {C}}}$ and a solution $\gamma (t)$. Then, all the maxima and minima of $\theta (t)$ correspond to points where $w=0$ and either $\theta =\theta _{a,b}$ or $v^2=2V(\theta )$.

Proof

By the third equation in (7), the extrema of $\theta (t)$ satisfy that $w(t)=0$. On the collision manifold ${\mathcal {C}}$, using (8), we have that

$$\begin{aligned} f(\theta )^2 v^2 = 2W(\theta )f(\theta ). \end{aligned}$$

If $f(\theta )=0$, then by definition $\theta =\theta _{a,b}$. If $f(\theta )\ne 0$, then $v^2= 2 W(\theta )/f(\theta )=2V(\theta )$. $\square$

Proposition 5

On the collision manifold ${\mathcal {C}}$, any solution is such that the variable $\theta$ oscillates from maxima to minima on $\Sigma$ and/or the curve $v^2=2V(\theta )$, $w=0$.

Proof

By Proposition 4 and Lemma 1, it is enough to see that the orbit cannot tend asymptotically to the curve $v^2=2V(\theta )$, $w=0$. Suppose that it does as v increases while $t\rightarrow \infty$. Then, $\displaystyle {\lim _{t\rightarrow \infty } \frac{\mathrm{d}w}{\mathrm{d}t}=0}$. But along any point on such curve, using (7) and (8), we have that

$$\begin{aligned} \frac{dw}{dt}=f(\theta ) \dfrac{V'(\theta )}{V(\theta )} \ne 0, \end{aligned}$$

which is a contradiction. $\square$

In Fig. 3, we show some orbits on the collision manifold in the SC4BP for different values of the parameter of the problem.

Remark. As a consequence of Proposition 4, any solution in ${{\mathcal {C}}}$ is such that forwards in time, $\theta (t)$ either oscillates infinitely between maxima and minima while $v(t)\rightarrow \infty$, or oscillates a finite number until the orbit tends to $E^{+}$ (analogously backwards in time). In particular, any heteroclinic orbit connecting $E^-$ and $E^+$ will describe a finite number of oscillations between $\Sigma _a$ and $\Sigma _b$.

Notice that on the collision manifold the variables $\theta$ and w are bounded, whereas the variable $v\in (-\infty ,+\infty )$. When a solution of Eq. (7) on ${\mathcal {C}}$ is such that $v\rightarrow \pm \infty$, we say that it escapes through the right arm if $\theta >\theta _c$, respectively, through the left arm if $\theta <\theta _c$.

3 Dynamics on the Invariant Manifolds

As stated in previous sections, on the one hand, the problem given by Eq. (7) has a collision manifold ${\mathcal {C}}$ corresponding to the blow-up performed at $r=0$, and on the other hand, there exist two hyperbolic equilibrium points, $E^{\pm }\in {\mathcal {C}}$, and their corresponding invariant manifolds, see Proposition 2. The knowledge of the qualitative behavior of the flow on the total collision manifold will lead us to read off the behavior of orbits passing near total collision, ejecting from or reaching total collision.

As stated in Proposition 2, the equilibrium points are hyperbolic and, for a fixed value of the energy h, each one has associated two invariant manifolds: one of dimension one, the other of dimension two. Due to the symmetry (9), the invariant manifolds associated with $E^-$ are symmetric to the ones associated with $E^+$. Therefore, it is enough to describe the behavior of, for example, $W^{u/s}(E^-)$. These invariant manifolds are already well known and studied in the three- and four-body problems mentioned in Sect. 2.2, see, for example, (Devaney 1980; Lacomba 1983; Simó and Lacomba 1982). In the next section, we will describe their behavior in detail and establish some nomenclature.

3.1 One-Dimensional Invariant Manifolds

We start by describing the behavior of $W^u(E^-)$ (and by symmetry, we have that of $W^s(E^+)$), which is a one dimensional invariant manifold with two branches, each one being specific solutions of the system. We will denote by $W^u_-(E^-)$ (respectively, $W^u_+(E^-)$) the branch going toward the half-space $w<0$ (resp. $w>0$). Notice that also, by the third equation of (7), the positive branch goes toward $\theta _b$, whereas the negative branch moves toward $\theta _a$. The first important property is that $W^u(E^-) \subset {{\mathcal {C}}}$. Second, as we have seen in Sect. 2.5, any given branch is an orbit that initially goes back and forth between $\Sigma _a$ and $\Sigma _b$ and then it can only exhibit two different behaviors: either it tends to $E^+$ (becoming an heteroclinic connection) or the trajectory “escapes” toward $v\rightarrow +\infty$ along one of the upper legs of the total collision manifold. See Figs. 3 and 4.

There exist three possible cases, named after Lacomba (1983): The non-degenerate case, in which there are no heteroclinic connections on ${\mathcal {C}}$ between the equilibrium points and the branches of $W^u_{\pm }(E^-)$ go through the upper legs of ${\mathcal {C}}$ (Fig. 3). In the symmetric degenerate case, both branches of $W^{u}_{\pm }(E^{-})$ coincide with the branches of $W^s_{\pm }(E^+)$, so there exist two heteroclinic connections between the equilibrium points (Fig. 4, center). In the (non-symmetric) degenerate case, only one branch of $W^{u}(E^{-})$ coincides with one branch of $W^{s}(E^{+})$, while the other branch of $W^u(E^-)$ escapes along one of upper legs of ${\mathcal {C}}$ (Fig. 4, left and right).

Fig. 3

Branches of the invariant manifolds $W_{+}^u(E^-)$ (in red) and $W_{-}^u(E^-)$ (in blue) on the collision manifold in the $(\theta ,w,v)$ space. The vertical lines correspond to $w=0, \theta =\theta _{a,b}$. Also their intersections with the section $\Sigma$ are shown. The plots show the four different scenarios in the non-degenerate cases: types I, II, III, IV (see the text and Table 1). The four samples plotted correspond to the SC4BP for different values of the mass parameter (see Sect. 2.2), which illustrate the behavior in our general setting

Fig. 4

Branches of the invariant manifolds $W_{+}^u(E^-)$ (in red) and $W_{-}^u(E^-)$ (in blue) on the collision manifold in the $(\theta ,w,v)$ space in the degenerate cases (not all of them are represented). The three samples correspond to the SC4BP for different values of the mass parameter

Observe that in the non-degenerate case, initially both branches of the invariant manifolds go through partial collisions $\theta =\theta _{a,b}$ alternatively and then exhibit the same type of partial collisions going up along one upper arm of ${\mathcal {C}}$. In the degenerate cases, the branches corresponding to heteroclinic connections only exhibit a finite number of partial collisions.

In fact, the branches of the one dimensional invariant manifolds can be characterized by the number of full turns around the total collision manifold ${\mathcal {C}}$ (the number of oscillations of the variable $\theta$ between $\theta _a$ and $\theta _b$). More concretely, we say that a branch of a 1D-invariant manifold makes a full turn if the variable $\theta$ varies from $\theta _c$ to $\theta _c$ passing through $\theta _a$ and $\theta _b$ just once. For example, the orbits in Fig. 3 top left make two full turns, whereas those on plot top right make one and a half turn.

The number of full turns and their intersections with the section $\Sigma$ allow us to characterize the 1D-invariant manifolds as follows. Consider the successive intersections of each branch with the the section $\Sigma$ (see Definition 2)

$$\begin{aligned} W^u_{\pm }(E^-)\cap \Sigma =\left\{ \mathbf{U}_j^{\pm }\right\} _{j\ge 1} \qquad \text {and} \qquad W^s_{\pm }(E^+)\cap \Sigma =\left\{ \mathbf{S}_j^{\pm }\right\} _{j\ge 1}, \end{aligned}$$

where $\mathbf{U}_j^{\pm }=(0,\theta _{a,b},u_j^{\pm },0)$, $\mathbf{S}_j^{\pm }=(0,\theta _{a,b},s_j^{\pm },0)$ and $\{u_j^{\pm }\}_{j\ge 1}$,$\{s_j^{\pm }\}_{j\ge 1}$ are increasing sequences (see Fig. 3). In the non-degenerate cases, the sequences are infinite, whereas in the degenerate cases some or all of them are finite. Notice that, using the symmetry of the system, we have that

$$\begin{aligned} s_j^- = -u_j^+ \quad \hbox {and} \quad s_j^+ = -u_j^-. \end{aligned}$$

For simplicity, we will simply just denote by $u_j^{\pm }, s_j^{\pm }$ the points $\mathbf{U}_j^{\pm }$, $\mathbf{S}_j^{\pm }$, respectively.

Let ${\mathcal {S}}$ be the set of all possible sequences, just taking into account the elements a and b. We define

$$\begin{aligned} \begin{array}{ccl} {{\mathcal {I}}^{+}}: W^{u}(E^{-}) &{} \longrightarrow &{} {{\mathcal {S}}}\\ \Gamma &{} \longrightarrow &{} \sigma =(\sigma _1,\sigma _2,\dots ,\sigma _n, \dots ) \end{array} \end{aligned}$$

where

$$\begin{aligned} \sigma _j=\left\{ \begin{array}{ll} a &{} \text{ if } \text{ the } j-\text{ th } \text{ intersection } \text{ of } \Gamma \text{ with } \Sigma \text{ is } \text{ at } \Sigma _a, \\ b &{} \text{ if } \text{ the } j-\text{ th } \text{ intersection } \text{ of } \Gamma \text{ with } \Sigma \text{ is } \text{ at } \Sigma _b, \end{array} \right. \quad \text{ for } \, j\ge 1. \end{aligned}$$

The sequence ${{\mathcal {I}}}^+(\Gamma )$ codes the partial collisions (intersections with $\Sigma$) forwards in time for the unstable manifold. Similarly, we can define ${{\mathcal {I}}}^-$ on $W^s(E^{+})$, obtaining a sequence of partial collisions backwards in time. Using the symmetry of the problem, we have that

$$\begin{aligned} {{\mathcal {I}}^+}(W^u_+(E^-)) = {{\mathcal {I}}^-}(W^s_-(E^+)) \qquad \hbox {and} \qquad {{\mathcal {I}}^+}(W^u_-(E^-)) = {{\mathcal {I}}^-}(W^s_+(E^+)). \end{aligned}$$

We classify the behavior of the 1-dimensional manifolds $W^u_{\pm }(E^-)$ and $W^s_{\pm }(E^+)$ using the number of full turns of each branch, their intersections with the section $\Sigma$ and the map ${{\mathcal {I}}}^+$. In what follows, the sequence $\underline{\star ,\bullet },\overset{n)}{\ldots },\star ,\bullet$ denotes that the sequence $\star ,\bullet$ is repeated n times. For example, the sequence $(\underline{b,a},\overset{n)}{\ldots },b,a,b,b,b,\ldots )$ represents an orbit with a sequence of n pairs of collisions b, a (a collision of type b followed by a collision of type a), and then, the orbit only has collisions of type b forwards in time. Analogous interpretations are given for other sequences.

The non-degenerate cases are classified in four types:

• (1) Type I Both branches make n full turns around ${{\mathcal {C}}}$ (see Fig. 3 top left), before escaping through different arm:

  $$\begin{aligned} {{\mathcal {I}}^+}(W^u_+(E^-))= & {} (\underline{b,a},\overset{n)}{\ldots },b,a,b,b,b,\ldots ),\\ {{\mathcal {I}}^+}(W^u_-(E^-))= & {} (\underline{a,b},\overset{n)}{\ldots },a,b,a,a,a,\ldots ). \end{aligned}$$

  Then, the sequences $u_j^{\pm }$ and $s_j^{\pm }$ are ordered as follows. Along the line ${{\mathcal {C}}}\cap \Sigma _b$:

  $$\begin{aligned} \begin{aligned}&\dots<s_{2n+3}^-<s_{2n+2}^-<s_{2n+1}^-<u_1^+<s_{2n}^+<u_2^-<s_{2n-1}^-<u_3^+<s_{2n-2}^+< \\&\quad \dots<s_3^-<u_{2n-1}^+<s_2^+<u_{2n}^-<s_1^-<u_{2n+1}^+<u_{2n+2}^+<u_{2n+3}^+ < \dots \end{aligned} \end{aligned}$$

  Along the line ${{\mathcal {C}}}\cap \Sigma _a$:

  $$\begin{aligned} \begin{aligned}&\dots<s_{2n+3}^+<s_{2n+2}^+<s_{2n+1}^+<u_1^-<s_{2n}^-<u_2^+<s_{2n-1}^+<u_3^-<s_{2n-2}^-< \\&\quad \dots<s_3^+<u_{2n-1}^-<s_2^-<u_{2n}^+<s_1^+<u_{2n+1}^-<u_{2n+2}^-<u_{2n+3}^-<\dots , \end{aligned} \end{aligned}$$

  see Fig. 5.

• (2) Type II Both branches make n full turns and a half (see Fig. 3 top right), before escaping through a different arm on ${{\mathcal {C}}}$:

  $$\begin{aligned} {{\mathcal {I}}^+}(W^u_+(E^-))= & {} (\underline{b,a},\overset{n+1)}{\ldots },b,a,a,a,\ldots ), \\ {{\mathcal {I}}^+}(W^u_-(E^-))= & {} (\underline{a,b},\overset{n+1)}{\ldots },a,b,b,b,\ldots ). \end{aligned}$$

  Then, the sequences $u_j^{\pm }$ and $s_j^{\pm }$ on ${{\mathcal {C}}}\cap \Sigma _b$ are ordered as follows:

  $$\begin{aligned} \begin{aligned}&\dots<s_{2n+4}^+<s_{2n+3}^+<s_{2n+2}^+<u_1^+<s_{2n+1}^-<u_2^-<s_{2n}^+<u_3^+<s_{2n-1}^-< \\&\quad \dots<s_3^-<u_{2n}^-<s_2^+<u_{2n+1}^+<s_1^-<u_{2n+2}^-<u_{2n+3}^-<u_{2n+4}^-\dots . \end{aligned} \end{aligned}$$

  To obtain the ordering on ${{\mathcal {C}}}\cap \Sigma _a$, change the sign plus by minus.

• (3) Type III The positive branch makes n full turns, whereas the negative branch makes n and a half (see Fig. 3 bottom left), before escaping both through the right arm:

  $$\begin{aligned} {{\mathcal {I}}^+}(W^u_+(E^-))= & {} (\underline{b,a},\overset{n)}{\ldots },b,a,b,b,b,\ldots ), \\ {{\mathcal {I}}^+}(W^u_-(E^-))= & {} (\underline{a,b},\overset{n+1)}{\ldots },a,b,b,b,\ldots ). \end{aligned}$$

  The sequences $u_j^{\pm }$ and $s_j^{\pm }$ along ${{\mathcal {C}}}\cap \Sigma _b$ satisfy

  $$\begin{aligned} \begin{aligned}&\dots<s_{2n+3}^-<s_{2n+3}^+<s_{2n+2}^-<s_{2n+2}^+<s_{2n+1}^-<u_1^+<u_2^-<s_{2n}^+< \\&\quad s_{2n-1}^-<u_3^+<u_4^-<\dots<s_4^+<s_3^-<u_{2n-1}^+<u_{2n}^-< \\&\quad s_2^+<s_1^-<u_{2n+1}^+<u_{2n+2}^-<u_{2n+2}^+<u_{2n+3}^-<u_{2n+3}^+<u_{2n+4}^-\dots . \end{aligned} \end{aligned}$$

  In this case, along ${{\mathcal {C}}}\cap \Sigma _a$ we have the following ordered finite sequence:

  $$\begin{aligned} \begin{aligned}&u_1^-<s_{2n+1}^+<s_{2n}^-<u_2^+<u_3^-<s_{2n-1}^+<s_{2n-2}^-< \\&\quad \dots<u_{2n-2}^+<u_{2n-1}^-<s_3^+<s_2^-<u_{2n}^+<u_{2n+1}^-<s_1^+. \end{aligned} \end{aligned}$$

• (4) Type IV The positive branch makes n full turns and a half, whereas the negative branch makes n turns (see Fig. 3 bottom right), before escaping both through the left arm:

  $$\begin{aligned} {{\mathcal {I}}^+}(W^u_+(E^-))= & {} (\underline{b,a},\overset{n+1)}{\ldots },b,a,a,a,\ldots ), \\ {{\mathcal {I}}^+}(W^u_-(E^-))= & {} (\underline{a,b},\overset{n)}{\ldots },a,b,a,a,\ldots ). \end{aligned}$$

  In this case, along ${{\mathcal {C}}}\cap \Sigma _b$ there is a finite number of intersections:

  $$\begin{aligned} \begin{aligned}&u_1^+<s_{2n+1}^-<s_{2n}^+<u_2^-<u_3^+<s_{2n-1}^-<s_{2n-2}^+< \\&\quad \dots<u_{2n-2}^-<u_{2n-1}^+<s_3^-<s_2^+<u_{2n}^-<u_{2n+1}^+<s_1^-. \end{aligned} \end{aligned}$$

  Along ${{\mathcal {C}}}\cap \Sigma _a$, the ordering is the following:

  $$\begin{aligned} \begin{aligned}&\dots<s_{2n+2}^+<s_{2n+2}^-<s_{2n+1}^+<u_1^-<u_2^+<s_{2n}^-< \\&\quad s_{2n-1}^+<u_3^-<u_4^+<\dots<s_4^-<s_3^+<u_{2n-1}^-<u_{2n}^+< \\&\quad s_2^-<s_1^+<u_{2n+1}^-<u_{2n+1}^+<u_{2n+2}^-<u_{2n+2}^+<u_{2n+3}^-<\dots . \end{aligned} \end{aligned}$$

Fig. 5

Ordering of sequences $\{s_{j}^{\pm }\}, \{u_{j}^{\pm }\}$ (see Sect. 3.1) and $\{p_j^{\pm }\}, \{q_j^{\pm }\}$ (see Sect. 3.2) along ${\mathcal {C}}\cap \Sigma _{a,b}$ for the non-degenerate case Type I. Figures left and right represent bottom and top parts of ${\mathcal {C}}$, respectively

Along the paper, we will refer to each one of the above cases. We summarize them in Table 1.

Table 1 Codes of the partial collisions exhibited by the branches of the unstable manifold $W^u(E^-)$ (and by symmetry, the stable manifold $W^s(E^+)$) in the non-degenerate cases depending on the number of full turns (n or n and a half)

In the degenerate cases, there are three cases. If it is non-symmetric, one of the branches connects with the equilibrium point $E^{+}$, so its image by ${{\mathcal {I}}^+}$ is a finite sequence, whereas the other one exhibits one of the behaviors described above. In the symmetric degenerate case, both branches have associated a finite sequence in ${{\mathcal {S}}}$, see Fig. 4.

3.2 Two-Dimensional Invariant Manifolds

Next, we describe some features of the behavior of the 2-dimensional invariant manifolds $W^u(E^+)$ and $W^s(E^-)$. In Fig. 6, we show a qualitative representation of such invariant manifolds. We observe that if $r>0$, then the projection of the motion in the space $(\theta ,w,v)$ takes place inside the collision manifold. This can be deduced from Eq. (8). For $\theta$ fixed, the motion takes place in an ellipse in the plane (v, w) with semiaxes that are maxima when $r=0$ (since $h<0$): $\theta _a \le \theta \le \theta _b$ and

$$\begin{aligned} W(\theta ) w^2 + f(\theta )^2 v^2 \le 2W(\theta )f(\theta ). \end{aligned}$$

However, we plot the manifolds outside ${\mathcal {C}}$ for a clearer visualization (following the first plots by Lacomba et al.)

Fig. 6

Qualitative behavior of the 2D-invariant manifolds $W^u(E^+)$ and $W^s(E^-)$

More concretely:

• The invariant manifolds are glued to the total collision manifold ${\mathcal {C}}$, not only by the equilibrium point: the intersections are

  $$\begin{aligned} W^u(E^+)\cap {{\mathcal {C}}}=\Gamma ^u_{\pm } \quad \hbox {and} \quad W^s(E^-)\cap {{\mathcal {C}}}=\Gamma ^s_{\pm }, \end{aligned}$$

  (12)

  where each $\Gamma ^{u}_{\pm }$ (resp. $\Gamma ^{s}_{\pm }$) is an orbit that escapes forwards (respectively, backwards) in the v-direction, $v\rightarrow +\infty$ (resp. $v\rightarrow -\infty$) through one of the legs of ${\mathcal {C}}$ (see, for instance, (Kaplan 1999) or (Lacomba and Simó 1982)). Here, as for the one-dimensional invariant manifolds, the sign $+$ (respectively, the sign −) means that the orbit initially moves with $w>0$ space (respectively, $w<0$) near the equilibrium point, $E^+$ when referring to $\Gamma ^{u}_{\pm }$ and $E^-$ for $\Gamma ^{s}_{\pm }$. See Fig. 7. As explained in Sect. 2.5, each trajectory performs an infinite sequence of partial collisions:

  $$\begin{aligned} {{\mathcal {I}}^+}(\Gamma ^u_+)=(b,b,b,\ldots ), \qquad {{\mathcal {I}}^+}(\Gamma ^u_-)=(a,a,a,\ldots ), \end{aligned}$$

  and

  $$\begin{aligned} {{\mathcal {I}}^-}(\Gamma ^s_+)=(a,a,a,\ldots ), \qquad {{\mathcal {I}}^-}(\Gamma ^s_-)=(b,b,b,\ldots ). \end{aligned}$$

  In fact,

  $$\begin{aligned} \Gamma ^u_+ \cap \Sigma = \{\mathbf{P}_j^{+}\}_{j\ge 1}\subset \Sigma _b, \quad \Gamma ^u_- \cap \Sigma = \{\mathbf{P}_j^{-}\}_{j\ge 1}\subset \Sigma _a, \end{aligned}$$

  where $\mathbf{P}_j^{+}=(0,\theta _b,p_j^{+},0)$, $\mathbf{P}_j^{-}=(0,\theta _a,p_j^{-},0)$, and

  $$\begin{aligned} \Gamma ^s_+ \cap \Sigma = \{\mathbf{Q}_j^{+}\}_{j\ge 1}\subset \Sigma _a, \quad \Gamma ^s_- \cap \Sigma = \{\mathbf{Q}_j^{-}\}_{j\ge 1}\subset \Sigma _b, \end{aligned}$$

  with $\mathbf{Q}_j^{+}=(0,\theta _b,q_j^{+},0)$, $\mathbf{Q}_j^{-}=(0,\theta _a,q_j^{-},0)$. The sequences $\{p_j^{\pm }\}$ are increasing and $\{q_j^{\pm }\}$ are decreasing ($q_j^{\mp }=-p_j^{\pm }$). See Fig. 7. These sequences can be combined with the sequences $\{u_j^{\pm }\}$ and $\{s_j^{\pm }\}$. In all the cases, it is clear that

  $$\begin{aligned} q_1^-< u_1^+, \qquad s_1^-< p_1^+, \qquad q_1^+< u_1^-, \qquad s_1^+ < p_1^-. \end{aligned}$$

  (13)

  See, for example, Fig. 5 for the non-degenerate case of Type I.

• The solution $\gamma _h(t)$ given in Proposition 3 belongs to $W^u(E^+)\cap W^s(E^-)$, that is, it is an ECO that connects both equilibrium points without any partial collision. Therefore, $\gamma _h(t)$ does not intersect $\Sigma$.

Fig. 7

Behavior of $\Gamma ^{u/s}_{\pm }$ and the homothetic solution $\gamma _h(t)$

From now on, we will simply just denote by $q_j^{\pm }, p_j^{\pm }$ the points $\mathbf{Q}_j^{\pm }$, $\mathbf{P}_j^{\pm }$, respectively.

4 Ejection–Collision Orbits

In this section, we prove the existence of different types of ECO depending on the behavior of the 1-dimensional invariant manifolds. Actually, we will characterize the ECO by its finite number of successive binary collisions with $\Sigma$. Let $\sigma$ be a finite sequence of collisions of type a and b. Following the notation in Sect. 3.1, we will say that an ECO is of type $\sigma$ if its orbit describes forwards in time the finite sequence of binary collisions encoded by $\sigma$.

The following result is straightforward from the symmetry (9).

Proposition 6

Let $\Gamma$ be an ECO of type $\sigma =(\sigma _1,\ldots ,\sigma _m)$. Then ${\overline{\Gamma }}$ defined as in (10) is an ECO of type ${\overline{\sigma }}=({\overline{\sigma }}_1,\ldots , {\overline{\sigma }}_m)$, with ${\overline{\sigma }}_k=\sigma _{m-k+1}$, $k=1,\ldots m$.

Along the proofs of the following results, we use the notation ${{\,\mathrm{int}\,}}(K)$ and ${\overline{K}}$ for the interior and the closure of a set K.

We start with a technical lemma and a general result for all the cases. We will denote by ${W}^u(E^+)\cap \Sigma _{a,b}^1$ and $W^s(E^-)\cap \Sigma ^1_{a,b}$ the first intersection (forwards and backwards in time, respectively) of the 2-dimensional manifolds with each one of the sections $\Sigma _{a,b}$.

Lemma 2

Each one of the intersections ${W}^u(E^+)\cap \Sigma ^1_{a,b}$ and $W^s(E^-)\cap \Sigma ^1_{a,b}$ is an arc contained in $\Sigma _{a,b}$ whose closure has endpoints contained on ${\mathcal {C}}\cap \Sigma _{a,b}$. More precisely,

$$\begin{aligned} \begin{array}{rclcrcl} J^{b}:=\overline{{W}^u(E^+)\cap \Sigma _{b}^1} &{} = &{} \langle u_1^+,p_1^+ \rangle , &{} \quad &{} J^{a}:=\overline{{W}^u(E^+)\cap \Sigma _{a}^1} &{} = &{} \langle u_1^-,p_1^- \rangle ,\\ K^{b}:= \overline{{W}^s(E^-)\cap \Sigma _{b}^1} &{} = &{} \langle q_1^-,s_1^- \rangle , &{} \quad &{} K^{a}:=\overline{{W}^s(E^-)\cap \Sigma _{a}^1} &{} = &{} \langle q_1^+,s_1^+ \rangle ,\\ \end{array} \end{aligned}$$

(14)

where $\langle x,y \rangle$ denotes a closed arc contained in $\Sigma$ with endpoints x, y.

Proof

We detail the proof for ${W}^u(E^+)\cap \Sigma _{b}^1$. The intersection with $\Sigma _a$ follows similar arguments, and the intersections of the stable manifold of $E^-$ are obtained using the symmetry of the problem. Let $\Phi _t$ be the flow of system (7).

Consider an arc of initial conditions contained in $W^u(E^+)$ and close enough to $E^+$, so that the arc is homeomorphic to a semicircle parametrized by an angle $\phi \in [0,\pi ]$, in such a way that $\phi =0,\pi ,$ corresponds to points $\mathbf{Z}^+$ in $\Gamma ^u_+$ and $\mathbf{Z}_-$ in $\Gamma ^u_-$, respectively (recall (12)), and $\phi =\frac{\pi }{2}$ corresponds to a point $\mathbf{Z}^h$ in the homothetic orbit $\gamma _h$. See Fig. 8.

Clearly, $\Phi _t(\mathbf{Z}^+)$ intersects $\Sigma _b$ at $p_1^+$. Therefore, by continuity, the flow transforms the subarc parameterized by $(0, \pi /2)$ into a continuous arc contained in $\Sigma _b$. Moreover, for any $\mathbf{Z}$ in this subarc close to $\mathbf{Z}^h$, the trajectory $\Phi _t(\mathbf{Z})$ has a close passage to $E^-$. Due to the hyperbolic character of the equilibrium point, the orbit will continue close to the unstable branch of $E^-$, whose intersection with $\Sigma _b$ is $u_1^+$. Therefore, ${W}^u(E^+)\cap \Sigma _{b}^1$ is an arc with end points $p_1^+$ and $u_1^+$.

In a similar way, the image of the subarc parametrized by $(\pi /2,\pi )$ is also a continuous arc, contained in $\Sigma _a$, with endpoints $u_1^-$ and $p_1^-$. $\square$

In Fig. 8, we show the idea of the proof of Lemma 2. The projection of the collision manifold in the $(\theta ,v)$ plane and the semiplane (r, v), $r\ge 0$ (that contain the projection of the arches) are depicted jointly glued to the section $\Sigma _b$. From now on, the pictures will follow this representation.

Fig. 8

Sketch of the proof of Lemma 2. The collision manifold and the semiplane (r, v), $r\ge 0$ (that contains the arches) are depicted jointly glued to the section $\Sigma _b$

Theorem 1

For any natural number $m\ge 1$, the system (7) has an ejection–collision orbit of type

$$\begin{aligned} ({\underline{a}},\overset{m)}{\ldots },a), \quad \hbox {and} \quad ({\underline{b}},\overset{m)}{\ldots },b). \end{aligned}$$

Proof

From Lemma 2, recall that $J^{a,b}$ and $K^{a,b}$ are the four arcs that correspond to the first intersection of the unstable ${W}^u(E^+)$ and stable $W^s(E^-)$ manifolds, respectively, with $\Sigma _{a,b}$. We give a proof of the existence of ECOs with only collisions of type b. The result for the other type of ECOs follows by repeating the same arguments considering the other branches of the invariant manifolds and section $\Sigma _a$.

For $n=1$, from Lemma 2 and the ordering (13), it follows that $J^b\cap K^b \ne \emptyset$. Let us denote by $E_1 \in J^b\cap K^b$ the point such that the arc $K^b_1:=\langle q_1^-,E_1 \rangle \subset K^b$ does not intersect $J^b$ except at $E_1$. Clearly $\Phi _t(E_1)\rightarrow E^{\pm }$ for $t\rightarrow \mp \infty$ with no other partial collisions. Thus, it is an ECO of type (b), see Fig. 8.

Fig. 9

Schematic idea of the proof of Theorem 1

To prove the claim for any $m>1$, we will follow the stable manifold $W^s(E^-)$ backwards in time to look for intersections with $J^b$. Recall that ${{\mathcal {P}}}$ is the Poincaré map (see (11)). Notice that ${{\mathcal {P}}}$ and ${{\mathcal {P}}}^{-1}$ are defined for any point on $\Sigma$ that does not correspond to an ECO.

We claim that ${{\mathcal {P}}}^{-1}({{\,\mathrm{int}\,}}(K^b_1))$ is an arc contained in $\Sigma _b$ whose closure is the arc $\langle q_2^-,s_1^- \rangle$, that is, $\overline{{{\mathcal {P}}}^{-1}({{\,\mathrm{int}\,}}(K^b_1))}=\langle q_2^-,s_1^- \rangle$. On the one hand, it is clear that ${{\mathcal {P}}}^{-1}(q_1^-)=q_2^-$. Consider $Z \in K^b_1$ close to $E_1$, and its orbit $\Phi _t(Z)$. Applying the same argument as in Lemma 2, the trajectory in backwards time will have a close passage to the equilibrium point $E^+$ and then will follow the branch $W^s_-(E^+)$. Therefore,

$$\begin{aligned} \lim _{\underset{Z\in K^b_1}{Z \rightarrow E_1}} {{\mathcal {P}}}^{-1}(Z) = s_1^-. \end{aligned}$$

Using the ordering of the points along $\Sigma _b$ (see Sect. 3.1 and Fig. 5), ${{\mathcal {P}}}^{-1}({{\,\mathrm{int}\,}}(K^b_1))$ intersects $J^b$ at a point that corresponds to an ECO of type (b, b).

Now consider $E_2\in {{\mathcal {P}}}^{-1}({{\,\mathrm{int}\,}}(K^b_1))\cap J^b$ such that the arc $K^b_2:=\langle q_2^-,E_2 \rangle \subset \langle q_2^- , s_1^-\rangle$ does not intersect $J^b$ except at $E_2$. Using the same argument as before, $\overline{{{\mathcal {P}}}^{-1}({{\,\mathrm{int}\,}}(K^b_2))} = \langle q_3^-,s_1^- \rangle \subset \Sigma _b$, which intersects $J^b$. Therefore, there exists an ECO of type (b, b, b).

By induction, ${\overline{\mathcal {P}^{-1}({{\,\mathrm{int}\,}}(K^b_{m-1}))}}=\langle q_m^-, s_1^- \rangle$ and there exists $E_m\in {{\mathcal {P}}}^{-1}({{\,\mathrm{int}\,}}(K^b_{n-1}))\cap J^b$ such that the arc $K^b_m:=\langle q_m^-,E_m \rangle \subset \langle q_m^-, s_1^- \rangle$ does not intersect $J^b$ except at point $E_m$. Therefore, for each m, there exists a point $E_m$ on $\Sigma _b$ that corresponds to an ECO of type $(b,b,\overset{m)}{\ldots },b)$, with m partial collisions of type b. $\square$

We notice that the results and proofs of Lemma 2 and Theorem 1 follow the same arguments as in the case of the C3BP (Kaplan 1999) or in the SC4BP (Lacomba and Medina 2004). We remark that we are analyzing a more general setting.

4.1 Non-degenerate Cases

Next, we will prove the existence of ECO exhibiting different number and type of partial collisions. The results will depend on the behavior of the 1D-invariant manifolds contained in the collision manifold ${\mathcal {C}}$, classified in types I, II, III and IV in Sect. 3.1, and the orderings explained in that section.

Theorem 2

Suppose that $W^u_{\pm }(E^-)$ are of type I, and let $n\ge 1$ be the number of full turns performed by the branches of the 1D-invariant manifolds before escaping through different arms of ${{\mathcal {C}}}$. Then,

• (a) There exist ejection–collision orbits exhibiting $2n+1$ collisions of types $(\underline{b,a},\overset{n)}{\ldots },b,a,b)$         and         $(\underline{a,b},\overset{n)}{\ldots },a,b,a).$

• (b) There exist ejection–collision orbits exhibiting any sequence that can be obtained by the following graph:

Proof

Recall that the fact that $W^u_{\pm }(E^-)$ are of type I means that the branches perform n full turns and exhibit the following behaviors, respectively (see Table 1 and Fig. 3, top left):

$$\begin{aligned} (\underline{b,a},\overset{n)}{\ldots },b,a,b,b,\ldots ), \quad (\underline{a,b},\overset{n)}{\ldots },a,b,a,a,\ldots ). \end{aligned}$$

Therefore, as shown in Sect. 3.1, the intersections of the 1D-invariant manifolds with the section $\Sigma$ give the sequences $u^{\pm }_j$, $s^{\pm }_k$ with a specific ordering, see also Fig. 5.

From Lemma 2, $K^{b}$ and $J^{b}$ are the arcs that correspond to the first intersection, backwards and forwards in time, of $W^s(E^-)$ and $W^u(E^+)$ with $\Sigma _b$, respectively (similarly, $K^a$ and $J^a$ and the section $\Sigma _a$). In Theorem 1, we have proved that $J^b\cap K^b \ne \emptyset$ ($J^a\cap K^a \ne \emptyset$).

The arguments are done by iterating the Poincaré map ${\mathcal {P}}$ backwards in time and following the preimages of the stable manifold $W^s(E^-)$ to look for intersections with $J^{a/b}$.

Remark. In most of the figures that illustrate the proofs, for simplicity, those arcs that intersect are shown as if they would intersect only once. In general, this is not necessarily the case. For this reason, in the proofs the reader will find points like E and ${\widetilde{E}}$ that in the figures seem to be the same one, but they are not in general.

• (a) First, we shall prove the existence of ECO of the form $(\underline{b,a},\overset{n)}{\ldots },b,a,b)$. The existence of an ECO of type $(\underline{a,b},\overset{n)}{\ldots },a,b,a)$ can be obtained repeating similar arguments using the arcs $J^a$ and $K^a$. Consider ${\widetilde{E}}_1 \in J^b\cap K^b$ such that the arc ${\widetilde{K}}^b:=\langle {\widetilde{E}}_1,s_1^- \rangle \, \subset K^b$ does not intersect $J^b$ except at ${\widetilde{E}}_1$, see Fig. 10. Clearly, ${{\mathcal {P}}}^{-1}(s_1^-)=s_2^-$ and

  $$\begin{aligned} \lim _{\underset{Z\in {\widetilde{K}}^b}{Z \rightarrow {\widetilde{E}}_1}} {{\mathcal {P}}}^{-1}(Z) = s_1^+. \end{aligned}$$

  Therefore, $\overline{{\mathcal {P}}^{-1}({{\,\mathrm{int}\,}}({\widetilde{K}}^b))}=\langle s_2^-,s_1^+ \rangle$ is a continuous arc contained in $\Sigma _a$. Let us suppose first that $\langle s_2^-,s_1^+ \rangle \cap J^a = \emptyset$, see Fig. 10, left. Therefore, we can take its preimage:

  $$\begin{aligned} \overline{{\mathcal {P}}^{-2}({{\,\mathrm{int}\,}}({\widetilde{K}}^b))}= {\mathcal {P}}^{-1}(\langle s_2^-,s_1^+ \rangle )=\langle {\mathcal {P}}^{-1}(s_2^-), {\mathcal {P}}^{-1}(s_1^+) \rangle =\langle s_3^-,s_2^+ \rangle , \end{aligned}$$

  which is an arc in $\Sigma _b$. Suppose also that we can repeat the argument $2n-1$ times. That is, suppose that iterating the Poincaré map ${{\mathcal {P}}}$ backwards, all the preimages

  $$\begin{aligned} \overline{{\mathcal {P}}^{-k}({{\,\mathrm{int}\,}}({\widetilde{K}}^b))} \cap W^u(E^+)=\langle s_{k+1}^-,s_{k}^+ \rangle \cap W^u(E^+) = \emptyset , \end{aligned}$$

  for $k=1,\ldots , 2n-1$. Then,

  $$\begin{aligned} \overline{{\mathcal {P}}^{-(2n)}({{\,\mathrm{int}\,}}({\widetilde{K}}^b))}=\langle s_{2n+1}^-,s_{2n}^+ \rangle \in \Sigma _b, \end{aligned}$$

  and it intersects $J^b=\langle u_1^+,p_1^+ \rangle$ because of the known ordering of the sequences on ${\mathcal {C}} \cap \Sigma _b$: $s_{2n+1}^-< u_1^+< s_{2n}^+.$ In consequence, $J^b\cap {\mathcal {P}}^{-(2n)}({{\,\mathrm{int}\,}}({\widetilde{K}}^b)) \ne \emptyset$. The orbit through any of the intersection points is an ECO of type $(\underline{b,a},\overset{n)}{\ldots },b,a,b)$, see Fig. 10, left. Now suppose that one of the preimages $\overline{{\mathcal {P}}^{-k}({{\,\mathrm{int}\,}}({\widetilde{K}}^b))}$ already intersects $W^u(E^+)$. We can suppose that $k=1$ is the first preimage of ${\widetilde{K}}^b$ that intersects the unstable manifold (the argument is similar for any other k), that is,

  $$\begin{aligned} \langle s_2^-,s_1^+ \rangle \cap J^a \ne \emptyset , \end{aligned}$$

  see Fig. 10, right. Then, we can consider $F_1$ a point on that intersection such that $\langle s_2^-,F_1 \rangle \subset \langle s_2^-,s_1^+ \rangle$ does not intersect $J^a$ except at $F_1$. Then, we take its preimage

  $$\begin{aligned} \overline{{\mathcal {P}}^{-1}({{\,\mathrm{int}\,}}(\langle s_2^-,F_1 \rangle ))}= \langle s_3^-,s_1^- \rangle \subset \Sigma ^b. \end{aligned}$$

  If this arc does not intersect $J^b$, then we consider its preimage $\langle s_4^-,s_2^-\rangle$. If it intersects, then there exists $F_2$ such that $\langle s_3^-,F_2 \rangle \subset \langle s_3^-,s_1^- \rangle$ does not intersect $J^b$ except at $F_2$, see Fig. 10, right. And we can consider its preimage, which is $\langle s_4^-,s_1^+\rangle$. Repeating the argument, at each step we can consider an appropriate subarc $\langle s_{k+1}^-,F_k \rangle$ such that the preimage of its interior is $\langle s_{k+2}^-,s_j^{\pm } \rangle$ for a certain $j\le k$. After 2n iterations of ${{\mathcal {P}}}^{-1}$, we will end with an arc

  $$\begin{aligned} \langle s_{2n+1}^-, s_{j}^-\rangle , \quad j \le 2n \end{aligned}$$

  that intersects $J^b$. Therefore, we obtain an ECO of type $(\underline{b,a},\overset{n)}{\ldots },b,a,b)$, see Fig. 10, right. Notice that in the above case, other ECO with less number of partial collisions exists, although a priori we cannot ensure their existence.

• (b) We notice that the existence of each one of the types that appear in the vertices of the diagram is already shown in Theorem 1 and the previous item. Furthermore, we will prove in detail the existence of the following diagram:

The ECOs corresponding to reverse the arrows can be proved using Proposition 6, and the remaining ones can be obtained by the fact that the 1D-invariant manifolds $W^u(E^-)$ and $W^s(E^+)$ are of type I, repeating the same arguments that we will show but using the negative branches of the manifolds.

First, we prove the connection

that is, the existence of ECOs of type $(\underline{b,a},\overset{n)}{\ldots },b,a,b,{\underline{b}},\overset{m)}{\ldots },b)$, for any $m\in {{\mathbb {N}}}$.

As seen in the proof of Theorem 1, for any $m>0$ an ECO of type $(b,\overset{m+1)}{\ldots },b)$ is obtained from the arc $K_1^b\subset K^b$, by showing the existence of a sequence of arcs $K_j^b\subset \overline{{\mathcal {P}}^{-1} ({{\,\mathrm{int}\,}}(K_{j-1}^b))}=\langle q_{j}^-,s_1^- \rangle \subset \Sigma ^b, j=2,\dots ,m+1$. See Fig. 9.

Consider $\overline{{\mathcal {P}}^{-1}({{\,\mathrm{int}\,}}(K_{m}^b))}= \langle q_{m+1}^-,s_1^- \rangle$, which intersects $J^b$, and consider a point ${\widetilde{E}}_{m+1}$ of that intersection such that $\langle {\widetilde{E}}_{m+1},s_1^- \rangle$ does not intersect $J^b$ except at ${\widetilde{E}}_{m+1}$. We now repeat the process explained in the previous item: $\overline{{\mathcal {P}}^{-1}({{\,\mathrm{int}\,}}(\langle {\widetilde{E}}_{m+1},s_1^- \rangle ))}=\langle s_2^-,s_{1}^+ \rangle$ in $\Sigma _a$, and iterating the Poincaré map backwards, the preimages belong alternatively to $\Sigma _a$ and $\Sigma _b$ until

$$\begin{aligned} \overline{{\mathcal {P}}^{-(2n)}({{\,\mathrm{int}\,}}(\langle {\widetilde{E}}_{m+1},s_1^- \rangle ))}=\langle s_{2n+1}^-,s_{2n}^+ \rangle \in \Sigma _b, \end{aligned}$$

which intersects $J^b$. See Fig. 11 left.

Second, we prove the connection

that is, the existence of an ECO of type $({\underline{a}},\overset{m)}{\ldots },a,\underline{b,a},\overset{n)}{\ldots } b,a,b)$, for any $m\in {{\mathbb {N}}}$.

In this case, we start with the last arc in the proof of item (a), $\overline{{\mathcal {P}}^{-(2n)}({{\,\mathrm{int}\,}}({\widetilde{K}}^b))}=\langle s_{2n+1}^-,s_{2n}^+ \rangle$ which intersects $J^b$ (recall Fig. 10). Consider point ${\widetilde{C}}_1$ on that intersection such that the arc $\langle {\widetilde{C}}_1,s_{2n}^+ \rangle \subset \langle s_{2n+1}^-,s_{2n}^+ \rangle$ does not have any point in common with $J^b$ except ${\widetilde{C}}_1$. Therefore, point ${\widetilde{C}}_1$ belongs to an ECO of type $(\underline{b,a},\overset{n)}{\ldots } b,a,b)$, $\overline{{\mathcal {P}}^{-1}({{\,\mathrm{int}\,}}(\langle {\widetilde{C}}_1,s_{2n}^+ \rangle ))}=\langle s_{2n+1}^+,s_1^+ \rangle$ belongs to $\Sigma _a$ and intersects the arc $J^a=\langle u_1^-,p_1^- \rangle \subset W^u(E^+)$. Each of these intersections correspond to an ECO of type $(a,\underline{b,a},\overset{n)}{\ldots } b,a,b)$.

Next, let $F_1\in \langle s_{2n+1}^+,s_1^+ \rangle \cap J^a$ such that that $\langle s_{2n+1}^+, F_1 \rangle$ does not intersect $J^a$ except at $F_1$. Its preimage $\overline{{\mathcal {P}}^{-1}({{\,\mathrm{int}\,}}(\langle s_{2n+1}^+, F_1 \rangle )}= \langle s_{2n+2}^+,s_1^+ \rangle$ also intersects $J^a$. Any point of that intersection corresponds to an ECO of type $(a,a,\underline{b,a},\overset{n)}{\ldots }, b,a,b)$. By the iteration of this process, we prove the existence of ECOs of type $({\underline{a}},\overset{m)}{\ldots },a,\underline{b,a},\overset{n)}{\ldots } b,a,b)$. See Fig. 11 right.

Third, we prove the connection

that is, the existence of an ECO of type $(\underline{a,b},\overset{n)}{\ldots },a,b,a,\underline{b,a},\overset{n)}{\ldots },a,b)$.

In the previous reasoning, we have seen that the orbit through ${\widetilde{C}}_1$ is an ECO of type $(\underline{b,a},\overset{n)}{\ldots } b,a,b)$ and ${\mathcal {P}}^{-1}({{\,\mathrm{int}\,}}(\langle {\widetilde{C}}_1,s_{2n}^+ \rangle ) \cap J^a \ne \emptyset$. Consider now a point on that intersection ${\widetilde{F}}_1$ such that $\langle {\widetilde{F}}_1,s_1^+ \rangle$ does not intersect $J^a$ except at ${\widetilde{F}}_1$. Then $\overline{{\mathcal {P}}^{-1}({{\,\mathrm{int}\,}}(\langle {\widetilde{F}}_1,s_1^+ \rangle ))}=\langle s_2^+,s_1^- \rangle$ is an arc in $\Sigma _b$. We iterate the Poincaré map ${{\mathcal {P}}}$ backwards:

$$\begin{aligned} \overline{{\mathcal {P}}^{-k}({{\,\mathrm{int}\,}}(\langle {\widetilde{F}}_1,s_1^+ \rangle ))}= \langle s_{k+1}^+,s_k^- \rangle \end{aligned}$$

for $k=2,\ldots ,2n-1$, provided that all the preimages do not intersect the unstable manifold. For simplicity, we will suppose this is the case. If ${\mathcal {P}}^{-k}({{\,\mathrm{int}\,}}(\langle {\widetilde{F}}_1,s_1^+ \rangle )) \cap W^u(E^+) \ne \emptyset$ for some k, then we proceed as in item (a). The last iterate

$$\begin{aligned} \overline{{\mathcal {P}}^{-2n}({{\,\mathrm{int}\,}}(\langle {\widetilde{F}}_1,s_1^+ \rangle ))} = \langle s_{2n+1}^+,s_{2n}^- \rangle \subset \Sigma _a, \end{aligned}$$

which intersects $J^a$. The points on that intersection correspond to ECOs of type $(\underline{a,b},\overset{n)}{\ldots },a,b,a,\underline{b,a},\overset{n)}{\ldots },a,b)$, see Fig. 12.

This concludes the proof of Theorem 2. $\square$

Fig. 10

Schematic idea of the proof of the existence of ECO of type $(\underline{b,a},\overset{n)}{\ldots },b,a,b)$

Fig. 11

Schematic idea of the proof of the existence of ECO of type $(\underline{b,a},\overset{n)}{\ldots },b,a,b,{\underline{b}},\overset{m)}{\ldots },b)$ (left) and $({\underline{a}},\overset{m)}{\ldots },a,\underline{b,a},\overset{n)}{\ldots } b,a,b)$ (right)

Fig. 12

Schematic idea of the proof of the existence of ECO of type $(\underline{a,b},\overset{n)}{\ldots },a,b,a,\underline{b,a},\overset{n)}{\ldots },a,b)$. It starts with the existence of ${\widetilde{C}}_1$, see the text for more details and Fig. 11

Remark: Notice that the proofs in Theorem 2 are based on the dynamical behavior of the 1D-invariant manifolds $W^s(E^+)$ and $W^u(E^-)$ and the fact that their branches are of type I and they escape through different arms of the collision manifold after performing n full turns. If the 1D-invariant manifolds are of type II, the behavior is similar with the only difference that they make n and a half full turns. Therefore, using similar arguments, the next result can be demonstrated.

Theorem 3

Suppose that $W^u_{\pm }(E^-)$ are of type II, so they perform n and a half number of full turns ($n\ge 1$), before escaping through different arms of ${{\mathcal {C}}}$. Then:

• (a) There exist ejection–collision orbits exhibiting $2(n+1)$ collisions of types $(\underline{b,a},\overset{n+1)}{\ldots },b,a)$         and         $(\underline{a,b},\overset{n+1)}{\ldots },a,b).$

• (b) There exist ejection–collision orbits exhibiting any sequence that can be obtained by the following graph:

Next we present the results of the existence of ECO in cases III and IV of the 1D-invariant manifolds.

Theorem 4

Consider the 1D-invariant manifold $W^u_{\pm }(E^-)$:

• (1) Suppose they are of type III, so the right and left branches perform n and n and a half, respectively, full turns before escaping through the right arm of ${{\mathcal {C}}}$. Then, there exist ejection–collision orbits of the following type for any integer $k\ge 1$:

  

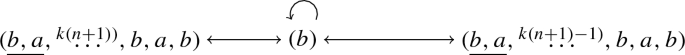
• (2) Suppose they are of type IV, so the right and left branches perform n and a half and n, respectively, full turns before escaping through the left arm of ${{\mathcal {C}}}$. Then, there exist ejection–collision orbits of the following type for any integer $k\ge 1$: integer $k\ge 1$:

  

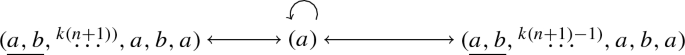
Proof

We prove the existence of ECOs in the first case (when the 1D-invariant manifolds are of type III). The case of invariant manifolds of type IV can be obtained straightforward by interchanging a and b.

First, we prove the existence of ECO of the desired type for $k=1$. The existence of ECOs of type $(\underline{b,a},\overset{n)}{\ldots },b,a,b)$ relies on the fact that the branch $W^u_{+}(E^-)$ (and its symmetric one, $W^s_{-}(E^+)$) escapes through the right arm of ${{\mathcal {C}}}$, which is the same scenario than in Theorem 2. Similarly, the proof of the existence of ECOs that can be obtained from the graph

follows the same arguments as in Theorem 2. See Fig. 13 and the iterations ${\mathcal {P}}^{-k}({{\,\mathrm{int}\,}}(\langle {\widetilde{E}}_1,s_1^- \rangle ))$, $k=1,\ldots ,2n$.

Fig. 13

Schematic idea of the proof of the existence of ECO: 1) of type $(\underline{b,a},\overset{n)}{\ldots },b,a,b)$ by the iteration of the Poincaré map backwards of the arc $\langle {\widetilde{E}}_1,s_1^- \rangle$; 2) of type $(b,a,\underline{b,a},\overset{n)}{\ldots },b,a,b)$ following the previous argument and iterating backwards the arc $\langle {\widetilde{C}}_1,s_{2n}^+ \rangle$

From the last step, there exists a point ${\widetilde{C}}_1 \in {\mathcal {P}}^{-(2n)}({{\,\mathrm{int}\,}}(\langle {\widetilde{E}}_1,s_1^- \rangle ))$ that corresponds to an ECO of type $(\underline{b,a},\overset{n)}{\ldots },b,a,b)$, and such that the arc $\langle {\widetilde{C}}_1, s_{2n}^+ \rangle$ does not intersects $J^b$. By iterating the Poincaré map backwards,

$$\begin{aligned} \overline{ {\mathcal {P}}^{-1}({{\,\mathrm{int}\,}}(\langle {\widetilde{C}}_1,s_{2n}^+ \rangle ))}=\langle s_{2n+1}^+,s_1^+ \rangle , \qquad \overline{ {\mathcal {P}}^{-2}({{\,\mathrm{int}\,}}(\langle {\widetilde{C}}_1,s_{2n}^+ \rangle ))}=\langle s_{2n+2}^+,s_2^+ \rangle . \end{aligned}$$

The last arc intersects $J^b$ (see Fig. 13), so there exists an ECO of type $(\underline{b,a},\overset{n+1)}{\ldots },b,a,b)$.

Now, consider the last arc $\langle s_{2n+2}^+,s_2^+ \rangle$, and $C_2$ and ${\widetilde{C}}_2$ such that the arcs

$$\begin{aligned} \langle s_{2n+2}^+, C_2 \rangle , \qquad \langle {\widetilde{C}}_2,s_2^+ \rangle , \end{aligned}$$

do not intersect $J^b$ except at $C_2$ and ${\widetilde{C}}_2$, respectively. Iterating the arc $\langle s_{2n+2}^+, C_2 \rangle$ using ${\mathcal {P}}$ backwards repeatedly, we can obtain an ECO of type

Using Proposition 6, we also obtain the reverse sequence. This concludes the proof for $k=1$.

To prove the case $k=2$, we apply the above arguments to the arc $\langle {\widetilde{C}}_2,s_2^+ \rangle$. First,

$$\begin{aligned} \overline{ {\mathcal {P}}^{-1}({{\,\mathrm{int}\,}}(\langle {\widetilde{C}}_2,s_{2}^+ \rangle ))}=\langle s_{3}^+,s_1^+ \rangle , \quad \ldots \quad \overline{ {\mathcal {P}}^{-(2n)}({{\,\mathrm{int}\,}}(\langle {\widetilde{C}}_2,s_{2}^+ \rangle ))}=\langle s_{2n+2}^+,s_{2n}^+ \rangle . \end{aligned}$$

The later intersects $J^b$, which corresponds to an ECO of type $(\underline{b,a},\overset{2n+1)}{\ldots },b,a,b)$. Next, from the last arc, we can consider again two subarcs: one of them is iterated backwards through the Poincaré map to add as many collisions of type b as desired; the other one is iterated backwards twice to obtain an ECO of type $(b,a,\underline{b,a},\overset{2n+1)}{\ldots },b,a,b)=(b,a,\overset{2n+2)}{\ldots },b,a,b)$. From this ECO, we can consider two new arcs: one of them allows to prove that we can add a sequence of collisions of type b; to finish the proof for $k=2$, the other one is the first step to construct the ECOs of the case $k=3$.

By iterating the process, the proof is completed. $\square$

4.2 Degenerate Cases

Next we consider two of the degenerate cases, the non-symmetric ones (see Sect. 3.1):

• Type $D_1$: there is a heteroclinic connection given by $W^u_{+}(E^-) = W^s_{-}(E^+)$, while the other branches escape along the right arm of the collision manifold. Let n be the number of full turns and a half performed by the coincident branches.

• Type $D_2$: there is a heteroclinic connection given by $W^u_{-}(E^-) = W^s_{+}(E^+)$, while the other branches escape along the left arm of the collision manifold. Let n be the number of full turns and a half performed by the coincident branches.

In the symmetric degenerate case, the only ECOs that can be proved to exist are the ones listed in Theorem 1. Next results state the ECO that exist for sure in the non-symmetric cases.

Theorem 5

Consider the 1D-invariant manifold $W^u_{\pm }(E^-)$, $W^s_{\pm }(E^+)$ of a degenerate type.

• (1) Suppose they are non-symmetric of type $D_1$, and n and a half be the full turns of the heteroclinic connection. Then, there exist ejection–collision orbits of the following type for any integer $k\ge 1$:

  

• (2) Suppose they are non-symmetric of type $D_2$, and n and a half be the full turns of the heteroclinic connection. Then, there exist ejection–collision orbits of the following type for any integer $k\ge 1$:

  

The proof follows the arguments shown in Theorems 1 and 2. We illustrate the case of type $D_1$ for $n=2$ in Fig. 14.

Fig. 14

Schematic idea of the proof of the existence of ECO in the case $D_1$