Abstract
In this paper, we contribute to studying the issue of quasistatic limit in the context of Griffith’s theory by investigating a one-dimensional debonding model. It describes the evolution of a thin film partially glued to a rigid substrate and subjected to a vertical loading. Taking viscosity into account and under suitable assumptions on the toughness of the glue, we prove that, in contrast to what happens in the undamped case, dynamic solutions converge to the quasistatic one when inertia and viscosity go to zero, except for a possible discontinuity at the initial time. We then characterise the size of the jump by means of an asymptotic analysis of the debonding front.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In most of the models within the theory of linearly elastic fracture mechanics, the evolution process is assumed to be quasistatic, namely the body is at equilibrium at every time. This postulate is believed to be reasonable, assuming that inertial effects can be neglected if the speed of external loading is very slow with respect to the one of internal oscillations. However, its mathematical proof is really far from being achieved in the general framework, due to the high complexity and diversity of the phenomena under consideration. We can rephrase the problem, commonly referred as quasistatic limit issue, as follows: is it true that quasistatic evolutions can be approximated by dynamic ones when the external loading becomes slower and slower, or equivalently the speed of internal vibrations becomes faster and faster? Nowadays, only partial results on the theme are available; we refer for instance to Lazzaroni et al. (2018) and Roubíček (2013) for damage models, to Dal Maso and Scala (2014) in a case of perfect plasticity and to Lazzaroni and Nardini (2018a, b) for the undamped version of the debonding model we analyse in this work. The issue of quasistatic limit has also been studied in a finite-dimensional setting where, starting from the works of Agostiniani (2012) and Zanini (2007) and with the contribution of Nardini (2017), an almost complete understanding on the topic has been reached in Scilla and Solombrino (2019). A common feature appearing both in finite both in infinite dimension is the validation of the quasistatic approximation only in the presence of a damping term in the dynamic model. Because of this consideration, in this paper we resume a particular kind of debonding model previously inspected in Lazzaroni and Nardini (2018b) taking in addition viscosity into account. In Lazzaroni and Nardini (2018b), the authors proved that, due to lack of viscosity, the resulting limit evolution turns out not to be quasistatic, even in the case of a constant toughness of the glue between the film and the substrate. Thanks to viscosity, we are instead able to give a positive answer to the quasistatic limit question in the model under examination, covering the case of quite general toughnesses.
We refer to Burridge and Keller (1978), Freund (1990), Hellan (1978a, b), Hellan (1984) for an introduction to one-dimensional debonding models from an engineering point of view; a first analysis on the quasistatic limit in these kinds of models is instead developed in Dumouchel et al. (2008), Lazzaroni et al. (2012). The rigorous mathematical formulation we will follow throughout the paper has been introduced in Dal Maso et al. (2016), used in Lazzaroni and Nardini (2018a, b), Lazzaroni and Nardini (2017) for the undamped case, and adopted in Riva (2019) and Riva and Nardini (2018) for well-posedness results in the damped case.
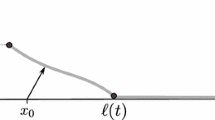
The mechanical system we consider describes the debonding of a perfectly flexible, inextensible and homogeneous thin film initially glued to a flat rigid substrate and subjected at an endpoint to a vertical loading w and to a horizontal tension which keeps the speed of sound in the film constant (in the whole paper normalised to one). The deformation of the film takes place in the half plane \(\{(x,y)\mid x\ge 0\}\) and at time \(t\ge 0\) is given by \((x,0)\mapsto (x+h(t,x),u(t,x))\), where the functions h and u are the horizontal and the vertical displacement of the point (x, 0), respectively. In the reference configuration, the debonded region is \(\{(x,0)\mid 0\le x< \ell (t)\}\), where \(\ell \) is a nondecreasing function representing the debonding front and satisfying \(\ell (0)=\ell _0>0\). See Fig. 1. By linear approximation and inextensibility of the film, the horizontal displacement h is uniquely determined by the vertical one u [see Dal Maso et al. 2016 or Riva and Nardini (2018)], so the only unknowns of the problem are u and the debonding front \(\ell \).
Since our aim is the analysis of the behaviour of the system in the case of slow loading and slow initial velocity, we introduce a small parameter \(\varepsilon \) in the model, so that the vertical displacement \(u_\varepsilon \) (we add the subscript to stress the dependence on \(\varepsilon \)) solves the dynamic problem:
where \(u_0\) and \(u_1\) are given initial data, while \(\nu \ge 0\) is a parameter which tunes viscosity. The evolution of the debonding front \(\ell _\varepsilon \) is instead established by suitable energy criteria, in the context of Griffith’s theory. Indeed, it has to fulfil, together with the vertical displacement \(u_\varepsilon \), an energy–dissipation balance and a maximum dissipation principle. As proved in Dal Maso et al. (2016), Riva and Nardini (2018), they can be equivalently rewritten in the form of the following system, called Griffith’s criterion:
The function \(\kappa \) appearing in the system is the toughness of the glue between the film and the substrate, while \(G_{{\dot{\ell }}_\varepsilon (\cdot )}(\cdot )\) is the so-called dynamic energy release rate. Its properties will be briefly explained in Sect. 1; we just want to say that if the vertical displacement is regular enough, then it can be written as \(G_{{\dot{\ell }}_\varepsilon (t)}(t)=\frac{1}{2} (1-{\dot{\ell }}_\varepsilon (t)^2)(u_\varepsilon )_x(t,\ell _\varepsilon (t))^2\). For more details, we refer to Dal Maso et al. (2016) and Riva and Nardini (2018).
In Eq. (0.1), the speed of the travelling waves is one, while the one of the external loading and initial velocity is of order \(\varepsilon \). Actually, we are interested in studying the limit as the speed of internal waves becomes faster and faster, so we need to consider the time-rescaled functions \(\Big ({u^\varepsilon }(t,x),{\ell ^\varepsilon }(t)\Big ):=\Big (u_\varepsilon \left( \frac{t}{\varepsilon },x\right) ,\ell _\varepsilon \left( \frac{t}{\varepsilon }\right) \Big )\), which solve:
plus the rescaled Griffith’s criterion (1.7) ruling the growth of \({\ell ^\varepsilon }\). In this rescaled setting, internal waves move with speed \(1/\varepsilon \), while the speed of the loading w and of the velocity \(u_1\) is of order one. The aim of the work is thus to investigate the limit as \(\varepsilon \) goes to \(0^+\) of this rescaled pair \(({u^\varepsilon },{\ell ^\varepsilon })\). To develop the analysis, several assumptions on the toughness \(\kappa \) will be crucial; for the sake of clarity, we list them here:
- (K0)
the function \(\kappa \) is not integrable in \([\ell _0,+\infty )\);
- (K1)
\(x\mapsto x^2\kappa (x)\) is nondecreasing on \([\ell _0,+\infty )\);
- (K2)
\(x\mapsto x^2\kappa (x)\) is strictly increasing on \([\ell _0,+\infty )\);
- (K3)
\(x\mapsto x^2\kappa (x)\) is strictly increasing on \([\ell _0,+\infty )\) and its derivative is strictly positive almost everywhere;
- (KW)
\(\displaystyle \lim \limits _{x\rightarrow +\infty }x^2\kappa (x)>\frac{1}{2}\max \limits _{t\in [0,T]}w(t)^2\) for every \(T>0\), and \(\displaystyle \kappa (\ell _0)\ge \frac{1}{2} \frac{w(0)^2}{\ell _0^2}\).
Condition (K0) states that an infinite amount of energy is needed to debond all the film, while conditions (K1), (K2), (K3) prevent the toughness from being too oscillating; (KW) is instead related to a stability condition for quasistatic evolutions; see (s2) in Proposition 2.3.
The paper is organised as follows. Section 1 deals with the dynamic model: we first introduce the energy criteria governing the evolution of the debonding front, see (1.5), and we present the concept of (dynamic) Griffith’s criterion. Then, we collect the known results, proved in Dal Maso et al. (2016), Lazzaroni and Nardini (2018b), Riva (2019) and Riva and Nardini (2018), on the time-rescaled problem (0.2) coupled with Griffith’s criterion. In particular, Theorem 1.6 states that there exists a unique dynamic evolution \(({u^\varepsilon },{\ell ^\varepsilon })\) for the debonding model and provides a representation formula for the vertical displacement \({u^\varepsilon }\).
In Sect. 2, we instead analyse the notion of quasistatic evolution in our framework; we refer to Mielke and Roubíček (2015) for the general topic of quasistatic and rate-independent processes. We first present the two different concepts of energetic and quasistatic solutions to our debonding problem (related to global and local minima of the energy, respectively), showing their equivalence under the strongest assumption (K3). Assuming in addition (KW), we then provide an existence and uniqueness result by writing down explicitly the solution; see Theorem 2.9.
The last two sections are devoted to the study of the limit of the pair \(({u^\varepsilon },{\ell ^\varepsilon })\) as \(\varepsilon \) goes to \(0^+\). In Sect. 3, we exploit the presence of the viscous term in the wave equation to gain uniform bounds and estimates for the vertical displacement \({u^\varepsilon }\) and the debonding front \({\ell ^\varepsilon }\). Main estimate (3.6) is an adaptation to our time-dependent domain setting of the classical estimate used to show exponential stability of the weakly damped wave equation; see for instance Misra and Gorain 2014. Of course, assumption \(\nu >0\) is crucial for its validity , while for the toughness only the minimal assumption (K0) is needed. It is worth noticing that in this section we do not make use of the explicit formula of the vertical displacement \({u^\varepsilon }\) given by Theorem 1.6, but we only need the fact that it solves Eq. (0.2).
Finally, in Sect. 4 we prove that if \(\nu >0\), namely when viscosity is taken into account, and requiring (K0) and (K3), the limit of dynamic evolutions \(({u^\varepsilon },{\ell ^\varepsilon })\) exists and it coincides with the quasistatic evolution we previously found in Sect. 2, except for a possible discontinuity at time \(t=0\) appearing if the initial position \(u_0\) is too steep; see Theorem 4.22. We first make use of the main estimate (3.6) proved in Sect. 3 to show the existence of the above limit; then, by means of the explicit representation formula of \({u^\varepsilon }\), we are able to pass to the limit in the stability condition of Griffith’s criterion and in the energy–dissipation balance (1.5a), getting a weak formulation of (s2) and (eb) in Proposition 2.3, conditions related to quasistatic evolutions; see Propositions 4.6 and 4.7. Up to this point, we only need the weakest assumption (K0), while to characterise the limit debonding front as the quasistatic one we need to require (K3) and to exploit the equivalence results of Sect. 2. We conclude the paper by giving a characterisation of the initial jump which might appear; we obtain this characterisation via an asymptotic analysis of the debonding front solving the unscaled coupled problem (4.15) and (4.16).
2 Notations
In this preliminary section, we collect some notation we will use several times throughout the paper. Similar notations have been introduced in Dal Maso et al. (2016), Riva and Nardini (2018) and also used in Lazzaroni and Nardini (2018a, b), Riva (2019).
Remark 0.1
In the paper, every function in the Sobolev space \(W^{1,p}(a,b)\), for \(-\infty<a<b<+\infty \) and \(p\in [1,+\infty ]\), is always identified with its continuous representative on [a, b].
Furthermore, the derivative of any function of real variable is denoted by a dot (i.e., \(\dot{f}\), \(\dot{\ell }\), \(\dot{\varphi }\), \(\dot{u}_0\)), regardless of whether it is a time or a spatial derivative.
Fix \(\ell _0>0\), \(\varepsilon >0\) and consider a function \({\ell ^\varepsilon }:[0,+\infty )\rightarrow [\ell _0,+\infty )\) satisfying:
These assumptions will be satisfied by the (rescaled) debonding front we will obtain in Theorem 1.6. Given such a function, for \(t\in [0,+\infty )\) we introduce:
and we define:
We notice that \(\psi ^\varepsilon \) is a bi-Lipschitz function since by (0.3b) it holds \(1\le \dot{\psi }^\varepsilon (t)< 2\) for almost every time, while \(\varphi ^\varepsilon \) turns out to be Lipschitz with \(0<{\dot{\varphi }}^\varepsilon (t)\le 1\) almost everywhere. Hence, \(\varphi ^\varepsilon \) is invertible and the inverse is absolutely continuous on every compact interval contained in \(\varphi ^\varepsilon ([0,+\infty ))\). As a by-product, we get that \(\omega ^\varepsilon \) is Lipschitz too and for a.e. \(t\in (\varepsilon \ell _0,+\infty )\) we have:
So also \(\omega ^\varepsilon \) is invertible and the inverse is absolutely continuous on every compact interval contained in \(\omega ^\varepsilon ([0,+\infty ))\). Moreover, given \(j\in \mathbb {N}\cup \{0\}\), and denoting by \((\omega ^\varepsilon )^j\) the composition of \(\omega ^\varepsilon \) with itself j times (whether it is well defined) one has:
It will be useful to define the sets:
For \((t,x)\in \Omega ^\varepsilon \), we also introduce:
In order to avoid the cumbersome definitions of \(m=m(\varepsilon ,t,x)\), \(n=n(\varepsilon ,t,x)\) and \(R^\varepsilon _i(t,x)\), we refer to the very intuitive Fig. 2.
Finally, for \(k\in \mathbb {N}\), let us define the spaces:
We say that a family \(\mathcal F\) is bounded in \(\widetilde{H}^k(0,+\infty )\) if for every \(T>0\) there exists a positive constant \(C_T\) such that \(\Vert u\Vert _{H^k(0,T)}\le C_T\) for every \(u\in \mathcal F\). We say that a sequence \(\{u_n\}_{n\in \mathbb {N}}\) converges strongly (weakly) to u in \(\widetilde{H}^k(0,+\infty )\) if for every \(T>0\) one has \(u_n\rightarrow u\) (\(u_n\rightharpoonup u\)) in \({H}^k(0,T)\) as \(n\rightarrow +\infty \).
3 Time-Rescaled Dynamic Evolutions
In this section, we give a presentation on the notion of dynamic evolutions for the considered debonding model, gathering all the known results about its well-posedness; see Theorems 1.6, 1.8 and Remark 1.7. We refer to Dal Maso et al. (2016), Lazzaroni and Nardini (2018b), Riva (2019) and Riva and Nardini (2018) for more details.
We fix \(\nu \ge 0\), \(\ell _0>0\), and we actually consider a slight generalisation of the rescaled problem (0.2):
in which also loading term and initial data depend on the (small) parameter \(\varepsilon >0\). We require they satisfy the following regularity assumptions:
and they fulfil the compatibility conditions:
Remark 1.1
By solution of problem (1.1), we mean an \(\widetilde{H}^1(\Omega ^\varepsilon )\) function which solves the (damped) wave equation in the sense of distributions in \(\Omega ^\varepsilon \) and attains the boundary values \({w^\varepsilon }\) and \(u^\varepsilon _0\) in the sense of traces, while the initial velocity \(u^\varepsilon _1\) in the sense of \(L^2(0,\ell _0)\).
To state the rules governing the evolution of the rescaled debonding front \({\ell ^\varepsilon }\), we consider the following rescaled energies, defined for \(t\in [0,+\infty )\):
They represent the sum of kinetic and (external) potential energy, the energy dissipated by viscosity and the work of the external loading, respectively. We refer to Dumouchel et al. (2008) and Lazzaroni et al. (2012) for more details about them. We postulate that our model is governed by an energy–dissipation balance and a maximum dissipation principle, namely the pair \(({u^\varepsilon },{\ell ^\varepsilon })\) has to satisfy:
where \(\kappa :[\ell _0,+\infty )\rightarrow (0,+\infty )\) is a measurable function representing the toughness of the glue, and:
where \(G^\varepsilon _{\varepsilon \alpha }\) is the (rescaled) dynamic energy release rate at speed \(\varepsilon \alpha \in [0,1)\). Formally, it can be seen as the opposite of the derivative of the total energy \(\mathcal E^\varepsilon +\mathcal A^\varepsilon +\mathcal W^\varepsilon \) with respect to the elongation of \({\ell ^\varepsilon }\) and it measures the amount of energy spent by the debonding process. In our context, it actually possesses an explicit formula, see (1.16), which for every \(\alpha \in [0,1/\varepsilon )\) can be expressed as:
being \(G^\varepsilon _0\) a given function depending on the data and on the debonding front \(\ell ^\varepsilon \) and the vertical displacement \(u^\varepsilon \) themselves. We refer to Dal Maso et al. (2016), Freund (1990), Lazzaroni and Nardini (2018b), Riva and Nardini (2018) and Slepyan (2002) for the rigorous definition and properties of the dynamic energy release rate and for the derivation of (1.6).
Remark 1.2
The maximum in (1.5b) is always achieved since by (1.6) the set \(\{\alpha \in [0,1/\varepsilon )\mid \kappa ({\ell ^\varepsilon }(t))\alpha =G^\varepsilon _{\varepsilon \alpha }(t)\alpha \}\) contains at most two elements.
As proved in Riva and Nardini (2018), the two principles (1.5) are equivalent to the (rescaled) dynamic Griffith’s criterion:
The first row is an irreversibility condition, which ensures that the debonding front can only increase, and moreover states that its velocity is always strictly less than \(1/\varepsilon \), namely the speed of internal waves; the second one is a stability condition and says that the dynamic energy release rate cannot exceed the threshold given by the toughness; the third one is simply the energy–dissipation balance (1.5a).
Remark 1.3
We recall that Griffith’s criterion (1.7) is also equivalent to an ordinary differential equation for \({\ell ^\varepsilon }\):
The reader pay attention to the presence of \(G^\varepsilon _0(t)\) instead of \(G^\varepsilon _{\varepsilon {\dot{\ell }}(t)}(t)\) in (1.8); see Dal Maso et al. (2016) and Riva and Nardini (2018) for more details. We will not make use of this formula in this work, but it can be helpful for further analysis and researches on the topic.
Before presenting the known results about the coupled problem (1.1) and (1.7), we introduce a function which will be useful in a representation formula for the solution of (1.1). Given a function \(\Theta \in \widetilde{L}^2(\Omega ^\varepsilon )\) we define:
where \(R^\varepsilon _\pm (t,x)\) are as in (0.6). Here are listed the main properties of \(H^\varepsilon \), under the assumption that \({\ell ^\varepsilon }\) satisfies (0.3):
Proposition 1.4
Let \(\Theta \in \widetilde{L}^2(\Omega ^\varepsilon )\), then the function \(H^\varepsilon [\Theta ]\) introduced in (1.9) is continuous on \(\overline{\Omega ^\varepsilon }\) and belongs to \(\widetilde{H}^1(\Omega ^\varepsilon )\). Moreover, setting \(H^\varepsilon [\Theta ]\equiv 0\) outside \(\overline{\Omega ^\varepsilon }\), it belongs to \(C^0([0,+\infty );H^1(0,+\infty ))\) and to \( C^1([0,+\infty );L^2(0,+\infty ))\).
Furthermore, for a.e. \(t\in (0,+\infty )\) one has:
where \(m^\varepsilon \!=\!m^\varepsilon (t)\) is the only natural number (including 0) such that \((\omega ^\varepsilon )^{m^\varepsilon }(t)\in [0,(\omega ^\varepsilon )^{{-}1}(0))\), while \(I^\varepsilon _1\) is defined as follows:
while if \((\omega ^\varepsilon )^{m^\varepsilon }(t)\in [\varepsilon \ell _0,(\omega ^\varepsilon )^{{-}1}(0))\) it is defined in this other way:
Finally, for a.e. \(t\in (0,+\infty )\) it holds:
where for a.e. \(s\in \varphi ^\varepsilon ([0,+\infty ))\) we define:
where \(n^\varepsilon =n^\varepsilon (s)\) is the only natural number (including 0) such that \((\omega ^\varepsilon )^{n^\varepsilon }(s)\in [-\varepsilon \ell _0,\varepsilon \ell _0)\), while
Proof
The regularity of \(H^\varepsilon [\Theta ]\) can be proved in the same way of Lemma 1.11 in Riva and Nardini (2018), so we refer to it for the details. The validity of (1.10) is a straightforward matter of computations; see Fig. 2 for an intuition and also Remark 1.12 in Riva and Nardini (2018). To get (1.11), always referring to Fig. 2 and to Riva and Nardini (2018), we compute:
and we conclude by using (0.5). \(\square \)
Lemma 1.5
Let \(\Theta \in \widetilde{L}^2(\Omega ^\varepsilon )\) and consider \(H^\varepsilon [\Theta ]\) and \(g^\varepsilon [\Theta ]\) given by (1.9) and (1.12), respectively. Then, for a.e. \(s\in \varphi ^\varepsilon ([0,+\infty ))\cap (0,+\infty )\) it holds:
Proof
We start computing by means of (1.10) and (1.12):
There are only two cases to consider: \(n^\varepsilon (s)=m^\varepsilon (s)\) or \(n^\varepsilon (s)=m^\varepsilon (s)+1\). We prove the lemma for the first case, being the other one analogous. So we have:
Exploiting the fact that in (1.14) there is now a telescopic sum and by using the explicit formulas of \(I_1^\varepsilon \) and \(I_2^\varepsilon \) given by Proposition 1.4, we hence deduce:
and we conclude. \(\square \)
Finally, we are in a position to state the main results about dynamic evolutions of the debonding model, namely solutions to coupled problem (1.1) and (1.7). These two theorems are obtained by collecting what the authors proved in Dal Maso et al. (2016), Lazzaroni and Nardini (2018b), Riva (2019) and Riva and Nardini (2018).
Theorem 1.6
(Existence and Uniqueness) Fix \(\nu \ge 0\), \(\ell _0>0\), \(\varepsilon >0\), assume the functions \({w^\varepsilon }\), \(u_0^\varepsilon \) and \(u_1^\varepsilon \) satisfy (1.2), (1.3) and let the toughness \(\kappa \) be positive and satisfy the following property:
Then, there exists a unique pair \(({u^\varepsilon },{\ell ^\varepsilon })\), with:
\({\ell ^\varepsilon }\in C^{0,1}([0,+\infty ))\), \({\ell ^\varepsilon }(0)=\ell _0\) and \(0\le {{\dot{\ell }}^\varepsilon }(t)<1/\varepsilon \) for a.e. \(t\in (0,+\infty )\),
\({u^\varepsilon }\in \widetilde{H}^1(\Omega ^\varepsilon )\) and \({u^\varepsilon }(t,x)=0\) for every (t, x) such that \(x>{\ell ^\varepsilon }(t)\),
solution of the coupled problem (1.1) and (1.7).
Moreover, \({u^\varepsilon }\) has a continuous representative which fulfils the following representation formula:
where \(f^\varepsilon \in \widetilde{H}^1(-\varepsilon \ell _0,+\infty )\) is defined by two rules:
- (i)
\(\displaystyle f^\varepsilon (s)={\left\{ \begin{array}{ll} \displaystyle \varepsilon {w^\varepsilon }(s)-\frac{\varepsilon }{2} u_0^\varepsilon \left( \frac{s}{\varepsilon }\right) -\frac{\varepsilon ^2}{2} \int _{0}^{s/\varepsilon }u_1^\varepsilon (\sigma )\,\mathrm {d}\sigma \\ \quad -\varepsilon {w^\varepsilon }(0)+\frac{\varepsilon }{2} u_0^\varepsilon (0),&{}\text {if }s\in (0,\varepsilon \ell _0],\\ \displaystyle \frac{\varepsilon }{2} u_0^\varepsilon \left( -\frac{s}{\varepsilon }\right) -\frac{\varepsilon ^2}{2} \int _{0}^{-s/\varepsilon }u_1^\varepsilon (\sigma )\,\mathrm {d}\sigma -\frac{\varepsilon }{2} u_0^\varepsilon (0),&{}\text {if }s\in (-\varepsilon \ell _0,0], \end{array}\right. }\)
- (ii)
\(\displaystyle {w^\varepsilon }(s+\varepsilon {\ell ^\varepsilon }(s))-\frac{1}{\varepsilon }f^\varepsilon (s+\varepsilon {\ell ^\varepsilon }(s))+\frac{1}{\varepsilon }f^\varepsilon (s-\varepsilon {\ell ^\varepsilon }(s))=0,\quad \quad \quad \) for every \(s\in (0,+\infty )\),
while \(H^\varepsilon \) is as in (1.9).
In particular, it holds:
Furthermore, one has:
and for \(\alpha \in [0,1/\varepsilon )\) the dynamic energy release rate can be expressed as:
where \(g^\varepsilon \) has been introduced in (1.12).
Remark 1.7
(Regularity) If the data are more regular, namely:
if the (positive) toughness \(\kappa \) belongs to \(\widetilde{C}^{0,1}([\ell _0,+\infty ))\) and if besides (1.3) also the following first-order compatibility conditions are satisfied:
then, the solution \({u^\varepsilon }\) is in \({\widetilde{H}}^2(\Omega ^\varepsilon )\).
Theorem 1.8
(Continuous Dependence) Fix \(\nu \ge 0\), \(\ell _0>0\), \(\varepsilon >0\), assume the functions \({w^\varepsilon }\), \(u_0^\varepsilon \) and \(u_1^\varepsilon \) satisfy (1.2), (1.3) and let the toughness \(\kappa \) be positive and belong to \(\widetilde{C}^{0,1}([\ell _0,+\infty ))\). Consider sequences of functions \(\{w^\varepsilon _n\}_{n\in \mathbb {N}}\), \(\{{u_0^\varepsilon }_n\}_{n\in \mathbb {N}}\) and \(\{{u_1^\varepsilon }_n\}_{n\in \mathbb {N}}\) satisfying (1.2) and (1.3), and let \((u^\varepsilon _n,\ell ^\varepsilon _n)\) and \(({u^\varepsilon },{\ell ^\varepsilon })\) be the solutions of coupled problem (1.1) and (1.7) given by Theorem 1.6 corresponding to the data with and without the subscript n, respectively. If the following convergences hold true as \(n\rightarrow +\infty \):
then for every \(T>0\) one has as \(n\rightarrow +\infty \):
\(\ell ^\varepsilon _n\rightarrow \ell ^\varepsilon \) in \(W^{1,1}(0,T)\);
\(u^\varepsilon _n\rightarrow {u^\varepsilon }\) uniformly in \([0,T]\times [0,+\infty )\);
\(u^\varepsilon _n\rightarrow {u^\varepsilon }\) in \(H^1((0,T)\times (0,+\infty ))\);
\(u^\varepsilon _n\rightarrow {u^\varepsilon }\) in \(C^0([0,T];H^1(0,+\infty ))\) and in \( C^1([0,T];L^2(0,+\infty ))\);
\((u^\varepsilon _n)_x(\cdot ,0)\rightarrow {u_x^\varepsilon }(\cdot ,0)\) in \(L^2(0,T)\).
4 Quasistatic Evolutions
This section is devoted to the analysis of quasistatic evolutions for the debonding model we are studying. We first introduce and compare two different notions of this kind of evolutions (we refer to Bourdin et al. (2008) or Mielke and Roubíček (2015) for a wide and complete presentation on the topic), then we prove an existence and uniqueness result under suitable assumptions; see Theorem 2.9.
Fix \(\ell _0>0\); throughout this section we consider a loading term \(w\in C^0([0,+\infty ))\) such that \(w\in AC([0,T])\) for every \(T>0\) and a toughness \(\kappa \in C^0([\ell _0,+\infty ))\) such that \(\kappa (x)>0\) for every \(x\ge \ell _0\).
Definition 2.1
Let \(\lambda :[0,+\infty )\rightarrow [\ell _0,+\infty )\) be a nondecreasing function such that \(\lambda (0)=\ell _0\), and let \(v:[0,+\infty )\times [0,+\infty )\rightarrow \mathbb {R}\) be a function which for every \(t\in [0,+\infty )\) satisfies \(v(t,\cdot )\in H^1(0,+\infty )\), \(v(t,0)=w(t)\), \(v(t,x)=0\) for \(x\ge \lambda (t)\) and such that \(v_x(t,0)\) exists for a.e. \(t\in (0,+\infty )\). We say that such a pair \((v,\lambda )\) is an energetic evolution if for every \(t\in [0,+\infty )\) it holds:
- (S)
\(\displaystyle \frac{1}{2}\int _{0}^{\lambda (t)}v_x(t,\sigma )^2\,\mathrm {d}\sigma +\int _{\ell _0}^{\lambda (t)}\kappa (\sigma )\,\mathrm {d}\sigma \le \frac{1}{2} \int _{0}^{\hat{\lambda }}\dot{\hat{v}}(\sigma )^2\,\mathrm {d}\sigma +\int _{\ell _0}^{\hat{\lambda }}\kappa (\sigma )\,\mathrm {d}\sigma ,\) for every \({\hat{\lambda }}\ge \lambda (t)\) and for every \(\hat{v}\in H^1(0,{\hat{\lambda }})\) satisfying \(\hat{v}(0)=w(t)\) and \(\hat{v}({\hat{\lambda }})=0;\)
- (EB)
\(\displaystyle \frac{1}{2}\int _{0}^{\lambda (t)}v_x(t,\sigma )^2\,\mathrm {d}\sigma +\int _{\ell _0}^{\lambda (t)}\kappa (\sigma )\,\mathrm {d}\sigma +\int _{0}^{t}\dot{w}(\tau )v_x(\tau ,0)\,\mathrm {d}\tau {=}\frac{1}{2}\int _{0}^{\ell _0}v_x(0,\sigma )^2\,\mathrm {d}\sigma .\)
Here, (S) stands for (global) stability, while (EB) for energy(-dissipation) balance. Roughly speaking an energetic evolution is a pair which fulfils an energy–dissipation balance being at every time a global minimiser of the functional \((v,\lambda )\mapsto \frac{1}{2} \int _{0}^{{\lambda }}{\dot{v}}(\sigma )^2\,\mathrm {d}\sigma +\int _{\ell _0}^{{\lambda }}\kappa (\sigma )\,\mathrm {d}\sigma \), which is sum of potential energy and energy dissipated to debond the film.
On the contrary, this second definition deals with local minima of the total energy:
Definition 2.2
Given \(\lambda \) and v as in Definition 2.1, we say that the pair \((v,\lambda )\) is a quasistatic evolution if:
- (i)
\(\lambda \) is absolutely continuous on [0, T] for every \(T>0\) and \(\lambda (0)=\ell _0\);
- (ii)
\(\displaystyle v(t,x)=w(t)\left( 1-\frac{x}{\lambda (t)} \right) \chi _{[0,\lambda (t)]}(x),\) for every \((t,x)\in [0,+\infty )\times [0,+\infty )\);
- (iii)
the quasistatic version of Griffith’s criterion holds true, namely:
$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{\lambda }}(t)\ge 0,\\ \frac{1}{2} \frac{w(t)^2}{\lambda (t)^2}\le \kappa (\lambda (t)),\\ \left[ \frac{1}{2} \frac{w(t)^2}{\lambda (t)^2}-\kappa (\lambda (t))\right] {\dot{\lambda }}(t)=0, \end{array}\right. }\quad \quad \text { for a.e. }t\in (0,+\infty ). \end{aligned}$$
Similarities with dynamic Griffith’s criterion (1.7) are evident, with the exception of the term \(\frac{1}{2} \frac{w(t)^2}{\lambda (t)^2}\) which requires some explanations: like in the dynamic case, we can introduce the notion of quasistatic energy release rate as \(G_{ qs }(t)=-\partial _\lambda \mathcal E_{ qs }(t)\), where the quasistatic energy \(\mathcal E_{ qs }\) is simply the potential one, kinetic energy being negligible in a quasistatic setting. By means of (ii), we can compute \(\mathcal E_{ qs }(t)=\frac{1}{2}\int _{0}^{\lambda (t)}v_x(t,\sigma )^2\,\mathrm {d}\sigma =\frac{1}{2} \frac{w(t)^2}{\lambda (t)}\), from which we recover \(G_{ qs }(t)=\frac{1}{2} \frac{w(t)^2}{\lambda (t)^2}\). Thus, (iii) is the correct formulation of quasistatic Griffith’s criterion.
For a reason which will be clear during the proof of the next proposition, we introduce for \(x\ge \ell _0\) the function \(\phi _\kappa (x):=x^2\kappa (x)\); we recall that \(\phi _\kappa \) actually appears in the assumptions (K1)-(KW) we listed in Introduction. It is worth noticing that (K1) ensures local minima of the energy are actually global, as stated in Proposition 2.3. Conditions (K2) and (K3) instead imply uniqueness of the minimum; see Proposition 2.7. Finally, the first assumption in (KW) is related to the existence of such a minimum, replacing the role of coercivity of the energy, which can be missing.
Proposition 2.3
Assume (K1). Then, a pair \((v,\lambda )\) is an energetic evolution if and only if:
- (o)
\(\lambda \) is nondecreasing on \([0,+\infty )\) and \(\lambda (0)=\ell _0\);
- (s1)
\(\displaystyle v(t,x)=w(t)\left( 1-\frac{x}{\lambda (t)} \right) \chi _{[0,\lambda (t)]}(x),\) for every \((t,x)\in [0,+\infty )\times [0,+\infty )\);
- (s2)
\(\displaystyle \frac{1}{2} \frac{w(t)^2}{\lambda (t)^2}\le \kappa (\lambda (t)),\) for every \(t\in [0,+\infty ),\)
- (eb)
\(\displaystyle \frac{1}{2} \frac{w(t)^2}{\lambda (t)}+\int _{\ell _0}^{\lambda (t)}\kappa (\sigma )\,\mathrm {d}\sigma -\int _{0}^{t}\dot{w}(\tau )\frac{w(\tau )}{\lambda (\tau )}\,\mathrm {d}\tau =\frac{1}{2} \frac{w(0)^2}{\ell _0},\) for every \(t\in [0,+\infty )\).
Proof
Let \((v,\lambda )\) be an energetic evolution, then (o) is satisfied by definition. Now fix \(t\in [0,+\infty )\) and choose \(\hat{\lambda }=\lambda (t)\) in (S). Then, we deduce that \(v(t,\cdot )\) minimises the functional \(\displaystyle \frac{1}{2} \int _{0}^{\lambda (t)}\dot{\hat{v}}(\sigma )^2\,\mathrm {d}\sigma \) among all functions \(\hat{v}\in H^1(0,\lambda (t))\) such that \(\hat{v}(0)=w(t)\) and \(\hat{v}(\lambda (t))=0\), and this implies (s1). Choosing now \(\hat{v}(x)=w(t)\left( 1-\frac{x}{{\hat{\lambda }}}\right) \chi _{[0,{\hat{\lambda ]}}}(x)\) in (S) and exploiting (s1), we get:
This means that the energy \(E_t:[\lambda (t),+\infty )\rightarrow [0,+\infty )\) defined by \(\displaystyle E_t(x):=\frac{1}{2}\frac{w(t)^2}{x}+\int _{\ell _0}^{x}\kappa (\sigma )\,\mathrm {d}\sigma \) has a global minimum in \(x=\lambda (t)\) and so \(\dot{E}_t(\lambda (t))\ge 0\), namely (s2) holds true. Finally, (eb) follows by (EB) exploiting (s1).
Assume now that (o), (s1), (s2) and (eb) hold true. To prove that \((v,\lambda )\) is an energetic evolution, it is enough to show the validity of (S), being (EB) trivially implied by (eb) and (s1). So let us fix \(t\in [0,+\infty )\) and notice that (s2) is equivalent to \(\phi _\kappa (\lambda (t))\ge \frac{1}{2} w(t)^2\). By (K1), we hence deduce that \(\phi _\kappa (x)\ge \frac{1}{2} w(t)^2\) for every \(x\ge \lambda (t)\), i.e., \(\dot{E}_t(x)\ge 0\) for every \(x\ge \lambda (t)\). This means that \(E_t\) has a global minimum in \(x=\lambda (t)\) and so we obtain:
which in particular implies (S), since affine functions minimise the potential energy. \(\square \)
If we do not strengthen the assumptions on the toughness \(\kappa \), there is no hope to gain more regularity on \(\lambda \), even in the case of a constant loading term \(w>0\). Indeed, it is enough to consider \(\kappa (x)=\frac{1}{2} \frac{w^2}{x^2}\) (in this case \(\phi _\kappa \) is constant) to realise that any function satisfying (o) automatically satisfies (s2) and (eb).
Lemma 2.4
Assume (K2). Then, any function \(\lambda \) satisfying (o), (s2) and (eb) is continuous.
Proof
Let us assume by contradiction that there exists a time \(\bar{t}\in [0,+\infty )\) in which \(\lambda \) is not continuous, namely \(\lambda ^-({\bar{t}}\,)<\lambda ^+({\bar{t}}\,)\). Here, we adopt the convention that \(\lambda ^-(0)=\lambda (0)=\ell _0\). Exploiting (s2), (eb) and the continuity of \(\kappa \) and w, we deduce that:
By using (K2), from (2.1) we get:
This leads to a contradiction and hence we conclude. \(\square \)
Lemma 2.5
Assume (K2) and let \(\lambda \) be a function satisfying (o), (s2) and (eb). If there exists a time \({\bar{t}}\in (0,+\infty )\) in which (s2) holds with strict inequality, then \(\lambda \) is constant in a neighbourhood of \({\bar{t}}\).
Proof
Let us consider the function:
which is continuous on its domain. Moreover, the derivative of \(\Phi \) in the direction x exists at every point and it is continuous on \([0,+\infty )\times [\ell _0,+\infty )\), being given by:
Since by assumption \(\Phi _x({\bar{t}},\lambda ({\bar{t}}\,))>0\), by continuity we deduce that:
where \([a,b]\times [c,d]\subset (0,+\infty )\times [\ell _0,+\infty )\) is a suitable rectangle containing the point \(({\bar{t}},\lambda (\bar{t}))\). By continuity of \(\lambda \) (given by Lemma 2.4), we can assume without loss of generality that \(\lambda ([a,b])\subset [c,d]\). Now, we fix \(t_1,\,t_2\in [a,b]\), \(t_1\le t_2\), and by the mean value theorem we deduce:
From this equality, exploiting (2.2) and (eb), we get:
Since w is absolutely continuous, we can also assume that the interval [a, b] is so small that:
From (2.3), we hence deduce that \(\lambda (t_2)=\lambda (t_1)\), and so we conclude. \(\square \)
Remark 2.6
Lemmas 2.4 and 2.5 hold true even weakening a bit assumption (eb). It is indeed enough to assume that:
The only changes in the proofs are in (2.1b) and in the first equality in (2.3): In this case, they become an inequality.
We now introduce a notation, already adopted in Almi et al. (2014) to deal with quasistatic hydraulic fractures: given a continuous function \(h:[a,b]\rightarrow \mathbb {R}\), we define by \(h_*\) the smallest nondecreasing function greater or equal than h, namely \(h_*(x):=\max \limits _{y\in [a,x]}h(y)\). We refer to Almi et al. (2014) for its properties, we only want to recall that if \(h\in W^{1,p}(a,b)\) for some \(p\in [1,+\infty ]\), then also \(h_*\) belongs to the same Sobolev space and \(\dot{h}_*(x)=\dot{h}(x)\chi _{\{h=h_*\}}(x)\) almost everywhere.
Proposition 2.7
Assume (K2) and let \(\lambda \) be a function satisfying (o), (s2) and (eb). Then:
Proof
Let \(\lambda \) satisfy (o), (s2) and (eb). By using (s2), we get \(\phi _\kappa (\lambda (t))\ge \frac{1}{2} w(t)^2\) for every \(t\in [0,+\infty )\), and since the left-hand side is nondecreasing we deduce:
Since by (K2) the function \(\phi _\kappa \) is invertible, we finally get that \(\lambda (t)\ge \bar{\lambda }(t)\) for every \(t\in [0,+\infty )\), where we denoted by \(\bar{\lambda }\) the function in the right-hand side of (2.5).
Since by Lemma 2.4 we know \(\lambda \) is continuous on \([0,+\infty )\) and since by construction the same holds true for \({\bar{\lambda }}\), we conclude if we prove that \(\lambda (t)={\bar{\lambda }}(t)\) for every \(t\in (0,+\infty )\). By contradiction let \({\bar{t}}\in (0,+\infty )\) be such that \(\lambda ({\bar{t}}\,)>{\bar{\lambda }}({\bar{t}}\,)\). By (K2) this in particular implies that \(\displaystyle \kappa (\lambda (\bar{t}\,))>\frac{1}{2}\frac{w({\bar{t}}\,)^2}{\lambda ({\bar{t}}\,)^2}\), and so by Lemma 2.5 we get that \(\lambda \) is constant around \(\bar{t}\). Since \({\bar{\lambda }}\) is nondecreasing, we can repeat this argument getting that \(\lambda \) is constant on the whole \([0,{\bar{t}}\,]\). This is absurd since it implies:
and so we conclude. \(\square \)
Remark 2.8
As in Remark 2.6, the conclusion of Proposition 2.7 holds true replacing (eb) by (2.4). This will be useful in the proof of Proposition 4.12.
Finally, we can state and prove the main result of this section, regarding the equivalence between the two Definitions 2.1 and 2.2 and about existence and uniqueness of quasistatic evolutions.
Theorem 2.9
Assume (K3). Then, a pair \((v,\lambda )\) is an energetic evolution if and only if it is a quasistatic evolution.
In particular, if we in addition assume (KW), the only quasistatic evolution \((\bar{v}, \bar{\lambda })\) is given by:
\(\displaystyle {\bar{v}}(t,x)=w(t)\left( 1-\frac{x}{{\bar{\lambda }}(t)} \right) \chi _{[0,{\bar{\lambda }}(t)]}(x),\quad \) for every \((t,x)\in [0,+\infty )\times [0,+\infty )\),
\(\displaystyle {\bar{\lambda }}(t)=\phi _\kappa ^{-1}\left( \max \left\{ \frac{1}{2} (w^2)_*(t),\phi _\kappa (\ell _0)\right\} \right) ,\quad \) for every \(t\in [0,+\infty )\).
Proof
Let \((v,\lambda )\) be an energetic evolution. By Proposition 2.3, we get v satisfies (ii) and \(\lambda \) satisfies (o), (s2) and (eb). Moreover, by Proposition 2.7\(\lambda \) is explicitly given by (2.5), and hence by (K3) it is absolutely continuous on [0, T] for every \(T>0\), being composition of two nondecreasing absolutely continuous functions. Differentiating (eb), we now conclude that quasistatic Griffith’s criterion (iii) holds true and so \((v,\lambda )\) is a quasistatic evolution.
On the other hand, checking that any quasistatic evolution satisfies (o), (s1), (s2) and (eb) is straightforward, and hence by Proposition 2.3 the other implication is proved.
Let us now verify that, assuming (KW), the pair \(({\bar{v}},{\bar{\lambda }})\) is actually a quasistatic evolution. By (KW) \({\bar{\lambda }}\) is well defined and (i) is fulfilled. The only nontrivial thing to check is the validity of the third condition in the quasistatic Griffith’s criterion (iii). We need to prove that for any differentiability point \(\bar{t}\in (0,+\infty )\) of \({\bar{\lambda }}\) such that \(\dot{{\bar{\lambda }}}(\bar{t}\,)>0\) it holds \(\displaystyle \kappa ({\bar{\lambda }}({\bar{t}}\,))=\frac{1}{2}\frac{w({\bar{t}}\,)^2}{{\bar{\lambda }}({\bar{t}}\,)^2}\). From the explicit expression of \(\dot{{\bar{\lambda }}}\), namely:
we deduce that in \(t={\bar{t}}\) we must have \(w(\bar{t}\,)^2=(w^2)_*({\bar{t}}\,)> 2\phi _\kappa (\ell _0)\) and so it holds:
and we conclude. \(\square \)
5 Energy Estimates
In this section, we provide useful energy estimates for the pair of dynamic evolutions \(({u^\varepsilon },{\ell ^\varepsilon })\) given by Theorem 1.6. These estimates will be used in the next section to analyse the limit as \(\varepsilon \rightarrow 0^+\) of both \({u^\varepsilon }\) and \({\ell ^\varepsilon }\). From now on, we always assume that the positive toughness \(\kappa \) belongs to \(\widetilde{C}^{0,1}([\ell _0,+\infty ))\). When needed, we will also require the following additional assumptions on the data:
- (H1)
the families \(\{{w^\varepsilon }\}_{\varepsilon >0}\), \(\{u_0^\varepsilon \}_{\varepsilon >0}\), \(\{\varepsilon u_1^\varepsilon \}_{\varepsilon >0}\) are bounded in \({\widetilde{H}}^1(0,+\infty )\), \(H^1(0,\ell _0)\) and \(L^2(0,\ell _0)\), respectively.
Remark 3.1
Whenever we assume (H1), we denote by \({\varepsilon _n}\) a subsequence for which we have:
for a suitable \(w\in \widetilde{H}^1(0,+\infty )\). This sequence can be obtained by weak compactness and Sobolev embedding. By abuse of notation, we will not relabel further subsequences.
The first step is obtaining an energy bound uniform in \(\varepsilon \) from the energy–dissipation balance (1.5a). As one can see, we must deal with the work of the external loading \(\mathcal W^\varepsilon \), so we need to find a way to handle the boundary term \({u_x^\varepsilon }(\cdot ,0)\). The next lemma shows how we can recover it via an integration by parts.
Lemma 3.2
Let the function \(h\in C^\infty ([0,+\infty ))\) satisfy \(h(0)=1\), \(0\le h(x)\le 1\) for every \(x\in [0,+\infty )\) and \(h(x)=0\) for every \(x\ge \ell _0\). Then, the following equality holds true for every \(t\in [0,+\infty )\):
Proof
We start with a formal proof, assuming that all the computation we are doing are allowed, and then we make it rigorous via an approximation argument. Performing an integration by parts, we deduce:
Exploiting the fact that \({u^\varepsilon }\) solves problem (1.1), we hence get:
Now, we conclude since it holds:
All the previous computations are rigorous if \({u^\varepsilon }\) belongs to \({\widetilde{H}}^2(\Omega ^\varepsilon )\), which is not the case. To overcome this lack of regularity, we perform an approximation argument, exploiting Remark 1.7 and Theorem 1.8.
Let us consider a sequence \(\{{u_0^\varepsilon }_n\}_{n\in \mathbb {N}}\subset H^2(0,\ell _0)\) such that \({u_0^\varepsilon }_n(0)=u_0^\varepsilon (0)\), \({u_0^\varepsilon }_n(\ell _0)=0\) and converging to \(u_0^\varepsilon \) in \(H^1(0,\ell _0)\) as \(n\rightarrow +\infty \); then, we pick a sequence \(\{w^\varepsilon _n\}_{n\in \mathbb {N}}\subset \widetilde{H}^2(0,+\infty )\) such that \(w^\varepsilon _n(0)={w^\varepsilon }(0)\) and converging to \(w^\varepsilon \) in \({\widetilde{H}}^1(0,+\infty )\) as \(n\rightarrow +\infty \); finally, we take another sequence \(\{{u_1^\varepsilon }_n\}_{n\in \mathbb {N}}\subset H^1(0,\ell _0)\) converging to \(u_1^\varepsilon \) in \(L^2(0,\ell _0)\) as \(n\rightarrow +\infty \) and satisfying:
Denoting by \((u^\varepsilon _n,\ell ^\varepsilon _n)\) the solution of coupled problem (1.1) and (1.7) related to these data, we deduce by Remark 1.7 that \(u^\varepsilon _n\) belongs to \(H^2(\Omega ^\varepsilon _T)\), and so by previous computations (3.2) holds true for it. By Theorem 1.8, equality (3.2) passes to the limit as \(n\rightarrow +\infty \) and hence we conclude. \(\square \)
Thanks to the previous lemma, we are able to prove the following energy bound:
Proposition 3.3
Assume (H1). Then, for every \(T>0\) there exists a positive constant \(C_T>0\) such that for every \(\varepsilon \in (0,1/2)\) it holds:
where \(\mathcal E^\varepsilon \) and \(\mathcal A^\varepsilon \) are the energies defined in (1.4a) and (1.4b).
Proof
We fix \(T>0\), \(t\in [0,T]\), \(\varepsilon \in (0,1/2)\), and by using the energy–dissipation balance (1.5a) we estimate:
By Lemma 3.2 and by applying Young’s inequality, we can continue the estimate getting:
We conclude by means of Grönwall lemma and exploiting (H1). \(\square \)
As an immediate corollary, we have:
Corollary 3.4
Assume (H1) and (K0). Then, for every \(T>0\) there exists a positive constant \(L_T>0\) such that \({\ell ^\varepsilon }(T)\le L_T\) for every \(\varepsilon \in (0, 1/2)\).
In order to improve the energy bound given by Proposition 3.3, we exploit the classical exponential decay of the energy for a solution to the damped wave equation. Following the ideas of Misra and Gorain (2014), we adapt their argument to our model in which the domain of the equation changes in time. For this aim, we introduce the modified energy:
where \(r^\varepsilon (t,x)\) is the affine function connecting the points \((0,{w^\varepsilon }(t))\) and \(({\ell ^\varepsilon }(t),0)\), namely:
The main result of this section is the following decay estimate:
Theorem 3.5
Assume (H1) and (K0) and let the parameter \(\nu \) be positive. Then, for every \(T>0\) there exists a constant \(C_T>0\) such that for every \(t\in [0,T]\) and \(\varepsilon \in (0,1/2)\) one has:
where \(\displaystyle m=m(\nu ,T):=\frac{1}{2} \min \left\{ \frac{1}{2\mu ^0_T},\,\frac{\nu }{2},\,\frac{1}{\mu _T^0+\mu ^1_T} \right\} >0\) and \(\mu ^0_T \), \(\mu ^1_T\) are defined as follows:
with \(L_T\) given by Corollary 3.4.
Remark 3.6
Estimate (3.6) actually still holds true for \(\nu =0\), but in this case \(m=0\) and so the inequality becomes trivial and useless.
To prove this theorem, we will need several lemmas. As before, we always assume that \(\varepsilon \in (0,1/2)\).
Lemma 3.7
Assume (H1). Then, for every \(T>0\) the modified energy \(\widetilde{\mathcal E}^\varepsilon \) is absolutely continuous on [0, T] and the following inequality holds true for a.e. \(t\in (0,T)\):
where \(C_T\) is a positive constant depending on T but independent of \(\varepsilon \).
Proof
By developing the square in (3.4) and exploiting (3.5), one can easily show that:
Now, fix \(T>0\). The modified energy \(\widetilde{\mathcal E}^\varepsilon \) is absolutely continuous on [0, T] because by (3.9) it is sum of two absolutely continuous functions [see also Proposition 2.1 in Riva and Nardini (2018)]. By (3.9) and the energy–dissipation balance (1.5a), we then compute for a.e. \(t\in (0,+\infty )\):
Recalling that \({\ell ^\varepsilon }(t)\ge \ell _0\) and since by (H1) the family \(\{{w^\varepsilon }\}_{\varepsilon >0}\) is uniformly equibounded in [0, T], we conclude by means of Young’s inequality. \(\square \)
Always inspired by Misra and Gorain (2014), for \(t\in [0,+\infty )\) we also introduce the auxiliary function:
Lemma 3.8
Assume (H1) and (K0). Then, for every \(T>0\) one has:
where \(\mu ^0_T\) and \(\mu ^1_T\) have been defined in (3.7).
Proof
We fix \(t\in [0,T]\) and by means of the sharp Poincarè inequality:
together with Young’s inequality we get:
From the above estimate, we hence deduce:
and we conclude. \(\square \)
Lemma 3.9
Assume (H1) and (K0). Then, for every \(T>0\) the function \(\widetilde{\mathcal F}^\varepsilon \) is absolutely continuous on [0, T] and the following inequality holds true for a.e. \(t\in (0,T)\):
where \(C_T\) is a positive constant depending on T but independent of \(\varepsilon \).
Proof
Fix \(T>0\). By exploiting the fact that \({u^\varepsilon }\) solves problem (1.1), we start formally computing the derivative of \(\widetilde{\mathcal F}^\varepsilon \) at almost every point \(t\in (0,T)\):
By means of an approximation argument similar to the one adopted in the proof of Lemma 3.2, one deduces that \(\widetilde{\mathcal F}^\varepsilon \) is absolutely continuous on [0, T] and that the formula for \(\dot{\widetilde{\mathcal F}^\varepsilon }\) found with the previous computation is actually true.
To get (3.12), we use the sharp Poincarè inequality (3.11) and Young’s inequality:
To conclude it is enough to use Corollary 3.4, (H1) and to exploit the explicit form of \(r^\varepsilon \) given by (3.5) getting:
\(\square \)
We are now in a position to prove Theorem 3.5:
Proof of Theorem 3.5
We fix \(T>0\) and we introduce the Lyapunov function:
From (3.10), we easily infer:
and so in particular by definition of m we deduce:
Moreover, we can estimate the derivative of \(\widetilde{\mathcal D}^\varepsilon \) for a.e. \(t\in (0,T)\) by using (3.8) and (3.12) and recalling that \(\varepsilon {{\dot{\ell }}^\varepsilon }(t)<1\) and that \(4m\le \nu \):
By (3.13), we hence deduce:
from which for every \(t\in [0,T]\) we get:
We conclude by using again (3.13). \(\square \)
6 Quasistatic Limit
In this section, we show how, thanks to the estimates of Sect. 3, dynamic evolutions \(\left( {u^\varepsilon },{\ell ^\varepsilon }\right) \) converge to a quasistatic one as \(\varepsilon \rightarrow 0^+\), except for a possible initial jump due to a steep initial position \(u_0\). The rigorous result is stated in Theorem 4.22. Also, in this section we assume that \(\kappa \) belongs to \(\widetilde{C}^{0,1}([\ell _0,+\infty ))\).
6.1 Extraction of Convergent Subsequences
We first prove that the sequence of debonding fronts \({\ell ^\varepsilon }\) admits a pointwise convergent subsequence.
Proposition 4.1
Assume (H1) and (K0). Then, there exists a subsequence \({\varepsilon _n}\searrow 0\) and there exists a nondecreasing function \(\ell :[0,+\infty )\rightarrow [\ell _0,+\infty )\) such that
Proof
The result follows by Corollary 3.4 and by a simple application of the classical Helly’s selection principle. \(\square \)
In order to deal with the convergence of the vertical displacements \({u^\varepsilon }\), we exploit the energy decay (3.5):
Proposition 4.2
Assume (H1) and (K0) and let \(\nu \) be positive. Then, for every \(T>0\) the modified energy \(\widetilde{\mathcal E}^\varepsilon \) converges to 0 in \(L^1(0,T)\) when \(\varepsilon \rightarrow 0^+\). Thus, there exists a subsequence \({\varepsilon _n}\searrow 0\) such that:
Proof
We fix \(T>0\). Theorem 3.5 ensures that:
where the symbol \(*\) denotes the convolution product and for a.e. \(t\in \mathbb {R}\) we define:
Furthermore, by (3.9) and (H1) we get that \(\widetilde{\mathcal E}^\varepsilon (0)\) is uniformly bounded in \(\varepsilon \), and so by classical properties of convolutions we estimate:
Now, we bound the \(L^1\)-norm of \(\rho ^\varepsilon \) by means of (H1), (K0) and recalling that by Lemma 3.2 and Proposition 3.3 we know that \(\Vert {u_x^\varepsilon }(\cdot ,0)\Vert _{L^2(0,T)}\) is uniformly bounded with respect to \(\varepsilon \):
Thus, we deduce that \(\widetilde{\mathcal E}^\varepsilon \rightarrow 0\) in \(L^1(0,T)\) when \(\varepsilon \rightarrow 0^+\) and so we conclude by using a diagonal argument. \(\square \)
Similarly to what we did in Lemma 3.2, we need to understand the behaviour of \({u_x^\varepsilon }(\cdot ,0)\) when \(\varepsilon \rightarrow 0^+\) before carrying on the analysis of the convergence of \({u^\varepsilon }\).
Lemma 4.3
Let the function h be as in Lemma 3.2. Then, the following equality holds true for every \(t\in [0,+\infty )\):
Proof
The proof follows by using exactly the same argument adopted in Lemma 3.2, recalling the explicit formula of the affine function \(r^\varepsilon \) given by (3.5). \(\square \)
Corollary 4.4
Assume (H1) and (K0) and let \(\nu >0\). Then, for every \(T>0\) one has:
Moreover, considering the subsequence \({\varepsilon _n}\) given by (3.1) and Proposition 4.1, one gets:
where w is given by (3.1) and \(\ell \) is the function obtained in Proposition 4.1.
Proof
We fix \(T>0\) and we simply estimate by using (4.1) and recalling that by (H1) the family \(\{{w^\varepsilon }\}_{\varepsilon >0}\) is uniformly equibounded in [0, T]:
By Hölder’s inequality and since \(\varepsilon {{\dot{\ell }}^\varepsilon }(t)<1\) almost everywhere, we then deduce:
By means of Proposition 3.3, we hence obtain:
We conclude by using (H1) and Proposition 4.2.
The proof of (4.2) trivially follows by triangular inequality, recalling that by (3.5) we know that \({r^\varepsilon }_x(t,0)=-\frac{{w^\varepsilon }(t)}{{\ell ^\varepsilon }(t)}\) for every \(t\in [0,+\infty )\). \(\square \)
We are now in a position to state our first result about the convergence of \({u^\varepsilon }\) to the proper affine function.
Theorem 4.5
Assume (H1), (K0), \(\nu >0\) and let \({\varepsilon _n}\) be the subsequence given by (3.1), Propositions 4.1 and 4.2. Let \(\ell \) be the nondecreasing function obtained in Proposition 4.1. Then, as \(n\rightarrow +\infty \) one has:
\({\varepsilon _n}{u_t^{\varepsilon _n}}(t,\cdot )\rightarrow 0\) strongly in \(L^2(0,+\infty )\), for every \(t\in (0,+\infty )\!\setminus \!J_\ell \),
\({u^{\varepsilon _n}}(t,\cdot )\rightarrow u(t,\cdot )\) strongly in \(H^1(0,+\infty )\), for every \(t\in (0,+\infty )\!\setminus \!J_\ell \),
where \(J_\ell \) is the jump set of \(\ell \) and:
with w given by (3.1).
Proof
By (3.1) and by Proposition 4.1, it is easy to see that for every \(t\in [0,+\infty )\) one has \({r^{\varepsilon _n}}(t,\cdot )\rightarrow u(t,\cdot )\) strongly in \(H^1(0,+\infty )\) as \(n\rightarrow +\infty \); thus, we deduce:
where we used Poincarè inequality.
To conclude it is enough to show that \(\lim \limits _{n\rightarrow +\infty }\widetilde{\mathcal E}^{\varepsilon _n}(t)=0\) for every \(t\in (0,+\infty )\!\setminus \!J_\ell \). By (3.1) and (3.9), this is equivalent to prove that:
By Proposition 4.2, we know that (4.3) holds true for a.e. \(t\in (0,+\infty )\). To improve the result, we then fix \(t\in (0,+\infty )\!\setminus \!J_\ell \) and we consider two sequences \(\{s_j\}_{j\in \mathbb {N}}\) and \(\{t_j\}_{j\in \mathbb {N}}\) such that \(0<s_j\le t\le t_j\), the limit in (4.3) holds true for \(s_j\) and \(t_j\) for every \(j\in \mathbb {N}\) and \(s_j\nearrow t\), \(t_j\searrow t\) as \(j\rightarrow +\infty \). By the energy–dissipation balance (1.5a), we hence get:
Passing to the limit as \(n\rightarrow +\infty \) and exploiting Corollary 4.4 together with (3.1), we deduce:
Passing now to the limit as \(j\rightarrow +\infty \), recalling that t is a continuity point of \(\ell \), we finally obtain:
and so we conclude. \(\square \)
We want to highlight that the viscous term in the wave equation forces the kinetic energy to vanish when \(\varepsilon \rightarrow 0^+\). Indeed, this phenomenon does not happen in Lazzaroni and Nardini (2018b), where on the contrary the presence of a persistent kinetic energy due to lack of viscosity is the main reason why the convergence of \({u^\varepsilon }\) to an affine function occurs only in a weak sense [see Theorem 3.5 in Lazzaroni and Nardini (2018b)] and the limit pair \((u,\ell )\) fails to be a quasistatic evolution.
6.2 Characterisation of the Limit Debonding Front
Our aim now is to understand if the limit function \(\ell \) solves quasistatic Griffith’s criterion. We thus need to pass to the limit in the dynamic Griffith’s criterion (1.7). The next proposition deals with the stability condition.
Proposition 4.6
Assume (H1), (K0), \(\nu >0\) and let \(\ell \) be the nondecreasing function obtained in Proposition 4.1. Then, for every \(0\le s\le t\) one has:
where w is given by (3.1).
In particular, the following inequalities hold true:
where \(\ell ^+\) and \(\ell ^-\) are the right limit and the left limit of \(\ell \), respectively.
Proof
Let \({\varepsilon _n}\) be the subsequence given by (3.1) and Proposition 4.1. By (1.16), we know that for a.e. \(t\in (0,+\infty )\) one has:
where we introduced the function:
Here, we adopt the notation \(\varphi ^{\varepsilon _n}(+\infty )=\lim \limits _{t\rightarrow +\infty }\varphi ^{\varepsilon _n}(t)\), which exists since \(\varphi ^{\varepsilon _n}\) is strictly increasing. We want also to remark that \(\varphi ^{\varepsilon _n}(+\infty )>0\) for n large enough (actually it diverges to \(+\infty \) as \(n\rightarrow +\infty \)); indeed, \(\varphi ^{\varepsilon _n}\) converges locally uniformly to the identity map as \(n\rightarrow +\infty \) by Corollary 3.4. By means of (1.15a) and of the explicit form of \(\dot{f}^{\varepsilon _n}\) and \(g^{\varepsilon _n}[{u_t^{\varepsilon _n}}]\) in \((-{\varepsilon _n}\ell _0,0)\), we deduce that:
Thus, thanks to (1.13), we obtain:
By the stability condition in dynamic Griffith’s criterion (1.7), we hence deduce that for every \(0\le s\le t\) one has:
Thus, by dominated convergence we infer:
We actually prove that the limit in the right-hand side exists and it holds:
If (4.7) is true, then we conclude; to prove it we reason as follows. We first assume \(s>0\), so that \(\varphi ^{\varepsilon _n}(s)>0\) (for n large enough) and we can write:
By means of the properties of \(\varphi ^{\varepsilon _n}\) and \(\psi ^{\varepsilon _n}\), see (0.4) and the subsequent discussion, and recalling Corollary 3.4 it is easy to see that the function \(\displaystyle a^{\varepsilon _n}(\sigma ):=\frac{\chi _{[\varphi ^{\varepsilon _n}(s),\varphi ^{\varepsilon _n}(t)]}(\sigma )}{{\dot{\psi }}^{\varepsilon _n}((\varphi ^{\varepsilon _n})^{-1}(\sigma ))}\) satisfies \(\Vert a^{\varepsilon _n}\Vert _{L^\infty (0,t)}\le 1\) and \(a^{\varepsilon _n}\rightarrow \chi _{[s,t]}\) in \(L^1(0,t)\) as \(n\rightarrow +\infty \). So we conclude if we prove that:
since the function \(w/\ell \) belongs to \(L^\infty (0,t)\). To prove (4.8), we estimate:
By (H1) and (4.2), the first and the second term go to zero as \(n\rightarrow +\infty \). For the third one, we continue the estimate:
which goes to zero by (3.3), and we conclude in the case \(s>0\).
If instead \(s=0\), we can write:
Reasoning as before, one can show that the second term goes to \(\displaystyle \frac{1}{2}\int _{0}^{t}\frac{w(\tau )^2}{\ell (\tau )^2}\,\mathrm {d}\tau \) as \(n\rightarrow +\infty \), so we conclude if we prove that the first one, denoted by \(J^{\varepsilon _n}\), vanishes in the limit. To this aim, we estimate:
We thus conclude by means of (H1) and (3.3), since \((\varphi ^{\varepsilon _n})^{-1}(0)\) is uniformly bounded with respect to \({\varepsilon _n}\) thanks to Corollary 3.4. \(\square \)
Now, we pass to the limit in the energy–dissipation balance (1.5a).
Proposition 4.7
Assume (H1), (K0), \(\nu >0\) and let w and \(\ell \) be given by (3.1) and Proposition 4.1, respectively. Then, there exists a positive measure \(\mu \) on \([0,+\infty )\) for which the following equality holds true for every \(t\in [0,+\infty )\):
where \({\varepsilon _n}\) is the subsequence given by (3.1) and by Propositions 4.1 and 4.2.
Moreover, for every \(0<s\le t\) one has:
Proof
By classical properties of BV functions in one variable [see for instance Ambrosio et al. (2000), Theorem 3.28], it is enough to prove that the function \(\rho :(-\delta ,+\infty )\rightarrow \mathbb {R}\) defined as:
belongs to the Lebesgue class of a nonincreasing function. Indeed, in that case \(\mu :=-D\rho \) does the job.
We actually prove that the right limit \(\rho ^+\) is nonincreasing. We fix \(s,t\in (-\delta ,+\infty )\) such that \(s<t\) and we consider all the possible cases.
If \(s\ge 0\), we pick two sequences \(\{s_j\}_{j\in \mathbb {N}}\), \(\{t_j\}_{j\in \mathbb {N}}\) such that for every \(j\in \mathbb {N}\) one has \(s<s_j<t<t_j\), \(s_j\) and \(t_j\) do not belong to the jump set of \(\ell \), and \(s_j\searrow s\), \(t_j\searrow t\) as \(j\rightarrow +\infty \). By the energy–dissipation balance (1.5a), we hence get:
Passing to the limit as \(n\rightarrow +\infty \), by Theorem 4.5 and by exploiting Corollary 4.4 together with (3.1), we deduce:
Passing now to the limit as \(j\rightarrow +\infty \) we get \(\rho ^+(t)\le \rho ^+(s)\).
If \(s\in (-\delta ,0)\) and \(t\ge 0\), we consider a sequence \(\{t_j\}_{j\in \mathbb {N}}\) as before, and by means of the energy–dissipation balance, we infer:
Passing to the limit as \(n\rightarrow +\infty \) and then \(j\rightarrow +\infty \), we hence deduce that also in this case \(\rho ^+(t)\le \rho ^+(s)\).
If finally both s and t belong to \((-\delta ,0)\), then trivially \(\rho ^+(t)=\rho ^+(s)\) and so we conclude. \(\square \)
The measure \(\mu \) introduced in the previous proposition somehow represents the amount of energy dissipated by viscosity which still is present in the limit. Indeed, it can be seen as a \(\hbox {weak}^*\)-limit of \(\mathcal A^\varepsilon \) as \(\varepsilon \rightarrow 0^+\). The rise of such a limit measure occurs also in Roubíček (2013) in a model of contact between two viscoelastic bodies. Of course, to obtain the desired quasistatic energy–dissipation balance (eb) we need to prove that \(\mu \equiv 0\), namely that \(\mathcal A^\varepsilon \) vanishes as \(\varepsilon \rightarrow 0^+\). Before doing that, we present a proposition which states that \(\mu \) is an atomic measure assuming (K1) and slightly stronger conditions on the limit loading w. For the result, we will need the following lemma, whose proof can be found in Scilla and Solombrino (2018), Lemma 5.2.
Lemma 4.8
Let \(\eta :[a,b]\rightarrow \mathbb {R}\) be continuous and such that the Dini upper right derivative of \(\eta \) is nonnegative for every \(t\in (a,b)\), namely:
Then, \(\eta \) is nondecreasing in [a, b].
Proposition 4.9
Assume (H1), (K0), (K1), \(\nu >0\) and let w and \(\ell \) be given by (3.1) and Proposition 4.1, respectively. Assume in addition that w satisfies at least one of the following properties:
- (a)
\(w^2\) is nonincreasing;
- (b)
w is locally Lipschitz.
Then, the measure \(\mu \) given by Proposition 4.7 is concentrated on the jump set of the function \(\rho \) defined in (4.11).
Proof
The proof follows the ideas proposed in Scilla and Solombrino (2019), Theorem 5.4, so we only sketch it, adding more details when differences come out. We first consider the right-continuous function:
which is nonincreasing and possesses the same jump set of \(\rho \). We now take the continuous and nonincreasing function \(\rho ^+-\rho ^J\); by Lemma 4.8, it is nondecreasing, and hence constant, if its Dini upper right derivative is nonnegative in \((0,+\infty )\). We indeed recall that it is already constant in \((-\delta ,0]\) by definition. If we prove this fact we conclude, since in that case \(\mu =-D\rho =-D\rho ^+=-D\rho ^J=-(D\rho )^J\), the latter being the jump part of the measure \(D\rho \). So we fix \(t\in (0,+\infty )\) and \(h>0\) and we start to estimate by exploiting the fact that \(\rho ^J\) is nonincreasing:
By the explicit expression of \(\rho \), we then continue exploiting (K1) and stability condition (4.4a):
If (a) is fulfilled, then \(\dot{w}(t)w(t)\le 0\) for a.e. \(t>0\) and thus (4.12) is nonnegative and we conclude. If instead w satisfies (b), then we actually prove that (4.12) goes to 0 as \(h\rightarrow 0^+\). To this aim, we estimate:
and we conclude since \(\ell ^+\) is right-continuous. \(\square \)
Remark 4.10
The requirement of conditions (a) or (b) seems artificial to us; indeed, we expect the same result still to hold without these additional assumptions. However, if w only belongs to \(\widetilde{H}^1(0,+\infty )\) and (a) does not hold previous proof does not work since in this case we are not able to show that (4.12) goes to zero, neither that its \(\limsup \) as \(h\rightarrow 0^+\) is nonnegative. Indeed, estimate (4.13) would become:
and nothing can be said about its limit when \(h\rightarrow 0^+\).
We also expect that the previous proposition still holds true removing assumption (K1), but also in this case our proof fails. This time the difficult term to estimate is \(\displaystyle \frac{1}{h}\int \limits _{\ell ^+(t)}^{\ell ^+(t+h)}\frac{\phi _\kappa (\sigma ){-}w(t)^2/2}{\sigma ^2}\,\mathrm {d}\sigma \); indeed, stability condition (4.4a) works well only in points of the form \(\ell ^+(t)\), so if t is a jump point for \(\ell ^+\) the integrand could be negative and the \(\liminf \) of the integral as \(h\rightarrow 0^+\) could be even \(-\infty \).
Unfortunately, the fact that \(\mu \) is concentrated on the jump set of \(\rho \) gives us no information about the limit debonding front. Let us indeed consider the following example: we take \(w(t)\equiv w>0\), \(\kappa (x)=\frac{1}{2}\frac{w^2}{x^2}\) if \(x\in [\ell _0,L]\), where \(L>>\ell _0\), and \(\kappa (x)=\frac{1}{2}\frac{w^2}{L^2}\) if \(x\ge L\). Moreover, we pick \(u_1^\varepsilon \equiv 0\) and \(u_0^\varepsilon (x)=w\left( 1-\frac{x}{\ell _0}\right) \). Then, any nondecreasing function \(\ell \) for which \(T^*:=\inf \{t>0\mid \ell ^+(t)\ge L\}\) is positive satisfies (4.4) with equality for every \(t\in [0,T^*)\); furthermore, in this case \(\rho (t)\equiv \frac{1}{2}\frac{w^2}{\ell _0^2}\) in \([-\delta ,T^*)\), and thus \(\mu \equiv 0\) on that interval.
To overcome this problem and to give a characterisation of the limit debonding front \(\ell \), we are forced to strengthen the assumptions on the toughness \(\kappa \), but in this way the annoying conditions (a) and (b) in Proposition 4.9 can be avoided. As we did in Sect. 2 to show equivalence between energetic and quasistatic evolutions, we first prove that \(\ell \) is a continuous function; this is, however, a crucial step for getting (eb) from (4.10).
Corollary 4.11
Assume (H1), (K0), (K2) and let \(\nu \) be positive. Then, the nondecreasing function \(\ell \) given by Proposition 4.1 is continuous in \((0,+\infty )\).
Proof
The result follows arguing as in the proof of Lemma 2.4 by means of (4.4b) and (4.10); see also Remark 2.6. \(\square \)
Proposition 4.12
Assume (H1), (K0), (K3) and let \(\nu \) be positive. Then, the following energy–dissipation balance holds true for the nondecreasing function \(\ell \) obtained in Proposition 4.1:
where w is given by (3.1).
Proof
By Corollary 4.11, we know \(\ell \) is continuous on \((0,+\infty )\), by (4.4a) we deduce that \(\ell \) satisfies stability condition (s2) in \((0,+\infty )\), while by (4.10) the function
is nonincreasing in \((0,+\infty )\). Thus, by Proposition 2.7 and Remark 2.8 we deduce that \(\ell \) has the form (2.5), with \(\ell ^+(0)\) in place of \(\ell _0\). By (K3) and by means of Theorem 2.9, we hence conclude. Indeed, we point out that, under our assumptions, condition (KW) is automatically satisfied: by (K0) and (K2), we deduce \(\lim \limits _{x\rightarrow +\infty }\phi _\kappa (x)=+\infty \) and by (4.4a) we have \(\phi _\kappa (\ell ^+(0))\ge \frac{1}{2} w(0)^2\). \(\square \)
The previous proposition shows that, assuming (K3), the measure \(\mu \) introduced in Proposition 4.7 is concentrated on the singleton \(\{0\}\). This means that viscosity dissipates all the initial energy at the initial time \(t=0\). Up to now, we have thus proved that, under suitable assumptions, the limit pair \((u,\ell )\) is a quasistatic evolution starting from the point \(\ell ^+(0)\). The aim of the next subsection will characterise the value \(\ell ^+(0)\).
6.3 The Initial Jump
In this subsection, we show that the (possible) initial jump of the limit debonding front \(\ell \) is characterised by the equality \(\ell ^+(0)=\lim \limits _{t\rightarrow +\infty }\tilde{\ell }(t)\), where \(\tilde{\ell }\) is the debonding front related to the unscaled dynamic coupled problem:
Here, we are assuming that \(u_0\in H^1(0,\ell _0)\) satisfies \(u_0(0)=w(0)\) and \(u_0(\ell _0)=0\). Moreover, as before, we consider \(\nu >0\) and a positive toughness \(\kappa \) which belongs to \(\widetilde{C}^{0,1}([\ell _0,+\infty ))\). We also need to introduce stronger conditions than (H1):
- (H2)
the family \(\{{w^\varepsilon }\}_{\varepsilon >0}\) is bounded in \({\widetilde{H}}^1(0,+\infty )\), \(u_0^\varepsilon \rightarrow u_0\) strongly in \(H^1(0,\ell _0)\), \(\varepsilon u_1^\varepsilon \rightarrow 0\) strongly in \(L^2(0,\ell _0)\) as \(\varepsilon \rightarrow 0^+\).
- (H3)
\({w^\varepsilon }\rightharpoonup w\) weakly in \({\widetilde{H}}^1(0,+\infty )\), \(u_0^\varepsilon \rightarrow u_0\) strongly in \(H^1(0,\ell _0)\), \(\varepsilon u_1^\varepsilon \rightarrow 0\) strongly in \(L^2(0,\ell _0)\) as \(\varepsilon \rightarrow 0^+\).
Remark 4.13
Assuming (H3), by the compact embedding of \(H^1(0,T)\) in \(C^0([0,T])\) we deduce that for every \(T>0\) we have \({w^\varepsilon }\rightarrow w\) uniformly in [0, T] as \(\varepsilon \rightarrow 0^+\).
Remark 4.14
As explained in Sect. 1, the pair \((\tilde{u},\tilde{\ell })\) solution of (4.15) and (4.16) fulfils the energy–dissipation balance:
where \(\mathcal E\) and \(\mathcal A\) are as in (1.4a) and (1.4b) with \(\varepsilon =1\) and \(\tilde{u}\), \(\tilde{\ell }\) in place of \({u^\varepsilon }\) and \({\ell ^\varepsilon }\).
We want to notice that, assuming (H2) and considering the subsequence \({\varepsilon _n}\) given by Remark 3.1, one can apply Theorem 1.8 deducing that actually the pair \((\tilde{u},\tilde{\ell })\) is the limit as \(n\rightarrow +\infty \) (in the sense of Theorem 1.8) of \((u_{\varepsilon _n},\ell _{\varepsilon _n})\), where this last pair is the dynamic evolution related to the unscaled problem (0.1) (replacing w, \(u_0\), \(u_1\) by \(w^{\varepsilon _n}\), \(u_0^{\varepsilon _n}\), \(u_1^{\varepsilon _n}\)) coupled with dynamic Griffith’s criterion.
We denote by \(\ell _1\) the limit of \(\tilde{\ell }(t)\) when t goes to \(+\infty \). Before studying the relationship between \(\ell _1\) and \(\ell ^+(0)\), we perform an asymptotic analysis of the pair \((\tilde{u},\tilde{\ell })\) as \(t\rightarrow +\infty \).
Lemma 4.15
Assume (K0). Then, for every \(\delta >0\) there exists a time \(T_\delta >0\) and a measurable set \(N_\delta \subseteq (T_\delta ,+\infty )\) such that \(|N_\delta |\le \delta \) and \(\dot{\tilde{\ell }}(t)\le \delta \) for every \(t\in (T_\delta ,+\infty )\!\setminus \!N_\delta \).
Proof
First of all, we notice that by (K0) we deduce from the energy–dissipation balance (4.17) that \(\ell _1\) is finite. Then, we fix \(\delta >0\) and we consider \(T_\delta >0\) in such a way that \(\ell _1-\tilde{\ell }(T_\delta )\le \delta ^2\). Introducing the sets:
we then define \(N_\delta :=ND_\delta \cup M_\delta \). By construction \(\dot{\tilde{\ell }}(t)\le \delta \) for every \(t\in (T_\delta ,+\infty )\!\setminus \!N_\delta \), while by means of Čebyšëv inequality we deduce:
and we conclude. \(\square \)
All the next propositions trace what we have done in the previous sections to deal with the analysis of the limit of the pair \(({u^\varepsilon },{\ell ^\varepsilon })\) when \(\varepsilon \rightarrow 0^+\). For this reason, the proofs are only sketched.
Proposition 4.16
Assume (K0). Then, one has \(\displaystyle \lim \limits _{t\rightarrow +\infty }{\mathcal E}(t)=\frac{1}{2}\frac{w(0)^2}{\ell _1}\).
Proof
As in Sect. 3, we introduce the modified energy:
where
Repeating the proof of Theorem 3.5, we deduce that the following estimate holds true:
where m is a suitable positive value and C is a positive constant independent of t. By means of Lemma 4.15, now we show that the second term in (4.18) goes to 0 when \(t\rightarrow +\infty \). Indeed, let us fix \(\delta >0\) and consider \(T_\delta \), \(N_\delta \) as in Lemma 4.15; then, for every \(t\ge T_\delta \) we can estimate:
Letting first \(t\rightarrow +\infty \) and then \(\delta \rightarrow 0^+\), we hence deduce that \(\displaystyle \lim \limits _{t\rightarrow +\infty }\mathrm{e}^{-mt}\int _{0}^{t}\dot{\tilde{\ell }}(\tau )\mathrm{e}^{m\tau }\,\mathrm {d}\tau =0\) and so we get \(\lim \limits _{t\rightarrow +\infty }\widetilde{\mathcal E}(t)=0\). Now, we conclude since like in (3.9) we have:
\(\square \)
Lemma 4.17
Assume (K0). Then, the following limit holds true:
Proof
The proof is analogous to the one of Corollary 4.4. By using (4.1) with the obvious changes, for every \(t>0\) we obtain the estimate:
From this, we conclude by applying de l’Hôpital’s rule since in Proposition 4.16 we proved that \(\lim \limits _{t\rightarrow +\infty }\widetilde{\mathcal E}(t)=0\). \(\square \)
Proposition 4.18
Assume (K0). Then, \(\ell _1\) satisfies the stability condition at time \(t=0\), namely:
Proof
The idea is to pass to the limit as \(t\rightarrow +\infty \) in the stability condition in Griffith’s criterion (4.16), as we did in Proposition 4.6. Since here we want to compute a limit when t grows to \(+\infty \), as in Lemma 4.17 we need to average the stability condition, getting:
By de l’Hôpital’s rule, the left-hand side in (4.19) converges to \(\kappa (\ell _1)\) as \(t\rightarrow +\infty \), while to deal with the right-hand side we argue as in the proof of Proposition 4.6. For the sake of simplicity, we introduce the time \(t^*>0\) which satisfies \(t^*=\tilde{\ell }(t^*)\), so that for every \(t\ge t^*\) we can write:
where we used the explicit formula for \({G}_{\dot{\tilde{\ell }}(\sigma )}(\sigma )\) given by (4.5) and (4.6), with the obvious changes. By means of Lemma 4.17 and since \(\lim \limits _{t\rightarrow +\infty }\frac{\tilde{\varphi }(t)}{t}=\lim \limits _{t\rightarrow +\infty }\frac{t-{\tilde{\ell }}(t)}{t}=1\) it is easy to infer:
Moreover, by using estimate (4.9) in the proof of Proposition 4.6 and recalling that the dissipated energy \(\mathcal A\) is bounded by (4.17), we deduce:
From (4.21) and (4.22), we can pass to the limit in (4.20) deducing that:
and so we conclude. \(\square \)
We are now in a position to compare the value of \(\ell ^+(0)\) with \(\ell _1\).
Lemma 4.19
Assume (H2) and (K0). Then, \(\ell _1\le \ell ^+(0)\).
Proof
We fix \(t>0\) and we consider the subsequence \({\varepsilon _n}\searrow 0\) given by Remark 3.1 and Proposition 4.1. Then, one has:
Now, we fix \(T>0\) and by monotonicity we deduce \(\ell _{\varepsilon _n}\left( \frac{t}{{\varepsilon _n}}\right) \ge \ell _{\varepsilon _n}\left( T\right) \) for n large enough. Thus, by means of Theorem 1.8, we get:
Hence, \(\ell (t)\ge \tilde{\ell }(T)\) and by the arbitrariness of \(t>0\) and \(T>0\) we conclude. \(\square \)
Proposition 4.20
Assume (H2), (K0) and (K3). Then, the following inequality holds true:
Proof
By Proposition 4.7, Corollary 4.11 and the energy–dissipation balance (1.5a), we know that for every \(t>0\) it holds:
where \({\varepsilon _n}\) is the subsequence given by (3.1) and by Propositions 4.1 and 4.2. By means of (4.14), we hence deduce:
By a simple change of variable, we now notice that:
and so, by Theorem 1.8, we get:
Putting together (4.23) and (4.24), we finally deduce:
To conclude it is enough to recall that by energy–dissipation balance (4.17) we have:
and so by Proposition 4.16 we obtain:
\(\square \)
Corollary 4.21
Assume (H2), (K0) and (K3). Then, \(\ell _1=\ell ^+(0)\).
Proof
By Lemma 4.19, we already know that \(\ell _1\le \ell ^+(0)\). As in Proposition 2.3, we introduce the energy:
By Proposition 4.20, we get \(E_0(\ell ^+(0))\le E_0(\ell _1)\), while by Proposition 4.18 and (K3) we deduce that \(\dot{E}_0(x)>0\) for every \(x>\ell _1\), namely \(E_0\) is strictly increasing in \((\ell _1,+\infty )\). Thus, we finally obtain \(\ell _1=\ell ^+(0)\). \(\square \)
Putting together all the results obtained up to now, we can finally deduce our main Theorem:
Theorem 4.22
Fix \(\nu > 0\), \(\ell _0>0\) and assume the functions \({w^\varepsilon }\), \(u_0^\varepsilon \) and \(u_1^\varepsilon \) satisfy (1.2) and (1.3) for every \(\varepsilon >0\). Let the positive toughness \(\kappa \) belong to \(\widetilde{C}^{0,1}([\ell _0,+\infty ))\) and assume (H2), (K0) and (K3). Let \(({u^\varepsilon },{\ell ^\varepsilon })\) be the pair of dynamic evolutions given by Theorem 1.6. Let \({\varepsilon _n}\) and w be the subsequence and the function given by Remark 3.1 and let \(\ell _1\) be defined as \(\ell _1:=\lim \limits _{t\rightarrow +\infty }\tilde{\ell }(t)\), with \((\tilde{u},\tilde{\ell })\) solution of (4.15) and (4.16). Then, for every \(t\in (0,+\infty )\) one has:
- (a)
\(\lim \limits _{n\rightarrow +\infty }{\ell ^{\varepsilon _n}}(t)=\ell (t)\),
- (b)
\({\varepsilon _n}{u_t^{\varepsilon _n}}(t,\cdot )\rightarrow 0\) strongly in \(L^2(0,+\infty )\) as \(n\rightarrow +\infty \),
- (c)
\({u^{\varepsilon _n}}(t,\cdot )\rightarrow u(t,\cdot )\) strongly in \(H^1(0,+\infty )\) as \(n\rightarrow +\infty \),
where \((u,\ell )\) is the quasistatic evolution given by Theorem 2.9 starting from \(\ell _1\) and with external loading w.
Moreover, if we assume (H3), then we do not need to pass to a subsequence and the whole sequence \(({u^\varepsilon },{\ell ^\varepsilon })\) converges to \((u,\ell )\) in the sense of (a), (b), (c) for every \(t\in (0,+\infty )\) as \(\varepsilon \rightarrow 0^+\).
Remark 4.23
Of course, stability condition at time \(t=0\), namely \(\frac{1}{2} \frac{w(0)^2}{\ell _0^2}\le \kappa (\ell _0)\), is a necessary condition to have \(\ell _1=\ell _0\), due to Proposition 4.18; however, it is not sufficient; indeed, it does not involve the initial position \(u_0\), which can produce the initial jump if steep enough, as the following example shows. Let us consider the case of a constant toughness \(\kappa =1/2\), a loading term satisfying \(0\le w(0)\le \ell _0\) (so that initial stability holds) and a smooth (\(C^1\) is enough) initial position \(u_0\) fulfilling compatibility conditions \(u_0(0)=w(0)\) and \(u_0(\ell _0)=0\). By means of the explicit equation solved by the debonding front \(\tilde{\ell }\), namely (1.8) with \(\varepsilon =1\), and thanks to (1.16), we deduce that under our assumptions \(\tilde{\ell }\) is actually \(C^1([0,+\infty ))\) [see also Riva and Nardini (2018)]. Moreover, we can compute:
from which we get \(\dot{\tilde{\ell }}(0)>0\), and thus \(\ell _1>\ell _0\), if \(\dot{u}_0(\ell _0)^2>1\).
On the other hand, if the initial position is an affine function, namely \(u_0(x)=w(0)\left( 1-\frac{x}{\ell _0}\right) \), then stability condition at time \(t=0\) becomes equivalent to the absence of initial jump. Indeed, in this case if \(\frac{1}{2} \frac{w(0)^2}{\ell _0^2}\le \kappa (\ell _0)\), then the pair \((\tilde{u},\tilde{\ell })\) is explicitly given by \(\tilde{u}(t,x)=w(0)\left( 1-\frac{x}{\ell _0}\right) \) and \(\tilde{\ell }(t)=\ell _0\), since by (1.16) we have \(G_0(t)\equiv \frac{1}{2}\frac{w(0)^2}{\ell _0^2}\), and thus trivially \(\ell _1=\ell _0\).
Remark 4.24
Under the same assumptions of the above theorem, the convergence of the debonding fronts can be slightly improved by classical arguments. Indeed, since \({\ell ^\varepsilon }\) are nondecreasing continuous functions and since the pointwise limit \(\ell \) is continuous in \((0,+\infty )\), we can infer that the convergence stated in (a) is actually uniform on compact sets contained in \((0,+\infty )\).
We want also to recall that for every \(T>0\) the convergences in (b) and (c) hold true, respectively, in \(L^2(0,T;L^2(0,+\infty ))\) and \(L^2(0,T;H^1(0,+\infty ))\) too, as we proved in Proposition 4.2 under weaker assumptions.
Remark 4.25
We want to notice that Theorem 2.9 ensures that the limit \(\ell \) is an absolutely continuous function, so one could guess that the convergence of the debonding fronts \({\ell ^\varepsilon }\) even occurs in \(W^{1,1}_{ loc }(0,+\infty )\), but unfortunately we were not able to prove it. Of course, this last conjecture could be true only under the assumptions of Theorem 4.22, otherwise neither the continuity of the function \(\ell \) is expected. Our idea to attack the problem was getting good a priori bounds on \({{\dot{\ell }}^\varepsilon }\) via the explicit formula (1.8), but we found the task hard due to the high nonlinearity of the formula. Thus, better ideas or better strategies are needed to validate or to disprove our conjecture.
7 Conclusions
In this paper, we have proved that dynamic evolutions of a damped debonding model are a good approximation of the quasistatic one when initial velocity and speed of the external loading are very slow with respect to internal vibrations. In light of Lazzaroni and Nardini (2018b), in which the failure of this approximation in the undamped case (even with constant toughness) is shown, it is clear that the presence of viscosity, or more generally the presence of some kind of friction, is crucial to get this kind of result. As previously said, the importance of viscosity was already observed in finite dimension and in some damage models.
Although in our work we have been able to cover cases of quite general toughness \(\kappa \), we, however, needed to require some assumptions on it to develop all the arguments. First of all, we have always assumed continuity of \(\kappa \) and furthermore conditions (K1), (K2) or (K3) have been used to prevent the case of a glue whose toughness oscillates dramatically. It is worth noticing that we did not make use of them until Proposition 4.9; thus, our previous analysis is suited to deal with wild oscillating (but still continuous) toughnesses too. Going further in the analysis without that assumptions possibly requires a deeper understanding of the measure \(\mu \) introduced in Proposition 4.7 and of its relationship with the jump set of the limit debonding front. This kind of study has been developed in Scilla and Solombrino (2019) in finite dimension, but a generalisation to our infinite-dimensional setting seemed hard to us. The idea in Scilla and Solombrino (2019) relies on the introduction of a suitable cost function which measures the energy gap of a limit solution after a jump in time and hence characterises their counterpart of measure \(\mu \).
As explained with the example under Proposition 2.3, without condition (K2) we lose uniqueness and continuity (in time) of quasistatic evolutions. However, a more careful analysis on the quasistatic limit might be useful to select and characterise those quasistatic evolutions coming from dynamic ones, and thus somehow more physical. We indeed expect that, as happens in Scilla and Solombrino (2019) and as happens in our problem at time \(t=0\), one could characterise the (possible) jumps of the limit debonding front at time \(t={\bar{t}}>0\) as the limit to infinity of a debonding front of a suitable unscaled problem: we conjecture the right one should be the solution to (4.15) and (4.16) with \(w({\bar{t}}\,)\) and \(u^-({\bar{t}}\,)\) in place of w(0) and \(u_0\), respectively, and starting from \(\ell ^-({\bar{t}}\,)\). Unfortunately, in this case the proof performed in Sect. 4.3 does not work anymore and, as said before, we were not able to transfer the strategy developed in Scilla and Solombrino (2019) to our infinite-dimensional case.
A more drastic scenario may even appear in the case of a discontinuous toughness, covered, however, by Theorem 1.6. The failure of the quasistatic approximation in this framework was observed in Dumouchel et al. (2008) and Lazzaroni et al. (2012) where the authors considered explicit examples of piecewise constant toughness \(\kappa \); they noticed that on discontinuity points of \(\kappa \) the limit solution does not fulfil Griffith’s criterion, which has to be replaced by a suitable energy balance. This is in line with Proposition 4.7 (which, however, should be proved without assuming continuity of \(\kappa \)), where the appearance of the measure \(\mu \) in (4.10) takes into account also this feature. A similar phenomenon emerges in Roubíček (2013) too. As we said before, a more complete comprehension of \(\mu \) may thus open new perspectives in the understanding of the topic of quasistatic limit.
Finally, we want to mention that different kinds of frictions may be considered in the dynamic model, replacing the viscous term \(u_t(t,x)\) in the wave equation for instance by \({-}u_{txx}(t,x)\) (Kelvin–Voigt model, see Dautray and Lions (1992), Slepyan (2002)) or by a convolution term of the form \(\int _{0}^{+\infty }{-}h(\tau )u_{txx}(t-\tau ,x)\,\mathrm {d}\tau \) (viscoelastic materials, see Conti et al. (2018), Dautray and Lions (1992), Slepyan (2002)). To our knowledge, an analysis of debonding models under the action of these kinds of viscoelastic dampings is still missing in the literature.
Furthermore, one might also wonder whether some nonlinear viscous term may change or not the main results of the paper; and also, what happens if inertia and viscosity go to zero in a different manner than \(\varepsilon ^2\) and \(\varepsilon \)?
We leave all of these questions and proposals open to further research.
References
Agostiniani, V.: Second order approximations of quasistatic evolution problems in finite dimension. Discrete Contin. Dyn. Syst. 32, 1125–1167 (2012)
Almi, S., Dal Maso, G., Toader, R.: Quasi-static crack growth in hydraulic fracture. J. Nonlinear Anal. 109, 301–318 (2014)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs. Clarendon Press, Oxford (2000)
Bourdin, B., Francfort, G.A., Marigo, J.-J.: The variational approach to fracture. J. Elast. 91, 5–148 (2008)
Burridge, R., Keller, J.B.: Peeling, slipping and cracking: some one-dimensional free boundary problems in mechanics. SIAM Rev. 20, 31–61 (1978)
Conti, M., Danese, V., Giorgi, C., Pata, V.: A model of viscoelasticity with time-dependent memory kernels. Am. J. Math. 140, 349–389 (2018)
Dal Maso, G., Scala, R.: Quasistatic evolution in perfect plasticity as limit of dynamic processes. J. Differ. Equ. 26, 915–954 (2014)
Dal Maso, G., Lazzaroni, G., Nardini, L.: Existence and uniqueness of dynamic evolutions for a peeling test in dimension one. J. Differ. Equ. 261, 4897–4923 (2016)
Dautray, R., Lions, J.-L.: Mathematical Analysis and Numerical Methods for Science and Technology. Volume 1, Physical Origins and Classical Methods. Springer, Berlin (1992)
Dumouchel, P.-E., Marigo, J.-J., Charlotte, M.: Dynamic fracture: an example of convergence towards a discontinuous quasistatic solution. Contin. Mech. Thermodyn. 20, 1–19 (2008)
Freund, L.B.: Dynamic Fracture Mechanics. Cambridge Monographs on Mechanics and Applied Mathematics. Cambridge University Press, Cambridge (1990)
Hellan, K.: Debond dynamics of an elastic strip-I. Timoshenko beam properties and steady motion. Int. J. Fract. 14, 91–100 (1978a)
Hellan, K.: Debond dynamics of an elastic strip-II. Simple transient motion. Int. J. Fract. 14, 173–184 (1978b)
Hellan, K.: Introduction to Fracture Mechanics. McGraw-Hill, New York (1984)
Lazzaroni, G., Nardini, L.: On the 1d wave equation in time-dependent domains and the problem of debond initiation. ESAIM: COCV. (2017). https://doi.org/10.1051/cocv/2019006
Lazzaroni, G., Nardini, L.: Analysis of a dynamic peeling test with speed-dependent toughness. SIAM J. Appl. Math. 78, 1206–1227 (2018a)
Lazzaroni, G., Nardini, L.: On the quasistatic limit of dynamic evolutions for a peeling test in dimension one. J. Nonlinear Sci. 28, 269–304 (2018b)
Lazzaroni, G., Bargellini, R., Dumouchel, P.-E., Marigo, J.-J.: On the role of kinetic energy during unstable propagation in a heterogeneous peeling test. Int. J. Fract. 175, 127–150 (2012)
Lazzaroni, G., Rossi, R., Thomas, M., Toader, R.: Rate-independent damage in thermo-viscoelastic materials with inertia. J. Dyn. Differ. Equ. 30, 1311–1364 (2018)
Mielke, A., Roubíček, T.: Rate-Independent Systems: Theory and Application, Applied Mathematical Sciences, vol. 193. Springer, New York (2015)
Misra, S., Gorain, G.C.: Stability of an inhomogeneous damped vibrating string. Appl. Appl. Math. 9, 435–448 (2014)
Nardini, L.: A note on the convergence of singularly perturbed second order potential-type equations. J. Dyn. Differ. Equ. 29, 783–797 (2017)
Riva, F.: A continuous dependence result for a dynamic debonding model in dimension one. Milan J. Math. (2019). https://doi.org/10.1007/s00032-019-00303-5
Riva, F., Nardini, L.: Existence and uniqueness of dynamic evolutions for a one-dimensional debonding model with damping. (2018). arXiv:1810.12006v2
Roubíček, T.: Adhesive contact of visco-elastic bodies and defect measures arising by vanishing viscosity. SIAM J. Math. Anal. 45, 101–126 (2013)
Scilla, G., Solombrino, F.: Multiscale analysis of singularly perturbed finite dimensional gradient flows: the minimizing movement approach. Nonlinearity 31, 5036–5074 (2018)
Scilla, G., Solombrino, F.: A variational approach to the quasistatic limit of viscous dynamic evolutions in finite dimension. J. Differ. Equ. 267, 6216–6264 (2019)
Slepyan, L.I.: Models and Phenomena in Fracture Mechanics. Springer, New York (2002)
Zanini, C.: Singular perturbations of finite dimensional gradient flows. Discrete Contin. Dyn. Syst. Ser. A 18, 657–675 (2007)
Acknowledgements
The author wishes to thank Prof. Gianni Dal Maso for many helpful discussions on the topic. The author is a member of the Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Dr. Anthony Bloch.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Riva, F. On the Approximation of Quasistatic Evolutions for the Debonding of a Thin Film via Vanishing Inertia and Viscosity. J Nonlinear Sci 30, 903–951 (2020). https://doi.org/10.1007/s00332-019-09595-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-019-09595-8
Keywords
- Thin films
- Dynamic debonding
- Quasistatic debonding
- Griffith’s criterion
- Quasistatic limit
- Vanishing inertia and viscosity limit