Two Limit Cycles in Liénard Piecewise Linear Differential Systems

Abstract

Some techniques for studying the existence of limit cycles for smooth differential systems are extended to continuous piecewise linear differential systems. Rigorous new results are provided on the existence of two limit cycles surrounding the equilibrium point at the origin for systems with three zones separated by two parallel straight lines without symmetry. As a relevant application, it is shown the existence of bistable regimes in an asymmetric memristor-based electronic oscillator.

1 Introduction and Statement of the Main Results

One of the most interesting problems in the qualitative theory of planar polynomial differential systems is the study of their limit cycles, known as the famous second part of the 16th Hilbert problem (1900). Due to the fact that this Hilbert problem becomes up to now intractable (see Ilyashenko 2002; Li 2003), Smale (1998) proposed to study this problem restricting it to polynomial Liénard differential systems. In the case of smooth Liénard systems, there are many results on the nonexistence, existence and uniqueness of limit cycles, see, for instance, Carletti and Villari (2005), Dumortier and Li (1996), Dumortier and Rousseau (1990), Gasull et al. (2009), Khibnik et al. (1998), Llibre et al. (2009), Llibre and Valls (2013), Xiao and Zhang (2003) and Zhang et al. (1992). Going beyond the smooth case, a natural step is to allow non-smoothness while keeping the continuity, as it has been done in some previous works (Freire et al. 2002; Hogan 2003; van Horssen 2005; Llibre et al. 2013; Llibre and Teruel 2014).

While the majority of results for piecewise linear differential systems deal with two zones separated by one straight line or three zones separated by two parallel straight lines with symmetry and study the existence of at most one limit cycle, in this paper we go beyond and focus the attention to non-symmetric systems. Particular cases of such non-symmetric systems but assuming a certain symmetry for the sign of their determinants and traces in the three regions and allowing only one equilibrium point have been studied in Ponce et al. (2015) and Chen et al. (2017). The quoted authors are able to show the existence of two limit cycles surrounding the only equilibrium under adequate hypotheses. Similar results have been recently obtained in Lima et al. (2017) by considering perturbations of systems without sign-symmetric traces but under rather non-generic hypotheses. In all the quoted cases, the location of the equilibrium is out of the central zone for having two limit cycles.

Here, we do not assume any symmetry at all and give an extensive list of cases where we prove the existence of two limit cycles surrounding the origin, a new result in this field. In Llibre et al. (2015), exploiting the fact that there are situations where, by moving only the parameter given by the trace of the central zone, it is possible to pass from a system with two zones to a system with three zones, the authors were able to prove the existence of at least two limit cycles surrounding the equilibrium at the origin in some particular cases. The characterization of all possible cases with two limit cycles is far from being completely solved, and this paper is the first rigorous paper toward this goal exploiting all possibilities in which we are able to prove the existence of at least two limit cycles surrounding the equilibrium at the origin. This is the aim of this paper, and the techniques used to achieve this goal are not the same as the ones in Llibre et al. (2015), because there one of the main tools was the Massera’s method for proving the uniqueness of the limit cycles, which here is unusable because we want to prove the existence of at least two limit cycles.

More precisely, in this work we will study the limit cycles of the Liénard piecewise linear differential systems

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}\tau }= x' = F(x)-y, \quad \frac{\hbox {d}y}{\hbox {d}\tau }= y' =g(x), \end{aligned}$$

(1)

where

$$\begin{aligned} F(x)= & {} {\left\{ \begin{array}{ll} T_{L} (x+u) - T_{C} u &{}\quad \text {if } x \le -u,\\ T_{C} x &{}\quad \text {if } -u \le x \le v, \\ T_{R} (x-v) + T_{C} v &{}\quad \text {if } x \ge v, \end{array}\right. } \quad \text{ and } \\ g(x)= & {} {\left\{ \begin{array}{ll} L (x+u) - u &{}\quad \text {if } x \le -u,\\ x &{}\quad \text {if } -u \le x \le v, \\ R (x-v) + v &{}\quad \text {if } x \ge v, \end{array}\right. } \end{aligned}$$

with the constants u and v being positive, so that the straight lines $x=-u$ and $x=v$ split the phase plane in three regions. In the case that these systems are symmetric with respect to the origin of coordinates, i.e., $u=v$, $T_{L}=T_{R}$ and $L=R$. The study of their limit cycles is carried out, see Carmona et al. (2002), Freire et al. (1999), Freire et al. (2002), Freire et al. (1997) and Llibre and Sotomayor (1996) and for a complete analysis the book (Llibre and Teruel 2014).

First, we classify the equilibria of system (1).

Proposition 1

The following statements hold for the Liénard piecewise linear differential system (1).

• (a) If $L \ge 0$ and $R \ge 0$, then the origin is the unique equilibrium.

• (b) If $L \ge 0$ and $R < 0$, then there are two equilibria: the origin and $e_R= (\bar{x}_R,\bar{y}_R)=((R-1)v/R ,(T_{C}R-T_{R})v/R)$, which is a saddle.

• (c) If $L <0$ and $R \ge 0$, then there are two equilibria: the origin and $e_L=(\bar{x}_L,\bar{y}_L)= ((1-L)u/L,(T_{L}-T_{C}L)u/L)$, which is a saddle.

• (d) If $L < 0$ and $R< 0$, then there are three equilibria: the origin, $e_L$ and $e_R$, being $e_L$ and $e_R$ saddles.

Proof

It follows easily by direct computations because when equilibrium points exist they belong to the interior of each one of the three zones where the differential system is linear. $\square$

We note that the equilibrium point $e_R$ exists if and only if $R<0$, and when $R>0$, we say that $e_R$ is a virtual equilibrium. Similarly, the equilibrium point $e_L$ exists if and only if $L<0$, and when $L>0$, we say that $e_L$ is a virtual equilibrium. It follows from Proposition 1 that when the Liénard piecewise linear differential system (1) has a dynamics of focus or node type in an external zone, then the corresponding focus or node is a virtual equilibrium point; however, when such dynamics is of saddle type, then the saddle is always a real equilibrium point.

We now introduce some notation. When $T_L^2 > 4L$, we can define $w_L>0$ such that $4w_L^2=T_L^2 - 4L$ and we are dealing with a dynamics of node or saddle type. If we also introduce $\sigma _L$ such that $2\sigma _L=T_L$, then the eigenvalues are $\sigma _L\pm w_L$, with eigenvectors $(1, \sigma _L\mp w_L)^\mathrm{T}$ and $L=\sigma _L^2-w_L^2$. Thus, the corresponding (real or virtual) equilibrium point has two linear invariant manifolds that intersect the straight line $x=-u$ in two points of coordinates $(-u, P^{\pm }_{L})$. For the focus case, that is $T_L^2 < 4L$, we define $\sigma _L$ as before, but we take $\omega _L>0$ such that $4\omega _L^2=4L-T_L^2$, so that the eigenvalues are now $\sigma _L\pm i\omega _L$.

Similarly, when $T_R^2 > 4R$, we can define $w_R>0$ such that $4w_R^2=T_R^2 - 4R$ for the node or saddle cases. If we take $\sigma _R$ such that $2\sigma _R=T_R$, then the eigenvalues are $\sigma _R\pm w_R$, with eigenvectors $(1, \sigma _R\mp w_R)^\mathrm{T}$ and $R=\sigma _R^2-w_R^2$. Thus, the corresponding (real or virtual) equilibrium point has two linear invariant manifolds that intersect the straight line $x=v$ in two points of coordinates $(v, P^{\pm }_{R})$. For the focus case, that is $T_R^2 < 4R$, we define $\sigma _R$ as before, but we take $\omega _R>0$ such that $4\omega _R^2=4R-T_R^2$, so that the eigenvalues are now $\sigma _R\pm i\omega _R$.

We remark that the non-generic cases $L=0$, $R=0$, corresponding to bifurcations of equilibrium points at infinity, and the cases of improper node dynamics $T_L^2 = 4L$, $T_R^2 = 4R$, will not be included in the subsequent analysis for the sake of brevity. However, the followed approach could be extended to deal with these cases without any special difficulty.

If we focus our attention in the cases with $T_C=0$, it is clear that the origin is a linear center, leading to a period annulus which is bounded by the vertical line $x=v$, being its outermost periodic orbit the one of equation $x^2+y^2=v^2$, see Fig. 1 (left). Furthermore, apart from the origin, the possible real or virtual equilibrium points are located at $e_L$ and $e_R$, namely

$$\begin{aligned} e_L=(\bar{x}_L,\bar{y}_L)=\left( \frac{u}{L}-u,\frac{T_L}{L}u\right) ,\quad e_R=(\bar{x}_R,\bar{y}_R)=\left( v-\frac{v}{R},-\frac{T_R}{R}v\right) . \end{aligned}$$

(2)

Fig. 1

On the left, phase portrait corresponding to the case of reference $0<v<u$, $T_{L}<0$, $T_{C}=0$, and $T_{R}>0$. The outermost periodic orbit of the annulus corresponds to the circle $x^2+y^2=v^2$ and is unstable from outside, as $T_R>0$. On the right, the orbit $\gamma$ starting at $(x,y)=(v,\sqrt{u^2-v^2})$ and arriving after surrounding the period annulus at a point (v, y) with $0<y<\sqrt{u^2-v^2}$ is not possible under hypotheses $0<v<u$, $T_{L}<0$, $T_{C}=0$ and $T_{R}>0$

Taking this situation as a main reference for our subsequent analysis, we can state the following proposition whose proof is given in Sect. 4.

Proposition 2

Consider the differential systems (1) with $0<v<u$, $T_{L}<0$ and $T_{C}=0$. The following statements hold.

• (a) If $T_L^2 > 4L$ and we take $2\sigma _L=T_L$ and $w_L>0$ such that $4w_L^2=T_L^2 - 4L$, then the equilibrium point $e_L$ is an attractive virtual node when $L>0$ and a real saddle for $L<0$.

  • (a.1) When $L>0$, the invariant manifolds of the virtual node intersect the line $x=-u$ at the points $(-u, P^{\pm }_{L})$ and such orbits enter the region $-u<x<v$ intersecting the line $x=v$ at the points $(v, Q^{\pm }_{L})$, where

    $$\begin{aligned} P^{\pm }_{L}=\dfrac{u}{\sigma _L \mp w_L}, \quad Q^{\pm }_{L}=-\sqrt{(P^{\pm }_{L})^2+u^2-v^2}, \end{aligned}$$

    (3)

    so that $P^-_L<P^+_L<0$ and $Q^-_L<Q^+_L<0$. A first integral for the orbits above such invariant manifolds, when restricted to the region $x\le -u$ is the function

    $$\begin{aligned} H_L^N(\tilde{x},\tilde{y})=\log \sqrt{ (\tilde{y}-\sigma _L\tilde{x})^2-w_L^2\tilde{x}^2}+\dfrac{\sigma _L}{w_L} {{\,\mathrm{arctanh}\,}}\left( \dfrac{w_L\tilde{x}}{\tilde{y}-\sigma _L\tilde{x}}\right) , \end{aligned}$$

    (4)

    where $(\tilde{x},\tilde{y})=(x-\bar{x}_L,y-\bar{y}_L)$ are relative coordinates to $e_L$, as given in (2).

  • (a.2) When $L<0$, the invariant manifolds of the real saddle intersect the line $x=-u$ at the points $(-u, P^{\pm }_{L})$ and such orbits enter the region $-u<x<v$ (one forward and the other backward in time) intersecting the line $x=v$ at the points $(v, Q^{\pm }_{L})$, where

    $$\begin{aligned} P^{\pm }_{L}=\dfrac{u}{\sigma _L \mp w_L}, \quad Q^{\pm }_{L}=\mp \sqrt{(P^{\pm }_{L})^2+u^2-v^2}, \end{aligned}$$

    (5)

    so that $P^+_L<0<P^-_L$ and $Q^+_L<0<Q^-_L$. A first integral for the orbits between such invariant manifolds, when restricted to the region $x\le -u$, is the function

    $$\begin{aligned} H_L^S(\tilde{x},\tilde{y})=\log \sqrt{ w_L^2\tilde{x}^2-(\tilde{y}-\sigma _L\tilde{x})^2}+\dfrac{\sigma _L}{w_L} {{\,\mathrm{arctanh}\,}}\left( \dfrac{\tilde{y}-\sigma _L\tilde{x}}{w_L\tilde{x}}\right) , \end{aligned}$$

    (6)

    where $(\tilde{x},\tilde{y})=(x-\bar{x}_L,y-\bar{y}_L)$ are relative coordinates to $e_L$, as given in (2).

• (b) If $T_L^2 < 4L$ and we take $2\sigma _L=T_L$ and $\omega _L>0$ such that $4\omega _L^2= 4L-T_L^2$, then the equilibrium point $e_L$ is an attractive virtual focus. A first integral for the orbits restricted to the region $x\le -u$, is the function

  $$\begin{aligned} H_L^F(\tilde{x},\tilde{y})=\log \sqrt{(\tilde{y}-\sigma _L\tilde{x})^2+\omega _L^2 \tilde{x}^2}-\dfrac{\sigma _L}{\omega _L}\arctan \left( \dfrac{\tilde{y}-\sigma _L\tilde{x}}{\omega _L\tilde{x}}\right) , \end{aligned}$$

  (7)

  where $(\tilde{x},\tilde{y})=(x-\bar{x}_L,y-\bar{y}_L)$ are relative coordinates to $e_L$, as given in (2).

A similar result for the dynamics associated with $e_R$ is given in the next proposition. Since the proof of this proposition is analogous to the proof of Proposition 2, we omit it.

Proposition 3

Consider the differential systems (1) with $0<v<u$, $T_{C}=0$ and $T_{R}>0$. The following statements hold.

• (a) If $T_R^2 > 4R$ and we take $2\sigma _R=T_R$ and $w_R>0$ such that $4w_R^2=T_R^2 - 4R$, then the equilibrium point $e_R$ is a repulsive virtual node when $R>0$ and a real saddle for $R<0$.

  • (a.1) When $R>0$, the invariant manifolds of the virtual node intersect the line $x=v$ at the points $(v, P^{\pm }_{R})$ and such orbits enter the region $-u<x<v$ backward in time intersecting the line $x=-u$ at the points $(-u, Q^{\pm }_{R})$, where $P^{\pm }_{R}=-\dfrac{v}{\sigma _R\mp w_R}$ and $Q^{\pm }_{R}=-\sqrt{(P^{\pm }_{R})^2+v^2-u^2}$, so that $P^+_R<P^-_R<0$ and $Q^+_R<Q^-_R<0$, where it is assumed $(P^-_R)^2\ge u^2-v^2$. A first integral for the orbits above such invariant manifolds, when restricted to the region $x\le v$, is the function

    $$\begin{aligned} H_R^N(\tilde{x},\tilde{y})=\log \sqrt{(\tilde{y}-\sigma _R\tilde{x})^2- w_R^2\tilde{x}^2}+\dfrac{\sigma _R}{w_R}{{\,\mathrm{arctanh}\,}}\left( \dfrac{w_R\tilde{x}}{\tilde{y}-\sigma _R\tilde{x}}\right) , \end{aligned}$$

    where $(\tilde{x},\tilde{y})=(x-\bar{x}_R,y-\bar{y}_R)$ are relative coordinates to $e_R$, as given in (2).

  • (a.2) When $R<0$, the invariant manifolds of the real saddle intersect the line $x=v$ at the points $(v, P^{\pm }_{R})$ and such orbits enter the region $-u<x<v$ (one forward and the other backward in time) intersecting the line $x=-u$ at the points $(-u, Q^{\pm }_{R})$, where

    $$\begin{aligned} P^{\pm }_{R}=-\dfrac{v}{\sigma _R\mp w_R},\quad Q^{\pm }_{R}=\pm \sqrt{(P^{\pm }_{R})^2+u^2-v^2}, \end{aligned}$$

    (8)

    so that $P^-_R<0<P^+_R$ and $Q^-_R<0<Q^+_R$. A first integral for the orbits between such invariant manifolds, when restricted to the region $x\le v$ is the function

    $$\begin{aligned} H_R^S(\tilde{x},\tilde{y})=\log \sqrt{w_R^2\tilde{x}^2-(\tilde{y}-\sigma _R \tilde{x})^2}+\dfrac{\sigma _R}{w_R}{{\,\mathrm{arctanh}\,}}\left( \dfrac{\tilde{y}-\sigma _R \tilde{x}}{w_R\tilde{x}}\right) , \end{aligned}$$

    (9)

    where $(\tilde{x},\tilde{y})=(x-\bar{x}_R,y-\bar{y}_R)$ are relative coordinates to $e_R$, as given in (2).

• (b) If $T_R^2 < 4R$ and we take $2\sigma _R=T_R$ and $\omega _R>0$ such that $4\omega _R^2= 4R-T_R^2$, then the equilibrium point $e_R$ is an repulsive virtual focus. A first integral for the orbits restricted to the region $x\le -u$, is the function

  $$\begin{aligned} H_R^F(\tilde{x},\tilde{y})=\log \sqrt{(\tilde{y}-\sigma _R\tilde{x})^2+ \omega _R^2\tilde{x}^2}-\dfrac{\sigma _R}{\omega _R}\arctan \left( \dfrac{\tilde{y} -\sigma _R\tilde{x}}{\omega _R\tilde{x}}\right) , \end{aligned}$$

  where $(\tilde{x},\tilde{y})=(x-\bar{x}_R,y-\bar{y}_R)$ are relative coordinates to $e_R$, as given in (2).

In what follows F, N and S denote a virtual focus, a virtual node and a real saddle, and the notation FN denotes that on the left-hand zone, we have a virtual focus and on the right-hand zone, we have a virtual node and similarly for any other combinations of two letters from $\{F,N,S\}$.

Our main result is as follows:

Theorem 4

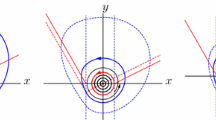
For the differential systems (1) with $0<v<u$, $T_{R}>0$, $T_{L}<0$, fulfilling one of the following sets of conditions,

(FF) :

$L, R>0$, $T_R< 2\sqrt{R}$, $|T_L| < 2 \sqrt{L}$ and

$$\begin{aligned} \dfrac{T_L}{\sqrt{L}} + \dfrac{T_R}{\sqrt{R}} <0, \end{aligned}$$

(10)

see Fig. 2 (left);

(NF) :

$L, R>0$, $T_R < 2 \sqrt{R}$, and $|T_L| > 2 \sqrt{L}$, see Fig. 2 (center);

(NN) :

$L, R>0$, $T_R> 2\sqrt{R}$, $|T_L| > 2 \sqrt{L}$, and $Q^+_{L} > P^-_R$, see Fig. 2 (right);

(SF) :

$L<0$, $R>0$, $T_R<2 \sqrt{R}$ and

$$\begin{aligned} H_R^F(v-\bar{x}_R,Q_L^{+} -\bar{y}_R)<H_R^F(v-\bar{x}_R, Q_L^{-}-\bar{y}_R), \end{aligned}$$

(11)

where $Q_L^{\pm }$ are as in (5) and $H_R^F$ as in (3), see Fig. 3 (left);

(FS) :

$L>0$, $R<0$, $|T_L|<2 \sqrt{L}$ and

$$\begin{aligned} H_L^F(-u-\bar{x}_L,Q_R^{+} -\bar{y}_L)<H_L^F(-u-\bar{x}_L, Q_R^{-}-\bar{y}_L), \end{aligned}$$

where $Q_R^{\pm }$ are as in (8) and $H_L^F$ as in (7), see Fig. 3 (center);

(SN) :

$L <0$, $R > 0$, $T_R > 2 \sqrt{R}$, $Q^+_{L} > P^-_R$ and

$$\begin{aligned} H_R^N(v-\bar{x}_R,Q_L^{+} -\bar{y}_R)<H_R^N(v-\bar{x}_R, Q_L^{-}-\bar{y}_R), \end{aligned}$$

where $Q_L^{\pm }$ are as in (5) and $H_R^N$ as in (3), see Fig. 3 (right);

(NS) :

$L >0$, $R < 0$, $|T_L| > 2 \sqrt{L}$ and

$$\begin{aligned} H_L^N(-u-\bar{x}_L,Q_R^{+} -\bar{y}_L)<H_L^N(-u-\bar{x}_L, Q_R^{-}-\bar{y}_L), \end{aligned}$$

where $Q_R^{\pm }$ are as in (8) and $H_L^N$ as in (4), see Fig. 4 (left), and condition (4) is automatically fulfilled if $P_L^{+}>Q_R^{-}$;

(SS) :

$L<0$, $R<0$, $Q^+_{L} > P^-_R$ and

$$\begin{aligned} H_R^S(v-\bar{x}_R,Q_L^{+} -\bar{y}_R)>H_R^S(v-\bar{x}_R, Q_L^{-}-\bar{y}_R), \end{aligned}$$

where $Q_L^{\pm }$ are as in (5), $P_R^{\pm }$ as in (8) and $H_R^S$ as in (9), see Fig. 4 (right), and condition (4) is automatically fulfilled if $P_R^{+}<Q_L^{-}$;

the following statements hold.

• (a) If $T_C=0$, then the origin is surrounded by a bounded period annulus whose most external periodic orbit, which is tangent to the straight line $x=v$, in its outer part is unstable. There exists also a stable limit cycle intersecting the three zones surrounding such period annulus.

• (b) There exists $\varepsilon >0$ such that if $-\varepsilon<T_C < 0$ the origin is surrounded by at least two limit cycles, the smaller is unstable and the bigger is stable.

Fig. 2

On the left, Poincaré disk corresponding to the FF case when $T_C=0$ and the hypotheses of Theorem 4 (FF) are satisfied, so that the periodic orbit at infinity is repulsive. Any nearby orbit allows to build a positively invariant compact set. Note that the vertical lines $x=-u$ and $x=v$ appear as arcs of circles connecting the north and south poles due to the compactification. On the center, Poincaré disk corresponding to the NF case when $T_C=0$. No additional hypotheses are required to get a compact positive invariant set containing the period annulus. We indicate only the values of ordinates, so that $P_L^-$ and $P_L^+$ are the ordinates of the intersection points for the invariant manifolds of the saddle $e_L$ with the straight line $x=-u$, and $Q_L^-$ (not shown) and $Q_L^+$ are their intersections with $x=v$. On the right, Poincaré disk corresponding to the NN case when $T_C=0$ and the hypotheses of Theorem 4 (NN) are satisfied. We indicate only the values of ordinates, so that $P_L^-$ and $P_L^+$ are the ordinates of the intersection points for the invariant manifolds of the virtual node $e_L$ with the straight line $x=-u$, and $Q_L^-$ (not shown) and $Q_L^+$ are their intersections with $x=v$. Similarly, $P_R^-$ and $P_R^+$ are the ordinates of the intersection points for the invariant manifolds of the virtual node $e_R$ with the straight line $x=v$

Fig. 3

On the left, Poincaré disk corresponding to the SF case when $T_C=0$ and the hypotheses of Theorem 4 (SF) are satisfied. On the center, Poincaré disk corresponding to the FS case when $T_C=0$ and the hypotheses of Theorem 4 (FS) are satisfied. On the right, Poincaré disk corresponding to the SN case when $T_C=0$ and the hypotheses of Theorem 4 (SN) are satisfied

Fig. 4

On the left, Poincaré disk corresponding to the NS case when $T_C=0$ and the hypotheses of Theorem 4 (NS) are satisfied. If $P_L^{+}>Q_R^{-}$, then the existence of a compact positive invariant set including the period annulus is guaranteed. On the right, Poincaré disk corresponding to the SS case when $T_C=0$ and the hypotheses of Theorem 4 (SS) are satisfied. If $P_R^{+}<Q_L^{-}$ then the existence of a compact positive invariant set including the period annulus is guaranteed

The proof of Theorem 4 is given in Sect. 5 where we have separated in different subsections the proofs of the cases FF, NF, NN and SF. Since the proofs of the remaining cases FS, SN, NS and SS are similar we omit them.

Different Poincaré disks, coming from the compactification of the phase portrait, illustrating the eight condition sets where Theorem 4 applies are drawn in Figs. 2, 3 and 4. See Chapter 5 of Dumortier et al. (2006) for details on the Poincaré compactification. We have chosen $1=v<u=2$ in all the cases, being $T_{L}$, $T_{R}$, L and R as given in Table 1.

Table 1 Numerical values chosen for drawing the Poincaré disks

After reversing the time and/or a change of variables that interchanges the left and the right zones (when needed), we can write similar results to the ones given in Theorem 4 for different hypotheses, as for instance, when $0<u<v$ or when $T_L>0$ and $T_R<0$ or both. Their precise statements and proofs are direct consequences of the one of Theorem 4, and they will not be provided.

Note that in Theorem 4 the case (FN) is not considered, since under the assumed hypotheses it is not possible to build a positively invariant compact set containing the period annulus in its interior. In fact, Theorem 4 relies in the fact that when such a compact set exists we must also conclude the existence of a stable limit cycle surrounding the period annulus that appears for $T_C=0$, that is not possible in the (FN) case, see below Remark 15.

We define the set $S_{\text {RVF}}=\mathbb {R}^2{\setminus }\{(x,y)\in \mathbb {R}^2: x g(x)< 0\}$. Note that $x g(x)< 0$ only in two situations, which can arise separately or not, namely when there are real equilibria of saddle type. Thus, if $L<0$, then $x g(x)< 0$ for $x<\bar{x}_L=-u(1-1/L)<-u,$, while if $R<0$, then $x g(x)< 0$ for $x>\bar{x}_R=v(1-1/R)>v.$ Therefore, $S_{\text {RVF}}$ is indeed the whole plane when $L>0$, $R>0$. Clearly, the two limit cycles predicted in Theorem 4 are located within such a set, which excludes any possible real saddle. Precisely, another important remark for system (1) is its character of being a rotated vector field whithin $S_{\text {RVF}}$ with respect to the parameter $T_C$, see Ye et al. (1986), Zhang et al. (1992). Effectively, the determinant

$$\begin{aligned} \left| \begin{matrix} F(x)-y &{} g(x) \\ \dfrac{\partial }{\partial T_C} (F(x)-y) &{} \dfrac{\partial }{\partial T_C} g(x) \end{matrix}\right| =\left| \begin{matrix} F(x)-y &{} g(x) \\ \dfrac{\partial }{\partial T_C} F(x) &{} 0 \end{matrix}\right| =-g(x) \dfrac{\partial }{\partial T_C} F(x) \end{aligned}$$

does not change its sign in $S_{\text {RVF}}$, since the expression

$$\begin{aligned} g(x) \dfrac{\partial }{\partial T_C} F(x)={\left\{ \begin{array}{ll} - u g(x)&{}\quad \text {if } x \le -u,\\ x g(x) &{}\quad \text {if }-u \le x \le v, \\ v g(x) &{}\quad \text {if } x \ge v, \end{array}\right. } \end{aligned}$$

is nonnegative there. Rotated vector fields have the non-intersection property; that is, closed trajectories of the system for two different values of the distinguished parameter $T_C$ cannot intersect. As a consequence, we can assure that the unstable limit cycle grows in size as long as $(-T_C)$ increases, while simultaneously the stable limit cycle shrinks, so that both limit cycles approach one another. In fact, they may collapse for a certain value $T_C^*<0$ in a semi-stable limit cycle, to disappear for bigger values of $(-T_C)$. Our last result indicates that this is indeed the case.

Theorem 5

For the differential systems (1) with $0<v<u$, $T_{R}>0$, $T_{L}<0$, fulfilling any of the sets of conditions of Theorem 4, there exists a value $T_C^*<0$ such that there are no limit cycles for $T_C<T_C^*$.

The proof of Theorem 5 is given in Sect. 6. The computation for each case of the greatest lower bound for the value $T_C^*$ predicted in Theorem 5, which will correspond with a saddle-node bifurcation of periodic orbits, is beyond the scope of this paper. Such global bifurcations are rather difficult to obtain by analytical techniques and typically one must resort to numerical methods.

The remaining sections are organized as follows. First, we show in Sect. 2 a relevant application of our results to the study of a memristor-based electronic oscillator, following the path initiated in Llibre et al. (2015). Next, we include in Sect. 3 some auxiliary results to be later needed. In Sect. 4, we compute the distinguished points and the first integrals that appear in the statements of Theorem 4, which is proved in Sect. 5. To finish, Sect. 6 is devoted to the proof of Theorem 5.

2 Bistability in a Simple Oscillator with One Memristor

Here, we revisit the study initiated in Llibre et al. (2015) on basic memristor oscillators without symmetry. These modern electronic devices are gaining relevance in electronic applications, and we will take advantage of the previous results by looking for possible bistable regimes, that is, the coexistence of two different attractors for certain configuration of parameters. See Llibre et al. (2015) and the references therein for a detailed derivation of state equations, and consider the elementary oscillator endowed with one flux-controlled memristor of Fig. 5. Note that to avoid conflict of notation, in this section we will use for the determinants of external zones the symbols $D_L$ and $D_R$.

In the shown circuit, the values of L and C for the impedance and capacitance are positive constants, while the resistor has a negative value $-R$. This negative resistor is typically realized by an auxiliary active device, responsible for the energy supplied to the circuit, see Corinto et al. (2011). After applying Kirchhoff’s laws and assuming that all the initial conditions are zero, we obtain the dynamical system

$$\begin{aligned} \frac{\hbox {d}x_1}{\hbox {d}\tau }= \frac{1}{C}\left[ -f_M(x_1)+x_2\right] , \qquad \frac{\hbox {d}x_2}{\hbox {d}\tau }= \frac{1}{L}\left[ -x_1+Rx_2\right] , \end{aligned}$$

(12)

where the state variables are $x_1(\tau )=\varphi _C(\tau )$ (the flux in the capacitor) and $x_2(\tau )=q_L(\tau )$ (the charge in the inductance), and the basic nonlinearity is given by the piecewise linear function relating the charge and the flux across the memristor M, namely

$$\begin{aligned} f_M(x)= {\left\{ \begin{array}{ll} b_L (x+u) - au &{}\quad \text {for } x \le -u, \\ a x &{}\quad \text {for } -u \le x \le v, \qquad \text{ with } \quad 0<v<u.\\ b_R (x-v) + av &{}\quad \text {for } x \ge v, \end{array}\right. } \end{aligned}$$

Fig. 5

The simple oscillator with one memristor analyzed in this section. Note that the negative value $-R$ considered for the resistor makes it the only active element in the circuit

After the change of variables $x=x_1$, $y=\nu x_1-x_2$ and the rescaling of time $\tau =C s$, we get the Liénard piecewise linear system

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}s}= \nu x-f_M(x)-y, \qquad \frac{\hbox {d}y}{\hbox {d}s}= \nu [G x- f_M(x)]. \end{aligned}$$

(13)

where we have introduced the positive parameters $G=1/R>0$, $\nu =RC/L= C/(GL)>0$.

As in Llibre et al. (2015), we assume in the sequel that the determinant D in the central region is positive, that is, $a<G$. We also introduce for convenience a positive constant $\omega$, such that $D=\nu (G- a)=\omega ^2>0.$ Therefore, under the above assumption, using the change $(x,y,s)\mapsto (X,Y,\tau )$ given by $X= x$, $Y= y/\sqrt{D}=y/\omega$ and $\tau = \omega \, s$, we get that system (12) can be written as in (1), with $T_L=(\nu -b_L)/\omega$, $T_C=(\nu -a)/\omega$, $T_R=(\nu -b_R)/\omega$, and

$$\begin{aligned} D_L=\frac{G\nu -b_L\nu }{G\nu -a\nu }=\frac{G-b_L}{G-a}, \quad D_R=\frac{G\nu -b_R\nu }{G\nu -a\nu }=\frac{G-b_R}{G-a}. \end{aligned}$$

We consider the case where the function $f_M$ giving the flux–charge characteristics of the memristor is non-symmetric, and in particular, we assume the conditions

$$\begin{aligned} b_R<\nu \le a< b_L, \end{aligned}$$

(14)

so that $T_R>0$, $T_L<0$, and $T_C\le 0$, a situation not covered by the results in Llibre et al. (2015).

Our previous assumption $a<G$ ensures that $b_R<G$. Also, we have $\nu <G$, that is, we are in a case with $R^2C<L$. After some algebra, the inequality $T_R<2\sqrt{D_R}$ translates to $(\nu +b_R)^2<4\nu G$, because $(\nu +b_R)^2<4\nu ^2 <4\nu G,$ and therefore, we have always a focus dynamics on the right zone. Regarding the left zone, several cases arise depending on whether the condition $G<b_L$ is satisfied or not.

If $b_L>G$, then $D_L<0$ and we have a saddle dynamics on the left zone. When $b_L<G$, we have $D_L>0$ and the topological type is determined by the sign of the expression $(\nu +b_L)^2-4\nu G$. Accordingly, we have a focus dynamics if $b_L<G^*$, being of node type in the case $b_L>G^*$, where the value $G^*$ satisfies

$$\begin{aligned} \sqrt{\nu G}<G^*= 2\sqrt{\nu G}- \nu <G. \end{aligned}$$

(15)

We conclude that the three cases (FF), (NF) and (SF) of Theorem 4 are feasible for our oscillator. Excluding the (SF) case for the sake of brevity, we can state the following result, which is a direct consequence of Theorem 4.

Proposition 6

Consider the asymmetric memristor-based oscillator under study with the assumption of zero initial conditions for the flux and charge in all the elements of the circuit, as modeled by (13). Assuming (14) and taking into account the value $G^*$ defined in (15), the following statements hold.

• (i) If $b_L<G^*$, then we are in the (FF) case of Theorem 4, and so when it is satisfied the additional condition

  $$\begin{aligned} \dfrac{\nu -b_L}{\sqrt{G-b_L}}+\dfrac{\nu -b_R}{\sqrt{G-b_R}}<0, \end{aligned}$$

  there exists $\varepsilon >0$ such that for $\nu<a<\nu +\varepsilon$ the equilibrium point is stable and surrounded by two limit cycles, being the biggest stable.

• (ii) If $G^*<b_L<G$, then we are in the (NF) case of Theorem 4, and so there exists $\varepsilon >0$ such that for $\nu<a<\nu +\varepsilon$ the equilibrium point is stable and surrounded by two limit cycles, being the biggest stable.

The existence of these bistable regimes, where the oscillatory behavior associated with the stable limit cycle coexists with a stable equilibrium point, is of great relevance for the design of these electronic oscillators, which are nowadays the subject of intensive research. Other different cases of multi-stable behavior have been recently reported in Amador et al. (2017) and Ponce et al. (2017).

3 Preliminary Results

We will need the following result whose proof is given in Dumortier et al. (2006).

Proposition 7

Let x(t) be a periodic solution of period T of the planar differential system $\dot{x} =f(x)$, and let $\mathcal {I}=\int _0^T \text {divergence }$(f(x))$|_{x=x(t)} \, \mathrm{d} t.$ If $\mathcal {I}>0$, then x(t) is an unstable hyperbolic limit cycle, and if $\mathcal {I} < 0$ then x(t) is a stable hyperbolic limit cycle.

The instability of the outermost periodic orbit for the bounded center that appears for $T_C=0$ under the hypothesis of the reference case, and the bifurcation of a unstable limit cycle from it when $T_C<0$, are shown next.

Proposition 8

Consider the differential systems (1) and assume $0<v<u$, $T_C=0$ and $T_{R}>0$. Then, the origin is surrounded by a bounded period annulus whose most external periodic orbit, which is tangent to the line $x=v$, is in its outer part unstable.

Proof

Since $T_C=0$ and $v < u$, we have a circular period annulus tangent to the line $x=v$ and totally contained in the band $-u < -v \le x \le v$. The most external periodic orbit which is tangent to the line $x=v$ passes through the point (v, 0). Recalling that the dynamics in the right-hand zone $x > v$ is given by $\dot{x} = T_R (x-v) -y, \quad \dot{y} =R (x-v) +v$, we conclude that

$$\begin{aligned} \left. \ddot{x}\right| _{(x,y)=(v,0)}=\left[ T_R(T_R (x-v) -y)-(R (x-v) +v)\right] _{(x,y)=(v,0)}=-v<0, \end{aligned}$$

so that we can define a local return map with respect to the straight line $x=v$. More precisely, if we take an orbit starting at the point $(v,y_0)$ with $y_0<0$ and small in absolute value, then is it assured that such an orbit enters the half plane $x>v$ and returns to the straight line $x=v$ at a point $(v,y_1)$ with $y_1>0$. In fact, we have the expansion $y_1=-y_0+\dfrac{2T_R}{3v}y_0^2+O(y_0^3),$ see, for instance, Proposition 8 in Freire et al. (2014). Consequently, as $T_R>0$, we get $y_1>|y_0|$ and the proof is complete. $\square$

Proposition 9

Consider differential systems (1) and assume $0<v<u$, $T_{R}>0$ and $T_{L}<0$. Taking $T_C$ as a bifurcation parameter, for $T_C=0$ the system undergoes a focus-center-limit cycle bifurcation, so that there exists $\varepsilon >0$ sufficiently small such that for $-\varepsilon< T_C < 0$ an unstable limit cycle bifurcates from the period annulus.

Proof

In view of Proposition 8 when $T_C=0$ the most external periodic orbit which is tangent to the line $x=v$ is in its outer part unstable.

Now, if we perturb system (1) with $T_C=0$ by taking $T_C < 0$ and sufficiently small, then in the central zone the origin becomes a stable focus, but since the external periodic orbit was unstable, by Bendixson–Poincaré theorem (recall that in the central zone the differential system is linear), there is a periodic solution $\gamma (t)$ crossing the straight line $x=v$. It remains to show that there is an unstable limit cycle. Note that the Poincaré map defined in a segment with end points (v, 0) and $(v+ \delta ,0)$ for some $\delta > 0$ is analytic (because it is the composition of two analytic maps). Assume that $\gamma (t)$ is not a limit cycle, i.e., $\gamma (t)$ is not isolated in the set of all periodic solutions of system (1). Then, by the analyticity of the Poincaré map it is the identity, in contradiction to the fact that the external periodic solution of the period annulus passing through the point (v, 0) is unstable. So all the periodic solutions crossing the straight line $x=v$ are isolated in the set of all periodic solutions of system (1). $\square$

For a quantitative characterization of the focus-center-limit cycle bifurcation of Proposition 9, which can appear in the more general setting of discontinuous systems without sliding dynamics, see Ponce et al. (2013).

4 Notable Points and First Integrals for $T_C=0$

Here, we compute notable points and first integrals under hypotheses $0<v<u$, $T_{R}>0$, $T_{L}<0$, for the case of reference $T_C=0$. This amounts to show Proposition 2.

Proof of Proposition 2

When $T_C=0$, if we are in a node or saddle case, then the coordinates of the virtual or real equilibrium $e_L$ turn out to be

$$\begin{aligned} e_L=\left( \frac{u}{\sigma _L^2-w_L^2}-u,\frac{2\sigma _L}{\sigma _L^2- w_L^2}u\right) , \end{aligned}$$

so that to find the intersection points of its invariant manifolds with the straight line $x=-u$ we must solve for $\alpha$ the linear system of equations

$$\begin{aligned} \left( \begin{array}{c}\frac{u}{\sigma _L^2-w_L^2}-u\\ \frac{2\sigma _L}{\sigma _L^2-w_L^2}u\end{array}\right) +\alpha \left( \begin{array}{c}1\\ \sigma _L\mp w_L\end{array}\right) =\left( \begin{array}{c} -u\\ P^{\pm }_{L}\end{array}\right) . \end{aligned}$$

We immediately obtain $\alpha =-u/(\sigma _L^2-w_L^2)$, and so

$$\begin{aligned} P^{\pm }_{L}=\dfrac{2\sigma _L}{\sigma _L^2-w_L^2}u- \dfrac{\sigma _L\mp w_L}{\sigma _L^2-w_L^2}u=\dfrac{\sigma _L\pm w_L}{\sigma _L^2-w_L^2}u=\dfrac{u}{\sigma _L\mp w_L}. \end{aligned}$$

Note that for $T_L<0$, the node case implies $\sigma _L<-w_L<0$ so that $P^-_L<P^+_L<0$, while in the saddle case we have $-w_L<\sigma _L<0$ and therefore $P^+_L<0<P^-_L$.

In computing the first integral for non-focus cases, we translate the left system to put $e_L$ at the origin so that, after eliminating time, the system becomes equivalent to the homogeneous differential equation $\dfrac{\hbox {d}y}{\hbox {d}x}=\dfrac{(\sigma _L^2-w_L^2)x}{2\sigma _L x-y},$ which after the substitution $y=sx$ becomes $\dfrac{\hbox {d}s}{\hbox {d}x}=\dfrac{(s-\sigma _L)^2-w_L^2}{(2\sigma _L -s)x}.$ Separating variables, we can write the decomposition

$$\begin{aligned} \dfrac{(\sigma _L-w_L) ds}{2w_L(s-\sigma _L-w_L)}-\dfrac{(\sigma _L+w_L) ds}{2w_L(s-\sigma _L+w_L)}=\dfrac{\hbox {d}x}{x}. \end{aligned}$$

Before making the integration, we note that in the node case we need to work, regarding the point $e_L$ once assumed to be in the origin, in the region with $x<0$ and $s=\dfrac{y}{x}<\sigma _L-w_L<\sigma _L+w_L<0,$ what leads to

$$\begin{aligned} \dfrac{(\sigma _L-w_L)}{2w_L}\log [-(s-\sigma _L-w_L)]-\dfrac{(\sigma _L+ w_L)}{2w_L}\log [-(s-\sigma _L+w_L)]=\log [-x]+C. \end{aligned}$$

We write

$$\begin{aligned} \dfrac{\sigma _L}{2w_L}\log \dfrac{s-\sigma _L-w_L}{s-\sigma _L+w_L}- \dfrac{1}{2}\log [(s-\sigma _L-w_L)(s-\sigma _L+w_L)]-\log [-x]=C, \end{aligned}$$

and so we choose as first integral the more compact expression given in (4).

In the saddle case we need to work, assuming the point $e_L$ to be at the origin, in the region with $x>0$ and $\sigma _L-w_L<s=\dfrac{y}{x}<\sigma _L+w_L,$ what leads to

$$\begin{aligned} \dfrac{(\sigma _L-w_L)}{2w_L}\log [-(s-\sigma _L-w_L)]-\dfrac{(\sigma _L +w_L)}{2w_L}\log (s-\sigma _L+w_L)=\log (x)+C, \end{aligned}$$

and we take the first integral given in (6).

The arguments in the proof of statement (b) are essentially the same as in statement (a.1), and consequently, we do not provide them. $\square$

5 Proof of Theorem 4

We first note that in view of Proposition 8 when $T_C=0$ we have a circular period annulus tangent to the line $x=v$, totally contained in the band $-u < -v \le x \le v$ and the outermost periodic orbit of the annulus is unstable. Furthermore, in view of Proposition 9 if we perturb this situation by taking $T_C<0$ and sufficiently small, then there is a bifurcation of an unstable limit cycle from the period annulus.

In order to complete the proof of Theorem 4, we will show that there exists a positively invariant set $\Omega$ homeomorphic to a closed disk containing the period annulus surrounding the origin. The next proposition ensures that this is enough to complete the proof of Theorem 4.

Proposition 10

Consider the Liénard piecewise linear differential system (1) with $T_C=0$. Assume that in each of the eight statements of Theorem 4 there exists a positively invariant compact set $\Omega$ homeomorphic to a closed disk containing the period annulus surrounding the origin. Then, there is a stable limit cycle $\gamma (t)$ surrounding the mentioned period annulus.

Proof

Under the assumptions of Proposition 10 and from Proposition 8, it follows by the Bendixson–Poincaré Theorem that there is a periodic solution $\gamma (t)$ surrounding the mentioned period annulus. It remains to show that there is a stable limit cycle. Again, the Poincaré map defined on a segment with end points (v, 0) and a point outside the region limited by $\gamma (t)$, but close to $\gamma (t)$ is analytic (because it is the composition of two or three analytic maps). The rest of the proof follows in a similar way to the last part of the proof of Proposition 9. Doing that we obtain that all the periodic solutions surrounding the period annulus are limit cycles of system (1). Due to the positive invariance of the set $\Omega$ minus the period annulus, at least one of these possible periodic solutions is a stable limit cycle. $\square$

Proposition 11

Assume that in each of the eight statements of Theorem 4 we are under the assumptions of Proposition 10. For $\varepsilon >0$ sufficiently small and $-\varepsilon< T_C < 0$, there exists at least two limit cycles of the Liénard piecewise linear differential systems (1), the smallest is unstable and the biggest is stable.

Proof

We perturb system (1) with $T_C=0$ by taking $T_C < 0$ and sufficiently small. Then, the stable limit cycle given in Proposition 10 remains, and by Proposition 9, one unstable limit cycle appears near the region previously occupied by the period annulus. Thus, this perturbed system has at least two limit cycles. This concludes the proof. $\square$

In view of Propositions 10 and 11 in order to prove Theorem 4, it only remains to show the existence of the compact set $\Omega$ defined in Proposition 10 when $T_C=0$.

Proof of statement (FF) of Theorem 4

We recall that $0<v<u, T_R > 0, T_L<0$ and

$$\begin{aligned} R,L>0, \ T_R< 2\sqrt{R}, \ |T_L|< 2 \sqrt{L}, \ \frac{T_L}{\sqrt{4 L -T_L^2 }} + \frac{T_R}{\sqrt{4 R-T_R^2}} <0, \end{aligned}$$

(16)

where the last inequality is easily deduced from condition (10), by using the monotony of the function $h(x)=x/\sqrt{4-x^2}$ for $x\in (-2,2)$. Note that under these assumptions system (1) has two virtual foci. We study the planar differential systems (1) in the Poincaré disk, see Fig. 2 (left). Since the differential system has no singular points at infinity, the set of points at infinity becomes a closed orbit, that is, we have a periodic orbit at infinity. We will show that under the assumptions of statement (FF) this periodic orbit is unstable.

To do so, we will use Proposition 7. First, we make the change of variables $x=\frac{\cos \theta }{r}, \quad y=\frac{\sin \theta }{r}, \quad \theta \in {{\mathbb {S}}}^1, \quad r > 0,$ either in the right and the left zones. On the right zone, if we denote by $(x_R,y_R)$ the old variables and by $(r_R,\theta )$ the new ones, where $\theta \in [-\pi /2,\pi /2]$ and $vr_R\le \cos \theta$, we get that

$$\begin{aligned} \begin{aligned} \dot{r}_R&= -(x_R \dot{x}_R + y_R \dot{y}_R )r_R^3 = -r_R\left\{ T_R \cos ^2 \theta +(R-1) \cos \theta \sin \theta \right. \\&\quad \left. - r_R v\left[ T_R \cos \theta +(R-1) \sin \theta \right] \right\} ,\\ {\dot{\theta }}&= r_R^2(\dot{y}_R x_R - y_R \dot{x}_R)= R \cos ^2 \theta +\sin ^2 \theta - T_R \cos \theta \sin \theta \\&\quad - r_R v\left[ (R-1) \cos \theta -T_R \sin \theta \right] , \end{aligned} \end{aligned}$$

while on the left zone, if we denote by $(x_L,y_L)$ the old variables and by $(r_L,\theta )$ the new ones, where $\theta \in [\pi /2,3\pi /2]$ and $-ur_L\le \cos \theta$, we get that

$$\begin{aligned} \begin{aligned} \dot{r}_L&= -r_L\left\{ T_L \cos ^2 \theta +(L-1) \cos \theta \sin \theta + r_L u\left[ T_L \cos \theta +(L-1) \sin \theta \right] \right\} ,\\ {\dot{\theta }}&= L \cos ^2 \theta +\sin ^2 \theta - T_L \cos \theta \sin \theta + r_L u\left[ (L-1) \cos \theta -T_L \sin \theta \right] . \end{aligned} \end{aligned}$$

We have the system $r_R' = \frac{\dot{r}_R}{{\dot{\theta }}}$ for $\theta \in [-\pi /2,\pi /2]$, and $r_L'=\frac{\dot{r}_L}{{\dot{\theta }}}$ for $\theta \in [\pi /2,3\pi /2]$. In this case, the divergence of these systems on the periodic orbit (which is $r_R=0$ with $\theta \in [-\pi /2,\pi /2]$ in the right zone and $r_L=0$ with $\theta \in [\pi /2,3\pi /2]$ in the left zone) is, using the divergence formula in polar coordinates, respectively,

$$\begin{aligned} \text {divergence}_S|_{r_S=0}= \frac{1}{r_S} \frac{\partial (r_S r_S')}{\partial r_S}|_{r_S=0} =-2 \frac{\mathcal {P}(S,T_S)}{\mathcal {Q}(S,T_S)}, \end{aligned}$$

where $S=R,L$, $\mathcal {P}(A,B)= B \cos ^2 \theta + (A-1) \cos \theta \sin \theta$, and $\mathcal {Q}(A,B)=1+ (A-1) \cos ^2 \theta -B\cos \theta \sin \theta$. In view of Proposition 7 we must compute

$$\begin{aligned} \mathcal {I}_{RL}= \int _{\pi /2}^{3 \pi /2} \text {divergence}_L|_{r_L=0} \, \mathrm{d} \theta + \int _{-\pi /2}^{\pi /2} \text {divergence}_R|_{r_R=0} \, \mathrm{d} \theta . \end{aligned}$$

For the calculations we can take advantage that

$$\begin{aligned} \dfrac{\hbox {d}}{\hbox {d}\theta }\left[ 1+ (A-1) \cos ^2 \theta -B\cos \theta \sin \theta \right] =-2(A-1)\cos \theta \sin \theta -2B \cos ^2 \theta +B, \end{aligned}$$

so that, for instance, for the right part,

$$\begin{aligned}&2\int _{-\frac{\pi }{2}}^{\frac{\pi }{2}} \dfrac{B \cos ^2 \theta + (A-1) \cos \theta \sin \theta }{1+ (A-1) \cos ^2 \theta -B\cos \theta \sin \theta } \mathrm{d}\theta \\&\quad = \int _{-\frac{\pi }{2}}^{\frac{\pi }{2}} \dfrac{B }{1+ (A-1) \cos ^2 \theta -B\cos \theta \sin \theta } \mathrm{d}\theta , \end{aligned}$$

because

$$\begin{aligned}&\int _{-\frac{\pi }{2}}^{\frac{\pi }{2}} \dfrac{B-2\left[ B \cos ^2 \theta + (A-1) \cos \theta \sin \theta \right] }{1+ (A-1) \cos ^2 \theta -B\cos \theta \sin \theta } \mathrm{d}\theta \\&\quad = \left[ \log \left( 1+ (A-1) \cos ^2 \theta -B\cos \theta \sin \theta \right) \right] _{-\frac{\pi }{2}}^{\frac{\pi }{2}}=0. \end{aligned}$$

Similar reduction can be achieved for the left part. Doing these integrals, we get that

$$\begin{aligned} \mathcal {I}_{RL}= -2 \pi \left( \frac{T_R}{\sqrt{4 R -T_R^2}} + \frac{T_L}{\sqrt{4 L -T_L^2}}\right) . \end{aligned}$$

By assumptions, see (16), $\mathcal {I}_{RL} > 0$ and it follows from Proposition 7 that the periodic orbit at infinity is unstable.

Taking an orbit starting at a point (0, M) with $M>0$ sufficiently big, the instability of the periodic orbit at infinity assures that after a turn the orbit will pass through a point (0, m) with $0<m<M$, as in Fig. 2 (left). Then, by joining these two points with a segment, we have a positively invariant compact set $\Omega$ containing the period annulus. This concludes the proof of statement (FF) of Theorem 4. $\square$

Note that we could also study the (FF) case by computing the local expansion of Poincaré map at infinity, by resorting to Proposition 6 of Llibre and Ponce (1999) in order to cope with piecewise defined vector fields. If this alternative approach is used, then the hypotheses assure that the derivative of such Poincaré map at $r=0$ is greater than one and the same conclusion follows.

Lemma 12

The Liénard piecewise linear differential system (1) with $0< v < u$, $T_C=0$, $T_R >0$ and $T_L<0$ cannot have an orbit $\gamma$ starting at $(x,y)=(v,\sqrt{u^2-v^2})$ and arriving after a turn at a point (v, y) with $0<y<\sqrt{u^2-v^2}$, as in Fig. 1 (right).

Proof

If such an orbit exists, then we could close the orbit with a segment on the line $x=v$, building a positively invariant compact set $\Omega$. Thus, from Proposition 10, we should have a stable limit cycle $\gamma _1(t)$ contained in $\Omega$ and surrounding the period annulus. Now from Proposition 9, we know that a second unstable limit cycle $\gamma _2(t)$ appears for $T_C < 0$ sufficiently small, and $\gamma _1(t)$ persists due to its stability. Note that $\gamma _1(t)$ and $\gamma _2(t)$ are contained in the half-space $x > -u$. But this is a contradiction since a piecewise linear differential system with two zones separated by a straight line has at most one limit cycle (see Freire et al. 1998; Llibre et al. 2013). $\square$

Proof of statement (NF) of Theorem 4

We recall that $0<v<u, T_R > 0, T_L<0$ and $L,R>0, \ T_R> 2 \sqrt{R}, \ |T_L| > 2 \sqrt{L}$.

Note that under these assumptions system (1) has one virtual focus on the right-hand zone and a virtual node on the left-hand zone. We shall describe the compact set $\Omega$ in the Poincaré disk, see Fig. 2 (center).

The point $e_L$ is a virtual attractor node whose invariant straight lines $\Gamma _{\pm }$ with director vectors the eigenvectors of the linear part at $e_L$ intersect the line $x=-u$ at the points $(-u,P^-_L)$ and $(-u,P^+_L)$ with $P^-_L<P^+_L<0$, see Proposition 2(a.1) and Fig. 2 (center).

Since $P^+_L < 0$ the orbit $\gamma (t)$ through $(-u,P^+_L)$ crosses the band $-u< x < v$ and enters the right-hand zone at the point $(v, Q^+_L)$, see (3). Since $\dot{x}_R|_{x =v} =-y$ and $\dot{y}_R |_{y=0} =R(x-v) +v > 0$, the orbit $\gamma (t)$ exits the right-hand zone. We note that $\gamma$ cannot intersect the segment $s_1$ on the line $x=v$ with $0\le y \le \sqrt{u^2-v^2}$, otherwise we have an orbit satisfying the assumptions of Lemma 12, and this is not possible. So the orbit $\gamma (t)$ crosses again the central zone as in Fig. 2 (center), and since at infinity the straight line $\Gamma _+$ has a saddle (see Fig. 2 (center) and use the Poincaré compactification described in Chapter 5 of Dumortier et al. (2006)), the orbit $\gamma (t)$ enters again the central zone. Using this orbit and an appropriate segment $s_2$ on the straight line $x=-u$, we obtain the compact set $\Omega$ homeomorphic to a closed disk surrounding the period annulus and positively invariant. This concludes the proof of statement (NF) of Theorem 4. $\square$

Proof of statement (NN) of Theorem 4

We recall that $0<v<u, T_R > 0, T_L<0$ and $L, R>0, \ T_R> 2\sqrt{R}, \ |T_L|> 2 \sqrt{L}, \ Q^+_{L} > P^-_R$. Note that under these assumptions system (1) has two virtual nodes. The point $e_R$ is a virtual unstable node whose invariant straight lines with director vectors the eigenvectors of the linear part of $e_R$ intersect the line $x=v$ on the points $(v,P^-_R)$ and $(v,P_R^+)$. From Proposition 3(a.1) we have $P^+_R<P^-_R< 0$. Moreover, the point $e_L$ is a virtual attractor node whose invariant straight lines with director vectors the eigenvectors of the linear part of $e_L$ intersect the line $x=-u$ on the points $(-u,P^-_L)$ and $(-u,P^+_L)$. From Proposition 2(a.1), we have $P^-_L<P^+_L < 0$. Now we compute the radius of the piece of circular orbit on the central zone passing through the point $(-u,P^+_L)$. Doing so we compute the point where this orbit intersects the line $x=v$ and we get the point $(v,Q^+_{L})$, see (3). By assumptions we have that $Q^+_{L} > P^-_R$. Moreover using the expressions of the Poincaré compactification (5.2) and (5.3) of Chapter 5 of Dumortier et al. (2006), at infinity we have two singular points at the end points of the invariant straight lines through $(-u,P^+_L)$ and $(v,P^-_R)$ being saddles. Hence, we can compute the compact set $\Omega$ in the Poincaré disk, see Fig. 2 (right), by following the orbit through the point $(v,Q^+_{L})$, as in the previous case, or by using the segment joining the points $(v,P^-_{R})$ and $(v,Q^+_{L})$, see Fig. 2 (right). This completes the proof of statement (NN) of Theorem 4. $\square$

Proof of statement (SF) of Theorem 4

We recall that $0<v<u, T_R > 0, T_L<0$ and $L<0, \ R>0, \ T_R<2 \sqrt{R}, \ H_R^F(v-\bar{x}_R,Q_L^+-\bar{y}_R)<H_R^F(v-\bar{x}_R, Q_L^--\bar{y}_R)$. Note that under these assumptions system (1) has one saddle on the left-hand zone and a virtual focus on the right-hand zone. The point $e_L$ is a saddle whose invariant manifolds intersect the line $x=-u$ at the points $(-u,P^-_L)$ and $(-u,P^+_L)$. By Proposition 2(a.2), we have $P^+_L< 0<P^-_L$. Furthermore, the point $e_R$ is a virtual unstable focus. Now, we compute the radius of the circular orbit on the central zone passing through the point $(-u,P^+_L)$. Doing so, we compute the point where this orbit intersects the line $x=v$ and we get the point $(v,Q^+_{L})$, see (5). Now we compute the radius of circular orbit in the central zone passing through the point $(-u,P^-_L)$ and then we compute the point where this orbit intersects the line $x=v$ in backward time and we get the point $(v,Q^-_{L})$, see (5).

Recall that the focus dynamics in the right-hand zone has the first integral $H_R^F(x,y)$ defined in (3). It is easy to conclude, by using the points on the vertical isocline $\tilde{y}=T_R\tilde{x}=2\sigma _R\tilde{x}$ and that $H_R^F(x,y)$ increases with the x-value of the intersection point of the orbit with such isocline, that assumption (11) assures that the orbit through $(v,Q^+_{L})$ arrives at the line $x=v$ below the point $(v,Q^-_{L})$. Then, we can obtain a positively invariant compact set $\Omega$ in the Poincaré disk, see Fig. 3 (left), by joining this arrival point with the point $(v,Q^-_{L})$, see Fig. 3 (left). This completes the proof of statement (SF) of Theorem 4. $\square$

6 Proof of Theorem 5

To show Theorem 5, we first recall a necessary condition for existence of limit cycles which is obtained from applying the Filippov’s transformations, see Ye et al. (1986) and Zhang et al. (1992). Working in the set of x-values corresponding to $S_{\text {RVF}}$, we define the function $G(x)=\int _0^x g(s) \,\mathrm{d}s$, positive for $x\ne 0$, since we exclude the possible regions with $xg(x)<0$. Thus, the function G is only defined for $x\ge \bar{x}_L$ if $L<0$ and for $x\le \bar{x}_R$ if $R<0$. Let $x_L(z)<0<x_R(z)$ be the two solution branches of the equation $G(x)=z>0$, where we also take $x_L(0)=x_R(0)=0$, and the domains of such functions could be different when real saddles appear. If we define the functions $F_{\{L,R\}}(z)=F(x_{\{L,R\}}(z)),$ it turns out that the differential equation $\dfrac{\hbox {d}y}{\hbox {d}z}= F_R(z)-y$ reproduces for $z\ge 0$ the orbits of system (1) for $x\ge 0$, while the differential equation $\dfrac{\hbox {d}y}{\hbox {d}z}= F_L(z)-y$ reproduces also for $z\ge 0$ the orbits of system (1) for $x\le 0$. This technique allows to ‘fold’ the phase plane and to apply comparison principles, so that, for instance, we can write the following result, which is a direct consequence of Theorem 5.4 of Ye et al. (1986).

Proposition 13

For the differential systems (1) with $0<v<u$, $T_{R}>0$, $T_{L}<0$, $L\ne 0$, $R\ne 0$, a necessary condition for the existence of periodic orbits is the existence of a value $z^*>0$ such that $F_L(z^*)=F_R(z^*)$.

In what follows, we will see that, in all the cases of Theorem 4, when $(-T_C)$ is big enough there are no intersections between the graphs of $F_L$ and $F_R$, so that Theorem 5 is a direct consequence of Proposition 13.

We start by computing

$$\begin{aligned} G(x)={\left\{ \begin{array}{ll} \frac{1}{2}\left[ L(x+u)^2-2u(x+u)+u^2\right] , &{}\quad \text {if } x\le -u,\\ \frac{1}{2}x^2, &{}\quad \text {if } -u<x<v,\\ \frac{1}{2}\left[ R(x-v)^2+2v(x-v)+v^2\right] , &{}\quad \text {if } x\ge v, \end{array}\right. } \end{aligned}$$

where we must add the restrictions $x+u>u/L$ or $x-v<-v/R$, whenever $L<0$ or $R<0$, respectively, or both if $L<0$ and $R<0$. Accordingly, we get

$$\begin{aligned} x_L(z)={\left\{ \begin{array}{ll}-\sqrt{2z}, &{}\quad \text {if } 2z\le u^2,\\ -u-\dfrac{1}{L}\left( \sqrt{u^2+L(2z-u^2)}-u\right) , &{}\quad \text {if } 2z> u^2,\\ \end{array}\right. } \end{aligned}$$

where we must add the restriction $2z\le u^2(1-1/L)$ when $L<0$, and

$$\begin{aligned} x_R(z)={\left\{ \begin{array}{ll}\sqrt{2z}, &{}\quad \text {if } 2z\le v^2,\\ v+\dfrac{1}{R}\left( \sqrt{v^2+R(2z-v^2)}-v\right) , &{}\quad \text {if } 2z> v^2,\\ \end{array}\right. } \end{aligned}$$

where we must add the restriction $2z\le v^2(1-1/R)$ when $R<0$. After composing these functions with the function F, we obtain

$$\begin{aligned} F_L(z)={\left\{ \begin{array}{ll}-T_C\sqrt{2z}, &{}\quad \text {if } 2z\le u^2,\\ -\dfrac{T_L}{L}\left( \sqrt{u^2+L(2z-u^2)}-u\right) -T_Cu, &{}\quad \text {if } 2z> u^2,\\ \end{array}\right. } \end{aligned}$$

(17)

and

$$\begin{aligned} F_R(z)={\left\{ \begin{array}{ll}T_C\sqrt{2z}, &{}\quad \text {if } 2z\le v^2,\\ \dfrac{T_R}{R}\left( \sqrt{v^2+R(2z-v^2)}-v\right) +T_Cv, &{}\quad \text {if } 2z> v^2,\\ \end{array}\right. } \end{aligned}$$

(18)

where the graph of $F_L$ should be restricted to $2z\le u^2(1-1/L)$ when $L<0$ and the graph of $F_R$ to $2z\le v^2(1-1/R)$ when $R<0$.

Assume first that we are in one of the cases with $L>0$ and $R>0$, that is, we are in cases (FF), (NF) or (NN), under the corresponding hypotheses of Theorem 4. We claim that by choosing $(-T_C)$ big enough we have $F_L(z)>F_R(z)$ for all $z>0$, so that from Proposition 13 we cannot have limit cycles and therefore the conclusion of this theorem holds.

To show the claim, note first that for $T_C=0$ the two graphs coincide for all $0\le 2z\le v^2$, since $v^2<u^2$ and then both functions vanish; this fact corresponds to the existence of the period annulus of statement (a) of Theorem 4. In any of these three cases of Theorem 4, we do know that there exists a stable limit cycle surrounding the period annulus, so that a straightforward extension of Proposition 13 implies the existence of a value $z^*$ with $2z^*>u^2$ where $F_L(z^*)=F_R(z^*)$. The situation is depicted in Fig. 6 (left) for the (FF) case of Table 1, where the fact that $F_L(z)<F_R(z)$ for $v^2<2z<2z^*$ tells us that orbits near the period annulus after a complete turn go far away from the annulus, agreeing with Proposition 8. It is precisely the intersection at $z^*$ leading to $F_L(z)>F_R(z)$ for $z>z^*$ what allows the existence of a closed orbit (the stable limit cycle surrounding the period annulus) that does return at the same point of the initial condition taken on the negative part of y-axis. Furthermore, the hypotheses of cases (FF) and (NF) imply that the condition

$$\begin{aligned} \dfrac{T_L}{\sqrt{L}}+\dfrac{T_R}{\sqrt{R}} <0 \end{aligned}$$

(19)

is fulfilled. On the other hand, we have

$$\begin{aligned} \lim _{z\rightarrow \infty }\left. \dfrac{F_R(z)}{F_L(z)}\right| _{T_C=0}=\lim _ {z\rightarrow \infty }\dfrac{\dfrac{T_R}{R}\left( \sqrt{v^2+R(2z-v^2)}-v\right) }{-\dfrac{T_L}{L}\left( \sqrt{u^2+L(2z-u^2)}-u\right) }= \dfrac{T_R/\sqrt{R}}{-T_L/\sqrt{L}}, \end{aligned}$$

(20)

so that condition (19) assures that the above limit is less than 1 and so $F_L(z)>F_R(z)$ for all z sufficiently big. Thus, since two parabolic branches have at most two intersections, we deduce that $F_L(z)>F_R(z)$ for all $z>z^*$ and therefore there is only one intersection in cases (FF) and (NF), as in Fig. 6 (left). This allows to define the positive quantity $H=\max _{z\ge 0} \left[ F_R(z)-F_L(z)\right] =\max _{0\le z \le z^*} \left[ F_R(z)-F_L(z)\right] >0.$

If starting from the situation of Fig. 6 (left), we allow $T_C<0$ and we see that for small values of z the functions do not vanish any longer, while the right parts of the graphs just undergo translations (recall (17)–(18)). Thus, for $2z\ge u^2$ the graph of $F_L(z)$ goes up an amount equal to $(-T_Cu)$, while for $2z\ge v^2$ the graph of $F_R(z)$ goes down an amount equal to $T_Cv$. Note that $F_L(z)>F_R(z)$ for all $0<2z\le v^2$, what indicates that the origin is now a stable focus, see Fig. 6 (center). In the figure, we observe two transversal intersections between the two graphs that correspond for sure to the two limit cycles predicted in statement (b) of Theorem 4 when $T_C$ is small enough, but it should be remarked that we cannot identify in general the number of intersections with the number of limit cycles; the only valid assertion is, from Proposition 13, that without intersections there are no limit cycles. If we increase more the value of $(-T_C)$, namely by taking $(-T_C)(u+v)>H$, we get a situation without intersections between the graphs of $F_L(z)$ and $F_R(z)$, see Fig. 6 (right). So, the above claim is proved and the theorem is completed for the cases (FF) and (NF).

In the (NN) case, we cannot guarantee condition (19) so that there could have in principle two intersections when $T_C=0$, a situation leading to $F_R(z)-F_L(z)>0$ (and not bounded) for z sufficiently big. Anyway, we do not have to consider all possibles values of $z>0$, since the stable limit cycle (and any other possible periodic orbit) must be surrounded by the orbit with initial condition $(v, Q_L^+)$, see Fig. 2 (right). Such an orbit defines a maximal value of $x_M$, so that the corresponding value $z_M$ with $x_R(z_M)=x_M$ bounds the interval where we must look for intersections of the graphs. Note that this bound is valid for all $T_C>0$ thanks to a property of rotated vector fields, which implies in our case that the stable limit cycle shrinks when $(-T_C)$ increases. Thus, if we now define the positive quantity $H=\max _{0\le z \le z_M} \left[ F_R(z)-F_L(z)\right] >0,$ we can follow the same reasoning as before to conclude that for $(-T_C)$ big enough there are no intersections for $z<z_M$ and therefore no periodic orbits in the (NN) case.

Fig. 6

The graphs of the functions $F_L(z)$ (solid line) and $F_R(z)$ (dashed line) for $T_C=0$ (left), for $T_C<0$ and small in absolute value (center) and for $(-T_C)(u+v)>H$ (right) in the case (FF) of Table 1

To show the cases where saddles zones are involved, we can follow a similar reasoning. The only difference is that at least one of the graphs is finite. Before ending the work, we write a couple of remarks.

Remark 14

For all the cases of Theorem 4, we can obtain a condition on $T_C<0$ that implies no intersections for the graphs of $F_R(z)$ and $F_R(z)$ when $0<2z<u^2$. More precisely, the condition $T_C+\dfrac{T_R}{\sqrt{R}} <0$ assures that there is no limit cycle totally contained in the half plane $x\ge -u$. So, the unstable limit cycle that bifurcates at $T_C=0$, if it still exists, lives in the three zones.

Remark 15

As mentioned before, Theorem 4 does not includes the (FN) case. The reasons that make this case different can now be clarified. Under the corresponding hypotheses $0<v<u$, $T_{R}>0$, $T_C=0$, $T_{L}<0$, $L,R>0$, $|T_L|<2/\sqrt{L}$ and $T_R>2/\sqrt{R}$, condition (19) is violated, since $\dfrac{T_L}{\sqrt{L}}+\dfrac{T_R}{\sqrt{R}} >-2+2=0.$ This together with (20) implies that $F_R(z)>F_L(z)$ not only for all z with $v^2<2z\le u^2$ (where $F_L(z)=0$) but also for z sufficiently big (and possibly for all z with $2z>v^2$). In this case, if we allow $T_C<0$, then we have always at least one intersection for the graphs of $F_R(z)$ and $F_L(z)$. In fact, by integrating backward in time the upper invariant manifold of the virtual node, it can be easily shown the existence of one unstable limit cycle for all values of $T_C<0$.