1 Introduction

1.1 Motivation and General Context

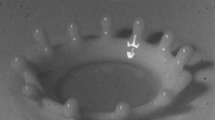
There are many natural systems which evolve on time-dependent spatial domains. A classical example is provided by fluid problems with a free interface that bounds a spatial domain and deforms in time owing to the motion within the domain, such as the drop-splash problem shown in Fig. 1a. In the situation depicted in Fig. 1a, the spatial domain is a circular rim, which evolves in time and experiences an instability responsible for the crown structure (Krechetnikov and Homsy 2009; Krechetnikov 2011; Hartong-Redden and Krechetnikov 2011). This system exhibits instabilities leading either to regular structures as in Fig. 1a or to irregular ones as in Fig. 1b. In particular, the number of spikes may stay constant over the time of evolution or, in appropriate regimes, may change as the crown evolves. Part of the goal here is to uncover, with the help of a simple model, the dynamical origins of the qualitative behavior observed in this and analogous systems. Thus, while the analysis that follows applies to a general class of systems, the accompanying discussion will be framed in terms of the crown problem. Since in such situations the domain size is determined by internal dynamics, we refer to it as an internal parameter.

Fig. 1
figure 1

Patterns observed in problems on growing domains: (a) drop-splash problem: regular crown (Krechetnikov and Homsy 2009; b) frustration pattern (Krechetnikov and Homsy 2009; Hartong-Redden and Krechetnikov 2011; c) pattern sequence on Pomacanthus semicirculatus (Painter et al. 1999; d) patterns on growing square domains (Madzvamuse et al. 2003)

Full size image

Besides fluid dynamics (Serrin 1959; Lions 1963; Fujita and Sauer 1970; Shahinpoor and Ahmadi 1972; Miyakawa and Teramoto 1982; Teramoto 1983; Vanneste and Wirosoetisno 2008), there are a large number of other processes involving time-dependent domains, including transport–reaction processes—crystal growth, metal casting, gas–liquid and gas–solid reaction systems—as well as classical electromagnetic cavity resonators with moving walls (Lee 1966; Rogak 1966; Borgnis and Papas 1972; Garcia and Minzoni 1981; Dittrich et al. 1998), quantum-mechanical problems (Dodonov et al. 1993), fluid–structure interaction (Fernández and Tallec 2003), and the formation of patterns and shapes in biology (morphogenesis) (Kondo and Asai 1995; Crampin et al. 1999; Neville et al. 2006; Gjorgjieva and Jacobsen 2007; Madzvamuse et al. 2010; Hetzer et al. 2012; Ueda and Nishiura 2012), cf. Fig. 1c. The latter phenomena include mammalian coat patterns, seashell pigmentation patterns, and skin patterns on tropical fish, as well as various symmetry-breaking events: branching processes in plants, initiation of single or multiple new organs in animals, and solid tumor growth. As suggested by Turing (1952), pattern formation in biology can be modeled by a system of reacting and diffusing chemicals (morphogens) that interact to produce stable patterns of morphogen concentrations \(\varvec{u}(\varvec{x},t)\) as described by the reaction–diffusion model \(\varvec{u}_{t} = \mathbf{D}\cdot \Delta \varvec{u} + \varvec{f}(\varvec{u})\), where \(\mathbf{D}\) is a matrix of diffusion coefficients and \(\varvec{f}\) is a reaction term. Such models are known to be able to capture complex evolving patterns arising from competition between reactions that create spikes in the concentration of the product and diffusion that smoothes out its gradient, cf. Fig. 1d. Recent interest has focused on incorporating other biologically relevant features such as domain growth, shape, and curvature into models of this type (Crampin et al. 1999; Neville et al. 2006; Gjorgjieva and Jacobsen 2007; Madzvamuse et al. 2010; Hetzer et al. 2012). In these problems the domain size is typically an externally imposed parameter, i.e., not controlled by internal dynamics.

The most common approach (Armaou and Christofides 2001) to analyze problems on time-dependent spatial domains is to map them onto a new fixed in space domain. The simplest case corresponds to the situation when the boundaries are deformed slowly compared with the inverse growth rate of the most unstable mode. In this case a solution can be constructed by multiple-scale asymptotic methods (Garcia and Minzoni 1981). Another common approach for studying stability and long-time behavior of these problems is by energy methods, as done in the context of fluid mechanics for the Navier–Stokes equations (Teramoto 1983), Cosserat fluids (Shahinpoor and Ahmadi 1972), wave equations (Garcia and Minzoni 1981; Dittrich et al. 1998), and the nonlinear beam equation (Ferreira et al. 1999). In the case when there is a well-defined map from the time-dependent spatial domain onto a fixed domain, the linearized stability problem is then about stability of a time-dependent base state, which usually reduces to the analysis of problems with nonautonomous linear operators, even if the original operator is autonomous. The best-studied case corresponds to time-periodic base states (Davis 1976) which allow a straightforward application of Floquet theory (Floquet 1883). In general, however, the arsenal of methods which enable one to obtain analytical results for problems with nonautonomous operators is very limited and amounts to either energy methods (Homsy 1973) or the computation of Lyapunov exponents (Farrell and Ioannou 1996, 1999) of the propagator \(\Phi _{[t,t_{0}]}\) which evolves the solution \(\varvec{u}(t,\varvec{x}) = \Phi _{[t,t_{0}]} \varvec{u}(t_{0},\varvec{x})\) from the initial condition \(\varvec{u}(t_{0},\varvec{x})\).

1.2 Key Questions and Scope of the Present Study

The key question is: what new behavior can one expect in the stability picture on time-dependent spatial domains versus stability on time-independent domains? Therefore, the idea of this work is to address the following questions for both dissipative and conservative systems:

  • May time dependence of the spatial domain lead to destabilization of a base state that is otherwise stable in the time-independent domain case?

  • How may the spatial structure of the solution be affected by the time evolution of the domain?

  • Does pattern coarsening take place in such problems?

While the class of systems evolving on time-dependent domains is very wide, as discussed in Sect. 1.1, in the present study we limit ourselves to one-dimensional (1D) systems where patterns form in the same spatial direction as the domain deformation and the dependent variable is not conserved, as opposed to systems with a conserved quantity or originating from a conservation law. For example, if the total amount (mass \(m\)) of a chemical is conserved (i.e., it is not being used up), then in one spatial dimension the material concentration \(u \propto 1/L\), where \(L\) is the length of the domain, so that the total mass \(m\equiv \int _0^L u\hbox {d}x\) remains constant. Thus as \(L\) increases, the concentration decreases. This effect is referred to as dilution (Crampin et al. 1999) and is present whenever the whole domain is stretching (somewhat like an elastic substrate). In this case the Lagrangian velocity of the domain translates into an Eulerian velocity \(v(x,t)\) at every point of the domain and the conservation law changes the time derivative \(\partial _{t}u\) to \(u_{t} + \partial _{x}(v \, u) \equiv u_{t} + v\partial _{x}u + u\partial _{x}v\), where the second term describes advection and the last term dilution. In the simplest case, \(v(x,t)\) is proportional to the motion of the boundary, \(v(x,t)=(L_t/L)x\), and the Eulerian velocity increases away from the center at \(x=0\). However, in a translation-invariant system on a periodic domain there is no preferred location and so \(v(x,t)\equiv 0\). Indeed, the motion of the boundaries alone does not, in general, result in dilution—if the system is conservative such motion may excite propagating waves; if it is dissipative, the effects of the boundary motion may be confined to the vicinity of the boundary. Below we give two examples of physical systems where dilution is absent.

Example 1

The crown formation problem discussed in Sect. 1.1 represents a good example, where the fluid domain (the rim) on which instability develops is evolving and its mass is not conserved (Krechetnikov and Homsy 2009; Krechetnikov 2011), since the rim originates from very thin ejecta at the time of the drop impact and subsequently grows in both radius and thickness (Krechetnikov and Homsy 2009; Krechetnikov 2011). While the domain (the rim) stretches, the stretching is uniform and because of the periodicity of the domain the spikes are not diluted/advected, but instead the wavelength increases in proportion to the domain stretch. Note that the crown formation problem may be conservative or dissipative, depending on the viscosity of the fluid.

Example 2

Certain systems exhibit spatially localized structures (Riecke 1999; Knobloch 2008), e.g., a pattern of rolls, embedded in a background trivial state. Such structures are quite common in many driven dissipative fluid systems. The amplitude of the rolls in such a state is independent of the distance between the fronts of the localized structure and is determined by the strength of the forcing, which in the case of convection is controlled by the applied temperature difference as measured by the Rayleigh number (a fixed parameter). Outside of the “pinning” region containing stationary structures of this type, the fronts connecting the periodic pattern to the trivial state depin and the structure grows in extent owing to the (outward) motion of the bounding fronts. Thus, no dilution is present and instead the structure has to supply additional rolls (of appropriate amplitude) as required by the motion of the fronts (Ma et al. 2010; Ma and Knobloch 2012).

It should be noted that there are examples of systems where domain change in one spatial direction leads to pattern wavelength change in another, e.g., propagation of waves on the surface of a leaky shallow tank. Here the frequency of the waves depends on the depth of the water as \(\sim \sqrt{k^{2} h}\) (Lighthill 1978; Lamb 1994). Thus, as water slowly drains out of the tank, the frequency of free waves changes. Conversely, if the waves are driven at fixed frequency, then their wavelength will change with time. In either case no dilution or advection terms are present in the equation describing the nonlinear evolution of the waves because the domain changes in a direction orthogonal to the direction in which the waves propagate. A different example is provided by pattern formation in melting boundary convection (Vasil and Proctor 2011).

In both Examples 1 and 2 one may ask if the wavelength of an initially periodic structure is stretched uniformly throughout the domain as in Example 1, or if new structures are nucleated in special locations, for example, near a moving front, as in Example 2. Our work is motivated by the current lack of understanding of the nucleation process whereby the system succeeds in replicating existing rolls (in the dissipative case) or crown spikes (in both conservative and dissipative cases) at just the right rate. As argued in the present work, the situations described above can be modeled by simpler equations describing the evolution of the amplitude of such structures on a growing domain—these take the form of amplitude equations and include the dissipative and conservative complex Swift–Hohenberg equation, the Ginzburg–Landau equation, and the nonlinear Schrödinger equation, appropriately modified to take into account the growing domain. For example, in the context of localized structures, the amplitude of the “rolls” in such equations is determined by \(\mu -\mu _{\mathrm {c}}(L)\), where \(\mu \) is the bifurcation parameter and \(\mu _{\mathrm {c}}(L)\) is its threshold value in a domain of length \(L\). Since \(|\mu _{\mathrm {c}}(L)-\mu _{\mathrm {c}}(\infty )|=O(L^{-2})\), it follows that the amplitude of the rolls is almost independent of \(L\) and hence no dilution is present. This is a fundamental property of amplitude equations of the aforementioned type. Instead, the lateral expansion of the domain manifests itself in the stretching of the wavelength of the pattern, and it is this stretching that pushes the wavelength into the Eckhaus-unstable regime, thereby triggering the nucleation of the new rolls required so that the growing domain continues to be filled with rolls corresponding to the given value of the bifurcation parameter.

Motivated by the above discussion, we use here (complex) amplitude equations as model problems for studying the effects of a time-dependent domain on the stability properties of simple uniform and periodic states. This approach allows us to respect translation invariance of the problem and hence to study analytically the onset and evolution of Eckhaus and Benjamin–Feir instabilities of periodic patterns and waves. We are therefore implicitly assuming/postulating that these amplitude equations can be derived from the underlying field equations such as the Navier–Stokes equations on slowly changing time-dependent domains in much the same way as universal amplitude equations on time-independent domains. In Appendix 2 we provide an example of such a derivation for a near-critical system on a time-dependent domain. In this context, one must note that a systematic derivation of the amplitude equation for the crown formation problem, which provided the original motivation for this work, is a prohibitive task, since even the base state—a temporally evolving flat rim—cannot be determined analytically (Betyaev 1995; Krechetnikov 2011).

1.3 Finite- versus Infinite-Dimensional Systems: Bifurcation Delay

Local phenomena, i.e., phenomena described by a local balance, on time-dependent domains can be formulated in one dimension as the following partial differential equation (PDE) problem:

$$\begin{aligned} \varvec{u}_t = \varvec{F}(\varvec{u}(t,x),\mu ), \end{aligned}$$
(1.1)

where \(\varvec{F}\) is a nonlinear differential operator and \(x \in [0,2\pi L(\varvec{u}(t,x),t)]\), i.e., \(x\) is defined on a time-dependent domain with moving boundary \(x=2\pi L\), and \(\mu \) is a (bifurcation) parameter. If \(L\) does not depend on \(\varvec{u}(t,x)\), we refer to it as an external variable; otherwise, \(L\) is determined as part of the solution and there may be a separate PDE governing the evolution of \(L\). In the latter case, one can view \(L\) as one of the components of the solution vector \(\varvec{u}\), i.e., an internal variable.

On the physical side, given the time dependence of the domain size and shape, two possible scenarios can be envisaged: (1) in experiments, one adjusts the domain size in any desired manner, implying that \(L\) is an external variable, and (2) the domain size changes solely as a result of the evolution of the system, i.e., without any external input from the experimenter (Vasil and Proctor 2011). In the latter case, the size becomes an internal variable of the system. In either case, it is natural to consider the associated instability phenomena within the realm of dynamic bifurcations (Benoit 1991), as informally defined above.

In the simplest case, for finite-dimensional systems, dynamic bifurcation problems can be formulated as follows:

$$\begin{aligned} \frac{\hbox {d}\varvec{u}}{\hbox {d} t} = \varvec{f}(\varvec{u}(t),\mu ), \end{aligned}$$
(1.2a)
$$\begin{aligned} \frac{\hbox {d} \mu }{\hbox {d} t} = \epsilon g(\varvec{u}(t),\mu ), \end{aligned}$$
(1.2b)

where \(\epsilon \ll 1\), firmly placing such problems in the framework of slow–fast systems. In what follows we focus on the case where \(L\) is an external parameter; i.e., we assume that \(g(\varvec{u}(t),\mu )\) does not depend on the solution \(\varvec{u}(t)\). Below we provide an example illustrating the main difference between static and dynamic bifurcations, and introduce the terminology necessary for subsequent discussion.

Example 3

(Maesschalck et al. 2009). Let us assume that \(u\) is a scalar, that \(\mu \) is an external parameter that varies linearly on the timescale \(\tau =\epsilon t\), and that (1.2a) admits linearization to the nonautonomous ordinary differential equation (ODE)

$$\begin{aligned} \epsilon {\hbox {d} u \over \hbox {d} \tau } = a(\tau ) u, \qquad u(0) = u_{0} > 0, \end{aligned}$$
(1.3)

where \(a\) is a sufficiently smooth function, which changes sign at some “turning” time \(\tau _{*} > 0\) with \(a(\tau ) < 0\) on \(t \in (0,\tau _{*})\) and \(a(\tau ) > 0\) on \(\tau \in (\tau _{*},\infty )\).

This problem has the solution

$$\begin{aligned} u(\tau ) = u_{0} \, \hbox {exp}{\left( {1 \over \epsilon } \int _{0}^{\tau }{a(s) \, \hbox {d}s}\right) }, \end{aligned}$$
(1.4)

implying that an initial condition \(u(0)\) decays over the time interval \(0 < \tau < \tau _{*}\) and then grows so that at some time \(\tau _{\mathrm{exit}} > \tau _{*}\) the exponent \({\int \limits _{0}^{\tau }{a(\tau ) \, \hbox {d} \tau }}\) vanishes and for \(\tau > \tau _{\mathrm{exit}}\) continues to grow. The time \(\tau _\mathrm{exit}\) then implies that for \(\tau >\tau _{\mathrm{exit}}\) the solution escapes (exits) from a ball of radius \(u(0)\) around \(u=0\) defined by the initial conditions; the two times, \(\tau _\mathrm{exit}\) and \(\tau _{*}\), characterizing the instability onset, do not depend on the value of \(u(0)\). Because \(\tau _{\mathrm{exit}} > \tau _{*}\), one usually speaks of a bifurcation delay since the solution \(u(\tau ,\epsilon )\) shows the following interesting property:

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} u(\tau ,\epsilon ) = 0, \ \forall \tau \in (0,\tau _{\mathrm{exit}}) \ \text {and} \ \lim _{\epsilon \rightarrow 0} u(\tau ,\epsilon ) = \infty , \ \forall \tau \in (\tau _{\mathrm{exit}},\infty ), \end{aligned}$$
(1.5)

where \(\tau _{\mathrm{exit}}\) is defined by the equality \(\int _{0}^{\tau _{\mathrm{{exit}}}}{a(s) \, \hbox {d}s} = 0\). Hence, the time at which the solution is repelled from the equilibrium \(u=0\) is given by \(\tau _{\mathrm{exit}}\), which is greater than the time \(\tau _{*}\) at which the equilibrium loses its stability should \(a(\tau )\) be considered as a fixed (time-independent) parameter.

Finite-time evolution of a dynamic instability is thus characterized by two characteristic times, the “turning” time \(\tau _{*}\) and the “exit” time \(\tau _{\mathrm{exit}}\). This discussion is developed further in Sect. 2.1 and Appendix 1.

While dynamic bifurcations and delays are reasonably well understood in finite dimensions, as discussed above and elsewhere (Eckhaus 1983; Mandel and Erneux 1987; Neishtadt 1987, 1988, 2009; Baer et al. 1989; Lythe 1996; Guckenheimer 2004), much less is known about the corresponding phenomena in extended systems. We argue below that, while many of the stability results from finite-dimensional systems carry over to the infinite-dimensional case, new effects arise in the latter in both linear and nonlinear regimes owing to the presence of spatial structure (Maesschalck et al. 2009). To incorporate spatial effects we study these phenomena within two nonlinear infinite-dimensional systems—the dissipative (Sect. 2) and conservative (Sect. 3) complex Swift–Hohenberg equation—and extract from their behavior lessons that apply generally to (nonconserved) PDEs on time-dependent domains. The Swift–Hohenberg equation has already proved to be immensely valuable as a reliable guide to the behavior of a wide variety of phenomena ranging from fluid flows (Bergeon et al. 2008; Schneider et al. 2010) to laser systems (Lega et al. 1994, 1995), and we anticipate here that this is the case on time-dependent domains as well.

2 Dissipative Swift–Hohenberg Model

Suppose one wishes to develop a low-dimensional phenomenological model capturing the crown behavior qualitatively. Since the reduction from the Navier–Stokes equations is a prohibitive task due to the time-dependent and complex geometry of the base state—the evolving rim of the crown—even when it is flat and no spikes are present, we develop an amplitude equation model based on experimental observations, which tell us that spikes may grow, appear, and disappear, and travel along the rim. Let us consider first evolution on a time-independent domain and assume that, as a simplest case, a steady-state bifurcation is present corresponding to a growing mode \(u \sim \mathrm {e}^{\lambda t + \mathrm {i} k x}\), where \(x\) refers to the azimuthal coordinate along the rim. This instability is described by a dispersion relation of the form \(\lambda =\lambda (k,\mu )\). Owing to translation and reflection symmetries w.r.t. \(x\), the growth rate \(\lambda \) is an even function of \(k\). If the instability is long-wave, \(\lambda = a_{0} + a_{2} k^{2} + \ldots \), so that, at lowest order, \(\lambda = \mu - k^{2}\). In this case, \(k=0\) is the most unstable wavenumber. In order to obtain a nonzero critical wavenumber \(k_0\) one needs to increase the order of \(\lambda (k)\), and thus one is naturally led to a quartic dispersion relation which reproduces (the linear part of) the Swift–Hohenberg equation. Note that, while in the linear picture the spikes do not move, they can move as a result of nonlinear mechanisms identified earlier by Dangelmayr (1986) and Armbruster et al. (1988) for systems with \(O(2)\) symmetry.

In view of the above argument and the requirement of translation invariance, we are led to consider the supercritical complex Swift–Hohenberg equation (Gelens and Knobloch 2010), hereafter CSHE, as a model for dissipative dynamics on a one-dimensional domain. If the domain is time dependent, i.e., the spatial variable is defined on \(x \in \Omega (t) = [0, 2 \pi L(t)]\), it can be scaled to \([0, 2 \pi ]\) by the transformation \(x \rightarrow L(t) x\), leading to

$$\begin{aligned} u_{t} = \mu \, u - L_{x} u-|u|^{2} u, \ \text {with} \ L_{x} = \left( \frac{1}{L^2(t)}\partial _{x}^{2}+k_{0}^2\right) ^{2}, \end{aligned}$$
(2.1)

where \(u(t,x): \, \mathbb {R}^{+} \times \mathbb {R} (\hbox {mod}\,2\pi )\rightarrow \mathbb {C}\) is a complex field periodic on \(\Omega (t)\), \(k_{0}\) represents an intrinsic wavenumber (i.e., a time-independent inverse length scale), and \(\mu \) is a parameter. Because of the periodicity and finite size (at finite time) of the domain, the spatial structure of the solution can be represented in terms of Fourier harmonics \(\mathrm {e}^{\mathrm {i} m x}\), \(m \in \mathbb {Z}\). PDEs over \(\mathbb {C}\) such as (2.1) are not uncommon in models of physical phenomena, and arise from PDEs over \(\mathbb {R}\) such as the Navier–Stokes equations for a real field \(v(t,x)\) via \(v = u \, \mathrm {e}^{\mathrm {i} k_{\mathrm {c}} x} + \overline{u} \, \mathrm {e}^{-\mathrm {i} k_{\mathrm {c}} x}\), where \(k_{\mathrm {c}}\) is the critical wavenumber.

The examples given in Sect. 1.2 explain why advection and dilution terms are not included in the formulation (2.1)—in this and subsequent problems the dynamical quantities of interest (amplitude, order parameter, etc.) are not conserved, and their evolution is not governed by a conservation law (unlike material concentration, for example).

2.1 Linear Stability of Spatially Homogeneous Base State \(u_{0}(t)\)

In what follows we use Lyapunov’s definition of stability, i.e., we explore the evolution of a perturbation in a “ball” centered on the base state \(u_{0}(t)\) even though the latter is time dependent. This is as opposed to the intuitive “convective” approach \(u(t,x) = u_{0}(t) (1 + u'(t,x))\), in which \(u' = \hbox {const.}\) would imply stability, but from Lyapunov’s point of view the solution is carried away from the base state a distance \(\sim u_{0}(t)\) and the base state \(u_{0}(t)\) is therefore unstable.

Base state. Equation (2.1) admits a real nonmodulated solution \(u_{0}(t) = R(t) \in \mathbb {R}\), which is independent of the domain size \(L(t)\) and satisfies the Landau equation

$$\begin{aligned} R_{t} = (\mu -k_{0}^{4}) R - R^{3}. \end{aligned}$$
(2.2)

This equation has fixed points \(R_{0} = 0\) and \(R_{0}^{2} = \mu - k_{0}^{4}\) provided \(\mu >k_{0}^{4}\). The former is stable w.r.t. spatially homogeneous perturbations when \(\mu <k_{0}^{4}\) and unstable when \(\mu >k_{0}^{4}\); the latter is stable w.r.t. such perturbations whenever it exists but may be unstable w.r.t. spatially inhomogeneous perturbations.

Stability of the homogeneous base state. We write \(u(t,x) = u_{0}(t) + u'(t,x)\), where \(u_{0}(t) \equiv R(t)\) is real, and linearize Eq. (2.1), obtaining

$$\begin{aligned} {\partial u' \over \partial t} = \mu \, u' - L_{x} u' - u_{0}^{2} \left( 2 u^{\prime } + \overline{u}^{\prime }\right) , \end{aligned}$$
(2.3)

where \(\overline{u}^{\prime }\) is the complex conjugate of \(u^{\prime }\). Let us represent the perturbation as

$$\begin{aligned} u'(t,x) = \alpha _{n}(t) \mathrm {e}^{\mathrm {i} n x} + \beta _{n}(t) \mathrm {e}^{- \mathrm {i} n x}, \end{aligned}$$
(2.4)

where \(\alpha _{n}, \beta _{n} \in \mathbb {C}\). Substituting this expression into Eq. (2.3) yields the equations

$$\begin{aligned} {\hbox {d} \alpha _{n} \over \hbox {d} t}&= \mu \, \alpha _{n} - \widehat{L}_{n} \alpha _{n} - R^{2} \left( 2 \alpha _{n} + \overline{\beta }_{n}\right) , \end{aligned}$$
(2.5a)
$$\begin{aligned} {\hbox {d} \beta _{n} \over \hbox {d} t}&= \mu \, \beta _{n} - \widehat{L}_{n} \beta _{n} - R^{2} \left( 2 \beta _{n} + \overline{\alpha }_{n}\right) , \end{aligned}$$
(2.5b)

with the “Fourier-transformed” operator \(L_{x}\) given by

$$\begin{aligned} \widehat{L}_{n} = \left( \frac{n^{2}}{L^2(t)}-k_{0}^2\right) ^{2} = k_{0}^{4}(\gamma _{n}-1)^{2}, \end{aligned}$$
(2.6)

where \(\gamma _{n} \equiv n^{2}/k_{0}^{2} L^2(t)\). Adding and subtracting equations for \(\alpha _{n}\) and \(\beta _{n}\), we obtain evolution equations for \(a_{n} \equiv \alpha _{n} + \beta _{n}\) and \(b_{n} \equiv \alpha _{n} - \beta _{n}\):

$$\begin{aligned} {\hbox {d} a_{n} \over \hbox {d} t}&= \left( \mu - \widehat{L}_{n}\right) a_{n} - R^{2} \left( 2 a_{n} + \overline{a}_{n}\right) , \end{aligned}$$
(2.7a)
$$\begin{aligned} {\hbox {d} b_{n} \over \hbox {d} t}&= \left( \mu - \widehat{L}_{n}\right) b_{n} - R^{2} \left( 2 b_{n} - \overline{b}_{n}\right) . \end{aligned}$$
(2.7b)

Writing \(a_{n} = a_{n}^{\mathrm {R}} + \mathrm {i} a_{n}^{\mathrm {I}}\) now leads to

$$\begin{aligned} {\hbox {d} a_{n}^{\mathrm {R}} \over \hbox {d} t}&= \left( \mu - \widehat{L}_{n} - 3 R^{2}\right) a_{n}^{\mathrm {R}},\end{aligned}$$
(2.8a)
$$\begin{aligned} {\hbox {d} a_{n}^{\mathrm {I}} \over \hbox {d} t}&= \left( \mu - \widehat{L}_{n} - R^{2}\right) a_{n}^{\mathrm {I}}. \end{aligned}$$
(2.8b)

The growth rate of any instability is therefore determined by the expressions in brackets: if they are positive, then the perturbation grows. Similarly, writing \(b_{n} = b_{n}^{\mathrm {R}} + \mathrm {i} b_{n}^{\mathrm {I}}\), one arrives at the same set of equations (2.8) with the only difference that \(a_{n}^{\mathrm {R}} \rightarrow b_{n}^{\mathrm {I}}\) and \(a_{n}^{\mathrm {I}} \rightarrow b_{n}^{\mathrm {R}}\). Note that, if \(R(t)\) grows monotonically, which is the case for initial conditions \(R(0) < R_{0} \equiv \sqrt{\mu - k_{0}^{4}}\), \(\mu - k_{0}^{4}>0\), then the mode \(a_{n}^{\mathrm {I}}\) (and thus \(b_{n}^{\mathrm {R}}\)) is the “least stable.”

Let us first discuss the instability from the point of view of the long-time behavior. The integrand in (2.8b) behaves as

$$\begin{aligned} \mu - \widehat{L}_{n} - R^{2} \rightarrow k_{0}^{4} \gamma _{n} (2-\gamma _{n}) \ \text {as} \ t \rightarrow \infty \quad (\text {since} \ R^{2} \rightarrow \mu - k_{0}^{4} \ \text {as} \ t \rightarrow \infty ), \end{aligned}$$
(2.9)

which is positive if \(2-\gamma _{n} > 0\). If \(L\) grows without bound, the latter condition is always satisfied, but the growth rate saturates at zero. Suppose now that the state \(R_0\) is set up on a faster timescale than the one on which \(L(t)\) varies, and that \(L(t)\) grows from \(L_{0}\) such that \(2-\gamma _{n} < 0\) to \(L_{\infty }\) such that \(2-\gamma _{n} > 0\), i.e., \(2-\gamma _{n}\) changes sign. Then this case will exhibit bifurcation delay as discussed in Sect. 1.3. For finite times, however, Eqs. (2.2) and (2.8b) must be integrated simultaneously.

Finally, the natural question one may ask is: under which conditions may a time-periodic domain lead to instability? A partial answer is given in Example 3 for a scalar equation, which tells us that, even if the “eigenvalue” oscillates periodically between positive and negative values, the cumulative effect may lead to the growth of the perturbation (as long as the time integral of the positive part of the eigenvalue outweighs the negative one). In higher dimensions one can get instability due to the time-varying domain even if the time-frozen eigenvalues are always negative, as can be seen from the following example.

Example 4

Consider the particular two-dimensional system (Knobloch and Merryfield 1992):

$$\begin{aligned} \left( \begin{array}{l} \dot{x} \\ \dot{y} \end{array}\right) = \left( \begin{array}{l@{\quad }r} - 1 - 9 \cos ^{2}{6 t} + 6 \sin {12 t} &{} 12 \cos ^{2}{6 t} + {9 \over 2} \sin {12 t} \\ - 12 \sin ^{2}{6 t} + {9 \over 2} \sin {12 t} &{} - 1 - 9 \sin ^{2}{6 t} - 6 \sin {12 t} \end{array}\right) \left( \begin{array}{l} x \\ y \end{array}\right) . \end{aligned}$$
(2.10)

It is easy to see that the eigenvalues of the \(2\times 2\) matrix are independent of time and equal to \(\lambda _{1,2} = -1, -10\), while Eq. (2.10) has the particular solution

$$\begin{aligned} x(t) = \mathrm {e}^{2 t} (\cos {6 t} + 2 \sin {6 t}), \ y(t) = \mathrm {e}^{2 t} (2 \cos {6 t} - \sin {6 t}), \end{aligned}$$
(2.11)

which grows exponentially.

2.2 Linear Stability of Spatially Inhomogeneous Base State \(u_{0}(t,x)\)

Base state. Equation (2.1) also admits a complex modulated solution \(u_{0}(t,x) = R_m(t) \, \mathrm {e}^{\mathrm {i} m x}\), \(m \in \mathbb {Z}\), with a real amplitude \(R_m(t)\) obeying

$$\begin{aligned} \frac{\mathrm{d}{ R}_{m}}{\mathrm{d}t} = \left[ \mu -k_{0}^{4} \left( \gamma _{m} - 1\right) ^{2}\right] R_m - R_m^{3}. \end{aligned}$$
(2.12)

Short-time behavior of \(R_m(t)\). Linearization of (2.12) shows that, for short times,

$$\begin{aligned} R_{mt}= R_m(0) \, \exp {\left[ (\mu -k_{0}^{4}) t + k_{0}^{4} \int _{0}^{t}{\gamma _{m} \left( 2-\gamma _{m}\right) \,\mathrm {d}\tau }\right] }. \end{aligned}$$
(2.13)

Thus, for \(m=0\) the solution grows if \(\mu >k_{0}^{4}\), while for \(m \ne 0\) the solution grows if

$$\begin{aligned} \mu -k_{0}^{4} + k_{0}^{4} \gamma _{m} \left( 2-\gamma _{m}\right) > 0, \end{aligned}$$
(2.14)

from some time \(t_{*}\) on to infinity. We anticipate that, as \(\mu \) increases, the mode numbers \(m\) such that \(\gamma _m\approx 1\), i.e., \(m\ne 0\), will grow first. In the following we identify such states with a growing \(m\)-spike crown in the drop-splash problem: as the domain grows in the original (unscaled) physical variable, the wavelength grows in proportion to \(2\pi L(t)/m\).

Long-time behavior of \(R_m(t)\). To determine the long-time behavior of \(R_m(t)\) we analyze (2.12) from the energy point of view: with \(E_m = R_m^{2}(t)\) and \(a_m(t)\equiv \mu -k_{0}^{4} \left( \gamma _{m} - 1\right) ^{2}\), Eq. (2.12) takes the form

$$\begin{aligned} {1 \over 2} \frac{\mathrm{d}{ E}_{m}}{\mathrm{d}t} = a_m \, E_m - E_m^{2}. \end{aligned}$$
(2.15)

While (2.15) does not allow separation of variables, it is of Bernoulli type and thus can be integrated in quadratures. With \(E_m(0) = E_{m0}\) at \(t=0\), the exact solution reads

$$\begin{aligned} E_m^{-1}(t) = F_m^{-1}(t) \left( 2 \int \nolimits _{0}^{t}{F_m(t) \, \hbox {d}t} + E_{m0}^{-1}\right) ,\,\,\, \ F_m(t) = \mathrm{exp}\left( 2 \int _{0}^{t}{a_m(t)\hbox {d}t}\right) , \end{aligned}$$
(2.16)

showing that the solution depends on the cumulative effect of the time-dependent coefficient \(a_m(t)\), as should be the case in problems with bifurcation delay. As discussed in Example 3, there are two characteristic times at the linear level of description—the turning time \(t^{*}\), at which \(a_m(t)\) changes sign from negative to positive, and the exit time \(t_{\mathrm {exit}}\), at which the integral \(\int _{0}^{t}{a_m(t) \, \hbox {d}t}\) in \(F_m(t)\) changes sign from negative to positive. These effects remain when the first term on the right side of (2.16), responsible for the nonlinear effects, is neglected so that \(E_m(t) = E_{m0} \, F_m(t)\). The nonlinear term, in turn, leads to the saturation of the instability, characterized by a third time scale \(t_{\mathrm {sat}}\).

In the case when \(L(t)\) and thus \(R_m(t)\) evolve on a slow timescale \(\tau = \epsilon \, t\), the base state satisfies the equation

$$\begin{aligned} \epsilon \frac{\mathrm{d}{ R}_{m}}{\mathrm{d}\tau } = \left[ \mu -k_{0}^{4} \left( \gamma _{m} - 1\right) ^{2}\right] R_m - R_m^{3}, \end{aligned}$$
(2.17)

which can be solved in terms of an asymptotic series, \(R_m(\tau ) = R_{m0}(\tau ) + \epsilon R_{m1}(\tau ) + \ldots \), where either \(R_{m0}=0\) or

$$\begin{aligned} R_{m0}^{2}(\tau ) = \mu -k_{0}^{4} \left( \gamma _{m} - 1\right) ^{2}, \ \text {and} \ R_{m1} = - {1 \over 2 R_{m0}^{2}} {\hbox {d} R_{m0} \over \hbox {d} \tau }. \end{aligned}$$
(2.18)

Thus \(R_{m0} = 0\) is repelling for \(\mu > k_{0}^{4} \left( \gamma _{m} - 1\right) ^{2}\), while the nontrivial solution \(R_{m0}\) is attracting, much as in the case discussed in Sect. 2.1. This result confirms our intuition that the mode with \(\gamma _m\approx 1\) will set in first.

Stability of the modulated base state. When the base state has spatial structure, as in the crown problem, it may be subject to Eckhaus instability (Eckhaus 1965; Raitt and Riecke 1995; Hoyle 2006), responsible for wavelength-changing processes. This instability generates phase slips (Kramer and Zimmermann 1985) which may result in the insertion of a new spike during time evolution. In the following we write \(u(t,x) = u_{0}(t,x) + u'(t,x)\), where \(u_{0}(t,x)=R_m(t)\mathrm {e}^{\mathrm {i}mx}\). Here, \(R_m^2\equiv \mu -\widehat{L}_m\) and \(\widehat{L}_{m}\) is defined by (2.6). Thus \(R_m\) varies on the same timescale as the domain. Linearization of Eq. (2.1) in \(u'(t,x)\) now yields

$$\begin{aligned} {\partial u' \over \partial t} = \mu \, u' - L_{x} u' - \left( 2 |u_{0}|^{2} u^{\prime }+u_{0}^{2} \overline{u}^{\prime }\right) . \end{aligned}$$
(2.19)

In order to study Eckhaus instability of the base state \(u_{0}(t,x)\), let us represent the perturbation as

$$\begin{aligned} u'(t,x) = \alpha _{n}(t) \mathrm {e}^{\mathrm {i} (m+n) x} + \beta _{n}(t) \mathrm {e}^{\mathrm {i} (m-n) x} \ \text {with} \ \alpha _{n}, \beta _{n} \in \mathbb {C}, \end{aligned}$$
(2.20)

which implies that the perturbation not only affects the amplitude of the base state \(u_{0}\) but may also change its wavenumber \(m\). Substitution of this representation into (2.19) and collection of terms in front of the independent exponentials \(\mathrm {e}^{\mathrm {i} (m \pm n)x}\) yields

$$\begin{aligned} {\hbox {d} \alpha _{n} \over \hbox {d} t}&= \mu \, \alpha _{n} - \widehat{L}_{m+n} \alpha _{n} - R_m^{2} \left( 2 \alpha _{n}+\overline{\beta }_{n}\right) , \end{aligned}$$
(2.21a)
$$\begin{aligned} {\hbox {d} \beta _{n} \over \hbox {d} t}&= \mu \, \beta _{n} - \widehat{L}_{m-n} \beta _{n} - R_m^{2} \left( 2 \beta _{n}+\overline{\alpha }_{n}\right) . \end{aligned}$$
(2.21b)

When the domain length \(L(t)\) evolves on a sufficiently slow time scale, we may ignore its time dependence and look for solutions of the form \((\alpha _{n}(t),\overline{\beta }_{n}(t))\propto (\alpha _{n}(0),\overline{\beta }_{n}(0))\exp \sigma _n t\), where \(\sigma _n\) is the growth rate. This growth rate satisfies the quadratic equation

$$\begin{aligned} \biggl [\sigma _n-\mu +2R_m^2+\biggl (k_0^2-{{m^2+n^2}\over L^2}\biggr )^2+{4m^2n^2\over L^4}\biggr ]^2-{16m^2n^2\over L^4}\biggl (k_0^2-{{m^2+n^2}\over L^2}\biggr )^2-R_m^4=0. \end{aligned}$$
(2.22)

When the perturbation wavenumber \(n\) is small, \(|n|\ll |m|\), one of the roots of this equation (the phase eigenvalue) is also small while the other (the amplitude eigenvalue) remains \(O(1)\) and negative. The phase instability that occurs when the former eigenvalue becomes positive is called the Eckhaus instability. In the limit \(n \ll m\) we can take \(\sigma _n =\sigma n^2+O(n^4)\) with \(m/L=O(1)\) and obtain

$$\begin{aligned} \sigma ={2\over L^2} {{{\mu \biggl (k_0^2-{3m^2\over L^2}\biggr )-\biggl (k_0^2-{m^2\over L^2}\biggr )^2\biggl (k_0^2-{7m^2\over L^2}\biggr )}\over {\mu -\biggl (k_0^2-{m^2\over L^2}\biggr )^2}} } + O(n^2). \end{aligned}$$
(2.23)

Thus Eckhaus instability is present whenever \(\sigma >0\), and this instability leads to the growth of perturbations with wavenumber \(m\pm n\); on a periodic domain, the growth of the instability leads to the appearance of discrete mode numbers \(m\pm 1\). This calculation should be compared with that for the Ginzburg–Landau equation \(u_t = \mu u + u_{xx} - |u|^{2} u\), for which the base state \(u=R_m \, \mathrm {e}^{\mathrm {i}mx}\) is stable with respect to long-wavelength perturbations when \(\mu >3m^2\) and unstable when \(m^2<\mu <3m^2\) (Eckhaus 1965; Hoyle 2006).

We emphasize that the above calculation is valid only when the growth rate of the Eckhaus instability is faster than the timescale on which the domain length changes. Since the instability is slow near threshold, this requirement provides a serious constraint on the usefulness of the prediction (2.23) for time-dependent domains.

In order to retain the effects of time dependence, we assume as in (2.17) that the base state evolves on a slow timescale \(\tau = \epsilon \, t\) and consider the case when the instability wavenumber \(n\) corresponds to a shorter wavelength, i.e., \(n = \epsilon ^{1/2} \widehat{n}\), where \(\widehat{n} = O(1)\). Thus

$$\begin{aligned} \widehat{L}_{m \pm n}&= \widehat{L}_{m \pm n}^{0} + \epsilon ^{1/2} \widehat{L}_{m \pm n}^{1/2} + \epsilon \widehat{L}_{m \pm n}^{1} + \ldots , \end{aligned}$$
(2.24)

where

$$\begin{aligned} \widehat{L}_{m + n}^{0}&= \widehat{L}_{m - n}^{0} = k_{0}^{4} (\gamma _{m} - 1)^{2}, \end{aligned}$$
(2.25a)
$$\begin{aligned} \widehat{L}_{m + n}^{1/2}&= - \widehat{L}_{m - n}^{1/2} = {4 k_{0}^{2} \, m \, \widehat{n} \over L^{2}} (\gamma _{m} - 1),\end{aligned}$$
(2.25b)
$$\begin{aligned} \widehat{L}_{m + n}^{1}&= \widehat{L}_{m - n}^{1} = {2 k_{0}^{2} \widehat{n}^{2} \over L^{2}} (3 \gamma _{m} - 1), \end{aligned}$$
(2.25c)

and we seek a solution of Eqs. (2.21) in the form

$$\begin{aligned} \alpha _{n}&= \alpha _{n}^{0} + \epsilon ^{1/2} \alpha _{n}^{1/2} + \epsilon \alpha _{n}^{1} + \ldots , \end{aligned}$$
(2.26a)
$$\begin{aligned} \beta _{n}&= \beta _{n}^{0} + \epsilon ^{1/2} \beta _{n}^{1/2} + \epsilon \beta _{n}^{1} + \ldots . \end{aligned}$$
(2.26b)

Taking into account that \(R_m^{2} = R_{m0}^{2} + 2 \epsilon R_{m0} R_{m1} + \ldots \) along with the relations (2.25), and collecting terms of the same order, we find

$$\begin{aligned} \epsilon ^{0}&:&\alpha _{n}^{0} + \overline{\beta }_{n}^{0} = 0, \end{aligned}$$
(2.27a)
$$\begin{aligned} \epsilon ^{1/2}&:&\widehat{L}_{m + n}^{1/2} \alpha _{n}^{0} = - R_{m0}^{2} \left( \alpha _{n}^{1/2} + \overline{\beta }_{n}^{1/2}\right) ,\end{aligned}$$
(2.27b)
$$\begin{aligned}&\widehat{L}_{m - n}^{1/2} \beta _{n}^{0} = - R_{m0}^{2} \left( \beta _{n}^{1/2} + \overline{\alpha }_{n}^{1/2}\right) , \end{aligned}$$
(2.27c)
$$\begin{aligned} \epsilon ^{1}&:&{\hbox {d} \alpha _{n}^{0} \over \hbox {d} \tau } = - \widehat{L}_{m + n}^{1} \alpha _{n}^{0} - 2 R_{m0} R_{m1} \alpha _{n}^{0} - \widehat{L}_{m + n}^{1/2} \alpha _{n}^{1/2} - R_{m0}^{2} \left( \alpha _{n}^{1} + \overline{\beta }_{n}^{1}\right) ,\nonumber \\ \end{aligned}$$
(2.27d)
$$\begin{aligned}&{\hbox {d} \beta _{n}^{0} \over \hbox {d} \tau } = - \widehat{L}_{m + n}^{1} \beta _{n}^{0} - 2 R_{m0} R_{m1} \beta _{n}^{0} + \widehat{L}_{m + n}^{1/2} \beta _{n}^{1/2} - R_{m0}^{2} \left( \overline{\alpha }_{n}^{1} + \beta _{n}^{1}\right) .\nonumber \\ \end{aligned}$$
(2.27e)

In view of the \(O(\epsilon ^{0})\) constraint, the \(O(\epsilon ^{1})\) equations yield

$$\begin{aligned} 2 R_{m0}^{2} \left( \alpha _{n}^{1} + \overline{\beta }_{n}^{1}\right) = \widehat{L}_{m + n}^{1/2} \left( \overline{\beta }_{n}^{1/2} - \alpha _{n}^{1/2}\right) . \end{aligned}$$
(2.28)

As a result, with the use of the \(O(\epsilon ^{1/2})\) equation, the linear amplitude equation for \(\alpha _{n}^{0}\) becomes

$$\begin{aligned} {\hbox {d} \alpha _{n}^{0} \over \hbox {d} \tau } = - \widehat{L}_{m + n}^{1} \alpha _{n}^{0} + {1 \over R_{m0}^{2}} \left( \widehat{L}_{m + n}^{1/2}\right) ^{2} \alpha _{n}^{0} - 2 R_{m0} R_{m1} \alpha _{n}^{0}, \end{aligned}$$
(2.29)

where \(R_{m0}(\tau )\) and \(R_{m1}(\tau )\) are given by Eq. (2.18). Equation (2.29) retains full time dependence of the perturbation amplitude on the domain dynamics.

At this point one can perform finite-time analysis of (2.29), i.e., based on the behavior of the exponent \(\int _{0}^{\tau }{a(\tau ') \, \hbox {d}\tau '}\), as well as long-time analysis based on the behavior of the time-dependent coefficient \(a(\tau )\) on the right side of (2.29), i.e., \({\hbox {d} \alpha _{n}^{0} / \hbox {d} \tau } = a(\tau ) \alpha _{n}^{0}\). Note that all the terms on the right side of (2.29) may be positive under certain conditions and thus contribute to the growth of the amplitude \(\alpha _{n}^{0}\), which means that Eckhaus instability takes place.

Example 5

Let us state the conditions under which all the terms on the right side of (2.29) are positive. First, \(R_{m1} < 0\), which implies based on (2.18) that \({\hbox {d} R_{m0} / \hbox {d} \tau } > 0\). The latter is true if \(\gamma _{m} < 1\) and \({\hbox {d} \gamma _{m} / \hbox {d} \tau } < 0\), thus requiring that \(L(\tau )\) grows with time monotonically. In this case the condition \(3 \gamma _{m} - 1 < 0\) is satisfied, thus making \(\widehat{L}_{m + n}^{1} < 0\) as required.

2.3 Nonlinear Evolution of the Eckhaus Instability

In this section, we extend the analysis in the previous section into the nonlinear regime by deriving a nonlinear evolution equation for the pattern wavenumber. The derivation is done on an infinite domain—the only difference for a finite domain is that the wavenumber spectrum is discrete, so that the Eckhaus instability generates states with wavenumbers \(m \pm 1\). We begin by extending the standard analysis of the Eckhaus instability for the complex Ginzburg–Landau equation on an infinite domain \(x \in \mathbb {R}\) in (Eckhaus 1965; Hoyle 2006) to the time-dependent domain case. Guided by the characteristic scales for the Eckhaus instability identified in the previous section, we introduce the slow scales \(\tau = \epsilon ^{2} t\) and \(\xi =\epsilon x\) and write the amplitude equation in the spatial variable \(\xi \) scaled by the time-dependent domain size \(L(\tau )\),

$$\begin{aligned} \epsilon ^{2} u_{\tau } = \mu \, u + {\epsilon ^{2} \over L^{2}(\tau )} u_{\xi \xi } - |u|^{2} u. \end{aligned}$$
(2.30)

Under these conditions one may seek a solution in the Wentzel–Kramers–Brillouin–Jeffreys (WKBJ) form (Bender and Orszag 1999)

$$\begin{aligned} u(\tau ,\xi ) = R(\tau ,\xi ) \mathrm {e}^{\mathrm {i} \phi (\tau ,\xi ) / \epsilon }, \end{aligned}$$
(2.31)

where without loss of generality we assume that \(R\), \(\phi \in \mathbb {R}\). The form (2.31) is designed to capture both the base state and its perturbation, i.e., it should reflect the time evolution of a general initial condition varying on the scale \(\xi =O(1)\). Substituting the Ansatz (2.31) into (2.30) and collecting terms of the same order gives

$$\begin{aligned} O(1)&:&\ \mu - R^{2} = \phi _{\xi }^{2} / L^{2}, \end{aligned}$$
(2.32a)
$$\begin{aligned} O(\epsilon )&:&\ R^{2} \phi _{\tau } = {1 \over L^{2}} {\partial \over \partial \xi } \left( R^{2} \phi _{\xi }\right) . \end{aligned}$$
(2.32b)

In terms of the wavenumber \(k \equiv \phi _{\xi }\) Eqs. (2.32) become

$$\begin{aligned} k_{\tau }={1\over L^{2}}{\partial \over \partial \xi } \left[ {{\mu - {3 k^{2} \over L^{2}}} \over {\mu - {k^{2} \over L^{2}}}} k_{\xi }\right] . \end{aligned}$$
(2.33)

This equation corresponds to nonlinear diffusion of porous medium type, \(\theta _{t} = \nabla \cdot (D(\theta ) \, \nabla \theta )\) (Pattle 1959; Heaslet and Alksne 1961; Shampine 1973; Aronson 1986), which arises in a number of different fields (Vázquez 2006). It is known that these problems have a rich variety of solutions, including solutions with compact support and steep fronts (Pattle 1959). Moreover, negative powers \(n\) in \(D(\theta ) = \theta ^{n}\) are not uncommon (King 1991) and for certain forms of \(D(\theta )\) may lead to self-similar solutions (Dresner 1983).

The factor \(1/L^2\) on the right side of (2.33) can be absorbed in a definition of the effective wavenumber \(\kappa \equiv k / L\). The diffusion coefficient \(D(k)\equiv \Big (\mu - {3 k^{2} \over L^{2}}\Big )/\Big (\mu - {k^{2} \over L^{2}}\Big )\) is singular when \(\mu = \kappa ^{2} = {k^{2} / L^{2}}\) (the existence boundary) and vanishes when \(\mu = 3\kappa ^{2} \equiv {3 k^{2} / L^{2}}\) (the Eckhaus boundary), as obtained from linear stability theory Hoyle (2006), and is positive in the Eckhaus-stable regime and negative in the Eckhaus-unstable regime. Equation (2.33) indicates that, as the domain grows, the effective wavenumber \(\kappa \) may be pushed across the Eckhaus stability boundary, thereby triggering instability. Equation (2.33) describes the evolution of this instability while the amplitude of the perturbation remains slaved to the evolution of the phase. The slaving breaks down near locations where the amplitude \(R(\tau ,\xi )\) vanishes, and the phase \(\phi (\tau ,\xi )\) becomes undefined. The formation of such a singularity results in a phase slip (Kramer and Zimmermann 1985), i.e., the insertion of a new spike into the crown, followed by wavelength readjustment. As the domain continues to expand, repeated phase slips triggered by the Eckhaus instability may take place.

With the introduction of the effective wavenumber \(\kappa \), Eq. (2.33) becomes

$$\begin{aligned} \kappa _{\tau } + {L_{\tau } \over L} \kappa = {1 \over L^{2}} {\partial \over \partial \xi } \left[ {{\mu - 3 \kappa ^{2}} \over {\mu - \kappa ^{2}}} \kappa _{\xi }\right] ; \end{aligned}$$
(2.34)

thus the presence of time-dependent \(L\) introduces an advective contribution to the wavenumber evolution. Near the time-independent Eckhaus instability threshold \(\mu = 3 \kappa _{0}^{2}\) we may write \(\kappa = \kappa _{0} + \kappa '\), \(\kappa _{0}>0\), and find that \(\kappa '\) satisfies a driven porous medium equation:

$$\begin{aligned} \kappa ^{\prime }_{\tau } = - {3 \over L^{2}}{\partial \over \partial \xi } \left[ {\kappa ' \kappa _{\xi }^{\prime } \over \kappa _{0}}\right] - {L_{\tau } \over L} \kappa _{0}. \end{aligned}$$
(2.35)

This equation describes the slow (compared with the original time scale \(t\)) drift of the system through the Eckhaus instability boundary arising from the time dependence of the domain: the effective diffusivity is positive when \(\kappa ^{\prime }<0\) (Eckhaus stable) but is negative when \(\kappa ^{\prime }>0\) (Eckhaus unstable). When the forcing term on the right side is small (namely, if the time dependence of \(L\) is too slow), this equation describes the generation of a phase slip in finite time. When this is not the case and both \(L\) and \(\kappa \) evolve on the same time scale \(\tau \), the situation is less clear. While it is likely that a sufficiently rapid variation of \(L\) may suppress the generation of a phase slip altogether, the fact that a phase slip generally forms in finite time suggests that the time scale on which \(\kappa \) changes decreases rapidly as the instability starts to develop and hence that the forcing on the right side ultimately becomes subdominant, and the phase slip proceeds to completion. Traditional derivations of the phase equation near the Eckhaus boundary employ a scaling that brings in \(\kappa _{\xi \xi \xi \xi }^{\prime }\) to regularize the solution (Hoyle 2006), resulting in the Kuramoto–Sivashinsky equation; this equation remains valid provided phase slips (\(R=0\)) do not take place.

Since \(\phi _x=\epsilon L(\tau )\kappa \) and the jump in \(\phi \) across a periodic domain is \(2\pi N\), where \(N\) is an integer, we see that, in the absence of phase slips that change the integer \(N\), the wavenumber \(\kappa \propto L^{-1}\), i.e., the wavelength of the pattern is stretched. This stretching ultimately carries the wavenumber \(\kappa \) across the Eckhaus boundary into the Eckhaus-unstable regime. When this is the case, the Eckhaus instability leads, after a delay, to a localized growth of \(\kappa \), and hence a local decrease in the amplitude of the wavetrain, as described by Eq. (2.32), i.e., \(R^2=\mu -\kappa ^2\). Once \(\kappa \) is so large that \(R\) falls to zero, the phase \(\phi \) ceases to be well defined and a phase slip occurs that inserts a new wavelength or spike into the pattern at the location of the phase slip. The pattern then relaxes, resulting in a new pattern with more or less uniform but shorter wavelength. When this wavelength falls in the Eckhaus-stable region, the stretching takes over and the above process repeats; when it does not, a further phase slip will be triggered until the wavelength falls in the Eckhaus-stable regime. Since the phase slips occur on a fast timescale (the Eckhaus instability is subcritical), the number of phase slips that will occur before stability is restored depends on the delay in triggering the instability. Thus, the time dependence of the domain plays a new and fundamental role in the evolution of the pattern. See Ma et al. (2010) and Ma and Knobloch (2012) for numerical studies of this process.

The same scaling assumptions as in Eq. (2.30) can also be applied to the CSHE (2.1), yielding

$$\begin{aligned} \epsilon ^{2} u_{\tau } = \mu \, u - L_{x} u-|u|^{2} u, \ \text {with} \ L_{x} = \left( \frac{\epsilon ^{2}}{L(\tau )^2}\partial _{x}^{2}+k_{0}^2\right) ^{2}. \end{aligned}$$
(2.36)

The WKBJ Ansatz (2.31) now leads to the following equation for the evolution of the (scaled) wavenumber \(\kappa \):

$$\begin{aligned} \kappa _{\tau } + {L_{\tau } \over L} \kappa = - {2 \over L^{2}} {\partial \over \partial \xi } \left[ {{\mu (k_{0}^{2} - 3 \kappa ^{2}) - (k_{0}^{2}-7\kappa ^{2}) (k_{0}^{2}-\kappa ^{2})^{2}} \over {\mu - (k_{0}^{2}-\kappa ^{2})^{2}}} \kappa _{\xi }\right] . \end{aligned}$$
(2.37)

As in the complex Ginzburg–Landau equation case, the diffusion coefficient \(D(\kappa )\equiv (\mu (k_{0}^{2} - 3 \kappa ^{2}) - (k_{0}^{2}-7\kappa ^{2}) (k_{0}^{2}-\kappa ^{2})^{2})/(\mu - (k_{0}^{2}-\kappa ^{2})^{2})\) is singular when \(\mu = (k_{0}^{2}-\kappa ^{2})^{2}\) (the existence boundary of the base state \(R_{m}\)) and vanishes when \(\mu = (k_{0}^{2}-7\kappa ^{2}) (k_{0}^{2}-\kappa ^{2})^{2}/(k_{0}^{2}-3 \kappa ^{2})\) [the Eckhaus boundary (2.23)], with \(D>0\) in the Eckhaus-stable and \(D<0\) in the Eckhaus-unstable region, respectively.

2.4 Coarsening

Domain growth also exerts considerable effect on pattern coarsening. To show this we derive the Cahn–Hilliard equation governing the evolution of small-wavenumber perturbations of the homogeneous state within the complex Swift–Hohenberg equation (2.1) on a time-dependent domain. Following a similar derivation by Gelens and Knobloch (2010), we write

$$\begin{aligned} u(t,x) = R_{\mathrm {s}} \left( 1 + \epsilon ^{2} u(\tau ,\xi )\right) \mathrm {e}^{\mathrm {i} \, \phi (\tau ,\xi )}, \end{aligned}$$
(2.38)

where \(R_{\mathrm {s}} = \sqrt{\mu - k_{0}^{4}}\), \(\xi = \epsilon x\), \(\tau = \epsilon ^{4} t\), and \(0<\epsilon \ll 1\) is an ordering parameter that may be taken as the wavenumber of the perturbation. The phase \(\phi (\tau ,\xi )\) is formally \(O(1)\), but its gradient is small, \(\phi _x=\epsilon v\), where \(v \equiv \phi _{\xi }\) is \(O(1)\). We anticipate that the phase will be a slow variable and hence assume that the perturbation \(u\) is slaved to it; i.e., we assume that \(u = \alpha \, v^{2} + O(\epsilon ^2)\) with \(\alpha = O(1)\).

We begin by setting \(u(t,x) = R(t,x) \mathrm {e}^{\mathrm {i} \, \phi (t,x)}\) and writing (2.1) as a pair of equations for the amplitude \(R\) and wavenumber \(k\equiv \phi _x\):

$$\begin{aligned} R_{t}&= \mu R - R^{3} - {2 k_{0}^{2}\over L^2} R_{xx} - \biggl (k_{0}^{2} - {k^{2}\over L^2}\biggr )^{2} R + {6 k^{2}\over L^4} R_{xx} \nonumber \\&+ {12 k k_{x}\over L^4} R_{x} + {3 k_{x}^{2}\over L^4} R + {4 k k_{xx}\over L^4} R - {1\over L^4}R_{xxxx}, \end{aligned}$$
(2.39a)
$$\begin{aligned} k_{t}&= - {4k_{0}^{2}\over L^2} \left[ {k R_{x}\over R}\right] _x - {4\over L^4}\left[ {k R_{xxx}\over R}\right] _x - {6\over L^4}\left[ {k_x R_{xx}\over R}\right] _x - {4\over L^4}\left[ {k_{xx} R_{x}\over R}\right] _x \nonumber \\&+ {4\over L^4} \left[ {k^3 R_{x}\over R}\right] _x - {2 k_{0}^{2}\over L^2} k_{xx} - {1\over L^4} k_{xxxx} + {2\over L^4} (k^{3})_{xx}. \end{aligned}$$
(2.39b)

We next write an equation for the perturbation \(u(\tau ,\xi )\) of the steady state \(R_\mathrm {s}\) introduced in (2.38):

$$\begin{aligned} \epsilon ^{4} u_{\tau }&= - 2 R_{\mathrm {s}}^{2}u + {2 k_{0}^{2}\over L^2} v^{2} + \epsilon ^{2} \biggl [- 3 R_{\mathrm {s}}^{2}u^{2} + {2 k_{0}^{2}\over L^2}u v^{2} + {3 v_{\xi }^{2}\over L^4} \\&+ {4 v v_{\xi \xi }\over L^4} - {v^{4}\over L^4} - {2 k_{0}^{2}\over L^2} u_{\xi \xi }\biggr ] + \hbox {h.o.t.} \end{aligned}$$

Thus \(\alpha = k_{0}^{2} / (L^2 R_{\mathrm {s}}^{2})\) and the expression for the phase reduces to

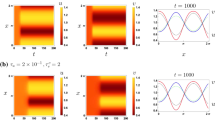
$$\begin{aligned} \epsilon ^2 v_{\tau }= - {1 \over L^{2}} \left[ 2 k_{0}^{2} v + {\epsilon ^2 \over L^{2}} v_{\xi \xi } + {\epsilon ^2\sigma \over L^{2}}v^{3}\right] _{\xi \xi } + O(\epsilon ^{3}), \end{aligned}$$
(2.40)

where \(\sigma \equiv {8\over 3}{k_{0}^{4}\over R_{\mathrm {s}}^{2}}-2\). For consistency we therefore require that \(k_0\sim \epsilon \ll 1\), and in this regime \(\sigma \approx -2\). Thus, when the intrinsic length scale \(2\pi /k_0\) is large and the domain size fixed, we expect coarsening as described by the autonomous Cahn–Hilliard equation (2.40) with \(L=1\), cf. Fig. 2a. Coarsening is not expected, however, for smaller values of this length scale when structures develop oscillatory tails and lock to one another, thereby arresting the coarsening process (Gelens and Knobloch 2010).

A different type of freezing out occurs when the domain length \(L\) varies on the coarsening timescale. Figure 2b shows that in this case the expansion of the domain also arrests the coarsening process. However, once the expansion timescale becomes longer than the coarsening timescale, the coarsening process resumes abruptly. Equation (2.40) with \(\epsilon =0.05\) should capture transitions of this type.

Fig. 2
figure 2

Coarsening in the complex Swift–Hohenberg equation on (a) a time-independent domain, \(L=1\) and (b) a time-dependent domain, \(L=1+(L(0)-1)\mathrm {e}^{-t/t_{\mathrm {c}}}\), where \(t_{\mathrm{c}} = 5000\). The domain varies on the same timescale as the coarsening process in the time-independent case. Periodic boundary conditions are used with parameters \(\mu = 1.0\) and \(k_{0} = 0.05\) (color figure online)

Full size image

The above derivation applies to long-wave modulation of a homogeneous state, \(R=R_\mathrm {s}\). A similar calculation may be made for the quasistationary \(m\)-spike state \(R=R_m(\tau )\), where

$$\begin{aligned} R_m^2(\tau )=\mu -\bigg ({m^2\over L^2(\tau )}-k_0^2\biggr )^2 \ \text {with} \ \tau =\epsilon t. \end{aligned}$$
(2.41)

In the following we write \(R=R_m+\delta u\), \(k=m+\delta v\) with \(0<\delta \ll 1\) and suppose that \(u=u(T,\tau ,\xi )\), \(v=v(T,\tau ,\xi )\), where \(\xi =\delta x\) and the slow time \(T\) is determined below. Once again we expect the amplitude perturbation to be slaved to the slow evolution of the wavenumber perturbation \(v\):

$$\begin{aligned} u=Av+\delta B v^2+\delta ^2 D v^3+\delta ^2 F v_{\xi \xi }+\dots \end{aligned}$$
(2.42)

Substituting this Ansatz into Eq. (2.39a), we obtain expressions for the coefficients \(A\), \(B\), \(D\), and \(F\). These depend on the time \(\tau \) through the domain length \(L(\tau )\). With this result, Eq. (2.39b) yields

$$\begin{aligned} v_t=-[\delta ^2\alpha v+\delta ^3\beta v^2+\delta ^4\gamma v_{\xi \xi }+\delta ^4\nu v^3]_{\xi \xi }+\dots , \end{aligned}$$
(2.43)

where

$$\begin{aligned} \alpha ={8m^2\over R_m^2}\biggl ({m^2\over L^4}-{k_0^2\over L^2}\biggr )^2 -{6m^2\over L^4}+{2k_0^2\over L^2}, \end{aligned}$$
(2.44)

with similar expressions for the remaining coefficients. It follows that as \(L\) varies the diffusion coefficient \(\alpha (\tau )\) may pass through zero, leading to destabilization of the \(m\)-spike state. In the regime where \(\alpha =O(\delta )\) the (nonlinear) evolution of the system occurs on the timescale \(T=\delta ^3t\) and nontrivial dynamics, including bifurcation delay, are expected when \(\delta ^3\sim \epsilon \). However, on this timescale the instability does not saturate. Equation (2.43) shows that, on the longer time scale \(T=\delta ^4t\), two new terms enter the dynamics, leading to Cahn–Hilliard-like dynamics and saturation whenever the coefficient \(\gamma (\tau )\) remains positive. See Gelens and Knobloch (2010) for a discussion of the \(L\equiv 1\) case.

3 Conservative Swift–Hohenberg Model

It is also possible to formulate the crown formation problem within ideal hydrodynamics. The corresponding model problem must also be conservative, and we adopt here a nonlinear Schrödinger-type equation with higher-order dispersion as a model for conservative dynamics on a one-dimensional time-dependent domain \(x \in \Omega (t) = [0, 2\pi L(t)]\). After rescaling the spatial variable \(x\) we obtain

$$\begin{aligned} \mathrm {i} \, u_{t} = \mu \, u - \left( \frac{1}{L^2(t)}\partial _{x}^{2}+k_{0}^2\right) ^{2} u-|u|^{2} u, \end{aligned}$$
(3.1)

where, as in Eq. (2.1), \(u(t,x): \, \mathbb {R}^{+} \times \mathbb {R} (\hbox {mod} \, 2\pi ) \rightarrow \mathbb {C}\), \(k_{0}\) represents an intrinsic wavenumber (i.e., a time-independent inverse length scale), and \(\mu \) is a parameter.

3.1 Benjamin–Feir Instability

Models of the type (3.1) also exhibit crown-like behavior and undergo long-wave instabilities leading to wavenumber changes via sideband instabilities. In the context of water waves such instability goes under the name of Benjamin–Feir instability (Benjamin and Feir 1967; Knobloch et al. 1994), and we consider here the onset of the corresponding instability on a growing domain.

Let us consider the spatially homogeneous base state \(u_{0}(t)\) satisfying

$$\begin{aligned} \mathrm {i} \, u_{0t} = (\mu -k_{0}^{4})u_{0} - |u_{0}|^{2} u_{0}. \end{aligned}$$
(3.2)

Thus \(|u_0|^2=R_0^2\), where \(R_0\) is a constant, and hence \(u_0(t)=R_0\exp \mathrm {i}\Omega t\), where

$$\begin{aligned} \Omega = -(\mu -k_{0}^{4}) + R_{0}^{2} \end{aligned}$$
(3.3)

is a constant. This solution is analogous to the Stokes solution of the nonlinear Schrödinger equation; we identify the half-period of \(u_0(t)\) with the evolution of the rim in the drop-splash problem, as it first grows and then collapses, with the crown-forming instability developing on top of this time-dependent base state (Krechetnikov and Homsy 2009).

An infinitesimal perturbation \(u'(t,x)\) superposed on the complex base state \(u_{0}(t)\) evolves according to the linearization of Eq. (3.1),

$$\begin{aligned} \mathrm {i} {\partial u' \over \partial t} = \mu \, u' - L_{x} u' - 2 |u_{0}|^{2} u^{\prime } - u_{0}^{2} \overline{u}^{\prime }, \end{aligned}$$
(3.4)

where \(\overline{u}^{\prime }\) is the complex conjugate of \(u^{\prime }\). We write the perturbation as

$$\begin{aligned} u'(t,x) = \alpha _{n}(t) \mathrm {e}^{\mathrm {i} \Omega t + \mathrm {i} n x} + \beta _{n}(t) \mathrm {e}^{\mathrm {i} \Omega t - \mathrm {i} n x} \ \text {with} \ \alpha _{n}, \beta _{n} \in \mathbb {C}, \end{aligned}$$
(3.5)

obtaining the equations

$$\begin{aligned} \mathrm {i} {\hbox {d} \alpha _{n} \over \hbox {d} t}&= (\mu +\Omega )\alpha _{n} - \widehat{L}_{n} \alpha _{n} - 2 R_{0}^{2} \alpha _{n} - R_{0}^{2} \overline{\beta }_{n}, \end{aligned}$$
(3.6a)
$$\begin{aligned} \mathrm {i} {\hbox {d} \beta _{n} \over \hbox {d} t}&= (\mu +\Omega )\beta _{n} - \widehat{L}_{n} \beta _{n} - 2 R_{0}^{2} \beta _{n} - R_{0}^{2} \overline{\alpha }_{n}, \end{aligned}$$
(3.6b)

where \(\widehat{L}_{n}\) is defined as in (2.6).

To solve these equations in the case of slowly varying \(L(t)\) we look for solutions of the form \(\big (\alpha _n(t),\overline{\beta }_n(t)\big )\!\propto \!\big (\alpha _n(0),\overline{\beta }_n(0)\big )\exp \, \big (\mathrm {i} \int _0^t\omega (t')\,\mathrm {d}t'\big )\) and find that the frequency \(\omega (t)\) satisfies the dispersion relation

$$\begin{aligned} \omega ^2=(R_0^2-k_0^4+\widehat{L}_{n})^2-R_0^4. \end{aligned}$$
(3.7)

Thus, when \(L\equiv 1\), the solution is stable (\(\omega ^2>0\)) whenever \(R_0^2<(k_0^4-\widehat{L}_{n})/2\) and unstable (\(\omega ^2<0\)) whenever \(R_0^2>(k_0^4-\widehat{L}_{n})/2\). However, if \(L(t)\) increases, the frequency \(\omega (t)\) may transition from being real to being imaginary, thereby triggering the Benjamin–Feir instability. This instability also experiences delay, and we surmise that it will manifest itself only once its growth rate exceeds that of the domain. Right after this instant, corresponding to a particular crown radius, the growth of the instability is expected to become explosive, and lead rapidly to an irregular crown.

3.2 Nonlinear Schrödinger Equation

We begin first with the nonlinear Schrödinger equation in the form

$$\begin{aligned} \epsilon \mathrm {i} u_{\tau } = \mu \, u + {\epsilon ^{2} \over L^{2}(\tau )} u_{\xi \xi } - |u|^{2} u, \end{aligned}$$
(3.8)

where \(\tau = \epsilon t\) and \(\xi =\epsilon x\). The use of these scales is motivated by the characteristic scales for the Benjamin–Feir instability identified above. Under these conditions one may again seek a solution in the WKBJ form (2.31). This time we obtain

$$\begin{aligned} O(1)&: \ \phi _{\tau } = - \mu + R^{2} + {\phi _{\xi }^{2} \over L^{2}}, \end{aligned}$$
(3.9a)
$$\begin{aligned} O(\epsilon )&: \ R_{\tau } = {1 \over {R \, L^{2}}} {\partial \over \partial \xi } \left( R^{2} \phi _{\xi }\right) . \end{aligned}$$
(3.9b)

In terms of the wavenumber \(k \equiv \phi _{\xi }\) Eqs. (3.9) become

$$\begin{aligned} k_{\tau } = {\partial \over \partial \xi } \biggl ({k^2\over L^2}+\rho \biggr ),\qquad \rho _{\tau } ={2\over L^2}{\partial \over \partial \xi }(\rho k), \end{aligned}$$
(3.10)

where \(\rho \equiv R^2\). This pair of conservation laws describes the evolution of the wavenumber \(k(\tau ,\xi )\) and amplitude \(R(\tau ,\xi )\) of the solution of (3.8).

Despite their nonlinear character, Eqs. (3.10) can be solved analytically. Indeed, let us rewrite (3.10) as a system in vector form:

$$\begin{aligned} A {\partial \Phi \over \partial \tau } + B {\partial \Phi \over \partial \xi } = 0, \ \Phi = \left[ \begin{array}{l} k \\ \rho \end{array}\right] , \ A = \left[ \begin{array}{ll} 1 &{} 0 \\ 0 &{} 1 \end{array}\right] , \ B = - \left[ \begin{array}{ll} 2 k \over L^{2} &{} 1 \\ 2 \rho \over L^{2} &{} 2 k \over L^{2} \end{array}\right] . \end{aligned}$$
(3.11)

The characteristic type of this system is determined from the following eigenvalue problem (Courant and Hilbert 1989):

$$\begin{aligned} \phi \, B = \lambda \, \phi , \end{aligned}$$
(3.12)

which yields the eigenvalues and left eigenvectors

$$\begin{aligned} \lambda _{1,2} = - {2 k \over L^{2}} \pm {\sqrt{2 \rho } \over L}, \ \phi _{1,2} = \left[ \mp {\sqrt{2 \rho } \over L}, 1\right] , \end{aligned}$$
(3.13)

respectively. Since both eigenvalues are real, the system is hyperbolic. With the knowledge of the left eigenvectors, we can bring the system (3.11) into the normal form

$$\begin{aligned} - {\sqrt{2 \rho } \over L} \left[ {\partial k \over \partial \tau } + \lambda _{1} {\partial k \over \partial \xi }\right] + \left[ {\partial \rho \over \partial \tau } + \lambda _{1} {\partial \rho \over \partial \xi }\right]&= 0, \end{aligned}$$
(3.14a)
$$\begin{aligned} {\sqrt{2 \rho } \over L} \left[ {\partial k \over \partial \tau } + \lambda _{2} {\partial k \over \partial \xi }\right] + \left[ {\partial \rho \over \partial \tau } + \lambda _{2} {\partial \rho \over \partial \xi }\right]&= 0. \end{aligned}$$
(3.14b)

Next, introducing characteristic coordinates \(\alpha (\tau ,\xi )\) and \(\beta (\tau ,\xi )\) such that

$$\begin{aligned} - {\alpha _{\tau } \over \alpha _{\xi }} = {\hbox {d} \xi \over \hbox {d}\tau }&= \lambda _{1}, \end{aligned}$$
(3.15a)
$$\begin{aligned} - {\beta _{\tau } \over \beta _{\xi }} = {\hbox {d} \xi \over \hbox {d}\tau }&= \lambda _{2}, \end{aligned}$$
(3.15b)

system (3.14) becomes

$$\begin{aligned} - {\sqrt{2 \rho } \over L} {\partial k \over \partial \beta } + {\partial \rho \over \partial \beta }&= 0, \end{aligned}$$
(3.16a)
$$\begin{aligned} {\sqrt{2 \rho } \over L} {\partial k \over \partial \alpha } + {\partial \rho \over \partial \alpha }&= 0. \end{aligned}$$
(3.16b)

The characteristic curves can be interpreted as representing “sound waves” propagating with velocity

$$\begin{aligned} {\hbox {d} \xi \over \hbox {d}\tau } = \lambda _{1,2}. \end{aligned}$$
(3.17)

Generic properties of Eqs. (3.16) include shock formation similar to gas dynamics, which can be described by identifying the Riemann invariants \(r(k,\rho )\) and \(s(k,\rho )\), i.e., functions constant along the characteristics

$$\begin{aligned} {\hbox {d} r \over \hbox {d}\alpha } = 0, \ \ \ {\hbox {d} s \over \hbox {d}\beta } = 0. \end{aligned}$$
(3.18)

These Riemann invariants are determined from

$$\begin{aligned} r_{k}&= {\sqrt{2 \rho } \over L} g, \, r_{\rho } = g, \end{aligned}$$
(3.19a)
$$\begin{aligned} s_{k}&= - {\sqrt{2 \rho } \over L} l, \, s_{\rho } = l, \end{aligned}$$
(3.19b)

and the compatibility conditions \(r_{k\rho } = r_{\rho k}\) and \(s_{k\rho } = s_{\rho k}\); here \(g(k,\rho )\) and \(l(k,\rho )\) are integrating factors. Solutions of (3.19) are given by \(r = r(k + L \, \sqrt{2 \rho })\) and \(s = s(k - L \, \sqrt{2 \rho })\), respectively, indicating that along characteristics, i.e., curves \(k \pm L \, \sqrt{2 \rho } = \hbox {const.}\), the wavenumber stretches or compresses as \(L\) increases, depending on the direction of the wave and the behavior of the amplitude. For example, along the characteristic \(k- L \, \sqrt{2 \rho } = \hbox {const.}\), the wavelength shrinks as \(L\) increases whenever the amplitude \(\rho \) remains constant. This illustrates an interesting property—evolution of the pattern wavelength \(2\pi /k\) with \(L\) depends on the time rate of change of the amplitude \(\rho \), which is in turn dictated by the initial conditions.

One can also get an idea of the type of solutions described by Eqs. (3.10) by considering the case \(|k|\ll 1\) and taking \(\rho =\rho _0+\rho ^{\prime }\), where \(|\rho ^{\prime }|\ll \rho _0\). The linearized equations that result can be combined into a wave equation for the wavenumber \(k\),

$$\begin{aligned} k_{\tau \tau }=c_0^2(\tau )\, k_{\xi \xi }, \end{aligned}$$
(3.20)

where \(c_0^2(\tau )\equiv 2\rho _0/L^2(\tau )>0\). Existing studies of the wave equation on time-dependent domains (Lee 1966; Rogak 1966; Borgnis and Papas 1972; Garcia and Minzoni 1981; Dittrich et al. 1998), though limited, reveal that energy may grow or decay. This is in contrast to the fixed domain case, which is a conservative problem. The time-dependent sound speed in (3.20) may result in the presence of parametric resonance (Cooper 2000; Ueda 2011), as can be seen by taking the Fourier transform of (3.20) in \(\xi \), resulting in Hill’s equation whenever \(L\) varies sinusoidally in time. The latter, depending on the exact shape of \(c(\tau )\), may have solutions bounded for all time or growing exponentially. Time-dependent sound speed is in fact used to control the solutions of the wave equation (Chambolle and Santosa 2002).

3.3 Conservative CSHE

In the case of the conservative CSHE:

$$\begin{aligned} \epsilon \mathrm {i} u_{\tau } = \mu \, u - L_{x} u - |u|^{2} u, \quad \mathrm{with}\quad \ L_{x} = \left( {\epsilon ^{2} \over L^{2}(\tau )} \partial _{\xi }^{2} + k_{0}^{2}\right) ^{2}, \end{aligned}$$
(3.21)

the WKBJ Anzatz (2.31) produces

$$\begin{aligned} O(1)&: \ \phi _{\tau } = - \mu + R^{2} + \left( {\phi _{\xi }^{2} \over L^{2}} - k_{0}^{2}\right) ^{2}, \end{aligned}$$
(3.22a)
$$\begin{aligned} O(\epsilon )&: \ R_{\tau } = {2 \over {R \, L^{4}}} {\partial \over \partial \xi } \left( R^{2} \phi _{\xi }^{3}\right) - {2 k_{0}^{2} \over {R \, L^{2}}} {\partial \over \partial \xi } \left( R^{2} \phi _{\xi }\right) . \end{aligned}$$
(3.22b)

In terms of the wavenumber \(k \equiv \phi _{\xi }\) and \(\rho \equiv R^2\), Eqs. (3.22) become

$$\begin{aligned} k_{\tau } = {\partial \over \partial \xi } \left[ \left( {k^2\over L^2}-k_{0}^{2}\right) ^{2}+\rho \right] ,\qquad \rho _{\tau } ={4\over L^4}{\partial \over \partial \xi }(\rho k^{3}) - {4 k_{0}^{2} \over L^2}{\partial \over \partial \xi }(\rho k). \end{aligned}$$
(3.23)

In the limit \(|k| \ll |k_{0}|\) one obtains

$$\begin{aligned} k_{\tau \tau } = - c_0^2(\tau ) \, k_{\xi \xi }, \end{aligned}$$
(3.24)

where \(c_0^2(\tau ) \equiv 4 k_{0}^{2}\rho _0 / L^{2}\), indicating the presence of a long-wave instability. In contrast, in the case \(k = k_{0} \, L + k'\), \(\rho = \rho _{0} + \rho '\), where \(|k'|\ll k_{0} \, L\) and \(|\rho '|\ll \rho _{0}\), we obtain for \(L \equiv 1\) the wave equation \(k_{\tau \tau } - 8 \rho _{0} k_{0}^{2} \, k_{\xi \xi } = 0\), indicating propagative dynamics.

4 Conclusions

In this paper we have described several new types of behavior associated with evolution and pattern formation on time-dependent domains. Our discussion was limited to the case where the domain dynamics are prescribed, i.e., the domain size is an external parameter, as opposed to systems in which the domain size is an internal parameter, i.e., the domain grows in response to the dynamics taking place within it. Both types of situation arise frequently in applications. As examples of the former we mention fluid flow in an expanding bubble or in an expanding universe (Knobloch 1978), in which the expansion of the domain is determined to a large extent by overpressure, with the internal dynamics contributing little to the domain dynamics. In contrast, processes such as tumor growth and solidification processes (Vasil and Proctor 2011), in which the domain grows in response to processes within it, constitute examples of systems in which the domain size is an internal parameter. In fact, the system which motivated this study—the drop-splash problem in which the perimeter of the crown grows rapidly and exhibits instabilities that may or may not coarsen in time—belongs to the latter class, but an externally imposed domain growth can be considered as a first approximation to the true dynamics.

With the help of the CSHE model we have seen two types of effects of time dependence. First, when the domain grows on a slow timescale, the wavelength of any pattern or structure within it is stretched, thereby pushing the pattern wavenumber out of the Eckhaus-stable regime. When this occurs, Eckhaus instability generates a phase slip that inserts a new cell into the pattern. If the resulting pattern, after wavelength readjustment, is still Eckhaus unstable, further phase slips take place. This process is typically fast compared with the timescale on which the domain evolves. Thus the gradual growth of the domain will lead to repeated phase slips as the pattern tries to keep its wavelength in the preferred, Eckhaus-stable, range. This type of behavior has recently been observed in localized patterns outside of the so-called pinning interval (Ma et al. 2010; Ma and Knobloch 2012): in this regime the fronts bounding the structure on either side move apart, triggering repeated phase slips in the structure between them. In fact, in some regimes the phase slip frequency and the front motion may be closely coupled. In such cases the domain size becomes an internal parameter. Second, we have also seen that the growth of the domain may suppress pattern coarsening if the timescale for domain growth is faster than the coarsening timescale. On the other hand, once the growth timescale exceeds the coarsening timescale, coarsening may resume in a dramatic fashion (Fig. 2). Thus domain growth may lead to the “freezing” of the structure, much as occurs in the presence of oscillatory tails in time-independent systems (Raitt and Riecke 1995; Gelens and Knobloch 2010). A similar wavelength-changing instability, the Benjamin–Feir instability, is present in conservative systems, but coarsening of the above type is not expected to occur.

Throughout this paper we have focused on systems in which dilution effects are absent. These effects are typically present in reaction–diffusion equations on a growing domain (Crampin et al. 1999) but in many studies appear to play a subordinate role (Ueda and Nishiura 2012). We do not expect dilution to be important in the phase instabilities we have focused on, except insofar as they reduce the amplitude of the solution and so potentially shorten the time to phase slip. These effects will be described in detail in a follow-up paper.

Our work suggests a number of interesting directions for further study. The properties of the nonautonomous nonlinear diffusion equations (2.33) and (2.37) governing wavenumber evolution in growing domains remain to be studied. Of particular interest is the behavior of these equations near the singularity in the nonlinear diffusion coefficient \(D(\kappa )\) leading to phase slips. Likewise, the nonlinear evolution of the Benjamin–Feir instability, as described by the conservation laws (3.10) and (3.23), requires further exploration. On the pattern coarsening side of the story, detailed properties of the Cahn–Hilliard equation (2.40) on an evolving domain are of great interest. From a broader perspective, the relation between systems with an externally prescribed domain size and systems in which the domain size is an intrinsic variable remains to be elucidated. The latter would necessitate the development of methods for analyzing problems with an intrinsic time-varying domain size. Also, the connection between the stability picture on evolving domains and dynamic bifurcations, bifurcation delay, canard solutions, and phase slips needs to be understood in greater detail.

Finally, time variation of the domain size suggests a new way to control instability phenomena in the context of PDEs. Traditionally (Burns and Kang 1991; Krstic 1999; Krstic et al. 2008), stabilization of equilibrium solutions of PDEs is achieved via control of boundary conditions with control actions either distributed over the entire spatial domain (or a part), or applied at the boundary of the spatial domain (boundary controls), or active only at specified points within the domain (point controls). The proposed study of the effects of time dependence of the domain size provides new avenues for the control of equilibria of PDEs.