The effects of picker-oriented operational factors on hand-off delay in a bucket brigade order picking system

Abstract

During collaboration between neighboring pickers in a bucket brigade order picking, the downstream picker frequently experiences productivity loss in the form of a hand-off delay while waiting for a new tote from the upstream picker. This paper proposes an analytical model to quantify the hand-off delay of downstream pickers under non-deterministic pick times and non-instantaneous walk times of the upstream pickers. Numerical analyses show the effects of the magnitude of pick time, the variation of pick time, and the forward walk time on the hand-off delay, and simulation models show the effects of the number of pickers and their skill differences. We conclude that stable pick times are especially important to reduce hand-off delays and that slowest-to-fastest picker assignments offset hand-off delays with the blocking delays.

1 Introduction

In a bucket brigade order picking system (OPS) with flow-rack shelving, managers assign multiple pickers to pick a single batch in the picking area associated with the order, and the pickers collect items at pick faces sequentially until the single batch is fully picked. An “upstream” picker picks an item and places it in the tote assigned to the batch and then moves to the next pick face if it is not occupied by a “downstream” picker. When meeting a downstream picker who has no tote, the upstream picker hands off the current tote, and then returns to retrieve a new batch and tote and begin a new picking as the downstream picker continues to fill the current tote. The bucket brigade order picking benefits from a fully flexible work range of pickers (Hopp and Spearman 2008), meaning that any picker can conduct picking operations at any pick face. The work area for any picker is not predetermined and the use of a pick-and-pass rule eliminates the need for work zone load balancing, which can be complicated and difficult (Bartholdi and Eisenstein 1996a).

In a bucket brigade OPS, however, transferring partially picked orders from upstream pickers to downstream pickers often causes delays for the downstream pickers because of the variability and uncertainty of the hand-off locations and the remaining pick times. Synchronization and a no-passing rule require the downstream picker to wait (“idle”) for the upstream picker to complete picking and handing off the tote to the downstream picker. To understand the hand-off delays and the operational rules, we interviewed the managers of several distribution centers. In general, they maintained a relatively large number of batches and released an additional work-in-process to mitigate the shortage probability of batches between adjacent pickers in an order picking line as reported in Koo (2009). Collaboration between neighboring pickers also reduced hand-off delay, which is similar to the side-by-side picking reducing blocking delay reported in Bartholdi and Eisenstein (1996a). These popular rules guaranteed high and stable performance for most picking operations.

A few studies have examined the performance issues caused by hand-off delays in bucket brigade order picking. Bartholdi and Eisenstein (1996b), who describe the existence of hand-off delay in bucket brigades, report cases of less hand-off delay, i.e., the delay is assumed as negligible. Later, Bartholdi and Eisenstein (2005) report the significance of hand-off time and propose four ways to measure the hand-off time, but again the delay is assumed as deterministic. Koo (2009) conducts a simulation study to investigate the productivity loss due to hand-off delay in a bucket brigade OPS. Similarly, Hong et al. (2015) capture the hand-off delay from a simulation study in a bucket brigade OPS. The few studies above rely on simulation models because it is difficult to monitor industry cases.

In this paper, we identify an analytical model and investigate the effects of the stochastic pick time and finite walk time on hand-off delays by conducting numerical analyses and simulation experiments. In order to take over a new tote from an upstream picker, a downstream picker confronts an upstream picker picking item(s) or walking forward at a neighboring upstream pick face, where the pick time at each pick face varies and the walk time also differs. The upstream picker’s remaining pick or walk time affects the downstream picker’s hand-off operation due to the randomness of the remaining times. We develop an analytical hand-off model for a two-picker situation with finite forward walk time over non-deterministic pick density situations in an order picking line. Our numerical analyses of the analytical model and simulation experiments identify the effects of pick time variability and picker skill difference on hand-off delays.

The paper is organized as follows. Section 2 reviews the bucket brigade literature and identifies new opportunities. Section 3 explains hand-off delays in a bucket brigade order picking system. Section 4 introduces the analytical models using a stochastic process. Section 5 describes numerical analyses of hand-off delays and summarizes a simulation study. Section 6 concludes and suggests additional research.

2 Literature review

2.1 Bucket brigades

In an early study of bucket brigade management, Bartholdi and Eisenstein (1996b) find that the highest throughput is obtained when pickers are sequenced with the slowest picker in the location most upstream and the fastest picker in the location most downstream. The authors suggest that picker blocking can be minimized when there are large capability differences among pickers, and that hand-off delay can be reduced as pickers learn to anticipate upcoming exchanges. Bartholdi et al. (2010) review serial bucket brigades where every item is handed off from one picker to another in a straight-line layout. Each picker processes an item only once.

Bartholdi and Eisenstein (1996a), who also describe the productivity improvements obtained from a bucket brigade OPS, emphasize that bucket brigades can achieve both high space utilization and high picker utilization. For instance, when higher space utilization makes passing difficult, they recommend bucket brigades for high-volume, limited-space picking operations over the more traditional zone picking strategy. Bartholdi et al. (2001) develop a general performance model where the workload is not uniform over the pick area. Demonstrating that bucket brigades are still advantageous and self-balancing despite the exponential distribution of pick locations, they assume that all pickers’ hand-offs occur simultaneously and synchronously with no delays. The chain of the hand-off occurs at the same time because walk speed is infinite.

Bucket brigade system also applies to an in-tree assembly network (Bartholdi et al. 2006). Bartholdi et al. (2009) study bucket brigades with significant walk-back time which allows pickers to overtake or pass each other and walk back with finite velocities. The bucket brigade system can avoid chaotic behavior when pickers are indexed from most impeded by work to least impeded by work. Lim and Yang (2009) analyze the dynamics of bucket brigades on discrete work stations and identify the policies that maximize throughput. A policy that fully cross-trains pickers and sequences them from slowest to fastest, however, is not always the best strategy, even though it outperforms other policies for most work-content distributions.

Lim (2011, 2012) introduce an approach, which they call cellular bucket brigades, which distributes the work content of an assembly line on both sides of an aisle in a “U-line.” Each picker works on one side when proceeding in one direction and then works on the other side when proceeding in the reverse direction. Lim and Wu (2014) present an operating protocol to coordinate pickers on a U-line, which allows management to configure the system for maximal productivity. Lim (2017) extends the analysis by considering the effects of hand-off times on the operational performance of cellular bucket brigades.

2.2 Delays and idleness in bucket brigades

Bartholdi and Eisenstein (1996a) report two delays in bucket brigade OPS, blocking delay and hand-off delay, and introduce batch picking and collaboration in a pick face. Koo (2009) confirms that picker blocking and hand-off delay reduce the productivity of a bucket brigade OPS when pickers have the same capability and the bucket brigade rules are applied tightly, assuming that workload is random, pick time is not deterministic, and walk time is negligible. Koo (2009) constrains each picker’s picking area by defining a downstream boundary where upstream pickers are allowed to leave totes at the boundary location if a downstream picker is not available to take over the tote.

Recently, Hong et al. (2015) identify analytical picker blocking models for bucket brigade order picking using a discrete-time Markov chain. Hong et al. (2015) show that a circular-aisle OPS approximates a picker blocking model in a bucket brigade OPS. They identify the effects of the hand-off delay on the blocking delay based on the operational characteristic that the hand-off increases the order picking lead times as much as the hand-off duration does. Hong et al. (2015) confirm the approximation using a simulation study, and Hong (2014) finds the same results analytically for a two-picker case with finite walk time.

Bartholdi and Eisenstein (1996b) consider the hand-off delay as the upstream picker’s interruption that can be reduced through practice. Bartholdi and Eisenstein (2005) analyze an assembly line where the walk speed is not infinite and the return trip of a picker after handing off a tote requires significant time. Specifically, they assume constant hand-off time to identify the operational stability, and then introduce four ways to measure the hand-off time. Koo (2009) attempts to quantify the hand-off delay by using a simulation study. Hong et al. (2015) also use simulation to estimate hand-off delay.

2.3 Motivations

Published studies of hand-off delays that only rely on empirical and simulation observations do not generate enough insights to understand the effect of a delay and its mitigation. Specifically, they lack an explanation of the amount of hand-off delay over the pick time variation and the finite walk time. The fact that our preliminary experiment also shows randomness between the hand-off delays per occurrence (see “The interdependency in the hand-off location and the hand-off delay” section in Appendix for the details) indicates the probable existence of a hand-off delay model. Therefore, we propose an analytical model of hand-off delay considering non-deterministic pick and finite walk time cases and explain the trade-off between less hand-off and longer lead time.

3 Problem definition

3.1 Bucket brigade order picking system

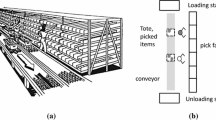
We consider a flow-rack shelving and picker-to-part-order picking case (Fig. 1). A bucket brigade order picking strategy is equipped with flow-rack shelving to achieve high throughput warehouse environments. This study refers to the combination of flow-rack shelving and the bucket brigade strategy discussed in Bartholdi adn Eisenstein (1996) as a bucket brigade order picking system (OPS).

Fig. 1

(Adapted from Bartholdi and Eisenstein (1996a))

A flow-rack OPS.

A bucket brigade OPS can cause a delay in two ways (Bartholdi and Eisenstein 1996a). First, when a downstream picker approaches an upstream picker to take over a new tote, the downstream picker has to wait until the upstream picker completes the pick and releases the tote. This is termed hand-off delay. Second, if an upstream picker attempts to move forward to the next pick face already occupied by a busy downstream picker, the upstream picker cannot transfer, or hand off the current tote to the downstream picker, since the downstream picker is still picking. Also, the upstream picker cannot pass the downstream picker, because the pickers’ sequence in the zone must be maintained. The delay of the upstream picker is termed picker blocking. See Hong et al. (2015) for further details on picker blocking.

3.2 The hand-off delay

To identify the hand-off delay of a downstream picker, we consider a hand-off case during picking and extend it into a hand-off case during walking. First, we assume a bucket brigade order picking case of two pickers in an F pick face system with finite walk speed in both forward and backward directions as shown in Fig. 2. The X-axis represents the location of pickers in a pick face number and the Y-axis traces the time per picker event. The upstream picker arrives at time t ₁ , starts a pick at pick face f − 1, and plans to pick batches during t ₃ − t ₁ . The downstream picker arrives at time t ₂ to take over a new tote, which is after t ₁ and before t ₃ . The downstream picker cannot move backward because the upstream picker occupies pick face f − 1. The occurring hand-off delay |t ₄  − t ₂ | is the time gap until the idle downstream picker obtains a new tote from the upstream picker, who is not yet ready, even though the downstream picker is waiting. After completing the picking, the upstream picker hands over the tote to the downstream picker. Because the pick face is not wide enough to accommodate the two pickers, the upstream picker conducts the hand-over without entering into pick face f.

Fig. 2

A spatial and temporal trajectory of two pickers and their hand-off operations when an upstream picker is picking

Observation 1

A hand-off delay occurs when a downstream picker arrives, but the upstream picker is still picking.

Second, because the picker’s walk speed is not infinite, i.e., the travel time between neighboring pick faces is not instantaneous as shown in Fig. 3, the downstream picker stays idle even though the upstream picker is walking in a neighboring pick face. In this case, which resembles a “first come first served” rule, if any picker enters a pick face, no other picker can enter the same pick face. For example, if an upstream picker leaves pick face f − 2 and decides to go to pick face f − 1 at time t ₅ , a downstream picker could arrive at pick face f at time t ₆ , which is later than t ₅ , but before the upstream picker’s arrival at pick face f − 1. Since the downstream picker cannot move to pick face f − 1 due to the upstream picker, the downstream picker stays idle to take over the tote until the upstream picker completes the forward walk. The upstream picker completes the walk at time t ₇ . If there is no additional pick, the upstream picker hands over the tote to the downstream picker. The downstream picker’s hand-off delay is |t ₇  − t ₆ |, but if the upstream picker continues a pick operation, the downstream picker’s waiting time becomes |t ₉  − t ₆ |.

Fig. 3

A spatial and temporal trajectory of two pickers when an upstream picker is walking

Observation 2

A hand-off delay occurs when a returning downstream picker meets an upstream picker who is still finishing a forward walk along a pick face. The hand-off delay lasts only if the upstream picker does not continue any pick, or the hand-off delay lasts as long as the upstream picker continues a pick (pick duration).

Observations 1 and 2 show hand-off situations under finite pick and walk times. The hand-offs occur when an upstream picker is picking and walking and the completion time of the picking and walking operations is not synchronized with the downstream picker’s readiness. Accordingly, the hand-off delay occurs when any picker (except the first one) takes over a tote from the previous picker. We analyze a hand-off delay model for a bucket brigade OPS with flow-rack shelving, i.e., hand-off delay (HD), with a variation of pick times and a finite walk speed. Pickers are numbered from 1 to PK from upstream to downstream. The hand-off delay occurs over 2 to PK pickers. We obtain the expected hand-off delay of one picker at a stop (E[HD]). We develop an analytical model for hand-off delays in a bucket brigade OPS of one picker when the pick time is non-deterministic and the forward walk time is non-instantaneous including infinite walk speed. Here, we consider only the downstream picker’s hand-off delay.

4 Analytical model

In this section, we develop an analytical model to quantify the hand-off delay between two neighboring pickers, which is a managerial concern. We identify a renewal process model to explain the hand-off operation between the two pickers.

4.1 Assumptions

Consider a discrete bucket brigade order picking system with F pick faces and the order picking scenarios (Fig. 4) defined in Hong et al. (2016). Assume two pickers have the same capability and a new order is ready when the most upstream picker requests a new one. The loading station is located at a 0.5 unit distance before pick face 1 and the unloading station is at a 0.5 distance after pick face F. Only one picker at a time can occupy a pick face. If a picker, i.e., tote, enters a pick face and occupies a part of the pick face, the other picker yields the pick face to the picker who reserves the location first. The bucket brigade protocol requires that pickers maintain exactly one order without any other buffer. Let ft denote the time to walk forward to a pick face, and let bt denote the time to walk backward from a pick face. A picker decides to pick one item at a pick face with probability p, or directly walk to the next pick face with probability 1 − p. The duration of each pick is denoted by τ. After a pick with duration τ, the picker repeats the same decision at the same pick face, i.e, pick with probability p or walk with probability 1 − p, while the cumulative number of picks at a stop is smaller than m. Note that if the total number of picks at a pick face reaches to m, i.e., an upper bound of the number of picks at a stop, the picker walks to the next pick face without any additional pick trial. See (Parikh and Meller 2009,2010) for details. For simplification, assume τ = 1 if there is no explanation. If the number of picks is i, then the pick time duration becomes τ·i = 1·i = i. A hand-off operation is required when two pickers occupy two pick faces f and f + 1 and the downstream picker is ready for a take-over. The picker hands the tote to the downstream picker and the switch (hand-off) time is ht. See Fig. 4.

Fig. 4

Order picking scenario with two pickers in F pick faces with the maximal number of picks = m

A picker starts a trip by taking one tote from a loading station or from the upstream picker. After taking over the new tote, the picker begins retrieving an item (s) or moves to the next pick face. A hand-off delay occurs when the upstream picker is not ready to release the current tote and the downstream picker has to stand idle to take over a new tote. The two pickers switch (i.e., hand off) a tote to continue the picking operation. The hand-off delay can be expressed by an expected remaining pick time of the upstream picker. Because the downstream picker’s arrival occurs randomly after releasing the previous tote and the upstream picker picks continuously, the duration becomes the expected remaining renewal time of the pick. Unlike the blocking delay, the hand-off delay occurs at the time the downstream picker takes over a new tote from the upstream picker. Note that blocking delay also occurs when two pickers are in a neighboring pick face and each picker is fulfilling an order. See Hong et al. 2015, Hong 2014 for the details.

4.2 Elementary models of hand-off delays

There are three hand-off delay situations: (1) hand-off delay during picking, (2) hand-off delay during walking, and (3) hand-off delay during walking-then-picking.

• i. hand-off delay during pick duration

A downstream picker confronts the upstream picker during picking. To calculate the expected hand-off delay during picking (HD _p ), we assume that both forward and backward walk speeds are infinite and denote the pick time at a pick as random variable PT. We know that picks are randomly and evenly distributed per pick face with pick time PT. It takes PT pick time for an upstream picker to complete picks at a pick face. The resulting hand-off delay is expressed by W time such that the downstream picker waits for W to take over a new tote. The locations of the two pickers are pick faces f − 1 and f, where f ≤ F. Passing is prohibited in both forward and backward directions.

In Fig. 5 we project PT, S, and W on a renewal process. In other words, PT ₁ , PT ₂ , PT ₃ ,… become inter-completion times between stops. From the inter-completion times, we obtain the arrival process of the upstream picker. The sequence, A ₁ , A ₂ ,…, represents the specific times when the upstream picker completes the retrieval operation at 1st stop (PT ₁ ), the retrieval operation at 2nd stop (PT ₂ ), …. The downstream picker takes over a batch from the upstream picker recursively. Here, the sequence, S ₁ , S ₂ , S ₃ ,… is the arrival time for the downstream picker to take over a tote from the upstream picker at the upstream picker’s next pick face. Denoting the waiting time of the downstream picker for each arrival by W ₁ , W ₂ , W ₃ ,…, the waiting time for jth hand-off (W _j ) becomes A _i  − S _j , where A _i stands for the completion time of pick(s) at ith stop of the upstream picker. This is the well-known excess-time model of a renewal process in Ross (2010). Thus, the expected waiting time of the downstream picker (E[W]) is E[PT²]/2E[PT] when pickers return randomly and walk speeds are infinite, as derived in “Detailed calculation of the expected waiting time (E[W])” section of Appendix. We obtain the expression of the expected hand-off delay as follows:

Fig. 5

A projection of a hand-off during picking on a renewal process

Theorem 1

When a downstream picker returns and meets an upstream picker who is picking, the expected waiting time of the downstream picker (E[HD _p ]) is

$$ E[HD_{p} ] = \frac{{E\left[ {PT^{2} } \right]}}{{2 \cdot E\left[ {PT} \right]}} = \frac{p + 1}{2(1 - p)} - \frac{{m \cdot p^{m} }}{{(1 - p^{m} )}} $$

(1)

(see “Proof of Theorem 1” section in Appendix for details).

Theorem 1 asserts that the hand-off delay relates to the magnitude and the variation of pick time over the maximal expected number of picks per pick face m. When there is no effect by the walk time, the hand-off delay comes from the variation of pick time as well as the magnitude of the pick time. However, in practice, the walk time, which is evidently shorter than pick time, could offset the impacts by the variation of pick time.

• ii. hand-off delay during walking only

In Fig. 6 the upstream picker makes stops 1, 2,… for picks whenever passing one pick face. Each stop can spend one unit forward walk time ft. FT ₁ , FT ₂ , FT ₃ ,… denote the time spent by the upstream picker until the upstream picker completes a trip to pass a pick face at a stop. The mean of the inter-completion times {FT ₁ , FT ₂ , FT ₃ ,…} is E[FT] = ft and is equivalent to the average walk time per stop, whereas the hand-off delay occurs on randomly chosen W at time S and its duration is assumed as W. The hand-off occurs at time S ₁ , S ₂ , S ₃ …, and each hand-off delay persists during W ₁ , W ₂ , W ₃ ,….

Fig. 6

A projection of a hand-off on a renewal process (walking case)

We also use Theorem 1. The negligible walk time assumption holds for the backward direction above. To obtain the expected hand-off delay during walking only (HD _wo ), we repeat the previous procedure. E[FT] = ft and E[FT²] = Var[FT] + E[FT]² = 0 + ft² = ft². Thus, we calculate the expected hand-off delay for walking only. Then,

$$ E[HD_{wo} ] = \frac{{E\left[ {FT^{2} } \right]}}{{2 \cdot E\left[ {FT} \right]}} = \frac{{ft^{2} }}{2ft} = \frac{ft}{2} $$

(2)

• iii. hand-off delay during walking-then-picking

The downstream picker is already under the hand-off delay by the upstream picker’s walking; thus, the expected length of the hand-off delay lags as much as the expected picking time. We define this hand-off delay as a hand-off delay during walking-then-picking (HD _wp ). The expected hand-off delay during walking-then-picking (E[HD _wp ] becomes

$$ \begin{aligned} E[HD_{wp} ] & = E[HD_{wo} ] + E[PT] \\ & = \frac{ft}{2} + \sum\limits_{i = 1}^{m} {p^{i} } = \frac{ft}{2} + \frac{{p(1 - p^{m} )}}{(1 - p)} \\ \end{aligned} $$

(3)

4.3 Expected duration of hand-off delay per occurrence

Since only one picker can occupy one single pick face regardless of picks or walks at the pick face, hand-offs occur at a boundary of neighboring pick faces after each picker completes the walk at each pick face. Assume that backward walk speed (empty travel walking speed) is infinite (bt = 0), similar to Bartholdi and Eisenstein (1996a), and the upstream picker’s forward walk time is still finite.

There are two initiation cases of the hand-off delay: 1) the downstream picker arrives when the upstream picker is picking (HD _p ), and 2) the downstream picker arrives when the upstream picker is walking (HD _w ). We condition on the arrival of the downstream picker to calculate the expected hand-off delay (HD) as follows:

$$ E\left[ {HD} \right] \, = E\left[ {HD_{p} } \right]\; \cdot \;P\left( {HD_{p} } \right) \, + E\left[ {HD_{w} } \right]\; \cdot \;P\left( {HD_{w} } \right). $$

(4)

When the downstream picker returns for a new tote, the status of the upstream picker is either pick, or walk. Since we apply the pick time as E[PT], each probability becomes:

$$ P(HD_{p} ) = \frac{E[PT]}{E[PT] + E[FT]} = \frac{{\sum\nolimits_{i = 1}^{m} {p^{i} } }}{{\sum\nolimits_{i = 1}^{m} {p^{i} } + ft}} $$

(5)

$$ P(HD_{w} ) = \frac{E[FT]}{E[PT] + E[FT]} = \frac{ft}{{\sum\nolimits_{i = 1}^{m} {p^{i} } + ft}} $$

(6)

We already obtain E[HD _p ] in Eq. (1). Last, the expected hand-off delay during walking (HD _w ) is the hand-off delay during walking plus the hand-off delay during walking-then-picking, which are conditioned on pick probability p.

$$ E\left[ {HD_{w} } \right] \, = P\left( {HD_{wp} } \right)E\left[ {HD_{wp} } \right] \, + P\left( {HD_{wo} } \right)E\left[ {HD_{wo} } \right]. $$

(7)

Given that the downstream picker experiences a walking hand-off delay, the downstream picker would experience a walking-then-picking hand-off delay if the upstream picker decides to continue a pick with probability p. Otherwise, the downstream picker would experience only the walking hand-off delay. Thus, P(HD _wp ) = p and P(HD _wo ) = 1 − p. Finally, E[HD _w ] becomes (see “Calculation of Eq. (8)” section in Appendix for details)

$$ \begin{aligned} E[HD_{w} ] & = p\left( {E[PT] + \frac{{E[FT^{2} ]}}{2E[FT]}} \right) + (1 - p)\frac{{E[FT^{2} ]}}{2E[FT]} \\ & = p\left( {\frac{{p(1 - p^{m} )}}{(1 - p)} + \frac{ft}{2}} \right) + (1 - p)\left( {\frac{ft}{2}} \right) \\ \end{aligned} $$

(8)

In this case the expected delay time per hand-off occurrence and the expected delay time per order are derived. We obtain the expected hand-off delay as (see “Calculation of Eq. (9)” section in Appendix for details):

$$ \begin{aligned} E[HD] & = E\left[ {HD_{p} } \right]\frac{E[PT]}{E[PT] + E[FT]} + E\left[ {HD_{w} } \right]\frac{E[FT]}{E[PT] + E[FT]} \\ & = \left[ {\frac{p + 1}{2(1 - p)} - \frac{{m \cdot p^{m} }}{{(1 - p^{m} )}}} \right]\frac{{p(1 - p^{m} )}}{{p(1 - p^{m} ) + ft\left( {1 - p} \right)}} + \frac{ft}{2}\frac{{p^{2} (1 - p^{m} ) + ft(1 - p)}}{{p(1 - p^{m} ) + ft\left( {1 - p} \right)}} \\ \end{aligned} $$

(9)

4.4 Validation

This section compares the simulation and analytical results of a validation experiment. Table 1 summarizes the simulation results validating the analytical models over a two-picker-order picking case in a 50 pick faces system with ft = 0.1 and bt = inf, where we set inf to 0.0005 s per unit distance according to the simulation’s best accuracy. The results of the simulation models include m = inf, 5, and 1. The comparison gap from the analytical models ranges from − 7.1 to 3.6%, where Gap % = (the time delayed by the analytical model – the time delay by the simulation model)/(the time blocked by the analytical model) × 100. When m = 1, the large gaps are due to the small amount of the value.

Table 1 Comparison of simulation and analytical results with ft = 0.1 and bt = inf

Figure 7 depicts the time delayed per occurrence over the maximal number of picks m across pick density p. We consider five different cases of m. Basically, when pick density is practical (less than 0.5), the gaps between impacts by m are very small, whereas when pick density is very dense (more than 0.9), the magnitude of m has a strong impact on the hand-off delay.

Fig. 7

Hand-off delay per occurrence over the maximal number of picks m (2 pickers, ft = 0.2)

5 Numerical analysis

This section explains the effects of operational environments on hand-off delays using the analytical model identified. From the analytical model we continue the numerical analyses with Eq. (9). Note that our simulation validation also confirms our analytical results below.

5.1 Limiting property on pick density

We analyze the impacts of sufficiently low and sufficiently high pick density conditions. The lower number of picks may reduce the hand-off delay of a downstream picker. Theorem 2 shows that under sufficiently low pick density, the downstream picker still experiences a hand-off delay from the upstream picker’s walking time, which amounts to ft/2. In other word, when pickers are only traveling, a hand-off delay is inevitable because the hand-off is available at the boundary location between neighboring pick faces.

Theorem 2

The expected hand-off delay (E[HD]) converges to ft/2 when p goes to 0.

Proof

From Eq. (9),

$$ \begin{aligned} & \mathop {\lim }\limits_{p \to 0} E[HD] \\ & = \mathop {\lim }\limits_{p \to 0} \left[ {\left[ {\frac{p + 1}{2(1 - p)} - \frac{{m \cdot p^{m} }}{{(1 - p^{m} )}}} \right]\frac{{p(1 - p^{m} )}}{{p(1 - p^{m} ) + ft\left( {1 - p} \right)}} + \frac{ft}{2}\frac{{p^{2} (1 - p^{m} ) + ft(1 - p)}}{{p(1 - p^{m} ) + ft\left( {1 - p} \right)}}} \right] \\ & = 0 + \frac{ft}{2}\frac{0 + ft}{0 + ft} = \frac{ft}{2} \\ \end{aligned} $$

(10)

□

Under very high pick density, as the work load increases and pick density p goes to 1, the average pick time converges to m. The average hand-off delay also converges to (m + ft)/2. Here, the convergence to m represents the average pick time at a stop since we assume a unit pick time of 1, i.e., the pick time becomes invariant and stable per pick face. Consistently, the walk time is valid as ft. The hand-off delay amounts to half of the sum of the expected pick time and walk time at the pick face.

Theorem 3

The expected hand-off delay (E[HD]) converges to (m + ft)/2 when p goes to 1.

(See “Proof of Theorem 3” in Appendix for details.)

Both states p = 0 and 1 mean that there is no variation of pick time; thus, hand-off delays converge to ft/2 and (m + ft)/2 as the average values of pick times and walk times.

5.2 Pick time variation

The pick time at a stop could vary due to pick capability, item weight, shelf height, etc. To clarify the impacts by the pick time variation, we consider different pick time distributions. The hand-off delay per occurrence consists of the expected pick time and the variance normalized by the pick time. From Eq. (9), we formulate the hand-off delay as a function of the magnitude and variable of pick time (see “General distributions and calculation steps of Eq. (11)” section in Appendix for details):

$$ \begin{aligned} E[HD] & = \frac{{E[PT^{2} ]}}{2E[PT]}\frac{E[PT]}{E[PT] + E[FT]} + \left[ {p\left( {E[PT] + \frac{{E[FT^{2} ]}}{2E[FT]}} \right) + (1 - p)\frac{{E[FT^{2} ]}}{2E[FT]}} \right]\frac{E[FT]}{E[PT] + E[FT]} \\ & = \left[ {\frac{E[PT]}{2} + \frac{Var[PT]}{2E[PT]}} \right]\frac{E[PT]}{E[PT] + E[FT]} + \left[ {p\left( {E[PT] + \frac{E[FT]}{2}} \right) + (1 - p)\frac{E[FT]}{2}} \right]\frac{E[FT]}{E[PT] + E[FT]} \\ \end{aligned} . $$

(11)

The derivation shows that both magnitude and variance of pick times affect the hand-off delay. The hand-off delay model in Eq. (9) is based on the fact that the hand-off delay relates to the magnitude and the variation of pick time over the maximal expected number of picks per pick face m.

To clarify the impact by the variation of pick time on the hand-off delay, we use regular pick time distributions instead of the discrete random pick time limited by the maximal number of pick m. We conduct a numerical analysis over three pick time distributions: Unif = uniform [min,max] = [0.0, 2.0]; Tri = triangular [min, mode, max] = [0.5, 1.0, 1.5]; and Exp = exponential [mean] = [1.0], where the time unit represents the time spent to retrieve an item. The expected hand-off delay models of p, ft, and F over distributions are derived in “General distributions and calculation steps” section of Appendix and the results are shown in Fig. 8. As Theorem 1 and the derivation above demonstrate, the high variation of pick time increases the hand-off delay.

Fig. 8

Hand-off delay trends over four different pick time distributions with the same average pick time (2 pickers, ft = 0.2, E[PT] = 1)

Fig. 9

Time delay results over upstream picker’s capability (2 pickers, ft = 0.2, m = 5)

Fig. 10

Time delay results over upstream walk time capability (2 pickers, m = 5)

Fig. 11

Simulation results over different numbers of pickers (ft = 0.2, m = 5)

5.3 Picker capability

Warehouse managers want to improve both OPS throughput and picker capabilities. Interviews with warehouse managers revealed that picker’s capability gap is a significant issue for higher OPS throughput, i.e., most newly hired pickers are less skilled in searching for items and require more picking time than experienced pickers. Pickers’ skills can range from 0.5 to 1.5 time to pick the same item, which is similar to Bartholdi and Eisenstein (1996a).

The hand-off operation is interconnected with the upstream pickers. Since most managers prefer slowest-to-fastest picker ordering, we conduct a simulation test to determine the impact of skill difference and slowest-to-fastest ordering. Management’s other major concern, congestion in order picking, is beyond the scope of this study.

We set the upstream picker’s picking capability as 1.4, 1.2, 1.0, 0.8, and 0.6 unit time per pick. Pick capability and pick difference both have equally strong impacts on hand-off delay. We know that slowest-to-fastest ordering performs best in bucket brigade order picking, but when hand-off delay is large compared to blocking delay, the sequence should be reversed. We also know that since blocking delay is of more concern in a regular-order picking, managers tend to assign beginners to packing or other tasks at the end of an order fulfillment (Fig. 9).

5.4 Forward walk time

The walk ratio per pick time may change in order picking situations. We use 0.5 to 0.01 as the slow to fast walk speed (Gue et al. 2006). If the walk time between two pick faces is longer, the opportunity to hand off while walking increases. Thus, duration and hand-off delay per occurrence increases. However, the hand-off duration per trip can decrease as walk speed slows. As p goes to 0, the hand-off delay converges to ft/2, then 0.25, 0.1, 0.05, 0.025 (Eq. (10), Theorem 2), and 0.005. As p goes to 1, the hand-off delay converges to (m + ft)/2 as 2.75, 2.60, 2.55, 2.525, and 2.505 (Theorem 3) (Fig. 10).

6 Simulation analysis

6.1 Simulation environments

We conduct a simulation study to investigate the effect of multiple pickers and their skill gaps on hand-off delay. As shown in Table 2, we use an order picking profile based on Bartholdi and Eisenstein (1996b), Koo (2009) to evaluate the proposed procedure. We conduct our simulation experiment on the Tecnomatix Plant Simulation 12. The base case has 100 pick faces and five pickers. A picker performs with ft = 0.1 and bt = 0.05. We assume a new batch is ready when the most upstream picker requests a new one and the most downstream picker returns after unloading a completed batch during uniform [0,1] unit time. The multiple-picker scenario has 100 pick faces and two to five pickers. The skill difference scenario, which relaxes the equal skill assumption, differentiates picking capabilities across the five pickers; the times per pick are 1.2, 1.1, 1.0, 0.9, and 0.8. We consider both slowest-to-fastest ordering and fastest-to-slowest ordering.

Table 2 Summary of experimental picking environments

6.2 Impacts of number of pickers

To improve throughput, warehouse managers add more pickers. Increasing the number of pickers in the OPS, i.e, the comparison between two, three, four, and five pickers in the same size OPS, tends to result in a shorter hand-off delay per occurrence as shown in Fig. 11, and produces a higher-order picking throughput. However, the number of hand-offs per trip increases as much as the number of pickers minus 1. Our simulation model shows that while adding more pickers increases the total amount of hand-off delay per trip, hand-off delay per occurrence continuously decreases as more pickers are assigned.

6.3 Impacts of skill difference

The hand-off operation of a picker is correlated with the upstream pickers’ pick and walk durations. The bucket brigade literature prefers slowest-to-fastest picker ordering for higher throughput (Bartholdi and Eisenstein 1996a, 1996b). Since most managers prefer slowest-to-fastest ordering, we conduct a simulation test to determine the impact of skill difference and slowest-to-fastest ordering. Again, the managerial concern, congestion in order picking, is beyond the scope of this study (Fig. 12).

Fig. 12

Time delay per occurrence over picker capability and assignment (5 pickers, 100 pick faces, 5 picks per stop): a simulation result and b analytical model

In a bucket brigade OPS, there are PK pickers. Thus, we extend the model. The expected hand-off delay per batch is determined by the picking capability of pickers 1 to PK − 1. When there are PK number of pickers, the hand-off delay per batch is:

$$ \sum\limits_{k = 1}^{PK - 1} {E[HD_{k} ]} = \sum\limits_{k = 1}^{PK - 1} {\left[ {\frac{{E[PT_{k}^{2} ]}}{{2E[PT_{k} ]}}\frac{{E[PT_{k} ]}}{{E[PT_{k} ] + E[FT]}} + \left[ {p\left( {E[PT_{k} ] + \frac{E[FT]}{2}} \right) + (1 - p)\frac{E[FT]}{2}} \right]\frac{E[FT]}{{E[PT_{k} ] + E[FT]}}} \right]} $$

Note that PK − 1 pickers are associated with the hand-offs for a batch and there is no hand-off for the first picker. Thus, slowest-to-fastest ordering by management could experience more hand-off delay and result in throughput drop if blocking delay does not offset the reduction in hand-off delay.

7 Conclusions

This paper has contributed to the analysis and understanding of the hand-off delay in bucket brigade order picking as follows. First, analytical models of hand-off delay in a bucket brigade OPS were developed. Second, based on numerical analysis, the limiting properties of hand-off delay over pick density, magnitude, variance of pick time, and forward walk time were identified. Third, additional simulation studies identified the conditions required for more efficient operations.

The analytical model quantified the delays related to hand-offs by extending the analogy of an excess-time renewal model to a bucket brigade OPS. The analytical results found that the reduction in variability of pick time reduced hand-off delay. Notably, hand-off delays occupied a larger portion of the throughput as the increase in the instability of pick time. We concluded that this type of hand-off delay required consistent and careful management of upstream pickers. In fact, the slowest-to-fastest picker ordering widely used by management could increase hand-off delay. The resulting gap is the difference between the slowest and fastest pickers’ capabilities.

To avoid the stock out due to fluctuations in production, management can add more inventory between processes, which is called the safety stock (Hopp and Spearman 2008). Incomplete picking by upstream pickers before the arrival of the downstream pickers results in an immediate shortage of a batch and incurs the hand-off delays of downstream pickers. In this case, management prevents much of the hand-off delay with an additional level of the work-in-process. Our analytical model confirms that the uncertainty of the hand-off delay from the variability of pick time requires the increase in the work-in-process, which lengthens the order picking lead times, but gains a higher throughput.

Based on our findings, we suggest two future research avenues: developing an integrated throughput model, and controlling hand-off delays. Since hand-off delay is tightly coupled with blocking delay and walk time, we prefer an integrated approach such as the blocking model in Hong et al. (2015). A new approach to reduce hand-off delays without hurting the responsiveness of order picking will remain challenging as variability increases because manufacturing and service have different operational properties.

Appendix

1.1 The interdependency in the hand-off location and the hand-off delay

Let X _i be the ith hand-off. Then, we evaluate the interdependency in the hand-off location and the hand-off delay. We conduct a simulation to observe the hand-off location and the hand-off delay between ith hand-off and i + 1st hand-off. Figure 13 shows the scatter plot of ith hand-off and the i + 1st hand-off. Figure 13a indicates the correlation between the hand-off locations, which is about − 0.47 correlation value. The correlation coefficient is relatively high as shown in the scatter plot comparison. Vice versa, in the scatter plot of the hand-off delay between ith hand-off and i + 1st hand-off, we look for a clear linear trend, which is close to a relative randomness. The correlation coefficient appears smaller than 0.1.

Fig. 13

Scatter plot of X _i and X_i+1 in n = 50, p = 0.1, m = 10, and unit pick time. a Hand-off location b hand-off delay

The autocorrelation analysis in Fig. 14 generalizes the result above. In Fig. 14a, the autocorrelation analysis of the hand-off location shows relatively high autocorrelation values and patterns over the increase in lags. However, in Fig. 14b, the autocorrelation analysis of the hand-off delay shows smaller values and it appears that there is little likelihood of dependence between delays.

Fig. 14

Autocorrelation plot over lags in n = 50, p = 0.1, and unit pick time. a Hand-off location b hand-off delay

An experiment over larger p and other pick time distribution in Figs. 15 and 16 confirms the observations. We consider an exponential pick time situation with higher pick probability. The similar results repeat over the hand-off locations and the hand-off delay. Consistently, the scatter plots and autocorrelation plots show a relatively high dependency in the hand-off location and a relatively high randomness in the hand-off delay.

Fig. 15

Scatter plot of X _i and X_i+1 in n = 50, p = 0.5, m = 1, and exp(1) pick time a hand-off location b hand-off delay

Fig. 16

Autocorrelation plot over lags in n = 50, p = 0.1, m = 1, and Exp(1.0) pick time. a Hand-off location b hand-off delay

In conclusion, the dependency in the hand-off location does not affect the hand-off delay under the stochastic pick time and the finite walk time. Intuitively, hand-off locations “remember” their last hand-offs while the arrival times of downstream pickers do not repeat the previous hand-off times in the stochastic picking.

1.2 Detailed calculation of the expected waiting time (E[W])

Excess-time model The expected waiting time (E[W]) is E[PT²]/2E[PT] when pickers return randomly, the walk speed is infinite, and there is no blocking delay.

Proof

The renewal process is derived based on the definition in Ross (2010). It follows that there is a renewal process {N(t), t ≥ 0} having inter-arrival times PT _n , n ≥ 1, and assuming a hand-off when a downstream picker meets an upstream picker. We assume the hand-off to be a reward. We define W(t) to equal the time from t until the next stop, a renewal, and, as such, it represents the remaining (residual or excess) life of the pick at time t. Over the renewal process {PT(t), t ≥ 0}, we measure the time of W(t) as the excess time Y(t) = A_n+1(t) – t.

Then, according to the renewal reward process (Ross 2010), the time to completion at time t is the time from t until the next renewal and becomes the remaining time to completion at time t. We assume the new waiting time t ₀ be a reward during a renewal cycle. We write the average value of the excess as,

$$ \begin{aligned} E\left[ W \right] & \equiv \mathop {\lim }\limits_{s \to \infty } \frac{{\int_{0}^{s} {W(t){\text{d}}t} }}{s} = \frac{{E\left[ {{\text{ Reward}}\;{\text{during}}\;{\text{a}}\;{\text{renewal}}\;{\text{cycle }}} \right]}}{{E\left[ {{\text{ Time}}\;{\text{of}}\;{\text{a}}\;{\text{renewal}}\;{\text{cycle}}} \right]}} \\ & = \frac{{E\left[ {{\text{ Hand - off delay}}\;{\text{during}}\;{\text{a}}\;{\text{stop }}} \right]}}{{E\left[ {{\text{ Pick}}\;{\text{time}}\;{\text{of}}\;{\text{a}}\;{\text{stop}}} \right]}} \\ \end{aligned} $$

In addition, over the given cycle length PT, we obtain the following expected value,

$$ \begin{aligned} E\left[ {{\text{Hand - off}}\;{\text{delay}}\;{\text{during}}\;{\text{a}}\;{\text{stop}}} \right] & = E\left[ {\int_{0}^{PT} {W(t) \cdot {\text{d}}t} } \right] \\ & = E\left[ {\int_{0}^{PT} {\left( {PT - t} \right) \cdot {\text{d}}t} } \right] \, \\ \end{aligned} $$

The expectation for the overall PT ranges from 0 to infinite and PT has a distribution F,

$$ \begin{aligned} E\left[ {\int_{0}^{PT} {\left( {PT - t} \right) \cdot {\text{d}}t} } \right] & = E\left[ {\int_{0}^{PT} {\left( {PT - t} \right) \cdot {\text{d}}t} } \right] = E\left[ {\left. {\left( {PTt - \frac{{t^{2} }}{2}} \right)} \right|_{0}^{PT} } \right] = E\left[ {\frac{{PT^{2} }}{2}} \right] \\ & = \frac{{E\left[ {PT^{2} } \right]}}{2} \\ \end{aligned} $$

where $\, E\left[ {\int_{0}^{X} {\left( {X - t} \right) \cdot {\text{d}}t} } \right] \, = \, \int_{0}^{\infty } {\int_{0}^{X} {\left( {X - t} \right) \cdot {\text{d}}t} \cdot {\text{d}}F\left( X \right)}$.

The time of a pick cycle is an inter-arrival time between the picks having the distribution function F. Then, $E\left[ {{\text{Pick}}\;{\text{time}}\;{\text{of}}\;{\text{a}}\;{\text{stop}}} \right] = E\left[ {PT} \right]$.

Thus, we express the expected waiting time (E[W]) as,

$$ E[W] = \frac{{E\left[ {{\text{Hand - off}}\;{\text{delay}}\;{\text{during}}\;{\text{a}}\;{\text{stop}}} \right]}}{{E\left[ {{\text{Pick}}\;{\text{time}}\;{\text{of}}\;{\text{a}}\;{\text{stop}}} \right]}} = \frac{{E\left[ {PT^{2} } \right]}}{{2 \cdot E\left[ {PT} \right]}} $$

□.

1.3 Proof of Theorem 1

When a downstream picker returns randomly and meets an upstream picker who is picking, the expected waiting time of the downstream picker (E[HD _p ]) is

$$ E[HD_{p} ] = \frac{{E\left[ {PT^{2} } \right]}}{{2 \cdot E\left[ {PT} \right]}} = \frac{p + 1}{2(1 - p)} - \frac{{m \cdot p^{m} }}{{(1 - p^{m} )}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (1) $$

Proof

The expected delay time per hand-off occurrence (HD _p ) is derived when an upstream picker is picking by replacing W with HD _p in Fig. 5. First, we estimate E[PT]. Given these pick and walk decision patterns, the expected pick time as a stop (PT) is equal to the expected number of picks at a pick face · unit pick time (τ) = the expected number of picks at a pick face. Formulate E[PT] as:

$$ \begin{aligned} E[PT] & = pq + 2p^{2} q + 3p^{3} q + \cdots + (m - 1)p^{m - 1} q + mp^{m} \\ & = p(1 - p) + 2p^{2} (1 - p) + 3p^{3} (1 - p) + \cdots + (m - 1)p^{m - 1} (1 - p) + mp^{m} \\ & = p + ( - p^{2} + 2p^{2} ) + ( - 2p^{3} + 3p^{3} ) + \cdots + ( - (m - 1)p^{m} + mp^{m} ) \\ & = p + p^{2} + p^{3} + \cdots + p^{m - 1} + p^{m} \\ & = \sum\limits_{i = 1}^{m} {p^{i} } = \frac{{p(1 - p^{m} )}}{(1 - p)}. \\ \end{aligned} $$

(12)

Second, E[PT²] becomes

$$ \begin{aligned} E[PT^{2} ] & = \sum\limits_{i = 1}^{m} {i^{2} p^{i} q} \\ & = pq + 2^{2} p^{2} q + 3^{2} p^{3} q + \cdots + (m - 1)^{2} p^{m - 1} q + m^{2} p^{m} \\ & = p(1 - p) + 2^{2} p^{2} (1 - p) + 3^{2} p^{3} (1 - p) + \cdots + (m - 1)^{2} p^{m - 1} (1 - p) + m^{2} p^{m} \\ & = (p - p^{2} ) + (2^{2} p^{2} - 2^{2} p^{3} ) + \cdots + ((m - 1)^{2} p^{m - 1} - (m - 1)^{2} p^{m} ) + mp^{m} \\ & = p + ( - p^{2} + 2^{2} p^{2} ) + ( - 2^{2} p^{3} + 3^{2} p^{3} ) + \cdots + ( - (m - 1)^{2} p^{m} ) + m^{2} p^{m} ) \\ & = \sum\limits_{i = 1}^{m} {(2i - 1)p^{i} } = 2\sum\limits_{i = 1}^{m} {i \cdot p^{i} } - \sum\limits_{i = 1}^{m} {p^{i} } \\ & = \frac{2}{1 - p}\left[ {\frac{{p(1 - p^{m} )}}{(1 - p)} - m \cdot p^{m + 1} } \right] - \frac{{p(1 - p^{m} )}}{(1 - p)} \\ & = \frac{{p(1 - p^{m} )(p + 1)}}{{(1 - p)^{2} }} - \frac{{2m \cdot p^{m + 1} }}{(1 - p)}. \\ \end{aligned} $$

(13)

Finally, we obtain the expected hand-off delay during picking(HD _p ) as

$$ \begin{aligned} E[HD_{p} ] & = \frac{{E\left[ {PT^{2} } \right]}}{{2 \cdot E\left[ {PT} \right]}}\quad \quad \quad \quad \quad {\text{from }}\left( {12} \right)\;{\text{and}}\;\left( {13} \right) \\ & = \frac{{\frac{{p(1 - p^{m} )(p + 1)}}{{(1 - p)^{2} }} - \frac{{2m \cdot p^{m + 1} }}{(1 - p)}}}{{2\frac{{p(1 - p^{m} )}}{(1 - p)}}} \\ & = \frac{p + 1}{2(1 - p)} - \frac{{m \cdot p^{m} }}{{(1 - p^{m} )}} \\ \end{aligned} $$

□.

1.4 Calculation of Eq. (8)

E[HD _w ] becomes

$$ \begin{aligned} E[HD_{w} ] & = p\left( {E[PT] + \frac{{E[FT^{2} ]}}{2E[FT]}} \right) + (1 - p)\frac{{E[FT^{2} ]}}{2E[FT]} \\ & = p\left( {\sum\limits_{i = 1}^{m} {p^{i} } + \frac{ft}{2}} \right) + (1 - p)\left( {\frac{ft}{2}} \right)\quad \quad \quad \quad {\text{from}}\;\left( {12} \right),E\left[ {FT} \right] \, = ft,\;{\text{and}}\;E\left[ {FT^{2} } \right] \, = ft^{2} \\ & = p\left( {\frac{{p(1 - p^{m} )}}{(1 - p)} + \frac{ft}{2}} \right) + (1 - p)\left( {\frac{ft}{2}} \right) \\ \end{aligned} $$

1.5 Calculation of Eq. (9)

The expected delay time per hand-off occurrence and the expected delay time per order are derived when there are instantaneous walk times, a large number of picks, and no picker blocking. Obtain the expected hand-off delay as

$$ \begin{aligned} E[HD] & = E\left[ {HD_{p} } \right]\frac{E[PT]}{E[PT] + E[FT]} + E\left[ {HD_{w} } \right]\frac{E[FT]}{E[PT] + E[FT]} \\ &= \left[ {\frac{p + 1}{2(1 - p)} - \frac{{m \cdot p^{m} }}{{(1 - p^{m} )}}} \right]\frac{{\frac{{p(1 - p^{m} )}}{1 - p}}}{{\frac{{p(1 - p^{m} )}}{1 - p} + ft}} + \left[ {\frac{{p^{2} (1 - p^{m} ) + ft(1 - p)}}{2(1 - p)}} \right]\frac{ft}{{\frac{{p(1 - p^{m} )}}{1 - p} + ft}} \\ & = \left[ {\frac{p + 1}{2(1 - p)} - \frac{{m \cdot p^{m} }}{{(1 - p^{m} )}}} \right]\frac{{\frac{{p(1 - p^{m} )}}{1 - p}}}{{\frac{{p(1 - p^{m} )}}{1 - p} + ft}} + \left[ {\frac{{p^{2} (1 - p^{m} ) + ft(1 - p)}}{2(1 - p)}} \right]\frac{ft}{{\frac{{p(1 - p^{m} )}}{1 - p} + ft}} \\ & = \left[ {\frac{p + 1}{2(1 - p)} - \frac{{m \cdot p^{m} }}{{(1 - p^{m} )}}} \right]\frac{{\frac{{p(1 - p^{m} )}}{1 - p}}}{{\frac{{p(1 - p^{m} ) + ft\left( {1 - p} \right)}}{1 - p}}} + \left[ {\frac{{p(1 - p^{m} )}}{(1 - p)}p + \frac{ft}{2}} \right]\frac{ft}{{\frac{{p(1 - p^{m} ) + ft\left( {1 - p} \right)}}{1 - p}}} \\ & = \left[ {\frac{p + 1}{2(1 - p)} - \frac{{m \cdot p^{m} }}{{(1 - p^{m} )}}} \right]\frac{{p(1 - p^{m} )}}{{p(1 - p^{m} ) + ft\left( {1 - p} \right)}} + \left[ {\frac{{p^{2} (1 - p^{m} ) + ft(1 - p)}}{2(1 - p)}} \right]\frac{{ft\left( {1 - p} \right)}}{{p(1 - p^{m} ) + ft\left( {1 - p} \right)}} \\ & = \left[ {\frac{p + 1}{2(1 - p)} - \frac{{m \cdot p^{m} }}{{(1 - p^{m} )}}} \right]\frac{{p(1 - p^{m} )}}{{p(1 - p^{m} ) + ft\left( {1 - p} \right)}} + \frac{ft}{2}\frac{{p^{2} (1 - p^{m} ) + ft(1 - p)}}{{p(1 - p^{m} ) + ft\left( {1 - p} \right)}} \\ \end{aligned} $$

1.6 Proof of Theorem 3

From Eq. (9), we define the lower bound and upper bound of the HD. The lower bound inequality holds by simplifying $E[PT^{2} ] = \sum\nolimits_{i = 1}^{m} {i^{2} \cdot p^{i} q} + m^{2} p^{m + 1} \ge m^{2} p^{m + 1}$ as follows:

$$ \left[ {\frac{{m^{2} \cdot p^{m + 1} }}{{2\sum\nolimits_{i = 1}^{m} {p^{i} } }}} \right]\frac{E[PT]}{E[PT] + E[FT]} + \left[ {p\left( {\sum\limits_{i = 1}^{m} {p^{i} } + \frac{ft}{2}} \right) + (1 - p)\left( {\frac{ft}{2}} \right)} \right]\frac{E[FT]}{E[PT] + E[FT]} \le E[HD] $$

The following limiting property shows that the lower bound is bounded by (m + ft)/2.

$$ \begin{aligned} &\mathop {\lim }\limits_{p \to 1} \left[ {\frac{{m^{2} \cdot p^{m + 1} }}{{2\sum\nolimits_{i = 1}^{m} {p^{i} } }}\frac{{\sum\nolimits_{i = 1}^{m} {p^{i} } }}{{\sum\nolimits_{i = 1}^{m} {p^{i} } + ft}} + \left[ {p\left( {\sum\nolimits_{i = 1}^{m} {p^{i} } + \frac{ft}{2}} \right) + (1 - p)\left( {\frac{ft}{2}} \right)} \right]\frac{ft}{{\sum\nolimits_{i = 1}^{m} {p^{i} } + ft}}} \right] \\ & \mathop { = \lim }\limits_{p \to 1} \left[ {\frac{{m^{2} \cdot p^{m + 1} }}{{2\sum\nolimits_{i = 1}^{m} {p^{i} } }}\frac{m}{m + ft} + \left[ {\left( {m + \frac{ft}{2}} \right)} \right]\frac{ft}{m + ft}} \right] \\ & = \left[ {\frac{{m^{2} }}{2m}} \right]\frac{m}{m + ft} + \left( {m + \frac{ft}{2}} \right)\frac{ft}{m + ft} \\ & = \left[ {\frac{m}{2}} \right]\frac{m}{m + ft} + \left( {\frac{2m + ft}{2}} \right)\frac{ft}{m + ft} \\ & = \frac{{m^{2} + 2m \cdot ft + ft^{2} }}{{2\left( {m + ft} \right)}} = \frac{{\left( {m + ft} \right)^{2} }}{{2\left( {m + ft} \right)}} = \frac{m + ft}{2} \\ \end{aligned} $$

(14)

Similarly, the upper bound inequality holds by replacing $E[PT^{2} ] = \sum\nolimits_{i = 1}^{m} {i^{2} \cdot p^{i} q} + m^{2} p^{m + 1} \le q\sum\nolimits_{i = 1}^{m} {i^{2} } + m^{2} p^{m + 1}$ as follows:

$$ E[HD] \le \left[ {\frac{{q\sum\nolimits_{i = 1}^{m} {i^{2} } + m^{2} \cdot p^{m + 1} }}{{2\sum\nolimits_{i = 1}^{m} {p^{i} } }}} \right]\frac{E[PT]}{E[PT] + E[FT]} + \left[ {p\left( {\sum\limits_{i = 1}^{m} {p^{i} } + \frac{ft}{2}} \right) + (1 - p)\left( {\frac{ft}{2}} \right)} \right]\frac{E[FT]}{E[PT] + E[FT]} $$

The upper bound also is bounded by (m + ft)/2 (see “Proof of Theorem 3” section in Appendix for details):

$$ \begin{aligned} &\mathop {\lim }\limits_{p \to 1} \left[ {\frac{{q\sum\nolimits_{i = 1}^{m} {i^{2} } + m^{2} \cdot p^{m + 1} }}{{2\sum\nolimits_{i = 1}^{m} {p^{i} } }}\frac{pt}{pt + ft} + \left[ {p\left( {\sum\nolimits_{i = 1}^{m} {p^{i} } + \frac{ft}{2}} \right) + (1 - p)\left( {\frac{ft}{2}} \right)} \right]\frac{ft}{pt + ft}} \right] \\ & = \mathop {\lim }\limits_{p \to 1} \left[ {\frac{{q\frac{m(m + 1)(2m + 1)}{6} + m^{2} \cdot p^{m + 1} }}{{2\sum\nolimits_{i = 1}^{m} {p^{i} } }}\frac{pt}{pt + ft} + \left[ {p\left( {m + \frac{ft}{2}} \right) + (1 - p)\left( {\frac{ft}{2}} \right)} \right]\frac{ft}{{\sum\nolimits_{i = 1}^{m} {p^{i} } + ft}}} \right] \\ & = \mathop {\lim }\limits_{p \to 1} \left[ {\frac{{(1 - p)\frac{m(m + 1)(2m + 1)}{6} + m^{2} \cdot p^{m + 1} }}{{2\sum\nolimits_{i = 1}^{m} {p^{i} } }}\frac{pt}{pt + ft} + \left[ {p\left( {m + \frac{ft}{2}} \right) + (1 - p)\left( {\frac{ft}{2}} \right)} \right]\frac{ft}{{\sum\nolimits_{i = 1}^{m} {p^{i} } + ft}}} \right] \\ & = \left[ {\frac{{m^{2} }}{2m}} \right]\frac{m}{m + ft} + \left( {m + \frac{ft}{2}} \right)\frac{ft}{m + ft} = \frac{m + ft}{2} \\ \end{aligned} $$

(15)

As both the lower bound (Eq. (14) and the upper bound (Eq. (15)) converge to the same value (m + ft)/2, E[HD] results in (m + ft)/2:

$$ \begin{aligned} & \frac{m + ft}{2} \le \mathop {\lim }\limits_{p \to 1} E[HD] \le \frac{m + ft}{2}, \\ & \mathop {\lim }\limits_{p \to 1} E[HD] = \frac{m + ft}{2} \\ \end{aligned} $$

□.

1.7 General distributions and calculation steps of Eq. (11)

$$ \begin{aligned} E[HD] & = \frac{{E[PT^{2} ]}}{2E[PT]}\frac{E[PT]}{E[PT] + E[FT]} + \left[ {p\left( {E[PT] + \frac{{E[FT^{2} ]}}{2E[FT]}} \right) + (1 - p)\frac{{E[FT^{2} ]}}{2E[FT]}} \right]\frac{E[FT]}{E[PT] + E[FT]} \\ & = \frac{{E[PT^{2} ]}}{2E[PT]}\frac{E[PT]}{E[PT] + E[FT]} + \left[ {p\left( {E[PT] + \frac{E[FT]}{2}} \right) + (1 - p)\frac{E[FT]}{2}} \right]\frac{E[FT]}{E[PT] + E[FT]} \\ & = \frac{{E[PT]^{2} + Var[PT]}}{2E[PT]}\frac{E[PT]}{E[PT] + E[FT]} + \left[ {p\left( {E[PT] + \frac{E[FT]}{2}} \right) + (1 - p)\frac{E[FT]}{2}} \right]\frac{E[FT]}{E[PT] + E[FT]} \\ & = \left[ {\frac{E[PT]}{2} + \frac{Var[PT]}{2E[PT]}} \right]\frac{E[PT]}{E[PT] + E[FT]} + \left[ {p\left( {E[PT] + \frac{E[FT]}{2}} \right) + (1 - p)\frac{E[FT]}{2}} \right]\frac{E[FT]}{E[PT] + E[FT]} \\ \end{aligned} $$

1.8 General distributions and calculation steps

If the pick duration follows the uniform distribution of Unif(a,b) where b ≥ a ≥ 0.

$$ \begin{aligned} E[HD_{\text{unif}} ] & = \left[ {\frac{{p((b - a)^{3} /6)}}{2p(a + b)/2}} \right]\frac{p}{p + ft} + \left[ {p\frac{a + b}{2} + \frac{ft}{2}} \right]\frac{ft}{p + ft} \\ & = \left[ {\frac{{(b - a)^{3} }}{6(a + b)}} \right]\frac{p}{p + ft} + \left[ {p\frac{a + b}{2} + \frac{ft}{2}} \right]\frac{ft}{p + ft} \\ \end{aligned} $$

If the pick duration follows the exponential distribution of mean = a where a > 0.

$$ \begin{aligned} E[HD_{\exp } ] & = \left[ {\frac{p(2a)}{2pa}} \right]\frac{p}{p + ft} + \left[ {pa + \frac{ft}{2}} \right]\frac{ft}{p + ft} \\ & = \frac{p}{p + ft} + \left[ {pa + \frac{ft}{2}} \right]\frac{ft}{p + ft} \\ \end{aligned} $$

If the pick duration follows the triangular distribution of triangular(a,b,c) where a ≥ c ≥ b ≥ 0.

$$ \begin{aligned} E[HD_{\text{tri}} ] & = \left[ {\frac{{p\left[ {\frac{{a^{2} + b^{2} + c^{2} - ab - bc - ca}}{18} + \left( {\frac{a + b + c}{3}} \right)^{2} } \right]}}{{2p\left( {\frac{a + b + c}{3}} \right)}}} \right]\frac{p}{p + ft} + \left[ {p\left( {\frac{a + b + c}{3}} \right) + \frac{ft}{2}} \right]\frac{ft}{p + ft} \\ & = \left[ {\frac{{p\left[ {\frac{{a^{2} + b^{2} + c^{2} + ab + bc + ca}}{6}} \right]}}{{2p\left( {\frac{a + b + c}{3}} \right)}}} \right]\frac{p}{p + ft} + \left[ {p\left( {\frac{a + b + c}{3}} \right) + \frac{ft}{2}} \right]\frac{ft}{p + ft} \\ & = \left[ {\frac{{a^{2} + b^{2} + c^{2} + ab + bc + ca}}{4(a + b + c)}} \right]\frac{p}{p + ft} + \left[ {p\left( {\frac{a + b + c}{3}} \right) + \frac{ft}{2}} \right]\frac{ft}{p + ft} \\ \end{aligned} $$

There are numerical examples of three pick time distributions: Uni = uniform [min,max] = uniform [a,b] = [0.0, 2.0]; Exp = exponential [mean] = exp[a] = [1.0]; and Tri = triangular [min, mode, max] = triangular [a, b, c] = [0.5, 1.0, 1.5], where the time unit represents the time spent to retrieve an item.

$$ \begin{aligned} E[HD_{unif} ] & = \left[ {\frac{2}{3}} \right]\frac{p}{p + ft} + \left[ {p + \frac{ft}{2}} \right]\frac{ft}{p + ft} \\ E[HD_{\exp } ] & = \frac{p}{p + ft} + \left[ {p + \frac{ft}{2}} \right]\frac{ft}{p + ft} \\ E[HD_{tri} ] & = \left[ {\frac{6.25}{12}} \right]\frac{p}{p + ft} + \left[ {p + \frac{ft}{2}} \right]\frac{ft}{p + ft} \\ \end{aligned} $$