“Conventional valuation which is established as the outcome of mass psychology of a large number of ignorant individuals is liable to change violently as the result of a sudden fluctuation of opinion”

Keynes (1936)

1 Introduction

A number of papers have expounded the limitations and flaws of risk-neutral option pricing in real-life economic and financial decision-making (Millo and MacKenzie 2009; Haug and Taleb 2011). Special attention has been paid to the mechanics of the Black and Scholes (1973), Merton (1973), Margrabe (1978), closed-form formulaeFootnote 1 (MMBS) and their extensions. These models are seen by critics as narrow and specific (e.g., they assume absence of frictions) and unable to capture the realities of financial markets and investment decision-makers’ behavior. MMBS models suffer from misvaluation and (imperfect) hedging problems when modeling the behavior and choices of “irrational” investors encountering extreme uncertainty or “never-seen-before” economic conditions (market crashes, financial crises, economic depressions). A recurring issue pertains to the omission of incalculable risk and the impact of investors’ sentiment and ambiguity attitudes on their cognitive assessment of option values (e.g., Smith and McCardle 1998; Nau 2006). The MMBS framework assumes that financial market participants and investment decision-makers follow a uniform approach towards risk and uncertainty prior to option exercise and investment maturity. While it may be roughly valid in normal times, this assumption can be challenged when markets are abnormally uncertain (Mandelbrot and Taylor 1967; Consigli 2002).

Under uncertainty, economic agents are no longer sure about the likelihoods of the states of nature and, as a result, their estimations of option payoffs are subject to vagueness, behavioral biases and partial ignorance. In such extreme conditions, the heterogenous attitudes of investors and decision-makers towards uncertainty dominate rational beliefs and expectations in a manner that distorts asset pricing norms and fundamentals, resulting in ambiguity and swings in investor valuation opinions (Keynes 1936). This brings ambiguity in economics and markets (Allais 1953; Ellsberg 1961). Ignorance and ambiguity attitudes influence the valuation processes and opinions of investors when abnormal uncertainty prevails in financial markets.

The aim of this article is to examine the extent to which uncertainty—viewed under a Choquet ambiguity modeling lens (e.g., De Waegenaere et al. 2003)—alters the standard analytical option pricing framework of MMBS, with particular focus on the value of the option to exchange one risky asset for another (which subsumes the other standard models as special cases). Useful from the perspective of investors’ discretion to switch resources among risky prospects, the option to exchange one risky (stochastic) asset for another (or an option with a stochastic strike price) is a general case of the standard option to buy or sell an asset at a fixed or predetermined exercise price (Margrabe 1978).Footnote 2 In times of economic turbulence, a more robust asset pricing and option valuation model ought to be able to account for swings in investor opinion, market overreactions and subjective ambiguity beliefs characterizing real investors’ choices. Our analysis is based on an uncertain environment, where ambiguity in true underlying asset values is specified in the form of Choquet–Brownian motions (Kast and Lapied 2010; Kast et al. 2014) and examines how the notion of c-ignorance affects investor valuation judgments. Relaxing the standard assumption of homogeneous investor beliefs and expectations underlying the MMBS modeling framework, we analyze the impact of ambiguity and (partial) ignorance on market decision-makers and investors’ option value estimates incorporating Choquet uncertainty (Schmeidler 1989) in the option pricing apparatus.

Our extended formulae and findings confirm that MMBS standard prices are special cases of more general price bounds that can be observed in the market when uncertainty is abnormally high and that, contrary to normative theory, option values can either increase or decrease with volatility subject to decision-makers’ perceived ambiguity as a result of model uncertainty (i.e., parametric ambiguity). We also show how investors’ heterogenous beliefs and ambiguity attitudes can be extracted from observed option prices.

Related works in decision analysis and financial economics include Muzzioli and Torricelli (2005) on binomial index option pricing in illiquid markets, Cherubini (1997) and Han and Zhou (2007) on ambiguity-adjusted Black–Scholes pricing using fuzzy measures, Liu et al. (2005) on robust option valuation under rare events, Coimbra-Lisboa and Gongalves (2006) and Riedel (2009) on multiple-priors option pricing, Araujo et al. (2012) on super replication pricing under ambiguity, Zhang and Li (2013) on contingent-claim pricing using set-valued differential inclusion, and Izhakian and Yermack (2014) on executive stock option pricing under uncertain expected utilities.Footnote 3 We extend this stream of research by developing general formulae to price European-type options (in finite-time) with stochastic (and fixed) exercise prices under Choquet uncertaintyFootnote 4 for a range of ambiguity averse and ambiguity-seeking market decision-makers. Pricing option instruments in finite-time is relevant as the vast majority of derivatives contracts traded in financial markets are of finite duration and contain crucial information about investors’ heterogenous beliefs and expectations regarding future prospects.

Our ambiguity-based analysis goes beyond the maxmin or worst-case criterion for valuation under uncertainty (e.g., Gilboa and Schmeidler 1989; Zymler et al. 2013) to consider negative and positive investment sentiment in option pricing. This is achieved with the use of (conditional) capacities (see, e.g., Chateauneuf et al. 1996; Araujo et al. 2012) representing decision-maker beliefs in the stochastic movement followed by underlying asset prices within the Choquet expected utility framework. Our ambiguity models nest the standard Margrabe–Merton–Black–Scholes formulae under risk and multiple-priors and show how ambiguity attitudes (aversion and seeking) and ignorance moderate non-monotonically the dynamics of option prices when markets are abnormally uncertain.

2 Margrabe exchange option pricing under Choquet uncertainty

Alternative approaches and paradigms for representing uncertainty in investment decision-making and option pricing include robust control (Hung and So 2010; Zymler et al. 2011), fuzzy sets (Carlsson and Fuller 2003; Muzzioli and Torricelli 2004; Zmeskal 2010), multiple-priors (Nishimura and Ozaki 2007; Riedel 2009), and Choquet ambiguity (Roubaud et al. 2010; Agliardi and Sereno 2011). In this article, ambiguity is characterized in the form of the Choquet–Brownian motions recently developed by Kast et al. (2014) in decision theory. This continuous-time ambiguous Brownian motion type specification relies on the concept of (non-additive) capacities acting as weighted probability functions, where decision weights capture decision-makers’ subjective degrees of confidence about probabilistic and economic judgment. Capacities have been used in the decision theory literature to provide formal definitions of ambiguity and uncertainty attitudes (Schmeidler 1989; Epstein 1999), degrees of confidence under additive probability measures (Eichberger and Kelsey 1999), pessimism or optimism (Wakker 2001; Chateauneuf et al. 2001), as well as sensitivity and robustness to changes in likelihood. Capacities have also been applied and extended in the context of the Choquet integral for discrete-time option pricing by Muzzioli and Torricelli (2002).

Our representation of uncertainty follows the dynamically consistent Choquet random walk of asset prices developed by Kast and Lapied (2010) and extended to continuous-time by Kast et al. (2014). This random walk is defined by a conditional capacity \(c\) with 0 \(< c <\) 1 which, in accordance with the properties of the Choquet expected utility, determines the nature of fluctuations of underlying asset values along investor time horizons (e.g., Chateauneuf et al. 1996).Footnote 5 \(^{,}\) Footnote 6 In continuous-time, the Choquet random walk converges to a general Wiener process \(W\) with mean \(m = 2c-1\) and variance \(s^{2} = 4c(1-c)\), resulting in a distorted (set of) Brownian motion(s) with ambiguous drifts and ambiguous variances that are functions of \(c\) (Kast and Lapied 2010; Roubaud et al. 2010; Agliardi and Sereno 2011). To account for the uncertainty preferences and sentiment of decision-makers, the Choquet integral is employed, through a linear transformation (see Proposition 4 of Kast et al. (2014)), to obtain the expected value of the asset price with respect to a specific capacity \(w\). The decision weights used in the computation of the Choquet integral overweight high outcomes if the capacity is concave and superadditive (\(c >\) 0.5) and favor low outcomes if the capacity is convex and subadditive (\(c <\) 0.5).Footnote 7

The basic intuition behind this formulation is that there is a range of possible values (determined by \(c)\) for the drift and volatility terms of the Brownian motion resulting in multiple probabilities of option exercise, imperfect hedging, and subjective valuation. The special case \(c\) = 0.5 corresponds (reduces) to the traditional probabilistic framework and standard Brownian motion used in risk-neutral option pricing. Capacity variable \(c\) acts as a proxy for decision-makers’ attitudes towards ambiguity; it summarizes investors’ ambiguity attitudes (aversion or seeking) about future prospects, with 0 \(< c <\) 0.5 (\(m <\) 0) representing aversion (convex capacities), and 0.5 \(< c < 1(m > 0)\) indicating ambiguity-seeking (concave capacities). This is in line with investors considering multiple Brownian motions under uncertainty and following subjective decision rules and criteria in their appraisal of investment prospects and option values. Under Choquet ambiguity, volatility is subjectively assessed as \(s\times \sigma ,\) with 0 \(< s \le \) 1.

In line with Kast et al. (2014), the dynamics of \(W\) can be written as:

$$\begin{aligned} \mathrm{d}W=m\mathrm{d}t+s\mathrm{d}Z \quad (\forall \, m\in \, ] {-1,1} [, \forall s \in ]0,1]) \end{aligned}$$
(1)

where \(Z\) is a standard Wiener process, and functions \(m = h(c)\) and \(s = k(c)\) are as defined above.

We consider the present value (\(E'_{0})\) of an option to exchange one risky asset (\(S_{1})\) for another (\(S_{2})\) under uncertainty by incorporating Choquet–Brownian motions in \(S_{1}\) and \( S_{2}\) pricing dynamics. These also represent (stochastic) exercise prices for the option. The pricing formula for the standard exchange option (Margrabe 1978) is a generalization of the Black–Scholes–Merton (1973) models with fixed (non-stochastic) strikes (\(X)\). Herein we revisit and extend the Margrabe (1978) apparatus under Choquet ambiguity and show how the resulting Choquet-based formula subsumes and nests the Merton (1973) and Black and Scholes (1973) models and their extensions under ambiguity. We obtain the price of exchange contingent claim, \(E(S_{1}, S_{2}, t)\), by adopting a Choquet-based pricing kernel with \(m\) and \(s\) acting as proxies for decision-makers’ subjective ambiguity beliefs. The resulting formula is derived using standard change of numeraire techniques (e.g., Margrabe 1978; Rady 1997). The situation with fixed strike (\(X)\) is covered as a special case in Sect. 3.

Suppose the price of underlying asset \( S_{i}\) follows a Brownian motion of the form:

$$\begin{aligned} \frac{\mathrm{d}S_i }{S_i }=\mu _i \mathrm{d}t+\sigma _i \mathrm{d}W \end{aligned}$$
(2)

Using the specification for \(\mathrm{d}W\) in Eq. (2), \(S_{1}\) and \(S_{2}\) follow the Choquet–Brownian motions described below:

$$\begin{aligned} \frac{\mathrm{d}S_i }{S_i }=( {\mu _i +m_i \sigma _i })\mathrm{d}t+s_i \sigma _i \mathrm{d}Z_i \quad ( {\forall m_i \in } ]-1,1\left[ { , \forall s_i\in } \right] 0,1]) \end{aligned}$$
(3)

where \(i=\left\{ {1 ,2} \right\} \) and \( \mathrm{d}Z\) \(_{1}\) and \(\mathrm{d}Z\) \(_{2}\) are correlated with correlation coefficient \(\rho \).

The above implies that investors consider multiple stochastic differential equations, Eq. (3), for their predictions of future underlying asset prices \(S_{1}\) and \(S_{2 }\) and assign subjective values according to capacity variable (judgment) \(c\). Heterogenous beliefs (e.g., see Li 2007) are accounted for via behavioral ambiguity drift and volatility-moderating parameters \(m_{i}\) and \(s_{i}\) (and the market pricing kernel discussed later). Eq. (3) can thus be interpreted as a stochastic Brownian process with model parameter uncertainty in both drift and volatility. This is a result of subjective volatility measurement under uncertainty as well as heterogenous discounting.

Following standard numeraire change techniques, we define the relative process \(U\):

$$\begin{aligned} U=\frac{S_1 }{S_2 } \end{aligned}$$
(4)

From multi-dimensional Ito’s Lemma, Eq. (4) implies:

$$\begin{aligned} \frac{\mathrm{d}U}{U}&= [ ( {\mu _1 +m_1 \sigma _1 })-( {\mu _2 +m_2 \sigma _2 })+( {s_2 \sigma _2 )^2-\rho ( {s_1 \sigma _1 })( {s_2 \sigma _2 })} ]\mathrm{d}t\nonumber \\&\quad \left. +( {s_1 \sigma _1 })\mathrm{d}Z_1 -(s_2 \sigma _2 \right) \mathrm{d}Z_{2 } \end{aligned}$$
(5)

Through the change of numeraire, the drift term in Eq. (5) under the \(S_{2}\) measure tends to zero (as if \(S_{2}\) remains constant at its initial level) while the diffusion part stays the same (e.g., Brigo and Mercurio 2007).

Substituting \(U\) from Eqs. (4), (5) then reduces to:

$$\begin{aligned} \mathrm{d}\left( \frac{S_1 }{S_2 }\right) =\frac{S_1 }{S_2 }(s_1 \sigma _1 )\mathrm{d}Z_1 -\frac{S_1 }{S_2 }(s_2 \sigma _2 )\mathrm{d}Z_2 \end{aligned}$$
(6)

In line with standard properties of the (single) Brownian motion process, one can write:

$$\begin{aligned} \mathrm{Var}(s_1 \sigma _1 \mathrm{d}Z_1 -s_2 \sigma _2 \mathrm{d}Z_2 )=\mathrm{Var}( {\sigma _0 \mathrm{d}Z_0 }) \end{aligned}$$
(7)

where the diffusion (stochastic) part of \(U\) is:

$$\begin{aligned} \sigma _0 =\sqrt{[(s_1 \sigma _1 )^2+(s_2 \sigma _2 )^2-2\rho ( {s_1 \sigma _1 })( {s_2 \sigma _2 })]} \text{ and } \mathrm{d}Z_1 \mathrm{d}Z_2 =\rho \end{aligned}$$
(8)

Rewriting Eq. (5) leads to:Footnote 8

$$\begin{aligned} \frac{\mathrm{d}U}{U}=\mu _{0 } \mathrm{d}t+\sigma _0 \mathrm{d}Z_0 \end{aligned}$$
(9)

where

$$\begin{aligned} \mu _{0 } \equiv [( {\mu _1 +m_1 \sigma _1 })-( {\mu _2 +m_2 \sigma _2 })+( {s_2 \sigma _2 )^2-\rho ( {s_1 \sigma _1 })( {s_2 \sigma _2 })} ] \end{aligned}$$
(10)

Having specified the reformulated price dynamics of \(S_{1}\), \(S_{2}\) and the relative price \(U\), the market pricing kernel can now be determined in the Choquet context. Let \(\xi \) represent the level(s) of marginal utility in the economy at time \(t.\) We assume that \(\xi \) dynamics follow (see Harrison and Kreps 1979):

$$\begin{aligned} \frac{\mathrm{d}\xi }{\xi }=f( {\xi , U})\mathrm{d}t+g( {\xi , U})\mathrm{d}W \end{aligned}$$
(11)

where \(f(\xi , U)\) and \(g(\xi , U)\) are general functions to be determined.

From Eqs. (1) and (9), we can now rewrite Eq. (11) in terms of \(U\) as:

$$\begin{aligned} \frac{\mathrm{d}\xi }{\xi }=\left[ {mg( {\xi , U})+f( {\xi , U})} \right] \mathrm{d}t+sg( {\xi , U})\mathrm{d}Z_0\quad (\forall m\in ] {-1,1} [ , \forall s \in ]0,1] ) \end{aligned}$$
(12)

This suggests that there can be more than one marginal utility level in the economy in the presence of ambiguity (see, e.g., Cochrane 2001). From martingale theory (with the drift term tending to zero):

$$\begin{aligned} f( {\xi , U})&= -mg( {\xi , U})\end{aligned}$$
(13)
$$\begin{aligned} \mathrm{d}( {\xi U})&= \xi U\left[ {( {\mu _0 })\mathrm{d}t+\sigma _0 \mathrm{d}Z_0 } \right] +U\xi \left\{ \left[ {mg( {\xi , U})-mg( {\xi , U})} \right] \mathrm{d}t\right. \nonumber \\&\quad \left. +sg( {\xi , U})\mathrm{d}Z_0 \right\} \nonumber \\&\quad +\xi U\sigma _0 sg( {\xi , U})\mathrm{d}t \end{aligned}$$
(14)

This further implies:

$$\begin{aligned}&\mu _0 \mathrm{d}t+\sigma _0 sg( {\xi , U})\mathrm{d}t=0\end{aligned}$$
(15)
$$\begin{aligned}&g( {\xi , U})=-\frac{\mu _0 }{\sigma _0 s} \end{aligned}$$
(16)

We assume that the market pricing kernel follows Harrison and Kreps (1979), but \(f\) and \(g\) are not unique (as they both depend on subjective ambiguity parameters \(m\) and \(s\), with \(-1 < m <\) 1 and 0 \(< s \le \) 1) otherwise we incrementally go back to the perfect hedging or risk-neutral case resulting in the Margrabe (1978), Merton (1973) and Black and Scholes (1973) equations.Footnote 9 This type of pricing kernel captures swings in fundamentals, but not the purely sentimental part of the market kernel (see, e.g., Shefrin 2005; Han 2008). If the market kernel was equal to the marginal utility level, perfect hedging would be possible (equivalent to the unlikely assumption of hedging against uncertainty).

Given imperfect hedging and market incompleteness, and substituting \( f( {\xi , U})\) and \(g(\xi , U)\) from Eqs. (13) and (16) in Eq. (11), we obtain:

$$\begin{aligned} \frac{\mathrm{d}\xi }{\xi }=m\frac{\mu _0 }{\sigma _0 s}\mathrm{d}t-\frac{\mu _0 }{\sigma _0 s}\mathrm{d}Z_0 \end{aligned}$$
(17)

As noted, this pricing kernel follows Harrison and Kreps (1979) dynamics but here \(f\) and \(g\) depend on subjective factors \(s\) and \(m\) from Eq. (12) and other behavioral parameters from Eqs. (8) and (10).

Let \(E\) be the price of a contingent claim or derivative security (namely, a European option to exchange one risky asset \( S_{1}\) for another \(S_{2})\) which depends only on \(U\) and time \(t\), \(E(U,t)\). From Ito’s lemma, the dynamics of option price \(E\) are:

$$\begin{aligned} \mathrm{d}E( {U, t})=\left[ {\frac{\partial E}{\partial t}+\frac{\partial E }{\partial U}( {\mu _0 })U+\frac{1}{2}\frac{\mathrm{d}^2E}{\mathrm{d}U^2}( {\sigma _0 })^2U^2} \right] \mathrm{d}t+\frac{\partial E}{\partial U}( {\sigma _0 })U\mathrm{d}Z \end{aligned}$$
(18)

This leads to the following valuation equation for the price of the European exchange option \(E\):

$$\begin{aligned} \mathrm{d}( {\xi E})&= \xi \left\{ {\left[ {\frac{\partial E}{\partial t}+\frac{\partial E }{\partial U}( {\mu _0 })U+\frac{1}{2}\frac{\mathrm{d}^2E}{\mathrm{d}U^2}( {\sigma _0 })^2U^2} \right] \mathrm{d}t+\frac{\partial E}{\partial U}( {\sigma _0 })U\mathrm{d}Z_0 } \right\} \nonumber \\&\quad +\xi E\left[ {m\frac{\mu _0 }{\sigma _0 s}\mathrm{d}t-\frac{\mu _0 }{\sigma _0 s}\mathrm{d}Z_0 } \right] \nonumber \\&\quad +\xi \left[ {-\frac{\partial E}{\partial U}( {\sigma _0 })U\frac{\mu _0 }{\sigma _0 s}\mathrm{d}t} \right] \end{aligned}$$
(19)

Rearranging terms, we get the following partial differential equation (pde):

$$\begin{aligned} \frac{\partial E}{\partial t}+U\frac{\partial E }{\partial U}\left( {\frac{\mu _0 [ {(\sigma _0 s-\sigma _0 )+m}]}{\sigma _0 s}}\right) +\frac{1}{2}\frac{\mathrm{d}^2E}{\mathrm{d}U^2}( {\sigma _0 })^2-E\left( {-m\frac{\mu _0 }{\sigma _0 s}}\right) =0 \end{aligned}$$
(20)

Analogous to Margrabe (1978), the solution to Eq. (20) under Choquet uncertainty is:

$$\begin{aligned} E_0 ^{\prime }=S_1 e^{-\varepsilon ^{\prime \prime \prime }T}N( {d_1 ^{\prime \prime \prime }})-S_2 e^{-r^{\prime \prime \prime }T}N( {d_2 ^{\prime \prime \prime }}) \quad \left( {\forall c \in } \right] 0,1[ ) \end{aligned}$$
(21)

where

$$\begin{aligned} m&= 2c-1 \quad \text{ and }\quad s=\sqrt{4c(1-c)} \\ r^{\prime \prime \prime }&= -m\frac{\mu _0 }{\sigma _0 s} \quad \text{ and }\quad \varepsilon ^{\prime \prime \prime }=\frac{\mu _0 [\sigma _0 ( {1-s})-m]}{\sigma _0 s} \\ d_1 ^{\prime \prime \prime }&= \frac{\ln ( {\frac{S_1 }{S_2 }})+( {r^{\prime \prime \prime }-\varepsilon ^{\prime \prime \prime }+0.5( {\sigma _0 })^2})T}{\sigma _0 \sqrt{T} },\quad d_2 ^{\prime \prime \prime }=d_1 ^{\prime \prime \prime }-\sigma _0 \sqrt{T} \\ \end{aligned}$$

\(r^{\prime \prime \prime }\) and \( \varepsilon '''\) account for investors’ ambiguous beliefs and subjective discounting traits. Behavioral variable \(s\) is reflective of subjective volatility moderation which arises under ambiguity or when shocks and innovations are unexpected. Although resembling the standard Margrabe (1978) formula under risk, Eq. (21) highlights the type of decision-rule or (sophisticated) heuristic that might be used by investors when appraising option instruments under uncertainty, confirming that multiple option prices can exist under Choquet ambiguity. The interval of possible prices for this exchange option corresponds to the set of values satisfying Eq. (21) for 0 \(< c <\) 1.

Subjective discounting and heterogenous investor valuations are reinforced by non-linear interactions between standard option pricing inputs and the ambiguous parameters characterizing the Choquet–Brownian motions described above. Because of parametric uncertainty in drifts and volatilities, market decision-makers often likely deviate from rational pricing assumptions valuing option-type investments somewhat above or below equilibrium prices according to their uncertainty preferences and perceptions of ambiguity. Effects from such dynamics tend to be more pronounced under uncertainty and normally disappear under risk-neutrality (i.e., standard Black–Scholes environment). It can be readily shown that Eq. (21) nests the classical Margrabe exchange and the Black–Scholes–Merton option pricing formulae under risk-neutrality (where \(c = 0.5\)) and under multiple-priors (where \(s= 1\) and \(m \ne \) 0).Footnote 10

3 Fixed strike case and illustration of ambiguity attitudes

We next examine the special (but more common) case of the European option to exchange (buy or sell) a risky asset \(S\) for a “riskless” (fixed) counterpart \(X\). Here, strike \(X\) is a predetermined constant.

Suppose the price of risky asset \(S\) follows a Choquet–Brownian motion of the form (recalling that \(\mathrm{d}W=m\mathrm{d}t+s\mathrm{d}Z)\):

$$\begin{aligned} \frac{\mathrm{d}S}{S}=(\mu +m\sigma )\mathrm{d}t+s\sigma \mathrm{d}W\quad ( {\forall m\in ] {-1,1} [ , \forall s \in } ]0,1] ) \end{aligned}$$
(22)

Interest rates are stochastic such that (\(r\) is the instantaneous rate of return of fixed-income security \(B\) and \(\sigma ^{\prime }\) is interest rate volatility):

$$\begin{aligned} \frac{\mathrm{d}B}{B}=r\mathrm{d}t+\sigma ^{\prime }\mathrm{d}W \end{aligned}$$
(23)

Then Eq. (21) simplifies to:

$$\begin{aligned} C{''}_0 =S_0 e^{-\varepsilon ^{\prime \prime }T}N( {\mathrm{d}''_1 })-Xe^{-r^{\prime \prime }T}N( {\mathrm{d}{''}_2 })\quad ( {\forall c \in } ]0,1[ ) \end{aligned}$$
(24)

where

$$\begin{aligned} m&= 2c-1 \text{ and } s=\sqrt{4c(1-c)} \\ r^{\prime \prime }&= r+m\left[ {( {r+m\sigma ^{\prime }})-( {\mu +m\sigma })} \right] /s^2(\sigma -\sigma ^{\prime })]+s^2\sigma ^{\prime }\left[ ( {r+m\sigma ^{\prime }})\right. \\&\quad \left. -( {\mu +m\sigma }) \right] /s^2(\sigma -\sigma ^{\prime })] \\ \varepsilon ^{\prime \prime }&= \left[ {r-( {\mu +m\sigma })} \right] +[(s\sigma -m-s^2\sigma ^{\prime })\left[ {( {\mu -r+m(\sigma -\sigma ^{\prime }})} \right] /s^2(\sigma -\sigma ^{\prime })] \\ \mathrm{d}''_1&= \frac{\ln ( {\frac{S_0 }{X}})+( {r^{\prime \prime }-\varepsilon ^{\prime \prime }+0.5( {s\sigma })^2})T}{s\sigma \sqrt{T} },\,\,\mathrm{d}''_2 =\mathrm{d}''_1 -s\sigma \sqrt{T} \\ \end{aligned}$$

A special case of Eq. (21), Eq. (24) is structurally analogous to the fundamental Merton (1973) European call option formula with stochastic interest rates, but additionally considers heterogenous beliefs and ambiguity in the pricing process resulting in multiple option prices under ambiguity aversion and ambiguity-seeking. The solution to pde (20), where \(X\) replaces \(S_{2}\) corresponds to the set of possible option values satisfying Eq. (24) (for \(-1 < m < 1\) and \(0 < s \le 1\)).

The above reaffirms that under ambiguity investors deviate from risk-neutrality using subjective (sometimes negative) discount rates (\(r^{\prime \prime })\), adjusting their expectations of underlying future values by a subjective dividend-yield-type factor or ignorance-based term (\(\varepsilon ^{\prime \prime })\).Footnote 11 \(N( {\mathrm{d}''_1 }) \) and \( N( {\mathrm{d}''_2 })\) are affected by heterogenous beliefs and ambiguity attitudes. Partial derivatives (option “Greeks”, where \(\tau \), \(\mathrm{d}''_1 \) and \(\mathrm{d}''_2 \) follow standard option pricing nomenclature) for Eq. (24) are as follows:Footnote 12

$$\begin{aligned} \Delta&= \frac{\partial C_t }{\partial S}=\mathrm{e}^{-\varepsilon ^{\prime \prime }t}N( {\mathrm{d}_1^{\prime \prime } }) , {\Theta }=\frac{\partial C_t }{\partial t}=\varepsilon ^{\prime \prime }{S}_\mathrm{t} {e}^{\varepsilon ^{\prime \prime }t}N( {\mathrm{d}_1^{\prime \prime } })-\frac{{S}_\mathrm{t} \mathrm{e}^{-\varepsilon ^{\prime \prime }t}( {s}\sigma )}{2\sqrt{\tau }}N'( {\mathrm{d}_1^{\prime \prime } })\\&\qquad \quad \qquad \qquad \qquad \qquad \qquad -r''Xe^{-r''t}N( {\mathrm{d}_2^{\prime \prime } })\\ \nu&= \frac{\partial C_t }{\partial \sigma }={S}_\mathrm{t} \mathrm{e}^{-\varepsilon ^{\prime \prime }t}s\sqrt{t} N^{\prime }(\mathrm{d}_1^{\prime \prime } )+{S}_\mathrm{t} \left( {\frac{t( {m[ {\sigma ^2( {s^2-s})-\mu +r} ]})}{s^2\sigma ^2}}\right) \mathrm{e}^{-\varepsilon ^{\prime \prime }t}N({\mathrm{d}_1^{\prime \prime } })\\&\quad -X\left( {\frac{t( {m\left[ {\mu -r} \right] })}{s^2\sigma ^2}}\right) e^{-r''t}N( {\mathrm{d}_2^{\prime \prime } }) \\ \Gamma&= \frac{\partial ^2C_t }{\partial ^2S}=\frac{e^{-\varepsilon ^{\prime \prime }t}}{S_{\mathrm{t}} ( {s}\sigma )\sqrt{t} } N^{\prime }( {\mathrm{d}_1^{\prime \prime } }),\quad \kappa =\frac{\partial C_t }{\partial X}=-e^{-r^{\prime \prime }\tau }N( {\mathrm{d}_2^{\prime \prime } }),\\ \rho ^{\prime }&= \frac{\partial C_t }{\partial r^{\prime \prime }}=X\tau .e^{-r^{\prime \prime }\tau }N( {\mathrm{d}_2^{\prime \prime } }) \\ \omega&= \frac{\partial C_t }{\partial c}=t\left[ {S}_{\mathrm{t}} \mathrm{e}^{-\varepsilon ^{\prime \prime }t}\left( {-N\left( {\mathrm{d}_1^{\prime \prime } }\right) \frac{\partial \varepsilon ''}{\partial c}-N^{\prime }\left( {\mathrm{d}_1^{\prime \prime } }\right) 2ms\sigma \sqrt{t} }\right) +X.e^{-r^{\prime \prime }t}N\left( {\mathrm{d}_2^{\prime \prime } }\right) \frac{\partial r''}{\partial c} \right] \end{aligned}$$

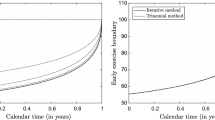
An interesting result is that “Vega” (\(v)\) can be either positive or negative, implying that option values can either increase or decrease with underlying volatility (\(\sigma \)) subject to investors’ perceived ambiguity (i.e., aversion or seeking). This is in contradiction to standard option pricing, where higher volatility tends to monotonically increase option value. This is explained by the fact that under Choquet ambiguity, the volatility measure \(\sigma \) is moderated by behavioral parameter \(s\) causing lower variance estimation (0 \(< s \le \) 1). Under ambiguity-seeking (aversion), the drift term \(\mu +m\sigma \) is overstated (understated) vis-à-vis \(\mu \) while volatility \(s\sigma \) is underestimated, having equivocal effects on option value. Such dynamics are accompanied by substantial changes in discount rates \(r^{\prime \prime }\) and ambiguity multipliers \(\varepsilon ^{\prime \prime }\) as uncertainty increases, reinforcing the non-monotonicity of the volatility-option value relationship. For example, ambiguity averse investors might be discounting at higher rates when \(\mu \) is high but require lower rates when \(\mu \) is low, and vice-versa for ambiguity-seeking counterparts. Figure 1 illustrates this non-monotonic behavior comparing (at-the-money) call option values under ambiguity aversion (\(c\) = 0.3) vs. ambiguity-seeking (\(c\) = 0.7) at different levels of asset volatility (assuming \(X\) = 1,000, \(r\) = 4.8 %, \(\mu \) = 8 %, \(\sigma ^{\prime }\)= 0 and \(T\) = 1). For \(c\) = 0.7 (ambiguity-seeking), the relation appears U-shaped. A similar pattern is found under ambiguity aversion (\(c\) = 0.3) when \(\mu \) = 0 %.

Under ambiguity, the effect of volatility on option value is moderated by subjective parameters \(c\), \(m\) and \(s\) and their interactions via discount rates (\(r^{\prime \prime })\), the value erosion/ambiguity multiplier (\(\varepsilon ^{\prime \prime })\) and expected return/drift variable (\(\mu \)). Similar non-monotonic relationships also hold for other partial derivatives, suggesting that the propensity to exercise an option or close an option position depends on subjective investor sentiment (proxied by behavioral parameters \(m\) and \(s)\). This is also reflected in the makeup of “Omega” (\(\omega \)). The above partial derivatives (Greeks) reduce to standard form under risk-neutrality when capacity variable \(c\) equals 0.5.

Fig. 1
figure 1

Choquet-based option value under c-ignorance vs. volatility

Full size image

Having analyzed the role of ambiguity in option pricing and investment decision-making, we now illustrate how investors’ subjective beliefs under uncertainty can be directly extracted from observed call and put option prices. By back-solving Eq. (21) for \(c\) numerically such that \(c=E{'}_0^{-1}(X,S,T,r,\mu ,\sigma ,\sigma {'})\), one can estimate the level of ambiguity aversion or ambiguity-seeking characterizing option investors in times of abnormal uncertainty. For this purpose, the 2007–2008 credit crunch (and the period leading to it) provides an exemplary time window for gauging market ambiguity and investors’ heterogenous beliefs in conditions of uncertainty. In the case of German equity options, we use Deutsche Bank and the DAX index as illustrative examples to highlight option investors’ tendencies to diverge from risk-neutrality when markets are fraught with ambiguity (i.e., the period surrounding the 2007–08 banking crisis). Figures 2 and 3 illustrate these dynamics for a series of 1-month maturity (at-the-money) call and put options, with the last maturity occurring in December 2008. Given the symmetric nature of the Choquet random walk and the quadratic form of \(s^{2}\), we are able to extract ambiguity averse (\(m < 0\)) and ambiguity-seeking (\(m > 0\)) sentiments directly from option prices. This is achieved by minimizing the distance between model prices and observed market prices. These implied ambiguity attitudes are reflective of option holders’ ambiguous beliefs about future underlying asset returns and volatility over the respective option maturities. Extended to other contracts and markets, these measures of ambiguity can serve as forward-looking indicators of ambiguity aversion and ambiguity-seeking for various stocks and indices.

Fig. 2
figure 2

Implied ambiguity attitudes of Deutsche Bank options holders during 2006–2008. (Data source: Thomson Datastream, coverage: 03/07/2006-31/12/2008)

Full size image
Fig. 3
figure 3

Implied ambiguity attitudes of DAX index options holders during 2006–2008. (Data source: Thomson Datastream, coverage: 03/07/2006-31/12/2008)

Full size image

Significant deviations from risk-neutrality (blue line in Figs. 2, 3) are observed throughout 2006–2008, with severe swings and dispersions during the credit crunch period and around the fall 2008 global banking crash. Shifts in ambiguity (from aversion to seeking and vice-versa) also occur near and after the crash, with Deutsche Bank option holders showing more evidence of ambiguity than their DAX counterparts. This reflects the heightened level of uncertainty/ambiguity surrounding major global banks at the time. Findings suggest that our ambiguity-based models should be more efficient in terms of informational content than their risk-neutral counterparts (e.g., Driouchi et al. 2012). Figures 2 and 3 verify empirically that call and put option investorsFootnote 13 tend to deviate from risk-neutrality during periods of economic stress, confirming that normative assumptions of rational option pricing do not necessarily hold under such conditions.

The above findings also challenge claims of robustness and effectiveness of delta-neutral trading strategies focused on creating a risk-free hedge between short and long option positions according to the values of their hedge ratios. Aimed at eliminating the effects of stock price movements in a portfolio, these strategies fail when markets are fraught with ambiguity and subjective discounting takes over rational beliefs and expectations (e.g., LTCM and the Russian sovereign default). Since the Delta changes with changes in \(c\), alternative trading strategies need to track investors’ changing uncertainty preferences and subjective beliefs. Although not directly observable in the market place, \(c, \quad m\) and \(s\) can be imputed from economic and market data (e.g., economic confidence indicators, policy and economic uncertainty proxies, disagreements among economic forecasters or CDS spreads, etc.) and can serve as inputs to more robust option pricing models. These variables can be employed as instruments for gauging and monitoring market sentiment and investor ambiguity.

4 Conclusions

We developed closed-form solutions for the pricing of European options with stochastic (and fixed) exercise prices under Choquet ambiguity. Our Choquet-based models subsume existing classical models, such as the Margrabe (1978) and Black–Scholes–Merton (1973) option pricing models. Our analysis confirms that MMBS standard option prices are special cases of more general price bounds that can be observed in the marketplace when uncertainty is abnormally high and that market ambiguity and investor ignorance significantly moderate the relationship between option prices and uncertainty. We find that option values can either increase or decrease with volatility subject to decision-makers’ perceived ambiguity (aversion or seeking) given a finite option maturity. The developed analytical formulae can help us capture how swings in investor opinions resulting from heightened uncertainty and ambiguity affect option prices, and how the notion of “fair value” is relative in the presence of model uncertainty. Given ample evidence of heterogenous attitudes towards uncertainty among investors and market decision-makers, the models developed in this paper should be useful in deriving more accurate option prices in situations of abnormal uncertainty and extreme market sentiment. It is worth examining the extent to which such models are in line with heuristics used in practice for financial options trading and real options decision-making (Miller and Shapira 2004; Haug and Taleb 2011).

Our analysis presents several opportunities as well as challenges for future research. We have not dealt with situations of complete ignorance or events with unbounded volatility. We also did not cover alternative stochastic processes (beyond lognormal diffusion) which may involve discontinuities in prices, jumps or higher-moment effects. Nonetheless, there are several important theoretical and empirical implications deriving from this research. These may motivate revisiting several well-known empirical option pricing puzzles, reexamining option implied volatility surfaces under ambiguity, extending option pricing modeling under ambiguity in discrete-time using alternative processes, and re-examining the relationships between discount rates, dividend yields, option values and heterogenous beliefs using behavioral experiments, managerial surveys or high frequency market data.