1 Introduction

Dealing with the stochasticity of commodity and electricity prices is a key issue in contemporary energy markets and cannot be neglected by the producers of electrical power. In this paper, we propose a multistage stochastic optimization model for market-oriented power production planning. Optimization has a long history in this field, and in the last years stochastic optimization approaches have become more and more important. See, e.g., Takriti et al. (1996), Gollmer et al. (2000), Philpott and Schultz (2006), Sen and Yu (1993) and the overview Wallace and Fleten (2003).

In particular, we formulate an optimization model for thermal electricity production. Different types of fuels are bought at spot markets and stored to produce electric energy. Finally, the production is sold at an electricity spot market. Costs involve fuel costs as well as fixed and variable operating costs. In addition, we allow for trading at CO\(_2\) spot markets to have available the necessary amount of emission certificates. The aim is to maximize the asset value—consisting of a cash position and the value of stored fuel—at the end of the planning horizon. Because the problem is stochastic, we maximize a mixture of expectation and average value at risk.

We aim at a simplified model for mid-term planning that can be used for repetitive calculation. Each step from data to final decisions is described. We implement and solve concrete 1-year planning problems for a fictitious configuration of thermal units optimizing against the market prices.

Besides formulating the multistage stochastic optimization problem, which will be done in Sect. 2, this paper also discusses the estimation of the related price models. Oil, gas, coal and CO\(_2\) prices are modeled as Geometric Brownian motions with jumps. Electricity prices have properties that differ considerably from those of other commodities. In particular, they show strong seasonalities as well as spiking behavior. We therefore estimate electricity spot prices based on the related forward curve and deviations between this curve and actual prices, by introducing a new regime switching model. We estimate these models for European price data and analyze their in- and out-of-sample performance.

The concrete formulation of the optimization model uses the framework of tree-based multistage stochastic optimization. Based on the distance concept developed in Pflug and Pichler (2012), trees are constructed accordingly to a novel tree approximation method proposed in Kovacevic and Pichler (2012). This approach builds on a multiperiod generalization of the Wasserstein distance to a distance between processes.

Based on the implemented framework, we bring evidence for two aspects to be considered in production planning: We implement a small realistic thermal system and use it to analyze the effects of increasing CO\(_2\) prices on the accumulated CO\(_2\) emissions. Furthermore, we demonstrate the use of the model to calculate indifference prices for electricity delivery contracts with given contract size.

The paper is organized as follows: In Sect. 2, we develop the optimization model. Section 3 then gives a deeper view of the involved risk factors, describes the price models used and the related estimation procedures, and analyzes the estimation quality. In the final section, we give an overview of a tree-based reformulation of the optimization model and describe the tree reduction approach as well as a basic numerical example. Also in Sect. 4, we utilize the implemented system for a case study on indifference pricing and for some sensitivity analysis of CO\(_2\) prices. Finally, in the appendices, we give further details of the estimation procedure, show some empirical results, and the full specification of the reformulated optimization model.

2 The optimization model

Consider the decision problem of an electricity producer, who owns some thermal production units \({\fancyscript{I}}=\{1,\ldots ,I\}\) and uses fuels \({\fancyscript{J}}=\{1,\ldots ,J\}\) to produce electrical power over some planning horizon \({\fancyscript{T}}=\{\tau _{0},\ldots ,\tau _{T}\}\). Fuels have to be bought, electricity is sold at an electricity spot market, and further restrictions and costs (in particular related to CO\(_2\) emissions) have to be observed.

Clearly the producer has to take some risk: All kinds of prices are considered as stochastic in the following, and hence these risk factors are modeled as stochastic processes. Starting with some state space \(\varOmega \) and defined on a related filtered probability space \((\varOmega ,\varSigma ,\mathbb{P })\), with \(\varSigma \) representing some filtration and \(\mathbb{P }\) a probability measure, we refer to the price processes in the following way: For each sample path \(\omega \in \varOmega \) and point in time \(\tau _t \in {\fancyscript{T}}\), we denote by \(P_{t,j}^\mathrm{f}(\omega )\) the fuel spot price for fuel \(j\in {\fancyscript{J}}\), by \(P_{t}^\mathrm{x}(\omega )\) the electricity spot price, and by \(P_{t}^\mathrm{c}(\omega )\) the spot price for CO\(_2\) emission certificates. As usual, the filtration \(\varSigma =(\varSigma _{t})_{t \in T}\) is modeled as the filtration generated by the random vector \((P_{t}^\mathrm{f},P_{t}^\mathrm{x},P_{t}^\mathrm{c}),\) i.e., \(\varSigma _{t}=\sigma ((P_{t,}^\mathrm{f},P_{t}^\mathrm{x},P_{t}^\mathrm{c}),t \in \{0,1,\ldots ,T\})\).

The basic decisions are made regarding the electric energy \(x_{t,ij}(\omega )\) produced by unit \(i \in {\fancyscript{I}}\) using fuel \(j\) over time period \([\tau _{t},\tau _{t}+\varDelta _{t}]\) (where \(\varDelta _{t}=\tau _{t+1}-\tau _{t}\) is measured in hours), the amount \(f_{t,j}(\omega )\) of fuel \(j\) bought at time \(t\), and the amount \(c_{t}(\omega )\) of CO\(_2\) emission certificates bought (if positive) or sold at time \(t\). In our setup it is possible for a generating unit to use more than one fuel during the same time period, which means that we are seeking for an optimal fuel mix. Further (derived) decision variables will be defined later on.

In practice, amounts of fuels are measured by a huge variety of units, depending on the particular fuel and the concrete market location. To avoid in this paper the usage of conversion factors as much as possible, all amounts of fuel are expressed by their energy content in MWh. As a consequence, all fuel prices as well as the price of electricity are expressed in EUR/MWh. CO\(_2\) emissions and the amounts of traded certificates are expressed in (metric) tons and hence the certificate price in EUR/tonne. Because electricity is produced and simultaneously sold over periods \([\tau _{t},\tau _{t+1}]\), the prices \(P_{t}^\mathrm{x}\) have to be interpreted as weighted mean prices achieved over the whole period.

In the following description, all decision variables related to time \(\tau _t\) are considered as \(\varSigma _{t}\)-measurable, which means that decisions have to be taken based on information available at time \(t\). In order to shorten notation, from now on we will not explicitly mention the dependence of random variables on states \(\omega \), if no confusion is possible. In any case, it should be kept in mind that equations and inequalities involving random variables have to be understood as holding almost surely. Furthermore, we follow the convention that equations containing free indices \(i\in {\fancyscript{I}},j\in {\fancyscript{J}}\) or \(t \in \{0,1,\ldots ,T\}\) are intended to hold for all possible values of these indices, i.e., \(\forall i \in {\fancyscript{I}}, j\in {\fancyscript{J}}\) and for \(0\le t \le T\), if no special assumptions are stated.

2.1 Thermal power plants, fuels and the basic cost model

It is not possible to produce negative amounts of energy, and we do not allow for selling back fuel, which leads to the restrictions

$$\begin{aligned} x_{t,ij}\ge 0,\quad f_{t,j}\ge 0. \end{aligned}$$
(1)

Different types of power plants are characterized by their efficiencies for producing electricity with different fuels, the maximum power produced and the cost structure, which together define the merit order of turbines in the system. In the simplest setup, the produced energy is modeled as proportional to the amount of fuel used for conversion, i.e., for each generator \(i\) we use multiplicative factors \(\eta _{ij}\) representing the efficiency of producing electric energy with fuel \(j\). The maximum power (in MW) that can be produced with generator \(i\) is denoted by \(\beta _{i}\). This means that the generated electric energy is restricted by

$$\begin{aligned} \sum _{j=1}^{J}x_{t,ij}\le \beta _{i}\cdot \varDelta _{t}. \end{aligned}$$
(2)

Three kinds of cost are used throughout this paper: fuel costs, variable and fixed operating costs. The fuel used for producing an amount of energy \(x_{t,ij}\) is given by \(x_{t,ij}/\eta _{ij}\); hence, the related fuel costs are given by \(P_{t+1,j}^\mathrm{f}(\omega )\cdot x_{t,ij}/\eta _{ij}\). It is assumed that the fuel price is known only after deciding about the amount of fuel used. The variable operating costs \(\gamma _{i}\) per operating time (in EUR/h) include variable personnel costs and maintenance costs. The usage time is estimated by \(x_{t,ij}/\beta _{i}\). Finally, we also model fixed operating costs, including personnel as well as maintenance and capital costs. At first glance, it might seem that fixed costs do not influence the optimal solution. However, we assume that fixed costs have to be paid at each decision period and we will distinguish between positive and negative amounts of cash. Because interest paid on a negative cash position (debt) is higher than interest on positive cash, fixed costs have an effect on the risk of the decision problem.

In our examples, we aim at mid-term planning with weekly decisions; therefore, we will not use switching, ramping, or minimum power production constraints. Such constraints are most relevant in hourly (or daily) decision models and lead to mixed integer models. While comparably efficient formulations exist for deterministic planning (see, e.g., Torre et al. 2002 or Carrion and Arroya 2006), it is very difficult to include mixed integer constraints in a large stochastic problem, especially if calculation time is critical. As an example see, e.g., Nowak et al. (2005). We also do not use production-dependent efficiencies, which would lead to nonconvex optimization problems. By avoiding such complications, it is possible to increase the complexity of the stochastic model, in particular to use more scenarios.

2.2 Storage, CO\(_2\) and cash accounting

In the following we introduce storages \(s_{t,j}(\omega )\) for each fuel \(j\) (in MWh), CO\(_2\) emissions \(e_{t}(\omega )\) cumulated up to time \(t\) (in metric tons), an account \(a_{t}(\omega )\) for CO\(_2\) allowance certificates cumulated up to time \(t\) (in metric tons), and a cash position \(w_{t}(\omega )\) (in EUR). These variables depend on the decisions described in the previous section and hence are also stochastic processes, adapted to the filtration \(\varSigma \). With initial amount \(s^0_{j}\) and maximum amount \({\bar{s}}_{j}\), each storage \(j\) develops according to

$$\begin{aligned}&s_{0,j}=s_{j}^{0},\quad s_{t,j}=s_{t-1,j} +f_{t,j}-\sum _{i=1}^{I}\frac{x_{t-1,ij}}{\eta _{ij}}\qquad \forall t>0,\end{aligned}$$
(3)
$$\begin{aligned}&0\le s_{t,j}\le {\bar{s}}_{j}. \end{aligned}$$
(4)

Note that Eq. (3) models storage as the amount stored immediately before the beginning of the next production period \((\tau _{t},\tau _{t+1}]\). It is assumed that fuels are bought and stored at times \(\tau _t\), while they are used for electricity production over periods \((\tau _{t},\tau _{t+1}]\).

The production during any period \((\tau _{t},\tau _{t+1}]\) is restricted by the stored amount of fuel at the beginning of the period, i.e.,

$$\begin{aligned} \sum _{i=1}^{I}\frac{x_{t,ij}}{\eta _{ij}}\le s_{t,j}. \end{aligned}$$
(5)

Storage costs are based on a cost factor \(\zeta _j\) (EUR/MWh/h) for each fuel and are averaged for each time period. CO\(_2\) emissions and the related costs are modeled in the following way: At the beginning, the amount \(e^0\) of CO\(_2\) emitted before the planning horizon is known and during each period emissions \(e_t\) accumulate as follows:

$$\begin{aligned} e_{0}=e^{0}, \quad e_{t}=e_{t-1}+\sum _{j=1}^{J}\sum _{i=1}^{I}\frac{\varepsilon _{ij}}{\eta _{ij}}\cdot x_{t-1,ij}\qquad \forall t>0. \end{aligned}$$
(6)

Here, \(\varepsilon _{ij}\) denotes the amount of emissions (in metric tons, \(t\)) per MWh of fuel \(j\) produced by unit \(i\). At each time, it is possible to buy (\(c_{t}>0\)) or sell (\(c_{t}<0\)) CO\(_2\) allowance certificates at prices \(P_{t}^\mathrm{c}\). The transactions are accumulated on an account \(a_t\), which is finally cleared against the actual cumulated emissions \(e_t\), both in tons. Again, we start with a known amount \(a^{0}\) of certificates bought before the beginning and describe the certificate position by

$$\begin{aligned} a_{0}=a^{0},\quad a_{t}=a_{t-1}+c_{t}\qquad \forall t>0. \end{aligned}$$
(7)

Clearly the emission accounts have to be restricted by

$$\begin{aligned} a_{t} \ge 0, \quad e_{t} \ge 0. \end{aligned}$$
(8)

As we will see, a penalty, payable at the end of the planning horizon, ensures that emissions do not exceed the certificates hold.

Given all cash flows from fuel usage, storage, CO\(_2\) emissions and certificates, we are able to define accounting equations for the cash position. At time \(t=0\) we start with

$$\begin{aligned} w_{0}=w^{0}-\sum _{j=1}^{J}P_{0,j}^\mathrm{f}f_{0,j}. \end{aligned}$$
(9)

For \(0<t<T\), it is necessary to account for interest, fuel costs, cash flows from selling electricity and from trading with certificates, storage costs, and finally for operating costs. The cash position is split into a positive and a negative part \(w_{t}^{+},w_{t}^{-}\) which allows to apply different interest rates for borrowing (\(w_{t}^{-}>0\)) and lending (\(w_{t}^{+}>0\)):

$$\begin{aligned} w_{t} = w_{t}^{+}-w_{t}^{-}, \quad w_{t}^{+} \ge 0 \quad w_{t}^{-} \ge 0 \qquad \forall t>0. \end{aligned}$$
(10)

We use interest rates \(\rho _{b}\) for borrowing and \(\rho _{l}\) for lending such that \(\rho _{b}>\rho _{l}\). Because of the difference between the two interest rates, it is possible to avoid the explicit complementarity constraints \(w_{t}^{+}\cdot w_{t}^{-}=0\): Any unnecessary amount \(w_t^-\) is penalized harder than its counterpart \(w_t^+\) by the higher interest rate. These effects accumulate in the cash position and finally influence the objective function (defined later on). Hence, superfluous amounts will be avoided in the optimal solution.

Finally, with \(\zeta _{j}\) denoting storage costs per MWh and hour for fuel \(j,\gamma _{i}\) (EUR/h) denoting variable operating costs of generating unit \(i\) per hour and \(\kappa _{i}\) (EUR/h) denoting fixed operating costs of generating unit \(i\) per hour, the cash position updates in the following way:

$$\begin{aligned} w_{t}&= (1+\rho _{l})w_{t-1}^{+}-(1+\rho _{b})w_{t-1}^{-}\\&-\sum _{j=1}^{J}P_{t,j}^\mathrm{f}f_{t,j} - P_{t}^\mathrm{c}c_{t}\nonumber \\&+ P_{t}^\mathrm{x}\cdot \sum _{i=1}^{I}\sum _{j=1}^{J}x_{t-1,ij}\nonumber \\&-\sum _{j=1}^{J}\zeta _{j}\frac{(s_{t,j}+s_{t-1,j})}{2}\varDelta _{t-1}\nonumber \\&-\sum _{i=1}^{I}\left( \frac{\gamma _{i}}{\beta _{i}} \cdot \sum _{j=1}^{J}x_{t-1,ij}-\kappa _{i}\cdot \varDelta _{t-1} \right) \qquad 0<t<T\nonumber \end{aligned}$$
(11)

At time \(T\) no fuel is bought, but the certificates have to be cleared. If the accumulated certificates \(a_T\) do not suffice, i.e., the difference between actual cumulative emissions \(e_T\) and \(a_T\) is positive, then this difference is valued at the actual certificate price plus a penalty of \(\theta =100\) EUR/t (see, e.g., Environmental Agency (GB) 2009). The resulting amount has to be paid. On the other hand, remaining certificates just lose their value.

Analogously to (10), the positive part \(u^+\) of the difference can be modeled by

$$\begin{aligned} e_T - a_T = u^{+}-u^{-}\!, \quad u^{+} \ge 0, \quad u^{-} \ge 0. \end{aligned}$$
(12)

Hence the cash position at time \(T\) is given by

$$\begin{aligned} w_{T}&= (1+\rho _{l})w_{T-1}^{+}-(1+\rho _{b})w_{T-1}^{-}\\&+P_{T}^\mathrm{x}\cdot \sum _{i=1}^{I}\sum _{j=1}^{J}x_{T-1,ij}\nonumber \\&-\sum _{j=1}^{J}\zeta _{j}\frac{(s_{T,j}+s_{T-1,j})}{2}\varDelta _{T-1}\nonumber \\&-\sum _{i=1}^{I}\left( \frac{\gamma _{i}}{\beta _{i}}\cdot \sum _{j=1}^{J}x_{T-1,ij}-\kappa _{i}\cdot \varDelta _{T-1} \right) \nonumber \\&-(\theta +P_{T}^\mathrm{c})u^+\nonumber \!. \end{aligned}$$
(13)

Note that because positive differences are penalized in the cash position and the cash position affects the objective function via (14), \(u^+\) and \(u^-\) will not be simultaneously positive in the optimal solution of the full optimization problem.

2.3 The objective function and the overall optimization problem

The producer aims at maximizing the revenue over the planning horizon. The decision is based on the sum of the cash position and the market value of fuels stored at time \(T\). This is the asset value \(v_{T}(\omega )\) at the end of the planning horizon, a \(\varSigma _T\)-measurable random variable:

$$\begin{aligned} v_{T}=w_{T}+\sum _{j=1}^{J}s_{T,j}\cdot P_{T,j}^\mathrm{f}. \end{aligned}$$
(14)

In this specification, it is assumed that the certificates lose their value at the clearing time \(T\). Because \(v_{T}\) is a random variable, we define the objective as a mixture of expectation and average value at risk. For a random variable \(X\) with c.d.f. \(F\) the average value at risk is defined as

$$\begin{aligned} \hbox {AV}@{\hbox {R}}_{\alpha }(X)=\int _{0}^{\alpha }F^{-1}(p). \end{aligned}$$
(15)

See Eichhorn and Römisch (2005), Pflug and Römisch (2007) for more details on \(\hbox {AV}@\hbox {R}\) and the related class of polyhedral risk and acceptability measures and Eichhorn et al. (2004) for further applications in electricity production. Summarizing the setup, we can write the decision problem of the producer as

$$\begin{aligned}&\max _{x,f,c,(s,w,w^+,w^-,v,a,e.u^+,u^-)} \lambda \cdot \mathbb{E }[v_{T}]+(1-\lambda )\cdot \hbox {AV}@{\hbox {R}}_{\alpha }(v_{T})\\&\text {s.t.}\quad (1){-}(14)\nonumber \\&x,f,c\triangleleft \varSigma \nonumber \\&s,w,v,a,e,u\triangleleft \varSigma .\nonumber \end{aligned}$$
(16)

The trade-off between the two objectives—the expectation and the \({\mathbb{A }}\)V@R—is defined by the weighting factor \(0\le \lambda \le 1\). The constraints \(x,f,c\triangleleft \varSigma \) and \(s,w,v,a,e\triangleleft \varSigma \)—the non-anticipativity constraints—require that all decision processes are adapted to the underlying filtration \(\varSigma \), i.e., that decisions at time \(t\) are based only on information available up to time \(t\).

3 Price models

In this section, we describe the underlying data used for the price models, show estimation procedures and discuss the results. For the calibration of the gas price model, we take daily GPL spot gas prices provided by Bloomberg, sample period April 2007–December 2011. For the oil prices, we look at Brent Crude daily spot oil prices over the sample period: May 2003–December 2011 (index EUCRBREN, source Bloomberg). Spot coal prices for Europe are published weekly, for example, by McCloskeys key physical prices for North West Europe (NWE) steam coal marker. We thus take the Index MSCMEUET, source Bloomberg, data sample from 9th December 2005 to 25th June 2012. We further look at CO\(_2\) emission allowances, taking daily observations (EUETSSY1 price index provided by Bloomberg) between April 2008 and December 2011. For electricity we take EEX Phelix hourly electricity prices quoted at the European Energy Exchange (EEX), between September 2008 and December 2011.

In Table 2, we show descriptive statistics of the gas, coal, oil and emission allowance (EUA) prices. The skewness and kurtosis coefficients suggest a leptokurtic distribution with negatively skewed returns in all three investigated markets. This is also confirmed by the Jarque–Bera test results which clearly reject the null hypothesis of a normal distribution for both levels and daily returns. Furthermore, autocorrelations die out slowly in levels, which is consistent with a very persistent, possibly non-stationary variation. To investigate the stationarity properties of the analyzed commodity prices we employ three-unit root tests (Table 3). The results suggest that, at conventional significance levels, logarithmic spot prices are non-stationary. This is similar to Daskalakis et al. (2009) and clearly contradicts the common assumption of mean reverting behavior in commodity prices.

3.1 Preliminaries

We aim at an optimization problem with five driving random factors (gas, coal, oil, CO\(_2\) and electricity prices). The first question in estimating the related price models is whether it is worthwhile to estimate a joint model. While it seems reasonable that some dependencies between those markets might be relevant, the literature on joint models for commodity prices is scarce. We can mention in this sense (Paschke and Prokopczuk 2009), who proposed a multi-factor model for the joint dynamics of related commodity spot prices in continuous time, with an application on crude/heating oil and gasoline prices. Another example is Pilz and Scholgl (2009), who derive a hybrid commodity and interest rate market model. However, the study refers mainly to futures commodity markets with application to oil prices. Miltersen (2003) shows how to build a stochastic model for commodity price behavior that matches the current term structure of forward and futures prices. Casassus et al. (2010) found that long-term co-movement among commodities is driven by economic relations, as an application for oil prices. However, all cited models are applied to oil/gasoline prices. To our knowledge, a joint model tested simultaneously for different European commodity prices (gas, oil, coal, etc.) was not published so far.

As a starting point we investigated whether there are significant co-movements in the commodity prices in such a way that a joint simulation model can be derived. Thus, we applied Principal Component Analysis (PCA) to identify possible joint factors driving the commodity prices. For this purpose, we looked at daily data between April 2008 and December 2011 for gas, (crude) oil, CO\(_2\) emission allowances and electricity prices as described in the previous section. The coal prices were left apart, since we have available only weekly observations in this case. In general, we observe very low correlations (see Table 4). There is some correlation (\({<}0.2\)) between CO\(_2\) emission rights and oil prices, between CO\(_2\) and gas (\({<}0.1\)) as well as between gas and electricity (\({<}0.1\)). The PCA shows that the first factor explains \(31~\%\), the first two factors explain \(58~\%\) of the variance, etc. The eigenvalues of all four factors are relatively close, so we cannot conclude clearly that there are factors which explain most of the variation of all included prices (see Table 5). The rotated component matrix also shows that basically each factor drives one commodity (see Table 6). Thus, there is no clear evidence for the use of a joint factor model. Furthermore, we performed a cointegration analysis pairwise and included all prices at once in the analysis, but did not get conclusive results.Footnote 1

3.2 Modeling commodity prices: gas, oil, CO\(_2\) and coal prices

3.2.1 Overall approach

The descriptive statistics of gas, oil and EUA spot prices indicates that they are likely to be characterized by non-stationarity and jumps, as indicated by the skewness and kurtosis. A model based on the standard Geometric Brownian motion process would be too limited in this case. We therefore apply Merton’s jump diffusion model (Merton 1976)—Geometric Brownian motion augmented by Poisson jumps (GBMPJ) which, according to the literature (e.g., Schwartz 1997; Bierbrauer et al. 2007 or Meade 2010), shows a good performance in modeling the dynamics of commodity prices.

We estimate the Merton model following the discussion in Honoré (1998). The occurrences of jumps are modeled as Poisson process with \(\hbox {d}J_t\sim \hbox {Po}(\lambda \hbox {d}t)\), and the jump amplitude \(Y_t\) is assumed to be log-normally distributed, i.e., \(\ln (1+Y_t)\sim N(\mu , \delta ^2)\). Thus, the log spot price \(\ln (S_t)\) at time \(t\) has the form:

$$\begin{aligned} \ln (S_t)=\ln (S_0)+\left( \alpha -\frac{1}{2}\sigma ^2\right) t+\sigma W_t+\sum _{0<s\le t}\ln (1+Y_s\hbox {d}J_s). \end{aligned}$$
(17)

The model parameters \(\psi =(\alpha , \sigma , \lambda , \mu , \delta )\) in Eq. (17) are estimated by maximum likelihood, following consistently the procedure proposed by Honoré (1998, pp. 3–8).

3.2.2 Results

Our parameter estimates for gas, oil, coal and EUA prices are summarized in Table 1. For a robustness check, we also perform an out-of-sample test by reestimating the parameters for a shorter sample which ends on 1st December 2010. It shows that the estimated parameters are not sample dependent. The jump intensity \(\lambda \) has the largest value for the gas prices. Oil prices show the lowest jump intensity estimates. This is consistent with the kurtosis, skewness and Jarque–Bera values which are the largest in case of gas (and the smallest for oil), as shown in Table 2.

Figures 9, 10, 11 and 12 show the means and quantiles of 50,000 scenarios simulated for oil, EUA, gas and coal spot prices based on the GBMPJ model starting in 1st December 2011 for a horizon of 300 days (52 weeks in case of coal) and compare it with the evolution of the real prices in the subsequent time period. One can see that the scenario means reflect the spot price dynamics in a realistic way for all commodities.

Table 1 ML estimation results of the GBMPJ model for oil, EUA, gas and coal spot prices
Full size table

3.3 Modeling electricity prices

3.3.1 Preliminaries

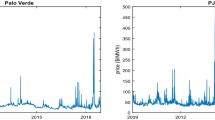
Electricity prices have properties that differ considerably from those of financial assets, or even of other commodities (see Keles et al. 2011; Blöchlinger 2008). Therefore, we treat them separately. The seasonal behavior of electricity prices is one of the most complicated among all commodities. It is predominantly caused by the almost inelastic short-term demand for electricity. Beside this, the capacity to store electricity is very limited and it is expensive or even damaging to change the production of big generating units. These facts can be seen as causes for spikes and for negative electricity prices. From an economic perspective, negative prices can be rational, e.g., if the costs to shut down or ramp up a power plant unit exceed the loss for accepting negative prices (see Keles et al. 2011). Therefore, since 1st September 2008, negative price bids are allowed at the German power exchange EEX. Historical spot market data over the investigated period show a total amount of about 100 h with negative prices. Mostly, they occur during the night and early morning hours (2300–0800) as displayed in Fig. 13.

Beside the deterministic impact factors, electricity spot prices are also influenced by uncertain factors like power plant outages and fluctuant renewable electricity generation. These uncertainties are drivers of the stochastic component of the spot prices. Thus, we derive a new regime switching model which takes into account the deterministic component of electricity prices, as well as the market expectation using an hourly price forward curve (HPFC) as input. Subsequently, the regime switching model reflects big fluctuations of the market spot price around the HPFC: upward and downward spikes may occur with a certain probability, which also allows simulating negative prices.

3.3.2 Regime switching model for electricity prices

An important characteristic of electricity prices is their spiking behavior, also called “jump groups” (see Keles et al. 2011): Prices may jump into another price level, called “spike regime”, and afterwards jump back to the base price level, called “base regime”. Therefore, regime switching approaches for electricity prices are often employed in literature (see, for e.g., Keles et al. 2011).

We calibrate our model using a HPFC generated for the next trading day at EEX (first day HPFC), but also consider the fluctuation of spot prices around the HPFC, due to risk factors such as power plant outages, fluctuant renewable electricity generation, etc. The HPFC gives us an important information about the expectation of the future spot prices. Since spot prices may vary for each hour of the day, probabilities for upward or downward spikes are derived for each hour of each week day (168 parameters). The probability values quantify the likelihood that the spot price is in the “base regime” or in one of the upper or lower spike regimes. Furthermore, we assume that upward or downward spikes are exponentially distributed and we determine the expected spike size for each hour of each week day. The model can be described by

$$\begin{aligned}&\hbox {MCP}_t = \left\{ \begin{array}{l@{\quad }l} f_t^\mathrm{L}-{\hbox {Spike}}_t^- &{} \text {with probability }p_h^-\\ f_t \cdot \exp (r_t) &{} \text {with probability }1-p_h^- - p_h^+\\ f_t^\mathrm{U}+{\hbox {Spike}}_t^+ &{} \text {with probability }p_h^+ \end{array} \right. \end{aligned}$$

with

$$\begin{aligned}&{\text {Spike}}_t^+ \sim \mathrm{Exp }(\lambda _h^+)\\&{\text {Spike}}_t^- \sim \mathrm{Exp }(\lambda _h^-)\\&r_t \sim N(0,\sigma _h^2)\\&f_t^\mathrm{L}=f_t*\exp (-\alpha _h)\\&f_t^\mathrm{U}=f_t*\exp (\alpha _h) \end{aligned}$$

where

\({\text {MCP}}_t\) :

Market clearing price (or spot price) for time \(t\) measured in hours

\(f_t\) :

Forward price for hour \(t\) from HPFC

\(h\) :

Index of the week hour that corresponds to time \(t\), i.e., \(h(t):\, t\rightarrow \{1,\ldots ,168\}\)

\({\text {Spike}}_t^+\) :

Spike (upward), exponentially distributed with parameter \(\lambda _h^+\)

\({\text {Spike}}_t^-\) :

Spike (downward), exponentially distributed with parameter \(\lambda _h^-\)

\(f_t^\mathrm{U}\) :

Upper limit of the Gauss dynamics

\(f_t^\mathrm{L}\) :

Lower limit of the Gauss dynamics

\(r_t\) :

Normally distributed random variable \(N(0,\sigma _h^2)\)

Parameters:

\(p_h^+\) :

Probability for spike upwards

\(p_h^-\) :

Probability for spike downward

\(\sigma _h^2\) :

Volatility of the Gaussian dynamics

\(\lambda _h^+\) :

Parameter of the exponential distribution for upward spikes

\(\lambda _h^-\) :

Parameter of the exponential distribution for downward spikes

\(\alpha _h\) :

Delimitates the upper/lower bounds of the “base regime.”

We calibrate our model using as input the first day HPFC. We generate one HPFC for each day between September 2008 and December 2011, and we extract always the first day of each curve. We construct this way the first day HPFC, which contains updated information about the next day expected price. It is of great importance to look at the updated curve, since the level of electricity prices can change significantly also on short term. In Appendix A, we describe the derivation of HPFCs. The Gaussian regime around the first day HPFC is delimited by the bands \(f_t^\mathrm{L}\) and \(f_t^\mathrm{U}\). Deviations from the HPFC are driven by the normally distributed random variable \(r_t\). Upper and lower spikes occur with probabilities \(p_h^+\) and \(p_h^-\), and their magnitude is exponentially distributed. The model parameters are estimated using a maximum likelihood estimation procedure, as discussed in the next subsection.

3.3.3 Estimation procedure for the electricity model

Observations are given at (hourly) time points \(t=1,\ldots ,T\). Let \(h(t) : t \rightarrow \{1, \ldots , H\}\) a function that maps to each time point \(t\) the index of the corresponding week hour (\(H=168\) is the number of hours per week). In the first step, the observations are assigned to different regimes. The values that separate the Gaussian from the lower or from the upper spike regime, respectively, for each time band \(h'=1,\ldots ,H\) are set to \(\alpha _{h'} := \alpha \cdot s_{h'}\). Parameter \(\alpha >0\) is unique for all hours and \(s_{h'}\) is the estimated standard deviation of \(r_t := \ln {\text {MCP}}_t - \ln f_t\) for all \(t=1,\ldots ,T\) with \(h(t)=h'\), i.e., before assigning the observations to different regimes, but taking into account only positive prices. Define for each hour \(h'=1,\ldots ,H\) the sets

$$\begin{aligned} {\fancyscript{D}}^\mathrm{L}(h')&:= \{ t = 1,\ldots ,T \,|\, h(t) = h' \,\wedge \, {\text {MCP}}_t < f_t \cdot e^{-\alpha _{h'}} \} \\ {\fancyscript{D}}^\mathrm{U}(h')&:= \{ t = 1,\ldots ,T \,|\, h(t) = h' \,\wedge \, {\text {MCP}}_t > f_t \cdot e^{\alpha _{h'}} \} \\ {\fancyscript{D}}^G(h')&:= \{ t = 1,\ldots ,T \,|\, h(t) = h' \,\wedge \, f_t \cdot e^{-\alpha _{h'}} \le {\text {MCP}}_t \le f_t \cdot e^{\alpha _{h'}} \} \end{aligned}$$

that contain the indices of the hours that belong to one of the three regimes. Then, for each \(h'=1,\ldots ,H\) the parameters are found by

$$\begin{aligned} \lambda _{h'}^-&= \frac{\#\hbox {elements in} {\fancyscript{D}}^\mathrm{L}(h') }{ \sum _{t\in {\fancyscript{D}}^\mathrm{L}(h')} (f_t \cdot e^{-\alpha _{h'}} - {\text {MCP}}_t) } \\ \lambda _{h'}^+&= \frac{\#\hbox {elements in} {\fancyscript{D}}^\mathrm{U}(h')}{ \sum _{t\in {\fancyscript{D}}^\mathrm{U}(h')} ({\text {MCP}}_t - f_t \cdot e^{\alpha _{h'}}) } \\ \sigma _{h'}^2&= \frac{1}{\#\hbox {elements in} {\fancyscript{D}}^G(h') }\sum _{t\in {\fancyscript{D}}^G(h')} (\ln {\text {MCP}}_t - \ln f_t)^2. \end{aligned}$$

The value of \(\alpha \) is chosen so that the log-likelihood function

$$\begin{aligned}&\ln \fancyscript{L}(\sigma _1,\ldots ,\sigma _H, \lambda _1^+,\ldots ,\lambda _H^+, \lambda _1^-,\ldots ,\lambda _H^- \,|\, \alpha ) \\&\quad =\sum _{h'=1}^H \sum _{t\in {\fancyscript{D}}^\mathrm{L}(h')} \ln \phi _\mathrm{exp}(f_t \cdot e^{-\alpha \cdot s_{h(t)}} -{\text {MCP}}_t \,|\, \lambda _{h'}^-) \\&\qquad + \sum _{h'=1}^H \sum _{t\in {\fancyscript{D}}^\mathrm{U}(h')} \ln \phi _\mathrm{exp}({\text {MCP}}_t - f_t \cdot e^{\alpha \cdot s_{h(t)}} \,|\, \lambda _{h'}^+) \\&\qquad + \sum _{h'=1}^H \sum _{t\in {\fancyscript{D}}^G(h')} \ln \phi _\mathrm{norm}(\ln {\text {MCP}}_t - \ln f_t \,|\, 0, \sigma _{h'}) \end{aligned}$$

is maximized, where

$$\begin{aligned} \phi _\mathrm{exp}(x \,|\, \lambda )&= \left\{ \begin{array}{l@{\quad }l} \lambda e^{-\lambda x}, &{} x \ge 0 \\ 0 &{} x < 0 \end{array} \right. , \\ \phi _\mathrm{norm}(x \,|\, \mu , \sigma )&= \frac{1}{\sqrt{2 \pi \sigma ^2}}\exp \left\{ -\frac{1}{2} \left( \frac{x-\mu }{\sigma } \right) ^2 \right\} \end{aligned}$$

are the densities of the exponential and the normal distribution with parameters \(\lambda >0\) and \(\mu =0, \sigma >0\), respectively.

3.3.4 Results

Our estimation results for all hours of each week day are presented in Tables 7 and 8. The expected values for each hour of the upward or downward spikes, \(1/\lambda _h^+\) and \(1/(-\lambda _h^-)\) are given in EUR/MWh. We observe that large spikes are expected to occur during the night hours, as well as during the midday and evening peak hours. Furthermore, we have a higher volatility \(\sigma _h^2\) during the midday and evening peak hours. For each hour \(h\), the probabilities for upward and downward spikes, \(p_h^+\) and \(p_h^-\), are denoted in \(\%\). There is a larger probability that electricity prices fall into the lower “spike regime” during the night hours. This result is in line with our findings from Fig. 13. For each day hour, there is a higher probability that large spikes occur during Sundays, which is also confirmed by the literature (see, for e.g., Keles et al. 2011). The parameter \(\alpha _h\) was estimated at \(1.6\).

After calibrating the model, several simulations were carried out to evaluate the goodness of fit in- and out-of-sample. Figure 14 summarizes the quantiles over 50,000 scenarios for the spot electricity prices, for a horizon of 1 month, starting in September 2008 (for an in-sample test) and in December 2011 (out-of-sample). We observe that the simulated electricity spot prices reflect the daily, weekly and annual cycles of electricity prices. Furthermore, the model generates important properties like single peaks or jump groups and the mean reverting property is captured very well by the model.

From the graphical comparison of simulated and historical prices, it can be concluded that the simulated electricity price curve is similar to the observed one. In addition, different quality factors such as the \(R^2\) and the mean average percentage error (MAPE)Footnote 2 are computed for different estimation samples. The results in the following table show that the model performance is not sample dependent:

Estimation sample

\(R^2\)

MAPE

01/09/2008–01/12/2011

\(0.559\)

\(0.168\)

01/09/2008–01/12/2010

\(0.572\)

\(0.157\)

4 Implementation of the production planning model and applications

In the following we apply the described optimization model to a concrete configuration of thermal power plants. The prices used for coal, gas and oil as well as for CO\(_2\) certificates were simulated from the price models analyzed in Sect. 3 and afterwards reduced to tractable trees. The implementation is used to consider two practical case studies: First, we analyze the effects of increasing CO\(_2\) prices on the decisions made and second, we analyze minimum production costs of electricity delivery contracts in the framework of indifference pricing.

4.1 The tree reformulation

Problem (16) cannot be solved directly. In order to solve concrete instances within the framework of multistage stochastic optimization, it has to be reformulated on a discrete probability space. The setup follows the approach described in Pflug and Swietanowski (2000), Pflug and Römisch (2007), see also Birge and Louveaux (1997) where alternative approaches can be found: Consider a finite probability space \(\varOmega =(\omega _{1},\ldots ,\omega _{K})\), representing \(K\) scenario paths. Any stochastic process defined on this sample space can be represented as a finite tree with node set \({\fancyscript{N}}=\{0,1,\ldots ,N\}\). The levels of the tree correspond to the decision stages. Let \({\fancyscript{N}}_{t}\) be the set of nodes at level \(t\), for \(t=0,\ldots ,T\). The last level \({\fancyscript{N}}_{T}\) contains the \(K\) leaves of the tree which can be identified with the scenario paths: \({\fancyscript{N}}_{T}=\varOmega =(\omega _{1},\ldots ,\omega _{K})\). The tree structure represents the filtration of the process and can be defined by stating the (unique) predecessor node \(n_{-}\) for each node \(n\). The set of child nodes is denoted by \(n_{+}\). There is a unique root node, by convention denoted with \(0\), which represents the present. Furthermore, each node \(n\) carries a probability \(Q_{n}\ge 0\) with \(\sum _{j\in {\fancyscript{N}}_{t}}Q_{j}=1\) for all points in time \(t\). By construction there is a one to one relation between any node \(n\) and an assigned pair \((\omega ,t\)), which means that each node is related to the state of the system at time \(t\) in sample path \(\omega \) and vice versa.

The price processes \(P^\mathrm{x},P^\mathrm{f},P^\mathrm{c}\) are represented w.r.t. the nodes \(n\) of the tree, i.e., we write \(P_{n}^\mathrm{x},P_{n}^\mathrm{f},P_{n}^\mathrm{c}\) instead of \(P_{t}^\mathrm{x}(\omega ),P_{t}^\mathrm{f}(\omega ),P_{t}^\mathrm{c}(\omega )\). In similar manner, the decision variables \(x,f,c,s,w,v,a,e\) are related to the nodes: So far \(x_{t,ij}\) denoted the random vector of produced energy in period \((t,t+1]\). From now on (in discretized models) \(x_{n,ij}\) will denote the value of the produced energy planned at node \(n\) and produced in the time period between \(n\) and its successor nodes. This formulation automatically ensures measurability.

Furthermore, almost sure constraints are obtained by formulating them for all nodes of a stage \({\fancyscript{N}}_t\) and the objective function is based on the probabilities related to the nodes: The expectation is directly calculated by weighting the values at each leaf node with the respective probability. For the \(\hbox {AV}@\hbox {R}\), we use its well-known epigraphical representation (see, e.g., Rockafellar and Uryasev 2000). Figure 8 shows the full finite state space reformulation, which is an LP.

It should be noted that typically the used trees are not very dense: If the time horizon is 1 year and the decision periods have a length of 1 week, a binary tree would lead to a number of nodes around \(9\times 10^{15}\). While for LPs without integer variables, it is easily possible to solve instances with several millions variables and constraints, even binary trees will lead to instances that cannot be calculated anymore. Therefore, the trees must be sparse, i.e., most of the paths in the tree do not branch most of the time.

In our model, it is possible to buy and sell emission certificates. This can lead to unbounded solutions (arbitrage opportunities) because predictability is high for sparse trees. In order to avoid this difficulty, we allow trading of certificates only in nodes with more than one significantly distinct successors: we add constraints

$$\begin{aligned} n\in {\fancyscript{N}}_{\lnot 0}^{b}:\;\; a_{n}=a_{n_{-}}+c_{n}, \end{aligned}$$
(18)

where \({\fancyscript{N}}^{b}_{\lnot 0}\) denotes the set (excluding the root) of nodes with more than two successor nodes such that the related prices go in different directions.

Tree construction is done in three steps: Starting from an estimated model for the relevant prices, we simulate scenario paths and use a tree reduction method (Dupacova et al. 2003, as an alternative Heitsch and Römisch 2011) to construct a big scenario tree (with, e.g., several thousand leaf nodes). In the last step, the big tree is reduced to a smaller tree (with several hundred leaf nodes), which is finally used as the basis for the reformulated optimization model as described above. We base this reduction on a multistage distance between trees, which generalizes the Wasserstein distance and was recently proposed and analyzed in Pflug and Pichler (2012). The exact algorithm can be found in Kovacevic and Pichler (2012).

The advantage of this approach lies in the fact that the multistage distance is able to account for the development of information over time in a proper way: While the Wasserstein distance evaluates the similarity between trees based on values and probabilities and uses only one relevant \(\sigma \)-algebra, the multistage distance uses values and probabilities as well, and also takes into account the whole filtrations represented by the respective tree structures using all conditional probabilities.

4.2 System specification and basic results

The thermal system consists of three combustion turbines, two combined cycle plants and one steam turbine. The steam turbine is fired with coal, whereas the other plants are able to use both gas and oil. The steam turbines are more efficient than the simple combustion turbines and the combined cycle plants are more efficient than the steam turbine. On the other hand, combustion turbines emit more CO\(_2\) than combined cycle turbines and steam turbines emit more CO\(_2\) than combustion turbines. The same order also holds for fixed and variable operating costs, and for the size (maximum power) of the turbines. The exact numbers have been derived from typical engines described in Konstantin (2007) and can be found at http://homepage.univie.ac.at/raimund.kovacevic/publications.html.

Storage capacity is sufficient for approximately 3 weeks full production and the system starts with a small amount of stored fuel at the beginning. Again the related data, including storage costs, can be found at the above homepage.

As described before, we use historical data to estimate models for gas, oil, coal and electricity prices as well as CO\(_2\) emission prices. The cash position starts with a budget of 1 million EUR. In addition, interest on the cash position is given by \(2.5~\%\) and interest on debt is \(12.5~\%\). Finally, the average value at risk is calculated at the level \(\alpha =0.05\). The mixture parameter \(\lambda \) is set to \(0.5\) in the standard case.

Fig. 1
figure 1

Simulated scenario paths for all used commodities

Full size image

From the estimated models, we simulate scenario paths for all commodities (see Fig. 1), calculate weekly averages, and finally construct a tree containing price and probability information. In particular, we use a medium size tree with 52 stages representing the weeks of a year, 350 leaf nodes, representing the scenarios, and all in all 5,950 nodes. The pure structure of the resulting tree is depicted in Fig. 2 and represents the filtration of the involved price and decision processes. This formulation resulted in LP problems with 331,665 constraints and 359,635 decision variables. The model was implemented in AIMMS 3.12 and the interior point algorithm of GUROBI 4.6 was used to solve all discussed instances. The mean running time for instances related to the efficient frontier calculation below was 1.92 s, while one instance of indifference pricing (see Sect. 4.3.2) took 22.3 s on average.

Fig. 2
figure 2

Tree structure representing the filtration of the approximating processes used for numerical examples

Full size image

As the first result, Fig. 3 shows the development of the asset value \(v_t\) over time, while Fig. 4 shows an estimated p.d.f. of the asset value at the end of the planning horizon in more detail.

Fig. 3
figure 3

Standard case: Development of the cash position over time

Full size image
Fig. 4
figure 4

Standard case: distribution (distribution function) of the cash position at the end of the planning horizon

Full size image

While we use the arbitrary value \(\lambda =0.5\) for the mixing parameter in the basic setup, it is possible to calculate an efficient frontier for the trade-off between expected end value and risk by calculating optimal solutions, when \(\lambda \) is varied between 0 and 1. The results are shown in Fig. 5: For a given risk, \(\mathbb{E }(v_T)-\hbox {AV}@\hbox {R}(v_T)\), the points on the line show the largest expected end value possible—which is related to a certain value of \(\lambda \).

Fig. 5
figure 5

Efficient frontier for the trade-off between expected end value \(\mathbb{E }[v_{T}]\) and riskiness \(\mathbb{E }[v_{T}]-\hbox {AV}@\hbox {R}_{\alpha }(v_{T})\) of the end value

Full size image

4.3 Two case studies

4.3.1 Varying CO\(_2\) emission prices

For political reasons, European CO\(_2\) emission prices are low at the time being and do not substantially reduce CO\(_2\) emissions. We use the basic model to implement a simple analysis of the effect of increasing CO\(_2\) prices on the optimal decisions. It should be kept in mind that this is an analysis from the viewpoint of a producer with a certain given thermal system, not a market view.

The price scenarios are varied such that all CO\(_2\) prices are increased by \(5,10,20,30\) and \(50~\%\). For each of these scenarios, problem (16) is solved to obtain the related optimal values and decisions. Figure 6 depicts the effect of these price variations on the (accumulated) amount of CO\(_2\), emitted over the whole planning horizon. Further results show that for the analyzed thermal system, an overall increase of CO\(_2\) prices by \(1~\%\) reduces the expected asset value by \(1.66~\%\), but (on average) reduces the accumulated CO\(_2\) emissions by only \(0.035~\%\). The bimodal shape of the p.d.f. is mainly caused by the two types of gas/oil plants—if CO\(_2\) prices increase, production is gradually switched to the more efficient combined cycle plants.

Fig. 6
figure 6

Effect of an increase in CO\(_2\) prices on the accumulated CO\(_2\) emissions. The distribution of emissions is represented by a kernel density estimate

Full size image

4.3.2 Indifference pricing for electricity delivery contracts

Assume now that in addition to producing electricity for the spot market, one also considers electricity delivery contracts with given contract size. For simplicity, we consider contracts with a fixed (and constant) amount \(E\) of electricity deliverable during all weeks (52) of the planning horizon at a fixed, agreed price \(K\) per MWh. Hence, the generator has to produce some electricity and sell it at a fixed price, regardless of the actual development of prices. Only excess production capacity can be used for trading at the spot market.

The question arises at which price \(K\)—given our thermal system—the producer is willing to close a deal with given contract size. In the following we use indifference pricing as an approach to find this minimum price: The indifference principle states that the seller of a product compares his optimal decisions with and without the contract and then requests a price such that he is at least not worse off when closing the contract. This idea goes back to insurance mathematics (Bühlmann 1972) but has been used for pricing a wide diversity of financial contracts in recent years; see Carmona (2009) for an overview.

To implement indifference pricing within our framework, problem (16) is solved to find the optimal value \(v^*\) without the analyzed contract. In the second step, a modified optimization problem is formulated to find the minimal bid price: Because the producer should be indifferent, one constraint is given by

$$\begin{aligned} \lambda \cdot \mathbb{E }[v_{T}]+(1-\lambda )\cdot \hbox {AV}@\hbox {R}_{\alpha }(v_{T}) \ge v^*. \end{aligned}$$
(19)

Next, it is allowed to buy electricity \(y_t\ge 0\) at the spot market, and we ensure that the contract is fulfilled:

$$\begin{aligned} \sum _{i\in I,j\in J}x_{t,ij}+y_{t}\ge E \end{aligned}$$
(20)

Finally, the calculation of the cash position has to be corrected for the fact that parts of the electricity are sold at the contracted price \(K\) instead of the actual spot prices: The third line of (11) is replaced by

$$\begin{aligned} P_{t}^\mathrm{x}\cdot \left( \sum _{i=1}^{I}\sum _{j=1}^{J}x_{t-1,ij}-E\right) + K\cdot E. \end{aligned}$$
(21)

In order to find the indifference price, we then solve the optimization problem

$$\begin{aligned} \begin{array}{r@{\quad }l} \min \limits _{x,f,c,y,K,(s,w,v,a,e)} &{} K\\ \text {s.t.} \ &{} (1)-(14), \hbox {using } (21) \\ (19),(20) &{} x,y,f,c\triangleleft \varSigma \\ &{} s,w,v,a,e\triangleleft \varSigma , \end{array} \end{aligned}$$
(22)

Figure 7 shows the indifference prices for different contract sizes. It can be seen that the price is very high for small amounts of energy and decreases fast, due to scale effects in production. For large contract sizes, the price increases again, because for those amounts it is necessary to buy more and more electricity and to bear the resulting price risk.

Fig. 7
figure 7

Indifference prices for varying contract size

Full size image

The indifference approach can easily be modified for pricing forward contracts as contracts with delivery during some (future) part of the planning horizon. In the same way, it is possible to analyze fuel contracts: In this case, the producer seeks for the maximum price he is willing to pay for a fixed amount of fuel delivered during some specified period, such that he is indifferent with respect to the objective value.

5 Conclusions

In this paper, we described a multistage stochastic optimization model for a thermal electricity production system with different types of fuels, the related random spot prices, fuel storage and CO\(_2\) emission certificates. In addition, costs involve fixed and variable operating costs. We maximize a mixture of expectation and average value at risk and derive the distribution of the asset value (a cash position plus the value of the fuel) at the end of the planning horizon. Going from data to some applications, several tasks had to be handled:

  • We specified a flexible model for mid-term planning, such that iterative analysis—repeatedly using the optimization model—can be done in reasonable time.

  • Our risk factors were the fuel prices for oil, gas, coal and CO\(_2\) emission certificates prices which are modeled as Geometric Brownian motions with jumps. We further estimated electricity spot prices based on the related forward curve and deviations between this curve and actual prices. All models show a good in- and out-of-sample performance and they can be used for a realistic simulation of the future evolution of prices.

  • Simulated hourly and daily commodity prices were aggregated to weekly average price scenarios and reduced to stochastic trees, suitable for stochastic multistage optimization.

  • A concrete instance of the multistage optimization model—modeling weekly decisions over a full year—was implemented with fictitious but reasonable data, and used for some case studies: We analyzed variations in the overall level of CO\(_2\) prices and their effects to the production. Furthermore, we investigated the pricing of electricity delivery contracts with fixed amount and price in the framework of indifference pricing.

The implementation was developed in discussion with practitioners from Siemens AG Austria and we hope to develop further some aspects of this work in our future research. In particular, we will work to enhance the tree construction. Furthermore we see indifference pricing as an important approach at energy markets (applicable to all kinds of delivery contracts and forward contracts) and will try to understand deeper its theoretical and practical properties and implications.