Revenue management for a make-to-order company with limited inventory capacity

Abstract

We consider the application of revenue management to a make-to-order manufacturing company with limited inventory capacity. Orders with different profit margins arrive stochastically over an infinite time horizon and the company has to decide which orders to accept and which orders to reject. We model the problem with a discrete-time Markov decision process and propose a heuristic procedure. In numerical tests we show the potential benefit of using revenue management instead of a FCFS policy and assess the performance of the heuristic procedure.

Introduction

Revenue management originates from the airline industry. In the late 1970s, airlines started to offer early-bird discounts in order to optimize the capacity utilization of their flights. One decision problem that emerged immediately was how many seats should be sold at the early-bird rate while reserving enough seats for the customers who would book shortly before their departure and pay the full price. This decision problem spawned a wide-ranging scientific literature, see (McGill and van Ryzin 1999), and started the era of yield management, which later became known as revenue management.

Today, revenue management has gained ground in a number of industries, see (Talluri and van Ryzin 2004). In order to see what revenue management presently encompasses, we will describe what steps a company has to take until the benefits of using revenue management can be reaped, see (Wong et al. 1993).

At first, the company has to segment its customers by their willingness to pay and set the prices for the different customer segments. It is common practice in revenue management to differentiate the customers by the time between the decision to buy the product and the actual use of the product. In the airline industry, for example, business customers usually have the right to book their flight very short in advance to the actual take-off and pay much higher prices compared to private customers who usually book their flight several weeks before take-off.

A company that wants to implement revenue management also has to make sure that customer segments which pay higher prices cannot buy capacity of customer segments with lower prices. In the airline industry this is done by different measures. One is binding private passengers to have a weekend between their outward and returning flights. This way, business passengers who are expected to buy the full-price ticket will probably not buy a ticket of the lower price segment because these passengers usually want to return home from their business trips before the weekend.

While the main developments in revenue management have taken place in the fields of service industries, relatively little research has been done for the manufacturing sector. We consider revenue management for a manufacturing company.

In detail, we consider the problem of allocating the capacity of a make-to-order company with limited inventory capacity. We assume that different customer classes have already been segmented and demand forecasts have been provided. Orders arrive stochastically with a certain probability in every discrete time period over an infinite planning horizon. Each order belonging to a certain class has a class-specific probability of arrival, lead time, capacity usage and profit margin.

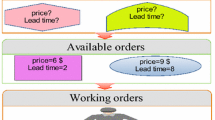
It is reasonable to assume that the company can demand a price premium for orders with shorter lead times, see (Li and Lee 1994). Thus, the company has to decide how much capacity it should reserve for orders with a higher profit margin while not rejecting too many orders with lower profit margins. We model this decision problem by an order acceptance problem. The decision of accepting or rejecting an incoming order will depend on the order class of the order, the company’s current capacity utilization and the company’s current inventory level. The company’s inventory capacity is limited and the company also has to decide how much of its inventory it should use for fulfilling accepted orders while reserving enough inventory for more profitable orders that might arrive in the future. The decision problem is outlined in Fig. 1.

Fig. 1

Decision problem

Literature review

When optimizing the capacity allocation in a manufacturing context, it becomes clear that instead of accepting or rejecting passengers the acceptance or rejection of manufacturing orders placed by customers becomes relevant. Thus, a high portion of the related literature deals with the decision problem of how many and which orders should be accepted over a finite or infinite time horizon in a stochastic environment with the optimization criterion of maximizing profits.

Within the order acceptance literature, a number of authors model the decision problem with Markov decision processes. Miller (1969) considers the problem of profit-maximizing admission control to a queue which is basically equivalent to the order acceptance problem. Miller models the problem by a continuous-time Markov decision process and provides a specialized solution algorithm for the problem that he considers. Lippman and Ross (1971) extend Miller’s model by allowing service times that are dependent on the customer classes, a general arrival process and an infinite number of customer classes and study this problem with a semi-Markov decision process. Lippman (1975) considers maximizing the average reward for a controlled M/M/c queue, adapts a new definition for the transition times in Markov decision processes and is able to derive several important results. Matsui (1982, 1985) uses semi-Markov decision processes to consider several order selection policies for stochastic job shops with the goal of maximizing the long-term average reward. Carr and Duenyas (2000) use a continuous-time Markov decision process to model a combined make-to-stock/make-to-order manufacturing system in order to decide which orders should be accepted and how many make-to-stock products to make. The authors are able to find the structure of optimal control and sequencing policies. Kniker and Burman (2001) propose a discrete-time Markov decision process for order acceptance at a make-to-order company and Defregger and Kuhn (2004) outline a heuristic for this approach.

Other modelling concepts for profit-maximizing order acceptance decisions in a stochastic manufacturing context have been used. Keilson (1970) and Balachandran and Schaefer (1981) provide nonlinear programming models and solution procedures for the order acceptance problem. In a series of papers (Balakrishnan et al. 1996, 1999; Patterson et al. 1997), Balakrishnan, Patterson and Sridharan use a decision-theoretic approach for reserving capacity of a make-to-order firm for orders with high profit margins. Caldentey (2001) approximates the order acceptance problem with a dynamic diffusion control model. In his model the price that the customers are willing to pay changes stochastically over time and the company has to decide about order acceptance and setting the inventory level. Missbauer (2003) uses a stochastic model to derive optimal lower bounds for the profit margin of stochastically arriving orders. Only orders whose contribution margins exceed the optimal lower bounds are accepted.

While direct order acceptance and rejection is an important technique for controlling the capacity of a manufacturing company, there are other possibilities as well. By using these possibilities, a company tries to influence external demand for the products by changing prices or quoted due dates. One possibility is the concept of dynamic pricing. Instead of directly accepting or rejecting certain orders the company can dynamically change the price for a certain product over time, thus in effect rejecting more orders when raising the price and accepting more orders when lowering the price.

Low (1974) studies a semi-Markov decision process for determining optimal pricing policies for a M/M/c queue. Harris and Pinder (1995) consider an assemble-to-order manufacturing company and determine optimal pricing and capacity reallocation policies for a static revenue management problem with an arbitrary number of customer classes. Gallego and van Ryzin (1997) consider pricing a given set of inventories of components that go into finished products over a finite time horizon. Swann (1999, 2001) examines the suitability of dynamic pricing in a manufacturing context and analyzes different dynamic pricing models. Chen and Frank (2001) analyze pricing policies for a company with homogeneous or heterogeneous customers where prices for admission to the queue depend on the size of the queue. Elimam and Dodin (2001) use nonlinear programming in order to determine optimal price discount levels during off-peak periods at a manufacturing company. Chan et al. (2003) consider dynamic pricing strategies in a finite horizon problem under non-stationary, stochastic demand.

Besides dynamic pricing, companies can also control their capacity by quoting different due dates to customers. By quoting longer due dates the company can decrease external demand and is thus effectively rejecting more orders, while quoting shorter due dates increases the demand. Duenyas (1995) and Duenyas and Hopp (1995) use semi-Markov decision processes to solve the problem of quoting optimal lead times to customers when the probability of a customer placing an order depends on the lead time quoted to him. Easton and Moodie (1999) develop a probabilistic model in order to determine optimal pricing and due date setting decisions and Watanapa and Techanitisawad (2005) extend Easton and Moodie’s model. Kapuscinski and Tayur (2000) are able to determine the structure of an optimal due date setting policy for a revenue management problem at a make-to-order company. Keskinocak et al. (2001) study several online and offline algorithms for quoting lead times to different customer classes where revenues obtained from the customers are sensitive to lead time.

For a literature review with mostly finite-horizon models on coordinating pricing with inventory and production decisions, see (Chan et al. 2004). If customers do not require an immediate reply whether their order will be accepted or not, the production capacity can also be auctioned off (Gallien and Wein 2005).

Mathematical model

Model formulation

The decision problem that we consider is an order acceptance problem with limited inventory capacity that we model with an infinite-horizon discrete-time Markov decision process with the optimization criterion of maximizing the average reward per period. All orders that arrive at the manufacturing company can be attributed to an order class n∈{1,...,N}. In each period at most one order can arrive and the probability of an order of class n arriving in each period is given by $p_{n} ,{\text{ }}{\sum\nolimits_{n = 1}^N {p_{n} < 1} }$. Each order of class n has a profit margin m _n , a capacity usage of u _n discrete time periods, and a maximum lead time of l _n time periods. If an order is accepted, the complete fulfillment of that order will take place at the latest within l _n periods after accepting the order. Partial deliveries to the customers are taking place whenever possible and without any additional costs incurred. It is possible that no order arrives in a time period. This event is modelled by the dummy order class 0. The probability that no order arrives in a period is given by $p_{0} = 1 - {\text{ }}{\sum\nolimits_{n = 1}^N {p_{n} ,p_{0} < 0} }$. The system state of the production system is measured at the beginning of a discrete time period and is modelled by three state variables:

• n∈{0,...,N} is the class of the order that arrived in the beginning of the current time period

• c is the number of periods the machine is still busy because of orders that have been accepted in the past and have not been finished yet

• i is the current level of inventory. This state variable is measured in the number of periods that the machine needed to produce the inventory level i.

The state space of all possible system states (n,c,i) is denoted by S. The inventory has a maximum capacity of I ^max. Furthermore, each unit that is on inventory for one period causes a holding cost of h monetary units. The number of states ∣S∣ is given by ∣S∣=(N+1)·max{max _n l _n ,1}·(I ^max+1). In each state (n,c,i)∈S the company can choose a decision from a set of decisions that depends on the state the system currently occupies. Basically, the company has at most four types of decisions at its disposal which are depicted in Fig. 2.

Fig. 2

Sequence of decisions

The four types of decisions are combinations of the decisions to accept or reject an incoming order and to raise the inventory level or not to raise it. If an order is accepted the company has to decide how many units of inventory should be used to fulfill this order. The possible decisions D for a given system state (n,c,i) are in detail:

$$D{\left[ {{\left( {n,{\text{ }}c,{\text{ }}i} \right)}} \right]} = \left\{ \begin{aligned} & D1\,\,\,\,\,\,\,\,\,: = {\text{reject and do not raise inventory level}},{\text{ }}\forall {\left( {n,c,i} \right)} \in S \\ & D2\,\,\,\,\,\,\,\,\,: = {\text{reject}}\,{\text{and}}\,{\text{raise}}\,{\text{inventory}}\,{\text{level}},\,\forall {\left( {n,c,i} \right)} \in {\left\{ {S:c = 0 \wedge i < I^{{\max }} } \right\}} \\ & D3{\left( r \right)}\,\,\,: = {\text{accept,}}\,{\text{do}}\,{\text{not}}\,{\text{raise}}\,{\text{inventory}}\,{\text{level}}\,{\text{and}}\,{\text{fulfill}}\,{\text{order}}\,{\text{by}}\,r\,{\text{units}}\,{\text{from}}\,{\text{the}}\,{\text{inventory}},\,\forall r \in {\left\{ {r_{{\min }} , \ldots ,r_{{\max }} } \right\}},\,\forall {\left( {n,c,i} \right)} \in {\left\{ {S:n > 0 \wedge {\left( {c + u_{n} \leqslant l_{n} + i \vee u_{n} \leqslant i} \right)}} \right\}} \\ & D4\,\,\,\,\,\,\,\,\,\,: = {\text{accept,}}\,{\text{fill}}\,{\text{order}}\;{\text{by}}\,{\text{inventory}}\,{\text{only}}\,{\text{and}}\,{\text{raise}}\,{\text{inventory}}\,{\text{level}},\,\forall {\left( {n,c,i} \right)} \in {\left\{ {S:n > 0 \wedge c = 0 \wedge u_{n} \leqslant i} \right\}} \\ \end{aligned} \right.$$

The maximum number of decisions ∣D∣ that can be taken in a certain system state is given by ∣D∣=min{I ^max, max _n u _n }+4.

D1

The company always has the option of rejecting an incoming order and not to raise the inventory level.

D2

The company can always reject any incoming order but can use the production capacity during the current time period for raising the inventory level if there are currently no orders waiting for the machine and the current inventory level is below the maximum inventory level I ^max. As the company’s decision only affects the current time period the inventory level i is raised by one unit.

D3(r)

This models the decision that the company accepts an order, takes r units from the inventory to fulfill that order and does not raise the inventory level. The company can only accept an order if in fact an order has arrived (n>0) and the current inventory and capacity booking levels i and c permit delivery of the order within its lead time l _n . Thus, it is feasible to accept an order if and only if c+u _n ≤l _n +i∨u _n ≤i. Furthermore, it is feasible to use the machine to completely satisfy an order if and only if c+u _n ≤l _n . It is feasible to use the machine for partially satisfying an order if and only if c<l _n .

The number of units r that are taken from the inventory to help fulfill the order is a decision variable and varies in the range between r _min. The minimum amount of inventory that has to be used in order to fulfill the accepted order is given by r _min=min{max{0, c+u _n −l _n }, u _n } while the maximum amount that can be used to fulfill the order is given by r _max=min{i, u _n }. The range [r _min, r _max] thus depends on the state (n,c,i) that the system occupies when the decision is taken.

One might argue that decision D3(r) could be simplified and replaced by a decision D3 which just takes all the necessary inventory to fulfill an order and uses the machine if the inventory is not enough. Decision D3(r) allows to reserve some inventory for highly profitable orders with very short lead times, though, which will have a positive effect on the long-term average reward of the company.

D4

The company can accept order n, fulfill it by inventory only and at the same time raise the inventory level if and only if the production capacity is currently not occupied by any outstanding orders, i.e. c=0, and the capacity requirement of the order u _n can be fulfilled by the current inventory level, i.e. u _n ≤i. As the company’s decision only affects the current time period the inventory level i is raised by one unit.

The reward R in a given system state (n,c,i)∈S that the company receives in a discrete time period results from the decision the company took in that period:

$$\begin{aligned} & R^{{D1}} \,\,\,\,\, = - h \cdot i \\ & R^{{D2}} \,\,\,\,\, = - h \cdot i \\ & R^{{D3{\left( r \right)}}} = m_{n} - h \cdot {\left( {i - r} \right)} \\ & R^{{D4}} \,\,\,\,\, = m_{n} - h \cdot {\left( {i - u_{n} } \right)} \\ \end{aligned} $$

It is assumed that if the decision to raise the inventory level has been taken, i.e. decision D2 or D4, the resulting increase of the inventory level will have taken place by the end of the period. Thus the additional inventory holding costs which result from the increase of the inventory level will apply only in the next period. If the company partially or completely fulfills an order by inventory, i.e. decision D3(r) or D4, the inventory holding costs decrease accordingly.

The transition probabilities P show which states can be reached from a state (n,c,i) once a certain decision has been taken. If the company rejects an order and does not raise the inventory level (decision D1), the capacity booking level c is reduced by one in the next period. If c has reached zero, it stays zero if the company continues to reject orders.

$$P^{{D1}} {\left[ {{\left( {n,c,i} \right)},{\left( {m,\,\max {\left\{ {c - 1,0} \right\}},i} \right)}} \right]} = p_{m} ,{\text{ }}\forall {\left( {n,c,i} \right)} \in S,{\text{ }}\forall m \in {\left\{ {0,{\text{ }} \ldots ,{\text{ }}N} \right\}}$$

If the company decides for D2 the inventory level increases by one unit:

$$P^{{D2}} {\left[ {{\left( {n,0,i} \right)},{\left( {m,0,i + 1} \right)}} \right]} = \left\{ \begin{aligned} & p_{m} ,\,\,\,\,\forall n \in {\left\{ {0, \ldots ,N} \right\}}, \\ & \,\,\,\,\,\,\,\,\,\forall m \in {\left\{ {0, \ldots ,N} \right\}}, \\ & \,\,\,\,\,\,\,\,\,\,\,\,\forall i \in {\left\{ {0, \ldots ,I^{{\max }} - 1} \right\}} \\ & 0,\,\,\,\,\,\,\,\,{\text{else}} \\ \end{aligned} \right.$$

If the company accepts an order and uses r units from the inventory to fulfill it, the capacity booking level c and the inventory level i are updated accordingly:

$$P^{{D3{\left( r \right)}}} {\left[ {{\left( {n,c,i} \right)},{\left( {m,\,\max {\left\{ {c - 1,0} \right\}} + u_{n} - r,i - r} \right)}} \right]} = \left\{ \begin{aligned} & p_{m} ,\,\,\forall r \in {\left\{ {r_{{\min }} , \ldots ,r_{{\max }} } \right\}}, \\ & \,\,\,\,\,\,\,\,\,\,\,\forall {\left( {n,c,i} \right)} \in {\left\{ {S:n > 0 \wedge c + u_{n} \leqslant l_{n} + i \vee u_{n} \leqslant i} \right\}}, \\ & \,\,\,\,\,\,\,\,\,\,\,\forall m \in {\left\{ {0, \ldots ,N} \right\}} \\ & 0,\,\,\,\,\,\,\,\,{\text{else}} \\ \end{aligned} \right.$$

If the company accepts an order, uses only the inventory to fulfill it and raises the inventory level, the system state evolves as follows:

$$P^{{D4}} {\left[ {{\left( {n,0,i} \right)},{\left( {m,0,i - u_{n} + 1} \right)}} \right]} = \left\{ \begin{aligned} & p_{m} ,\,\,\,\,\,\forall n \in {\left\{ {{\left\{ {1, \ldots ,N} \right\}}:u_{n} \leqslant i} \right\}}, \\ & \,\,\,\,\,\,\,\,\,\,\forall m \in {\left\{ {0, \ldots ,N} \right\}}, \\ & \,\,\,\,\,\,\,\,\,\,\,\,\forall i \in {\left\{ {0, \ldots ,I^{{\max }} - 1} \right\}} \\ & 0,\,\,\,\,\,\,\,\,{\text{else}} \\ \end{aligned} \right.$$

All system states, decisions, transition probabilities and rewards specify an infinite-horizon, discrete-time Markov decision process. In order to determine which solution procedure can be applied, this Markov decision process has to be classified.

Model classification

As we will describe below, the Markov decision process can be classified as multichain and communicating. A deterministic policy specifies which decision is taken at each state every time the system occupies this state. Once a policy has been selected, the Markov decision process becomes a discrete-time Markov reward process with a corresponding transition probability matrix.

Following (Puterman 1994), the Markov decision process that we specified in the previous section can be classified as multichain as there exists at least one policy which induces two or more closed irreducible classes. This can be seen in Fig. 3 which shows the stochastic process resulting from such a policy. The policy-maker can choose an arbitrary inventory threshold t∈{1,...,I ^max}. If the system’s inventory level is below t, the policy prescribes that the inventory level is never raised above t. If the inventory level is above t, the inventory level is never decreased below t. Thus this policy induces a multichain transition matrix and the Markov decision process can be classified as multichain.

Fig. 3

Stochastic process resulting from a policy which induces a multichain structure

The Markov decision process can also be classified as communicating. A Markov decision process is called communicating if for every pair of states a, b∈S there exists any arbitrary policy under which a is accessible from b. To show that this Markov decision process is communicating we show that there exist policies by which all possible outcomes of the state variables n, c and i can be reached.

Order class n

With regards to the state variable n, the Markov decision process is communicating because any order of class n∈{0,...,N} can arrive in all time periods.

Capacity booking level c

Under any policy the capacity booking level c can always decrease to 0 if for a very long number of periods no orders arrive which is possible because of the condition p ₀>0. On the other hand, there is a positive probability that the booking level c can reach its maximum c ^max=max _n l _n if an order arrives in every period and all incoming orders are accepted without using the inventory for those orders. Thus, all possible capacity booking levels c∈{0,...,c ^max} can be reached, independently of the inventory level i.

Inventory level i

By a similar argument, the state variable i can also be shown to classify the Markov decision process as communicating. By fulfilling all incoming orders by the inventory as far as possible, the inventory level i can be brought to zero. On the other hand, by another policy all incoming orders can be rejected and the capacity booking level c will decrease to zero. Then the inventory level i can be raised to any i∈{1,...,I ^max}. Thus all inventory levels i∈{0,...,I ^max} can be reached.

As there exist policies by which all capacity booking levels c∈{0,...,c _max} can be reached at any inventory level i and all inventory levels i∈{0,...,I ^max} can be reached, we have shown that all possible outcomes of the state variables n, c and i can be realized and thus the Markov decision process can be classified as communicating.

As the Markov decision process is multichain and communicating, the unichain versions of solution procedures like value iteration, policy iteration or linear programming do not apply. Instead, the communicating versions of these solution procedures have to be used. The communicating value iteration method was chosen because of its relative simplicity with regards to implementation compared to the other solution procedures. But in order to be able to use value iteration, one has to show that the transition matrices of optimal policies are aperiodical (Puterman 1994).

We now show that all possible policies induce aperiodical transition matrices. First we consider the unichain case, i.e. the decision maker does not set a threshold t as seen in Fig. 3 and it is possible that the inventory level can always decrease to zero. A transition matrix is aperiodical if one system state in each recurrent class of the transition matrix can be found which allows a transition into itself. To find these states one can make the assumption that no orders arrive during a large number of time periods which is possible because of the condition p ₀>0. Then the capacity booking level c will decrease to 0 and the stochastic process will remain in the states (n,0,i). Now, two cases depending on the inventory policy can be distinguished. If the policy does not prescribe to fill up the inventory level for any i∈{0,...,I ^max−1} in the system state (n,0,i), the system state will not change and the transition matrix will thus be aperiodic. If the policy prescribes to fill up the inventory level until I ^max, the inventory level will increase to I ^max. If no order arrives (n=0) which is possible because of the assumption p ₀>0, the state will make a transition into itself as the state variables n, c and i remain unchanged. Thus the transition matrix is aperiodic.

This argument can be extended to multichain policies as well, see Fig. 4. No matter in which closed recurrent class the stochastic process is evolving, the inventory level can always rise to its maximum with respect to the recurrent class and then there is a positive probability that the system state remains unchanged. Thus, for multichain policies all possible transition matrices are aperiodic as well.

Fig. 4

Example for a multichain policy which induces two aperiodic recurrent classes

As we have shown all possible policies to be aperiodic, we can use the communicating value iteration algorithm to find the optimal policy for the Markov decision process. As we will show in the numerical results, the value iteration algorithm does not converge in a reasonable amount of time for large problem instances, though. Thus, we suggest the following heuristic procedure with a complexity of the running time of O(N) in the number of order classes N.

Heuristic procedure

The idea for the heuristic is to reject orders from unprofitable order classes and to accept orders from more profitable order classes. The profitability of an order class n∈{1,⋯,N} will not be measured by its profit margin m _n , but rather by its relative profit margin m _n /u _n , i.e. m _n divided by the capacity usage u _n . The relative profit margin is an indicator of how profitable it is to allocate the machine for one period to an order of class n. The relative profit margin for the dummy order class 0 is set to 0. Before the heuristic can start, the order classes are sorted ascendingly by their relative profit margins.

Figure 5 shows how a good heuristic policy might look like for five hypothetical order classes which are sorted in ascending order by their relative profit margins, m _n /u _n ≤m _n+1/u _n+1, n∈{1,2,...,N−1}. For each order class the policy specifies if and under which circumstances this order class is rejected or not. The dummy order class 0, which represents the case that no order arrives in a given period is always set to rejection. The exemplary policy in Fig. 5 rejects order class 1, the order class with the lowest relative profit margin, in all system states even if it could be accepted in some system states. This rejection of order class 1 might increase the average reward of the company in order to reserve capacity for order classes with higher profit margins. Order classes 2 and 3 are only partially rejected which means that they are accepted in some system states but rejected in all other system states, even if they could be accepted in some of those other system states. Order classes 4 and 5 which have the highest relative profit margins are accepted in all system states where acceptance is possible. The optimal policy will be the optimal combination of which order classes are completely rejected, which order classes are partially rejected and which order classes are fully accepted.

Fig. 5

Accepting and rejecting order classes

Figure 6 illustrates the concept of partial rejection of a certain order class, e.g. order class 2 or 3 in Fig. 5. We consider a hypothetical order class n that is partially rejected and has a capacity usage u _n of 3 units and a lead time l _n of 4 time periods. The inventory capacity I ^max is 7. It can be seen in Fig. 6 that there are some states in which the company is forced to reject orders and cannot decide otherwise because it cannot deliver the product within the lead time l _n wanted by the customer, even if there is some inventory i on hand.

Fig. 6

Partial rejection of order class n, l _n =4, u _n =3

For example, the company can accept the order of class n in the state (n, c=3, i=2) but not in the state (n,3,1) because the lead time cannot be met even if the one unit of inventory that is available is used to help fulfill the order of class n. The policy for a partial rejection of an order class is based on the assumption that one unit of inventory has roughly the same value to the company as one period of the capacity of the machine. This can be seen by the fact that an order of class n in Fig. 6 is accepted when the capacity is not booked out at all (c=0) and there are 2 or more units of inventory at hand (i≥2) or when c=1 and i≥3 etc. Order class n is only partially accepted because it is rejected in some states where it could be accepted, e.g. (n,0,0) or (n,0,1).

In order to develop a heuristic procedure it is helpful to approximate each policy of mapping an action to each state by an N-dimensional vector A ^T=(a ₀, a ₁,...,a _N). The element a _n specifies what the minimum inventory level i is for accepting an order when c=0, e.g. in Fig. 6, a _n =2. For c>0 the decision at what minimum inventory level to accept or reject an order is given by a _n +c, e.g. with a _n =2 and c=1, the order is accepted at a minimum inventory level i of 3 units, see Fig. 6.

Each a _n thus specifies exactly in which states orders of class n should be accepted and in which states they should be rejected. The lower bound of the range for each element a _n is max{0, u _n −l _n } as this is the minimum inventory needed to accept the order of class n when the machine capacity is not booked out, i. e., c=0. The upper bound for the range of each a _n is I ^max. If all orders of class n are rejected, a _n is set to I ^max+1. The dummy order class 0 which models the event that no order arrives in a given period is always set to rejection, so a ₀=I ^max+1 for any policy.

Figure 7 shows how a policy with five order classes is approximated by the vector A ^T=(a ₀, a ₁,...,a ₅). In this example, the order class with the lowest relative profit margin m _n /u _n is fully rejected while order classes 2 and 3 are partially rejected. Order classes 4 and 5 are fully accepted.

Fig. 7

Policy approximation

In order to account for the decision to raise the inventory level or not the additional assumption is made that it is always profitable to raise the inventory level whenever possible. This assumption seems reasonable as long as there are no excessive inventory holding costs and demand is high enough to clear the inventory on a regular basis.

Denote by π the policy that the order classes n∈{0,...,π} are completely rejected and the order classes n∈{π+1,...,N} are completely accepted. The idea of the heuristic is to evaluate various policies and find good policies by simulation comparisons. Each policy π results in a Markov reward process with an associated average reward per period R _π whose estimate $\widehat{R}_{\pi }$can be obtained by simulation. The heuristic starts by comparing policies π=0 and π=1 by simulation (see Fig. 8). If $\widehat{R}_{0} > \widehat{R}_{1}$ policy 0 of accepting all order classes is accepted as the optimal policy and the heuristic stops. Otherwise, π→π+1 and the procedure continues likewise until $\widehat{R}_{\pi } > \widehat{R}_{{\pi + 1}}$. At that point, policy π has the highest average reward of all policies compared so far and is denoted by π* (see Fig. 9 for an example).

Fig. 8

Comparing policies

Fig. 9

Policy π*=2

Now, the heuristic tries to further optimize policy π* by comparing it to policy π*⁺ which is obtained by setting

$${\text{a}}_{{\pi * + 1}} \leftarrow {\left\lfloor {\frac{{I^{{\max }} + 1 - \max {\left\{ {0,u_{{\pi * + 1}} - l_{{\pi * + 1}} } \right\}}}}{2}} \right\rfloor } + \max {\left\{ {0,u_{{\pi * + 1}} - l_{{\pi * + 1}} } \right\}},$$

see Fig. 10. If $\widehat{R}_{{\pi *^{ + } }} > \widehat{R}_{{\pi *}}$policy π*⁺ is accepted to be the best policy found by the heuristic. Otherwise, policy π* is compared to policy π*^- which is obtained by setting

$$a_{{\pi *}} \leftarrow {\left\lfloor {\frac{{I^{{\max }} + 1 - \max {\left\{ {0,u_{{\pi *}} - l_{{\pi *}} } \right\}}}}{2}} \right\rfloor } + \max {\left\{ {0,u_{{\pi *}} - l_{{\pi *}} } \right\}}.$$

If $\widehat{R}_{{\pi * - }} > \widehat{R}_{{\pi *}}$policy π*⁻ is set to the best policy.

Fig. 10

Policies π*⁺ and π*⁻

Two policies are compared following the paired-t confidence interval approach (see Law and Kelton 2000, chapter 10). Thus a policy is determined to outperform another policy and the sequential simulation comparison is stopped after n replications if the following criterion is fulfilled:

$${\left| {\overline{Z} {\left( n \right)}} \right|} - t_{{n - 1,1 - \alpha /2}} {\sqrt {\widehat{{Var}}{\left[ {\overline{Z} {\left( n \right)}} \right]}} } > 0$$

where $\overline{Z} {\left( n \right)} = \overline{R} _{1} {\left( n \right)} - \overline{R} _{2} {\left( n \right)}$ is the difference of the estimated averages of the average rewards per period $\overline{R} _{1} {\left( n \right)}\,{\text{and}}\,\overline{R} _{2} {\left( n \right)}$ of the two policies after n simulation replications and $t_{{n - 1,1 - \alpha /2}} {\sqrt {\widehat{{Var}}{\left[ {\overline{Z} {\left( n \right)}} \right]}} }$ is the half-width of the 100(1−α) percent confidence interval for the true difference of the two average rewards being compared.

If two average rewards to be compared are very close, no significant difference between the two policies can be detected within a reasonable amount of replications. For this case the stopping criterion to end the comparison is:

$${\left| {\overline{Z} {\left( n \right)}} \right|} + t_{{n - 1,1 - \alpha /2}} {\sqrt {\widehat{{Var}}{\left[ {\overline{Z} {\left( n \right)}} \right]}} } < 0.5\% \cdot \min {\left\{ {\overline{R} _{1} {\left( n \right)},\,\overline{R} _{2} {\left( n \right)}} \right\}}$$

Here the simulation comparison stops if the policies do not differ significantly by more than half a percent. In this case, the policy which accepts more orders overall is set to dominate the policy it was compared to.

Numerical results

We compared both an FCFS policy which accepts all incoming orders as long as they can be fulfilled within their lead time and the heuristic procedure to the communicating value iteration algorithm which is an optimal procedure. Five problem classes of 100 problem instances each were created and are outlined in Table 1. The problem classes vary in the number of states and 100 instances were created randomly with certain parameters and parameter distributions for each problem class. The number of order classes for each of the 100 problem instances of a problem class was drawn randomly from a [5,20] uniform distribution for problem classes 1 and 2, from a [10,30] uniform distribution for problem class 3 and from [20,50] uniform distributions for problem classes 4 and 5. The limited inventory capacity was raised through the five problem classes as well. The relative profit margin m _n /u _n for each order class of each problem instance was drawn from a [1,3] uniform distribution for all problem classes.

Table 1 Problem classes

By specifying the number of states, the inventory capacity and the minimum number of order classes for each problem class, the maximum lead time for each problem instance of a certain problem class can be calculated as depicted in Table 1. For example, when looking at problem class 1, if the number of order classes for a certain problem instance is drawn to be the minimum of 5, the maximum lead time has to be set at 151 so that the desired number of 10,000 states can be reached approximately. If the number of order classes is drawn to be the maximum of 20, the maximum lead time for this problem instance has to be set to 43 in order to create a problem instance with approximately 10,000 states. Thus, for problem class 1 the maximum lead time for the 100 problem instances was in the range between 43 and 151.

The inventory cost was set to 0.01 in each problem class and the overall traffic intensity for each problem instance was drawn from a [1.5,2.5] uniform distribution. The overall traffic intensity for a problem instance is given by ${\sum\nolimits_{n = 1}^N {p_{n} \cdot u_{n} } }$. In order to account for a higher willingness to pay of customers with shorter lead times, each problem instance was created such that order classes with shorter lead times had higher relative profit margins than order classes with longer lead times. This was done by sorting the order classes of each problem instance in ascending order by their lead times and matching them with relative profit margins which were drawn randomly and sorted in descending order.

Table 2 shows the benefits of using revenue management compared to a simple FCFS policy which accepts all orders as long as they can be fulfilled within their lead time. The optimal policy applying revenue management was obtained by value iteration with ε=0.1%, i. e., the average reward obtained by value iteration differed at most by 0.1% from the optimal average reward. A time limit of 1 h for the value iteration algorithm was set for all problem instances so that the experiments could finish within a reasonable amount of time. Table 2 shows the average running time of the value iteration algorithm to reach the ε-optimal policy for each problem class. The column “proportion optimum” shows for how many of the 100 instances in each problem class the ε-optimal policy could actually be calculated within the time limit. It turns out that even in small problem classes there were some instances where the optimal policy could not be calculated within the time limit although the average running time of value iteration for these problem classes is clearly below the 1 h time limit. For the large problem classes, the optimal policy could not be calculated within the time limit for any problem instance.

Table 2 Percentage deviations of average rewards per period of the value iteration algorithm compared to a FCFS policy

The average running times of value iteration for problem classes 4 and 5 are larger than the 1 h time limit because the time to obtain the actual average reward by simulation of the policy that was obtained after 1 h of running time of value iteration was included when measuring the running time. For problem instances where the ε-optimal policy could be calculated, the average reward did not have to be obtained by simulation but was rather an output of the value iteration algorithm.

The average reward of the FCFS policy for each problem instance, AR^FCFS, was obtained by simulation after applying the procedure of Welch to determine a warm-up phase for each problem class by a representative simulation run (see Law and Kelton (2000), chapter 9). For each problem instance within a problem class, the percentage deviation Δ ^FCFS-VI of the average reward obtained by a FCFS policy compared to the average reward AR^VI obtained by the value iteration algorithm was calculated by Δ ^FCFS-VI=(AR^VI−AR^FCFS)/AR^FCFS[%]. The average, minimum, maximum and standard deviation over the percentage deviations Δ ^FCFS-VI of the 100 problem instances within each problem class were calculated and are given in Table 2.

It can be seen that on average the ε-optimal policy dominates the FCFS policy between 4.5 and 4.9% for problem classes 1 to 3 where the ε-optimal policy could be calculated for most problem instances. For problem classes 4 and 5 it can be seen that applying the 1-h time limit to the value iteration algorithm leads to inferior results, especially for problem class 5. On average, value iteration performs 6.7% worse compared to a FCFS policy so applying value iteration to large problem instances cannot be recommended when results are expected within a tolerable time limit. The reason that value iteration cannot even accomplish the average of the FCFS policy in problem class 5 is that value iteration first obtains an optimal policy as if the planning horizon was only one period long, in the next iteration as if the planning horizon was two periods long and so on. So during the first iterations of the value iteration algorithm it is not advantageous to raise the inventory level because of the inventory holding costs that are incurred. Not replenishing the inventory has a negative effect on the average reward that can be obtained, though, and this is the reason that the value iteration algorithm is not able to accomplish the average rewards of the FCFS policy for large problem instances.

For some problem instances the percentage deviation of the average reward between FCFS and the optimal policy was notably higher than the average percentage deviation as can be seen in the maximum of the percentage deviation within each problem class. This shows that for some problem instances it is quite profitable to use revenue management instead of using a simple FCFS policy (Table 3).

Table 3 Percentage deviations of average rewards per period of the value iteration algorithm compared to the heuristic procedure

We now proceed to assessing the performance of the heuristic procedure. We first compared value iteration to the heuristic procedure for problem classes 1 to 3 where most problem instances could be solved optimally. On average, value iteration outperforms the heuristic procedure between 0.8 and 1.1%. Figure 11 shows the histograms of the distributions of the percentage deviations and it can be seen that for most individual problem instances within problem classes 1 to 3, the percentage deviation in the average reward between value iteration and the heuristic procedure is between 0 and 1%.

Fig. 11

Histograms of the distributions of the percentage deviations of average rewards per period of value iteration compared to the heuristic procedure

In order to assess the performance of the heuristic procedure for large problem instances we compared it to a FCFS policy because a comparison to the value iteration algorithm for problem instances 4 and 5 would not be meaningful as the value iteration algorithm did not converge to the ε-optimal policy in any of the problem instances of problem classes 4 and 5 (see Table 2). Table 4 shows the data for the percentage deviations of average rewards of the heuristic procedure compared to the FCFS policy and Fig. 12 gives the corresponding histograms of the distributions of the percentage deviations for each problem class. It can be seen that on average the heuristic procedure outperforms the FCFS policy between 4.0 and 2.2%. As the heuristic starts out with a FCFS policy, it never performs worse than the FCFS policy. For some problem instances, the heuristic outperforms the FCFS policy significantly. This shows the potential benefits of the heuristic policy in practice, where each problem instance corresponds to a possible environment that an individual company is operating in.

Table 4 Percentage deviations of average rewards per period of the heuristic procedure compared to a FCFS policy

Fig. 12

Histograms of the distributions of the percentage deviations of average rewards per period of the heuristic procedure compared to a FCFS policy

When looking at the runtimes for obtaining the average reward of the FCFS policy, one notices that the average runtimes are similar for problem classes 2 through 4, although the number of states increases considerably from problem class 2 to problem class 4. This can be explained by the fact that the number of order classes in these problem classes also increases and that simulation runs to estimate the average reward tend to be shorter with a higher number of order classes.

Conclusion

We modeled the application of revenue management to a make-to-order company which has limited inventory capacity. After classifying the underlying Markov decision process, we introduced a heuristic procedure. In numerical tests, we showed the potential benefits of using revenue management compared to a FCFS policy and also demonstrated the usefulness of the heuristic procedure. Furthermore we showed that it is not feasible to use the optimal procedure value iteration for large problem instances.

Our model does not take into account that already accepted orders whose lead times are not tight cannot be resequenced in order to accept orders with tight lead times that have to be rejected otherwise. Allowing the resequencing of the current queue of already accepted orders would cause an explosion of the state space as each member of the queue would have to be modelled by at least one additional state variable. Thus, this feature would make the model intractable.

Furthermore, we only consider one product and one machine. More products can be considered by introducing one additional state variable for each additional product in order to represent the current inventory level of the product. The new number of states, ∣S∣^new, is obtained by multiplying ∣S∣ by the maximum inventory level of each additional product. Thus, adding more products will lead to an explosion of the state space as well. Similarly, for each additional parallel machine one state variable would suffice to model the current booking level of the machine, but the state space will increase exponentially as well. Nevertheless, we think that our model provides valuable insight for applying revenue management to a manufacturing company with limited inventory capacity.

Future research will be concerned with setting an appropriate maximum inventory level in the case of high inventory costs and modelling sequence-dependent setup times and costs between different order classes for the multi-product, one-machine case.