Introduction

It is well-known that properties of immiscible polymer blends are strongly dependent on their phase structure which is formed during their mixing and processing. Therefore, control of the blend phase structure evolution during their mixing and processing is an object of intensive scientific and industrial interest, especially for blends of biodegradable polymers, where conditions of mixing and processing are less established than for blends of synthetic polymers. It is generally accepted that the size of droplets in flowing blends with the droplets-in-matrix morphology is determined by the competition between the droplet breakup and coalescence [1–3]. The phase structure formed during blend mixing is affected by a number of parameters as mixing rate and time, mixer type, temperature, and the blend composition. Among these, blend composition is a crucial parameter [4]. Comparison of the shape of the dependence of average droplet radius, R, on volume fraction of the dispersed phase, φ, predicted theoretically and determined experimentally, can provide better insight into mechanism of the phase structure formation in flow.

Most available theories describe systems, where dynamic equilibrium between the droplet breakup and coalescence is established [1–3]. It relates to the situation in a batch mixer if mixing continues for a long enough time and degradation of the blend components is avoided. The theories were mostly derived for blends of Newtonian liquids in simple shear flow. Therefore, the choice the parameters of effective shear flow, \(\dot{\gamma }\) ef, which properly can model flow fields in a batch mixer, is necessary. Dynamic equilibrium between the droplet breakup and coalescence of monodispersed droplets in shear flow can be described by the equation [2, 5]:

$$F(R) = \frac{4}{\pi }\dot{\gamma }\varphi P_{\text{c}} (R)$$
(1)

where F(R) is breakup frequency, \(\dot{\gamma }\) is the shear rate which must be substituted with \(\dot{\gamma }\) ef and P c(R) is probability that the droplet collision, calculated without consideration of any inter-droplet interaction, will be followed by their fusion. Recent theories of flow induced coalescence [6–10] show that P c is practically independent of R in the region of small R. For monodisperse system, steep decrease in P c appears at critical R, relating to remarkable deformation of colliding droplets. A decrease of P c with average R is substantially less steep and starts at its lower value in systems containing droplets polydisperse in size than in the related monodisperse systems [10]. It was shown that character of the dependence of P c on R does not change if the effect of the matrix elasticity on P c is considered [7, 8].

Unfortunately, much more limited is our knowledge of the dependence of F on R [2, 11]. Generally, F is zero for R smaller than its critical value R c, related to critical capillary number, Ca c [1–3]. Dependence of Ca c on system parameters is well-known, at least for blends of Newtonian liquids in simple shear and extensional flows. On the other hand, generally accepted dependence of F on R does not exist and strongly differing expressions were used in various theories describing competitions between the breakup and coalescence [2, 5]. Various breakup mechanisms are operative in dependence of R/R c ratio and other system parameters [2, 3]. Theoretical calculations of the breakup time must be done numerically, which complicates determination of its dependence on system parameters. Also, experimental determination of F is much more difficult than that of Ca c due to the necessity to simultaneously determine the breakup time and number and size distribution of daughter’s droplets.

Various shapes of the dependences of R on φ were determined experimentally. A part of the experimental results shows a steeper than linear increase of the average R with φ [11–19]. Slower than linear growth of R with φ has been found only rarely [20, 21]. On the other hand, and additional part of the experimental results showed a linear growth of R with φ [15, 21–24]. Recently, strictly linear growth of average R with φ was found for polypropylene/ethylene–propylene rubber blend [25]. This shape of the dependence can be explained using assumption that F is proportional to R − R c. On the other hand, using effective shear rate, \(\dot{\gamma }\) ef, calculated by the method successfully applied for determination of flow curves [26], calculation of R c and slope of the dependence led to strong disagreement between theory and experiment [25].

The phase structure of immiscible polymer blends formed during their mixing changes substantially during compression molding. Our recent study [27] showed that the main contribution to the growth of dispersed droplets in polymer blends during compression molding is caused by the droplet coalescence in a hot press. Smaller contribution can be a consequence of the droplet rejection by crystallizing matrix.

The aim of the paper is to study and correctly evaluate the phase structure evolution during mixing and processing in practically important biodegradable poly(lactic acid)/ε-polycaprolactone (PLA/PCL) blends. PLA is fully biodegradable polymer promising for broad substitution of plastics made from fossil fuels. However, range of its applicability is limited by its brittleness. Blending of PLA with PCL is one of the most frequently used ways to improve its toughness [28]. However, this improvement is limited by the low compatibility of PLA/PCL blends. Therefore, efficient compatibilizer for PLA/PCL blends has been intensively asked [28–31]. Less care has been paid to study effect of the properties of the component, and mixing and processing conditions on the morphology of PLA/PCL blends [32]. We believe that better understanding of the applicability and limits of available theories for prediction of the phase structure evolution in PLA/PCL blends during their mixing and processing is essential for their tailoring, i.e., preparation of their samples with required properties.

The further aim of the paper is to contribute to verification of general applicability of available theories, derived for model systems in simple flows, to the phase structure evolution in real immiscible polymer blends during their mixing and annealing.

Experimental

Materials

Two biodegradable polymers were used in this study: polycaprolactone (PCL; Capa 6800; The Perstorp Group; Sweden; T m = 60 °C) and polylactide (PLA; Ingeo 4032D; NatureWorks LLC, USA; T m = 166 °C). Tetrahydrofuran (THF; Lachner, Czech Republic) were used as an etching substance of PCL phase. Properties of PCL and PLA are summarized in Table 1.

Table 1 Characteristics of the blend components
Full size table

Blend preparation

Before mixing, the neat polymers were dried in vacuum oven: PCL at 40 °C for 12 h and PLA at 80 °C for 4 h. PLA/PCL blends were prepared in the wide range of compositions (from 95/5 to 50/50 of weight ratios). The samples were produced by melt mixing (180 °C, 50 rpm, 10 min.) inside the chamber B 50 EHT of a Brabender Plasticorder (Brabender, Germany). Each sample was processed in two ways: (1) fast cooling in liquid nitrogen immediately after opening the mixer chamber (quenching) and (2) compression molding by hydraulic press (Fontijne Grotnes, Netherlands; 180 °C, 2 min at 50 kN + 8 min at 220 kN); after that, the samples were transferred into another press cooled with water. The resulting samples (irregular shapes from quenching and 2 mm plates from compression molding) were used for further characterization by microscopy and rheometry, as described below.

Scanning electron microscopy and morphology determination

Morphology of PLA/PCL blends was determined by means of scanning electron microscopy (SEM) followed by image analysis of the resulting micrographs. SEM micrographs were obtained with microscope Vega Plus TS 5135 (Tescan, Brno, Czech Republic). The specimens for SEM investigations were prepared as follows: the samples were smoothed under liquid nitrogen [33] and then etched (tetrahydrofuran vapor at 45 °C for 4 min) to visualize blend morphology (tetrahydrofuran vapors etch PCL particles faster than PLA matrix). Before observation in the electron microscope, the smoothed and etched surfaces were fixed on a metallic support using conductive double-adhesive carbon tape (Christine Groepl, Austria), and further fixed with conductive silver paste (Leitsilber G302, Christine Groepl, Austria) and sputtered with Pt (vacuum sputter coater, SCD 050, Balzers, Lichtenstein) to minimize charging and sample damage. All micrographs were taken in high vacuum at accelerating voltage 30 kV, using secondary electrons detector.

Image analysis was performed in two ways. For the PLA/PCL blends with particulate morphology (compositions from 95/5 to 70/30), we determined particle size distributions, which were based on EquivalentDiameter of the particles (ED = [4A/π]1/2, where A is the area of the particle and ED represents the diameter of a circle with the same area as the corresponding object; Ref. [34]). For the whole concentration range, we determined an overall measure structure coarseness—MeanChordLength (CL, which is calculated as the mean length of secants in pseudo-random directions within the micrograph, where the edges of the secants are defined by the interphase boundaries [33]). Main advantage of CL is that it can be used for systems with both particulate and co-continuous morphology, and its value increases with structure coarseness. Both ED’s and CL’s can be determined with a standard image analysis software; in this work, we used NIS Elements AR version 4.0. (Laboratory Imaging, Czech Republic).

The particle size distributions in the blends with particulate structure (composition range 95/5–70/30) were calculated with our recently developed program MDISTR [35]. The program is optimized for accurate calculation of particle sizes in systems with complex morphology, such as polymer blends with very broad particle size distributions or blends containing domains with different particle sizes. This complex morphology was observed in PLA/PCL blends with higher amounts of minority phase (starting from compositions 85/15). MDISTR combines the size distributions from several sets of micrographs with different magnifications and/or coming from different locations. It produces averaged histograms of particle sizes and substantially improves the accuracy of average particle sizes. Except for histograms showing overall distributions, the MDISTR program outputs the following parameters: ED n and σ(N) = the arithmetic mean and the width of number distribution of particle sizes; ED V and σ(V) = the arithmetic mean and the width of volume distribution of particle sizes; Min and Max = the minimal and maximal particle size in given dataset; S and B = the percent of particles smaller and bigger than 1 μm.

Rheometry

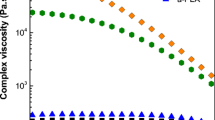
Rheological properties of PLA, PCL and PLA/PCL (90/10) and (80/20) blends were determined in dynamic mode, at a temperature of 180 °C with a Physica MCR 501 rheometer (Anton Paar, Austria) equipped with a convection temperature device CTD 450 and parallel plate fixture of 25 mm diameter. The dependence of absolute value of complex viscosity, η *, on angular frequency, ω, for PLA and PCL (plotted in Fig. 1) was used for determination of their Newtonian viscosity (extrapolated to zero shear rate) and viscosity at effective shear rate in the Brabender chamber using Carreau–Yasuda model based on the assumption that Cox–Merz rule is valid [36]. The dependences of complex modulus, G*, of PLA, PCL and PLA/PCL blends on angular frequency, ω, were used for an attempt to determine the interfacial tension, σ, between PLA and PCL.

Fig. 1
figure 1

The absolute value of complex shear viscosity as a function of angular frequency of the used PLA (filled circle) and PCL (filled square) biopolymers measured at 180 °C

Full size image

Melt flow ratio (MFR) of PLA and PCL was measured according to ISO 1133 at 210 °C with a weight of 2.16 kg using Meltflixer 2000 (Thermo Haake, Germany).

Determination of the effective shear rate in the Brabender chamber

The effective shear rate in the chamber of a Brabender Plasticorder is estimated by the method successfully used by Bousmina et al. [26] for determination of flow curves for set of polymers. The data obtained in our previous paper [25] for the ratio β of the radii of adjacent cylinders, modeling a wall and rotor of the chamber are used. For the rate 50 rpm, the effective shear rate in the chamber, \(\dot{\gamma }\) eff, is 154 s−1.

Determination of the interfacial tension

We tried to determine the interfacial tension between PLA and PCL from measurements of dependence of the blend, G*, on ω using Palierne’s theory [37]. G* can be expressed as:

$$\frac{G^*(\omega )}{{G^*_{\text{m}} (\omega )}} = \frac{1 + 3\varphi H(\omega )}{1 - 2\varphi H(\omega )}$$
(2)

where, for the ratio of the volume average of the droplet radius, R V , to its number average, R n , less than about 2, H(ω) is given by [38]:

$$H(\omega ) = \frac{{4(\sigma /R_{V} )(5G_{\text{d}}^{*} + 2G_{\text{m}}^{*} ) + (G_{\text{d}}^{*} - G_{\text{m}}^{*} )(19G_{\text{d}}^{*} + 16G_{\text{m}}^{*} )}}{{40(\sigma /R_{V} )(G_{\text{d}}^{*} + G_{\text{m}}^{*} ) + (2G_{\text{d}}^{*} + 3G_{\text{m}}^{*} )(19G_{\text{d}}^{*} + 16G_{\text{m}}^{*} )}}$$
(3)

where \(G_{\text{d}}^{{^{*} }}\) is complex modulus of the dispersed phase (PCL) and \(G_{\text{m}}^{{^{*} }}\) is complex modulus of the matrix (PLA). For known R V , σ can be determined by adjusting to G * vs. ω dependence, calculated with Eq. (2), to the experimentally determined one.

Determination of density in melt

Density of PLA (ρ PLA) and PCL (ρ PCL) was determined from comparison of MFR with volume melt flow ratio [MVR (cm3/10 min)] measured with Meltflixer 2000 (Thermo Haake, Germany) at 180 °C. Average value from two measurements was used.

Results and discussion

Phase structure development during mixing of PLA/PCL blends

The phase structure of the samples of PLA/PCL blends with different PCL content, quenched immediately after mixing, is shown in Fig. 2. It is visible that the blends with content of PCL till 30 wt % have typical droplets-in-matrix morphology and, therefore, the size of PCL droplets in this concentration range is controlled by the competition between their breakup and coalescence during mixing. Above this concentration, highly anisometric particles of PCL were detected (see Fig. 2) and PCL phase showed a certain degree of continuity. Start of remarkable partial co-continuity above 30 % of the dispersed phase has been detected for a number of polymer blends [39, 40]. Fineness of the phase structure of the blends is characterized with mean chord length (CL), number (ED n ) and volume (ED V ) averages of equivalent diameters. These parameters are summarized in Table 2. It follows from Table 2 that blends prepared by melt mixing of PLA and PCL, having similar viscosities at mixing conditions, show quite fine phase structure till 30 wt % of PCL, i.e., for compositions where toughening of PLA is common blending reason. Our further analysis is focused on blends with droplets-in-matrix morphology, i.e., with content of PCL till 30 wt %. These blends should behave like toughened PLA.

Fig. 2
figure 2

Dependence of the morphology of quenched samples of PLA/PCL blends on the weight fraction of PCL

Full size image
Table 2 Volume fractions of PCL and morphological parameters of PLA/PCL blends
Full size table

Theories considering dynamic equilibrium between the droplet breakup and coalescence [1–3, 5, 12] provide dependence of the droplet radius on volume fraction of the dispersed phase. Unfortunately, the relation between average equivalent diameter and related average radius cannot be determined for random section of a system of spheres with unknown radius distribution. For a system of monodisperse spheres, the following relation is valid between ED and R [41]:

$$R = \, \left( { 3/ 2} \right)^{ 1/ 2} {\text{ED}}/ 2$$
(4)

Because distribution of ED for quenched samples is not broad and particle pictures are nearly circular, Eq. (4) is used to compare our experimental result with theory. Dependences of R n and R V , calculated with Eq. (4) from the related ED n and ED V , on volume fraction, φ, of PCL are plotted in Fig. 3. The dependences of both R n vs. φ and R V vs. φ are well fitted by a quadratic form in φ. The fitting leads to R n  = 0.137 μm and R V  = 0.158 μm for φ → 0. Difference from linearity is substantially more remarkable for the dependence of R V on φ. While linear regression for the R n dependence provides fair prediction of this limit, its application to the R V leads to totally misleading results.

Fig. 3
figure 3

Dependence of the number average (R n ) and volume average (R V ) radii of quenched samples of PLA/PCL blends on the volume fraction of PCL

Full size image

Shear flow induced breakup of the droplets is controlled by the value of capillary number, Ca [2, 3].

$$Ca = \frac{{\eta_{m} \dot{\gamma }R}}{\sigma }$$
(5)

where σ is interfacial tension. Critical capillary number, Ca c, for breakup of Newtonian droplets in a Newtonian system is described by the equation [42]:

$$\log Ca_{c} = - 0.506 - 0.0995\log p + 0.124\left( {\log p} \right)^{2} - \frac{0.115}{\log p - log4.08}$$
(6)

where p is the ratio of viscosity of the dispersed droplets, η d and of the matrix, η m. For polymer blends, Ca c is also a function of elasticity parameters of the disperse phase and matrix. However, equation for Ca c, analogical to Eq. (6) is not available for viscoelastic systems. Critical droplet radius, R c, calculated by combination of Eqs. (5) and (6), should relate to average droplet radius, determined by extrapolation of R vs. φ dependence for quenched samples to φ → 0. In comparison, viscosities of the dispersed phase and matrix at \(\dot{\gamma }\) eff (154 s−1) are considered (see Table 1). The related viscosity ratio p is equal to 1.20.

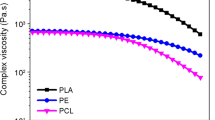
Besides η d, η m and \(\dot{\gamma }\) eff, also interfacial tension, σ, is needed for calculation of R c. Unfortunately, it has been found that σ cannot be determined from rheological measurements using Palierne’s theory for system under study. Comparison of measured and calculated complex moduli for PLA/PCL (90/10) and (80/20) blends shows that experimentally determined modulus is smaller than that calculated with Eqs. (2) and (3) in the region of large ω (see Fig. 4 for PLA/PCL (80/20); graphs for (90/10) blend lead to the same conclusion), where the blend G * is insensitive to σ and should be described by the Kerner equation [43]. The blend modulus has been found even lower than modulus of any blend component. It seems that PLA and PCL do not show perfect adhesion at the interface, which is the condition for validity of the Kerner equation. This imperfect adhesion is apparently interrelated to the slip at the interface, which is commonly accepted explanation to the negative deviation of the viscosity dependence of many immiscible polymer blends on their composition from additivity [44]. Due to this discrepancy, Palierne’s theory cannot be utilized for determination of σ in our system. However, we have tried to compare shapes of the curves of dependence of both real and loss modulus of the blend on angular frequency for experimental data with estimates for a set of interfacial tensions. For this purpose, we have used a shifted curve obtained by multiplication of measured blend moduli by such a factor that the derived data agree with an estimate for zero interfacial tension for high angular frequency (where the estimates for different interfacial tensions differ negligibly). For PLA/PCL (80/20), the estimated G′ curve for 3 mN/m gave best agreement for ω > 0.5 rad/s, and between those for 1.9 and 1.2 mN/m for lower ω, while for the loss component, the curve for 1.2 mN/m provided the best fit. It shows that not even this empirical procedure can serve for determination of the interfacial tension, however, suggests its probable range. Available literature data [45, 46] provides for PLA/PCL blends values of σ from about 1.2 mN/m to about 6 mN/m. Therefore, this range of interfacial tensions is considered in further discussion.

Fig. 4
figure 4

Comparison of experimental and calculated with the Palierne theory dependences of storage, G′, and loss, G″, moduli on the angular frequency, ω

Full size image

For σ = 1.2 mN/m, R c = 0.0041 μm follows from Eqs. (5) and (6); R c = 0.0205 μm relates to σ = 6 mN/m. The both values are much lower than the extrapolated values of R n and R V to φ → 0, which should lay between R c and R c/(2)1/3 when droplet breakup into two daughter’s droplets is assumed. Besides the method of Bousmina et al. [26], other methods of determination of \(\dot{\gamma }\) eff have been used in the literature [25]. For \(\dot{\gamma }\) eff = 20 s−1, which can be considered as lower limit of possible effective shear rates at used mixing conditions, R c one order of magnitude smaller than the extrapolated values of R n and R V follows from Eqs. (5) and (6) for σ = 1.2 mN/m and R c is about of half of extrapolated values for σ = 6 mN/m. Substantially smaller values of R c, calculated for effective shear flows using equations for Newtonian systems, than experimentally determined extrapolated radii of droplet in polymer blends, were found in several previous papers [22, 25, 47]. It seems that using effective shear rate and equations for a Newtonian system leads to a prediction of substantially smaller critical droplet radius than that determined for polymer blends. It is valid with p not substantially large than 1. For systems with p ≫ 1, droplet breakup is apparently affected by extensional component of the flow field in a mixing chamber.

It was suggested to consider the effect of elasticity of the droplets and matrix on the droplet breakup by substituting for the interfacial tension, σ, by its effective value, σ eff, defined as [48]:

$$\sigma_{\text{eff}} = \sigma_{0} + \frac{1}{6}R\left( {N_{{1,{\text{d}}}} - N_{{ 1 , {\text{m}}}} } \right)$$
(7)

where N 1,d and N 1,m are first normal stress differences for the dispersed phase and matrix, respectively. The first normal stress differences can be determined using Laun’s equation [49]:

$$N_{1} (\dot{\gamma }) = 2G^{{\prime }} (\omega )\left[ {1 + \left( {\frac{{G^{{\prime }} (\omega )}}{{G^{{\prime \prime }} (\omega )}}} \right)^{2} } \right]^{0.7} {\text{ for }}\dot{\gamma } = \omega \,$$
(8)

Using Eq. (8), for the first normal stress differences, leads to negative value of the second term on the right hand side of Eq. (7) for \(\dot{\gamma }\) eff = 154 or 20 s−1. Therefore, using σ eff instead of equilibrium σ in the above procedure leads to even stronger discrepancy between calculated and experimentally determined values of the critical droplet radius. The same result was obtained in our preceding study for polypropylene/ethylene–propylene rubber blends [25].

For monodisperse system, P c(R) from Eq. (1) is independent of R in the region of small R’s and starts to steeply decrease with R from a certain R [6–9]. Decrease in dependence of P c on average R for polydisperse system is less steep and starts at lower average R than for the related monodisperse system [10]. F(R) is a function of R − R c. It is obviously equal to 0 for R < R c. Linear dependence of R on φ follows from Eq. (1) if P c(R) is independent of R and F(R) is directly proportional to R − R c. We observed steeper than linear increase of R with φ in our PLA/PCL blends. For P c(R) independent of R, such an increase follows from Eq. (1) if F(R) grows with R − R c slower than linearly [2, 5]. Unfortunately, present state of art unable to predict dependence of F(R) on R − R c. It should be mentioned that only binary collisions of droplets were considered in derivation of Eq. (1), which is a quite rough approximation for typical polymer blends [2]. Therefore, terms proportional to higher powers of φ, relating to simultaneous collisions of three and more droplets, can affect observed dependence of R on φ.

It follows from comparison of results of the theory of flow induced coalescence, based on the switch between equations for coalescence of spherical and highly deformed droplets, and Janssen’s theory of coalescence that they provide very near values of probability of coalescence, P c, for Rs, where steep decrease in P c in the first theory appears (see Fig. 8 in Ref. [7]). Therefore, Janssen’s theory is used for estimation of the set of parameters for which coalescence in the system is remarkable. Using arbitrarily mobile interface model for matrix drainage between deformed droplets [9], Janssen’s theory leads to the following equation for P c:

$$P_{c} = exp\left\{ { - \frac{{9Ca^{2} R^{2} }}{{4\left( {1 + 3a/p} \right)}}\left[ {\frac{1}{{2h_{c}^{2} }} + \frac{a}{{pCaR^{2} }}ln\left( {\frac{{1 + \frac{3a}{p} - \frac{3a}{p}exp\left\{ { - \frac{p}{3a}\left( {\frac{{3CaR^{2} }}{{2ah_{c}^{2} }} - 1 + bp} \right)} \right\}}}{{1 + \frac{3a}{p} - \frac{3a}{p}exp\left\{ { - \frac{p}{3a}\left( {\frac{{3CaR^{2} }}{{2ah_{0}^{2} }} - 1 + bp} \right)} \right\}}}} \right)} \right]} \right\}$$
(9)

where it is assumed that the inter-droplet distance at the coalescence origin, h 0, is much larger than the critical inter-droplet distance for their fusion, h c. a and b are dimensionless parameters. The choice a = 8 and b = 1 leads to good agreement with more sophisticated Rother and Davis theory [6].

Substitution to Eq. (9) leads to negligible P c even for smallest R n , determined for PLA/PCL (95/5) and the largest estimated σ (6 mN/m). It is valid both for effective shear rate determined by the method of Bousmina et al. [26] (154 s−1) and for the lower shear rate 20 s−1. It means that the theory predicts no coalescence and, therefore, zero growth of the droplet size with their volume fraction, for the system under study if flow field in the mixing chamber is substituted by effective shear rate. The same contrast between prediction and experiment was found also in our preceding paper [25]. Equation (9) was derived for the coalescence of Newtonian droplets in a Newtonian matrix. However, the theory, considering the effect of the matrix elasticity on coalescence [7, 8], predicts only negligible effect of the matrix elasticity on R and Ca at which P c starts to steeply decrease.

Phase structure evolution during compression molding

The phase structure of compression molded samples of PLA/PCL blends is shown in Fig. 5. PLA/PCL blends with a content of PCL till 30 wt % contain spherical droplets of PCL. Microphotographs document that average droplet sizes and the width of the droplet size distribution increase in comparison with quenched samples having the same content of PCL. PLA/PCL (60/40) blend shows coarse morphology containing some domains with co-continuous structure and others with dispersed PCL particles in PLA matrix. Nonuniform phase is apparently a consequence of the shape relaxation and coalescence of anisometric particles simultaneously with coarsening of co-continuous domains during quiescent annealing at compression molding. PLA/PCL (50/50) blend shows coarse co-continuous structure, formed by rapid coarsening of the structure at the end of mixing (cf. Fig. 2) during compression molding. Number and volume averages of equivalent diameters of PCL droplets, evaluated by MDSTIR method, and their CL’s are summarized in Table 2. CL = 8.92 μm and CL = 20.13 μm were determined for PLA/PCL (60/40) and (50/50), respectively. Comparison of these values with CL’s in Table 2 for lower content of PCL clearly demonstrates that chord length consistently characterizes coarseness of blends with dispersed and co-continuous structures.

Fig. 5
figure 5

Dependence of the morphology of compression molded samples of PLA/PCL blends on the weight fraction of PCL

Full size image

Droplet radii, used for comparison the phase structure evolution during compression molding with theory, are recalculated from the related ED’s using Eq. (4). It can be assumed due to low degree of crystallinity of PLA that the effect of the matrix crystallization on the growth of PCL droplets during compression molding [27, 50] is insignificant. In this case, the growth of the droplet size during compression molding is caused by coalescence at rest [27]. Therefore, the difference between droplet size in quenched and compression molded samples should match to the theory of coalescence at rest. Theory considering main features of the coalescence in quiescent polymer blends is available only for monodisperse systems [51]. It follows from Table 2 that polydisperzity, i.e., the ratio ED V /ED n , of compression molded samples grows quite rapidly with φ and is substantially larger than for the related quenched samples.

Our study of coalescence in quiescent state induced by van der Waals forces [51] showed that the theory using average starting inter-droplet distance, 〈h 0〉, lead to a better agreement with experiments than the theories using other methods of calculation of the average coalescence time, t c. When 〈h 0〉 is substantially larger than the critical distance for droplet fusion, h c, the following equation is valid for the time dependence of the droplet radius, R:

$$R^{3} = R_{0}^{3} + \frac{{Ap^{4} }}{{27\pi \eta_{\text{m}} \left[ {G(0) - G\left( {p\sqrt {4H(\varphi )} } \right)} \right]}}t$$
(10)

where R 0 is the average droplet radius at the coalescence origin, η m is zero shear viscosity of the matrix, A is the effective Hamaker constant, p is the ratio of η d and η m for \(\dot{\gamma }\) → 0, equal to 0.89 (cf. Table 1). The function G is defined as [51]:

$$\begin{aligned} G\left( z \right) = & \frac{{ ( 2 { }g_{{ 2 {\text{k}}}}^{2} \text{ - }{ 4 }g_{{ 1 {\text{k}}}}^{2} g_{{ 2 {\text{k}}}} + g_{{1{\text{k }}}}^{ 4} ) {\text{g}}_{\text{mk}} \text{ - } 5 { }g_{{ 1 {\text{k}}}} g_{{ 2 {\text{k}}}}^{ 2} + 5g_{{ 1 {\text{k}}}}^{ 3} g_{{ 2 {\text{k}}}} \text{ - }g_{{ 1 {\text{k}}}}^{ 5} )}}{{ 2 { }\sqrt {g_{{ 1 {\text{k}}}}^{ 2} - 4g_{{ 2 {\text{k}}}} } }}{ \ln }\left( {\frac{{ 2 { }g_{{ 2 {\text{k}}}} + z \, \left({\text{ - }\sqrt {g_{{ 1 {\text{k}}}}^{ 2} { - } 4g_{{ 2 {\text{k}}}} } + \, g_{{ 1 {\text{k}}}} } \right)}}{{ 2 { }g_{{ 2 {\text{k}}}} \, + z\left( {\sqrt {g_{{ 1 {\text{k}}}}^{ 2} - 4g_{{ 2 {\text{k}}}} } + \, g_{{ 1 {\text{k}}}} } \right)}}} \right) \\ - \frac{{\left( { 2g_{{ 1 {\text{k}}}} g_{{ 2 {\text{k}}}} \text{ - }g_{{1{\text{k}}}}^{3} } \right)g_{\text{mk}} \, + \, g_{{ 2 {\text{k}}}}^{ 2} \text{ - } 3g_{{ 1 {\text{k}}}}^{2} g_{{ 2 {\text{k}}}} \, + \, g_{{ 1 {\text{k}}}}^{4} }}{ 2}{ \ln }\left( {g_{{ 2 {\text{k}}}} \, + {\text{ g}}_{{ 1 {\text{k}}}} z \, + \, z^{2} } \right) \\ + & \left[ {\left( { \, g_{{ 2 {\text{k}}}} - g_{{ 1 {\text{k}}}}^{2} } \right)g_{\text{mk}} - 2g_{{ 1 {\text{k}}}} g_{{ 2 {\text{k}}}} + g_{{ 1 {\text{k}}}}^{ 3} } \right]z + \frac{{\left( {g_{{ 1 {\text{k}}}} g_{\text{mk}} + g_{{ 2 {\text{k}}}} { - }g_{{ 1 {\text{k}}}}^{2} } \right)}}{2}z^{2} + \frac{{g_{{ 1 {\text{k}}}} { - }g_{\text{mk}} }}{ 3}z^{3} { - }\frac{{z^{4} }}{ 4} \\ \end{aligned}$$
(11)

with g 1k = 1.711, g 2k = 0.461 and g mk = 0.402. The function H(φ) can be expressed as:

$$H(\phi ) = \frac{{\left\langle {h_{0} } \right\rangle }}{2R} = \int\limits_{1}^{\infty } {exp\left\{ { - \frac{8\phi (1 + \varphi )}{{(1 - \varphi )^{3} }}(x^{3} - 1) + \frac{{6\varphi^{2} (3 + \varphi )}}{{(1 - \varphi )^{3} }}(x^{2} - 1) - \frac{{12\phi^{3} }}{{(1 - \varphi )^{3} }}(x - 1)} \right\}dx}$$
(12)

When it is assumed that the growth of the average droplet radius during compression molding is caused by the coalescence, Eq. (10) can be used for verification of plausibility of predicted dependence of the rate of coalescence on volume fraction of the dispersed phase. In this case, t is the time of the compressing molding in a hot press, R is an average droplet radius in compression molded sample of a blend and R 0 is the related average droplet radius in the blend quenched at the end of mixing. It follows from Eq. (10) that the function Φ, equal to

$$\varPhi = (R^{3} - R_{0}^{3} )\left( {G(0) - G\left( {p\sqrt {4H(\varphi )} } \right)} \right)\frac{{27\pi \eta_{\text{m}} }}{{Ap^{4} t}}$$
(13)

should be a constant equal to 1 if the theory describes the coalescence precisely.

Values of the function Φ calculated for R n and R V in dependence on volume fraction of PCL are summarized in Table 3. Values of zero shear viscosity, η 0, of PLA and PCL from Table 1, volume fractions of PCL at 180 °C, φ PCL,  from  Table 2 and t = 600 s were used. Value of the effective Hamaker constant, which is not available for PLA/PCL blends, was adjusted to 10−19 J. Dependences of functions Φ-R n and Φ-R V on volume fraction of PCL differ qualitatively. For small φ PCL, increase in R n due to coalescence during compression molding is small and Φ-R n shows large scatter due to unavoidable error in experimental determination of the particle sizes. For larger φ PCL, Φ-R n values are not far from 1. It indicates that the theory of coalescence in quiescent state can serve for semiquantitative prediction of the R n vs. φ dependence during annealing for system under study. On the other hand, Φ-R V is substantially larger than 1 for φ PCL = 0.057 and rapidly increases with φ PCL. Therefore, available theory of coalescence for monodisperse system [51] cannot be utilized for prediction of the dependence of R V on φ at annealing of immiscible polymer blends. These results show that new theory of the coalescence in quiescent state, reflecting increasing width of the droplet size distribution during annealing, should be derived.

Table 3 Dependence of the function Φ [defined by Eq. (13)], calculated for R n (Φ-R n ) and for R V (Φ-R V ) on φ PCL
Full size table

Conclusions

Melt mixing of PLA/PCL blends in a batch mixer results in fine phase structure if viscosities of the blend components are similar. The blends contain small PCL particle in PLA matrix up to 20 wt % of minority phase, somewhat bigger PCL particles with a broader size distribution up to 30 wt % of PCL, and co-continuous morphologies for higher PCL weight fractions. Dependences of average size of PCL droplets on their volume fraction (φ) are well fitted by quadratic function of φ; this holds for the average radii determined from both number and volume particle size distributions.

Procedure of the determination of the interfacial tension based on the Palierne theory cannot be applied to the blend under study, apparently due to incomplete adhesion between PCL droplets and PLA matrix in the melt.

Comparison of experimental data with available theories of the phase structure evolution in flowing polymer blends, based on the assumption that flow field in a batch mixer can be substituted by the shear flow with effective shear rate, leads to the conclusion that theories strongly underestimate the values of the critical radius for a droplet breakup and efficiency of flow induced coalescence.

Changes in the phase structure of PLA/PCL blends during compression molding are caused by the droplet coalescence as well as by breakup, coalescence and coarsening of fully or partially co-continuous structures in quiescent melts. Comparison of an increase in droplet radii during compression molding with available theory for monodisperse system [51] leads to the conclusion that the theory provides fair semiquantitative prediction for the number average of droplet radii, but totally fails at prediction for the volume average of droplet radii.