With the recent availability of flexible intravascular stents, a new therapeutic approach has become possible in the endovascular treatment of intracranial aneurysms. In first-case reports and case series, stents were mainly used in combination with coils to treat aneurysms that were difficult to treat with coils only [1, 2]. However, evidence from experimental studies also showed that use of stents without coils might hemodynamically uncouple the aneurysm from the parent vessel, leading to thrombosis of the aneurysm [1–5] and Vanninen et al. described recently their observations of broad-based saccular intracranial aneurysms that showed a spontaneous thrombosis after stent placement only [6].

Computer simulations applying finite element modeling have been shown to be an effective tool to provide insight into cerebral hemodynamics [7]. For example, Burleson et al., who investigated shear stress and pressure on a model of a side wall cerebral aneurysm, found these parameters to be maximal at the downstream site of the ostium rather than at the aneurysm dome, the site that is commonly considered to be the rupture site [8]. Aenis et al. used the finite element method to study the effect of stent placement on a side wall aneurysm and found the flow activity as well as the pressure inside the stented aneurysm to be diminished [9], and Steinman et al. recently demonstrated the ability to perform computational simulation of flow dynamics from patient-specific studies using datasets from rotational angiography [10]. These studies focused on the hemodynamic factors of flow velocity and wall shear stress. However, for the assessment of hemodynamic changes in aneurysms after stenting, the influence of viscosity of the blood is also important, as these changes likely influence thrombus formation.

In this report, changes in dynamic viscosity after stent placement were investigated by finite element analysis of a bifurcation aneurysm. For that purpose, the non-Newtonian viscosity of blood was taken into account by including an experimentally derived equation, yielding a viscosity, which decreases as the shear rate increases.

We hypothesized that this approach might give important information for a better understanding of rheological changes that occur within aneurysms after treatment with a stent.

Materials and Methods

Model Geometry

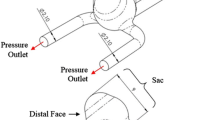
A two-dimensional model with a parent artery, a smaller branching artery (branching angle 90°), and an aneurysm located at the bifurcation was used for simulation. The geometric parameters of the model are given in Figure 1. Simulations were carried out with and without a stent located at the parent artery, covering the aneuyrsmal orifice and the smaller branching artery. The stent was simulated to have a wire diameter of 0.2 mm with a wire interval of 1.5 mm.

Figure 1
figure 1

Schematic of the vessel model. The model has an aneurysm at the branch.

Full size image

Assumptions

The following assumptions were made in each simulation: (1) two-dimensional study; (2) laminar flow; (3) pulsatile flow rate; (4) rigid walls; (5) non-Newtonian fluid (viscosity related to shear rate). The following inlet parameters were chosen: mean velocity in vessel A, 20 cm/sec; peak velocity in vessel A, 45 cm/sec; in branch B, 50 cm/sec, flow rate 2.4 cm3/sec, cardiac frequency 1 Hz. The Reynolds number based on the entrance flow conditions was defined by

$${\rm R}_{\rm e} = \rho{\rm U}_0{\rm D} \over {\mu_\infty}$$

where U0 refers to the peak or mean velocity near the tube axis, D is the tube diameter, ρ is the density of blood (1.1 g/cm3), and μ∞ is the dynamic viscosity of blood at an infinite shear rate (0.0035 Pa.s). With this definition, the Reynolds number varied from 200 (mean value) up to 450 (peak value).

Up to now, most of the computational hemodynamical approaches simplified blood to be a Newtonian fluid (shear stress is linearly proportional to the strain rate), an assumption that holds true for relatively high shear rates encountered in large vessels [9]. Because our model included an aneurysm with stagnant flow and low shear rates, high variations in viscosity values were expected. Therefore, to take the rheology of a non-Newtonian fluid into account, a constitutive equation that yields a dynamic viscosity that decreases as the shear rate increases was included. This formula was derived from our own experimental studies and the results were fitted to the Cross law according to the following formula:

$$\mu = \mu_\infty + (\mu_0 - \mu_\infty)/\left[1 + (\dot\gamma/\dot\gamma_{\rm C})^p\right]$$

where μ∞ is the dynamic viscosity at very high shear rate (0.0035 Pa.s), μ0 is the value for the null shear rate (0.0364 Pa.s), \(\dot\gamma\) is the shear rate, \(\dot\gamma_{\rm C}\) is a constant (2.63 sec−1, the abscissa at the inflexion point), and p a constant exponent (p = 1.45) (Fig. 2).

Figure 2
figure 2

Relationship between shear rate and dynamic viscosity. When the shear rate is high, the dynamic viscosity becomes low.

Full size image

Finite Element Method and Numerical Scheme

Fluid dynamic modeling based on the finite element method was performed on a Sun ULTRA 5 station (Sun Computer, Mountain View, CA), using software (N3S) developed by Electricite de France and improved in house. The mesh from 8000–10,000 nodes was created with a triangle element. Spatial derivatives were approximated with second-order accuracy using Navier–Stokes equations. Time derivatives were approximated with first-order accuracy by the method of characteristics. The solution was approached in an iterative fashion using about 10,000 time steps per period. The computations were continued over four periods to check the periodicity of the solutions. The solution for each case was reached after a computation time of 20–40 h.

Results

Velocity

Summarized results for the two-dimensional velocity vector plots during different phases of the cardiac cycle are graphically depicted in Figure 3. Before stent placement, the volume flow into the aneurysm sac originated from the downstream end of the aneurysm ostium. The peak velocities in the main vortex were reduced by a factor of about 2 compared to peak velocities in the main artery, and a smaller countercirculating vortex during systole, located near the dome of the aneurysm, was visualized. After stent placement, the main inflow vortex was “broadened” and peak velocities in the main vortex were lowered by a factor of about 4–40 compared to peak velocities in the main artery. The smaller countercirculating vortex was no longer present; instead an area of stagnant flow—even during systole—was observed near the dome of the aneurysm.

Figure 3
figure 3

Flow pattern of before and after stent. The flow speed in the aneurysm was reduced after stent placement.

Full size image

Wall Shear Stress

Wall shear stress values were highest at peak systole before and after stent simulation. The wires of the stent diminished the viscous stress exerted by the fluid onto the wall of the main artery. In the dome area of the aneurysm, known to be the usual rupture site, a small shear stress was observed on the aneurysm wall in the prestent simulation, which disappeared in the after-stent simulation. On the other hand, the peak wall shear stress of the branch vessel was slightly amplified (Fig. 4).

Figure 4
figure 4

Wall shear stresses before and after stent. The stress disappears in the after-stent simuation at the dome area of the aneurysm.

Full size image

Viscosity

In the prestent simulation, the dynamic viscosity was low in almost the entire aneurysm and also in the adjacent arteries. Only near the dome during diastole were slightly elevated viscosity rates observed, which vanished during the acceleration phase. In the poststent simulation, viscosity values increased by up to a factor of 10 compared to viscosity values in the parent artery (Fig. 5). Main changes in viscosity were observed in a large area of the aneurysm opposite the orifice and persisted over the entire cardiac cycle: Detailed computations revealed that over 60% of the time, the viscosity values were at least threefold increased in a major part (>50%) of the aneurysm.

Figure 5
figure 5

Viscosity changes before and after stent during diastole (left). The viscosity near the dome was elevated after stent, even during systole (right).

Full size image

Discussion

Computational fluid dynamic simulations using the finite element method have been extensively applied to assess local changes of velocity and shear stress in aneurysms, and these hemodynamic parameters are fairly well understood. Using an idealized geometry of a spherical aneurysm located at a bifurcation with a smaller branch, our findings were similar to those reported by Burleson et al. [8], showing the volume flow into the aneurysm and the maximal shear stress located at the downstream edge of the orifice. Furthermore, Aenis et al. [9] investigated the impact of stent placement on a side wall aneurysm. They found substantially changed flow patterns within the aneurysm after stent placement and an increase of wall shear stress at the distal neck of the aneurysm comparable to our results.

An insight into changes of flow velocity and shear stress is certainly of value in examining the potential impact of stent placement. However, one aim of stent placement of cerebral aneurysms in vivo is the induction of thrombosis within the sac, thereby excluding the aneurysm from the circulation [6]. It is known from experimental and clinical observations that thrombus formation does occur in areas of stagnant flow near the dome of an aneurysm, where high viscosities are expected. We, therefore, applied finite element simulations to determine not only changes in velocity and shear stress but also of dynamic viscosity before and after stent placement. For that purpose, an experimentally derived equation yielding values for dynamic viscosity dependent on the shear rate was incorporated into our assumption.

The most interesting finding of our study was the observation that viscosity changes were considerably increased over the entire cardiac circle after stent placement, especially near the dome of the aneurysm. This area is known from clinical experience to be the region where thrombosis of aneurysms starts, which can be regarded to a certain extent as a validation of our computed results.

However, as with any modeling study, a number of assumptions to simplify the model were made, such as the idealized two-dimensional (2-D) geometry and the simple stent “design.” It is certainly the goal to perform simulations on patient specific three-dimensional (3-D) geometric data, as recently described Steinman et al. [10], and it is to be assumed that advances in computer performance will ultimately lead to that goal. The assumption of a rigid vessel is a second simplification. However, this is probably acceptable, as intracranial arteries and aneurysms are less distensible compared to extracranial arteries [11–15]. Finally, it should be pointed out that the mechanism of thrombus formation and growth is of a complex nature. The efficiency with which platelets adhere and aggregate is dependent on the synergistic action of various adhesive and soluble agonist receptors that depend on prevailing flow condition [16]. Therefore, even if a non-Newtonian behavior of blood was assumed and regions of high viscosity with regions where thrombus formation usually occurs were compared, caution should be exercised when attempting to extrapolate from measurements of viscosity to thrombus formation.

A next logical step would be to perform simulations on viscosity changes induced by stent placement on 3-D models of aneurysms. Three-dimensional modeling would also allow investigation of the impact of different stent designs on viscosity changes in a more realistic way. It was recently shown using 2-D models that the design pattern and effective porosity of stents have a marked impact on hemodynamic alterations within a side wall aneurysm [17]. If the 3-D models were obtained from real patient data, this would ultimately enable a treatment simulation and a more rational therapeutic decision. Finally, thixotropic effects (the initial extra flow resistance linked to developing orientation and disaggregation of erythrocytes) should be experimentally analyzed and incorporated into flow simulations, to obtain an even more detailed and realistic impression of blood flow behavior [18].

In summary, our computer simulations support the experimental and clinical assumptions that intracranial stents act in two ways: by the reduction of shear stress onto the aneuyrsmal wall and by increasing the viscosity inside the aneuyrsmal sac. The decrease of shear stress in our model was most pronounced at the aneuyrsmal dome, the area of expected rupture. One could, therefore, hypothesize that stents will lead to an immediate reduction of shear stress, resulting in an immediate reduction of rupture risk, and will create a region with high blood viscosity.