Introduction

Most real materials are not single crystals but consist of crystalline grains of various sizes, misorientated with respect to each other. The bulk properties of single crystals have been extensively studied but grain boundary (GB) properties are much less understood, even though the grain boundaries influence many of the material properties. For instance, when considering mantle rocks, grain and phase boundaries become important since they facilitate creep and fast diffusion (Duffy 1986; Keller et al. 2006; Faul et al. 2011), which are assumed to control mantle rheology. Olivine, a complex silicate, is a major component of the Earth’s upper mantle, and therefore, it is of considerable importance to study its physical and thermodynamic polycrystalline properties.

Despite the importance of silicate GBs, the knowledge of their structure, physical and thermodynamic properties is limited. Low-angle GBs can be described by the dislocation model (Read and Shockley 1950), which describes the GB as a series of dislocations. With increasing misorientation angle, the cores of dislocations interact and overlap. In high-angle GBs, individual dislocations are commonly not observed. Furthermore, the misorientation angle is related to the distance between dislocations and their Burgers vectors by Frank’s (1951) formula. The transition from low to high-angle GBs is suggested to occur in metals at misorientation ∼15° (Smith 1996). For olivine, Poirier and Nicolas (1975) gave a maximum misorientation of 15° and de Kloe (2001) estimated 11.6°. Recently, Heinemann et al. (2005) experimentally studied Mg2SiO4 forsterite GBs with tilt angle ranging from 9.9 to 21.5° using HRTEM. They have shown that low-angle GBs with arrays of dislocations exist for misorientation angles up to 21.5°. So far, the structure of GBs and the transition from low to high-angle GBs in olivine are not well constrained. In addition, geometrical models for GBs are mainly developed for metals and oxides (Gleiter and Chalmers 1972; Sutton and Balluffi 1995).

The structural arrangement at GBs produces an excess free volume which influences processes at GBs such as grain growth (Estrin et al. 2000). GB properties depend on the atomic structures of GBs, which depend in turn on macroscopic and microscopic degrees of freedom such as axis and angle of misorientation, GB planes, and the rigid displacement of one grain with respect to another (Sutton and Balluffi 1995). Therefore, systematic studies of the atomic structures of GBs are required to understand their properties. To gain such information, there are several experimental methods such as HRTEM (Heinemann et al. 2001, 2003, 2005; Nishimura et al. 2003; Wirth 2004; Hartmann et al. 2010), electron back-scattered diffraction (EBSD) (Rohrer 2011, and references therein), and light microscopy (Saiz et al. 1999; Duyster and Stöckhert 2001). The driving force for grain growth is controlled by the GB energy (Mullins 1956; MacPherson and Srolovitz 2007). Because of this importance, Duyster and Stöckhert (2001) have determined low- and high-angle olivine GB energies from natural samples using triple junction dihedral angles. Using this method, the angles are measured using a universal stage on a light microscope. It is a time-consuming method and not well suited to the acquisition of large data sets.

Experimental methods are limited by their huge experimental demands and time consumption. Furthermore, the determination of the detailed atomic structure of the GB even using HRTEM is not directly available. Usually, a geometric model, deduced from the experimental images or resulting from atomistic modeling, is assumed to simulate HRTEM images. The comparison of the simulated HRTEM images to the experimental results gives an indication of the correctness of the geometrical model (Nishimura et al. 2003; Sato et al. 2007). Atomistic simulations are not only useful to provide the structural model needed for the interpretation of the HRTEM images, but they are also a unique tool to link structure and physical or thermodynamic properties of grain boundaries. Therefore, computational methods are needed to supplement experimental results for covering both structure and properties.

The atomic structures of GBs can be studied using first-principles calculations based on density functional theory (DFT) (Dawson et al. 1996; Sato et al. 2009; Körner and Elsässer 2010; Verma and Karki 2010; Mitsuma et al. 2011) or empirical potential simulations (Duffy 1986; Watson et al. 1996; Mishin and Farkas 1998; Karakasidis and Meyer 2000; Nishimura et al. 2003; Sato et al. 2005). First-principles calculations are accurate and transferable, but they are computationally expensive, and cell sizes for simulations are limited to few hundred atoms. Due to periodic boundary conditions used in the simulations, the individual grains have to be large enough to avoid interaction between repeated GBs. In addition, the repeat unit length along the grain boundary increases with decreasing misorientation angle between the two grains. Also, for complex silicates with many atoms in the unit cell and low symmetry, large simulation cells are required to obtain reliable structures and properties of GBs. Empirical potentials are often used efficiently to explore physical properties for large system sizes and long run durations. However, the accuracy of such potentials may suffer from the fact that they are fit to experimental data for specific systems and their transferability between different coordination environments, compositions or different thermodynamic conditions is uncertain.

So far, computational simulations of the atomic structures of GBs were mainly performed for metallic systems (Farkas 2000) and ceramics (Fabris and Elsaesser 2001; Verma and Karki 2010). For silicates, which have complex atomic structures in which the issues such as local charge neutrality and surface termination become much more important, there are only a few atomistic simulation studies. de Leeuw et al. (2000) have performed atomistic simulations to study structure and stabilities of a range of stepped tilt high-angle GBs in Mg2SiO4 forsterite using classical interaction potentials. Recently, Dobson et al. (2007) have combined transmission electron microscopy (TEM) study and classical potentials simulations to study the enrichment of iron on MgSiO3 perovskite GBs.

Here, we perform atomistic simulations for a series of GBs in Mg2SiO4 forsterite with misorientation angle ranging from 9° to 60°. We apply an advanced ionic model that is derived from electronic structure calculations and considers important contributions to the bonding explicitly. A so-called Aspherical Ion Model (AIM) (Aguado et al. 2003; Madden et al. 2006) was parameterized for oxides and silicates of Ca–Mg–Al–Si–O system (Jahn and Madden 2007). The main goals of this study are to address the following issues: (1) the identification of low energy GB structures, (2) the variation of GB energy and excess free volume as function of misorientation angle and linking them to the GB structure, (3) the transition from low to high-angle GBs in forsterite, (4) the validity of Read-Shockley model (Read and Shockley 1950) for forsterite GBs, and (5) the validation of the modeled structures by comparison to HRTEM.

Methodology

Atomistic modeling

Mg2SiO4 forsterite crystallizes in an orthorhombic structure with space group Pbnm (a = 4.7535 Å, b = 10.1943 Å, c = 5.9807 Å, and α = β = γ = 90°) (Hazen 1976). It consists of isolated SiO4 tetrahedra linked by magnesium cations. We constructed [100] symmetric tilt grain boundaries with tilt angle θ by aligning a chosen crystallographic plane (0kl) parallel to the tilt axis [100] and misoriented with θ/2 to the (010) plane. The crystal is cut along the (0kl) plane into two crystal grains. One crystal grain is rotated by 180° relative to the other grain about the normal [0kl]. The (0kl) planes were cut in two different ways: (1) by keeping SiO4 tetrahedra intact and (2) by breaking Si-O bonds and allowing the formation of bridging oxygens and free oxygens. Since the Mg2SiO4 forsterite structure is based on a distorted hexagonal arrangement of oxygen atoms, we constructed also an asymmetric tilt GB with a misorientation of 60.80° formed between surfaces (010) and (011). This structure is a good candidate for a low energy GB as it preserves the hexagonal arrangement of oxygen atoms in GB region. In order to eliminate surface effects, we used three-dimensional periodic boundary conditions. This leads to two distinct GBs, in our setup one on the center of the simulation cell and another one on the parallel edges (Fig. 1). The distance between the two GBs should be large enough to exclude the interactions between them. We will further discuss this issue in the “Results and discussion”. The repeat length of the simulation cell in the x direction (along the tilt axis) is chosen to be 4a = 19.014 Å, whereas the repeat unit length, L GB, in y direction (perpendicular to the tilt axis in the GB plane) depends on the particular GB, as indicated in Table 1. For the initial setup, it is necessary to separate the two grains slightly (∼2 Å) to avoid very short interatomic distances.

Fig. 1
figure 1

Example of simulation cell containing a relaxed (012)/[100] symmetric tilt GB with misorientation 32.70°, which is projected a along and b perpendicular to the tilt axis [100]. x, y, and z present the simulation cell vectors. The tilt axis [100] is aligned along the x direction. The two bold arrows show the two GBs in the simulation cell. Black dashed rectangles illustrate the orientation of the Mg2SiO4 forsterite orthorhombic unit cells projected down the [100] axis, containing isolated SiO4 tetrahedra alternately pointing up and down

Full size image
Table 1 Characteristics of (0kl)/[100] grain boundaries with misorientation θ in Mg2SiO4 forsterite
Full size table

To take account of rigid-body translation, we calculated grain boundary energies as a function of relative displacements of one grain with respect to another grain by a vector \({\bf t} = (t_{x}, t_{y})\) along the grain boundary plane. The atomic configuration is relaxed after each translation using conjugate gradient method (Press et al. 1992). The translation t x is measured as a fraction of the lattice parameter a, and the translation t y is measured as a fraction of the GB unit length L GB, which depends on the misorientation angle θ. The increment of t x was 0.25a and for t y was 0.02 L GB. Before every new translation, the system was returned to its initial unrelaxed and non-translated state. For each translation t x , the GB energy was calculated as a function of t y . Most of the local minima of the GB energy were attained at the translational state with zero component along the tilt axis (t x  = 0). After that, molecular dynamics simulation is run starting with two to four configurations around each local energy minimum.

Molecular dynamics (MD) simulations were performed for a series of [100] symmetric tilt GBs with 12 different misorientations θ in the the range 9°–60°. The simulation cells consist of 4,032–9,408 atoms (Table 1). A time step of 1 fs is used for the numerical integration of the equations of motion. During the simulation, atomic coordinates, simulation cell parameters and shape are fully relaxed. Simulations are performed at zero (ambient) pressure and a constant temperature of 100 K. The equilibration is done using an anisotropic barostat (Martyna et al. 1994) coupled to a Nosé-Hoover thermostat (Nosé and Klein 1983) for a few ps before data collection runs of 10 ps were carried out. The AIM interaction model and its parameterization are described elsewhere (Madden et al. 2006; Jahn and Madden 2007). The model takes into account: the Coulomb interaction between charged particles, short-ranged repulsion due to the overlap of the electronic charge densities, dispersion, ionic polarization effects, and ion shape deformations. The set of AIM potentials used here was parameterized for the Ca–Mg–Al–Si–O system by reference to electronic structure calculations (Jahn and Madden 2007), and it was found that the potential predicts lattice parameters, elastic constants, and volume compression as a function of pressure in good agreement with experimental data. The model has successfully been applied to study crystalline magnesiosilicates (Jahn and Martoňák 2008, 2009; Jahn 2010), oxide and silicate melts (Jahn 2008; Adjaoud et al. 2008, 2011) as well as melt wetted forsterite GBs (Gurmani et al. 2011). Here, the same set of interatomic potentials is used.

The energy of a grain boundary is calculated with respect to a reference state, which is a single crystal containing the same number of atoms as the bicrystal:

$$ E_{\rm GB} = \frac{E_{\rm bc} - E_{\rm sc}}{2 A_{\rm GB}} $$
(1)

where E bc and E sc are the total energies of the supercell with a GB and without a GB, respectively. A GB is the area of one GB, that is, the cross-section of the simulation cell in the GB plane. Similarly, the excess free volume of the grain boundary:

$$ \Updelta V_{\rm GB} = \frac{V_{\rm bc} - V_{\rm sc}}{2 A_{\rm GB}} $$
(2)

where V bc and V sc are total volumes of supercell with GB and without GB, respectively.

HRTEM image

A TEM image of a 12° tilt grain boundary about the common [100] direction was kindly provided by Stefan Heinemann, which was part of his study published in 2005 (Heinemann et al. 2005). It was obtained from a forsterite bicrystal bonded using the direct bonding technique (e.g. Haisma et al. 1994; e.g. Plössl and Kraeuter 1999).

For the TEM analysis, the bicrystal sample was prepared using a focused ion beam instrument FEI FIB200TEM, which prevents preferential thinning of the grain boundary (e.g. Wirth 2004). Preparing a TEM lamella (10 × 15 μm2) with a small window where the final thickness can be reduced to about 50–80 nm and thus is for suitable HRTEM lattice fringe imaging. In the present case, an even thinner area could be obtained as the sample bent during FIB cutting and a wedge shaped edge was generated. The HRTEM image was obtained using a Philips CM200 TEM equipped with a LaB6 filament and a GATAN imaging filter (GIF). The presented image was obtained applying a 10 eV slit to the zero loss peak.

HRTEM image simulation

Multislice calculations were carried out using the software EMS (Stadelmann 1987) for HRTEM image simulation. It was developed by Pierre Stadelmann at the Centre Interdisciplinaire de Microscopie Electronique of the École Polytechnique Fédérale de Lausanne. Here, we used HRTEM image simulation to understand the contrast of the experimental micrographs and calculate images for comparison with this image and test whether or not the calculated grain boundary structure model is able to describe the previously made observations.

The EMS software package only allows to simulate images of cells with at least orthorhombic structure. Therefore, the final calculated models that have triclinic symmetry were slightly distorted to become orthorhombic. This results in a small distortion of at most 1.21° for the γ angle. The extensions of the supercell are x = 7.305 nm, y = 5.644 nm, z = 1.896 nm ((0 2 11)/[100] relaxed GB, see Table 1). The general working scheme of EMS is as follows. (1) Usually, the crystal or defect structure needs to be modeled. In the present case, we used one snapshot of equilibrated MD supercell obtained from atomistic modeling described above. (2) The propagation of the incident electron wave through the supercell slabs is calculated. To do so, the supercell is sliced in small wafers parallel to the later imaged surface. In the present study, we sliced the crystal in 19 slices of about 0.1 nm. The crystal potential of each wafer is projected onto its entrance plane. This introduces a modulation of the transmittance of this wafer. The modified wave front passes through vacuum for a very small distance (wafer thickness) and then propagates through the next plane with its projected potentials. (3) The transfer of the scattered wave by the microscope optics is calculated. This procedure is repeated for different crystal thicknesses and different defocus values until a best fit between experimental and simulated image is reached.

Results and discussion

Grain boundary energy and excess free volume

The convergence of GB energy with respect to the grain size perpendicular to the GB plane which should be large enough to avoid the interaction between GBs was tested by defining two supercells with different size of the same GB (e.g., (011)/[100] 60.80°). One contained 4,032 atoms, resulting in a GB distance 3.17 nm and one of 6,720 atoms, a GB distance of 5.23 nm. The difference of GB energies of the two supercells is less than 2 %. We considered this to be sufficiently converged. For all calculations, we used a grain size perpendicular to the GB plane of 3.17 nm or larger.

To illustrate the procedure of rigid-body translation, we use the (012)/[100] symmetric tilt GB with misorientation 32.70° as an example, see Fig. 2. The variation of the GB energy depends significantly on t y  is not smooth and shows jumps and sudden sharp peaks (Fig. 2).

Fig. 2
figure 2

(012)/[100] symmetric tilt GB with misorientation 32.70° as an example for grain boundary energy as a function of displacements t x , t y along the grain boundary plane. t x is defined as fraction of lattice parameter a = 4.7535 Å and t y as fraction of GB unit length, L GB, in this case L GB = 21.25 Å

Full size image

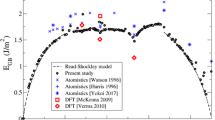
Figure 3a shows the calculated GB energies for two series of GB planes (01l) and (02l). The (01l) symmetric tilt GB energies are lower than the ones of the (02l) symmetric tilt GB, consistent with EBSD observations of the GB plane distribution in MgO, SrTiO3, Al, TiO2, MgAl2O4, and nickel-based superalloy (Miller et al. 2004; Rohrer et al. 2010; Saylor et al. 2003a, b, 2004a, b) suggesting that low index GB planes have low GB energies. For the (01l) symmetric tilt GBs, all calculated GB energies assuming isolated SiO4 tetrahedra only at the GB plane are lower than the ones for partly dimerized SiO4 tetrahedra at GB plane, except for the two misorientations 9.58° and 13.38°, which suggests that free oxygens can exist in GBs with low misorientation angles. The maximum GB energy value for (01l) symmetric tilt GB is ∼1.45 J/m2, in agreement with the value ∼1.4 J/m2 measured by Duyster and Stöckhert (2001) on natural samples of olivine GB using triple junction dihedral angles. Our model gives lower GB energies compared to those calculated for stepped tilt GBs in Mg2SiO4 forsterite by de Leeuw et al. (2000), except for their GB formed with (100) wall and (010) terrace, which corresponds to the smallest terrace in their study and which has a GB energy (1.32 J/m2) comparable to our study.

Fig. 3
figure 3

GB energy (a) and GB excess free volume (b) as a function of misorientation angle. The (01l) symmetric tilt GB energies (a) and GB excess free volume (b) are shown for only isolated SiO4 tetrahedra at GB plane (circles) and partly dimerized SiO4 tetrahedra at GB plane (triangles). Black filled circles represent GB energy (a) and GB excess free volume (b) of the asymmetric GB with a misorientation of 60.80°. The squares are the (02l) symmetric tilt GB energies (a) and GB excess free volume (b) with isolated SiO4 tetrahedra at GB plane. Solid line shows the fit to Eq. 4. Dashed lines are guides to the eye

Full size image

Figure 3b shows the variation of GB excess free volume as a function of misorientation angle for two series of GB planes (01l) and (02l). The (01l) symmetric tilt GB excess free volume are lower than the ones of the (02l) symmetric tilt GBs, except for the (023)/[100] symmetric tilt GB with a misorientation of 42.72°. For the (01l) symmetric tilt GB, excess free volume for partly dimerized SiO4 tetrahedra at the GB plane are lower than the ones with isolated SiO4 tetrahedra at the GB plane up to the misorientation angle of 22.13°. Then, the excess free volumes becomes approximately the same for the misorientations 32.70° and 60.80°. Generally, there is a positive correlation between the excess free volume and the GB energy: high excess free volumes show high GB energies (Fig. 4). Compared to the GBs in pure metallic systems where GB energy increases linearly with increasing excess free volume (Seki et al. 1996; Huang et al. 2006; Uesugi and Higashi 2011), this correlation is less pronounced for Mg2SiO4 forsterite symmetric tilt GBs especially for (01l) symmetric tilt GBs (Fig. 4). This is likely due to the complexity of Mg2SiO4 forsterite structure, which contains two cations and consists of isolated SiO4 tetrahedra, and also to the requirement of the local charge neutrality. Our calculated excess free volumes in (01l)/[100] Mg2SiO4 forsterite symmetric tilt GBs (0.43−0.61 (10−10 m3/m2)) are lower than the excess free volumes in [001] MgO tilt GB (0.81–0.93 (10−10 m3/m2)) obtained with ab initio calculations (Verma and Karki 2010). For comparison, the GB excess free volume for semiconductors, metals, alloys, and oxides is in the range of 10−12 − 10−10 m3/m2 (e.g. Seki et al. 1996; Shvindlerman et al. 2006; Shen et al. 2008; Uesugi and Higashi 2011).

Fig. 4
figure 4

GB energy as a function of GB excess free volume. The line shows a linear fit for (02l) symmetric tilt GB

Full size image

Grain boundary structure

Figures 5, 6 and 7 show relaxed structures of some of the [100] symmetric tilt GBs in Mg2SiO4 forsterite studied here, projected on the (100) plane. Each structure corresponds to the minimum energy configuration among many metastable states (Fig. 2) for the specific GB. Most of the ground state structures were found after rigid translation with t x and/or t y in the GB plane, meaning that a relative shift of grains is favorable for Mg2SiO4 forsterite symmetric tilt GBs. To investigate the structural origin of GB stability, average cation coordination numbers were obtained from equilibrated molecular dynamics trajectories. They were computed by counting all oxygens within a distance smaller than a given cutoff radius for Si and Mg, which was chosen to be at the position of the respective first minimum of the partial radial distribution function. For GBs with isolated SiO4 tetrahedra at the GB plane, the Si coordination number in the GB region stayed four-coordinated as in the single crystal, while some Mg have a coordination that is lower and/or higher than in the single crystal where Mg is six-coordinated (Table 2).

Fig. 5
figure 5

Atomic structure of (017)/[100] symmetric tilt GB with misorientation 9.58°, a keeping SiO4 tetrahedra intact at GB and b breaking Si-O bonds at GB. The thick black dashed lines show Burgers circuits for partial edge dislocation with Burgers vector \(\frac{1}{2}[001]\) and perfect edge dislocation with Burgers vector [001]. Thick black lines show the array of edge dislocations separated with distances d1 and d2 with d1 + d2 = d, where \(\hbox{d} =\frac{L_{\rm GB}}{2}\) is the spacing of perfect dislocations and L GB is given in Table 1

Full size image
Table 2 Density distribution of Mg atoms with a coordination number different from the single crystal (6-coord.) and of oxygen–oxygen (O–O) pairs with a distance shorter than the smallest distance in the single crystal (∼2.5 Å) per GB area
Full size table

For the geometrical analysis of grain boundaries, Frank (1951) proposed a relation between the spacing of perfect dislocations, d, the misorientation, θ, and the Burgers vector length, b:

$$ d = \frac{b}{2 {\hbox {sin}}(\theta/2)} \approx \frac{b}{\theta}. $$
(3)

Using θ and d = L GB/2 values from Table 1, we get b = [001] ∼5.98 Å, which is the lattice constant c of Mg2SiO4 forsterite. This is consistent with the model suggested to interpret HRTEM observations (Heinemann et al. 2005). The spacing between the perfect dislocations d decreases with misorientation angle θ, which is consistent with Frank’s formula (Fig. 8).

After atomic relaxation, the perfect edge dislocations of low-angle GBs (up to 22°) with Burgers vector [001] dissociate into an array of partial edge dislocations with Burgers vector \(\frac{1}{2}[001]\) and a stacking fault between pairs, as illustrated in Fig. 5 for the (017)/[100] GB. This GB structure is similar to the one observed in low-angle tilt GBs in alumina (Ikuhara et al. 2003). At and around the GB, there are regions with high and regions with low particle densities. The partial dislocation cores are separated by regions of almost perfect lattice (perfect stacking for a distance d 1) and regions of distorted lattice (stacking fault for distance d 2), see Fig. 5. The structures of (017)/[100] GB with misorientation 9.58° for intact SiO4 tetrahedra and partly dimerized SiO4 tetrahedra at the GB plane are presented in Fig. 5a, b, respectively. These structures have the same energy (1.46 J/m2, see Fig. 3a), which suggests that both partly dimerized SiO4 tetrahedra and free oxygens may exist in low-angle Mg2SiO4 forsterite symmetric tilt GBs.

Figure 6 shows the stable atomic structure for a (012)/[100] symmetric tilt GB with a misorientation of 32.70° which consists of an array of the structural units a + b + c. This structure obtained with rigid translation of one grain with respect to another with 0.64 nm along y direction and no translation in x direction showed the lowest GB energy (1.01 J/m2) among all GBs considered here. This lowest energy can be related to the distribution of coordination environments in the GB region. Stable GB structures are expected to preserve the local atomic coordination of the single crystal as much as possible (Oba et al. 2000). The coordination number of Mg in forsterite single crystal is 6, but in the GB some Mg atoms are lower or higher coordinated. In (012)/[100] GB with misorientation 32.70°, the coordination number of those Mg ions that are different from the single crystal is only fivefold coordination and they have the lowest density (5.7 nm2) (Table 2). Other GBs, in addition to fivefold coordination, contain also small amounts of three, four, and/or sevenfold coordination, and their density is higher than 5.7 nm2 (Table 2). A relation between GB stability and the occurrence of coordination numbers that are different from single crystal was also reported for ZnO GBs (Sato et al. 2005, 2007). The occurrence of oxygen–oxygen pairs with shorter distances than the smallest distance in single crystal (∼2.5 Å) can be also expected to influence GB energies. The repulsive interactions between those oxygen–oxygen pairs contribute to increase the GB energy. The lowest density (3.9 nm2) corresponds to the (012)/[100] GB with misorientation 32.70° which has the lowest GB energy (Table 2).

Fig. 6
figure 6

Atomic structure of (012)/[100] symmetric tilt GB with misorientation 32.70° formed with a + b + c structural units, which are presented with thick black lines

Full size image

Figure 7 shows the stable atomic structures for (011)/[100] tilt GB with misorientation 60.80°, (a) symmetric (structure A) and (b) asymmetric (structure B) which consist of an array of the structural units a + b and c, respectively. Structure A was found by rigid translation of one grain with respect to another with 0.57 nm in y direction and 0.24 nm in x direction. Structure B was formed with surface (010) and surface (011) which is displaced rigidly by 0.45 nm in y direction and no translation in x direction with respect to the surface (010). As for (012)/[100] GB with misorientation 32.70°, the distribution of Mg coordinations apart from the crystalline sixfold environment is restricted to fivefold coordination with a density of 7.1 nm2. This is higher than the one of the (012)/[100] GB with misorientation 32.70° but still lower than the ones of other GBs (Table 2). Hence, the GB of structure A (1.28 J/m2) has the second lowest energy after the one of the (012)/[100] GB with misorientation 32.70°. However, the GB energy of structure B is lower than the one of structure A even if structure B has Mg in fivefold (with the same density as structure A) and in fourfold coordination (1.6 nm2) (Table 2). This difference in energy between structures A and B maybe due to the different density of oxygen–oxygen pairs with short distance, which is higher for structure A (6.1 nm2) than for structure B (4.4 nm2) (Table 2).

Fig. 7
figure 7

a Atomic structure of (011)/[100] tilt GB with misorientation 60.80°, a symmetric and b asymmetric formed with the structural units a + b and c, respectively, which are presented with thick black lines. The gray dashed lines show the orientation of the grains

Full size image
Fig. 8
figure 8

Spacing between perfect dislocations as function of misorientation angle. Line is Frank’s formula and circles are values calculated from geometry of our simulation cells (Table 1)

Full size image

To validate our structural models, we used the stable structure obtained with MD simulations for 12.18° symmetric tilt GB as input to simulate the HRTEM image and we compare it to the experimental HRTEM image (Fig. 9). The best correlation between the simulated HRTEM image (b) and experimental HRTEM image (c) was found assuming a sample of 10 nm thickness and a defocus value of −10 nm. With these thickness and defocus values, the simulated HRTEM image showed quite similar contrast features to the experimental HRTEM image. This shows that the 12° tilt GB is formed with an array of partial edge dislocations with Burgers vector \(\frac{1}{2}[001]\) separated with a stacking fault (Fig. 9).

Fig. 9
figure 9

Comparison between experimental and simulated HRTEM image. a HRTEM image of a 12° tilt grain boundary by Heinemann et al. (2005), b HRTEM simulated image based on calculated structure, c FFT filtered image for a 12° tilt grain boundary by Heinemann et al. (2005), and d atomic structure of (0 2 11)/[100] symmetric tilt GB with misorientation 12.18° modeled by atomistic calculations (this study)

Full size image

Dislocation model for low-angle grain boundary

As discussed in the previous section (“Grain boundary structure”), GB structures for misorientation angles ranging from 9.58 to 22.13° consist of an array of partial edge dislocations with Burgers vector \(\frac{1}{2}[001]\) associated with stacking faults. Therefore, GB energy can be written as the sum of the partial dislocation energy, E d , and the stacking fault energy, E SF:

$$ E_{\rm GB} = 2 E_d + \alpha E_{\rm SF}, $$
(4)

where α = (d 2/d) is a stacking fault area fraction in the GB. The factor 2 arises because each perfect edge dislocation dissociates into two partial edge dislocations. E d can be calculated according to the Read and Shockley (1950) model:

$$ E_{d} = E_{0} \theta(A-{\hbox{ln}}(\theta)), $$
(5)

and E SF can be derived from the Peach-Koehler equation (Hirth and Lothe 1982; Ikuhara et al. 2003):

$$ E_{\rm SF} = E_0\left(\frac{b_{p}}{d}\right)\sum\limits_{n=0}^{\infty}\left(\frac{1}{n + \alpha} - \frac{1}{n + 1 - \alpha}\right). $$
(6)

The energy factor E 0 contains information about the elastic properties and the constant A = 1 + ln (b p /2πr 0) depends on the size of the dislocation cores. r 0 is an effective radius defining the extent of the core of the dislocations. b p  = b/2 = 2.99 Å is the Burgers vector magnitude of partial dislocations.

In the present case, we have an edge dislocation lying parallel to [100] with Burgers vector parallel to [001]; thus, the energy factor for an anisotropic material with orthorhombic symmetry is given by Eshelby et al. (1953), Foreman (1955), Steeds (1973) and Shadrake and Guiu (1976):

$$ E_{0} = \left(\frac{b_{p}}{4\pi}\right) \left(\frac{c_{33}}{c_{22}}\right)^{\frac{1}{2}} \left((c_{22}c_{33})^{\frac{1}{2}}+c_{23}\right) \left[\frac{c_{44}\left((c_{22}c_{33})^{\frac{1}{2}}-c_{23}\right)}{c_{33} \left((c_{22}c_{33})^{\frac{1}{2}}+c_{23}\right)+2c_{44}}\right]^{\frac{1}{2}}, $$
(7)

where c 22, c 23, c 33, and c 44 are the elastic constants.

For an isotropic material, the elastic constants are c 22 = c 33 = λ + 2μ, c 23 = λ, c 44 =  μ. Then, Eq. 7 reduces to:

$$ E_{0} = \left(\frac{b_{p}}{4\pi}\right) \left(\frac{2(\lambda + \mu)\mu}{\lambda + 2\mu}\right) = \frac{\mu b_{p}}{4\pi(1-\nu)}, $$
(8)

where μ is the shear modulus and ν is Poisson’s ratio.

Using the values of d and d2 calculated from our simulations, Eq. 7, the elastic constants of forsterite from Jahn and Madden (2007), and Eq. 6, we obtain E SF = 0.45 J/m2. This value of E SF is higher than the one of \(\Upsigma 3\) GB in alumina (0.32 J/m2) estimated from measured values of d and d 2 (Ikuhara et al. 2003).

By combining Eqs. 3 and 6, the misorientation angle θ can be defined as a function of α:

$$ \frac{1}{\theta} = \frac{1}{E_{SF}} \left(\frac{E_0}{2}\right)\sum\limits_{n=0}^{\infty}\left(\frac{1}{n + \alpha} - \frac{1}{n + 1 - \alpha}\right). $$
(9)

Then, the length of perfect stacking d 1 = (1 − α)d, the distance between two partial edge dislocations d 2 = αd, and the periodicity of the GB d can be calculated as a function of θ, which are shown in Fig. 10. The lengths d and d 1 decrease with θ and extremely increase with decreasing θ for angles smaller than 5°. The maximum value of d 2 (∼1.5 nm) appears for a misorientation angle of ∼0°, then decreases with θ and reaches ∼0.6 nm for a misorientation angle of 22°.

Fig. 10
figure 10

Spacing between perfect dislocations d, length of perfect stacking d 1 = (1 − α)d, and the distance between two partial edge dislocations d 2 = αd as a function of misorientation angle

Full size image

The best fit of Eq. 4 to our calculated GB energies gives E 0 = 5.53 ± 0.3 J/m2 and A =  −0.56 (Fig. 3a). This value of A corresponds to r 0 = 0.4b ∼2.4 Å, consistent with 0.5b = 2.4 Å (b = 4.76 Å) value for a dislocation line parallel to [001] in olivine GB derived from dihedral angles (Duyster and Stöckhert 2001) and the value 2.6 Å for [001](010) edge dislocations in forsterite calculated by Durinck et al. (2007) using the Peierls-Nabarro model. Harding et al. (1999) have calculated the [100] and [110] MgO tilt GB energies using classical atomistic simulations and they fit their results to the Read and Shockley (1950) equation. They derived A of 0.25 and −0.24 for [100] and [110] MgO tilt GBs, which correspond to r 0 of 0.34b = 1.4 Å (b ∼4.21 Å) and \(0.55b = 1.6\,\AA\,(b\,\sim 4.21/\sqrt 2 \AA),\) respectively. This implies that the core radius of dislocations in [100] Mg2SiO4 forsterite symmetric tilt GBs is larger than the ones of [100] and [110] MgO tilt GBs. The transition from low to high-angle GBs occurs when the cores of partial dislocations overlap, that is, when the distance between two partials d 2 smaller than 2r 0 = 4.8 Å. With our model, this occurs for a misorientation angle between 22° and 32° (see Fig. 10, inset).

Alternatively, we used Eqs. 7 and 8 to evaluate E 0 using experimental elastic constants by Suzuki et al. (1983) and the calculated ones with atomic simulations based on the same interatomic potential (Jahn and Madden 2007). Considering an anisotropic material (Eq. 7), we obtained E 0 = 4.66 J/m2 using experimental elastic constants and E 0 = 4.41 J/m2 using calculated elastic constants. In the case of an isotropic material (Eq. 8), we used Voigt-Reuss-Hill approximation (Hill 1952) for bulk (B) and shear (μ) moduli. Poisson’s ratio ν for an isotropic material is given by ν = (3B − 2μ)/(6B + 2μ). We obtain μ = 81.37 GPa and ν = 0.24 for experiment, and μ = 76.30 GPa and ν = 0.26 for atomic simulations. This gives E 0 = 5.10 J/m2, E 0 = 4.91 J/m2 for experiment and atomic simulations, respectively. As in the case of screw dislocation in MgO (Walker et al. 2005), we found the anisotropic energy factor is lower than the isotropic energy factor. Our fitted value of E 0 (5.57 ± 0.3 J/m2) is somewhat larger than that expected from elastic theory. Reasons for that could be that the obtained GB structures do not represent the global energy minima or the elastic theory does not account for details of the atomic structure of GBs in complex materials. Nevertheless, the energy factors calculated analytically from Eqs. 7 and 8 are in reasonable agreement with the one obtained from linear elastic theory (Eq. 4), E 0 = 5.57 ± 0.3 J/m2. This suggests that the energies of [100] Mg2SiO4 forsterite symmetric tilt GBs for small angles (up to ∼22°) are well explained by a model which combines the Read-Shockley model (Read and Shockley 1950) and the Peach-Koehler equation (Hirth and Lothe 1982; Ikuhara et al. 2003).

Conclusions

Molecular dynamics simulations provide an insight into the atomic structure of a series of [100] symmetric tilt grain boundaries in Mg2SiO4 forsterite and link their structures to the corresponding GB energies and excess free volumes. Our results show that grain boundary energy depends significantly on misorientation and low index GB planes have low GB energies. GB structures consist of an array of partial edge dislocations with Burgers vector \(\frac{1}{2}[001], \) associated with stacking faults between the partials, up to 22° and their energies can readily be fit with a model based on the Read-Shockley dislocation model for GB and the Peach-Koehler equation. GB energies and the size of the edge dislocation cores are consistent with previous estimates on natural samples of olivine GB using triple junction dihedral angles (Duyster and Stöckhert 2001). With increasing misorientation angle from 32.7° to 60.8° the dislocation cores interact and overlap to form repeated structural units. To compare our GB atomic model to HRTEM image (Heinemann et al. 2005), we used the stable atomic structure for misorientation of 12.18° as input to simulate HRTEM image. Both experiment and computation give a consistent image of GB.

Our study shows that the molecular modeling approach serves as an efficient tool to predict the energies and structures of GB in forsterite, which is a representative of silicates. The present results can be used as inputs for continuum models to understand processes in geomaterials such as diffusion and also as input to interpret HRTEM images.