Refining the Use of Habitat Equivalency Analysis

Abstract

When natural resources are injured or destroyed in violation of certain U.S. federal or state statutes, government agencies have the responsibility to ensure the public is compensated through ecological restoration for the loss of the natural resources and services they provide. Habitat equivalency analysis is a service-to-service approach to scaling restoration commonly used in natural resource damage assessments. Calculation of the present value of resource services lost due to injury and gained from compensatory restoration projects is complicated by assumptions concerning the within-time period crediting of losses and gains. Conventional beginning-of-period accounting leads to an underestimate of the loss due to injury and an overestimate of the gains from compensatory projects in cases with linear recovery projections. The resulting compensatory requirement is often insufficient to offset the true loss suffered by the public. Two algebraic equations are offered to correct for these estimation inaccuracies, and a numerical example is used to illustrate the magnitude of error for a typical, though hypothetical, injury scenario.

Introduction

Various U.S. federal and state government agencies and Native American tribes are trustees for natural resources. These entities have the responsibility to manage and protect resources for the benefit of their respective constituencies. When trust resources are injured in the United States, several federal and state statutes require trustees to seek damages from persons liable for the natural resource injury [see the Comprehensive Environmental Response, Compensation, and Liability Act (CERCLA, also known as Superfund), the Oil Pollution Act, the National Marine Sanctuaries Act, and the Clean Water Act]. Injuries most often occur as a result of the release of hazardous substances or oil into the environment, either from chronic discharges or from acute spills. Recovered damages must be used to restore the injured resources to the extent practical, to pay for restoration to compensate for interim service loss and any loss of the injured resources into perpetuity, and to repay reasonable response and assessment costs incurred by the trustees (Jones and Pease 1997).

Persons liable for natural resource injuries are responsible for restoring the resources and the services they provide to their baseline condition. The term “services” in the context of natural resource damage assessments (NRDAs) refers to the functions performed by a natural resource for the benefit of another natural resource and/or the public. Measures taken to restore the injured resources and services to, or as close as is practical to, baseline are defined as primary restoration. In natural resource damage assessment, baseline refers to those conditions that would have existed but for the incident. Even if the injured resources are fully restored to baseline, the public has not received compensation for the interim loss of natural resources and their services between the time of incident and the time at which the injured resources return to baseline. In addition, if the injured resource cannot be restored fully to baseline, there is some loss into perpetuity for which the public is entitled to compensation. To make the public whole from the injury, additional resource services are required to compensate for these interim and perpetual service losses. Actions taken to address interim and perpetual service loss are defined as compensatory restoration.

Habitat equivalency analysis (HEA) and resource equivalency analysis (REA) are methods often used in natural resource damage assessments to facilitate scaling of compensatory restoration (Unsworth and Bishop 1994; Mazzotta and others 1994; Allen and others 2004a; Hampton and Zafonte 2005; Zafonte and Hampton, 2007). Since the algebraic formulations of HEA and REA are identical, the revisions discussed in this article will refer solely to the HEA method for simplicity. Scaling refers to the process of determining the quantity of compensatory restoration required to offset interim and perpetual losses. Service-to-service approaches to scaling restoration seek to identify restoration actions that will yield benefits to natural resources and/or the public equivalent to those services associated with a lost natural resource. HEA is a service-to-service approach that relies on the implicit assumption that the public is willing to accept some trade-off between natural resource services lost because of the injury and those provided through compensatory restoration projects (Jones and Pease 1997). The interim and perpetual service losses and compensatory benefits are quantified in nonmonetized units. The objective of HEA is to calculate a quantity of restoration (often expressed in real units of a particular habitat) that equates the present value of the losses due to injury with the present value of the benefits from the compensatory project (Unsworth and Bishop 1994; Mazzotta and others 1994; Allen and others 2004a; Hampton and Zafonte 2005; Zafonte and Hampton 2007).

A thorough description of the method and its algebraic expressions are included in the articles cited previously and a primer prepared by the National Oceanic and Atmospheric Administration’s (NOAA’s) Damage Assessment and Restoration Program (NOAA 2000). The purpose of this article is to offer refinements to allow more accurate estimations of the amount of compensatory restoration required to offset natural resource injuries. The first alteration is to use the within-period mean percent service provision rather than beginning- or end-of-period accounting for both the injured resource’s recovery and compensatory project’s maturation functions. The second change is to capitalize service gains and/or losses such that the quantification is not unbounded when such services are provided or lost in perpetuity. These refinements solve certain of the problems associated with using discrete models to represent continuous recovery functions. This article provides a brief overview of the use of HEA, analyzes the current NOAA model, offers algebraic refinements that reduce systemic bias in the compensatory restoration estimate, and illustrates the proposed equations using a hypothetical numerical example.

Background

Habitat equivalency analysis entails three steps: (1) quantifying the present value of natural resource service losses due to injury, (2) quantifying the present value of service gains provided by the compensatory restoration project(s) per unit, and (3) calculating the quantity of compensatory restoration required to equate the losses and gains. Each will be discussed in turn.

Step 1: Quantify the Interim and Perpetual Service Losses Due to Injury

To quantify service losses, it is necessary to know eight parameters concerning the injury and affected resources:

• 1. When the injury began

• 2. Baseline service level over time

• 3. Service decline function

• 4. Extent of injury (area for habitats or counts for individual organisms)

• 5. Degree of injury (percent service level decrease)

• 6. When the injury begins to recover

• 7. Service recovery function (time path of service restoration)

• 8. Maximum percent service provision following restoration

For any given incident, it is likely that some of these parameters can be known with objective certainty, including the timing of the injury, the baseline service level (often defined as 100%), the decline function (often instantaneous), the extent of injury, and when the injury will begin to recover. The others often require an analysis of biological data. A discussion of the best approach for determining these parameters is beyond the scope of this article (see Barnthouse and Stahl 2002; Cacela and others 2005; Strange and others 2002). For the purposes of exploring changes to the algebraic equations, it is assumed that the parameters are given with certainty.

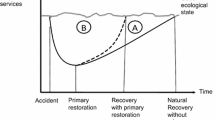
With the exception of the extent of injury, these parameters can be used to graphically depict the interim and perpetual service losses (Strange and others 2002). Figure 1 is such a depiction. The heavy line traces the resource service level through time. There is an initial baseline condition (line segment (a)), precipitous loss of service that accompanies an acute injury (b), stabilization at some service level below baseline (c), recovery of services following the completion of some primary restoration project or via natural recovery (d), and eventual return to baseline service provision (e). The shaded area, L, bounded by the heavy line and the baseline service level, is a graphical representation of the interim loss associated with this injury, in undiscounted form. Since the injured resource returns to full baseline condition, there is no perpetual loss in this depiction.

Fig. 1

Graphical representation of service losses associated with a generic injured resource

Step 2. Quantify the Service Gains Provided by Compensatory Restoration

Analogous information is required to quantify the benefits provided by a compensatory project, whether such projects involve creation of new habitat, enhancement of existing habitat, or prevention of future degradation of resources. These parameters include the following:

• 1. Initial service level of the compensatory project

• 2. Time that provision of additional services begins

• 3. Compensatory project maturity function (time path of service provision)

• 4. Maximum service provision following restoration action

• 5. Compensatory project duration

• 6. Relative value of the compensatory resource compared to the injured resource

If new habitat is to be created, then the initial percent service level may be 0%. For those compensatory restoration projects that seek to improve an existing, degraded habitat as compensation, the initial service level will be some positive value. Because it is recognized that created or restored habitat often may not provide the same level of services as a pristine natural environment of the same type, the maximum percent service provision is often less than 100%. Certain restorations are expected to be of limited duration and senesce at some time in the future. For projects that do not continue providing services into perpetuity, the life span of the project must be specified.

As with quantification of the losses, benefits gained from compensatory restoration can be depicted graphically (Fig. 2) (Strange and others 2002). In this example, the compensatory project is the improvement of degraded habitat, and therefore it is already providing some level of service prior to restoration actions (line segment (a) in Figure 2). Following action, the habitat provides an increasing level of service (b), up to the maximum percent service provision (c). The baseline condition of the injured site (dashed line) has been included in Figure 2 to illustrate that the maximum percent service provision of the compensatory project is less than the baseline level of service provision at the injured site. The arrow on the end of the heavy line indicates that the project continues into perpetuity. The shaded area, G, above the initial service provision level and below the heavy service provision line, continuing to infinity, represents the undiscounted gain from one unit of the compensatory project.

Fig. 2

Graphical representation of service gains provided by a generic compensatory restoration project

Step 3. Calculate the Quantity of Restoration Required

The timing of the interim and perpetual service losses and the gains from a compensatory project must be considered to derive the present value of each (Lyon 1996). It is common practice to use a constant discount rate of 3% in natural resource damage assessments (NOAA 1999), although this convention has been questioned (Cline 1999; Weitzman 1998, 1999; Dunford and others 2004). Once the service losses and gains have been appropriately discounted, restoration is scaled by dividing the present value of the losses by the present value of the gains per unit of compensatory restoration. The dividend is the number of restoration units necessary to compensate the public for lost natural resource services. See Penn and Tomasi (2002), Allen and others (2004b), Hampton and Zafonte (2005), and Zafonte and Hampton (2007) for examples of HEA applications.

NOAA HEA Model

The deterministic formula used in the NOAA HEA calculation is contained in the primer (NOAA 2000). To scale restoration, let t represent the time period, and define the following time points:

t = 0 :

injury occurs

t = C :

the base for discounting (when discount factor = 1.0)

t = B :

the injured resource returns to baseline

t = N :

the injured resource reaches maximum service provision

t = I :

compensatory project begins to provide additional services

t = M :

compensatory project reaches maximum service provision

t = L :

compensatory project senesces

The other necessary parameters, as discussed previously, are defined as follows:

$x_{t}^{j}$ :

the level of services provided per unit by the injured resource at the end of time period t

$x_{t}^{p}$ :

the level of services provided per unit by the compensatory project at the end of time period t

b ^j :

the baseline level of services provided by the injured resource

b ^p :

the initial level of services provided by the resources at the compensatory site

V _j :

the value per unit of the services provided by the injured resource (at baseline service provision)

V _p :

the value per unit of the services provided by the compensatory project

r :

the per time period discount rate

J :

the extent of the injury (number of units)

P :

the compensatory requirement (number of units)

With the parameters defined, the calculation to scale restoration is:

$$ P = J*{V_{j}\over V_{p}}*{\sum\limits_{t = 0}^B (1 + r)^{c - t}*{(b^{j} - x^{j}_{t})\over b^{j}}\over \sum\limits_{t = I}^L (1 + r)^{c - t}*{(x^{p}_{t} - b^{p})\over b^{j}}} $$

(1)

The last term in Eq. 1 is the ratio of the present value of the loss of one unit of the injured resource to the present value of the gain from one unit of compensatory restoration. This present value ratio is multiplied by the extent of the loss, J, and a ratio of the relative values of the injured resource and compensatory project, Vj and Vp. In nearly all contexts, it is assumed that Vj = Vp, and the ratio is reduced to a value of 1. However, the capacity to cope with resources of different values is maintained with this algebraic formulation.

The service metric x is a quantification of the services provided by the resource and may be a single measurement or a weighted composite of many. The term $x_{t}^{j}$ represents that level of service provided at the end of time period t by the injured resource j. With the baseline level of services, b ^j, measured in the same units as $x^{j}_{t}$, (b ^j − $x_{t}^{j}$) describes the loss of services in period t attributable to the incident. To convert this loss of service to a percent service loss, the quantity (b ^j − $x^{j}_{t}$) is divided by the baseline, b ^j. The present value of the loss in a single time period is calculated by multiplying the percent service loss, (b ^j − $x_{t}^{j}$)/b ^j, by the discount factor, (1 + r)^{C − t}. The numerator of the third term on the right-hand side of Eq. 1 sums these present values from the time of initial injury, t = 0, to the time period in which the baseline service level is reestablished, t = B. Thus, the numerator is the present value of the loss of one unit of the injured resource, quantified in units of x.

The denominator of this term is the present value of one unit of the compensatory project. The benefit of the project is the difference between the level of service provided by one unit, $x^{p}_{t}$, and the initial level of service provision, b ^p. These measurements must be in the same unit as the corresponding measures taken for the injured resource. The benefit is converted to a percent service gain by dividing the quantity ($x^{p}_{t}$− b ^p) by the baseline percent service level of the injured resource, b ^j. This normalizes the percent services provided by the compensatory project to the scale used in the numerator. The present value of the individual yearly gains is summed from the date the compensatory project begins to provide services, t = I, to the time of project senescence, t = L.

Analysis of the NOAA HEA Model

The specification of the present value ratio in Eq. 1 raises issues concerning the assumption of when services appear and are credited within a time period. By their definition, $x_{i}^{j}$ and $x_{t}^{p}$ are the levels of service being provided at the end of a period. It is implicit with these definitions that services are assumed to be credited at the end of that period. With end-of-period accounting, the resulting discrete, step functions used to approximate the true recovery and compensatory maturity functions yield an overestimate of the compensation required, P, in most NRDAs. The direction of bias associated with both beginning- and end-of-period accounting methods is only the same if (1) the injury is either instantaneous (i.e., acute oil or hazardous waste releases and physical resource destruction) or occurred prior to the first period included in the HEA (CERCLA sites with chronic releases that ceased prior to 1981) or (2) the recovery or maturation functions contain periods of declining service provision. However, although theoretically possible, these scenarios are rarely, if ever, encountered in NRDAs.

An example can be used to clarify this point. Suppose that an acute incident occurred in the 2000, affecting 20 ha of marsh and resulting in a percent service decline from a baseline of 100% to 50% following the injury. Primary restoration action is taken, and the injured resource begins to recover in 2002. It is predicted that a return to baseline will occur in 8 years, and that the recovery function is linear. Years are used as the time interval. This specific scenario is taken from the NOAA HEA primer (2000) and is used in the numerical example later in this article.

By focusing on the recovery portion of the graphical representation of HEA, it is possible to discern the implications of end-of-period accounting. Figure 3A illustrates the recovery function for this example. The heavy line is the theoretical true recovery in continuous form. The discrete step function used to approximate this continuous recovery is also depicted. The service recovery for the 2002 period occurs on the last day and is shown as an increase from 50% to 56.25% of service. However, the theoretical true recovery function shows that services are gradually restored. The end-of-period step function is continually below the theoretical true recovery function, with the top left corner of each step touching the true function at the end of each period. The loss overestimate, in undiscounted form, is the sum of the areas of the triangles formed by the theoretical true recovery line and the end-of period step function. Although not depicted in the figure, the same logic can be used to show that end-of-period accounting produces an underestimate of the benefits of compensatory restoration.

Fig. 3

Graphical depiction of the recovery horizon under three different assumptions concerning the timing of service provision

In addition to the inadequacy of the end-of-period step function, the graphical depiction calls into question the appropriate method of discounting services. Because the incident occurs at the beginning of the 2000 period, that instant is assumed to represent the base for discounting purposes (when the discount factor is 1.0). However, if services are not provided until the end of the period, those services should be discounted back to the base, which is nearly one full time period from when the services are credited. In essence, with end-of-period discounting, it is as if the services appeared at the t + 1 period. Although perhaps counterintuitive, discounting losses in all time periods by one additional time period is justified and theoretically correct with end-of-period accounting.

In the example, the incident occurs on January 1, 2000. Recovery begins on January 1, 2002, but end-of-year accounting does not credit these services until December 31, 2002. If C = 0, then these services are discounted by 2 years even though they appear 1 day shy of 3 years from the base time point. If, however, the services appeared on the next day, January 1, 2003, they would be discounted by 3 years. The difference in present values of services that are credited 364 days apart (January 1 to December 31) must be greater than the difference in present values of services credited 1 day apart (December 31 to January 1). Therefore, if end-of-period accounting is used, the appropriate discount factor is (1 + r)^C−t−1, which is functionally equivalent to crediting those services at the beginning of the t + 1 period and using the standard discount factor (1 + r)^C−t.

In practice, natural resource services that are lost or gained in the base time period are not discounted in this manner. Despite the published definition of $x^{j}_{t}$ and $x^{p}_{t}$ as the levels of service being provided at the end of the period, the customary practice of several federal and state trustees, private consultants, and academia is rather to use $x^{j}_{t}$ and $x^{p}_{t}$ as the level of services provided at the beginning of the period. In this instance, first-period discounting is not necessary because services appear at integer periods from the base time point. These differences in definitions have not been explicitly noted in any previously published accounts of natural resource damage assessments.

Beginning-of-period accounting alleviates the counterintuitive discounting problem but is still inadequate as an estimate of loss due to injury and gain from compensatory restoration. Figure 3B illustrates beginning-of-period accounting. The discrete step function is continually above the theoretically true recovery line, touching it at the top right of each step. Correspondingly, the loss due to injury is underestimated and the benefit due to the compensatory project is overestimated. The result is that the compensation requirement, P, is not sufficient to make the public whole from the loss.

Proposed Algebraic Refinements

There is a relatively simple solution to these service provision timing and discounting problems. If the mean within-period service provision level is used, the resulting step function is a more accurate estimation of any linear, continuous theoretical true recovery line. With the proposed mean accounting, it is assumed that the mean service provision level to be experienced within the period is credited at the beginning of the period and continues to the end. The effect of mean accounting can be seen in Figure 3C. If the theoretical true recovery function is linear, the overestimation of service provision in the first half of each period offsets the underestimation in the second half. Thus, the outcome is a more precise estimate of the loss due to injury. When the same reasoning is applied to the maturity function of a compensatory project, the resulting compensatory requirement, P, is a better estimate of the amount of restoration necessary.

This mean accounting refinement has been incorporated into Eq. 1 to form Eq. 2. The service levels $x^{j}_{t}$ and $x^{p}_{t}$ are still strictly defined as the end-of-period service provision levels. However, the present value ratio expressed as the third term on the right-hand side uses both these values and those for the previous period, t - 1, to compute the means. Since the discount factor exponent is maintained as C - t, the equation specifies that this mean service level is credited at the beginning of the t period. No other changes to Eq. 1 are necessary to solve the service provision timing and discounting problems.

$$ P = J*{V_{j}\over V_{p}}*{\sum\limits_{t = 0}^B (1 + r)^{c - t}*{b^{j} - 0.5(x^{j}_{t - 1} + x^{j}_{t})\over b^{j}}\over \sum\limits_{t = I}^L (1 + r)^{c - t}*{0.5(x^{p}_{t - 1} + x^{p}_{t}) - b^{p}\over b^{j}}} $$

(2)

There is, however, one challenge that makes the use of Eq. 2 untenable. These equations are unbounded if the loss due to injury or gain from the compensatory project is to continue into perpetuity. Specifically, the summations are without end if B = ∞ or L = ∞. In practice, if such perpetual losses or gains are to be incorporated into a HEA, the researcher must arbitrarily stop the calculations after a sufficiently large number of time periods. With a discount rate of 3%, the researcher will capture approximately 90% of the present value of an infinite stream of losses or gains by running the calculation for 80 annual periods. Continuation for 100 annual periods will capture approximately 95% of the present value, and 99% can be obtained with 160 annual time steps.

The HEA equation can be augmented to produce a closed solution for the compensatory requirement if the compensatory project’s service flows are finite:

$$ P = J*{V_{j}\over V_{p}}*{\sum\limits_{t = 0}^{N + 1} \left[(1 + r)^{c - t}*{b^{j} - 0.5(x^{j}_{t - 1} + x^{j}_{t})\over b^{j}}\right] + \left[{\left({b^{j} - x^{j}_{t = N + 1}\over b^{j}}\right)}*{1\over r}*(1 + r)^{c - (N + 1)}\right]\over \sum\limits_{t = 1}^L (1 + r)^{c - t} *{0.5(x^{p}_{t - 1} + x^{p}_{t}) - b^{p}\over b^{j}}} $$

(3)

and a similar equation for perpetual gains:

$$ P = J*{V_{j}\over V_{p}}*{\sum\limits_{t = 0}^{N + 1} \left[(1 + r)^{c - t}*{b^{j} - 0.5(x^{j}_{t - 1} + x^{j}_{t})\over b^{j}}\right] + \left[{\left({b^{j} - x^{j}_{t = N + 1}\over b^{j}}\right)}*{1\over r}*(1 + r)^{c - (N + 1)}\right]\over \sum\limits_{t = 1}^{M + 1} \left[(1 + r)^{c - t}*{0.5(x^{p}_{t - 1} + x^{p}_{t})} - b^{p}\over b^{j}\right] + {\left[{\left({x^{p}_{t = M + 1} - b^{p}\over b^{j}}\right)}*{1\over r}*(1 + r)^{c - (M + 1)}\right]}} $$

(4)

In both Eq. 3 and Eq. 4, the summation in the numerator is the per unit present value ratio truncated at the time period following the period in which the service provision level reaches its maximum point, t = N + 1. It is assumed that the nominal service provision level from t = N into the future is constant. The present value of the infinite stream of nominally constant services is added to this truncated summation. This is capitalized by dividing the percent service level loss associated with the $x^{j}_{N\,+\,1}$ quantity by the discount rate, r. This is then discounted back to the C base period by the discount factor (1 + r)^{C − (N + 1)}. In this manner, the infinite stream of benefits is condensed into the second bracketed term in the numerator.

The same rationale is used for the denominator of the per unit present value ratio in Eq. 4. The summation is truncated at the period following the period in which the maximum service provision level of the compensatory project achieved, t = M. The service level $x^{p}_{M\,+\,1}$ is divided by the discount rate and then discounted to the base period C. This closes the equation for both infinite losses and infinite gains, and it eliminates the need for arbitrarily ceasing the summation of Eq. 2.

Casual inspection reveals that the present value ratio numerators in Eq. 3 and Eq. 4 are identical. The per unit present value calculation for loss described here can be used whether or not the baseline service level is reestablished. If $x^{j}_{N}$< $x^{j}_{B}$, then there is a perpetual loss. The summation will cease at t = N + 1, and the second term in the numerator will calculate the present value of the nominally constant, continuing loss. If, however, the baseline is reestablished, then $x^{j}_{N}$ = $x^{j}_{B}$ and t = N is equal to t = B. The summation will cease at t = B − 1, as it does in Eq. 2 (technically, the summation continues through period t = B + 1; however, since $x^{j}_{N}$ = $x^{j}_{B}$ at t = N and t = N + 1, the summation will record zero service loss for these two periods). However, since the baseline has been reestablished, b ^j = $x^{j}_{N\,+\,1}$ and the second bracketed term in the present value ratio numerator collapses to zero. In this regard, the present value of the loss calculation is generally applicable to all injury scenarios.

The same does not hold for the present value ratio denominator. Since $x^{j}_{N}$ is bound by $x^{j}_{B}$, the second bracketed term in the numerator collapses to zero if the loss is not perpetual. The compensatory service level, $x^{p}_{M}$, is not bound by a similar parameter. Therefore, a single algebraic specification cannot accommodate both a compensatory project with a defined life span and one that is perpetual. Thus, Eq. 3 should be used if the compensatory project has a limited life span, whereas Eq. 4 should be used if a perpetual flow of services is expected.

It is relatively uncommon, though certainly possible, for losses examined in the context of a natural resource damage assessment to continue into perpetuity. One example of when the closed form solution for an infinite loss may be helpful is in the assessment of damage to coral reef framework as a result of vessel groundings. Individual coral colonies are quite slow growing, and restoration of live tissue injury may take 50–100 years. However, the ancient coral reef framework upon which living colonies settle is the result of hundreds or thousands of years of accretion. When such framework is crushed, little can be done to speed the recovery of the resource. Such a loss is best described as perpetual.

A far more common use of the closed form solution is for the perpetual provision of services by a compensatory restoration project. Indeed, absent strong information about why a project may senesce, a common default assumption is that the project will provide an infinite stream of services. For these applications, the closed form solution offered as Eq. 4 will eliminate the need for the researcher to arbitrarily cease the summation calculations.

Numerical Example

The effects of these algebraic changes are illustrated in the following hypothetical example. The parameter values are the same as those used in the NOAA HEA primer (2000). Necessary information concerning the injury and primary restoration is provided at the beginning of the Analysis of the NOAA HEA Model section of this article. The compensatory project seeks to improve degraded marsh at a location near the injury site. The initial level of service at the compensatory site is 25%, and the maximum level of service provision is 100%. Thus, the compensatory site will provide the same per unit level of service as the injured marsh. The compensatory project began providing additional services in 2002 and will mature in 10 years following a linear maturation function. The compensatory project is expected to provide a perpetual stream of services. The relative values of the services provided at the injured and compensatory marsh are equal, so V _j = V _p . The measurement unit for both the loss and the gain is marsh service hectare-years, and a 3% annual discount rate is used.

The compensatory requirement is calculated via the three methods heretofore described: (1) end-of-period accounting using the corrected discount factor that credits services at the beginning of the t + 1 period; (2) beginning-of-period accounting, which is most commonly practiced; and (3) mean accounting using Eq. 4. Table 1 details the three accounting methods’ estimates of the loss due to injury. The commonly employed beginning-of-period accounting method yields the smallest loss estimate, 50.85 discounted service hectare-years (DSHYs). The end-of-period method, which delays crediting of service improvements until the beginning of the t + 1 period, produces the largest estimate of 59.37 DSHYs lost. The mean accounting method estimates the loss at 55.11 DSHYs. The calculations in this example confirm the graphical illustrations of Figure 3.

Table 1 Estimation of service loss due to a hypothetical injury using three service accounting methods

The benefits of the compensatory restoration project are listed in Table 2. Beginning-of-period accounting overestimates the benefits of compensatory restoration and yields a gain of 21.26 DSHYs per hectare. As expected, the end-of-period accounting method underestimates the credit at 20.63 DSHYs per hectare. Both beginning- and end-of-period calculations were computed for 200 years; use of Eq. 4 for the mean accounting method truncated the calculations after 13 time periods. Table 2 also restates the three loss estimates from Table 1, computes the compensatory restoration requirement P, and contains the percentage difference between the two inaccurate methods and the mean accounting P estimate.

Table 2 Estimation of service gains from a hypothetical compensatory project using three service accounting methods

By employing mean accounting and using the closed form solution offered in Eq. 4, the resulting compensatory requirement is 2.62 ha. This is a significantly more accurate estimate than that derived from either the beginning-of-period accounting method, which yields a requirement of 2.39 ha or 8.8% less restoration, or the end-of-period method, which produces a P of 2.88 ha an overestimate of 9.7%.

Discussion

Caution should be exercised in interpreting the results of this hypothetical example. The difference between the theoretically accurate mean and the standard beginning-of-period accounting is dependent on the timing of both primary and compensatory restoration, the recovery and maturation functions, maximum service provision levels, and the length of the periods. The 8.8% underestimate produced by this hypothetical scenario should be considered a single example, and it is not necessarily representative of the underestimates of compensation derived in actual natural resource damage assessments.

Acknowledging that caveat, this hypothetical scenario is similar to many real-world cases. An injury recovery period of 10 years following an incident is within the common range used for moderate and heavy oiling following a spill. The compensatory restoration maturation function of a decade to full service provision is also within the range considered in many assessments. It can be concluded then that use of the common beginning-of-period accounting results in restoration that is insufficient to completely compensate the public for lost natural resource services if the true recovery trajectory is best described as linear over time. For extensive or long-lasting injuries, it is possible that such inaccuracies can result in substantial uncompensated service losses. Although the difference of a few tenths of a hectare found in this example will not lead to a significant undercompensation for the public’s loss, an 8–10% difference in the compensatory requirement for a natural resource damage assessment of hundreds of injured hectares and millions of dollars of restoration costs can be quite substantial. In certain situations, if use of traditional beginning-of-period accounting continues, the cumulative undercompensation of environmental services has the potential to become significant. Although a few HEA practitioners, both trustees and consultants often employed by responsible parties, have moved toward some form of mean accounting in practice, this is far from universal (Kohler and Dodge 2006).

The use of HEA to scale compensatory restoration in natural resource damage assessment has gained widespread acceptance in the past decade. When conducting an NRDA, the trustees are required by regulations to use the most efficient and cost-effective means of accurately determining injury and restoration requirements. These regulations act to reduce both overall assessment costs and the time to complete restoration. Because many of the necessary input parameters can be derived from data collected during the response to the incident and subsequent primary restoration or obtained from the existing literature, HEA is often less expensive than economic valuation studies. Given that many NRDAs are cooperative endeavors between the trustees and those responsible for the injury, HEA is often selected as preferred over economic valuation because it is less costly and time-consuming (Unsworth and Bishop 1994).

The accuracy of the point estimate of the restoration requirement produced by HEA is directly related to the quality of the parameter inputs used in the model (Dunford and others 2004). In practice, there is often substantial uncertainty concerning the percent service losses following injury, the recovery function of the injured resource, and the maturation function of the compensatory project. Depending on the application, very small changes in these input parameters can have a substantial effect on the estimated restoration requirement. It is likely that additional restoration science research, including long-term monitoring of previously impacted resources and compensatory projects, will improve the accuracy of and reduce the uncertainty associated with recovery and maturation functions for various habitat types. Such improvement in parameter estimates can significantly reduce the difference between the theoretically true restoration requirement and that estimated by HEA. The improvements in the accuracy of the method made by refining the algebraic equations are likely modest compared to the improvements that can be made through reduction of input parameter uncertainty. However, systemic bias in the current HEA equations can be eliminated immediately and for virtually no cost.

This article offers a pair of improved algebraic expressions for use in HEA. These equations eliminate the casual redefinition of $x^{j}_{t}$ and $x^{p}_{t}$ from the service levels provided at the end of periods to that provided at the beginning of periods. They also alleviate counterintuitive requirements associated with strict end-of-period accounting. If used in future natural resource damage assessments, these equations will enable both trustees and responsible parties to more accurately estimate the amount of compensatory restoration required to offset interim and perpetual service losses due to natural resource injuries.