Introduction

Contamination of surface and groundwaters causes shortages and even restricts their use. Generally groundwaters can suffer direct undiluted contamination when pollution reaches the groundwaters directly through abandoned, deficiently constructed wells, and indirectly through diluted contamination. In the indirect case the pollution reaches the groundwaters after passing through areas with solid residue deposition (urban and industrial), petroleum leaks, or mining wastes. Fully understanding, estimating, and mapping spatial variations of heavy metal water pollution using efficient techniques enables accurate monitoring and remedial action.

Univariate geostatistical techniques have been widely used in Earth Science to analyze spatial patterns and variations in pollutant concentrations, but multivariate geostatistical studies are less common than univariate analysis. Two frequently observed features are correlations between variables and scale-dependent spatial variability. The combination of these two features means that regionalized variables can have different degrees of correlation at different spatial scales. To analyze multivariate spatial data sets, Matheron (1982) proposed a geostatistical method named factorial kriging analysis that involves semivariographic multivariate modeling, principal component analysis, and cokriging. This method allows correlation structures found at different scales to be distinguished and produces a group of regionalized factors summarizing the main data characteristics at each spatial scale. Factorial kriging analysis has been applied to geophysics (Chiles and Guilen 1984; Galli et al. 1984), geochemistry (Sandjiv 1984; Wakernagel and Butenuth 1989), soil science (Goulard 1989; Goovaerts 1991; Castrignanò et al. 2000; Lin et al. 2002), and hydrogeology (Rouhani and Wackernagel 1990).

This study applies factorial kriging to assess the potential contamination of heavy metals in the soil, surface waters and groundwaters caused by decades of intense mining activity in the district of Santana, State of Amapá, in northern Brazil. Analyses of the spatial scales of variation in contamination were applied in this study as a way to separate local and regional phenomena characteristics, and also to verify relationships seen between different metal concentrations. In this way, it was possible to ascertain whether the origin of contamination from certain metals is due to human activities or the natural environment.

Study area

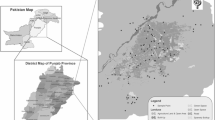
The study area is located in the district of Santana, Amapá State, in the extreme north of Brazil, approximately between 50° and 55° W and 0° to 5°N (Fig. 1a). Santana City has a population of 80,439 inhabitants, the second largest in the state (IBGE 2000). In 1953, following the discovery of high quality manganese in Serra do Navio, about 200 km from Macapá, the state’s capital (Fig. 1b, c), the Ore Trade Industry Inc (ICOMI) was established to exploit and commercialize the ore. In order to carry out the mining, ICOMI constructed a residential colony near the manganese mines in Serra do Navio and Santana with a complete infrastructure, including sanitation, recreation facility, schools, supermarket, hospital, and housing for the company’s employees and their families, in addition to the industrial installation. The industrial Santana area with approximately 129 hectares, was defined to be strictly for industrial purposes. The area was basically used to stock manganese and iron ores, products (pellets/sinter and alloys), and raw materials (fuel, coke, etc.) that arrived and departed through the ICOMI port and rail terminal (PCA/Environmental Control Plan 2001). The manganese and chromite ore were transported by railway from the Serra do Navio mines to the ICOMI industrial area in the Port of Santana, a distance of approximately 200 km.

Fig. 1
figure 1

a The location of the state of Amapá; (b) and (c) the state of Amapá, showing the municipalities of Serra do Navio, where the mining occurred, and Santana, where the manganese ore (pellets/sinter) was shipped

Full size image

Geologically, the studied area, which extrapolates the perimeter of ICOMI, is over sediments of the Barreiras Formation consisting of silty organic clays, clay silts, and hard clay with occasional intercalations of fine and coarse sand. The hydrograph is an important element in the physical landscape and the area’s economy. Santana Port fronts the Northern Channel of the Amazon River, where almost all its waters are discharged into the Atlantic Ocean. The study area is drained by several tributaries, which are generally narrow, sinuous water courses, just navigable by small boats. It is drained by the Elesbão 1 and Elesbão 2 tributaries that cross the ICOMI industrial area. It is totally covered by Quaternary sediments, silt rich in organic matter, and covered with a 0.30 to 0.50 m thick humus layer (PCA/Environmental Control Plan 2001).

Until its closure in 1997, the Serra do Navio deposit was one of the most important sources of high-grade manganese ore in the world. Tropical lateritic weathering processes from metasedimentary manganese protoliths in the Serra do Navio Formation (Paleoproterozoic) derived the high-grade manganese oxide ores. The ores were composed of manganese oxyhydroxides derived from metasedimentary protore lithologies rich in rhodochrosite, spessartine, rhodonite and tephroite. High-grade manganese oxide ore is composed chiefly of cryptomelane, pyrolusite and manganite.Through processes as dissolution, migration, minerals deposition and replacement formed also other type of manganese oxides, with high contents of iron, silica and aluminum.

Sampling and analysis

Due to lack of financial resources, logistical support, and local political questions, sampling did not totally adhere to the initially proposed plan for around 80 water samples. During the field work, it was only possible to acquire 42 water samples, with 26 from shallow wells inside the residential area, 10 from control drilling wells inside ICOMI’s industrial area and 6 from superficial waters and creeks, locally so-called “igarapés”. Moreover the results from 7 control drilling well water samples provided by ICOMI were used. Figure 2 exhibits the sampling area with the points of collection. For sample gathering a spherical sampling device and polyethylene bottle of 100 ml were used. For the sampling location points a global positioning system, Magellan type, was used. All water samples were analyzed by atomic spectrometry absorption in order to measure the concentrations, in mg/l, of 16 elements, shown in Table 1 (Queiroz 2003).

Fig. 2
figure 2

Samples location map

Full size image
Table 1 Statistics values for each element and maximum values allowed (in mg/l) for drinking water
Full size table

Geostatistical methods

Geostatistical methods are based on regionalized variable theory that states that variables in an area exhibit both random and spatially structured properties. The general assumption in spatial geostatistics is that the regionalized variable is second-order stationary.

Let z i (u), i  =  1,…, p, where u is the vector of location coordinates for the regionalized variables p (i.e., variables related to some location space u-measurement at all locations). In this case, Z i(u); i  =  1,…, p, is a random function defined in the random variables set in a study area. A spatial increment (z i (u) – z i(u + h)) is defined as the difference between z i -values at sites u and u + h for an interval lag distance and direction class h-vector. Assuming that the variable is second-order stationary, the two moments: mean and variance, are independent of location u and depend only on the h-vector.

The fundamental relations are

Mean-value vector:

$$m =E\{{{\mathbf{Z}}}({{\mathbf{u}}})\}$$

Co-variance matrix:

$${{\mathbf{C}}}({{\mathbf{h}}}) = E[\{{{\mathbf{Z}}}({{\mathbf{u}}})- m\}^{T} \{{{\mathbf{Z}}}({{\mathbf{u+h}}}) - m\}]$$

Semi-variogram matrix:

$${\Upgamma} ({{\mathbf{h}}}) = 1/2 E[\{Z({{\mathbf{u}}})-Z({\bf u+h})\}^{T}\{Z({\bf u})-Z({{\mathbf{u+h}}})\}]$$

where transposed matrices are indicated by superscript T. For h = 0 (lag zero), the co-variance C(h)-matrix is equal to the classic variance–covariance V-matrix:

$${{\mathbf{C}}}(0) = E[\{{{\mathbf{Z}}}({\bf u})-m\}^{T}\{{{\mathbf{Z}}}({\bf u})-m\}] = {{\mathbf{V}}}$$
(1)

Also, C(h) and \({\Upgamma} ({{\mathbf{h}}})\) are related by the expression

$${\Upgamma} ({\bf h}) = {{\mathbf{C}}}({\bf 0}) - 1/2 ({{\mathbf{C}}}({\bf h}) + {{\mathbf{C}}}(-{{\mathbf{h}}}))$$
(2)

The experimental semivariogram \(\hat{\Upgamma}({h})\) -matrix is a (p × p)-matrix in which the diagonal and off-diagonal are, respectively, the direct values and cross semivariogram values for a lag h:

$$\hat{\Upgamma}({{\mathbf{h}}}) = {\left[ {\begin{array}{*{20}c} {{\hat{\gamma}_{{11}} ({{\mathbf{h}}})}}& {\cdots}& {{\hat{\gamma}_{1{p}} ({{\mathbf{h}}})}} \\ {\vdots}& {\ddots}& {\vdots} \\ {{\hat{\gamma}_{{p}1} ({{\mathbf{h}}})}}& {\cdots}& {{\hat{\gamma}_{{\rm pp}} ({{\mathbf{h}}})}} \\\end{array}} \right]}$$
(3)

An experimental semivariogram \(\hat{\gamma}_{ij} ({\mathbf{h}})\) is computed as

$$\hat{\gamma}_{{ij}} ({\bf h}) = \frac{1}{{2N_{h}}} {\sum\limits_{\alpha = 1}^{N_{h}} {\{{z}_{i} ({\bf u}_{\alpha}) - z_{i} ({\bf u}_{\alpha} + {\bf h})\} \{z_{j} ({\bf u}_{\alpha}) - z_{j} ({\bf u}_{\alpha} + {\bf h})\}}}$$
(4)

where N h represents the number of pairs for a lag distance and direction class, h.

In most cases, the experimental semivariogram is fitted by combining theoretical models. This can occur when data are available for a large extension and the experimental semivariogram along that extension can reveal several scales of spatial variability. Each variability scale can be represented by a semivariogram model so that the space variability is modeled by the sum of the semivariograms (nested). Multivariate fatorial kriging allows us to analyze the relationships between Z i (u) in the spatial scales detected by the experimental semivariograms (nested).

One of the major practical difficulties found in multivariate factorial kriging is modeling the p(p +  1)/2 experimental semivariograms. To ensure that the variances of all finite linear combinations of the random Z i(u) functions are positive, the semivariogram functions-matrix must be conditionally negative semi-definite (Journel and Huibregts 1978). The formulation that has received the most attention is the linear model of coregionalization (LMC) which assumes that the original set of random correlated functions {Z i (u), i = 1,…, p} can be decomposed into an uncorrelated random functions {Y u k (u), k  =  1,…, p; s  =  1,…,S (number of different space scales)} with transformation coefficients a u is :

$$Z_{i} ({{\mathbf{u}}}) = {\sum\limits_{s = 0}^S {{\sum\limits_{k = 1}^p {a^{u}_{{ik}} Y^{u}_{k} ({{\mathbf{u}}})}}}}$$
(5)

where Y u k (u) are called regionalized factors with k denoting the different factors at a given spatial scale s. For a fixed scale s, the p regionalized factors have the same semivariogram function γ s(h). Also, Y u k (u) are mutually orthogonal by construction:

$$ 1/2 E[\{ {Y^{u}_{k} ({\mathbf{u}})-Y^{u}_{k} ({\mathbf{u}} + {\mathbf {h}})}{Y^{{u^{\prime}}}_{{k^{\prime}}} ({\mathbf {u}})-Y^{{u^{\prime}}}_{{k^{\prime}}} ({\mathbf{u}} + {\mathbf{h}})}\}] = \gamma_{s} ({\mathbf{h}}),\quad \hbox{if s} = s' \enspace \hbox{and} \enspace k = k^{\prime} $$

and = 0 otherwise.

The direct and cross semivariograms γ ij (h) can be expressed as a linear combination of the basic semivariogram γ s (h) with coefficients b u ij :

$$ \begin{aligned} \gamma_{ij}({{\mathbf{h}}})& = 1/2 E[\{Z_{i}({\bf u})- Z_{i}({\bf u+h})\}\{Z_{j}({\bf u}+{{\mathbf{h}}})- Z_{j}({\bf u+h})\}]\\ &= {\sum\limits_{u = 1}^S {{\sum\limits_{u' = 1}^S {{\sum\limits_{k = 1}^p {{\sum\limits_{k' = 1}^p {a^{s}_{{ik}} \,a^{{s'}}_{{ik'}} \,\raise0.5ex\hbox{$\scriptstyle 1$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle 2$}\,{E}[\{Y^{s}_{k} ({{\mathbf{u}}}) - Y^{s}_{k} ({{\mathbf{u}}} + {{\bf h}})\} \{Y^{{s'}}_{{k'}} ({{\mathbf{u}}}) - Y^{{s'}}_{{k'}} ({{\mathbf{u}}} + {{{\mathbf{h}}}})\} ]}}}}}}}} \\ &= {\sum\limits_{s = 0}^S {{\sum\limits_{k = 1}^p {a^{s}_{{ik}} a^{s}_{jk} \,\gamma_{s} ({{{\mathbf{h}}}})\, = \,{\sum\limits_{s = 0}^S {b^{s}_{ij} \,\gamma_{s} ({{{\mathbf{h}}}})}}}}}} \end{aligned} $$
(6)

By grouping the regionalized factors Y s k (u) with their respective semivariogram function γ s (h), each random function Z i (u) can be expressed as the sum of random orthogonal functions Z s i (u) called spatial components:

$$Z_{i}({{\mathbf{u}}}) = {\sum\limits_{s = 0}^S {Z}^{s}_{i} ({{\mathbf{u}}})} \quad \hbox{with} \quad Z^{s}_{i} ({{\mathbf{u}}})\, = {\sum\limits_{k = 1}^p {a}^{s}_{{ik}} \,Y^{s}_{k} ({{\mathbf{u}}})}$$
(7)

where Z s i (u) represents the behavior of the random function Z i(u) at a given spatial scale s. Eq. 6 then becomes:

$$\gamma_{ij}({{\mathbf{h}}}) = {\sum\limits_{s = 0}^S {\gamma^{s}_{ij} ({{{\mathbf{h}}}})}} \quad \hbox{with} \quad \gamma^{s}_{ij} ({{{\mathbf{h}}}}) = b^{s}_{ij} \gamma_{s} ({{{\mathbf{h}}}})$$
(8)

where γ s ij (h) are the cross semivariograms between spatial components Z s i (u) and Z s j (u).

The linear model of coregionalization, Eqs. 6 and 7 can be rewritten using matrix notation:

$$Z({{\mathbf{u}}}) = {\sum\limits_{s = 0}^S {{Y}^{s} ({{\bf u}})({A}^{s})^{T}}}.$$
(9)
$${{\mathbf{B}}}^{s} = {{\mathbf{A}}}^{s}({{\mathbf{A}}}^{s})^{T};$$
(10)

with \(Z({\bf u}) = [Z_{1}({\bf u}),\ldots, Z_{p}({\bf u})], Y^{s} ({\bf u}) = [Y^{s}_{1} ({x}),\ldots, Y^{s}_{p} ({x})]\) and A s (i,j) =  a s ij , and B s is a positive semi-definite matrix of coefficients, b s ij , called the coregionalization matrix.

The linear correlation between any two spatial components Z s i (u) and Z s j (u) is then measured by the structural correlation coefficient:

$$\rho^{s}_{ij} = {\rm Corr}\{Z^{s}_{i} ({{\mathbf{u}}}),Z^{s}_{j} ({{\mathbf{u}}})\} = \frac{b^{s}_{ij}}{\sqrt {b_{{ii}}^{s} \cdot b^{s}_{{jj}}}}.$$
(11)

The structural correlation coefficients matrix is defined as R s =  [ρs ij ].

Multivariate factorial kriging accounts for the regionalized nature of variables by analyzing the coregionalization B s-matrix or structural correlation coefficients R s -matrix separately. By so doing, each correlation structure is distinguished by filtering the structures belonging to the other spatial variation scales.

The practical implementation of multivariate factorial kriging involves the following procedures:

  1. 1.

    A coregionalization must be modeled that, in practice, involves the following steps:

    1. (i)

      Compute the p(p +  1)/2 direct and cross experimental semivariograms;

    2. (ii)

      Chose the number (S) and characteristics (type and range) of the basic semivariogram functions γ s (h). Webster et al. (1994) recommend that before fitting a coregionalization model, Principal Components Analysis be performed on the variance–covariance V-matrix (or correlation R-matrix) of the original variables, and the spatial correlation structure of the principal components should be evaluated by computing their semivariograms.

    3. (iii)

      Fit the selected model to the experimental values, i.e., estimate the b s ij coefficients under the constraint of positive semi-definiteness of the coregionalization matrices-B s (Pardo-Igúzquiza and Dowd 2002).

  2. 2.

    Multivariate methods, such as Principal Components Analysis, must then be applied to each matrix B s. Elements of each coregionalization matrix B s thus represent the relative contributions of the basic model, γ s (h), to direct and cross semivariograms. A Principal Components Analysis in the coregionalization matrix B s would lead to the following spectral decomposition:

    $${{\mathbf{B}}}^{s} = {{\mathbf{Q}}}^{s} \Uplambda^{s} ({Q}^{{s}})^{T} = {{\mathbf{A}}}^{s} ({{\mathbf{A}}}^{s})^{T} \quad \hbox{with} \quad {{\mathbf{A}}}^{s} = {{\mathbf{Q}}}^{s}({\varvec{\Uplambda}}^{s})^{1/2}$$
    (12)

    where Q s =  [q s ik ] is the orthogonal matrix of eingenvectors and \({\Lambda}^{s} = \lambda^{s}_{k}\) is the diagonal matrix of eigenvalues. The correlation coefficient between spatial component Z s i (u) and t regionalized factor Y s k (u) is

    $$\rho_{ik}^{s} \, = \,\frac{q_{ki} \,{\sqrt {\lambda^{s}_{k}}}}{\sqrt {b_{{ii}}^{s}}}.$$
    (13)

    where b s ii is the sill of the basic model γ I (h) of the direct semivariogram. The correlation representation graph indicates that interrelations between metals change as a function of the spatial scale.

  3. 3.

    The regionalized factors Y s k (u) are estimated by ordinary cokriging as (Pardo-Igúzquiza and Dowd 2002):

    $$\hat{Y}^{s}_{k} ({{\mathbf{u}}}) = {\sum\limits_{i = 1}^p {{\sum\limits_{\alpha = 1}^n {\lambda_{{i\alpha}} ({{\mathbf{u}}})Z_{i} ({{\mathbf{u}}}_{\alpha})}}}}$$
    (14)

    where \(\hat{Y}^{s}_{k} ({\bf u})\) is the ordinary cokriging estimator of the k-th regionalized factor at the s-th spatial scale, p is the number of variables, n is the number of data points surrounding u α used in the estimate, and \(\lambda_{{i\alpha}} ({{\bf u}})\) is the weight assigned to the datum Z i (u α). Minimizing the estimation subject to the unbiased conditions yields the following system of p(n + 1) linear equations, whose solution supplies the weights \(\lambda_{{i\alpha}} ({\bf u})\) :

    $$ \begin{aligned} \, & {\sum\limits_{i = 1}^p {{\sum\limits_{\beta = 1}^n {\lambda_{{\beta \,i}} \gamma_{ij} ({\mathbf{u}}_{\alpha} - {\mathbf{u}}_{\beta}) - \mu_{i} = a^{s}_{{ik}} \gamma_{s} ({\mathbf{u}}_{\alpha} - {\mathbf{u}}_{0})}}}}\\ \,&{\sum\limits_{\beta = 1}^n {\lambda_{{\beta \,i}} = 0}} \quad \hbox{for }i = 1, \ldots, p \enspace \hbox{and} \enspace \alpha = 1,\ldots, n.\\ \end{aligned} $$
    (15)

    The estimator is unbiased as a consequence of the conditions imposed on the weights. The condition that the sum of the weights be zero means that the local mean of each regionalized factor is a set of zeros.

  4. 4.

    In the same way, an unbiased estimate of a spatial component may be obtained by cokriging (Pardo-Igúzquiza and Dowd 2002):

    $$\hat{Z}^{s}_{i} ({{\mathbf{u}}}_{0}) = {\sum\limits_{i = 1}^p {{\sum\limits_{\alpha = 1}^n {\lambda_{{i\alpha}} ({{\mathbf{u}}})Z_{i} ({{\mathbf{u}}}_{\alpha})}}}}.$$
    (16)

    The system to be solved is

    $$ \begin{aligned} \,& {\sum\limits_{i = 1}^p {{\sum\limits_{\beta = 1}^n {\lambda_{{\beta \,i}} \gamma_{ij} ({{\mathbf{u}}}_{\alpha} - {{\mathbf{u}}}_{\beta}) - \mu_{i} = b^{s}_{{ik}} \gamma_{s} ({{\mathbf{u}}}_{\alpha} - {{\mathbf{u}}}_{0})}}}}.\\ \, & {\sum\limits_{\beta = 1}^n {\lambda_{{\beta \,i}} = 0}} \quad \hbox{to} \quad i =1,\ldots, p \enspace \hbox{and} \enspace \alpha = 1,\ldots, n \end{aligned} $$
    (17)

    where \(\gamma_{s}({\bf u}_{\alpha}-{\bf u}_{o})\) is the value of the s-th basic semivariogram between the α-th sampling point and u o, the point at which the estimate is made.

The elements of \(b^{s}_{{ik}} \gamma_{s}({\bf u}_{\alpha}-{\bf u}_{o}) = \gamma_{{ik}} ({\bf u}_{\alpha}-{\bf u}_{o})\) are the cross semivariances between Z i (u α) and Z s i (u 0). The condition where the sum of the weights is zero means that the local mean of each spatial component is a set of zeros.

Results and discussion

Table 1 presents the 16 variables and the statistics for each element. Iron shows a larger average value followed by manganese, aluminum and arsenic. The median of each variable is also presented and it is generally a unlike value from the corresponding mean indicating no variables with normal distributions. That was confirmed by observing that most elements exhibit accentuated positive asymmetry. Some elements presented values inside the limits established by the Brazilian environmental legislation (Table 1). The first column in Table 1 shows the maximum limits allowed by the environmental legislation (CONAMA 1986). Thus this study considered only 8 elements that show concentration levels above those established by the Brazilian environmental legislation. Aluminum presented the largest pollution percentage (75.5%), followed by selenium (46.3%), iron (36.6%), manganese (27%), arsenic (9.8%), cadmium (7.3%) lead (4.9%) and copper (4.9%). These elements were submitted to multivariate factorial kriging analysis. Metal concentrations are to some extent linearly correlated. The correlation matrix, R, listing the ordinary product-moment correlation coefficients is shown in Table 2. It shows strong correlations between lead and selenium (r = 0.965) and iron and cadmium (r = 0.934).

Table 2 Variables correlation matrix
Full size table

All selected variables are standardized to zero mean and unit variance. Relationships between the selected variables were first studied by the classic method of principal components analysis (PCA) applied to the correlation matrix. Table 3 summarizes the eigenvalues, the factor loadings and the explained variance for the first axis of PCA. The first three principal components account for 74.1% of the total variance. There were strong contributions from lead, selenium, cadmium and iron in first component, evidenced by the high values of the factorial loads for these elements highlighted in boldface in the Table 3. Arsenic and manganese contributed most to the third component, according to the biggest values of the factorial loads highlighted in Table 3, and the most important contributions in the second component were from aluminum, iron and cadmium in opposition to the copper variable (Table 3).

Table 3 Loading factors of principal components (PC)
Full size table

A linear coregionalization model was used to fit the semivariograms of the principal components. All the semivariograms have a nugget effect and show two scales of spatial variation. The solid lines in Fig. 3 show these fitted models, where C 0 is the nugget variance, C 1 is the sill for the first structure (short-range variance), C 2 is the sill for the second structure (large-range variance) and a 1 and a 2 are the amplitudes for the first and second structures, respectively.

Fig. 3
figure 3

Experimental omnidirectional semivariograms of the three principal components (lines linking points) and the linear coregionalization model fitted semivariograms (solid lines)

Full size image

Omnidirectional semivariograms were modeled using a nugget effect and two spherical schemes with ranges of 0.33 and 2.0 km, respectively. Both short and large-range structures are apparent in the first component whereas the short-range structure (0.33 km) plays an increasing role for the second and third principal components. All 36 direct and cross experimental semivariograms were computed and modeled as the sum of a nugget effect and two spherical schemes with a range of 0.33 and 2.0 km, respectively. Queiroz (2003) presents the 36 direct and cross experimental semivariograms fitted by linear coregionalization model.

In the selection of contrasting semivariograms for Fe, Cd, Pb, and Se (Fig. 4) the large-range structure (2 km) dominates the Pb and Se semivariograms and the short-range structure (0.33 km) dominates the Fe and Cd semivariograms. The relative contributions of both structures to the direct semivariograms reflects the role played by human and geological factors in the spatial pattern displayed by each element.

Fig. 4
figure 4

Experimental omnidirectional semivariogram of iron, cadmium, lead and selenium (lines linking points) and the linear model coregionalization fitted semivariograms (solid lines)

Full size image

Sill values for the two models, i.e., the b s ij coefficients, were assembled into two coregionalization matrices B 1 and B 2. These describe the correlation structures of the variable to small (0.33 km) and large (2 km) spatial scales, respectively. The PCA results of these two coregionalization matrices provide the regionalized factors which are the principal components of each coregionalization matrix, in their respective “s” scale and spatial components, Z s i (u).

Table 4 presents the results of the Principal Component Analysis of matrices B 1 and B 2. A strong correlation can be observed in iron and cadmium for the B 1-matrix (small spatial scale) with the first regionalized factor. Manganese correlated strongly with the second regionalized factor and arsenic gave the strongest contribution to the third regionalized factor. This suggests a possible relationship between the contamination from these elements and contamination linked to human activities. This source of contamination generally occurs on a small spatial scale, the case described by the B 1-matrix. For the B 2-matrix (large spatial scale), the first regionalized factor accounts for most of the variability (84.1%), and all variables correlate from 0.415 to 0.735, except copper with 0.097. This is interpreted as a dispersion effect, although lead, selenium and arsenic contribute the most. Copper is more strongly correlated with the second factor, and no single variable significantly contributes to the third factor which explains only 3.2% of the total variability. Aluminum has a stronger correlation with the first regionalized factor on the large scale than to the small scale. This indicates that arsenic, manganese, iron, and cadmium have stronger correlations to the small variability scale, the one linked to human activities. Meanwhile the high concentrations observed for aluminum, lead, selenium, arsenic and copper are due to the natural environment itself, deduced from their stronger correlations with the large scale.

Table 4 Regionalized factors on the small (B 1) and large (B 2) spatial scale
Full size table

It is clear in Table 4 that the correlation structure changes from one spatial scale to the other. Analyzing the coregionalization matrices brings to light the scale-dependent relationships that could not simply be detected by analyzing the conventional correlation R-matrix (or variance-covariance V-matrix). For example, the correlation between iron and cadmium is stronger in the small scale while selenium and lead have stronger correlation in the large scale. The load values of the first regionalized factors of the B 1 and B 2 matrix show more probability of some correlation to occur between arsenic and manganese on the large, rather than the small spatial scale. For the first regionalized factor in the large scale, it can be observed that the contribution, or load, of the arsenic variable is similar to that of the selenium variable. This relation between arsenic and selenium does not appear on the correlation matrix R.

The regionalized factors Y s k (u) and spatial components Z s i (u), s =  1,2 and i,k =  1, ..., 8 were mapped through cokriging. Figures 5 and 6 show maps of the first regionalized factor at the small and large spatial scales, respectively. The value of any regionalized factor equals zero at a distance greater than 0.33 km on the small scale, and at a distance greater than 2.0 km on the large scale.

Fig. 5
figure 5

Plot of first regionalized factor associated with the small spatial-scale spherical model

Full size image
Fig. 6
figure 6

Plot of first regionalized factor associated with the large spatial scale spherical model (white lines refer to drainage)

Full size image

Regionalized Factor 1 on the small spatial scale, Y 1 1, which mainly denotes iron and cadmium, takes high values in an area belonging to ICOMI indicated by a rectangle (Fig. 5). Iron and cadmium association can be related with the chemical aggregation capacity with manganese present in the mineral deposit. The drainage is plotted on the maps in white colors (Figs. 6 and 8). The spatial pattern related to area drainage agrees well with low values of the regionalized factor 1 at the large spatial scale showing the effect of metal dispersion. This regionalized factor accounts for 84.1% of the variability with reasonable contribution from almost all element variables, except copper.

Arsenic components on the small and large spatial scales are shown in Figs. 7 and 8, respectively. On the small spatial scale, the contribution from arsenic is more relevant in only the third principal component (or third regionalized factor) which accounts for only 11.2% of the total variance (Table 4). Two small negative anomalies can be seen on the small scale map, one within the ICOMI industrial area and the other in the Elesbão neighborhood by the Amazon River (Fig. 7). Webster et al. (1994) and Goovaerts et al. (1993) show that low and high values, meaning positive and negative anomalies, observed in the regionalized factors maps are, in general, associated with the geology of the area due to interactions among metals and soil types. Due to the lack of data such as a reliable geology map of the area in study, it was not possible to assess associations between type and soil use and the locations of negative and positive anomalies. On the large spatial scale, the contribution from arsenic is more relevant in the first principal component (or third regionalized factor) which accounts for only 84.1% of the total variance (Table 4). Figure 8, the large spatial scale map shows substantial areas with high positive values in the ICOMI area, the Elesbão neighborhood—to the northwest, and the residential area—in the Hospitality estate, which seem to indicate that arsenic is disseminated across the study area. The large spatial scale map also shows a certain similarity between spatial pattern and study area drainage.

Fig. 7
figure 7

Plot of the arsenic spatial component associated with the small spatial scale spherical model

Full size image
Fig. 8
figure 8

Plot of the arsenic spatial component associated with the large spatial scale spherical model (white lines refer to drainage)

Full size image

Conclusions

Environmental characterization is fundamental in evaluating risk analysis. Multivariate factorial kriging yields a regionalized factor set that summarizes the main features of data at each spatial scale, thus allowing identification of pollutant sources and patterns and supplying quantitative measurements of the complex interactions between analyzed variables. Modeling semivariograms allows distinction between small and large range variations. The small-scale structure is likely to be due to local sources of contamination linked to human activities. The large-scale structure probably reflects regional changes in the natural environment. Results in this study could probably be improved by information on area geology and analysis of pollutant concentrations at several different soil levels. Even so, the manganese exploration and commercialization activities in Santana have probably contributed to the high concentrations of manganese, arsenic, iron, and cadmium, in the study area. The high concentrations of aluminum, selenium, lead, and copper seem to be more closely related to the natural environment.