A method for analysis of lipid vesicle domain structure from confocal image data

Abstract

Quantitative characterization of the lateral structure of curved membranes based on fluorescence microscopy requires knowledge of the fluorophore distribution on the surface. We present an image analysis approach for extraction of the fluorophore distribution on a spherical lipid vesicle from confocal imaging stacks. The technique involves projection of volumetric image data onto a triangulated surface mesh representation of the membrane, correction of photoselection effects and global motion of the vesicle during image acquisition and segmentation of the surface into domains using histograms. The analysis allows for investigation of the morphology and size distribution of domains on the surface.

Introduction

In the last decade giant unilamellar vesicles (GUVs) became a very popular membrane model to explore the lateral structure of diverse artificial and natural lipid mixtures containing membranes (Bagatolli 2006). The cell size dimension of GUVs (mean diameter ~25 μm) makes this versatile membrane model system very appropriate for applying several fluorescence microscopy-related techniques in order to study membrane lateral structure. This type of experiment opened for the first time the possibility to obtain spatially resolved information from distinct free-standing membrane regions at the level of single vesicles (Bagatolli and Gratton 1999; 2000; Korlach et al. 1999; Dietrich et al. 2001). This information has been used to construct phase diagrams for various lipid mixtures (Veatch and Keller 2005), but also to evaluate lateral heterogeneity in compositionally complex mixtures [GUVs composed of natural lipid extracts or native membranes (Bernardino de la Serna et al. 2004; Plasencia et al. 2007; Montes et al. 2007)] as well as to evaluate partitioning of different membrane proteins into these different membrane regions (Kahya et al. 2005).

The distinct membrane domains observed in GUVs are generally related with equilibrium thermodynamic phases typically using: (1) the partitioning of different fluorescence probes into the distinct coexisting regions in the membrane or (2) by performing comparative analysis of different fluorescence parameters (such as fluorescence probe diffusion coefficient, or fluorescence emission shift) measured in the different membrane regions [see, for example, (Korlach et al. 1999; Bagatolli and Gratton 2000)]. However, differences in the aforementioned parameters between coexisting membrane domains are necessary but not sufficient conditions to demonstrate the presence of equilibrium thermodynamic phases. In a previous work (Fidorra et al. 2009), we introduced a sequential image analysis approach (involving segmentation and 3D reconstruction) for confocal fluorescence microscopy data of GUVs. We showed that lipid domain area fractions can be retrieved from GUVs and this information can be used to validate predictions from equilibrium thermodynamic phase diagrams (such as the lever rule). Among other observations, our results proved that the composition in the whole GUV population is representative of the initial composition utilized to prepare GUVs. Similar approaches have been tested by others for other lipid mixtures and further validated with information obtained from other biophysical techniques, i.e., NMR (see Juhasz et al. 2009). Image analysis approaches not only provide a necessary tool to properly determine phase equilibrium in compositionally simple lipid bilayers, but potentially also offer the possibility to obtain additional morpho-topological parameters normally lacking in fluorescence microscopy experiments involving GUVs. Honerkamp-Smith et al. (2008) have used a single confocal plane near one of the poles to measure correlation lengths along the domain boundary for a single domain. For 2D lipid monolayers observed by time lapse microscopy in Langmuir troughs, image processing routines have opened access to a quantitative description of morpho-topological properties (Härtel et al. 2005) and improved our understanding of enzyme coupled lipid domain formation significantly (Fanani et al. 2010). For free-standing lipid bilayers, the diverse morphologies observed for solid domains in GUVs require refined analysis of the fluorescence images.

In this article we present a new image analysis approach that facilitates a detailed quantitative analysis of the morpho-topological characteristics of domain structures in quasi-spherical GUVs imaged by confocal fluorescence microscopy. This is achieved by reconstructing an image of the membrane in a two-dimensional representation, in particular a spherical surface, from the volumetric image data. Our method takes into account the characteristics of the fluorophores involved and the specific experimental setup. Thus, the effects of photoselection are accounted for, and the domains are identified on the basis of an analysis of the fluorescence intensity map. Specific advantages of this method are that it provides identification of domains and their boundaries (as closed curves), and it provides a global characterization of the lateral structure. We demonstrate that a range of surface quantifiers for the domains can be identified such as vertex angles on polygonal domains and curvature of domain boundaries. The setup can easily be extended to quantify new properties of heterogeneous GUVs. The emphasis in the presentation is put on the image analysis technique rather than new insights in specific biophysical phenomena, and the presented results are proof of concept examples of quantitative characterizations.

The article is organized as follows: the “Materials and methods” section lists the materials used and describes the procedures for preparation and imaging of GUVs. In “Projection of confocal data,” the techniques of representing confocal image data of a GUV on a sphere are introduced. In “Analysis on the surface,” the tools for analysis of the lateral structure of the GUV based on the projected images will be presented. In “Domain characterization,” examples of the results from the described analysis are given for two example vesicles. The article is closed with a short discussion.

Materials and methods

Materials

1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), sphingomyelin (egg, chicken), ceramide (egg, chicken), cholesterol and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (ammonium salt) (Rh-DOPE) were purchased from Avanti Polar Lipids, Inc. 1,1′-Dioctadecyl-3,3,3′,3′-tetramethylindocarbocyanine perchlorate (DiIC₁₈) and 2-(4,4-difluoro-5,7-dimethyl-4-bora-3a,4a-diaza-sindacene-3-pentanoyl)-1-hexadecanoyl-sn-glycero-3-phosphocholine (Bodipy-PC) were purchased from Molecular Probes (Invitrogen). Naphtopyrene was purchased from Sigma.

Preparation of GUVs and confocal laser scanning fluorescence microscopy experiments

GUVs of different compositions were prepared following the electroformation method described by Angelova et al. (1992) using a custom-built chamber (Fidorra et al. 2006). Briefly, aliquots of the desired lipid mixture containing the fluorescent probes dissolved in organic solvent (Cl₃CH/MetOH 2:1 v/v) were deposited on each Pt electrode (4 μl of 0.2 mg/ml lipid stock solution), and the solvent was evaporated under vacuum. After the removal of the organic solvent the chamber was filled with a sucrose 200 mM solution and an AC field was applied to the chamber using a function generator (Vann Draper Digimess^® Fg 100, Stenson, Derby, UK) with an amplitude of 1.3V and a frequency of 10 Hz. The electroformation was carried out for 90 min at temperatures above the main phase transition temperature of the different lipid mixtures. Subsequently, the GUVs chamber was cooled at room temperature in a time span of approximately 5 h in an oven (J.P. Selecta, Barcelona, Spain) using a temperature ramp (∼0.2°C/min). The last step was done in order to achieve equilibrium conditions in our samples. Once the solution reached room temperature, the vesicles were transferred to an iso-osmolar glucose solution in a special chamber (200 μl of glucose + 50 μl of the GUVs in sucrose in each of the eight wells of the plastic chamber used; Lab-tek Brand Products, Naperville IL). The density difference between the interior and exterior of the GUVs induces the vesicles to sink to the bottom of the chamber, and within a few minutes the vesicles are ready to be observed using an inverted microscope. The temperature during image acquisition was controlled at 20.0 ± 0.5°C. The GUV mixtures used in this article are: (1) DOPC/DPPC/cholesterol with various molar fractions doped with 0.5 and 0.2 mol% with respect to total lipids of Naphtopyrene and Rh-DOPE, respectively (Figs. 1, 4); (2) DLPC/DPPC (30:70) doped with 0.25 mol% with respect to total lipids of DiIC₁₈ and Bodipy-PC (Figs. 3, 6, 7, 8, 9, 12); (3) egg SM/egg ceramide (70:30) doped with 0.5 mol% of DiIC₁₈ (Figs. 10, 11). The temperatures for electroformation were (1) 55°C, (2) 50°C and (3) 70°C.

Confocal image stacks were acquired on a Zeiss LSM 510 Meta confocal laser scanning fluorescence microscope. A C-Apochromat 40× water immersion objective with a NA 1.2 was used in our experiments. Two channel image stacks were acquired using multi-track mode. Argon and NeHe lasers (458 and 543 nm for Naphtopyrene and Rh-DOPE and 488 nm and 543 nm for BodipyPC and DiIC₁₈ respectively) were used as excitation sources. The laser lines were reflected to the sample through the objective using different dichroic mirrors (HFT 488/543/633 for exciting Rhodamine-DOPE, DiIC₁₈ and Bodipy-PC and HFT 458 for Naphtopyrene). The fluorescence emission collected through the objective was directed to the PMT detectors using a mirror. Generally, a beam splitter was used to eliminate remnant scatter from the laser sources (NFT 545 or NFT 490) in a two channel configuration. Additional filters were incorporated in front of the PMT detectors in the two different channels to measure the fluorescent intensity, i.e., a long pass filter >560 nm for Rhodamine-DOPE and DiIC₁₈, and band pass filters of 500 ± 20 nm and 525 ± 25 for Naphtopyrene and BodipyPC. The acquired intensity images were checked to avoid PMT saturation and loss of offsets by carefully adjusting the laser power, the detector gain and the detector offset. The image stacks were acquired at a sampling rate of 70 nm for Δx and Δy, and 340 nm for Δz, which is slightly above the Nyquist frequency, which was calculated to ∼40 nm for Δx and Δy, and ∼140 nm for Δz with Huygens Scripting Software (Scientific Volume Imaging, Hilversum, The Netherlands). The sampling above the Nyquist frequency was necessary to guarantee sufficient scan speed, which minimizes vesicle movement and photobleaching. The obtained confocal raw fluorescence image stacks were deconvolved by Huygens Scripting Software using an algorithm based on the Classic Maximum Likelihood Estimator.

Projection of confocal data

Confocal microscopes provide bitmap images of GUVs with fluorophores partitioned into the membrane. If multiple fluorophores are in use, the intensities of fluorescence are recorded in separate channels. In this article, we refer to these channels as red, green and blue (RGB) values for each pixel. Three-dimensional image data are provided in the form of stacks of bitmap images, slices, each corresponding to a constant z, i.e., a plane parallel to the xy-plane. Typically, the physical separation between slices is greater than the physical separation between neighboring pixels in the xy-plane by a factor of 3–6, so the resolution in the z-direction is lower than in the xy-focal plane. The point spread function of the imaging technique is rather broad (compared to the voxel separation) in the z-direction, so the image stack can benefit significantly from deconvolution.

Alignment of confocal stacks

In order to project the image onto a sphere, we need to align the model sphere with the vesicle in the image. This is carried out by choosing points by intensity thresholds applied to the individual channels and fitting the resulting point cloud to a sphere.

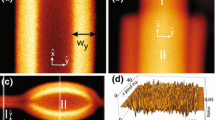
Unfortunately, GUVs can undergo significant random motion while the image stack is acquired, which may take several minutes. Translational motion of a spherical vesicle is seen by displacements between the centers of the circles depicted on adjacent slices. We do not see significant distortion within the individual slices. To correct for the displacements, a circle is fitted to each slice, and the slices are then translated to have the circle centers on a common axis (see Fig. 1). The circle fits are calculated as least squares solutions (see “Appendix 1”) of the equation

$$ \left(x - x_c\right)^2\, +\, \left(y-y_c\right)^2 = r^2 $$

(1)

using a set of (x, y)-coordinates obtained by thresholding the image by intensity.

Fig. 1

A circle is fitted to each slice, which is then translated so the center of the circle is on a common axis for the whole stack. The circle radii are then used for another circle fit (the thick circle on the top right), essentially fitting a sphere to the whole point cloud. For clarity the scaling factor c = Δz/Δx has been applied to both the “before” and “after” images in this figure, even though it is a fitting parameter

This does not correct for motion in the remaining degrees of freedom, i.e., rotation and translation in the z-direction. The latter is reduced, however, as the vesicles are resting on the bottom of the chamber because of the density difference of the sugar solutions described in “Materials and methods.” The motion of the vesicles may be further reduced using an adaption of the immobilization technique described by Lohse et al. (2008) to GUVs.

Another type of motion, which cannot easily be corrected for, is the motion of domains on the surface, which causes a distortion in the shapes and sizes of domains. Domains near the equator ¹ are more distorted than domains near the poles, since they span a greater number of slices and thus are imaged over a longer period of time. For this reason, GUVs with a percolated gel phase are most suitable for morphological characterization of domain boundaries, since the gel phase in this case fixes the domain structure in place. Concerning liquid-liquid coexistence, our images are not suitable for such characterizations, so we extracted only total area information from these. Faster imaging techniques, such as spinning-disk confocal microscopy, might enable morphological characterizations of the domain structure on these systems as well.

Fig. 2

θ is the polar angle, i.e., the angle from the z-axis, and takes values in the range (0, π] (in radians), while ϕ is the azimuth angle, i.e., the angle from the x-axis of the projection onto the xy-plane, and takes values in the range (−π, π]. We refer to θ = 0,π as the poles and $\theta=\frac{\pi}{2}$ as the equator

The circle fits provide a set of $(\tilde z, r)$ pairs, where r is the circle radius and $\tilde z$ is the slice number, i.e., the z-coordinate is given by $z=c\tilde z,$ where c = Δz/Δx is the ratio between the voxel depth in the z-direction and the width in the x- and y-directions. These pairs are then used for another circle fit, which essentially constitutes a fit of a sphere to the entire point cloud. This second fit is the least squares solution of the equation

$$ r^2 + \left(c \tilde z - z_c\right)^2 = R^2, $$

(2)

where R is the sphere radius and z _c is the z-coordinate of the center. The scaling parameter c can be provided as known from the equipment settings during acquisition or included as a fitting parameter. We have in general chosen to do the latter and check the result with the expected value.

Triangulation of the sphere

The sphere is approximated by a deltahedron, i.e., a polyhedron with triangular faces. The vertices are located on the sphere, and the deltahedron corresponds to a triangulation of the sphere.² The only convex, regular³ polyhedra are the five Platonic solids (Heath and Euclid 1956), and of these the tetrahedron (4 faces), the octahedron (8 faces) and icosahedron (20 faces) are deltahedra. Since we generally want a much finer triangulation, we cannot use a perfectly regular deltahedron, but only an approximation.

A triangulation with a desired characteristic spacing Δ is constructed by first generating a set of points that are approximately evenly distributed on a spherical surface. In terms of the spherical coordinates θ and ϕ defined in Fig. 2, the range of θ is first subdivided evenly into $\left\lceil \frac{\pi}{\Updelta} \right\rceil$ discrete values θ _i , and for each i, the range of ϕ is subdivided into $\left\lceil \frac{2\pi\sin\theta_i}{\Updelta} \right\rceil$discrete values.

The triangulation is then calculated as the triangulated⁴ convex hull of this set of points. The software Qhull (Barber et al. 1996) was chosen for this purpose. The resulting triangulation has triangles with internal angles between 45° and 90° and nearly identical areas. There are a few notable defects in the form of triangles that are half the area of the majority. These make up a vanishing fraction of the total area though. A triangulation with Δ = 0.06 radians is shown in Fig. 3.

Fig. 3

Conceptual diagram of the projection of a point cloud (bottom left) onto a triangulation of a sphere (top left). A triangular cone is defined by the center of the sphere and a triangle on the surface. The integral of the intensity over the enclosed volume is assigned to this triangle in the projection. The resulting projection on the right is using a finer triangulation than depicted on the left, so the individual triangles cannot be seen here

Using a mesh with these properties provides a uniform resolution throughout the surface. A local neighborhood consisting of a triangle and its nearest neighbors (see Fig. 5) has approximately the same shape and size throughout the surface, which facilitates simple implementations of local calculations such as finding gradients and applying filters, e.g., a Gaussian or a median filter, on image data on the surface using these small neighborhoods. It also avoids the risk of numerical stability problems because of triangles of vanishing area or with a vanishing vertex angle.

Projection

The objective of the projection is to use the triangles of the mesh as pixels for an image of the vesicle surface, thus producing a two-dimensional representation of the image. This representation, which we will refer to as a surface image, is suitable for investigating structures, i.e., domains, that are confined to the geometry of the surface. In order to produce the surface image, the point cloud is aligned and scaled as described above, filtered by intensity and optionally by radial coordinate, e.g., 0.8 R < r < 1.2 R, where r is the radial coordinate, and R is the radius of the sphere. It is then “projected” onto the triangular mesh, the details of which are discussed below.

The idea is to integrate the image data that are seen when looking from the center of the sphere out through a triangle on the surface and assign it to that triangle (see Fig. 3). This reduces the dimensionality by integrating out the radial coordinate. This should be reasonable as the image stack does not provide a true radial resolution of the membrane, since it is much thinner than the resolution limit of the microscopy technique by a factor of ∼50.

In the first attempts, each voxel is treated as a point located at the voxel center, and the intensity value for each channel of the voxel is simply added to the triangle that intersects the line from the the center of the sphere to this point. In other words, for each channel the intensity value assigned to a triangle is the sum of the intensities of the voxels with centers inside the triangular cone with its apex at the center of the sphere and the triangle as its base (see Fig. 3).

This approach produces good results for coarse triangular meshes, where the side lengths of the triangles are large compared to the voxel depth (Δz). However, for finer meshes, which are needed to utilize the available resolution throughout the surface, this approach breaks down, since the triangles become small enough that their corresponding cones may completely miss any points from the point cloud and thus not get any intensity information. This is particularly the case near the equator, where the gaps between points from adjacent slices can be seen from the center of the sphere and result in black bands on the surface. To prevent this, each voxel of the point cloud is instead treated as a box with side lengths equal to the voxel separation for each dimension rather than just a single point in space. In this way, every point in the imaged volume is part of some voxel and has intensity data. For a given channel, the intensity value assigned to a triangle is now the integral of the intensity over the corresponding triangular cone.

Calculating this integral involves calculation of the volumes of the intersections between the box-shaped voxels and the triangular cone. This region is a convex polyhedron and can be represented by a set of linear inequalities. A point r is inside the triangular cone if and only if it is on the internal side of each of the three planes containing the center of the sphere and one edge of the triangle:

$$ {\bf r} \cdot \left( {\bf v}_1 \times {\bf v}_2 \right) > 0, \quad {\bf r} \cdot \left( {\bf v}_2 \times {\bf v}_3 \right) > 0, \quad {\bf r} \cdot \left( {\bf v}_3 \times {\bf v}_1 \right) >0, $$

(3)

where v _i s are the position vectors of the vertices.⁵ The box-shaped voxel is described by inequalities that are simply constant bounds on x, y and z.

The algorithm used for this volume calculation (Ong et al. 2003) recursively constructs polynomials as integrands and bounds in integrals over different parts of the volume, while the inequalities are regarded one at a time. Due to the number of branches that typically occur and the corresponding number of polynomials that are constructed, this volume calculation is by far the most computationally demanding part of the projection.

The voxels are stored as a list of coordinates and intensities in order to allow for the coordinate displacements in the aligning step and the removal of individual voxels in the filtering step. Since the voxels are thus not easily located by their coordinates, the projection is carried out by looking at the voxels one at a time and for each locating the triangles to project it to. First, a triangle is located by walking the surface mesh towards increasing dot product between the position vectors of the voxel center and the triangle center. The volume of intersection with the cone of this triangle is calculated, and the channel intensities of the voxel are added to the triangle using this volume as a weight. The nearest neighbor triangles are then recursively tested for intersection between their corresponding cones and the voxel, and the projection is carried out for these as well in case of non-zero intersection.

Analysis on the surface

Once the image is represented on a surface, we can start doing image manipulation and analysis in this geometry. The image is stored in the OFF format of the geometry language OOGL used by the program Geomview (Amenta et al. 1995), which can be used to visually inspect the surface image. Figure 3 shows an example of such a visualization, and Fig. 12 shows a derived surface image in six different orientations. Another way of visualizing the surface is a (θ, ϕ) map, i.e., an equirectangular projection, as exemplified in Fig. 4. This has the advantage that the whole surface can be seen at once at the cost of shapes being distorted.

Fig. 4

An example of correction of a photoselection effect. The images are (θ, ϕ) maps of the surface with the poles at the left and right (see Fig. 2). Spherical harmonics with (ℓ, m) = (0, 0), (2, 0), (2,  ±2), (4, 0), (4,  ±2), (4,  ±4) have been included in this case

Correction of photoselection effect

A problem with fluorescence microscopy of GUVs is that some probes are subject to a photoselection effect because of their orientation with respect to the polarization of the incoming laser light (Bagatolli 2006). Since the orientation of the probe is correlated to the orientation of the surface (and therefore the position on the surface), the result is an angular dependence of the intensity response of the fluorophore.

The surface representation of the image data makes it possible to correct for this effect if it can be modeled as a function of the spherical coordinates θ and ϕ. Say the concentration of a fluorophore is c(θ, ϕ), and there is an orientation specific factor, F(θ, ϕ), due to photoselection for this molecule, such that the measured intensity becomes

$$ i(\theta,\phi) = F(\theta,\phi) c(\theta,\phi). $$

(4)

This factor can be approximated as a linear combination of a number of spherical harmonics (see “Appendix 2”):

$$ \begin{array}{c} F(\theta,\phi) \approx \sum\limits_{\ell,m} F_{\ell}^m Y_{\ell}^m (\theta,\phi) = \langle F \rangle \left( 1 + \sum\limits_{\ell>0,m} f_\ell^m Y_\ell^m (\theta,\phi) \right), \quad f_\ell^m = \frac{F_\ell^m}{\langle F \rangle}, \end{array} $$

(5)

where we have taken the mean value to be given by $\left\langle F \right\rangle = F_0^0 Y_0^0.$If we can determine the factors $f_\ell^m,$ we can correct for the photoselection effect:

$$ \tilde i(\theta,\phi) \equiv \langle F \rangle c(\theta,\phi) \approx \frac{i(\theta,\phi)}{1 + \sum_{\ell>0,m} f_\ell^m Y_\ell^m (\theta,\phi)}. $$

(6)

The coefficients $f_{\ell}^m$ can be determined using a reference vesicle that is expected to have a constant concentration c of the fluorophore by taking the inner product of the measured intensity with the corresponding spherical harmonics:

$$ c F_{\ell}^m = i_\ell^m \equiv \iint_S i(\theta,\phi)Y_{\ell}^m(\theta,\phi) {\text {d}}\Upomega, $$

(7)

from which we get

$$ f_\ell^m = \frac{i_\ell^m}{i_0^0 Y_0^0}. $$

(8)

Figure 4 shows an example of correction for such a photoselection effect. Before the correction, the surface image has two regions where the intensity in the red channel is high, and the structure in the green channel characteristic for the rest of the surface cannot easily be seen. After the correction, the representation of the structure in these regions on the surface image is significantly improved.

Noise reduction

A noisy image can be problematic for the various image analysis techniques. In segmentation and domain identification, it may lead to many very small domains consisting of only a few triangles to be erroneously identified, e.g., near the edges of the proper domains. In edge identification (see Sect. “Edge map”) the noise is amplified by taking gradients and may dominate the signal from the actual edges.

The effect of noise can be reduced by applying filters, e.g., a Gaussian or a median filter, to the surface image. For simplicity these are implemented by only looking at very small neighborhoods including a triangle and its three nearest neighbors. The non-normalized convolution mask used for a Gaussian filter is shown in Fig. 5. This way of applying the filter is directly applicable to general (not necessarily spherical) triangular meshes as long as the shapes and areas of the triangles are within a satisfyingly narrow distribution. In order to increase the spread, the filter can be applied multiple times, thus gradually smoothing the image.

Fig. 5

A small neighborhood consisting of four triangles showing the non-normalized convolution kernel used for an approximately Gaussian filter

Histograms and segmentation

Information about the distribution of the fluorophores on the membrane can be gained from histograms of the channel intensities (see Fig. 6). Since we have the image data represented on a spherical surface, the histogram can be calculated over the surface rather than the imaged volume. This is desirable when investigating the lateral structure of the membrane.

Fig. 6

Top A two-dimensional histogram of the channel intensities of a two-channel surface image (the one shown in Fig. 3). Bottom A histogram of the value $\phi=\tan^{-1}\left(\frac{i_g}{i_r}\right),$ the angle from the red axis in the two-dimensional histogram, over the surface. The local minimum indicated at ϕ = 0.679 on the ϕ histogram is found using the smoothed curve. This value as well as $\phi=\frac{\pi}{4}$ is also represented as lines (possible choices of threshold) on the two-channel histogram. Finally, the total red area as a function of the chosen threshold value of ϕ is shown. The areas are on the unit sphere, i.e., solid angle

In general, the fluorophores are expected to have different affinities to the different thermodynamic phases of the lipid membrane. This results in the phases occupying different positions in the intensity histogram. Thus, for a two-phase system we expect to see two peaks in the histogram as is the case in the example shown in Fig. 6.

The image can now be segmented into phases by fixing a threshold, which for a two-channel image takes the form of a curve that divides the (i _r , i _g )-space into two regions. The choice of threshold is guided by the observed behavior of the histogram and the criterion that the threshold curve should have one peak on either side and preferably pass through a low-valued region of the histogram so that the sensitivity of the segmentation to small variations of the curve is low. Once a choice has been made, it can be evaluated by visual inspection of the resulting segmentation of the surface image.

Ideally the phases give rise to sharp peaks such that the threshold curve can easily be chosen to pass through a zero-valued region of the histogram. However, typical histograms show rather broad peaks that overlap in the tail regions as in Fig. 6, so the threshold has to be chosen with care. A number of effects may cause such broadening, including noise, the area near domain boundaries (if the transition across them is smooth) or effects such as the photoselection effect that may lead to position specific variations of the recorded fluorescence intensity, if these effects are not perfectly corrected.

If for simplicity the curve is chosen as a straight line through the origin, it is defined by only one parameter: the angle $\phi = \tan^{-1} \frac{i_g}{i_r}$ from the red axis, where i _r and i _g are the red and green intensities. A histogram of this value over the surface is also shown in Fig. 6. On this one-dimensional histogram, two peaks corresponding to the two coexisting phases are easily seen, and the local minimum between them is a good candidate for a threshold that satisfies the above considerations. This minimum is identified by first smoothing the histogram by convolution with a Gaussian kernel and then walking the curve in the direction of decreasing value.

This method provides a systematic means of segmentation for a variety of vesicles with these general properties with a reasonable tolerance to differences in the positions and sizes of the peaks. It can, however, also be unstable in cases where there is a wide non-zero “floor” between the two peaks, such that small differences in this region may cause the threshold to end up in vastly different locations. Thus, for comparison of a number of vesicles, where care is taken to keep the experimental conditions equal except for the varied parameter (e.g., composition), it may be a better choice to simply fix the threshold value of ϕ to a constant, since this approach is simpler and more stable.

The information in the histogram along with a choice of threshold yields the total area of one of the phases and hence provides a measure of the degree of transition between them. The area fraction of the red phase is also shown as a function of the threshold in the ϕ histogram in Fig. 6. By measuring this value for a range of compositions, the anatomy of the coexistence region in the phase diagram can be characterized in detail. Such a study is being worked on by the authors for the liquid-ordered/liquid-disordered coexistence region of the DOPC/DPPC/cholesterol mixture.

Domain characterization

The segmentation described in the previous section provides a way to determine the phase of each triangle and thus trivially a way to calculate the total area of the individual phases coexisting on the membrane. If we are interested in more specific information about the lateral structure, such as the size distribution or morphology of the domains, we need a way to identify the individual domains. This is achieved by finding the connected regions of the same phase on the surface. In this section we present examples of quantitative characterization of the domains on the vesicle in Fig. 3.

Domain size distribution

The histograms of the surface image of the example vesicle (Fig. 3) are shown in Fig. 6. Since the histograms show a clear separation into two phases, the example is suitable for this analysis. The threshold determined by the local minimum in the ϕ histogram was used for segmentation of the surface image into the two phases. The segmentation produces a set of 286 domains in total (red and green domains combined), but many of these are most likely due to noise or below-resolution structures leading to an incorrect subdivision into many very small domains of only a few triangles. In Fig. 7 the areas of the green domains are sorted by decreasing area and plotted on a logarithmic scale.

Fig. 7

Top domain area vs. number when domains are sorted by decreasing area. The dashed line is a fit of an exponential function. Bottom Kernel density histograms of domain areas (excluding domains with area A < 0.01) using various spreads for a Gaussian kernel compared to the hyperbola corresponding to exponential fit above

Despite the limited number of domains, it appears we can still say something about the area distribution. Apparently the areas of the first 20 domains follow an exponential decay when plotted against their index in the ordering, i.e.,

$$ A(n) = a e^{-bn}. $$

(9)

Inverting this function gives

$$ n(A) = \frac{1}{b} \ln \frac{a}{A}. $$

(10)

The area distribution of the domains can now be approximated by

$$ \left|\frac{\text{d}n}{\text{d}A}\right| = \frac{1}{bA}. $$

(11)

This distribution can only apply for a limited range of areas, as it is not normalizable for the range $A\in [0:4\pi],$ and an upper bound of the domain area is given by the total area of the phase.

Figure 7 also shows histograms of the domain areas (for domains with A > 0.01) generated by kernel density estimation (Rosenblatt 1956; Parzen 1962) using a Gaussian kernel, i.e.,

$$ \hat \rho(A) = \frac{1}{\sqrt{2\pi\sigma^2}} \sum_i e^{\frac{(A-A_i)^2}{2\sigma^2}}, $$

(12)

along with the distribution from Eq. 11. Equation 12 provides an estimate of the probability distribution of the area of a domain picked at random from an ensemble of vesicles with the same size and composition. The histogram seems to follow the model distribution somewhat, but it is clearly a very small sample of domains to produce a reliable histogram. A proper statistical analysis of domain areas would require a large sample of vesicles with the same size and composition.

Domain morphology

Apart from domain sizes, our method also allows investigating the morphology of the domain boundaries. Domains in a lipid bilayer with liquid-liquid phase separation are expected to be circular because of minimization of the interfacial energy, while textures in more ordered phases can give rise to different shapes (Bernchou et al. 2009). Due to the high mobility of domains in liquid-liquid separated systems, we have not been able to reliably characterize the boundary morphology from confocal images of these systems.⁶ We will thus continue with the vesicle in Fig. 3, in which the red phase is a percolated gel phase, to give examples of boundary characterizations.

On this vesicle, the boundaries of many of the domains appear to be curvilinear polygons (i.e., they have vertices), so we would like to characterize them as such. This involves identifying the vertices, characterizing the edges between them (e.g., their geodesic curvature) and measuring the vertex angles. This characterization requires good fidelity in the domain shape in order to unambiguously identify the vertices and to reliably fit simple curves (e.g., circles) to the edges. The triangular domain shown in Fig. 8 is quite adequate for this purpose.

Fig. 8

A rather simple, triangular domain. The green curves are geodesics (great circles) approximating the edges of the triangle. The leftmost edge is apparently better approximated by the blue curve, which is a non-geodesic circle on the sphere, while the remaining two edges cannot be concluded to deviate from the geodesics from this data. The radius of the blue curve (on the unit sphere) is r = 0.87, and hence its geodesic curvature is κ _g  = 0.56

After the segmentation, the domains are provided as sets of triangles of the same phase on the triangular mesh. The domain boundaries can then be obtained as lists of vertices from the mesh, defining the boundaries as closed space curves. These curves suffer from noise as well as artifacts from the mesh (they follow the triangle edges of the mesh) and from the original voxel lattice, which gives rise to staircase-like curves near the equator. Therefore, geometric properties should be measured over sufficiently large length scales to overcome these effects.

We can estimate the curvature at a point of the curve by fitting a parabola to a small segment surrounding the point (Lewiner et al. 2005). The resulting curvature estimate is shown in Fig. 9. Since we are interested in characterizing the curve as a curvilinear polygon (in this case a triangle), we wish to identify the vertices of this polygon. This is done by applying a threshold to the curvature estimate and identifying the positions of peaks of large curvature as vertices and the segments between them as edges.

Fig. 9

The local curvature of the domain boundary depicted in Fig. 8 determined by fitting of small segments (7 points) by parabolas. The threshold is used to identify the vertices and edges of the curvilinear triangle

Figure 8 also shows approximations of the edges by simple curves and estimates of vertex angles and geodesic curvature. The three green curves are geodesics, while the blue curve is a non-geodesic circle on the spherical surface. A geodesic approximating an edge is determined by simply connecting two points on the edge by a geodesic. The blue circle was found by least-squares minimization of the distance of the edge to the osculating plane of the circle, i.e., the least squares solution of the system

$$ {\bf r}_i \cdot \frac{{\bf r}_c}{|{\bf r}_c|^2} = 1, $$

(13)

where {r _i } is the collection of position vectors of the boundary segment, and r _c is the vector from the center of the sphere to the center of the circle and hence also defines the osculating plane by ${\bf r} \cdot {\bf r}_c = |{\bf r}_c|^2.$

The latter method suffers from not minimizing the distance to the model circle but to a plane, and therefore tends to favor a near-tangential plane when applied to short segments, where the deviation from a tangent plane due to the curvature of the sphere is small compared to the noise. However, for longer segments it can provide good results and has been chosen for the blue curve in the figure, since it clearly provides a better fit than the geodesic. For the remaining two edges of the triangular domain the geodesics were found to be the best fits. The measured angles are between the tangent vectors of the model curves at their intersections.

Area and perimeter

Figure 10 shows a surface image of a vesicle prepared from a mixture of egg sphingomyelin and egg ceramide. The vesicle shows an intriguing domain structure with flower-shaped domains and is thus a good candidate for morphological characterizations of domain boundaries. Since only one fluorophore was used in the preparation, the image has only one channel, and the segmentation is achieved using a constant threshold value, i _r,0, for this channel. The value is chosen such that the segmentation captures much of the morphology of the domain boundaries while producing a reasonable identification of domains.

Fig. 10

Surface image of a GUV prepared from a mixture of egg sphingomyelin and egg ceramide. Also shown are the identified domain boundaries, when using the threshold i _r,0 = 0.15

A simple characterization facilitated by our method is the relationship between the domain perimeter p and domain area A. Figure 11 shows these these variables plotted against each other in a double-logarithmic coordinate system. The domain areas were determined by simply adding up the areas of the triangles constituting a domain. For the perimeter calculation, the boundaries were first smoothed in order to avoid the artifact imposed by the triangular mesh. The two straight lines indicate separate power law behaviors, which apply at two different regimes of domain sizes with a cross-over at a perimeter around p ≈ 1 or equivalently A ≈ 0.05. If we define the fractal dimensions D _p and D _A for the perimeter and area respectively by

$$ \begin{aligned} p &= C_p L^{D_p} \\ A &= C_A L^{D_A}, \end{aligned} $$

(14)

where L is measure of the linear extent of a domain, our identified power law behavior provides an estimate of the ratio $\frac{D_A}{D_p}.$

For the small domains, this ratio is $\frac{D_A}{D_p} \approx 1.93,$ which is approximately the characteristic value for compact two-dimensional regions, for which the fractal dimensions are D _p  = 1 and D _A  = 2. For the larger domains, however, the ratio is only $\frac{D_A}{D_p} \approx 1.15,$ i.e., a non-compact behavior. This parameter is easy to measure using our method and provides a means of testing models of the growth dynamics and underlying textures of the domains.

Fig. 11

Domain perimeters and areas on the vesicle depicted in Fig. 10. The lengths and areas are on the unit sphere

Edge map

Another means of investigating the domain morphology is an edge map, which is any scalar field on the surface that takes high values near domain boundaries and low values elsewhere. This map can be used to overcome the lattice artifact when determining tangent vectors along the boundary: By taking the edge map as the density, a moment of inertia tensor can be constructed in a neighborhood of a small boundary segment, and the local orientation of the boundary can thus be determined as the principal axis with the smallest moment of inertia. The edge map might also be used for setting up an active contour method (Kass et al. 1988; Xu and Prince 1997) on the spherical surface as another means of investigating domain morphology.

One approach for defining an edge map is to first define a suitable scalar field (say, the “greenness,” g) on the surface as a map from the channel intensities, which will have a large gradient near the edges of domains. For a two-channel image with two phases as in the histogram in Fig. 6, this could be the signed distance to the threshold line in the two-channel histogram or the angle from the red axis (ϕ in Sect. “Histograms and segmentation”). For this example, we will use the latter. In order to make this function change more rapidly when crossing the threshold line compared to changing within either side, it can be wrapped in the inverse tangent function:

$$ g = \tan^{-1}\left(k(\tilde g - \tilde g_0)\right) $$

(15)

where k is a constant, $\tilde g$ is the original greenness function, and $\tilde g = \tilde g_0$ represents the threshold line in the histogram. This reduces the gradients due to noise or structure within the individual domains. This trick requires some confidence in the proper location of the threshold, though, as it can make domains appear smaller or larger on the edge map depending on the value of $\tilde g_0.$ A Gaussian filter can also be used to reduce noise at the cost of broadening the edges in the edge map.

To complete the definition of an edge map of the vesicle in Fig. 3 we have used the square norm of the gradient of this field:

$$ e = |\nabla g|^2, \quad g = \tan^{-1}\left( 5 (\phi - 0.718) \right), \quad \phi = \tan^{-1}\left(\frac{i_g}{i_r}\right). $$

(16)

This value at a triangle is calculated by first evaluating the components of the gradient along the vectors from the triangle to to its three nearest neighbors. The position of a triangle is here taken as its barycenter, i.e., the mean of the three vertex positions. Pairwise these determine the gradient vector, so an average is taken of the square norms obtained using the three possible pairs. For the purpose of this calculation, the four-triangle neighborhood is first flattened by rotating the outer triangles around their common edge with the center triangle, such that the three distance vectors become coplanar.

The difference in the scalar field between the triangle and its ith nearest neighbor is to first order

$$ \Updelta g_i \approx {\bf v}_i \cdot \nabla g, $$

(17)

where v _i is the distance vector between the centers of the two triangles. For two directions i and j, we get a system of linear equations

$$ A \nabla g \approx b, $$

(18)

where

$$ A = \left(\begin{array}{cc} v_{ix} & v_{iy} \\ v_{jx} & v_{jy} \end{array}\right) \quad \hbox{and} \quad b = \left(\begin{array}{cc}\Updelta g_i \\ \Updelta g_j \end{array}\right), $$

(19)

where the vectors have been represented in an orthonormal basis of the plane of the flattened surface patch. The solution of the system is

$$ \begin{aligned} \nabla g &\approx A^{-1} b \\ \Rightarrow|\nabla g|^2 &= \nabla g^{\! \top} \! \nabla g \approx b^{\! \top} \! \left( A^{-1} \right)^{\! \top} \! A^{-1} b = b^{\! \top} \! \left( AA^{\! \top} \! \right)^{-1} b. \end{aligned} $$

(20)

Since

$$ \begin{aligned} AA^{\! \top} \! &= \left(\begin{array}{cc} |{\bf v}_i|^2 & {\bf v}_i \cdot {\bf v}_j \\ {\bf v}_i \cdot {\bf v}_j & |{\bf v}_j|^2 \end{array} \right) \quad \Rightarrow \\ \left(AA^{\! \top} \!\right)^{-1} &= \frac{1}{\det\left(AA^{\! \top} \!\right)} \left(\begin{array}{cc} |{\bf v}_j|^2 & -{\bf v}_i \cdot {\bf v}_j \\ -{\bf v}_i \cdot {\bf v}_j & |{\bf v}_i|^2 \end{array}\right), \end{aligned} $$

(21)

we get

$$ \begin{aligned} |\nabla g|^2 &\approx \\ e_{ij} &\equiv \frac{|{\bf v}_j|^2 \Updelta g_i^2 + |{\bf v}_i|^2 \Updelta g_j^2 - 2 ({\bf v}_i\cdot {\bf v}_j) \Updelta g_i \Updelta g_j}{|{\bf v}_i|^2 |{\bf v}_j|^2 - ({\bf v}_i\cdot{\bf v}_j)^2}. \end{aligned} $$

(22)

The distance vectors are coplanar 3-vectors, but since the result is expressed in terms of dot products of the vectors, we avoid the need to transform them to a two-dimensional orthonormal basis.

The edge map is now given by

$$ e = \frac{\left(e_{12} + e_{23} + e_{31}\right)} {3}. $$

(23)

An example edge map is shown in Fig. 12.

Fig. 12

An edge map of the vesicle shown in Fig. 3. For this image, the greenness is chosen as $g=\tan^{-1}\left( 5 (\phi - 0.718) \right),$ where $\phi = \tan^{-1}\left(\frac{i_g}{i_r}\right)$ is the angle from the red axis in the histogram. The same vesicle is depicted in six different orientations

Conclusion

We have presented a methodology to perform detailed analysis of the lateral domain characteristics of GUVs imaged by confocal fluorescence microscopy. A starting point for the analysis is the construction of a surface image from the confocal imaging stack, which faithfully represents the variations of fluorophore concentrations over the membrane. This construction takes into account the experimental setup, i.e., optical resolution, confocal stacking distance and orientation, lateral motion of the vesicle during image acquisition and photoselection effect. The surface image is triangulated to provide a discretization that allows for analysis of morphological characteristics of lateral domain structures. The domains are identified using image intensity histograms, which provide effective determinations of domain areas and boundaries. We show that the approach provides characterization of global properties of the lateral structure, e.g., domain size distribution, and single domain characterization, e.g., lengths, angles and geodesic curvatures of domain boundaries.

The rapid development in confocal fluorescence microscopy techniques with respect to stack acquisition time (e.g., spinning disk confocal microscopy), fluorophore development and GUV preparation techniques (e.g., fixation of vesicles) continues to improve the quality of confocal imaging stacks. Our method facilitates a very detailed characterization of the lateral structure of near-spherical vesicles based on the stacks and thus helps close the increasing gap between the level of detail available in confocal imaging of vesicles and the quantitative characterization the lateral structure obtained from it.

Appendices

Appendix 1: Linear least squares fitting

Least squares is a method for finding an approximate solution to an overdetermined system of equations. Specifically, the least squares solution to the system is the one that minimizes the sum of the squares of the residuals, which are defined as the difference between the right- and left-hand sides of each equation. The method is used for fitting a model equation with n adjustable parameters to a set of m data points, where m > n.

If the system is linear, it can be written in matrix form as

$$ A{\bf q} = {\bf b}, $$

(24)

where A is an m × n matrix with m > n. The vector q contains the unknowns, i.e., the parameters to be determined. The vector of residuals for a given choice of q is given by

$$ {\bf r}({\bf q}) = {\bf b} - A{\bf q}. $$

(25)

The problem of minimizing the sum of squares of the residuals can be written as

$$ \begin{aligned} 0 &= \frac{\partial}{\partial q_i} \left( {\bf r}^{\! \top} \! {\bf r} \right) \\ &= \frac{\partial}{\partial q_i} \left( {\bf q}^{\! \top} \! A^{\! \top} \! A {\bf q} + {\bf b}^{\! \top} \! {\bf b} - {\bf b}^{\! \top} \! A{\bf q} - {\bf q}^{\! \top} \! A^{\! \top} \! {\bf b} \right) \\ &= 2\sum_j \left(A^{\! \top} \! \! A\right)_{ij} q_j -2 \sum_j A^{\! \top} \!_{ij} b_j = 2 \sum_j \left( A^{\! \top} \! A{\bf q} - A^{\! \top} \! {\bf b} \right)_i, \end{aligned} $$

(26)

so the least squares solution to the overdetermined system is the solution to the corresponding “normal equations”:

$$ A^{\! \top} \! A {\bf q} = A^{\! \top} \! {\bf b} $$

(27)

Circle fits

For the circle fits, the overdetermined system is

$$ (x_i-x_c)^2 + (y_i - y_c)^2 = r^2, $$

(28)

which can be rewritten as

$$ x_i^2 + y_i^2 = r^2 - x_c^2 - y_c^2 + 2x_c x + 2y_c y, $$

(29)

or

$$ \left(\begin{array}{ccc} 1 &2x_1 & 2y_1 \\ \vdots & \vdots & \vdots \\ 1 & 2x_N & 2y_N \end{array}\right)\,\left(\begin{array}{c} r^2 - x_c^2 - y_c^2 \\ x_c \\ y_c \end{array}\right) = \left(\begin{array}{c} x_1^2 + y_1^2 \\ \vdots \\ x_N^2 + y_N^2 \end{array} \right) $$

(30)

defining A, q and b in equation (24). From the least squares solution for q, the desired parameters can be found as

$$ x_c = q_2, \quad y_c = q_3 \quad \hbox{and} \quad r = \sqrt{q_1 + q_2^2 + q_3^2 } $$

(31)

Sphere fit

For fitting a sphere using the radii r _i of the circle fits, the overdetermined system is

$$ r_i^2 + \left(c(\tilde z_i - \tilde z_c)\right)^2 = R^2, $$

(32)

where c = Δz/Δx is the scaling factor for the z-direction, and R is the radius of the sphere. The system can be rewritten as

$$ r_i^2 = R^2 - c^2 \tilde z_c^2 + 2c^2\tilde z_c \tilde z_i - c^2\tilde z_i^2 $$

(33)

or

$$ \left(\begin{array}{ccc} 1 & 2\tilde z_1 & -\tilde z_1^2 \\ \vdots & \vdots & \vdots \\ 1 & 2\tilde z_N & -\tilde z_N^2 \end{array}\right) \left(\begin{array}{c} R^2 - c^2 \tilde z_c^2 \\ c^2 \tilde z_c \\ c^2 \end{array}\right) = \left(\begin{array}{c} r_1^2 \\ \vdots \\ r_N^2 \end{array}\right). $$

(34)

From the least squares solution, the parameters are:

$$ c = \sqrt{q_3}, \quad \tilde z_c = \frac{q_2}{q_3} \quad {\text {and}} \quad R = \sqrt{q_1 + \frac{q_2^2}{q_3}} $$

(35)

Appendix 2: Spherical harmonics

The spherical harmonics are defined on the unit sphere using spherical coordinates (see Fig. 2) as

$$ \begin{aligned} &Y_{\ell}^m (\theta,\phi) = {\sqrt{\frac{2{\ell}+1}{4\pi}\frac{({\ell}-m)!}{({\ell}+m)!}}} \,P_{\ell}^m(\hbox{cos}\theta) e^{im\phi},\\ &{\ell}=0,1,{\ldots}, \quad m=-{\ell},-{\ell}+1,{\ldots},{\ell}-1,{\ell}, \end{aligned} $$

(36)

where $P_\ell^m$ is the associated Legendre polynomial of degree $\ell$ and order m. They are orthonormal, i.e.,

$$ \iint Y_\ell^m (\theta,\phi) Y_{\ell'}^{m'}(\theta, \phi) {\rm d}\Upomega = \delta_{\ell\ell'}\delta_{mm'}, $$

(37)

where ${\rm d}\Upomega = \sin\theta {\rm d}\theta {\rm d}\phi.$They form a complete basis for the set of square-integrable functions on the unit sphere, i.e., any such function can be written as

$$ f(\theta,\phi)=\sum_{\ell=0}^\infty \sum_{m=-\ell}^\ell f_\ell^m Y_\ell^m(\theta,\phi). $$

(38)

If the coefficients $f_\ell^m$ decrease rapidly with $\ell,$ the function can be approximated as a linear combination of only a few spherical harmonics. The least squares fit of a linear combination of some number of spherical harmonics is found by minimizing the integral of the square of the residual

$$ \iint \left(f(\theta,\phi) - \sum_{\ell,m} f_{\ell}^{m} Y_{\ell}^{m} (\theta,\phi) \right)^2 \text{d}\Upomega $$

(39)

with respect to the coefficients $f_\ell^m:$

$$ \begin{aligned} 0&= \frac{\partial}{\partial f_\ell^m} \iint \left(f(\theta,\phi) - \sum_{\ell',m'} f_{\ell'}^{m'} Y_{\ell'}^{m'} (\theta,\phi) \right)^2 \text{d}\Upomega\\ &= 2 \left( \sum_{\ell',m'} f_{\ell'}^{m'} \underbrace{\iint Y_\ell^m(\theta,\phi) Y_{\ell'}^{m'}(\theta,\phi) \text{d}\Upomega }_{\delta_{\ell\ell'} \delta_{mm'}}- \iint f(\theta,\phi) Y_\ell^m (\theta,\phi) \text{d}\Upomega \right)\\ &= 2\left( f_\ell^m - \iint f(\theta,\phi) Y_\ell^m (\theta,\phi) \text{d}\Upomega \right) \end{aligned} $$

(40)

So the coefficient for a particular spherical harmonic is simply the inner product of the function with the spherical harmonic:

$$ f_\ell^m = \iint f(\theta,\phi) Y_\ell^m (\theta,\phi) \text{d}\Upomega. $$

(41)