On an Ergodic Two-Sided Singular Control Problem

Abstract

Motivated by applications in natural resource management, risk management, and finance, this paper is focused on an ergodic two-sided singular control problem for a general one-dimensional diffusion process. The control is given by a bounded variation process. Under some mild conditions, the optimal reward value as well as an optimal control policy are derived by the vanishing discount method. Moreover, the Abelian and Cesàro limits are established. Then a direct solution approach is provided at the end of the paper.

1 Introduction

This work is motivated by applications in reversible investment [6, 8], optimal harvesting and renewing [10, 11], and dividend payment and capital injection [14, 19]. In the aforementioned applications, the systems of interests are controlled by bounded variation processes in order to achieve certain economic benefits. It is well known that any bounded variation process can be written as a difference of two nondecreasing and càdlàg processes. The two nondecreasing processes will often introduce rewards and costs to the optimization problems, respectively. For example, in natural renewable resource management problems such as forestry, while harvesting brings profit, it is costly to renew the natural renewable resource. One needs to balance the harvesting and renewing decisions so as to achieve an optimal reward. Similar considerations prevail in reversible investment and dividend payment and capital injection problems. In terms of the reward (or cost) functional, the two singular control processes have different signs. We call such problems two-sided mixed singular control problems. In contrast, in the traditional singular control formulation, the reward or cost corresponding to the singular control is expressed in terms of the expectation of its total variation.

We note that most of the existing works on two-sided mixed singular control problems are focused on discounted criteria. In many applications, however, optimizations using discounted criteria are not appropriate. For example, in optimal harvesting problems, discounted criteria largely favor current interests and disregard the future effect. As a result, they may lead to a myopic harvesting policy and extinction of the species. We refer to [2, 20, 23] for examples in which the optimal policy under the discounted criterion is to harvest all at time 0, resulting in an immediate extinction. Thus, this paper aims to investigate a two-sided mixed singular control problem for a general one-dimensional diffusion on $[0,\infty )$ using a long-term average criterion. Ergodic singular control problems have been extensively studied in the literature; see, for example, [12, 13, 15, 22, 24, 26, 27] and many others. In the aforementioned references, the cost (or reward) associated with the singular control is expressed in terms of expectation of the total variation. Our formulation in (2.3) is different. In particular, in (2.3), while $\eta (T)$ contributes positively toward the reward, the contribution from $\xi (T)$ is negative. On the one hand, this is motivated by the such applications as reversible investment, harvesting and renewing, and dividend payment and capital injection problems. On the other hand, the mixed signs also add an interesting twist to singular control theory as the gradient constraints in the corresponding HJB equation are different from those in the traditional setup as those in Karatzas [15], Menaldi and Robin [22], Weerasinghe [24, 26].

To find the optimal value $\lambda _{0}$ of (2.3) and an optimal control policy, one may attempt to use the guess-and-check approach. That is, one first finds a smooth solution to the HJB equation (3.1) and then uses a verification argument to derive the optimal long-term average value as well as an optimal control. Indeed this is the approach used in Karatzas [15], in which the Abelian and Cesàro limits are established for a singular control problem when the underlying process is a one-dimensional Brownian motion. The result was further extended to an ergodic singular control problem for a one-dimensional diffusion process in Weerasinghe [24] in which the drift and diffusion coefficients satisfy certain symmetry properties. While this approach seems plausible, it is not easy to guess the right solution. In particular, since the underlying process $X_{0}$ is a general one-dimensional diffusion on $[0,\infty )$ (to be defined in (2.1)) and the rewards associated with the singular controls $\xi$ and $\eta$ have mixed signs in (2.3), our problem does not have the same kind of symmetry as in Karatzas [15] and Weerasinghe [24]. In addition, the gradient constraint $c_{1} \le u'(x) \le c_{2}$ brings much difficulty and subtlety in finding the free boundaries that separate the action and non-action regions. Besides, this approach does not reveal how the ergodic, discounted and finite-time horizon problems (to be defined in (2.3), (2.6), and (2.7), respectively) are related to each other.

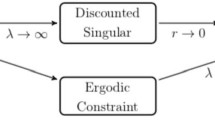
In view of the above considerations, we adopt the vanishing discount approach developed in Menaldi and Robin [22] and Weerasinghe [26]. First, we observe that under Assumption 3.2, careful analysis using reflected diffusion process on an appropriate interval [a, b] reveals that $\lambda _{0} > 0$. We next use Assumptions 4.2 and 4.3 to show that $\lim _{r\downarrow 0} r V_{r}(x) = \lambda _{0}$ for any $x \ge 0$ and that there exist two positive constants $a_{*} < b_{*}$ for which the reflected diffusion process on $[a_{*}, b_{*}]$ is an optimal state process, where $V_{r}(x)$ is the value function of the discounted problem (2.6). These results are summarized in Theorem 4.4. Furthermore, we show in Theorem 5.1 that the Cesàro limit holds as well. As an illustration, we study an ergodic two-sided singular control problem for a geometric Brownian motion model using this framework in Sect.  6. This approach fails when some of our assumptions are violated. Indeed, the case study in Sect. 6.1 indicates that the long-term average reward can be arbitrarily large under suitable settings. Upon the completion of this paper, we learned the recent paper [1], which deals with an ergodic two-sided singular control problem for a general one-dimensional diffusion on $(-\infty , \infty )$. The formulation in Alvarez [1] is different from ours because the rewards associated with the singular controls are both positive. Under certain conditions, the paper first constructs a solution to the associated HJB equation and then verifies that the local time reflection policy is optimal. The approach is different from the vanishing discount method used in this paper, which also helps to establish the Abelian and Cesàro limits.

Thanks to the referee who also brought our attention to the paper [3], which studies the optimal sustainable harvesting of a population that lives in a random environment. It proves that there exists a unique optimal local time reflection harvesting strategy and establishes an Abelian limit under certain conditions. In contrast to the problem considered in this paper, Alvarez and Hening [3] is focused on a one-sided singular control problem without running rewards and hence it is simpler than our formulation in (2.3).

Motivated by the two papers mentioned above, we add Sect. 7 to provide a direct solution approach to (2.3). Following the idea in Alvarez [1] and Alvarez and Hening [3], we first impose conditions so that the long-term average reward for an (a, b)-reflection policy $\lambda (a, b)$ achieves its maximum value $\lambda _{*} = \lambda (a_{*}, b_{*})$ at a pair $0< a_{*}< b_{*}< \infty$. The maximizing pair $(a_{*}, b_{*})$ further allows us to derive a $C^{2}$ solution to the HJB equation (3.1). This, together with the verification theorem (Theorem 3.1), reveals that $\lambda _{0} = \lambda _{*}$ and the $(a_{*}, b_{*})$-reflection policy is optimal.

The rest of the paper is organized as follows. Section 2 begins with the formulation of the problem; it also presents the main results of the paper. Section 3 collects some preliminary results. The Abelian and Cesàro limits are established in Sects. 4 and 5, respectively. Section 6 is devoted to an ergodic two-sided singular control problem when the underlying process is a geometric Brownian motion with Sect. 6.1 providing a case study for $\mu =0$ and $h(x) = x^{p}, p\in (0,1)$. Finally, we provide a direct solution approach in Sect. 7. An example on ergodic two-sided singular control for Verhulst-Pearl diffusion is studied in Sect. 7 as an illustration.

2 Formulation and Main Results

To begin, suppose the uncontrolled process is given by the following one-dimensional diffusion process with state space $[0, \infty )$:

$$\begin{aligned} \mathrm dX_{0}(s)= \mu (X_{0}(s))\mathrm ds +\sigma (X_{0}(s))\mathrm dW(s), \quad X_{0}(0) = x_{0} \in [0, \infty ), \end{aligned}$$

(2.1)

where W is a one-dimensional standard Brownian motion, and $\mu$ and $\sigma$ are suitable functions so that a weak solution $X_{0}$ exists and is unique in the sense of probability law. We refer to Sect. 5.5 of Karatzas and Shreve [16] for such conditions. Assume throughout the paper that 0 is an unattainable boundary point (entrance or natural) and that $\infty$ is a natural boundary point; see Chapter 15 of Karlin and Taylor [17] or Sect. 5.5 of Karatzas and Shreve [16] for more details on classifications of boundary points for one-dimensional diffusions. Note that if 0 is an entrance point, then it is part of the state space for $X_{0}$; otherwise, if 0 is a natural point, then it is not in the state space. While an entrance point cannot be reached from the interior, it is possible that the process $X_{0}$ will start from an entrance boundary point and quickly move to the interior and never return to it. The choice of $[0, \infty )$ as the state space for $X_{0}$ is motivated by the following consideration. The states of interest in applications such as reversible investment, optimal harvesting and renewing, and dividend payment and capital injection problems are all bounded from below. For notational convenience, we then choose $[0, \infty )$ as the state space for $X_{0}$.

Throughout the paper, we suppose that both the scale function S and the speed measure M of the process $X_{0}$ are absolutely continuous with respect to the Lebesgue measure. The scale and speed densities are given by

$$\begin{aligned} s(x) : = \exp \bigg \{-\int _{1}^{x} \frac{2\mu (y)}{\sigma ^{2} (y) } \mathrm dy\bigg \}, \ \ \ m(x): = \frac{1}{\sigma ^{2}(x) s(x)}, \qquad x > 0, \end{aligned}$$

respectively. The infinitesimal generator of the process $X_{0}$ is

$$\begin{aligned} {\mathcal {L}}f(x): = \frac{1}{2}\sigma ^{2}(x) f''(x) + \mu (x) f'(x)= \frac{1}{2} \frac{\mathrm d}{\mathrm dM}\bigg (\frac{\mathrm df(x)}{\mathrm dS} \bigg ), \ \quad \forall f\in C^{2}([0,\infty )). \end{aligned}$$

We now introduce a bounded variation process $\varphi = \xi -\eta$ to (2.1), resulting in the following controlled dynamics:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm dX(s)= \mu (X(s))\mathrm ds +\sigma (X(s))\mathrm dW(s) +\mathrm d\xi (s) - \mathrm d\eta (s), &{}\quad s\ge 0,\\ X(0-)=x \ge 0. \end{array}\right. } \end{aligned}$$

(2.2)

Throughout the paper, we assume that the control process $\varphi (\cdot )= \xi (\cdot )- \eta (\cdot )$ is an adapted, càdlàg process that admits the minimal Jordan decomposition $\varphi (t) = \xi (t) - \eta (t)$, $t\ge 0$. In particular, $\xi , \eta$ are nonnegative and nondecreasing processes satisfying $\xi (0-) =\eta (0- )= 0$ such that the associated Borel measures $\mathrm d\xi$ and $\mathrm d\eta$ on $[0,\infty )$ are mutually singular. In addition, it is required that under the control process $\varphi (\cdot )$, (2.2) admits a unique nonnegative weak solution $X(\cdot )$. Such a control process $\varphi (\cdot )$ is said to be admissible.

The goal is to maximize the expected long-term average reward:

$$\begin{aligned} \lambda _{0} : =\sup _{\varphi (\cdot )\in {\mathscr {A}}_{x}} \liminf _{T\rightarrow \infty }\frac{1}{T}{\mathbb {E}}_{x}\bigg [\int _{0}^{T} h(X(s) ) \mathrm ds +c_{1} \eta (T)- c_{2} \xi (T) \bigg ], \end{aligned}$$

(2.3)

where $c_{1} < c_{2}$ are two positive constants, h is a nonnegative function, and ${\mathscr {A}}_{x}$ is the set of admissible controls, i.e.,

$$\begin{aligned} \begin{aligned} {\mathscr {A}}_{x}&: = \big \{\varphi =(\xi ,\eta ) \text { is admissible and satisfies } \\&\quad { {\mathbb {E}}_{x}[\xi (T) ] \le K_{1}(x) T^{n} + K_{2}(x) } \text { for all } T >0\}, \end{aligned} \end{aligned}$$

(2.4)

where $K_{ 1}(x)$ and $K_{2}(x)$ are positive real-valued functions, and $n \in {\mathbb {N}}$ is a positive integer. The requirement that ${\mathbb {E}}_{x}[\xi (T) ] \le K_{1}(x) T^{n} + K_{2}(x)$ ensures that the expectation in the right-hand side of (2.3) as well as the discounted and finite-time horizon problems (2.6) and (2.7) are well-defined. The set is clearly nonempty because the “zero control” $\varphi (t) \equiv 0$ is in ${\mathscr {A}}_{x}$. Lemma 3.4 below indicates that ${\mathscr {A}}_{x}$ includes local time controls as well. It is also apparent that the value of $\lambda _{0}$ does not depend on the initial condition x since an initial jump dose not alter the value of the limit in (2.3). In addition, it is obvious that $\lambda _{0} \ge 0$.

In this paper, we aim to find the value $\lambda _{0}$ and an optimal control policy $\varphi ^{*}$ that achieves the value $\lambda _{0}$. Motivated by Weerasinghe [26], we will approach this problem via the vanishing discount method and show that $\lambda _{0}$ is equal to the Abelian limit as well as the Cesàro limit. In other words, we will demonstrate that

$$\begin{aligned} \lambda _{0} = \lim _{r\downarrow 0} r V_{r}(x)= \lim _{T\rightarrow \infty } \frac{V_{T}(x)}{T}, \end{aligned}$$

(2.5)

where $V_{r}(x)$ and $V_{T}(x)$ denote respectively the value functions for the related discounted and finite horizon problems

$$\begin{aligned} V_{r}(x)&: = \sup _{\varphi (\cdot )\in {\mathscr {A}}_{x}} {\mathbb {E}}_{x}\bigg [\int _{0}^{\infty } e^{-rs}[ h(X(s)) \mathrm ds + c_{1} \mathrm d\eta (s) - c_{2}\mathrm d\xi (s)]\bigg ], \end{aligned}$$

(2.6)

$$\begin{aligned} V_{T}(x)&: = \sup _{\varphi (\cdot )\in {\mathscr {A}}_{x}}{\mathbb {E}}_{x}\bigg [\int _{0}^{T} h(X(s) ) \mathrm ds +c_{1} \eta (T)- c_{2} \xi (T) \bigg ]. \end{aligned}$$

(2.7)

The main result of this paper is given next.

Theorem 2.1

Under Assumptions 3.2, 4.2, and 4.3, the following assertions hold:

• (i) There exist $0< a_{*}< b_{*} < \infty$ so that the reflected diffusion process on the interval $[a_{*}, b_{*}]$ (if the initial point is outside this interval, then there will be an initial jump to the nearest point of the interval) is an optimal state process for the ergodic control problem (2.3). Hence the optimal control policy is given by $\varphi _{*} = L_{a_{*}} - L_{b_{*}}$, in which $L_{a_{*}}$ and $L_{b_{*}}$ denote the local time processes at $a_{*}$ and $b_{*}$, respectively.

• (ii) The Abelian and Cesàro limits in (2.5) hold.

The proof of Theorem 2.1 follows from Theorems 4.4 and 5.1, which will be presented in the subsequent sections.

Remark 2.2

Since the optimal state process is a reflected diffusion on the interval $[a_{*}, b_{*}]\subset (0, \infty )$, it follows that it possesses a unique invariant measure $\pi$. According to Chapter 15 of Karlin and Taylor [17], the invariant measure is $\pi (\mathrm dx) = \frac{1}{M[a_{*}, b_{*}]} M( \mathrm dx)$. Moreover, using the ergodicity for linear diffusions in Chapter II, section 6 of Borodin and Salminen [4], we have

$$\begin{aligned} \lambda _{0} = \int _{a_{*}}^{b_{*}} h(x) \pi (\mathrm dx)+ \frac{c_{1}}{2M[a_{*}, b_{*}] s(b_{*})} -\frac{c_{2}}{2M[a_{*}, b_{*}] s(a_{*})}. \end{aligned}$$

3 Preliminary Results

In this section, we provide some preliminary results.

Theorem 3.1

Suppose there exists a nonnegative function $u\in C^{2}([0,\infty ))$ and a nonnegative number $\lambda$ such that

$$\begin{aligned} \max \big \{ {\mathcal {L}}u( x) + h(x)-\lambda , \ u' (x) - c_{2}, \ -u' (x) + c_{1} \big \} = 0. \end{aligned}$$

(3.1)

Then $\lambda _{0} \le \lambda$.

Proof

Let $x\in [0,\infty )$ and $\varphi (\cdot )=(\xi (\cdot ),\eta (\cdot ))\in {\mathscr {A}}_{x}$ be an arbitrary control policy and denote by X the controlled state process with $X(0-)=x$. For $n\in {\mathbb {N}}$, let $\beta _{n}: = \inf \{t\ge 0: X(t) \ge n\}$. By Ito’s formula we have

$$\begin{aligned} u(X(T\wedge \beta _{n}))&= u(x) + \int _{0}^{T\wedge \beta _{n}} {\mathcal {L}}u(X(s))\mathrm ds - \int _{0}^{T\wedge \beta _{n}}u'(X(s-)) (\mathrm d\eta _{s}^{c} - \mathrm d\xi _{s}^{c} ) \nonumber \\&\quad + \int _{0}^{T\wedge \beta _{n}}u'(X(s))\sigma (X(s))\mathrm dW(s) \nonumber \\&\quad +\sum _{0\le s \le T\wedge \beta _{n}}\left[ u(X(s)) - u(X(s-))\right] . \end{aligned}$$

(3.2)

The HJB equation (3.1) implies that $c_{1} \le u' (x) \le c_{2}$. Note also that $\Delta X(s) = \Delta \xi (s) - \Delta \eta (s)$. Consequently, we can use the mean value theorem to obtain

$$\begin{aligned} u( X(s)) - u( X(s-)) \le c_{2}\Delta \xi (s) - c_{1}\Delta \eta (s). \end{aligned}$$

(3.3)

Note that (3.1) also implies that ${\mathcal {L}}u(x) \le -h(x) + \lambda$. Plugging this and (3.3) into (3.2) gives us

$$\begin{aligned}&u(X(T\wedge \beta _{n})) \le u(x) - \int _{0}^{T\wedge \beta _{n}} h(X(s))\mathrm ds + \lambda (T\wedge \beta _{n}) \\&\quad + \int _{0}^{T\wedge \beta _{n}}u'(X(s))\sigma (X(s))\mathrm dW(s) - c_{1}\eta (T\wedge \beta _{n}) + c_{2} \xi (T\wedge \beta _{n}). \end{aligned}$$

Rearranging terms and then taking expectations, we arrive at

$$\begin{aligned}&{\mathbb {E}}_{x}\bigg [ \int _{0}^{T\wedge \beta _{n}} h(X(s))\mathrm ds + c_{1}\eta (T\wedge \beta _{n}) - c_{2} \xi (T\wedge \beta _{n}) \bigg ] \\&\quad + {\mathbb {E}}_{x}[u(X(T\wedge \beta _{n}))] \le u(x) + \lambda {\mathbb {E}}_{x}[T\wedge \beta _{n}]. \end{aligned}$$

Passing to the limit as $n\rightarrow \infty$ and then dividing both sides by T, we obtain from the nonnegativity of u and the monotone convergence theorem that

$$\begin{aligned} \limsup _{T\rightarrow \infty }\frac{1}{T} {\mathbb {E}}_{x}\bigg [ \int _{0}^{T} h(X(s))\mathrm ds + c_{1}\eta (T) - c_{2} \xi (T) \bigg ] \le \lambda . \end{aligned}$$

Finally, taking supremum over $\varphi (\cdot )$ yields the assertion that $\lambda _{0} \le \lambda$. $\square$

To proceed, we make the following assumption.

Assumption 3.2

• (i) $\lim _{x\downarrow 0} [h(x) + c_{2} \mu (x)] \le 0$ and $\lim _{x\rightarrow \infty } [h(x) + c_{1} \mu (x)] < 0$.

• (ii) There exist $0< a< b < \infty$ satisfying

  $$\begin{aligned} \int _{a}^{b}h(y) m(y) \mathrm dy + \frac{c_{1}}{2s(b)} - \frac{c_{2}}{2s(a)} > 0. \end{aligned}$$

  (3.4)

Lemma 3.3

Suppose Assumption 3.2 holds. Then there exists a positive number $\lambda = \lambda (a, b)$ so that the following boundary value problem has a solution:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{1}{2} \sigma ^{2}(x) u''(x) + \mu (x) u'(x) + h(x) = \lambda , &{}\quad x\in (a, b),\\ u'(a) = c_{2}, \quad u'(b) = c_{1}. \end{array}\right. } \end{aligned}$$

(3.5)

Proof

For any $0< a< b<\infty$ and $\lambda \in {\mathbb {R}}$ given, a solution to the differential equation $\frac{1}{2} \sigma ^{2}(x) u''(x) + \mu (x) u'(x) + h(x) = \lambda$ is given by

$$\begin{aligned} u(x) = c_{1} x+ \int _{a}^{x} 2s(u) \int _{u}^{b}[c_{1} \mu (y) + h(y) - \lambda ] m(y) \mathrm dy\mathrm du, \quad x\in [a, b]. \end{aligned}$$

(3.6)

Note that $u'(b) = c_{1}$. The other boundary condition $u'(a) = c_{2}$ gives

$$\begin{aligned} c_{1} +2 s(a) \int _{a}^{b} [c_{1} \mu ( y) + h(y) - \lambda ] m(y) \mathrm dy =c_{2}. \end{aligned}$$

Note that

$$\begin{aligned} \int _{a}^{b} \mu (y) m(y) \mathrm dy = \frac{1}{2s(b)} - \frac{1}{2s(a)}, \quad \forall [a, b] \in (0, \infty ). \end{aligned}$$

(3.7)

Hence it follows that

$$\begin{aligned} \lambda =\lambda (a, b) = \frac{1}{2 M[a, b]} \bigg (\frac{c_{1}}{s(b)} - \frac{c_{2}}{s(a)} + 2 \int _{a}^{b}h(y) m(y) \mathrm dy \bigg ), \end{aligned}$$

(3.8)

where $M[a, b] = \int _{a}^{b} m(y) \mathrm dy > 0$ is the speed measure of the interval [a, b]. In particular, it follows from (3.4) that $\lambda$ is positive. $\square$

Lemma 3.4

For any $0< a< b < \infty$, let X be the reflected diffusion process on [a, b]:

$$\begin{aligned} X(t) = x + \int _{0}^{t}\mu (X(s)) \mathrm ds + \int _{0}^{t}\sigma ( X(s)) \mathrm dW(s) + L_{a}(t) - L_{b}(t), \end{aligned}$$

(3.9)

where without loss of generality we can assume that the initial condition $x\in [a,b]$, and $L_{a}$ and $L_{b}$ denote the local time processes at a and b, respectively. Then there exist some positive constants $K_{1}$ and $K_{2}$ so that

$$\begin{aligned} {\mathbb {E}}_{x} [L_{a}(t) + L_{b}(t) ] \le K_{1} t + K_{2}, \quad \text { for any } t \ge 0. \end{aligned}$$

In particular, the policy $L_{a}- L_{b} \in {\mathscr {A}}_{x}$.

Proof

For the given $0< a< b < \infty$, as in the proof of Lemma 3.3, we can verify that the function given by

$$\begin{aligned} v(x) : = -x + a + 2 \int _{a}^{x}s(y) \int _{y}^{b}[-\mu (z) + K_{1}] m(z) \mathrm dz\mathrm dy, \quad x\in [a, b] \end{aligned}$$

is a solution to the boundary value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{1}{2} \sigma ^{2} (x) v''(x) +\mu ( x) v'(x) + K_{1} =0, &{} x\in (a, b), \\ v'(a) = 1, \ \ v'(b) = -1, \end{array}\right. } \end{aligned}$$

where $K_{1} = K_{1}(a, b ) = \frac{1}{2 M[a,b]} ( \frac{1}{s(a)} + \frac{1}{s(b)}) > 0.$

It is well-known that equation (3.9) has a unique solution X; see, for example, [9, Sect. 2.4] or [5]. We now apply Itô’s formula to the process v(X(t)) and then take expectations,

$$\begin{aligned} {\mathbb {E}}_{x}[v(X(t))]&= v(x) + {\mathbb {E}}_{x}\bigg [ \int _{0}^{t}\bigg (\mu (X(s)) v'(X(s)) + \frac{1}{2}\sigma ^{2} (X (s)) v''(X(s))\bigg )\mathrm ds\bigg ] \\&\quad +{\mathbb {E}}_{x}\big [v'(a) L_{a}(t) - v'(b) L_{b}(t) \big ] \\&= v(x) - K_{1} t + {\mathbb {E}}_{x}[L_{a}(t) + L_{b}(t)]. \end{aligned}$$

Since v is continuous and $X(t) \in [a, b]$ for all $t\ge 0$, it follows that there exists a positive constant $K_{2} = K_{2}(a, b)$ such that ${\mathbb {E}}_{x}[L_{a}(t) + L_{b}(t)] \le K_{1} t + K_{2}.$ The lemma is proved. $\square$

Corollary 3.5

Suppose Assumption 3.2 holds, then $\lambda _{0} > 0$.

Proof

To show that $\lambda _{0} > 0$, we consider the function u of (3.6) in which we choose $0< a< b<\infty$ so that $\lambda = \lambda (a, b)$ of (3.8) is positive. Now let X be the reflected diffusion process on [a, b] given by (3.9). Thanks to Lemma 3.4, the policy $L_{a}- L_{b}\in {\mathscr {A}}_{x}$. Apply Itô’s formula to u(X(t)) and then take expectations to obtain

$$\begin{aligned} {\mathbb {E}}_{x}[u(X(t))]&= u(x) + {\mathbb {E}}_{x}\bigg [ \int _{0}^{t}\bigg (\mu (X(s)) u'(X(s)) + \frac{1}{2}\sigma ^{2}( X(s)) u''(X(s))\bigg )\mathrm ds\bigg ]\\&\quad +{\mathbb {E}}_{x}\big [u'(a) L_{a}(t) - u'(b) L_{b}(t) \big ] \\&= u(x) + {\mathbb {E}}_{x}\bigg [ \int _{0}^{t} [\lambda -h(X(s))] \mathrm ds + c_{2} L_{a}(t) - c_{1} L_{b}(t)\bigg ]. \end{aligned}$$

Rearranging terms, dividing by t, and then passing to the limit as $t\rightarrow \infty$, we obtain

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{1}{t}{\mathbb {E}}_{x}\bigg [ \int _{0}^{t} h(X(s)) \mathrm ds - c_{2} L_{a}(t) + c_{1} L_{b}(t) \bigg ] =\lambda = \lambda (a, b), \end{aligned}$$

where $\lambda (a, b)$ is defined in (3.8). In other words, the long-term average reward of the policy $L_{a}- L_{b}$ is $\lambda (a, b) >0$. Now by the definition of $\lambda _{0}$, we have $\lambda _{0} \ge \lambda > 0$. $\square$

4 The Abelian Limit

For a given $r > 0$, recall the discounted value function $V_{r}(x)$ defined in (2.6). Also recall the definition of $\lambda _{0}$ given in (2.3). The following proposition presents a relationship between the discounted and long-term average problems.

Proposition 4.1

We have $\liminf _{r\downarrow 0} r V_{r}(x) \ge \lambda _{0}$ for any $x\in [0,\infty )$.

Proof

Since $V_{r}(x) \ge 0$, the relation $\liminf _{r\downarrow 0} r V_{r}(x) \ge \lambda _{0}$ holds trivially when $\lambda _{0} =0$. Now assume that $\lambda _{0} > 0$. Let $x\in [0,\infty )$. For any $0< K< \lambda _{0}$, there exists a policy $\varphi =\xi -\eta \in {\mathscr {A}}_{x}$ so that

$$\begin{aligned} \lambda _{0}\ge \liminf _{T\rightarrow \infty } \frac{1}{T} {\mathbb {E}}_{x}\bigg [\int _{0}^{T} h(X(s))\mathrm ds - c_{2} \xi (T) + c_{1}\eta (T) \bigg ] \ge K; \end{aligned}$$

(4.1)

here X is the controlled process corresponding to the policy $\varphi$ with initial condition $X(0-) =x$. Let $F(T): = {\mathbb {E}}_{x}[\int _{0}^{T} h(X(s))\mathrm ds - c_{2} \xi (T) + c_{1}\eta (T) ]$ and $G(T) := \frac{F(T)}{T+1}$ for $T>0$. Thanks to (4.1), there exists a $T_{1} > 0$ such that $F(T) > 0$ for all $T \ge T_{1}$. Consequently we can use integration by parts and Fubini’s theorem to obtain

$$\begin{aligned} {\mathbb {E}}_{x} \bigg [\int _{0}^{T} e^{-r s} (h(X(s))\mathrm ds - c_{2}\mathrm d\xi (s) + c_{1}\mathrm d\eta (s)) \bigg ]&= e^{-r T } F(T) + r\int _{0}^{T} e^{-rs} F(s) \mathrm ds\\&\ge r\int _{0}^{T} e^{-rs} F(s) \mathrm ds, \end{aligned}$$

for all $T \ge T_{1}$. Then it follows from the dynamic programming principle (see [8]) that for all $T \ge T_{1}$,

$$\begin{aligned} r V_{r}(x)&\ge \sup _{\varphi \in {\mathscr {A}}_{x}} r {\mathbb {E}}_{x} \bigg [\int _{0}^{T} e^{-r s} (h(X(s))\mathrm ds - c_{2}\mathrm d\xi (s) + c_{1}\mathrm d\eta (s)) + e^{-r T} V_{r}(X(T)) \bigg ] \\&\ge r {\mathbb {E}}_{x} \bigg [\int _{0}^{T} e^{-r s} (h(X(s))\mathrm ds - c_{2}\mathrm d\xi (s) + c_{1}\mathrm d\eta (s)) \bigg ] \\&\ge { r^{2} \int _{0}^{\infty } e^{-r s} F(s) \mathrm ds} = r^{2} \int _{0}^{\infty } e^{-r s} (s+1) G(s) \mathrm ds \\&= \int _{0}^{\infty } e^{-t}(t+r) G(t/r) \mathrm dt. \end{aligned}$$

In view of (4.1), for any $\varepsilon > 0$, we can find a $T_{2}>0$ so that $G(T) = \frac{F(T)}{T+1} \ge K-\varepsilon$ for all $T\ge T_{2}$. Denote $T_{0} : = T_{1}\vee T_{2}$. Then we can estimate

$$\begin{aligned} r V_{r}(x)&\ge \int _{0}^{ r T_{0}} e^{-t}(t+r) G(t/r) \mathrm dt + \int _{r T_{0}}^{\infty } e^{-t}(t+r) G(t/r) \mathrm dt\\&\ge \int _{0}^{ r T_{0}} e^{-t} F(t/r) \mathrm dt + \int _{r T_{0}}^{\infty } e^{-t}(t+r) (K-\varepsilon ) \mathrm dt\\&\ge -r^{2} T_{0} \max _{t\in [0, T_{0}]} F(t) + (K-\varepsilon ) (1+r -r^{2}(T_{0}+1)). \end{aligned}$$

Letting $r\downarrow 0$, we obtain $\liminf _{r\downarrow 0} r V_{r}(x) \ge K -{\varepsilon }$. Since $\varepsilon > 0$ and $K < \lambda _{0}$ are arbitrary, we obtain $\liminf _{r\downarrow 0} r V_{r}(x) \ge \lambda _{0}$, which completes the proof. $\square$

Usually one can show that the value function $V_{r}$ of (2.6) is a viscosity solution to the HJB equation

$$\begin{aligned} \min \{rv(x) -{\mathcal {L}}v(x) -h(x), -v'(x) + c_2, v'(x)-c_1\} = 0, \quad x\in (0,\infty ). \end{aligned}$$

(4.2)

Under additional assumptions such as concavity of the function h, for specific models (such as geometric Brownian motion in Guo and Pham [8]), one can further show that $V_{r}$ is a smooth solution to (4.2) and that there exist $0< a_{r}< b_{r} < \infty$ so that the reflected diffusion process on the interval $[a_{r}, b_{r}]$ is an optimal state process. In other words, the policy $L_{a_{r}}- L_{b_{r}}$ is an optimal control policy, where $L_{a_{r}}$ and $L_{b_{r}}$ denote the local times of the controlled process X at $a_{r}$ and $b_{r}$, respectively. If the initial position $X(0-)$ is outside the interval $[a_{r}, b_{r}]$, then an initial jump to the nearest boundary point is exerted at time 0. We also refer to Matomäki [21] and Weerasinghe [25] for sufficient conditions for the optimality of such policies for general one-dimensional diffusion processes under different settings.

Motivated by these recent developments, we make the following assumption:

Assumption 4.2

For each $r> 0$, there exist two numbers with $0< a_{r}< b_{r} < \infty$ so that the discounted value function $V_{r}(x)$ of (2.6) is $C^{2}([0,\infty ))$ and satisfies the following system of equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} r V_{r}(x) -{\mathcal {L}}V_{r}(x) -h (x) =0, \quad \ c_{1} \le V_{r}'(x) \le c_{2}, &{} x\in (a_{r}, b_{r}), \\ r V_{r}(x) -{\mathcal {L}}V_{r}(x) -h (x) \ge 0, \quad \ V_{r}'(x) = c_{1}, &{} x\ge b_{r},\\ r V_{r}(x) -{\mathcal {L}}V_{r}(x) -h (x) \ge 0, \quad \ V_{r}'(x) = c_{2},&{} x\le a_{r}. \end{array}\right. } \end{aligned}$$

(4.3)

In addition, the following assumption is needed for the proof of Theorem  4.4.

Assumption 4.3

The functions h, $\mu$, and $\sigma$ are continuously differentiable and satisfies $\inf _{x\in [a, b]} \sigma ^{2}(x) > 0$ for any $[a, b] \subset (0, \infty )$.

We now state the main result of this section.

Theorem 4.4

Let Assumptions  3.2, 4.2, and  4.3 hold. Then there exist positive constants $a_{*} < b_{*}$ so that the following statements hold true:

• (i) $\lim _{r\downarrow 0}rV_r(x) = \lambda _{0}$ for all $x \in {\mathbb {R}}$.

• (ii) The reflected diffusion process on the state space $[a_{*}, b_{*}]$ (if the initial point is outside this interval, then there will be an initial jump to the nearest point of the interval) is an optimal state process for the ergodic control problem (2.3). Hence the optimal control policy here is given by $\varphi _{*} = L_{a_{*}} - L_{b_{*}}$, in which $L_{a_{*}}$ and $L_{b_{*}}$ denote the local time processes at $a_{*}$ and $b_{*}$, respectively.

To prove Theorem 4.4, we first establish a series of technical lemmas.

Lemma 4.5

Suppose Assumptions 3.2 (i) and 4.2 hold. Then $\lambda _{0} > 0$ if and only if $\liminf _{r\downarrow 0} a_{r} >0$.

Proof

Recall that the function $V_{r}\in C^{2}(0, \infty )$ satisfies $r V_{r}(x) - \mu ( x) V_{r}'(x) - \frac{1}{2} \sigma ^{2}(x) V''_{r} (x) - h(x) = 0$ for $x\in (a_{r}, b_{r})$ and $V_{r}(x) = c_{2} x + V_{r}(0+)$ for $x\le a_{r}$, where $V_{r}(0+)= \lim _{x\downarrow 0} V_{r}(x) = V_{r}(a_{r}) - c_{2} a_{r}$. Therefore the smooth pasting principle for $V_{r}$ at $a_{r}$ implies that $V_{r}'(a_{r}) = c_{2}$ and $V_{r}''(a_{r}) =0$. Thus it follows that

$$\begin{aligned}&r(c_{2}a_{r} + V_{r}(0+)) -c_{2}\mu (a_{r}) - h(a_{r}) =0 \quad \text { or } \nonumber \\&rV_{r}(0+) = h(a_{r}) +c_{2}\mu (a_{r})- r c_{2}a_{r}. \end{aligned}$$

(4.4)

• (i) Suppose first that $\lambda _{0} > 0$. Then Proposition 4.1 implies that any limit point of $\{r V_{r}(0+)\}$ must be greater than 0. If there exists a sequence $\{r_{n}\} \subset (0, 1]$ for which $\lim _{n\rightarrow \infty } a_{r_{n}} =0$, then passing to the limit as $n\rightarrow \infty$ in (4.4) will give us $\lim _{n\rightarrow \infty } r_{n} V_{r_{n}}(0+) = \lim _{n\rightarrow \infty }[ h(a_{r_{n}}) + c_{2} \mu (a_{r_{n}}) ] \le 0$ thanks to Assumption 3.2 (i). This is a contradiction.

• (ii) Now if $\liminf _{r\downarrow 0} a_{r} =0$, then using (4.4) again, we obtain $\lim _{n\rightarrow \infty } r_{n} V_{r_{n}}(0+) = 0$ for some sequence $\{r_{n}\}$ such that $\lim _{n\rightarrow \infty } r_{n } =0$ and $\lim _{{n }\rightarrow \infty } a_{r_{n}} =0$. This, together with Proposition 4.1, indicates that $\lambda _{0} =0$.

$\square$

Lemma 4.6

Suppose Assumptions 3.2 (i) and 4.2 hold. Then $\limsup _{r\downarrow 0 } b_{r} < \infty$.

Proof

As in the proof of Lemma 4.5, we can use the smooth pasting for the function $V_{r}$ at $b_{r}$ to obtain

$$\begin{aligned} 0 < r V_{r} (b_{r}) = c_{1} \mu (b_{r}) + h(b_{r}). \end{aligned}$$

(4.5)

Suppose that there exists some sequence $\{r_{n}\} \subset (0, 1]$ so that $\lim _{n\rightarrow \infty } r_{n} =0$ and $\lim _{n\rightarrow \infty } b_{r_{n}} =\infty$. Now passing to the limit as $n\rightarrow \infty$ in (4.5), we obtain

$$\begin{aligned} 0\le \lim _{n\rightarrow \infty } r_{n} V_{r_{n}} (b_{r_{n}}) = \lim _{n\rightarrow \infty } ( c_{1} \mu ( b_{r_{n}}) + h(b_{r_{n}})) < 0 \end{aligned}$$

thanks to Assumption 3.2 (i). This is a contradiction. Hence $\limsup _{r\downarrow 0 } b_{r} < \infty$ and the assertion of the lemma follows. $\square$

The following lemma can be obtained directly from Corollary 3.5 and Lemmas 4.5 and 4.6.

Lemma 4.7

Suppose Assumptions 3.2 (i) and 4.2 hold. Then there exist constants $0<r_{0} <1$ and $0< K_{1}< K_{2} < \infty$ so that $K_{1} \le a_{r} < b_{r} \le K_{2}$ for all $0 < r \le r_{0}$.

Lemma 4.8

Let Assumptions  3.2, 4.2, and  4.3 hold. Then there exists a function $w_{r}\in C^{1}((0,\infty )) \cap C^{2}((0,\infty )\setminus \{a_{r}, b_{r}\})$ satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{1}{2} \sigma ^{2}( x) w_{r}''(x) + (\sigma (x) \sigma '(x) + \mu (x) ) w_{r}'(x) - (r - \mu '(x) ) w_{r}(x) + h'(x) = 0, &{}\quad x\in (a_{r}, b_{r}); \\ c_{1} \le w_{r}(x) \le c_{2}, &{}\quad x\in (a_{r}, b_{r}), \\ w_{r} (x) = c_{2}, \ \ w'_{r} (x) = 0, &{}\quad x\le a_{r}, \\ w_{r}(x) = c_{1}, \ \ w'_{r} (x) = 0, &{}\quad x\ge b_{r}. \end{array}\right. } \end{aligned}$$

(4.6)

Proof

Recall Assumption 4.2 indicates that $V_{r}$ of (2.6) satisfies

$$\begin{aligned}&\frac{1}{2} \sigma ^{2} (x) V_{r}''(x) + \mu ( x) V_{r}'(x) - r V_{r}(x) + h(x) = 0, \quad x\in (a_{r}, b_{r}),\\&c_{1}< V_{r}'(x) < c_{2}, \quad x\in (a_{r}, b_{r}),\nonumber \end{aligned}$$

(4.7)

and

$$\begin{aligned} V_{r}'(x)&= c_{2}, \text { for } x\le a_{r}, \ \ V_{r}'(x) = c_{1}, \text { for }x\ge b_{r}, \text { and }\\ V_{r}''(x)&=0 \text { for }x \le a_{r} \text { or }x \ge b_{r}. \end{aligned}$$

Now differentiating (4.7) and denoting $w_{r}: = V'_{r}$, then $w_{r}$ satisfies (4.6). $\square$

Lemma 4.9

Let Assumptions 3.2, 4.2, and 4.3 hold. Then there exist two positive constants $a_{* } < b_{*}$, a constant $l_{0}>0$, and a function $w_{0}\in C^{1}(0,\infty )$ satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{1}{2} \sigma ^{2} (x) w_{0}'(x) + \mu (x) w_{0}(x) + h(x) = l_0, &{} \quad x\in (a_{*}, b_{*}),\\ c_{1} \le w_{0}(x) \le c_{2}, &{} \quad x\in (a_{*}, b_{*}),\\ w_{0} (x) = c_{2}, \ \ w'_{0} (x) = 0, &{} \quad x\le a_{*},\\ w_{0}(x) = c_{1}, \ \ w'_{0} (x) = 0, &{} \quad x\ge b_{*}. \end{array}\right. } \end{aligned}$$

(4.8)

Proof

Thanks to (4.6), $w_{r}$ is uniformly bounded. Next we integrate the first equation of (4.6) from $a_{r}$ to x ($x\in (a_{r}, b_{r})$) to obtain

$$\begin{aligned} \frac{1}{2} \sigma ^{2} (x) w_{r}'(x) = c_{2}\mu (a_{r}) + h(a_{r}) - \mu (x) w_{r}(x) + r \int _{a_{r}}^{x} w_{r}(y) \mathrm dy - h(x). \end{aligned}$$

(4.9)

Thanks to Lemma 4.7 and the continuity of h and $\mu$, the right-hand side of (4.9) is uniformly bounded on $[K_{1}, K_{2}]$ for all $r\in (0, r_{0}]$, where $r_{0}, K_{1}$, and $K_{2}$ are the positive constants found in Lemma 4.7. This, together with Assumption 4.3, implies that $\{w_{r}'(x), r\in (0, r_{0}] \}$ is uniformly bounded on $[K_{1}, K_{2}]$. Consequently, $\{w_{r}(x), r\in (0, r_{0}] \}$ is equicontinuous.

Now we rewrite the first equation of (4.6) as

$$\begin{aligned}&\frac{1}{2} \sigma ^{2} (x) w_{r}''(x) = -(\sigma (x) \sigma '(x) + \mu (x) ) w_{r}'(x) + (r - \mu '(x) ) w_{r}(x) - h'(x),\\&\quad x\in (a_{r}, b_{r}). \end{aligned}$$

Since $\{w_{r}'\}$ and $\{w_{r}\}$ are uniformly bounded and $\sigma , \sigma '$, $\mu '$, and $h'$ are continuous, it follows from Assumption 4.3 that there exists a positive constant K independent of r such that

$$\begin{aligned} |w_{r}''(x)| \le K, \text { for all }x\in (a_{r}, b_{r}) \subset [K_{1}, K_{2}], \text { for any } r\in (0, r_{0}]. \end{aligned}$$

This, together with the fact that $w'_{r}(x) =0$ for all $x\in [K_{1}, K_{2}]\setminus (a_{r}, b_{r})$ (c.f. (4.6)), implies that $\{w_{r}', r\in (0, r_{0}] \}$ is equicontinuous on $[K_{1}, K_{2}]$.

Meanwhile, Lemma 4.7 implies that there exists a sequence $\{r_{n}\}_{n\ge 1}$ such that $\lim _{n\rightarrow \infty }r_{n} = 0$ for which

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }a_{r_{n}} = a_{*}, \ \quad \ \lim \limits _{n\rightarrow \infty }b_{r_{n}} = b_{*} \end{aligned}$$

(4.10)

for some $0<K_1 \le a_{*} \le b_{*} \le K_2 < \infty$. Since $\mu$ and h are continuous, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }( c_{2}\mu ( a_{r_{n}}) + h(a_{r_{n}}) ) =c_{2} \mu ( a_{*}) + h(a_{*}) =: l_{0}. \end{aligned}$$

Recall that (4.4) indicates $r V_{r}(0+) = h(a_{r}) + c_{2} \mu (a_{r})-r c_{2} a_{r}$. Thus $l_{0}$ is a limiting point of $\{rV_r(0+)\}$. This, together with Proposition 4.1, implies that $l_{0}\ge \lambda _{0}$.

Since $\{w_{r_{n}}\}$ and $\{w'_{r_{n}}\}$ are equicontinuous and uniformly bounded sequences on $[K_1, K_2]$, by the Arzelà–Ascoli theorem, there exists a continuously differentiable function $w_0$ on $[K_1,K_2]$ such that for some subsequence of $\{r_{n}\}$ (still denoted by $\{r_{n}\}$), we have

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }w_{r_{n}}(x) = w_0(x)\ \quad \ \lim \limits _{n\rightarrow \infty }w'_{r_{n}}(x) = w_0'(x). \end{aligned}$$

(4.11)

Passing to the limit along the subsequence $\{r_{n}\}$ in (4.9) and noting that $w_{r_{n}}$ is uniformly bounded, we obtain from (4.10) and (4.11) that

$$\begin{aligned} \frac{1}{2} \sigma ^{2}(x) w_{0}'(x) + \mu (x) w_{0}(x) + h(x) =l_{0}, \quad x\in (a_{*},b_{*}). \end{aligned}$$

Since $\{w_{r_{n}}\}$ and $\{w'_{r_{n}}\}$ are equicontinuous, we can extend $w_{0}$ to $(0,\infty )$ so that $w_{0}$ is continuously differentiable and that the third and fourth lines of (4.8) are satisfied. That $c_{1} \le w_{0}(x) \le c_{2}$ for all $x\in (a_{*}, b_{*})$ is obvious. This completes the proof of the lemma. $\square$

We are now ready to prove Theorem 4.4.

Proof

Let the positive constants $l_{0}$ and $a_{*} < b_{*}$ and the function $w_{0}$ be as in the statement of Lemma 4.9. Define the function Q by

$$\begin{aligned} Q(x) = \int _{0}^{x}w_{0}(u)\mathrm du, \quad x\in (0,\infty ). \end{aligned}$$

Since $w_{0}$ is positive and satisfies (4.8), it is easy to see that Q is nonnegative and satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{1}{2} \sigma ^{2}( x) Q''(x) + \mu (x) Q'(x) + h(x) = l_{0}, \ \ &{}\quad x\in (a_{*},b_{*}), \\ Q'(x) = c_{2}, \ \ &{}\quad x\le a_{*},\\ Q'(x) = c_{1}, \ \ &{}\quad x\ge b_{*}. \end{array}\right. } \end{aligned}$$

(4.12)

Without loss of generality, we assume that x is in the interval $[a_{*},b_{*}]$. Let $X_{*}$ be the reflected diffusion process on the interval $[a_{*}, b_{*}]$ with $X_{*}(0) =x$; that is,

$$\begin{aligned} X_{*}(t) = x + \int _{0}^{t} \mu (X_{*}(s)) \mathrm ds + \int _{0}^{t} \sigma ( X_{*}(s)) \mathrm dW(s) + L_{a_{*}}(t) - L_{b_{*}}(t), \end{aligned}$$

where $L_{a_{*}}$ and $L_{b_{*}}$ denote the local time processes at $a_{*}$ and $b_{*}$, respectively. Thanks to Lemma 3.4, $L_{a_{*}}-L_{b_{*}} \in {\mathscr {A}}_{x}$ and $X_{*}$ is an admissible process.

We now apply Itô’s formula to $Q(X_{*}(T))$ and use (4.12) to obtain

$$\begin{aligned}&{\mathbb {E}}_{x}\left[ Q(X_{*}(T))\right] \\&\quad = Q(x) + l_{0} T + {\mathbb {E}}_{x}\bigg [-\int _{0}^{T} h (X_{*}(s))\mathrm ds + c_{2} L_{a_{*}}(t) -c_{1} L_{b_{*}}(t) \bigg ]. \end{aligned}$$

Rearranging terms, dividing both sides by T, and then letting $T\rightarrow \infty$, we obtain

$$\begin{aligned} \lim _{T \rightarrow \infty }\frac{1}{T}{\mathbb {E}}_{x}\bigg [\int _{0}^{T}h(X(s))ds + c_1L_{b_{*}}(T) - c_2L_{a _{*}}(T) \bigg ] = l_0. \end{aligned}$$

This implies that $l_{0}\le \lambda _{0}$. Recall we have observed in the proof of Lemma 4.9 that $l_{0}\ge \lambda _{0}$. Hence we conclude that $l_{0}= \lambda _{0}$ and $\varphi _{*} = L_{a_{*}} - L_{b_{*}}$ is an optimal policy.

Recall from the proof of Lemma 4.9 that $l_{0}$ is a limiting point of $\{r V_{r}(0+)\}$. Since $\lambda _{0} = l_{0}$, it follows that any limiting point of $\{r V_{r}(0+)\}$ is equal to $\lambda _{0}$. Moreover, for any $x \in (0,\infty )$, we have

$$\begin{aligned} \lim _{r\downarrow 0} r V_{r}(x)&= \lim _{r\downarrow 0} r (V_{r}(x) - V_{r}(0+)) + \lim _{r\downarrow 0} r V_{r}(0+) \\ {}&= \lim _{r\downarrow 0} r w_{r} (\theta x) x + \lambda _{0} \\&= \lambda _{0}, \end{aligned}$$

where $\theta \in [0,1]$. Note that we used the fact that $w_{r}$ is uniformly bounded to obtain the last equality. The proof is complete. $\square$

5 The Cesàro Limit

This section establishes the Cesàro limit $\lim _{T\rightarrow \infty }\frac{1}{T}V_{T}(x) = \lambda _{0}$, where $V_{T}(x)$ is the value function for the finite-horizon problem defined in (2.7).

Theorem 5.1

Let Assumptions  3.2, 4.2, and  4.3 hold. Then we have

$$\begin{aligned} \lim _{T\rightarrow \infty }\frac{1}{T}V_{T}(x) = \lambda _{0}. \end{aligned}$$

(5.1)

Proof

The proof is divided into two steps.

Step 1. We first prove

$$\begin{aligned} \liminf \limits _{T\rightarrow \infty }\frac{1}{T} V_T(x) \ge \lambda _{0}. \end{aligned}$$

(5.2)

Note that (5.2) is obviously true when $\lambda _{0} =0$. Now we consider the case when $\lambda _{0} > 0$ and let K be a constant so that $K <\lambda _{0}$. By (2.3) there exits an admissible control $\varphi :=(\xi ,\eta )\in {\mathscr {A}}_{x}$ so that

$$\begin{aligned} \liminf _{T\rightarrow \infty } \frac{1}{T}{\mathbb {E}}_{x}\left[ \int _{0}^{T} h(X(s))\mathrm ds +c_1\eta (T) - c_2\xi (T)\right] > K. \end{aligned}$$

For any $T > 0$, by the definition of $V_{T}(x)$, we have ${\mathbb {E}}_{x}[\int _{0}^{T} h(X(s)) \mathrm ds +c_1\eta (T) - c_2\xi (T)] \le V_{T}(x)$ and hence

$$\begin{aligned} K < \liminf _{T\rightarrow \infty } \frac{1}{T}{\mathbb {E}}_{x}\left[ \int _{0}^{T} h(X(s)) \mathrm ds +c_1\eta (T) - c_2\xi (T)\right] \le \liminf _{T\rightarrow \infty } \frac{1}{T}V_{T}(x). \end{aligned}$$

Since $K < \lambda _{0}$ is arbitrary we conclude that $\lambda _{0} \le \liminf _{T\rightarrow \infty } \frac{1}{T}V_{T}(x)$. This gives (5.2).

Step 2. We now show that

$$\begin{aligned} \limsup _{T\rightarrow \infty } \frac{1}{T}V_{T}(x) \le \lambda _{0}. \end{aligned}$$

(5.3)

To this end, consider any $\varphi \in {\mathscr {A}}_{x}$ for which ${\mathbb {E}}_{x}[\int _{0}^{T} h(X(s)) \mathrm ds + c_{1} \eta (T) - c_{2}\xi (T)] \ge (V_{T}(x) -1)\vee 0$, where X is the corresponding controlled process with $X(0-) =x \in (0, \infty )$.

Let $r> 0$ and consider the functions $V_{r}$ and $w_{r}$ defined respectively in (2.6) and (4.6). Recall that $w_{r} = V_{r}'\in [c_{1}, c_{2}]$. Hence for any $x> 0$, we can write

$$\begin{aligned} V_{r}(x) = V_{r}(0) + \int _{0}^{x} w_{r}(y) \mathrm dy \ge V_{r}(0) + c_{1} x. \end{aligned}$$

(5.4)

We now apply Itô’s formula to the process $e^{-r T} V_{r}(X(T))$ to obtain

$$\begin{aligned}&{\mathbb {E}}_{x} [e^{-r(T\wedge \beta _{n})} V_{r}(X(T\wedge \beta _{n}))] \\&\quad = V_{r} (x) + {\mathbb {E}}_{x}\bigg [ \int _{0}^{T\wedge \beta _{n}} e^{-rs} (-r V_{r} + {\mathcal {L}}V_{r}) (X(s)) \mathrm ds \\&\qquad + e^{-rs} V_{r}' (X(s)) (\mathrm d\xi ^{c} (s) - \mathrm d\eta ^{c} (s))\bigg ] \\&\qquad + {\mathbb {E}}_{x}\Bigg [\sum _{0\le s \le T\wedge \beta _{n}} e^{-rs}\left[ V_{r} (X(s)) - V_{r} (X(s-))\right] \Bigg ], \end{aligned}$$

where $\beta _{n}: = \inf \{t\ge 0: X(t) \ge n\}$ and $n \in {\mathbb {N}}$. Since $V_{r}$ satisfies the HJB equation (4.2), we have

$$\begin{aligned}&{\mathbb {E}}_{x} [e^{-r(T\wedge \beta _{n})} V_{r}(X(T\wedge \beta _{n}))] \le V_{r} (x) \\&\quad + {\mathbb {E}}_{x}\bigg [ \int _{0}^{T\wedge \beta _{n}} e^{-rs} [-h(X(s)) \mathrm ds+ c_{2}\mathrm d\xi (s) - c_{1} \mathrm d\eta (s) ]\bigg ]. \end{aligned}$$

Rearranging terms and using (5.4) yield

$$\begin{aligned}&{\mathbb {E}}_{x}\bigg [ \int _{0}^{T\wedge \beta _{n}} e^{-rs} [h(X(s))\mathrm ds- c_{2}\mathrm d\xi (s) + c_{1} \mathrm d\eta (s)] \bigg ]\\&\quad \le V_{r} (x) - {\mathbb {E}}_{x} [e^{-r(T\wedge \beta _{n})} V_{r}(X(T\wedge \beta _{n}))] \\&\quad \le V_{r} (x) - {\mathbb {E}}_{x} [e^{-r (T\wedge \beta _{n})} V_{r}(0) +e^{-r(T\wedge \beta _{n})} c_{1} X(T\wedge \beta _{n})]\\&\quad \le V_{r} (x) - {\mathbb {E}}_{x} [e^{-r (T\wedge \beta _{n})} V_{r}(0) ]. \end{aligned}$$

Then it follows that

$$\begin{aligned} {\mathbb {E}}_{x} \bigg [ \int _{0}^{T } e^{-rs} (h(X(s))\mathrm ds - c_{2}\mathrm d\xi (s) + c_{1}\mathrm d\eta (s)) \bigg ] \le V_{r} (x) - e^{-r T} V_{r}(0). \end{aligned}$$

(5.5)

Using integration by parts, we have

$$\begin{aligned}&e^{-r T} {\mathbb {E}}_{x}\bigg [\int _{0}^{T } h(X(s))\mathrm ds - c_{2}\xi (T) + c_{1} \eta (T)\bigg ]\\ {}&\ \ = {\mathbb {E}}_{x} \bigg [ \int _{0}^{T } e^{-rs} (h(X(s))\mathrm ds - c_{2}\mathrm d\xi (s) + c_{1}\mathrm d\eta (s)) \bigg ] \\&\qquad - r{\mathbb {E}}_{x}\bigg [\int _{0}^{T}\!\! e^{-r t}\bigg [ \int _{0}^{t} h(X(s))\mathrm ds - c_{2}\xi (t) + c_{1} \eta ( t)\bigg ]\mathrm dt\bigg ]. \end{aligned}$$

Plugging this observation into (5.5), we obtain

$$\begin{aligned}&e^{-r T} {\mathbb {E}}_{x}\bigg [\int _{0}^{T } h(X(s))\mathrm ds - c_{2}\xi (T) + c_{1} \eta (T)\bigg ] \\&\quad \le V_{r} (x) - e^{-r T} V_{r}(0) - r{\mathbb {E}}_{x}\bigg [\int _{0}^{T}e^{-r t} \bigg [\int _{0}^{t} h(X(s))\mathrm ds - c_{2}\xi (t) + c_{1} \eta ( t)\bigg ]\mathrm dt\bigg ]\\&\quad \le V_{r} (x) - e^{-r T} V_{r}(0) + r c_{2} \int _{0}^{T}e^{-r t} {\mathbb {E}}[\xi (t) ] \mathrm dt\\&\quad \le V_{r} (x) - e^{-r T} V_{r}(0) + r c_{2} \int _{0}^{T}e^{-r t} ( K_{1}(x) t^{n} +K_{2}(x) )\mathrm dt\\&\quad = V_{r} (x) - e^{-r T} V_{r}(0) + \frac{c_{2}K_{1}(x) n!}{r^{n}}\bigg ( 1 - e^{-rT}\sum _{j=0}^{n} \frac{ (rT)^{j}}{j!} \bigg ) + K_{2}(x)(1- e^{-r T})\\&\quad = (1- e^{-r T}) V_{r}(0) + [ V_{r} (x) - V_{r}(0)] + \frac{c_{2}K_{1}(x)n!}{r^{n}}\bigg ( 1 - e^{-rT}\sum _{j=0}^{n} \frac{ (rT)^{j}}{j!} \bigg ) \\&\qquad + K_{2}(x)(1- e^{-r T}), \end{aligned}$$

where the third last step follows from (2.4). Now we pick $r = \frac{\delta }{T}$ for some $\delta \in (0,1)$ and divide both sides by T to obtain

$$\begin{aligned}&e^{-\delta } \frac{1}{T}{\mathbb {E}}_{x}\bigg [\int _{0}^{T } h(X(s))\mathrm ds - c_{2}\xi (T) + c_{1} \eta (T)\bigg ] \\&\quad \le \frac{1- e^{- \delta }}{\delta } r V_{r}(0) + \frac{V_{r} (x) - e^{-\delta } V_{r}(0) }{T} + \frac{c_{2}K_{1}(x)n! T^{n-1}}{\delta ^{n}} \bigg ( 1 - e^{-\delta }\sum _{j=0}^{n} \frac{ \delta ^{j}}{j!} \bigg ) \\&\qquad + \frac{K_{2}(x)(1- e^{- \delta })}{T}. \end{aligned}$$

Since $\lim _{r\downarrow 0} r V_{r}(0) = \lambda _{0}$ thanks to Theorem 4.4, we first let $\delta \downarrow 0$ and then let $T \rightarrow \infty$ to obtain

$$\begin{aligned} \limsup _{T\rightarrow \infty } \frac{1}{T}{\mathbb {E}}_{x}\bigg [\int _{0}^{T } h(X(s))\mathrm ds - c_{2}\xi (T) + c_{1} \eta (T)\bigg ] \le \lambda _{0}. \end{aligned}$$

This is true for any $\varphi \in {\mathscr {A}}_{x}$ and hence it follows that $\limsup _{T\rightarrow \infty } \frac{V_{T}(x)}{ T} \le \lambda _{0}$; establishing (5.3). The proof is complete. $\square$

6 Geometric Brownian Motion Models

In this section, we apply the vanishing discount method to study a two-sided singular control problem when the underlying process is a geometric Brownian motion. That is, we consider the following long-term average singular control problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda _{0} : =\displaystyle \sup _{\varphi (\cdot )\in {\mathscr {A}}_{x}} \liminf _{T\rightarrow \infty }\frac{1}{T}{\mathbb {E}}_{x}\bigg [\int _{0}^{T} h(X(s) ) \mathrm ds +c_{1} \eta (T)- c_{2} \xi (T) \bigg ],\\ \text {subject to }{\left\{ \begin{array}{ll}\mathrm dX(s)= \mu X(s)\mathrm ds +\sigma X(s)\mathrm dW(s) +\mathrm d\xi (s) - \mathrm d\eta (s), \quad s\ge 0,\\ X(0-)=x \ge 0, \end{array}\right. } \end{array}\right. } \end{aligned}$$

(6.1)

where $\mu < 0$, $\sigma > 0$, $0< c_{1} < c_{2}$ are constants, h is a nonnegative function satisfying Assumption 6.2 below, and the singular control $\varphi = \xi -\eta$ is admissible as in Sect. 2.

In problem (6.1), the underlying uncontrolled process is a geometric Brownian motion with state space $(0, \infty )$. Using the criteria in Chapter 15 of Karlin and Taylor [17], we see that both 0 and $\infty$ are natural boundary points. Moreover, the scale and speed densities are respectively given by $s(x)=x^{-\frac{2\mu }{\sigma ^{2}}}$ and $m(x)= \frac{1}{\sigma ^{2}} x^{\frac{2\mu }{\sigma ^{2}}-2}$, $x> 0$.

Remark 6.1

Let us explain why we need to assume $\mu < 0$ in (6.1). Suppose that $\mu > 0$, then one can show that $\lambda _{0}=\infty$. Indeed, for any $x > 0$ and any sequence $t_{k}\rightarrow \infty$ as $k\rightarrow \infty$, we can construct an admissible policy $\varphi (\cdot )=(\xi (\cdot ),\eta (\cdot ))$ as follows. Let $\xi (t)\equiv 0$ for all $t\ge 0$, $\eta (t) = 0$ for $t< t_{k}$ and $\eta (t) \equiv \Delta \eta (t_{k}) = X_{0}(t_{k}):= x \exp \{(\mu -\frac{1}{2} \sigma ^{2})t_{k} + \sigma W(t_{k}) \}$ for all $t\ge t_{k}$. In other words, under the policy $\varphi (\cdot )$, the manager does nothing before time $t_{k}$ and then harvests all at time $t_{k}$. Since $X_{0}(t_{k}) = x \exp \{(\mu -\frac{1}{2} \sigma ^{2})t_{k} + \sigma W(t_{k}) \}$, we have

$$\begin{aligned} \lambda _{0} \ge \lim _{k\rightarrow \infty } \frac{1}{t_{k}} {\mathbb {E}}_{x}[c_{1} \eta (t_{k})] = \lim _{k\rightarrow \infty } \frac{1}{t_{k}} {\mathbb {E}}_{x}[c_{1} X_{0}(t_{k})] = \lim _{k\rightarrow \infty } \frac{1}{t_{k}} c_{1} x e^{\mu t_{k}} = \infty . \end{aligned}$$

When $\mu =0$, in the presence of Assumption 6.2 below, we no longer have $\lim _{x\rightarrow \infty } (h(x) +c_{1} \mu x ) <0$, thus violating Assumption 3.2 (i). Consequently the vanishing discount method is not applicable. We will present in Sect. 6.1 a case study which indicates for the Cobb Douglas function $h(x) = x^{p}, p\in (0,1)$, the optimal long-term average reward can be arbitrarily large.

We need the following assumption throughout this section:

Assumption 6.2

The function h is nonnegative and satisfies the following conditions:

• (i) h is strictly concave, continuously differentiable and nondecreasing on $[0,\infty )$, and satisfies $h(0)=0$;

• (ii) h has a finite Legendre transform on $(0,\infty )$; that is, for all $z > 0$

  $$\begin{aligned} \Phi _{h}(z) : = \sup _{x\ge 0}\left\{ h( x) - z x\right\} < \infty . \end{aligned}$$

  (6.2)

• (iii) h satisfies the Inada condition at 0, i.e.,

  $$\begin{aligned} \lim _{x\downarrow 0} \frac{h(x)}{x} = \infty . \end{aligned}$$

  (6.3)

Remark 6.3

Assumption 6.2 is common in the finance literature; see, for example, Guo and Pham [8] and De Angelis and Ferrari [6]. The Inada condition at 0 implies that the right derivative $h'(0+)$ of the function h is infinity. If this condition is violated, say, there exists some $c\in [c_{1}, c_{2}]$ such that

$$\begin{aligned} h'(0+) + \mu c \le 0, \end{aligned}$$

(6.4)

then one can show that $\lambda _{0} =0$.

Indeed, in the presence of (6.4), we can immediately verify that the function $u(x) = c x$ and $\lambda =0$ satisfy (3.1). Consequently it follows from Theorem 3.1 that $\lambda _{0} =0$. Moreover, we can construct an optimal policy in the following way. Suppose $X(0-) = x \ge 0$. Let $\xi (t) \equiv 0$ and $\eta (t) \equiv \Delta \eta (0) = x$; that is, the policy harvests all and brings the state to 0 at time 0. The long-term average reward for such a policy is 0.

The main result of this section is presented next.

Theorem 6.4

Under Assumption 6.2, there exist $0< a_{*}< b_{*} < \infty$ such that the reflected geometric Brownian motion on the interval $[a_{*}, b_{*}]$ is an optimal state process (if the initial point is outside this interval, then there will be an initial jump to the nearest point of the interval). In other words, the optimal value $\lambda _{0}$ of (6.1) is achieved by $\varphi _{*}(\cdot ): = L_{a_{*}}(\cdot )- L_{b_{*}}(\cdot )$, in which $L_{a_{*}}(\cdot )$ and $L_{b_{*}}(\cdot )$ denote respectively the local times of X at $a_{*}$ and $b_{*}$. Moreover, the Abelian and the Cesàro limits (2.5) hold.

Proof

In view of Theorem 2.1, we only need to verify Assumptions 3.2, 4.2, and  4.3 hold. Assumption  4.3 obviously holds. Under Assumption 6.2, it is established in Guo and Pham [8] that there exist two positive numbers $a_{r} < b_{r}$ so that the discounted problem $V_{r}$ is a classical solution to (4.3), which verifies Assumption 4.2.

It remains to show Assumption 3.2 holds. Since $h(0) =0$, we have $\lim _{x\downarrow 0} [h(x) + c_{2} \mu x] =0$. In view of (6.2) and the fact that $\mu < 0$, we have $h(x) - ( \frac{-c_{1}\mu }{2} )x \le \Phi _{h}(\frac{-c_{1}\mu }{2} ) < \infty$. Consequently it follows that

$$\begin{aligned} \lim _{x\rightarrow \infty } [h(x) + c_{1}\mu x] \le \lim _{x\rightarrow \infty } \bigg [\Phi _{h}\bigg (\frac{-c_{1}\mu }{2} \bigg ) - \frac{c_{1}\mu }{2} x + c_{1}\mu x\bigg ] =-\infty . \end{aligned}$$

Assumption  3.2 (i) is therefore verified. To verify Assumption  3.2 (ii), we recall that the scale and speed densities of the geometric Brownian motion are respectively given by $s(x)=x^{-\frac{2\mu }{\sigma ^{2}}}$ and $m(x)= \frac{1}{\sigma ^{2}} x^{\frac{2\mu }{\sigma ^{2}}-2}$, $x> 0$. Next we observe that condition (6.3) implies that there exists a positive constant $\delta$ so that $\frac{h(y)}{y} > -2\mu c_{2}$ for all $y\in (0, \delta )$. Now let $b> \delta > a$. Then we have

$$\begin{aligned} \frac{c_{1}}{2s(b)} - \frac{c_{2}}{2s(a)} + \int _{a}^{b}h(y) m(y) \mathrm dy&\ge - \frac{c_{2}}{2s(a)} + \int _{a}^{\delta }\frac{h(y)}{y} y \frac{1}{\sigma ^{2}}y^{\frac{2\mu }{\sigma ^{2}}-2} \mathrm dy \\&> - \frac{c_{2}}{2s(a)} + \frac{1}{\sigma ^{2}} \int _{a}^{\delta }( -2\mu c_{2}) y^{\frac{2\mu }{\sigma ^{2}}-1} \mathrm dy\\&= - \frac{c_{2}}{2s(a)} + c_{2} \bigg ( \frac{1}{s(a)} -\frac{1}{s(\delta )}\bigg ) \\&= \frac{c_{2}}{2s(a)}- \frac{c_{2}}{s(\delta )} > 0, \end{aligned}$$

by choosing $a > 0$ sufficiently small so that $\frac{1}{s(a)} > \frac{2}{s(\delta )}$. This gives (3.4) and hence verifies Assumption  3.2 (ii). $\square$

6.1 Case Study: $\mu =0$ and $h(x) = x^{p}, p\in (0, 1)$

In this subsection, we consider the problem (6.1) in which $\mu =0$ and $h(x) = x^{p}, p\in (0, 1)$. We will demonstrate via probabilistic arguments that $\lambda _{0} =\infty$. To this end, we first present the following lemma.

Lemma 6.5

Suppose $\mu =0$ and $h(x) = x^{p}$ for some $p \in (0,1)$, then for all $\lambda > 0$ sufficiently large satisfying

$$\begin{aligned} \frac{2p}{\sigma ^{2}(1-p)} \lambda ^{1-\frac{1}{p}} < \frac{c_{2}-c_{1}}{2} \quad \text { and } \quad c_{2} \lambda ^{\frac{1}{p}-1} > \frac{2}{\sigma ^{2}p} \ln \lambda , \end{aligned}$$

(6.5)

the function

$$\begin{aligned} u(x) : ={\left\{ \begin{array}{ll}\frac{2}{\sigma ^{2} p (1-p)} x^{p} -\frac{2\lambda }{\sigma ^{2}} \log x + C x, &{}\quad \text { if }x > a_{*},\\ c_{2}(x-a_{*}) + u(a_{*}), &{}\quad \text { if } 0\le x \le a_{*} \end{array}\right. } \end{aligned}$$

(6.6)

is twice continuously differentiable, nonnegative, and satisfies the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {L}}u(x) + h(x) - \lambda =0, &{}\quad \text { if } x> a_{*},\\ c_{1} \le u'(x) \le c_{2}, &{} \quad \text { if }x > a_{*}, \\ {\mathcal {L}}u(x) + h(x) - \lambda \le 0, &{} \quad \text { if } x \le a_{*},\\ u'(x) = c_{2}, &{} \quad \text { if } x \le a_{*}. \end{array}\right. } \end{aligned}$$

(6.7)

Here $a_{*} = \lambda ^{1/p}$ and $C= c_{2} -\frac{2p}{\sigma ^{2} (1-p)} \lambda ^{1-\frac{1}{p}}$.

Proof

Note that condition (6.5) implies that $C> c_{2} - \frac{c_{2}-c_{1}}{2} = \frac{c_{2}+c_{1}}{2} > c_{1}$. The fact that $u \in C^{1}((0,\infty )) \cap C^{2}((0,\infty )\setminus \{a_{*}\})$ is a direct consequence of the definition of u in (6.6). Detailed calculations reveal that $\lim _{x\downarrow a_{*}} u''(x) = 0$ and hence $u \in C^{2}(0,\infty )$. In addition, the equalities in (6.7) can be verified by direct computations. We next show the inequalities in (6.7) hold as well.

For $x< a_{*}$, we have

$$\begin{aligned} {\mathcal {L}}u(x) + h(x) - \lambda&= h(x) -\lambda \le h(a_{*}) -\lambda =0. \end{aligned}$$

For $x> a_{*}$, we have

$$\begin{aligned} u'(x)&= \frac{2}{\sigma ^{2}(1-p)} x^{p-1} - \frac{2\lambda }{\sigma ^{2}} x^{-{1}} + C,\\ u''(x)&= -\frac{2}{\sigma ^{2} } x^{p-2}+ \frac{2\lambda }{\sigma ^{2}} x^{-2 } = \frac{2\lambda }{\sigma ^{2}} x^{-2 } (1- x^{p}) \le 0. \end{aligned}$$

These imply that $u'(x) \le u'(a_{*}) = c_{2}$ for all $x> a_{*}$. Also we notice that $\lim _{x\rightarrow \infty } u'(x) = C > c_{1}$. Hence it follows that $c_{1} < u'(x) \le c_{2}$ for all $x> a_{*}$.

Also observe that $u(a_{*}) = \frac{2}{\sigma ^{2} p}(\frac{\lambda }{1-p} -\lambda \ln \lambda ) + C \lambda ^{\frac{1}{p}}= \frac{2}{\sigma ^{2} (1-p)}(\frac{1}{p} - p) \lambda + (c_{2}\lambda ^{\frac{1}{p}-1}- \frac{2}{\sigma ^{2}p} \ln \lambda ) \lambda > 0$ thanks to the second inequality of (6.5). Hence $u(x) > 0$ for all $x>0$. The proof is complete. $\square$

Proposition 6.6

Suppose $\mu =0$ and $h(x) = x^{p}$ for some $p \in (0,1)$, then $\lambda _{0} =\infty$.

Proof

For any $\lambda > 0$ satisfying (6.5), we construct a policy whose long-term average reward equals $\lambda$. Since $\lambda$ is arbitrary, it follows that $\lambda _{0} =\infty$. To this end, recall that $a_{*} = \lambda ^{1/p}$. Let $b_{*}: = \log a_{*}$ and consider the drifted Brownian motion reflected at $b_{*}$:

$$\begin{aligned} \psi (t) : = b_{*} -\frac{1}{2} \sigma ^{2} t + \sigma W(t) + \phi (t) \ge b_{*}, \quad t\ge 0, \end{aligned}$$

where $\phi (t) = - \inf _{0\le s \le t}\{ - \frac{1}{2} \sigma ^{2} s + \sigma W(s)\}$. One can verify immediately that $\phi$ is a nondecreasing process that increases only when $\psi (t) =b_{*}$; i.e.,

$$\begin{aligned} \phi (t) = \int _{0}^{t} {\mathbf {1}}_{\{ b_{*}\}} (\psi (s)) \mathrm d\phi (s). \end{aligned}$$

(6.8)

Now let $X(t) : = e^{\psi (t)}$. Note that $X(0) = a_{*}$. By Itô’s formula, we have

$$\begin{aligned} \mathrm dX(t)= & {} \bigg ( -\frac{\sigma ^{2}}{2} + \frac{\sigma ^{2}}{2} \bigg )X(t) \mathrm dt + \sigma X(t) \mathrm dW(t) + X(t) \mathrm d\phi (t)\nonumber \\= & {} \sigma X(t) \mathrm dW(t) + \mathrm dL_{a^*}(t), \end{aligned}$$

(6.9)

where $L_{a_{*}}(t): = \int _{0}^{t} X(s) \mathrm d\phi (s)$. We make the following observations.

• (i) $X(t) \ge a_{*}$ for all $t\ge 0$. This is obvious since $\psi (t) \ge b_{*}$ for all $t\ge 0$.

• (ii) $L_{a_{*}}$ is a nondecreasing process that increases only when $X(t) =a_{*}$. Indeed, using (6.8) and note that $X(t) =a_{*}$ if and only if $\psi (t) =b_{*}$, it follows that

  $$\begin{aligned} \begin{aligned} L_{a_{*}}(t)&= \int _{0}^{t} X(s) \mathrm d\phi (s)= \int _{0}^{t} X(s) {\mathbf {1}}_{\{ b_{*}\}} (\psi (s)) \mathrm d\phi (s)\\&= \int _{0}^{t} {\mathbf {1}}_{\{ a_{*}\}} (X(s)) X(s) \mathrm d\phi (s)= \int _{0}^{t} {\mathbf {1}}_{\{ a_{*}\}} (X(s)) \mathrm dL_{a^*}(s). \end{aligned} \end{aligned}$$

  (6.10)

We now apply Itô’s formula to the process u(X(t)), where X is given by (6.9) with $X(0) = a_{*}$. Since $X(t) \ge a_{*}$ for all $t\ge 0$ and u satisfies (6.7), we have

$$\begin{aligned} {\mathbb {E}}[u(X(t\wedge \beta _{n})]&= u(a_{*}) + {\mathbb {E}}\bigg [\int _{0}^{t\wedge \beta _{n}} {\mathcal {L}}u(X(s)) \mathrm ds + \int _{0}^{t\wedge \beta _{n}} u'(X(s)) \mathrm dL_{a_{*}}(s) \bigg ] \\&= u(a_{*}) + {\mathbb {E}}\bigg [-\int _{0}^{t\wedge \beta _{n}} h(X(s)) \mathrm ds + c_{2} L_{a_{*}}(t\wedge \beta _{n}) \bigg ] + \lambda {\mathbb {E}}[t\wedge \beta _{n}], \end{aligned}$$

where $\beta _{n}: = \inf \{ t\ge 0: X(t) \ge n\}$ and $n\in {\mathbb {N}}\cap (a_{*},\infty )$. Since u is nonnegative, rearranging the terms yields

$$\begin{aligned} {\mathbb {E}}\bigg [ \int _{0}^{t\wedge \beta _{n}} h(X(s)) \mathrm ds - c_{2} L_{a_{*}}(t\wedge \beta _{n}) \bigg ] \le u(a_{*})+ \lambda {\mathbb {E}}[t\wedge \beta _{n}]. \end{aligned}$$

Now dividing both sides by t, and passing to the limit first as $n\rightarrow \infty$ and then as $t\rightarrow \infty$, we obtain

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t} {\mathbb {E}}\bigg [\int _{0}^{t} h(X(s)) \mathrm ds - c_{2} L_{a_{*}}(t) \bigg ] \le \lambda . \end{aligned}$$

(6.11)

In view of Sect. 15.5 of Karlin and Taylor [17], the process X of (6.9) has a unique stationary distribution $\pi (\mathrm dx) =a_{*} x^{-2} \mathrm dx, x\in (a_{*},\infty )$. The strong law of large numbers [18, Theorem 4.2] then implies that as $t\rightarrow \infty$

$$\begin{aligned} \frac{1}{t}\int _{0}^{t}h_{n}(X(s))\mathrm ds \rightarrow \int _{a_{*}}^{\infty } h_{n}(x) \pi (\mathrm dx), \ \ \text { a.s.} \end{aligned}$$

where $h_{n}(x) : = h(x) \wedge n$ and $n\in {\mathbb {N}}$. For each $n\in {\mathbb {N}}$, the random variables $\{\frac{1}{t} \int _{0}^{t} h_{n}(X(s)) \mathrm ds, t> 0 \}$ are non-negative and bounded above by n. Thus we can apply the bounded convergence theorem to obtain

$$\begin{aligned} \lim _{t\rightarrow \infty } {\mathbb {E}}\bigg [ \frac{1}{t} \int _{0}^{t} h_{n}(X(s)) \mathrm ds\bigg ] = \int _{a_{*}}^{\infty } h_{n}(x) \pi (\mathrm dx). \end{aligned}$$

On the other hand, since $h\ge h_{n}$ and $h_{n} \uparrow h$, we have

$$\begin{aligned} \liminf _{t\rightarrow \infty } {\mathbb {E}}\bigg [ \frac{1}{t} \int _{0}^{t} h(X(s)) \mathrm ds\bigg ]&= \lim _{n\rightarrow \infty } \liminf _{t\rightarrow \infty } {\mathbb {E}}\bigg [ \frac{1}{t} \int _{0}^{t} h(X(s)) \mathrm ds\bigg ]\nonumber \\&\ge \lim _{n\rightarrow \infty } \liminf _{t\rightarrow \infty } {\mathbb {E}}\bigg [ \frac{1}{t} \int _{0}^{t} h_{n}(X(s)) \mathrm ds\bigg ] \nonumber \\&= \lim _{n\rightarrow \infty } \int _{a_{*}}^{\infty } h_{n}(x) \pi (\mathrm dx)\nonumber \\&= \int _{a_{*}}^{\infty } h(x) \pi (\mathrm dx)\nonumber \\&= \frac{(a_{*})^{p}}{1-p} = \frac{\lambda }{1-p} \ge \lambda , \end{aligned}$$

(6.12)

where the second to the last line follows from the monotone convergence theorem and the equality in the last line follows from the fact that $a_{*} = \lambda ^{1/p}$.

We next estimate ${\mathbb {E}}[L_{a_{*}}(t)]$. To this end, we observe from the third equality of (6.10) that

$$\begin{aligned} L_{a_{*}}(t) = \int _{0}^{t} {\mathbf {1}}_{\{ a_{*}\}} (X(s)) X(s) \mathrm d\phi (s)= a_{*} \phi (t), \end{aligned}$$

and hence ${\mathbb {E}}[L_{a_{*}}(t)]= a_{*} {\mathbb {E}}[\phi (t)]$. On the other hand, since $\phi (t) = - \inf _{0\le s \le t}\{ - \frac{1}{2} \sigma ^{2} s + \sigma W(s)\}= \sup _{0\le s \le t}\{ \frac{1}{2} \sigma ^{2} s + \sigma (-W(s))\}$, it follows from (1.8.11) of Harrison [9] that

$$\begin{aligned} {\mathbb {P}}\{\phi (t) \le y \} = \Phi \bigg (\frac{y-\frac{1}{2} \sigma ^{2}t}{\sigma \sqrt{t}}\bigg ) - e^{y} \Phi \bigg (\frac{-y-\frac{1}{2} \sigma ^{2}t}{\sigma \sqrt{t}}\bigg ), \end{aligned}$$

where $\Phi$ is the standard normal distribution function $\Phi (x): = \int _{-\infty }^{x} \frac{1}{\sqrt{2\pi }} e^{-\frac{z^{2}}{2}}\mathrm dz$. Then we can compute

$$\begin{aligned}&{\mathbb {E}}[\phi (t)] \nonumber \\&\quad = \int _{0}^{\infty } y\bigg ( \frac{1}{\sqrt{2\pi \sigma ^{2}t}} e^{-\frac{(y-t\sigma ^{2}/2)^{2}}{2\sigma ^{2} t}} -e^{y} \Phi \bigg ( \frac{-y-t\sigma ^{2}/2}{\sigma \sqrt{t}}\bigg ) + e^{y} \frac{1}{\sqrt{2\pi \sigma ^{2}t}} e^{-\frac{(y+t\sigma ^{2}/2)^{2}}{2\sigma ^{2} t}} \bigg )\mathrm dy \nonumber \\&= \sigma ^{2} t \Phi (\sigma \sqrt{t}/2) +\frac{\sqrt{2t}\sigma e^{-\frac{\sigma ^{2}t}{8}}}{\sqrt{\pi }}- \int _{0}^{\infty } y e^{y} \Phi \bigg ( \frac{-y-t\sigma ^{2}/2}{\sigma \sqrt{t}}\bigg ) \mathrm dy. \end{aligned}$$

(6.13)

To estimate the last integral, we use the tail estimate for the standard normal distribution function (see, for example, [7, Sect. 7.1]):

$$\begin{aligned} 1- \Phi (x) = \int _{x}^{\infty } \frac{1}{\sqrt{2\pi }} e^{-\frac{y^{2}}{2}} \mathrm dy \ge [x^{-1} - x^{-3}] \frac{1}{\sqrt{2\pi }} e^{-\frac{x^{2}}{2}}, \quad x> 0, \end{aligned}$$

to obtain

$$\begin{aligned}&\Phi \bigg ( \frac{-y-t\sigma ^{2}/2}{\sigma \sqrt{t}}\bigg ) = 1- \Phi \bigg ( \frac{y+t\sigma ^{2}/2}{\sigma \sqrt{t}}\bigg ) \\&\quad \ge \frac{\sigma \sqrt{t}}{y+t\sigma ^{2}/2}\bigg [1- \frac{\sigma ^{2} t}{(y+t\sigma ^{2}/2)^{2}} \bigg ]\frac{1}{\sqrt{2\pi }} e^{-\frac{(y+t\sigma ^{2}/2)^{2}}{2\sigma ^{2} t}}. \end{aligned}$$

Moreover, we have

$$\begin{aligned} \lim _{y\rightarrow \infty } y \frac{\sigma \sqrt{t}}{y+t\sigma ^{2}/2}\bigg [1- \frac{\sigma ^{2} t}{(y+t\sigma ^{2}/2)^{2}} \bigg ]= \sigma \sqrt{t}. \end{aligned}$$

Therefore, for any $\varepsilon > 0$, there exists an $M>0$ so that

$$\begin{aligned} y \frac{\sigma \sqrt{t}}{y+t\sigma ^{2}/2}\bigg [1- \frac{\sigma ^{2} t}{(y+t\sigma ^{2}/2)^{2}} \bigg ] \ge \sigma \sqrt{t} (1-\varepsilon )\quad \text { for all } y\ge M. \end{aligned}$$

Then we can compute

$$\begin{aligned}&\int _{0}^{\infty } y e^{y} \Phi \bigg ( \frac{-y-t\sigma ^{2}/2}{\sigma \sqrt{t}}\bigg ) \mathrm dy\\&\quad \ge \int _{M}^{\infty } y e^{y} \Phi \bigg ( \frac{-y-t\sigma ^{2}/2}{\sigma \sqrt{t}}\bigg ) \mathrm dy \\&\quad \ge \int _{M}^{\infty } y e^{y} \frac{\sigma \sqrt{t}}{y+t\sigma ^{2}/2}\bigg [1- \frac{\sigma ^{2} t}{(y+t\sigma ^{2}/2)^{2}} \bigg ]\frac{1}{\sqrt{2\pi }} e^{-\frac{(y+t\sigma ^{2}/2)^{2}}{2\sigma ^{2} t}}\mathrm dy \\&\quad \ge \int _{0}^{\infty }\sigma \sqrt{t} (1-\varepsilon ) \frac{1}{\sqrt{2\pi }} e^{y }e^{-\frac{(y+t\sigma ^{2}/2)^{2}}{2\sigma ^{2} t}}\mathrm dy \\&\qquad - \int _{0}^{M}\sigma \sqrt{t} (1-\varepsilon ) \frac{1}{\sqrt{2\pi }} e^{y }e^{-\frac{(y+t\sigma ^{2}/2)^{2}}{2\sigma ^{2} t}}\mathrm dy\\&\quad \ge \sigma \sqrt{t} (1-\varepsilon )\sigma \sqrt{t} \Phi (\sigma \sqrt{t}/2)- \sigma \sqrt{t} (1-\varepsilon ) \frac{M e^{M}}{\sqrt{2\pi }}. \end{aligned}$$

Plugging this estimation into (6.13) gives

$$\begin{aligned} {\mathbb {E}}[\phi (t)]&\le \sigma ^{2} t \Phi (\sigma \sqrt{t}/2) +\frac{\sqrt{2t}\sigma e^{-\frac{\sigma ^{2}t}{8}}}{\sqrt{\pi }}- \sigma \sqrt{t} (1-\varepsilon )\sigma \sqrt{t} \Phi (\sigma \sqrt{t}/2)\\&\quad + \sigma \sqrt{t} (1-\varepsilon ) \frac{M e^{M}}{\sqrt{2\pi }} \\&= \sigma ^{2} t \Phi (\sigma \sqrt{t}/2) \varepsilon +\frac{\sqrt{2t}\sigma e^{-\frac{\sigma ^{2}t}{8}}}{\sqrt{\pi }}+ \sigma \sqrt{t} (1-\varepsilon ) \frac{M e^{M}}{\sqrt{2\pi }}. \end{aligned}$$

Hence, we have

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t}{\mathbb {E}}[L_{a_{*}}(t)] = \limsup _{t\rightarrow \infty } \frac{1}{t}{\mathbb {E}}[ a_{*} \phi (t)] \le a_{*}\sigma ^{2}\varepsilon . \end{aligned}$$

(6.14)

Now combining (6.12) and (6.14) yields

$$\begin{aligned} \liminf _{t\rightarrow \infty } {\mathbb {E}}\bigg [ \frac{1}{t} \int _{0}^{t} h(X(s)) \mathrm ds -c_{2}L_{a_{*}}(t) \bigg ] \ge \lambda - c_{2} a_{*}\sigma ^{2}\varepsilon . \end{aligned}$$

Since $\varepsilon > 0$ is arbitrary, it follows that

$$\begin{aligned} \liminf _{t\rightarrow \infty } {\mathbb {E}}\bigg [ \frac{1}{t} \int _{0}^{t} h(X(s)) \mathrm ds -c_{2}L_{a_{*}}(t) \bigg ] \ge \lambda . \end{aligned}$$

This, together with (6.11), implies that the policy $L_{a_{*}}$ of (6.10) has a long-term average reward of $\lambda$. The proof is concluded. $\square$

7 A Direct Solution Approach

In the previous sections, we obtained the solution to the ergodic two-sided singular control problem (2.3) via the vanishing discount method. A critical condition for this approach is that we need to first solve the discounted problem (2.6). In this section, we provide a direct solution approach to the problem (2.3).

Let us briefly explain the strategy on how to derive $\lambda _{0}$ of (2.3). First we focus on a class of policies that keeps the process in the interval [a, b] . The proof of Corollary 3.5 shows that the long-term average reward for such a policy is equal to $\lambda (a, b)$ of (3.8). Next we impose conditions so that $\lambda (a, b)$ achieves its maximum value $\lambda _{*} = \lambda (a_{*}, b_{*})$ at a pair $0< a_{*}< b_{*}< \infty$. The maximizing pair $(a_{*}, b_{*})$ further allows us to derive a $C^{2}$ solution to the HJB equation (3.1). This, together with the verification theorem (Theorem 3.1), reveals that $\lambda _{0} = \lambda _{*}$ and the $(a_{*}, b_{*})$-reflection policy is an optimal policy.

This approach is motivated by the recent paper [1], which solves an ergodic two-sided singular control problem for general one-dimensional diffusion processes. Note that the setups in Alvarez [1] are different from ours. In particular, the cost rates associated with the singular controls are all positive in Alvarez [1]. By contrast, our formulation in (2.3) has mixed signs for the singular controls $\eta$ and $\xi$. We also note that Theorem 2.5 in Alvarez [1] only proves that the $(a_{*}, b_{*})$-reflection policy is optimal in the class of two-point reflection policies. Here we observe that the $(a_{*}, b_{*})$-reflection policy is optimal among all admissible controls by the verification theorem.

Recall from the proof of Corollary 3.5 that the long-term average reward for the (a, b)-reflection policy is equal to $\lambda (a, b)$ of (3.8). Now we wish to maximize the long-term average reward $\lambda (a, b)$. First, detailed computations reveal that

$$\begin{aligned} \frac{\partial }{\partial a} \lambda (a, b)&= \frac{m(a)}{M[a, b]} [ \lambda (a, b)- \pi _{2}(a)], \\ \frac{\partial }{\partial b} \lambda (a, b)&= \frac{m(b)}{M[a, b]} [\pi _{1}(b) -\lambda (a, b) ]. \end{aligned}$$

where

$$\begin{aligned} \pi _{1}(x) = h(x) + c_{1} \mu (x), \quad \text { and }\quad \pi _{2}(x) = h(x) + c_{2} \mu (x). \end{aligned}$$

(7.1)

Therefore the first order optimality condition says that a maximizing pair $a_{*} < b_{*}$ must satisfy

$$\begin{aligned} \lambda (a_{*}, b_{*} ) = \pi _{1}(b_{*}) = \pi _{2} (a_{*}). \end{aligned}$$

(7.2)

Furthermore, (7.2) is equivalent to

$$\begin{aligned}&\int _{a_{*}}^{b_{*}} (\pi _{2}(x) - \pi _{2}(a_{*})) m(x) \mathrm dx + \frac{c_{1} - c_{2}}{2 s(b_{*})} =0, \end{aligned}$$

(7.3)

$$\begin{aligned}&\int _{a_{*}}^{b_{*}} (\pi _{1}(x) - \pi _{1}(b_{*})) m(x) \mathrm dx + \frac{c_{1} - c_{2}}{2 s(a_{*})}=0. \end{aligned}$$

(7.4)

To see this, we note that using the definition of $\lambda (a, b)$ in (3.8), we can write

$$\begin{aligned}&\frac{\partial }{\partial b} \lambda (a, b) = \frac{m(b)}{M[a, b]} [\pi _{1}(b) -\lambda (a, b) ] \\&\quad = \frac{m(b)}{M^{2}[a, b]} \bigg (\int _{a}^{b} \pi _{1}(b) m(x) \mathrm dx - \int _{a}^{b} h(x) m(x) \mathrm dx - \frac{c_{1}}{2 s(b) } + \frac{c_{2}}{ 2 s(a)} \bigg )\\&\quad = \frac{m(b)}{M^{2}[a, b]} \bigg (\int _{a}^{b}( \pi _{1}(b) - \pi _{1}(x) ) m(x) \mathrm dx + \int _{a}^{b} c_{1} \mu (x) m(x) \mathrm dx - \frac{c_{1}}{2 s(b) } + \frac{c_{2}}{ 2 s(a)} \bigg )\\&\quad = \frac{m(b)}{M^{2}[a, b]} \bigg (\int _{a}^{b}( \pi _{1}(b) - \pi _{1}(x) ) m(x) \mathrm dx + \frac{c_{2} - c_{1}}{ 2 s(a) } \bigg ). \end{aligned}$$

This gives the equivalence between $\lambda (a_{*}, b_{*} ) = \pi _{1}(b_{*})$ and (7.4). The equivalence between $\lambda (a_{*}, b_{*} ) = \pi _{2}(a_{*})$ and (7.3) can be established in a similar fashion.

To show that the first order condition (7.2) or equivalently the system of equations (7.3)–(7.4) has a solution, we impose the following conditions:

Assumption 7.1

• (i) The functions h and $\mu$ are continuously differentiable with $h'(x) > 0$ for all $x >0$. In addition, $h(0) = \mu (0) =0$.

• (ii) For $i =1,2$, there exists an ${{\hat{x}}}_{i} > 0$ such that $\pi _{i} (x)$ is strictly increasing on $(0, {{\hat{x}}}_{i})$ and strictly decreasing on $[{{\hat{x}}}_{i}, \infty )$. In addition $\lim _{x\rightarrow \infty } \pi _{1}(x) < 0$. Consequently, there exists a $b_{0} > {{\hat{x}}}_{1}$ such that $\pi _{1} (b_{0}) =0$.

• (iii) It holds true that

  $$\begin{aligned} \liminf _{a\downarrow 0} \bigg [ \int _{0}^{b_{0}}[\pi _{1}(y) - \pi _{1}(b_{0})] m(y)\mathrm dy + \frac{c_{1} - c_{2}}{2s(a)}\bigg ] > 0. \end{aligned}$$

  (7.5)

Remark 7.2

We remark that Assumption 7.1 (i) is standard in the literature of singular controls; see, for example, [1, 3] and [26]. Condition (ii) is motivated by similar conditions in Alvarez [1] and Weerasinghe [26]. In addition, these conditions are satisfied under the setup in Guo and Pham [8] as well. Condition (iii) is a technical one and it guarantees the existence of an optimizing pair $0< a_{*}< b_{*} < \infty$ satisfying the system of equations (7.3)–(7.4); see the proof of Proposition 7.4.

Remark 7.3

We also note that the extreme points ${{\hat{x}}}_{2}, {{\hat{x}}}_{1}$ in Assumption 7.1 must satisfy ${{\hat{x}}}_{2} < {{\hat{x}}}_{1}$. Suppose on the contrary that ${{\hat{x}}}_{1} \le {{\hat{x}}}_{2}$. Then since $\pi _{1}$ achieves its maximum at ${{\hat{x}}}_{1}$ and $\pi _{2}$ is strictly increasing on $(0, {{\hat{x}}}_{2})$, we have

$$\begin{aligned} \pi _{1}' ({{\hat{x}}}_{1} ) = h'({{\hat{x}}}_{1} ) + c_{1} \mu '({{\hat{x}}}_{1}) =0,\quad \text { and } \quad \pi _{2}' ({{\hat{x}}}_{1} ) = h'({{\hat{x}}}_{1} ) + c_{2} \mu '({{\hat{x}}}_{1}) \ge 0. \end{aligned}$$

(7.6)

On the other hand, Assumption 7.1 (i) says that $h'({{\hat{x}}}_{1}) > 0$. This, together with fact that $0< c_{1}< c_{2} < \infty$, implies that

$$\begin{aligned} \pi _{2}' ({{\hat{x}}}_{1} ) = h'({{\hat{x}}}_{1} ) + c_{2} \mu '({{\hat{x}}}_{1}) = h'({{\hat{x}}}_{1} ) - c_{2} \frac{h'({{\hat{x}}}_{1} ) }{c_{1}} = - \frac{c_{2} - c_{1}}{ c_{1}} h'({{\hat{x}}}_{1} ) < 0; \end{aligned}$$

resulting in a contradiction to (7.6).

Proposition 7.4

Let Assumption 7.1 hold. Then there exists a unique pair $0< a_{*}< b_{*} < \infty$ satisfying the system of equations (7.3)–(7.4).

Proof

Since ${{\hat{x}}}_{2} < {{\hat{x}}}_{1}$ thanks to Remark 7.3, we only need to consider two cases: $\pi _{2} ({{\hat{x}}}_{2}) \ge \pi _{1} ({{\hat{x}}}_{1})$ and $\pi _{2} ({{\hat{x}}}_{2}) < \pi _{1} ({{\hat{x}}}_{1})$.

Case (i): $\pi _{2} ({{\hat{x}}}_{2}) \ge \pi _{1} ({{\hat{x}}}_{1})$. In this case, thanks to Assumption 7.1, there exists a $y_{1} \in (0, {{\hat{x}}}_{2}]$ such that $\pi _{2}(y_{1} ) = \pi _{1} ({{\hat{x}}}_{1})$. In view of Remark 7.3, we have $y_{1} \le {{\hat{x}}}_{2} < {{\hat{x}}}_{1}$. In addition, Assumption 7.1 also implies that for any $a\in [0, y_{1}]$, there exists a unique $b_{a} \in [{{\hat{x}}}_{1}, b_{0})$ such that $\pi _{1}(b_{a}) = \pi _{2}(a)$. Consequently we can consider the function

$$\begin{aligned} \ell (a): = \int _{a}^{b_{a}} h(x) m(x) \mathrm dx - \pi _{1} (b_{a}) M[a, b_{a}] + \frac{c_{1}}{ 2 s(b_{a})} - \frac{c_{2}}{2 s(a)}, \quad a\in [0, y_{1}].\nonumber \\ \end{aligned}$$

(7.7)

Using (3.7) and the fact that $\pi _{1}(b_{a}) = \pi _{2}(a)$, we can rewrite $\ell (a)$ as

$$\begin{aligned} \ell (a)= & {} \int _{a}^{b_{a}} [\pi _{2}(x) - \pi _{2}(a)] m(x) \mathrm dx + \frac{c_{1}-c_{2}}{2s(b_{a})} \\= & {} \int _{a}^{b_{a}} [\pi _{1}(x) - \pi _{1}(b_{a})] m(x) \mathrm dx + \frac{c_{1}-c_{2}}{2s({a})}. \end{aligned}$$

Since $b_{y_{1}}= {{\hat{x}}}_{1}$, we have

$$\begin{aligned} \ell (y_{1})&= \int _{y_{1}}^{{{\hat{x}}}_{1}} [\pi _{1} (x) - \pi _{1}({{\hat{x}}}_{1})]m(x)\mathrm dx + \frac{c_{1} - c_{2}}{2 s(y_{1})}. \end{aligned}$$

Recall from Assumption 7.1 that $\pi _{1}$ is strictly increasing on $(0, {{\hat{x}}}_{1})$ and $c_{1} < c_{2}$. Hence it follows that $\ell (y_{1}) < 0.$

Next we show that $\ell$ is decreasing on $[0, y_{1}]$ and hence $\ell (0+): = \lim _{a\downarrow 0} \ell (a)$ exists. To this end, we consider $0\le a_{1} < a_{2} \le y_{1}$ and denote $b_{i} = b_{a_{i}}$ for $i= 1, 2$. Since $\pi _{1} (b_{1}) = \pi _{2} (a_{1}) < \pi _{2}(a_{2}) = \pi _{1}(b_{2})$ and $\pi _{1}$ is decreasing on $[{{\hat{x}}}_{1}, \infty )$, it follows that ${{\hat{x}}}_{1} \le b_{2} < b_{1}$. As a result, we can compute

$$\begin{aligned} \ell (a_{1}) -\ell (a_{2})&= \int _{a_{1}}^{a_{2}} h(x) m(x)\mathrm dx + \int _{b_{2}}^{b_{1}} h(x) m(x)\mathrm dx \\&\quad - \pi _{1}(b_{1}) M[a_{1}, b_{1}] + \pi _{1}(b_{2}) M[a_{2}, b_{2}] \\&\quad + \frac{c_{1}}{2s(b_{1})} - \frac{c_{2}}{2s(a_{1})}- \frac{c_{1}}{2s(b_{2})} + \frac{c_{2}}{2s(a_{2})} \\&= \int _{a_{1}}^{a_{2}} [\pi _{2}(x) - \pi _{2}(a_{1})] m(x) \mathrm dx + \int _{b_{2}}^{b_{1}} [\pi _{1}(x)- \pi _{1}(b_{1})] m(x)\mathrm dx\\&\quad + [\pi _{1}(b_{2}) - \pi _{1}(b_{1}) ] M[a_{2}, b_{2}]. \end{aligned}$$

Thanks to Assumption 7.1, the terms $\pi _{2}(x) - \pi _{2}(a_{1})$, $\pi _{1}(x)- \pi _{1}(b_{1})$, and $\pi _{1}(b_{2}) - \pi _{1}(b_{1})$ are all positive. Therefore $\ell (a_{1}) -\ell (a_{2}) > 0$ as desired.

Using Assumption 7.1 (iii), we have $\ell (0+) > 0$. Since the function $\ell$ is also continuous, there exists a unique $a_{*}\in (0, y_{1}]$ such that $\ell (a_{*}) =0$. Denote $b_{*} = b_{a_{*}} \in [{{\hat{x}}}_{1}, b_{0})$. Then

$$\begin{aligned} 0&= \ell (a_{*}) = \int _{a_{*}}^{b_{*}} h(x) m(x) \mathrm dx - \pi _{1} (b_{*}) M[a_{*}, b_{*}] + \frac{c_{1}}{ 2 s(b_{*})} - \frac{c_{2}}{2 s(a_{*})} \\&= \int _{a_{*}}^{b_{*}} [\pi _{2} (x) - \pi _{2} (a_{*}) ] m(x) \mathrm dx - \frac{c_{2}}{2s(b_{*})} + \frac{c_{2}}{2s(a_{*})} + \frac{c_{1}}{ 2 s(b_{*})} - \frac{c_{2}}{2 s(a_{*})} \\&= \int _{a_{*}}^{b_{*}} [\pi _{2} (x) - \pi _{2} (a_{*}) ] m(x) \mathrm dx + \frac{c_{1} - c_{2}}{2 s(b_{*})}. \end{aligned}$$

This gives (7.3). Similar calculations reveal that

$$\begin{aligned} 0&= \ell (a_{*}) = \int _{a_{*}}^{b_{*}} [\pi _{1} (x) - \pi _{1} (b_{*}) ] m(x) \mathrm dx + \frac{c_{1} - c_{2}}{2 s(a_{*})}, \end{aligned}$$

establishing (7.4).

Case (ii): $\pi _{2} ({{\hat{x}}}_{2}) < \pi _{1} ({{\hat{x}}}_{1})$. In this case, for any $a\in [0, {{\hat{x}}}_{2}]$, there exists a $b_{a} \in [{{\hat{x}}}_{1}, \infty )$ such that $\pi _{2}(a) = \pi _{1}(b_{a})$. Consequently we can define the function $\ell (a)$ as in (7.7) for all $a\in [0, {{\hat{x}}}_{2}]$. Let $y_{2} \in [{{\hat{x}}}_{1}, \infty )$ be such that $\pi _{2}({{\hat{x}}}_{2}) = \pi _{1}(y_{2})$. Then we have $b_{{{\hat{x}}}_{2}} = y_{2}$ and

$$\begin{aligned} \ell ({{\hat{x}}}_{2})&= \int _{{{\hat{x}}}_{2}}^{y_{2}} [ \pi _{2}(x) - \pi _{2}({{\hat{x}}}_{2})] m(x) \mathrm dx + \frac{c_{1} - c_{2}}{2 s(y_{2})} < 0. \end{aligned}$$

The rest of the proof is very similar to that of Case (i). We shall omit the details for brevity. $\square$

Proposition 7.5

Let Assumption  7.1 hold. Then there exist a function $u \in C^{2}([0, \infty ))$ and a positive number $\lambda _{*}$ satisfying the HJB equation (3.1).

Proof

Let $0< a_{*}< b_{*} < \infty$ be as in Proposition 7.4 and define

$$\begin{aligned} \lambda _{*}: = \frac{1}{M[a_{*}, b_{*}]} \bigg [\int _{a_{*}}^{b_{*}} h(x) m(x) \mathrm dx + \frac{c_{1}}{2s(b_{*})} - \frac{c_{2}}{2s(a_{*})} \bigg ]. \end{aligned}$$

(7.8)

In addition, we consider the function

$$\begin{aligned} u(x) = {\left\{ \begin{array}{ll} c_{1} x+ \int _{a_{*}}^{x} 2s(u) \int _{u}^{b_{*}}[\pi _{1} (y) - \lambda _{*}] m(y) \mathrm dy\mathrm du, &{}\quad x\in [a_{*}, b_{*}], \\ c_{1} (x-b_{*}) + u(b_{*}), &{}\quad x > b_{*}, \\ c_{2} (x-a_{*}) + u(a_{*}), &{}\quad x < a_{*}. \end{array}\right. } \end{aligned}$$

(7.9)

We next verify that the pair $(u, \lambda _{*})$ satisfies (3.1). First it is obvious that u is continuously differentiable and satisfies $u'(x) = c_{1}$ for $x \ge b_{*}$ and $u'(x) = c_{2}$ for $x \le a_{*}$.

Next we show that u is $C^{2}$ and satisfies ${\mathcal {L}}u( x) + h(x)-\lambda _{*}=0$ for $x\in (a_{*}, b_{*})$. To this end, we compute for $x\in (a_{*}, b_{*})$:

$$\begin{aligned} u'(x)&= c_{1}+ 2 s(x) \int _{x}^{b_{*}}[ \pi _{1} (y) - \lambda _{*}] m(y) \mathrm dy, \\ u''(x)&= -4s(x) \frac{\mu (x)}{\sigma ^{2}(x)} \int _{x}^{b_{*}}[ \pi _{1} (y) - \lambda _{*}] m(y) \mathrm dy + 2 s(x) [- \pi _{1} (x) + \lambda _{*}]m(x). \end{aligned}$$

Consequently it follows that u satisfies ${\mathcal {L}}u( x) + h(x)-\lambda _{*} =0$ for $x\in (a_{*}, b_{*})$.

To show that u is $C^{2}$, it suffices to show that u is $C^{2}$ at the points $a_{*}$ and $b_{*}$. Recall that $a_{*} < b_{*}$ and $\lambda _{*}$ satisfy (7.2) thanks to Proposition 7.4. Therefore it follows immediately that $u'(b_{*}-) = c_{1}$ and $u''(b_{*}-) = 0$. In addition, we can use (7.4) to compute

$$\begin{aligned} u'(a_{*}+) =c_{1}+ 2 s(a_{*}) \int _{a_{*}}^{b_{*}}[ \pi _{1} (y) - \lambda _{*}] m(y) \mathrm dy = c_{1} + 2 s(a_{*}) \frac{c_{2}- c_{1}}{2s(a_{*})} = c_{2}, \end{aligned}$$

and

$$\begin{aligned} u''(a_{*}+)&= -4s(a_{*}) \frac{\mu (a_{*})}{\sigma ^{2}(a_{*})} \int _{a_{*}}^{b_{*}}[ \pi _{1} (y) - \lambda _{*}] m(y) \mathrm dy + 2 s(a_{*}) [- \pi _{1} (a_{*}) + \lambda _{*}]m(a_{*}) \\&= -4s(a_{*}) \frac{\mu (a_{*})}{\sigma ^{2}(a_{*})} \cdot \frac{c_{2}- c_{1}}{2s(a_{*})} + \frac{2}{\sigma ^{2}(a_{*})} [- \pi _{1} (a_{*}) + \lambda _{*}]\\&= -\frac{2}{\sigma ^{2}(a_{*})}[(c_{2}- c_{1} ) \mu (a_{*}) + \pi _{1} (a_{*}) - \lambda _{*}]\\&=0, \end{aligned}$$

where the last equality follows from (7.2). Therefore we have shown that $u\in C^{2}((0,\infty ))$.

Recall that the function $\pi _{1}$ is decreasing on $[{{\hat{x}}}_{1}, \infty )$ and $b_{*} \in [{{\hat{x}}}_{1}, \infty )$ by the proof of Proposition 7.4. Therefore for any $x\ge b_{*}$,

$$\begin{aligned} {\mathcal {L}}u( x) + h(x)-\lambda _{*} = c_{1} \mu (x) + h(x) - \lambda _{*} = \pi _{1}(x) -\lambda _{*} \le \pi _{1}(b_{*}) -\lambda _{*} =0. \end{aligned}$$

Similar argument reveals that ${\mathcal {L}}u( x) + h(x)-\lambda _{*} \le 0$ for all $x\in a_{*}$.

It remains to show that $u'(x) \in [c_{1}, c_{2}]$ for $x\in (a_{*}, b_{*})$. To this end, we first consider the function

$$\begin{aligned} k(x): = \int _{x}^{b_{*}}[ \pi _{1} (y) - \lambda _{*}] m(y) \mathrm dy, \quad x\in [a_{*}, b_{*}]. \end{aligned}$$

We claim that k is nonnegative, which, in turn, implies that $v'(x) = c_{1} + 2 s(x) k(x) \ge c_{1}$ on $[a_{*}, b_{*}]$. To see the claim, we consider two cases. (i) If $\pi _{1} (y) \ge \lambda _{*}$ for all $y\in [a_{*}, b_{*}]$, then $k(x) \ge 0$ for all $x\in [a_{*}, b_{*}]$. (ii) Otherwise, since $a_{*} \le {{\hat{x}}}_{2} < {{\hat{x}}}_{1}$, $b_{*} > {{\hat{x}}}_{1}$, the monotonicity of $\pi _{1}$ implies that there exists a $y_{1} \in (a_{*}, b_{*})$ so that $\pi _{1} (y) - \lambda _{*}$ is negative on $[a_{*}, y_{1})$ and positive on $(y_{1}, b_{*})$. Consequently the function k is increasing on $[a_{*}, y_{1})$ and then decreasing on $(y_{1}, b_{*})$. On the other hand, we have $k(b_{*}) =0$, and thanks to (7.4), $k(a_{*}) = \frac{c_{2}-c_{1}}{2 s(a_{*})} > 0$. Therefore we again have the claim that $k(x) \ge 0$ for all $x\in [a_{*}, b_{*}]$.

Finally, to show that $v'(x) \le c_{2}$ on $[a_{*}, b_{*}]$, we consider the function

$$\begin{aligned} \rho (x): = k(x) + \frac{c_{1}-c_{2}}{2s(x)}, \quad x\in [a_{*}, b_{*}]. \end{aligned}$$

Note that $\rho (b_{*}) = \frac{c_{1}-c_{2}}{2s(b_{*})} < 0$. In addition, $\rho (a_{*}) = \ell (a_{*}) =0$ thanks to the proof of Proposition 7.4. Next we compute

$$\begin{aligned} \rho '(x) = -(\pi _{1} (x) - \lambda _{*} ) m(x) + \frac{c_{1}-c_{2}}{2}\cdot \frac{2\mu (x) }{\sigma ^{2}(x) s(x)} = (\lambda _{*}-\pi _{2}(x)) m(x). \end{aligned}$$

As a result, if $\lambda _{*}-\pi _{2}(x) < 0$ for all $x\in [a_{*}, b_{*}]$, then $\rho (x) \le \rho (a_{*}) = 0$ for all $x\in [a_{*}, b_{*}]$. Otherwise, using the monotonicity assumption of $\pi _{2}$ in Assumption 7.1, there exists some $y_{2} \in (a_{*}, b_{*})$ so that $\lambda _{*}-\pi _{2}(x) <0$ for $x\in [a_{*}, y_{2})$ and $> 0$ for $x\in (y_{2}, b_{*}]$. This, in turn, implies that $\rho (x)$ is decreasing on $[a_{*}, y_{2})$ and increasing on $(y_{2}, b_{*}]$. In such a case, we still have $\rho (x) \le 0$ for all $x\in [a_{*}, b_{*}]$. Then it follows that $2 s(x) k(x) \le c_{2}- c_{1}$ and hence $v'(x) = c_{1} + 2 s(x) k(x) \le c_{2}$.

To summarize, we have shown that the function u of (7.9) is $C^{2}$ and satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {L}}u(x) + h(x) - \lambda _{*} =0, \ \ c_{1} \le u'(x) \le c_{2}, &{}\quad x\in (a_{*}, b_{*}), \\ {\mathcal {L}}u(x) + h(x) - \lambda _{*} \le 0, \ \ u'(x) = c_{2}, &{}\quad x\le a_{*}, \\ {\mathcal {L}}u(x) + h(x) - \lambda _{*} \le 0, \ \ u'(x) = c_{1}, &{}\quad x\ge b_{*}. \end{array}\right. } \end{aligned}$$

In particular, $(u, \lambda _{*})$ satisfies the HJB equation (3.1). This concludes the proof. $\square$

Now we present the main result of this section.

Theorem 7.6

Let Assumption 7.1 hold. Then there exist $0< a_{*}< b_{*} < \infty$ so that the $(a_{*}, b_{*})$-reflection policy is optimal for problem (2.3). In addition, $\lambda _{0} = \lambda _{*}$, where $\lambda _{*}$ is defined in (7.8).

Proof

Since $(u, \lambda _{*})$ is a solution to the HJB equation, where the function u of (7.9) is bounded from below, it follows from Theorem 3.1 that $\lambda _{0} \le \lambda _{*}$. Furthermore, the proof of Corollary 3.5 says that the long-term average reward of the $(a_{*}, b_{*})$-policy is equal to $\lambda _{*}$ and therefore optimal. The proof is complete. $\square$

Example 7.7

In this example, we consider the ergodic two-sided singular control problem for the Verhulst-Pearl diffusion:

$$\begin{aligned} \mathrm dX(t) = \mu X(t) (1 - \gamma X(t)) \mathrm dt+ \sigma X(t) \mathrm dW( t)+ \mathrm d\xi (t) -\mathrm d\eta (t), \end{aligned}$$

where $\mu > 0$ is the per-capita growth rate, $\frac{1}{\gamma } > 0$ is the carrying capacity, and $\sigma ^{2}>0$ is the variance parameter measuring the fluctuations in the per-capita growth rate. The singular control $\varphi : = \xi -\eta$ is as in Sect. 2. Here, we can regard $\xi (t)$ and $\eta (t)$ as the cumulative renewing and harvesting amount up to time t, respectively. The scale and speed densities are

$$\begin{aligned} s(x) = x^{-\alpha } e^{\gamma \alpha (x-1)}, \quad m(x) = \frac{1}{\sigma ^{2}} x^{\alpha -2} e^{-\gamma \alpha (x-1)}, \quad x >0, \end{aligned}$$

where $\alpha =\frac{2\mu }{\sigma ^{2}}$. Detailed computations using the criteria given in Chapter 15 of Karlin and Taylor [17] reveal that both 0 and $\infty$ are natural boundary points.

For positive constants $c_{1} < c_{2}$ and a nonnegative function h satisfying Assumption 6.2 (i) and (ii), we consider the problem

$$\begin{aligned} \lambda _{0}: = \sup _{\varphi (\cdot )\in {\mathscr {A}}_{x}} \liminf _{T\rightarrow \infty } \frac{1}{T} {\mathbb {E}}_{x}\bigg [ \int _{0}^{T} h(X(t))\mathrm dt + c_{1}\eta ( T) - c_{2} \xi (T)\bigg ], \end{aligned}$$

(7.10)

where ${\mathscr {A}}_{x}$ is the set of admissible controls as defined in (2.4).

We now claim that Assumption 7.1 is satisfied and hence in view of Theorem 7.6, the optimal value $\lambda _{0}$ of (7.10) is achieved by the $(a_{*}, b_{*})$-reflection policy, where $0< a_{*}< b_{*} < \infty$. Assumption 7.1 (i) is obviously satisfied. We now verify Assumption 7.1 (ii). For $i=1,2$, we have $\pi _{i} (x) = h(x) +c_{i} \mu x(1-\gamma x)$ and hence

$$\begin{aligned} \pi '_{i}(x) = h'(x) +c_{i}\mu -2c_{i}\mu \gamma x,\ \quad x\ge 0. \end{aligned}$$

Noting that $h'(x) > 0$ and $c_{i}, \mu > 0$, we see from the above equation that $\pi '_{i}(x) > 0$ for $x> 0$ in a neighborhood of 0. Since h satisfies Assumption 6.2 (i) and (ii), it follows that there exists some positive number M so that $h'(x) < 1$ for all $x\ge M$. Thus $\lim _{x\rightarrow \infty }\pi '_{i} (x) = -\infty$. Then the continuity of $\pi '_{i}(x)$ implies that there exists a ${{\hat{x}}}_{i}>0$ so that $\pi '_{i}({{\hat{x}}}_{i})=0$. Furthermore, since h is strictly concave, $h'(x)$ is deceasing. Therefore $\pi '_{i}(x)< 0$ for all $x> {{\hat{x}}}_{i}$. Hence $\pi _{i}$ is first increasing on $[0, {{\hat{x}}}_{i})$ and then decreasing on $[{{\hat{x}}}_{i},\infty )$. On the other hand, using Assumption 6.2 (ii), we have $\lim _{x\rightarrow \infty } \pi _{i}(x)=-\infty$ and hence there exists a $b_{0} > {{\hat{x}}}_{1}$ so that $\pi _{1}(b_{0}) =0$. Assumption 7.1 (ii) is verified.

Finally, note that the arguments in the previous paragraph also reveal that $\pi _{1}$ is strictly positive on $(0, b_{0})$. This, together with facts that $\pi _{1}(b_{0}) =0$ and $\lim _{a\downarrow 0} \frac{1}{s(a)} = 0$, leads to (7.5) and hence Assumption 7.1 (iii) is in force. The proof is complete.