Generalized Penalty Method for Elliptic Variational–Hemivariational Inequalities

Abstract

We consider an elliptic variational–hemivariational inequality with constraints in a reflexive Banach space, denoted $\mathcal{P}$, to which we associate a sequence of inequalities $\{\mathcal{P}_n\}$. For each $n\in \mathbb {N}$, $\mathcal{P}_n$ is a variational–hemivariational inequality without constraints, governed by a penalty parameter $\lambda _n$ and an operator $P_n$. Such inequalities are more general than the penalty inequalities usually considered in literature which are constructed by using a fixed penalty operator associated to the set of constraints of $\mathcal{P}$. We provide the unique solvability of inequality $\mathcal{P}_n$. Then, under appropriate conditions on operators $P_n$, we state and prove the convergence of the solution of $\mathcal{P}_n$ to the solution of $\mathcal{P}$. This convergence result extends the results previously obtained in the literature. Its generality allows us to apply it in various situations which we present as examples and particular cases. Finally, we consider a variational–hemivariational inequality with unilateral constraints which arises in Contact Mechanics. We illustrate the applicability of our abstract convergence result in the study of this inequality and provide the corresponding mechanical interpretations.

1 Introduction

Variational and hemivariational inequalities represent a powerful tool in the study of a large number of nonlinear boundary value problems. The theory of variational inequalities was developed in early sixty’s, by using arguments of monotonicity and convexity, including properties of the subdifferential for convex functions. In contrast, the analysis of hemivariational inequalities uses as main ingredient the properties of the subdifferential in the sense of Clarke, defined for locally Lipschitz functions which may be nonconvex. Hemivariational inequalities were first introduced in early eighty’s by Panagiotopoulos in the context of applications in engineering problems. Studies of variational and hemivariational inequalities can be found in monographs [1, 7, 8, 18, 21, 22] and research papers [2, 11, 16, 17, 20, 23, 30,31,32,33,34,35,36,37,38, 40, 42].

Variational–hemivariational inequalities represent a special class of inequalities, governed by both convex and nonconvex functions. A recent reference in the field is the monograph [28]. There, existence, uniqueness and convergence results have been obtained for the elliptic, history-dependent and evolutionary cases. These results have been used in the study of various mathematical models which describe the contact between a deformable body and a foundation. Recently, a considerable effort was done to derive error estimates for discrete scheme associated to variational–hemivariational inequalities. At the best of our knowledge, paper [11] represents the first paper that provides an optimal order error estimate for the linear finite element method in solving hemivariational or variational–hemivariational inequalities. We refer the readers to [12, 13] for internal numerical approximations of variational–hemivariational inequalities, and [9] for both internal and external numerical approximations of such inequalities.

In this paper we consider the following inequality problem.

Problem

$\mathcal{P}$. Find an element $u\in K$ such that

$$\begin{aligned} \langle A u, v - u \rangle + \varphi (u, v) - \varphi (u, u) + j^0(u; v - u) \ge \langle f, v - u \rangle \qquad \forall \, v \in K. \end{aligned}$$

(1)

Here and everywhere in this paper X is a real reflexive Banach space, $\langle \cdot ,\cdot \rangle$ denotes the duality pairing between X and its dual $X^*$, $K\subset X$, $A :X \rightarrow X^*$, $\varphi :X \times X \rightarrow \mathbb {R}$, $j :X \rightarrow \mathbb {R}$ and $f\in X^*$. Moreover, $j^0(u;v)$ represents the generalized directional derivative of j at the point u in the direction v. Note that the function $\varphi (u, \cdot )$ is assumed to be convex for any $u\in X$ and the function j is locally Lipschitz and, in general, nonconvex. Therefore, (1) is a variational–hemivariational inequality and, since the data and the solution do not depend on the time variable, we sometimes refer to this inequality as an elliptic variational–hemivariational inequality.

The existence and uniqueness of the solution to the problem (1) was proved [19], based on arguments of multivalued pseudomonotone operators and the Banach fixed point theorem. The continuous dependence of the solution with respect to the data A, $\varphi$, j, f and K has been studied in [39, 41], where convergence results have been obtained, under various assumptions. A comprehensive reference on the numerical analysis Problem $\mathcal{P}$ is the survey paper [10].

Note that Problem $\mathcal{P}$ is governed by a set of constraints K. Therefore, for both theoretical and numerical reasons, it is useful to approximate it by using a penalty method. The classical penalty method aims to replace Problem $\mathcal{P}$ by a sequence of problems $\{\overline{\mathcal{P}}_n\}$ which, for every $n\in \mathbb {N}$, can be formulated as follows.

Problem

$\overline{\mathcal{P}}_n$. Find an element $\overline{u}_n\in X$ such that

$$\begin{aligned}&\langle A \overline{u}_n, v - \overline{u}_n \rangle + \frac{1}{\lambda _n} \langle P\overline{u}_n, v - \overline{u}_n \rangle + \varphi (\overline{u}_n,v) - \varphi (\overline{u}_n,\overline{u}_n)\nonumber \\&\quad + \, j^0(\overline{u}_n; v - \overline{u}_n) \ge \langle f, v - \overline{u}_n \rangle \qquad \forall \, v \in X. \end{aligned}$$

(2)

Note that Problem $\overline{\mathcal{P}}_n$ is formally obtained from Problem $\mathcal{P}$ by removing the constraint $u\in K$ and including a penalty term governed by a parameter $\lambda _n>0$ and an operator $P:X\rightarrow X^*$. Penalty methods have been used as an approximation tool to treat constraints in variational inequalities [8, 15, 26, 29] and variational–hemivariational inequalities [19, 28, 31]. In particular, the existence of a unique solution to Problem $\overline{\mathcal{P}}_n$ together with its convergence to the solution of Problem $\mathcal{P}$ as $\lambda _n\rightarrow 0$ was proved in [19, 28], under the assumption that P is a penalty operator of the set K, see Definition 7 below.

An extension of $\overline{\mathcal{P}}_n$ can be obtained by replacing in (2) the operator P with an operator $P_n:X\rightarrow X^*$ which depends on n. This problem can be stated as follows.

Problem

$\mathcal{P}_n$. Find an element $u_n\in X$ such that

$$\begin{aligned}&\langle A u_n, v - u_n \rangle + \frac{1}{\lambda _n} \langle P_nu_n, v - u_n \rangle + \varphi (u_n,v) - \varphi (u_n,u_n)\nonumber \\&\quad + \, j^0(u_n; v - u_n) \ge \langle f, v - u_n \rangle \qquad \forall \, v \in X. \end{aligned}$$

(3)

Note that Problem $\mathcal{P}_n$ is formally obtained from Problem $\mathcal{P}$ by removing the constraint $u\in K$ and including a penalty term governed by a parameter $\lambda _n>0$ and an operator $P_n:X\rightarrow X^*$ which, in contrast to (2), depends on n.

The aim of this paper is twofold. The first one is to prove the unique solvability of Problem $\mathcal{P}_n$ and the convergence of its solution to the solution of Problem $\mathcal{P}$. The main difficulty on this matter consists in constructing appropriate assumptions to establish a link between the operators $P_n$ and the set K, which guarantees the convergence $u_n\rightarrow u$ in X. Note that in the particular case of Problem $\overline{\mathcal{P}}_n$ this convergence follows from the assumption that P is a penalty operator of K, which represents a simple and elegant condition. Extending this condition to conditions which still guarantee the convergence when P is replaced by $P_n$ represents the first trait of novelty of this paper.

Our second aim is to illustrate some applications of the convergence result $u_n\rightarrow u$ in X. Note that this convergence extends the convergence result $\overline{u}_n\rightarrow u$ in X, obtained in [19, 28]. It shows that for n large enough, the solution of Problem $\mathcal{P}$ (with constraint) can be approximated by the solution of problem $\mathcal{P}_n$ (without constraint), which is more general than Problem $\mathcal{\overline{P}}_n$. The generality of our convergence result allows us to obtain various consequences which are new and interesting in their own. This represents the second trait of novelty of this paper.

The remainder of the paper is structured as follows. In Sect. 2 we introduce some preliminary material, and then we recall the existence and uniquenss result obtained in [19, 27]. In Sect. 3 we state and prove our main results, Theorems 9 and 10. The proofs are based on arguments of compactness, monotonicity and semicontinuity, combined with the properties of the Clarke subdifferential. In Sect. 4 we deduce some consequences of Theorems 9 and 10 that we present in a form of relevant particular cases. Finally, in Sect. 5 we illustrate the use of these theorems in the study of a variational–hemivariational inequalty which arises in Contact Mechanics and provide the corresponding mechanical interpretations.

2 Preliminaries

We start with some notation and preliminaries and refer the readers to [4,5,6, 14, 24, 43] for more details on the material presented below in this section. We use $\Vert \cdot \Vert _X$ and $\Vert \cdot \Vert _{X^*}$ for the norm on the spaces X and $X^*$, and $0_X$, $0_{X^*}$ for the zero element of X and $X^*$, respectively. All the limits, upper and lower limits below are considered as $n\rightarrow \infty$, even if we do not mention it explicitly. The symbols “$\rightharpoonup$” and “$\rightarrow$” denote the weak and the strong convergence in various spaces which will be specified.

For real valued functions defined on X we recall the following definitions.

Definition 1

A function $\varphi :X \rightarrow \mathbb {R}$ is lower semicontinuous (l.s.c.) if $x_n \rightarrow x$ in X implies $\liminf \varphi (x_n)\ge \varphi (x)$. A function $\varphi :X \rightarrow \mathbb {R}$ is weakly lower semicontinuous (weakly l.s.c.) if $x_n \rightharpoonup x$ in X implies $\liminf \varphi (x_n)\ge \varphi (x)$.

Definition 2

A function $j :X \rightarrow \mathbb {R}$ is said to be locally Lipschitz, if for every $x \in X$, there exist $U_x$, a neighborhood of x, and a constant $L_x>0$ such that $|j(y) - j(z)| \le L_x \Vert y - z \Vert _X$ for all y, $z \in U_x$. For such functions the generalized Clarke’s directional derivative of j at the point $x \in X$ in the direction $v \in X$ is defined by

$$\begin{aligned} j^{0}(x; v) = \limsup _{y \rightarrow x, \ \lambda \downarrow 0} \frac{j(y + \lambda v) - j(y)}{\lambda }. \end{aligned}$$

The generalized Clarke’s gradient (subdifferential) of j at x is a subset of the dual space $X^*$ given by

$$\begin{aligned} \partial j (x) = \{\, \zeta \in X^* \mid j^{0}(x; v) \ge {\langle \zeta , v \rangle } \quad \forall \, v \in X \, \}. \end{aligned}$$

The function j is said to be regular (in the sense of Clarke) at the point $x \in X$ if for all $v \in X$ the one-sided directional derivative $j' (x; v)$ exists and $j^0(x; v) = j'(x; v)$.

We shall use the following properties of the generalized directional derivative and the generalized gradient.

Proposition 3

Assume that $j :X \rightarrow \mathbb {R}$ is a locally Lipschitz function. Then the following hold:

• (i) For every $x \in X$, the function $X \ni v \mapsto j^0(x;v) \in \mathbb {R}$ is positively homogeneous and subadditive, i.e., $j^0(x; \lambda v) = \lambda j^0(x; v)$ for all $\lambda \ge 0$, $v\in X$ and $j^0 (x; v_1 + v_2) \le j^0(x; v_1) + j^0(x; v_2)$ for all $v_1$, $v_2 \in X$, respectively.

• (ii) For every $v \in X$, we have $j^0(x; v) = \max \, \{ \, \langle \xi , v \rangle \ :\ \xi \in \partial j(x) \, \}$.

Next, we proceed with some definitions for nonlinear operators.

Definition 4

An operator $A :X \rightarrow X^*$ is said to be:

• (a) monotone, if for all u, $v \in X$, we have $\langle Au - A v, u-v \rangle \ge 0$;

• (b) strongly monotone, if there exists $m_A > 0$ such that

  $$\begin{aligned} \langle Au - Av, u-v \rangle \ge m_A \Vert u - v \Vert _X^{2}, \quad \text{ for } \text{ all } \ u,\, v \in X; \end{aligned}$$

• (c) bounded, if A maps bounded sets of X into bounded sets of $X^*$;

• (d) pseudomonotone, if it is bounded and $u_n \rightarrow u$ weakly in X with

  $$\begin{aligned} \displaystyle \limsup \,\langle A u_n, u_n -u \rangle \le 0 \end{aligned}$$

  implies $\displaystyle \liminf \, \langle A u_n, u_n - v \rangle \ge \langle A u, u - v \rangle$ for all $v \in X$;

• (e) demicontinuous, if $u_n \rightarrow u$ in X implies $A u_n \rightarrow Au$ weakly in $X^*$.

We shall use the following results related to the pseudomonotonicity of operators.

Proposition 5

For a reflexive Banach space X the following statements hold.

• (a) If the operator $A:X \rightarrow X^*$ is bounded, demicontinuous and monotone, then A is pseudomonotone.

• (b) If A, $B :X \rightarrow X^*$ are pseudomonotone operators, then the sum $A+B :X \rightarrow X^*$ is pseudomonotone.

We turn now to the study of (1) and, to this end, we consider the following hypotheses on the data.

$$\begin{aligned}&K \ \text{ is } \text{ nonempty, } \text{ closed } \text{ and } \text{ convex } \text{ subset } \text{ of } \ X. \end{aligned}$$

(4)

$$\begin{aligned}&\left\{ \begin{array}{l}A :X \rightarrow X^* \ \text{ is } \text{ pseudomonotone } \text{ and }\\ \text{ strongly } \text{ monotone } \text{ with } \text{ constant }\ m_A>0. \end{array}\right. \end{aligned}$$

(5)

$$\begin{aligned}&\left\{ \begin{array}{l} \varphi :X \times X \rightarrow \mathbb {R}\ \text{ is } \text{ such } \text{ that }\\ \ \ \hbox {(a)} \ \varphi (\eta , \cdot ) :X \rightarrow \mathbb {R}\ \text{ is } \text{ convex } \text{ and } \text{ lower } \text{ semicontinuous },\\ \qquad \ \ \text{ for } \text{ all } \ \eta \in X. \\ \ \ \hbox {(b)} \ \text{ there } \text{ exists } \ \alpha _\varphi > 0 \ \text{ such } \text{ that } \\ \qquad \varphi (\eta _1, v_2) - \varphi (\eta _1, v_1) + \varphi (\eta _2, v_1) - \varphi (\eta _2, v_2)\\ \qquad \quad \le \alpha _\varphi \Vert \eta _1 - \eta _2 \Vert _X \, \Vert v_1 - v_2 \Vert _X,\ \ \ \ \text{ for } \text{ all } \ \eta _1, \eta _2, v_1, v_2 \in X. \end{array} \right. \end{aligned}$$

(6)

$$\begin{aligned}&\left\{ \begin{array}{l} j :X \rightarrow \mathbb {R}\ \text{ is } \text{ such } \text{ that }\\ \ \ \hbox { (a)} \ j \ \text{ is } \text{ locally } \text{ Lipschitz. } \\ \ \ \hbox { (b)} \ \Vert \xi \Vert _{X^*} \le c_0 + c_1 \, \Vert v \Vert _X \ \text{ for } \text{ all } \ v \in X,\ \xi \in \partial j(v), \ \text{ with } \ c_0, c_1 \ge 0. \\ \ \ \hbox { (c)} \ \text{ there } \text{ exists } \ \alpha _j > 0 \ \text{ such } \text{ that } \\ \qquad j^0(v_1; v_2 - v_1) + j^0(v_2; v_1 - v_2) \le \alpha _j \, \Vert v_1 - v_2 \Vert _X^2, \ \text{ for } \text{ all } \ v_1, v_2 \in X. \end{array} \right. \end{aligned}$$

(7)

$$\begin{aligned}&\alpha _\varphi + \alpha _j < m_A. \end{aligned}$$

(8)

$$\begin{aligned}&f \in X^*. \end{aligned}$$

(9)

It can be proved that for a locally Lipschitz function $j :X \rightarrow \mathbb {R}$, hypothesis (7)(c) is equivalent to the so-called relaxed monotonicity condition see, e.g., [18]. Note also that if $j :X \rightarrow \mathbb {R}$ is a convex function, then (7)(c) holds with $\alpha _j = 0$, since it reduces to the monotonicity of the (convex) subdifferential. Examples of functions which satisfy condition (7)(c) have been provided in [18, 19, 28], for instance.

The unique solvability of the variational–hemivariational inequality (1) is provided by the following version of Theorem 18 in [19], provided by Remark 13 in [28].

Theorem 6

Assume (4)–(9). Then, inequality (1) has a unique solution $u \in K$.

The Proof of Theorem 6 is carried out in several steps, by using the properties of the subdifferential, a surjectivity result for pseudomonotone multivalued operators and the Banach fixed point argument.

We conclude this section by introducing the notion of the penalty operator.

Definition 7

An operator $P :X \rightarrow X^*$ is said to be a penalty operator of the set $K\subset X$ if P is bounded, demicontinuous, monotone and $K = \{ x \in X \mid Px = 0_{X^*} \}$.

Note that the penalty operator always exists. Indeed, we recall that any reflexive Banach space X can be always considered as equivalently renormed strictly convex space and, therefore, the duality map $J :X \rightarrow 2^{X^*}$, defined by

$$\begin{aligned} J x = \{ \, x^* \in X^* \mid \langle x^*, x \rangle = \Vert x \Vert _X^2 = \Vert x^* \Vert _{X^*}^2 \, \}, \quad \hbox { for all}\ \ x \in X, \end{aligned}$$

is a single-valued operator. Then, the following result holds.

Proposition 8

Let X be a reflexive Banach space, K a nonempty closed and convex subset of X, $J :X \rightarrow X^*$ the duality map, $I:X \rightarrow X$ the identity map on X, and $\widetilde{P}_K :X \rightarrow K$ the projection operator on K. Then $P_K= J (I - \widetilde{P}_K):X\rightarrow X^*$ is a penalty operator of K.

Recall that if X is a Hilbert space then $J:X\rightarrow X^*$ is the canonical isometry. Therefore, for the operator $P_K = J (I_X - \widetilde{P}_K):X\rightarrow X^*$ in Proposition 8 we deduce that

$$\begin{aligned} \Vert P_K x \Vert _{X^*}= \Vert x -\widetilde{P}_Kx\Vert _{X}\qquad \forall \, x\in X. \end{aligned}$$

(10)

Moreover, recall that for each $x\in X$, $\widetilde{P}_Kx$ is the unique element in K which satisfies the inequality

$$\begin{aligned} \Vert x -\widetilde{P}_Kx\Vert _{X}\le \Vert x -y\Vert _{X}\qquad \forall \, y\in K. \end{aligned}$$

(11)

Relations (10), (11) will be used in various places in Sects. 4 and 5 of this paper.

3 Main Results

In this section we state and prove our existence, uniqueness and convergence result, Theorems and 9 and 10. To this end, we consider a family of operators $\{P_n\}$ and a sequence $\{\lambda _n\}\subset \mathbb {R}$ such that, for each $n\in \mathbb {N}$, the following hold:

$$\begin{aligned}&\left\{ \begin{array}{l}P_n:X_n\rightarrow X_n^* \ \ \text{ is } \text{ a } \text{ bounded, } \text{ demicontinuous }\\ \text{ and } \text{ monotone } \text{ operator. }\end{array}\right. \end{aligned}$$

(12)

$$\begin{aligned}&\lambda _n>0. \end{aligned}$$

(13)

The existence of a unique solution to Problem $\mathcal{P}_n$ is a direct consequence of Theorem 6.

Theorem 9

Assume (5)–(9), (12) and (13). Then, for each $n\in \mathbb {N}$, there exists a unique solution $u_n\in X$ to Problem $\mathcal{P}_n$.

Proof

Let $n\in \mathbb {N}$. Assumptions (12), (13) and Proposition 5(a) imply that the operator $\frac{1}{\lambda _n}P_n:X\rightarrow X^*$ is pseudomonotone. Therefore, Proposition 5(b) shows that the operator $A_n:X\rightarrow X^*$ defined by $A_n=A+\frac{1}{\lambda _n}P_n$ is pseudomonotone, too. Moreover, since $P_n$ is monotone and $\lambda _n>0$, using assumption (5)(b) we deduce that $A_n$ is strongly monotone with constant $m_A$. We conclude from above that the operator $A_n$ satisfies condition (5). This allows us to use Theorem 6 with K and A replaced by X and $A_n$, respectively. In this way we obtain the unique solvability of the inequality (2) which concludes the proof. $\square$

To study the behavior of the sequence of solutions to Problems $\mathcal{P}_n$ as $n\rightarrow \infty$, we consider the following additional hypotheses.

$$\begin{aligned}&\forall \,v\in K,\ \exists \, \{v_n\}\subset X \ \text{ s.t. }\ \ P_nv_n=0_{X^*}\ \ \forall \,n\in \mathbb {N}\ \ \hbox { and} \ \ v_n\rightarrow v\ \ \text{ in }\ \ X. \end{aligned}$$

(14)

$$\begin{aligned}&\lambda _n\rightarrow 0\quad \hbox { as}\quad n\rightarrow \infty . \end{aligned}$$

(15)

$$\begin{aligned}&\left\{ \begin{array}{ll}\text{ There } \text{ exists } \text{ an } \text{ operator } P:X\rightarrow X^* \text{ such } \text{ that }\\ \text{(a) } \ \text{ for } \text{ any } \text{ sequence }\ \{u_n\}\ \text{ satisfying }\ \, u_n\rightharpoonup u\ \text{ in }\ X\ \text{ and }\\ \qquad \displaystyle \limsup \,\langle P_nu_n, u_n -u \rangle \le 0\ \ \text{ we } \text{ have }\\ \qquad \displaystyle \liminf \, \langle P_nu_n, u_n - v \rangle \ge \langle P u, u - v \rangle \ \text{ for } \text{ all }\ v \in X.\\ \text{(b) }\ Pu=0_{X^*} \ \Longrightarrow \ u\in K. \end{array}\right. \end{aligned}$$

(16)

$$\begin{aligned}&\left\{ \begin{array}{ll}\text{ There } \text{ exists } \text{ a } \text{ continuous } \text{ function } c_\varphi :\mathbb {R}_+\rightarrow \mathbb {R}_+ \text{ such } \text{ that }\\ \varphi (u,v_1)-\varphi (u,v_2)\le c_\varphi (\Vert u\Vert )_X{\Vert v_1-v_2\Vert _X}\quad \forall \,u,\,v_1,\,v_2\in X. \end{array}\right. \end{aligned}$$

(17)

$$\begin{aligned}&\left\{ \begin{array}{ll}\text{ For } \text{ all } \text{ sequences }\ \{u_n\},\ \{v_n\}\ \text{ such } \text{ that }\\ u_n\rightharpoonup u\ \text{ in }\ X,\ v_n\rightarrow v\ \text{ in }\ X, \text{ we } \text{ have }\\ \limsup \,\big (\varphi (u_n,v_n)-\varphi (u_n,u_n)\big )\le \varphi (u,v)-\varphi (u,u). \end{array}\right. \end{aligned}$$

(18)

$$\begin{aligned}&\left\{ \begin{array}{ll}\text{ For } \text{ all } \text{ sequences }\ \{u_n\},\ \{v_n\}\ \text{ such } \text{ that }\\ u_n\rightharpoonup u\ \text{ in }\ X,\ v_n\rightarrow v\ \text{ in }\ X, \text{ we } \text{ have }\\ \limsup \,j^0(u_n;v_n-u_n)\le j^0(u;v-u). \end{array}\right. \end{aligned}$$

(19)

A simple exemple of function $\varphi$ which satisfies conditions (17) and (18) is given by

$$\begin{aligned} \varphi (u,v)=\int _{\varGamma } u|v|\,da\qquad \forall \,\,u,\,v\in H^1(\varOmega ). \end{aligned}$$

Here $X=H^1(\varOmega )$ is the Sobolev space of the first order associated to a bounded domain $\varOmega \subset \mathbb {R}^d$ with smooth boundary $\varGamma$ and, for each $u\in X$ we still write u for the trace of u to $\varGamma$.

Our main result in this section is the following.

Theorem 10

Assume (4)–(9), (12)–(19) and denote by $u_n$ the solution of Problem $\mathcal{P}_n$. Then $u_n\rightarrow u$ in X, as $n\rightarrow \infty$, where $u \in K$ is the unique solution of Problem $\mathcal{P}$.

Proof

The proof of Theorem 10 is carried out in several steps.

• (i) We claim that there is an element ${\widetilde{u}} \in X$ and a subsequence of $\{ u_n \}$, still denoted $\{ u_n \}$, such that $u_n \rightharpoonup {\widetilde{u}}$ in X as $n\rightarrow \infty$.

To prove the claim, we establish the boundedness of $\{ u_n \}$ in X. Let v be a given element in K. We use assumption (14) and consider a sequence $\{v_n\}\subset X$ such that $P_nv_n=0_{X^*}$ for all $n\in \mathbb {N}$ and

$$\begin{aligned} v_n\rightarrow v\quad \text{ in }\quad X. \end{aligned}$$

(20)

Let $n\in \mathbb {N}$. We now put $v_n\in X$ in (3) and use the strong monotonicity of the operator A to obtain

$$\begin{aligned}&m_A \, \Vert u_n - v_n \Vert _X^2 \le \langle A v_n, v_n - u_n \rangle + \frac{1}{\lambda _n} \langle P_nu_n, v_n - u_n \rangle \nonumber \\&\quad +\, \varphi (u_n,v_n) - \varphi (u_n,u_n)+ \, j^0(u_n; v_n - u_n) + \langle f, u_n - v_n \rangle . \end{aligned}$$

(21)

Next, since $P_nv_n=0_{X^*}$, assumption (12) implies that

$$\begin{aligned} \langle P_nu_n, v_n - u_n \rangle \le 0 \end{aligned}$$

(22)

and assumptions (6)(b), (17) yield

$$\begin{aligned}&\varphi (u_n,v_n) - \varphi (u_n,u_n)\nonumber \\&\quad =\big (\varphi (u_n,v_n) - \varphi (u_n,u_n)+ \varphi (v_n,u_n) - \varphi (v_n,v_n)\big )+\big (\varphi (v_n,v_n) - \varphi (v_n,u_n))\nonumber \\&\quad \le \alpha _\varphi \Vert u_n - v_n \Vert _X^2+c_\varphi (\Vert v_n\Vert _X) \Vert u_n - v_n \Vert _X. \end{aligned}$$

(23)

On the other hand, by (7) and Proposition 3(ii), we have

$$\begin{aligned}&j^0 (u_n; v_n - u_n) \nonumber \\&\quad = j^0(u_n; v_n - u_n) + j^0 (v_n; u_n - v_n) - j^0 (v_n; u_n - v_n)\nonumber \\&\quad \le j^0(u_n; v_n - u_n) + j^0 (v_n; u_n - v_n) + | j^0 (v_n; u_n - v_n)| \nonumber \\&\quad \le \alpha _j \Vert u_n - v_n \Vert _X^2 + |\max \, \{ \,\langle \xi , u_n - u_0 \rangle \, :\, \xi \in \partial j(v_n)\, \} | \nonumber \\&\quad \le \alpha _j \Vert u_n - v_n \Vert _X^2 + (c_0 + c_1 \Vert v_n \Vert _X) \Vert u_n - v_n \Vert _X, \end{aligned}$$

(24)

and, obviously,

$$\begin{aligned} \langle A v_n, v_n - u_n \rangle +\langle f, u_n - v_n \rangle \le \Vert Av_n-f \Vert _{X^*}\Vert u_n - v_n \Vert _X. \end{aligned}$$

(25)

We now combine inequalities (21)–(25) to see that

$$\begin{aligned}&m_A \, \Vert u_n - v_n \Vert _X^2 \le \Vert Av_n -f\Vert _X\Vert u_n - v_n \Vert _X+ c_\varphi (\Vert v_n\Vert _X) \Vert u_n - v_n \Vert _X \nonumber \\&\quad +\,\alpha _\varphi \Vert u_n - v_n \Vert _X^2+\alpha _j \Vert u_n - v_n \Vert _X^2 + (c_0 + c_1 \Vert v_n \Vert _X) \Vert u_n - v_n \Vert _X. \end{aligned}$$

(26)

Note that by (20) we know that the sequence $\{v_n\}$ is bounded in X. Therefore, using inequality (26), the smallness assumption (8) and the properties of the operator A and function $c_\varphi$ we deduce that there is a constant $C > 0$ independent of n such that $\Vert u_n-v_n\Vert _X \le C$. This implies that $\{u_n\}$ is bounded sequence in X. Thus, from the reflexivity of X, by passing to a subsequence, if necessary, we deduce that

$$\begin{aligned} u_n \rightharpoonup {\widetilde{u}} \ \ \hbox { in} \ \ X, \ \ \text{ as }\ \ n\rightarrow \infty , \end{aligned}$$

(27)

with some ${\widetilde{u}} \in X$. This implies the claim.

• (ii) Next, we show that ${\widetilde{u}} \in K$ is a solution to Problem $\mathcal{P}$.

Let v be a given element in X. We use (3) to obtain that

$$\begin{aligned}&\frac{1}{\lambda _n} \langle P_nu_n, u_n - v \rangle \le \langle Au_n, v-u_n \rangle \nonumber \\&\quad +\,\varphi (u_n,v)-\varphi (u_n,u_n)+j^0(u_n,v-u_n)+\langle f, u_n - v \rangle . \end{aligned}$$

(28)

Then, by conditions (5), (7), (17), using the boundedness of the sequence $\{u_n\}$ and arguments similar to those used in the proof of (26), we deduce that each term in the right hand side of inequality (28) is bounded. This implies that there exists a constant $D>0$ which does not depend on n such that

$$\begin{aligned} \langle P_nu_n, u_n - v \rangle \le \lambda _n D. \end{aligned}$$

We now pass to the upper limit in this inequality and use the convergence (15) to deduce that

$$\begin{aligned} \limsup \,\langle P_nu_n, u_n -v \rangle \le 0. \end{aligned}$$

(29)

We now take $v=\widetilde{u}$ in (29) to find that

$$\begin{aligned} \limsup \,\langle P_nu_n, u_n - \widetilde{u}\rangle \le 0, \end{aligned}$$

then we use assumptions (16)(a) and (27) to obtain that

$$\begin{aligned} \langle P {\widetilde{u}}, {\widetilde{u}} - v \rangle \le \liminf \, \langle P_nu_n, u_n - v \rangle \end{aligned}$$

and, finally, we combine this inequality with (29) to find that $\langle P {\widetilde{u}}, {\widetilde{u}} - v \rangle \le 0$. Hence, choosing $v = {\widetilde{u}} + w$ with $w \in X$, we get $\langle P {\widetilde{u}}, w \rangle = 0$ for all $w \in X$. So, it is clear that $P {\widetilde{u}} = 0_{X^*}$ and, therefore, (16)(b) implies that ${\widetilde{u}} \in K$.

Consider now a given element $v\in K$. We use assumption (14) to find a sequence $\{v_n\}$ such that $P_nv_n=0_{X^*}$ for all $n\in \mathbb {N}$ and (20) holds. Let $n\in \mathbb {N}$. We now put $v_n\in X$ in (3) and use the equality $P_nv_n=0_{X^*}$ to obtain that

$$\begin{aligned}&\langle A u_n, u_n - v_n \rangle \le - \frac{1}{\lambda _n} \langle P_nv_n - P_nu_n, v_n - u_n \rangle \\&\quad + \,\varphi (u_n,v_n) - \varphi (u_n,u_n) + j^0(u_n; v_n - u_n) + \langle f, u_n - v_n \rangle . \end{aligned}$$

Therefore, by the monotonicity of the operator $P_n$ we find that

$$\begin{aligned} \langle A u_n, u_n - v_n \rangle \le \varphi (u_n,v_n) - \varphi (u_n,u_n) + j^0(u_n; v_n - u_n) + \langle f, u_n - v_n \rangle . \end{aligned}$$

(30)

Next, using (27), (20) and assumption (18) we have

$$\begin{aligned} \limsup \, \big (\varphi (u_n,v_n) - \varphi (u_n,u_n)\big )\le \varphi ({\widetilde{u}},v) - \varphi ({\widetilde{u}},{\widetilde{u}}). \end{aligned}$$

(31)

On the other hand, from (27), (20) and (19), it follows that

$$\begin{aligned} \limsup j^0(u_n; v_n - u_n) \le j^0(\widetilde{u},v-\widetilde{u}). \end{aligned}$$

(32)

Moreover,

$$\begin{aligned} \langle f, u_n - v_n \rangle \rightarrow \langle f, \widetilde{u} - v \rangle . \end{aligned}$$

(33)

We now gather relations (30)–(33) to see that

$$\begin{aligned} \limsup \,\langle A u_n, u_n - v_n \rangle \le \varphi ({\widetilde{u}},v) - \varphi ({\widetilde{u}},{\widetilde{u}}) + j^0(\widetilde{u},v-\widetilde{u}) + \langle f, \widetilde{u} - v \rangle . \end{aligned}$$

(34)

Next, the properties of A combined with the convergences (27) and (20) imply that $\langle A u_n, v - v_n \rangle \rightarrow 0$. Therefore, writing

$$\begin{aligned} \langle A u_n, u_n - v_n \rangle =\langle A u_n, u_n - v \rangle +\langle A u_n, v - v_n \rangle , \end{aligned}$$

we deduce that

$$\begin{aligned} \limsup \,\langle A u_n, u_n - v_n \rangle =\limsup \,\langle A u_n, u_n -v \rangle . \end{aligned}$$

This equality combined with inequality (34) yields

$$\begin{aligned} \limsup \,\langle A u_n, u_n - v \rangle \le \varphi ({\widetilde{u}},v) - \varphi ({\widetilde{u}},{\widetilde{u}}) + j^0(\widetilde{u},v-\widetilde{u}) + \langle f, \widetilde{u} - v \rangle , \end{aligned}$$

(35)

for all $v\in K$. Now, taking $v= {\widetilde{u}} \in K$ in (35) and using Proposition 3(i) we obtain that

$$\begin{aligned} \limsup \, \langle A u_n, u_n - {\widetilde{u}} \rangle \le 0. \end{aligned}$$

(36)

This inequality together with (27) and the pseudomonotonicity of A implies

$$\begin{aligned} \langle A {\widetilde{u}}, {\widetilde{u}} - v \rangle \le \liminf \, \langle A u_n, u_n - v \rangle \ \ \text{ for } \text{ all } \ \ v \in X. \end{aligned}$$

(37)

Combining now (37) and (35), we have

$$\begin{aligned} \langle A {\widetilde{u}}, {\widetilde{u}} - v \rangle \le \varphi (\widetilde{u},v) - \varphi ({\widetilde{u},\widetilde{u}}) + j^0({\widetilde{u}}; v - {\widetilde{u}}) + \langle f, {\widetilde{u}} - v \rangle , \end{aligned}$$

for all $v \in K$. Hence, it follows that ${\widetilde{u}} \in K$ is a solution to Problem $\mathcal{P}$, as claimed.

• (iii) We now prove the weak convergence of the whole sequence $\{u_n\}$.

Since Problem $\mathcal{P}$ has a unique solution $u \in K$, we deduce that ${\widetilde{u}} = u$. A careful analysis of the proof in step (ii) reveals that every subsequence of $\{ u_n \}$ which converges weakly in X has the weak limit u. Moreover, we recall that the sequence $\{ u_n \}$ is bounded in X. Therefore, using a standard argument we deduce that the whole sequence $\{ u_n \}$ converges weakly in X to u, as $n\rightarrow \infty$.

• (iv) In the final step of the proof, we prove that $u_n \rightarrow u$ in X, as $n\rightarrow \infty$.

We take $v = {\widetilde{u}} \in K$ in (37) and use (36) to obtain

$$\begin{aligned} 0 \le \liminf \, \langle A u_n, u_n - {\widetilde{u}} \rangle \le \limsup \,\langle A u_n, u_n - {\widetilde{u}} \rangle \le 0, \end{aligned}$$

which shows that $\langle A u_n, u_n - {\widetilde{u}} \rangle \rightarrow 0$, as $n\rightarrow \infty$. Therefore, using equality $\widetilde{u}=u$, the strong monotonicity of A and the convergence $u_n \rightharpoonup u$ in X, we have

$$\begin{aligned} m_A \Vert u_n - u \Vert _X^2 \le \langle A u_n - Au, u_n - u \rangle = \langle A u_n, u_n - u \rangle - \langle A u, u_n - u \rangle \rightarrow 0, \end{aligned}$$

as $n\rightarrow \infty$. Hence, it follows that $u_n \rightarrow u$ in X, which completes the proof. $\square$

We end this section by considering the following condition.

$$\begin{aligned} \left\{ \begin{array}{ll} P:X\rightarrow X^* \text{ is } \text{ a } \text{ pseudomonotone } \text{ operator } \text{ and }\\ \Vert P_nu_n-Pu_n\Vert _{X^*}\rightarrow 0,\ \text{ whenever } \{u_n\} \text{ is } \text{ weakly } \text{ convergent } \text{ in } X. \end{array}\right. \end{aligned}$$

(38)

The interest in this condition follows from the next lemma.

Lemma 11

Assume that (38) holds. Then, the operator P satisfies condition (16)$(\mathrm{a})$.

Proof

Let $v\in X$ and let $\{u_n\}\subset X$ be a sequence such that $u_n\rightharpoonup u\ \text{ in }\ X$ and

$$\begin{aligned} \displaystyle \limsup \,\langle P_nu_n, u_n -u \rangle \le 0. \end{aligned}$$

(39)

It follows from here that $\{u_n\}$ is bounded and, therefore, assumption (38) yields

$$\begin{aligned} \langle P_nu_n-Pu_n,v-u_n\rangle \rightarrow 0\quad \mathrm{as}\quad n\rightarrow \infty . \end{aligned}$$

(40)

On the other hand, for each $n\in \mathbb {N}$ we write

$$\begin{aligned} \langle P_nu_n,u_n-v\rangle = \langle P_nu_n-Pu_n,u_n-v\rangle + \langle Pu_n,u_n-v\rangle \end{aligned}$$

and, using (40) we deduce that

$$\begin{aligned} \displaystyle \limsup \,\langle P_nu_n, u_n -v \rangle= & {} \limsup \,\langle Pu_n, u_n -v\rangle , \end{aligned}$$

(41)

$$\begin{aligned} \displaystyle \liminf \,\langle P_nu_n, u_n -v \rangle= & {} \liminf \,\langle Pu_n, u_n -v\rangle . \end{aligned}$$

(42)

We now take $v=u$ in (41) and use (39) to obtain that

$$\begin{aligned} \displaystyle \limsup \,\langle Pu_n, u_n -u \rangle \le 0. \end{aligned}$$

Then, using the pseudomonotonicity of P and (42) we find that

$$\begin{aligned} \langle Pu,u-v\rangle \le \liminf \,\langle Pu_n,u_n-v\rangle =\liminf \,\langle P_nu_n, u_n -v \rangle \end{aligned}$$

which concludes the proof. $\square$

Lemma 11 shows that condition (38) implies (16)(a). Moreover, note that checking (38) is more convenient in various applications than checking (16)(a). For this reason condition (38) will be used in several places in the rest of the paper.

4 Relevant Particular Cases

In this section we present some particular cases of penalty problems of the form (3) for which the results in Theorems 9 and 10 hold, and which have some interest on their own. Everywhere below we assume that (5)–(9), (13), (15) and (17)–(19) hold. With these data we consider problems $\mathcal{P}$ and $\mathcal{P}_n$ in which both K and ${P_n}$ will change from place to place and, for this reason, will be described below, in each particular case. For each example, we shall prove that conditions (4), (12), (14) and (16) are satisfied. Therefore, the existence of a unique solution to the corresponding Problem $\mathcal{P}_n$ will be provided by Theorem 9 and its convergence to the solution of Problem $\mathcal{P}$ is guaranteed by Theorem 10.

(a) The classical penalty method. This particular case is obtained when K satisfies (4) and $P_n=P$ where P is a penalty operator of K. Note that in this case inequality (3) becomes the penalty inequality (2).

We now prove the validity of conditions (12), (14) and (16). First, we use Definition 7 to see that the operator P is bounded, demicontinuous and monotone, and, therefore, condition (12) holds. Moreover, conditions (14) and (16)(b) are obviously satisfied, since $P_n=P$ and P is a penalty operator of K. In addition, Proposition 5(a) guarantees that P is pseudomonotone. Assume now that $u_n\rightharpoonup u$ in X and $\displaystyle \limsup \,\langle P_nu_n, u_n -u \rangle \le 0$, which implies that $\displaystyle \limsup \,\langle Pu_n, u_n -u \rangle \le 0$. Then, using equality $P_n=P$ and the pseudomonotonicity of P, we have

$$\begin{aligned} \liminf \,\langle P_nu_n,u_n-v\rangle = \liminf \,\langle Pu_n,u_n-v\rangle \ge \langle Pu,u-v\rangle \quad \hbox { for all}\ v\in X \end{aligned}$$

which shows that (16)(a) holds.

We are now in a position to apply Theorems 6 and 9 in order to obtain the following result.

Corollary 12

Assume (4)–(9), (13) and, moreover, assume that $P:X\rightarrow X^*$ is a penalty operator of the set K. Then, for each $n\in \mathbb {N}$, there exists a unique solution $\overline{u}_n\in X$ to Problem $\overline{\mathcal{P}}_n$. In addition, if (15) and (17)–(19) hold, then $\overline{u}_n\rightarrow u$ in X, as $n\rightarrow \infty$, where $u \in K$ is a unique solution to Problem $\mathcal{P}$.$\Box$

Corollary 12 was obtained in [19], in the particular case when $\varphi (u,v)=\varphi (v)$. Its proof in the general case, when $\varphi$ depends on both u and v, was given in [28].

(b) An unconstrained variational–hemivariational inequality. This particular case is obtained when $K=X$ and, for each $n\in \mathbb {N}$, $P_n:X\rightarrow X^*$ is a penalty operator of the closed ball $B_n=\{\,v\in X\ :\ \Vert v\Vert _X\le n\,\}$. Note that in this case Problem $\mathcal{P}$ reads as follows : find an element $u\in X$ such that

$$\begin{aligned} \langle A u, v - u \rangle + \varphi (u, v) - \varphi (u, u) + j^0(u; v - u) \ge \langle f, v - u \rangle \qquad \forall \, v \in X. \end{aligned}$$

(43)

We now prove the validity of conditions (12) (14) and (16). First, we use Definition 7 to see that the operator $P_n$ is bounded, demicontinuous and monotone, for each $n\in \mathbb {N}$. Therefore, condition (12) holds. Let $v\in X$. Then, it is easy to see that the sequence $\{v_n\}\subset X$ defined by

$$\begin{aligned} v_n=\left\{ \begin{array}{lll} \ 0_X &{} \hbox { if}&{} n\le \Vert v\Vert _X,\\ \ v &{} \hbox { if}&{} n>\Vert v\Vert _X\end{array}\right. \end{aligned}$$

satisfies condition (14). Let $P:X\rightarrow {X^*}$ be such that $Pv=0_{X^*}$ for any $v\in X$, and let $u_n\rightharpoonup u$ in X. Then the sequence $\{u_n\}$ is bounded in X and, therefore, for n large enough we have $\Vert u_n\Vert _X\le n$, i.e., $u_n\in B_n$, which implies that $P_nu_n=0_{X^*}$. We deduce from here that condition (38) holds and, by Lemma 11 it follows that (16)(a) holds, too. Finally, note that condition (16)(b) is obviously satisfied.

We now use Theorems 9 and 10 to deduce that for each $n\in \mathbb {N}$, there exists a unique solution ${u}_n\in X$ to Problem $\mathcal{P}_n$ and, moreover, ${u}_n\rightarrow u$ in X, as $n\rightarrow \infty$, where u is a unique solution to the variational–hemivariational inequality (43).

We note that the previous convergence result is not surprising. Indeed, it follows from the proof of Theorem 9 that the sequence $\{u_n\}$ is bounded in X. Therefore, with the choice above on $P_n$ we have $P_nu_n=0$ for n large enough. It follows from here that Problem $\mathcal{P}_n$ becomes Problem $\mathcal{P}$ for n large enough, which shows that $u_n=u$ for n large enough and confirms the convergence $u_n\rightarrow u$ in X.

(c) Penalty method associated to the Hausdorff convergence of sets. For this example we assume that X is a Hilbert space, K satisfies condition (4) and, for each $n\in \mathbb {N}$, $P_n=J(I-\widetilde{P}_{n}):X\rightarrow X^*$ where $J:X\rightarrow X^*$ is the canonical isometry, $I:X\rightarrow X$ is the identity map and $\widetilde{P}_{n}$ is the projection operator on a set $K_n$, assumed to satisfy condition (4). In addition, we assume that

$$\begin{aligned} \mathcal{H}(K_n,K)\rightarrow 0,\quad \mathrm{as}\quad n\rightarrow \infty . \end{aligned}$$

(44)

Here and below $\mathcal{H}(A,B)$ denotes the Hausdorff distance of the sets $A, B\subset X$, assumed to be nonempty. For the convenience of the reader we recall that

$$\begin{aligned} \mathcal{H}(A,B)=\mathrm{max}\,\{e(A,B), e(B,A)\}, \end{aligned}$$

(45)

where

$$\begin{aligned} e(A,B)= & {} \sup _{a\in A}\,d(a,B),\qquad e(B,A)=\sup _{b\in B}\,d(b,A), \end{aligned}$$

(46)

$$\begin{aligned} d(a,B)= & {} \displaystyle \inf _{b\in B} \Vert a - b \Vert _X,\quad \quad d(b,A)= \displaystyle \inf _{a\in A} \Vert a - b \Vert _X. \end{aligned}$$

(47)

We now prove the validity of conditions (12), (14) and (16). First, we use Proposition 8 and Definition 7 to see that (12) holds. Assume now that $v\in K$. Then, using (11) and (45)–(47) we have

$$\begin{aligned} \Vert v-\widetilde{P}_{n}v\Vert _X= & {} \displaystyle \inf _{w\in K_n} \Vert v-w \Vert _X= d(v,K_n)\\ \displaystyle\le & {} \sup _{z\in K}d(z,K_n)=e(K,K_n)\le \mathcal{H}(K_n,K) \end{aligned}$$

and, therefore, assumption (44) implies that $\widetilde{P}_{n}v\rightarrow v$ in X. Denote $v_n=\widetilde{P}_{n}v$. Then $v_n\in K_n$ and, therefore, $P_nv_n=J(v_n-\widetilde{P}_{n}v_n)=0_{X^*}$. Moreover, recall that $v_n\rightarrow v$ in X. We conclude from here that condition (14) is satisfied.

Next, let $P:X\rightarrow X^*$ be the operator defined by $P=J(I-\widetilde{P})$ where $\widetilde{P}:X\rightarrow K$ denotes the projection operator on K. Let $\{u_n\}\subset X$ be a sequence which is weakly convergent. Then, using (10) and (45)–(47) we deduce that

$$\begin{aligned} \Vert P_nu_n-Pu_n\Vert _{X^*}= & {} \Vert \widetilde{P}_{n}u_n-\widetilde{P}u_n\Vert _X=\displaystyle \inf _{w\in K_n} \Vert w -\widetilde{P}u_n\Vert _X\\= & {} d(\widetilde{P}u_n,K_n) \displaystyle \sup _{z\in K}d(z,K_n)=e(K,K_n)\le \mathcal{H}(K_n,K), \end{aligned}$$

for each $n\in \mathbb {N}$. Therefore condition (44) implies

$$\begin{aligned} \Vert P_nu_n-Pu_n\Vert _{X^*}\rightarrow 0. \end{aligned}$$

On the other hand, by Propositions 8, Definition 7 and Proposition 5 we see that P is a pseudomonotone operator. We deduce from above that condition (38) holds and, by Lemma 11 it follows that (16)(a) holds, too. In addition, condition (16)(b) is obviously satisfied.

We are now in a position to apply Theorems 9 and 10 in order to obtain the following result.

Corollary 13

Let X be a Hilbert space. Assume (4)–(9), (13) and, moreover, and, for each $n\in \mathbb {N}$ assume that $P_n=J(I-\widetilde{P}_{n}):X\rightarrow X^*$ where $J:X\rightarrow X^*$ is the canonical isometry, $I:X\rightarrow X$ is the identity map and $\widetilde{P}_{n}$ is the projection operator on the set $K_n$, assumed to satisfy (4). Then, for each $n\in \mathbb {N}$, there exists a unique solution ${u}_n\in X$ to Problem $\mathcal{P}_n$. In addition, if (15), (17)–(19) and (44) hold, then ${u}_n\rightarrow u$ in X, as $n\rightarrow \infty$, where $u \in K$ is the unique solution to Problem $\mathcal{P}$.

(d) Penalty method associated to affine transformation of the set of constraints. For this last example in this section we assume that X is a Hilbert space, K satisfies conditions (4) and, for each $n\in \mathbb {N}$, $P_n=J(I-\widetilde{P}_{n}):X\rightarrow X^*$ where $\widetilde{P}_{n}$ is the projection operator on the set

$$\begin{aligned} K_n=a_nK+b_n\theta , \end{aligned}$$

(48)

where $a_n$, $b_n>0$ and $\theta \in K$ is given. In addition, we assume that

$$\begin{aligned} a_n\rightarrow 1,\qquad b_n\rightarrow 0\quad \mathrm{as}\quad n\rightarrow \infty . \end{aligned}$$

(49)

Here and below the operators J and I are those defined in the previous example. Note that assumption (4) combined with (48) guarantees that $K_n$ is a closed convex nonempty subset of X and, therefore, the operator $P_n$ is well defined. Denote by $P:X\rightarrow X^*$ the operator given by $P=J(I-\widetilde{P})$ where $\widetilde{P}:X\rightarrow K$ denotes the projection operator on K. With these notations we prove the validity of conditions (12), (14) and (16).

First, we use Proposition 8 and Definition 7 to see that (12) holds. Next, condition (14) is guaranteed by definition (48) and assumption (49) with $v_n=a_nv+b_n\theta$, for each $v\in K$ and $n\in \mathbb {N}$. Let $\{u_n\}\subset X$ be a weakly convergent sequence and let $n\in \mathbb {N}$. Using (10) we deduce that

$$\begin{aligned} \Vert P_nu_n-Pu_n\Vert _{X^*}= \Vert \widetilde{P}_nu_n-\widetilde{P}u_n\Vert _{X}. \end{aligned}$$

(50)

On the other hand, an elementary calculus based on the definition of the projection, (11), combined with equality (48) reveals that

$$\begin{aligned} \widetilde{P}_nz= a_n \widetilde{P}\Big (\frac{z-b_n\theta }{a_n}\Big )+b_n\theta \qquad \forall \, z\in X. \end{aligned}$$

(51)

Recall also the nonexpansivity of the projector on Hilbert spaces, that is

$$\begin{aligned} \Vert \widetilde{P}y-\widetilde{P}z\Vert _X\le \Vert y-z\Vert _X \qquad \forall \, y,\, z\in X. \end{aligned}$$

(52)

We now substitute inequality (51) in (50), then use the triangle inequality and (52) to deduce that

$$\begin{aligned} \Vert P_nu_n-Pu_n\Vert _{X^*}\le \frac{1}{a_n}|a_n-1|\Vert u_n\Vert _X+ |b_n|\Vert \theta \Vert _X. \end{aligned}$$

(53)

Recall also that the sequence $\{u_n\}$ is bounded in X. Therefore, (53) and (49) imply that

$$\begin{aligned} \Vert P_nu_n-Pu_n\Vert _{X^*}\rightarrow 0. \end{aligned}$$

(54)

The convergence (54) combined with the pseudomonotonicity of P, guaranteed by Proposition 5(a), shows that condition (38) holds and, by Lemma 11 it follows that (16)(a) holds, too. On the other hand, condition (16)(b) is a consequence of Proposition 8.

We are in a position to use Theorems 9 and 10 in order to obtain the following result.

Corollary 14

Let X be a Hilbert space. Assume (4)–(9), (13) and, moreover, for each $n\in \mathbb {N}$ assume that $P_n=J(I-\widetilde{P}_{n}):X\rightarrow X^*$ where $\widetilde{P}_{n}$ is the projection operator on the set $K_n$, given by (48) with $a_n$, $b_n>0$. Then, for each $n\in \mathbb {N}$, there exists a unique solution ${u}_n\in X$ to Problem $\mathcal{P}_n$. In addition, if (15), (17)–(19) and (49) hold, then ${u}_n\rightarrow u$ in X, as $n\rightarrow \infty$, where $u \in K$ is the unique solution to Problem $\mathcal{P}$.

We end this section with two remarks. The first one is that in the particular case when the set K is bounded, then the example d) is a particular case of the example c). Indeed, it is easy to see that in this case assumptions (48), (49) imply that (44) holds. The second remark is that that Theorems 9 and 10 can be applied to various elliptic variational–hemivariational inequalities which do not cast in the particular cases presented above. The last section of this manuscript is devoted to the study of such example, which arises in Contact Mechanics.

5 An application in Contact Mechanics

The results presented in Sects. 3 and 4 can be used in the study of various mathematical models which describe the equilibrium of elastic bodies in contact with an obstacle, the so-called foundation. References in the field are the books [3, 18, 26, 28]. Providing a description of such contact models requires to introduce a long list of preliminaries and notation. Therefore, in order to keep this paper in a reasonable length we consider only the variational formulation of a representative contact model which was already studied in [25]. The reason of this choice is two fold. First, the results obtained in [25] provide part of the ingredients we need in our study below. Second, we obtain here a new result, Theorem 16, which extends some of the results obtained in [25].

Let $\varOmega \subset \mathbb {R}^d$ ($d=2,3$) be a domain with smooth boundary $\varGamma$, divided into three measurable disjoint parts $\varGamma _1$, $\varGamma _2$ and $\varGamma _3$ such that ${ meas}\,(\varGamma _1)>0$. A generic point in $\varOmega \cup \varGamma$ will be denoted by ${\varvec{x}}=(x_i)$. We use the notation $\mathbb {S}^d$ for the space of second order symmetric tensors on $\mathbb {R}^d$. Moreover, $``\cdot ''$ and $\Vert \cdot \Vert$ will represent the canonical inner product and Euclidian norms on $\mathbb {R}^d$ and $\mathbb {S}^d$, and ${\varvec{\tau }}^D$ denotes the deviator of the tensor ${\varvec{\tau }}\in \mathbb {S}^d$. We use standard notation for the Sobolev and Lebesgue spaces associated to $\varOmega$ and $\varGamma$ and for an element ${\varvec{v}}\in H^1(\varOmega )^d$ we still write ${\varvec{v}}$ for the trace of ${\varvec{v}}$ to $\varGamma$. In addition, we consider the following spaces:

$$\begin{aligned} V= & {} \{\,{\varvec{v}}\in H^1(\varOmega )^d:\ {\varvec{v}}={\varvec{0}}\ \ \hbox { on }\varGamma _1\,\},\\ Q= & {} \{\,{\varvec{\sigma }}=(\sigma _{ij}):\ \sigma _{ij}=\sigma _{ji} \in L^{2}(\varOmega )\,\}. \end{aligned}$$

The spaces V and Q are real Hilbert spaces endowed with the inner products given by

$$\begin{aligned} ({\varvec{u}},{\varvec{v}})_V= \int _{\varOmega } {\varvec{\varepsilon }}({\varvec{u}})\cdot {\varvec{\varepsilon }}({\varvec{v}})\,dx,\qquad ( {\varvec{\sigma }},{\varvec{\tau }})_Q = \int _{\varOmega }{{\varvec{\sigma }}\cdot {\varvec{\tau }}\,dx}, \end{aligned}$$

(55)

where, here and below, ${\varvec{\varepsilon }}({\varvec{v}})$ denotes the linearized strain of ${\varvec{v}}$. The associated norms on these spaces are denoted by $\Vert \cdot \Vert _V$ and $\Vert \cdot \Vert _{Q}$, respectively. We use notation $V^*$ and $\langle \cdot ,\cdot \rangle$ for the topological dual of V and the duality pairing between $V^*$ and V, respectively. We also denote by ${\varvec{0}}_V$ the zero element of V and, for any element ${\varvec{v}}\in V$, we denote by $v_\nu$ and ${\varvec{v}}_\tau$ its normal and tangential components on $\varGamma$ given by $v_\nu ={\varvec{v}}\cdot {\varvec{\nu }}$ and ${\varvec{v}}_\tau ={\varvec{v}}-v_\nu {\varvec{\nu }}$, respectively. Finally, we recall that the Sobolev trace theorem yields

$$\begin{aligned} \Vert {\varvec{v}}\Vert _{L^2(\varGamma _3)^d}\le \Vert \gamma \Vert \,\Vert {\varvec{v}}\Vert _{V}\qquad \forall \,{\varvec{v}}\in V, \end{aligned}$$

(56)

where $\Vert \gamma \Vert$ represents the norm of the trace operator $\gamma :V \rightarrow L^2(\varGamma _3)^d$.

Consider in what follows the data $\mathcal{A}$, k, ${\varvec{f}}_0$,${\varvec{f}}_2$, F, g and $j_\nu$, assumed to satisfy the following conditions.

$$\begin{aligned}&\left\{ \begin{array}{ll} \hbox { (a)}\ \mathcal{A}:\varOmega \times \mathbb {S}^d\rightarrow \mathbb {S}^d.\\ \hbox { (b) There exists}\ L_\mathcal{A}>0\ \hbox { such that}\\ {}\qquad \Vert \mathcal{A}({\varvec{x}},{\varvec{\varepsilon }}_1)-\mathcal{A}({\varvec{x}},{\varvec{\varepsilon }}_2)\Vert \le L_\mathcal{A} \Vert {\varvec{\varepsilon }}_1-{\varvec{\varepsilon }}_2\Vert \\ {}\qquad \qquad \forall \,{\varvec{\varepsilon }}_1,{\varvec{\varepsilon }}_2 \in \mathbb {S}^d,\ \hbox { a.e.}\ {\varvec{x}}\in \varOmega .\\ \hbox { (c) There exists}\ m_\mathcal{A}>0\ \hbox { such that}\\ {}\qquad (\mathcal{A}({\varvec{x}},{\varvec{\varepsilon }}_1)-\mathcal{A}({\varvec{x}},{\varvec{\varepsilon }}_2)) \cdot ({\varvec{\varepsilon }}_1-{\varvec{\varepsilon }}_2)\ge m_\mathcal{A}\, \Vert {\varvec{\varepsilon }}_1-{\varvec{\varepsilon }}_2\Vert ^2\\ {}\qquad \quad \forall \,{\varvec{\varepsilon }}_1, {\varvec{\varepsilon }}_2 \in \mathbb {S}^d,\ \hbox { a.e.}\ {\varvec{x}}\in \varOmega .\\ \hbox { (d) The mapping}\ {\varvec{x}}\mapsto \mathcal{A}({\varvec{x}},{\varvec{\varepsilon }})\ \hbox { is measurable on }\varOmega ,\\ {}\qquad \hbox { for any }{\varvec{\varepsilon }}\in \mathbb {S}^d.\\ \hbox { (d) The mapping } {\varvec{x}}\mapsto \mathcal{A}({\varvec{x}},{\varvec{0}})\ \hbox { belongs to}\ Q. \end{array}\right. \end{aligned}$$

(57)

$$\begin{aligned}&k>0. \end{aligned}$$

(58)

$$\begin{aligned}&{\varvec{f}}_0 \in L^2(\varOmega )^d. \end{aligned}$$

(59)

$$\begin{aligned}&{\varvec{f}}_2\in L^2(\varGamma _2)^d. \end{aligned}$$

(60)

$$\begin{aligned}&F\in L^2(\varGamma _3),\qquad F({\varvec{x}})\ge 0\quad \hbox { a.e.}\ {\varvec{x}}\in \varGamma _3. \end{aligned}$$

(61)

$$\begin{aligned}&g>0. \end{aligned}$$

(62)

$$\begin{aligned}&\left\{ \begin{array}{ll} j_\nu :\varGamma _3 \times \mathbb {R}\rightarrow \mathbb {R}\ \text{ is } \text{ such } \text{ that } \\ \ \ \hbox { (a)} \ j_\nu (\cdot , r) \ \text{ is } \text{ measurable } \text{ on } \ \varGamma _3 \ \text{ for } \text{ all } \ r \in \mathbb {R}\ \text{ and } \text{ there }\qquad \\ \qquad \text{ exists } \ {\overline{e}} \in L^2(\varGamma _3) \ \text{ such } \text{ that } \ j_\nu (\cdot , {\overline{e}} (\cdot )) \in L^1(\varGamma _3). \\ \ \ \hbox { (b)} \ j_\nu ({\varvec{x}}, \cdot ) \ \text{ is } \text{ locally } \text{ Lipschitz } \text{ on } \ \mathbb {R}\ \text{ for } \text{ a.e. } \ {\varvec{x}}\in \varGamma _3. \\ \ \ \hbox { (c)} \ | \partial j_\nu ({\varvec{x}}, r) | \le {\overline{c}}_0 + {\overline{c}}_1 \, | r | \ \text{ for } \text{ a.e. } \ {\varvec{x}}\in \varGamma _3, \\ \qquad \text{ for } \text{ all } \ r \in \mathbb {R}\ \text{ with } \ {\overline{c}}_0, \, {\overline{c}}_1 \ge 0. \\ \ \ \hbox { (d)} \ j_\nu ^0({\varvec{x}}, r_1; r_2 - r_1) + j_\nu ^0({\varvec{x}}, r_2; r_1 - r_2) \le \alpha _{j_\nu } \, | r_1 - r_2 |^2 \\ \qquad \text{ for } \text{ a.e. } \ {\varvec{x}}\in \varGamma _3, \ \text{ all } \ r_1,\, r_2 \in \mathbb {R}\ \text{ with } \ \alpha _{j_\nu } \ge 0.\\ \ \ \hbox { (e)} \ \hbox { either}\ j_\nu ({\varvec{x}},\cdot )\ \hbox { or}\ -j_\nu ({\varvec{x}},\cdot ) \ \hbox { is regular on } \ \mathbb {R} \ \hbox { for a.e.}\ {\varvec{x}}\in \varGamma _3. \end{array} \right. \end{aligned}$$

(63)

$$\begin{aligned}&\alpha _{j_\nu } \Vert \gamma \Vert ^2 < m_{\mathcal {A}}. \end{aligned}$$

(64)

Note that in (63) and below we denote by $\partial j_\nu ({\varvec{x}},\cdot )$ and $j^0({\varvec{x}},\cdot ;\cdot )$ the generalized gradient and the generalized directional derivative of $j_\nu$ with respect to the second variable, for a.e. ${\varvec{x}}\in \varGamma _3$.

We now introduce the sets U, W and K defined by

$$\begin{aligned} U= & {} \{\,{\varvec{v}}\in V : v_\nu \le g\ \ \hbox {a.e. on}\ \varGamma _3\,\}, \end{aligned}$$

(65)

$$\begin{aligned} W= & {} \{\,{\varvec{v}}\in V : \Vert {\varvec{\varepsilon }}^D({\varvec{v}})\Vert \le k\ \ \hbox {a.e. in}\ \varOmega \,\}, \end{aligned}$$

(66)

$$\begin{aligned} K= & {} U\cap W. \end{aligned}$$

(67)

Moreover, let A, $\varphi$, j, ${\varvec{f}}$ be defined as follows:

$$\begin{aligned} A:V \rightarrow V^*, \langle A{\varvec{u}},{\varvec{v}}\rangle= & {} \int _{\varOmega }\mathcal{A}{\varvec{\varepsilon }}({\varvec{u}})\cdot {\varvec{\varepsilon }}({\varvec{v}})\,dx, \end{aligned}$$

(68)

$$\begin{aligned} \varphi :V\times V\rightarrow \mathbb {R}, \varphi ({\varvec{u}},{\varvec{v}})= & {} \int _{\varGamma _3}Fv_\nu ^+\,da, \end{aligned}$$

(69)

$$\begin{aligned} j:V\rightarrow \mathbb {R}, j({\varvec{v}})= & {} \int _{\varGamma _3}j_\nu (v_\nu )\, da, \end{aligned}$$

(70)

$$\begin{aligned} {\varvec{f}}\in V^*,\langle {\varvec{f}}, {\varvec{v}}\rangle= & {} \int _{\varOmega }{\varvec{f}}_0\cdot {\varvec{v}}\,dx + \int _{\varGamma _2}{\varvec{f}}_2\cdot {\varvec{v}}\,da, \end{aligned}$$

(71)

for all ${\varvec{u}},{\varvec{v}}\in V$. Assumptions (57)–(63) guarantee that the set K is nonempty and the integrals in (68)–(71) are well-defined. Moreover, (63) implies that j is a locally Lipschitz function on V and, therefore, its directional derivative at any the point ${\varvec{u}}\in V$ in any the direction ${\varvec{v}}\in V$, denoted $j^0({\varvec{u}};{\varvec{v}})$, is well defined. Finally, note that the function $\varphi$ does not depend on ${\varvec{u}}$.

With these notations we consider the following problem.

Problem

$\mathcal{Q}$. Find a function ${\varvec{u}}\in K$ such that

$$\begin{aligned}&\langle A{\varvec{u}},{\varvec{v}}- {\varvec{u}}\rangle + \varphi ({\varvec{u}},{\varvec{v}}) - \varphi ({\varvec{u}},{\varvec{u}}) + j^0({\varvec{u}};{\varvec{v}}-{\varvec{u}})\nonumber \\&\quad \ge \langle {\varvec{f}}, {\varvec{v}}- {\varvec{u}}\rangle \ \ \text{ for } \text{ all } \ \ {\varvec{v}}\in K. \end{aligned}$$

(72)

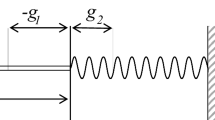
Problem $\mathcal{Q}$ was introduced in our recent paper [25]. It represents the variational formulation of a mathematical model which describes the equilibrium of an elastic body made of a locking material in frictionless contact with a foundation. Here, the operator $\mathcal{A}$ is the elasticity operator, assumed to be nonlinear, k represents the yield limit of the von Mises convex which governs the locking constraints of the material, ${\varvec{f}}_0$ denotes the density of body forces and ${\varvec{f}}_2$ represents the density of surface tractions which act on $\varGamma _3$. The body is fixed on $\varGamma _1$ and is in potential contact on $\varGamma _3$ with a foundation made of a rigid body covered by a deformable layer of thickness g and a rigid-plastic crust of yield limit F. The function $j_\nu$ is the so-called normal compliance function which describes the behaviour of the deformable layer of the foundation.

In the study of Problem $\mathcal{Q}$ we recall the following existence and uniqueness result.

Theorem 15

Assume that (57)–(64) hold. Then Problem $\mathcal{Q}$ has a unique solution ${\varvec{u}}\in K$.

The proof of Theorem 15 can be found in [25], based on the abstract existence and uniqueness result provided by Theorem 6. There, it was proved that assumptions (57)–(64) imply conditions (4)–(9) with $X=V$ and A, $\varphi$, j, ${\varvec{f}}$ given by (68)–(71).

We now illustrate the use of the abstract results in Theorems 9 and 10 in the study of Problem  $\mathcal{Q}$. To this end we consider a normal compliance function $p_\nu$ which satisfies the following condition.

$$\begin{aligned} \left\{ \begin{array}{ll} p_\nu :\varGamma _3\times \mathbb {R}\rightarrow \mathbb {R}_+ \ \text{ is } \text{ such } \text{ that } \\ \ \ \hbox { (a) there exists}\ L_{p_\nu }>0 \hbox { such that}\\ \qquad |p_\nu ({\varvec{x}},r_1)-p_\nu ({\varvec{x}},r_2)|\le L_{p_\nu } |r_1-r_2|\\ \qquad \quad \text{ for } \text{ all } \, r_1,\,r_2\in \mathbb {R},\ \hbox { a.e. } {\varvec{x}}\in \varGamma _3, \\ \ \ \hbox { (b) } (p_\nu ({\varvec{x}},r_1)-p_\nu ({\varvec{x}},r_2))\,(r_1-r_2)\ge 0\\ \qquad \quad \text{ for } \text{ all } \, r_1,\,r_2\in \mathbb {R},\ \hbox { a.e. } {\varvec{x}}\in \varGamma _3, \\ \ \ \hbox { (c)} \ p_\nu (\cdot , r) \hbox { is measurable on}\ \varGamma _3 \ \hbox { for all }r\in \mathbb {R}, \\ \ \ \hbox { (d)}\ p_\nu ({\varvec{x}},r)=0 \ \ \text{ if } \text{ and } \text{ only } \text{ if } \ \ r \le 0, \ \hbox { a.e.}\ {\varvec{x}}\in \varGamma _3. \end{array}\right. \end{aligned}$$

(73)

A typical example of function satisfying (73) is $p_\nu ({\varvec{x}},r)=r^+$ for all $r\in \mathbb {R}$, a.e. ${\varvec{x}}\in \varGamma _3$. Next, for each $n\in \mathbb {N}$ we assume that $k_n$ and $g_n$ satisfy

$$\begin{aligned}&k_n>0 \end{aligned}$$

(74)

$$\begin{aligned}&g_n>0, \end{aligned}$$

(75)

and we define the sets

$$\begin{aligned} U_n= & {} \{\,{\varvec{v}}\in V : v_\nu \le g_n\ \ \hbox {a.e. on}\ \varGamma _3\,\}, \end{aligned}$$

(76)

$$\begin{aligned} W_n= & {} \{\,{\varvec{v}}\in V : \Vert {\varvec{\varepsilon }}^D({\varvec{v}})\Vert \le k_n\ \ \hbox {a.e. in}\ \varOmega \,\}, \end{aligned}$$

(77)

$$\begin{aligned} K_n= & {} U_n\cap W_n, \end{aligned}$$

(78)

$$\begin{aligned} \varSigma _n= & {} \{\,{\varvec{\tau }}\in Q : \Vert {\varvec{\tau }}^D\Vert \le k_n\ \ \hbox {a.e. in}\ \varOmega \,\}. \end{aligned}$$

(79)

Note that $\varSigma _n$ is a closed convex subset of the Hilbert space Q. These properties allows us to consider the projection operator on $\varSigma _n$, denoted $\widetilde{P}_n$. Moreover, using the Riesz representation theorem we define the operator $P_n:V\rightarrow V^*$ by equality

$$\begin{aligned} \langle P_n{\varvec{u}},{\varvec{v}}\rangle= & {} \int _{\varOmega }({\varvec{\varepsilon }}({{\varvec{u}}})-\widetilde{P}_n{\varvec{\varepsilon }}({{\varvec{u}}}))\cdot {\varvec{\varepsilon }}({\varvec{v}})\,dx\nonumber \\&+ \int _{\varGamma _3}\,p_\nu (u_\nu -g_n)v_\nu \,da \qquad \forall \,{\varvec{u}},\, {\varvec{v}}\in V. \end{aligned}$$

(80)

Assume (13). Then, for each $n\in \mathbb {N}$, we consider the following problem.

Problem

$\mathcal{Q}_n$. Find a function ${\varvec{u}}_n\in V$ such that

$$\begin{aligned}&\langle A{\varvec{u}}_n,{\varvec{v}}- {\varvec{u}}_n\rangle +\frac{1}{\lambda _n} \langle P_n{\varvec{u}}_n, {\varvec{v}}- {\varvec{u}}_n \rangle + \varphi ({\varvec{v}}) - \varphi ({\varvec{u}}_n)\nonumber \\&\quad + j^0({\varvec{u}}_n;{\varvec{v}}-{\varvec{u}}_n)\ge \langle {\varvec{f}}, {\varvec{v}}- {\varvec{u}}_n \rangle \qquad \forall \, {\varvec{v}}\in X. \end{aligned}$$

(81)

We also consider the following assumption:

$$\begin{aligned} g_n\rightarrow g \quad \text{ and }\quad k_n\rightarrow k. \end{aligned}$$

(82)

We now state and prove the following existence, uniqueness and convergence result.

Theorem 16

Assume (57)–(64), (73)–(75) and (13). Then:

• (i) For each $n\in \mathbb {N}$, there exists a unique solution ${\varvec{u}}_n$ to Problem $\mathcal{Q}$.

• (ii) If, in addition (82) and (15) hold, the solution ${\varvec{u}}_n$ of Problem $\mathcal{Q}_n$ converges to the solution ${\varvec{u}}$ of Problem $\mathcal{Q}$, i.e., ${\varvec{u}}_n \rightarrow {\varvec{u}}$ in V, as $n \rightarrow \infty$.

Before presenting the proof of Theorem 16 we make the following comments. First, the sets K and $K_n$ defined by (67) and (78), respectively, do not satisfy an equality of the form (48). Moreover, the operator $P_n$ is not expressed in terms of the projection operator on $K_n$. We conclude from here that we are not in a position to obtain Theorem 16 as a consequence of Corollaries 13 or 14. In fact, Problem $\mathcal{Q}_n$ represents a type of penalty problem which does not cast in the particular cases treated in Sect. 4. This example shows, once more, that our results in this paper can be used in the study of a large class of the penalty problems.

Next, we consider the closed convex subset of Q given by

$$\begin{aligned} \varSigma =\{\,{\varvec{\tau }}\in Q : \Vert {\varvec{\tau }}^D({\varvec{v}})\Vert \le k\ \ \hbox {a.e. in}\ \varOmega \,\} \end{aligned}$$

(83)

and denote by $\widetilde{P}:Q\rightarrow \varSigma$ the projection operator on $\varSigma$. Moreover, we use the Riesz representation theorem, again, to define the operator $P:V\rightarrow V^*$ by equality

$$\begin{aligned} \langle P{\varvec{u}},{\varvec{v}}\rangle= & {} \int _{\varOmega }({\varvec{\varepsilon }}({{\varvec{u}}})-\widetilde{P}{\varvec{\varepsilon }}({{\varvec{u}}}))\cdot {\varvec{\varepsilon }}({\varvec{v}})\,dx\nonumber \\&+ \int _{\varGamma _3}\,p_\nu (u_\nu -g)v_\nu \,da \qquad \forall \,{\varvec{u}},\, {\varvec{v}}\in V. \end{aligned}$$

(84)

The proof of Theorem 16 requires some preliminaries that we recall in what follows together with the corresponding references.

Lemma 17

Under the assumption (63), the function (70) satisfies the following property:

$$\begin{aligned} \left\{ \begin{array}{ll}\text{ For } \text{ all } \text{ sequences }\ \{{\varvec{u}}_n\},\ \{{\varvec{v}}_n\}\ \text{ such } \text{ that }\\ {\varvec{u}}_n\rightharpoonup {\varvec{u}}\ \text{ in }\ V,\ {\varvec{v}}_n\rightarrow {\varvec{v}}\ \text{ in }\ V, \text{ we } \text{ have } \\ \limsup \,j^0({\varvec{u}}_n;{\varvec{v}}_n-{\varvec{u}}_n)\le j^0({\varvec{u}};{\varvec{v}}-{\varvec{u}}). \end{array}\right. \end{aligned}$$

Lemma 18

Assume that $g_n$, g, $k_n$, $k>0$. Then, the operators $P_n:V\rightarrow V^*$ and $P:V\rightarrow V^*$ are penalty operators to the sets $K_n$ and K, respectively, i.e., they satisfy the conditions in Definition 7 with $X=V$ and $K_n$, K given by (78) and (67).

Lemma 19

Assume that $k_n$, $k>0$. Then, the projection operators $\widetilde{P}_n:Q\rightarrow \varSigma _n$ and $\widetilde{P}:Q\rightarrow \varSigma$ satisfy the following condition:

$$\begin{aligned} \Vert \widetilde{P}_n{\varvec{\tau }}-\widetilde{P}{\varvec{\tau }}\Vert _{Q}\le |k_n-k|\qquad \forall \, {\varvec{\tau }}\in Q. \end{aligned}$$

(85)

Lemma 17 is a direct consequence of Lemma 6 in [28, p. 123]. Lemma (18) was proved in [25] for the operator P and, therefore, is valid for the operator $P_n$, too. Finally, Lemma 19 corresponds to Proposition 4.6 in [26, p. 102].

We now have all the ingredients to provide the proof of Theorem 16.

Proof

• (i) Let $n\in \mathbb {N}$. It follows from Lemma 18 and Definition 7 that the operator $P_n$ is bounded, demicontinuous and monotone and, therefore, it satisfies condition (12). The existence of a unique solution of Problem $\mathcal{Q}$ is now a direct consequence of Theorem 9.

• (ii) Let ${\varvec{u}},\,{\varvec{v}}_1,\, {\varvec{v}}_2\in V$. We use definition (69) and the trace inequality (56) to see that

  $$\begin{aligned} \varphi ({\varvec{u}},{\varvec{v}}_1)-\varphi ({\varvec{u}},{\varvec{v}}_2)\le \Vert F\Vert _{L^2(\varGamma _3)}\Vert {\varvec{v}}_1-{\varvec{v}}_2\Vert _{L^2(\varGamma _3)^d}\le \Vert \gamma \Vert \Vert F\Vert _{L^2(\varGamma _3)}\Vert {\varvec{v}}_1-{\varvec{v}}_2\Vert _V, \end{aligned}$$

  which shows that condition (17) is satisfied. Assume now that $\{{\varvec{u}}_n\}$, $\{{\varvec{v}}_n\}$ are sequences of V such that ${\varvec{u}}_n\rightharpoonup {\varvec{u}}$ and ${\varvec{v}}_n\rightarrow {\varvec{v}}\ \text{ in }\ V$. Then, using the compactness of the trace we have

  $$\begin{aligned}&\varphi ({\varvec{u}}_n,{\varvec{v}}_n)-\varphi ({\varvec{u}}_n,{\varvec{u}}_n)=\int _{\varGamma _3} F(v_{n\nu }^+-u_{n\nu }^+)\,da\\&\quad \rightarrow \int _{\varGamma _3}F(v_{\nu }^+-u_{\nu }^+)\,da=\varphi ({\varvec{u}},{\varvec{v}})-\varphi ({\varvec{u}},{\varvec{u}}), \end{aligned}$$

  which shows that condition (18) holds. Moreover, Lemma 17 guarantees that condition (19) is satisfied, too.

Let ${\varvec{v}}\in K$, $n\in \mathbb {N}$ and let ${\varvec{v}}_n=\alpha _n{\varvec{v}}$ where

$$\begin{aligned} \alpha _n=\min \Big \{\frac{g_n}{g},\frac{k_n}{k}\Big \}>0. \end{aligned}$$

(86)

Then, using the definitions of the sets $K_n$ and K it is easy to see that ${\varvec{v}}_n\in K_n$. We now use Lemma 18 and Definition 7 to see that $P_n{\varvec{v}}_n=0_{V^*}$. On the other hand, definition (86) and assumption (82) show that $\alpha _n\rightarrow 1$. Therefore, since ${\varvec{v}}_n=\alpha _n{\varvec{v}}$ we deduce that ${\varvec{v}}_n\rightarrow {\varvec{v}}$ in V. We conclude from here that condition (14) is satisfied.

Let ${\varvec{v}}\in V$, ${\varvec{w}}\in V$ and let $n\in \mathbb {N}$. Then, using the definitions (80) and (84) combined with inequality (85), assumption (73)(a) and (56) we find that

$$\begin{aligned}&\langle P_n{\varvec{v}}-P{\varvec{v}},{\varvec{w}}\rangle =\int _{\varOmega }(\widetilde{P}{\varvec{\varepsilon }}({{\varvec{v}}})-\widetilde{P}_n{\varvec{\varepsilon }}({{\varvec{v}}}))\cdot {\varvec{\varepsilon }}({\varvec{w}})\,dx\\&\qquad + \int _{\varGamma _3}\,\big (p_\nu (v_\nu -g_n)-(p_\nu (v_\nu -g)\big ) w_\nu \,da\\&\quad \le \Vert \widetilde{P}_n{\varvec{\varepsilon }}({{\varvec{v}}})-\widetilde{P}{\varvec{\varepsilon }}({{\varvec{v}}})\Vert _{Q}\Vert {\varvec{\varepsilon }}({\varvec{w}})\Vert _{Q}+L_p|g_n-g|\int _{\varGamma _3}\Vert {\varvec{w}}\Vert \,da\\&\quad \le |k_n-k|\Vert {\varvec{w}}\Vert _{V}+L_p|g_n-g|(meas\,\varGamma _3)^{\frac{1}{2}}\Vert {\varvec{w}}\Vert _{L^2(\varGamma _3)^d}\\&\quad \le \Big (|k_n-k|+L_p|g_n-g|(meas\,\varGamma _3)^{\frac{1}{2}}\Vert \gamma \Vert \Big )\Vert {\varvec{w}}\Vert _{V}. \end{aligned}$$

It follows from here that

$$\begin{aligned} \Vert P_n{\varvec{v}}-P{\varvec{v}}\Vert _{V^*}\le |k_n-k|+L_p|g_n-g|(meas\,\varGamma _3)^{\frac{1}{2}}\Vert \gamma \Vert \qquad \forall \,{\varvec{v}}\in V,\ n\in \mathbb {N}. \end{aligned}$$

(87)

Consider now a sequence $\{{\varvec{u}}_n\}$ of elements of V. We write (87) with ${\varvec{v}}={\varvec{u}}_n$ then we use (82) to deduce that

$$\begin{aligned} \Vert P_n{\varvec{u}}_n-P{\varvec{u}}_n\Vert _{V^*}\rightarrow 0. \end{aligned}$$

(88)

The convergence (88) combined with the pseudomonotonicity of P shows that condition (38) holds and, by Lemma 11 it follows that (16)(a) holds, too. On the other hand, condition (16)(b) is a consequence of Lemma 18.

We conclude from above that conditions (14), (16), (17), (18) and (19) are satisfied. Moreover, recall that assumptions (57)–(64) imply conditions (4)–(9) with $X=V$ and A, $\varphi$, j, ${\varvec{f}}$ given by (68)–(71). We are in a position to use Theorem 10 in order to conclude the proof. $\square$

In addition to the mathematical interest in the convergence result in Theorem 10(ii), it is important from the mechanical point of view, since it provides the link between the weak solutions of two different models of contact. Indeed, Problem $\mathcal{Q}_n$ describes the frictionless contact of an elastic material, with a deformable foundation covered by a crust. In contrast, Problem $\mathcal{Q}$ describes the frictionless contact of a locking material with a rigid-deformable foundation covered by a crust. Note that Problem $\mathcal{Q}$ is nonsmooth since it contains unilateral constraints both in the constitutive law and the contact boundary condition. In contrast, Problem $\mathcal{Q}_n$ is smoother, since these constraints have been removed. Theorem 10 shows that we can approach the solution of the nonsmooth contact problem $\mathcal{Q}$ by the solution of a smoother contact problem $\mathcal{Q}_n$, as the penalty parameter $\lambda _n$ converges to zero and the convergences (82) hold. The novelty of this result arises from the fact that it guarantees the convergences of the solution even when the penalty problems are constructed with the parameters $g_n$ and $k_n$, different from g and k, provided that (82) holds. This is important in applications, since the data g and k are obtained from experiments and, therefore, their value can slightly vary due to the error measurements.