A Simple Derivation and Classical Representations of Energy Variations for Curved Cracks

Abstract

We consider configurational variations of a homogeneous (anisotropic) linear elastic material $\Omega \subset \mathbb {R}^n$ with a crack K. First, we provide a simple way to compute configurational variations of energy by means of a volume integral. Then, under increasing information on the regularity of the displacement field we show how to obtain classical representations of the energy release due to Eshelby, Rice and Irwin. A rigorous functional setting for these representations to hold is provided.

1 Introduction

In fracture mechanics it is common to employ a variational approach in which evolutions are defined in terms of energies and their variations, most often with respect to variations of the crack set. This approach dates back to Griffith’s criterion [5] which is formulated right in terms of energy release G (i.e. variations of potential energy with respect to variations of crack surface area) and toughness $G_c$ (a material parameter). Actually, the mathematical argument of [5] was “just” an algebraic estimate of the energy release in terms of material and geometrical parameters, based on the results of Inglis [8] on stress singularities around elliptical holes and cracks.

After [5] energy release became a fundamental concept in Mechanics, through the years it attracted much attention and has been the object of several fundamental contributions. A milestone is the study of Ehselby [4] which lead to volume and surface integral representations of the energy release in terms of energy momentum tensor $\mathbb {E}$. It is noteworthy that Eshelby’s works gave general integral representations applicable in many different context; this is indeed a substantial theoretical improvement after [5].

Later, Irwin [9] devised an explicit formula for the energy release in terms of the stress intensity factors, based on Westergaard’s expansions [14] of the stress around the tip, and Rice [13] introduced a contour integral representation of the energy release, called the J-integral; this is again a general representation result, infact similar to that of [4], which does not rely on the singular behaviour of the stress.

Let us turn to the mathematical literature on configurational energy variations for elasticity problems. First we will make a couple of considerations of technical importance on outer variations and singularities.

Consider a crack $K_0$ and an incremental variation $K_h$. Being $K_h$ increasing, the spaces $\mathcal {W}_h$ of admissible displacement and the corresponding spaces $\mathcal {V}_h$ of admissible variations are increasing as well. If $w_h$ (for $h \ge 0$) denote the equilibrium configuration in $\mathcal {W}_h$, then for $h>0$ and $h=0$ respectively the variational formulation yields

$$\begin{aligned} \int _{\Omega {\setminus } K_h} \varvec{\sigma }(w _h) : \varvec{\epsilon }( v_h ) = 0 \qquad \text {for every}\;v_h \in \mathcal {V}_h, \\ \int _{\Omega {\setminus } K_0} \varvec{\sigma }(w _0) : \varvec{\epsilon }( v_0 ) = 0 \qquad \text {for every}\;v_0 \in \mathcal {V}_0. \end{aligned}$$

Since the spaces are monotone it holds also

$$\begin{aligned} \int _{\Omega {\setminus } K_h} \varvec{\sigma }( w_h ) : \varvec{\epsilon }( v_h - v_0 ) \, dx = 0 \qquad \text {for every}\;v_h \in \mathcal {V}_h\;\mathrm{and}\; v_0 \in \mathcal {V}_0 . \end{aligned}$$

Hence by symmetry and coercivity the variation of energy can be written as

$$\begin{aligned} \tfrac{1}{2} \int _{\Omega {\setminus } K_h} \varvec{\sigma }(w _h) : \varvec{\epsilon }( w_h ) - \varvec{\sigma }(w _0) : \varvec{\epsilon }( w_0 ) \, dx&= \tfrac{1}{2} \int _{\Omega {\setminus } K_h} \varvec{\sigma }( w_0 + w_h ) : \varvec{\epsilon }( w_0 - w_h ) \, dx \\&= \tfrac{1}{2} \int _{\Omega {\setminus } K_h} \varvec{\sigma }( w_0 ) : \varvec{\epsilon }( w_0 - w_h ) \, dx \\&= \tfrac{1}{2} \int _{\Omega {\setminus } K_h} \varvec{\sigma }( w_0 - w_h ) : \varvec{\epsilon }( w_0 - w_h ) \, dx \\&\ge C \Vert w_h - w_0 \Vert ^2 , \end{aligned}$$

where $\Vert \cdot \Vert$ denotes the norm in $\mathcal {W}_h$. Hence, if the variation of energy is O(h) it tuns out that $w_0 - w_h = O ( h^{1/2})$ in $\mathcal {W}_h$. In particular the “speed” $w'_0$ is not well defined.

For this reason, it seems not convenient, even if natural, to frame the energy release in terms of linear outer variations; as we shall see it is more effective to employ inner variations, including in a broad sense blow up techniques.

Let us turn to regularity, which is a delicate point often behind the mathematical difficulties on energy release rate. In the mathematical literature there are several results under many different hypothesis; here we will just mention a couple of them, a classical and a recent one. The first is a well known result of Grisvard [7] characterizing the regular and singular part of solutions; more precisely, it asserts that for a polygonal planar domain the displacement field in a neighbourhood of the crack tip takes the form

$$\begin{aligned} u = K_{{\mathrm{I}}} \hat{u}_{\mathrm{I}}+ K_\mathrm{II}\hat{u}_\mathrm{II}+ \tilde{u} , \end{aligned}$$

where $K_{\mathrm{I}}$ and $K_\mathrm{II}$ are the stress intensity factors and $\hat{u}_i = \rho ^{1/2} U_i (\theta )$ (in local polar coordinates) while $\tilde{u}$ belongs to the Sobolev space $W^{2,2}$.

A remarkable generalization for a wide class of cracks has been recently obtained by Babadjian et al. [1] (extending [2]) together with an “indirect representation” of the energy release, written in terms of a minimization problem. Another recent result, in the same spirit of our work but with a different technical approach, may be found in [10].

Now, we present the content of our paper. First of all, we will work with curved cracks, technically of class $W^{1,\infty }$ or $W^{2,\infty }$ in $\mathbb {R}^n$ for $n \ge 2$, and we will employ homogeneous linear (anisotropic) elasticity. Using a family of diffeomorphisms $\Psi _h$ to represent the variation of the domain, as a sort of shape or configuration derivative, we will provide first a simple way to compute a volume integral representation of energy variations. We remark that our proof does not employ the primal-dual formulation of linear elasticity employed by Destuynder and Djaoua [3], it is indeed purely based on variational formulations; moreover it does not rely on regularity (or singularity) properties of solutions. For this reason it holds in any space dimensions and for anisotropic elasticity.

Then, we show how to recast our volume integral representation in terms of energy momentum tensor, contour integrals and stress intensity factors. It is interesting to remark that for the first it is basically enough to employ symmetry of the stress while for the second and the third some more information on the regularity of solutions is needed: for the contour integral we employ the fact that solutions are of class $W^{2,2}$ away from the crack front while for the stress intensity factors we obviously need the exact form of the singularities (and thus the representation holds true only in the plane strain setting and for isotropic elasticity).

To conclude, it is fair to say that it is still not clear (but under investigation) a possible way to extend the current proof to more general variations of the domain, including in particular the case of kinked cracks.

2 Notation

Let $\Omega \subset \mathbb {R}^n$ (for $n\ge 2$) be a bounded, connected, open set with Lipschitz boundary $\partial \Omega$. Assume that the initial crack $K \subset \Omega$ is closed and of class $W^{1,\infty }$. Variations of the crack will be of the form $K_h = \Psi _h (K)$ for a suitable family $\Psi _h$ of bi-Lipschitz diffeomorphisms. More precisely, assume that $\Psi _h$ is a diffeomorphism of $\Omega$ of the form $\Psi _h (x) = x + h \Phi _h (x)$ for $\Phi _h$ uniformly bounded in $W^{1,\infty } (\Omega ,\mathbb {R}^n)$ with $\Phi _h (x) = 0$ on $\partial \Omega$ and such that $D \Phi _h \rightarrow D \Phi$ a.e. in $\Omega$ (and thus $\Phi _h \mathop {\rightharpoonup }\limits ^{*}\Phi$ in $W^{1,\infty }( \Omega , \mathbb {R}^n)$). Note that configurational variations of this type are not necessarily “incremental”, i.e. the family of cracks $K_h = \Psi _h (K)$ is not necessarily increasing. Incremental variations are possible but they require more regularity of the crack set K, as explained in the next example.

2.1 Incremental Variations in the Plane Strain Setting

Assume that the initial crack K and its incremental variations $K_h$ are both represented by the graph of a function k of class $W^{2,\infty }$, i.e. that $K_h = \{ ( x_1 , k (x_1) ) : x_1 \in [- l, h ] \}$ for $h \ge 0$. Assume also, for simplicity, that $k(0) = k'(0)=0$.

Let us represent the variations $K_h$ in terms of configurational variations of the initial crack K. To this end, let $\phi \in W^{1,\infty } ( \Omega , [0,1] )$ with $\phi =1$ in a neighbourhood of the origin and $\mathrm {supp} (\phi ) \subset \subset \Omega$ and define

$$\begin{aligned} \Psi _h ( x_1 , x_2 ) = \big ( x_1 + h \phi (x_1, x_2) , x_2 + k ( x_1 + h \phi (x_1, x_2)) - k (x_1) \big ) . \end{aligned}$$

Let us write $\Psi _h (x) = x + h \Phi _h (x)$ (for $h > 0$) where

$$\begin{aligned} \Phi _h (x_1 , x_2) = \left( \phi (x_1, x_2) \, , \frac{k ( x_1 + h \phi (x_1, x_2)) - k (x_1) }{h} \right) \end{aligned}$$

and let $\Phi (x_1 , x_2) = \phi (x_1, x_2) ( 1 , k' (x_1) )$. Note that $\Phi _h = \Phi = 0$ if $\phi =0$.

Lemma 2.1

$\Phi _h \rightarrow \Phi$ strongly in $L^{\infty }( \Omega , \mathbb {R}^n)$. Moreover $D \Phi _h \rightarrow D \Phi$ a.e. in $\Omega$ and $D \Phi _h$ is bounded in $L^{\infty }( \Omega , \mathbb {R}^{2 \times 2})$.

Proof

It is easy to check that $\Phi _h \rightarrow \Phi$ a.e. in $\Omega$. Write $D \Phi = \nabla \phi \times ( 1 , k') + \phi \, k'' \, \hat{e}_{2} \times \hat{e}_1$ and

$$\begin{aligned} D \Phi _h = \left( \begin{array}{ccc} \phi _{,1} &{} &{} \phi _{,2} \\ {\displaystyle \frac{k' ( x_1 + h \phi ) - k'(x_1)}{h} } + k' ( x_1 + h \phi ) \phi _{,1} &{} &{} k' ( x_1 + h \phi ) \phi _{,2} \end{array} \right) . \end{aligned}$$

Then, by continuity and a.e. differentiability of the Lipschitz function $k'$, it follows that $D \Phi _h \rightarrow D \Phi$ a.e. in $\Omega$. Finally, $D \Phi _h$ is uniformly bounded in $L^\infty ( \Omega , \mathbb {R}^{2 \times 2})$. $\square$

Remark 2.2

It is fair to remark that within these variations it is not possible to include kinked cracks, since in that case only $h D \Phi _h$ is bounded in $L^\infty ( \Omega , \mathbb {R}^{2 \times 2})$.

2.2 Incremental Variations in the Three Dimensional Setting

Assume again that the initial crack $K \subset \Omega$ is represented by a graph, i.e. that $K = {\mathcal K} (K^\flat )$ with ${\mathcal K} (x_1, x_2) = (x_1, x_2 , k (x_1 , x_2) )$ for k of class $W^{2,\infty }$ and $K^\flat \subset \mathbb {R}^2$ compact and connected. Let $\phi \in W^{1,\infty } (\Omega , \mathbb {R}^3)$ with $| \phi | \le 1$ and $\mathrm {supp}(\phi ) \subset \subset \Omega$. For $h > 0$ define the mapping

$$\begin{aligned} \Psi _h (x) = x + \big ( h \phi _1 (x) , h \phi _2 (x) , k ( x_1 + h \phi _1 (x) , x_2 + h \phi _2 (x) ) - k (x_1,x_2) \big ) \end{aligned}$$

and the corresponding variations of the crack $K_h = \Psi _h ( K)$. Denote also ${\mathcal K} _h (x_1 , x_2) = \Psi _h \circ {\mathcal K} ( x_1 , x_2)$ so that $K_h = {\mathcal K}_h (K^\flat )$. Introducing $\phi ^\flat (x_1 , x_2) = \phi ( x_1 , x_2 , k (x_1 , x_2))$ the map ${\mathcal K} _h$ can be written as

$$\begin{aligned} {\mathcal K} _h (x_1 , x_2)&= \big (x_1 + h \phi ^\flat _1 (x) , x_2 + h \phi ^\flat _2 (x) , k ( x_1 + h \phi ^\flat _1 (x) , x_2 + h \phi ^\flat _2 (x) ) \big ) = {\mathcal K} ( x^h_1 , x^h_2) , \end{aligned}$$

where $( x^h_1 , x^h_2) = ( x_1 , x_2) + h \phi ^\flat (x_1 , x_2)$ represent the corresponding variation of the domain $K^\flat$.

2.3 Energy

We consider homogeneous linearized energy with density

$$\begin{aligned} W ( D u) = \tfrac{1}{2} \, Du : \mathbf {C}[Du] = \tfrac{1}{2} \, \varvec{\epsilon }(u) : \varvec{\sigma }(u) , \end{aligned}$$

for $\varvec{\epsilon }(u) = (Du + Du^T) / 2$ and $\mathbf {C}[Du] = \varvec{\sigma }(u)$. Note that for the moment, and in most of the paper, we will not assume isotropic elasticity, which will be needed only in Sect. 6 to obtain Irwin’s formula.

For $\partial _D \Omega$ relatively open in $\partial \Omega$ and $g \in W^{1,2} (\Omega , \mathbb {R}^n)$ let

$$\begin{aligned} {\mathcal U}_h = \{ u \in W^{1,2} (\Omega {\setminus } K_h , \mathbb {R}^n) : u = g \ \partial _D\Omega \} \end{aligned}$$

be the space of admissible displacements.

For $f \in W^{1,p} (\Omega , \mathbb {R}^n)$ (for some $p>1$) the energy is of the form $F (u) = E (u) - L (u)$ where

$$\begin{aligned} E(u) = \int _{\Omega {\setminus } K_h} W ( D u ) \, dx , \qquad L(u) = \int _{\Omega {\setminus } K_h} f \cdot u \, dx . \end{aligned}$$

Now, given $u \in \,{\mathcal U}_h$ by a change of variable, write

$$\begin{aligned} E ( u) = E_h ( u \circ \Psi _h) = \tfrac{1}{2} \int _{\Omega {\setminus } K} D (u \circ \Psi _h) : \mathbf {C}_h [ D (u \circ \Psi _h) ] \, dx \end{aligned}$$

(1)

where $\mathbf {C}_h [ F ] = \mathbf {C}[ F D \Psi _h^{-1} ] D \Psi _h^{-T} \det D \Psi _h$ and

$$\begin{aligned} L (u) = L_h (u \circ \Psi _h ) = \int _{\Omega {\setminus } K} f_h \cdot ( u \circ \Psi _h) \, dx \end{aligned}$$

(2)

for $f_h = (f \circ \Psi _h) \, \det D \Psi _h$. Since $\Psi _h$ induces a one to one correspondence between ${\mathcal U}_0$ and ${\mathcal U}_h$ for our purposes it will be equivalent to consider the energy $F_h (u) = E_h (u) - L_h(u)$ in ${\mathcal U}_0$ instead of the energy $F (u) = E (u) - L (u)$ in ${\mathcal U}_h$.

3 Variational Representation of Energy Variations

3.1 Expansions

Lemma 3.1

$\Psi _h \rightarrow \mathrm {id}$ in $W^{1,\infty } (\Omega , \mathbb {R}^n)$. Moreover, for $h \ll 1$ we have the following expansions

$$\begin{aligned} D \Psi _h^{-1} = \sum _{n=0}^\infty ( - h D \Phi _h )^n&= I - h D \Phi _h + o (h) \\ \det D \Psi _h&= 1 + h \, \mathrm {tr} D \Phi _h + o (h) , \end{aligned}$$

which hold in $L^\infty (\Omega , \mathbb {R}^{n \times n})$ (and thus a.e. in $\Omega$).

Proof

Since $D \Psi _h (x) = I + h D \Phi _h (x)$ with $D \Phi _h$ uniformly bounded it is clear that $\Psi _h \rightarrow \mathrm {id}$ in $W^{1,\infty } (\Omega , \mathbb {R}^n)$. Moreover for $h \ll 1$ the inverse matrix can be expanded as

$$\begin{aligned} D \Psi _h^{-1} = \sum _{n=0}^\infty ( - h D \Phi _h )^n = I - h D \Phi _h + o (h) . \end{aligned}$$

Finally $\mathrm {det} D \Phi _h = 1 + h \, \mathrm {tr} D \Phi _h + o (h)$. All the expansions above hold in $L^\infty (\Omega , \mathbb {R}^{n \times n} )$. $\square$

Lemma 3.2

Let $w \in W^{1,2} ( \Omega {\setminus } K , \mathbb {R}^n)$, then $\mathbf {C}_h [ Dw ] \rightarrow \mathbf {C}[Dw]$ in $L^2 ( \Omega {\setminus } K , \mathbb {R}^{n \times n})$ and

$$\begin{aligned} \frac{ \mathbf {C}_h [Dw] - \mathbf {C}[Dw]}{h} \ \rightarrow \ \mathbf {C}' [Dw] = - \mathbf {C}[Dw D{\Phi }_0] - \mathbf {C}[Dw] D{\Phi ^T_0} + \mathbf {C}[Dw] \mathrm {tr} D{\Phi }_0 \end{aligned}$$

in $L^2 ( \Omega {\setminus } K , \mathbb {R}^{n \times n})$. Moreover $f_h \rightarrow f$ in $L^p ( \Omega , \mathbb {R}^n)$ and

$$\begin{aligned} \frac{ f_h - f }{h} \rightharpoonup f' = Df \, \Phi + f \, \mathrm {tr} D \Phi \quad \text{ in } L^p ( \Omega , \mathbb {R}^n)\text{. } \end{aligned}$$

Proof

Write $\mathbf {C}_h [Dw] = \mathbf {C}[ Dw D \Psi _h^{-1} ] D \Psi _h^{-T} \det D \Psi _h$. Since $D\Psi _h^{-1} \rightarrow I$ in $L^{\infty } (\Omega , \mathbb {R}^{n \times n})$ (by Lemma 3.1) it follows that $\mathbf {C}_h [Dw] \rightarrow \mathbf {C}[Dw]$ in $L^2 ( \Omega {\setminus } K , \mathbb {R}^{n \times n})$.

From the expansions of Lemma 3.1 we get, a.e. in $\Omega$,

$$\begin{aligned} \mathbf {C}_h [Dw]= & {} \mathbf {C}\big [ Dw D \Psi _h^{-1} \big ] \, D \Psi _h^{-T} \mathrm {det}D \Psi _h \\= & {} \mathbf {C}\big [ Dw \big (I - h D{\Phi _h} + o(h) \big ) \big ] \big (I - h D{\Phi _h} + o(h)\big )^{T} \big (1 + h \mathrm {tr} D {\Phi _h} + o(h) \big ) \\= & {} \mathbf {C}[ Dw ] + h \big ( - \mathbf {C}[Dw D{\Phi _h}] - \mathbf {C}[Dw] D{\Phi ^T_h} + \mathbf {C}[Dw] \mathrm {tr} D {\Phi _h} \big ) + o(h) \\= & {} \mathbf {C}[ Dw ] + h \mathbf {C}'_h [Dw] + o (h) , \end{aligned}$$

where

$$\begin{aligned} \mathbf {C}'_h [Dw] = - \mathbf {C}[Dw D{\Phi _h}] - \mathbf {C}[Dw] D{\Phi ^T_h} + \mathbf {C}[Dw] \mathrm {tr} D{\Phi _h}. \end{aligned}$$

Since $D\Phi _h$ is uniformly bounded in $L^2 ( \Omega {\setminus } K , \mathbb {R}^{n \times n})$ and converge a.e. to $D \Phi$, by dominated convergence it follows that $\mathbf {C}'_h [ Dw] \rightarrow \mathbf {C}' [Dw]$ in $L^2 ( \Omega {\setminus } K , \mathbb {R}^{n \times n})$.

The convergence to $f'$ of the difference quotient follows from Lemmas 2.1 and 3.1 together with a classical result on difference quotient for Sobolev functions, see instance [11]. $\square$

3.2 Variational Representation

In this section we show a volume integral representation of the energy release, obtained without any regularity assumption on the displacement field.

Let $w_h \in \mathrm {argmin} \,\{ F (w) : w \in {\mathcal U}_h \}$ be the displacement field in $\Omega {\setminus } K_h$ and let $u_h \in \mathrm {argmin} \,\{ F_h (u) : u \in {\mathcal U}_0 \}$ be its pull back in $\Omega {\setminus } K$. We will denote by $G_\Phi (u_0)$ the variation of energy, i.e.

$$\begin{aligned} G_\Phi ( u_0 ) = \lim _{h \rightarrow 0} \frac{ F (w_h) - F (u_0) }{h} = \lim _{h \rightarrow 0} \frac{ F_h (u_h) - F (u_0) }{h} , \end{aligned}$$

(3)

since $F (w_h) = F_h (u_h)$.

Theorem 3.3

The variation of energy reads

$$\begin{aligned} G_\Phi (u_0) = \tfrac{1}{2} \int _{\Omega {\setminus } K} D u_0 : \mathbf {C}' [D u_0] \, dx - \int _{\Omega {\setminus } K} f' \cdot u_0 \, dx , \end{aligned}$$

(4)

where $\mathbf {C}'$ and $f'$ have been defined in Lemma 3.2.

Proof

First, let us see that $u_h \rightharpoonup u_0$ in $W^{1,2} ( \Omega {\setminus } K, \mathbb {R}^n)$. For convenience, let us introduce the bilinear forms

$$\begin{aligned} A_h(u,v) = \int _{\Omega {\setminus } K} Dv : \mathbf {C}_h [D u_h ] \, dx , \qquad A ( u,v) = \int _{\Omega {\setminus } K} Dv : \mathbf {C}[ Du ] \, dx , \end{aligned}$$

so that the Euler–Lagrange equation for $u_h$ reads $A_h ( u_h , v) = L_h(v)$ for every $v \in {\mathcal V}_0$. It is not difficult to check that $A_h$ is elliptic and continuous in $W^{1,2} (\Omega {\setminus } K , \mathbb {R}^n)$ uniformly with respect to h. It follows that $u_h$ is bounded in $W^{1,2} (\Omega {\setminus } K , \mathbb {R}^n)$ and thus (up to subsequences) that $u_h \rightharpoonup w$ in $W^{1,2} (\Omega {\setminus } K , \mathbb {R}^n)$ and thus strongly in $L^2 (\Omega {\setminus } K , \mathbb {R}^n)$. Passing to the limit in the variational formulation $A_h ( u_h,v ) = L_h (v)$ leads to $A ( w, v) = L (v)$ for every $v \in {\mathcal V}_0$. Hence $w=u_0$ and $u_h \rightharpoonup u_0$ in $W^{1,2} (\Omega {\setminus } K , \mathbb {R}^n)$.

By the variational formulations, for every $u \in {\mathcal U}_0$ we have

$$\begin{aligned} A_h ( u_h , u_h) = A_h ( u_h - u , u_h) + A_h ( u , u_h) = L_h ( u_h - u) + A_h ( u , u_h) . \end{aligned}$$

Hence

$$\begin{aligned} F_h ( u_h)&= \tfrac{1}{2} A_h ( u_h , u_h) - L_h ( u_h) = \tfrac{1}{2} L_h ( u_h - u_0) + \tfrac{1}{2} A_h ( u_0 , u_h) - L_h ( u_h) \\&= \tfrac{1}{2} A_h ( u_0 , u_h) - \tfrac{1}{2} L_h ( u_h+u_0) . \end{aligned}$$

In the same way $F ( u_0 ) = \tfrac{1}{2} A ( u_h , u_0) - \tfrac{1}{2} L ( u_0+u_h)$. Writing explicitly we get

$$\begin{aligned} \tfrac{1}{2} A_h ( u_0 , u_h ) - \tfrac{1}{2} A ( u_h , u_0) = \tfrac{1}{2} \int _{\Omega {\setminus } K} Du_h : \big ( \mathbf {C}_h [ D u_0 ] - \mathbf {C}[ Du_0 ] \big ) \, dx \end{aligned}$$

and

$$\begin{aligned} \tfrac{1}{2} L_h (u_h + u_0) - \tfrac{1}{2} L (u_h + u_0) = \tfrac{1}{2} \int _{\Omega {\setminus } K} (f_h - f) \cdot ( u_h + u_0) \, dx . \end{aligned}$$

Hence by Lemma 3.2

$$\begin{aligned} \frac{F_h ( u_h) - F ( u_0)}{h} \ \rightarrow \ \tfrac{1}{2} \int _{\Omega {\setminus } K} Du_0 : \mathbf {C}' [ D u_0 ] \, dx - \int _{\Omega {\setminus } K} f' \cdot u_0 \, dx , \end{aligned}$$

which concludes the proof. $\square$

Note that Theorem 3.3 employs only the weak convergence of $u_h$, in particular it does not rely on quantitative estimates of $u_h - u_0$. Note also that $G_\Phi (u_0)$ is the sum of a configurational force $f'$ and a configurational stress $\mathbf {C}' [ Du_0]$. Finally, introducing $F' (u) = \tfrac{1}{2} A' (u , u) - L' (u)$ where

$$\begin{aligned} A' ( u , w) = \int _{\Omega {\setminus } K} Du : \mathbf {C}' [Dw] \, dx , \qquad L' (u) = \int _{\Omega {\setminus } K} f' \cdot u \, dx , \end{aligned}$$

Eq. (4) reads simply $G_\Phi ( u_0 ) = F' (u_0)$.

Remark 3.4

In the case of “incremental variations” $G_\Phi$ provides the energy release up to a multiplicative constant. Strictly speaking, the classical definition of elastic energy release (for incremental cracks) would be

$$\begin{aligned} {\mathcal {G}} ( u_0) = - \lim _{h \rightarrow 0} \frac{ F_h (u_h) - F (u_0) }{ {\mathcal H}^{n-1} ( K_h {\setminus } K) }, \end{aligned}$$

i.e. the negative derivative with respect to variations of crack surface area, and not with respect the parametrization parameter h. Thus, apart from the minus sign, $G_\Phi (u_0)$ differs from $\mathcal {G}(u_0)$ by a multiplicative constant, which measures the variation of surface area with respect to h. (Under the assumptions of Sect. 2.1 it turns out that $G_\Phi (u_0) = - \mathcal {G} (u_0)$ since the length $\ell (h)$ of the cracks $K_h$ is

$$\begin{aligned} \ell (h) = \int _{-l}^h (1 + (k'(s))^2 )^{1/2} \, ds \end{aligned}$$

and thus $\ell '(0)=1$). Finally, note that $G_\Phi (u_0)$ depends linearly on $\Phi$, through $\mathbf {C}'$ and $f'$. As a matter of fact the energy release depends only on the variations of the crack; indeed, if $K_h = \Psi _h (K) = \hat{\Psi }_h (K)$ for every $h>0$ then $F_h ( u_h ) = F_h ( \hat{u}_h ) = F (w_h)$ and thus by definition (3) it is independent of the choice of the configurational map.

In the next sections we will obtain from (4) a cascade of classical representations of energy variations (including of course the energy release): to re-write (4) we will use both algebraic and regularity properties of $u_0$ but we will not use any more the definition (3).

4 Representation with the Energy Momentum Tensor

With few algebraic manipulations which do not require further regularity of $u_0$ we can write (4) in terms of the Eshelby tensor

$$\begin{aligned} \mathbb {E} (u_0) = W ( D u_0) I - Du^T_0 \varvec{\sigma }(u_0) . \end{aligned}$$

Theorem 4.1

The variation of energy can be written as

$$\begin{aligned} G_\Phi (u_0) = \int _{\Omega {\setminus } K} \mathbb {E} (u_0) : D \Phi \, dx - \int _{\Omega {\setminus } K} f' \cdot u_0 \, dx , \end{aligned}$$

(5)

where $f' = D\!f \, \Phi + f \, \mathrm {tr} D \Phi$.

Proof

Since

$$\begin{aligned} F : \mathbf {C}[F] M^T = F M : \mathbf {C}[F] = \mathbf {C}[FM] : F = F : \mathbf {C}[FM] \end{aligned}$$

we can write (for $M= D \Phi$)

$$\begin{aligned} F : \mathbf {C}' [ F ]= & {} F : ( - \mathbf {C}[ F D \Phi ] - \mathbf {C}[F] D \Phi ^T + \mathbf {C}[F] \mathrm {tr} D \Phi ) = \\= & {} F : ( - 2 \mathbf {C}[F] D \Phi ^T + \mathbf {C}[F] \mathrm {tr} D \Phi ) \\= & {} F : \mathbf {C}[F] ( -2 D \Phi ^T + \mathrm {tr} D \Phi I ) . \end{aligned}$$

Remembering that $D \Phi : I = \mathrm {tr} D \Phi$ and that $\tfrac{1}{2} F : \mathbf {C}[F] = W (F)$ we can write

$$\begin{aligned} \tfrac{1}{2} F : \mathbf {C}' [F] = - D \Phi : F^T \mathbf {C}[F] + D \Phi : W (F) I . \end{aligned}$$

For $F = Du_0$ we get

$$\begin{aligned} \tfrac{1}{2} D u_0 : \mathbf {C}' [D u_0] = - D \Phi : D u_0^T \varvec{\sigma }(u_0) + D \Phi : W (D u_0) I = D \Phi : \mathbb {E} (u_0). \end{aligned}$$

Hence (5) follows from (4). $\square$

5 Representation with Contour Integrals

In this section we will show the representation of $G_\Phi$ by means of contour integrals. We will get first a “generalized J-integral” [12] and then, under special hypothesis, the classical path-independent J-integral [13]. We will assume that the crack is of class $W^{2,\infty }$, that the map $\Phi$ is compactly supported, tangent to the crack (i.e. that $\Phi \cdot \hat{n} = 0$ on K) and that $f'=0$.

In order to define a contour integral it is necessary to have more information on the regularity of the displacement field $u_0$. Singular expansions in terms of the stress intensity factors are not strictly necessary; what is actually needed is indeed the “elliptic regularity” of $u_0$. Let $\Gamma$ denote the crack front or tip, then by [6, 7] $u_0 \in W^{2,2} ( \Omega ' {\setminus } K , \mathbb {R}^n)$ for every $\Omega ' \subset \Omega$ with $\bar{\Omega }' \subset \Omega$ and $\Gamma \cap \bar{\Omega }' = \emptyset$ (note that $\Omega '$ may intersect to crack K but not its front/tip $\Gamma$). Therefore, $\mathbb {E} (u_0) \in W^{1,q} ( \Omega ' {\setminus } K , \mathbb {R}^n)$ for some $q > 1$ and $\varvec{\sigma }( u_0) \hat{n} = 0$ in $K^\pm \cap \Omega '$ in the sense of traces, and thus in $L^1 ( K \cup \Omega ' , \mathbb {R}^n)$.

Lemma 5.1

The following representation holds,

$$\begin{aligned} G_\Phi (u_0) = \int _{\Omega {\setminus } K} \mathrm {div}( \mathbb {E}^T (u_0) \Phi ) \, dx . \end{aligned}$$

In particular $\mathrm {div}( \mathbb {E}^T (u_0) \Phi ) \in L^1 ( \Omega {\setminus } K)$.

Proof

Denote for simplicity $\mathbb {E} = \mathbb {E} (u_0)$, $\varvec{\sigma }= \varvec{\sigma }(u_0)$ and $u=u_0$.

Since $\Phi \in W^{1,\infty }$ we have $\mathbb {E}^T \Phi \in W^{1,q}_{\text{ loc }}(\Omega {\setminus } K)$ for some $q > 1$. Let us check that

$$\begin{aligned} \mathrm {div}( \mathbb {E} ) = 0 , \qquad \mathrm {div}( \mathbb {E}^T \Phi ) = \mathrm {div}(\mathbb {E} ) \cdot \Phi + \mathbb {E} : D \Phi = \mathbb {E} : D \Phi . \end{aligned}$$

(6)

Denote by ${\mathrm {div}_k}$ the k-component of the vectorial divergence. Being $\mathbf {C}_{ijmn} = \mathbf {C}_{mnij}$ and $u \in W^{2,2}_{\text{ loc }}(\Omega {\setminus } K, \mathbb {R}^2)$ we have

$$\begin{aligned} {\mathrm {div}_k}\big ( W (Du) I \big )&= \tfrac{1}{2} ( \varvec{\sigma }: D u )_{,k} = \tfrac{1}{2} ( \varvec{\sigma }_{ij} \, u_{i,j} )_{,k} = \tfrac{1}{2} ( \mathbf {C}_{ijmn} u_{m,n} \, u_{i,j} )_{,k} \\&= \tfrac{1}{2} \mathbf {C}_{ijmn} u_{m,nk} \, u_{i,j} + \tfrac{1}{2} \mathbf {C}_{mnij} u_{m,n} \, u_{i,jk} = \varvec{\sigma }_{ij} \, u_{i,jk} , \end{aligned}$$

$$\begin{aligned} {\mathrm {div}_k}( Du^T \varvec{\sigma })&= ( Du^T \varvec{\sigma })_{kj,j} = ( u_{i,k} \, \varvec{\sigma }_{ij} )_{,j} = u_{i,kj} \, \varvec{\sigma }_{ij} + u_{i,k} \, \varvec{\sigma }_{ij,j}\\&= u_{i,jk} \, \varvec{\sigma }_{ij} + u_{i,k} \, \varvec{\sigma }_{ij,j} . \end{aligned}$$

Hence ${\mathrm {div}_k}( \mathbb {E} ) = {\mathrm {div}_k}( W I - D u^T \varvec{\sigma }) = - u_{i,k} \, \varvec{\sigma }_{ij,j} = - u_{,k} \cdot \mathrm {div}(\varvec{\sigma }) = 0$.

By the regularity of $\mathbb {E}^T \Phi$, we can write

$$\begin{aligned} \mathrm {div}( \mathbb {E}^T \Phi ) = ( \mathbb {E}_{ji} \Phi _j )_{,i} = \mathbb {E}_{ji,i} \Phi _j + \mathbb {E}_{ji} \Phi _{j,i} = \mathrm {div}(\mathbb {E} ) \cdot \Phi + \mathbb {E} : D \Phi = \mathbb {E} : D \Phi , \end{aligned}$$

which concludes the proof by Theorem 4.1. $\square$

Let us introduce the contour integral: consider a family $U_r$ of Lipschitz neighbourhoods of the crack front/tip $\Gamma$. Assume that $U_r \subset \{ x : d ( x , \Gamma ) < r \}$. Denoting, $\Gamma _r = \partial U_r {\setminus } K$ the contour integral or “generalized J-integral” [12] will be

$$\begin{aligned} J_\Phi ( u_0, \Gamma _r) = \int _{\Gamma _r} \Phi ^T \mathbb {E} (u_0) \, \hat{n} \, ds \end{aligned}$$

(7)

where $\hat{n}$ denotes the outward unit normal for $U_r$.

Note that in the case of curved cracks the contour integral depends both on the tangent field $\Phi$ and on the boundary $\Gamma _r$. We will recover the classic path-independent J-integral of [13] in the case of a straight crack in § 5.1. Let us see the relationship between $G_\Phi$ and $J_\Phi$.

Theorem 5.2

The following asymptotic contour integral representation holds,

$$\begin{aligned} - G_\Phi ( u_0) = \lim _{r \rightarrow 0} J_ {\Phi } (u_0 , \Gamma _r) = \lim _{r \rightarrow 0} \int _{\Gamma _r} \Phi ^T \mathbb {E} (u_0) \, \hat{n} \, ds \,. \end{aligned}$$

(8)

Proof

Denote $\mathbb {E} = \mathbb {E}(u_0)$, $\varvec{\sigma }= \varvec{\sigma }(u_0)$ and $\Omega _r = \Omega {\setminus } ( K \cup \bar{U}_r)$. Without loss of generality we assume that $r \ll 1$. Being $\mathrm {div}( \mathbb {E}^T \Phi ) \in L^1 ( \Omega {\setminus } K )$

$$\begin{aligned} \int _{\Omega {\setminus } K} \mathrm {div}( \mathbb {E}^T \Phi ) \, dx = \lim _{r \rightarrow 0} \int _{\Omega _r} \mathrm {div}( \mathbb {E}^T \Phi ) \, dx . \end{aligned}$$

(9)

As $\Phi$ is compactly supported in $\Omega$ we have $\mathbb {E}^T \Phi \in W^{1,q} ( \Omega _r , \mathbb {R}^n)$ for some $q > 1$ and we are allowed to write

$$\begin{aligned} \int _{\Omega _r} \mathrm {div}( \mathbb {E}^T \Phi ) \, dx = - \int _{\partial \Omega _r} \Phi ^T \mathbb {E} \, \hat{n} \, ds , \end{aligned}$$

because $\mathbb {E}^T \Phi \in L^1 (\partial \Omega _r , \mathbb {R}^n)$ and because $\hat{n}$ is the inward unit normal to $\Omega _r$. Let us split $\partial \Omega _r$ as $\partial \Omega \cup (K^\pm \cap \partial \Omega _r) \cup \Gamma _r$ and check that

$$\begin{aligned} \int _{\partial \Omega } \Phi ^T \mathbb {E} \, \hat{n} \, ds = 0 , \qquad \int _{K^\pm \cap \,\partial \Omega _r} \Phi ^T \mathbb {E} \, \hat{n} \, ds = 0 . \end{aligned}$$

The first integral vanishes simply because $\Phi$ has compact support in $\Omega$. The second vanishes since $\Phi ^T \mathbb {E} \, \hat{n} = 0$ on $K^\pm \cap \partial \Omega _r$, indeed we have

$$\begin{aligned} \Phi ^T \mathbb {E} \, \hat{n} = \Phi ^T ( W I - D u ^T \varvec{\sigma }) \hat{n} = ( \Phi ^T \hat{n} ) \, W - \Phi ^T Du_0^T ( \varvec{\sigma }\hat{n} ) = 0 , \end{aligned}$$

(10)

being $\Phi \cdot \hat{n} = 0$ (because here $\Phi$ is tangent to the crack) and $\varvec{\sigma }\hat{n} = 0$ (by equilibrium). Hence by (9)

$$\begin{aligned} \int _{\Omega {\setminus } K} \mathrm {div}( \mathbb {E}^T (u_0) \Phi ) \, dx = - \lim _{r \rightarrow 0} \int _{\Gamma _r} \Phi ^T \mathbb {E} (u_0) \, \hat{n} \, ds = - \lim _{r \rightarrow 0} J_ { \Phi } (u_0 , \Gamma _r) , \end{aligned}$$

(11)

which concludes the proof $\square$

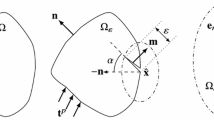
Corollary 5.3

(Path Dependence) Let $U_i$ (for $i=1,2$) be admissible neighbourhoods for (7). Assume that $\bar{U}_2 \subset U_1$.

Then we have

$$\begin{aligned} J_\Phi ( \Gamma _1) - J_\Phi (\Gamma _2) = \int _{U_1 {\setminus } U_2} \mathrm {div}( \mathbb {E}^T (u_0) D \Phi ) \, dx . \end{aligned}$$

(12)

Note that $\mathrm {div}( \mathbb {E}^T (u_0) D \Phi ) = \mathbb {E} (u_0) : D \Phi$ in general does not vanish in $U_1 {\setminus } U_2$.

Proof

It is sufficient to write

$$\begin{aligned} \int _{U_1 {\setminus } U_2} \mathrm {div}( \mathbb {E}^T (u_0) D \Phi ) \, dx = \int _{\partial (U_1 {\setminus } U_2)} \Phi ^T \mathbb {E} (u_0) \, \hat{n} \, ds , \end{aligned}$$

where $\hat{n}$ is the outward unit normal for $U_1 {\setminus } U_2$. Since $\mathbb {E} (u_0) \hat{n} = 0$ on $\partial ( U_1 {\setminus } U_2) \cap K^\pm$ (see the proof of Theorem 5.2) and since $- \hat{n}$ on $\Gamma _2$ is the outward unit vector for $\partial U_2$ we get (12) (Fig. 1). $\square$

Fig. 1

A curved crack and a couple of admissible contours for the evaluation of $J_\Phi$

5.1 Path Independent J-Integral

In this subsection we will restrict ourselves to the setting of [13]: assume that $\Omega \subset \mathbb {R}^2$ and consider a straight crack $K = [-l , 0 ] \times \{ 0 \}$.

Consider also a simple Lipschitz curve $\gamma : [0,1] \rightarrow \Omega {\setminus } \{ 0\}$ with $\gamma (1) \in K^+$ and $\gamma (0) \in K^-$. Denote $\Gamma = \gamma ([0,1])$ and define the J-integral as

$$\begin{aligned} J = - \int _\Gamma \hat{e}_1 \mathbb {E} (u_0) \hat{n} \, ds , \end{aligned}$$

where $\hat{n}$ is again the outward normal.

Let $\varphi \in C^\infty _0 ( \Omega , [0,1])$ with $\varphi = 1$ in a (small) neighbourhood of the origin (the crack tip). Let $\Phi = \hat{e}_1 \varphi$. For $h \ll 1$ the map $\Psi _h (x) = x + h \Phi (x)$ is a smooth diffeomorphism of $\Omega$ with $K_h = \Phi _h ( K)$. Clearly $- G_\Phi (u_0)$ is the energy release with respect to the variations $K_h$ of K.

Proposition 5.4

J is independent of $\Gamma$ and $J = - G_\Phi (u_0)$.

Proof

By the assumptions on $\Gamma$ for r sufficiently small we can apply Corollary 5.3 with $\Gamma _1= \Gamma$ and $\Gamma _2 = \partial B_r$. Denoting by A the region “enclosed” by $\Gamma$, $\partial B_r$ and $K^\pm$, we get by (6)

$$\begin{aligned} \int _{\Gamma } \hat{e}_1 \mathbb {E} (u_0) \hat{n} \, ds - \int _{\partial B_r} \hat{e}_1 \mathbb {E} (u_0) \hat{n} \, ds = \int _{A} \mathbb {E} (u_0) : D \hat{e}_1 \, dx = 0 . \end{aligned}$$

On the other hand, by (7)

$$\begin{aligned} G_\Phi ( u_0) = - \lim _{r \rightarrow 0} \int _{\partial B_r} \hat{e}_1 \mathbb {E} (u_0) \, \hat{n} \, ds = - \int _{\Gamma } \hat{e}_1 \mathbb {E} (u_0) \hat{n} \, ds , \end{aligned}$$

(13)

which gives the representation of the energy release in terms of the J-integral [13]. This argument holds for every curve $\Gamma$ and thus J is independent of $\Gamma$. $\square$

To be precise, the original way [13] of writing the J-integral is the following:

$$\begin{aligned} J = \int _{\Gamma } W dx_2 - \varvec{T} \cdot u_{,1} \, ds , \end{aligned}$$

where the first term is a differential form (and $\Gamma$ denotes a counter-clockwise contour) while the second is a (non-oriented) line integral. Now, consider a counter-clockwise arc length parametrization $\gamma$ of $\Gamma$. Since $\dot{\gamma }$ is the unit tangent vector and $\hat{n}$ is the unit outward vector, we have $\dot{\gamma }_2 = \hat{n}_1$ and thus the differential form $W dx_2$ reads

$$\begin{aligned} \int _{\Gamma } W dx_2 = \int _0^L W \big ( Du_0 ( \gamma (t) ) \big ) \dot{\gamma }_2 (t) \, dt = \int _{\Gamma } W ( D u_0) \hat{n}_1 \, ds = \int _{\Gamma } W ( D u_0 ) \hat{n} \cdot \hat{e}_1 \, ds . \end{aligned}$$

The second is instead a line integral for $\varvec{T} = \varvec{\sigma }( u_0 ) \hat{n}$ and $u_{,1} = D u_0 \hat{e}_1$. Thus

$$\begin{aligned} \int _{\Gamma } u_{,1} \cdot \varvec{T} \, ds = \int _{\Gamma } (Du_0 \hat{e}_1)^T \varvec{\sigma }(u_0) \hat{n} \, ds = \int _{\Gamma } \hat{e}_1^T Du_0^T \varvec{\sigma }(u_0) \, \hat{n} \, ds . \end{aligned}$$

Taking the difference, we get

$$\begin{aligned} J = \int _{\Gamma } W ( D u_0 ) \, \hat{e}_1^T \hat{n} - \hat{e}_1^T Du_0^T \varvec{\sigma }(u_0) \, \hat{n} \, ds = \int _{\Gamma } \hat{e}^T_1 \mathbb {E} (u_0) \hat{n} \, ds . \end{aligned}$$

6 Representation with the Stress Intensity Factors

In this section we will work under the following assumptions: $\Omega \subset \mathbb {R}^2$ and the crack K is of class $W^{2,\infty }$ (in particular it is not necessarily straight). Without loss of generality we assume that the tip is in the origin with tangent $\hat{e}_1$. Finally, we assume that $f'=0$ and, most important, we consider isotropic elasticity with $\mathbf {C}[Du] = \varvec{\sigma }(u) = 2 \mu \varvec{\epsilon }(u) + \lambda \mathrm {tr} (\varvec{\epsilon }(u) ) I$, for $\lambda , \mu >0$ the Lamé constants. First of all let us introduce the singular displacement fields

$$\begin{aligned} \hat{u}_{\mathrm{I}}= \rho ^{1/2} \hat{U}_{\mathrm{I}}(\theta ) , \qquad \hat{u}_\mathrm{II}= \rho ^{1/2} \hat{U}_\mathrm{II}(\theta ) , \end{aligned}$$

where the fields $\hat{U}_i$ take the form

$$\begin{aligned} \hat{U}_{\mathrm{I}}(\theta )&= ( a_{\mathrm{I}}\cos (\theta /2) + b_{\mathrm{I}}\cos (3\theta /2) , c_{\mathrm{I}}\sin (\theta /2) + d_{\mathrm{I}}\sin (3 \theta /2) ) , \\ \hat{U}_\mathrm{II}(\theta )&= ( a_\mathrm{II}\sin (\theta /2) + b_\mathrm{II}\sin (3 \theta /2) , c_\mathrm{II}\cos (\theta /2) + d_\mathrm{II}\cos (3\theta /2) ) \\ \hat{U}_{\mathrm{I}}(\theta )&= \alpha ( \cos (\theta /2) (\beta - \cos \theta ) , \sin (\theta /2) (\beta - \cos \theta ) ) , \\ \hat{U}_\mathrm{II}(\theta )&= \alpha ( \sin (\theta /2) (\beta +2 + \cos \theta ) , - \cos (\theta /2) (\beta -2 + \cos \theta ) ) , \end{aligned}$$

for a suitable choice of the scalars depending only on the Lamé parameters. Now, given $u_0$ let us introduce the rescaled field

$$\begin{aligned} u^{(r)} (x) = r^{-1/2} u_0 ( r x) . \end{aligned}$$

Then by [1] there exist $K_{\mathrm{I}}, K_{\mathrm{II}}$ (the stress intensity factors) such that

$$\begin{aligned} D u^{(r)} \rightarrow K_{\mathrm{I}}D \hat{u}_{\mathrm{I}}+ K_{\mathrm{II}} D \hat{u}_{\mathrm{II}} \qquad \text {strongly in}\,\, L^2 ( B_1 , \mathbb {R}^{2 \times 2}). \end{aligned}$$

(14)

In the case of a smooth crack the above convergence follows easily from the singular expansion proved by Grisvard in [7].

The following result gives Irwin’s formula for the representation of the energy release $-G_\Phi ( u_0)$ in terms of the stress intensity factors.

Theorem 6.1

Let the map $\Phi$ be compactly supported and tangent to the crack K. Then

$$\begin{aligned} - G_\Phi (u_0) = (1-\nu ^2) ( K^2_{\mathrm{I}}+ K^2_\mathrm{II}) / E , \end{aligned}$$

(15)

where $\nu = \lambda / 2 (\lambda + \mu )$ and $E = 2 ( 1 + \nu ) \mu$ are respectively Poisson’s ratio and Young’s modulus.

Proof

For $0 < r \ll 1$ let $\varphi _r (x) = | 1 - |x|/r |_+$ (where $| \cdot |_+$ denotes the positive part). Given the tangent field $\Phi$ let $\Phi _{r} (x_1, x_2) = \varphi _r (x) \Phi (x)$. Clearly $\nabla \varphi _r (x)= 0$ in $\Omega {\setminus } B_r$ and $\nabla \varphi _r (x) = \hat{e}_\rho /r$ in $B_r$, thus

$$\begin{aligned} D \Phi _r = \hat{e}_\rho \otimes \Phi /r + \varphi _r D \Phi . \end{aligned}$$

By (5) we have

$$\begin{aligned} G_\Phi (u_0) = \lim _{r \rightarrow 0} \int _{B_r {\setminus } K} \mathbb {E} (u_0) : D \Phi _r \, dx . \end{aligned}$$

(16)

In the ball $B_r$ it holds $|\Phi - \hat{e}_1 | \le c r$ and hence $| D \Phi _r - \hat{e}_\rho \otimes \hat{e}_1 / r | \le C$, with C independent of r. Since $\mathbb {E}(u_0) \in L^1$ it follows that

$$\begin{aligned} G_\Phi (u_0) = \lim _{r \rightarrow 0} \int _{B_r {\setminus } K} \mathbb {E} (u_0) : D \Phi _r \, dx = \lim _{r \rightarrow 0} r^{-1} \int _{B_r {\setminus } K} \mathbb {E} (u_0) : \hat{e}_\rho \otimes \hat{e}_1 \, dx \,. \end{aligned}$$

In terms of the rescaled field $u^{(r)}$ the variation of energy reads

$$\begin{aligned} G_\Phi (u_0) = \lim _{r \rightarrow 0} \int _{B_1 {\setminus } K^{(r)}} \mathbb {E} (u^{(r)}) : \hat{e}_\rho \otimes \hat{e}_1 \, dx , \end{aligned}$$

where $K^{(r)} = K/r$. By (14) it follows that $\mathbb {E} (u^{(r)}) \rightarrow \mathbb {E} ( K_{\mathrm{I}}\hat{u}_{\mathrm{I}}+ K_{\mathrm{II}} \hat{u}_{\mathrm{II}} )$ strongly in $L^1 (B_1 , \mathbb {R}^{2 \times 2})$ and thus

$$\begin{aligned} G_\Phi (u_0) = \int _{B_1} \mathbb {E} ( K_{\mathrm{I}}\hat{u}_{\mathrm{I}}+ K_{\mathrm{II}} \hat{u}_{\mathrm{II}} ) : \hat{e}_\rho \otimes \hat{e}_1 \, dx . \end{aligned}$$

It is convenient to write explicitly the Eshelby tensor as

$$\begin{aligned} \mathbb {E} ( K_{\mathrm{I}}\hat{u}_{\mathrm{I}}+ K_{\mathrm{II}} \hat{u}_{\mathrm{II}} ) = \sum _{i,j\,=\,{\mathrm{I}}}^{\mathrm{II}} K_i K_j \, \hat{\mathbb {E}}_{i,j} , \end{aligned}$$

where $\hat{\mathbb {E}}_{i,j} = \varvec{\epsilon }( \hat{u}_i ) : \varvec{\sigma }(\hat{u}_j) I - D\hat{u}^T_i \varvec{\sigma }(\hat{u}_j)$ is of the form $\rho ^{-1} \hat{S}_{i,j} (\theta )$ (for $i,j = \text{ I, } \text{ II }$). Denoting

$$\begin{aligned} \hat{C}_{i,j} = \int _{B_1} \hat{\mathbb {E}}_{i,j} : \hat{e}_\rho \otimes \hat{e}_1 \, dx&= \int _{B_1} \rho ^{-1} \hat{S}_{i,j} (\theta ) : \hat{e}_\rho (\theta ) \otimes \hat{e}_1 \, \rho \, d\rho \, d\theta \\&= \int _{-\pi }^{\pi } \hat{S}_{i,j} (\theta ) : \hat{e}_\rho (\theta ) \otimes \hat{e}_1 \, d\theta \end{aligned}$$

we obtain

$$\begin{aligned} G_\Phi (u_0) = \sum _{i,j\,=\,{\mathrm{I}}}^{\mathrm{II}} \hat{C}_{i,j} K_i K_j . \end{aligned}$$

From the classical result of Irwin it holds $\hat{C}_{{\mathrm{I}},\mathrm{II}} = \hat{C}_{\mathrm{II},{\mathrm{I}}}= 0$ (by symmetry arguments) and that $\hat{C}_{{\mathrm{I}},{\mathrm{I}}} = \hat{C}_{\mathrm{II},\mathrm{II}} = -(1-\nu ^2)/E$. $\square$

To conclude this section, we observe that in our setting Green’s formula

$$\begin{aligned} \int _{\Omega {\setminus } K} \mathrm {div}( \mathbb {E}^T (u_0) \Phi ) \, dx = \int _{\partial (\Omega {\setminus } K)} \Phi ^T \mathbb {E} (u_0) \, \hat{n} \, ds \end{aligned}$$

does not hold true. Indeed,

$$\begin{aligned} G_\Phi (u_0) = \int _{\Omega {\setminus } K} \mathrm {div}( \mathbb {E}^T (u_0) \Phi ) \, dx \qquad \text {while} \qquad \int _{\partial (\Omega {\setminus } K)} \Phi ^T \mathbb {E} (u_0) \, \hat{n} \, ds = 0 , \end{aligned}$$

since $\Phi ^T \mathbb {E} (u_0) \, \hat{n} = 0$ a.e. on $K^\pm$, as shown in (10). However, by Lemma 5.1 and Theorem 6.1 the following “generalized Green’s formula” holds

$$\begin{aligned} \int _{\Omega {\setminus } K} \mathrm {div}( \mathbb {E}^T (u_0) \Phi ) \, dx = \int _{\partial (\Omega {\setminus } K)} \Phi ^T \mathbb {E} (u_0) \, \hat{n} \, ds - (1-\nu ^2) ( K_{\mathrm{I}}^2 + K_\mathrm{II}^2 ) / E . \end{aligned}$$

In general, since $\mathbb {E}$ belongs to $L^1( \mathrm {div}; \Omega {\setminus } K , \mathbb {R}^{n\times n} )$ Green’s formula (cf. Theorem 7.1) takes the form

$$\begin{aligned} \int _{\Omega {\setminus } K} \mathrm {div}( \mathbb {E}^T (u_0) \Phi ) \, dx = \langle \Gamma _{\hat{n}} ( \mathbb {E} (u_0) ) , \Phi \rangle , \end{aligned}$$

(17)

where $\Gamma _{\hat{n}} : L^1(\mathrm {div}; \Omega {\setminus } K , \mathbb {R}^{n \times n}) \rightarrow (W^{1,\infty } ( K , \mathbb {R}^n))^*$ is a bounded linear operator. In general $\Gamma _{\hat{n}}$ does not enjoy an integral representation, i.e. it does not belong to $L^1(K, \mathbb {R}^n)$. In our setting, given $u_0$, if $\Phi$ is tangential it holds

$$\begin{aligned} \Gamma _{\hat{n}} ( \mathbb {E} (u_0) ) = - (1-\nu ^2) ( K_{\mathrm{I}}^2 + K_\mathrm{II}^2 ) / E . \end{aligned}$$

Appendix: Green’s Formula in \(L^1 (\text {div})\)

Let A be a bounded, Lipschitz domain in $\mathbb {R}^n$ and define

$$\begin{aligned} L^1 ( \mathrm {div}; A , \mathbb {R}^{n\times n} ) = \{ \xi \in L^1 ( A , \mathbb {R}^{n \times n}) : \mathrm {div}(\xi ) \in L^1 (A , \mathbb {R}^n)\} \end{aligned}$$

endowed with the norm $\Vert \xi \Vert _{L^1 (\mathrm {div})} = \Vert \xi \Vert _{L^1} + \Vert \mathrm {div}(\xi ) \Vert _{L^1}$. The following Theorem defines the normal trace in $L^1(\mathrm {div}; A , \mathbb {R}^{n \times n})$ as an element of $(W^{1,\infty } ( \partial A, \mathbb {R}^n) )^*$, the dual of $W^{1,\infty } (\partial A,\mathbb {R}^n)$.

Theorem 7.1

Let $\xi \in L^1 (\mathrm {div}; A , \mathbb {R}^{n \times n})$. There exists a bounded linear operator

such that $\Gamma _{\hat{n}} ( \xi ) = \xi \, \hat{n}$ for $\xi \in C^1 ( \bar{A}, \mathbb {R}^{n\times n})$ and such that

$$\begin{aligned} \int _{A} \mathrm {div}( \xi \tilde{\psi }) = \int _{A} \mathrm {div}( \xi ) \cdot \tilde{\psi }+ \xi : D \tilde{\psi }\, dx = \langle \Gamma _{\hat{n}} ( \xi ) , \psi \rangle \end{aligned}$$

holds for any $\psi \in W^{1,\infty } ( \partial A , \mathbb {R}^n )$ and any $\tilde{\psi }\in W^{1,\infty } ( A , \mathbb {R}^n)$ with $\tilde{\psi }_{|\partial A}=\psi$. Brackets $\langle \cdot ,\cdot \rangle$ above denote the duality between $W^{1,\infty } ( \partial A , \mathbb {R}^n)$ and its dual $(W^{1,\infty } ( \partial A, \mathbb {R}^n) )^*$.

Proof

Let us define $\Gamma _{\hat{n}} : C^1 ( \bar{A}, \mathbb {R}^{n\times n}) \rightarrow (W^{1,\infty } (\partial A, \mathbb {R}^n))^*$ by

$$\begin{aligned} \langle \Gamma _{\hat{n}} (\xi ) , \psi \rangle = \int _{A} \mathrm {div}( \xi ) \cdot \tilde{\psi }+ \xi : D \tilde{\psi }\, dx , \end{aligned}$$

where $\tilde{\psi }\in W^{1,\infty } ( A , \mathbb {R}^n)$ is a lifting of $\psi \in W^{1,\infty } ( \partial A , \mathbb {R}^n)$. Note that $\xi \tilde{\psi }\in W^{1,\infty } (A , \mathbb {R}^n)$ and thus classical Green’s formula holds in integral form as

$$\begin{aligned} \langle \Gamma _{\hat{n}} (\xi ) , \psi \rangle = \int _{A} \mathrm {div}( \xi \tilde{\psi }) = \int _{\partial A} \psi \cdot \xi \, \hat{n} \,ds . \end{aligned}$$

In particular $\Gamma _{\hat{n}}$ is independent of the (non-unique) lifting operator. Moreover $\Gamma _{\hat{n}}$ is linear and bounded with respect to the norm of $L^1(\mathrm {div}; A , \mathbb {R}^{n \times n})$, indeed by definition

$$\begin{aligned}&\Vert \Gamma _{\hat{n}} (\xi ) \Vert _{(W^{1,\infty } ( \partial A , \mathbb {R}^n))^*}\\&\quad = \sup \big \{ \langle \Gamma _{\hat{n}} (\xi ) , \psi \rangle : \psi \in W^{1,\infty } ( \partial A ,\mathbb {R}^n) \text { with } \Vert \psi \Vert _{W^{1,\infty } (\partial A, \mathbb {R}^n)} \le 1 \big \} \end{aligned}$$

and by continuity of the lifting operator

$$\begin{aligned} \langle \Gamma _{\hat{n}} (\xi ) , \psi \rangle = \int _{A} \mathrm {div}( \xi ) \cdot \tilde{\psi }+ \xi : D \tilde{\psi }\, dx \le C \Vert \xi \Vert _{L^1(\mathrm {div}, A , \mathbb {R}^{n \times n})} . \end{aligned}$$

We conclude extending $\Gamma _{\hat{n}}$ (in a unique way) since $C^1 ( \bar{A}, \mathbb {R}^{n \times n})$ is dense in $L^1(\mathrm {div}; A , \mathbb {R}^{n \times n})$. $\square$