A Dynamic Model for the Evolution of Protein Structure

Abstract

Domains are folded structures and evolutionary building blocks of protein molecules. Their three-dimensional atomic conformations, which define biological functions, can be coarse-grained into levels of a hierarchy. Here we build global dynamical models for the evolution of domains at fold and fold superfamily (FSF) levels. We fit the models with data from phylogenomic trees of domain structures and evaluate the distributions of the resulting parameters and their implications. The trees were inferred from a census of domain structures in hundreds of genomes from all three superkingdoms of life. The models used birth–death differential equations with the global abundances of structures as state variables, with one set of equations for folds and another for FSFs. Only the transitions present in the tree are assumed possible. Each fold or FSF diversifies in variants, eventually producing a new fold or FSF. The parameters specify rates of generation of variants and of new folds or FSFs. The equations were solved for the parameters by simplifying the trees to a comb-like topology, treating branches as emerging directly from a trunk. We found that the rate constants for folds and FSFs evolved similarly. These parameters showed a sharp transient change at about 1.5 Gyrs ago. This time coincides with a period in which domains massively combined in proteins and their arrangements distributed in novel lineages during the rise of organismal diversification. Our simulations suggest that exploration of protein structure space occurs through coarse-grained discoveries that undergo fine-grained elaboration.

Introduction

The biological machinery of living cells is composed of proteins. The machine’s three-dimensional structure determines the machine’s function. Since structure determines function, it is also more likely to be conserved (Caetano-Anollés and Caetano-Anollés 2003; Nasir et al. 2011). Thus, if we understand the evolutionary history of protein structure, we can reconstruct some of the evolutionary history of life itself. This is the inspiration for this research.

Proteins are linear polymers of amino acids. This sequence of amino acids corresponds to a three-dimensional structure that determines the functions a protein can perform. As Caetano-Anollés et al. (2009) detail, Linderstrøm-Lang and Schellman proposed in the 1950s that protein structure had a four-tiered hierarchy, which they called primary, secondary, tertiary, and quaternary structure. These corresponded, respectively, to (i) the amino acid sequence linked by peptide bonds, (ii) the helices and sheet elements of a fold that arise as a result of the hydrogen-bonding patterns, (iii) the molecular fold itself, and (iv) the aggregate of such chains into a larger biological construct from which function arises. Recognition of repeating motifs in protein structure led to the advent of (v) supersecondary structure. The further observation that protein folds have modular components that act alone or with other modules in proteins forms the basis for (vi) protein domains.

This research begins with domains. There are dozens of domain classification systems, but Caetano-Anollés et al. (2009) present a solid argument for the use of the Structural Classification of Proteins (SCOP) gold standard to which we adhere. SCOP domains with >30 % pairwise amino acid residue identities are pooled into fold families (FFs), FFs with functional and structural features suggesting a common origin are grouped into fold superfamilies (FSFs), and FSFs with secondary structures that maintain a similar topology and arrangement are grouped into protein folds. Finally, folds are grouped into classes according to secondary structure organization in the fold, giving rise to the $\alpha / \beta$, $\alpha + \beta$, all-$\alpha$, all-$\beta$, small, and multidomain groups. Note that each classification, from fold families to classes, is a subset of the next. This research specifically focuses on folds and FSFs because all relevant pieces, but most significantly a “molecular clock” (described below in the “Issue of a Time Scale” section) has been discovered for these two levels of the structural hierarchy.

Caetano-Anollés and Caetano-Anollés (2003), Nasir and Caetano-Anollés (2015), and Caetano-Anollés et al. (2011) have constructed phylogenomic trees that describe the evolution of folds and FSFs using parsimony methods and genomic abundances of folds or FSFs as phylogenetic characters. Reconstruction of rooted trees assumes that the character states are linearly polarized by abundance, i.e., that the structures which are currently present in greater numbers have older origins than those present in lower numbers. This assumption complies with Weston’s generality criterion of rooting, which takes advantage of the wide distribution of early originating character states in branches at the base of a rooted tree and the increasingly restricted distribution of those that originate later. The implementation of this generality criterion involves selecting most parsimonious unrooted trees from searches of the space of all possible trees and rooting these trees a posteriori with the Lundberg method, which reorients and roots the tree by pulling down the branch that yields a minimum increase in tree length. This study uses and builds upon data from these previous phylogenomic studies.

The topology of the trees provides a static characterization of the evolution of protein structure, a word which we use throughout this paper to mean either folds or FSFs. A given structure has potentially many different proteins that are classified within this structure, and we call these the structure’s variants. In the tree of protein structures, each node corresponds to a structure with a vector of character states, the abundance of variants of each type of structure in a set of genomes. The structure originates at its node of origin which is an internal node of the tree.

What is missing from this tree, however, is a dynamic model detailing the kinetic parameters relevant to describing the evolution of such a tree. Such a phenomenological description of the dynamics of the evolutionary process would specify parameters for the study of protein history. We have provided such a description, building on previous models that attempted to explain the evolution of protein structure.

The models of Qian et al. (2001) and Karev et al. (2002) aim to explain the existence of the power law distribution of fold occurrence in genomes in which a few folds occur in many copies per genome and many folds are rare. However, Qian et al. (2001) take a “local” perspective, i.e., the focus of their model is the distribution within a single genome over time. This does not capture a given fold’s history as it develops in many organisms across the entire planet. Moreover, their model also assumes that the “rate of fold flow” (or fold acquisition − fold deletion) is the same value for all folds within a given organism and that the initial rates of fold duplications within an organism are also identical. Both assumptions seem implausible, as there are different selection pressures on different folds, since different folds hold different functions. We believe that a model taking a global perspective, with the fold or FSF across all organisms as its subject, and allowing the two rates discussed to change as they may, is more realistic.

Similarly, in order for the model of Karev et al. (2002) to be compatible with the power law distributions it hopes to explain, it assumes that domain families are commonly in a state of equilibrium with respect to the total number of domain families over time and the total number of domain families of a given size in a given genome over time. This approach appears implausible. There does not appear to be anything like environmental equilibrium at many time scales throughout history. There are constantly changing selection pressures on organisms and therefore on the genetics and proteins they contain and encode. Again, we believe that a model relinquishing the assumption of such an equilibrium can shed light on evolutionary history.

Another attempt to explain the power law distributions of protein structures, by Magner et al. (2015), takes an information-theoretic approach. They conclude that the power laws of sequences have different origins than those of folds; “protein sequences exhibit a power law distribution to achieve efficient coding of necessary folds,” while that of folds “is based on the thermodynamic stability of folds.” But here, too, the focus is on a local model, rather than a global model, so the insights and benefits of a global perspective are missed.

Yet, another approach, by Zeldovich et al. (2006), attempts to reconstruct protein evolutionary history via simulation. The study demonstrates that, given stability as the selection mechanism in each iteration, random protein sequences often converge on proteins with specific structures, the so-called “wonderfolds.” The authors consider these emergent thermostable wonderfolds as potential pre-biotic precursors to the biotic protein structure hierarchy, ones that likely arose in a hot environment and needed their thermostability. This study, however, focuses only on the pre-biotic world. In contrast, our study is independent of assumptions of pre-biotic and biotic worlds and focuses on the evolution of the protein world.

Still another approach, by Zeldovich et al. (2007), takes the organism, rather than the protein structure, as its point of focus, with organisms evolving in a simulation under the assumption that an organism’s fitness corresponds to its proteins’ abilities to be in their native conformations. This model, too, successfully recovers known power laws and structural hierarchy, but again does not take our global perspective and the implications that arise from it. To the best of our knowledge, no other group has taken the global perspective.

While local models capture details of organismal distribution of domains in proteomes, they must address the effects of horizontal transfer of genetic information. For example, the model of Karev et al. (2002) is a birth–death model with an additional term of innovation, which pools both the generation of novelties and the import of novelties from other proteomes via horizontal gene transfer. This adds complexity and uncertainty to the modeling exercise. The global model we implement here avoids modeling horizontal gene transfer and possible heterogeneities in organismal superkingdoms by focusing on domain innovation at a planetary level. Local models are not comparable to this global model unless they address the heterogeneities of horizontal gene transfer, which are largely unknown and difficult to evaluate. Local models focus on organismal lineages, which are delimited by population biology parameters. However, diversification operates at different temporal scales for genes and folds. Populations change on a time scale of approximately 10–1000 years, whereas fold and FSF diversification and innovation occur on scales of millions to billions of years.

Here we use the data from the phylogenomic tree reconstructions described to build global, dynamical models for the evolution of folds and FSFs and evaluate their parameters. In contrast to the preceding models, our models predict the abundances of individual folds or FSFs throughout the living world and generate a non-steady-state time course for their evolution. This paper describes our models, the evaluation of their parameters using a large sample of real data from all three superkingdoms of life, and the implications for the history of protein structure.

The Model

The Global Model of Fold Evolution

We built dynamic models of evolution that correspond to our trees of protein structures. We assume that structures evolved in a stochastic branching process from a primordial structure. Our models are inspired by the Galton–Watson process, elaborated by Harris (1963), that models propagation of branching as a delicate balance between birth, survival, and extinction. Our models are also variants of the birth–death model. We consider the ensemble of possible realizations of the branching process. We model the time course of changes in the ensemble-averaged abundance of each structure. The parameters of the model are transition probabilities per unit time, or rate constants, for transition to a new variant of a structure and for transition from one kind of structure to another. An approximation technique is presented which allows the calculation of these rates and their changes over time.

In considering a possible model, one must take into account the ways in which a structure can be lost, copied, or transformed into another structure. A new structure can evolve through the mutation of an existing structure (structure transitions), de novo evolution from a non-coding region, or horizontal transfer from another genome. We describe structure transitions in the structure transition matrix: It gives the probability per unit time, per domain, that a structure will be transformed into any other structure. We assume that de novo evolution is very improbable, as the probability of an open reading frame (the portion of DNA which is transcribed and can eventually be translated into a protein) evolving from a non-coding region is very low. We ignore this. However, it is worth noting that Carvunis et al. (2012) demonstrated that, at least in Saccharomyces cerevisiae, de novo evolution may not be unlikely through translation of transitory proto-genes in non-genic sequences. Momentarily, it is difficult to account for this term in our model as there is not enough information on how widespread this proto-gene mechanism is across the three superkingdoms, how much similarity can be detected among the proto-genes between species, and whether these proto-genes fall into classifiable three-dimensional structures. However, if it turns out that the mechanism is important and data can be collected on the three-dimensional structures’ abundances among and between species, it may then be possible to repeat our study by creating a tree of structures and proto-structures (corresponding to proto-genes), and proceeding as below.

We opted to use a global model (which deals with the distribution of structures in all organisms), as opposed to a local model (which deals with the distribution of structures in individual organisms). The global model avoids using separate terms for horizontal transfer. Moreover, it focuses on the structures that have been successful, thus including selection bias in the structure transition probabilities. The global model is a variant of the birth–death model for domain structures within the constraints of the stochastic branching process. The total abundance of a domain structure is the state variable, which changes through two kinds of birth (transitions into the structure or growth of variants) and one kind of death (transitions out of the structure). Moreover, a death for one structure via a transition is a birth for another structure and its state variable. Thus, we model two types of birth and one death with a death in one structure causing a birth in some other. The global model is a deterministic model for the ensemble-average global abundance of a structure, not a stochastic model.

Governing Equations of the Global Model

We consider a simple model which allows evaluations of all parameters from the data. We call this model the irreversible tree-hugging model (ITH). In ITH, we assume that we only have “forward” transitions. That is, the only transition probabilities that are non-zero are those from an ancestral structure to a neighboring descendant; thus transitions are irreversible. We set the transition probabilities for all “reverse” transitions equal to 0. The model also assumes that the only possible transitions are the ones seen in the tree, thus it is tree-hugging. The governing equations of a complete global model are

$$\begin{aligned} \frac{{\mathrm {d}}N_j}{{\mathrm {d}}t} = \left(\lambda _j -\sum _{i\ne j}a_{ij}\right)N_j + \sum _{i\ne j}a_{ji}N_i, \end{aligned}$$

(1)

where $N_j(t)$ is the global abundance of a structure of type j at time t. $t = 0$ at the origin of the primordial structure ($j=1$). We assume $N_1(0)=1$ and $N_j(0)=0$ for $j > 1$. If structure j is ancestral to structure i, $j < i$.

$\lambda _j$ is the net rate (birth minus death) per copy of structure j of generating new variants of structure j.

$a_{ij}$ is the rate of transition from structure j to structure i (forward transition). Note that $a_{ij}\ne 0$ only when structure i is the neighboring descendant of structure j. In particular, this means that each of the two sums in Eq. 1 only has one non-zero term, yielding:

$$\begin{aligned} \frac{{\mathrm{ d}}N_1}{{\mathrm{ d}}t}&= \lambda _{1}N_1 -a_{2,1}N_1 \end{aligned}$$

(2)

$$\begin{aligned} \frac{{\mathrm{ d}}N_j}{{\mathrm{ d}}t}&= (\lambda _j -a_{j+1,j} )N_j + a_{j,j-1}N_{j-1}. \end{aligned}$$

(3)

The ITH strategy does not restrict the number of folds. It only restricts allowed transitions among folds. Global abundances of structures are the state variables, which range over all non-negative integers. In the data processing, however, data were allowed to range over any non-negative integer values but were normalized to a linearly ordered scale (0–20 and 0–23 for folds or FSFs, respectively) to accommodate the requirements of phylogenetic analysis. The ITH assumption does not inherently restrict the range of the state space. It does eliminate certain values of a, which indirectly affect the values of the state variables. However, it does not limit the potential range of the space.

Structure Abundance and Funnels

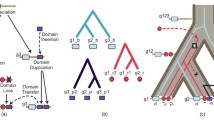
Each internal node in the tree of protein structures has two child nodes, one of them representing the continuation of the old structure and the other the creation of a new structure. Starting from a particular parent node which represents some structure j, we can follow the path through the branches on the tree, which correspond to structure j up to the present (see Fig. 1). The number of copies of a particular structure is increasing in an approximately exponential manner, and thus we say it corresponds to a funnel (see Fig. 2). The number of copies of a particular structure at a certain time is represented by the cross-section of the funnel. Each new branch coming off this path corresponds to the initiation of a new structure $j'$ (see Fig. 1), and thus of a new funnel (see Fig. 2). Each new funnel initially starts out with one copy of a new structure. We thus note that all the internal nodes represent present-day structures, even though the examples of the structures may have changed over time due to mutations. It is thus possible to identify each one uniquely using its global abundance: the structure with the greater abundance will be the older branch.

Fig. 1

Identification of internal nodes. Red and blue colors correspond to j and j′, respectively (Color figure online)

Fig. 2

Funnels corresponding to folds j and j′. A horizontal cross-section of a funnel measures that funnel’s total abundance with respect to time, N(t)

Estimating the Global Abundances of Structures

Our strategy is to estimate the global abundances of structures, and then to use these estimates to estimate the $\lambda$’s and a’s from N’s.

The phylogenomic tree was derived from data for the local abundances of the J folds in K genomes. The relation between the global abundance of structure j, $N_j$, and the vector of local popularities [$s_{j1}, s_{j2}, ...s_{jK}$] is

$$\begin{aligned} N_j = \sum _{k}m_ks_{jk}. \end{aligned}$$

(4)

Here $m_k$ is the effective population size of species k. The breeding population size is the intuition behind the formal effective population size which is defined by Caballero (1994) as the size of the ideal population which assumes no selection, random mating, and a random chance for each offspring to have a particular parent. For ancestral nodes, species k will not in fact be the present species k, but rather the lineage leading to the present species k. Thus, we are not saying that species k existed in the remote past.

We have data for the present abundance vectors. We require a method of estimating the present effective population sizes, denoted by $m_k^*$ for species k. Figure 1b by Lynch and Conery (2003) offers the relationship $\log (m_k^* \mu ) = -1.3 -0.55 \log G_k$ where $G_k$ is the genome size of species k in millions of bases, Mb, and the logarithm is in base 10. $\mu _k$ represents, for species k, mutations/base/cell division. Cell division corresponds to genome duplication for unicellular organisms such as prokaryotes and lower eukaryotes. For multicellular organisms such as higher eukaryotes $\mu _k = \mu _{bs}/c$ where $\mu _{bs}$ represents mutation rate/base/generation from Fig. 3 by Lynch (2006), and $c$ is the number of germline cell divisions per generation from Lynch and Conery (2003). However, Lynch and Conery (2003) also reference an average $\mu _k$, which we call $\mu$, and offer its value as $\mu = 2.3 \times 10^{-10}$. Using this value, we can solve for $m_k^*$:

$$\begin{aligned} m_k^* = 2.2 \times 10^8 \times G_k^{-0.55}. \end{aligned}$$

(5)

One caveat of using an average $\mu$ value is that mutation rates vary not only between but within organisms, for example in CG-rich versus AT-rich regions. Thus, an average captures an approximate snapshot.

Issue of a Time Scale

We do not know how to directly assign times to the origins of most domain structures. However, Wang et al. (2011) graph the geological times of origin of known structures, determined from independent paleontological evidence, against their normalized distance in nodes (nd) from the hypothetical ancestral structure at the base of a phylogenomic tree of structures.

The number of bifurcations in the tree from the root to any structure can be determined by counting. For example, in Fig. 1, there have been three bifurcations that lead to the birth of leaf 1, but four bifurcations that lead to leaf 6. The maximum number of bifurcations that lead to a structure on the tree is 4, and we call this the normalization. When taking the number of bifurcations leading to a particular structure and dividing it by the normalization, one arrives at the normalized node distance (nd) of a node.

The relation between t and nd for folds, as given by Wang et al. (2011), is

$$\begin{aligned} t = -3.8023nd + 3.8137, \end{aligned}$$

(6)

while for FSFs it is

$$\begin{aligned} t = -3.8314nd + 3.6284. \end{aligned}$$

(7)

Here t is in gigayears.

We assume that these relations hold for all nodes of the respective trees. Since we can calculate $\lambda$’s, a’s, and nd’s for folds and FSFs, we can use the above equations to relate our results to real time and make statements about the history of protein structure.

Estimating $\lambda$’s

We assume that transitions to new structures are rarer than transitions to variants, so $a_{j'j} \ll \lambda _j$. Applying this to Eqs. 2 and 3 reduces them to $\frac{{\mathrm {d}}N_j}{{\mathrm {d}}t} = \lambda _j N_j$. It follows that, for a given node h, $N_h = v_{h-1}*e^{\lambda _h (t_h - t_{h-1})}$ where $v_{h-1} = 1$ if node h represents a new structure originating from the structure at node $h -1$, and $v_{h-1} = N_{h-1} - 1 \approx N_{h-1}$ if the structure at node h is the same as the structure at node $h-1$. Note that $t_h$ is the time of origin of node h. Note also that since t is in gigayears $\lambda$ is in $(Gy)^{-1}$. If the node represents a new structure we call it a novel structure, and if the node is the same we say it is a persistent structure. This approximation is reasonable because $N_{h-1} \gg 1$ for a persistent structure if $a_{j'j} \ll \lambda _j$, as our results show.

In any case, a novel structure requires knowledge of the present total abundance and time to determine $\lambda,$ while a persistent structure requires, in addition, the total abundance one tree step back. As such, we are faced with several difficulties: (1) determining which structures are novel and which are persistent and (2) determining ancient abundances for persistent structures. Since both of these tasks are difficult to accomplish correctly in principle without making unsavory assumptions, we instead resort to an approximation.

Note that every n-furcation on a tree contains exactly one persistent structure. The rest are novel. Thus, there are numerous labelings of novelty and persistence on a tree to consider in search of the historically accurate one. We consider two interesting extremes which we call a p-comb and an n-comb. A p-comb, as illustrated in Fig. 3, is a binary tree in which, at each bifurcation, the persistent structure becomes a leaf (as witnessed by the second subscript p labels in the figure and equations). An n-comb, as illustrated in Fig. 4, is a binary tree in which, at each bifurcation, the novel structure becomes a leaf (as witnessed by the second subscript n labels in the figure and equations). In both comb figures, leaves represent the present though their branches have not been extended.

Fig. 3

A p-comb

Fig. 4

An n-comb

For the p-comb, the following equations follow from the above discussion:

$$\begin{aligned} N_{0,n}&= e^{\lambda _0 t} \\ N_{1,p}&= N_{1,n}^* e^{\lambda _1 t} \\ N_{1,n}^*&= e^{\lambda _1 t} \\ N_{1,p}&= e^{2\lambda _1 t}, \end{aligned}$$

where the last equation follows from the previous two and the first equation gives $\lambda _{0,n}$ directly. Similarly,

$$\begin{aligned} N_{2,p}&= N_{2,n}^* e^{\lambda _2 (2t)} \\ N_{2,n}^*&= e^{\lambda _2 t} \\ N_{2,p}&= e^{3\lambda _2 t}. \end{aligned}$$

Note here that t has been replaced by 2t in the first equation since this structure has been around for that length of time since its origin. It follows by a generalization of the above that:

$$\begin{aligned} N_{j,p}&= e^{(j+1)\lambda _j t} \end{aligned}$$

(8)

$$\begin{aligned} \lambda _{j,p}&= \frac{\ln N_j}{(j+1)t} \end{aligned}$$

(9)

$$\begin{aligned} \lambda _{0,n}&= \frac{\ln N_0}{t}. \end{aligned}$$

(10)

For the n-comb, however, the calculation is different:

$$\begin{aligned} N_{0,p}&= N_{1,p}^* e^{\lambda _0 t}& \quad \quad N_{1,n}&= e^{\lambda _1 t}\\ N_{1,p}^*&= N_{2,p}^* e^{\lambda _0 t}& \quad \quad N_{2,n}&= e^{\lambda _2 (2t)}\\ N_{2,p}^*&= N_{3,p}^* e^{\lambda _0 t}& \quad \quad N_{3,n}&= e^{\lambda _2 (3t)}. \end{aligned}$$

Clearly, the left-hand side of the above is a chain of equations that can be easily solved, while the right-hand side can be generalized to:

$$\begin{aligned} N_{0,p}^*&= N_{J,p}^* e^{\lambda _{0} t}& \quad \quad N_{j,n}&= e^{\lambda _j (jt)}. \end{aligned}$$

This can be solved to yield

$$\begin{aligned} \lambda _{j,n}&= \frac{\ln N_j}{jt} \end{aligned}$$

(11)

$$\begin{aligned} \lambda _{0,n}&= \frac{\ln \frac{N_0}{N_j}}{jt}. \end{aligned}$$

(12)

By combining our analysis for p-comb and n-comb trees, we get the ratio:

$$\begin{aligned} \frac{\lambda _{j,n}}{\lambda _{j,p}}&= \frac{j+1}{j}, \ j = 1,\ldots ,J. \end{aligned}$$

(13)

This equation suggests that whether we are dealing with an n-comb or a p-comb the results for $\lambda$’s will not differ by much. We say that these two extremes bracket the space of real solutions, though we do not know whether they bound the space.

If we imagine a random walk in sequence space, one interpretation for a p-comb is that new structures arise at the boundary of a region for a previously new structure. An n-comb, on the other hand, implies that the first structure is the stem line and its boundary contacts regions for all other structures.

Clearly, the real tree is neither a p-comb nor an n-comb nor, in fact, binary (though it departs from binaryness in only a handful of nodes). We will discuss how comb-like our tree is and delve into easing these approximations in the “Finding the Nodes in a Comb” section.

Note, finally, that our solutions for the total abundances can take on non-integer values, though abundances are clearly integer valued. This is a consequence of modeling an integer-valued variable with a differential equation, and any non-integer values are taken to be approximations of the true values.

Estimating a’s

To derive the a’s, we use an approximation which we call the “nuclear decay” approximation for reasons that will become clear. Consider structure j during the time interval between its origin and the time at which a new structure, $j'$, originates from j. For convenience of notation, we take $t=0$ as the time at which j originated—that is, $N_j(0)= 1$. Suppose transitions to new structure are rare, so $a_{j'j} \ll \lambda _j$. Then approximately, $N_j(t)=e^{\lambda _j t}$. $t(N_j)$ has been plotted as a logarithmic curve with the axes $N_j$ (abscissa) versus time (ordinate) in Fig. 5. To each value of $N_j$ corresponds a value of $\tau (N_j)$, the mean time interval from t to the first transition of a copy of structure j to $j'$. $\tau$ decreases as $N_j$ increases because the more copies of structure j exist the more likely it is that one of them will make the transition to $j'$. Below we show that $\tau = \frac{1}{N_j^2a_{j'j}}$. We have plotted $\tau (N_j)$, $t(N_j),$ and their sum, $t(N_j) + \tau (N_j)$, in Fig. 5. This sum has a minimum value which is the mean time at which the first transition to $j'$ will occur.

Fig. 5

Graph of $t(N_j)$, $\tau (N_j)$, and $t(N_j) + \tau (N_j)$

To find an analytic expression for this minimum value, note that the transition $j \rightarrow j'$ is analogous to the radioactive decay of an atom, which is described by a Poisson process. Let the probability that an atom decays in the time interval dt be adt. The probability that one of N atoms will first decay between t and $t + {\mathrm d}t$ is ${Pr(no\ decay\ before\ t)}{Pr(one\ decay\ in\ } {\mathrm d}t \mathrm {)} = ([e^{-at}]^N)(a{\mathrm d}t)$. Then the mean first decay time for N atoms is

$$\begin{aligned}&\tau = \int _0^{\infty }t'e^{-Nat'}a{\mathrm d}t' \end{aligned}$$

$$\begin{aligned}\mathrm {so\ } \tau = \frac{1}{N^2a}. \end{aligned}$$

Now consider the transition $j \rightarrow j'$. From the preceding,

$$t = \frac{1}{{\lambda _{j} }}\ln N_{j} \;{\text{and}}\;\tau = \frac{1}{{N_{j}^{2} a_{{j'j}} }}$$

$${\text{ so}}\;\frac{{{\text{d}}(t + \tau )}}{{{\text{d}}N_{j} }} = \frac{1}{{\lambda _{j} N_{j} }} - \frac{2}{{a_{{j'j}} N_{j}^{3} }}$$

$$ {\mathrm{which}}\;{\mathrm{is}}\;{\mathrm{zero}}\;{\mathrm{at }}\frac{{a_{{j^{\prime}j}} }}{{\lambda _{j} }} = \frac{2}{{N_{{jmin}}^{2} }}. $$

(14)

Thus, the ratio $\frac{a_{j'j}}{ \lambda _j}$ can be determined from the value of $N_j$ when the transition occurs. Because $N_{j min}^2 \gg 1$, the ratio is $\ll 1$, as we assumed. Since the value of $\lambda _j$ has been determined, we can get $a_{j'j}$ from the ratio. Note that Eq. 14 implies that the units of a are $(Gy)^{-1}$.

Notice that the above model was explicated for the trees of protein folds and FSFs but can be adapted without modification for any level of the protein structural hierarchy for which all the relevant pieces discussed are available, namely abundance data and a known relationship between nd and time.

Materials and Methods

Phylogenomic Analysis

Two analyses were performed at different levels of the protein structure hierarchy, the first on folds and the second on fold superfamilies (FSFs). The data used to construct the trees consisted of fold and FSF abundances. There were 1030 folds in 749 species across all three superkingdoms. There were 1733 FSFs in 981 species across all three superkingdoms. SCOP was used for both fold and FSF classification. These numbers were the latest available at the time of retrieval. An argument for the virtues of SCOP over other classification schemes such as CATH is given by Caetano-Anollés et al. (2011).

PAUP* was used to construct phylogenomic trees for both FSFs and folds following the previously described methods of Caetano-Anollés et al. (2011), with genomic abundance within species, g, serving as characters. A single g value for each structure in each species resulted in two matrices (structures $\times$ species), $1733 \times 981$ and $1030 \times 749$ for FSFs and folds, respectively. Since large genomes are more likely to have larger protein structure abundances, we normalized the abundances (g) to a linearly ordered 0–23 scale using the formula (for FSFs):

$$\begin{aligned} g_{ab}{\mathrm {\_norm}} = {\mathrm {round}}\left[ \frac{23\ln (g_{ab}+1)}{(g_{\mathrm {max}} + 1)}\right]. \end{aligned}$$

(15)

And for folds, on a linearly ordered 0–20 scale:

$$\begin{aligned} g_{ab}{\mathrm {\_norm}} = {\mathrm {round}}\left[ \frac{20\ln (g_{ab}+1)}{(g_{\mathrm {max}} + 1)}\right]. \end{aligned}$$

(16)

Here, $g_{ab}$ is the g value of the FSF (or fold) a in species b. $g_{\mathrm {max}}$ is the maximum g value in the matrices above. These normalized matrices were then handed to PAUP* in a standard NEXUS file to compute the trees described above.

Calculating nd

Trees for folds and FSFs were returned in Newick format. In Newick format, numbers represent leaves and parentheses around two or more nodes represent an immediate common ancestor among those. For example, ((1,2),(3,4),5) corresponds to the tree in Fig. 6. The leaves of this tree are 1, 2, 3, 4,  and 5 and the internal nodes of the tree are (1,2),(3,4),  and ((1,2),(3,4),5) representing nodes 6, 7, and 8, respectively. In order to calculate the nd value of any node in a tree given in Newick format, one must count the number of left parentheses, ‘ ( ,’ to the left of the node and subtract from this the number of right parentheses, ‘ ) ,’ to the left of the node. For example, for leaf 3 there are 3 left parentheses to its left and 1 right parenthesis to its left, so its unnormalized nd value is 2, which is confirmed by inspection. Similarly, the internal node (3,4) has 2 left parentheses and one right parenthesis to its left so its unnormalized nd value is 1, as can again be verified by inspection.

Fig. 6

A tree corresponding to Newick format ((1,2),(3,4),5)

A Java program was written to de-nest the tree, i.e., to get a listing of all its internal nodes and leaves, find the location of each node within the tree’s Newick format, and count the number of left and right parentheses to the left of the node to yield the node’s nd value.

Collecting Genomes

Genome sizes for all organisms were mainly downloaded from NCBI, genomesonline.org, and project webpages. As a check of sanity, the sum of genome abundances for a given species was graphed against that species’ genome size. We expected, and found, a generally increasing trend; a species with a larger genome is more likely to have a larger sum. No extreme or unexpected outliers were found, though the data did have an expected scatter. These are presented in the “Sum of Genome Abundances Versus Genome Size” section.

Finding the Nodes in a Comb

The comb analysis, i.e., calculating $\lambda$’s and a’s assuming p-combs and n-combs described in “The Model” section, was first performed only on the comb-like terminal nodes, that is, those nodes that sprang directly from the stem line of the tree. There were 187 such nodes for FSFs and 147 for folds, discovered by manual inspection, accounting for 11 and 14 % of the nodes of the respective trees. The analysis was then repeated for all leaves of the trees, assuming each sprang directly from the stem line (i.e., assuming the tree was a perfect comb), and the results of the previous calculation were compared. There were no major differences in the results.

Justification for the comb approach was sought by binning the count of nd for each of the comb nodes; each comb node’s nd value was binned in one of a sequence of bins of size $\frac{1}{30}$ spanning the entire range of possible nd values, [0, 1], for a structure tree. A uniform distribution was discovered, with one spike at the combinatorial explosion of domains, as one might expect given a look at the spiky nature of the raw data at this point. These results are presented, defined, and discussed in the “No Comb Bias” section. Thus, the comb approach has, as a merit, a mostly uniform sampling over time, without biased over-representation of certain periods in time.

Calculating the Total Abundances, $\lambda$’s, and a’s

As denoted in Eq. 4, the total abundance of a protein structure is given by the dot product of the effective population size vector and the local genomic abundance vector. The effective population size of a particular species depends on the genome size of that species as noted in Eq. 5, so the effective population size vector is dependent on the corresponding genome size vector. Note, however, that the exponent of G in Eq. 5 is a derivation from population genetics. We were curious as to how robust our qualitative results were to variations in this exponent and this was explored by repeating the analysis through a range of different exponents from -2 to 2. This procedure was performed in an Excel spreadsheet using array formulas. The $\lambda$’s and a’s were also calculated in this spreadsheet and all results were graphed against time using Eqs. 6 and 7. Qualitatively, the results presented in this paper appeared to hold well for values of G’s exponent in that range, and the overall pattern evinced disappeared in a continuous fashion as we got further away from the exponent’s actual value, leading us to believe that our results are robust in the face of a potentially oversimplified population genetics model.

Results and Discussion

Evolutionary Patterns Emerging from the Model

In Wang et al. (2011), we postulated a molecular clock of FSFs and folds and plotted character state changes and terminal branch lengths against domain age derived from phylogenomic trees. No model was defined beyond the use of ordered characters and assumptions of maximum parsimony for the search of optimal trees. The plots revealed a biphasic pattern with an inflection point that coincided with the time of occurrence of an explosive event of domain combination in multidomain proteins and the rise of Eukarya. Wang and Caetano-Anollés (2009) offered possible mechanisms that could have been culprits of this combinatorial “big bang,” all of which likely enhanced the movement of genes in genomes. These mechanisms include the evolutionary inception of chromosomal and intronic recombination, faulty excision of introns, domain insertions and deletions at protein termini, and activity of ancient transposable elements. The combinatorial big bang persists today, but at a decreasing rate as noted by Caetano-Anollés et al. (2009). This is probably because of constraints imposed by the sizes of proteomes and the number of domains a protein can accommodate that increases its cost at a cellular level, as observed by Shahzad et al. (2015). Thus, a trade-off between economy, flexibility, and robustness exists lest domain function be degraded if indefinite increase in domains per protein is allowed.

In the present manuscript, we make the model of protein evolution explicit. We use the ITH strategy to calculate parameters of diversification of FSFs and folds. As we will show, our modeling exercise reveals that these parameters of domain growth and diversification also exhibit an emergent biphasic pattern. The fact that the pattern was not a foregone conclusion of the exercise makes its discovery through the model, and its correspondence to the biphasic pattern shown in Wang et al. (2011), even more remarkable.

Sum of Genome Abundances Versus Genome Size

As discussed in the “Collecting Genomes” section, as a check, the sum of fold abundances for a given species was graphed against that species’ genome size. A generally increasing trend was expected and found, as shown in Fig. 7, with species with a larger genome more likely to have a larger sum. The data for folds are presented separately by superkingdom because, while the data are increasing for all superkingdoms, for Archaea and Bacteria the graphs are linear. They show an abundance of about 1.25 copies per gene. For Eukaryotes a power law is a much better fit. The Metazoan kingdom is the largest contributor to the scatter in this power law. When Metazoa are removed, the $R^2$ noticeably increases as can be seen from Fig. 8.

Fig. 7

Archaeal, bacterial, and eukaryotic sums of fold abundances vs genome size

Fig. 8

Top sums of fold abundances vs genome size for fungi, metazoa, plants, and protista. Bottom sums of fold abundances vs genome size for fungi, plants, and protista

No Comb Bias

As discussed in the “Finding the Nodes in a Comb” section, justification for the lack of bias in the comb approach was sought by binning the count of nd for each of the comb nodes. A uniform distribution was discovered, with one spike near the combinatorial explosion of domains, before it for FSFs and after it for folds, since a larger nd corresponds to an earlier time. In the spike, the percentage of comb nodes is higher than elsewhere. The combinatorial explosion of structural domains, or “big bang” discussed by Wang and Caetano-Anollés (2009), refers to the sudden, punctuated appearance of a large number of terminal leaves (structures) following the evolutionary halfway mark (at nd ${\sim}0.6$), primarily due to the high combination and rearrangement of domains and distribution of these new combinations in novel lineages, and the rise of organismal diversification. The presence of this spike near the combinatorial explosion is discussed in the “ N _j 's” section. However, the presence of a uniform distribution across the entire timeline suggests that the comb approach will not yield a biased sampling. The graph for both FSF and fold nodes is presented in Fig. 9.

Fig. 9

Binned count of nd for comb nodes for FSF and fold data. Comb nodes are leaves diverging directly off the stem line on the trees of FSFs and folds. The bins are of size $\frac{1}{30}$

Graphs for $N_j$, $\lambda _j$, and $a_j$ and Their Interpretation

As described in “Materials and Methods” section, both the a’s and $\lambda$’s were graphed as functions of the time of origin of a structure. The results for both FSFs and folds are presented in Figs. 10, 11, and 12. While we have placed the graphs for folds and FSFs alongside each other to demonstrate the similar evolution of folds and FSFs, the graphs are not directly comparable because of the different numbers of organisms present in each study.

$N_j$’s

Figure 10 shows log$(N_j)$ versus time for both folds and FSFs for present-day p-comb-like nodes. Note that the present is at $t = 0$. Qualitatively, both fold and FSF total abundances have experienced a similar history, with total abundances dropping with time until a spike occurs around 1.5 Gyrs, at which point total abundances increase until the present. FSFs experienced this spike just prior to 1.5 Gyrs, while folds experienced it just after. In general, also, FSFs had larger total abundances over time.

Since only present-day structures are used in this graph, the time on the x-axis represents a given structure’s time of origin. Thus, in general, the present structures that came into existence earlier have had longer to grow in abundance and, therefore, have greater total abundances than structures that came into existence later. However, after the spike, $\lambda$’s increase rapidly (Fig. 11) and variants diversify so rapidly that the newer structure abundances actually catch up to and outpace older structure abundances. Clearly, a biphasic pattern emerges.

Moreover, the spike in the graph is present in all plots, Figs. 10, 11, and 12, always just prior to 1.5 Gyrs in FSFs and just after that time in folds. This time period corresponds to the combinatorial explosion of domains.

Fig. 10

log($N_j$) vs time (in Gyrs) for p-comb-like fold and FSF nodes

$\lambda _j$’s

Figure 11 shows log$(\lambda _j)$ versus time for both folds and FSFs for present-day p-comb-like nodes. Note again that the present is at $t = 0$. Again, qualitatively, both fold and FSF total abundances have experienced a similar history, with $\lambda$’s increasing with time until a spike occurs around 1.5 Gyrs, at which point $\lambda$’s increase much faster until the present, yet another emergent biphasic pattern. In general, also, FSFs had larger $\lambda$’s over time. The initial value of $\lambda$ for FSFs is approximately 7 $(Gyr)^{-1}$. It ranges from approximately 7 to 12 $(Gyr)^{-1}$ at the spike, and peaks at 867 $(Gyr)^{-1}$ at present.

The super-exponential growth in $\lambda$’s after the combinatorial explosion is to be expected for the following reasons. Consider a particular structure X. Once structure combinations are possible at a greater rate, X will appear in combination with other structures more often. Moreover, this new combination gets selected for its functionality. That additional selection pressure, above that of X’s on its own, speeds X’s diversification. As combinations proceed and generations of new structures are born, the new structures form combinations with each other as well as with structures existing prior to the explosion. This same super-exponential tendency in the $\lambda$’s following the combinatorial explosion is also the reason why newer structure abundances outpace older structure abundances around this time in Fig. 10.

Note that in Fig. 10 there are two inflection points, one at $-2.3$ Gyrs and another at $-1.6$ Gyrs for FSFs. If $\log \lambda$ were constant over time, $N_j$ would decrease as a function of time since an older present-day fold would have had longer to grow in abundance. $\log \lambda$ is nearly constant until the second inflection point resulting in only minor deviation from linear decline in $N_j$ until after this inflection point when $\log \lambda$ begins to increase sharply causing a similar increase in total abundance. Caetano-Anollés et al. (2011) show, in Fig. 4, at $nd = 0.4$ and 0.45, between the time of the two inflection points, that there is a drop in the number of functions. A drop in the number of functions means a drop in selection on the number of variants which results in a drop in total abundance.

Fig. 11

log($\lambda$) vs time (in Gyrs) for p-comb-like fold and FSF nodes

$a_j$’s

Figure 12 shows log$(a_{j^{\prime}j})$ versus time for both folds and FSFs for present-day p-comb-like nodes. Note again that the present is at $t = 0$. Again, qualitatively, both fold and FSF total abundances have experienced a similar biphasic history, with a’s increasing with time until a spike occurs around 1.5 Gyrs, at which point a’s decrease until the present. FSFs experienced this spike just prior to 1.5 Gyrs, while folds experienced it just after. Interestingly, unlike in Figs. 10 and 11 where FSFs dominate folds, folds had larger $\ln (a_{j^{\prime}j})$’s over time. That is, at a given time, transitions between folds occur with larger rate constants than transitions between FSFs. a’s and N’s have an inverse square relationship as seen in Eq. 14, and FSFs dominate folds in total abundances over time. Thus, folds dominate FSFs in log$(a_{j^{\prime}j})$’s over time because folds’ total abundances are generally lower.

Domination aside, the values of a’s increase consistently for both structures until the spike. This spike occurs nearer the end of superkingdom specification and into the epoch of organismal diversification described by Wang et al. (2007). An analogy to this time course is that of a developing field of knowledge. The initial researchers cannot help but make many novel discoveries. The next wave of researchers, however, usually do not make as many fundamental discoveries, perhaps due in part to the scarcity of such results in the field, but also because it is easy to combine many of the basic results into novel combinations. A similar biphasic pattern theorizing about the emergence of modules was elaborated on by Mittenthal et al. (2012).

Following the combinatorial explosion values of a’s decreased. As described earlier, old structures’ appearances in various combinations result in high numbers of old structures being preserved relative to low numbers of entirely new structures. This explains the simultaneous rise in $\lambda$ in Fig. 11 and fall of a in Fig. 12 following the combinatorial explosion. It also suggests that once combinations arose more rapidly access to new niches was faster via combinations rather than novel domain discoveries.

Note that $a_{j^{\prime}j}$ is approximately $10^{-17}$ per Gyr for a typical FSF. So aN is approximately $10^{-17}$ per year. The probability of $a_{j^{\prime}j}$ is small because that term represents a structure transitioning from ${j}$ specifically to $j^{\prime}$, not from ${j}$ to any other structure. In addition, at any given time the ability of a variant to transition from j to $j^{\prime}$ might be zero because most variants may not be able to directly access j. While we do not know how likely it is for a variant of j to access $j^{\prime}$, a particular structure and function may occupy fractions from $10^{-11}$ to $10^{-77}$ of sequence space, depending on how widely adopted the structure is, as reviewed by Ferrada and Wagner (2010). The probability of transitioning to $j^{\prime}$ is a proportion of fold space, while the probability of transitioning to $j^{\prime}$ from j is $a_{j^{\prime}j}$ and should thus be a smaller proportion of fold space. Thus, values for $a_{j^{\prime}j}$ fall into the expected range for the probability of transitioning to $j^{\prime}$ given by previous work.

Fig. 12

log($a_{j^{\prime}j}$) for present j to future j′ vs time (in Gyrs) for perfect p-comb fold and FSF nodes

Comparing Folds to FSFs

It should be clear that, qualitatively, $\lambda$’s, a’s, and N’s for both FSFs and folds experienced very similar qualitative histories. While FFs and FSFs clearly derive from a common ancestor by SCOP definition, it is uncertain whether folds do. Our results suggest that folds may indeed retain an evolutionary relationship after all. This is not unexpected as a tight correlation between folds and FSFs has been previously noted by Caetano-Anollés et al. (2011), Wang and Caetano-Anollés (2009), and Wang et al. (2007).

Data from the SCOP 1.75 database reveal that there are, on average, about 1 to 2 FSFs in each fold, with an overall average of 1.64 FSFs per fold across all protein classes. Thus, it is no surprise that the history of folds and FSFs is quite similar in Figs. 10, 11, and 12. If there was only one FSF in each fold, then the $\lambda$ of the FSF would be the same as the $\lambda$ of the fold. This equality would then make the plots of N’s and a’s for FSFs and folds similar by virtue of Eqs. 11 and 14.

Yet, there is a gap between the two curves, especially evident in Figs. 10 and 12. Moreover, in all curves, the spike in the data occurs at slightly different times, just before 1.5 Gyrs in FSFs and just after that in folds. However, as mentioned in the “Calculating nd ” section, while the graphs of folds and FSFs are laid alongside each other, they are not directly comparable. The significantly larger number of organisms in the FSF study, as compared to the fold study, accounts for the gap between the curves in Fig. 10, causing the total abundances of FSFs, which are functions of the number of organisms, to be consistently above the total abundances of folds. The gap between the total abundances cause the gaps in the remaining graphs due to the mathematical relationships between N, $\lambda$, and a. Specifically, Eq. 11 shows a direct proportionality between log(N) and $\lambda$, resulting in FSFs being above folds in Fig. 11. Since $\lambda$ is only proportional to log(N) the visible gap shrinks. Similarly, Eq. 14 shows an inverse relationship between N and a so in Fig. 12 we expect the fold curve to dominate the FSF curve.

Finally, note that the time in Figs. 10, 11, and 12 was determined via the linear relationship between t and nd in Eqs. 6 and 7. However, nd is a normalized node distance so the larger the number of structures present in the study, the larger the normalization. A larger normalization pushes back the nd value, and thus the time, of older structures. Since there are more FSFs than folds in our study, the FSFs have a larger normalization and this is a contributor to the FSF curve having a downward spike earlier than the fold curve in Fig. 10. Again, the mathematical relationships between N, $\lambda$, and a then maintain this spike separation in Figs. 11 and 12.

Conclusions

We have produced a model for the evolution of protein folds and FSFs and offer approximate solutions. We believe that the biological assumptions incorporated into our dynamic model are more plausible than the equilibrium assumptions of previous models. Our model is cast in linear ordinary differential equations which have exponentials as solutions. When more refined data are available, non-linear models with more parameters may be appropriate. We used our model to conclude (1) that there appears to be a tight connection between the history of folds and FSFs, (2) that the parameters of domain growth and diversification, $\lambda$ and a, exhibit an emergent biphasic pattern, (3) that, more specifically, the corresponding transition probabilities to new variants of a fold experienced a sharp increase just as the transition probabilities to new folds experienced a steep decline, and (4) that this simultaneous sharp increase in $\lambda$ and the decline in a are explainable by and consistent with the combinatorial explosion of domains and the rise of organismal diversification. We believe that variations of our simple model will be applicable to other problems dealing with the evolution of protein structure, and may have uses whenever the simple assumptions of a birth–death model with available abundances and a molecular clock exist. For example, there may be an analogy to be made with language. Written words are to protein sequences, as spoken words are to protein domains, as meaning is to function. A previous connection between language and protein domains was shown by Shahzad et al. (2015) who demonstrated that average domain length decreases as the domain number grows in a protein just as average syllable length decreases as syllable number grows in a word, the so-called Menzerath–Altmann law. In another direction, this research could be used to bootstrap a new phylogenomic tree reconstruction strategy. This paper gives values for a’s via parsimony methods. These values can potentially be used to generate a new tree via maximum likelihood.