Modelling and simulation of a moving interface problem: freeze drying of black tea extract

Abstract

The moving interface separates the material that is subjected to the freeze drying process as dried and frozen. Therefore, the accurate modeling the moving interface reduces the process time and energy consumption by improving the heat and mass transfer predictions during the process. To describe the dynamic behavior of the drying stages of the freeze-drying, a case study of brewed black tea extract in storage trays including moving interface was modeled that the heat and mass transfer equations were solved using orthogonal collocation method based on Jacobian polynomial approximation. Transport parameters and physical properties describing the freeze drying of black tea extract were evaluated by fitting the experimental data using Levenberg–Marquardt algorithm. Experimental results showed good agreement with the theoretical predictions.

1 Introduction

Freeze drying known as “Lyophilization” is a key separation processes (the sublimation of frozen solvent (water) content from the material being dried) mainly used in pharmaceuticals, biotechnology, fine chemicals, and food industries. The conventional drying processes (evaporative drying, drum drying, spray drying, etc.) may cause loss of aroma, taste, texture, and nutrition utilize higher operation temperatures compared to the freeze drying. Thus, the highest quality products can be obtained by freeze drying compare to the conventional drying processes.

Freeze drying process consists of the preparation stages, freezing, primary drying stage, secondary drying stage, packaging, and storage. In order to keep prime properties (activity, stability, structure, flavor, taste, etc.) and obtain the finest quality products, each stage is critical and requires maximum care possible. Freeze-drying is a relatively expensive separation process requiring long processing time and high energy demand. There are two stages in drying process; primary drying and secondary drying. To supply energy for vacuum and sublimation of frozen water, among the stages of freeze drying, the primary drying stage requires time and energy as compared to the other stages of freeze drying such as freezing and secondary drying stage [15]. Therefore, optimization of primary drying stage becomes crucial for the freeze drying process.

The freeze drying process fits perfect to the high market value products such as pharmaceuticals, fine chemicals, biotechnological products, and expensive foods. During drying, the water in the product changes its physical phase from solid to gas by sublimation. This process can be modeled as a moving interface while the product is drying. Duration of primary drying stage can be determined by estimating the position of moving interface.

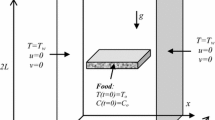
Figure 1 shows a typical temperature distribution during the primary drying stage while the moving interface position changes. T_x, states the temperature of the moving interface is also the lowest point of the temperature profile during primary drying stage. The interface position approaches the length of the material until the primary drying stage of freeze drying has been completed. The heat and mass transfer mechanism of freeze drying stages has been extensively investigated in the literature [5, 9, 13, 16, 22]. In contrast, Sadikoglu et al. has constructed a mathematical model for skim milk. The best fit of heat and mass transfer coefficients to the experimental results of freeze drying of skim milk has been determined. Their mathematical model utilizes the dusty-gas model which does not require detailed information about the porous matrix structure of the dried layer [2, 6, 11, 12]. However, a detailed freeze drying of the black tea extract has not been investigated.

Fig. 1

Temperature distribution of T_UP, T_X and T_LP during primary drying stage

The orthogonal collocation method can be successfully applied to the solution of moving boundary problems in finite media. On the other hand, finite element analysis is also a successful method, however it could make a difficulty in applying moving boundary to the sublimation interface [1, 10]. An empirical and statistical approach using the response surface method gives a predicted property of the resultant dried product, but doesn’t give the status of products during drying [3, 14].

In this study, the aim is to determine heat and mass transport parameters during freeze drying black tea extract. The equations associated with heat and mass transfer mechanisms established by [16] were used as the model equations, successfully transformed due to solve moving interface problem. Then the parameter estimation was accomplished by Levenberg–Marquardt minimization algorithm, also known as the damped least-squares (DLS) method is actually a combination of two minimization methods: the gradient descent method and the Gauss–Newton method. One dimensional mathematical model devised using conservation of mass and energy presented to describe dynamic behavior of drying stages of freeze drying of bulk solution of black tea extract in trays.

1.1 Mathematical model of freeze-dried black tea extract

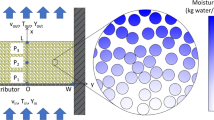
The free water (frozen) and bound water (unfrozen) are removed from the material by sublimation occurs as a result of heat being conducted to the sublimation interface through dried layer I and frozen layer II. As shown in Fig. 2, the terms of N_t and N_w state the total mass flux and water vapor mass flux in dried layer. N_t is the sum of the mass flux of water and inert vapor gas. The q₁ represents the heat input to the upper surface of dried layer of the product that is being freeze-dried by radiation, while q_II represent the heat input to the frozen bottom surface the material being freeze dried by conduction. The term q_III depicts the heat input to side surfaces of the material being freeze dried but the top and bottom surfaces of the tray loaded by black tea extract are much larger than the side surfaces of the tray. The heat input from the side surfaces of the tray can be neglected throughout the calculation without introducing any significant error. The magnitude of q_I and q_II are altered by changing the upper and lower plate temperatures because freeze dryer designs do not allow to control the upper and lower plate temperatures independently. Thus, the heat input from the frozen bottom surface is always larger than the heat input from the dried top surface of the product.

Fig. 2

Diagram of a material on a tray during freeze-drying [the variable X denotes the position of the sublimation between the freeze-dried layer (layer I) and the frozen layer (layer II)]

1.1.1 Primary drying stages

During the primary drying stage, the heat required for sublimation of frozen water at interface that separates the dried and frozen layers, supplied by heating plates through dried (I) and frozen (II) layers by radiation and by conduction, respectively. In order to construct the mathematical model to represent primary drying stages of the freeze drying of black tea extract in tray, the following assumptions have been made:

• One dimensional heat and mass transfer modeled assumed to occur normal to the interface and surface,

• Sublimation occurs at an interface parallel to and at a distance X from the surface of the sample,

• The thickness of interface is taken to be infinitesimal,

• A binary mixture of water vapor and inert gas flows through the dried layer,

• The concentration of water vapor is assumed to be under equilibrium with the ice at the moving interface,

• Solid matrix and the gas has been assumed to be thermal equilibrium in the porous region,

• The frozen region is considered to be homogeneous, thermal conductivity, density and specific heat are assumed to be constant,

• The frozen region contains a negligible proportion of dissolved gas [8, 12].

The temperature distributions in dried (I) and frozen (II) layers, water vapor and inert concentration distributions in dried (I) region, can be determined using Eqs. 1–3 for dried (I) and frozen (II) layers.

$$\frac{{\partial {\text{T}}_{\text{I}} }}{{\partial {\text{t}}}} = {{\upalpha }}_{\text{Ie}} \frac{{\partial^{2} {\text{T}}_{\text{I}} }}{{\partial {\text{x}}^{2} }} - \frac{{{\text{C}}_{\text{pg}} }}{{{{\uprho }}_{\text{Ie}} {\text{C}}_{\text{Ie}} }}\frac{{\partial \left( {{\text{N}}_{\text{t}} {\text{T}}_{\text{I}} } \right)}}{{\partial {\text{x}}}} + \frac{{{{\Delta H}}_{\text{v}} {{\uprho }}_{\text{I}} }}{{{{\uprho }}_{\text{Ie}} {\text{C}}_{\text{Ie}} }}\frac{{\partial {\text{C}}_{\text{sw}} }}{{\partial {\text{t}}}} \quad 0 \le {\text{x}} \le {\text{X}}$$

(1)

$$\frac{{\partial {\text{T}}_{\text{II}} }}{{\partial {\text{t}}}} = {{\upalpha }}_{\text{II}} \frac{{\partial^{2} {\text{T}}_{\text{II}} }}{{\partial {\text{x}}^{2} }}\quad {\text{X}} \le {\text{x}} \le {\text{L}}$$

(2)

$$\frac{1}{\text{R}}\frac{\partial }{{\partial {\text{t}}}}\left( {\frac{{{\text{P}}_{\text{w}} }}{{{\text{T}}_{\text{I}} }}} \right) = - \frac{1}{{{\text{M}}_{\text{w}} {{\upvarepsilon }}}}\frac{{\partial {\text{N}}_{\text{w}} }}{{\partial {\text{x}}}} - \frac{{{{\rho }}_{\text{I}} }}{{{\text{M}}_{\text{w}} {{\upvarepsilon }}}}\frac{{\partial {\text{C}}_{\text{sw}} }}{{\partial {\text{t}}}}\quad 0 \le {\text{x}} \le {\text{X}}$$

(3)

$$\frac{1}{\text{R}}\frac{\partial }{{\partial {\text{t}}}}\left( {\frac{{{\text{P}}_{\text{in}} }}{{{\text{T}}_{\text{I}} }}} \right) = - \frac{1}{{{\text{M}}_{\text{in}} {{\varepsilon }}}}\frac{{\partial {\text{N}}_{\text{in}} }}{{\partial {\text{x}}}}\quad 0 \le {\text{x}} \le {\text{X}}$$

(4)

The parameters water vapor mass flux, N_w and inert mass flux, N_in that appear in Eqs. (3) and (4), respectively can be determined by using the dusty-gas model:

$${\text{N}}_{\text{w}} = - \frac{{{\text{M}}_{\text{w}} }}{{{\text{RT}}_{\text{I}} }}\left( {{\text{k}}_{1} \frac{{\partial {\text{p}}_{\text{w}} }}{{\partial {\text{x}}}} + {\text{k}}_{2} {\text{p}}_{\text{w}} \left( {\frac{{\partial {\text{p}}_{\text{w}} }}{{\partial {\text{x}}}} + \frac{{\partial {\text{p}}_{\text{in}} }}{{\partial {\text{x}}}}} \right)} \right)$$

(5)

$${\text{N}}_{\text{in}} = - \frac{{{\text{M}}_{\text{in}} }}{{{\text{RT}}_{\text{I}} }}\left( {{\text{k}}_{3} \frac{{\partial {\text{p}}_{\text{in}} }}{{\partial {\text{x}}}} + {\text{k}}_{4} {\text{p}}_{\text{in}} \left( {\frac{{\partial {\text{p}}_{\text{w}} }}{{\partial {\text{x}}}} + \frac{{\partial {\text{p}}_{\text{in}} }}{{\partial {\text{x}}}}} \right)} \right)$$

(6)

The Eqs. (5) and (6) must be differentiated with respect to space coordinate x, before replacing them in Eqs. (3) and (4). One expression to describe the removal of the bound (unfrozen) water from the inside of the solid is based on the linear desorption rate of the bound water using a proper desorption rate constant [16]. In this work, we utilized the linear desorption rate equation to describe (removal) of bound water:

$$\frac{{\partial C_{sw} }}{\partial t} = - k_{d} C_{sw}$$

(7)

where k_d is the desorption rate constant. The initial and boundary conditions of Eqs. (1)–(6) and (7) are as follows:

$$T_{I} = T_{II} = T_{x} = T^{0} , \quad t = 0,\quad 0 \le x \le L$$

(8)

$$p_{w} = p^{0}_{w} , \quad p_{in} = p^{0}_{in }, \quad t = 0,\quad 0 \le x \le X$$

(9)

$$C_{sw} = C^{0}_{sw} , \quad t = 0,\quad 0 \le x \le L$$

(10)

$$q_{I} = - k_{Ie} \left. {\frac{{\partial T_{I} }}{\partial x}} \right|_{x = 0} \quad x = 0\quad t > 0$$

(11)

For dried layer I, heat transfer to the upper dried surface by radiation,

$$q_{I} = \sigma \varepsilon \left( {T^{4}_{up} - \left( {T_{I} \left( {t,0} \right)} \right)^{4} } \right)\quad t > 0$$

(12)

The material and energy balances at infinitesimal thickness of interface result the following equation from where the temperature of interface can be determined.

$$k_{II} \left. {\frac{{\partial T_{n} }}{\partial x}} \right|_{x = X} -\,k_{Ie} \left. {\frac{{\partial T_{I} }}{\partial x}} \right|_{x = X} + V\left( {\rho_{II} C_{pII} \left. {T_{II} } \right|_{x = X} - \rho_{I} C_{pI} \left. {T_{I} } \right|_{x = X} } \right) +\, N_{t} C_{pg} T_{x} = - {{\Delta }}H_{S} N_{t}\quad {\hbox{at}}\quad x = X {\text{ and }}0 < t \le t_{x = L}$$

(13)

The interface temperature is also the right boundary condition of the frozen section and the left boundary condition of the dried section.

$$T_{I} = T_{x} = T_{II} \quad x = X\quad t > 0$$

(14)

$$q_{II} = - k_{II} \left. {\frac{{\partial T_{II} }}{\partial x}} \right|_{x = L} \quad x = L\quad t > 0$$

(15)

There is a thin film between the frozen material and lower surface of the tray and k_f is the thermal film conductivity coefficient.

$$q_{II} = k_{f} \left( {T_{LP} - \left( {T_{II} \left( {t,L} \right)} \right)} \right)\quad {\text{t}} > 0$$

(16)

P_o implies the sum of water vapor pressure (P_w) and inert gas pressure (P_in).

$$p_{w} = p^{o}_{w} \quad x = 0\quad t > 0$$

(17)

$$p_{in} = p^{o}_{in} = P_{o} - p^{o}_{w} \quad x = 0\quad t > 0$$

(18)

The variable $p^{o}_{w}$, is the chamber water vapor pressure, usually determined by the condenser design and assumed constant within the drying chamber. The variable P_o denotes the total pressure $\left( {P_{o} = p^{o}_{w} + p^{o}_{in} } \right)$ at x = 0, and is usually considered to be approximately equal to the total pressure in the drying chamber.

$$p_{w} = f\left( {T_{x} } \right)\quad x = X\quad 0 < t \le t_{x = L}$$

(19)

$$\left. {\frac{{\partial p_{in} }}{\partial x}} \right|_{x = X} = 0 \quad x = X\quad 0 < t \le t_{x = L}$$

(20)

where V is the velocity of interface that is calculated by the mass flux of water vapor at interface (x = X) dividing of difference of frozen layer II density and equilibrium density at interface.

$$V = \frac{dX}{dt} = \frac{{ - \left. {N_{w} } \right|_{x = X} }}{{\rho_{II - } \rho_{I} }}\quad X = 0\quad t = 0$$

(21)

Minus sign at the in front of water vapor mass flux indicate the direction and it is the opposite direction of the moving interface velocity.

1.1.2 Secondary drying stage

The secondary drying stage starts at the end of the primary drying stage where the frozen free water content of the material is completely removed. This drying stage involves the removal of bound water from inside the sample resulted by physical and chemical adsorption, or crystallization [19]. During the secondary drying stage, the energy and material balance equations representing the temperature, phase pressures, and bound water concentration are same equations those are derived in the primary drying stage. However, in this stage those equations are also to be solved for the varying thickness of the drying material. The resulting equation is shown in Eq. 22,

$$\frac{{\partial T_{I} }}{\partial t} = \alpha_{Ie} \frac{{\partial^{2} T_{I} }}{{\partial x^{2} }} - \frac{{C_{pg} }}{{\rho_{Ie} C_{Ie} }}\frac{{\partial \left( {N_{t} T_{I} } \right)}}{\partial x} + \frac{{\Delta H_{v} \rho_{I} }}{{\rho_{Ie} C_{Ie} }}\frac{{\partial C_{sw} }}{\partial t}\quad 0 \le x \le L$$

(22)

Initial and boundary conditions for Eq. (22) are as follows:

$$T_{I} = \gamma \left( x \right),\, t = t_{x = L},\, 0 \le x \le L$$

(23)

$$q_{I} = - k_{Ie} \left. {\frac{{\partial T_{I} }}{\partial x}} \right|_{x = 0} \quad x = 0 \quad t > t_{x = L}$$

(24)

Heat transfer to the upper dried surface by radiation,

$$q_{I} = \sigma \varepsilon \left( {T^{4}_{up} - \left( {T_{I} \left( {t,0} \right)} \right)^{4} } \right)\quad t > t_{x = L}$$

(25)

$$q_{II} = - k_{Ie} \left. {\frac{{\partial T_{I} }}{\partial x}} \right|_{x = L} \quad x = L\quad t > t_{x = L}$$

(26)

Initial and boundary conditions of Eqs. (2)–(3) and (5) for the second drying stage are as follows:

$$p_{w} = \delta \left( x \right) \quad t = t_{X = L} \quad 0 \le x \le L$$

(27)

$$p_{in} = \theta \left( x \right) \quad t = t_{X = L} \quad 0 \le x \le L$$

(28)

$$C_{sw} = v\left( x \right) \quad t = t_{X = L} \quad 0 \le x \le L$$

(29)

$$p_{w} = p_{wo} \quad p_{in} = p_{ino} = P_{o} - p_{wo} \quad x = 0\quad t \ge t_{X = L}$$

(30)

$$\left. {\frac{{\partial p_{w} }}{\partial x}} \right|_{x = L} = 0\quad x = L\quad t > t_{x = L}$$

(31)

$$\left. {\frac{{\partial p_{in} }}{\partial x}} \right|_{x = L} = 0\quad x = L\quad t > t_{x = L}$$

(32)

γ(x), $\delta \left( x \right)$, θ(x) and v(x) are functions position, x and contain profile of T_I, p_w, p_in, and C_sw, obtained from the solution of the mathematical models at the end of the primary drying stage and they serve as initial conditions for the secondary drying stage. Immediately after the first dried layer come to existence during the primary drying stage, the secondary drying stage start taking place. But during the primary drying the concentration gradient between solid and dried pores is not significant. As a result the contribution of the removal of bound water to the total mass flux of the water removed during primary drying is not also significant. Subject to the physical properties of the material being freeze-dried, the secondary drying stage could be as long as the primary drying stage. Practically, 10–30% of the total water content of the material is removed by desorption during the secondary drying stage [19]. The required desorption heat to remove the bound water molecules in the dried layer during the secondary drying stage is provided by the radiation from the top of the sample and by conduction from the bottom of the sample. Both heat inputs from top and bottom surfaces of the sample are transferred by the conduction throughout the porous dried layer [16, 17, 19].

2 Materials and methods

2.1 Materials

Çay Çiçeği black tea (produced by Çaykur) is a well- known and widely used trademark in Turkey used in this study. Commercial black tea extracted with distilled water, filtered then concentrated to 10% (w/w) in an evaporator under vacuum.

2.2 Freeze dryer

In freeze-drying experiments, the pilot scale freeze dryer (Virtis Ultra 25 XL, New York, NY) was used. The temperature of heating plates of the freeze dryer used in the drying experiment can be adjusted from −40 to 60 °C while the condenser temperature can be set as low as −70 °C. The four trays of the freeze dryer are capable to hold 25 L of solution. The condenser where sublimated and desorbed water vapor removed from the drying chamber by condensation has surface area of 3264 cm². The vacuum system of the freeze dryer equipped with one compressor with a power of 1.12 kW, and capable of supplying vacuum as low as 10 Pa.

2.3 Experimental verification

Five hundred grams of black tea was added into 5000 L of boiling distilled water in a steel container to allow soluble solids of black tea to infuse into boiling water. Solution filtered and concentrated to 10% (w/w) in an evaporator under vacuum. Concentrated 10% (w/w) 150 mL solution poured in the tray (0.10 m × 0.15 m × 0.04 m) of the freeze dryer. The heating plates temperature of the freeze dryer was set at −35 °C for 4 h to completely freeze the concentrated solution for each experiment. On completion of freezing, the drying chamber pressure was set to 10 Pa and kept constant during the drying. The air in the drying chamber evacuated by the vacuum pump in 30 min to reach set pressure of 10 Pa. Detailed information about freeze drying of black tea solution was not available in the literature, but it is known that the primary drying stage of freeze drying is a mass transfer controlled process while the secondary drying stage of freeze drying is a heat transfer controlled process. Therefore, the drying chamber pressure was set to 50 Pa that is minimum value can reached for employed freeze dryer, well below the ice vapor pressure of the sample to increase water vapor mass flux through the pores of the dried material resulted by the sublimation during the primary drying stage [17, 18].

Moderately high chamber pressure could be beneficial for the heat transfer limited secondary drying stage by increasing the heat transfer capacity of the dried matrix, to facilitate the removal of bound water from the solid phase of the material being freeze dried. The problem is distinguishing the primary and secondary drying stages for freeze drying of black tea extract is almost impossible. Therefore, the drying chamber pressure was set its minimum value during both the primary and secondary drying stages. The heating plate temperatures of the freeze dryer and chamber pressures are given in Table 1. From the beginning to the end of the freeze-drying process, weight measurements were taken for every 2 h to obtain the weight loss of the samples.

Table 1 Freeze drying conditions of black tea extract

2.4 Moisture content analysis

Certain amount of tea sample were placed into a pre-weighed dish and evaporated in an oven at 100 °C (±2) for 24 h. Then sample was cooled in a desiccator and brought to constant weight. From the weight of residue, moisture content and the amount of total solids in the tea leaves were obtained.

2.5 Numerical solution of developed mathematical model

As mentioned before, the mathematical models that given in this work to represent dynamic behavior of both the primary and secondary drying stages of freeze drying of black tea extract in the tray solved by numerical techniques of orthogonal collocation that demands less computational time because it generates smaller problems [4]. In the primary drying, the Eqs. (1)–(4) along with the constitutive equations of water vapor and inert mass fluxes [Eqs. (5)–(6)], boundary [Eqs. (8)–(10)] and initial conditions [Eqs. (11)–(20)] are the set of nonlinear parabolic partial differential equations with moving boundary [Eq. (21)] and requires simultaneous solution. Before using the orthogonal collocation method, all equations were put in dimensionless by defining dimensionless spatial direction for both the dried (I) and frozen (II) layers.

$$\xi = \frac{x}{X} \quad 0 \le x \le X$$

(33)

$$\eta = \frac{x - X}{L - X}\quad X \le x \le L$$

(34)

Then the transformed models are conveniently discretized using orthogonal collocation with the collocation points in the spatial direction. The trial functions chosen to be sets of orthogonal Jacobi polynomials [21] which satisfied the boundary conditions and the roots to the polynomials gave the collocation points. Thus, collocation points are taken as the roots of orthogonal Jacobi polynomials whose all roots are located between 0 and 1. The first and the second partial derivative with respect to dimensionless spatial direction can defined as follows:

$$\frac{\partial Y\left( i \right)}{\partial \xi } = \mathop \sum \limits_{j = 1}^{N + 2} A\left( {i,j} \right)Y\left( i \right), \quad 0 \le \xi \le 1$$

(35)

$$\frac{{\partial^{2} Y\left( i \right)}}{{\partial \xi^{2} }} = \mathop \sum \limits_{j = 1}^{N + 2} B\left( {i,j} \right)Y\left( i \right), \quad 0 \le \xi \le 1$$

(36)

In Eqs. (35)–(36), ξ is the dimensionless spatial direction, Y represents dependent variable such as temperature of the dried layer T_I, temperature of the frozen layer T_II, water vapor pressure p_w, and inert pressure p_in, i represents root of orthogonal polynomial (collocation points) while A and B represent discretization matrices come from orthogonal collocation method. The roots of the Jacobi polynomials and discretization matrices of A and B for required number of collocation points were calculated by using the method developed by [23]. Employing discretization matrices of A and B for required number of collocation points, the energy balances in the dried (I) and frozen (II) layers and the material balances in the dried layer (I), become as follows:

$$\begin{aligned} \frac{{\partial T_{I} \left( i \right)}}{\partial t} & = \frac{{\alpha_{Ie} }}{{X^{2} }}\mathop \sum \limits_{j = 1}^{N + 2} B\left( {i,j} \right)T_{I} \left( i \right) + \frac{1}{X}\left( \xi \left( i \right)\frac{\partial X}{\partial t} - \frac{{C_{pg} }}{{\rho_{Ie} C_{Ie} }}\left( {N_{t} \left( i \right)\mathop \sum \limits_{j = 1}^{N + 2} A\left( {i,j} \right)T_{I} \left( i \right)} \right.\right. \\ & \quad +\left.\left.T_{I} \left( i \right)\mathop \sum \limits_{j = 1}^{N + 2} A\left( {i,j} \right)N_{t} \left( i \right) \right) \right) \\ & \quad + \frac{{\Delta H_{v} \rho_{I} }}{{\rho_{Ie}C_{Ie}}}\frac{{\partial C_{sw} }}{\partial t}\quad 0 \le \xi \le 1 \end{aligned}$$

(37)

$$\begin{aligned} \frac{{\partial T_{II} \left( i \right)}}{\partial t} = \frac{{\alpha_{II} }}{{(L - X)^{2} }}\mathop \sum \limits_{j = 1}^{N + 2} B\left( {i,j} \right)T_{II} \left( j \right) + \frac{dX}{dt}\left( {\frac{{L\left( {\eta - 1} \right) + X\left( {1 - \eta } \right)}}{{(L - X)^{2} }}} \right)\mathop \sum \limits_{j = 1}^{N + 2} A\left( {i,j} \right)T_{II} \left( j \right) \hfill \\ 0 \le \eta \le 1 \hfill \\ \end{aligned}$$

(38)

$$\frac{{\partial p_{w} \left( i \right)}}{\partial t} = \frac{\xi \left( i \right)}{X}\frac{\partial X}{\partial t}\mathop \sum \limits_{j = 1}^{N + 2} A\left( {i,j} \right)p_{w} \left( i \right) - \frac{{RT_{I} \left( i \right)}}{{\varepsilon_{p} M_{w} }}\left( {\frac{1}{X}\mathop \sum \limits_{j = 1}^{N + 2} A\left( {i,j} \right)N_{t} \left( i \right) + \rho_{Ie} k_{d} C_{sw} } \right)\, 0 \le \xi \le 1$$

(39)

$$\frac{{\partial p_{in} \left( i \right)}}{\partial t} = \frac{\xi \left( i \right)}{X}\frac{\partial X}{\partial t}\mathop \sum \limits_{j = 1}^{N + 2} A\left( {i,j} \right)p_{in} \left( i \right) - \frac{{RT_{I} \left( i \right)}}{{\varepsilon_{p} M_{in} }}\left( {\frac{1}{X}\mathop \sum \limits_{j = 1}^{N + 2} A\left( {i,j} \right)N_{t} \left( i \right)} \right)\quad 0 \le \xi \le 1$$

(40)

$$\frac{{\partial C_{sw} \left( i \right)}}{\partial t} = \frac{\xi \left( i \right)}{X}\frac{\partial X}{\partial t}\mathop \sum \limits_{j = 1}^{N + 2} A\left( {i,j} \right)C_{sw} \left( i \right) - k_{d} C_{sw} \quad 0 \le \xi \le 1$$

(41)

$$\frac{\partial X}{\partial t} = - \frac{{\left. {N_{w} } \right|_{\xi = 1} }}{{\rho_{II} - \rho_{I} }}$$

(42)

For all equation presented above i (i = 1, 2, 3, …, N) represents internal collocation points that corresponds to roots of the orthogonal Jacobi polynomials except 0 and 1. Index j (j = 1, 2, 3, …., N + 2) also represents the internal collocation points where j = 1 and j = N + 2 means the first and last collocation points that correspond the first and final root of the Jacobi polynomial that is 0 and 1, respectively.

Eventually, the partial differential equations that given in Eqs. (1)–(4) and (7), (21) are transformed to ordinary differential equations system [Eqs. (37)–(42)] with following initial and boundary conditions:

$$\left. {T_{I} } \right|_{\xi = 0} = \left. {T_{I} } \right|_{\xi = 1} = \left. {T_{II} } \right|_{\eta = 1} = T^{0} \quad t = 0\quad 0 \le \xi \le 1$$

(43)

$$p_{w} = p^{0}_{w} \quad t = 0 \quad 0 \le \xi \le 1$$

(44)

$$p_{in} = p^{0}_{in} \quad t = 0\quad 0 \le \xi \le 1$$

(45)

$$C_{sw} = C^{0}_{sw} \quad t = 0\quad 0 \le \xi \le 1$$

(46)

$$\left. T \right|_{\xi = 0} = \frac{{ - k_{Ie} \mathop \sum \nolimits_{j = 2}^{N + 2} A\left( {1,j} \right)T_{I} \left( j \right) - X\sigma F_{up} \left( {\left. {T^{4} } \right|_{\xi = 0} - T_{up}^{4} } \right)}}{{k_{Ie} \left( {A\left( {1,1} \right)} \right)}}$$

(47)

$$\left. {T_{I} } \right|_{\xi = 1} = \left. {T_{II} } \right|_{\eta = 1} = \frac{{\frac{{k_{Ie} }}{X}\left( {A\left( {N + 2,1} \right)\left. {T_{I} } \right|_{\xi = 0} + \mathop \sum \nolimits_{j = 2}^{N + 1} A\left( {N + 2,j} \right)T_{I} \left( j \right)} \right) - \Delta H_{s} \left. {N_{t} } \right|_{\xi = 1} }}{{\left. {N_{t} } \right|_{\xi = 1} \left( {C_{pg} - \frac{{\rho_{II} C_{pII} - \rho_{I} C_{pI} }}{{\rho_{II} - \rho_{I} }}} \right) - \frac{{k_{Ie} }}{X}A\left( {N + 2,N + 2} \right)}}$$

(48)

$$\left. {T_{II} } \right|_{\eta = 1} = \frac{{\frac{{k_{II} }}{L - X}T_{X} + k_{f} T_{LP} }}{{\left( {\frac{{k_{II} }}{L - X} + k_{f} } \right)}}$$

(49)

$$p_{w} = p^{o}_{w} \quad \xi = 0\quad t > 0$$

(50)

$$p_{in} = p^{o}_{in} = P_{o} - p^{o}_{w} \quad \xi = 0\quad t > 0$$

(51)

$$p_{w} = f\left( {\left. T \right|_{\xi = 1} } \right)\quad \xi = 1\quad t > 0$$

(52)

$$\left. {p_{in} } \right|_{\xi = 1} = - \frac{{\mathop \sum \nolimits_{j = 1}^{N + 1} A\left( {N + 2,j} \right)p_{in} \left( j \right)}}{{A\left( {N + 2,N + 2} \right)}}\quad \xi = 1\quad t > 0$$

(53)

The initial condition for Eq. (42) is X = 0.0001 at t = 0, but this means that there exist dried layer at the beginning of freeze drying, this not realistic but it required for the numerical solution. In the secondary drying stage, there is no moving boundary and froze (II) layer. Therefore, Eq. (38) totally eliminated and X is set to L while derivative of X is set equal zero to obtain numerical solution for the secondary drying stage.

2.6 Algorithm of numerical solution

Time dependent ordinary and partial differential equations for freeze drying process are complex to simulate the process. In order to solve the models equations, explicit and implicit approaches are used. While the explicit method calculates the state of a system at a later time from the state of the system at the current time, the implicit method solves an equation involving both the current state and later state of the system [20]. The expressions of explicit and implicit methods are given below, respectively. Mathematically, t denotes the current system state and t + Δt denotes the state at later time.

$$T\left( {t + \Delta t} \right) = F\left( {T\left( t \right)} \right)$$

(54)

$$F\left( {T\left( t \right),T\left( {t + \Delta t} \right)} \right) = 0$$

(55)

Equation (55) is implicitly solved to find T(t + Δt). As shown from Eq. (55), although implicit form involves extra term and requires extra a computational effort, it uses larger time steps and takes less computational time. In our study, the model equations transformed to the implicit form like Eq. (55) and it was seen from the numerical analysis, implicit approach is more suitable for the our model equations. The ode15i Matlab solver was used to solve our model and all equation transformed fully implicit form as:

$$F\left( {t, y\left( t \right), y^{\prime } \left( t \right)} \right) = 0$$

(56)

There are novelties because there are two Jacobian matrices, ${\text{dF}}/{\text{dy}}$ and ${\text{dF}}/{\text{dy'}}$ that can be given manually; also solver can estimate approximate Jacobian. Specific vectorized format is needed for the ode15i Matlab solver, in the present model all equation vectorized [like Eq. (57)] and solved simultaneously.

$$if\, y^{\prime}\left( t \right) = G\left( t \right) = > 0 = y^{\prime}\left( t \right) - G\left( t \right)$$

(57)

Orthogonal collocation uses collocation at the zeros of some orthogonal polynomial (Jacobi polynomial for this work) to transform the partial differential equation (PDE) to a set of ordinary differential equations (ODEs). In our system, to describe the dynamic behavior of the primary drying stage, there are 5 PDEs (Eqs. 1–4, 7) and 1 ODE [Eq. (21)]. With the A and B matrices which are difference operators established by collocation method, our PDE equations can be easily converted ODEs that shown before (Eqs. 37–42). Then 5n + 1 ODE equations are solved with ode15i solver.

The solution algorithm is:

Step 1:

Determine n, the number of collocation points in axial direction. Set initial data: $T_{I} = T_{II} = T_{x} = T^{0} , p_{w} = p^{0}_{w} ,p_{in} = p^{0}_{in} ,C_{sw} = C^{0}_{sw}$ and set initial time interval for ode15i.

Step 2:

Calculate position of collocation points r₁, r₂ vectors and difference operators A and B matrices using the methods described by Villadsen and Michelsen (Collocation points r₁ and r₂ represent ξ and η respectively).

Step 3:

Calculate heat and mass transfer parameters (ρ₁, ρ₂, Cp₁, Cp₂, k₁, k₂).

Step 4:

Compute $T_{I} , T_{II} , T_{x} , p_{w} ,p_{in} \, \rm {and} \, C_{sw}$ for t = t_old + Δt by solving the nonlinear algebraic system using ode15i solver.

Step 5:

If the relative error of two iterates is less than a prescribed tolerance, stop the iteration and set new time interval go back to Step 4. Otherwise, save data at prescribed time intervals, set new time interval. Check whether the stopping criterion (X (t) = L) is met. If not then go to the Step 3 otherwise (T = T_II) and go to the Step 6. (Please note that frozen and dried are solved in ξ and η domain respectively. Interior points positions can be calculated for frozen and dried part x = Xξ and x = η(L − X) + X) respectively).

Step 6:

Compute ${\text{T}},p_{w} ,p_{in} \, {\text{and}} \, C_{sw}$ for specific time interval by solving the secondary drying equation set with ode15i solver.

Step 7:

If the relative error of two iterates is less than a prescribed tolerance, stop the iteration and set new time interval go back to Step 6. Otherwise, check water vapor mass flux N_w. If the product is dried stop the iteration, otherwise set new time interval go back to Step 6.

3 Result and discussion

The theoretical results for the freeze drying of black tea extract were obtained by solving simultaneously Eqs. (37)–(42) with the initial and boundary conditions that given in from Eqs. (43)–(53) for primary drying stage. The numerical solution for the secondary drying stage obtained by eliminating Eq. (38) and (42) and setting X equal to L, also setting the derivative of X to equal because there is no frozen (II) layer or no moving interface. The values of the parameters as well as the expressions employed in the evaluation of certain parameters of the theoretical model are presented in Tables 2 and  3. The melting T_m and scorch T_scor temperatures of black tea extract chosen to be −10 and 40 °C, respectively.

Table 2 Parameters and values for freeze drying model of black tea extract

In this work, the dynamic behavior of the removal of bound water was presented with the first-order rate desorption mechanism that given in Eq. (7). Detailed model calculations performed in this work have indicated that the total mass flux of the water removed during primary drying mainly resulted by sublimation of free water at interface, the contribution of the removal of bound water is limited. The result is in agreement with work of [16], therefore, the mechanism of the removal of bound water in the mathematical model during primary drying can be neglected without introducing a significant error.

3.1 Parameter estimation

The freeze drying of skim milk model developed by [16]. In their work, they considered freeze drying of skim milk in the sense that it can be acknowledged as a complex pharmaceutical product because it contains enzymes and proteins. Compared to freeze drying of black tea extract with skim milk, the ice crystals formed during the freezing stage that determines the size and shape of the pores, the pore size distribution, and the pore connectivity of the porous network of the dried layer formed by the sublimation of frozen water during the primary drying stage, could be substantially different.

That means the parameter of the dusty gas model (water vapor Knudsen diffusivity, K_w, inert gas Knudsen diffusivity, K_in, along with the free gas mutual diffusivity in a binary mixture of water vapor and inert, D_w,in, and film thermal conductivity, k_f should be determined for freeze drying of black tea extract in tray. Parameters estimation done by searching the best-fit transport properties of the dried layer and the film thermal conductivity between heating plate and bottom surface of the tray, during freeze drying of black tea extract. In order to achieve this task, an iterative computation procedure is employed. For each iteration, if the difference between experimental data and computed data that obtained by solving dynamic mathematical model, is high, the initial guess of parameters was altered until the difference is minimum [7]. This procedure identical to the nonlinear least-square method where the sum of the square of the error that defined as difference between experimental data, y_ex, and theoretical data, y_t, minimized to obtain best fit values of the parameters.

$$SSE = \mathop \sum \limits_{i = 1}^{N} \left( {y_{ex} - y_{t} } \right)^{2}$$

(57)

In Eq. (57) N denotes number of the experimental data while i is the index (i = 1, 2,…N). Levenberg–Marquardt algorithm requires initial guesses and range (maximum and minimum tolerable values) for the parameters, given input data (y_ex) and observed output data (y_t) to perform parameter estimation. Both the given input data and observed output data must be the same size matrices or vectors. In this work, the given input data is the experimental amount of removed water that measured for every two hours starting at the beginning to end of the experiments. The observed output data calculated for the same time span of the given input data, by solving dynamic mathematical model that presented in this work. Nonlinear least-square algorithm continuously try to minimize the sum of square of error (SSE) between the given input data and observed output data, by adjusting the parameters in the given range. The parameters that give the minimum value of the SSE, are considered to be the best-fitted parameters of the dynamic mathematical model.

The estimated transport parameters shown in Table 3 can be used to reveal the heat and mass mechanisms involved in the freeze drying process. The structure of the porous matrix of the dried layer is very complex in order to model. Therefore the dusty gas model was used to describe mass transport in black tea extract. The structural parameters C₀₁, C₁ and pair of C₂, D_w,in characterize the mechanism of intra-particle convective flow, and they used in calculation of self-diffusivity constant, Knudsen diffusivity and bulk diffusivity constant, respectively (detailed information can be seen in nomenclature). The diffusivity values are directly related to the pore structures of the materials. Knudsen diffusivity is important when the average free path of the gas molecules is greater than the pore diameter of the porous material and plays an effective role in the diffusion phenomena occurring in the porous materials.

Table 3 Estimated model parameters

3.2 Evaluation of simulated results

During primary drying stage, the theoretical and experimental temperature distributions on upper plate and lower plate against time were shown in Fig. 3. At the beginning of the primary drying stage frozen sample temperature is T_F = 238.15 K at x = 0 and drying heat treated to upper and lower surface by radiation and conduction, shelf temperature was 283.15 K. It is obvious that sudden temperature drop at first as a result of sublimation under the vacuum condition and higher temperature difference between the product surface and shelf temperature. The amount of heat required for sublimation enthalpy ∆Hs was obtained from this sudden temperature drop. TE_UP and TE_LP increased with time and at the end of the primary drying stage (t = 10 h) it is observed that temperatures of TE_UP and TE_LP were almost equal. The reason that moving sublimation interface ended its downward movement and primary drying stage was completed and secondary drying stage started. The downward movement of interface caused porous rigid structures in dried layer and amount of free water in porous rigid structures decreased with time. In other words, amount of heat required for sublimation is less that at the beginning and that causes temperature differences between upper plate and lower plate.

Fig. 3

The time variation of the theoretical top surface, T₀, theoretical bottom surface, T_L, experimental top surface TE_UP and experimental bottom surface TE_LP, temperatures during the primary drying stage

Figure 4 shows that theoretical results for mass flux of water vapor, N_w│_x=0 evaluated at the top surface of material being dried at various drying times during the primary drying stage. As shown from Fig. 3, initial water vapor mass flux rate is maximum value due to the thickness of dried layer is almost infinitesimal and resistance to mass transfer may be ignored. As the primary drying stage proceeds porous dried layer is occurred by the moving sublimation interface and the porous dried layer provides a significant resistance to mass and heat transfer.

Fig. 4

The time variation of the water vapor mass flux, Nw│x = 0, during the primary drying stage

Figure 5 represents experimental data and the theoretical results for the amount of water removed in the sample at various drying times during the secondary drying stage. The mechanisms of mass transfer of water vapor and inert gas in the pores of the dried layer consider Knudsen diffusion, bulk diffusion, and convective flow. It should be noted again at this point that during the secondary drying stage, the water vapor in the pores of the dried layer is formed from the removal of bound (unfrozen) water from the phase of the solute (instant tea). Therefore, the contribution of the removal of bound water to the total mass flux of water removed during the secondary drying stage is dominant, and the value of the k_d in Fig. 5 is two order of magnitude larger than the value of the k_d, during the primary drying stage (Table 2). This result clearly indicates mass transfer occur as a result of desorbing bound water from the phase of the solute, during the secondary drying stage. Further analyzing the profile in Fig. 4, the agreement between the experimental and the theoretical data is, for all practical purposes, good. During the secondary drying stage, the major mass transfer mechanisms are removal of bound water from the phase of the solute, Knudsen diffusion, bulk diffusion and the convective flow, for the freeze drying of black tea extract that studied in this work.

Fig. 5

Amount of residual water versus time during the secondary drying stage of the freeze-drying of instant tea

The three major mass transfer mechanisms during secondary drying were as follows: (I) removal of bound water from the phase of the solute, (2) Knudsen diffusion, and (3) bulk diffusion. In general, it is recommended that the mechanism of convective flow should be included in the mathematical model used to describe the dynamic behavior of the secondary drying stage, since one, for a given system of interest, cannot accurately estimate a priori the effect of the contribution of the convective flow on the drying rate during secondary drying; if, of course, numerous comparisons of theoretical results with experimental data from the system of interest indicate that the contribution of the mechanism of convective flow in the pores of the dried material is not significant during secondary drying, then one could neglect the mechanism of convective flow in the mathematical model used to describe the dynamic behavior of the secondary drying stage.

4 Conclusion

We constructed a mathematical model for freeze drying of black tea extract and transformed space due to moving interface. Thus, orthogonal collocation method is applied which involving transformations of PDEs to ODEs. In the solution of model equations, ODEs were adjusted in an implicit form and it is prior to solve the moving interface problems which are relatively stiffness. Using A and B discretization matrices come from orthogonal collocation and solving implicitly model equations enable to simulate the dynamic behavior of the processes accurately and with less effort. The estimated transport parameters that are difficult to measure directly can be used to predict the duration of freeze drying of black tea extract and reduce processing time and energy consumption in the next studies.