1 Introduction

Boundary layer flow and heat transfer over a stretched surface has received considerable attention in recent years. The problem has scientific and engineering applications such as aerodynamic extrusion of plastic sheets and fibers, drawing, annealing and tinning of copperwire, paper production, crystal growing and glass blowing. Such applications involve cooling of a molten liquid by drawing it into a cooling system. In drawing the liquid into the cooling system it is sometimes stretched as in the case of a polymer extrusion process. The fluid mechanical properties desired for the outcome of such a process depends mainly on the rate of cooling and the stretching rate. It is important that a proper cooling liquid is chosen and flow of the cooling liquid due to the stretching sheet is controlled so as to arrive at the desired properties for the outcome. In view of these applications Sakiadis [1] was the first mathematician who studied boundary layer flow over a stretched surface moving with a constant velocity. Crane [2] initiated the analytical study of boundary layer flow due to a stretching sheet. Grubka and Bobba [3] carried out heat transfer studies by considering the power-law variation of surface temperature.

When modeling the boundary layer flow and heat transfer of stretching surface, the boundary conditions that are usually applied are either a specified surface temperature or a specified surface heat flux. However, there is boundary layer flow and heat transfer problems in which the surface heat transfer depends on the surface temperature. This situation arises in conjugate heat transfer problems and when there is Newtonian heating of the convective fluid from the surface. Newtonian heating occurs in many important engineering devices, for example, inheat exchangers, where the conduction in a solid tubewall is greatly influenced by the convection in the fluid flowing over it. On the basis of above discussions and application Aziz [4] investigated the heat transfer problems for boundary layer flow concerning with a convective boundary condition and exhibit that similarity solution it is possible if the convective heat transfer associated with the hot fluid on the lower surface of the plate is proportional to x −1/2. Makinde [5] extend the work of Aziz [4] by including hydromagnetic field and mixed convection heat and mass transfer over a vertical plate. Olanrewaju et al. [6] examined the combined effects of internal heat generation and a convective boundary condition on the laminar boundary layer flow over a flat plate. Ishak et al. [7] obtained the dual solution for laminar boundary layer flow over a moving plate in a moving fluid with convective surface boundary condition in the presence of thermal radiation. Apart from these works, various aspects of flow and heat transfer of viscous fluid over a stretching surface with convective boundary condition were investigated by many researchers (see [8–13]).

All the above investigations are concerned with single phase flows. In nature, the fluid in pure form is rarely available. Air and water contains impurities such as dust particles and foreign bodies. Therefore the study of two-phase flows in which solid spherical particles are distributed in a clean fluid are of interest in practical applications such as petroleum industry, purification of crude oil, physiological flows, etc. Other important applications involving dust particles in boundary layers include soil salvation by natural winds, lunar surface erosion by the exhaust of a landing vehicle and dust entrainment in a cloud formed during a nuclear explosion. Chakrabarti [19] analyzed the boundary layer formed by a dusty gas. Datta and Mishra [14] studied the two phase boundary layer flow over a semi-infinite flat plate in the region of high and small slip velocities. Evgeny and Sergei [15] discussed the stability of a dusty gas laminar boundary layer on a flat plate. Further Xie et al. [16] extended work of Datta and Mishra [14] and studied the hydrodynamic stability of a particle-laden flow over a flat plate boundary layer. Palani and Ganesan [17] studied heat transfer effects on dusty gas flow past a semi-infinite inclined plate. Agranat [18] studied dusty boundary layer flow and heat transfer, with the effect of pressure gradient. Vajravelu and Nayfeh [20] analyzed the hydromagnetic flow of dusty fluid over a stretching sheet with the effect of suction. Recently Ramesh et al. [21] investigate the MHD flow of a dusty fluid near the stagnation point over a permeable stretching sheet with non-uniform source/sink and studied for two types of heating process PST and PHF cases.

The present study has been undertaken in order to study the dusty fluid behavior on boundary layer flow and heat transfer over a stretching sheet with convective boundary condition. Appropriate similarity transformations are used to reduce the governing partial differential equations into a set of nonlinear ordinary differential equations. The resulting equations are solved numerically using the fourth-fifth order Runge–Kutta method with the help of Maple. The effect of variations of several pertinent emerging parameters on the flow and heat transfer characteristics is analyzed in detail.

1.1 Flow analysis of the problem

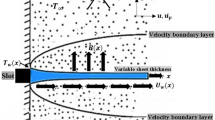
Consider a steady two dimensional laminar boundary layer flow of an incompressible viscous dusty fluid over a stretching sheet. The sheet is coinciding with the plane y = 0, with the flow being confined to y > 0 Two equal and opposite forces are applied along the x-axis, so that the sheet is stretched, keeping the origin fixed. The temperature of sheet surface (to be determined later) is the result of a convective heating process which is characterized by a temperature T f and a heat transfer coefficient h f . Far from the surface, both the fluid and the dust particles are in equilibrium and are assumed to be at rest. The dust or particle-phase volume fraction is assumed to be small and the suspension is assumed to be dilute in the senses that inter particle collision is neglected. The dust particles are assumed to be spherical in shape and uniform in size and number density of these are taken as a constant throughout the flow. Under the foregoing assumptions the basic two dimensional boundary layer equations of motion for clean fluid and dust fluid with usual notation are [see 20].

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(1)
$$\rho_{\infty } \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) = \mu \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\rho_{p} }}{\tau }(u_{p} - u),$$
(2)
$$u_{p} \frac{{\partial u_{p} }}{\partial x} + v_{p} \frac{{\partial u_{p} }}{\partial y} = \frac{{\rho_{p} }}{\tau }(u - u_{p} ),$$
(3)
$$u_{p} \frac{{\partial v_{p} }}{\partial x} + v_{p} \frac{{\partial v_{p} }}{\partial y} = \frac{1}{\tau }(v - v_{p} ),$$
(4)
$$\frac{\partial }{\partial x}(\rho_{p} u_{p} ) + \frac{\partial }{\partial y}(\rho_{p} v_{p} ) = 0,$$
(5)
$$\rho_{\infty } c_{p} \left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}} \right) = k\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{c_{s} \rho_{p} }}{{\gamma_{T} }}(T_{p} - T),$$
(6)
$$u_{p} \frac{{\partial T_{p} }}{\partial x} + v_{p} \frac{{\partial T_{p} }}{\partial y} = - \frac{1}{{\gamma_{T} }}(T_{p} - T) ,$$
(7)

where (u,v) and (u p ,v p ) are the velocity components of the fluid and dust particle phases along x and y directions respectively. μ, ρ ∞ , ρ p and m are the co-efficient of viscosity of the fluid, density of the fluid, mass of dust particles per unit volume of the fluid, mass of the dust particle, K is the Stokes’ resistance (drag co-efficient) respectively. T and T p is the temperature of the fluid and temperature of the dust particle, c p and c s are the specific heat of fluid and dust particles, γ T is the temperature relaxation time, τ is the relaxation time of the of dust particle, k is the thermal conductivity. In deriving these equations, the drag force is considered for the interaction between the fluid and dust phases.

The boundary conditions of the problem are

$$u = U_{w} (x),\quad \,v = 0,\,\quad - k\frac{\partial T}{\partial y} = h_{f} (T_{f} - T)\quad {\text{at}}\;y = 0$$
(8)
$$u \to 0,\quad u_{p} \to 0,\quad v_{p} \to v,\quad \rho_{p} \to \omega \rho_{\infty } ,\quad T \to T_{\infty } ,\quad T_{p} \to T_{\infty } \quad \;{\text{as}}\;y \to \infty ,$$

where U w (x) = cx is the stretching sheet velocity, c > 0 is stretching rate, ω is the density ratio, T f is the hot fluid temperature and h f is the heat transfer coefficient.

To convert the governing equations into a set of similarity equations, now we introduce the following transformation as,

$$\begin{aligned} u & = cxf^{\prime } ,\quad v = - \sqrt {vc} \;f,\quad \eta = \sqrt {\frac{{U_{w} }}{\nu x}} y,\quad \theta = \frac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }} \\ u_{p} & = cxF,\quad v_{p} = \sqrt {vc} \;G,\quad \;\rho_{r} = H,\quad \theta_{p} = \frac{{T_{p} - T_{\infty } }}{{T_{f} - T_{\infty } }} \\ \end{aligned}$$
(9)

Substituting (8) into (1)–(7), we obtain the following non-linear ordinary differential equations:

$$f^{\prime \prime \prime } + ff^{\prime \prime } - (f^{\prime } )^{2} + \beta H[F - f^{\prime } ] = 0,$$
(10)
$$GF^{\prime } + (F)^{2} + \beta [F - f^{\prime } ] = 0,$$
(11)
$$GG^{\prime } + \beta [f + G] = 0,$$
(12)
$$HF + HG^{\prime } + GH^{\prime } = 0,$$
(13)
$$\frac{1}{\Pr }\theta^{\prime \prime } + f\theta^{\prime } + \frac{2H\beta }{3}[\theta_{p} - \theta ] = 0$$
(14)
$$G\theta^{\prime }_{p} + L_{0} \beta [\theta_{p} - \theta ] = 0,$$
(15)

where a prime denotes differentiation with respect to η and ρ r = ρ p/ρ ∞, τ = 1/K is the relaxation time of the particle phase, β = 1/cτ is the fluid particle interaction parameter and ρ r = ρ p/ρ is the relative density, \(\Pr = {\nu \mathord{\left/ {\vphantom {\nu \alpha }} \right. \kern-0pt} \alpha }\) is the Prandtl number, \(Bi = (v/a)^{1/2} h_{f} /k\) is the Biot number and L 0 = τ/γT is the temperature relaxation parameter.

The boundary conditions defined as in (8) will take the form,

$$\begin{aligned} f & = 0,\quad f^{\prime } = 1,\quad \;\theta^{\prime } = - Bi(1 - \theta )\quad at\quad \eta = 0, \\ f^{\prime } & \to 0,\quad F \to 0,\quad G \to - f,\quad H \to \omega ,\quad \theta \to 0,\quad \theta_{p} \to 0\quad as\quad \eta \to \infty . \\ \end{aligned}$$
(16)

If β = 0, the analytical solution of (10) was given by Crane [2] as

$$f(\eta ) = 1 - e^{ - \eta } .$$
(17)

The wall shear stress is given by:

$$\tau_{w} = \mu \frac{\partial u}{\partial y}|y = 0$$
(18)

The friction factor is given by:

$$C_{fx} = \frac{{2\tau_{w} }}{{\rho U_{w}^{2} }} = - 2\text{Re}_{x}^{ - 1/2} f^{\prime \prime } (0)$$
(19)

The surface heat transfer rate is given by:

$$q_{w} = k\frac{\partial T}{\partial y}|y = 0$$
(20)

The local Nusselt number may be written as:

$$Nu_{x} = \frac{{q_{w} }}{{k(T_{f} - T_{\infty } )}} = - \text{Re}_{x}^{1/2} \theta^{\prime } (0)$$
(21)

2 Results and discussion

The nonlinear ordinary differential Eqs. (10)–(15) subject to the boundary conditions (16) are solved numerically using Runge–Kutta–Fehlberg fourth-fifth order method (RKF45 Method). To solve these equations we adopted symbolic algebra software Maple which is described in [4]. The accuracy of the employed numerical method is tested by direct comparisons with the values of \(\theta^{\prime } (0)\) with those reported by Wang [22] and Gorla and Sidawi [23] in Table 1 for special case of the present problem and an excellent agreement between the results is found. Further, the impact of some important physical parameters on the friction factor, surface particle velocity, surface heat transfer rate, wall temperature and dust phase wall temperature which are proportional to \(f^{\prime \prime } (0),F(0), - \theta^{\prime } (0),\theta (0)\) and \(\theta_{p} (0)\), respectively, may be analyzed from Table 2. It may be noted that the effect of increasing fluid particle interaction parameter, β is to decrease the wall shear stress \(f^{\prime \prime } (0)\), surface heat transfer rate −\(\theta^{\prime } (0)\) and increase the surface particle velocity, wall temperature and dust phase wall temperature proportional to \(F(0),\theta (0)\) and \(\theta_{p} (0)\), respectively.

Table 1 Comparison results for the temperature gradient −θ′(0) in the case of L 0  = 1, β, ω = 0 and Bi = 1,000
Full size table
Table 2 Computations of f″(0), F(0), θ′(0), θ(0) and θ p (0) for different values of Biot number (Bi) with ω = 0.02
Full size table

In order to study the behaviour of velocity \((f^{\prime } ,F)\) and temperature \((\theta ,\theta_{p} )\) fields for dusty fluid, a comprehensive numerical computation is carried out for various values of the parameters that describe the flow characteristics, and the results are reported in terms of Figs. 1 and 2. Figure 1 exhibits the velocity and temperature profiles (fluid phase) for several values of fluid-particle interaction parameter β. By analyzing the graphs it reveals that the effect increasing the β is to decrease the velocity and temperature distribution. This is due to the fact that for a large value of β the relaxation time of the dust particle decreases. Figure 2 represents the effect of β on the velocity and temperature (dust phase) distribution. It is noticed that the velocity and temperature increases with the increase of β. From these figures we noted that when increasing the values of β small variation can be found in fluid phase and when compare to dust phase. Further observation shows that if the dust is very fine, that is, mass of the dust particles is negligibly small, then the relaxation time of dust particle decreases, and ultimately as \(\tau \to 0\), the fluid phase and dust phase will be the same.

Fig. 1
figure 1

Effect of β on velocity and temperature distribution (fluid phase)

Full size image
Fig. 2
figure 2

Effect of β on velocity and temperature distribution (dust phase)

Full size image

The effect of Prandtl number Pr on both fluid and dust phase temperature distributions are displayed in Fig. 3. It can be seen that the fluid-phase temperature and dust-phase temperature decrease with increase of Prandtl number, which implies momentum boundary layer is thicker than the thermal boundary layer. This is due to the fact that for higher Prandtl number, fluid has a relatively low thermal diffusivity, which reduces conduction. We note that, the Pr gives no influence to the development of the velocity boundary layer, which is clear from Eqs. (10)–(13).

Fig. 3
figure 3

Effect of Pr on temperature distribution

Full size image

Figure 4 depict the variation in the temperature distribution of \(\theta (\eta )\) and \(\theta_{p} (\eta )\) for different values of Bi. It is observed that temperature field \(\theta (\eta )\) and \(\theta_{p} (\eta )\) increases rapidly near the boundary by increasing Biot number (Bi). Form Table 2, we can see that the values of the friction factor, −\(f^{\prime \prime } (0)\) increase with the values of fluid particle interaction parameter considered. Table 3 indicates that the heat transfer rate increases with the Biot number Bi. Figures 1, 2, 3 and 4, it is observed that the fluid phase velocity and temperature fields are similar to that of dust phase and also the fluid phase velocity and temperature are higher than the dust phase values.

Fig. 4
figure 4

Effect of Bi on temperature distribution

Full size image
Table 3 Computations of −θ′(0), θ(0) and θ p (0) for different values of Biot number (Bi) with β = 0.5, Pr = 3.0 and ω = 0.02
Full size table

3 Conclusions

In this paper, the heat transfer characteristics of a fluid particle suspension over a stretching sheet have been studied numerically. Different from previous investigations, the effect of convective boundary condition on the development of the thermal boundary layer flow has been taken into consideration. We discussed the effects of the governing parameters Biot number, Prandtl number and fluid particle interaction parameter Bi, Pr and β, respectively, on the heat transfer characteristics. Form the Table 3, it is found that when Bi increases from 0.1 to 50, the heat transfer rate \(- \theta^{\prime } (0)\), surface temperature function of both fluid \(\theta (0)\) and dust \(\theta_{p} (0)\) phases increase significantly. However, a further increase in Bi has only minor effect on the values of \(- \theta^{\prime } (0)\), \(\theta (0)\) and \(\theta_{p} (0)\). When \(Bi \to \infty\) (i.e., for large value), no significant change is observed for the values of \(- \theta^{\prime } (0)\), \(\theta (0)\) and \(\theta_{p} (0)\).

Following are brief conclusions drawn from the investigation:

  • Increase of fluid-particle interaction parameter reduces the velocity and temperature distribution (fluid phase), opposite effect can be seen in dust phase.

  • Increase of Prandtl number reduces the thermal boundary layer thickness.

  • Increase of Biot number is to increase the thermal boundary layer.