Estimation of moisture transport coefficients in porous materials using experimental drying kinetics

Abstract

From experimental drying kinetics, an inverse technique is used to evaluate the moisture transport coefficients in building hygroscopic porous materials. Based on the macroscopic approach developed by Whitaker, a one-dimensional mathematical model is developed to predict heat and mass transfers in porous material. The parameters identification is made by the minimisation of the square deviation between numerical and experimental values of the surface temperature and the average moisture content. Two parameters of an exponential function describing the liquid phase transfer and one parameter relative to the diffusion of the vapour phase are identified. To ensure the feasibility of the estimation method, it is initially validated with cellular concrete and applied to lime paste.

1 Introduction

To be able to predict the drying kinetics of hygroscopic porous material, good knowledge of the product’s physical properties and their evolutions according to moisture content and/or temperature is a necessity. Some properties can be determined experimentally, such as isothermal desorption, thermal conductivity, heat capacity, density… However, other parameters, like moisture transport coefficients, are not easily measured. By definition, these coefficients express the capacity of water in its different states (liquid or vapour) to move through the solid matrix under the effect of temperature gradient or concentration gradient.

The Wet-cup method is one of the stationary techniques usually used for studying vapour diffusion through a porous material [1]. However, this technique requires long experimental duration and is badly adapted to heterogeneous materials with high moisture contents. In a transient state, there are several analytical solutions [2, 3] that can be used to estimate the global diffusion coefficient. However some of these solutions are given for isothermal Dirichlet conditions and do not take into account the dependency of diffusion coefficient of the state variables. In view of the limits of analytical solutions and the development of numerical methods and computing power, the estimation of the transport coefficients through the inverse method seems attractive. However, there are few works in literature which use the inverse approach by taking into account the initial and boundary conditions as well as the coupling of heat and mass transfer equations to determine unknown parameters of the model [4–8].

Danta et al. [7, 8] recently analyzed the application of Levenberg–Marquardt method with the help of simulated measurements temperatures and moisture contents with random errors to the estimation of thermophysical properties of drying materials appearing in Luikov’s formulation. Dietl et al. [8] developed an inverse procedure to determine two unknown transport coefficients using experimental drying kinetics. For these authors, the moisture conductivity (liquid transport coefficient) is introduced like a parametric function of the local moisture content and temperature and the vapour diffusivity as a function of the vapour diffusion resistance which is approximated by a constant.

In the present work, experimental and numerical studies have been carried out. We are interested to the heat and mass transfer modelling of two different hygroscopic porous materials: lime paste and cellular concrete. The latter is regarded as a reference material [9].

Initially, we will give the different experiments conducted with the materials. Thereafter, based on the fundamental physical laws that govern the migration of liquid and gaseous phases in porous media, a 1D mathematical model is used to predict heat and mass transfer in capillary porous material. Finally, to determine the moisture transport coefficients from experimental drying kinetics, two different methods have been applied. The first one is based on the analytical solution of second Fick’s law given by Crank [2] which allows for the determining of an order of magnitude of effective diffusion coefficients by linear regression. The second one is based on the parameter estimation approach taking into account the coupling of heat and mass transfer equations by minimizing the sum of square deviations between the observed output variables and the calculated ones. A sequential quadratic programming algorithm [10] is used. After numerical tests, the methodology is applied to experimental drying kinetics.

2 Material and experimental setup

Cellular concrete is chosen as a material of reference because it has been widely studied and characterized in literature [9]. It is a hygroscopic porous material with porosity close to 0.8; the industrial production of the material guarantees consistency in its properties.

The samples of lime binder are manufactured in our laboratory. They are composed of 71 wt% of lime-based binder (Tradical^® PF80 M: 35 wt% mineral load and 65 wt% binder: 85 wt% hydrate lime, 15 wt% natural hydraulic lime), and 29 wt% of water. So the water/lime ratio is about 0.4. To obtain a good homogenization of the components, the mixture is made in a mixer.

2.1 Kinetics of lime hydration

Figure 1 presents the hydration kinetics of lime binder Tradical^® PF 80 M obtained by isothermal calorimeter at 25°C with a water/lime ratio of 0.4. The energy generated by the kinetic reaction according to time is traced. We can distinguish three principal stages of hydration: acceleration, deceleration and steady state. The acceleration occurs during the first 12 h and characterized by an important reaction rate. The deceleration and steady state stages are controlled by the diffusion process. The reaction rate in these periods is relatively low and gradually decreases toward zero. We notice that the major quantity of heat released by the reaction is in the first 20 h.

Fig. 1

Kinetics of Tradical^® PF 80 M hydration (T = 25°C, water/lime = 0.4)

Later, in order to avoid the interaction between drying process and hydration kinetics, the specimens of lime paste are dried after 2 days of their manufacturing.

2.2 Isothermal desorption

The isothermal desorption of the lime binder are obtained experimentally by assessing the moisture content of the product in equilibrium with different air relative humidities at a temperature of 20°C (Fig. 2).

Fig. 2

Isothermal desorption kinetics of lime binder (L.B) and cellular concrete (C.C)

The GAB model presented by the Eq. 1 provides a good representation of experimental desorption kinetics of lime binder and cellular concrete. The values of unknown parameters (W _m , C and K) of the GAB model are given in Table 1.

$$ W = \frac{{W_{m} \;C\;K\;a_{w} }}{{\left( {1 - K\;a_{w} } \right)\;\left( {1 - K\;a_{w} + C\;K\;a_{w} } \right)}} $$

(1)

Table 1 Parameters of GAB model

2.3 Physical properties of the materials

The physical properties of the cellular concrete and the lime binder, which have been used to supply the model, are listed in Table 2. Some have been obtained experimentally. However, all of cellular concrete properties have been found in the literature.

Table 2 Properties of lime binder and cellular concrete

2.4 Experimental drying pilot

The drying kinetics is obtained using a pilot designed in our laboratory [12]. This drier makes it possible to vary the aerodynamic and thermal conditions by controlling velocity and temperature of air. The studied samples are disposed in parallelepiped crucible with cross section of 10 × 10 cm². In the context of a one-dimension thermal and mass transfer, only the upper face is in contact with airflow. An optical pyrometer measures the surface temperature of the product and two thermocouples are implanted to give the temperature in the bottom and the middle. An electronic scale is used to acquire the product mass as a function of time. All temperature sensors and scale are connected to an acquisition system (Fig. 3).

Fig. 3

Experimental design

2.5 Drying kinetics

Figure 4 shows a drying kinetic of cellular concrete. The test is carried out on material with a thickness of 2.5 cm, and an initial moisture content of 0.8 kg kg⁻¹. The air of drying has a temperature of 50°C and a velocity of 3 m s⁻¹.

Fig. 4

Drying kinetic of cellular concrete (50°C, 3 m s⁻¹)

Figure 5 shows an example of drying kinetic of lime paste after 2 days of its manufacturing. The kinetic are obtained with air velocity of 2 m s⁻¹, temperature of 29°C and humidity around 35%. Initially, the sample’s cross section is 9.9 × 9.9 cm² and its thickness is 2.5 cm. After drying, we notice shrinkage of about 2.7% of the thickness and 2% of the cross section. We also note that the great amount of moisture was removed during the first 15 h of drying. After this, moisture content decreases towards the equilibrium.

Fig. 5

Drying kinetic of lime binder (29°C, 2 m s⁻¹)

Figure 6 gives a comparison between the drying rate of lime binder at two different air velocities (1 and 2 m s⁻¹) for an air temperature of 29°C. We show through these curves that the air velocity has a significant role, particularly at the beginning of drying. Indeed, the raising of the air velocity makes it possible to increase the coefficient of heat transfer by convection and consequently, the mass transfer coefficient.

Fig. 6

Evolutions of evaporated mass flux (29°C)

According to the expression of evaporated mass flux given by the Eq. 2, the mass transfer coefficient k _m have been determined.

$$ F_{m} = k_{m} \frac{{P_{\text{atm}} \,M_{v} }}{{{\text{RT}}_{f} }}\ln \left( {\frac{{P_{\text{atm}} - P_{v\infty } }}{{P_{\text{atm}} - a_{W} P_{\text{vsat}} }}} \right) $$

(2)

with knowledge of air temperature, humidity, surface temperature and evaporated mass flux of each test during the isenthalpic phase (water activity equal to 1), the Colburn analogy between heat and mass transfer (Eq. 3) allows to deduce coefficient of convection h _c for a Lewis number (Le) closer to 1. The values of calculated convective coefficient are given in Table 3.

$$ \frac{{h_{c} }}{{k_{m} \rho \,C_{p} }} = Le^{2/3} = \left( {\frac{Sc}{\Pr }} \right)^{2/3} $$

(3)

where Pr and Sc are respectively the Prandtl number and the Schmidt number.

Table 3 Values of the convective heat transfer coefficient

3 Physical problem and mathematical formulation

The setting in equations of combined heat and moisture transfer in hygroscopic porous material has been the subject of extensive investigations since several years. It was initially established by Philip and De Vries [13]; these equations are based on the mass, momentum and energy conservations expressed by Fourier’s law, Darcy’s law and Fick’s second law to explain respectively heat diffusion, liquid transfer, and vapour diffusion through porous matrix. Whitaker [14] proposes the concept of representative elementary volume to allow for the homogenisation of a multiphase system by smoothing discontinuous properties in interfaces. The hypotheses made by Whitaker are generally satisfactory for the process of heat transfer and mass encountered in building materials. Therefore, the selected model reflects this approach and the global equations are developed with the same simplifying assumptions; thus the studied materials are treated as a multiphase system with three phases, the solid one is supposed homogeneous and isotropic, the liquid phase contains free and bound water, and the gas phase is a perfect mixture of air and water vapour. Moreover, its total pressure is supposed constant and equal to atmospheric pressure in the case of convective drying at low temperatures. The convective transport in the material and the thermomigration of the liquid phase are neglected. The effect of hydration on the drying process is also neglected; thus the heat transfer occurs merely in two forms: conduction and latent heat moved outward by the vapour diffusion.

3.1 Heat and mass equations

The fields of temperature and moisture content (T and W) are obtained by the resolution of the following system of equations:

$$ \frac{\partial W}{\partial t} - \vec{\nabla } \cdot \left[ {\frac{1}{{\rho_{s} }}\left( {\left( {D_{v}^{T} } \right) \, \vec{\nabla }T + \left( {D_{l}^{W} + D_{v}^{W} } \right) \, \vec{\nabla }W} \right)} \right] = 0 $$

(4)

$$ \overline{{\rho C_{p} }} \frac{\partial T}{\partial t} - \vec{\nabla } \cdot \left( {\lambda^{*} \vec{\nabla }T} \right) - \vec{\nabla } \cdot \left( {D_{v}^{T} \vec{\nabla }T + D_{v}^{W} \vec{\nabla }W} \right)\Updelta H_{v} = 0 $$

(5)

$\lambda^{*}$ and $\overline{{\rho C_{p} }}$ are respectively the effective thermal conductivity and the effective volumetric heat capacity.

The transport of the liquid phase obeys Darcy’s law, it occurs in the direction of increasing negative pressure to regions where the liquid is in tension. It is described by the isothermal liquid transport coefficient $D_{l}^{W}$ given in Eq. 6

$$ D_{l}^{W} = \rho_{l} \frac{{K\,K_{r}^{l} }}{{\mu_{l} }}\frac{{\partial P_{c} }}{\partial W} $$

(6)

$K_{r}^{l} ,\;K,\;P_{c}$ and $\mu_{l}$ are respectively the relative and intrinsic permeability’s, the capillary pressure, and the water dynamic viscosity.

The vapour diffusion process is governed by Fick’s law and expressed by two coefficients, isothermal vapour transport coefficient $D_{v}^{W}$ and thermal vapour transport coefficient $D_{v}^{T}$. The isothermal vapour transport is a result of vapour concentration gradients established by vapour pressure decrease, while the thermal vapour transport is due to vapour concentration established by temperature gradient. They are presented by Eqs. 7 and 8.

$$ D_{v}^{W} = \mu f\,D_{0} \left( {\frac{{M_{a} M_{v} }}{\text{MRT}}} \right)\left( {\frac{{\partial P_{v}^{g} }}{\partial W}} \right) $$

(7)

$$ D_{v}^{T} = \mu f\,D_{0} \left( {\frac{{M_{a} M_{v} }}{\text{MRT}}} \right)\left( {\frac{{\partial P_{v}^{g} }}{\partial T}} \right) $$

(8)

where D ₀ is the binary diffusion coefficient of the vapour in air [15] given by Eq. 9 in m² s⁻¹, and M is the equivalent molar mass of the vapour/air mixture expressed by Eq. 10. f, μ and $P_{v}^{g}$ are, respectively, the relative vapour permeability, the tortuosity factor and the partial vapour pressure.

$$ D = 2.17 \times 10^{ - 5} \left( {\frac{T}{{273.14}} + 1} \right)^{1.88} $$

(9)

$$ M\,P_{g}^{g} = M_{a} \,P_{a}^{g} + M_{v} \,P{}_{v}^{g} $$

(10)

3.2 Initial and boundary conditions

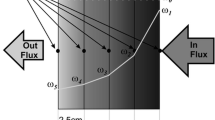
Referring to Fig. 7, the boundary conditions at the surface and the bottom of the product are expressed as follows:

Fig. 7

Boundary conditions

• At the surface, in contact with air flow, the heat exchange takes place mainly by convection and radiation, thus the energy conservation equation can be written as:

$$ - \lambda^{ * } \,\nabla T + \rho_{l} \bar{v}_{l} \,\Updelta H_{v} = h_{c} \left( {T_{a} - T_{1} } \right) + h_{r} \left( {T_{p} - T_{1} } \right) $$

(11)

h _r is expressed by the Eq. 12:

$$ h_{r} = 4\;\zeta \;\sigma \;T_{m} $$

(12)

where T _m is the mean between the surface temperature and air temperature.Similarly, the mass flux can be written as:

$$ - \left( {\bar{\rho }_{v}^{g} \bar{v}_{v} + \rho_{l} \bar{v}_{l} } \right) = F_{m} $$

(13)

• At the interface product/crucible, the wall is impermeable and the temperature of the product in the bottom is equal to the experimental one.

$$ T_{n} = T_{\exp } $$

(14)

The initial temperature and moisture content of the material are considered uniform and equal to averaging values given by the experimental data at the beginning of drying.

3.3 Numerical resolution

The system of equations is solved by the finite volume method [16] based on the notion of control volume. The temporal resolution is obtained by an iterative method, thus each equation is independently integrated by an implicit scheme.

4 Estimation of mass transfer coefficients and results

The prediction of the hydrothermal behaviour of a capillary porous material can be achieved only through the knowledge of moisture transfer coefficients. Initially, to give an approximation of these coefficients, we attempted to estimate an global diffusion coefficient using the analytical solution of Fick’s second law with the help of experimental drying kinetics. When considering the diffusivity and thickness of the material invariable, and neglecting the effects of gravity, temperature, and pressure on mass transfer, the analytical solution of Fick’s equation is written as follows [2]:

$$ \frac{{W\left( t \right) - W_{\text{ini}} }}{{W_{\infty } - W_{\text{ini}} }} = 1 - \frac{8}{{\pi^{2} }}\sum\limits_{k = 0}^{\infty } {\frac{1}{{\left( {2k + 1} \right)^{2} }}\exp \left[ { - \left( {2k + 1} \right)^{2} \frac{{\pi^{2} }}{4}\frac{D}{{e^{2} }}t} \right]} $$

(15)

Supposing that the effect of moisture content on mass diffusivity negligible in short intervals of time, Eq. 15 is solved by means of a stepping method and an optimisation procedure. Figure 8 shows the evolution of the global diffusion coefficient obtained with the drying kinetics of lime binder and cellular concrete. It can observed that the global diffusion coefficients of the lime binder and that of cellular concrete have a same order of magnitude, it varied between 4.5 × 10⁻⁹ and 6.7 × 10⁻⁹ m² s⁻¹ for the cellular concrete and, between 2 × 10⁻⁹ and 3.5 × 10⁻⁹ m² s⁻¹ for the lime binder.

Fig. 8

Global diffusion coefficients determined by analytical solution of Fick’s law

It should be noted that the principal objective of using the analytical solution of Fick’s law as a first approach is to have an idea of the diffusion coefficient magnitude, however, the number of simplifying assumptions used to reach this analytical solution, including not taking into account the combined heat and mass equations and external resistance to transfer is a non-negligible source of error for correct estimation of this parameter.

In the second stage, we attempt to estimate the moisture transfer coefficients by inverse technique in combination with the coupled heat and mass transfer equations. As shown in Eq. 6, the determination of $D_{l}^{W}$ requires knowledge of intrinsic and relative permeability’s of the liquid phase and capillary pressure as a functions of moisture content. Generally, the capillary pressure and the relative permeability can be obtained from the desorption isotherm using Kelvin’s relation. For high relative humidity (between 90 and 100%), this method is not accurate because the measurement of the desorption isotherm is less precise in this range of humidity. Therefore, some empirical correlations have been proposed to give an approximation of the liquid transport coefficient [8, 17, 18], as example, the Eq. 16 proposed by Navarri and Andrieu [17]. According to these authors, the global diffusion coefficient of the liquid phase is a multiple exponential function of the product moisture content and its temperature.

$$ D_{l} = D_{0} \exp \left( { - \frac{a}{W}} \right)\exp \left( { - \frac{{E_{a} }}{\text{RT}}} \right) $$

(16)

By considering the independency of the diffusion coefficient from temperature variation, thus the liquid diffusion coefficient is expressed as an exponential function of moisture content with two unknown parameters:

$$ D_{l}^{W} = \exp \left( {p_{1} + \frac{{p_{2} }}{W}} \right) $$

(17)

The vapour diffusion coefficients, $D_{v}^{T}$ and $D_{v}^{W}$, given previously by Eqs. 8 and 9 have as common unknown parameters the tortuosity coefficient μ and the relative vapour permeability f. Some authors have suggested that the value of the product μf is constant [19], other use empirical polynomial forms to present the relative vapour permeability f as a function of liquid saturation [20–23]. Based on the forms found in the literature [23], we have expressed the product μf as a polynomial function of normalized moisture content with three unknown parameters.

$$ \mu f = p_{3} + p_{4} W_{\text{eq}}^{2} + p_{5} W_{\text{eq}}^{3} $$

(18)

where $W_{\text{eq}} = \frac{{W - W_{\text{hyg}} }}{{W_{\text{sat}} - W_{\text{hyg}} }}$

Thus, we will attempt to estimate through the inverse technique the parameters p ₁, p ₂, p ₃, p ₄ and p ₅. In what follows, we provide more detail on the assuming methodology and a discussion about the results.

4.1 Description of the inverse method

Equations 4 and 5, which are relative to heat and fluid transfer, make up the system of equations to be solved. The unknown parameters of the system are: p ₁, p ₂, p ₃, p ₄ and p ₅; the output variables are T and W. The inverse problem consists to identify the unknown parameters from the output variables using an optimization method based on the sequential quadratic programming algorithm [10]. This method is adapted for solving the nonlinear constrained problem. Its basic idea is to transform the nonlinear problem of optimization with constraints into a sequence of quadratic sub problems.

The identification of parameters is done by minimizing an objective function S(p) which is the sum of square deviations between the observed output variables and the simulated ones. The minimum of this function matches the set of optimal parameters. We use two variables: surface temperature and average moisture content, therefore it is important to give the same order of magnitude for the standard deviation of each variable dividing by dividing each one by its maximal (Eq. 19).

$$ S(p) = \sum\limits_{i = 1}^{N} {\left[ {\alpha \left( {\frac{{W_{i}^{\text{av}} - \tilde{W}_{i}^{\text{av}} (p)}}{{\max \left( {W^{\text{av}} } \right)}}} \right)^{2} + (1 - \alpha )\;\left( {\frac{{T_{i}^{\text{surf}} - \tilde{T}_{i}^{\text{surf}} (p)}}{{\max \left( {T^{\text{surf}} } \right)}}} \right)^{2} } \right]} $$

(19)

with N, the number of measurements and α, a weighted coefficient. The parameter values are bounded and the minimization is carried out under two constraints:

$$ \left\{ {\begin{array}{*{20}c} {\mu \,f\left( {W_{{{\text{eq}}\max }} = 1} \right) = 0} \\ {\mu \,f\left( {W_{{{\text{eq}}\min }} = 0} \right) \le 1} \\ \end{array} } \right. $$

(20)

The calculation is stopped when one of the following criteria is satisfied:

$$ S\left( {p^{k + 1} } \right) - S\left( {p^{k} } \right) < \varepsilon \quad {\text{or}}\quad \,\left\| {p^{k + 1} - p^{k} } \right\| < \varepsilon^{\prime} \, $$

(21)

with k the number of iteration.

4.2 Sensitivity analysis

To know if it is possible to estimate parameters p ₁, p ₂, p ₃, p ₄ and p ₅ simultaneously with a sufficient accuracy, it is important to quantify their influence on the output variables and detect the correlation that can exist between these parameters. These can be accomplished only through the sensitivity study. Thus, we define a reduced sensitivity given in Eq. 22. The partial deviation expressed in this equation is calculated by using a centred difference approximation by applying a small variation to parameter p _i (1% of p _i ).

$$ \left. {{\text{SY}}_{ij} \left( {t,p} \right) = p_{i} \frac{{\partial \tilde{Y}_{j} }}{{\partial p_{i} }}} \right|_{{p_{k,k \ne i} }} $$

(22)

We have investigated the sensitivities of surface temperature and average moisture content to the variation of parameter p _i . The study was initially carried out with cellular concrete. The input parameters introduced in the numerical model are those which have been previously given (Table 2). The temperature and the moisture content of the material are about 22°C and 0.82 kg kg⁻¹ and, the drying conditions are those given earlier in Fig. 7.

A significant dominance of sensitivities to p ₁ and p ₂ is registered. It reaches 106°C for surface temperature and 2 kg kg⁻¹ for average moisture content. These values are largely higher than the measurement error. However, the lowest sensibilities are given by parameters p ₄ and p ₅, which are widely below the measurement noise. To make out the profile of the sensitivity curves relative to each parameter, the reduced sensitivities are presented in a standardized form by dividing them by their maximal values (Fig. 9).

Fig. 9

Normalized relative sensitivity of surface temperature (a) and mean moisture content (b) (convective drying of cellular concrete)

Figure 9a and b show that the sensitivity curves of surface temperature and moisture content to p ₄ and p ₅ are inversely proportional; this is probably due to the linear dependency between the parameters. Less linear dependency is noted between the couple p ₁ and p ₂. However, sensitivities to p ₃ have a different appearance from those of other parameters, so is an advantage for accurately estimation.

To evaluate the estimator variance of the different parameters and to quantify their correlation index, it is necessary to determine the variance matrices and correlation factors that are represented by the following expressions:

$$ {\text{Var}}\left( {p_{i} ,p_{m} } \right) = \sigma_{n}^{2} \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\sum\nolimits_{k = 1}^{N} {\left( {{\text{SY}}_{ij} \left( {t_{k} ,p} \right)} \right)} } & {\sum\nolimits_{k = 1}^{N} {{\text{SY}}_{ij} \left( {t_{k} ,p} \right) \cdot \left( {SY_{mj} \left( {t_{k} ,p} \right)} \right)} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\sum\nolimits_{k = 1}^{N} {{\text{SY}}_{ij} \left( {t_{k} ,p} \right) \cdot \left( {{\text{SY}}_{mj} \left( {t_{k} ,p} \right)} \right)} } & {\sum\nolimits_{k = 1}^{N} {\left( {{\text{SY}}_{mj} \left( {t_{k} ,p} \right)} \right)} } \\ \end{array} } \\ \end{array} } \right] $$

(23)

$$ \rho \left( {p_{i} ,p_{m} } \right) = \frac{{{\text{Cov}}\left( {p_{i} ,p_{m} } \right)}}{{\sqrt {{\text{Var}}\left( {p_{i} } \right) \cdot {\text{Var}}\left( {p_{m} } \right)} }} $$

(24)

Table 4 presents the correlation matrices deduced from temperature and moisture content sensitivities of cellular concrete. We notice that the pair (p ₁, p ₂) presents an important correlation coefficient; it is about 0.985 for the surface temperature, this value is slightly higher compared to that of the average moisture content (0.959). The pair (p ₄, p ₅) also means an important dependence; its correlation coefficient is about 0.973 for temperature and 0.920 for water content. However, the correlation factors of other pairs are far from one.

Table 4 Correlation matrix “cellular concrete”

From the study of sensitivity and correlation matrices, we can conclude that the linear dependence relating some parameters can affect their estimation. It is also noted that neither surface temperature alone or average moisture content alone have enough information to correctly estimate the five parameters. Therefore, it is necessary to exploit both contributions simultaneously.

4.3 Estimation in the case of cellular concrete

Several estimations are carried out with various initial parameter sets. In Table 5, we give the estimation results for cellular concrete tested with different weighted coefficients. These results prove the validity of the study, but we can not judge the independence of the final solutions on the initial parameters set. It is important to note that in some cases, the estimated values of parameters p ₃ and p ₄ are joined as saying that the parameter p ₅ tends towards its lower bound (10⁻³). This result can be explained by the lower sensitivity of surface temperature and moisture content to parameters p ₄ and p ₅.

Table 5 Minimisation test with experimental drying kinetics of cellular concrete

In addition, we have highlighted the complimentary of temperature and moisture content contributions in the minimization of the objective function. It is clearly shown in Table 5, that the set of estimated parameter obtained with a weighted coefficient of 0.5 presents the lowest square deviation between the experimental and simulated kinetics.

Figure 10 shows a comparison between experimental and simulated kinetics obtained with a weighted coefficient of 0.5. We notice that the experimental moisture content is correctly presented by the numerical model with an average error of 0.001 kg kg⁻¹. We also observe a distinction between the measured and simulated surface temperatures, particularly during the isenthalpic phase, in which an important deviation is recorded (about 2°C). After this, the increase of simulated temperature is overlapped with the experimental one. The curves separate again during the steady state, thus the simulated temperature is slightly higher than the experimental one; this may be caused by a probable over-estimation of the diffusion coefficient in the vapour phase.

Fig. 10

Confrontation of experimental and simulated drying kinetics of cellular concrete (α = 0.5)

The numerical profiles of moisture content and temperature as function of position and time are presented respectively in Fig. 11a and b. We can distinguish on the profile of moisture contents a zone with high water evaporation located at the surface extremity of the material between 0 and 15 mm to this zone of strong evaporation is associated a zone with thermal depression of 2–4°C.

Fig. 11

Numerical profiles of moisture content (a) and temperatures (b) as functions of space and time «cellular concrete»

Secondly, to improve the estimation results and reduce computing time, we will attempt to estimate only three parameters instead of five, thus replacing Eq. 18 by the following equation:

$$ \mu \,f = p_{3} \left( {1 - W_{\text{eq}}^{2} } \right) $$

(25)

On the basis of the same initial parameter set, the estimation results for various values of α are shown in Table 6. The result of estimation of three parameters is identical to that of the first estimation.

Table 6 Minimisation test with experimental drying kinetics of cellular concrete

Therefore, the estimation of three parameters makes it possible to reduce the computing time, as well as to ensure more stability in the solution.

The evolutions of the diffusion coefficients of cellular concrete as a function of moisture content are given in Fig. 12. We note that the diffusion coefficient of the vapour phase is higher than the liquid phase. This is probably due to the size distribution of pores.

Fig. 12

Moisture transport coefficients «cellular concrete»

4.4 Estimation for the lime binder

Table 7 gives the estimation result obtained with the lime binder, using the previously presented procedure. These results prove the validity of the study and the independence of the final solution on the initial parameters. In addition, the equality of surface temperature and moisture content contributes to the minimization of the objective function.

Table 7 Minimisation test with experimental drying kinetics of lime binder

Figure 13 shows the confrontation between the experimental and simulated drying kinetics of the lime binder. We observe distinction between the measured surface temperatures and simulated ones, particularly, during the isenthalpic phase; it is about 1°C. After this period the two variables are superposed. The most important error recorded with average moisture content is at the end of drying during the steady state; it is less than 0.006 kg kg⁻¹. Therefore, the evolution of the average moisture content is well predicted.

Fig. 13

Simulated and experimental dying kinetics of lime binder (30°C, 2 m s⁻¹)

Figure 14 presents the evolutions of estimated diffusion coefficients of the lime binder. It occurs that the liquid phase diffusion is dominant until water content of 0.026. Below this value, vapour diffusion takes over. So the diffusion of the liquid phase is more important than the vapor diffusion. The vapour transport coefficient due to the temperature gradient is about 2 × 10⁻¹⁰ kg m⁻¹ s⁻¹ K⁻¹. This value is much lowers then those of the two other coefficients.

Fig. 14

Evolution of moisture transport coefficients «lime binder»

To confirm the validity of the estimated transport coefficients, the values obtained previously are used to simulate dying kinetic of lime binder in other conditions (air velocity of 1 m s⁻¹ and air temperature of 30°C). The result of simulation is compared with experimental data in Fig. 15. We notice a good conformity between experimental and simulated moisture content and temperature. Then we can conclude that the estimated moisture transport coefficients are suitable to get a good evaluation of temperature and moisture evolution in the case of convective drying.

Fig. 15

Comparison between simulated and experimental drying kinetics of lime binder (30°C, 1 m s⁻¹)

5 Conclusion

We have shown through this study that it is possible to estimate simultaneously two parameters describing the dependence of the liquid phase transfer coefficient on the moisture content and one parameter relative to the diffusion of the vapour phase in the material. The estimation procedure is applied successfully to two different construction materials. For different initial parameters, the problem converges regularly to the same solution and the drying kinetics are correctly predicted. The experimental and simulated moisture contents are perfectly superimposed; however, the simulated surface temperature is below the experimental temperature during the constant rate period. This difference may be due to the measurement error of temperature and the probable evolution of product’s emissivity with moisture content which is not taken into account in this study.

At early age, the exposure of material to a changeable environment (temperature, relative humidity and air velocity) often leads to the interaction between the hydration and the evaporation processes. Future developments will concern the understanding to this interaction by introducing the degree of hydration as the third output variable in the model to find a suitable compromise between the drying time, the energy consumption and hydration.