1 Introduction

The demand for high power lasers for precise welding has been increased in the last decades. Simultaneous to this trend, laser welding computation techniques have been improved to the point where numerical modelling [1–6] began more and more acceptable as a guide to the prediction of geometries of weld and the profile of temperature.

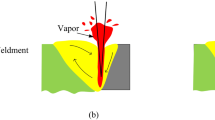
The laser welding keyhole (Fig. 1) model was proposed in the earliest studies as an alternative to both Gaussian and Double Ellipsoidal (DE) models. In the end of the last decade, two relevant models were consecutively proposed and discussed by Singh et al. [1] and Anisimov [2]. The latter model was more realistic, since it did not adopt the assumption of isothermal expansion inside the keyhole.

Fig. 1
figure 1

Laser welding disposal

Full size image

In this study, we tried to set a cylindrical model as a guide to solve the heat equation inside the heated keyhole and evaluate the cooling velocity in the relaxation phase.

2 Keyhole model features

For establishing the keyhole approximation model, we presumed that the keyhole vertical edges temperature is equal to the boiling point of the material and that the heat transfer along directions perpendicular to the incident laser beam is invariant under cylindrical symmetry.

Parallel to these assumptions, it as supposed that the heat source is Gaussian (Fig. 2) and centred along the keyhole axis. The exciting beam thermal and optical profiles were also supposed to be coherent.

Fig. 2
figure 2

Keyhole scheme

Full size image

The source cut-off date was set as the starting point of the modelling procedure.

It was also supposed that keyhole dimensions h and b (Fig. 1), are small when compared to bulk.

3 Theory

First, the maximal central temperature T 0 is obtained analogically to Coulomb approximation [7, 8]:

$$ T_{0} = \frac{{\hat{P}}}{2\pi k}\frac{1}{{\hat{b}}} $$
(1)

where k is the thermal conductivity, \( \hat{P} \) and \( \hat{b} \) are defined by:

$$ \left\{ \begin{gathered} \hat{b} =\frac{2b}{\sqrt \pi } \hfill \\ \hat{P} = \int\limits_{ - h}^{0} {\left( {\int\limits_{0}^{ + \infty } {Q_{v} \times {\text{e}}^{{ - \frac{{x^{2} }}{{2b^{2} }}}} 2\pi x{\text{d}}x} } \right){\text{d}}z = \frac{{8P_{ak} }}{\sqrt \pi }} \hfill \\ \end{gathered} \right. $$
(2)

where Q v is the power per unit volume absorbed by the keyhole and P ak is the total power absorbed by the keyhole volume:

$$ Q_{v} = \frac{{P_{ak} }}{{V_{\text{keyhole}} }} = \frac{{4P_{ak} }}{{h \pi b_{{}}^{ 2} }} $$
(3)

Maximal central temperature T 0 is then:

$$ T_{0} = \frac{{2P_{ak} }}{\pi kb} = \frac{{hbQ_{v} }}{2k} $$
(4)

The main heat equation inside the keyhole is then:

$$ \begin{array}{*{20}l} {\left\{ \begin{aligned} & \frac{\partial T(x,t) }{{\partial {\text{ t}}}} = \frac{1}{D} \frac{{\partial^{2} T(x,t) }}{{\partial {\text{ x}}^{ 2} }},t > 0;\left| x \right| < b\\ & \left. {T(x,t)} \right|_{t = 0} = \frac{{hbQ_{v} }}{2k} \times {\text{e}}^{{ - \frac{{x^{2} }}{{2b^{2} }}}} ;\left. {T(x,t)} \right|_{t \to \infty } = T_{\infty } \end{aligned} \right.} \end{array} $$
(5)

where T ∞ is the room temperature and D is the thermal diffusivity.

T(x, t) is first expressed as an infinite sum of the Boubaker polynomials [9–13], whose expression fits boundary condition.

$$ T(x,t) = T_{0} \times {\text{e}}^{{ - \frac{{x^{2} }}{{2b^{2} }}}} \times \frac{1}{{2N_{0} }}\sum\limits_{n = 1}^{{N_{0} }} {\xi_{n} B_{4n} \left( {t\frac{{\alpha_{n} }}{{t_{m} }}} \right)} $$
(6)

where α n are the minimal positive roots (Fig. 3) of the Boubaker 4n-order polynomials B 4n [9–11], t m is the maximum time range (when the temperature is supposed to be room one), N 0 is an even given integer, T 0 is the calculated maximal central temperature and ξ n are coefficients which verify the system (7):

$$ \left\{ \begin{gathered} \sum\limits_{n = 1}^{{N_{0} }} {\xi_{n} } = - N_{0} \hfill \\ \sum\limits_{n = 1}^{{N_{0} }} {\xi_{n} \frac{{\alpha_{n} }}{{t_{m} }}B_{4n}^{\prime } (\alpha_{n} )} = 0 \hfill \\ \end{gathered} \right. $$
(7)
Fig. 3
figure 3

Minimal positive roots (α n ) of the Boubaker 4n-order polynomials B 4n

Full size image

The system (7), due to the Boubaker polynomials properties, is reduced to:

$$ \left\{ \begin{gathered} \sum\limits_{n = 1}^{{N_{0} }} {\xi_{n} } = - N_{0} \hfill \\ \sum\limits_{n = 1}^{{N_{0} }} {\xi_{n} \times u_{n} } = 0;{\text{ with : }}u_{n} = \left[ {\alpha_{n}^{2} (\alpha_{n}^{2} - 1)^{2} (3\alpha_{n}^{2} + 4)} \right] \hfill \\ \end{gathered} \right. $$
(8)

A solution to the system (8) is:

$$ \xi_{n} = \left\{ \begin{gathered} - N_{0} \frac{{u_{{\left( {N_{0} - n + 1} \right)}} }}{\varpi }{\text{ if }}n < \frac{{N_{0} }}{2} \hfill \\ N_{0} \frac{{u_{{\left( {N_{0} - n + 1} \right)}} }}{\varpi }{\text{ if }}n > \frac{{N_{0} }}{2} \hfill \\ {\text{where }}\varpi = \left( {\sum\limits_{n = 1}^{{N_{0} }} {u_{{\left( {N_{0} - n + 1} \right)}} } } \right) \hfill \\ \end{gathered} \right. $$
(9)

The correspondent calculated parameters are shown in Fig. 4.

Fig. 4
figure 4

Absolute value of the coefficients ξ n

Full size image

4 Results and discussion

The obtained temperature values are presented in Table 1 along with theoretical results.

Table 1 Temperature values versus time
Full size table

It is known that a good knowledge of the cooling velocity profile is necessary for predicting and monitoring many interesting items like initial solidification uniformity, slab solidification structure, and metal purity. In this context, the cooling velocity profile (Fig. 5) was derived from the results shown in Table 1. It is noted that the time (t = 0) corresponds to the cooling phase starting date (≈0.6 s in Fig. 5).

Fig. 5
figure 5

The cooling velocity and acceleration profiles

Full size image

The shape of this profile (Fig. 3) is in concordance with the profiles presented by Paul et al. [14], Andreassen et al. [15] and Belcher [16]. The velocity range (0–82°C s−1) is also agreeing with the values published by Santos et al. [17] and more recently by Mughal et al. [18].

5 Conclusion

In this paper, a theoretical–experimental model of heat transfer inside a cylindrical keyhole laser welding [19–28] was presented. We have being tried to exploit the model, by implementing real-time velocity measurements, to prove that the cooling velocity can be reduced by the presence of appropriate alloying elements. This feature is very interesting since it is an issue for hardening with mild quenching. Our numerical results have been compared with both experimental results and recently published results [14–43]. This comparison shows that our model was well-adapted in order to evaluate the cooling velocity and acceleration.