1 Introduction

The effect of thermal radiation on convective heat transfer is very important in space technology and in processes involving high temperatures such as nuclear power plants, gas turbines and thermal energy storage.

Alam et al. [1] analyzed a two-dimensional steady MHD mixed convection and mass transfer flow over a semi-infinite porous inclined plate in the presence of thermal radiation with variable suction and thermophoresis. Yih [2] studied the effect of radiation on mixed convection flow optically dense viscous fluids about an isothermal wedge embedded in a saturated porous medium. Al-Odat et al. [3] investigated the influences of radiation on mixed convection flow of an optically dense viscous fluid along an isothermal wedge embedded in non-Darcy porous medium. Chamkha et al. [4] investigated on the steady-state, hydromagnetic forced convective boundary-layer flow of an incompressible Newtonian, electrically conducting and heat-generating/absorbing fluid over a non-isothermal wedge in the presence of thermal radiation effects. Elbashbeshy and Bazid [5] determined the effect of radiation on forced convection flow of a micropolar fluid over a horizontal plate. Hossain and Takhar [6] analyzed the effect of radiation using the Rosseland diffusion approximation on mixed convection along a vertical plate with uniform free stream velocity and surface temperature. Hossain et al. [7] determined the effect of radiation on the natural convection flow of an optically dense incompressible fluid along a uniformly heated vertical plate with a uniform suction. Hossain et al. [8] investigated effect of thermal radiation on the natural convection flow along a uniformly heated vertical porous plate with variable viscosity and uniform suction velocity. Duwairi [9] and Damseh et al. [10] studied the radiation and magnetic effects on the skin friction and heat transfer for forced convection conditions.

The study of magneto-hydrodynamic flow for an electrically conducting fluid past a heated surface has attracted the interest of many researchers in view of its important applications in many engineering problems such as plasma studies, petroleum industries, MHD power generators, cooling of nuclear reactors, the boundary layer control in aerodynamics, and crystal growth [10, 11]. Chen [11] investigated the momentum, heat and mass transfer characteristics of MHD natural convection flow over a permeable, inclined surface with variable wall temperature and concentration, taking into consideration the effects of ohmic heating and viscous dissipation. Seddeek [12] analyzed the effect of variable viscosity and magnetic field on the flow and heat transfer past a continuously moving porous plate. Abdelkhalek [13] investigated the effects of mass transfer on steady two-dimensional laminar MHD mixed convection. Aldoss and Ali [14] studied the effects of suction and blowing on convection heat transfer from a horizontal cylinder in cross magnetohydrodynamic flow. Nanousis [15] analyzed the effects of an applied magnetic field on the mixed convection boundary-layer flow over a wedge with suction or injection.

The aim of the present study is focused at highlighting the combined effects of gas radiation and magnetic field on the mixed convection flow from a permeable vertical plate.

2 Analysis

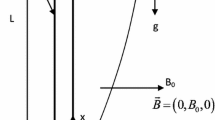
Consider a semi-infinite vertical permeable plate at a uniform temperature T w which is played vertical in a quiescent fluid of infinite extent at constant temperature T ∞. The fluid is assumed to be a gray, emitting and absorbing, but non-scattering medium. The following assumptions are made in the analysis: (a) variations in fluid properties are limited only to those density variations which affect the buoyancy terms, (b) viscous dissipation effects are negligible, and (c) the radiative heat flux in the x-direction is considered negligible in comparison with that in the y-direction, where the physical coordinates (x, y) are chosen such that x is measured from the leading edge in the streamwise direction and y is measured normal to the surface of the plate. The coordinates system and the flow configuration are shown in Fig. 1.

Fig. 1
figure 1

The schematic of the problem

Full size image

Under the usual Boussinesq approximation, the conservation equations for the steady, laminar, two-dimensional boundary-layer flow problem under consideration can be written as

$$ \frac{{\partial u}}{{\partial x}} + \frac{{\partial \upsilon }}{{\partial y}} = 0 $$
(1)
$$ u\,\frac{{\partial u}}{{\partial x}} + \upsilon \frac{{\partial u}}{{\partial y}} = v\,\frac{{\partial ^{2} u}}{{\partial y^{2} }} + g\,\beta \,\left( {T - T_{\infty } } \right) - \frac{{\sigma B_{0}^{2} }}{\rho }\left( {u - u_{\infty } } \right) $$
(2)
$$ u\frac{{\partial T}}{{\partial x}} + \upsilon \frac{{\partial T}}{{\partial y}} = \frac{v}{{Pr}}\left( {\frac{{\partial ^{2} T}}{{\partial y^{2} }}} \right) - \frac{1}{{\rho c_{p} }}\frac{\partial }{{\partial y}}\left( {q_{{\text{R}}} } \right) $$
(3)

Here u and υ are the velocity components in the x and y-direction, respectively, T is the temperature of the fluid, β is the coefficient of thermal expansion, v is the kinematic viscosity, ρ is the fluid density, g is the acceleration due to gravity, σ is the electrical conductivity of the fluid and B 0 is the magnetic flux density.

The quantity q R on the right-hand side of Eq. (3) represents the radiative heat flux in the y-direction. For simplicity and comparison, the radiative heat flux term in the energy equation is analyzed by utilizing the Rosseland diffusion approximation [16] for an optically thick boundary layer as follows:

$$ q_{r} = - \frac{{4a}}{{3\alpha _{{\text{R}}} }}\frac{{\partial T^{4} }}{{\partial y}}\quad {\text{and}}\quad \frac{{\partial q_{r} }}{{\partial y}} = - \frac{{16a}}{{3\alpha _{{\text{R}}} }}\frac{\partial }{{\partial y}}\left( {T^{3} \frac{{\partial T}}{{\partial y}}} \right) $$
(4)

where a is the Stefan–Boltzmann constant, α R is the Rosseland mean absorption coefficient. This approximation is valid at points optically far from the bounding surface, and is good only for intensive absorption, that is, for an optically thick boundary layer [8].

The appropriate boundary conditions for the velocity and temperature of this problem are

$$ \begin{array}{*{20}l} {x = 0} & {y > 0} & {T = T_{\infty } } & {u = u_{\infty } } & {} & {} \\ {x > 0} & {y = 0} & {T = T_{w} } & {u = 0} & {} & {v = \pm V_{w} } \\ {y \to \infty } & {} & {T \to T_{\infty } } & {} & {u \to u_{\infty } } & {} \\ \end{array} $$
(5)

The minus sign for the conductive gray fluid vertical velocity means the suction from the permeable wall, where the plus sign means the gray fluid injection. To seek a solution, the following dimensionless variables are introduced:

$$ \xi = \frac{x}{L},\quad \psi \left( {x,y} \right) = \left( {vu_{\infty } x} \right)^{{1/2}} f(\xi ,\eta ),\quad \eta = y\left( {\frac{{u_{\infty } }}{{vx}}} \right)^{{1/2}} ,\quad \theta = \frac{{T - T_{\infty } }}{{T_{{\text{w}}} - T_{\infty } }} $$
(6)

where ψ(x, y)is the free stream function that satisfies Eq. (1) with u = ∂ψ/∂y and υ = −∂ψ/∂x.

In terms of these new variables, the velocity components can be expressed as

$$ u = u_{\infty } f^{\prime} , $$
(7)
$$ \upsilon = - \frac{{\left( {vu_{\infty } x} \right)^{{1/2}} }}{x}\left\{ {\frac{1}{2}f + \xi \frac{{\partial f}}{{\partial \xi }} - \frac{\eta }{2}f^{\prime}} \right\} $$
(8)

The transformed momentum and energy equations together with the boundary conditions, Eqs. (2), (3) and (5), can be written as

$$ f^{\prime \prime \prime} + \frac{1}{2}ff^{\prime \prime} + Ri\xi \theta - M\xi \left( {f^{\prime} - 1} \right) = \xi \left( {f^{\prime} \frac{{\partial f^{\prime} }}{{\partial \xi }} - f^{\prime \prime} \frac{{\partial f}}{{\partial \xi }}} \right) $$
(9)
$$ \frac{1}{{Pr}}\theta ^{\prime \prime} + \frac{1}{2}f\theta^{\prime} + \frac{4}{{3PrR_{d} }}\left\{ {\left[ {\theta \left( {\theta _{{\text{w}}} - 1} \right) + 1} \right]^{3} \theta^{\prime} } \right\}^{\prime } = \xi \left( {f^{\prime} \frac{{\partial \theta }}{{\partial \xi }} - \theta^{\prime} \frac{{\partial f}}{{\partial \xi }}} \right) $$
(10)

with the boundary conditions;

$$ f\left( {\xi ,0} \right) + 2\xi \frac{{\partial f}}{{\partial \xi }} = f_{{\text{w}}} \xi ^{{1/2}} ,\quad f^{\prime} \left( {\xi ,0} \right) = 0,\quad \theta \left( {\xi ,0} \right) = 1, $$
$$ f^{\prime} \left( {\xi ,\infty } \right) = 1,\quad \theta \left( {\xi ,\infty } \right) = 0 $$
(11)

where \( f_{{\text{w}}} = - 2\frac{L}{v}V_{{\text{w}}} Re_{L}^{{ - 1/2}} , \) the case f w > 0 designates suction while f w < 0 indicates injection or blowing. The corresponding dimensionless groups that appeared in the governing equations defined as

$$ Pr = \frac{{\mu c_{p} }}{k} = \frac{v}{\alpha },\quad Ri = \frac{{Gr}}{{Re^{2} }},\quad Gr = \frac{{g\beta \left( {T_{{\text{w}}} - T_{\infty } } \right)L^{3} }}{{v^{2} }},\quad Re = \frac{{u_{\infty } L}}{v},\quad M = Ha/\text{Re} $$
$$ Ha = \frac{{\sigma B_{0}^{2} L^{2} }}{\mu },\quad R_{d} = \frac{{k\alpha _{{\text{R}}} }}{{4aT_{\infty }^{3} }},\quad {\text{and}}\quad \theta _{{\text{w}}} = \frac{{T_{{\text{w}}} }}{{T_{\infty } }} $$
(12)

where Pr is the Prandtl number, Ri is the Richardson number, Gr is the Grashof number, Re is the Reynolds number, M is the magnetic parameter which is the ratio of the Hartman number to the Reynolds number, Ha is the Hartman number, R d is the Planck number (radiation–conduction parameter), θ w is the surface temperature ratio to the ambient fluid.

In the above system of equations, the radiation–conduction parameter is absent from the MHD mixed convection heat transfer problem when R d  → ∞. It should be mentioned that the optically thick approximation should be valid for relatively low values of the radiation–conduction parameter, R d . According to Ali et al. [17], some values of R d for different gases are: (1) Rd = 10–30: carbon dioxide (100–650°F) with corresponding Prandtl number range 0.76–0.6; (2) R d  = 30–200: ammonia vapor (120–400°F) with corresponding Prandtl number range 0.88–0.84; (3) R d  = 30–200: water vapor (220–900°F) with corresponding Prandtl number 1.

The system of transformed equations together with the boundary conditions, Eqs. (9)–(11), have been solved numerically using the Keller box scheme, an efficient and accurate finite-difference scheme, similar to that described in Cebeci and Bradshaw [18]. For the sake of brevity, details of the numerical method are not described, referring the reader to Cebeci and Bradshaw [18]. This is a very popular implicit scheme, which demonstrates the ability to solve systems of differential equations of any order as well as featuring second-order accuracy (which can be realized with arbitrary non-uniform spacing), allowing very rapid x or ξ (streamwise distance) variations [10]. In the calculations, a uniform grid of the step size 0.01 in the η-direction and a nonuniform grid in the ξ-direction with a starting step size 0.001 and an increase of 0.05 times the previous step size were found to be satisfactory in obtaining sufficient accuracy within a tolerance better than 10−6 in nearly all cases.

3 Results and discussion

At first, in order to verify the accuracy of the numerical results, the validity of the numerical code developed has been checked for some limiting cases. For Pr = 1.0, Ri = 0.0, and R d  → ∞, we compare our −θ′(0, 0) results with those given by Chamkha et al. [4], Lin and Lin [19], Yih [20] and Nield and Kuznetsov [21] (Table 1). For different f w and ξ, we compare our −θ′(ξ, 0)results with those given by Chamkha et al. [22] (Table 2). As it is seen from Tables 1 and 2 excellent agreements have been observed.

Table 1 Comparison of the values −θ′(0, 0) for various values Pr at Ri = 0.0, M = 0.0, R d  → ∞ and f w = 0.0
Full size table
Table 2 Comparison of the values −θ′(ξ, 0) for various values ξ and fw at M = 1, Ri = 1, R d  → ∞ and Pr = 0.7
Full size table

In this paper, the mixed convection effects of ionized gas adjacent to radiate porous wall are investigated including the magnetic field. The following ranges of the main parameters are considered: Ri = 0, 1, 2 and 3; Pr = 1.0; f w = −0.1, 0.0, 0.1; magnetic parameter M = 1, 2 and 3; radiation parameter R d  = 1, 10, and 50; and surface temperature parameter θ w = 1.7, 2.0, and 2.3. The mixed convection parameter Ri, the radiation parameter R d , the surface temperature parameter θ w, the suction/injection effects f w and magnetic parameter M on the momentum and heat transfer are analyzed and discussed. The Richardson number, Ri represents a measure of the effect of the buoyancy in comparison with that of the inertia of the external forced or free stream flow on the heat and fluid flow. Outside the mixed convection region, either the pure forced convection or the free convection analysis can be used to describe accurately the flow or the temperature field. Forced convection is the dominant mode of transport when Ri → 0, whereas free convection is the dominant mode when Ri → ∞. Buoyancy forces can enhance the surface heat transfer rate when they assist the forced convection, and vice versa [23].

Figure 2 shows the effect of the buoyancy parameter Ri on the dimensionless velocity and temperature profiles. The velocity and temperature gradients increase with Ri and the momentum and thermal boundary layers decrease.

Fig. 2
figure 2

Dimensionless velocity (a) and temperature (b) profiles for different Ri while Pr = 1.0, M = 1, R d = 1, θ w = 1.7 and ξ = 0.4

Full size image

The effect of injection/suction of fluid from the plate on the dimensionless velocity and temperature profiles is also clear from Fig. 2. Injecting fluid into the boundary layer broadens the velocity distribution and increases the hydrodynamic boundary layer thicknesses. Also, the wall shear stress would be increased with the application of suction whereas injection tends to decrease wall shear stress. This can be explained by the fact that the wall velocity gradient is increased with the increasing value of f w. The effect of injection is found to broaden the temperature distribution, decrease the wall temperature gradient, and hence reduce the heat transfer rate. On the other hand, the thermal boundary layer becomes thinner and the wall temperature gradient becomes larger when suction is applied.

The effect of the mixed convection parameter Ri on the local skin friction and the local heat transfer parameters are shown in Fig. 3. Both the local skin friction and the local heat transfer parameters increase with an increase in the mixed convection parameter Ri.

Fig. 3
figure 3

Numerical values of local skin friction (a) and local heat transfer (b) against the streamwise distance ξ for different Ri while Pr = 1.0, M = 1, R d  = 1 and θ w = 1.7

Full size image

Figure 4 shows the dimensionless velocity and temperature profiles inside the boundary layer for different values of the radiation parameter R d . The increasing of the radiation parameter R d increases the momentum boundary layer thickness and decreases the temperature boundary layer thickness (i.e. increases temperature gradients at the permeable wall).

Fig. 4
figure 4

Dimensionless velocity (a) and temperature (b) profiles for different R d while Pr = 1.0, M = 1, Ri = 1, θ w = 1.7 and ξ = 0.4

Full size image

In Fig. 5 the effects of the radiation parameter R d on the local skin friction and the local heat transfer parameters are displayed. The increasing of the radiation parameter R d decreases the local skin friction parameter and increases the local heat transfer parameter as a result of increased hydrodynamic boundary layer thickness and decreased thermal boundary layer thickness.

Fig. 5
figure 5

Numerical values of local skin friction (a) and local heat transfer (b) against the streamwise distance ξ for different R d while Pr = 1.0, M = 1, Ri = 1 and θ w = 1.7

Full size image

The effect of surface temperature parameter θ w on the velocity and temperature profiles is shown in Fig. 6. Increasing the surface temperature ratio increases dimensionless velocity profile (Fig. 6), which is shown to increase the local skin friction parameter (Fig. 7). Moreover increasing the temperature ratio also increased the temperatures inside the boundary layer (Fig. 6) and consequently decreases the local heat transfer parameter (Fig. 7).

Fig. 6
figure 6

Dimensionless velocity (a) and temperature (b) profiles for different θ w while Pr = 1.0, M = 1, Ri = 1, R d = 1 and ξ = 0.4

Full size image
Fig. 7
figure 7

Numerical values of local skin friction (a) and local heat transfer (b) against the streamwise distance ξ for different θ w while Pr = 1.0, M = 1, Ri = 1 and R d = 1

Full size image

Figure 8 shows the dimensionless velocity and temperature profiles inside the boundary layer for different values of the magnetic parameter M. The increasing of the magnetic parameter M decreases the momentum and the temperature boundary layer thicknesses (i.e. increases velocity and temperature gradients at the permeable wall). Both the local skin friction and the local heat transfer parameters increase with the magnetic parameter M (Fig. 9). Since the magnetic parameter M is multiplied by ξ [see Eq. (9)], the effect of M increases with the streamwise distance ξ.

Fig. 8
figure 8

Dimensionless velocity (a) and temperature (b) profiles for different M while Pr = 1.0, Ri = 1, R d  = 1, θ w = 1.7 and ξ = 0.4

Full size image
Fig. 9
figure 9

Numerical values of local skin friction (a) and local heat transfer (b) against the streamwise distance ξ for different M while Pr = 1.0, Ri = 1, R d  = 1 and θw = 1.7

Full size image

It is also clear from Figs. 3, 5, 7, and 9 increasing f w increases local skin friction and local heat transfer parameter.

4 Conclusions

In this article, we have studied numerically the effects of suction/injection and thermal radiation on a steady MHD mixed convective flows of a viscous incompressible fluid about a permeable vertical plate. A transformed set of non-similar equations have been solved using the Keller box scheme, an efficient and accurate finite-difference scheme. From the present numerical investigation, the following conclusions can be drawn:

  1. 1.

    An increase in the mixed convection parameter increases the local skin friction and the local heat transfer parameters.

  2. 2.

    An increase in the radiation parameter decreases the local skin friction parameter and increases the local heat transfer parameter.

  3. 3.

    An increase in the surface temperature parameter increases the local skin friction parameter and decreases the local heat transfer parameter.

  4. 4.

    An increase in the magnetic parameter increases the local skin friction and the local heat transfer parameters.

  5. 5.

    It is found that the presence of suction makes the thermal boundary layer thinner and therefore enhances the heat transfer, while the injection presents an opposite effect.