1 Introduction

Extensive literature is now available on the flow and heat transfer from an infinitely long circular cylinder to Newtonian fluids, e.g., see [1, 17, 18, 30–32]. Undoubtedly, in addition to the Reynolds and Prandtl numbers, the rate of heat transfer from a cylinder to the streaming fluid is also influenced by the type of thermal boundary condition prescribed at the surface of the cylinder, namely, constant temperature or uniform heat flux. While in practice, the boundary conditions tend to be mixed and complex, these two limiting thermal boundary conditions represent the cases of a general thermal boundary condition, i.e., linear heat transfer to a fixed temperature, isoflux for very low and isothermal for very high heat transfer coefficients. Further complications arise from the variety of the possible flow regimes depending upon the value of the Reynolds number. It is now generally agreed that the flow characteristics past an unconfined cylinder transit from one regime to another as follows: steady flow without separation at Re < 5, steady flow with two symmetric vortices up to Re < 49, the onset of laminar vortex shedding at Re ≈ 49, three-dimensional (3D) wake-transition at Re ≈ 190–260, and shear-layer transition at Re ≈ 103–2 × 105 [30].

An inspection of the available literature clearly shows that the flow characteristics have been studied much more extensively than the heat transfer characteristics. Furthermore, the bulk of the available literature on the heat transfer from a cylinder relates to the flow of air (Pr = 0.71), e.g., see [1, 2, 17]. Indeed, little numerical and experimental work is available on the effect of Prandtl number on heat transfer from a cylinder in the cross-flow configuration. Thus, for instance, Dennis et al. [8] numerically solved the flow and energy equations for the values of Prandtl number up to 3.3 × 104 and of the Reynolds number up to 40 for the constant temperature case. Subsequently, the range of these results has been extended by Chang and Finlayson [6] for Reynolds numbers up to 150 and Prandtl number up to 104 for the constant temperature case.

Similarly, very few investigations have studied heat transfer from a cylinder subjected to the constant heat flux condition. Both Ahmad and Qureshi [2] and Badr [3] have reported numerical results for mixed convection heat transfer with air for the uniform heat flux and constant temperature boundary conditions, respectively, in the Reynolds number range 1 ≤ Re ≤ 60 and 1 ≤ Re ≤ 40, respectively. More recently, Soares et al. [26] have studied the heat transfer from a cylinder to power-law fluids. In the limit of Newtonian fluid behavior, they have presented very few results for Prandtl number values up to 100. The effect of temperature-dependent physical properties (viscosity and density) on the rate of heat transfer for air has been studied by Shi et al. [25]. Similarly, Eckert and Soehngen [11] and Krall and Eckert [16] reported the experimental values of the local Nusselt number on the surface of the cylinder for the flow of air. Combined together, these two studies encompassed a wide range of Reynolds numbers as 10 ≤ Re ≤ 400.

The role of the two types of thermal boundary conditions was elucidated experimentally by Baughn and Saniei [4] with air and for a fixed value of the Reynolds number, Re = 34,000. As expected, not only they reported higher values of the Nusselt number for the uniform heat flux case than that for an isothermal cylinder, but the type of boundary condition exerted greater influence on heat transfer in the front part than that in the rear of the cylinder. Wang and Travnicek [29] have explored the role of temperature-dependent viscosity on heat transfer for air. Nakamura and Igarashi [19–21] have experimentally explored the unsteady and 3D characteristics of the heat transfer from a circular cylinder to air in different flow regimes and presented the Nusselt number correlation for the range of Reynolds number 70–30,000. More recently, Sanitjai and Goldstein [22] have reported experimental results for a cylinder subjected to the constant heat flux condition for a range of values of the Prandtl number by using air, water and ethylene glycol mixtures of varying concentrations in the range 103 ≤ Re ≤ ∼105. The flow regime was found to exert a strong influence on the nature of dependence on Reynolds and Prandtl numbers. Aside from these results based on the experimental investigation and/or solution of the complete governing equations, there have been some studies based on the boundary layer flow approximations (Khan et al. [15]).

It is thus fair to say that the adequate information is now available for estimating the value of the Nusselt number as a function of Reynolds and Prandtl numbers for an isothermal cylinder. On the other hand, much less is known about the effect of Prandtl number on the heat transfer from an isoflux cylinder, except the experimental results [4, 22] which relate to Re > 1,000 or the numerical results [7, 23] for the flow of air for Re > 50.

Hence, the present work is aimed to study the role of Prandtl number and of the two limiting thermal boundary conditions on the rate of heat transfer from a circular cylinder in the low Reynolds numbers in the steady cross-flow regime. Extensive numerical results are presented for the Reynolds number range 10 ≤ Re ≤ 45, and Prandtl number range 0.7 ≤ Re ≤ 400, respectively. These values have been used to develop simple predictive correlations.

2 Problem statement and mathematical formulation

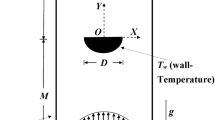
Consider the 2D, steady and incompressible flow of an uniform velocity U ∞ and temperature T ∞ over a circular cylinder of diameter, D. The unconfined flow is simulated here by considering the flow in a channel with the cylinder placed symmetrically between two plane walls with slip boundary conditions, as shown in Fig. 1. The cylinder is situated at a distance of L u from the inlet and at a distance of L d from the outflow boundary (Fig. 1). The surface of the cylinder is taken to be either at a constant wall temperature (CWT) T w, or at a uniform heat flux (UHF) q w. Furthermore, the thermo-physical properties of the fluid are assumed to be temperature independent and with negligible viscous dissipation. Admittedly, the temperature dependence of thermo-physical properties (or of Prandtl number) varies from one substance to another, the objective here is to elucidate the role of Prandtl number over a wide range of conditions rather than focusing on any specific fluid. Furthermore, it is also appropriate to make a comment about the role of free convection over the range of conditions studied herein. Vilimpoc et al. [28] reported that the forced convection (0.02 ≤ Re ≤ 64; 5.5 ≤ Pr ≤ 2,700) heat transfer from a cylinder in Newtonian liquids dominates for the high Prandtl number fluids up to a value of Richardson number (Ri = Gr/Re 2  = gβΔTD/U 2 ∞) of 4. Since the ranges of conditions covered herein are generally within this range, it is reasonable to neglect the buoyancy effects in the present work.

Fig. 1
figure 1

Schematics of the unconfined flow around a circular cylinder

Full size image

The momentum and energy equations are non-dimensionalized using D, U ∞, D/U ∞ and ρU 2 ∞ as scaling variables for length, velocity, time and pressure, respectively. The temperature is non-dimensionalized using (T w  − T ∞) for the CWT case or q w D/k for the UHF condition. Only dimensionless equations, variables and values are reported hereafter.

In a Cartesian coordinate system, the flow and heat transfer together with the above-noted simplifying assumptions are governed by the following equations:

  • Continuity equation

    $$ \frac{{\partial V_{x} }} {{\partial x}} + \frac{{\partial V_{y} }} {{\partial y}} = 0 $$
    (1)

  • x-Momentum equation

    $$ \frac{{\partial V_{x} }} {{\partial t}} + \frac{{\partial (V_{x} V_{x} )}} {{\partial x}} + \frac{{\partial (V_{y} V_{x} )}} {{\partial y}} = - \frac{{\partial p}} {{\partial x}} + \frac{1} {{Re}}{\left( {\frac{{\partial ^{2} V_{x} }} {{\partial x^{2} }} + \frac{{\partial ^{2} V_{x} }} {{\partial y^{2} }}} \right)} $$
    (2)

  • y-Momentum equation

    $$ \frac{{\partial V_{y} }} {{\partial t}} + \frac{{\partial (V_{x} V_{y} )}} {{\partial x}} + \frac{{\partial (V_{y} V_{y} )}} {{\partial y}} = - \frac{{\partial p}} {{\partial y}} + \frac{1} {{Re}}{\left( {\frac{{\partial ^{2} V_{y} }} {{\partial x^{2} }} + \frac{{\partial ^{2} V_{y} }} {{\partial y^{2} }}} \right)} $$
    (3)

  • Thermal energy equation

    $$ \frac{{\partial T}} {{\partial t}} + \frac{{\partial (V_{x} T)}} {{\partial x}} + \frac{{\partial (V_{y} T)}} {{\partial y}} = \frac{1} {{Pe}}{\left( {\frac{{\partial ^{2} T}} {{\partial x^{2} }} + \frac{{\partial ^{2} T}} {{\partial y^{2} }}} \right)} $$
    (4)

    where, the Reynolds, Prandtl and Peclet numbers are defined as

    $$ Re = \frac{{DU_{\infty } \rho }} {\mu };\quad Pr = \frac{{c_{p} \mu }} {k}{\text{ and }}Pe = Re \times Pr. $$
    (5)

The boundary conditions for this problem may be written as follows.

  • At the inlet boundary: uniform flow condition

    $$ V_{x} = 1,\quad V_{y} = 0,\quad \frac{{\partial p}} {{\partial x}} = 0{\text{ and }}T = 0 $$
    (6)

  • At the upper boundary: slip flow condition

    $$ \frac{{\partial V_{x} }} {{\partial y}} = 0,\quad V_{y} = 0,\quad \frac{{\partial p}} {{\partial y}} = 0{\text{ and }}\frac{{\partial T}} {{\partial y}} = 0{\text{ (adiabatic)}} $$
    (7)

  • On the circular cylinder: no slip condition

    $$ V_{x} = 0,\quad V_{y} = 0,\quad \frac{{\partial p}} {{\partial n_{{\text{s}}} }} = 0{\text{ and }}\left\{ \begin{aligned}{} & T = 0\quad {\text{(CWT}\; {\text{case)}}} \\ & \frac{{\partial T}} {{\partial n_{{\text{s}}} }} = - 1\quad {\text{(UHF}\;{\text{case)}}} \\ \end{aligned} \right. $$
    (8)

    where n s represents the unit normal vector on s, the surface of the cylinder.

  • At the exit boundary: the homogeneous Neumann boundary condition has been used:

    $$ \frac{{\partial \phi }} {{\partial x}} = 0{\text{ and }}p = p_{\infty } = 0 $$
    (9)

    where φ is a scalar (i.e., V x , V y and T).

  • At the plane of symmetry, i.e., center line: symmetric flow condition

    $$ \frac{{\partial V_{x} }} {{\partial y}} = 0,\quad V_{y} = 0,\quad \frac{{\partial p}} {{\partial y}} = 0{\text{ and }}\frac{{\partial T}} {{\partial y}} = 0. $$
    (10)

Owing to the symmetry, the solution is obtained only in the upper half of the domain in Fig. 1. The numerical solution of Eqs. (1)–(4) along with the above-noted boundary conditions yields the velocity, pressure and temperature fields and these, in turn, are used further to deduce the global characteristics like drag coefficients and Nusselt number, as outlined elsewhere [5]. The local Nusselt number on the surface of the circular cylinder is evaluated by the following expressions:

$$ Nu_{{{\text{local}}}} = \frac{{hD}} {k} = \left\{ \begin{aligned}{} & - \frac{{\partial T}} {{\partial n_{{\text{s}}} }}{\text{(CWT}\;{\text{case)}}} \\ & \frac{1} {T}{\text{(UHF}\;{\text{case)}}} \\ \end{aligned} \right.$$
(11)

Such local values have been further averaged over the entire cylinder to obtain the surface averaged (or overall mean) Nusselt number.

$$ Nu = \frac{1} {\pi }{\int\limits_0^\pi {Nu_{{{\text{local}}}} \;{\text{d}}\theta } }. $$
(12)

The average Nusselt number can be used in process engineering design calculations to estimate the rate of heat transfer from the cylinder in the CWT case, or to estimate the average surface temperature of the cylinder for the UHF condition.

3 Numerical methodology

Since detailed description of the solution procedure and of the choice of numerical parameters is available elsewhere [5], only the salient features are recapitulated here. The governing equations have been discretized using the semi-implicit finite volume method [12] on a non-staggered and non-uniform grid, QUICK scheme [9, 10, 14, 24] for convective terms and central difference scheme for other terms. The final equations were solved using a Gauss–Seidel iterative algorithm. The steady-state solution has been obtained using the false-transient method. A zero-volume cell at each boundary condition has been used to implement the boundary conditions, which enables the exact boundary conditions at the surface of the cylinder. The fully converged velocity field [5] was used as the input for the thermal energy equation. The fully converged temperature field, then, is used to deduce the values of the local and average Nusselt number on the surface of the cylinder. The results presented herein are based on the domain size, L u  = L d  = L y  = 30.5 and a 101 × 283 grid, which was found to be adequate to capture all possibilities of the flow and heat transfer phenomena [5].

4 Results and discussion

Numerical computations have been carried out for Re = 10–45 in steps of 5 and for a range of values of the Prandtl number varying from 0.7 to 400. However, the maximum value of the Peclet number never exceeded 4,000.

4.1 Domain and grid independence

The domain independence study was performed with the non-uniform grid at Re = 10, Pr = 0.7 and 400 and at Re = 45, Pr = 0.7 and 75, respectively for both thermal boundary conditions. The domain is assumed to have L u  = L d  = L y , and these dimensions simultaneously were varied to find a domain size that is sufficiently large to justify the unconfined flow approximation. The G3 grid used for the domain study has a minimum spacing of 0.05 in the region 2.5D upstream and downstream of the cylinder and a spacing of 0.5 in the outer domain. The number of grid points on the half surface of the cylinder was 101. Table 1 shows the change of five units in the domain size results in a very slight change in the values of the average Nusselt number. Therefore, bearing in the mind the slight change in the results from a domain size of 30.5–35.5 at the expanse of a rather significant increase in CPU time, the domain size of 30.5 is believed to be adequate to obtain the results free of the domain effects.

Table 1 Domain independence study for the average Nusselt number
Full size table

Having fixed the domain size, the grid independence study was carried out for six non-uniform grids for the same values of the Reynolds and Prandtl numbers. Table 2 shows the effect of the grid size on the average Nusselt number. The refinement in the grid from G5 to G6 shows change < 1%, in the results. Therefore, the grid G6 (101 × 283) is believed to be sufficiently refined to resolve the heat-transfer phenomena. Also, the grid G6 has the grid spacing of 0.01 in the inner region of the domain, which is fine enough to resolve the thermal boundary layers for the ranges of the conditions covered in this study. Therefore, the results presented herein are based on the domain size 30.5 and a 101 × 283 grid.

Table 2 Grid independence study for the average Nusselt number
Full size table

4.2 Validation of results

The numerical methodology used in this work has already been validated extensively in terms of the recirculation length, separation angle, individual and total drag coefficients, surface vorticity, and pressure coefficient and their value at the stagnation points, all of which show excellent correspondence with the literature values [5]. Since most of the previous studies for heat transfer in the range of Reynolds number 10–45 relate to the flow of air, the present results for air at Re = 10, 20 and 40 have been compared with some of the prior numerical and experimental results (Table 3). There present results are well within ± 2–3% of the previous numerical results and are within 10–15% of the experimental results estimated using the correlation the correlation of Sparrow et al. [27]. The extent of the differences seen in Table 3 is not uncommon in such studies. These inherent uncertainties in the results are due to (a) modelling error (i.e., the differences in the flow schematics, problem formulations, etc.), (b) discretization error (i.e., discretization schemes, etc.), (c) numerical error due to iteration, round-up and programming, and (d) grid and accuracy of the scheme, etc. The Nusselt number values reported in the literature [3, 8] itself differ by as much as 5–6% and the present results are well within the range of values. Similarly, the experimental results in this field frequently entail errors up to ∼ 15–20%. Bearing in mind all these factors, it is fair to conclude that the present results are probably reliable to within 3–4%. Finally, based on the idea of equal surface area available for heat transfer, Ahmad [1] has outlined a method to link the results for a circular and square cylinder. This approach has been used to predict the results for a circular cylinder from that for a square cylinder as reported by Dhiman et al. [10]. These values are seen to deviate from the present values at most by 5% and the correspondence improves as the Reynolds number increases. This inspires confidence in the reliability and accuracy of the present method.

Table 3 Comparison of the average Nusselt number (Pr = 0.7) with the literature values
Full size table

4.3 Heat transfer results

The heat transfer results in terms of isotherm patterns, distribution of local Nusselt number on the surface of the cylinder and the average Nusselt number for 10 ≤ Re ≤ 45, 0.7 ≤ Pr ≤ 400 and two thermal boundary conditions are presented and discussed in next sections. The average Nusselt number has also been presented in terms of the Colburn heat transfer factor, j for both the thermal boundary conditions.

4.3.1 Isotherm patterns

Figure 2a–d shows representative isotherms in the vicinity of the cylinder for Re = 10 and 45 at different Prandtl numbers. The upper half and lower half of the figures show the isotherms for CWT and UHF conditions, respectively. It is seen that the front surface has the maximum clustering of temperature isotherms which indicates high temperature gradients (and thus highest local Nusselt number), as compared to the other points on the surfaces of the cylinder. For a fixed Reynolds number, the temperature gradients near the rear surface of the cylinder increases with an increase in the Prandtl number for both thermal boundary conditions. The clustering of isotherms also increases with an increase in the Reynolds number and/or Prandtl number or both. This is due to the increase in the recirculation region with Reynolds number and/or due to the thinning of the thermal boundary layer at high Prandtl numbers.

Fig. 2
figure 2

Isotherm plots [upper and lower half represents the constant wall temperature (CWT) and uniform heat flux (UHF) conditions, respectively] for Re = 10 and 45 at various Prandtl numbers

Full size image

4.3.2 Local Nusselt number

Owing to the underlying inherent differences, the results for the two thermal boundary conditions are discussed separately.

CWT condition

The variation of the local Nusselt number on the surface of the cylinder at Re = 10, 20 and 45 for a range of Prandtl numbers is shown in Fig. 3a–c. As expected, the Nusselt number increases with an increase in the Reynolds number and/or Prandtl number. These figures show that the relatively large values of the Nusselt number seen at the front stagnation point (θ = 0) decrease gradually along the surface of the cylinder, to a minimum value near the point of separation due to the thickening of the thermal boundary layer. A gradual increase in the values of the Nusselt number can be seen with an increase in the Reynolds number and Prandtl number in the rear part of cylinder, i.e. from the point of separation to the rear stagnation point (θ = π). The change in the slope in the Nusselt number variation after the separation points indicates the existence of a vortex. The local Nusselt number is seen to be strongly affected by the value of the Prandtl number. At Re = 10, the local Nusselt number at the front stagnation point increases from 2.73 to 25.32 as the Prandtl number increases from 0.7 to 400. However, the increase in the Nusselt number at the rear stagnation point is comparatively small, i.e. from 0.94 to 1.77. At Re = 45, the front stagnation Nu increases from 5.88 to 31.96 while the rear stagnation Nu increases from 1.22 to 10.06 as Pr increases from 0.7 to 75. The variation of the Nusselt number, Nu fs at the front stagnation point (θ = 0°) for the ranges of this study can be best represented by the following correlation:

$$ Nu_{{{\text{fs}}}} \;({\text{at }}\theta = {\text{0}}) = 0.85\;Re^{{0.555}} \;Pr^{{0.355}} $$
(13)

which has an average and maximum deviation of 1.32 and 4.63%, respectively. Note that the Eq. (13) compares favorably with the corresponding expression of Goldstein [13] for the flow of air.

Fig. 3
figure 3

Local Nusselt number variation on the surface of the cylinder for Re = 10, 20 and 45 at various Prandtl numbers for CWT and UHF conditions, respectively

Full size image

UHF condition

Representative results on the variation of the local Nusselt number on the surface of the cylinder for this case are shown in Fig. 3d–f for a range of the Reynolds and Prandtl numbers. These figures show qualitatively similar features as seen in Fig. 3a–c for the CWT condition. In this case also, the variation of the Nusselt number at the front stagnation point for the whole range of Re and Pr is best represented by Eq. (13), with the resulting average and maximum deviation of 1.48 and 4.42%, respectively.

4.3.3 Average Nusselt number

The average Nusselt number is obtained by averaging the local Nusselt number over the surface of cylinder (Eq. 12). In the engineering literature, it is convenient to use the Colburn heat transfer factor, j, which affords the possibility of reconciling the results for a range of Reynolds and Prandtl numbers on to a single curve. This is in contrast to the earlier investigations where Nusselt number correlations have been presented for fixed values of Prandtl number e.g., see [1, 2, 11].

Figure 4a–b shows the variation of the average Nusselt number with the Reynolds number at different Prandtl numbers for the two thermal boundary conditions. As expected, that the average Nusselt number for the cylinder increases with the Reynolds number and/or Prandtl number. Further analysis of data suggested the Nusselt number exhibits the classical dependence on Prandtl number, i.e. Nu α Pr 1/3. This allows the reconciliation of the results for different Prandtl numbers through use of the j-factor as shown in Fig. 5. A least-squares method applied to the present results for 10 ≤ Re ≤ 45 and 0.7 ≤ Pr ≤ 400 yields the following expression

$$ j = 0.6738\;Re^{{ - 0.5321}} $$
(14)

for the CWT case. Equation (14) correlates the present numerical data with the maximum and average deviations of 5.65 and 1.55%. The corresponding expression for the UHF condition is given by

$$ j = 0.7837\;Re^{{ - 0.5342}} $$
(15)

which shows maximum and average deviations of 3.16 and 0.95%, respectively. Attention is drawn to the almost identical power indices of the Reynolds number in Eqs. (14) and (15). However, the average Nusselt number is always higher for the UHF condition than that for CWT condition as indicated by the multiplicative constant in two equations.

Fig. 4
figure 4

Average Nusselt number as a function of the Reynolds number at different Prandtl number for CWT and UHF conditions, respectively

Full size image
Fig. 5
figure 5

Colburn j-factor as a function of the Reynolds number at different Prandtl number for CWT and UHF conditions, respectively

Full size image

Finally, it is appropriate to make some general remarks about the utility of the results reported herein from an engineering application viewpoint. Admittedly, the thermo-physical properties, notably viscosity, (and hence Prandtl number) of fluids do vary with temperature. However, since the average Nusselt number varies only as Pr 1/3, even a 100% increase in the value of Prandtl number will change the value of the Nusselt number by 26%. Therefore, the assumption of constant thermo-physical properties used in this work is not as bad as it seems. Thus, the present results can be used when moderate variation in the value of Prandtl number is encountered by using the physical properties evaluated at the mean temperature. Therefore, the results reported herein can be used at least as a first-order approximation even when there is a moderate variation in the values of Prandtl number due to temperature-dependent properties. However, in case of large variations, one needs to solve the coupled non-linear differential equations which further adds to the computational difficulty, as is reflected by the lack of such results in the literature even for air and water.

5 Conclusions

In the present study, the effect of Prandtl number (0.7 ≤ Pr ≤ 400) and of two different thermal boundary conditions on the forced convection heat transfer from an unconfined circular cylinder has been investigated in the Reynolds number range 10 ≤ Re ≤ 45 in the steady cross-flow regime. At a fixed point on the surface of the cylinder, the local Nusselt number increases with an increase in the values of the Reynolds number and/or of the Prandtl number. On the other hand, for a fixed values of Re and Pr, the local Nusselt number on the surface of cylinder decreases from the front stagnation point to the point of separation. However, it is seen to increase again from the point of separation to the rear stagnation point. The maximum value of the Nusselt number corresponding to the front stagnation point also increases with Reynolds number and/or Prandtl number. The Nusselt number at the front stagnation point is always higher for UHF than that for CWT condition. Finally, the numerical results are correlated in terms of the Colburn j-factor which allows an easy calculation of the Nusselt number for intermediate values of the Prandtl and Reynolds numbers.