1 Introduction

The modeling of high temperature phenomena in a moving bed of porous pellets is a challenging task, involving fluid mechanics, heat and mass transfer together with heterogeneous chemical reactions between pellets and gaseous mixture [6]. Such flows have been observed in chemical and metallurgical reactors. The overall performance of such reactors is strongly affected by reactional treatment of the solid matrix of bed with the gaseous mixture in aspect of heat and mass transfer. Therefore the simulation of a porous pellet behavior, as specimen of this moving bed, with a gaseous mixture is a necessary prerequisite of understanding and modeling of such moving bed reactors. A general review of previous works on the modeling of heterogeneous reactions between gaseous reactant and solid pellets is presented in Table 1. Relying largely on the computational effort and chemical complexities much of the work in this field has been based on relatively simple formulations [38]. The most important simplifications that have been used in the literature can be classified as follows.

  • Pseudo-steady state approximation

Table 1 General summary of previous investigations on noncatalytic gas–solid reactions
Full size table

By this approximation, the accumulation term in the gaseous phase is neglected and the governing equations are relatively simplified for analytical solution. It has extensively been used in the previous works except reports in which a numerical method is applied for solution of the equations (See Table 1). However pseudo steady state approximation has been shown to be valid for isothermal gas–solid reactions [22]. It leads to significant error when this assumption is used in the case of nonisothermal models [40].

  • Isothermal condition

This is usually made in the majority of gas–solid reaction models (See Table 1). This assumption can significantly simplify the solution of equations. However most of the chemical and physical properties of the gaseous mixture as well as the solid matrix are dominantly affected by temperature variation. It must be questioned whenever the reaction is exothermic or endothermic. Also this assumption may lead to error, when a temperature variation is imposed in the gas flow or size of the pellet is quite large [20, 21].

  • Single reactant for gas and solid

As it is shown in Table 1, most of the models that have been presented previously have used a single reactant in the gas phase and/or in the solid phase for modeling. However a multicomponent gas and/or solid phase with a multireaction system coexists in the practical application of these models [17, 34, 36, 37].

  • Simplification in physico-chemical properties

For gas and solid phase physical properties such as thermal conductivity, viscosity, heat capacity, etc. and chemical properties such as diffusivity, reaction rate constant, heat of reaction, etc. usually depend on the gas and solid composition, temperature, pressure and also solid structure. Therefore it may lead to error if we do not take into account these dependencies. As an example a simplification on diffusivity estimation is shown in Table 1 corresponding to earlier studies. It can be seen that the most of previous models have applied the constant value for diffusion or some of them have estimated diffusivity as linear proportional of temperature [11–13, 22, 41, 42]. Moreover Knudsen diffusivity is withdrawn in the most of models which presented in Table 1. However it may significantly restrict the gaseous diffusion in practical cases, when the pellet pores are small enough [28].

  • Equimolar counter diffusion assumption

This is the last major assumption that is frequently made in the literature. It implies that the reactant and product gas flux are equal and opposite of each other for any reaction. However this assumption is not normally valid except under the pseudo steady state approximation in which the stochiometric coefficients of each gaseous reactant and product are equal [20, 21].

  • Gas–solid reaction models

To study gas–solid reaction, different techniques have already been applied for modeling. They can be divided in three categories as the following:

Heterogeneous model

When the porosity of the unreacted solid is very small so that the solid is practically impervious to the gaseous reactants. The chemical reactions are narrowly confined to the interface between the unreacted solid reactant and product. The USCM Footnote 1 technique has been used frequently to analyze this type of reaction [28, 40, 41]. This model generally implemented in the modeling of nonporous solid reactants as Sharp Interface Model Footnote 2 [12, 13]. Szekely and Evans [29–31] have shown that the shrinking core model has been successful for interpretation experimental data. However it has some major shortcomings in that the sharp reaction boundary was not necessarily supported by the experimental data.

Homogeneous model

When the solid contains enough pores to pass freely the gaseous agents, gaseous reactants could be available at all over the pellet at nearly bulk concentration. So that the chemical reactions take place at all over the pellet in which solid reactants have been distributed homogeneously. This type of reaction model has also been used in the literature for highly porous solid phase [7, 20, 21, 40].

Intermediate model

In practical case the distributions of the solid reactant may be considered as an ensemble of small lumps of reactant distributed throughout the solid phase. The reaction rates between each small lump of the solid reactants and the gas reactants that diffuse into the solid may be described by one of the above mentioned cases. The overall reaction rate depends on many parameters such as distribution of the small lumps of reactant in the solid, structure of solid, intrinsic reaction velocities, and transport properties of gaseous species within the porous media. This type of model has been used in porous solid reactants as zone model [11, 27, 35] or grain model [29–31, 35–38] in the literature.

As previously discussed, a gas–solid reaction are further complicated by occurring of multiple reactions in the mostly practical applications. Simultaneous gas–solid reactions may generally be divided into three classes as independent, parallel and consecutive reactions. When a multireactant gaseous mixture does react with a multireactant solid matrix as Eq. (1), a general form of reaction including all of these three classes appears simultaneously.

$$\begin{aligned} \,& \alpha _{1} G_{1} + \beta _{1} S_{1} \to \gamma _{1} P_{1} + \zeta _{1} S_{2} \\ \,& \vdots \\& \alpha _{i} G_{i} + \beta _{i} S_{1} \to \gamma _{i} P_{i} + \zeta _{i} S_{2} \\ \,& \vdots \\ \,& \alpha _{n} G_{n} + \beta _{n} S_{1} \to \gamma_{n} P_{n} + \zeta _{n} S_{2} \\ \end{aligned} \ldots \begin{aligned} \,& \alpha _{1} G_{1} + \beta _{1} S_{i} \to \gamma _{1} P_{1} + \zeta _{1} S_{{i + 1}} \\ \,& \vdots \\ \,& \alpha _{i} G_{i} + \beta _{i} S_{i} \to \gamma _{i} P_{i} + \zeta _{i} S_{{i + 1}} \\ \,& \vdots \\ \,& \alpha _{n} G_{n} + \beta _{n} S_{i} \to \gamma _{n} P_{n} + \zeta _{n} S_{{i + 1}} \\ \end{aligned} \ldots \begin{aligned} \,& \alpha _{1} G_{1} + \beta _{1} S_{{m - 1}} \to \gamma _{1} P_{1} + \zeta _{1} S_{m} \\ \,& \vdots \\ \,& \alpha _{i} G_{i} + \beta _{i} S_{{m - 1}} \to \gamma _{i} P_{i} + \zeta _{i} S_{m} \\ \,& \vdots \\ \,& \alpha _{n} G_{n} + \beta _{n} S_{{m - 1}} \to \gamma _{n} P_{n} + \zeta _{n} S_{m} \\ \end{aligned}$$
(1)

Among the studies devoted to earlier gas–solid reaction modeling, Hindmarsh and Johnson [14, 15] have been reported a quite complete model considering multiple reactions but their approach is quite cumbersome to handle. They used the multipurpose differential algebraic equation solver for solution the nonlinear system of Stefan–Maxwell equation which is coupled with continuity equation. It should therefore be presented a general model which is applicable easily under a wide variety of conditions and it can be covered the models which were mentioned and discussed above.

Hence, in this paper a model has been developed to simulate any kind of heterogeneous exothermic or endothermic reactions like Eq. (1) which take place within the multireactant porous pellet as specimen of moving packed bed. Also, the reactions are simultaneously proceeded in nonisothermal transient conditions in the whole of the pellet. A grain model which describes the solid phase as a juxtaposition of dense grains is used as intermediate model for modeling of the reactions in a spherical porous pellet. So that, the chemical reactions and gaseous diffusion proceed simultaneously in the pellet composed of small grains. A Finite Volume Method (FVM) as a fully implicit formulation is used for solving the governing equations of this model.

2 Concepts of phenomenon

The system under study is a porous solid pellet which is generally made up of a number of grains of different sizes, separated by pores. A possible representation of the solid pellet is shown in Fig. 1b, in which the pellet is in fact an agglomerate of dense grains of different sizes. Let us consider that the reactions in Eq. (1) are simultaneously taken place inside of a grain at interfaces which move spatially with reaction time. Regarding to mass transfer the following phenomena must be considered for modeling.

  • Gaseous mass transfer of species from the bulk flow of gas mixture to the external surface of the solid pellet.

  • Diffusion transport of the gaseous species through the pores of the solid matrix, which could consist of a solid reactant and solid products.

  • Heterogeneous chemical reactions at the interfaces of the grain of the pellet.

  • Diffusion of the gaseous products through the pores of the pellet.

  • Gaseous mass transfer of the reaction products from the external surface of the pellet to the bulk flow of the gas mixture.

Fig. 1
figure 1

Schematic Configuration of a Counter-current moving bed reactor, b multicomponent porous solid pellet, c grain model conversion

Full size image

Considering that, each of these steps has its own kinetics that it can limit or help to limit the overall rate of the pellet conversion.

In the case of nonisothermal condition the following phenomena must be taken in to account in regard to heat transfer.

  • Convection (and possibly radiation) heat transfer between the gas stream and the surface of the solid pellet.

  • Heat generation or consumption by progressing of reactions.

  • Conduction (and possibly radiation) heat transfer within the porous domain.

3 Mathematical model

The energy and mass equations together with initial and boundary conditions are presented here. Some of the general necessary assumptions for derivation of these equations are as following:

  • The pellet is spherical with constant diameter and any cracks do not form during the reaction.

  • Total pressure of mixture is constant inside the pellet.

  • The reactions are assumed to proceed reversibly without interaction between the gaseous species.

  • In the porous pellet the local thermal equilibrium between gas and solid is employed.

  • The pellet composed of spherical grains with radius r g.

3.1 Energy equation

The energy equation for heat transfer in porous media, in principle, should include conductive, radiant and convective terms [27]. The relative importance of these mechanisms varies, depending on solid properties, pore structure, temperature range and gaseous flow in each case. The common approach in treating radiant heat transfer in a porous media at high temperature is to include it in conductive heat transfer formulation by using effective heat conductivity [10, 23, 24]. By neglecting convective heat transfer inside the porous pellet, the energy equation can then be written as follows:

$$(\rho C_{\rm P})_{{\rm eff}} \frac{{\partial T}}{{\partial t}} = \nabla \cdot (\lambda _{{\rm eff}} \nabla T) + {\sum\limits_{k = 1}^{m - 1} {{\sum\limits_{j = G_{i}}^{G_{n}} {\dot{R}g_{{j,k}} {\left({- \Delta H_{{T,j,k}}}. \right)}}}}}$$
(2)

3.2 Mass transfer equations

Mass equations for gaseous reactants G i :

$$ \frac{{\partial (\varepsilon C_{t} Y_{{G_{i}}})}}{{\partial t}} + \nabla \cdot N_{{G_{i}}} = - \alpha _{{G_{i}}} {\sum\limits_{k = 1}^{m - 1} {\dot{R}g_{{G_{i}, k}}}} .$$
(3)

Mass equations for gaseous product P i :

$$ \frac{{\partial (\varepsilon C_{t} Y_{{P_{i}}})}}{{\partial t}} + \nabla \cdot N_{{P_{i}}} = \gamma _{{P_{i}}} {\sum\limits_{k = 1}^{m - 1} {\dot{R}g_{{P_{i}, k}}}} .$$
(4)

Equation for local conversion of solid reactant

$$ \rho _{{0,k}} \frac{{\partial f_{k}}}{{\partial t}} = {\sum\limits_{j = G_{i}}^{G_{n}} {\alpha _{j} \dot{R}g_{{j,k}}}} .$$
(5)

A simplified formulation is applied here for the fluxes involving effective diffusion coefficients as pseudo-binary diffusivity for each species. The applied methodology for estimation effective diffusivity will be discussed in Section 4.6.2.

$$ N_{j} = - C_{t} D^{e}_{j} \hbox{grad}\,Y_{j}, \quad j = G_{i}, P_{i} .$$
(6)

3.3 Auxiliary equations

Some other equations will be needed to close the set of governing equations. These are as follows:

$${\sum\limits {Y_{j}}} = 1.0, \quad j = G_{i}, P_{i}$$
(7)
$$C_{j} = Y_{j} C_{t}, \quad j = G_{i}, P_{i}$$
(8)
$$C_{t} = \frac{P}{{\bar{R}T}}$$
(9)
$$F_k = \left.\int\limits_{r = 0}^{R} 4\pi r^2 f_k \hbox{d}r \right/ \left(4/3\pi R_0^3 \right).$$
(10)

3.4 Reaction rate equation

The reaction rate per unit volume of solid reactant is generally expressed for each reaction as follows:

$$\dot{R}g_{{G_{i}, k}} = a_{\rm s} kr_{{G_{i}, k}} g{\left({f_{k}} \right)} \left(C_{{G_{i}}} - \frac{{C_{{P_{i}}}}}{{Ke_{{j,k}}}} \right)$$
(11)

where kr j,k , is the rate constant for reaction between G i and kth solid reactant, is assumed to obey the Arrhenius law as follows,

$$ kr_{{G_{i}, k}} = ko_{{G_{i}, k}} \hbox{Exp}{\left({\frac{{- Ea_{{G_{i}, k}}}}{{\bar{R}T}}} \right)}$$
(12)

And a s is also the specific area (area per unit volume) of solid reactant. But in this paper for grain model is defined as follows,

$$a_{\rm s} = \frac{{3(1 - \varepsilon)}}{{r_{g}}}$$
(13)

And g(f k )is a function of local degree conversion of kth solid reactant, f k , which is to describe the geometries of the solid reactants and change during the reactions. For applying in grain model this function is defined as follows [35]:

$$g(f_{k}) = \left({1 - f_{k}} \right)^{2/3}$$
(14)

3.5 Boundary and initial conditions

For continuity of heat and mass fluxes on the surface of pellet,r = R 0 we have:

$$ - \lambda _{{\rm eff}} \frac{{\partial T(R_0,t)}}{{\partial r}} = h^{*} (T^{\rm s} - T^{\rm b}) = \left(h_{\rm r} + h_{\rm C} \right) \left(T^{\rm s} - T^{\rm b} \right)$$
(15)
$$ - D^{e}_{j} \frac{{\partial Y_{j} (R_0,t)}}{{\partial r}} = km_{j} \left(Y^{\rm s}_{j} - Y^{\rm b}_{j} \right), \quad j = G_{i}, P_{i}$$
(16)
$$ f_{k} (R_0,t) = 1.0 $$
(17)

Due to spherical symmetry, at the center of the pellet, r = 0 :

$$\frac{{\partial T(0,t)}}{{\partial r}} = 0$$
(18)
$$\frac{{\partial Y_{j} (0,t)}}{{\partial r}} = 0, \quad j = G_{i}, P_{i}$$
(19)
$$\frac{{\partial f_{k} (0,t)}}{{\partial r}} = 0, \quad j = G_{i}, P_{i}.$$
(20)

For initial condition at t = 0,

$$ T(r,0) = T^{0} $$
(21)
$$ Y_{j} (r,0) = Y^{0}_{j}, \quad j = G_{i}, P_{i} $$
(22)
$$ f_{k} (r,0) = 0 $$
(23)

3.6 Physico-chemical properties

In the nonisothermal condition, thermo-physical and chemical properties of solid matrix, gaseous mixture, and gaseous species depend on the temperature and gaseous composition dominantly. In this section estimation of these properties will be discussed.

3.6.1 Heat and mass transfer coefficient

Heat transfer coefficient, h *, between bulk gaseous mixture and porous pellet is included two terms: convective heat transfer coefficient, h C, and radiative heat transfer coefficient. Convective heat transfer coefficient is calculated from classical correlation expressing Nu number as a function of the Re and Pr numbers. In the case of single pellet, the correlation of Ranz and Marshal should be applied if the radiative heat transfer could be evaluated quantitatively [2]:

$$Nu = 2.0 + 0.6Re^{{\frac{1}{2}}}_{p} Pr^{1/3}$$
(24)

In this case the radiative heat transfer coefficient will be estimated as following correlation:

$$h_{\rm r} = e\sigma (T^{2}_{s} + T^{2}_{b})(T_{s} + T_{b})$$
(25)

But in the case of porous pellet in the counter-current moving bed, the following empirical relation was used for determining the convective heat transfer coefficient [2].

$$Nu = 2.0 + 0.39Re^{1/2}_{p} Pr^{1/3}$$
(26)

And the following correlation have been proposed by Schotte[24] for radiative heat transfer coefficient.

$$h_{\rm r} = 0.692e\,{\left({\frac{{T^{3}}}{{10^{8}}}} \right)}.$$
(27)

A mass transfer coefficient for both reactants and products is obtained by using the analogy between heat and mass transfer. Hence, mass transfer coefficient, km j , between each gaseous agent and porous pellet is calculated from classical correlation expressing Sh number as a function of the Re and Sc numbers.

For single pellet in the gaseous flow:

$$Sh_{j} = 2.0 + 0.6Re^{1/2}_{p} Sc_{j} ^{1/3}, \quad j = G_{i}, P_{i}$$
(28)

For porous pellet in the counter-current moving bed reactor:

$$Sh_{j} = 2.0 + 0.39Re^{1/2} Sc_{j} ^{1/3}, \quad j = G_{i}, P_{i}$$
(29)

3.6.2 Effective diffusivity

The diffusion of a gaseous species through a porous media is strongly depended on solid matrix structure: void fraction, tortuosity, and pore size distribution as well as thermo-physical property of gaseous agents. When the pore size is large comparing with the mean free path of gas molecules, molecular diffusion is predominant, and the binary diffusivity for a pair of gaseous species can be found by use of the Wilke and Lee correlation [9]. Conversely, in a porous media with fine pores the Knudsen diffusion mechanism prevails. The Knudsen diffusivity for a gaseous species is given by the following relation [28].

$$D_{{Kj}} = \frac{{4K_{0}}}{3}{\left({\frac{{8\bar{R}T}}{{\pi M_{j}}}} \right)}^{1/2}, \quad j = G_{i}, P_{i},$$
(30)

where K 0 is the effective Knudsen flow parameter with dimension of the length Footnote 3

But in pores with intermediate size, transition or mixed type of diffusion may be occurred. In the intermediate region all types of transport mechanisms might be significant and a general relation combining these transport modes should therefore be developed.

By using the dusty gas model were able to show the possibility of additively of momentum transfer of Knudsen and ordinary diffusion as follows [9]:

$$ - C_{t} \hbox{grad}\,Y_{j} = \frac{{N_{j}}}{{D^{e}_{{kj}}}} + {\sum\limits_{j \ne l} {\frac{{Y_{l} N_{j} - Y_{j} N_{l}}}{{D^{e}_{{jl}}}}}}, \quad j = G_{i}, P_{i}$$
(31)

This model is not easy to implement for a multicomponent system. Therefore the simplified equation has been used for calculating effective diffusivity.

The ordinary diffusion term in the Stefan–Maxwell equation are thus approximated as follows [9]:

$$\frac{{N_{j}}}{{D^{e}_{{jm}}}} \cong {\sum\limits_{j \ne l} {\frac{{Y_{l} N_{j} - Y_{j} N_{l}}}{{D^{e}_{{jl}}}}}}, \quad j = G_{i}, P_{i}$$
(32)

Where, D e jm is the effective molecular diffusivity of component j in a multicomponent mixture.

By combination of Eqs. (6), (31) and (32), the effective diffusivity is obtained as,

$$\frac{1}{{D^{e}_{j}}} = \frac{1}{{D^{e}_{{kj}}}} + \frac{1}{{D^{e}_{{jm}}}}$$
(33)

The D jm is obtained from the equation for diffusion of component j through other stagnant components of a mixture as follows [9, 34]:

$$\frac{1}{{D_{{jm}}}} = \frac{1}{{1 - Y_{j}}}{\sum\limits_{j \ne l} {\frac{{Y_{j}}}{{D_{{jl}}}}}}$$
(34)

Because of the tortuous nature of pores in a porous pellet the diffusivity species must overcome a greater resistance than when diffusing is in straight pore capillaries. The effective diffusivity is therefore given by:

$$D^{e}_{{jm}} = \frac{\varepsilon}{\tau}D_{{jm}}$$
(35)

Here, τ represent the tortuosity factor which is varied between 1.5 and 10 in practically [28].

3.6.3 Effective thermal conductivity and heat capacity

As previously mentioned, the effective thermal conductivity must be included the radiant and conductive terms as follow:

$$\lambda_{{\rm eff}} = \lambda _{{\rm eff},C} + \lambda _{{\rm eff},R}$$
(36)

λeff,R which is a function of temperature, solid property and pore structure, is obtained from the following correlation [10, 24, 27]:

$$\lambda_{{\rm eff},R} = \frac{{1 - \varepsilon}}{{1/\lambda _{S} + 1/\lambda ^{o}_{r}}} + \varepsilon \lambda ^{o}_{r}$$
(37)

Where, \(\lambda ^{o}_{r} = 0.690822e\,{\text {d}}_{g} {\left({\frac{{T^{3}}}{{10^{8}}}} \right)}\)

λeff,C which is a function of temperature, gaseous mixture properties, solid properties and pore structure, is obtained from the following correlation with considering that the arrangement of solid matrix and pores is in parallel and series at the same time[1]:

$$\lambda _{{\rm eff},C} = \frac{1}{3}{\left\{{\varepsilon \lambda _{\rm g} + (1 - \varepsilon)\lambda _{\rm S}} \right\}} + \tfrac{2}/{3}{\left\{{\frac{\varepsilon}{{\lambda _{\rm g}}} + \frac{{(1 - \varepsilon)}}{{\lambda _{\rm S}}}} \right\}}^{{- 1}}$$
(38)

Effective heat capacity is also obtained by the following relation:

$$(\rho C_{\rm P})_{{\rm eff}} = \varepsilon (\rho C_{\rm P})_{\rm f} + (1 - \varepsilon)(\rho C_{\rm P})_{\rm S}$$
(39)

4 Numerical solution

Regarding to the complex nature of governing equations including multireaction system, nonlinear kinetics and nonisothermal condition, it requires a numerical method to be employed. So far some schemes like numerical integration [25, 26] and Finite Difference Method (FDM) [5, 8, 35], were used in different studies. However in the case of nonisothermal simulation with using FDM, it took so much computation time [35]. Also sometimes a special skill is needed for reducing computation time that this may distribute some errors in solution results [35]. So the FVM, which has already been established as an effective scheme to model the systems including convection and diffusion is preferred to analyze and handle the present model [18]. To our knowledge the FVM has not yet been applied so much to analyze grain model of noncatalytic multireaction gas–solid in a porous pellet. However Gupta and Saha [11] have already developed a zone model of pseudo steady isothermal FVM solution for the steady conversion of a porous pellet. Also formerly Patisson et al. [21] has applied a FVM method for solution the homogeneous model of porous pellet. But their application is restricted by a single reaction both in the solid matrix and the gas flow.

4.1 Discretization

The governing equations have been discretized by using of the FVM approach as a fully implicit formulation [39]. This method ensures numerical stability and also allows using of large time step which is a desirable feature to deal with reaction problems.

As it is shown in Fig. 2, the solution domain is generally divided into n + 1 equal grid. A control volume is considered around the grid point P with the neighboring grid points W and E in the west and east of the grid respectively. The midpoint of the control volume interfaces are w and e in the west and east respectively. Considering that for boundary grids, I = 2 and I = IN, we have to apply special discritization due to boundary conditions.

Fig. 2
figure 2

Schematic representation of the grids and the control volumes

Full size image

The governing equations are integrated over the control volumes which are shown in Fig. 2 with regard to r from the western face w to the eastern face e and with regard to time from t to t + Δt. Afterward the discrete equations should be rearranged as the following general form:

$$a_{\rm P} \phi _{\rm P} = a_{\rm W} \phi _{\rm W} + a_{\rm E} \phi _{\rm E} + a^{0}_{\rm P} \phi ^{0}_{\rm P} + S_{\rm u}$$
(40)

Where a P is defined as follow

$$a_{P} = a_{W} + a_{E} + a^{0}_{P} - S_{P}$$
(41)

a W , a E , a 0 P , S P and S u are defined as Table 2 for each governing equations.

Table 2 Coefficients of discretized Eq. (40) based on nonisothermal grain intermediate model for multiple reactions
Full size table

Physical and chemical properties on the interfaces of control volumes, e and w, are considered as meaning between two neighborhood control volumes \(\left(\hbox{i.e.}\, {\left(\xi \right)}_{e} = \frac{{{\left(\xi \right)}_{E} + {\left(\xi \right)}_{P}}}{2},\; {\left(\xi \right)}_{w} = \frac{{{\left(\xi \right)}_{W} + {\left(\xi \right)}_{P}}}{2} \right).\)

4.2 Solution methodology

Formerly the governing equations were rendered to set of algebraic equations by discretization based on FVM. These algebraic equations are solved by an iterative method as Tri-Diagonal Matrix Algorithm (TDMA). TDMA is used as it saves computing time and memory space to a great extent. The solution procedure is schematically shown in Fig.  3. To reduce the effect of grid size on the result of model, a set of grid indecency study was established. Then it was found an efficient grid number in the practical size of pellet which is usually applied in the commercial moving bed reactors (6 mm < d p  < 20 mm) is about 100.

Fig. 3
figure 3

The schematic illustration of the flowchart of the model

Full size image

5 The model validation

In order to validate the model estimations, the results are compared with experimental data of iron ore reduction for two cases: the single pellet and the counter-current moving bed of the pellets. The pellet which is contained one or three solid reactants, reacts with a gaseous mixture including one or two reactants.

5.1 Single pellet

In this case, the present model is used to simulate the reduction process of a single reactant pellet which is made of wustite (FeO), a form of iron oxide, with a mixture of hydrogen and water vapor as following reaction:

$$\hbox{FeO}_{({\rm s})} + \hbox{H}_{2({\rm g})} \to \hbox{Fe}_{({\rm s})} + \hbox{H}_{2} \hbox{O}_{({\rm g})}$$
(42)

The experimental results reported by Usui et al. [35] have been used for validation of model estimations. Figure 4 shows a comparison between experimentally measurements and numerically predicted overall conversion for hydrogen as a reactant agent. It has been shown that there is reasonable agreement between the model predictions and the experiments. A comparison between the model assessments and the analytical solutions of wustite conversion has been illustrated in Fig. 5. It has been obviously shown that the numerical solution based on FVM is considerably agreement with the analytical solution.

Fig. 4
figure 4

Comparison of the model estimations with the experimental data [35] for wustite conversion (d P  = 13 mm, ɛ = 0.49, T b = 1173 K)

Full size image
Fig. 5
figure 5

Comparison of the model results with the analytical solution of wustite pellet conversion. (d P  = 13 mm, ɛ = 0.44, T b = 1173 K)

Full size image

In this case the modeling has also been done to simulate the reduction of hematite (Fe2 O3) pellet to iron using a gaseous mixture of hydrogen and carbon monoxide. During the hematite reduction, a set of noncatalytic reactions (i.e. conversion hematite to magnetite, magnetite to wustite and wustite to iron) are observed which are taken place simultaneously as the following reactions:

$$3\hbox{Fe}_{2} \hbox{O}_{3} + \hbox{H}_{2} \to 2\hbox{Fe}_{3} \hbox{O}_{4} + \hbox{H}_{2} \hbox{O}$$
(43)
$$\hbox{Fe}_{3} \hbox{O}_{4} + \hbox{H}_{2} \to 3\hbox{FeO} + \hbox{H}_{2} \hbox{O}$$
(44)
$$\hbox{FeO} + \hbox{H}_{2} \to \hbox{Fe} + \hbox{H}_{2} \hbox{O}$$
(45)
$$3\hbox{Fe}_{2} \hbox{O}_{3} + \hbox{CO} \to 2\hbox{Fe}_{3} \hbox{O}_{4} + \hbox{CO}_{2}$$
(46)
$$\hbox{Fe}_{3} \hbox{O}_{4} + \hbox{CO} \to 3\hbox{FeO} + \hbox{CO}_{2}$$
(47)
$$\hbox{FeO} + \hbox{CO} \to \hbox{Fe} + \hbox{CO}_{2}$$
(48)

The published experimental data by Towhidi and Szekely [33] for overall conversion have been used to validate the model prediction results for overall conversion rate. Figure 6 illustrates conversion rate of each solid component separately with overall conversion rate. A comparison between model estimation and experimental results of overall conversion shows that the model can considerably reproduce the experimental data.

Fig. 6
figure 6

Comparison of the model predictions and the experimental data [33] for the reduction of hematite to iron in a mixture of hydrogen and carbon monoxide \(\left(\frac{{{\hbox {H}}_{2}}}{{{\hbox {CO}}}} = \frac{{75}}{{25}}, d_{P} = 15.2\,{\rm mm}, \varepsilon = 0.15, T^{b} = 1173\,{\rm K} \right)\)

Full size image

5.2 Moving bed

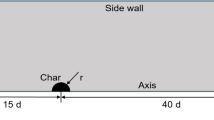
The reduction of hematite pellet (Fe2O3) in a scale model of moving packed bed, as a multireactant case, has been investigated and the model results have been validated. A schematic of the configuration of the bed has been illustrated in Fig. 1. The pellets are continuously charged from top of the bed and are descended alongside the bed with closely uniform velocity due to gravity. Conversely, a hot gaseous mixture including CO, CO2, H2, and H2O is admitted to the lower section of bed comes into contact with the pellets and is counter-currently ascended in the bed. The pellets are gradually heated and reduced to iron as the reactions (43, 44, 45, 46, 47, 48). A one dimensional model including overall mass and energy balances has been used for estimating the longitudinal (z direction) profile of temperature and concentration of gaseous reactants.

In this case, the experimental results reported by Takenaka et al. [32], have been used for validation of the model. As it has been shown in Fig. 7, the results of the present model for overall conversion rate and the experimental data are agreeable whitin the acceptable margin of error.

Fig. 7
figure 7

Comparing the model prediction with the experimental results in case of the moving bed reactor \(\left({\hbox {H}}_{2}/{\hbox {CO}} = 1.41,{\hbox {H}}_{2} + {\hbox{CO}}/{\hbox {CO}}_{2} + {\hbox{H}}_{2} {\hbox {O}} = 15,Q_{g} = 103\,{\hbox {Nm}}^{3}/{\hbox {h}}, \dot{m}_{p} = 51\,{\hbox {kg/h}} \right)\)

Full size image

6 Conclusions

A mathematical model has been developed for investigation of a multireaction treatment of a porous pellet. It is a specimen of a moving packed bed which is immersed in a mixture of multicomponent gas mixture. It takes into account the external mass transfer; the internal diffusion transport through the pores; the chemical reactions; the heat generation or consumption by reactions and its transport by the effective conduction in all over the solid matrix. This model is comprehensive and easy to applicable to modeling of the multireactant systems both in solid phase and in the gas phase. A grain model has been used to mathematically representation of the reactions which are take place in the solid interfaces. The implicit FVM as a powerful scheme has been implemented and verified for solving the governing equation. The model has been validated with the experimental data for two cases: the single pellet and the moving bed. In the single pellet scale the model has been carried out to simulate a pellet containing one of a single reactant which is reacted by a single gaseous reactant. Besides, it has been used to simulate the pellet containing of three reactants which are simultaneously reacted with two reactants gaseous mixture. It was found that the results of model and the published experimental data are considerably agreeable. In the moving bed scale, modeling has been carried out to simulate a solid matrix including three reactants which are simultaneously reacted with a gaseous mixture containing of two reactants. It has been shown that the model can significantly reproduce the experimental data. Considerably agreement among the model predictions and the experimental and analytical data implies that the FVM is a powerful technique for numerical solution of gas–solid reaction models, however according to the literature this approach has rarely been used in the previous studies.