Experimental validation of heat transfer models for flow through a porous medium

Abstract

Unsteady heat transfer in a fluid saturated porous medium contained in a tube is studied. The porous medium is a bed of uniform diameter spheres, made of glass or steel, while the flowing fluid is water. The flow field is time invariant in the simulation as well as experiments. Step response of the bed when the temperature of the incoming water is suddenly increased, and oscillatory response when hot and cold fluids alternately flow through the tube are studied. Heat transfer models are based on thermal equilibrium between the fluid and the solid phase (one-equation) and thermal non-equilibrium (two-equation) between the two phases. The predictions of these models are compared against experiments conducted in a laboratory-scale apparatus. The comparison is in terms of time evolution of temperature profiles at selected points in the bed, as well as global properties of the temperature distribution such as attenuation and phase lag with respect to the boundary perturbations. The range of Peclet numbers considered in the study is 500–4,000, for which the flow can be considered laminar. Results show that the predictions of the two-equation model are uniformly superior to the one-equation model over the range of Peclet numbers studied. The differences among the three approaches diminish when the thermophysical properties of the solid and fluid phases are close to one another. The differences also reduce in the step response test as steady state is approached.

1 Introduction

Fluid flow and transport in porous media have received considerable attention owing to a large number of related engineering applications. Examples are thermal energy storage systems, regenerators in Stirling cycles, enhancement of cooling of electrical and electronic components, automobile catalytic reactors and geothermal reservoirs. Mathematical models of fluid flow and heat transfer have been extensively studied in the literature. In the context of heat transfer, a fundamental approximation often employed in modeling is that of local thermal equilibrium between the fluid and the solid phases at every instant of time. Depending on the nature of the transient process and the thermophysical properties of the individual phases, the phase temperatures can be different. In such an application, it is necessary to represent correctly the exchange of thermal energy between the solid and fluid media. In applications such as regenerators and thermal energy storage in underground reservoirs, the transport process is inherently unsteady (though periodic). The performance of the device depends on the degree of non-equilibrium between the fluid and the solid phases. The approximation of thermal equilibrium is not valid for these processes. The validation of equilibrium and non-equilibrium models against laboratory-scale, step and oscillatory flow experiments is reported in the present study.

Vafai and Sozen [1] numerically investigated forced convective heat transfer for gas flow in a packed bed allowing for thermal non-equilibrium between fluid and solid phases. Their studies indicate that the local thermal equilibrium condition is sensitive to particle Reynolds number and Darcy number. Amiri and Vafai [2] performed a comprehensive numerical analysis of various effects in a flow field on forced convection heat transfer through porous medium. These include inertia, dispersion, variable porosity and boundary effects, validity of local thermal equilibrium and two-dimensionality. The mathematical model for energy transfer was based upon thermal non-equilibrium between fluid and solid phase. Most studies deals with a steady flow field in which a step change in temperature is introduced at one of the boundaries and the thermal field evolves towards a steady state. Transport processes in oscillatory flow have also been reported in the literature. Peak et al. [3] studied experimentally the transient cool-down of a porous medium in pulsating flow of air, wherein an oscillating component of velocity is added to the time-averaged flow. Results show that there is minor effect on the temperature field when the pulsation amplitude is so small that no reverse flow is induced. When the pulsation amplitude is greater than unity, its effect on temperature field is large in such a way that the temperature–time curve becomes less steep. The amplitude of temperature oscillations decreases with distance from the inflow plane. The heat transfer rate from the solid phase of the porous medium to the fluid medium decreases with decreasing frequency. Muralidhar and Suzuki [4] analyzed numerically the pulsating flow of gas within a regenerator made from mesh screens. The metallic mesh was modeled as a non-Darcy porous medium in which heat transfer takes place under thermal non-equilibrium conditions. The fully developed unsteady flow field was solved by a harmonic analysis technique. The resulting friction factor and regenerator effectiveness were also calculated. Fu et al. [5] studied heat transfer from the wall of a heated porous channel to the fluid medium experimentally when subjected to both steady and oscillatory flow. The length-averaged Nusselt number for oscillating flow was higher than that for steady flow. Hence, a porous channel subjected to oscillatory flow was found to be a superior method of cooling. Wong et al. [6] studied numerically the consequences of local thermal equilibrium in forced convection past a heated cylinder embedded in a porous medium. Under thermal non-equilibrium conditions, the thermal fronts in the fluid and solid phases were found to have distinct speeds.

A survey of the literature shows that under identical flow conditions, a direct comparison of one- and two-equation models of heat transfer in a porous medium has not been reported. In this context, the present study deals with convective heat transfer in a porous medium contained in a tube. The fluid medium is water, while spherical glass and steel beads have been used for the solid phase. The equilibrium and non-equilibrium models have been compared under transient conditions arising from a step change in temperature and in oscillatory flow. In the second configuration, hot and cold flows enter the tube at one of its ends and pass through the porous medium for half a time period each. The differential equations arising from the mathematical models have been numerically solved. Experiments that represent the above flow configurations have been conducted over a range of flow rates and temperature differences. The comparison between simulation and experiments is in terms of temperature distribution, front speed, phase differences and attenuation in the temperature amplitude.

2 Mathematical model

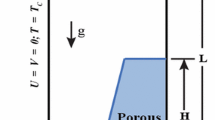
A model of heat transfer for flow in a saturated porous medium is first presented. The model is implemented with boundary conditions that include a step increase in temperature and hot/cold fluid alternately flowing through the porous region in a given direction. For definiteness, the porous bed is composed of spherical particles of uniform diameter. It is taken to be homogeneous and isotropic. This approximation requires that the bead diameter is sufficiently smaller than the tube diameter so that wall effects (such as channeling) are not significant. The tube length is much larger than its diameter so that flow development effects are negligible. The fully developed velocity profile in a homogeneous isotropic porous medium confined to a tube is simply a uniform distribution, equal to the average fluid speed. The porous region analyzed in the present work is shown in Fig. 1a along with the cylindrical coordinate system. In a step response study, the bed is saturated at all times and is initially at the cold (ambient) temperature. At times greater than zero, the inflow temperature increases to a new value. The interest then is in the propagation of a thermal front in the porous medium. In the oscillatory flow experiment, hot water enters the tube from the left side for half a cycle, while cold water enters the tube from the same side for the remaining half cycle. The velocity of the fluid medium is spatially constant at all instants of time.

Fig. 1

a Physical model and coordinate system, b step response, c oscillatory response

The one- and two-equation models of heat transfer in a porous medium are presented below. The one-equation model assumes that the fluid and solid phases are locally at identical temperatures at every instant of time. This approximation leads to an equation that is similar to the advection–diffusion equation for energy transport in a homogeneous fluid [7]. The fact that heat capacity effects are associated with both solid and fluid phases, while convection effects arise from fluid velocity alone is reflected in the governing equation. In contrast, the two-equation model assigns individual temperatures to the two phases and permits inter-phase heat transfer between them. The material properties appearing in the two-equation model are those of the individual phases and not the porous region as a whole. The model is thus capable of permitting thermal non-equilibrium between the solid spheres and the flowing fluid. The derivation of the two-equation model has been discussed in [7, 8], while it has been used for analysis in [1–4, 8]. The governing equations in dimensional form are first presented below.

One-equation model

$${({\rho C_{{\rm p}}})}_{{\rm m}} \frac{{\partial T}}{{\partial t}} + {({\rho C_{{\rm p}}})}_{{\rm f}} u \frac{{\partial T}}{{\partial r}} = \frac{\partial}{{\partial r}}{\left({{\left({{{k}}_{{{{\rm eff,m}}}}} \right)}_{z} \frac{{\partial {\text{T}}}}{{\partial z}}} \right)} + \frac{1}{r}\frac{\partial}{{\partial r}}{\left({{\left({{{k}}_{{{\rm eff,m}}}} \right)}_{r} r \frac{{\partial {\text{T}}}}{{\partial r}}} \right)}.$$

(1)

Two-equation model

$${{\rm Fluid}}: \quad \varepsilon {({\rho C_{{\rm p}}})}_{{\rm f}} {\left({\frac{{\partial T}}{{\partial t}} + \frac{u}{\varepsilon}\frac{{\partial T}}{{\partial z}}} \right)} = \frac{\partial}{{\partial z}}{\left({{\left({k_{{\rm eff,f}}} \right)}_{z} \frac{{\partial T}}{{\partial z}}} \right)} + \frac{1}{r}\frac{\partial}{{\partial r}}{\left({{\left({k_{{\rm eff,f}}} \right)}_{r} r\frac{{\partial T}}{{\partial r}}} \right)} + Q_{{{\rm f} \leftarrow {\rm s}}},$$

(2)

$${{\rm Solid}}: \quad {({1 - \varepsilon})}{({\rho C_{{\rm p}}})}_{{\rm s}} \frac{{\partial T}}{{\partial t}} = \frac{\partial}{{\partial z}}{\left({{({k_{{\rm eff,s}}})}\frac{{\partial T}}{{\partial z}}} \right)} + \frac{1}{r}\frac{\partial}{{\partial r}}{\left({{({k_{{\rm eff,s}}})}\, r\frac{{\partial T}}{{\partial r}}} \right)} + Q_{{{\rm f} \to {\rm s}}}.$$

(3)

In the energy equations above, $Q_{{{\rm f} \to {\rm s}}}$ refers to the heat transfer from the fluid to solid phase ( $Q_{{{\rm f} \leftarrow {\rm s}}}$ being equal and opposite in sign to $Q_{{{\rm f} \to {\rm s}}}$)and is evaluated in terms of the heat transfer coefficient as:

$$Q_{{{\rm f} \to {\rm s}}} = h A _{{\rm IF}}(T_{{\rm f}}- T_{{\rm s}}).$$

(4)

Here, A _IF is the interfacial area between the fluid and the solid phases per unit volume of the porous medium.

The formulation presented below is in dimensionless form, with T representing the dimensionless temperature (T − T _C)/(T _H−T _C), whose value is between zero and unity. The length scale is the tube radius R and the time scale is R ² / α. The velocity u appearing in the equations below is the Darcian velocity, namely the velocity obtained by locally averaging the energy equation over a small volume of the porous medium. The governing equations are stated below as follows:

One-equation model

$$\frac{{{1}}}{{{{Pe \, \beta }}_{{{\rm m}}}}}\frac{{\partial {{T}}}}{{\partial {{t}}}} + {{u}}\frac{{\partial {{T}}}}{{\partial z}} = \frac{{{1}}}{{{{Pe}}}}{\left({\frac{\partial}{{\partial z}}{\left({{\left[{\frac{{{\left({{{k}}_{{{{\rm eff,m}}}}} \right)}_{z}}}{{{{k}}_{{{\rm f}}}}}} \right]}\frac{{\partial {{T}}}}{{\partial z}}} \right)} + \frac{1}{r}\frac{\partial}{{\partial r}}{\left({{\left[{\frac{{{\left({{{k}}_{{{{\rm eff,m}}}}} \right)}_{r}}}{{{{k}}_{{{\rm f}}}}}} \right]}r\frac{{\partial {{T}}}}{{\partial r}}} \right)}} \right)}.$$

(5)

Two-equation model

$$\begin{aligned} & {{\rm Fluid}} : \quad \varepsilon {\left({\frac{1}{{Pe}}\frac{{\partial T}}{{\partial t}} + \frac{u}{\varepsilon}\frac{{\partial T}}{{\partial z}}} \right)} = \frac{1}{{Pe}}{\left({\frac{\partial}{{\partial z}}{\left({{\left[{\frac{{{\left({k_{{\rm eff,f}}} \right)}_{z}}}{{k_{{\rm f}}}}} \right]}\frac{{\partial T}}{{\partial z}}} \right)} + \frac{1}{r}\frac{\partial}{{\partial r}}{\left({{\left[{\frac{{{({k_{{\rm eff,f}}})}_{r}}}{{k_{{\rm f}}}}} \right]}r\frac{{\partial T}}{{\partial r}}} \right)}} \right)} \\ & \, - \frac{{NuA_{{\rm f}}}}{{Pe}}{\left({T_{{\rm f}} - T_{{\rm s}}} \right)}, \\ \end{aligned}$$

(6)

$${{\rm Solid}} : \quad \frac{{{({1 - \varepsilon})}}}{{Pe}}\frac{{\partial T}}{{\partial t}} = \frac{{\beta / \lambda }}{{Pe}}{\left({\frac{\partial}{{\partial z}}{\left({{\left[{\frac{{k_{{\rm eff,s}}}}{{k_{{\rm s}}}}} \right]}\frac{{\partial T}}{{\partial z}}} \right)} + \frac{1}{r}\frac{\partial}{{\partial r}}{\left({{\left[{\frac{{k_{{\rm eff,s}}}}{{k_{{\rm s}}}}} \right]}r\frac{\partial}{{\partial r}}} \right)}} \right)} + \frac{{Nu\,A_{{\rm f}} \beta}}{{Pe}}{({T_{{\rm f}} - T_{{\rm s}}})}.$$

(7)

The thermal conductivities in the one- and two-equation models are corrected for dispersion effects as follows [9, 10]:

$${{\rm Longitudinal}} : \quad ({k_{{\rm eff,f}}})_{z} = \varepsilon k_{{\rm f}} + 0.5 Pe \, k_{{\rm f}},$$

(8)

$${{\rm Transverse}} : \quad ({k_{{\rm eff,f}}})_{r} = \varepsilon k_{{\rm f}} + 0.1 Pe \, k_{{\rm f}}.$$

(9)

The following expression has been used for Nusselt number that represents solid-to-fluid heat transfer [9, 10]:

$$Nu_{{\rm p}} = 2 + 1.1 {Pr}^{0.33} {Re}_{{\rm p}}^{0.6}.$$

(10)

In Eq. 10, the non-dimensional parameters Nu _p and Re _p are defined on the basis of the particle diameter d _p. In Eqs. 6 and 7, these are expressed in terms of the tube radius. The correlation is valid for steady flow conditions. In the present study, it has been taken to be applicable for unsteady conditions as well, with heat transfer being driven by the instantaneous temperature difference between the solid and the fluid media. The specific surface area of the porous bed composed of spheres is given as [7]:

$$A_{{\rm f}} = \frac{{6{({1 - \varepsilon})}R}}{{d_{{\rm p}}}}.$$

(11)

The governing equations subjected to suitable initial and boundary conditions are numerically solved. An implicit finite difference method has been utilized. The QUICK approach [11] is used to approximate the (first order) convective terms, while central differencing scheme is used for the second order partial derivatives. A forward difference formula evaluates the time derivatives. Gauss-Seidel iterations are used to solve the system of algebraic equations. Time steps and space grids are chosen such that the results obtained are independent of number of time steps and nodes. Typically, the time step is 0.01% of the total time and grid size is 0.1% of the total length of the porous region. The numerical algorithm used is quite similar to the one described in [4]. It has been further validated against analytical solutions available in the literature.

2.1 Initial and boundary conditions

In the problem analyzed, the porous bed is initially saturated with water at room temperature that also serves as the minimum temperature at any point in the porous medium during the experiment. This statement can be expressed in dimensionless form as:

$$T({z,r,t})= 0, \quad 0 < z < L, \quad {\rm for} \; t \leqslant 0.$$

(12)

The boundary condition for step response simulation is that hot water is introduced through the inlet plane for all times. Hence

$$T {({0, r, t})} = 1, \quad {\rm for} \; t > 0.$$

(13)

For oscillatory response simulation, hot and cold water flow for half of the time period each through the inflow plane. Hence

$$\begin{aligned}T{({0,r,t})} &= 1, \quad {\rm for} \; 0 < t \leqslant {({t_{{\rm p}}/2})}, \\ T {({0,r,t})} &= 0, \quad {\rm for} \; {({t_{{\rm p}}/2})} < t \leqslant t_{{\rm p}}.\\ \end{aligned}$$

(14)

At the far field, the zero gradient outflow boundary condition is applied for fluid and solid phases as follows:

$${\left({\frac{\partial T}{\partial z}}\right)}_{{z = L}}=0.$$

(15)

The boundary condition at the tube wall is a heat loss condition in terms of Biot number and is given for fluid and solid phase as:

$$ - {\left({\frac{{\partial T_{{\rm f}}}}{{\partial r}}} \right)}_{{r = 1}} = \frac{{Bi}}{\lambda}{\left({{({T_{{\rm f}}})}_{{r = 1}} - T_{{\rm a}}} \right)},$$

(16)

$$ - {\left({\frac{{\partial T_{{\rm s}}}}{{\partial r}}} \right)}_{{r = 1}} = Bi{\left({{({T_{{\rm s}}})}_{{r = 1}} - T_{{\rm a}}} \right)}.$$

(17)

For an adiabatic wall, Biot number is set to zero. In addition, the sensitivity of the temperature distribution to Biot number has been studied. The above-stated initial and boundary conditions carry over unchanged to the two-equation model in terms of the individual phase temperatures.

For the experimental conditions described in Section 3, various parameters appearing in the calculations for glass and steel–water beds, respectively, are as follows: porosity ɛ=0.37 and 0.4; particle diameter d _p=2.25 and 4.76 mm; specific area of pore surface A _IF=48.7 and 21.9. Pipe radius R for both the beds is 29 mm. The length of the bed L for glass–water bed is 25R and for steel–water is 16R. The cold water temperature corresponds to the ambient conditions and hot water temperature is set 10–15 K higher than the cold temperature. Peclet number varies in glass–water bed from 500 to 1,600 and for steel–water bed from 800 to 3,000. The average velocity of flow in the tube realized in the experiments varied from 0.25 to 1.5 cm s⁻¹. The Biot number in experiments is estimated by matching maximum temperature obtained with numerical results under identical conditions. Table 1 gives the thermophysical properties of glass and steel used in the analysis.

Table 1 Thermophysical properties of glass and steel spheres

The following thermophysical properties of water at 300 K have been used for calculations: ρ=995.7 kg m⁻³, C _p=4,178 J (kg K)⁻¹, k=0.61 W (m K)⁻¹, ν=0.00802 cm² s⁻¹, α=0.00146 cm² s⁻¹ and Pr=5.46. Hence the thermal capacity ratio is β=2.2 (water–glass) and 1.1 (water–steel), the thermal conductivity ratio is λ=0.56 (water–glass) and 0.04 (water–steel).

3 Experiments

In order to validate the mathematical models, the experimental set up is fabricated as shown in Fig. 2. The test section is of diameter D=58 mm while the length L=725 and 465 mm, respectively, for glass–water and steel–water beds. The length given here excludes the extra sections added for flow development on the inlet side and for exit. The test section is insulated at the tube boundary. The solid phase of the porous bed consists of glass spheres of diameter (d _p) 2.25 mm and steel spheres of diameter 4.76 mm.

Fig. 2

Schematic drawing of the experimental set up

The spherical particles are closely packed in a PVC pipe and mesh screens are placed at both the ends. The pipe to particle diameter ratios are 12 and 25, respectively, for steel and glass–water beds. This being quite large, wall effects can be neglected and the flow can be regarded as essentially one-dimensional. The fluid temperatures are measured along the centerline of the test section. K-type thermocouples of 0.32 mm diameter wire (bead diameter 0.62 mm) have been employed. Each thermocouple is passed through a 1 mm diameter copper sheath and introduced at the centre plane. The dimensions involved are quite small, with estimate time constant in the range of 10–100 ms. Since the time scales in experiments are of the order of 1 h (step response) and 10–200 s (oscillatory response), transient effects associated with the thermocouple itself are expected to be negligible for the present work.

In order to supply hot water to the bed, a constant temperature bath is utilized. The bath is regulated by a PID type controller with a temperature resolution of 0.1°C. After a sufficiently long period of time, water reaches a constant temperature under flow conditions, and water is supplied to the bed. In oscillatory flow experiments, an electronic timer actuates solenoid valves so that hot and cold water is alternately supplied to the bed. The output of the thermocouples is measured via a data acquisition card (National Instruments) and processed in a PC (Zenith) afterwards. All the electrical instruments are carefully grounded to remove stray voltages that can adversely affect the thermocouple readings.

4 Results and discussion

Results are presented for a step change as well as pulsatile variation in fluid temperature at the inflow plane of the tube. The inflow temperature condition in simulation has been taken as the reading of the first thermocouple in the experimental apparatus. This approach eliminates flow development effects in the experimental apparatus. Temperatures as measured in experiments at selected locations along the tube axis and the predictions of the one- and two-equation models have been compared. The sensitivity of the model predictions to wall heat transfer has been studied. Other quantities of interest are the front speed and the spread of the thermal front as a function of axial position within the tube.

4.1 Step response of the porous medium

Figure 3 shows the temperature distribution measured as a function of time at various points in the porous bed when it is subjected to step response. Figure 3a, b shows the temperature distribution for glass–water bed while Fig. 3c, d shows temperature variation for the steel–water bed. Temperatures at various locations are plotted at two distinct Peclet numbers for each bed. The location, z=0 in each of the figures refers to the first thermocouple closest to the inflow plane of the test section. Figure 3 shows that temperature at a given location increases with time and subsequently reaches a steady state. Over the distance covered, the steady state temperature is less than unity at the lower Peclet numbers of 915 and 961, while it approaches unity at higher Peclet numbers of 1,615 and 2,190.

Fig. 3

Experimental record of step response of porous bed: a, b glass–water bed, c, d steel–water bed

Figure 4 compares the temperature variation recorded in step response experiments with the one- and two-equation models. The glass–water bed is first considered. Figure 4a shows the comparison when Biot number for numerical models is set to zero. The Biot number is 1 in Fig. 4b. At the location z=0, the inflow condition of one- and two-equation models are matched with experimental data using curve fitting. In Fig. 4a, the numerical profiles match well the experimental profile at z=11. At a downstream point of z=22 the individual difference between the models and experiments increases but the overall trends are similar to those at z=11. The one-equation model predicts a faster increase in temperature when compared to the two-equation model. This could because of the absence of inter-phase heat transfer in the one-equation model. In Fig. 4b, with an increase in Biot number to unity, the match improves but the steady state temperatures predicted by numerical results fall at downstream locations.

Fig. 4

Step response: variation of temperature with time in experiments, one- and two-equation model for glass–water bed. a Bi=0, b Bi=1

Figure 5 compares temperature variations recorded in experiments with the one- and two-equation models. The porous bed comprises spherical balls of steel and water. In Fig. 5a, Biot number for numerical models is zero while it is 0.05 in Fig. 5b. At a location z=0, one- and two-equation model profiles are again matched with experimental profile using curve fitting. In Fig. 5a, the two-equation model predicts a good match with experiments at locations z=5 and 10; though the one-equation model profile is quite similar to experimental profile but its slope is distinct from the experiments. In general, the numerical profiles are close to experiments at zero Biot number. In Fig. 5b, a Biot number of 0.05 improves the match of the two-equation model with experiments, whereas the one-equation model fails to predict meaningfully the experimental temperature profile. The one-equation model totally fails to predict the experimental profiles at non-zero Biot number for steel–water bed. However, Figures 4 and 5 do provide qualitative validation of the numerical models with experiments.

Fig. 5

Step response: variation of temperature with time in experiments, one- and two-equation model for steel–water bed. a Bi=0, b Bi=0.05

4.2 Front speed and spread

In order to compare the numerical simulation closely with experimental results, quantities such as front speed and front spread have been employed. These are defined as:

Front speed

It is the ratio of the spatial distance (Z) between the two locations divided by the time difference Δ τ for the dimensionless temperature to reach 0.5 at each location. In non-dimensional form, the front speed is given as:

$${{\rm Front\,speed}} = \frac{1}{{Pe}}{\left({\frac{Z}{{\Delta \tau}}} \right)}.$$

(18)

In experiments, the front speed is calculated with data recorded by thermocouples that are spaced apart. In numerical simulation, the separation is set equal to the experimentally set spacing.

Front spread

It is the time taken for the dimensionless fluid temperature to rise from 0.25 to 0.75 at a particular location.

The front speed and front spread for the glass–water and steel–water beds are presented in the following section.

4.2.1 Glass–water bed

Figures 6 and 7, respectively, give the front speed and front spread for the step response experiments along with the results of the one- and two-equation models. The results are presented for various Peclet numbers. Since the front speed is calculated from front displacement between two points, the value of z-coordinate in Fig. 6 is chosen to be their mid-point. The front speed in a porous bed is a weak function of Peclet number, but a stronger function of dispersion, heat loss to the atmosphere and the thermal properties of fluid and solid phases. In general, higher the heat loss, lower is the front speed. The front spread is indicative of dispersion and decreases with an increase in Peclet number.

Fig. 6

Step response: front speed in glass–water experiments, one- and two-equation model

Fig. 7

Step response: spread of front in glass–water experiments, one- and two-equation model

The front speed is seen to be smaller in experiments when compared to simulation (Fig. 6). The model predictions are sensitive to Biot number. The two-equation model predicts values closer to experiments, in particular at the higher Peclet number. The front spread in experiments is seen to be quite close when compared to the numerical models (Fig. 7). Once again, the effect of Biot number is seen. The predictions of the two-equation model are marginally superior to the one-equation model, in particular at higher Peclet numbers. At a Peclet number of 1,615 in Figs. 6c and 7c, the front speed and spread are reasonably close to the numerical values. The one-equation model assumes a homogeneous single phase, and therefore has no interphase heat transfer present. As interphase heat transfer between the fluid and the solid slows the front movement, the one-equation model predicts a higher front speed when compared to the two-equation model. The difference decreases with an increase in Peclet number, Fig. 6, indicating a higher contribution of interphase heat transfer at lower Peclet numbers. The dependence of the front speed and spread on Biot number is brought out in Figs. 6 and 7. At a lower Peclet number, the front spread increases with an increase in Biot number while the front speed decreases. At higher Peclet numbers, the effect of an increase in Biot number upon front speed and spread is smaller. Thus, dispersion and heat loss effects are cumulative with distance from the inflow plane.

4.2.2 Steel–water bed

The steel–water bed differs from a glass–water bed since the solid phase has a higher thermal conductivity and a higher thermal diffusivity as compared to water. As a result, a hot pulse moving with the liquid will diffuse into the solid phase and will experience a fall in speed with distance. A second factor affecting fluid speed is the appearance of an independent diffusion path within the solid phase that in turn transfers thermal energy back to the fluid. Figure 8 shows the front speed for step response of the steel–water bed in experiments and simulation using one- and two-equation models. The results of one-equation model being excessively sensitive to Biot number, are subsequently only shown for zero Biot number. At a lower Peclet number (Pe=545), diffusive transport within the solid phase itself is important and there is a possibility of front speed increasing with distance, Fig. 8a. At higher Peclet numbers, where advective transport of energy dominates diffusive transport, the effect of higher thermal diffusivity of the solid phase is to lower the front speed with distance, Fig. 8b, c. The two-equation model follows these trends, though the increase and reduction of front speed with distance is slight for zero Biot number. The sensitivity to Biot number is seen. The predictions of one-equation model are also in conformity to experiments, and the match is seen to be closer to experiments. The predicted values are seen to be sensitive to the choice of Biot number, with Bi=0.05 resulting in a great reduction in the front speed.

Fig. 8

Step response: front speed in steel–water experiments, one- and two-equation model

The data on spread of the thermal front as determined from experiments and models are compared in Fig. 9. The front spread predictions of the two-equation model are seen here to be quite close to experiments. The two-equation model does not show excessive sensitivity to Biot number. On the other hand, the predictions of the one-equation model are poor at a Biot number of zero; they deteriorate excessively with an increase in Biot number.

Fig. 9

Step response: spread of front in steel–water experiments, one- and two-equation model

The anomalous behavior of the one-equation model can be explained in terms of the effective medium properties employed. The model accounts for energy storativity in the fluid as well as the solid phases, while advection is present in the liquid phase. It uses an effective thermal conductivity as a weighted mean the solid and liquid phases, being quite large for the steel–water system. The larger effective thermal conductivity results in a higher dispersion coefficient and hence a large spread of the thermal front. It also reflects a lowered internal conduction resistance with respect to heat losses to the ambient. Since Biot number is defined in terms of this conductivity, even a small value of Bi indicates large loss heat losses. In the two-equation model, the properties used are those of the individual phases. The phase energy equations are linked through the interphase Nusselt number that in turn depends on Peclet number. Thus, the two-equation model, while predicting the direction of heat transfer between phases correctly, is not excessively sensitive to the disparity of their thermophysical properties.

4.2.3 Thermal non-equilibrium

Thermal non-equilibrium conditions between the fluid and solid phase is dominant during transient heating and cooling of the porous bed. At steady state, the energy exchange is zero and consequently the one-equation model can be used to predict the temperature field in the porous region. The two-equation model can predict the individual temperatures of fluid and solid phases during steady as well transient processes. The degree of non-equilibrium can be calculated in a step response test, in terms of the percentage temperature difference between the fluid and solid phases with respect to the maximum temperature change applied to the porous bed. The estimates given below are from numerical simulation. Thermal non-equilibrium in a glass–water bed at Peclet numbers of the order of 100 was less than 0.4%. It decreased with distance from inflow plane and fell to 0.1% at locations around z=30. With an increase in Peclet number, the extent of thermal non-equilibrium was found to increase. At a Peclet number of 5,000, the temperature difference between the two phases rose to 4.1% at points near inlet plane. At points away from the inlet plane, for example, z=30, it fell to 1.4%. The degree of non-equilibrium can be related to relative importance of thermal resistance to inter-phase heat transfer with respect to thermal resistances within the individual phases. Referring to Eq. 6, the inter-phase to convective resistance in the liquid is seen to be proportional to Pe / (Nu × A _f). It has a lower value at low Peclet numbers, so that interphase heat transfer is (relatively) higher and the resulting temperature difference is small. At a higher Peclet number, energy transport occurs preferentially within the liquid, heat transfer to the solid phase is delayed and a greater degree of thermal equilibrium is obtained.

When the solid phase (such as steel) has a high thermal conductivity, a diffusion path separately established in the solid phase is important. The speed of front movement in the solid phase is closer to that in the liquid at low Peclet numbers and interphase heat transfer is not important. Hence, conditions closer to thermal equilibrium are realized. At a low Peclet number of 100, temperature differences are around 0.4% at locations near the inflow plane and fall to 0.2% at downstream locations. In contrast, at a Peclet number of 5,000, the front speed in the liquid is higher and non-equilibrium is again highlighted. The respective values of thermal non-equilibrium at locations closer to the inflow plane and far downstream were found to be 4.9 and 1.6%.

4.3 Oscillatory response of the porous medium

In oscillatory flow, the boundary conditions at the inflow plane change periodically from hot to cold temperatures. The hot fluid gives energy to the cold domain during the first half and the cold fluid retrieves energy from the heated domain in the second half. The total time taken for the passage of one hot and one cold pulse is the time period (t _p). The corresponding frequency is ω=2 π / t _p (rad s⁻¹). Since the thermophysical properties have been taken constant, the heat exchange process in the porous medium is linear. Therefore, the oscillatory response of the porous medium occurs at the same frequency as the inflow pulsation. It comprises temperature maxima and minima at downstream points with a phase lag, both of which are functions of frequency.

The response of the porous bed is characterized in terms of the amplitude [namely, half the separation of the maximum and minimum (dimensionless) temperatures at a point] and phase lag (ϕ). The latter is defined as the average time elapsed between successive peaks or valleys (expressed in terms of an angle). In a conduction-dominated transport process, the phase lag increases as the square root of distance from the inflow plane. Using this result, phase lag has been non-dimensionalized by the multiplicative factor ${\sqrt{2 \alpha_{{\rm f}} / {\omega}}}\,(1/z)$. In addition, one can introduce a reference frequency for each experiment in terms of the time period required for the hot and cold pulses to travel the entire length of the bed while moving with the average fluid speed. The dimensionless reference frequency is given as

$$\omega_{{\rm ref}} = \pi R\,Pe/L.$$

(19)

Here R and L are radius of the tube and its length.

Figure 10 shows the experimentally recorded oscillatory response of a glass–water bed at various Peclet numbers and frequencies. The reference frequencies are separately given. Figure 10a shows the oscillatory response at a Peclet number of 948 and a pulsing of frequency of 0.022 rad s⁻¹. Hot and cold water flow alternately at z=0. During the time period, the temperature at z=0 varies from a value close to zero to a value of near unity for the hot phase and falls to the initial value at the end of cold half phase. The inflow amplitude of temperature is 0.5. The oscillatory responses at locations z=11 and 22 are shown in Fig. 10. It is interesting to compare the frequency with the reference frequency at this Peclet number. The comparison estimates whether hot/cold water will reach the end of the bed within half of the time period. The reference frequency for the flow rate in Fig. 10 is 0.021 rad s⁻¹. Thus, adequate time is available to heat and cool portions of the porous medium in such a way that they reach their respective maximum and minimum temperatures. Figure 10 shows that the maximum temperature obtained at z=11 is slightly smaller than at z=0 and the minimum temperature is slightly higher. Consequently, there is a fall in temperature amplitude with distance. The amplitude attenuates further at a location of z=22. In Fig. 10b, the Peclet number is close to that in Fig. 10a, but the frequency of oscillation is set to a value larger as compared to reference frequency. Hence, less time is available for the hot and cold pulses to traverse the length of the bed. The respective amplitudes of temperature are further diminished. Figure 10c, d shows the oscillatory response of the glass–water bed at a higher Peclet number. In general, as the frequency approaches the reference frequency, the amplitude of the oscillations increases and the corresponding attenuation is smaller. At a frequency much higher than the reference frequency, the amplitudes fall and attenuation of temperature is higher.

Fig. 10

Experimental record of oscillatory response of glass–water bed

Figure 11 shows the oscillatory response of temperature in a steel–water bed. Figure 11a, b shows the response at a Peclet number of around 1,000 whereas Fig. 11c, d shows the response at a Peclet number of around 2,000. In Fig. 11a, the frequency is less than reference and in Fig. 11b, it is higher than reference. In general, the attenuation is large when the forcing frequency is higher than the reference value.

Fig. 11

Experimental record of oscillatory response of steel–water bed

Figure 12 compares variations of temperature as a function of time in experiments, one- and two-equation models for oscillatory response of the porous bed. A Biot number of unity has been used for glass–water bed in numerical simulation to indicate mild heat losses to the ambient. For steel–water bed, the Biot number is 0.05. Figure 12a shows the variations in temperature for the glass–water bed while Fig. 12b is for the steel–water bed. The oscillatory response at various downstream locations is shown in the figures. In Fig. 12a, the oscillatory response of the glass–water bed at z=11 shows that numerical models match well with experiments. Though, during the cold phase, numerical models predict lower temperatures as compared to experiments. Of the two numerical models, the one-equation model is faster than the two-equation model. These trends are magnified at z=22. The attenuation of temperature is higher in experiments than numerical models. Figure 12b presents the oscillatory response in a steel–water bed. Here the two-equation model is slightly faster than experiments; the one-equation model is much slower than experiments at Biot number of 0.05. The lowest temperature obtained during a cycle should increase with distance since attenuation increases with distance. The one-equation model does not predict this trend correctly. The minima predicted by one-equation model actually increase with distance. The above discussion shows that the two-equation model out-performs the one-equation model in oscillatory heat transfer. It is clearly because of the correct representation of inter-phase heat transfer between the solid and the fluid phases during the transient process.

Fig. 12

Oscillatory response: variation of temperature with time in experiments, one- and two-equation model. a glass–water, b steel–water

In the following sections, temperature amplitudes and dimensionless phase lag are presented over a range of Peclet numbers and forcing frequencies. The mathematical models have once again been compared against experiments.

4.3.1 Glass–water bed

Figure 13 shows attenuation of temperature (in terms of amplitude) for a glass–water bed as a function of distance from the inflow plane at various forcing frequencies. Figure 13a presents attenuation at a Peclet number of around 950, while Fig. 13b is for a Peclet number of around 1,550. In both figures, attenuation is plotted at three distinct frequencies starting from a value near the reference frequency. At a frequency near reference value, for example, 0.022 rad s⁻¹ (Fig. 13a), the amplitude of temperature is closer to 0.5, the maximum possible value. The attenuation of temperature in experiments is close to those of numerical models. When the frequency increases, the amplitude falls and the attenuation increases. The two-equation model predicts a larger attenuation when compared to the one-equation model. For these conditions, experiments show a greater attenuation when compared to numerical models. At a higher Peclet number of around 1,550, Fig. 13(b), similar effects are observed.

Fig. 13

Oscillatory response: attenuation of temperature as a function of distance in glass–water bed. a ω_ref=0.021 rad s⁻¹, b ω_ref= 0.034 rad s⁻¹. Bi=1

Figures 14 and 15 show phase lag of temperature in a glass–water bed at nominal Peclet numbers of 950 and 1,050, respectively. The phase lag at a location z > 0 is plotted with respect to location z=0. It is seen that phase lag remains constant with distance in experiments as well as simulation. This is a confirmation of an inverse square root dependence of phase lag on distance. Since this variation is based on a conduction model, it is to be concluded that oscillatory heat transfer in a porous medium resembles conduction heat transfer on a cycle averaged basis (even in the presence of through flow in the porous bed). The experiments predict a higher phase lag when compared to numerical models. At a frequency near reference value, the difference is quite small. The difference increases when the frequency increases with respect to reference frequency. The two-equation model predicts a slightly higher phase lag as compared to one-equation model and the difference decreases with an increase in Peclet number. For a given Peclet number, the phase lag increases with frequency, while it decreases with an increase in Peclet number.

Fig. 14

Oscillatory response: phase lag in glass–water bed as a function of distance. Peclet number (Pe)=927–981, ω_ref=0.021 rad s⁻¹, Bi=1

Fig. 15

Oscillatory response: phase lag in glass–water bed as a function of distance. Pe=1,545–1,562, ω_ref=0.034 rad s⁻¹, Bi=1

4.3.2 Steel–water bed

Figure 16 shows attenuation in steel–water bed in the form of temperature amplitudes for various distances from the inflow plane and frequencies. Figure 16a shows attenuation at a Peclet number of around 1,000 and Fig. 16b at around Pe=2,000. At a frequency near the reference value, attenuation in experiments is small and quite close to two-equation model but one-equation model predicts a large attenuation even at zero Biot number. At higher frequencies the attenuation is, however, closer to the predictions of numerical simulation. The amplitudes fall with an increase in frequency. In general, the prediction of attenuation by the two-equation model is closer to experiments.

Fig. 16

Oscillatory response: attenuation of temperature as a function of distance in steel–water bed. a ω_ref=0.033 rad s⁻¹, b ω_ref=0.065 rad s⁻¹

Figures 17 and 18 present the phase lag at Peclet numbers of nominal values of 1,000 and 2,000, respectively. The phase lag again nearly follows an inverse square root dependence on distance. The phase lag in steel–water bed is higher than the glass–water bed, an indicative of distortion of thermal front in the highly diffusive solid phase. At a frequency near the reference value, the phase lag in experiments is quite close to simulation (Fig. 17a). As the frequency increases the phase lag increases and the predictions of the two-equation model become lower than in experiments. The one-equation model predicts a very small phase lag (Fig. 17b, c). At a higher Peclet number there is a slight increase in phase lag with distance at frequencies larger than reference (Fig. 18b, c).

Fig. 17

Oscillatory response: phase lag in steel–water bed as a function of distance. Pe=966–1,024, ω_ref=0.033 rad s⁻¹

Fig. 18

Oscillatory response: phase lag in steel–water bed as a function of distance. Pe=1,950–2,019, ω_ref=0.065 rad s⁻¹

The one-equation model does not predict the maximum temperature during hot phase and minimum temperature during cold phase. Hence, as discussed in the context of the step response calculations, it is not appropriate for solid media that have thermal properties widely different from the fluid medium.

5 Conclusions

In the present study, one- and two-equation models of heat transfer in a porous medium have been compared against experiments. Step and oscillatory response of glass–water and steel–water beds have been considered. The governing equations have been numerically solved. A direct comparison of numerical prediction with experiments showed that the models followed experiments quite closely in terms of temperatures. The differences between the two-equation model and experiments were uniformly smaller than the one-equation model. Thus, the two-equation model is seen as more appropriate than the one-equation model for unsteady transport in porous media. The following additional conclusions have been drawn in the study:

• 1. In step response studies, the thermal front speed and its spread are matched well by the two-equation model of heat transfer in glass–water beds.

• 2. For a steel–water bed, the one-equation model predicts the front speed better, but is excessively sensitive to the Biot number. The front spread predicted by the two-equation model matches experiments better.

• 3. Experiments generally show a larger front spread as compared to the one- and two-equation models and a lower front speed. This aspect is particularly seen for locations at larger distances from the inflow plane.

• 4. For oscillatory heat transfer, the two-equation model is closer to experiments, while the one-equation model fails for the steel–water bed. Attenuation and phase lag of the thermal pulsations with respect to the inflow plane are matched well by the two-equation model, while the one-equation model shows large errors. The phase lag scales with the inverse square root of distance from the inflow plane. Steel–water bed reveals large attenuation of temperature when compared to a glass–water bed. The frequency defined in terms of the fluid velocity and bed length emerges as a reference value that determines the impact of the forcing frequency.