Theoretical analysis of dehumidification process in a desiccant wheel

Abstract

A mathematical model based on the one-dimensional Navier–Stokes equation is described. The current model is capable of predicting the transient and steady-state transport in a desiccant wheel. It reveals the moisture and temperature in both the airflow channels and the sorbent felt, in detail, as a function of time. The predicted results are validated against the data taken from experimental results, with reasonable accuracy. Therefore, the numerical model is a practical tool for understanding and accounting for the complicated coupled operational process inside the wheel. Consequently, it is useful for parameter studies. As a demonstration of its utility, the model is employed to study the effect of felt thickness and passage shape on the performance of a desiccant wheel.

1 Introduction

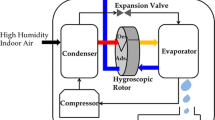
In a conventional air-conditioning unit, air cooling and dehumidification are achieved simultaneously through heat transfer between supply air and the cool surface of the evaporator. The dehumidification process, however, can result in poor space comfort control under same conditions. Fortunately, the technology of desiccant-based dehumidification offers an effective way to enhance dehumidification control and space comfort conditions through utilizing waste heat or solar energy in summer. In an open cycle of an air-conditioning system with a desiccant wheel, a desiccant medium is employed to remove moisture from humid air, and the resulting dry air is then cooled by indirect evaporative cooling. The sensible and latent loads are reduced, and as a result, both the thermal comfort of the supply air and the system efficiency are greatly improved. A well-designed desiccant wheel can recover 60–80% of the energy used in dehumidification. It lowers building operating costs and reduces equipment costs because more compact and efficient devices can be installed. Therefore, desiccant wheels are extensively used in the heating, ventilating and air-conditioning (HVAC) industry, especially in air dehumidification and energy recovery [1].

The design and optimization of these system, however, require a quantitative knowledge of momentum and energy and mass transfer between the airflow and the sorbent medium in both the adsorption and regeneration sections. Assessing the great number of available options and their optimum combinations is a time-intensive task that needs to be addressed through a combination of experimentation and analysis. Undoubtedly, carefully conducted experiments can provide relatively precise results for a specific test; therefore, testing is needed for ultimate product certification. However, the cause-and-effect relationships implicit in the test results are often hard to interpret, making it difficult to establish strategies that carry over from one design iteration to the next through experimentation alone. On the other hand, modeling and simulation approaches, although less precise in predicting the outcome of a specific test, can effectively isolate one variable at a time and point out trends and causes. Therefore, mathematical modeling and numerical analysis become highly effective tools in designing a desiccant wheel.

Much work on mathematical modeling and simulation has been conducted to assess the performance of desiccant wheels for given operating conditions. The simultaneous heat and mass transfer in a rotary dehumidifier was computed by both finite difference techniques and approximate analytic solutions in those early models [2, 3]. In all of these studies, the dehumidifier was modeled using particular sets of matrix properties. Therefore, Mitchell and co-authors [4, 5] presented several models that considered the effects of matrix properties on the performance of a rotary dehumidifier. The periodic steady-state performance of the desiccant wheel was considered, as the real transient process of heat and mass transfer still could not be reflected in the matrix channels. Later, Pesaran and Mills [6] presented a model that accounts for detailed diffusion of moisture within a particle and combined it with a model for thin-bed performance as a whole, incorporating gas-phase mass and heat transfer resistances. However, like other early models, Pesaran and Mills’ model [6] did not fully consider the effects of both fluid flow and the geometrical size of matrix channels on the performance of a desiccant wheel.

Recently, several models further considered the effect of fluid flow and operating parameters on predicting the performance of a desiccant wheel [7–10]. Compared with earlier models, these mathematical models were based on one-dimensional transient heat and mass conservation. The models can be modified to support the parametric study of a desiccant wheel. Unfortunately, these models still didn’t fully consider the effect of geometry and ignored the effect of the shapes of element channels on their heat transfer performance [7, 8]. These gaps affect the validation of the model as a general design tool for desiccant wheels.

Actually, the geometry and shape of element channels are important in improving the transport process in a desiccant wheel [10]. More research is needed to obtain detailed information on heat and mass transfer in ducts with different cross-sectional geometries. The present work is an attempt to develop a mathematical model that can be used to predict the effect of passage shape and the geometrical size of the matrix on the performance of a desiccant wheel. The mathematical model is presented to simulate the heat and mass transfer process in a porous composite structure and conventional heat exchanger. The study is conducted on the basis of theoretical simulation. A computer code has been developed as a design tool for a desiccant wheel.

2 Mathematical formulation

A desiccant wheel is mathematically described as a rotating cylindrical porous-medium wheel of length L_w and diameter D_w, which is divided into two sections: an adsorption section (angle fraction: α) and a regeneration section (angle fraction: 1−α). The rotary wheel revolves at a constant velocity ω and is cyclically exposed to two physically separated air streams. The two air streams are in a counterflow arrangement through the adsorption and regeneration sections. A schematic of the desiccant wheel is shown in Fig. 1a. Each section is a matrix composed of numerous elementary channels, parallel to the rotation axis, with relatively small cross-section areas. Each elementary structure includes flow passages and sorbent felt, as is illustrated in Fig. 1b. The sorbent felt consists of a mixture of commercially available silica gels with compatible inert material particles that have high thermal capacitance. For convenience of analysis, the matrerial is modeled as a homogeneous porous medium in which both gas and adsorbed liquid phases coexist.

Fig. 1

Schematic of the desiccant wheel

The transport phenomena occurring in a desiccant wheel are usually simplified by considering a single channel structure, ignoring radial and angular heat conduction between adjacent channels. An exact representation of the system can be exceedingly complex, requiring a prohibitive computational effect to obtain excessively detailed information. In fact, the cross-sectional area of an elementary channel is relatively small, and the sorbent materilal is very thin. The Bi numbers (h_t d/k) or Bi_m number (h_m δ/k) for both airflow channel and sorbent felt are less than or close to 0.1. Therefore, the temperature and the mass gradient across the cross-section of desiccant and airflow channel are small. The numerical results predicted by Sphaier and Worek [11], using a two-dimensional model, support this assumption. To avoid prohibitive costs for computation, it is reasonable to ignore the effect of heat and mass transfer across the thickness of desiccant and airflow channel. Consequently, a one-dimensional model is considered an accurate method to describe the thermal conduction and diffusion that occur within the porous desiccant.

For convenience, the following simplifications are assumed for the next analysis and calculation: (1) the variables, i.e., temperature and moisture, are considered as a function of θ(t), t and z; (2) one-dimensional airflow in each channel is assumed at constant pressure and velocity; (3) there exists no heat and mass transfer between adjacent flow channels; (4) the sorbent is composed of a homogeneous material with a constant porosity; (5) heat and mass transfer caused by conduction and diffusion within the sorbent is negligible in the radial direction; (7) heat transfer between the wheel and atmosphere is also ignored; (8) the effect of gravity on the fluid mixture is negligible; (9) no chemical reaction takes place, nor are there any energy sources within the system.

2.1 Governing equations for transport phenomena

Based on these assumptions, the relocation, energy, and mass balances for each elementary volume are expressed individually.

As mentioned earlier, a desiccant wheel is a rotating cylindrical porous-medium wheel. Each elementary channel in the desiccant wheel alternates periodically between adsorption and regeneration processes. The transient angle location of each elementary volume is the function of time, rotating speed, and its initial location, as follows:

$$\theta = \bmod {\left({\theta _{0} + \frac{{2\pi \omega t}}{{3600}},2\pi} \right)}$$

(1)

where mod is modulus, a symbol of the mathematical calculation for remainder after division. Herein, the elementary volume is located within the adsorption section if θ is less than 2απ; otherwise, it is located within the regeneration section.

Heat and mass conservation equations for an unsteady-state wet air stream in a narrow duct are mathematically described in the following:

$$\frac{{\partial \rho _{{\text{g}}} c_{{{\text{pg}}}} T_{{\text{g}}}}}{{\partial t}} + \varphi \frac{{\partial \rho _{{\text{g}}} c_{{{\text{pg}}}} T_{{\text{g}}}}}{{\partial \theta}} + u_{{\text{g}}} \frac{{\partial \rho _{{\text{g}}} c_{{{\text{pg}}}} T_{{\text{g}}}}}{{\partial z}} = \Phi _{{\text{T}}} + \Phi _{{{\text{TM}}}} $$

(2)

$$\frac{{\partial \rho _{{\text{g}}} Y_{{\text{g}}}}}{{\partial t}} + \varphi \frac{{\partial \rho _{{\text{g}}} Y_{{\text{g}}}}}{{\partial \theta}} + u_{{\text{g}}} \frac{{\partial \rho _{{\text{g}}} Y_{{\text{g}}}}}{{\partial z}} = \Phi _{{\text{M}}} $$

(3)

where Φ _T, Φ_TM, and Φ _M are source terms caused by heat and mass transfer between wet airflow and sorbent felt, respectively. They are given as follows:

$$\Phi _{{\text{T}}} = \frac{{h_{{\text{t}}}}}{{{f_{{\text{v}}}} \mathord{\left/{\vphantom {{f_{{\text{v}}}} {f_{{\text{s}}}}}} \right. \kern-\nulldelimiterspace} {f_{{\text{s}}}}}}{\left({T_{{\text{f}}} - T_{{\text{g}}}} \right)}$$

(4a)

$$\Phi _{{{\text{TM}}}} = \frac{{\rho _{{\text{f}}} h_{{\text{m}}}}}{{{f_{{\text{v}}}} \mathord{\left/{\vphantom {{f_{{\text{v}}}} {f_{{\text{s}}}}}} \right. \kern-\nulldelimiterspace} {f_{{\text{s}}}}}}c_{{{\text{pg}}}} T_{{\text{g}}} {\left({Y_{{\text{f}}} - Y^{*}_{{\text{f}}} {\left({T_{{\text{g}}}, Y_{{\text{g}}}} \right)}} \right)}$$

(4b)

$$\Phi _{{\text{M}}} = \frac{{\rho _{{\text{f}}} h_{{\text{m}}}}}{{{f_{{\text{v}}}} \mathord{\left/{\vphantom {{f_{{\text{v}}}} {f_{{\text{s}}}}}} \right. \kern-\nulldelimiterspace} {f_{{\text{s}}}}}}{\left({Y_{{\text{f}}} - Y^{*}_{{\text{f}}} {\left({T_{{\text{g}}}, Y_{{\text{g}}}} \right)}} \right)}$$

(4c)

In the above equations, f_v /f_s is the ratio of volume to surface area and is equal to D/4. The ratio of f_v /f_s reflects the basic characteristics of flow passage shape. h _m =h _t /ρ _f c _pf Le, and h _t is determined by the Nusselt number (Nu _D =h _t D/k _g ). The Le is the Lewis number. For air and water vapor mixtures, Le is 0.894 [1]. An air stream inside the small channels of the desiccant wheel is considered a fully turbulent flow (i.e., Re _D > 2300). A classical expression for computing the local Nusselt number for fully developed turbulence in an internal flow may be obtained from the Dittus–Boelter equation. The equation is of the form found in Incropera and DeWitt [12]:Nu _D =0.023Re^0.8_D Prⁿ, where n = 0.4 for adsorption (T_f > T_g) and 0.3 for regeneration (T_f < T_g).

Unlike in the air channels, heat and mass transfer in the desiccant is dominated by both thermal conductivity and diffusivity. Thus, the equations of energy and mass conservation for the desiccant are described as follows:

$$\frac{{\partial \rho _{{\text{f}}} c_{{{\text{pf}}}} T_{{\text{f}}}}}{{\partial t}} + \varphi \frac{{\partial \rho _{{\text{f}}} c_{{{\text{pf}}}} T_{{\text{f}}}}}{{\partial \theta}} = \frac{\partial}{{\partial z}}{\left({k_{{\text{f}}} \frac{{\partial T_{{\text{f}}}}}{{\partial z}}} \right)} + \Psi _{{\text{T}}} + \Psi _{{{\text{TM}}}} $$

(5)

$$\frac{{\partial \rho _{{\text{f}}} Y_{{\text{f}}}}}{{\partial t}} + \varphi \frac{{\partial \rho _{{\text{f}}} Y_{{\text{f}}}}}{{\partial \theta}} = \frac{\partial}{{\partial z}}{\left({D_{{\text{S}}} \frac{{\partial \rho _{{\text{f}}} Y_{{\text{f}}}}}{{\partial z}}} \right)} + \Psi _{{\text{M}}} $$

(6)

where Ψ _{T, Ψ_TM}, and Ψ _M are source terms caused by heat and mass transfer between air flow and desiccant felt, respectively. They are given as follows:

$$\Psi _{{\text{T}}} = \frac{{h_{{\text{t}}}}}{{\delta/2}}{\left({T_{{\text{g}}} - T_{{\text{f}}}} \right)}$$

(7a)

$$\Psi _{{{\text{TM}}}} = \frac{{\rho _{{\text{f}}} qh_{{\text{m}}}}}{{\delta/2}}{\left({Y^{*}_{{\text{f}}} {\left({T_{{\text{g}}}, Y_{{\text{g}}}} \right)} - Y_{{\text{f}}}} \right)}$$

(7b)

$$\Psi _{{\text{M}}} = \frac{{\rho _{{\text{f}}} h_{{\text{m}}}}}{{\delta/2}}{\left({Y^{*}_{{\text{f}}} {\left({T_{{\text{g}}}, Y_{{\text{g}}}} \right)} - Y_{{\text{f}}}} \right)}$$

(7c)

In the above equations, all the thermal properties are described in the next section.

2.2 Thermoproperties model and equilibrium isotherm

The density, thermal conductivity, and specific heat of the fluid mixture in the process stream are given by the following equations:

$$\rho _{{\text{g}}} = {\left({1 + Y_{{\text{g}}}} \right)}\rho _{{\text{a}}} $$

(8a)

$$k_{{\text{g}}} = {{\left({\rho _{{\text{a}}} k_{{\text{a}}} + Y_{{\text{g}}} \rho _{{\text{a}}} k_{{\text{v}}}} \right)}} \mathord{\left/{\vphantom {{{\left({\rho _{{\text{a}}} k_{{\text{a}}} + Y_{{\text{g}}} \rho _{{\text{a}}} k_{{\text{v}}}} \right)}} {\rho _{{\text{g}}}}}} \right. \kern-\nulldelimiterspace} {\rho _{{\text{g}}}}$$

(8b)

$$c_{{{\text{pg}}}} = {{\left({\rho _{{\text{a}}} c_{{{\text{pa}}}} + Y_{{\text{g}}} \rho _{{\text{a}}} c_{{{\text{pv}}}}} \right)}} \mathord{\left/{\vphantom {{{\left({\rho _{{\text{a}}} c_{{{\text{pa}}}} + Y_{{\text{g}}} \rho _{{\text{a}}} c_{{{\text{pv}}}}} \right)}} {\rho _{{\text{g}}}}}} \right. \kern-\nulldelimiterspace} {\rho _{{\text{g}}}}$$

(8c)

The properties of sorbent can be described as a function of desiccant porosity. Therefore, the density, specific heat, and thermal conductivity are given as follows:

$$\rho _{{\text{f}}} = {\left({1 - \varepsilon _{{\text{f}}}} \right)}\rho _{{\text{d}}} + \varepsilon _{{\text{f}}} \rho _{{\text{g}}} $$

(9a)

$$k_{{\text{f}}} = {{\left({{\left({1 - \varepsilon _{{\text{f}}}} \right)}\rho _{{\text{d}}} k_{{\text{d}}} + \varepsilon _{{\text{f}}} \rho _{{\text{g}}} k_{{\text{g}}}} \right)}} \mathord{\left/{\vphantom {{{\left({{\left({1 - \varepsilon _{{\text{f}}}} \right)}\rho _{{\text{d}}} k_{{\text{d}}} + \varepsilon _{{\text{f}}} \rho _{{\text{g}}} k_{{\text{g}}}} \right)}} {\rho _{{\text{f}}}}}} \right. \kern-\nulldelimiterspace} {\rho _{{\text{f}}}}$$

(9b)

$$c_{{{\text{pf}}}} = {{\left({{\left({1 - \varepsilon _{{\text{f}}}} \right)}\rho _{{\text{d}}} c_{{{\text{pd}}}} + \varepsilon _{{\text{f}}} \rho _{{\text{g}}} c_{{{\text{pg}}}}} \right)}} \mathord{\left/{\vphantom {{{\left({{\left({1 - \varepsilon _{{\text{f}}}} \right)}\rho _{{\text{d}}} c_{{{\text{pd}}}} + \varepsilon _{{\text{f}}} \rho _{{\text{g}}} c_{{{\text{pg}}}}} \right)}} {\rho _{{\text{f}}}}}} \right. \kern-\nulldelimiterspace} {\rho _{{\text{f}}}}$$

(9c)

Since most heat and mass transfer between airflow and desiccant occur only on the solid surface of a desiccant particle, the effect of the diffusivities of combined ordinary and Knudsen diffusion is small compared with the surface mass diffusion. Therefore, in Eq. 6, only the surface mass diffusion is considered. The diffusion coefficient, D_s, can be evaluated using the following expression [7, 13].

$$D_{{\text{S}}} = \frac{{D_{0}}}{\tau}\exp {\left({- {\text{0}}{\text{.974e}} - {\text{3}}q \mathord{\left/{\vphantom {q {T_{{\text{f}}}}}} \right. \kern-\nulldelimiterspace} {T_{{\text{f}}}}} \right)}$$

(10)

The adsorption heat of silica gel of regular density is given by Pesaran and Mills [6], as follows:

$$ q = \left\{ {\begin{array}{*{20}c} {{3500 - 13,400Y_{{\text{f}}} ,}} & {{Y_{{\text{f}}} \leqslant 0.05}} \\ {{2950 - 1400Y_{{\text{f}}} ,}} & {{Y_{{\text{f}}} \succ 0..05}} \\ \end{array} } \right. $$

(11)

The system equation governing the dynamics of sorption has to be solved along with the equilibrium sorption isotherm of the desiccant, which is given by Majumdar [13] and is simplified as follows:

$$Y^{*}_{{\text{f}}} = a_{1} + a_{2} T^{2}_{{}} + a_{3} {\text{RH}}^{2} + a_{4} {\text{RH}}^{3} + a_{5} T^{3}_{{}} {\text{RH}}^{2} + a_{6} T^{3}_{{}} {\text{RH}}^{3} $$

(12)

where a₁ = 0.0329, a₂ = −4.113e−6, a₃ = 1.05e−5, a₄ = 6.586e−7, a₅ = 7.894e−11, and a₆ = 6.747e−13. In Eq. 12, the relative humidity ratio is given by

$${\text{RH}} = \frac{{264.0727Y_{{\text{g}}}}}{{\exp {\left({{17.2694{\left({T - 273.15} \right)}} \mathord{\left/{\vphantom {{17.2694{\left({T - 273.15} \right)}} {{\left({T - 34.85} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left({T - 34.85} \right)}}} \right)}}}$$

(13)

2.3 Boundary conditions and gross-parameters process

As discussed earlier, a desiccant wheel is a rotating cylindrical porous-medium wheel, where two air streams are blown in counterflow through an adsorption section and a regeneration section. Each elementary volume in the desiccant wheel alternates periodically between the adsorption and regeneration processes. The transient angle location of each elementary volume is described by Eq. 1.

Therefore, boundary conditions for airflows are given by

$$ \begin{array}{*{20}l} {{{\text{If}}\;{\text{0}} \leqslant \theta < 2\pi \alpha \;{\text{then}}\;T_{{g,z = 0}} = T_{{{\text{a}},{\text{in}}}} ,Y_{{g,z = 0}} = Y_{{{\text{a}},{\text{in}}}} }} \\ {{{\text{If}}\;2\pi \alpha \leqslant \theta < 2\pi \;{\text{then}}\;T_{{g,z = L}} = T_{{{\text{r}},{\text{in}}}} ,Y_{{g,z = L}} = Y_{{{\text{r}},{\text{in}}}} }} \\ \end{array} $$

(14)

For boundary conditions for the desiccant felts, assume the surface of the desiccant is coated with a layer of insulating material. Hence, the boundary conditions are given by

$$\frac{{\partial T_{{\text{f}}}}}{{\partial z}}\left| {_{{z = 0}}} \right. = \frac{{\partial T_{{\text{f}}}}}{{\partial z}}\left| {_{{z = L}}} \right. = \frac{{\partial Y_{{\text{f}}}}}{{\partial z}}\left| {_{{z = 0}}} \right. = \frac{{\partial Y_{{\text{f}}}}}{{\partial z}}\left| {_{{z = L}}} \right. = 0$$

(15)

In addition, the overall values of the temperature and moisture content of supply air are evaluated, after the outlet of each section in the desiccant wheel, using the following expressions:

$$ \begin{aligned} & {\text{If}}\,{\text{0}} \leqslant \theta < 2\pi \alpha \,{\text{then}} \\ & T_{{{\text{a}},{\text{out}}}} = \frac{1} {{2\pi \alpha }}{\int\limits_0^{2\pi \alpha } {T_{g} (\theta ,L){\text{d}}\theta \,{\text{and}}\,Y_{{{\text{a}},{\text{out}}}} = \frac{1} {{2\pi \alpha }}{\int\limits_0^{2\pi \alpha } {Y_{g} (\theta ,L){\text{d}}\theta } }} } \\ \end{aligned} $$

(16a)

$$ \begin{aligned} & {\text{If}}\;{\text{2}}\pi \alpha \leqslant \theta {\text{ $<$ 2}}\pi \;{\text{then}} \\ & T_{{{\text{r,out}}}} = \frac{1} {{2\pi {\left( {1 - \alpha } \right)}}}{\int\limits_{2\pi \alpha }^{2\pi } {T_{{\text{g}}} {\left( {\theta ,0} \right)}} }{\text{d}}\theta \,\begin{array}{*{20}c} {{{\text{and}}\,}} \\ \end{array} Y_{{{\text{r,out}}}} = \frac{1} {{2\pi {\left( {1 - \alpha } \right)}}}{\int\limits_{2\pi \alpha }^{2\pi } {Y_{{\text{g}}} {\left( {\theta ,0} \right)}} }{\text{d}}\theta \\ \end{aligned} $$

(16a)

These boundary conditions are based on the impermeable surface of the desiccant wheel. The gross process ignores the effect of the profile of moisture and density along the wheel. These simplifications are considered in order to avoid the complexity of the system, and the result is reasonably accurate.

3 Numerical solution

The conservation equations described by Eqs. 2, 3 and 5, 6 can be cast into the common form:

$$\frac{{\partial {\left({\rho \phi} \right)}}}{{\partial t}} + \frac{{\partial {\left({\rho w\phi} \right)}}}{{\partial \theta}} + \frac{{\partial {\left({\rho u\phi} \right)}}}{{\partial z}} = \frac{\partial}{{\partial z}}{\left({\Gamma _{\phi} \frac{{\partial \phi}}{{\partial z}}} \right)} + S_{\phi} $$

(17a)

Integrating the differential Eq. 17a over a control volume gives

$$ \begin{aligned} & \frac{{{\left( {\rho \phi } \right)}^{{\text{n}}}_{{\text{P}}} - {\left( {\rho \phi } \right)}^{{\text{o}}}_{{\text{P}}} }} {{\Delta t}}{\text{d}}V \\ & + \frac{{{\left( {\rho w\phi } \right)}^{{\text{n}}}_{{\text{P}}} - {\left( {\rho w\phi } \right)}^{{\text{o}}}_{{\text{P}}} }} {{\Delta \theta }}{\text{d}}V \\ & + {\left( {{\left( {\rho u\phi } \right)}^{{\text{n}}}_{{\text{E}}} - {\left( {\rho u\phi } \right)}^{{\text{n}}}_{{\text{W}}} } \right)}{\text{d}}A \\ & = {\left( {{\left( {\Gamma _{\phi } \frac{{\phi _{{\text{E}}} - \phi _{{\text{P}}} }} {{z_{{\text{E}}} - z_{{\text{P}}} }}} \right)}^{{\text{n}}} - {\left( {\Gamma _{\phi } \frac{{\phi _{{\text{P}}} - \phi _{{\text{W}}} }} {{z_{{\text{P}}} - z_{{\text{W}}} }}} \right)}^{{\text{n}}} } \right)}{\text{d}}A + S^{{\text{o}}}_{\phi } {\text{d}}V \\ \end{aligned} $$

(17b)

where n and o represent new and old time levels; P is the CV center, E the east CV neighbor, and W is the west CV neighbor. In the foregoing formula, a fully implicit form is chosen in order to achieve the stability to evaluate all terms in connection with large time steps.

After gathering all coefficients of Φ_P, Φ_E, Φ_W, and S_Φ, we obtain the following formation:

$$a^{{\text{n}}}_{{\text{P}}} \phi ^{{\text{n}}}_{{\text{P}}} - a^{{\text{n}}}_{{\text{E}}} \phi ^{{\text{n}}}_{{\text{E}}} - a^{{\text{n}}}_{{\text{W}}} \phi ^{{\text{n}}}_{{\text{W}}} = a^{{\text{o}}}_{{\text{P}}} \phi ^{{\text{o}}}_{{\text{P}}} + s^{{\text{o}}}_{\phi} {\text{d}}V$$

(18)

After accounting for all grid points in the domain, a matrix equation is available: $[A] \cdot \Phi = B.$. In order to solve the matrix equation, a fast solver is adopted: line-by-line TDMA along Z-direction. The grid in Z-direction is considered to be uniform.

The corresponding program is written in the Visual Fortran 6.1 language and executed on a Pentium-IV desktop computer. In brief, the numerical solution stages consist of (1) assignment of initial and inlet condition for both the adsorption and regeneration section; (2) computation of heat and mass transfer for both flow channel and sorbent in each section; (3) calculation of gross parameters in the exit of the two sections; (4) rezoning of the adsorption and regeneration section and reassignment of their inlet condition.

The sensitivity of mesh generation was thoroughly analyzed before the numerical simulation was conducted. The initial calculation found that the numerical result approaches constant if the mesh numbers on the cross-sectional area of the wheel and the Z-direction are beyond 2000 and 25, respectively. Consequently, the authors conclude that the result is independent of mesh generation. When mesh numbers across the wheel surface are less than 1000, the numerical calculation breaks down because the geometry of each air channel is quite small. Therefore, in the next analysis, the mesh generation adopted is 2000 units for the cross-sectional area of the wheel and 25 units for the Z-direction.

4 Results and discussion

4.1 Model validation

In order to validate the current model, several comparisons are conducted in this section between measured results derived from experimental investigation [14] and the ones predicted by the current model. The wheel used in the comparison is a commercially available desiccant dehumidification wheel. The dimensions of the wheel are listed in Table 1. The cross-area of each elementary channel is assumed to be 0.81 mm², and the number of gross elements is assumed as 14,642. In addition, the thickness of the adsorption is 0.1 mm. The initial conditions in the cases are 20°C temperature and 25% relative humidity (or 3.69 g/kg-DA). The moisture content in the dessicant is in equilibrium with the ambient condition and is determined by Eq. 12 on the basis of inlet air temperature and humidity. The inlet parameters, including temperature and humidity ratio, are considered as a function of time and gradually increased from the ambient condition to the set points. The delay timing is around 4 min in accordance with the experimental data. Wheel rotational speed is 18 rph, and airflow rates for both the adsorption and regeneration sections are 0.897 m³/s.

Table 1 Specific parameters of desiccant wheel

Figure 2 plots the comparison of predicted and measured parameters, such as adsorption outlet air temperature and moisture removal capacity (MRC), in a transient process. In this case, adsorption inlet temperature is 31°C and regeneration inlet temperature is 88°C. Both inlet air humidity ratios are 12.5 g/kg-DA, which represents 45.1 and 3.1% RM, respectively. From Fig. 2a and b, the prediction approaches the steady state a little more quickly than in the actual experiment. This is because the prediction is conducted under ideal operating conditions, while the actual system is affected by many uncertain factors, e.g. unstable heating and flow leakage.

Fig. 2

Comparison of predicted and measured transient gross outlet parameters in an unsteady state. a Adsorption outlet air temperature. b The MRC. The broken line shows experimental data [14]; the solid line shows predicted results; the adsorption inlet temperature is 31°C

Figure 3 shows the comparison of predicted and measured gross outlet parameters in a steady state. In this case, regeneration inlet temperature is still 88°C, but adsorption inlet temperature is 35°C. The result illustrates that the predicted adsorption outlet temperature is slightly less than the temperature in the experimental data. The difference is between 2 and 3°C. The MRC is close to that of the experimental result. The regeneration outlet temperature is not compared because data were unavailable.

Fig. 3

Comparison of predicted and measured gross outlet parameters in a steady state. The solid line is MRC; the broken line is air temperature at the exist; the diamond shape denotes experimental data [14]; the square denotes predicted data

The model can reveal the moisture and temperature morphology in both the airflow channel and the sorbent in detail. A typical periodic profile of the thermal parameters of an element in a steady state, including temperature and moisture content, is shown in Fig. 4. The adsorption inlet humidity ratio is 75% in the case shown. The periodic profile is formed as a result of the periodic alternation between adsorption and regeneration. The numerical model provides a strong tool for understanding and accounting for the complicated coupled processes inside the wheel.

Fig. 4

Periodic profile of predicted transient parameters of an element in a steady state: a air temperature, b moisture content of airflow, c sorbent temperature, d moisture content of sorbent felt

Based on the analyses of Figs. 2, 3, and 4, the authors conclude that although there exists a slight difference between the experimental data and the results simulated by the current model, the model can generally predict the transient and steady-state performance of a desiccant wheel with reasonable accuracy.

4.2 Sensitivity analyses of Desiccant geometry

After obtaining confidence in the predictive capabilities of the model, this section aims at investigating the sensitivity of the performance of the desiccant wheel to the desiccabt thickness. The desiccant wheel previously analyzed is used for this analysis. The flow passage shape of each element is assumed to be square. For the convenience of analysis, no time delay in inlet setting is considered. The moisture content in the sorbent is considered to be immediately at equilibrium with the local ambient condition. Airflow rates in both adsorption and regeneration are still 0.897 m³/s.

Figure 5 reflects the effect of the thickness of sorbent on MRC, which is calculated for the adsorption section. The result illustrates that a thicker sorbent requires much more time to reach a steady state and has a higher MRC. The difference in MRC resulting from sorbent thickness could be 25% or more. From the view of both energy savings and dehumidification, a lower rotational speed is better when a thicker sorbent is employed in a desiccant wheel.

Fig. 5

Effect of sorbent thickness on MRC

Figure 6 plots the effect of the thickness of the sorbent on the air temperature and humidity ratio at the exit of each section in a rotational wheel. Apparently, the thickness of the sorbent influences both the transient and steady-state performance of a desiccant wheel. In the case of a thicker sorbent felt, a longer time is required to approach the steady state. Once in the steady state, there is a difference in air temperature at the exit of each section. Fig. 6a and b show the detailed information. A similar situation appears in humidity ratio, as seen in Fig. 6c and d. The reason for these phenomena is that a thicker sorbent possesses a stronger capacity for heat and mass transfer. Therefore, increasing the sorbent’s thickness has a positive effect on MRC in a desiccant wheel.

Fig. 6

Effect of sorbent thickness on the performance of the rotational wheel: a adsorption outlet temperature, b regeneration outlet temperature, c adsorption outlet humidity ratio, d regeneration outlet humidity ratio

In Fig. 6c and d, there is a significant change in the humidity ratio at the exits of the adsorption and regeneration sections when the working time is less than 300 s. During the period of transient process, airflow with enriched moisture enters the flow channel of the adsorption section while high-temperature airflow goes through the flow passage of the regeneration section. The transport phenomenon in both the adsorption and regeneration processes becomes quite strong as a result of the significant difference in temperature and moisture. Then each element, including flow channel and desiccant, undergoes the periodic alternation between adsorption and regeneration and slowly leads these gross processing parameters to regain a stable state. The phenomenon is also reflected in Fig. 5.

In general, the performance of a desiccant wheel is closely related to geometry, in addition to the properties of the desiccant material and motor rotational speed. The optimization of motor rotational speed in a desiccant wheel is also determined by the thickness of the sorbent. Usually, thicker sorbents require a lower rotational speed.

4.3 Effect of flow channel shapes on the performance of the desiccant wheel

To design a desiccant wheel with better performance for a desiccant wheel, another important factor to consider is the shape of the flow channel. It is of interest to determine, which shape offers better performance under a given set of conditions. The f_v /f_s is considered here as shape factor to evaluate the effect of flow passage shapes on the performance of desiccant wheels. This is because f_v/f_s is the ratio of volume to surface area and reflects the basic characteristics of flow passage shape.Currently available commercial desiccant wheels, the typical flow channel shapes include triangular, square, quadrilateral, sinusoidal, and hexagonal (Fig. 7). To ensure a relevant comparison, the cross-sectional area of the flow channel in each case is assumed to be the same. Based on this assumption, shape factors can be derived from the cross-sectional area of the flow channel and the ratio of a and b, respectively, for variable flow passage shapes. The cross-sectional area of each elementary channel is considered here to be 0.81 mm² and the thickness of the adsorption matrerialto be 0.1 mm.

Fig. 7

Schematic of flow channel shapes

To determine accurately the effect of each channel shape on the performance of a desiccant wheel, the performance parameters at steady state are compared first. Figure 8 plots the effect of passage shape on MRC as a function of adsorption inlet humidity ratio. Based on the data in Fig. 8, the influence of airflow passage shape on MRC is significant, especially in the case of a high humidity ratio. The difference could approach up to 20%. The result points out that a sinusoidal airflow passage possesses the best potential for MRC; the triangular shape is second-best; and the hexagonal shape is the worst. This is due to the fact that the hydraulic diameter in the sinusoidal channel is relatively small at the same cross-area of the airflow channel. As a result, the airflow in the sinusoidal channel has a higher flow velocity and a better heat transfer coefficient. Further analysis also shows that the small ratio of a and b could lead to the higher MRC, as is proved by the comparison between cases 3 and 4.

Fig. 8

Comparison of predicted MRC for variable passage shape in a steady state

Figure 9 plots the comparison of predicted gross outlet parameters at the exit of each channel shape in a steady state. With the increase of adsorption inlet relative humidity, the air temperature at the adsorption exit rises, while that at the regeneration exit is reduced. This is mainly because of the heat transfer of counter airflows and heat generated in the process of moisture transport between adsorption and regeneration. The air humidity ratio at both the adsorption and regeneration exits seems to rise with the increase in adsorption inlet relative humidity. The air humidity ratio at the adsorption exit, however, increases faster than that at the regeneration exit.

Fig. 9

Comparison of predicted gross outlet parameters for variable passage shape in a steady state; a adsorption outlet air temperature;b adsorption outlet air humidity ratio; c regeneration outlet air temperature d regeneration outlet air humidity ratio

Figure 10 shows a comparison of predicted MRC at the exit of each passage shape in a transient process. There is a similar transient process for all cases, especially during the earlier period. Once the system enters and operates at steady state, the performance is quite different. A situation occurs that is similar to the air temperature and humidity ratio at the exit of each section (To avoid unnecessary repetition, their curves are not plotted here.)

Fig. 10

Effect of passage shape on MRC in a transient process

The foregoing results illustrate that the flow channel shape is important in efforts to improve the performance of a dehumidification process. Understanding this point is very useful in the future design of desiccant wheels.

5 Conclusion

A mathematical model based on the one-dimensional Navier–Stokes equation was developed in an effort to investigate the transport phenomena occurring within the porous sorbent and the airflow channels in a desiccant wheel. These governing equations include those terms due to heat and mass transfer within the sorbent and between the sorbent and the flow channel. The model can reveal the moisture and temperature in both the airflow channel and the sorbent in detail as a function of time. The results predicted by the current model are further validated with reasonable accuracy against data taken from experimental results. Therefore, the numerical model is assumed to be a positive tool that accounts for the transport phenomena within the wheel and, consequently, is ideal for parameter studies that can lead to design optimization.

As a demonstration of its utility, the model is employed to study the effect of desiccant thickness. The results illustrate that the thickness of the sorbent influences both the transient and the steady-state performance of a desiccant wheel. As the thickness of the sorbent increases, a longer time is required to approach a steady state, and the MRC of the desiccant wheel improves. A further parametric study focuses on the effect of passage shape on the performance of a desiccant wheel. The influence of airflow passage shape on MRC is significant, approaching up to 20%. The predicted result points out that a sinusoidal airflow passage employed in a desiccant wheel possesses more potential for MRC. The triangular shape is second-best, and the hexagon shape is worst. The further analysis shows that a small ratio between a and b could achieve a higher MRC.