LES study of heat transfer augmentation and wake instabilities of a rotating disk in a planar stream of air

Abstract.

Large-eddy-simulations are performed for the heat transfer and the wake flow of a thin rotating disk subjected to an outer parallel passing stream of air. Above a critical value for the angular velocity of the disk, heat transfer augmentation sets on. This is strongly related to a flow instability that leads to a periodic vortex generation at the counter-moving disk side. The resulting phenomena are captured by the classical Landau model. For higher angular velocities the wake becomes fully turbulent, and here the transition to turbulence seems to be very abrupt. In this regime, a periodic vortex generation is observable at the co-moving disk side, too.

Zusammenfassung.

Grobstruktur-Simulationen werden für die Wärmeübertragung und die Nachlaufströmung für eine dünne rotierende Scheibe in einem äußeren parallelen Luftstrom durchgeführt. Oberhalb eines kritischen Wertes für die Rotationsgeschwindigkeit setzt eine Verstärkung der Wärmeübertragung ein. Dies ist eng mit einer hydrodynamischen Instabilität, die zu einer periodischen Wirbelablösung an der gegenläufigen Scheibenseite führt, verbunden. Die resultierenden Phänomene werden gut durch das klassische Landau-Modell erfaßt. Für größere Rotationsgeschwindigkeiten wird der Nachlauf stark turbulent, und der Übergang in die Turbulenz scheint im vorliegenden Fall abrupt zu sein. In diesem Bereich findet eine periodische Wirbelablösung auch an der mitlaufenden Scheibenseite statt.

1 Introduction

Heat transfer characteristics of rotating systems are not only of considerable theoretical interest, but are also of great technical importance. Usually, the flow in and over rotating systems is three-dimensional and flow separation often takes place. Since the convective heat transfer in rotating systems is intimately related to the flow characteristics, they too are quite complex and offer challenges to theoreticians as well as to experimental scientists. Almost every rotating system exhibits new and often unexpected phenomena when it is subjected to a detailed investigation. Even for the very fundamental rotating systems, namely rotating disks, the range of phenomena seems to be nearly unlimited; this becomes obvious, for instance, by inspecting the reviews of Zandbergen and Dijkstra [1], Kreith [12], or Owen and Rogers [3]. However, the available investigations have excluded nearly the problem of a thin rotating disk subjected to an additional outer parallel flow. Such a flow configuration destroys the similar solution of the velocity field and leads to a complex symmetry breaking of the resulting flow and heat transfer. Some general properties of related laminar boundary layer flows have been proposed by Rott and Lewellen [4], but their infinite configuration allows only the deduction of results with minor technical importance. Dennis et al. [5] performed an experimental study of the heat transfer from a rotating disk subjected to an air crossflow, but they revealed that the flow was always turbulent due to the rotation.

Recently, the heat transfer from a thin rotating disk in an outer forced flow parallel to the disk surface has been investigated numerically [6]. In that work the Nusselt number at the disk surface has been calculated by means of computational fluid dynamics using the classical k-ɛ-model of turbulence. There, it has been found that heat transfer augmentation due to rotation not begins until a critical angular velocity is reached. In the vicinity of the critical value, the resulting heat transfer augmentation has been captured by the phenomenological Landau model of instability [7, 8]. However, the physical basis of this instability phenomenon was not understood so far. This gap was caused by the numerical approach chosen in [6], because the heat transfer augmentation is directly related to the wake and its small scale fluctuations. The k-ɛ-model of turbulence is usually not able to resolve such small-scale fluctuations within the resulting wake with the necessary accuracy [9]. Whereas the mean values of heat transfer can be calculated successfully by means of the k-ɛ-model (or other related turbulence models), this approach fails in cases where small spatial and temporal effects are in question, because the smoothing and dissipative influence of the approach dominates on that scale. Though full simulation of (turbulent) flow at practically high Reynolds numbers is still unrealistic, the capacity of digital computers has come to allow large-eddy-simulations (LES) of such flows, which is expected to do better then the Reynolds averaged equation methods.

The objective of the present paper is therefore to investigate the thermal wake and the flow instabilities generated by a thin rotating disk in an outer parallel flow by means of LES. It is supposed that periodic vortex shedding forms the physical mechanism of heat transfer augmentation near to the critical angular velocity. This effect can be described in terms of the universal Landau model.

2 Background and problem formulation

The present paper focused on the flow situation illustrated by means of Fig. 1. A thin disk rotates with angular velocity Ω subjected to an outer stream of air parallel to the disk surface with constant inflow velocity u _1,in . The disk of radius r may be located in the x,y-plane and the direction normal to the disk surface may be given by the z-axis. In the following, the disk surfaces are assumed to be kept at constant temperature T _d whereas the air far away from the disk has the temperature T _∞ assumed to be constant, too. The parameters used in the following are listed in Table 1; they correspond directly to the data used in [6]. The material parameters are assumed to be constant, i.e. the fluid is treated as incompressible. In terms of physics, they correspond to air at normal pressure and at ambient temperature of about 20°C.

Fig. 1.

Schematics of the flow problem considered

Table 1. Parameters used for calculations

In the flow domain, the governing equations call in the usual tensor notation

$$ {{\partial u_i} \over {\partial x_i}} = 0 $$

(1)

$$ {{\partial u_i} \over {\partial t}} + u_j {{\partial u_i} \over {\partial x_j}} = - {1 \over \rho}{{\partial p} \over {\partial x_i}} + {\partial \over {\partial x_j}}\left({\nu{{\partial u_i} \over {\partial x_j}}} \right) $$

(2)

$$ \rho c{{\partial T} \over {\partial t}} + \rho cu_i {{\partial T} \over {\partial x_i}} = {\partial \over {\partial x_i}}\left({\lambda {{\partial T} \over {\partial x_i}}} \right) $$

(3)

Equation (1) is the continuity equation for an incompressible fluid, equation (2) represents the Navier-Stokes-equation for a Newtonian fluid, and the energy equation (3) contains the rather mighty simplifications due to very small Mach and Eckert numbers, respectively.

The main problem in heat transfer is to determine the heat transfer coefficient

$$ h \equiv {{\dot q} \over {T_d - T_\infty}} $$

(4)

It is for engineering purposes convenient to focus on the mean Nusselt number Nu _m defined by means of

$$ Nu_m \equiv {{h_m r} \over \lambda} = {{\dot q_m r} \over {\lambda (T_d - T_\infty)}} $$

(5)

where the mean heat flux q̇ _m is the surface-average value

$$ \dot q_m = {1 \over {\pi r^2}}\int\limits_0^{2\pi} {\int\limits_0^r {\dot q\,r^{\prime}\,dr^{\prime}\,d\varphi}} $$

(6)

Correlations for the mean Nusselt number Nu _m as function of the applied Reynolds number Re _u have been deduced in [6] by means of computational fluid dynamics using the standard k-ɛ-model of turbulence.

For instance, in case of a non-rotating disk (Ω = 0) the correlation

$$ Nu_m = 0.470 \cdot Re_u^{1/2} \cdot Pr^{1/3} \quad \hbox{for}\ 10^3\leq Re_u\leq 5 \cdot 10^4 \quad \hbox{and}\quad 0.5\leq Pr\leq1.0 $$

(7)

has been derived for laminar flow. The resulting heat transfer as function of the applied translational Reynolds number for Ω = 0 is shown in Fig. 2. Three convective heat transfer regimes can be distinguished: a laminar regime captured by equation (7), a transition zone, and a turbulent regime. In the later regime, the flow over the resting disk becomes turbulent. The present paper is addressed to the laminar boundary layer problem for Re _u < 5.0 · 10⁴.

Fig. 2.

Mean Nusselt number for non-rotating disk

When the angular velocity Ω is increased, the numerical results derived in [6] indicate an augmentation of the mean Nusselt number not until a critical angular velocity Ω _cr is reached. Some numerical results are shown in Fig. 3. The logarithm of the normalised mean Nusselt number is plotted as function of the logarithm of the ratio between the rotational Reynolds number $Re_\Omega = {{\Omega r^2} \over \nu}$ and the translational one, $Re_u = {{u_{1,in} r} \over \nu}$ . Below a certain critical value (0 ≤ Ω < Ω _cr ) the mean Nusselt number remains constant, i.e. it is equal to the non-rotating value. This effect can be explained on the basis that disk rotation augments heat convection on the ascending (co-moving) side and diminishes it on the descending (counter-moving) side in such a way that the average heat transfer is almost unaffected. However, for sufficient high angular velocities Ω a flow separation has to be expected which destroys any exact compensation. In addition to the numerical data a simple correlation line related to the Landau model is given in Fig. 3, too. It seems to be the case that near the critical value, where the heat transfer augmentation sets on, the Landau model can correlate the data very well. Since the Landau model captured effects related to periodic vortex shedding (von Karman vortex shedding) as well [8], it is therefore assumed that such a flow instability effect forms the basis of the heat transfer augmentation reported here, too. It should be kept in mind that in case of vortex shedding the Landau model is applied usually for much smaller translational Reynolds numbers.

Fig. 3.

Normalised mean Nusselt number for rotating disk

The numerical approach based on the Reynolds averaged Navier-Stokes equations (RANS) used in [6] was not able to resolve the complex flow separation and wake turbulence with the required accuracy. The unsteady RANS equations may be considered to represent the phase-averaged flow, and the time-dependent solution is conceivable [10, 11], but periodic phenomena on a small time scale cannot be captured well by such RANS simulations, and one gets only the time-independent mean values with high accuracy. Because of this, in the present paper large-eddy-simulations (LES) are employed to get more physical insight into the underlying augmentation mechanism.

3 Large-eddy-simulation

The basic equations used in the present large-eddy-simulation (LES) are discussed in this section. The LES technique that was been thought to be too expensive for practical calculations has now reached a high potential to be exploited in various engineering applications [12]. However, despite of the various LES procedures developed in the past no single LES procedure has yet emerged as a standard.

3.1 General LES considerations

Turbulent flows are characterised by eddies with a wide range of length and time scales. The largest eddies are typically comparable in size to characteristic lengths of the mean flow; whereas the smallest eddies are mainly responsible for the turbulent dissipation. It is theoretically possible to directly resolve the whole spectrum of turbulent scales using a so-called direct-numerical-simulation (DNS) approach. However, DNS is not feasible for technical engineering problems, because the mesh sizes and the computer capabilities required for DNS are prohibitive. Conceptually, LES is situated somewhere between DNS and the classical Reynolds-averaged-Navier-Stokes (RANS) approach. The k-ɛ-model of turbulence is certainly one of the most popular RANS examples, but it fails often in case of flow separation and wake flows. For a detailed discussion of that, the reader is referred, for instance, to the monograph written by Leder [9].

Basically, in LES the large eddies are resolved directly while small eddies are modelled by subgrid-scale (SGS) models. Like in case of DNS, LES are three-dimensional and time-dependent. The main ideas behind LES can be summarised as follows: (i) momentum, mass, and energy are transported mostly by large eddies, (ii) the large eddies are more problem-dependent and governed by the specific mean flow problem, whereas the small eddies are less geometry dependent and tend to be more isotropic and universal, and (iii) in LES sets of (spatial) filtered equations are chosen. Filtering is essentially a manipulation of the exact governing equations to remove only the eddies that are smaller than the size of the filter.

3.2 Filtered governing LES equations

The governing equations employed for LES are obtained by filtering the time-dependent three-dimensional governing equations (1)–(3). In general, a filtered variable, for example, the velocity component u _i , is denoted by an overbar and is defined by

$$ \bar u_i (x, y, z, t) \equiv \mathop{\int\!\!\!\int\!\!\!\int}\limits_{V} {u_i (x^{\prime},y^{\prime},z^{\prime},t) \cdot G(x,y,z,x^{\prime},y^{\prime},z^{\prime},t)dx^{\prime}\,dy^{\prime}\,dz^{\prime}} $$

(8)

In the present study, the rather simple box-filter

$$ G = \cases{{1/(\Delta x\Delta y\Delta z)} & $ {\hbox{for }(x^{\prime},y^{\prime},z^{\prime}) \in V} $ \cr 0 & $ {\hbox{otherwise}}$} $$

(9)

for the filter function G is used for all variables (u _i , p, and T).

Filtering of the governing equations (1) and (2) gives therefore

$$ {{\partial \bar u_i} \over {\partial x_i}} = 0 $$

(10)

$$ {{\partial \bar u_i} \over {\partial t}} + {\partial \over {\partial x_j}}(\bar u_i \bar u_j) = - {1 \over \rho}{{\partial \bar p} \over {\partial x_i}} + {\partial \over {\partial x_j}}\left({\nu {{\partial \bar u_i} \over {\partial x_j}}} \right) + {\partial \over {\partial x_j}}\tau _{ij} $$

(11)

where ρ and ν are the fluid density and the molecular kinematic viscosity, respectively. In equation (11) the subgrid-scale stress tensor is defined by

$$ \tau _{ij} = - \overline {u_i u_j} + \bar u_i \bar u_j $$

(12)

The popular eddy-viscosity model for the subgrid-scale stresses, namely,

$$ \tau _{ij} = {2 \over 3}\hbox{k}\delta _{ij} + 2\nu _t \bar{\hbox{S}}_{ij} $$

(13)

with the subgrid turbulence kinetic energy k is chosen in the present study. In equation (13) ν _t is the turbulent viscosity and $\bar S_{ij}$ is the corresponding filtered strain rate tensor. In order to close the above set of equations, the Smagorinsky model [13] is used to model the eddy viscosity. In detail, one gets

$$ \nu _t = 2(\Delta x\Delta y\Delta z)^{2/3} C_S^2 \sqrt {\bar{\hbox{S}}_{ij} \bar{\hbox{S}}_{ij}} = (\Delta x\Delta y\Delta z)^{2/3} C_S^2 \sqrt {{{\partial \bar u_i} \over {\partial x_j}}\left({{{\partial \bar u_i} \over {\partial x_j}} + {{\partial \bar u_j} \over {\partial x_i}}} \right)} $$

(14)

$$ k = {{\nu _t^2 } \over {C_k^2 (\Delta x\Delta y\Delta z)^{2/3} }} $$

(15)

with the Smagorinsky constants C _S = 0.1 and C _k = 0.094, respectively.

The same filtering procedure is chosen for the temperature equation (3). In this case, an eddy thermal diffusivity is introduced such that the resulting filtered temperature equation can be closed by setting the turbulent Prandtl number to Pr _t = 1.0.

3.3 Numerical approach

To solve the governing LES equations formulated a numerical approach based on the finite-volume-method is chosen. The discretisation of the partial differential equations is performed on a Cartesian mesh with staggered grid arrangement for the velocities. The chosen semi-implicit formulation for the pressure forces results in coupled sets of equations that must be solved by an iterative technique. In the present study, the successive over-relaxation (SOR) method is applied [14]. Time advancing of the equations is done by the second-order Adams-Bashforth method.

The chosen basic numerical method has a formal accuracy that is second-order with respect to time and space increments; for sake of convergence, a second-order monotonicity preserving upwind-difference method [15] for the convective terms is applied. Furthermore, for the velocity profile near boundaries a fifth-order approach is applied. The fractional area and volume obstacle representation [6, 16] is employed to represent the disk. The great advantage of this method is certainly the possibility to use a rectangular Cartesian grid that circumvents convergence problems as in case of cylindrical grids (e.g. at the origin) and enables a rather transparent generation of the discretisated equations. The disadvantage of this method in comparison to body-fitted co-ordinates is the comparable poor resolution of curved obstacles. However, since the LES approach requires usually fine grids, this disadvantage is mainly invalidated in the present study.

3.4 Computational grid and boundary conditions

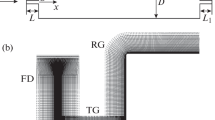
The computational region and the boundary conditions are illustrated by means of Fig. 4. The uniform inflow condition (u ₁ = u _1,in , u ₂ = u ₃ = 0, k = 10^–4 u _1,in ², T = T _∞) and the radiation outflow condition are applied at the corresponding y,z-planes. At the x,y-planes and x,z-planes the slip-condition is prescribed. The disk with radius r = 0.1m and thickness d = 0.002m is located at the origin in the x,y-plane (z = 0, see also Fig. 1). With regard to the global co-ordinate system the rotation is anti-clockwise with angular velocity Ω. At the disk surface the velocity is prescribed by the non-slip condition leading to non-trivial velocity boundary conditions at the obstacle's boundary. The computational region extends from x = –3r to x = +8r, from y = –3r to y = +3r, and from z = –r to z = +r, respectively. These dimensions have to be found sufficient after some preliminary studies.

Fig. 4.

Computational region and boundary conditions

The computational region is discretised by a Cartesian rectangular mesh. For LES a sufficient high grid resolution is required in spite of the large eddies. From elementary laminar boundary layer theory [17] the following minimal grid width relation can be deduced

$$ {{\Delta z} \over r} \approx {1 \over {\sqrt {Re_u}}} $$

(16)

with the translational Reynolds number Re _u = u _1,in r/ν. The same minimum grid width may be required for the other spatial directions, too. The grid is more closely spaced near to the obstacle, satisfying relation (16). The mesh parameters used for the present study are listed in Table 2.

Table 2. Mesh parameters

The initial condition for the flow domain is equal to the uniform inflow condition. At time t = 0 the disk starts to rotate. In order to avoid convergence problems due to non-continuos steps of the applied boundary condition at the disk, the angular velocity Ω increases linearly from Ω = 0 within t = 0 to t = 1.0s. For t > 1.0s the angular velocity Ω reaches its final constant value (for sake of simplicity called Ω in the following).

3.5 Remarks

Upwind differencing used for convective terms may introduce unknown numerical dissipation, but in agreement with the numerical experiences of A. Nakayama [11, 12] it was found by preliminary studies that central differencing leads to serious convergence problems and diverging results.

The grid width far away from the rotating disk may be a little bit too large, but the LES are performed on a standard PC with its typical processor and memory restrictions. However, in the literature [11, 12] it has been recently demonstrated that even such moderate LES could calculate separating flows very well.

4 Numerical results

For two angular velocities Ω = 20rad/s (in the following also called case A) and Ω = 100rad/s (so-called case B) corresponding numerical case studies by means of the above LES method are performed. The main characteristics of the both cases are listed in Table 3, too. By inspection of Fig. 3 it can be seen that case A corresponds to a flow case well captured by the phenomenological Landau model, whereas case B should lead to significant departure from it.

Table 3. Rotational case study parameters

4.1 Cell heat flux distributions

The main objective of [6] has been the calculation of the cell heat fluxes at the disk surface. This was done by means of the RANS method. In the present paper, LES technique is employed to resolve the small time-scale and spatial fluctuations that would be smoothed out by the k-ɛ-model.

The LES-calculated distributions of q̇ are shown in Fig. 5 and Fig. 6 for case A and case B, respectively. The chosen time moment t = 3.0s corresponds to the "steady-state" where no explicit transient effects due to the onset of rotation at t = 0.0s are observable. However, later it will be shown that the situation never reaches a rigorous steady-state. The zig-zag contour curves in Fig. 5 and Fig. 6 are caused artificially by the basic post-processing; they have no real physical meaning. For a sufficient small angular velocity (case A, Fig. 5) the plate boundary layer profile (half-moon-shape) of the heat flux is affected only slightly. For a high angular velocity (case B, Fig. 6), the heat flux distribution tends to be more uniform. The LES lead mainly to the same heat flux distributions as the RANS method [6]. The mean heat transfer values are in fact nearly the same, and the correlations deduced in [6] and the results plotted in Fig. 2 and Fig. 3 remain valid.

Fig. 5.

Heat flux for Ω = 20rad/s (case A)

Fig. 6.

Heat flux for Ω = 100rad/s (case B)

Due to the small time-scale fluctuations of the velocities, the LES values of the local cell flux exhibit small fluctuations, too. This can be observed in Fig. 7 and Fig. 8 where the heat flux profiles along the x-axis (y = 0) at the disk surface are shown. The superposition of profiles calculated at different moments gives a nice illustration of the fluctuations. For a small angular velocity (case A, Fig. 7) the fluctuations are of only minor importance: the profiles remain nearly the same for all moments. In case B, Fig. 8, the fluctuations get major importance that can be seen by the comparable large differences between the profiles. This growing of fluctuations indicates that the flow situation changes dramatically for sufficient high angular velocities.

Fig. 7.

Heat flux for Ω = 20rad/s (case A)

Fig. 8.

Heat flux for Ω = 100rad/s (case B)

4.2 Thermal wakes

The different flow situations caused by different angular velocities are well illustrated by means of the thermal wakes. The LES-calculated temperature distributions in the fluid for z = 0 in the x,y-plane are shown in Fig. 9 and Fig. 10 for Ω = 20rad/s (case A) and Ω = 100rad/s (case B), respectively. The symbol H indicates maximum values. In case A an asymmetric thermal wake is observable due to the anti-clockwise rotation, Fig. 9. Furthermore, a periodic vortex shedding at the upper counter-moving side of the wake is indicated also by means of Fig. 9. For a sufficient high angular velocity (case B), the thermal wake is fully turbulent, Fig. 10. Strong spatial temperature fluctuations can be clearly observed. Due to convection, the temperature fluctuates in case of turbulent wakes also in time. This is illustrated by means of Fig. 11 where a time-wise superposition of different temperature profiles T(x,y = 0, z = 0, t) is plotted. The RANS method is not able to resolve such small time-scale fluctuations, but the mean profile (strongly decreasing temperature with increasing co-ordinate x) may be conceivable as well.

Fig. 9.

Thermal wake for Ω = 20rad/s (case A)

Fig. 10.

Thermal wake for Ω = 100rad/s (case B)

Fig. 11.

Fluctuating temperature profile for Ω = 100rad/s (case B)

The time-evolution of the thermal wake reflects the different flow situations also very well. Some temperature distributions for Ω = 20rad/s and Ω = 100rad/s in the x,y-plane (z = 0) are shown in Fig. 12 and Fig. 13 respectively. The symbol L indicates minimum values. Whereas in case A a deterministic periodic vortex shedding is present (Fig. 12, counter-moving disk boundary), the results in Fig. 13 (case B) demonstrate the turbulent motion of the fluid. However, a vortex shedding is present in case B as well (co-moving disk boundary). From Fig. 13 it becomes clear that the RANS method would be not able to calculate the turbulent effects in greater detail; the LES approach for understanding flow separation and heat transfer augmentation due to rotation is therefore necessary.

Fig. 12.

Thermal wake for Ω = 20rad/s (case A)

Fig. 13.

Thermal wake for Ω = 100rad/s (case B)

4.3 Turbulence for high angular velocity

For high values of the angular velocity (case B) the wake becomes fully turbulent. The regions of high turbulence activities is represented by means of the total viscosity. Corresponding distributions in the x,y-plane (z = 0) and in the x,z-plane (y = 0) at different moments are shown in Fig. 14 and Fig. 15, respectively. Mainly, they corresponds to the temperature distributions of the last subsection. The vortex shedding at the disk boundary is observable. The total value of the viscosity may be compared with the molecular value (see Table 1) to indicate the turbulence centres within the wake.

Fig. 14.

Dynamic viscosity for Ω = 100rad/s (case B)

Fig. 15.

Dynamic viscosity for Ω = 100rad/s (case B)

In Fig. 16 the broadening of the wake in z-direction normal to the disk is shown in greater detail. In case A the wake remain in the disk plane, i.e. the x,y-plane, that is shown in Fig. 17. From Fig. 17 it becomes also clear that the flow separation is mainly two-dimensional in case of small angular velocities. The flow over the disk remains comparable to the plate boundary layer flow in case A; the vortex shedding is a singular phenomenon. It is therefore no surprise that the wake flow in case A is very different from the turbulent wake for higher angular velocities. For example, the distribution of the viscosity for Ω = 20rad/s (Fig. 18) should be compared to the corresponding distribution in case B (Fig. 19). The upper vortex shedding in case of near-critical angular velocity Ω = 20rad/s becomes observable from Fig. 18 and should be compared with the thermal wake shown in Fig. 9. Also, for Ω = 100rad/s the turbulent wake distribution of Fig. 19 is well related to the thermal wake shown in Fig. 10.

Fig. 16.

Dynamic viscosity for Ω = 100rad/s (case B)

Fig. 17.

Dynamic viscosity for Ω = 20rad/s (case A)

Fig. 18.

Dynamic viscosity for Ω = 20rad/s (case A)

Fig. 19.

Dynamic viscosity for Ω = 100rad/s (case B)

Finally, the sake of comparison with the RANS approach of [6], a so-calculated viscosity distribution in the x,y-plane (z = 0) is shown in Fig. 20. Note, that the time moments in Fig. 20 are not rigorously comparable to the moments shown in the corresponding LES-distributions of Fig. 14. The RANS-distributions of Fig. 20 based on a step-boundary condition for the angular velocity Ω (Ω = 0 for t ≤ 0, Ω = constant for t > 0), whereas the LES-distributions of Fig. 14 based on a linear increase of Ω within 0 < t < 1.0s. The turbulent mixing and the small-scale fluctuations cannot be resolved by means of the RANS-method chosen in [6]; the LES method leads to a more realistic picture of the wake. Remarkable is although the fact that even the smoothing RANS-method lead to the same periodic vortex shedding at the lower co-moving wake boundary.

Fig. 20.

RANS-calculated dynamic viscosity for Ω = 100rad/s (case B)

5 The transition to turbulence

From the last section it becomes obvious that near to the critical angular velocity Ω _cr , where the rotation heat transfer augmentation sets on, the wake remains mainly non-turbulent. A periodic vortex shedding at the counter-moving disk boundary occurs due to the slightly supercritical rotation of the disk (case A). For further increased angular velocities (case B) the wake becomes obviously turbulent.

In this situation it cannot be expected that results from simple low-dimensional dynamics should be very relevant to the considered turbulent flow problem. At the transition to turbulence, on the other hand, it is however possible that low-dimensional dynamics could lead to important physical insight. Such a remarkable model of the physics near an instability point has been proposed first by Landau [18]. Even if the Landau-route into chaotic motion may be questionable in principle, the original Landau model works however very well in the vicinity of instability points, i.e. for near-critical control parameters. Important examples for its success are vortex shedding and wake transitions in case of cylinders and spheres [8, 19, 20].

First, the main ideas behind the Landau model are recapitulated in this section; and, second, it is faced with the transition to turbulence and heat transfer augmentation investigated in the present numerical study of a rotating thin disk subjected to an outer parallel stream of air.

5.1 The Landau model

The Landau model describes the physical effects near a critical point in terms of a suitable introduced order-parameter (or amplitude) A that is a function of a suitable chosen control-parameter Ψ. The later one may be identified in the present case with the rotational Reynolds number Re _Ω or directly with the angular velocity Ω. The amplitude A is a global property of the model, i.e. it could be the velocity component at a certain point, or an integral energy variable of the flow. It is convenient to normalise the control-parameter Ψ in such a way that for Ψ ≤ 0 the order-parameter A remains zero, i.e. A = 0 for Ψ ≤ 0. At Ψ = 0 the critical point is reached.

In the following, a mode superposition with the j-th perturbation amplitude

$$ A_j (t) \propto \exp (\sigma_j t) = \exp (\sigma _j^r t + i\sigma _j^i t) $$

(17)

(the usual approach in linear stability analyses) is assumed to be valid for the resulting flow. For under-critical angular velocities Ω < Ω _cr all of the perturbation modes A _j are damped exponentially, i.e. σ _j ^r for Ω < Ω _cr . For Ω ≤ Ω _cr at least one perturbation mode (j) grows exponentially, i.e. σ _j ^r > 0 for Ω > Ω _cr . In case of two or more growing perturbation modes, the following is restricted to the mode j with the largest amplification factor, i.e. with the largest value for the real part σ _j ^r. In the vicinity of the critical point, where the instability sets on, a general complex expression for the perturbation in lowest order is given by means of

$$ {{dA_j} \over {dt}} = (\sigma_j^r + i\sigma_j^i)A_j - B{\vert}{A_j}{\vert}^2 A_j $$

(18)

Equation (18) could be deduced from a Taylor series; then the constant B can be understood as an expansion coefficient. Sometimes, equation (18) is also called Hopf normal form (of the ambient Hopf-bifurcation) [21].

From equation (18) the relation

$$ 2\pi f_{sep} = \sigma _j^i $$

(19)

for the observed perturbation (separation) frequency f _sep follows directly; the limit or saturated amplitude value |A _j |₀ of the perturbation is then

$$ {\vert}{A_j}{\vert}_0 = \sqrt{{{\sigma _j^r} \over B}} $$

(20)

Expanding the real part of the complex factor σ _j leads in lowest order to a linear relationship for the amplification factor

$$ \sigma _j^r \cong k(\Omega - \Omega _{cr}) $$

(21)

where k is a suitable expansion coefficient. This leads directly to the relation

$$ {\vert}{A_j}{\vert}_0 = \sqrt{{{k(\Omega - \Omega _{cr})} \over B}} \equiv \hbox{constant} \cdot (\Omega - \Omega _{cr})^m \quad \hbox{for}\ \Omega > \Omega_{cr} $$

(22)

where m is the critical exponent of the critical point at Ω = Ω _cr . Thus, the critical exponent m in the framework of the Landau model is equal to m = 1/2 which has been plotted in Fig. 3 for the normalised Nusselt number. Sometimes, a different value for the critical exponents may be found; the canonical value m = 1/2 corresponds to the so-called mean-field approximation [8]. A remarkable fact of the Landau model is its universality: the critical behaviour of the system is independent on the underlying microscopic dynamics, because the Landau model averages over the whole control volume. And because of this, for several classes of systems the critical exponents are the same, i.e. they values are universal.

5.2 Rotating disk instability

In the present paper the instability (vortex shedding) due to a rotating disk in an outer parallel stream of air is considered. From Fig. 3 it becomes obvious that a critical angular velocity Ω _cr obviously exists. For Ω > Ω _cr the heat transfer augmentation due to rotation sets on. Quite near to the critical point the above Landau model states that mainly one separation frequency (the imaginary part of the dominant perturbation mode with largest amplification factor) should be observable in the spectrum of the flow. The vortex shedding should be thus periodic in time within this regime.

The numerical investigations of the flow instability lead to the results listed in Table 4. In case A, the near-critical case, the Landau model seems to be well applicable. In the spectrum only one comparable sharp separation frequency f _sep occurs. The periodic vortex generation at the counter-moving disk boundary can be seen by means of Fig. 12 for instance. It is convenient to express the frequency in terms of the Strouhal number

$$ Str \equiv {{f \cdot r} \over {u_{1,in}}} $$

(23)

With f _sep = 1.5 ± 0.2 Hz, r = 0.1m, and u _1,in = 1m/s the value Str = 0.15 ± 0.02 results from equation (23). The magnitude of the present Strouhal number is well comparable to values found in case of von Karman vortex shedding [8, 9]. The velocity profile at the lower disk boundary remains mainly static in case A. This is illustrated by means of Fig. 21 where profiles u ₁(x = 0, y, z = 0, t) for different time moments t = 1.8s to t = 2.8s are shown. There is no significant difference observable for the ten profiles plotted in Fig. 21, in other words: the velocity field has reached a steady-state. The small sketch in Fig. 21 illustrates that the profiles are established at the negative y-axis for x = z = 0. At the upper disk boundary (positive y-axis) detaching eddies are generated in case A. This periodic behaviour is contained in the periodicity of the velocity field in this region. In spite of this, profiles u ₁(x = 0, y, z = 0, t) for different time moments t = 1.8s to t = 2.8s are shown for the positive y-axis at x = z = 0 in Fig. 22. The periodic and deterministic characteristics of the near-critical flow is well illustrated by means of the regular profiles plotted in Fig. 22.

Table 4. Results

Fig. 21.

Velocity profiles u₁ for Ω = 20rad/s (case A) at lower y-axis

Fig. 22.

Velocity profiles u₁ for Ω = 20rad/s (case A) at lower y-axis

For large angular velocities (case B) the assumptions for the Landau model are not satisfied and turbulent motion appears in the wake. The resulting frequency spectrum tends to be more uniform. Even at the lower co-moving disk boundary a vortex generation can be observed. However, the velocity field is irregular, even at this periodic source region. To underline this, the reader may be referred to Fig. 23 and Fig. 24 where the resulting profiles u ₁(x = 0, y, z = 0, t) for different time moments t = 1.8s to t = 2.8s are plotted. Along the complete y-axis there is no simple, regular pattern observable. The differences with regard to the regular flow patterns of Fig. 21 and Fig. 22 are hence dramatic.

Fig. 23.

Velocity profiles u₁ for Ω = 100rad/s (case B) at lower y-axis

Fig. 24.

Velocity profiles u₁ for Ω = 100rad/s (case B) at upper y-axis

The original picture of the transition to turbulence suggested by Landau argued that turbulence may be viewed as a hierarchy of instabilities. As the control parameter increases from zero, a succession of unstable modes appear and saturate in non-linear periodic states having frequencies which are not rationally related. The motion would appear more and more complicated as the number of frequencies increases. However, usually the experiments indicate an abrupt transition to an aperiodic spectrum (turbulent behaviour). This seems to be valid in the present case, too. The numerical investigations are not able to identify a second frequency; the wake becomes turbulent after the first instability. This fast transition has to be expected since the translational and the rotational Reynolds numbers are quite large in the present flow scenario.

6 Conclusion

Large-eddy simulations of the flow field and the heat transfer over a rotating thin disk subjected to an outer forced parallel flow have been performed. The LES method is able to resolve the small-scale fluctuations, despite of its comparable basic filtering and closure approach used in the present study. The numerical results for the mean heat transfer coefficients that have been recently calculated by means of the k-ɛ-model have been well reproduced.

Based on the LES, the heat transfer augmentation due to rotation has been explained in terms of the universal Landau model. The critical exponent m = 1/2 in the vicinity of the critical angular velocity has been found. Here, the periodic vortex generation at the counter-moving disk side is responsible for the effective mean heat transfer augmentation. The co-moving disk boundary is not a source of eddies in case of small angular velocities. If the angular velocity is increased sufficiently, the wake becomes fully turbulent. Then, eddies are created at both edges of the disk, but there is no sharp separation spectrum observable.