Introduction

Marine invertebrates are being fished at an increasing rate worldwide (Keesing and Hall 1998), and some fisheries are experiencing serious declines. Sea urchin fisheries are a case in point. Although there is a long history of exploitation especially in the Atlantic coast of Europe, the Mediterranean, northern Asia, New Zealand and Chile; sea urchin fisheries have experienced significant declines in landings over the past decade almost in all regions (Williams 2002). As a result, the Chilean sea urchin (Loxechinus albus) fishery has become the most important in the world (Andrew et al. 2002), accounting for almost 65% of the world’s landings in some years (Williams 2002; Moreno et al. 2007) and with an overall average landing of 43,000 metric tons for the 2000–2008 period (Chilean Fisheries Service, www.sernapesca.cl).

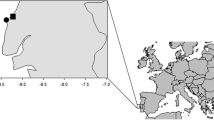
The Chilean sea urchin fishery operates along almost the entire coast of Chile, but the bulk of the catch comes from the southern region (Figs. 1 and 2), where sea urchin beds are scattered in a maze of fjords and islands that span 15 degrees of latitude (42°–57° S), posing a serious challenge to their assessment and fishery management (Moreno et al. 2007). The spatial pattern of exploitation has been highly dynamic, experiencing successive contractions and expansions (Orensanz et al. 2005). Its spatial complexity and the postulated sequential depletion of the grounds (Barahona and Jerez 1997; Andrew et al. 2002; Williams 2002) have led to suggestions that rotational harvesting strategies combined with permanent reserves may offer a suitable alternative to the regional-quota system currently in place (Barahona et al. 2003). To evaluate such policies, a spatially explicit simulation model of the fishery in regions X and XI (Fig. 2) has been developed, which requires specification of fishery and biological parameters at different scales. Growth is one of the key processes that need to be quantified, as optimal rotational strategies may be very sensitive to the assumed growth rates (Botsford et al. 1993; Quinn et al. 1993).

Fig. 1
figure 1

Annual landings of sea urchin fisheries in Chile by geographical zone from 1968 to 2008. Lines and dots correspond to overall landings

Full size image
Fig. 2
figure 2

Location of the three sampling sites in southern Chile (Chonos Archipelago)

Full size image

The estimation of growth parameters in sea urchins has been based on analyses of length frequency distributions (Botsford et al. 1994; Smith et al. 1998; Vadas et al. 2002), size-increments from mark–recapture experiments (Russell 1987; Rowley 1990; Kenner 1992; Ebert and Russell 1992, 1993; Ebert et al. 1999; Lamare and Mladenov 2000; Morgan et al. 2000; Rogers-Bennett et al. 2003; Ebert and Southon 2003) and size-at-age data obtained by reading annual growth bands on shell plates (Crapp and Willis 1975; Nichols et al. 1985; Sime and Cranmer 1985; Gage et al. 1986; Comely and Ansell 1988; Soualili et al. 1999; Agatsuma and Nakata 2004; Shelton et al. 2006; Blicher et al. 2007). In the case of L. albus, growth bands on genital plates (GP) have been used for aging (Gebauer 1992; Gebauer and Moreno 1995; Duran et al. 1999; Barahona et al. 2003), their annual periodicity was validated through the analysis of marginal increments on plates sampled monthly (50 sea urchin/month) from an experimental cohort kept in tidepools over a 12-month period (Gebauer 1992; Gebauer and Moreno 1995).

Different models have been used to represent growth in sea urchins (see Grosjean 2001); asymptotic models being the most common. However, Ebert and Russell (1993) questioned the assumption of asymptotic growth at least for large, long-lived species such as Strongylocentrotus franciscanus and to suggest the use of non-asymptotic models (e.g., Tanaka 1982). They noted that there is no universally best model to characterize sea urchin growth in general. Furthermore, model choice may vary depending on location, as was observed in S. franciscanus (Shelton et al. 2006). Therefore, the selection of an appropriate model is an important first step in quantifying growth for management strategy evaluation.

L. albus is a slow-growing species (Stotz et al. 1992; Gebauer 1992; Gebauer and Moreno 1995; Duran et al. 1999; Barahona et al. 2003). Barahona et al. (2003) suggested that its growth was linear based on size-at-age data, but the range of ages analyzed was too narrow to be conclusive. The aim of this paper is to characterize the growth pattern of L. albus and to examine whether the choice of an appropriate model is invariant over space. To address this goal, we measured and aged a large collection of sea urchin shells sampled from three different locations in southern Chile and compared the performance of asymptotic and non-asymptotic growth models using the Information Theoretic Approach [ITA (Burnham and Anderson 2002)] and Bayesian inference.

Materials and methods

Data sets

Three sets of size-at-age data were obtained by reading growth bands on genital plates and taking measures of test size (at 0.1 mm) of sea urchins collected from three locations in southern Chile: Stokes Is., Amita Is. and Williams Is. (Fig. 2). A stratified-by-size sampling scheme was used following Bromaghin (1993). The samples were collected from surveys (fishery-independent, January 2007) and from the commercial landings (September–October 2006/2007). Aging methodology was based on Gebauer (1992) and Gebauer and Moreno (1995). Mean sizes-at-age from Gebauer (1992) were also analyzed for comparative purposes. In addition, subsamples from Stokes Is. (n = 196) and Amita Is. (n = 162) were used to evaluate the uncertainty in the age estimation by comparing the ages obtained by three blind age readings done by the same reader (LF). Aging errors were evaluated according to the average percent error (APE) and coefficient of variation (CV) (Campana 2001). The APE and CV were estimated according to the following equations:

$$ {\text{APE}}_{j} = 100\% \times {\frac{1}{R}}\sum\limits_{i = 1}^{R} {{\frac{{\left| {X_{ij} - X_{j} } \right|}}{{X_{j} }}}} $$
(1)

where X ij is the ith age determination of the jth sea urchin, X j is the mean age estimate of the jth sea urchin, and R is the number of times each sea urchin is aged. When APE j is averaged across many sea urchins, it becomes an index of average percent error. The CV j is the age precision estimate for the jth sea urchin and also can be averaged across sea urchin to produce a mean CV:

$$ {\text{CV}}_{j} = 100\% \times {\frac{{\sqrt {\sum\nolimits_{i = 1}^{R} {{\frac{{(X_{ij} - X_{j} )^{2} }}{R - 1}}} } }}{{X_{j} }}} $$
(2)

Models

Asymptotic and non-asymptotic models were applied to each data set. The asymptotic models were the Von Bertalanffy (1938) and Richards (1959); the re-parameterizations proposed by Schnute and Fournier (1980) and by Ohnishi and Akamine (2006) were used, respectively, to avoid numerical problems encountered during parameter estimation. The non-asymptotic models proposed by Schnute (1981) and by Tanaka (1982) were also evaluated in addition to a linear model. The parameterizations used are shown in Table 1.

Table 1 Alternative growth models fitted to size-at-age data of L. albus
Full size table

Parameter estimation and model selection

Parameters of the candidate models m i (i = 1–5) were estimated using nonlinear regression, implemented in AD Model Builder (ADMB v 6.0.2, Otter Research Ltd). Model selection was based on the ITA and Bayesian inference. The Akaike information criteria [AIC (Akaike 1973)] and Bayesian or Schwarz information criteria [BIC (Schwarz 1978)] were used to assess model performance. The model with the smallest AIC and BIC value (AICmin and BICmin) was chosen as the model that “best” represented the growth pattern observed in the sea urchin data. In addition, we computed normalized weights of each model (Ward 2008) following Burnham and Anderson (2002) to quantify the plausibility of each model given the data and the set of models as follows:

$$ w_{i} = {\frac{{e^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}\,({\text{IC}}_{m} - {\text{IC}}_{\min )} }} }}{{\sum\nolimits_{m = 1}^{5} {e^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}\,({\text{IC}}_{m} - {\text{IC}}_{\min )} }} } }}}, $$
(3)

where IC corresponds to the AIC or BIC depending on which criterion was used. The weights range between 0 and 1 and are interpreted as the weight of evidence in favor of model i as the best model among the set of all candidate models examined (Burnham and Anderson 2004). Ideally, the ranking of performances, or at least for the choice of best model, would be independent of the criteria or dataset used although this is not necessarily the case.

Results

Size-at-age pattern

The size and age ranges of the sea urchins differed among the datasets. The sample from Stokes Is. had the widest size range (7.7–139.5 mm), followed by Williams Is. (13.2–126.2 mm), and then by Amita Is. (11.8–109.7 mm). As a reference, the minimum and maximum sizes sampled during the 1995–2004 fisheries monitoring program in the area were 31 mm and 145 mm, respectively, and the sizes of sea urchins collected for this analysis extended well beyond the typical size structure of fisheries data of each site (Fig. 3). However, not all the size classes were equally represented in our study. The widest age range was also registered in the sample from Stokes Is. (0–13 years); its age range was similar to that obtained in Williams Is. (1–12 years), while less old animals were registered in Amita Is. (1–10 years) (Fig. 4). Aging errors were generally small (CVs less than 6% and APEs < 5%) except in the smallest size classes (10–30 mm for Stokes Is. and 10–40 mm for Amita Is.) (Table 2). Age differences between repeated readings were size-dependent and variable. For example, in Stokes Is., the size classes with the highest differences were 80–90 mm (7–10 years) and 100–110 mm (8–11 years) (Table 2). Aging errors were larger in Amita Is. than in Stokes Is.

Fig. 3
figure 3

Overall size structure by site obtained from 1995 to 2004 fisheries sampling program. Arrows represent minimum and maximum test sizes from sea urchin collected and aged in this study

Full size image
Fig. 4
figure 4

Size-at-age data (dots) and fitted models (solid line Von Bertalanffy; dashed line Richards; dotted line Schnute; dot dashed line Tanaka; long dashed line linear)

Full size image
Table 2 Uncertainty in age estimation (three readings) based on average percent error (APE) and coefficient of variation (CV) estimated for subsamples from the collections of Stokes and Amita Islands
Full size table

The size-at-age relationship was linear in Stokes Is. and almost linear in Amita Is. and Williams Is. When only the mean size-at-age was considered, the trend was clearly linear in the three datasets (Fig. 4). No departures from linearity were apparent in scatter plots of the residuals of the linear model fitted to the size-at-age data, plotted as a function of age in any of the three locations (Fig. 5).

Fig. 5
figure 5

Residual values at age for the linear models fitted to the data from Amita Is. (a), Stokes Is. (b), and Williams Is. (c)

Full size image

Growth model selection

The results of the model selection for the three locations are presented in Table 3, which includes maximum likelihood parameter estimates, negative log-likelihood values, AIC, AIC differences, BIC and normalized weights for AIC and BIC.

Table 3 Parameter estimates and standard deviation (in parenthesis), and results of model selection for the respective age range in each zone: Amita Is. (1–10), Stokes Is. (0–13), and Williams Is. (1–12)
Full size table

The Tanaka model (m 4 ) was the best in Amita Is. and Williams Is. according to the normalized weights based on both AIC and BIC. This model was supported by a weight of evidence of 47.20 and 43.00% for Amita and 42.84 and 42.67% for Williams, respectively. In Stokes Is., the ranking of models based on the AIC and BIC differed. The Schnute model (m 3 ) had the highest AIC weight (30.89%), while the linear model (m 5 ) was favored by the BIC weight (82.19%) (Table 3).

In order to evaluate whether model choice was affected by the different age ranges present in the three samples, the analysis was repeated using only the data in the age range between 2 and 10 years for the three samples (Table 4). In this case, the rankings differed between areas and also depending on the performance statistics used (AIC and BIC). The AIC still favored the Tanaka model for Amita (44.22% of W i ) and Williams (36.27% of W i ), and the Schnute model (m 3 ) for Stokes (30.23% of W i ). On the other hand, the BIC showed that the linear model (m 5 ) was the best among all candidates for Stokes (80.34% of W i ), Amita (64.91% of W i ), and Williams (61.87% of W i ).

Table 4 Parameter estimates and standard deviation (in parenthesis), and results of the model selection using data for the age range between 2 and 10 years
Full size table

The comparison of the five models showed that von Bertalanffy model had the worst performance, and its estimated rho parameter (c) was always near 1, which implies a linear growth pattern. This non-asymptotic behavior was also observed in the Richard model, which showed a very large asymptotic parameter, much larger than the maximum historic observed size. These results support the use of non-asymptotic growth models for L. albus.

Discussion

Observed pattern in the size-at-age relationship

The size-at-age relationship found in this study for L. albus is similar to that reported by Barahona et al. (2003), but different from the relationships reported by Gebauer (1992), Gebauer and Moreno (1995), and Duran et al. (1999). The mean size-at-age of Gebauer (1992) and Gebauer and Moreno (1995) were slightly nonlinear, but with a similar age range (0–11 years) of this study. On the other hand, a markedly nonlinear pattern was evident in the size-at-age plot reported by Duran et al. (1999). In general, we found evidence of a linear pattern in the size-at-age relationship of the three analyzed data sets (at least in the age range between 2 and 10 years), even though there was evidence of a small curvature at young ages for the datasets from Amita Is. and Williams Is. These results differ also from the growth patterns described for many sea urchin species worldwide (Crapp and Willis 1975; Nichols et al. 1985; Gage and Tyler 1985; Gage et al. 1986; Gage 1987; 1992; Brady and Scheibling 2006; Shelton et al. 2006; Blicher et al. 2007). Most sea urchin species are characterized by a nonlinear growth pattern with an asymptotic or sigmoidal shape.

The quality of parameter estimation depends on the quantity of the information (Chen et al. 2003). In this sense, the sample size and the age range could affect the patterns observed in the size-at-age relationship reported for L. albus. This problem is apparent in the analysis presented by Duran et al. (1999) where some age groups are absent or under represented especially sea urchins of younger (<3 years) and older ages (>7 years). In our study, we had few data points in the small and large sea urchin size classes (e.g., age 1). The same problems related to the sample size (some age groups poorly represented) also could have affected studies conducted on other sea urchin species. The influence of both the sampling design and sample size in the characterization of a pattern in the size-at-age relationship has been emphasized for finfish (e.g., Chen 1996; Chen et al. 2003; Brouwer and Griffiths 2005) and should also be considered for sea urchin species.

Another important factor is the variability in the size-at-age data. In Duran et al. (1999) and Barahona et al. (2003), this variability was considerably larger than in our study. This variability could be a consequence of aging errors. An element of subjectivity is always retained in the interpretation of periodic features in the calcified structures used for aging (e.g., genital plates), which tend to vary markedly in appearance and relative size (Campana et al. 1995). The level of variability is characteristic of each species. Therefore, validation of the aging technique, such as was done by Gebauer (1992) and Gebauer and Moreno (1995) using L. albus, is an important first step. In other sea urchin species, the growth lines in echinoid ossicles have been found to be unreliable indicators of age (e.g., Russell and Meredith 2000).

Uncertainty in the aging, specifically in relation to the precision, reproducibility or aging consistency, could have affected the size-at-age relationship observed in Amita Is. and Williams Is., and perhaps also the pattern reported by Duran et al. (1999). In this sense, the degree of uncertainty (APE and CV) quantified in this study is an important auxiliary information. In all previous studies on sea urchins, no estimates of aging precision were provided. Lai and Gunderson (1987), assessing the effect of aging errors on some population parameters, observed that the magnitude of the changes in the under- or over-estimation of the mean length-at-age increased when the CV of aging error increased. In our study, aging error levels remained low; therefore, we believe that a conspicuous departure from linearity in the data at larger ages seems rather unlikely.

Growth model selection

Several models have been used to estimate the individual growth of sea urchin species (Table 5), but the von Bertalanffy, Richards and Gompertz models have been the most common (Grosjean 2001). Also for L. albus, the von Bertalanffy model in its traditional (Stotz et al. 1992; Gebauer 1992; Gebauer and Moreno 1995; Duran et al. 1999) and re-parameterized (Barahona et al. 2003) formulation have been used.

Table 5 Models used to fit sea urchin growth data in multi-model studies (in bold the model chosen)
Full size table

The choice of a growth model often remains arbitrary or is a question of personal preference (Fletcher 1974; Grosjean 2001). This tendency is well illustrated by the variety of models used to represent sea urchin individual growth (Table 5). The application of the information theory approach (Burnham and Anderson 2002) or Bayesian methods provides a means for using objective criteria in model selection. These approaches encompass a set of basic steps, including an a priori specification of a set of candidate models, the estimation of parameters and their precision, and the model selection based on parsimonius approaches such as Akaike information criterion (Akaike 1973) or Bayesian information criterion (Schwarz 1978). The principle of parsimony implies the selection of a model with the smallest possible number of parameters for an adequate representation of the data, a bias versus variance trade-off. The application of this approach in sea urchin growth studies has been limited and most often the model selection has been based on other statistical analysis (Table 5).

The model selection approach revealed differences in the behavior of the AIC and BIC. The AIC always favored the Tanaka model in Amita Is. and Williams Is., and the Schnute model in Stokes Is., irrespective of whether the complete or restricted age ranges were used. The BIC yielded the same results only for Amita and Williams islands when all data were analyzed. This contrasted with the linear pattern favored for all locations when the age ranges were restricted (ages 2–10). According to Quinn and Deriso (1999), the AIC tends to favor models with more parameters (what we see in this study), while the BIC is more likely to result in a more parsimonious model, as it more heavily penalizes the inclusion of additional parameters.

The differences among the size-at-age relationships observed and modeled could be an effect of the individual variability (process error) and related to the uncertainty in the age estimation (observation error). Katsanevakis and Maravelias (2008) emphasized that model selection is not only dependent on the species-specific growth pattern but also on the quality of the data and the amount of information, which may explain different results among different datasets for the same species.

The difficulty in the selection of a growth model for L. albus, and perhaps for other sea urchin species, is evident. In none of the samples was the best model a clear winner (w i  > 0.9 or 90%), even if the asymptotic models were omitted. But the BIC supported values of w i  > 72% in contrast to the AIC that resulted in values of w i  < 61%. This supports the conclusion by Ebert and Russell (1993) that a unique growth model for sea urchins in general does not exist, but that some generalization of the Tanaka function seems promising. Other examples of this problem have been seen to Strongylocentrotus franciscanus where Ebert and Russell (1993) and Shelton et al. (2006) found that Tanaka (1982) model was the best option, while Rogers-Bennett et al. (2003) reported a logistic dose–response model as the best one. Lamare and Mladenov (2000) suggested that the growth of Evechinus chloroticus was non-asymptotic but still selected the Richards model as the best candidate.

The use of asymptotic models to represent the growth of long-lived species has been questioned (Ebert and Russell 1993). In this study, a non-asymptotic model was clearly the best option, and the von Bertalanffy model was the least supported. Besides, although the Richards model was also supported by the data (Δ i  < 2), the asymptotic size estimated with this model was unrealistically large and should be interpreted as just a model parameter with no biological meaning. This justified the rejection of both the von Bertalanffy (1938) and the Richards (1959) models. Furthermore, the model-based size-at-age predictions made by the linear and von Bertalanffy models were almost identical (Fig. 4). Based on our analysis, we believe that the choice of a model for L. albus should be conditioned on the goal of the model. While the Tanaka model was favored by the information approach, from a practical viewpoint, a linear model would be perfectly adequate in fisheries applications, for example to estimate the age composition from length data.

Implications for further analyses

Further issues such as growth modeling based on repeated-age readings and assessment of the effect of aging error on model selection based on simulations should be considered in future growth studies on this species. According to Cope and Punt (2007), the first topic considered is important, because they demonstrate a consistent bias in parameter estimates when only one age reading is used, regardless of sample size and method used to incorporate the information obtained from multiple readings. They recommend the use of a random-effect method using a gamma distribution in the estimation.

The linear growth pattern reported in this study and its consistency over space is important for further studies, such as the analysis of spatial variability in growth. According to Turon et al. (1995), the use of a single model to fit all growth data is preferable for comparison purposes. In our case, a linear model approach (e.g., linear mixed-effect models) would provide a useful framework to assess simultaneously the effect of several factors and scales on sea urchin growth. It implies a simplification over the models commonly used in population dynamic and stock assessment.