Introduction

Wood has always been a vital factor in human existence and artefacts of wood, both utilitarian and decorative, form a significant part of our cultural heritage.

Uncontrolled variations of ambient temperature (T) and relative humidity (RH) are the principal hazards to the preservation of wooden cultural objects, which are usually exposed to real-world dynamically changing environments.

The climate-induced stress is caused by the hygroscopic nature of wood and the restrained dimensional response to the moisture sorption/desorption. The restraint of the dimensional response is universally present in real-world conditions. It may result from the rigid construction restricting movement, or by joining wood elements with different mutual orientations of their fibre direction. Wood can also experience internal restraint, as the moisture diffusion is not instantaneous and the outer part of the wood will dry more quickly than the interior on reduction of RH. The dry outer part will be restrained from the shrinkage by the still wet core beneath, which will result in mechanical stress: the outer shell will go into tension and the core into compression. Internal structural restraint is a further component of the internal restraint. It is a result of anisotropy in the moisture-related dimensional change: in all wooden objects in which the curvature of the growth rings is significant (e.g. objects of a cylindrical symmetry) the large tangential shrinkage or swelling will not be accommodated because of an insufficient radial change. This would give rise to an internal stress even for slow, quasi-static changes in RH producing no gradient of moisture content in bulk wood.

Investigations of the response of wood to variations in ambient RH showed that the external zone of wooden objects, at least to the depth of several millimetres, continually absorbs and releases water vapour, which results in a gradient of moisture content and stress development (Padfield 1999; Time 2002; Svensson and Toratti 2002). The most extensive efforts to determine the response of wood to fast RH variations have been undertaken so far in the context of heritage science. Vici et al. (2006) have recently reported an extensive research on wooden boards 4 cm thick, simulating the supports of panel paintings, subjected to step variations in RH. Although the time-to-equilibrium was approximately 3 months, very fast responses lasting hours or even minutes were also detected, when asymmetrical moisture gradients were produced by waterproofing one face of the boards. Mecklenburg et al. (1998) quantified changes in RH inducing restrained dimensional change at which wood begins to deform plastically or fails mechanically. The largest dimensional response related to the tangential direction was considered, as this represented the worst-case condition. The authors assumed that the yield point of wood, i.e. the strain at which wood begins to deform plastically, is generally around 0.004 and postulated that the allowable RH variations should not cause strains exceeding this critical value. As the dimensional change coefficients depend strongly on RH, the allowable RH variations were presented as functions of starting RH levels.

The described approach, however, suffers from limitations. The model does not predict stresses resulting from the internal structural restraints: it neglects the curvature of the growth-rings and is therefore, valid for pieces of wood cut from positions away from the axis of the tree trunk. Such simplification is not valid for wooden sculptures, which can be regarded as carved of a tree trunk with the sculpted surfaces loosely following the tangential planes parallel to the trunk axis. Further, the model provides only maximum values of stress corresponding to maximum possible restraint of the object without showing how the stress levels depend on the time periods over which the RH variation occurs. The time-dependent analysis of the wood response to an RH variation is also necessary because dimensional change is a direct function of moisture content in wood rather than ambient RH, and the former depends on the history of RH changes due to the sorption hysteresis.

Historic wooden objects can experience complex patterns of RH variations on one hand and varying restraint levels on the other, as their shapes and construction can be complex. The aim of the present paper has been to model the moisture movement in wooden cultural objects in response to RH variations, as well as resulting internal stresses and risks of damage. A case of a massive wooden cylinder, simulating a wooden sculpture, has been considered, as it constitutes one of the worst cases in terms of risk of climate-induced damage to wooden objects.

A particularly important aim has been to determine the allowable thresholds, i.e. the amplitude and rate of variation in RH, which wooden cylindrical objects can safely endure.

Of the several elementary strains that add up to the total strain of a specimen, our model considered the elastic strain only. The investigations focussed on the acceptable levels of the wood’s response completely recoverable after the stress is removed. Therefore, the model did not consider plastic deformations, which account for tensional stresses in the core at the final stage of drying (Kowalski et al. 2004; Svensson and Toratti 2002). Further, the visco-elastic strain was neglected as its contribution at normal indoor temperatures is very small in comparison to the elastic strain (Toratti and Svensson 1997). Also the thermal strain is insignificant as thermal expansion is almost isotropic and the heat diffusivity is fast when compared with rates of temperature variations in the usual display environments.

Material and measurements of wood properties

Lime wood (Tilia sp.) has been selected for laboratory measurements as this wood species was widely used in the past to produce wooden sculptures and decorations for reasons of availability and ease of processing. The specimens were cut from the outer part of the trunk, air-seasoned for 3 years under shelter. Mean dry density of the specimens was 530 g/cm3.

Two material properties are required to model moisture transport in wood subjected to climatic fluctuations: equilibrium moisture contents (EMC) and moisture diffusion coefficients.

To determine EMC, moisture adsorption/desorption isotherms were determined gravimetrically with the use of a Sartorius vacuum microbalance. Typically, a 0.05 g piece of wood was weighed and outgassed prior to measurement under a vacuum of a residual pressure less than 10−3 mbar. The aim was to move air out of the wood and to eliminate most of the species physisorbed during storage of the sample so that a well-defined, reproducible state was obtained from which the moisture sorption of water vapour could start. Vacuum was maintained until a constant weight was obtained, then subsequent portions of water vapour were introduced and the respective mass increases due to the sorption, and the respective equilibrium pressures were recorded. The isotherms thus determined at 15, 24 and 35°C are shown in Fig. 1. They were used for calculations of the EMC at specific RH values required in the modelling. Linear interpolation was used to derive an EMC for the specific temperature required. As a distinctive and reproducible hysteresis loop appears between adsorption and desorption branches, a similarity-hypothesis approach of Peralta and Bangi (1998) was used to generate intermediate curves (scanning isotherms) reflecting the progress of adsorption and desorption steps. A comparison of the predicted scanning curves with actual experimental data for lime wood, illustrated in Fig. 2, indicates that the approach is highly reliable.

Fig. 1
figure 1

Adsorption isotherms of water vapour for lime wood at several temperatures

Full size image
Fig. 2
figure 2

Adsorption isotherm of water vapour for lime wood at 20°C. The desorption and re-adsorption path following the changes in RH 85 → 20 → 85% predicted by modelling and measured experimentally

Full size image

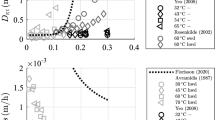
To determine moisture diffusion coefficients, a modified ASTM E 96-80 permeance cup procedure was used. The water vapour transport was measured for a set of cylindrical wood specimens of thickness varying from 2 to 40 mm, and of diameter 35 mm. Values of the moisture diffusion coefficients were obtained for two anatomical directions: longitudinal and radial, for two temperatures (7 and 24°C) and a range of RH between 17 and 91%, controlled by saturated salt solutions placed in the measuring vessels. The RH difference applied across the specimens was around 10%. Moisture diffusion coefficients obtained are plotted in Fig. 3 as a function of moisture content in wood.

Fig. 3
figure 3

Moisture diffusion coefficients for lime wood plotted as a function of moisture content

Full size image

Two material properties are required to calculate internal stresses due to non-uniform moisture distribution on drying or wetting: mechanical properties of wood and swelling/shrinkage in response to changes in T and RH.

The determination of the tensile properties in an extensometer followed the procedures of the ISO Standard 3346 (1985) “Wood; determination of ultimate tensile stress perpendicular to grain”. The rate of the tension loading was between 0.7 and 2 mm/min along the radial and tangential directions. Moduli of elasticity, yield points (strains necessary to produce permanent plastic deformation) and strengths were determined. Yield point was arbitrarily defined as the strain at which the stress–strain curve deflects from a straight line by more than 1%. Prior to measurements, the specimens were preconditioned for 2 months at a constant RH, controlled by a saturated salt solution, to allow for full hygroscopic equilibrium and relaxation of internal stresses. The RH levels selected were 20, 35, 50, 65 and 80%. The measurements were carried out at two temperatures, 7 and 24°C. The tensile parameters are listed in Table 1.

Table 1 Tensile properties of lime wood
Full size table

The amount by which wood specimens swell or shrink was expressed as strain versus EMC. The dimensions of wood specimens coincided with the principal anatomical directions in wood – radial 2 cm × tangential 2 cm × longitudinal 0.5 cm. The dimensional change in radial and tangential direction was measured using two inductive transducers of accuracy 2 μm. The measurements were taken in a specially built specimen holder placed in a vacuum vessel. The vessel was connected to the same outgassing and water vapour dosing system, which was used to determine water vapour sorption isotherms; in fact, the two measurements were taken simultaneously. Both absorption and desorption branches of the dimensional change isotherm were recorded. The tangential and radial strain values obtained are plotted as a function of the EMC in Fig. 4. Dimensional change coefficients determined by the linear fit across the entire range of EMC were αρ = 0.13 and α T  = 0.28.

Fig. 4
figure 4

Dimensional change of lime wood in the radial and tangential directions plotted as a function of the equilibrium moisture content

Full size image

Modelling transport of moisture

The modelling aimed to analyse water vapour movement into or out of wood in response to variations in T and RH in its environment and thus to calculate the evolution of the moisture content gradient across wood. The numerical technique employed sought to change the continuous process of water vapour diffusion into a discrete one in the time and spatial domain. The finite element method as described by Press et al. (1992) was used.

A cylindrical computational mesh was used, commensurable with the symmetry of a tree trunk. Moisture transport along the radial direction only was considered and the calculation was limited to the cross-section of the cylinder. In this way, the moisture exchanges and related stress field were independent of the length of a cylinder. Our preliminary calculations indicated that wood did not experience any change in moisture content within 48 h in response to the variation in the external RH at distances from the top or bottom of a cylinder greater than 5 cm. Therefore, the selected model replicated well the moisture transport occurring for example in wooden sculptures.

The two-dimensional computational mesh consisted of concentric rings of radii changing in steps of 10 μm, which imitated a cell diameter in wood. The rings were further divided into trapezoid elements 10 μm wide in the middle of their height. As the width of the elements remained constant, their number decreased with a decrease of the ring radius.

The formulation of the problem was obtained starting from appropriate equations expressing mass conservation. In each cell of wood, there is equilibrium between water absorbed in the cell wall and water vapour present in the remaining free volume of the cell. The free volume accessible to gases was estimated to be 70%, as an average value for hardwoods (Simpson and TenWolde 1999). If small changes in the cell dimensions during sorption–desorption are neglected, the free volume remains constant. Water vapour contained in each cell is considered to behave as a perfect gas, “trapped in a box” which can leave the box only by diffusion.

On the change of RH in the environment, the moisture content in wood attains a new level of EMC. The EMC at a specific RH value was established from the scanning curves inside the water sorption hysteresis loop reflecting the sorption history as described above.

The immediate response to the RH change in the environment of the wooden element occurs only on its surface. The change to the new level of EMC in elements situated inside the wood requires movement of water vapour into or out of wood, which is described by the equation of diffusion applied for one dimensional case, along direction ρ in Fig. 5, in the following form:

$$ \begin{aligned}{} \frac{{\delta c(\rho ,t)}} {{\delta t}} & = \nabla (D(c(\rho ,t))\nabla c(\rho ,t) = \frac{1} {\rho }\frac{\delta } {{\delta \rho }}(\rho D(c(\rho ,t))\frac{{\delta c(\rho ,t)}} {{\delta \rho }} \\ & = \frac{{D(c(\rho ,t)}} {\rho }\frac{{\delta c(\rho ,t)}} {{\delta \rho }} + \frac{{\delta D(c(\rho ,t))}} {{\delta \rho }}\frac{{\delta c(\rho ,t)}} {{\delta \rho }} + D(c(\rho ,t))\frac{{\partial ^{2} c(\rho ,t)}} {{\partial \rho ^{2} }} \\ \end{aligned} $$
(1)

in which c is the water content in the element at the position ρ and moment t, and D is the diffusion coefficient which is a function of this water content.

Fig. 5
figure 5

Two-dimensional computational mesh and progress of calculation of water content across wood in time and space

Full size image

As D(c(ρ,t)) is not a constant and c(ρ,t) cannot be separated into parts depending on ρ and t, respectively, Eq. 1 has no analytical solution and c(ρ,t) can be determined numerically using, e.g. the least square method.

Making use of the definition of partial derivatives

$$ \begin{aligned}{} & \frac{{\delta c(\rho ,t)}} {{\delta t}} = {\mathop {\lim }\limits_{\Delta t \to 0} }\frac{{c(\rho ,t + \Delta t) - c(\rho ,t)}} {{\Delta t}} \\ & \frac{{\delta c(\rho ,t)}} {{\delta \rho }} = {\mathop {\lim }\limits_{\Delta \rho \to 0} }\frac{{c(\rho + \Delta \rho ,t) - c(\rho ,t)}} {{\Delta \rho }} \\ & \frac{{\partial ^{2} c(\rho ,t)}} {{\partial \rho ^{2} }} = {\mathop {\lim }\limits_{\Delta \rho \to 0} }\frac{{c(\rho + \Delta \rho ,t) - 2c(\rho ,t) + 2c(\rho - \Delta \rho ,t)}} {{\Delta \rho ^{2} }} \\ \end{aligned} $$
(2)

c(ρ,t) can be expressed as c n j , where index n signifies a subsequent step in time Δt, and index j a subsequent step in space Δρ. Then

$$ \begin{aligned}{} & \frac{{\delta c(\rho ,t)}} {{\delta t}} = {\mathop {\lim }\limits_{\Delta t \to 0} }\frac{{c^{{n + 1}}_{j} - c^{n}_{j} }} {{\Delta t}} \\ & \frac{{\delta c(\rho ,t)}} {{\delta \rho }} = {\mathop {\lim }\limits_{\Delta \rho \to 0} }\frac{{c^{n}_{{j + 1}} - c^{n}_{j} }} {{\Delta \rho }} \\ & \frac{{\partial ^{2} c(\rho ,t)}} {{\partial \rho ^{2} }} = {\mathop {\lim }\limits_{\Delta \rho \to 0} }\frac{{c^{n}_{{j + 1}} - 2c^{n}_{j} + 2c^{n}_{{j - 1}} }} {{\Delta \rho ^{2} }}. \\ \end{aligned} $$
(3)

Substituting the above in Eq. 1, one obtains

$$ \frac{{c^{{n + 1}}_{j} - c^{n}_{j} }} {{\Delta t}} = \frac{{D_{j} }} {{\rho _{j} }}\frac{{c^{n}_{{j + 1}} - c^{n}_{j} }} {{\Delta \rho }} + \frac{{D_{{j + 1}} - D_{j} }} {{\Delta \rho }}\frac{{c^{n}_{{j + 1}} - c^{n}_{j} }} {{\Delta \rho }} + D_{j} \frac{{c^{n}_{{j + 1}} - 2c^{n}_{j} + c^{n}_{{j - 1}} }} {{\Delta \rho ^{2} }} $$
(4)

in which

$$ D_{j} = D(c^{n}_{j} ){\text{ and }}\rho _{j} = j\Delta \rho . $$

Equation 4 can be implemented numerically and the moisture content can be determined in any place within the wood and at any time (Fig. 5).

The response of wood to the change in the second environmental parameter, i.e. air temperature is much more immediate. Thermal diffusivity in wood is 4–5 orders of magnitude higher than the time constant of water vapour transport. Therefore, the response of wood to the temperature variations in real-world display conditions can be considered instantaneous and hence a uniform distribution of temperature across wood at any moment was assumed.

The change in temperature gives rise to an isochoric change in the water vapour present in the cell. Assuming that water vapour in wood behaves as a perfect gas, one can write

$$ \frac{{p(T)}} {T} = \text{const} . $$
(5)

in which p(T) is pressure of water vapour at a given temperature T.

Also the saturation pressure of water vapour (p s) depends on temperature as described by Teten’s law:

$$ p_{{\text{s}}} (T) = 6.11 \times 10^{{\frac{{aT}} {{b + T}}}} {\text{ hPa}} $$
(6)

with a = 7.5 and b = 237.3°C for T > 0.

As both water vapour pressure and saturation water vapour pressure undergo change, RH will also change

$$ {\text{RH}}_{{{\text{new}}}} = {\text{RH}}_{{{\text{old}}}} \frac{{T_{{{\text{new}}}} }} {{T_{{{\text{old}}}} }}\frac{{p_{{\text{s}}} (T_{{{\text{old}}}} )}} {{p_{{\text{s}}} (T_{{{\text{new}}}} )}}. $$
(7)

The temperature induced change in RH will bring about in turn an adjustment of the EMC in the element. On the release or uptake of water vapour, the pressure inside the element will change according to Eq. 8

$$ \Delta p = \frac{{\Delta m}} {{{\text{M}}_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}\frac{{RT}} {{V_{{\text{a}}} }} = \frac{{dRT}} {{0.7{\text{M}}_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}\Delta {\text{EMC}} $$
(8)

where Δp is the pressure change, Δm is the change in the moisture content, M H20 is the molecular mass of water, R is the gas constant, T is the temperature, V a is the volume accessible to water vapour in the cell being V a = 0.7 V, where V is the total volume of the cell, d is the density of wood, and ΔEMC is the change in the equilibrium moisture content.

A change in water vapour pressure will change RH, which in turn will lead to a change in the content of water adsorbed. The process is repeated until a new equilibrium is established. Calculating the new EMC in the given finite element which has adapted to the new RH level is numerically analysed by using the above iterative procedure.

Modelling forces in elemental cells

For each moisture distribution, corresponding stress field develops across the wood. For a wooden cylinder, stress is caused by the internal restraint – dynamic and structural – of the dimensional change. As described in “Introduction”, internal dynamic restraint is generated by a gradient of the moisture content and related differential dimensional change across bulk wood, whereas the structural restraint is a result of the curvature of the growth rings.

The field of stress for each moisture distribution and the related restrained dimensional change was obtained with the use of the finite elements procedure using the same cylindrical computation mesh as for determining the transport of moisture. The formulation of the problem for the two-dimensional cross-section of the cylinder and moisture transport limited to the radial direction is obtained starting from five appropriate equations:

  • Two geometrical equations describing deformation:

    $$ \begin{aligned}{} & \varepsilon _{\rho } = \frac{{\delta u}} {{\delta \rho }} \\ & \varepsilon _{t} = \frac{u} {\rho } \\ \end{aligned} $$
    (9)

    where ε ρ and ε t are deformations in the radial and tangential directions, respectively, and u is displacement.

  • Two physical equations:

    $$ \begin{aligned}{} & \sigma _{\rho } = E_{\rho } (1 - \nu _{{\rho t}} \nu _{{t\rho }} ){\left\{ {\varepsilon _{\rho } - \alpha _{\rho } \Delta {\text{RH}}} \right\}} + E_{\rho } \nu _{{t\rho }} (1 - \nu _{{\rho t}} \nu _{{t\rho }} ){\left\{ {\varepsilon _{t} - \alpha _{t} \Delta {\text{RH}}} \right\}} \\ & \sigma _{t} = E_{t} (1 - \nu _{{\rho t}} \nu _{{t\rho }} ){\left\{ {\varepsilon _{t} - \alpha _{t} \Delta {\text{RH}}} \right\}} + E_{t} \nu _{{\rho t}} (1 - \nu _{{\rho t}} \nu _{{t\rho }} ){\left\{ {\varepsilon _{\rho } - \alpha _{\rho } \Delta {\text{RH}}} \right\}} \\ \end{aligned} $$
    (10)

    where σ ρ and σ t are stresses in the radial and tangential directions, respectively, E ρ and E t are moduli of elasticity in the radial and tangential directions, respectively, ν ρt and ν tρ are Poisson’s ratio for the forces applied along the radial and tangential directions, respectively, α ρ and α t are dimensional change coefficients in the radial and tangential directions, respectively, and ΔRH is the change in RH in the finite element analyzed.

  • One equation describing the condition that the resultant force must be zero at any moment

    $$ \frac{{\delta \sigma _{\rho } }} {{\delta \rho }} + \frac{{\sigma _{\rho } - \sigma _{t} }} {\rho } = 0 $$
    (11)

    E ρ and E t are not constants, but they depend on the moisture content as given in Table 1.

It was further assumed that ν ρt  = ν tρ  = 0.4 (Green et al. 1999).

Computational algorithm

Each modelling is started with a uniform distribution of moisture in the object, corresponding to the initial, constant RH selected. Furthermore, presence of no forces is assumed.

Then variable boundary conditions, reflecting microclimatic variations, are imposed on the perimeter of the computational mesh. For each modelling step, the initial condition is moisture distribution in the elements of the mesh. In all calculations, the moisture distribution is of axial symmetry, which simplifies the computation.

Then, the following numerical operations are cyclically performed for the time interval assumed:

  1. 1.

    Iteration of the equation of the water vapour diffusion.

  2. 2.

    Calculation of the new EMC level, if temperature outside the cylinder has been changed.

  3. 3.

    Calculation of the tangential and radial stresses appearing in the mesh as a result of the release or uptake of moisture.

Results and discussion

The calculations were performed for a cylinder of diameter 13 cm using the material properties of lime wood specified above.

A first series of calculations was performed for a step RH variation in which RH was lowered instantaneously from 70 to 30%. EMC for wood fully equilibrated at the initial and final RH levels were 14 and 6%, respectively. The time interval was 5 s. The change in moisture content distribution across wood in response to the described RH variation is shown in Fig. 6. As anticipated, early in drying, the change in moisture content is concentrated in the outer part of the cross-section. The surface shell, the first ring of a width of 10 μm, attains the new EMC almost immediately. However, the core of the cylinder, lying deeper than 1 cm in the wood, does not experience any change in the moisture content before 3 h. After 24 h, the change in the EMC at this distance from the surface is only 30% of the change at the surface.

Fig. 6
figure 6

Change in the distribution of moisture content at selected distances from the external surface of a wooden cylinder for a step RH variation from 70 to 30%

Full size image

The presented strong gradient in the moisture content gives rise to a considerable drying stress, due to the differential shrinkage being restrained (Fig. 7). A magnitude of the tangential stress is most significant; therefore, further discussion will be limited just to this parameter as the worst-case condition. The plots mirror the changes in the moisture contents at different strata of wood. The maximum tension of 5.5 MPa is attained very quickly at the surface layer. At such a stress level, wood is endangered by plastic deformation, as the elastic limit of approximately 2 MPa at 30% RH is exceeded 2.5 times. The tension is even close to the plastic range limit of approximately 6.3 MPa at 30% RH and hence mechanical failure – surface cracking can occur.

Fig. 7
figure 7

Tangential stress developing in wood as a result of the gradient of moisture content shown in Fig. 6

Full size image

The stress decreases very slowly as the moisture gradient gradually vanishes on a progressive drying of the interior layers in wood, as illustrated in Fig. 8.

Fig. 8
figure 8

Evolution of moisture content gradient and tangential stress levels, visualized using a grey scale, in the cross-section of a wooden cylinder after 24 h (a) and 10 days (b) from a step RH variation between 70 and 30%. The lightest tone corresponds to the initial moisture content of 14% and lack of stress. The darkest tone corresponds to the final moisture content of 6 % and the stress level of 5.75 MPa

Full size image

The maximum stress induced by the RH variation depends not only on the magnitude of that variation, but also on the RH range within which the variation occurs. Therefore, the maximum stress levels have to be expressed as a map of values, which takes into account the starting RH levels. Such a map calculated for a wooden cylinder of diameter 13 cm is shown in Fig. 9. Domains of RH variations endangering wood by deformation or complete failure are marked, as well as tolerable RH variations producing stress within the elastic domain. The map shows that any RH variation exceeding 10–15% produces stresses going beyond the elastic limit so that wood can experience damaging plastic deformations. The risk of failure appears already for an RH variation of 40% if the change occurs from a high initial RH level of above 95%. The variations centred on 50% RH could be considered the safest, confirming the established observation of the conservation practice. The reason for that is the least slope of dependence between RH and EMC in the mid-region of the water vapor adsorption isotherm (Fig. 1).

Fig. 9
figure 9

Maximum stress induced by step RH variations between 10 and 90% plotted as a function of the initial RH level from which the variation starts. Domains of RH variations endangering the wood by irreversible response (deformation) or complete failure are marked together with the domain of tolerable variations producing safe, reversible response of the wood

Full size image

Figure 10 shows a similar map derived for the RH drop from 70 to 30%, but which occurred over a time period of 24 h, i.e. the variation changed from instantaneous to diurnal. The map indicates an increase in the domain of RH variations, which produce stress levels within the elastic limit safe for the material. RH variations potentially leading to failure have been practically eliminated.

Fig. 10
figure 10

Maximum stress induced by RH variations between 10 and 90% occurring over the time period of 24 h plotted as a function of the initial RH level from which the variation starts. Domains as in Fig. 9

Full size image

Finally, Fig. 11 shows the final stress field reached when the wooden cylinder is in a full equilibrium with the new RH, i.e. no gradient in EMC across the cylinder is observed. The stress is entirely due to the contribution from the structural internal restraint. Such stress levels would be produced if the material is subjected to changes in RH over a sufficiently long time. The map indicates the maximum possible expansion of the domain of RH variations, which produce stress within the elastic limit safe for the material.

Fig. 11
figure 11

Stress induced by RH variations between 10 and 90% after a full equilibrium with the new RH is reached, i.e. no gradient in EMC is observed. Domains as in Fig. 9

Full size image

The numerical simulation allows determining time periods of drop in the RH, which would produce stress below the yield point of wood. Such time periods for the RH drop from 70 to 30% are plotted as a function of the diameter of a cylinder in Fig. 12. The time necessary for a safe adaptation of the wooden cylinder to the RH change increases exponentially with the diameter, for example reaching 20 days for a diameter of 13 cm. The measurements illustrate directly and quantitatively the old wisdom of preventive conservation that even a significant RH change can be safe if the adaptation time for a wooden object is long enough.

Fig. 12
figure 12

Time periods of the RH variation from 70 to 30% which produce stress below the yield point of the wood as a function of cylinder diameter

Full size image

Finally, stresses due to temperature driven changes in EMC at a constant RH were calculated. Fig. 13 shows a map of maximum stresses produced by an instantaneous temperature change at a constant RH of 50% for a cylinder of diameter 13 cm. It should be noted that even for huge temperature variations, e.g. from 10 to 50°C, the stress values do not reach even the yield point, which is 2.06 MPa at 50% RH. Therefore, stresses produced by real-world variations in temperature specially recorded indoors are safe for wooden objects.

Fig. 13
figure 13

Stress induced by temperature variations from −15 to +45°C due to changes in EMC across wood

Full size image

Conclusions

A systematic numerical modelling of the moisture movement and resulting stress field has provided insight into the response of a wooden cylinder, an important case imitating wooden sculptures, to variations in ambient T and RH. The allowable RH variations, below which mechanical damage will not occur, were derived as functions of the amplitude, time period and the starting RH level of the variation. In this way, domains of reversible and irreversible response of wood, as well as of material failure could be determined. The middle RH region (close to 50%) is optimal from the standpoint of risk of damage due to the least slope of dependence between RH and EMC at this RH level. Lime wood can endure step RH variations of up to 15% in this moderate region but the allowable domain narrows when RH levels shift from the middle range. The allowable amplitude of the variations increases when time allowed for the change increases. However, the stress field does not vanish even for slow, quasi-static changes in RH due to structural internal restraint resulting from anisotropy in the moisture-related dimensional change.