A fully anisotropic mechanism for formation of trapped surfaces in vacuum

Abstract

We present a new, fully anisotropic, criterion for formation of trapped surfaces in vacuum. More precisely we provide local conditions on null data, concentrated in a neighborhood of a short null geodesic segment (possibly flat in all other directions) whose future development contains a trapped surface. This extends considerably the previous result of Christodoulou (Monographs in Mathematics. European Mathematical Society, Switzerland, 2009) which required instead a uniform condition along all null geodesic generators. To obtain our result we combine Christodoulou’s mechanism for the formation of a trapped surface with a new deformation process which takes place along incoming null hypersurfaces.

1 Introduction

According to the celebrated incompleteness result of Penrose, the future Cauchy development of a non-compact initial data set of the Einstein vacuum¹ equations,

$$\begin{aligned} \text{ Ric }(g)=0 \end{aligned}$$

which contains a trapped surface, must be incomplete. Thus, in a sense, the fundamental issue of formation of spacetime singularities in gravitational collapse is reduced to the somewhat more tangible problem of formation of trapped surfaces. This, on the other hand, is still a highly non-trivial problem. Indeed, the expansions of both null geodesic congruences generated by a compact, trapped surface $S$ is required, by definition, to be negative at every point on $S$. To show that such surfaces can form in evolution, starting with regular initial data sets which contain no trapped surfaces, requires a deep understanding of the dynamics of the Einstein equations. It is for this reason that the problem has remained open for more than forty years, in the wake of Penrose’s result, until the recent breakthrough of Christodoulou. In [2] he was able to identify an open set of regular² initial conditions, on a finite outgoing null hypersurface, with trivial data on an incoming null hypersurface, whose future development must contain a trapped surface. The main condition in Christodoulou’s result is that the data verify a uniform lower bound condition, with respect to all short, null geodesic generators of the outgoing initial null hypersurface. The goal of this paper is to significantly relax this uniform condition by showing that a trapped surface forms even if the local null outgoing data is only concentrated in a neighborhood of a short null geodesic segment (possible flat in all other directions).

We recall that Christodoulou’s proof in [2] rests on two main ingredients:

• (1) A semi-global existence result for the characteristic initial value problem with large initial data³ measured relative to a small parameter $\delta >0$. The precise dependence on $\delta$, which Christodoulou calls the short pulse method, was subsequently relaxed in [4, 5]; see also [7]. In all these results the data on the incoming null hypersurface is assumed to be flat. This restriction has been recently removed in [6]. The semi-global result allows one to construct the future development of the initial data, together with a double null foliation⁴ $(u,{\underline{u}}),\,0\le u\le u_*,\,0\le {\underline{u}}\le {\underline{u}}_*$, and full control on all the geometric quantities associated to it.

• (2) An amplification mechanism for the integrals $\int _\gamma |\hat{\chi }|^2$ along outgoing null geodesic segments $\gamma$, (with $\hat{\chi }$ denoting the outgoing null shear). This mechanism, which requires the estimates obtained in the constructive step (1), combines with a uniform lower bound assumption of these integrals on the initial null hypersurface, and leads to the formation of a trapped surface. It is important to note that all trapped surfaces found in this fashion belong to the concentric spheres generated by the double null foliation $(u,{\underline{u}})$, i.e. are of the form $S=\{u=u_1, {\underline{u}}={\underline{u}}_1\}$, for some $0 <u_1\le u_*, \,0<{\underline{u}}_1\le {\underline{u}}_*$.

The new result we present in this paper relies heavily on the hard part of the above results, i.e. the construction of the spacetime in (1). We modify however part (2) by combining Christodoulou’s argument with a new deformation argument along the incoming null hypersurfaces $\{{\underline{u}}=\text{ const }\}$. This allows us to dramatically weaken his uniform condition merely to a localized condition in a neighborhood of a null geodesic of $\{u=0\}$. The deformation is determined by solving a simple elliptic inequality on the standard sphere $S_{0,0}=\{{\underline{u}}=0\} \cap \{u=0\}$, see (20). We note that the trapped surface we find by our argument does not belong any longer to the double null foliation constructed in step (1).

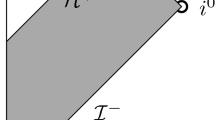
1.1 Geometry of a double null foliation

As in [4] we consider a region ${\mathcal {D}}={\mathcal {D}}(u_*,{\underline{u}}_*)$ of a vacuum spacetime $(M,g)$,

$$\begin{aligned} \text{ Ric }(g)=0, \end{aligned}$$

spanned by a double null foliation generated by the optical functions $(u,{\underline{u}})$ increasing towards the future⁵, where $0\le u\le u_*$ and $0\le {\underline{u}}\le {\underline{u}}_*$ (see Fig. 1). These spacetimes will be constructed via solving a characteristic initial value problem.

Fig. 1

The shaded region on the right represents the domain ${\mathcal {D}}(u_*,{\underline{u}}_*),\,{\underline{u}}_*= \delta$. The same picture is represented on the left, by emphasizing that all points in the diagram on the right are in fact $2$-surfaces

We denote by $H_u$ the outgoing null hypersurfaces generated by the level surfaces of $u$ and by $\underline{H}_{{\underline{u}}}$ the incoming null hypersurfaces generated level hypersurfaces of ${\underline{u}}$. We write $S_{u,{\underline{u}}}=H_u\cap \underline{H}_{{\underline{u}}}$ and denote by $H_{u}^{({\underline{u}}_1,{\underline{u}}_2)}$ and $\underline{H}_{{\underline{u}}}^{(u_1,u_2)}$ the regions of these null hypersurfaces defined by ${\underline{u}}_1\le {\underline{u}}\le {\underline{u}}_2$ and respectively $u_1\le u\le u_2$. Let $L=-2g^{\alpha \beta }\partial _\alpha u\partial _\beta ,\,\, {\underline{L}}=-2g^{\alpha \beta }\partial _\alpha {\underline{u}}\partial _\beta ,\,\,$ be the geodesic vectorfields associated to the two foliations and define,

$$\begin{aligned} g(L,{\underline{L}}):=-2\Omega ^{-2}=4g^{\alpha \beta }\partial _\alpha u\partial _\beta {\underline{u}}. \end{aligned}$$

(1)

As is well known, the space-time slab ${\mathcal {D}}(u_*, {\underline{u}}_*)$ is completely determined (for small values of $u_*, {\underline{u}}_*$) by data along the null hypersurfaces $H_0,\,{\underline{H}}_0$ corresponding to ${\underline{u}}=0$ and $u=0$ respectively. We assume that $\Omega =1$ along $H_0$ and $\underline{H}_0$, i.e.,

$$\begin{aligned} \Omega (0,{\underline{u}})&= 1, \qquad 0\le {\underline{u}}\le {\underline{u}}_*,\end{aligned}$$

(2)

$$\begin{aligned} \Omega (u,0)&= 1, \qquad 0\le u\le u_*. \end{aligned}$$

(3)

We denote by $r=r(u,{\underline{u}})$ the area-radius of the $2$-surface $S=S_{u,{\underline{u}}}$, i.e. $|S_{u,{\underline{u}}}|=4\pi r(u,{\underline{u}})^2$. In this paper, we assume $r(0,0)=1$.⁶

Throughout this paper we work with the normalized null pair $(e_3,e_4)$ defined by

$$\begin{aligned} e_3=\Omega {\underline{L}},\quad e_4=\Omega L \end{aligned}$$

which satisfy

$$\begin{aligned} g(e_3,e_4)=-2. \end{aligned}$$

Given a 2-surfaces $S_{u,{\underline{u}}}$ and $(e_a)_{a = 1,2}$ an arbitrary frame tangent to it we define the Ricci coefficients,

$$\begin{aligned} \Gamma _{(\lambda )(\mu )(\nu )}=g(e_{(\lambda )}, D_{e_{(\nu )}} e_{(\mu )} ),\quad \lambda ,\mu ,\nu =1,2,3,4. \end{aligned}$$

(4)

These coefficients are completely determined by the following components,

$$\begin{aligned} \chi _{ab}&= g(D_a e_4,e_b),\, \,\, \quad \,\,\, \underline{\chi }_{ab}=g(D_a e_3,e_b),\nonumber \\ \eta _a&= -\frac{1}{2} g(D_3 e_a,e_4),\quad \underline{\eta }_a=-\frac{1}{2} g(D_4 e_a,e_3)\nonumber \\ \omega&= -\frac{1}{4} g(D_4 e_3,e_4),\quad \,\,\, {\underline{\omega }}=-\frac{1}{4} g(D_3 e_4,e_3),\nonumber \\ \zeta _a&= \frac{1}{2} g(D_a e_4,e_3) \end{aligned}$$

(5)

where $D_a=D_{e_{(a)}}$. We also introduce the null curvature components,

$$\begin{aligned} \alpha _{ab}&= R(e_a, e_4, e_b, e_4),\quad \, \,\, {\underline{\alpha }}_{ab}=R(e_a, e_3, e_b, e_3),\nonumber \\ \beta _a&= \frac{1}{2} R(e_a, e_4, e_3, e_4) ,\quad {\underline{\beta }}_a =\frac{1}{2} R(e_a, e_3, e_3, e_4),\nonumber \\ \rho&= \frac{1}{4} R(Le_4,e_3, e_4, e_3),\quad \sigma =\frac{1}{4} \,^*R(e_4,e_3, e_4, e_3). \end{aligned}$$

(6)

Here $\,^{*}R$ denotes the Hodge dual of $R$. We denote by $\nabla$ the induced covariant derivative operator on $S_{u,{\underline{u}}}$ and by $\nabla _3$, $\nabla _4$ the projections to $S_{u,{\underline{u}}}$ of the covariant derivatives $D_3$, $D_4$. Observe that,

$$\begin{aligned} \omega&= -\frac{1}{2} \nabla _4 (\log \Omega ),\qquad {\underline{\omega }}=-\frac{1}{2} \nabla _3 (\log \Omega ),\nonumber \\ \eta _a&= \zeta _a +\nabla _a (\log \Omega ),\quad \underline{\eta }_a=-\zeta _a+\nabla _a (\log \Omega ). \end{aligned}$$

(7)

We recall the integral formulas⁷ for a scalar function $f$ in ${\mathcal {D}}$,

$$\begin{aligned} \frac{d}{ d{\underline{u}}} \int _{S_{u,{\underline{u}}}} f&= \int _{S_{u,{\underline{u}}}} \left( \frac{df}{d{\underline{u}}}+ \Omega \text{ tr }\chi f\right) = \int _{S_{u,{\underline{u}}}} \Omega (e_4(f)+ \text{ tr }\chi f),\nonumber \\ \frac{d}{ du } \int _{S_{u,{\underline{u}}}} f&= \int _{S_{u,{\underline{u}}}} \left( \frac{df}{du}+\Omega \text{ tr }\underline{\chi }f\right) = \int _{S_{u,{\underline{u}}}}\Omega (e_3(f)+ \text{ tr }\underline{\chi }f). \end{aligned}$$

(8)

In particular,

$$\begin{aligned} \frac{dr}{d{\underline{u}}}=\frac{1}{8\pi }\int _{S_{u,{\underline{u}}}}\Omega \text{ tr }\chi , \qquad \frac{dr}{du}=\frac{1}{8\pi }\int _{S_{u,{\underline{u}}}}\Omega \text{ tr }\underline{\chi }. \end{aligned}$$

(9)

We also recall the following commutation formulae⁸ between $\nabla$ and $\nabla _4, \nabla _3$ in [3]:

Lemma 1

For a scalar function $f$:

$$\begin{aligned} \left[ \nabla _4,\nabla \right] f&= \frac{1}{2} (\eta +\underline{\eta }) D_4 f -\chi \cdot \nabla f,\end{aligned}$$

(10)

$$\begin{aligned} \left[ \nabla _3,\nabla \right] f&= \frac{1}{2} (\eta +\underline{\eta }) D_3 f -\underline{\chi }\cdot \nabla f. \end{aligned}$$

(11)

For a 1-form tangent to $S$:

$$\begin{aligned} \left[ \nabla _4,\nabla _a\right] U_b&= -\chi _{ac} \nabla _c U_b +\in _{ac}\, ^*\beta _b U_c +\frac{1}{2}(\eta _a+\underline{\eta }_a) D_4 U_b \\&-\chi _{ac} \,\underline{\eta }_b\, U_c +\chi _{ab} \,\underline{\eta }\cdot U,\\ \left[ \nabla _3,\nabla _a\right] U_b&= -\underline{\chi }_{ac} \nabla _c U_b +\in _{ac} ^*{\underline{\beta }}_b U_c + \frac{1}{2}(\eta _a+\underline{\eta }_a) D_3 U_b \\&- \underline{\chi }_{ac} \eta _b\,U_c+\underline{\chi }_{ab} \, \eta \cdot U. \end{aligned}$$

In particular,

$$\begin{aligned} \left[ \nabla _4,\mathrm{div}\right] U\!&= \!-\frac{1}{2} \text{ tr }\chi \, \mathrm{div} U\!-\!\hat{\chi }\cdot \nabla U -\beta \cdot U \!+\!\frac{1}{2} (\eta +\underline{\eta })\cdot \nabla _4 U- \underline{\eta }\cdot \hat{\chi }\cdot U ,\\ \left[ \nabla _3,\mathrm{div}\right] U\!&= \!-\frac{1}{2} \text{ tr }\underline{\chi }\, \mathrm{div} U\!-\!\underline{\hat{\chi }}\,\cdot \nabla U \!+\! {\underline{\beta }}\cdot U +\frac{1}{2} (\eta +\underline{\eta })\cdot \nabla _3 U\! -\! \eta \cdot \underline{\hat{\chi }}\,\cdot U. \end{aligned}$$

1.2 Main theorem

For simplicity of our presentation⁹ we describe our main result in the context of the class of initial data used by Christodoulou. This class of initial data gives rise to a class of spacetimes endowed with a double null foliation as described in the previous subsection. As in [2], we prescribe the null incoming data to be trivial, i.e. corresponding to null cones in Minkowski space. In particular $S_{0,0}$ is the standard sphere of radius $1$. To prescribe null data on $H_0$ amounts to prescribe an arbitrary symmetric, traceless, smooth tensor $\hat{\chi }_0$, called initial shear. In [2], the initial shear is prescribed only in a region with a short characteristic length scale, i.e., $0\le {\underline{u}}\le \delta$.

Definition 1

Given $\delta >0$ and $B>0$, we say that a smooth shear $\hat{\chi }_0$, supported on $H_0^{(0,\delta )}$, verifies Christodoulou’s $\delta$-short pulse condition with constant $B$ if,

$$\begin{aligned} \sup _{{\underline{u}}}\sum _{i\le 5}\sum _{k\le 3}\delta ^{\frac{1}{2}+k}||\nabla _4^k\nabla ^i\hat{\chi }_0||_{L^\infty (S_{0,{\underline{u}}})}\le B. \end{aligned}$$

(12)

It is proved in [2] that given any $B>0$ and $u_*<1$, there exists $\delta$ sufficiently small such that any prescribed shear $\chi _{0}$ satisfying (12) gives rise to a unique smooth spacetime $\mathcal D(u_*,\delta )$. In particular, the final inner sphere $S_{u_*,0}$ has radius

$$\begin{aligned} r_* = 1-u_*, \end{aligned}$$

which can be arbitrarily small, as long as $\delta$ is also chosen to be sufficiently small. This is summarized in the following theorem:

Theorem 1

(Christodoulou¹⁰ [2]) For every $B>0$ and $u_*<1$ there exists $\delta >0$ sufficiently small such that if the null shear $\hat{\chi }_0$ along $H_0$ verifies Christodoulou’s $\delta$-short pulse condition with constant $B$, then the future development of the corresponding initial data contains ${\mathcal {D}}(u_*,\delta )$ as a regular spacetime in which, in particular, the conditions MA1–MA4 below are satisfied, with $\delta _0=\delta ^{1/2}$.

• MA1.   $\Omega$ is comparable with its initial value

  $$\begin{aligned} \Omega = 1 +O(\delta _0). \end{aligned}$$

• MA2.    The Ricci coefficients $\chi , \omega , \eta , \underline{\eta }, \nabla (\log \Omega ), \underline{\chi }, {\underline{\omega }}$ verify

  $$\begin{aligned} |\hat{\chi }, \omega |&= O(\delta ^{-1/2}), \\ |\text{ tr }\chi |&= O(1), \\ |\eta , \underline{\eta }, \underline{\hat{\chi }}\,, \text{ tr }\underline{\chi }+\frac{2}{r}, {\underline{\omega }}, \nabla (\log \Omega )|&= O(\delta _0).\\ \end{aligned}$$

• MA3.   The derivatives of Ricci coefficients satisfy

  $$\begin{aligned} |\nabla \eta |&= O(\delta _0 \delta ^{-1/2}), \\ |\nabla \underline{\hat{\chi }}\,, \nabla \text{ tr }\underline{\chi }, \nabla {\underline{\omega }}|&= O(\delta _0). \end{aligned}$$

• MA4.   $\text{ tr }\chi$ is close to its Minkowskian value on the initial cone ${\underline{H}}_0$

  $$\begin{aligned} \left| \text{ tr }\chi -\frac{2}{r}\right|&= O(\delta _0),\quad \text{ on } \quad {\underline{H}}_0. \end{aligned}$$

To show that a trapped surface forms in ${\mathcal {D}}(u_*,\delta )$, Christodoulou needs in addition a uniform lower bound on the function $M_0=M_0[\hat{\chi }_{0}]$ defined on $S_{0,0}$ as follows,

$$\begin{aligned} M_0(\omega )=M_0[\hat{\chi }_0](\omega ):= \int _0^{\delta } |\hat{\chi }_0|^2({\underline{u}}',\omega ) d{\underline{u}}', \end{aligned}$$

(13)

where the integral is taken along the null geodesic generators on $H_0$, transversal to $S_{0,0}$, initiating at $\omega \in S_{0,0}$. More precisely, he proved

Theorem 2

(Christodoulou [2]) Assume that the initial null shear $\hat{\chi }_0$ along $H_0$ verifies both Christodoulou’s $\delta$-short pulse condition with constant $B$ and the isotropic condition

$$\begin{aligned} \inf _{\omega \in S_{0,0} } M_0(\omega )\ge M_* >0. \end{aligned}$$

(14)

Then, for any given $r_*>0$,

$$\begin{aligned} r_*<\frac{M_*}{2},\quad u_*=1-r_*, \end{aligned}$$

there exists $\delta >0$ sufficiently small (depending only on $B$ and $M_*$) such that surface $S_{u_*,\delta }\subset {\mathcal {D}}(u_*,\delta )$, with ${\mathcal {D}}(u_*,\delta )$ constructed by Theorem 1, is necessarily trapped.

We now state our main result, which replaces the condition of the uniform lower bound (14) by merely the condition that $M_0$ is positive somewhere:

Theorem 3

(Main theorem) Assume that the initial null shear $\hat{\chi }_0$ along $H_0$ verifies both Christodoulou’s $\delta$-short pulse condition with constant $B$ and the following anisotropic condition

$$\begin{aligned} \sup _{\omega \in S_{0,0}} M_0(\omega )>0. \end{aligned}$$

(15)

Then, there exists $u_*>0$ sufficiently close to $1$ and $\delta >0$ sufficiently small (depending on $B$ and the function $M_0$) such that the future development ${\mathcal {D}}(u_*,\delta )$, constructed by Theorem 1, contains a trapped surface.

By continuity of $M_0$, the condition (15) implies that there exists $\epsilon$ and $M_*$ such that

$$\begin{aligned} \inf _{\omega \in B_p(\epsilon ) } M_0(\omega )\ge M_* >0, \end{aligned}$$

(16)

where $B_p(\epsilon )$ is a geodesic ball of radius $\epsilon$ around some $p\in S_{0,0}$. Our main theorem therefore follows from the more quantitative version below:

Theorem 4

Assume that the initial null shear $\hat{\chi }_0$ along $H_0$ verifies both Christodoulou’s $\delta$-short pulse condition with constant $B$ and the non-isotropic condition (16) with constants $\epsilon$ and $M_*$. Then, for any given $r_*>0$ verifying

$$\begin{aligned} r_*= c_0M_*\epsilon ^5,\quad u_*=1-r_*, \end{aligned}$$

(17)

(where $c_0$ is a universal constant) there exists $\delta >0$ sufficiently small (depending on $B$, $M_*$ and $\epsilon$) such that the future development ${\mathcal {D}}(u_*,\delta )$, constructed by Theorem 1, contains a trapped surface of area at least $\gtrsim M_*^2 \epsilon ^{10}$.

Remark 1

In Chapter 2 of [2], Christodoulou also constructed a class of initial data satisfying the assumptions of Theorems 1 and 2. The construction, which is based on solving ordinary differential equations along the null generators of the initial outgoing null hypersurface, can also be applied to construct initial data which obey the assumptions of our main theorem (Theorem 3). In particular, since the initial data at any point $p$ on the initial hypersurface depend only on the prescribed conformal part of the metric along the null generator passing through $p$, we can prescribe initial data which are flat except in a small neighborhood of an outgoing generator on the initial hypersurface.

Remark 2

The conditions MA1–MA4 are needed to implement part (2) of our main theorem. Though strictly speaking Christodoulou’s theorem implies MA1–MA4 with $\delta _0=\delta ^{1/2}$, we prefer to write them in this more general form with respect to a second parameter $\delta _0$, such that $\delta _0$, $\delta _0^{-1}\delta$ are sufficiently small. This formulation allows us to adapt our result to the more general initial data used in [4–6].

Remark 3

The original theorem of Christodoulou [2] also applies to the case when the initial area-radius is $r_0$. In that case, (12) can be replaced by $\sup _{{\underline{u}}}\sum _{i\le 5}\sum _{k\le 3}\delta ^{\frac{1}{2}+k}r_0^{1+i}||\nabla _4^k\nabla ^i\hat{\chi }_0||_{L^\infty (S_{0,{\underline{u}}})}\le B,$ and the definition of $M$ is similarly modified, i.e. $M(\omega ;r_0)=\int _0^{\delta } r_0^2|\hat{\chi }_0|^2({\underline{u}}',\omega )d{\underline{u}}'.$ With this definition, if the initial data satisfy $\inf _{\omega \in S_{0,0} } M_0(\omega ;r_0)\ge M_* >0,$ the formation of trapped surface theorem (Theorem 2) still holds after choosing $\delta$ sufficiently small depending on $B$ and $M_*$. By the same rescaling argument our main theorem (Theorem 3) holds in the case where the initial area-radius is $r_0$ if the condition $\sup _{\omega \in S_{0,0} } M_0(\omega ;r_0) >0$ is verified. Moreover, in [2], Christodoulou proved that one can take $r_0\rightarrow \infty$ and construct a spacetime from null infinity. For such spacetimes, our anisotropic condition can be replaced by the condition $\sup _{\omega \in S_{0,0} } M_0(\omega ;\infty ) >0$ and still guarantee the formation of a trapped surface.

Remark 4

Note that while in [2] the desired trapped surface can be found among the surfaces $S_{u,{\underline{u}}}$, consistent with the double null foliation, this is no longer the case in our theorem. Instead, we will identify a different 2-sphere, embedded in the null hypersurface $\{{\underline{u}}=\delta \}$, which can be shown to be trapped. Note also that the function $M_0[\hat{\chi }](\omega )=\int _0^\delta |\hat{\chi }({\underline{u}}, \omega )|^2 d{\underline{u}}'$ is invariant¹¹ with respect to a change of foliation along the initial hypersurface $H_0$. It is thus impossible to change the foliation on the initial hypersurface $H_0$ so that the isotropic condition in Theorem 2 holds.

We show that a trapped surface exists in ${\mathcal {D}}(u_*,\delta )$ by finding an embedded trapped 2-sphere in the incoming null hypersurface ${\underline{H}}_\delta$. Notice that by MA2, $\text{ tr }\underline{\chi }<0$ on ${\underline{H}}_{\delta }$. Therefore, it suffices to find a 2-sphere such that the outgoing null expansion is also pointwise negative. We will achieve this in two steps. In Sect. 2 we make use of the conditions MA1–MA4 to reduce the problem of existence of a trapped surface to that of finding appropriate solutions to an elliptic inequality, see (20), on $S_{0,0}$. In Sect. 3, we prove that under the assumption (16) of the main theorem, a desired solution to the elliptic inequality exists.

2 Reduction to an elliptic inequality on the initial sphere $S_{0,0}$

In this section, we show that under the assumptions MA1–MA4, the existence of a trapped surface can be reduced to constructing a solution to an elliptic inequality (20). The main result of the section is stated in Theorem 5.

We first make a remark concerning the global parametrization of points in ${\mathcal {D}}(u_*,\delta )$ by $u$, ${\underline{u}}$ and coordinates $\omega$ on $S_{0,0}$.

Proceeding as in [2] we associate to each coordinate patch on $S_{0,0}$, a system of transported coordinates defined by

(18)

and

(19)

where is the restriction of the Lie derivative to $T S_{u,{\underline{u}}}$ (see [2], chapter 1). This provides an identification of each point in the spacetime $\mathcal {D}(u_*, \delta )$ with a point in the initial sphere $S_{0,0}$ by the value of the coordinate functions.

It follows that any point in $\mathcal D(u_*, \delta )$ can also be uniquely specified by the coordinates $({\underline{u}}, u, \omega )$, where $\omega \in S_{0,0}$.

We can now state the main result of this section:

Theorem 5

Assume that the spacetime ${\mathcal {D}}(u_*,\delta )$ satisfies MA1–MA4. Let $M_0$ be the function on the initial sphere $S_{0,0}$ defined by (13), i.e.,

$$\begin{aligned} M_0(\omega ) := \int _0^{\delta } |\hat{\chi }|^2(u=0,{\underline{u}}',\omega ) d{\underline{u}}'. \end{aligned}$$

Assume $R$ is a smooth function on $S_{0,0}$ satisfying $r_*+C\delta _0 < R< 1$ as well as the elliptic inequality¹² on $S_{0,0}$

$$\begin{aligned} -\Delta _0 R+ R^{-1}|\nabla _0 R|^2 + R <2^{-1}M_0-C\delta _0, \end{aligned}$$

(20)

with $C>0$ a constant depending only on $\sum \nolimits _{i\le 2} ||\nabla _0^i R||_{L^\infty (S_{0,0})}$.

Then, for $\delta \delta _0^{-1}$, $\delta _0$ sufficiently small, the $2$-sphere defined by $\{({\underline{u}},u,\omega ) : {\underline{u}}=\delta , 1-u = R(\omega )\}$ is a trapped surface.

We prove Theorem 5 in this section and leave for the next section the task to show that a smooth solution $R$ to (20) exists, provided that $M_0$ satisfies the assumptions of our main theorem.

The proof of Theorem 5 will be achieved in two steps. In Sect. 2.1, we will carry out Christodoulou’s argument in [2] to estimate $\text{ tr }\chi$ with respect to the original foliation on ${\underline{H}}_{\delta }$. In Sect. 2.2, we will then deform the foliation on ${\underline{H}}_{\delta }$ in such a way that the 2-sphere $\{({\underline{u}},u,\omega ) : {\underline{u}}=\delta , 1-u = R(\omega )\}$ is a level surface adapted to the new foliation. We then compute the desired outgoing expansion $\text{ tr }\chi '$ on the 2-sphere $\{({\underline{u}},u,\omega ) : {\underline{u}}=\delta , 1-u = R(\omega )\}$.

We note that the derivation in Sect. 2.2 can be simplified by taking into account the specific properties of the spacetime constructed in Theorem 1. We will include the simplified argument in Sect. 2.3. Nevertheless, we prefer to proceed below with the general derivation in view of possible applications to a more general setting.

2.1 Christodoulou’s argument

In [2], it was shown that under the assumptions MA1–MA4, the expansion $\text{ tr }\chi$ on each of the spheres $S_{u, \delta }$ on $\underline{H}_{\delta }$ can be computed up to a small error depending on $\delta$. In the context of [2], where a uniform lower bound on $M_0$ is assumed, this is sufficient to conclude the existence of a trapped surface $S$ of the form $S=S_{u,\delta }$. In the case of our weaker condition (16), his argument only shows that $\text{ tr }\chi$ becomes sufficiently negative in part of the sphere $S_{u,\delta }$. To obtain a trapped surface we need to combine that fact with a new deformation argument of the foliation on ${\underline{H}}_{\delta }$.

Christodoulou’s argument for the formation of trapped surfaces in [2] rests on the equations¹³,

$$\begin{aligned} \nabla _4 \text{ tr }\chi&= -|\hat{\chi }|^2 -\frac{1}{2} (\text{ tr }\chi )^2 -2\omega \text{ tr }\chi \\ \nabla _3\hat{\chi }+\frac{1}{2} \text{ tr }\underline{\chi }\hat{\chi }&= \nabla \widehat{\otimes } \eta +2{\underline{\omega }}\hat{\chi }-\frac{1}{2} \text{ tr }\chi \underline{\hat{\chi }}\,+\eta \widehat{\otimes } \eta \end{aligned}$$

In view of our Ricci coefficients assumptions we can rewrite,

$$\begin{aligned} \nabla _4 \text{ tr }\chi&= -|\hat{\chi }|^2 +O(\delta ^{-1/2}) \\ \nabla _3\hat{\chi }+\frac{1}{2} \text{ tr }\underline{\chi }\hat{\chi }&= O(\delta _0 \delta ^{-1/2}) \end{aligned}$$

Multiplying the second equation by $\hat{\chi }$,

$$\begin{aligned} \nabla _3 |\hat{\chi }|^2+\text{ tr }\underline{\chi }|\hat{\chi }|^2&= O(\delta _0 \delta ^{-1}) \end{aligned}$$

Using also our assumptions for $u, {\underline{u}}, \Omega$ we deduce¹⁴,

$$\begin{aligned} \frac{\partial }{\partial {\underline{u}}}\text{ tr }\chi&= -|\hat{\chi }|^2+O(\delta ^{-1/2}) \end{aligned}$$

(21)

$$\begin{aligned} \frac{\partial }{\partial u}|\hat{\chi }|^2+\text{ tr }\underline{\chi }|\hat{\chi }|^2&= O(\delta _0\delta ^{-1}) \end{aligned}$$

(22)

Integrating (21) we obtain,

$$\begin{aligned} \text{ tr }\chi (u,{\underline{u}})&= \frac{2}{r(u,0)}-\int _0^{{\underline{u}}} |\hat{\chi }|(u,{\underline{u}}')^2 d{\underline{u}}' +O(\delta _0) \end{aligned}$$

(23)

In view of our assumptions for $\text{ tr }\underline{\chi }$ and $\frac{dr}{du}$, (22) implies

$$\begin{aligned} \frac{d}{du} (r^2 |\hat{\chi }|^2)&= r^2\frac{d}{du}|\hat{\chi }|^2+2 r \frac{dr}{du} |\hat{\chi }|^2=r^2\big [-\!\text{ tr }\underline{\chi }|\hat{\chi }|^2 +O(\delta _0\delta ^{-1})\big ]\\&+\,2r\big [ -\!1+O(r\delta _0) \big ] |\hat{\chi }|^2 \\&= O(\delta _0\delta ^{-1}). \end{aligned}$$

Therefore,

$$\begin{aligned} r^2 |\hat{\chi }|^2(u,{\underline{u}})=r^2(0,{\underline{u}}) |\hat{\chi }|^2(0 ,{\underline{u}})+O(\delta _0\delta ^{-1}) \end{aligned}$$

Let $\hat{\chi }_0$ denote the initial data for $\hat{\chi }$:

$$\begin{aligned} \hat{\chi }_0({\underline{u}})=\hat{\chi }(0,{\underline{u}}). \end{aligned}$$

(24)

We deduce,

$$\begin{aligned} |\hat{\chi }|^2(u,{\underline{u}})&= \frac{ r^2(0,{\underline{u}})}{r^2(u,{\underline{u}})} |\hat{\chi }_0|^2({\underline{u}})+O(\delta _0\delta ^{-1} ) \end{aligned}$$

Since $r(u,{\underline{u}})=r(u,0)+O(\delta )$,

$$\begin{aligned} |\hat{\chi }|^2(u,{\underline{u}})=\frac{ 1}{r^2(u,0)} |\hat{\chi }_0|^2({\underline{u}})+O(\delta _0\delta ^{-1}). \end{aligned}$$

Thus, returning to (23), and recalling that

$$\begin{aligned} M_0(\omega )=\int _0^{\delta } |\hat{\chi }_0|^2({\underline{u}}',\omega ) d{\underline{u}}', \end{aligned}$$

we deduce the following:

Proposition 1

Under the assumptions MA1–MA4 we have, for $\delta _0$, $\delta _0^{-1}\delta$ sufficiently small,

$$\begin{aligned} \text{ tr }\chi (u,{\underline{u}}=\delta ,\omega )=\frac{2}{r(u, 0)} - \frac{ 1}{r^2(u,0)}M_0(\omega )+ O(\delta _0) \end{aligned}$$

(25)

Since $r(u,0)=1-u+O(\delta _0)$, this implies

Corollary 1

For $\delta _0$, $\delta _0^{-1}\delta$ small, the necessary and sufficient condition to have $\text{ tr }\chi < 0$ everywhere on the sphere $S_{u,\delta }$ is that

$$\begin{aligned} {2(1-u)}< M_0(\omega )- O(\delta _0) \end{aligned}$$

(26)

holds uniformly for every $\omega \in S_{0,0}$.

Under the assumptions of our main theorem, we can only hope that the outgoing null expansion $\text{ tr }\chi$ adapted to the foliation $(u,{\underline{u}})$ becomes negative in the part where $M_0$ is positive. Thus to prove our main theorem, we need to combine this argument with the new deformation mechanism which leads to the formation of a trapped surface that is no longer adapted to the double null foliation $(u,{\underline{u}})$. Instead, as stated in Theorem 5, the trapped surface will be a topological 2-sphere embedded in the incoming null hypersurface $\{{\underline{u}}= \delta \}$ defined by $\{({\underline{u}},u,\omega ): {\underline{u}}=\delta , 1-u=R(\omega )\}$.

2.2 Main transformation formula

According to the statement of Theorem 5, $\{({\underline{u}},u,\omega ): {\underline{u}}=\delta , 1-u=R(\omega )\}$ will correspond to a trapped surface provided that $R$ satisfies (20). To verify that, we need to compute its null expansion, which differs from the null expansion $\text{ tr }\chi$ relative to the double null foliation $(u,{\underline{u}})$ restricted to $\{({\underline{u}},u,\omega ): {\underline{u}}=\delta , 1-u=R(\omega )\}$. To compute the correct null expansion $\text{ tr }\chi '$, we introduce the new null frame adapted to this set,

$$\begin{aligned} e_3'=e_3,\qquad e_a'=e_a- \Omega e_a(R)e_3, \qquad e_4'=e_4-2\Omega e^a(R) e_a+ \Omega ^{2} |\nabla R|^2 e_3\nonumber \\ \end{aligned}$$

(27)

Recall that by definition $e_3(u)=\Omega ^{-1}$. Thus we have, $e_a'(u+R-1)=e_a(R)- e_a(R) \Omega e_3(u)= 0$. Also, since $e_3$ is orthogonal to any vector tangent to ${\underline{H}}$ we easily check that

$$\begin{aligned} g(e_a', e_b')=g(e_a,e_b)=\delta _{ab},\quad g(e_4', e_a')= g(e_4', e_4')=0,\quad g(e_3', e_4')=-2. \end{aligned}$$

We prove the following

Proposition 2

The trace of the null second fundamental form $\chi '$, relative to the new frame (27), is given by

$$\begin{aligned} \text{ tr }\chi '&= \text{ tr }\chi -2\Omega \Delta R -4\Omega \eta \cdot \nabla R-4\Omega ^2\underline{\hat{\chi }}\,_{b c} \nabla ^b R\nabla ^c R -\Omega ^2\text{ tr }\underline{\chi }|\nabla R|^2\nonumber \\&-\,8\Omega ^2{\underline{\omega }}|\nabla R|^2. \end{aligned}$$

(28)

Proof

Let $F_a=\Omega (\nabla _a R)$. We can then write $e_4'=e_4-2F+|F|^2 e_3$ with $F=F^c e_c$ and $e_b'=e_b-F_b e_3$. We have,

$$\begin{aligned} \chi '(e_a', e_b'):=g(D_{a'} e_4', e_b')=g(D_a e_4', e_b')- F_a g(D_3 e_4', e_b') \end{aligned}$$

The first term is given by

$$\begin{aligned} g(D_a e_4', e_b')&= g\big (D_a(e_4-2F +|F|^2 e_3)\,, \,e_b- F_b e_3\big )\\&= \chi (e_a, e_b)-2F_b \zeta _a-2\nabla _a F_b +2 F_b g(D_a F, e_3)\\&+|F|^2g(D_a e_3, e_b-F_b e_3)\\&= \chi _{ab}-2\zeta _a F_b-2\nabla _ a F_b-2 F_b\, \underline{\chi }(F, e_a)+|F|^2\underline{\chi }_{ab}\\&= \chi _{ab}-2\zeta _a F_b-2\nabla _ a F_b-2 F_b\, F^c \, \underline{\chi }_{ac}+|F|^2\underline{\chi }_{ab} \end{aligned}$$

Also,

$$\begin{aligned} g(D_3 e_4', e_b')&= g\big (D_3(e_4-2F+|F|^2 e_3)\,,\, e_b- F_b e_3\big )\\&= g(D_3 e_4, e_b)-F_b g(D_3e_4, e_3)-2\nabla _3 F_b\\&= 2\eta _b+4F_b {\underline{\omega }}-2\nabla _3 F_b \end{aligned}$$

Hence,

$$\begin{aligned} \chi '_{ab}&=\chi _{ab}-2\zeta _b F_a-2\nabla _ a F_b-2 F_b F^c \underline{\chi }_{ac}\\&\quad +|F|^2\underline{\chi }_{ab}- F_a \big (2\eta _b+4F_b {\underline{\omega }}-2\nabla _3 F_b)\\&=\chi _{ab}-2\nabla _ a F_b+2 F_a \nabla _3 F_b-2\zeta _b F_a -2 F_a\eta _b\\&\quad + |F|^2 \underline{\chi }_{ab}-2 F_b F^c \underline{\chi }_{ac} -4 {\underline{\omega }}F_a F_b \end{aligned}$$

By symmetry in $a, b$ we deduce the formula,

$$\begin{aligned} \chi '_{ab}&= \chi _{ab}-(\nabla _ a F_b+\nabla _b F_a) + \nabla _3(F_a F_b) -(\zeta _b +\eta _b)F_a-(\zeta _a+\eta _a )F_b\nonumber \\&+ |F|^2 \underline{\chi }_{ab}- F_b F^c \underline{\chi }_{ac}- F_a F^c \underline{\chi }_{bc} -4 {\underline{\omega }}F_a F_b \end{aligned}$$

(29)

and, taking the trace,

$$\begin{aligned} \text{ tr }\chi '&= \text{ tr }\chi -2\mathrm{div} F+\nabla _3|F|^2-2(\eta +\zeta )\cdot F+(|F|^2 \text{ tr }\underline{\chi }-2\underline{\chi }_{bc} F^b F^c)\\&-\,\,4{\underline{\omega }}|F|^2\\&= \text{ tr }\chi -2\mathrm{div} F+\nabla _3|F|^2-2(\eta +\zeta )\cdot F -2\underline{\hat{\chi }}\,_{bc} F^b F^c-4{\underline{\omega }}|F|^2. \end{aligned}$$

We next calculate $\nabla _3|F|^2$ using

$$\begin{aligned} \nabla _3 R=0 \end{aligned}$$

and the commutation formula

$$\begin{aligned}{}[\nabla _3, \nabla ] h =(\nabla \log \Omega ) \nabla _3 h-\underline{\chi }\cdot \nabla h. \end{aligned}$$

Since $F=\Omega \nabla R$ we deduce,

$$\begin{aligned} \nabla _3 F_a&= \nabla _3( \Omega \nabla R)= \Omega (\nabla _3 \nabla R)+(\nabla _3\Omega ) \nabla R\\&= \Omega \nabla \nabla _3 R+(\nabla \log \Omega )\Omega \nabla _3 R- \Omega \underline{\chi }\cdot \nabla R- 2{\underline{\omega }}\Omega \nabla R\\&= - \Omega \underline{\chi }\cdot \nabla R- 2{\underline{\omega }}\Omega \nabla R. \end{aligned}$$

from which we derive,

$$\begin{aligned} \nabla _3|F|^2&= -\Omega ^2 \text{ tr }\underline{\chi }|\nabla R|^2 -2\Omega ^2\underline{\hat{\chi }}\,_{b c} \nabla _b R \nabla _c R -4\Omega ^2{\underline{\omega }}|\nabla R|^2. \end{aligned}$$

Therefore,

$$\begin{aligned} \text{ tr }\chi '&= \text{ tr }\chi -2\mathrm{div} F-2(\eta +\zeta )\cdot F -2\underline{\hat{\chi }}\,_{bc} F^b F^c-4{\underline{\omega }}|F|^2\\&-\Omega ^2 \text{ tr }\underline{\chi }|\nabla R|^2 -2\Omega ^2\underline{\hat{\chi }}\,_{b c} \nabla _b R \nabla _c R -4\Omega ^2{\underline{\omega }}|\nabla R|^2\\&= \text{ tr }\chi -2\Omega \Delta R -4\Omega \eta \cdot \nabla R-4\Omega ^2\underline{\hat{\chi }}\,_{b c} \nabla _b R\nabla _c R -\Omega ^2\text{ tr }\underline{\chi }|\nabla R|^2\\&-\,8\Omega ^2{\underline{\omega }}|\nabla R|^2 \end{aligned}$$

as desired. $\square$

We combine this with the main assumptions MA1–MA4 to derive the following proposition:

Proposition 3

The trace of the null second fundamental form $\chi '$, relative to the new frame (27), evaluated at the set $\{({\underline{u}},u,\omega ):{\underline{u}}=\delta , 1-u=R(\omega )\}$ is given by

$$\begin{aligned}&\text{ tr }\chi '(u=1-R(\omega ),{\underline{u}}=\delta ,\omega )\nonumber \\&\quad =\text{ tr }\chi (u=1-R(\omega ),{\underline{u}}=\delta ,\omega ) -\frac{2\Delta _0 R}{R^2} +\frac{2|\nabla _0 R|^2}{R^3}+O_R(\delta _0),\quad \qquad \end{aligned}$$

(30)

where $O_R(\delta _0)$ denotes a term bounded by $C\delta _0$, where $C$ depends only on the $L^\infty$ norm of $R$, $\nabla _0 R$ and $\nabla _0^2 R$, and $\nabla _0$, $\Delta _0$, as before, are defined with respect to the connection on the initial sphere $S_{0,0}$.

Proof

By MA1–MA4, $\Omega -1$, $\eta$, $\underline{\hat{\chi }}\,$, $\text{ tr }\underline{\chi }+\frac{2}{r}$ and ${\underline{\omega }}$ are small in terms of $\delta _0$. Thus

$$\begin{aligned}&\text{ tr }\chi '(u=1-R(\omega ),{\underline{u}}=\delta ,\omega )\\&\quad = \text{ tr }\chi (u=1-R(\omega ),{\underline{u}}=\delta ,\omega ) -2 {\Delta R} +\frac{2|\nabla R|^2}{R}+O_R(\delta _0). \end{aligned}$$

To achieve the proposition, we need to compare¹⁵ $\nabla R$ with $\nabla _0 R$. To this end, we consider the equation

$$\begin{aligned} \nabla _3 R=0 \end{aligned}$$

and commute with angular derivatives. The commutation formulae in Lemma 1 and MA1–MA4 imply that

$$\begin{aligned} \nabla _3 \nabla R+\frac{1}{2} \text{ tr }\underline{\chi }\nabla R = O_R(\delta _0), \end{aligned}$$

and

$$\begin{aligned} \nabla _3 \nabla ^2 R+ \text{ tr }\underline{\chi }\nabla ^2 R = O_R(\delta _0). \end{aligned}$$

This implies, via the condition $|\text{ tr }\underline{\chi }+\frac{2}{r}|= O(\delta _0)$ in MA2, that

$$\begin{aligned} \nabla _3 (r\nabla R) = O_R(\delta _0), \end{aligned}$$

and

$$\begin{aligned} \nabla _3 (r^2\nabla ^2 R) = O_R(\delta _0). \end{aligned}$$

Therefore,

$$\begin{aligned} |\nabla R|^2=\frac{|\nabla _0 R|^2}{R^2}+O_R(\delta _0),\quad \Delta R=\frac{\Delta _0 R}{R^2}+O_R(\delta _0). \end{aligned}$$

The conclusion thus follows. $\square$

We now combine the results of Propositions 1 and 3. According to Proposition 1, $\text{ tr }\chi$ evaluated at $\{({\underline{u}},u,\omega ): {\underline{u}}=\delta , 1-u=R(\omega )\}$ is given by

$$\begin{aligned} \text{ tr }\chi (u\!=\!1-R(\omega ),{\underline{u}}\!=\!\delta ,\omega )\!=\!\frac{2}{R(u,0)} \!-\! \frac{ 1}{R^2(u,0)}\!\int _0^{\delta } |\hat{\chi }_0|^2({\underline{u}}',\omega ) d{\underline{u}}'\!+\!\! O(\delta _0). \end{aligned}$$

Thus, inserting in (30), we have

$$\begin{aligned} \text{ tr }\chi '(u\!=\!1-R(\omega ),{\underline{u}}\!=\!\delta ,\omega )&\le \frac{2}{R} - \frac{2\Delta _0 R}{R^2} +\frac{2|\nabla _0 R|^2}{R^3} \!-\! \frac{ 1}{R^2} M_0 -O_R(\delta _0). \end{aligned}$$

where

$$\begin{aligned} M_0= \int _0^{\delta } |\hat{\chi }_0|^2({\underline{u}}') d{\underline{u}}'. \end{aligned}$$

This concludes the Proof of Theorem 5.

2.3 An alternative derivation

In the context of our specific situation we outline¹⁶ here a slightly easier argument leading to the formula for $\text{ tr }\chi '$ on ${\underline{H}}_{\delta }$ in terms of $\text{ tr }\chi$ on ${\underline{H}}_{\delta }$ and the function $R$ in the limit $\delta \rightarrow 0$. Note however that the derivation below depends on further properties of the Ricci coefficients, in addition to MA1–MA4, proved in [2]. This provides an alternative Proof of Theorem 5.

We recall from [2] that in the limit $\delta \rightarrow 0$, the following curvature components tend to zero:

$$\begin{aligned} {\underline{\beta }}\rightarrow 0,\quad {\underline{\alpha }}\rightarrow 0. \end{aligned}$$

(31)

Also,

$$\begin{aligned} \underline{\hat{\chi }}\,=O(\delta ^{\frac{1}{2}}),\quad \text{ tr }\underline{\chi }\rightarrow -\frac{2}{r}, \end{aligned}$$

(32)

$\hat{\chi }$ is of the order $O(\delta ^{-\frac{1}{2}})$ and all the remaining Ricci coefficients are at least $O(1)$.

By (32), in the limit $\delta \rightarrow 0$

holds along the incoming null hypersurface ${\underline{H}}_{\delta }$, where $\gamma$ is a induce Riemannian metric on $S_{u,\delta }$.

It follows that at the $\delta \rightarrow 0$ limit, the metric $\gamma '$ on the sphere defined by $\{({\underline{u}},u,\omega ): {\underline{u}}=\delta , 1-u=R(\omega )\}$ is conformal to the metric on the standard sphere $\gamma _0$ with the conformal factor given by

$$\begin{aligned} \gamma ' = R^2 \gamma _0. \end{aligned}$$

(33)

Let $K'$ denote the Gauss curvature of the sphere $\{({\underline{u}},u,\omega ): {\underline{u}}=\delta , 1-u=R(\omega )\}$ and $K_0$ be the Gauss curvature on the initial sphere $S_{0,0}$. Then, in view of (33),

$$\begin{aligned} K'=R^{-2}(K_0-\Delta _{0} (\log R)) = R^{-2}(1-\Delta _{0} (\log R)) . \end{aligned}$$

(34)

Consider the Gauss equation for the sphere $\{({\underline{u}},u,\omega ): {\underline{u}}=\delta , 1-u=R(\omega )\}$,

$$\begin{aligned} K'=-\rho '+\frac{1}{2} \hat{\chi }'\cdot \underline{\hat{\chi }}\,'-\frac{1}{4} \text{ tr }\chi '\text{ tr }\underline{\chi }'. \end{aligned}$$

(35)

Also the Gauss equation for the $2$-spheres adapted to the original foliation,

$$\begin{aligned} K=-\rho +\frac{1}{2} \hat{\chi }\cdot \underline{\hat{\chi }}\,-\frac{1}{4} \text{ tr }\chi \text{ tr }\underline{\chi }. \end{aligned}$$

(36)

We will derive $\text{ tr }\chi '$ in terms of $\text{ tr }\chi$ and $R$ using Eqs. (35) and (36). By definition, $e_a'=e_a- \Omega e_a(R)e_3$ and $e_3'=e_3$. Since $e_3$ is normal to $e_a$, $e_a'$ and $e_3$, and

$$\begin{aligned} D_{e_3} e_3=-2\omega e_3, \end{aligned}$$

we have

$$\begin{aligned} \underline{\chi }'_{ab}=\frac{1}{2} g(D_{a'} e_3, e_b')=\frac{1}{2} g(D_{a} e_3, e_b)=\underline{\chi }_{ab}. \end{aligned}$$

Therefore, as $\delta \rightarrow 0$,

$$\begin{aligned} \text{ tr }\underline{\chi }'=\text{ tr }\underline{\chi }\rightarrow -\frac{2}{r} \end{aligned}$$

and

$$\begin{aligned} |\underline{\hat{\chi }}\,'|= O(\delta ^{\frac{1}{2}}). \end{aligned}$$

(37)

On the other hand, $e_4'=e_4-2 \Omega e_a(R) e_a+ \Omega ^{2} |\nabla R|^2 e_3$, $\hat{\chi }'$ can be expressed as $\hat{\chi }$ plus a linear combination of the Ricci coefficients with respect to the original frame which are bounded independent of $\delta$. Therefore,

$$\begin{aligned} |\hat{\chi }'-\hat{\chi }| = O(1), \end{aligned}$$

(38)

where the implicit constant may depend on $R$. Note that (37) and (38) together imply in the limit $\delta \rightarrow 0$,

$$\begin{aligned} |\hat{\chi }\cdot \underline{\hat{\chi }}\,-\hat{\chi }'\cdot \underline{\hat{\chi }}\,'|\rightarrow 0. \end{aligned}$$

Since $e_4'=e_4-2 \Omega e_a(R) e_a+ \Omega ^{2} |\nabla R|^2 e_3$ and $e_3'=e_3$, $\rho '-\rho$ can be written as a linear combination of ${\underline{\beta }}$ and ${\underline{\alpha }}$. Thus, by (31), in the limit $\delta \rightarrow 0$,

$$\begin{aligned} \rho '\rightarrow \rho . \end{aligned}$$

In the $\delta \rightarrow 0$ limit the Gauss equations (36) becomes

$$\begin{aligned} \rho&= -K -\frac{1}{4} \text{ tr }\chi \text{ tr }\underline{\chi }=-R^{-2}+\frac{1}{2R}\text{ tr }\chi \end{aligned}$$

On the other hand, the $\delta \rightarrow 0$ limit of the Gauss equations (35) becomes

$$\begin{aligned} K'=-\rho '-\frac{1}{4} \text{ tr }\chi '\text{ tr }\underline{\chi }'=-\rho +\frac{1}{2 R}\text{ tr }\chi '= R^{-2}-\frac{1}{2R}\text{ tr }\chi +\frac{1}{2 R}\text{ tr }\chi ' \end{aligned}$$

Thus, making use of (34), we have

$$\begin{aligned} \text{ tr }\chi '&= \text{ tr }\chi -\frac{1}{2R}+2R K'=\text{ tr }\chi -\frac{2}{R}\Delta _0 (\log R)\\&= \text{ tr }\chi + \frac{2}{R} \left( -\frac{\Delta _0 R}{R}+\frac{|\nabla _0 R|^2}{R^2}\right) . \end{aligned}$$

Combining this with Proposition 1, we thus have

$$\begin{aligned} \text{ tr }\chi '=\frac{2}{R}\left( 1-\frac{\Delta _0 R}{R}+\frac{|\nabla _0 R|^2}{R^2}\right) -\frac{M_0}{R^2} \end{aligned}$$

in the limit $\delta \rightarrow 0$.

3 Solutions to the deformation equation on $S_{0,0}$

To prove our main Theorem 3 it suffices¹⁷ now to show that if $M_0$ verifies the assumption (16), then an appropriate solution to the differential inequality on the standard sphere $S=S_{0,0}$,

$$\begin{aligned} -\Delta R+ R^{-1}|\nabla R|^2+R< 2^{-1} M_0, \end{aligned}$$

(39)

can be found.¹⁸

Let $R=e^{-\phi }$. Then the main deformation Eq. (39) reduces to

$$\begin{aligned} \Delta \phi +1< \frac{1}{2} M_0 e^\phi . \end{aligned}$$

(40)

We show below that (40) can be solved as long as $M_0\ge 0$ and $M_0\ge M_*>0$ on some open ball of $S$. Our approach provides an explicit construction using the Green’s function for the Laplacian on $S$. The main observation is that given any function $\tilde{\phi }$, there exists a sufficiently large constant $C$ such that (40) is satisfied by $\phi =\tilde{\phi }+C$ on the set where $M_0$ has a positive lower bound. It is therefore sufficient first to construct a function $\tilde{\phi }$ satisfying (40) only on the complement of the set where $M_0$ has a positive lower bound. It turns out that an appropriately rescaled and cut-off version of the Green’s function for the Laplacian satisfies this property.

We prove the following proposition, which together with Theorem 5, implies our main theorem (Theorems 3 and 4):

Proposition 4

Let $M_*=\min _{B_p(\epsilon )} M_0$. Then there exists a function $\phi _{\epsilon ,M_*}$ verifying the inequality (40) and such that

$$\begin{aligned} \phi _{\epsilon ,M_*}&\le \log \left( \frac{1}{M_* \epsilon ^5}\right) +O(1) \end{aligned}$$

(41)

$$\begin{aligned} |\nabla \phi _{\epsilon ,M_*}|&= O(\epsilon ^{-1}), \quad |\nabla ^2\phi _{\epsilon ,M_*}|=O(\epsilon ^{-2}). \end{aligned}$$

(42)

3.1 Proof of the main theorem

Returning to our task of constructing a trapped surface, note that the upper bound (41) for $\phi$ corresponds to our desired lower bound for $R$. More precisely, (41) implies that for some $C>0$,

$$\begin{aligned} \max _S \frac{1}{R}\le e^{\max _S \phi }\le \frac{C }{M_* \epsilon ^5}. \end{aligned}$$

In particular, for $M_0$ satisfying the assumption of Theorem 4, i.e.,

$$\begin{aligned} \inf _{B_p(\epsilon )} M_0 \ge M_*> 0, \end{aligned}$$

the proposition implies the existence of a function $R$ verifying (39) and a lower bound $R> c_0{M_* \epsilon ^5}$, for some constant $c_0$. Therefore, by Theorem 1, given $M_*$ and $\epsilon$, we can choose $\delta$ sufficiently small such that the spacetime solution for the characteristic initial value problem remains smooth in ${\mathcal {D}}(u_*,\delta )$ for $u_*= 1-r_*<1-c_0{M_* \epsilon ^5}$. This guarantees that the sphere $\{({\underline{u}},u,\omega ) : {\underline{u}}=\delta , 1-u = R(\omega )\}$ lies within ${\mathcal {D}}(u_*,\delta )$. Moreover, given a function $R$ verifying (39), the term $C\delta _0$ in (20) can be made arbitrarily small by choosing $\delta$ small. Thus, by Theorem 5, the sphere defined by $\{({\underline{u}},u,\omega ) : {\underline{u}}=\delta , 1-u = R(\omega )\}$ is a trapped surface in ${\mathcal {D}}(u_*,\delta )$. Since $R \ge r_*$, the constructed trapped surface has area at least $\gtrsim r_*^2 \approx M_*^2 \epsilon ^{10}$.

This concludes the proof of the main theorem. It thus remains to prove Proposition 4.

3.2 Proof of Proposition 4

To this end, we use the following bounds for the Green’s function of the standard sphere $S$.

Lemma 2

Given a point $p$ in the standard unit sphere, define $\lambda$ to be the distance function from $p$. Then the function given by

$$\begin{aligned} w=\sin \left( \log \left( \frac{\lambda }{2}\right) \right) \end{aligned}$$

satisfies

$$\begin{aligned} \Delta _d w +\frac{1}{2 }= 2\pi \delta _p \end{aligned}$$

(43)

where $\Delta _d$ is the distributional Laplacian on the standard sphere and $\delta _p$ is the Dirac measure at $p$. Moreover, $w$ obey the following bounds:

$$\begin{aligned} w= \log \lambda +O(1),\quad |\nabla w|=O(\lambda ^{-1}),\quad |\nabla ^2 w|=O(\lambda ^{-2}). \end{aligned}$$

Remark 5

In a more general setting where the metric $\gamma$ on $S$ is not the metric on the standard unit sphere, we can still use the Green’s function to construct a desired solution to the elliptic inequality. More precisely, given a smooth riemannian metric $\gamma$ on $S$, there exists a function $w$, smooth outside the point $p$, such that

$$\begin{aligned} \Delta _d w +\frac{1}{2r_0 }= 2\pi \delta _p \end{aligned}$$

(44)

where $\Delta _d$ is the distributional Laplacian associated to the metric $\gamma$, $\delta _p$ is the Dirac measure at $p$, and $r_0$ is defined by $\text{ Area }(S)= 4\pi r_0$. Moreover, if $\lambda _p$ denotes the distance function from $p$,

$$\begin{aligned} w = \chi \log \lambda _p + v \end{aligned}$$

(45)

with $v$ smooth in $S{\setminus }\{p\}$ and satisfying

$$\begin{aligned} |v|\le C,\quad |\nabla v|=o(\lambda ^{-1}),\quad |\nabla ^2 v|=o(\lambda ^{-2}); \end{aligned}$$

and $\chi$ a smooth cut-off function identically equals to 1 in a small neighborhood of $p$.

We refer the readers to Theorem 4.13 in [1] for a proof of this fact.

Using Lemma 2, we now proceed to the Proof of Proposition 4:

Proof of Proposition 4

Consider the cut-off function

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \chi _\epsilon =0&{} \text{ on } \quad B_p(\epsilon /2)\\ \chi _\epsilon =1&{} \text{ on } \quad S{\setminus } B_p(\epsilon ) \end{array}\right. \end{aligned}$$

and define $\tilde{w}_\epsilon = \chi _\epsilon w + (1-\chi _\epsilon ) \log \epsilon$. Note¹⁹ for that $\tilde{w}_\epsilon$ verifies the following properties:

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \tilde{w}_\epsilon =\log \epsilon ,&{} \text{ on }\qquad B_p(\epsilon /2)\\ \tilde{w}_\epsilon = \log \epsilon +O(1),&{} \text{ on }\quad B_p(\epsilon ){\setminus } B_p(\epsilon /2) \\ \tilde{w}_\epsilon = \log \lambda +O(1),&{} \text{ on }\quad S {\setminus } B_p(\epsilon ) \\ \nabla \tilde{w}_\epsilon = O(\epsilon ^{-1}),&{} \text{ on }\quad S{\setminus } B_p(\epsilon /2) \\ \nabla ^2 \tilde{w}_\epsilon = O(\epsilon ^{-2}),&{} \text{ on }\quad S{\setminus } B_p(\epsilon /2) \\ \Delta \tilde{w}_\epsilon +\frac{1}{2}=0, &{} \text{ on }\quad S{\setminus } B_p(\epsilon ) \end{array}\right. \end{aligned}$$

(46)

Consider now the function $\tilde{\phi }_\epsilon =3 \tilde{w}_\epsilon$ and observe that, on $S{\setminus } B_p(\epsilon )$, we must have,

$$\begin{aligned} \Delta \tilde{\phi }_\epsilon +1=- \frac{3}{2} +1<0. \end{aligned}$$

Thus, we have,

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \tilde{\phi }_\epsilon = 3\log \epsilon ,&{} \text{ on }\qquad B_p(\epsilon /2)\\ \tilde{\phi }_\epsilon = 3\log \epsilon +O(1),&{} \text{ on }\quad B_p(\epsilon ){\setminus } B_p(\epsilon /2) \\ \tilde{\phi }_\epsilon = 3\log \lambda +O(1),&{} \text{ on }\quad S {\setminus } B_p(\epsilon ) \\ \nabla \tilde{\phi }_\epsilon = O(\epsilon ^{-1}),&{} \text{ on }\quad S{\setminus } B_p(\epsilon /2) \\ \nabla ^2 \tilde{\phi }_\epsilon = O(\epsilon ^{-2}),&{} \text{ on }\quad S{\setminus } B_p(\epsilon /2) \\ \Delta \tilde{\phi }_\epsilon +1<0, &{} \text{ on }\quad S{\setminus } B_p(\epsilon ) \end{array}\right. \end{aligned}$$

(47)

Finally, we add a large constant to the function $\tilde{\phi _\epsilon }$ to obtain the desired solution to the inequality (40). More precisely, we let

$$\begin{aligned} \phi _{\epsilon , M_*}=-\log s_{\epsilon , M_*}+\tilde{\phi }_\epsilon , \end{aligned}$$

(48)

where $s_{\epsilon , M_*}$ is some small constant to be chosen later.

Clearly,

$$\begin{aligned} \Delta \phi _{\epsilon ,M_*}=\Delta \tilde{\phi }_\epsilon . \end{aligned}$$

Therefore, on $S{\setminus } B_p(\epsilon )$,

$$\begin{aligned} \Delta \phi _{\epsilon ,M_*}+1=\Delta \tilde{\phi }_\epsilon +1<0. \end{aligned}$$

By (47), there exists a positive constant $C'_0$ such that, everywhere,

$$\begin{aligned} \Delta \tilde{\phi }_\epsilon \le \frac{C'_0}{\epsilon ^2}. \end{aligned}$$

Thus, on $B_p(\epsilon )$,

$$\begin{aligned} \Delta \phi _{\epsilon ,M_*}+1=\Delta \tilde{\phi }_\epsilon +1<\frac{C_0}{\epsilon ^{2}} \end{aligned}$$

for some positive constant $C_0>0$. To ensure our inequality (40) we need to make sure that $\frac{C_0}{\epsilon ^{2}}$ does not exceed $\frac{1}{2} M_* e^{\phi _{\epsilon ,M_*}}$ on $B_p(\epsilon )$. We therefore need,

$$\begin{aligned} \inf _{B_p(\epsilon )} \phi _{\epsilon ,M_*} \ge \log \left( \frac{2 C_0}{M_*\epsilon ^2}\right) . \end{aligned}$$

Recall that (47) implies

$$\begin{aligned} \inf _{B_p(\epsilon )} \phi _{\epsilon ,M_*}\ge -\log s_{\epsilon , M_*}+3\log \epsilon -\log C_1 \end{aligned}$$

for some $C_1>0$. Therefore, it suffices to choose

$$\begin{aligned} s_{\epsilon , M_*}=\frac{M_* \epsilon ^{5}}{2 C_0 C_1} \end{aligned}$$

(49)

and (40) is verified everywhere on $S$.

Finally, we use (47), (48) and (49) to check that $\phi _{\epsilon , M_*}$ obeys the bounds asserted in the proposition. By (47), we have the one-sided bound

$$\begin{aligned} \phi _{\epsilon } \le C, \end{aligned}$$

for some $C>0$. This, together with (48) and (49) implies

$$\begin{aligned} \sup _S \phi _{\epsilon ,M_*} \le -\log \left( \frac{M_* \epsilon ^{5}}{C_0 C_1}\right) +O(1) = \log \left( \frac{1}{M_* \epsilon ^5}\right) +O(1). \end{aligned}$$

(50)

For the bounds for the first and second derivatives of $\phi _{\epsilon ,M_*}$, notice that since $s_{\epsilon ,M_*}$ is a constant, by (47), we have

$$\begin{aligned} |\nabla \phi _{\epsilon ,M_*}|&= |\nabla \phi _{\epsilon }|=O(\epsilon ^{-1}),\\ |\nabla ^2\phi _{\epsilon ,M_*}|&= |\nabla ^2\phi _{\epsilon }|=O(\epsilon ^{-2}). \end{aligned}$$

$\square$