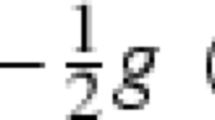Désingularisation de métriques d’Einstein. I

Abstract

We find a new obstruction for a real Einstein 4-orbifold with an A ₁-singularity to be a limit of smooth Einstein 4-manifolds. The obstruction is a curvature condition at the singular point.

For asymptotically hyperbolic metrics, with boundary at infinity a conformal metric, we prove that if the obstruction vanishes, one can desingularize Einstein orbifolds with such singularities.

The Dirichlet problem consists in finding Einstein metrics with given conformal infinity on the boundary: we prove that our obstruction defines a wall in the space of conformal metrics on the boundary, and that all the Einstein metrics must have their conformal infinity on one side of the wall.

1 Introduction

Cet article est consacré aux limites de métriques d’Einstein en dimension 4. Par les théorèmes d’Anderson et Bando-Kasue-Nakajima [1, 5], une suite (g _i ) de métriques d’Einstein sur des variétés compactes de dimension 4, à volume minoré et diamètre borné, et norme L ² de la courbure bornée, converge vers une métrique d’Einstein sur un orbifold ; en outre, près des singularités qui apparaissent, une limite d’éclatements $(\frac{g_{i}}{\epsilon_{i}})$, où ϵ _i tend vers 0, converge vers une variété Ricci plate asymptotiquement localement euclidienne (ALE), c’est-à-dire modelée à l’infini sur le quotient de ℝ⁴ par un sous-groupe fini de $\operatorname {SO}(4)$.

L’idée générale dans laquelle s’inscrit cet article est de raffiner le théorème de compacité en comprenant les limites possibles des suites de métriques d’Einstein. C’est une question importante en géométrie ou pour les applications des techniques géométriques en topologie. Plus précisément, nous étudions les métriques d’Einstein sur des orbifolds pour lesquelles on peut reconstruire les suites de métriques d’Einstein lisses convergeant vers la métrique orbifold. Si une telle construction est connue en géométrie kählérienne—l’exemple de certaines surfaces K3 construites par désingularisation de surfaces de Kummer singulières—, ce n’est pas le cas en géométrie riemannienne, car l’équation d’Einstein réelle est difficile à manipuler : en particulier, elle est toujours obstruée dans cette situation.

Les métriques ALE Ricci-plates ne sont pas classifiées, mais on suppose souvent qu’elles se réduisent aux instantons gravitationnels ALE, classifiés par Kronheimer [9, 10]. Ce sont des métriques ALE hyperkählériennes, désingularisations ou lissifications des singularités kleiniennes ℂ²/Γ, où Γ est un sous-groupe fini de $\operatorname {SU}(2)$. Leur 2-homologie est engendrée par les classes d’une configuration de sphères d’auto-intersection −2, contractées sur la singularité dans ℂ²/Γ. Le cas le plus simple est donc celui de la singularité ℂ²/ℤ₂, dans laquelle est contractée la seule sphère de sa désingularisation, la métrique de Eguchi-Hanson définie sur T ^∗ S ².

C’est ce cas que nous étudions dans cet article : le cas général d’une singularité kleinienne, nettement plus technique, sera traité dans un autre article. La singularité ℂ²/ℤ₂ est aussi le cas le plus « générique » de convergence vers une singularité kleinienne, au sens où l’on ne contracte qu’une seule sphère d’auto-intersection −2. Une autre limitation de cet article est que nous ne résolvons la question que dans un cadre non compact, où un bout à l’infini est asymptotiquement hyperbolique (AH)—le cas compact posant les problèmes supplémentaires connus d’obstruction dans les équations d’Einstein. Néanmoins, une grande partie de notre construction est valable dans le cas compact et y soulève des questions intéressantes. Elle éclaire aussi le problème de Dirichlet à l’infini sur les variétés AH, étudié par Anderson, dans le cas où la variété possède un H ² qui ne provient pas de son bord.

Passons maintenant aux résultats de cet article. On part d’un orbifold M ₀, à bord ∂M ₀={x=0} (où x est une équation du bord), muni d’une métrique d’Einstein AH g ₀, au sens où près du bord ∂M ₀ on a $g_{0}\sim \frac{dx^{2}+\gamma_{0}}{x^{2}}$, où γ ₀ est une métrique sur ∂M ₀. Le bord ∂M ₀ apparaît donc comme bord à l’infini, sur lequel g ₀ n’induit intrinsèquement que la classe conforme [γ ₀], appelée infini conforme de g ₀. Le but est de désingulariser la métrique aux points orbifold, ce qui sera possible sous une hypothèse de courbure. Pour l’énoncer, rappelons que la courbure riemannienne peut être vue comme endomorphisme symétrique des 2-formes, et qu’en dimension 4, celles-ci se décomposent en formes autoduales et anti-autoduales :

$$\varOmega^2=\varOmega^2_+\oplus\varOmega^2_-. $$

La courbure se décompose alors en

où W ⁺ et W ⁻, à trace nulle, sont les parties autoduales et anti-autoduales du tenseur de Weyl W.

Enfin, précisons que g ₀ est dite non dégénérée si elle n’admet pas de déformation d’Einstein infinitésimale L ².

Théorème 1.1

Supposons que (M ₀,g ₀) ait une singularité de la forme ℝ⁴/ℤ₂ au point p ₀, et que g ₀ soit non dégénérée. Soit M la variété obtenue à partir de M ₀ en éclatant p ₀ en une sphère d’auto-intersection −2. Supposons en outre qu’au point p ₀ on ait

$$ \det \mathbf {R}^+_{g_0}(p_0)=0. $$

(1)

Alors il existe une famille g _t (t>0) de métriques d’Einstein AH sur M, telle que

• le volume de la sphère éclatant p ₀ est t ;

• quand t→0, on a g _t →g ₀, avec convergence C ^∞ sur tout compact en dehors de p ₀ ;

• à la singularité, une bulle se forme : quand t→0, on a $\frac{g_{t}}{t}\to \mathrm {eh}$.

Si M ₀ compte plusieurs singularités de la forme ℝ⁴/ℤ₂, le même résultat reste vrai : on peut désingulariser ou bien toutes les singularités simultanément, ou bien seulement un sous-ensemble en laissant les singularités orbifold aux autres points.

Un exemple explicite de désingularisation est connu : la famille de métriques AdS-Taub-Bolt, construite par Page-Pope [13], voir aussi [12]. C’est une famille à 1 paramètre de métriques d’Einstein AH sur T ^∗ S ², dégénérant vers une métrique orbifold g ₀. Cette métrique g ₀ vérifie l’hypothèse de courbure detR ⁺(p ₀)=0. En fait, elle coïncide avec le quotient par ℤ₂ d’une métrique de Pedersen [14], et en particulier est autoduale ; par [8, prop. 4.5.3], elle est non dégénérée.

La méthode de démonstration du théorème consiste à recoller la métrique de Eguchi-Hanson de T ^∗ S ², asymptote à ℝ⁴/ℤ₂, à la métrique orbifold après un changement d’échelle dépendant de t. Dans ce recollement apparaît un paramètre de jauge, $\varphi\in \operatorname {SO}(4)$, indiquant comment la carte à l’infini de Eguchi-Hanson est recollée à une carte de M ₀ au point singulier. Comme la métrique de Eguchi-Hanson est $\operatorname {U}(2)$-invariante, le paramètre φ habite dans $\operatorname {SO}(4)/\operatorname {U}(2)$, qui s’identifie aux directions de $\varOmega^{2}_{+}\mathbb {R}^{4}$.

Choisissons sur Eguchi-Hanson la carte à l’infini qui est complexe pour la structure complexe de $T^{*}P^{1}_{\mathbb {C}}$. Alors, dans notre méthode de recollement, il faut que la droite de $\varOmega^{2}_{+}\mathbb {R}^{4}$ déterminée par φ soit dans le noyau de R ⁺(p ₀). Dans le cas non dégénéré où une seule valeur propre de R ⁺(p ₀) s’annule, la jauge de recollement est donc complètement déterminée ; dans le cas dégénéré où deux valeurs propres s’annulent, il y a plus de liberté.

Cela correspond bien à ce qui se passe dans le cas kählérien : les valeurs propres de R ⁺ sont alors $(\frac{\operatorname {Scal}}{4},0,0)$ ; si la courbure scalaire de M ₀ est non nulle, la structure complexe de M ₀ ne peut pas être recollée à celle de $T^{*}P^{1}_{\mathbb {C}}$, la métrique Kähler-Einstein ne pouvant pas admettre de courbe holomorphe d’auto-intersection −2. Il faut donc la recoller à une autre structure complexe de Eguchi-Hanson, pour laquelle la section nulle n’est pas holomorphe.

Enfin, si la métrique orbifold satisfait plutôt $\det \mathbf {R}^{-}_{g_{0}}(p_{0})=0$ en l’un des points singuliers, le théorème reste valable en recollant en p ₀ une métrique de Eguchi-Hanson avec l’orientation opposée. Par conséquent, compte tenu de la forme diagonale de R pour une métrique d’Einstein, on peut considérer que la vraie condition de courbure pour rendre possible le recollement est

$$\det \mathbf {R}_{g_0}(p_0)=0, $$

et une droite du noyau détermine un paramètre de recollement dans $\mathrm{O}(4)/\allowbreak \operatorname {U}(2)$, c’est-à-dire à la fois un choix d’orientation et un choix de structure complexe dans l’espace de Eguchi-Hanson recollé.

Une partie de la démonstration du théorème 1.1 est valable sur les variétés compactes. Cela permet de penser que, M ₀ compacte ou non compacte, la condition de courbure detR ⁺(p ₀)=0 soit nécessaire pour que g ₀ soit la limite d’une suite (g _i ) de métriques d’Einstein convergeant vers g ₀, telle que $(\frac{g_{i}}{\epsilon_{i}})$ converge vers la métrique de Eguchi-Hanson. Voici un premier résultat dans cette direction. Pour l’énoncer, soit $g_{t}^{0}$ la métrique qu’on obtient en recollant une grande boule de rayon $t^{-\frac{1}{4}}$, contractée d’un facteur $t^{\frac{1}{2}}$, dans une petite boule de rayon $t^{\frac{1}{4}}$ de M ₀. Il s’agit du recollement le plus simple possible entre g ₀ et la métrique de Eguchi-Hanson qui désingularise la singularité. Soit ρ≥1 une fonction, qui satisfait :

• en dehors d’un compact de Eguchi-Hanson, ρ coïncide avec le rayon ;

• sur M ₀, dans une boule fixe B autour de la singularité, la fonction ρ coïncide avec $t^{-\frac{1}{2}}r$, où r est le noyau ;

• dans M ₀−B, la fonction ρ est tronquée par une constante (donc de l’ordre de $t^{-\frac{1}{2}}$).

Il y a bien sûr un recollement sur la zone de transition entre les deux métriques. Alors :

Théorème 1.2

Supposons que (M ₀,g ₀) soit un orbifold compact, d’Einstein, non dégénéré, avec singularité de la forme ℝ⁴/ℤ₂ au point p ₀. Supposons qu’au point p ₀ on ait

$$\det \mathbf {R}_{g_0}^+(p_0)\neq0. $$

Soit δ ₀>0 petit. Alors il existe ϵ>0, tel que si g est une métrique sur M, proche dans C ² de $g_{t}^{0}$ au sens où, pour k=0,1,2,

$$\bigl|\nabla^k\bigl(g-g_t^0\bigr)\bigr|_{g_t^0} \leq\epsilon\rho^{-\delta_0-k} $$

(en fait il suffit d’avoir cette borne dans C ^1,α), alors g n’est pas d’Einstein.

Voir l’énoncé technique précis C ^1,α dans le corollaire 9.3, qui traite aussi le cas non compact (un autre poids est alors nécessaire à l’infini). Notons tout de suite que la condition sur la différence n’est pas trop forte, au sens où la borne C ² exigée sur $g-g_{t}^{0}$ est loin d’empêcher g d’être Einstein par un argument local. Par ailleurs, la proximité demandée entre g et $g_{t}^{0}$ est d’ordre $t^{\frac{\delta_{0}}{2}}$, ce qui est raisonnable puisqu’on s’attend à ce qu’une éventuelle métrique d’Einstein diffère en O(t) de la métrique $g_{t}^{0}$ (c’est le cas pour les métriques produites par le théorème 1.1).

On montrera dans un autre article que la condition de courbure (1) est nécessaire aussi, dans le même sens, pour désingulariser les autres singularités kleiniennes. Évidemment il serait souhaitable de démontrer que la condition est nécessaire sous des hypothèses beaucoup plus faibles sur la suite de métriques d’Einstein convergeant vers g ₀ :

Question

Supposons qu’on ait une suite de métriques d’Einstein (g _i ), convergeant vers un orbifold g ₀ avec une singularité ℂ²/Γ au point p, et telle qu’un éclatement au point p, soit $\frac{g_{i}}{\epsilon_{i}}$, converge vers un instanton gravitationnel ALE. Alors a-t-on $\det \mathbf {R}^{+}_{g_{0}}(p_{0})=0$ ?

L’hypothèse de non dégénérescence est évidemment satisfaite pour les métriques hyperboliques réelles, qui en revanche ne satisfont jamais la condition de courbure detR ⁺(p ₀)=0. Donc le théorème 1.2 dit qu’on ne peut pas désingulariser un orbifold hyperbolique réel, avec des singularités d’ordre 2, par la métrique de Eguchi-Hanson. Il est intéressant de spécialiser la question précédente aux variétés hyperboliques :

Sous-question

Si (M ₀,g ₀) est un orbifold compact de dimension 4, hyperbolique réel, avec des singularités kleiniennes, est-il possible qu’existe une suite g _i de métriques d’Einstein sur des variétés compactes, convergeant vers g ₀ en dehors des singularités, et telle qu’un éclatement aux singularités converge vers un instanton gravitationnel ALE ?

La même question fait également sens dans le cadre non compact.

Dans le théorème 1.1, les métriques g _t modifient l’infini conforme de g ₀, et le comportement de l’infini conforme par rapport à t est déterminé. Cela éclaire le problème de Dirichlet à l’infini pour les métriques d’Einstein AH : étant donné une métrique conforme [γ] sur ∂M, trouver une métrique d’Einstein AH sur M dont l’infini conforme est [γ]. Pour le résoudre, Anderson [2, 3] propose une théorie du degré comptant le nombre de métriques d’Einstein d’infini conforme donné, sous l’hypothèse que toute la 2-homologie de M provienne de ∂M, ce qui permet justement d’éviter la dégénérescence vers un orbifold. La démonstration du théorème 1.1 donne une indication sur ce cas, si les singularités sont kleiniennes. Notons $\mathcal {C}$ l’espace des métriques conformes sur ∂M ₀. Pour $\gamma\in \mathcal {C}$, proche de γ ₀, il existe [6] une métrique d’Einstein AH g ₀(γ), d’infini conforme γ. Soit

$$ \mathcal {C}_0 = \bigl\{ \gamma\in \mathcal {C}, \det \mathbf {R}^+_{g_0(\gamma)}(p_0)=0 \bigr\}. $$

(2)

Alors le résultat suivant dit que, génériquement, on peut désingulariser d’un seul côté de $\mathcal {C}_{0}$, et qu’ainsi $\mathcal {C}_{0}$ est un « mur » pour le problème de Dirichlet à l’infini ; les énoncés précis se trouvent sections 14 et 15 :

Théorème 1.3

Sous une hypothèse « générique » sur γ ₀, l’hypersurface $\mathcal {C}_{0}\subset \mathcal {C}$ est lisse en γ ₀, et :

• (1) les infinis conformes des métriques désingularisées construites par le théorème 1.1 remplissent l’intersection d’un voisinage ouvert de γ ₀ avec un seul côté de $\mathcal {C}_{0}$ ;

• (2) si une métrique d’Einstein AH g sur M, d’infini conforme γ, est proche au sens du théorème 1.2 d’un recollement de la métrique de Eguchi-Hanson avec une métrique orbifold d’Einstein, alors il faut que γ soit du côté de $\mathcal {C}_{0}$ déterminé ci-avant, et g est déterminée par γ.

Ce théorème indique manifestement que, dans le cas général, chaque sphère d’auto-intersection −2 dans la 2-homologie de M donne naissance à un mur défini par (2) sur l’orbifold obtenu par contraction de cette sphère : si l’on savait définir le degré d’Anderson dans cette situation, il changerait à travers ce mur, avec une contribution des métriques que nous avons construites égale à 1. Pour en déduire que la formule de passage de mur donne une différence égale à 1, il faudrait en outre montrer qu’il n’y a pas d’autre moyen de dégénérer vers g ₀ à travers des métriques d’Einstein, que par des métriques proches, au sens du théorème 1.2, des recollements modèles $g_{t}^{0}$. Voir l’exemple de T ^∗ S ² à la fin de la section 15.

Pour des sphères d’auto-intersection différente de −2, il y a dans [3] quelques remarques tendant à suggérer que ce type de phénomène ne se produira pas.

Les autres singularités kleiniennes correspondent à certaines configurations de sphères d’auto-intersection −2. On peut aussi les désingulariser, mais les obstructions à annuler portent non seulement sur R ⁺, mais aussi sur les dérivées de la courbure. Ce problème beaucoup plus technique sera traité dans un autre article. Par rapport à la question ci-dessus, on s’attend à trouver les dégénérescences vers ces singularités plus compliquées aux intersections des diverses hypersurfaces $\mathcal {C}_{0}$ définies par les différentes sphères d’auto-intersection −2. On voit donc que la codimension sera supérieure à 1, et qu’il s’agit d’un cas beaucoup moins générique que celui traité dans cet article.

Passons à présent au plan de cet article. On commence par analyser en profondeur l’équation infinitésimale d’Einstein pour la métrique de Eguchi-Hanson en section 2. Pour recoller la métrique de Eguchi-Hanson, après changement d’échelle, à la métrique orbifold donnée g ₀, on modifie en section 3 la métrique de Eguchi-Hanson pour la faire coller à l’infini avec les termes d’ordre 2 de g ₀ au point singulier. C’est possible sous une condition sur ses termes d’ordre 2, interprétée en section 4 comme condition de courbure sur g ₀ au point singulier. Cette condition permet donc de fabriquer en section 5 un recollement qui est approximativement d’Einstein. Malheureusement, on ne peut pas le déformer en une vraie métrique d’Einstein, à cause des obstructions provenant de Eguchi-Hanson, et on est amené à définir en section 6 un problème d’Einstein modulo obstructions. On a été concis dans la résolution, effectuée en sections 7–9, car elle suit un schéma général classique : néanmoins la démonstration reste délicate, car il faut d’une part contrôler une géométrie dont le rayon d’injectivité tend vers 0, et d’autre part obtenir un développement précis des obstructions. De ce développement est déduit en particulier le corollaire 9.3 qui dit que, sous certaines hypothèses, la condition de courbure $\det \mathbf {R}^{+}_{g_{0}}(p_{0})=0$ est nécessaire. Jusque là, toute la construction, y compris ce corollaire, reste valable si M ₀ est compacte.

La résolution complète de l’équation exige de trouver de nouvelles déformations pour tuer les obstructions : celles-ci proviennent des déformations de l’infini conforme de M ₀ (ce n’est donc qu’ici qu’on utilise la non compacité de M ₀), permettant de perturber le germe de g ₀ au point singulier en sections 10–11 (ceci repose sur le théorème de continuation unique de [7]), puis on construit les métriques d’Einstein en section 12. Déterminer l’asymptotique précis des infinis conformes nécessaires requiert un raffinement des obstructions et des solutions approchées mené en sections 13–14. Finalement, un argument de transversalité développé en section 15 donne l’unicité générique des solutions.

2 La linéarisation de l’équation d’Einstein pour Eguchi-Hanson

La métrique de Eguchi-Hanson, eh, est une métrique hyperkählérienne sur $T^{*}P^{1}_{\mathbb {C}}$. À l’infini, elle est ALE (asymptotiquement localement euclidienne), c’est-à-dire asymptotique à la métrique plate de ℝ⁴/ℤ₂. On rappelle ici quelques faits standards. Choisissons des coordonnées (x ¹,x ²,x ³,x ⁴) sur ℝ⁴, soient r le rayon et (α ₁,α ₂,α ₃) une base de 1-formes invariantes sur la sphère S ³, satisfaisant dα ₁=2α ₂∧α ₃,… Plus précisément, on prend

On peut alors écrire la métrique de Eguchi-Hanson comme

$$ \mathrm {eh}= \frac{r^2}{\sqrt{1+r^4}} \bigl(dr^2+r^2 \alpha_1^2 \bigr)+\sqrt{1+r^4} \bigl( \alpha_2^2+\alpha_3^2 \bigr), $$

(3)

où la section nulle de $T^{*}P^{1}_{\mathbb {C}}$ est représentée par r=0, et la métrique y est équivalente à

$$d\biggl(\frac{r^2}{2}\biggr)^2+4\biggl(\frac{r^2}{2} \biggr)^2\alpha_1^2+\alpha_2^2+ \alpha_3^2. $$

Pour obtenir une métrique qui s’étende de manière lisse à l’origine, on voit qu’il faut que 2α ₁ soit de longueur 2π sur les cercles autour du P ¹, c’est-à-dire qu’il faut quotienter par l’action de ℤ₂ sur ces cercles ; la formule (3) définit ainsi une métrique lisse sur $T^{*}P^{1}_{\mathbb {C}}$.

Comme métrique hyperkählérienne, Eguchi-Hanson est kählérienne par rapport à trois structures complexes I ₁, I ₂ et I ₃ ; on choisira I ₁ comme la structure complexe donnant $T^{*}P^{1}_{\mathbb {C}}$, elle est donnée explicitement par les coordonnées complexes x ¹+ix ² et x ³+ix ⁴. Les structures complexes I ₂ et I ₃ sont asymptotes, à l’infini, aux structures complexes de ℝ⁴ données respectivement, d’une part par les coordonnées complexes x ¹+ix ³ et x ²−ix ⁴, d’autre part par les coordonnées complexes x ¹+ix ⁴ et x ²+ix ³.

Enfin, à l’infini, notant la métrique euclidienne

$$\mathrm {e}= dr^2+r^2\bigl(\alpha_1^2+ \alpha_2^2+\alpha_3^2\bigr), $$

on a le développement asymptotique

$$ \mathrm {eh}= \mathrm {e}+\frac{1}{2r^4} \bigl(- \bigl(dr^2+r^2 \alpha_1^2 \bigr)+\alpha_2^2+ \alpha_3^2 \bigr) +O \biggl(\frac{1}{r^6} \biggr), $$

(4)

qui montre que la métrique de Eguchi-Hanson est asymptotique à la métrique plate de ℂ²/ℤ₂ à des termes en $O(\frac{1}{r^{4}})$ près.

La cohomologie L ² de eh, concentrée en degré 2, est de dimension 1 et représentée par la 2-forme anti-autoduale fermée

$$ \varOmega= \frac{1}{1+r^4} \biggl(\frac{r^2}{\sqrt{1+r^4}}dr \land r\alpha_1-\sqrt{1+r^4}\alpha_2\land \alpha_3 \biggr). $$

(5)

L’opérateur de linéarisation de l’équation d’Einstein, agissant sur les 2-tenseurs symétriques, est

$$d_\mathrm {eh}\operatorname {Ric}(h)=\frac{1}{2} \nabla_\mathrm {eh}^*\nabla_\mathrm {eh}h - \overset {\circ }{R}_\mathrm {eh}h - \delta_\mathrm {eh}^* B_\mathrm {eh}h , $$

où $B_{\mathrm {eh}}=\delta_{\mathrm {eh}}h+\frac{1}{2}d\operatorname {tr}_{\mathrm {eh}}h$ est l’opérateur de Bianchi.

Dans la suite, sauf ambiguïté, on évitera les indices indiquant par rapport à quelle métrique est défini l’opérateur.

Généralement, on considère h en jauge de Bianchi Bh=0, ce qui mène à étudier plutôt

$$P = \frac{1}{2} \nabla^*\nabla- \overset {\circ }{R}. $$

Puisque $\operatorname {Ric}_{\mathrm {eh}}=0$, l’identité de Bianchi $B_{g} \operatorname {Ric}_{g}=0$ implique $B_{\mathrm {eh}}\circ d_{\mathrm {eh}}\operatorname {Ric}=0$, d’où on déduit immédiatement

$$B_\mathrm {eh}P_\mathrm {eh}= B_\mathrm {eh}\delta_\mathrm {eh}^* B_\mathrm {eh}= \frac{1}{2} \nabla_\mathrm {eh}^*\nabla_\mathrm {eh}B_\mathrm {eh}. $$

Une conséquence de cette formule est le fait suivant : si P _eh h=0 et h=O(r ^δ) pour un δ<1, alors B _eh h=0. Par conséquent, le noyau de P, et particulièrement son noyau L ², paramètre bien des déformations infinitésimales d’Einstein.

Proposition 2.1

L’opérateur P _eh pour la métrique de Eguchi-Hanson satisfait les propriétés suivantes :

• (1) Le noyau L ² de P _eh, noté $\mathcal {O}_{\mathrm {eh}}$, est de dimension 3, engendré par les trois tenseurs

  $$o_i(x,y) = \varOmega(I_ix,y), $$

  où Ω est la 2-forme harmonique L ², et les I _i sont les trois structures complexes de la métrique de Eguchi-Hanson.

• (2) Le noyau de P _eh sur les tenseurs u tels que |u|=O(r ^−δ) pour un δ>0 se réduit à $\mathcal {O}_{\mathrm {eh}}$.

• (3) Si v=O(r ^−δ) pour un δ∈(0,4), δ≠2, alors il existe u tel que

  $$P_\mathrm {eh}u=v, \quad u=O\bigl(r^{2-\delta}\bigr) $$

  si et seulement si le produit scalaire (v,o _i )=0 pour 1≤i≤3.

• (4) Une solution $\hat{k}_{i}$ de $P_{\mathrm {eh}}\hat{k}_{i}=o_{i}$ est donnée par

  $$\hat{k}_i = -\frac{1}{12} \bigl(1+r^4\bigr)^{\frac{3}{2}}o_i. $$

• (5) Une solution k _i , à trace nulle, de $d_{\mathrm {eh}}\operatorname {Ric}k_{i}=o_{i}$ est donnée par

  

Démonstration

On a $\operatorname {tr}P(h) = \Delta \operatorname {tr}h$, donc si P(h)=0, il faut que $\operatorname {tr}h=0$. On est donc ramené au cas sans trace. On utilise alors l’isomorphisme $\operatorname {Sym}_{0}^{2}=\varOmega_{-}^{2}\varOmega_{+}^{2}$ pour identifier h avec une 2-forme anti-autoduale à valeurs dans les 2-formes autoduales. Par la formule (4.6) dans [8], on a alors la formule

$$ P h = d_- d_-^* h , $$

(6)

où $d_{-}:\varOmega^{1}\varOmega_{+}^{2} \to\varOmega_{-}^{2}\varOmega_{+}^{2}$ est la différentielle extérieure. Comme la métrique est hyperkählérienne, le fibré $\varOmega_{+}^{2}$ est trivial, et trivialisé par les trois structures complexes parallèles I _i : l’identification de $\varOmega_{-}^{2}\varOmega_{+}^{2}$ avec $\varOmega_{-}^{2}\otimes \mathbb {R}^{3}$ qui en résulte est donnée par h↦(ω _i (x,y)=h(x,I _i y)). Ainsi l’opérateur $d_{-}d_{-}^{*}$ devient le laplacien ordinaire sur les ω _i . Comme la cohomologie L ² est de dimension 1, on obtient la première assertion.

Pour la seconde assertion, observons que si, pour une 2-forme anti-autoduale ω telle que |ω|=O(r ^−δ) on a $d_{-}d_{-}^{*}\omega=0$, alors par régularité elliptique |∇ω|=O(r ^−δ−1) ; par conséquent, dans l’intégration par parties

$$\int_{r<R} \bigl\langle d_-d_-^*\omega,\omega\bigr\rangle= \int _{r<R} \bigl|d_-^*\omega\bigr|^2 - \int_{r=R} d_-^*\omega\land\omega $$

le terme de bord est O(r ^−δ−1 r ^−δ r ³)=O(r ^2(1−δ)), et donc, si δ>1 on obtient $d_{-}^{*}\omega=0$, c’est-à-dire dω=0. On en déduit alors facilement qu’en réalité ω doit coïncider avec un multiple de la forme harmonique Ω.

On utilise alors la théorie des opérateurs elliptiques dans les espaces à poids pour constater que l’opérateur $d_{-}d_{-}^{*}$ n’a pas de poids critique dans l’intervalle (0,2), et donc le noyau dans cet intervalle ne dépend pas du poids δ∈(0,2). Puisque, pour δ>1, il est réduit au noyau L ², il est donc réduit au noyau L ² sur tout l’intervalle (0,2).

La troisième assertion résulte aussi de la théorie des opérateurs elliptiques dans les espaces à poids. En effet, si δ n’est pas critique (d’où la restriction δ≠2), le conoyau de l’opérateur P:r ^δ−2 C ^2,α→r ^δ C ^α est égal au noyau de P sur r ^4−δ C ^α. Mais si δ∈(0,4) alors 4−δ∈(0,4) et le noyau dans cet intervalle se réduit au noyau L ².

Compte tenu de la formule (6), la quatrième assertion se ramène à l’égalité $d_{-}d_{-}^{*}\varXi=\varOmega$, où

$$\varXi= -\frac{1}{12}\bigl(1+r^4\bigr)^{\frac{3}{2}} \varOmega. $$

Or on calcule

$$ d^*\varXi= \frac{r^4}{2\sqrt{1+r^4}}\alpha_1 , $$

(7)

qui mène à

$$ dd^*\varXi= \omega_1 + \varOmega. $$

(8)

La partie anti-autoduale est donc Ω, d’où la formule.

La dernière assertion est plus compliquée : le problème est que les $\hat{k}_{i}$ ne sont plus en jauge de Bianchi, donc le calcul de $P_{\mathrm {eh}}\hat{k}_{i}$ n’est pas suffisant pour obtenir $d_{\mathrm {eh}}\operatorname {Ric}\hat{k}_{i}$. Calculons donc le terme de jauge dans $P_{\mathrm {eh}}\hat{k}_{i}$. Observons que la formule (7) indique que d ^∗ Ξ est duale (au sens de la métrique) du champ de vecteurs de Killing $\frac{1}{2} I_{1} r\frac{\partial}{\partial r}$. Il en résulte

$$ \nabla d^*\varXi= \frac{1}{2} dd^*\varXi= \frac{1}{2}( \omega_1+ \varOmega). $$

(9)

Compte tenu de $\hat{k}_{i}(\cdot,\cdot)=\varXi(I_{i}\cdot,\cdot)$, on en déduit $\delta\hat{k}_{i}=I_{i}d^{*}\varXi$, d’où, à l’aide de (8),

$$ \nabla B\hat{k}_i(\cdot,\cdot) = -\frac{1}{2}(\omega_1+ \varOmega) (\cdot,I_i\cdot). $$

En prenant la partie symétrique, on obtient

Puisque $d\operatorname {Ric}=P-\delta^{*}B$, on en déduit l’assertion sur k ₂ et k ₃. En revanche,

$$ d_\mathrm {eh}\operatorname {Ric}\hat{k}_1=\frac{1}{2}(o_1-\mathrm {eh}). $$

(10)

Pour compenser le terme eh, on introduit un terme à trace : la fonction $f(r)=\sqrt{1+r^{4}}$ satisfait Δf=−8, et, plus précisément, df=−4I ₁ d ^∗ Ξ, donc par (9),

$$\nabla df = 2(\mathrm {eh}+ o_1). $$

Il en résulte

Combinant avec (10), on en déduit que $d_{\mathrm {eh}}\operatorname {Ric}\frac{3}{2}(\hat{k}_{1}-\frac{1}{12}f\mathrm {eh})=o_{1}$. Le terme de jauge additionnel dans la proposition, $\frac{1}{12}\delta^{*} (\frac{(1+r^{4})^{\frac{3}{2}}-1}{r^{3}}\partial_{r} )$, permet d’annuler la trace (calcul laissé au lecteur). □

3 Le problème linéarisé sur Eguchi-Hanson

Soit dans ℝ⁴ un 2-tenseur symétrique H dont les coefficients sont des polynômes homogènes de degré 2, ainsi

$$ H=H_{ijkl}x^ix^jdx^kdx^l. $$

(11)

On pense à H comme le terme d’ordre 2 dans le développement à l’origine d’une métrique g=e+H+⋯ sur ℝ⁴. La courbure en 0 de g ne dépend que de H et sera notée R(H). Il est important de noter que R(H) est linéaire en H. Les composantes de R(H) (courbure de Weyl, tenseur de Ricci et courbure scalaire) seront notées W(H), $\operatorname {Ric}(H)$ et $\operatorname {Scal}(H)$. On déduit aussi l’opérateur de courbure,

$$\mathbf {R}(H) : \varLambda^2\mathbb {R}^4 \to\varLambda^2 \mathbb {R}^4. $$

Dans la décomposition $\varLambda^{2}\mathbb {R}^{4}=\varLambda^{2}_{+}\mathbb {R}^{4}\oplus \varLambda^{2}_{-}\mathbb {R}^{4}$, cet opérateur s’écrit

(12)

Enfin, il sera important dans la suite de noter que le tenseur H n’est pas forcément donné en jauge de Bianchi par rapport à la métrique euclidienne, et le défaut à être en jauge de Bianchi est mesuré par la 1-forme

$$B_\mathrm {e}H = \sum_k (-2 H_{kjkl}+H_{jlkk}) x^j dx^l . $$

Dans cette section, on étudie un problème infinitésimal de déformation de eh par un tenseur asymptotique à l’infini à un tenseur H donné de type (11).

Supposons que le tenseur H soit d’Einstein, c’est-à-dire

$$\operatorname {Ric}(H)=\varLambda\sum\bigl(dx^i\bigr)^2 $$

pour un réel Λ. Fixons les coordonnées (x ⁱ) sur ℝ⁴ comme dans la section 2, avec la métrique de Eguchi-Hanson donnée par la formule (3). Le problème que nous regardons s’écrit :

$$ \begin{aligned} d_\mathrm {eh}\operatorname {Ric}(h) &= \varLambda \mathrm {eh}, \\ h &= H + O \bigl(r^{-2+\epsilon} \bigr) \quad \text{pour tout} \ \epsilon>0. \end{aligned} $$

(13)

Le but de cette section est le résultat suivant :

Proposition 3.1

Le problème (13) a une solution si et seulement si, pour i=1,2,3, on a

$$\lim_{r\to\infty} \int_{S_r/\mathbb {Z}_2} \biggl(\frac{3}{r} \langle H,o_i \rangle+o_i\biggl(BH,\frac{\partial}{\partial r} \biggr) \biggr) \operatorname {vol}_{S_r/\mathbb {Z}_2}=0, $$

où les o _i sont les solutions L ² de P _eh h=0.

Remarquons que les termes principaux de H, BH et o _i sont respectivement en r ², r et r ⁻⁴, tandis que le volume des sphères est en r ³, donc la limite est bien définie. De même, le choix de la métrique euclidienne ou de la métrique de Eguchi-Hanson pour calculer BH est sans importance, puisque seul le terme principal contribue à la limite.

Démonstration

Remarquons qu’on peut mettre H en jauge de Bianchi, en trouvant un champ de vecteurs V sur ℝ⁴, dont les coefficients sont des polynômes homogènes de degré 3, tel que

$$B_\mathrm {e}\tilde{H}=0, \quad\text{o\`{u} } \ \tilde{H}=H+ \delta_\mathrm {e}^*V. $$

En effet, il suffit de résoudre l’équation $B_{\mathrm {e}}\delta_{\mathrm {e}}^{*}V=-B_{\mathrm {e}}H$, or $B_{\mathrm {e}}\delta_{\mathrm {e}}=\nabla_{\mathrm {e}}^{*}\nabla_{\mathrm {e}}=-\sum\frac{\partial^{2}}{(\partial x^{i})^{2}}$ donc c’est toujours possible, $\tilde{H}$ est encore un tenseur dont les coefficients sont des polynômes de degré 2.

Si on a une solution du système (13), alors on peut mettre h en jauge de Bianchi en résolvant

$$ \begin{aligned} B_\mathrm {eh}\delta_\mathrm {eh}^*v &= - B_\mathrm {eh}h , \\ v &= V + O \bigl(r^{-1} \bigr) , \end{aligned} $$

(14)

et en posant $\tilde{h}=h+\delta_{\mathrm {eh}}^{*}v$, qui est alors solution du système

$$ \begin{aligned} d_\mathrm {eh}\operatorname {Ric}(\tilde{h}) &= \varLambda \mathrm {eh}, \\ B_\mathrm {eh}\tilde{h}&= 0, \\ \tilde{h} &= \tilde{H} + O \bigl(r^{-2+\epsilon} \bigr), \end{aligned} $$

(15)

donc, en particulier,

$$ \begin{aligned} P_\mathrm {eh}\tilde{h} &= 0, \\ \tilde{h} &= \tilde{H} + O \bigl(r^{-2+\varepsilon} \bigr). \end{aligned} $$

(16)

Réciproquement, une solution de l’équation (16) satisfait automatiquement le système (15) : en effet, puisque $B_{\mathrm {eh}}P_{\mathrm {eh}}=\frac{1}{2}\nabla_{\mathrm {eh}}^{*}\nabla_{\mathrm {eh}}B_{\mathrm {eh}}$, si $P_{\mathrm {eh}}\tilde{h}=0$, alors $w=B_{\mathrm {eh}}\tilde{h}$ satisfait $\nabla_{\mathrm {eh}}^{*}\nabla_{\mathrm {eh}}w=0$ ; en outre, compte tenu de l’asymptotique de $\tilde{h}$, on a w=O(r ^−3+ϵ), donc il faut que ∇_eh w=0 ce qui entraîne w=0. On a donc montré que la résolution du système (13) se ramène à la résolution du système (16), où $\tilde{H}$ est en jauge de Bianchi à l’infini.

Or, la résolution du système (16) est maintenant facile : soit χ une fonction de coupure, donc

$$\chi(x)= \begin{cases} 1, &|x|>2R, \\ 0, &|x|<R, \end{cases} $$

alors il faut trouver $k=\tilde{h}-\chi\tilde{H}$ satisfaisant

$$ \begin{aligned} k&=O \bigl(r^{-2} \bigr), \\ P_\mathrm {eh}k&=-P_\mathrm {eh}(\chi\tilde{H}). \end{aligned} $$

(17)

Sachant que $\tilde{H}$ est en jauge de Bianchi à l’infini, et que $\operatorname {Ric}(\tilde{H})=\varLambda \mathrm {e}$, on voit que

$$B_\mathrm {eh}\tilde{H}=O\bigl(r^{-3}\bigr), \qquad d_\mathrm {eh}\operatorname {Ric}(\tilde{H})-\varLambda \mathrm {eh}=O\bigl(r^{-4}\bigr), $$

donc au total

$$P_\mathrm {eh}(\chi\tilde{H})=O\bigl(r^{-4}\bigr) . $$

Par la proposition 2.1, une solution de (17) est donc possible si et seulement si

$$ \bigl(P_\mathrm {eh}(\chi\tilde{H}),o_i \bigr)=0, \quad i=1,2,3, $$

(18)

où les o _i engendrent le noyau de P _eh. Dans ce cas, la solution k satisfait k=O(r ^−2+ϵ) pour tout ϵ>0.

Puisque $P=\frac{1}{2} \nabla^{*}\nabla-\overset {\circ }{R}$, l’équation P _eh o _i =0 entraîne

$$ \int_{r\leq R} \langle P_\mathrm {eh}v,o_i \rangle \operatorname {vol}_\mathrm {eh}= \frac{1}{2} \int_{r=R} \bigl( \langle- \nabla_{\vec{n}}v,o_i \rangle+ \langle v, \nabla_{\vec{n}}o_i \rangle\bigr) \operatorname {vol}_{S_R/\mathbb {Z}_2} . $$

(19)

Sachant que o _i admet à l’infini un développement suivant les puissances de $\frac{1}{r}$, dont le terme principal est en r ⁻⁴, on déduit

$$\nabla_{\vec{n}}o_i \sim\frac{-4}{r} o_i . $$

De même, à l’infini, $\tilde{H}$ est homogène de degré 2, donc

$$\nabla_{\vec{n}}\tilde{H} \sim\frac{2}{r} \tilde{H} . $$

Passant à la limite dans (19), on déduit

$$ \bigl(P_\mathrm {eh}(\chi\tilde{H}),o_i \bigr) = -3 \lim_{r\to\infty} \frac{1}{r}\int_{S_r/\mathbb {Z}_2} \bigl\langle\tilde{H},o_i \bigr\rangle \operatorname {vol}_{S_R/\mathbb {Z}_2}. $$

(20)

Il reste à exprimer cette intégrale en fonction de H plutôt que $\tilde{H}$. Pour cela nous modifions un peu le calcul précédent : rappelons que $\tilde{H}=H+\delta_{\mathrm {e}}^{*}V$, où V a été choisi de sorte que $B_{\mathrm {e}}\delta_{\mathrm {e}}^{*}V=-B_{\mathrm {e}}H$. Prolongeons V de manière quelconque sur tout $T^{*}P_{\mathbb {C}}^{1}$, en préservant son asymptotique, alors $\chi\tilde{H}=H'+\delta_{\mathrm {eh}}^{*}V$, avec H′=H+O(r ⁻²). La même intégration par parties que précédemment mène à :

$$ \bigl(P_\mathrm {eh}H',o_i \bigr) = -3 \lim_{r\to\infty} \frac{1}{r}\int_{S_r/\mathbb {Z}_2} \langle H,o_i \rangle \operatorname {vol}_{S_R/\mathbb {Z}_2}. $$

(21)

Faisons en revanche une intégration par parties différente sur l’autre terme : puisque $P_{\mathrm {eh}}\delta_{\mathrm {eh}}^{*}=\delta_{\mathrm {eh}}^{*}B_{\mathrm {eh}}\delta_{\mathrm {eh}}^{*}$ et B _eh o _i =0, on obtient

$$\int_{r\leq R} \bigl\langle P_\mathrm {eh}\delta_\mathrm {eh}^*V,o_i\bigr\rangle \operatorname {vol}_\mathrm {eh}= \int_{S_R/\mathbb {Z}_2} * \bigl(B_\mathrm {eh}\delta_\mathrm {eh}^*V\lrcorner o_i \bigr). $$

Compte tenu de $B_{\mathrm {e}}\delta_{\mathrm {e}}^{*}V=-B_{\mathrm {e}}H$ près de l’infini, en passant à la limite R→∞, on obtient

$$ \bigl(P_\mathrm {eh}\delta_\mathrm {eh}^*V,o_i \bigr) = \lim_{r\to\infty} \int_{S_r/\mathbb {Z}_2} * (-BH\lrcorner o_i ). $$

(22)

La somme de (21) et (22) donne le résultat de la proposition. □

Si la condition de la proposition 3.1 n’est pas satisfaite, on ne peut plus résoudre le système (13). Néanmoins, on peut résoudre modulo l’espace d’obstruction $\mathcal {O}_{\mathrm {eh}}$, c’est-à-dire résoudre le système suivant :

$$ \begin{aligned} d_\mathrm {eh}\operatorname {Ric}(h) &= \varLambda \mathrm {eh}+ \sum_1^3 \lambda_io_i, \\ h &= H + O \bigl(r^{-2+\epsilon} \bigr) \quad \text{pour tout} \ \epsilon>0, \end{aligned} $$

(23)

où les λ _i sont des constantes inconnues à trouver.

Proposition 3.2

Le problème (23) a toujours une solution h. Les constantes λ _i sont déterminées par H :

$$ \lambda_i = - \frac{1}{\|\varOmega\|_{L^2}^2} \lim_{r\to\infty} \int_{S_r/\mathbb {Z}_2} \biggl(\frac{3}{r}\langle H,o_i \rangle+o_i \biggl(BH,\frac{\partial}{\partial r} \biggr) \biggr) \operatorname {vol}_{S_r/\mathbb {Z}_2}. $$

(24)

La solution est déterminée modulo jauge et modulo le noyau $\mathcal {O}_{\mathrm {eh}}$. En mettant H en jauge de Bianchi, on peut fixer une solution particulière en demandant

$$ B_\mathrm {eh}h=0, \qquad \int_{S^2} \langle h,o_j\rangle_\mathrm {eh}\operatorname {vol}= 0. $$

(25)

Démonstration

Observons que les tenseurs k _i de la proposition 2.1 n’ont pas de raison particulière d’être en jauge de Bianchi, mais on peut les mettre en jauge de Bianchi en posant $\tilde{k}_{i}=k_{i}+\delta_{\mathrm {eh}}^{*}v_{i}$, où v _i résoud le système (14).

On montre alors la proposition en reprenant la démonstration de la proposition 3.1 : il s’agit de résoudre le système (17) pour un $\tilde{H}$ en jauge de Bianchi à l’infini. La solution est possible pourvu que les trois conditions (18) soient satisfaites. En posant $\tilde{H}=\tilde{H}'+\sum_{1}^{3}\lambda_{i}\tilde{k}_{i}$, où les λ _i sont données par (24), alors $\tilde{H}'$ satisfait les conditions (18) et on peut donc résoudre le problème. Le prix à payer est que $P_{\mathrm {eh}}\tilde{k}_{i}=d_{\mathrm {eh}}\operatorname {Ric}\tilde{k}_{i}=o_{i}$, donc on n’a résolu que l’équation (23). □

4 Reformulation des obstructions

Le but de cette section est de recalculer la condition de résolution du système (13) sous une forme différente. En effet, la condition sur H trouvée dans la proposition 3.1 doit manifestement être invariante par difféomorphismes infinitésimaux de ℝ⁴ dont la différentielle est l’identité à l’origine : donc cette condition ne peut être qu’une condition sur la courbure R(H) associée à H. En effet, on obtient une condition simple sur l’opérateur de courbure R(H) agissant sur Ω ²ℝ⁴ :

Théorème 4.1

Le système (13) a une solution si et seulement si

$$ \mathbf {R}^+(H) \bigl(dx^1\land dx^2+dx^3\land dx^4 \bigr)=0 . $$

(26)

Notons qu’on pourrait écrire aussi bien la condition sur R(H), puisque la métrique est d’Einstein.

Dans ce théorème, les coordonnées (x ⁱ) ne sont pas quelconques, puisqu’à l’infini x ¹+ix ² et x ³+ix ⁴ sont complexes pour la structure complexe I ₁ de la métrique de Eguchi-Hanson—à savoir la structure de $T^{*} P^{1}_{\mathbb {C}}$.

Pour démontrer le théorème, on commence par calculer explicitement les obstructions provenant de la proposition 3.1. Compte tenu de la proposition 2.1 de la formule (5), on a les asymptotiques explicites suivantes pour les o _i :

$$ \begin{aligned} o_1 &\sim \frac{1}{r^2} \biggl( \frac{dr^2}{r^2} + \alpha_1^2 - \alpha_2^2 - \alpha_3^2\biggr), \\ o_2 &\sim\frac{1}{r^2} \biggl( \frac{dr}{r} \cdot \alpha_3 + \alpha_1 \cdot\alpha_2 \biggr), \\ o_3 &\sim\frac{1}{r^2} \biggl(-\frac{dr}{r} \cdot \alpha_2 + \alpha_1 \cdot\alpha_3 \biggr). \end{aligned} $$

(27)

Manifestement, la condition d’existence d’une solution au système (13) est invariante sous la transformation H→H+δ ^∗ V, où V est un champ de vecteurs dont les coefficients sont homogènes de degré 3. Par conséquent, il suffit de tester la condition de la proposition 3.1 sur H mis en jauge radiale : $\frac{\partial}{\partial r}\lrcorner H=0$. Cela implique que H s’écrive sous la forme

$$ H = \sum_{ij} H_{ij} \beta_i\beta_j, $$

(28)

où les H _ij sont des fonctions homogènes de degré 0, et on a posé

$$\beta_i = r^2\alpha_i = x^1 dx^{i+1} - x^{i+1} dx^1 + \cdots $$

On calcule alors :

Lemme 4.2

On a

(29)

et pour i=2,3,

$$ \lim_{r\to\infty} \int_{S_r/\mathbb {Z}_2} \biggl(\frac{3}{r} \langle H,o_i \rangle+o_i \biggl(BH,\frac{\partial}{\partial r} \biggr) \biggr) \operatorname {vol}_{S_r/\mathbb {Z}_2} = \int_{S^3/\mathbb {Z}_2} 6 H_{1i}\operatorname {vol}_{S^3/\mathbb {Z}_2} . $$

(30)

Démonstration

On a ∇β ₁=dx ¹⊗dx ²−dx ²⊗dx ¹+dx ³⊗dx ⁴−dx ⁴⊗dx ³=I ₁, et, plus généralement,

$$\nabla\beta_i = I_i . $$

On calcule alors aisément, toujours pour la métrique euclidienne,

Enfin, on aura besoin, pour une fonction f, de la formule :

$$B(fT) = f BT + \biggl(-\nabla f \lrcorner T + \frac{1}{2}(\operatorname {tr}T)df \biggr) . $$

Remarquons à présent que H=H _ij β _i β _j avec H _ij homogène de degré 0, donc $\frac{\partial H_{ij}}{\partial r}=0$. On obtient alors immédiatement

$$o_1\biggl(BH,\frac{\partial}{\partial r}\biggr)=BH\biggl(\frac{\partial}{\partial r}\biggr)=2(H_{11}+H_{22}+H_{33}); $$

d’un autre côté,

$$\langle H,o_1\rangle=H_{11}-H_{22}-H_{33} ; $$

ces deux formules ensemble donnent la première formule du lemme, les deux autres s’établissent de la même manière. □

Démonstration du théorème 4.1

Il reste à interpréter l’annulation de ces trois quantités en termes de la courbure R(H). Bien qu’un calcul explicite soit possible, nous préférons l’approche abstraite suivante. Notons S ₊ et S ₋ les représentations spinorielles de $\operatorname {Spin}(4)=\operatorname {SU}(2)\times \operatorname {SU}(2)$, ce sont donc les représentations standard dans ℂ² des deux copies de $\operatorname {SU}(2)$ ; notons $S_{\pm}^{k}$ leur produit symétrique, alors les représentations de $\operatorname {SO}(4)$ se décomposent en somme de produits tensoriels $S_{+}^{k}S_{-}^{l}$. En particulier, ℝ⁴=S ₊ S ₋ (en fait c’est la partie réelle, mais comme toutes nos représentations sont réelles, nous oublierons ce détail dans la suite), les 2-formes se décomposent en $\varOmega^{2}\mathbb {R}^{4}=\varOmega^{2}_{+}\oplus\varOmega^{2}_{-}=S_{+}^{2}\oplus S_{-}^{2}$, et les 2-tenseurs symétriques en $S^{2}\mathbb {R}^{4}=S_{+}^{2}S_{-}^{2}\oplus \mathbb {R}$. Finalement, les deux demi-tenseurs de Weyl W _± vivent dans les représentations $S_{\pm}^{4}$.

Le 2-tenseur H=H _ijkl x ⁱ x ^j dx ^k dx ^l vit dans la représentation

$$\mathcal {H}=S^2\mathbb {R}^4\otimes S^2 \mathbb {R}^4, $$

mais la condition qu’il soit radial se traduit par

$$V(H):=x^i\frac{\partial}{\partial x^i}\lrcorner H=0 . $$

Or les coefficients du vecteur V(H) sont homogènes de degré 3, donc $V(H)\in \mathcal {V}=S^{3}\mathbb {R}^{4}\otimes \mathbb {R}^{4}$. On a les décompositions :

(31)

(32)

Il est clair que $V:\mathcal {H}\to \mathcal {V}$ est surjectif. Comme il est aussi $\operatorname {SO}(4)$-équivariant, on en déduit que l’espace des 2-tenseurs H radiaux, à savoir kerV, se décompose suivant les représentations présentes dans (31) mais absentes dans (32), donc

$$ \ker V = \mathbb {R}\oplus S_+^2S_-^2 \oplus S_+^4 \oplus S_-^4 . $$

(33)

Cette décomposition coïncide avec celle de l’ensemble $\mathcal {R}$ des tenseurs de courbure à l’origine de ℝ⁴, qui, au vu des différentes composantes irréductibles de la courbure, voir (12), s’écrit aussi

$$ \mathcal {R}= \mathbb {R}\oplus S_+^2S_-^2 \oplus S_+^4 \oplus S_-^4 . $$

(34)

Cette coïncidence traduit le fait bien connu de géométrie riemannienne suivant lequel, dans des coordonnées géodésiques, les dérivées secondes de la métrique à l’origine sont déterminées par la courbure à l’origine. En conséquence, la courbure

$$ R : \ker V \to \mathcal {R}, $$

(35)

est un isomorphisme. Compte tenu de la décomposition en facteurs irréductibles, cet isomorphisme est complètement déterminé par la décomposition, à une constante près dans chaque facteur.

Nous pouvons donc expliciter l’isomorphisme (35) en calculant un exemple pour fixer les constantes. Dans notre cas, il suffira de traiter les facteurs ℝ et $S_{+}^{4}$. Utilisons la description suivante des éléments de $\mathbb {R}\oplus S_{+}^{4}$ :

• dans kerV, il s’agit des tenseurs qui se laissent écrire H=∑H _ij β _i β _j , où les H _ij sont constantes ;

• dans $\mathcal {R}$, on peut identifier, via l’opérateur de courbure, le facteur $\mathbb {R}\oplus S_{+}^{4}$ aux endomorphismes symétriques de $\varOmega_{+}^{2}$ : on les écrira donc comme des matrices dans la base de $\varOmega_{+}^{2}$ donnée par les ω _i (⋅,⋅)=g(I _i ⋅,⋅)=dβ _i .

Passons maintenant au calcul d’un exemple : la métrique hyperbolique complexe, à courbure sectionnelle holomorphe −1, s’écrit

$$g=dr^2+\sinh^2(r)\alpha_1^2+4 \sinh^2\biggl(\frac{r}{2}\biggr) \bigl(\alpha_2^2+ \alpha_3^2\bigr), $$

ce qui correspond à

$$ H = \frac{1}{3} \biggl( \beta_1^2 + \frac{\beta_2^2+\beta_3^2}{4} \biggr) ; $$

(36)

on a $\operatorname {Scal}=-6$ et, comme pour toute métrique I ₁-kählérienne, l’opérateur de courbure, restreint à $\varOmega_{+}^{2}$ est donné par

(37)

La comparaison de (36) et (37) permet de fixer les constantes sur les facteurs ℝ et $S_{+}^{4}$, on obtient

(38)

Via le lemme 4.2, il apparaît ainsi que les annulations requises sont équivalentes à R ⁺(H)(I ₁)=0. Le théorème est démontré. □

Remarque 4.3

La formule (38), avec le lemme 4.2, donne une formule directe pour les coefficients λ _i de la proposition 3.2 en termes de R(H)(I ₁).

5 Construction d’une solution approchée

Soit (M ₀,g ₀) une variété d’Einstein, donc $\operatorname {Ric}_{g_{0}}=\varLambda g_{0}$. Supposons que M ₀ ait une singularité orbifold de type ℝ⁴/ℤ₂ au point p ₀. On va construire sur la désingularisation M de la variété une famille de métriques (g _t ) _t>0, satisfaisant approximativement l’équation d’Einstein, modulo les obstructions présentes sur Eguchi-Hanson. Jusqu’à la section 9 incluse, la variété M ₀ peut être aussi bien compacte que non compacte.

Dans des coordonnées géodésiques (x ⁱ) au point p ₀, on écrit

$$ g_0 = \mathrm {e}+ H + O \bigl(|x|^4 \bigr), \quad \text{avec} \ H = H_{ijkl}x^ix^jdx^kdx^l. $$

(39)

(Le développement ne contient que des termes pairs, au vu de l’invariance sous ℤ₂.) Par la proposition 3.2, il existe sur Eguchi-Hanson une solution h au système (23), c’est-à-dire une solution de $d_{\mathrm {eh}}\operatorname {Ric}(h)=\varLambda \mathrm {eh}+\sum_{1}^{3}\lambda_{i}o_{i}$, asymptote à H à l’infini, où les constantes λ _i sont déterminées par H. On prendra h normalisée par (25).

Remarquons la présence d’un paramètre de jauge dans la construction : si $\varphi\in \operatorname {SO}(4)$, alors on peut appliquer φ à la carte dans laquelle est exprimée g ₀, ce qui a pour effet de modifier H dans (39), et donc la solution h. De manière équivalente, on peut penser qu’on a appliqué φ ⁻¹ à la métrique de Eguchi-Hanson. Comme celle-ci est $\operatorname {U}(2)$-invariante, il ne reste en réalité que deux paramètres réels, dans $\operatorname {SO}(4)/\operatorname {U}(2)$. Donc on ne perd rien à restreindre φ à être dans le groupe $\operatorname {Sp}_{1}\subset \operatorname {SO}(4)$ qui fixe $\varOmega^{2}_{-}\mathbb {R}^{4}$, et le vrai paramètre est dans $\operatorname {Sp}_{1}/U_{1}=\operatorname {SO}(4)/\operatorname {U}(2)$.

Notons que ce paramètre de jauge peut être déjà utilisé de la manière suivante : dans le cas où $\mathbf {R}^{+}_{g_{0}}(p_{0})|_{\varOmega_{+}^{2}\mathbb {R}^{4}}$ a un noyau non trivial, quitte à appliquer une jauge $\varphi\in \operatorname {Sp}_{1}/U_{1}$, on peut supposer que ce noyau contient la forme dx ¹∧dx ²+dx ³∧dx ⁴. Alors, par le théorème 4.1, on a λ _j =0. Plus généralement, toujours grâce à ce paramètre de jauge, on peut assurer que dx ¹∧dx ²+dx ³∧dx ⁴ soit un vecteur propre de R(H), ce qui implique au moins

$$\lambda_2=\lambda_3=0. $$

Considérons alors sur Eguchi-Hanson le 2-tenseur

$$h_{t,\varphi} = \mathrm {eh}+ t h . $$

La notation ici garde en mémoire le paramètre de jauge $\varphi\in \operatorname {Sp}_{1}/U_{1}$. A priori il ne s’agit pas d’une métrique, puisque le terme th explose à l’infini et n’a pas de raison d’être positif. Néanmoins, h _t,φ est une métrique sur des régions de plus en plus larges de Eguchi-Hanson. Pour l’énoncer correctement, voyons Eguchi-Hanson dans les coordonnées de la section 2, donc identifiée en dehors de la section nulle avec ℝ⁴/ℤ₂, et définissons des régions de Eguchi-Hanson par

où $\beta\in{]0,\frac{1}{2}[}$ sera fixé ultérieurement. Définissons sur Eguchi-Hanson une fonction ρ≥1 asymptote au rayon r près de l’infini : ρ est une fonction croissante de r satisfaisant

$$\rho= \begin{cases} r & \text{si} \ r>2, \\ 1 & \text{si} \ r\leq1. \end{cases} $$

Lemme 5.1

Soit $\beta\in{]0,\frac{1}{2}[}$, si t≪1 alors h _t,φ est une métrique sur la région EH^t. En outre, sur cette région,

$$\Biggl|\nabla^k \Biggl(\operatorname {Ric}_{h_{t,\varphi}}-t\varLambda h_{t,\varphi}-t\sum_1^3 \lambda_jo_j \Biggr) \Biggr|_\mathrm {eh}\leq c_k t^2 \rho^{2-k}. $$

Démonstration

Puisque h=O(ρ ²), sur EH^t on a |h|≤ct ^1−2β ; or $\beta<\frac{1}{2}$, d’où il résulte que h _t,φ est une métrique dès que t est assez petit.

Comme h est solution de $d_{\mathrm {eh}}\operatorname {Ric}(h)=\varLambda \mathrm {eh}+\sum_{1}^{3}\lambda_{i}o_{i}$, le membre de gauche de l’inégalité est constitué de −t ² h et de termes au moins quadratiques de $\operatorname {Ric}$ appliqués à th : comme th est petit, les termes les plus grands sont les termes quadratiques, qui contiennent toujours au moins 2 dérivées de h (termes en ∇² h⋅h, ou ∇h⋅∇h) ; vu que |∇^k h|≤c _k ρ ^2−k, on en déduit le résultat. □

Considérons l’homothétie $s_{t}:\mathrm {EH}^{t,\beta}_{>}\to M_{0}$ donnée par $s_{t}(x)=\sqrt{t}x$. Alors $\frac{1}{t} \varphi^{*}s_{t}^{*}g_{0}$ est proche de h _t,φ : sur $\mathrm {EH}^{t,\beta}_{>}$,

et la dérivée k-ième satisfait la même estimation, avec les erreurs multipliées par r ^−k. Une coïncidence optimale est obtenue avec le choix

$$\beta=\frac{1}{4}, $$

qui sera dorénavant fixé. Par conséquent, sur $\mathrm {EH}^{t}_{>}$,

$$\biggl|\nabla^k\biggl(\frac{1}{t} \varphi^*s_t^*g_0 - h_{t,\varphi}\biggr)\biggr|_\mathrm {e}\leq c_k t^{2+\frac{k}{4}}. $$

Choisissons une fonction de coupure χ _t =χ _t (r), à support dans EH^t, telle que

$$ \chi_t(r) = 1 \quad \text{si} \ r\leq\frac{1}{2} t^{-\frac{1}{4}}, \qquad\bigl|\partial_r^k \chi_t\bigr|\leq c_k t^{\frac{1}{4} k}. $$

(40)

Il suffit de choisir $\chi_{t}(\rho)=\chi_{1}(t^{\frac{1}{4}}\rho)$. On construit une métrique g _t,φ en recollant :

• la métrique g ₀ de M ₀ dès que $r\geq2t^{\frac{1}{4}}$,

• la métrique $t[(1-\chi_{t})\frac{s_{t}^{*}g_{0}}{t}+\chi_{t}\varphi_{*}h_{t,\varphi}]$ sur EH^t,

via l’homothétie s _t . Les deux métriques coïncident au voisinage de $r=2t^{\frac{1}{4}}$, donc on a bien défini une métrique sur la désingularisation M de M ₀, obtenue comme

$$M = M_0^t \cup_{s_t} \mathrm {EH}^t , \quad \text{avec} \ M_0^t=\biggl\{r>\frac{1}{2} t^{\frac{1}{4}} \biggr\}\cap M_0 . $$

On montre de manière similaire au lemme 5.1 :

Lemme 5.2

La métrique g _t,φ satisfait l’estimation sur EH^t :

$$\Biggl|\nabla^k\Biggl(\operatorname {Ric}_{g_{t,\varphi}}-\varLambda g_{t,\varphi}-t \sum_1^3\lambda_j \chi_to_j\Biggr) \Biggr|_\mathrm {eh}\leq c_k t^2 \rho^{2-k}. $$

On prendra garde que, dans ce lemme, le membre de gauche est concentré sur EH^t, et la norme est exprimée par rapport à la métrique de Eguchi-Hanson, comme l’indique la notation. Par ailleurs, comme on a vu, les λ _j dépendent aussi de φ.

On remarquera également que l’erreur sur o _j provoquée par la troncature est absorbée dans le terme d’erreur t ² ρ ².

Remarque

Un choix plus simple de recollement serait la métrique

$$ g_{t,\varphi}^0 = \chi_t t\mathrm {eh}+ (1- \chi_t)\varphi^*g_0, $$

(41)

dans laquelle on n’a pas fait coïncider les termes quadratiques de g ₀ en p ₀ avec ceux d’une métrique sur EH. Mais on vérifie immédiatement que cette métrique est une moins bonne approximation d’une métrique d’Einstein, car elle vérifie seulement sur EH^t

$$ \bigl|\nabla^k \bigl(\operatorname {Ric}_{g_{t,\varphi}^0}-\varLambda g_{t,\varphi}^0 \bigr) \bigr|_\mathrm {eh}\leq c t \rho^{-k}, $$

(42)

qui est moins bon que l’estimation du lemme 5.2.

Notation

Pour alléger les notations dans la suite, on oubliera généralement la dépendance en φ pour noter g _t au lieu de g _t,φ . La dépendance en φ sera écrite quand elle est utilisée.

6 Équation d’Einstein modulo les obstructions

On a construit dans la section 5 une solution approchée g _t de l’équation d’Einstein sur M. On souhaite déformer g _t en une solution exacte, en appliquant la méthode de [6, chapitre I] : pour chaque t>0 assez petit, on cherche une métrique g proche de g _t , telle que

$$ \varPhi_{g_t}(g) := \operatorname {Ric}_g-\varLambda g+ \delta_g^*B_{g_t}g = 0 . $$

(43)

En effet, par l’identité de Bianchi, une solution g doit satisfaire

$$B_g\delta_g^*B_{g_t}g=0 . $$

Souvent [6, lemme I.1.4], l’opérateur $B_{g}\delta_{g}^{*}$ est injectif, donc en réalité $B_{g_{t}}g=0$ et donc $\operatorname {Ric}_{g}=\varLambda g$. Le lemme 8.1 donnera des conditions sous lesquelles $B_{g}\delta_{g}^{*}$ est inversible.

Or, l’application de cette méthode nécessite un contrôle de la norme de l’inverse de la linéarisation de Φ. Comme P _eh n’est pas inversible pour la métrique de Eguchi-Hanson, un tel contrôle n’existe pas. Le conoyau $\mathcal {O}_{\mathrm {eh}}$ de P _eh, étudié dans la section 2, apparaît ainsi comme obstruction à la résolution de l’équation d’Einstein. Aussi, dans un premier temps, résoudra-t-on seulement « modulo les obstructions ».

Par la proposition 2.1, l’espace $\mathcal {O}_{\mathrm {eh}}$ est engendré par les trois tenseurs o _i . Pour poser l’équation d’Einstein modulo ce conoyau, on peut définir un espace d’obstructions tronquées, de dimension trois, $\mathcal {O}=\langle\chi_{t}o_{i}\rangle$, et écrire

$$ \operatorname {Ric}_g - \varLambda g \in \mathcal {O}. $$

Néanmoins, cette équation pose problème, car le membre de gauche satisfait l’identité de Bianchi $B_{g}(\operatorname {Ric}_{g}-\varLambda g)=0$, qu’un élément de $\mathcal {O}$ n’a pas de raison de satisfaire a priori. Il semble ainsi difficile de résoudre l’équation en appliquant la méthode de l’équation (43).

On contourne cette difficulté en faisant dépendre le second membre de l’équation de la métrique inconnue g. Pour toute métrique g, telle que l’opérateur $B_{g}\delta_{g}^{*}$ sur les champs de vecteurs soit un isomorphisme (voir le lemme 8.1), on définit la projection

$$ \pi_g:L^2 \bigl(\varOmega^1 \bigr)\to L^2 \bigl(\varOmega^1 \bigr)\cap\ker B_g, $$

(44)

par

$$ \pi_g = 1 - \delta_g^* \bigl(B_g\delta_g^* \bigr)^{-1}B_g. $$

(45)

Faisons dépendre l’espace d’obstruction de la métrique g en posant

$$ \mathcal {O}_g = \bigl\langle\pi_g(\chi_to_i) \bigr\rangle. $$

(46)

L’équation à résoudre devient

$$ \operatorname {Ric}_g - \varLambda g \in \mathcal {O}_g. $$

(47)

À présent, la méthode de l’équation (43) peut être appliquée : en intégrant la jauge dans l’équation, on résout

$$ \varPhi_{g_t}(g) = \operatorname {Ric}_g-\varLambda g+ \delta_g^*B_{g_t}g \in \mathcal {O}_g. $$

(48)

Puisque $\mathcal {O}_{g}\subset\ker B_{g}$, la même méthode que ci-dessus assure, si $B_{g}\delta_{g}^{*}$ est injectif, qu’une solution de $\varPhi_{g_{t}}g\in \mathcal {O}_{g}$ satisfait en réalité l’équation de jauge $B_{g_{t}}g=0$. On a donc montré :

Lemme 6.1

Si la métrique g satisfait $\varPhi_{g_{t}}g\in \mathcal {O}_{g}$, et si l’opérateur $B_{g}\delta_{g}^{*}$ est injectif, alors $B_{g_{t}}g=0$ et $\operatorname {Ric}_{g}-\varLambda g\in \mathcal {O}_{g}$. □

7 Espaces fonctionnels

Construisons maintenant les espaces fonctionnels nécessaires à la résolution du problème (47).

Fixons un rayon $r_{p_{0}}$ inférieur au rayon d’injectivité de g ₀ au point p ₀. Soit $\tilde{r}$ une fonction réelle définie sur M ₀ par

$$\tilde{r} = \begin{cases} r & \text{si} \ r\leq\frac{1}{2} r_{p_0}, \\ 1 & \text{sur} \ M_0-B(p_0,r_{p_0}). \end{cases} $$

Par ailleurs, si M ₀ est AH, on dispose d’un bout N=]0,x ₀[×∂M de M ₀, où la première coordonnée, x, est une équation du bord à l’infini. On prolonge x sur M ₀ de sorte que x ₀≤x≤1 sur M ₀−N.

Soit un fibré tensoriel E, et δ ₀∈ℝ un poids. On définit sur EH un espace à poids $C^{k,\alpha}_{\delta_{0}}(\mathrm {EH},E)$ de sections de E par :

Ici i _eh est le rayon d’injectivité de la métrique de Eguchi-Hanson, et la différence |s(x)−s(y)| est évaluée, de manière usuelle, en transportant parallèlement s(y) en E _x le long de la géodésique de x à y.

De manière similaire, on définit un espace à poids $C^{k,\alpha}_{\delta_{0}}(M_{0},E)$ par

(49)

puis, pour un couple de poids (δ ₀,δ _∞), un espace à poids $C^{k,\alpha}_{\delta_{0},\delta_{\infty}}(M_{0},E)$ par

(50)

(Dans le cas où M ₀ est compact, on n’a plus besoin du poids x à l’infini, on peut garder la même définition en convenant que x≡1, donc le poids δ _∞ ne joue plus de rôle.)

Finalement la norme effectivement utilisée dans cet article est un recollement des normes sur EH et sur M ₀ : si (δ ₀,δ _∞) est un couple de poids comme ci-dessus, on définit $C^{k,\alpha}_{\delta _{0},\delta_{\infty};t}(M,E)$ par la norme, pour une section s de E,

$$ \| s \|_{C^{k,\alpha}_{\delta_0,\delta_\infty;t}} = t^{\frac{\delta_0+\ell}{2}}\|\chi_ts \|_{C^{k,\alpha}_{\delta_0}(EH)} + \bigl\|(1-\chi_t)s\bigr\|_{C^{k,\alpha}_{\delta _0,\delta_\infty}(M_0)}. $$

(51)

Ici ℓ:=ℓ ₊−ℓ ₋ est le poids conforme du fibré $E\subset TM^{\otimes\ell_{+}}\otimes T^{*}M^{\otimes\ell_{-}}$. C’est le poids qui permet d’identifier les normes des sections de E pour deux métriques g et $\frac{g}{t}$ :

$$t^{\frac{\ell}{2}}|s|_{\frac{g}{t}} = |s|_g . $$

Compte tenu que, dans la région $\mathrm {EH}^{t}_{>}$, on a

$$\rho\sim\frac{\tilde{r}}{\sqrt{t}} , $$

le facteur $t^{\frac{\delta_{0}}{2}}$ dans (51) fait exactement coïncider les normes à poids de EH et M ₀ dans la région de recollement. En particulier, les normes des espaces $C^{k,\alpha}_{\delta_{0},\delta _{\infty};t}(M)$ et $C^{k,\alpha}_{\delta_{0},\delta_{\infty}}(M_{0})$ sont uniformément équivalentes pour les sections à support dans M _t −EH ^t : pour tout t>0, si s est à support dans M _t −EH ^t, alors

$$ C^{-1} \| s \|_{C^{k,\alpha}_{\delta_0,\delta_\infty}(M_0)} \leq\| s \|_{C^{k,\alpha}_{\delta_0,\delta_\infty;t}(M)} \leq C \| s \|_{C^{k,\alpha}_{\delta_0,\delta_\infty}(M_0)} , $$

(52)

pour une constante C indépendante de t.

Dans la suite de l’article, on considère les poids δ ₀>0 et δ _∞>0 fixés et suffisamment petits.

8 La jauge de Bianchi

Le lemme suivant montre que la projection π _g définie par (45) existe de manière très générale pour les perturbations de g _t :

Lemme 8.1

Soit k≥1 un entier, soient δ∈]−1,3[ et δ′∈]0,4[. Il existe des constantes η ₁,η ₂>0, telles que si t<η ₁ et

$$ \|g-g_t\|_{C^{k,\alpha}_{\delta_0,\delta_\infty;t}}< \eta_2 t^{\frac{\delta_0}{2}}, $$

(53)

alors $B_{g}\delta_{g}^{*}:C^{k+1,\alpha}_{\delta,\delta';t}\to C^{k-1,\alpha }_{\delta+2,\delta';t}$ soit inversible, et la norme de l’inverse soit bornée indépendamment de t et g.

Démonstration

Tout d’abord, on vérifie que, sous l’hypothèse du lemme, toutes les métriques g ont des cartes dans lesquelles leurs coefficients se comparent de manière uniforme. Faisons le sur la partie EH^t de M (c’est similaire sur la partie $M_{0}^{t}$ de M ₀). Remarquons que sur EH^t on peut tester la condition (53) indifféremment par rapport à g _t ou teh, puisque $|\nabla^{k}(\frac{g_{t}}{t}-\mathrm {eh})| = O_{\mathrm {eh}}(t\rho^{2-k})$, donc la condition (53) est largement satisfaite pour la différence teh−g _t .

Sur un compact fixé de EH, la condition (53), compte tenu de la définition (51), nous dit que

$$\biggl\| \frac{g}{t} - \mathrm {eh}\biggr\|_{C^{k,\alpha}(\mathrm {EH})} < \eta_2 . $$

Si η ₂>0 est assez petit, alors $\frac{g}{t}$ se compare uniformément à la métrique eh.

Sur la partie non compacte : soit un anneau de la forme

$$A_R = \{ R \leq r \leq2R \} . $$

Considérons l’homothétie h de rapport R qui envoie l’anneau A ₁ dans l’anneau A _R , alors on vérifie immédiatement que

$$\|g-t\mathrm {eh}\|_{C^{k,\alpha}_{\delta_0,\delta_\infty;t}(A_R)} \sim t^{\frac{\delta_0}{2}}R^{\delta_0} \biggl\|\frac{1}{R^2}h^*\biggl(\frac{g}{t} - \mathrm {eh}\biggr)\biggr\|_{C^{k,\alpha}(A_1)}. $$

La métrique $\frac{1}{R^{2}}\frac{g}{t}$ devient de plus en plus proche de la métrique plate de l’anneau A _R quand R devient grand. Sous l’hypothèse (53), ces métriques sont se comparent uniformément.

Les estimations elliptiques dans les espaces de Hölder à poids se montrent justement en se ramenant à un nombre fini d’ouverts relativement compacts sur lesquels la métrique est uniformément bornée par rapport à une métrique de référence :

• un compact de EH ;

• un anneau A ₁ (après changement d’échelle) ;

• un compact de M ₀ ;

• une boule hyperbolique pour les boules centrées sur des points allant vers ∂M ₀.

Soit un opérateur elliptique géométrique P, d’ordre d≤k+1. Sur chacun de ces ouverts, on dispose d’estimations elliptiques avec constante uniforme pour l’opérateur P. Les espaces fonctionnels définis section 7 sont justement obtenus à partir de ces ouverts par changement d’échelle, et on en déduit immédiatement, si d≤ℓ≤k+1, l’estimation elliptique

$$ \|s\|_{C^{\ell,\alpha}_{\delta_0,\delta_\infty;t}} \leq c \bigl( \|s\|_{C^0_{\delta_0,\delta_\infty;t}} + \|Ps \|_{C^{\ell-d,\alpha}_{\delta_0+d,\delta_\infty;t}} \bigr) , $$

(54)

où la constante c peut être choisie indépendante de la métrique g satisfaisant (53).

Passons à l’assertion sur $B_{g}\delta_{g}^{*}$. Il s’agit de montrer une estimation

$$ \|X\|_{C^{k+1,\alpha}_{\delta,\delta';t}} \leq c \bigl\|B_g\delta_g^*X \bigr\|_{C^{k-1,\alpha}_{\delta+2,\delta';t}} , $$

(55)

avec constante indépendante de g. Compte tenu de la régularité elliptique (54), avec constantes uniformes, il suffit de montrer une estimation

$$ \|X\|_{C^0_{\delta,\delta';t}} \leq c \bigl\|B_g \delta_g^*X\bigr\|_{C^0_{\delta+2,\delta';t}} . $$

(56)

Le raisonnement se fait classiquement par l’absurde, et on sera donc bref : s’il existe

• des réels t _i →0,

• des métriques g _i telles que $\|g_{i}-g_{t_{i}}\|_{C^{k,\alpha}_{\delta_{0},\delta_{\infty};t}}< \eta_{2}$ ,

• des champs de vecteurs X _i tels que $\|X_{i}\|_{C^{0}_{\delta,\delta';t}}=1$ et

  $$\bigl\|B_{g_i}\delta_{g_i}^*X\bigr\|_{C^0_{\delta+2,\delta';t}}\to0, $$

alors, en regardant le point x _i ∈M où la norme $\|X_{i}\|_{C^{0}_{\delta,\delta';t}}$ est atteinte, on extrait de X _i (éventuellement après changement d’échelle) une limite non nulle X _∞ sur une variété limite M _∞ vers laquelle x _i converge. La limite satisfait Bδ ^∗ X _∞=0, et on montre pour les trois limites possibles de M _∞ que c’est impossible :

• (1) M _∞=M ₀ : alors $X_{\infty}\in C^{0}_{\delta,\delta'}(M_{0})$, donc X _∞∈L ²(M ₀) (δ=2 n’est pas un poids critique en p ₀ à cause de l’action de ℤ₂), mais $B_{g_{0}}\delta_{g_{0}}^{*}=\frac{1}{2}(\nabla^{*}\nabla-\operatorname {Ric})$ est injectif sur L ²(M ₀) ;

• (2) M _∞=EH : alors $X_{\infty}\in C^{0}_{\delta}(\mathrm {EH})$, à nouveau $B_{\mathrm {eh}}\delta_{\mathrm {eh}}^{*}=\frac{1}{2} \nabla^{*}\nabla$ n’a pas de noyau sur $C^{0}_{\delta}(M_{0})$ ; à nouveau c’est l’action de ℤ₂ qui interdit le poids critique 0 à l’infini ;

• (3) M _∞=ℂ²/ℤ₂ (la partie intermédiaire entre EH et M ₀) : même argument.

 □

On en déduit en particulier que toute métrique assez proche de g _t peut se mettre en jauge de Bianchi par rapport à g _t :

Lemme 8.2

Soit k≥1 un entier. Il existe des constantes η,ϵ,ϵ′>0, tels que pour tout t<η et toute métrique g sur M telle que $\|g-g_{t}\|_{C^{k,\alpha}_{\delta_{0},\delta_{\infty};t}}<\epsilon t^{\frac {\delta_{0}}{2}}$, il existe un difféomorphisme $\varphi=\exp_{g_{t}}X$ avec $\|X\|_{C^{k+1,\alpha }_{\delta_{0}-1,\delta_{\infty};t}} < \epsilon' t^{\frac{\delta_{0}}{2}}$, tel que $B_{g_{t}}\varphi^{*}g=0$.

C’est une application du théorème des fonctions inverses, sous la forme explicite donnée par le lemme suivant :

Lemme 8.3

Soit Φ:E→F une application lisse entre espaces de Banach, et soit Q=Φ−Φ(0)−d ₀ Φ. Supposons qu’existent des constantes strictement positives q, r ₀ et c telles que

• (1) ∥Q(x)−Q(y)∥≤q∥x−y∥(∥x∥+∥y∥) pour tous x,y∈B(0,r ₀) ;

• (2) d ₀ Φ est un isomorphisme, et ∥(d ₀ Φ)⁻¹∥≤c.

Si $r\leq\min(r_{0},\frac{1}{2qc})$ et $\|\varPhi(0)\| \leq\frac{r}{2c}$, alors l’équation Φ(x)=0 admet une solution unique dans B(0,r). □

Démonstration du lemme 8.2

On applique le lemme 8.3 à l’opérateur

$$X \mapsto\varPhi(X,g) = B_{(\exp_{g_t}X)^*g_t}g , $$

entre les espaces

$$ t^{-\frac{\delta_0}{2}}C^{k+1,\alpha}_{\delta_0-1,\delta_\infty;t} \to t^{-\frac{\delta_0}{2}}C^{k-1,\alpha}_{\delta_0+1,\delta_\infty;t}. $$

(57)

Le facteur $t^{-\frac{\delta_{0}}{2}}$ s’explique de la manière suivante : sur un grand compact K⊂EH, on a

Sachant que

$$B_{(\exp_{g_t}X)^*g_t}g=tB_{(\exp_{\frac{g_t}{t}}X)^*\frac{g_t}{t}}\frac{g}{t}, $$

on voit que sur K l’opérateur Φ entre les espaces (57) est identique à l’opérateur $X\mapsto B_{(\exp_{\frac{g_{t}}{t}}X)^{*}\frac{g_{t}}{t}}\frac{g}{t}$ entre les espaces standards C ^k+1,α→C ^k−1,α pour la métrique de Eguchi-Hanson.

Sur chaque ouvert où la métrique se ramène, par changement d’échelle, à une métrique uniformément proche d’un modèle (voir la démonstration du lemme 8.1), on peut faire la même opération et vérifier que l’opérateur Φ se ramène, après changement d’échelle, au même opérateur pour la métrique contrôlée, entre des espaces

$$ \lambda C^{k+1,\alpha}\to\lambda C^{k-1,\alpha}, $$

(58)

avec λ≥1 (le cas ci-dessus où λ=1 étant le plus défavorable).

La géométrie ainsi bien contrôlée, on peut passer à la démonstration du lemme : on a Φ(X,g)=0 si et seulement si $B_{g_{t}}(\exp_{g_{t}}X)_{*}g=0$, et

$$\frac{\partial\varPhi}{\partial X} \bigg|_{(0,g_t)}(X) = B_{g_t}\delta_{g_t}^*X , $$

qui, par le lemme 8.1, est inversible, avec constante contrôlée indépendamment de t. Si $\|g-g_{t}\|_{C^{k,\alpha }_{\delta_{0},\delta_{\infty};t}}< \epsilon t^{\frac{\delta_{0}}{2}}$, et ϵ est assez petit, alors la norme d’opérateur $\|\frac{\partial\varPhi}{\partial X}(0,g_{t})-\frac{\partial\varPhi }{\partial X}(0,g)\|$ est petite (c’est une question locale qui se voit dans les cartes ci-dessus), donc $\frac {\partial\varPhi}{\partial X}(0,g)$ demeure inversible, et la norme de l’inverse est contrôlée. En outre,

$$ \bigl\|\varPhi(0,g)\bigr\|_{C^{k-1,\alpha}_{\delta_0+1,\delta_\infty;t}} \leq c \epsilon t^{\frac{\delta_0}{2}}. $$

(59)

On applique le lemme 8.3 à l’opérateur X→Φ(X,g) entre les espaces (57), en écrivant

$$\varPhi(X,g) = \varPhi(0,g) + \frac{\partial\varPhi}{\partial X} \bigg|_{(0,g)}(X) + Q(X) . $$

Il reste à montrer l’estimation

C’est une estimation locale, qu’il suffit de vérifier dans chacune des cartes où Φ se ramène à un opérateur entre les espaces de Hölder standards (58). Comme Q représente des termes au moins quadratiques, une telle estimation est immédiate entre les espaces de Hölder standards. Quand on multiplie les normes par λ comme dans (58), l’inégalité continue d’aller dans le bon sens si λ≥1, ce qui est justement le cas. On notera qu’obtenir exactement λ≥1 avec un minimum égal à 1 est la raison d’être du facteur $t^{-\frac{\delta _{0}}{2}}$ dans (57).

La constante q du lemme 8.3 est donc contrôlée. Si on prend ϵ assez petit dans (59), le lemme 8.3 fournit donc une unique solution. □

9 Résolution de l’équation modulo les obstructions

Le lemme 8.1 donne un sens au problème $\varPhi_{g_{t}}(g)\in \mathcal {O}_{g}$ quand g est une perturbation de g _t dans $C^{2,\alpha}_{\delta_{0},\delta_{\infty}}$. Avant de résoudre le problème, définissons pour υ=(υ ₁,υ ₂,υ ₃)∈ℝ₃ assez petit une métrique

$$ g_{t,\upsilon} = g_t + t \chi_t \sum _1^3 \upsilon_j o_j . $$

(60)

Nous utilisons ainsi explicitement l’ambiguïté de la solution dans la proposition 3.2. Remarquons que

$$ \|t o_j\|_{C^{2,\alpha}_{\delta_0,\delta_\infty;t}}=O \bigl(t^{1+\frac {\delta_0}{4}} \bigr), $$

(61)

donc g _t,υ est une petite perturbation de g _t .

Proposition 9.1

Soit (M ₀,g ₀) une métrique orbifold Einstein, avec singularité de type ℝ⁴/ℤ₂ au point p ₀. Supposons M ₀ compacte, ou alors non compacte AH ; dans tous les cas non dégénérée. Alors il existe η,ϵ>0 tels que, pour t<η et υ=(υ ₁,υ ₂,υ ₃) avec |υ|<ϵ, il existe une unique solution $\hat{g}_{t}$ de l’équation

$$\operatorname {Ric}_{\hat{g}_t}-\varLambda\hat{g}_t \in \mathcal {O}_{\hat{g}_t} , $$

satisfaisant les conditions suivantes :

• (1) $\|\hat{g}_{t}-g_{t}\|_{C^{2,\alpha}_{\delta_{0},\delta_{\infty}}} \leq \epsilon t^{\frac{\delta_{0}}{2}}$ ;

• (2) $\hat{g}_{t}$ est en jauge de Bianchi par rapport à g _t , c’est-à-dire $B_{g_{t}}\hat{g}_{t}=0$ ;

• (3) pour j=1,2,3, on a sur la section nulle dans EH :

  $$ \int_{S^2} \biggl\langle\frac{1}{t}(\hat{g}_t-g_t),o_j\biggr\rangle_\mathrm {eh}\operatorname {vol}_\mathrm {eh}= \upsilon_j. $$

  (62)

En outre, écrivant $\operatorname {Ric}_{\hat{g}_{t}}-\varLambda\hat{g}_{t}=\sum_{1}^{3}\lambda_{j}(t)\pi_{\hat{g}_{t}}(\chi_{t}o_{j})$, on a les estimations

(63)

(64)

Les estimations sont uniformes par rapport à υ et à une variation de l’infini conforme et donc de la métrique orbifold d’Einstein g ₀.

Quand nous faisons varier la métrique orbifold Einstein g ₀ à partir d’une variation γ de son infini conforme γ ₀, nous notons explicitement la dépendance des objets intervenant dans la proposition par rapport à la jauge $\varphi\in \operatorname {Sp}_{1}/U_{1}$ et à γ : λ _j (φ,γ), λ _j (t,φ,γ), g _t,φ,υ,γ , $\hat{g}_{t,\varphi,\upsilon,\gamma}$… Le paramètre υ sera rapidement oublié car il ne sert en réalité que dans le corollaire 9.3 ci-dessous.

Remarque 9.2

On peut remarquer que, par rapport à la métrique recollée plus naïve $g_{t}^{0}$ donnée par (41), on a

$$ \bigl\|g_t-g_t^0\bigr\|_{C^{2,\alpha}_{\delta_0,\delta_\infty;t}}=O \bigl(t^{\frac{1}{2}+\frac{\delta_0}{4}} \bigr). $$

(65)

Il en résulte immédiatement que les (1), (2) et (3) de la proposition restent vrais en remplaçant g _t par $g_{t}^{0}$. On obtient un gain en remplaçant $g_{t}^{0}$ par la meilleure solution approchée g _t dans les estimations (63) et (64) sur la solution.

On peut déduire de la proposition un énoncé montrant que la condition de courbure sur g ₀ au point p ₀ est une condition nécessaire pour résoudre l’équation d’Einstein par notre méthode de recollement :

Corollaire 9.3

Sous les hypothèses de la proposition 9.1, si la condition de courbure $\det \mathbf {R}^{+}_{g_{0}}(p_{0})=0$ n’est pas satisfaite, alors il existe ϵ,η>0 tels que si γ est assez proche de γ ₀ et t<η, alors il n’existe pas de jauge $\varphi\in \operatorname {Sp}_{1}/U_{1}$ et de métrique d’Einstein g telle que

$$\bigl\|g-g^0_{t,\varphi,\gamma}\bigr\|_{C^{1,\alpha}_{\delta_0,\delta_\infty;t}} \leq\epsilon t^{\frac{\delta_0}{2}} . $$

L’utilisation de la métrique recollée naïve $g_{t,\varphi,\gamma}^{0}$ dans l’énoncé permet d’avoir les hypothèses les plus simples possibles.

Démonstration du corollaire 9.3

Pour tous les γ suffisamment proches de γ ₀ et tous les $\varphi\in \operatorname {Sp}_{1}$, les λ _i (φ,γ) ne sont pas tous nuls, par exemple

$$\bigl|\lambda_1(\varphi,\gamma)\bigr| > \epsilon \quad \text{pour un} \ \epsilon>0. $$

Si g est une métrique d’Einstein, proche de $g^{0}_{t,\varphi,\gamma}$ au sens du du corollaire, alors elle est également proche de g _t,φ,γ par (65), donc, par le lemme 8.2, peut être mise en jauge de Bianchi par rapport à g _t,φ,γ .

La régularité de l’équation d’Einstein en jauge de Bianchi permet de déduire qu’en réalité, on dispose d’une borne

$$\|g-g_{t,\varphi,\gamma}\|_{C^{2,\alpha}_{\delta_0,\delta_\infty;t}} \leq\epsilon t^{\frac{\delta_0}{2}} . $$

Toujours par l’hypothèse, on a alors $|\int_{S^{2}} \langle \frac{1}{t}(g-g_{t}),o_{j}\rangle_{\mathrm {eh}}\operatorname {vol}_{\mathrm {eh}}|<\epsilon$, donc on peut appliquer l’unicité dans la proposition 9.1 pour conclure que g coïncide avec l’une des métriques $\hat{g}_{t,\varphi,\upsilon,\gamma}$. Mais, pour t<η avec η assez petit, uniforme pour tous les infinis conformes γ proches de γ ₀, la métrique $\hat{g}_{t,\varphi,\upsilon,\gamma}$ ne peut pas être Einstein à cause de (64). □

Démonstration de la proposition 9.1

On considère l’opérateur

$$ \varPhi(h,x) = \operatorname {Ric}_g - \varLambda g+\delta_g^*B_{g_t}g - \sum_1^3x_j \pi_g(\chi_to_j) , \quad\text{o\`{u}} \ g=g_{t,\upsilon}+h , $$

(66)

vu comme agissant entre les espaces

$$ t^{-\frac{\delta_0}{2}} \ ^0 C^{2,\alpha}_{\delta_0,\delta_\infty;t} \oplus \mathbb {R}^3 \to t^{-\frac{\delta_0}{2}} C^\alpha_{\delta _0+2,\delta_\infty;t}, $$

(67)

l’espace ⁰ C ^2,α défini par la condition (62) sur g _t,υ =g−h.

La proposition se ramène à résoudre le problème Φ(h,x)=0, et à en estimer la solution. En effet, si on a une solution (h,x), par les lemmes 6.1 et 8.1, la métrique $\hat{g}_{t}=g_{t}+h$ satisfait alors l’équation $(\operatorname {Ric}-\varLambda)\hat{g}_{t}\in \mathcal {O}_{\hat{g}_{t}}$ tout en étant en jauge de Bianchi par rapport à g _t .

À nouveau, il s’agit de voir qu’on peut appliquer le lemme 8.3, avec des constantes c et q uniformément bornées. Comme, par le lemme 5.2 et l’estimation (61), on a au départ

$$\bigl\| \varPhi(0) \bigr\|_{C^\alpha_{\delta_0+2,\delta_\infty;t}} = O\bigl(t^{1+\frac{\delta_0}{4}}\bigr), $$

alors pour t assez petit on peut appliquer le lemme 8.3, et l’estimation (63) en résultera automatiquement. Dans la suite, le paramètre υ ne joue plus aucun rôle et on l’omettra.

La différentielle de l’opérateur Φ s’écrit

$$ d_0\varPhi(h,x)=\varPsi(h,x)+\frac{1}{2}( \operatorname {Ric}_{g_t}\circ h+h\circ \operatorname {Ric}_{g_t}-2\varLambda h), $$

(68)

où

$$ \begin{aligned} \varPsi(h,x)&=P_th+\sum _1^3 x_j\pi_{g_t}( \chi_to_j), \\ P_t h&=\frac{1}{2}\nabla_{g_t}^*\nabla_{g_t} h- \overset {\circ }{R}_{g_t} h. \end{aligned} $$

(69)

Compte tenu de $\|{\operatorname {Ric}_{g_{t}}-\varLambda g_{t}}\|_{C^{2,\alpha}_{\delta_{0}+2,\delta_{\infty}}} =O(t^{1+\frac{\delta_{0}}{4}})$, l’opérateur $d_{(g_{t},0)}\varPhi$ est une petite perturbation de Ψ et il nous suffira de borner inférieurement la norme de Ψ ⁻¹ entre les espaces apparaissant dans (67).

On notera que $\|\chi_{t}o_{j}\|_{C^{\alpha}_{\delta_{0},\delta_{\infty};t}} \sim t^{\frac{\delta_{0}}{2}}$, donc la norme standard sur ℝ³ est exactement la norme adéquate dans (67). On en déduit, comme dans la démonstration du lemme 8.2, que tout l’opérateur Φ est lisse avec des coefficients contrôlées dans les cartes locales par la norme de $t^{-\frac{\delta_{0}}{2}}C^{2,\alpha}_{\delta_{0},\delta_{\infty};t}\oplus \mathbb {R}^{3}$. Il en résulte que les termes non linéaires de l’opérateur Φ satisfont l’estimation uniforme requise dans la condition (1) du lemme 8.3.

Pour appliquer ce lemme, il reste donc à montrer que l’opérateur d ₀ Φ admet un inverse borné uniformément, donc à montrer une estimation

$$ t^{-\frac{\delta_0}{2}} \|h\|_{C^{2,\alpha}_{\delta_0,\delta _\infty;t}} + |x| \leq c t^{-\frac{\delta_0}{2}} \bigl\| \varPsi(h,x) \bigr\|_{C^\alpha_{\delta_0+2,\delta_\infty;t}} $$

(70)

pour une constante c indépendante de t. Le raisonnement se fait par contradiction, comme dans le lemme 8.1. Supposons donnés une suite t _i →0, et (h _i ,x _i ) tels que

$$t_i^{-\frac{\delta_0}{2}} \|h_i\|_{C^0_{\delta_0,\delta_\infty;t_i}} + |x_i| = 1, $$

mais

$$t_i^{-\frac{\delta_0}{2}} \bigl\| \varPsi(h_i,x)\bigr\|_{C^0_{\delta_0+2,\delta _\infty;t_i}} \to0 . $$

Supposons dans un premier temps que x _i →0. Alors le raisonnement est très similaire à celui fait pour le lemme 8.1 : la norme est atteinte à un point p _i , et on extrait, éventuellement après changement d’échelle, une limite h _∞ de h _i sur une variété limite M _∞ vers laquelle p _i converge. Les trois cas sont les mêmes :

• (1) M _∞=M ₀ : alors $\|h_{\infty}\|_{C^{0}_{\delta_{0},\delta_{\infty}}}=1$ et $P_{g_{0}}h_{\infty}=0$ ; cela impliquerait que h _∞ soit L ², mais par hypothèse, P n’a pas de noyau sur M ₀, contradiction ;

• (2) M _∞=EH : alors $\|h_{\infty}\|_{C^{0}_{\delta_{0}}}=1$ et P _eh h _∞=0, et en outre on a (62) ; or le noyau de P _eh dans $C^{0}_{\delta_{0}}$ consiste précisément des o _j , mais ceux-ci sont interdits par la condition (62), d’où la contradiction ;

• (3) M _∞=ℂ²/ℤ₂ : alors $\|h_{\infty}\|_{C^{0}_{\delta _{0}}}=1$ et $Ph_{\infty}=\frac{1}{2} \nabla^{*}\nabla h_{\infty}=0$, mais la condition $h_{\infty}\in C^{0}_{\delta _{0}}$ implique que h _∞ soit lisse à l’origine (au sens orbifold), et tende vers 0 à l’infini : il n’existe pas de telle solution, d’où la contradiction.

Finalement nous avons réduit la démonstration à établir x _i →0. Cela sera établi comme conséquence des faits suivants sur les produits scalaires L ² (il faut noter que le produit scalaire de 2-tenseurs symétriques est invariant conforme) :

(71)

(72)

(73)

En effet, de (72) et (73) on déduit, puisque $t^{-\frac{\delta_{0}}{2}} \|h_{i}\|_{C^{2,\alpha}_{\delta_{0},\delta_{\infty};t}}\leq1$ et $(o_{j},o_{k})_{\mathrm {eh}}= \|o_{1}\|_{\mathrm {eh}}^{2}\delta_{jk}$,

$$\|o_1\|_\mathrm {eh}^2 x_{i,j} = \bigl( \varPsi(h_i,x_i),\chi_t o_j\bigr)_{g_t} + O\bigl(t^{\frac{1}{2}-\delta}\bigr) , $$

donc, par (71), pour j=1, 2, 3,

$$|x_{i,j}| \leq c t^{-\frac{\delta_0}{2}} \bigl\|\varPsi(h_i,x_i)\bigr\|_{C^\alpha_{\delta_0,\delta_\infty;t}} + O\bigl(t^{\frac{1}{2}}\bigr). $$

Cela prouve bien x _i →0 comme voulu.

Il nous reste donc à démontrer les estimations (71), (72) et (73). L’estimation (71) s’obtient immédiatement par intégration à partir de la définition de la norme de l’espace $C^{\alpha}_{\delta_{0},\delta_{\infty};t}$. Pour l’estimation (72), on fait l’intégration par parties

$$ (P_th,\chi_to_j )_{g_t} = \bigl(h,P_t(\chi_t o_j) \bigr)_{g_t} = \biggl(\frac{h}{t},P_{\frac{g_t}{t}}(\chi_t o_j) \biggr)_{\frac{g_t}{t}} . $$

(74)

La seconde égalité est juste le résultat d’une homothétie sur la métrique. Comme les métriques $\frac{g_{t}}{t}$ et eh sont uniformément équivalentes sur EH^t, on peut estimer le second membre par rapport à eh. Or

(75)

Intégrant contre h, sachant que $|\frac{h}{t}|_{\mathrm {eh}}\leq t^{-\frac{\delta_{0}}{2}}\rho^{-\delta_{0}}\|h\|_{C^{2,\alpha}_{\delta _{0},\delta_{\infty};t}}$, on déduit

$$\bigl| (P_th,\chi_to_j )_{g_t} \bigr| \leq c t^{\frac{1}{2}-\frac{\delta_0}{4}}\|h\|_{C^{2,\alpha}_{\delta_0,\delta _\infty;t}}, $$

ce qui prouve bien (72).

Enfin, pour la dernière estimation (73), remarquons tout d’abord que, puisque $B_{g_{t}}=\frac{1}{t^{2}} B_{\frac{g_{t}}{t}}$, on a sur EH ^t

$$ \bigl|B_{g_t}(\chi_t o_j)\bigr|_{\frac{g_t}{t}} \leq c t^{-2} \biggl( \frac{1_{EH^t_>}}{\rho^5} + \frac{t}{\rho^3}\biggr), $$

(76)

et par conséquent,

$$ \bigl\| B_{g_t}(\chi_t o_j) \bigr\|_{C^{k,\alpha}_{\delta+2}} = t^{\frac{\delta+3}{2}} \sup\rho^{2+\delta} \bigl|B_{g_t}(\chi_t o_j)\bigr|_{\frac{g_t}{t}} \leq c t^{\frac{\delta}{4}}. $$

(77)

Si −1<δ<3, il en résulte, par le lemme 8.1,

$$ \bigl\| \delta_{g_t}^* \bigl(B_{g_t}\delta_{g_t}^*\bigr)^{-1}B_{g_t}(\chi_t o_j) \bigr\|_{C^{k+1,\alpha}_{\delta+1}} \leq c t^{\frac{\delta}{4}}. $$

(78)

En intégrant contre χ _t o _k , il en résulte, dès que δ>0,

$$ \bigl| \bigl( \delta_{g_t}^* \bigl(B_{g_t}\delta_{g_t}^*\bigr)^{-1} B_{g_t}(\chi_t o_j),\chi_t o_k \bigr) \bigr| \leq c t^{\frac{1}{2}-\frac{\delta}{4}}. $$

(79)

Les autres termes dans (73) viennent du fait que la métrique par rapport à laquelle on mesure le produit scalaire est $\frac{g_{t}}{t}$ plutôt que eh, et le terme de reste $\int_{r>t^{-\frac{1}{4}}}|o_{j}|^{2}$, mais tous sont O(t) et on en déduit le résultat.

Passons maintenant à la démonstration de l’estimation (64). On part de l’estimation du lemme 5.2,

$$\Biggl| (\operatorname {Ric}-\varLambda) (g_t) - \sum_1^3t \lambda_j(\gamma) \chi_to_j \Biggr|_\mathrm {eh}\leq c \rho^2 t^2 , $$

avec les estimations similaires pour les dérivées. En particulier,

$$ \Biggl| \Biggl( (\operatorname {Ric}-\varLambda) (g_t) - \sum_1^3 t \lambda_j(\gamma) \chi_to_j,\chi_to_k\Biggr)_{g_t} \Biggr| \leq c t^{\frac{3}{2}}. $$

(80)

On écrit la solution de l’équation d’Einstein avec obstruction comme

$$\hat{g}_t = g_t + j_t , \qquad \|j_t\|_{C^{2,\alpha}_{\delta_0,\delta_\infty;t}}\leq ct^{1+\frac{\delta_0}{4}}. $$

Par l’estimation (72), on obtient

$$ \bigl| (P_tj_t,\chi_to_j)_{g_t}\bigr| \leq c t^{\frac{3}{2}} . $$

(81)

Par ailleurs, les estimations (78) et (79) restent valables pour $\hat{g}_{t}$, et on en déduit, pour tout δ>0 petit,

$$ \bigl| \bigl( \delta_{\hat{g}_t}^* \bigl(B_{\hat{g}_t} \delta_{\hat{g}_t}^* \bigr)^{-1}B_{\hat{g}_t}(\chi_t to_j),\chi_t o_k\bigr)_{g_t} \bigr| \leq c t^{\frac{3}{2}-\delta}. $$

(82)

Enfin, observons que

$$ (\operatorname {Ric}-\varLambda) (\hat{g}_t)=(\operatorname {Ric}-\varLambda) (g_t)+P_t(j_t)+Q_t(j_t), $$

(83)

où Q _t contient les termes au moins quadratiques de $\operatorname {Ric}-\varLambda$. Or on a vu

$$\bigl\|Q_t(j_t)\bigr\|_{C^\alpha_{\delta_0+2,\delta_\infty;t}} \leq c t^{-\frac{\delta_0}{2}} \|j_t\|_{C^{2,\alpha}_{\delta_0,\delta_\infty;t}}^2 \leq c' t^2, $$

d’où résulte l’estimation

$$ \bigl| ( Q_tj_t,\chi_to_j)_{g_t} \bigr| \leq c t^{2-\frac{\delta_0}{2}} . $$

(84)

Finalement, mettant ensemble (81), (82) et (84) dans l’équation (83), nous obtenons

$$\Biggl| \Biggl( (\operatorname {Ric}-\varLambda) (\hat{g}_t) -\sum_1^3t\lambda_j(\gamma) \pi_{\hat{g}_t}(\chi_to_j),\chi_to_j \Biggr)_{g_t} \Biggr| \leq c t^{\frac{3}{2}-\delta}. $$

Compte tenu de (73), également valable pour $\hat{g}_{t}$, on en déduit le lemme.

Enfin, l’uniformité des estimations par rapport à une variation de l’infini conforme est claire, puisque g ₀(γ) (et en particulier λ _j (γ)) dépend de manière lisse de γ, et tous les opérateurs différentiels dépendent aussi de manière lisse de γ. □

Remarque

L’estimation (72) indique qu’un éventuel inverse de $P_{t}:\allowbreak C^{2,\alpha}_{\delta_{0},\delta_{\infty};t}\to C^{\alpha}_{\delta_{0}+2,\delta_{\infty};t}$ ne peut pas être borné sur χ _t o _j .

10 Solutions singulières sur l’orbifold

Dans cette section, on commence à utiliser la non compacité de M ₀, pour y construire des solutions particulières des équations linéarisées, avec terme principal singulier donné au point orbifold. Le but est le lemme 10.1, qui garantit l’injectivité de l’opérateur associant au terme principal au point singulier le terme indéterminé à l’infini. Celui-ci sera appliqué dans la section 11 pour étendre par dualité des germes de solutions sur l’orbifold, et dans la section 13 pour construire des vecteurs propres approchés de P _t .

Les deux opérateurs que nous avons en vue sont l’opérateur

$$B\delta^*=\frac{1}{2}\bigl(\nabla^*\nabla-\operatorname {Ric}\bigr) $$

sur TM ₀, et l’opérateur

$$P=\frac{1}{2}\bigl(\nabla^*\nabla-\overset {\circ }{R}\bigr) $$

sur $\operatorname {Sym}^{2}_{0}T^{*}M$. Le lien entre les deux opérateurs provient de la formule Pδ ^∗=δ ^∗ Bδ ^∗, qui garantit qu’à une solution X de Bδ ^∗ X=0 correspond une solution h=δ ^∗ X de Ph=0.

D’une manière générale, soit E un fibré tensoriel, muni d’un laplacien géométrique $P=\nabla^{*}\nabla+\mathcal {R}$, où $\mathcal {R}$ est un opérateur d’ordre 0 (typiquement, un terme de courbure). Un voisinage du point orbifold p ₀ s’identifie à $({]0,r_{p_{0}}[}\times S^{3})/\mathbb {Z}_{2}$, on trivialise E sur ce voisinage, alors les termes principaux de P à l’origine sont ceux du laplacien de l’espace plat ℝ⁴, à savoir

$$ -\frac{1}{r^3}\partial_r \bigl(r^3 \partial_r \bigr)-\frac{1}{r^2}\Delta_{S^3} ; $$

(85)

en particulier on obtient comme solution approchée les

$$ r^k f_k, \quad r^{-2-k} f_k, \quad \text{o\`{u}} \ \Delta_{S^3}f_k=kf_k. $$

(86)

Les valeurs propres k du laplacien de la sphère S ³ sont des entiers naturels, mais compte tenu de l’invariance sous ℤ₂, on a en fait

$$k\in k_0+2\mathbb {N}, \quad \text{o\`{u}} \ k_0= \begin{cases} 0 & \text{si le poids conforme de $E$ est pair,}\\ 1 & \text{s'il est impair.} \end{cases} $$

Notons F _k l’espace propre du laplacien scalaire sur la sphère S ³, constitué de fonctions polynomiales de degré k.

Supposons P inversible dans L ²(M ₀). Étant donné $\sigma_{k_{0}}\in E_{p_{0}}\otimes F_{k_{0}}$, compte tenu de (86), la section $s'=\frac{\sigma_{k_{0}}}{r^{2+k_{0}}}$ est une solution approchée de l’équation Ps′=0 près de p ₀, et plus précisément

$$ Ps'=O \biggl(\frac{1}{r^{2+k_0}} \biggr). $$

(87)

Par inversibilité de P, on peut alors résoudre Ps″=−Ps′ avec $s''=O(\frac{1}{r^{k_{0}}})$ et on obtient une solution s=s′+s″ de Ps=0 qui satisfait s∼s′ près de p ₀, et s est L ² à l’infini.

Le procédé s’étend en partant d’une solution approchée s ₀=r ^−2−k σ _k , avec $\sigma_{k}\in E_{p_{0}}\otimes F_{k}$. Alors Ps ₀∼r ^−2−k, et on peut corriger s ₀ par un s ₁∼r ^−k (ou bien s ₁∼r ^−klnr) ; on construit ainsi une somme finie s′=s ₀+s ₁+⋯+s _[k/2], solution de $Ps'=O(r^{-2-k_{0}})$, qu’on peut à nouveau corriger en une vraie solution s=s′+s″, équivalente à s ₀ en p ₀, et L ² à l’infini. L’ambiguïté dans la construction consiste en les solutions s de Ps=0, croissant moins vite en p ₀ que s ₀, donc satisfaisant s=O(r ^−k).

À l’infini, l’opérateur P a la forme suivante : dans une trivialisation le long de géodésiques aboutissant à l’infini, les solutions de Ps=0 ont un comportement gouverné par l’opérateur indiciel,

$$\operatorname {Ind}P=-(x\partial_x)^2-H x\partial_x+P_0, $$

où H=3 est la trace de la seconde forme fondamentale, et P ₀ est un opérateur d’ordre 0 agissant sur $E|_{\partial M_{0}}$. Une valeur propre μ de P ₀, d’espace propre E _μ , donne un poids critique

$$ \delta^\pm=\frac{1}{2} \Bigl(H\pm\sqrt{H^2+4\mu} \,\Bigr), $$

(88)

ce qui signifie que x ^δ e est une solution de l’opérateur indiciel si e∈E _μ . Soit $\delta_{0}^{+}>\frac{H}{2}$ le plus petit poids critique L ², correspondant à la valeur propre μ ₀, alors la solution s fabriquée plus haut satisfait

$$s \sim\sigma_\infty x^{\delta_0^+}, \quad\sigma_\infty\in E_{\mu_0}. $$

Ce procédé définit une application linéaire

$$ S_k^\infty: E_{p_0}\otimes F_k \to\varGamma(\partial M_0,E_{\mu_0}), \quad\sigma_k \mapsto\sigma_\infty, $$

(89)

défini à l’image près des $S_{\ell}^{\infty}$ pour ℓ<k.

Décomposons maintenant le produit tensoriel $E_{p_{0}}\otimes F_{k}$ sous l’action du groupe $\operatorname {SO}(4)$ dans les cas que nous considérons :

• pour E=TM ₀, on a k ₀=1 et

  $$ E_{p_0}\otimes F_1 = S_+S_-\otimes S_+S_- = S_+^2S_-^2\oplus S_+^2\oplus S_-^2\oplus \mathbb {R}; $$

  (90)

• pour $E=\operatorname {Sym}_{0}^{2}TM_{0}$, on a k ₀=0 et

  $$ \begin{aligned} E_{p_0}\otimes F_0 &= S_+^2S_-^2 , \\ E_{p_0}\otimes F_2 &= S_+^2S_-^2 \otimes S_+^2S_-^2 = \bigl(S_+^4\oplus S_+^2\oplus \mathbb {R}\bigr) \bigl(S_-^4\oplus S_-^2\oplus \mathbb {R}\bigr). \end{aligned} $$

  (91)

Le lemme suivant indique des cas d’injectivité de l’opérateur $S_{k}^{\infty}$.

Lemme 10.1

Supposons M ₀ asymptotiquement hyperbolique, non dégénérée, alors :

• (1) pour P=Bδ ^∗ agissant sur TM ₀, l’opérateur $S_{1}^{\infty}$ restreint à $S_{+}^{2}S_{-}^{2}\oplus S_{+}^{2}\oplus S_{-}^{2}$ est injectif  ;

• (2) pour $P=\frac{1}{2}(\nabla^{*}\nabla-\overset {\circ }{R})$ agissant sur $\operatorname {Sym}_{0}^{2}T^{*}M_{0}$ :

  • l’opérateur $S_{0}^{\infty}$ est injectif  ;

  • l’opérateur $S_{2}^{\infty}$ est injectif sur $S_{+}^{4}S_{-}^{4}\oplus S_{+}^{4}(S_{-}^{2}\oplus \mathbb {R})\oplus(S_{+}^{2}\oplus \mathbb {R})S_{-}^{4}$.

Démonstration

Commençons par le premier cas. L’opérateur $P=B\delta^{*}=\frac{1}{2}(\nabla^{*}\nabla-\operatorname {Ric})=\frac{1}{2}(\nabla^{*}\nabla+3)$ a 2 poids critiques à l’infini :

• $\delta_{0}^{+}=4$, avec espace propre les champs de vecteurs tangents au bord (les sections de T∂M ₀)

• $\delta_{1}^{+}>4$, avec espace propre les champs de vecteurs normaux au bord.

Les solutions L ² de Ps=0 ont un développement formel en les puissances de x, déterminé par les deux termes indéterminés correspondant aux deux poids critiques. Observons également qu’on a un procédé de fabrication de solutions de Ps=0 : identifiant TM ₀ avec Ω ¹ M ₀, et compte tenu de la formule de Bochner satisfaite par le laplacien de Hodge-De Rham sur Ω ¹,

$$\Delta= \nabla^*\nabla+ \operatorname {Ric}, $$

on voit que $P=\frac{1}{2}(\Delta+6)$. On déduit que si f est une fonction telle que (Δ+6)f=0, alors df satisfait Pdf=0. En particulier le poids critique de Δ+6 sur les fonctions est égal à $\delta_{1}^{+}$.

On comprend alors pourquoi le facteur ℝ dans (90) a disparu dans l’énoncé du lemme : en effet, il existe une solution de l’équation (Δ+6)f=0, telle que $f\sim\frac{1}{r^{2}}$ en p ₀, et f est L ² à l’infini. Alors P(df)=0 donc df fournit un élément du noyau de $S_{1}^{\infty}$.

En fait, cela représente la seule possibilité de non injectivité de $S_{1}^{\infty}$. En effet, si une solution s de Ps=0 a un premier terme indéterminé σ _∞ qui est nul, alors le développement formel de s à l’infini est de la forme df pour le développement formel d’une fonction f telle que (Δ+6)f=0. Il en résulte que le développement formel de ds à l’infini est identifiquement nul. Mais si s satisfait Ps=0, alors ds satisfait (Δ+6)ds=0 aussi, et, par unique continuation [11], on déduit que ds est identiquement nulle sur M ₀. En particulier, au voisinage de p ₀, on a s=df avec $f=O(\frac{1}{r^{2}})$. Cela n’est possible que si le terme principal $\frac{\sigma_{1}}{r^{3}}$ de s en p ₀ satisfait en réalité que σ ₁ soit dans la composante ℝ de la décomposition (90).

Passons maintenant au second cas, de l’opérateur P agissant sur le fibré $\operatorname {Sym}_{0}^{2}T^{*}M_{0}$. Il y a trois poids critiques à l’infini :

• $\delta_{0}^{+}=3$, avec espace propre $\operatorname {Sym}_{0}^{2}T^{*}\partial M_{0}$ ;

• $\delta_{1}^{+}=4$, avec espace propre s’identifiant à T∂M ₀ (par produit intérieur avec le vecteur normal) ;

• $\delta_{2}^{+}>4$, avec espace propre (3dx ²−γ)/x ².

Comme on a vu, si un champ de vecteurs satisfait Bδ ^∗ X=0, alors s=δ ^∗ X satisfait Ps=0. Cela explique les poids $\delta_{1}^{+}$ et $\delta_{2}^{+}$, qui coïncident avec les deux poids critiques de Bδ ^∗.

Analysons maintenant les opérateurs $S_{0}^{\infty}$ et $S_{2}^{\infty}$ : si une solution s de Ps=0 a son premier terme indéterminé nul, σ _∞=0, alors son développement à l’infini est celui de δ ^∗ X, pour X un champ de vecteurs satisfaisant Bδ ^∗ X=0. En fait, le théorème d’unique continuation [7], voir aussi [4], indique que, dans un voisinage de l’infini, on a exactement s=δ ^∗ X. Comme cette équation contrôle complètement X et ses dérivées en fonction de celles de s, le champ de vecteurs X peut être continué analytiquement le long de n’importe quel chemin. Il en résulte que, près de p ₀, on a aussi s=δ ^∗ X avec Bδ ^∗ X=0 (mais, suivant la topologie, ce n’est pas forcément vrai globalement).

Dans le cas où $s\sim\frac{\sigma_{0}}{r^{2}}$, il faut que $X\sim\frac{1}{r}$, et un tel X satisfaisant Bδ ^∗ X=0 n’existe pas. D’où l’injectivité de $S_{0}^{\infty}$.

Dans le cas où $s\sim\frac{\sigma_{2}}{r^{4}}$, il faut que $X\sim\frac {X_{1}}{r^{3}}$, ce qui est possible. Alors les comportements asymptotiques possibles de X en p ₀ sont donnés par (90). Le terme dominant de s est obtenu algébriquement à partir de celui de X : en effaçant dans la seconde décomposition de (91) les représentations de $\operatorname {SO}(4)$ qui apparaissent dans (90), on déduit que ces comportements asymptotiques de s ne peuvent pas être obtenus comme δ ^∗ X et par conséquent $S_{2}^{\infty}$ est injectif sur ces représentations. □

11 Extension de germes sur l’orbifold

L’existence de petites valeurs propres de l’opérateur P _t va être compensée par des déformations de la métrique, modifiant l’infini conforme de g ₀. Par la proposition 2.1, l’espace des obstructions de l’équation d’Einstein pour la métrique de Eguchi-Hanson peut être tué par des tenseurs symétriques sur Eguchi-Hanson, à croissance quadratique, donc asymptotes à σ ₂ r ² avec $\sigma_{2}\in S_{+}^{2}S_{-}^{2}\otimes S_{+}^{2}S_{-}^{2}$ comme dans (91). Certains de ces germes correspondent à l’action infinitésimale de $\operatorname {SO}(4)$ sur Eguchi-Hanson, donc à l’infini à δ ^∗ X avec X∼X ₁ r.

Dans le recollement, l’infini de Eguchi-Hanson est vu, après homothétie, comme le voisinage de p ₀. Un ingrédient essentiel sera de prolonger σ ₂ r ² (ou X ₁ r dans le cas d’un champ de vecteurs), vu comme un germe sur l’orbifold M ₀ en p ₀, en une solution globale s de Ps=0 sur M ₀. Évidemment, un tel s ne saurait être L ² au vu de la non dégénérescence de M ₀. Il y a un plus petit poids critique $\delta_{0}^{-}$ non L ², voir (88), plus précisément

$$\delta_0^- = \begin{cases} -1 & \text{pour} \ B\delta^*\text{ agissant sur }TM_0, \\ 0 & \text{pour} \ P \text{ agissant sur }\operatorname {Sym}_0^2T^*M_0. \end{cases} $$

Le but de cette section est le lemme suivant, dans lequel on se rappellera les décompositions (90) et (91) : en particulier, on notera $(E_{p_{0}}\otimes F_{2})_{0}$ le sous-espace de $(S_{+}^{2}S_{-}^{2})^{\otimes2}$ orthogonal au facteur trivial ℝ, c’est-à-dire orthogonal à la partie sans trace du 2-tenseur r ² dr ².

Lemme 11.1

Supposons M ₀ asymptotiquement hyperbolique, non dégénérée. Alors

• (1) pour tout $X_{1}\in S_{+}^{2}S_{-}^{2}\oplus S_{+}^{2}\oplus S_{-}^{2}$, il existe un champ de vecteurs X sur M ₀, satisfaisant Bδ ^∗ X=0, tel qu’en p ₀ on ait X∼X ₁ r et à l’infini on ait X∼X _∞ x ⁻¹, où X _∞ est un champ de vecteurs sur ∂M ₀ ;

• (2) pour tout $\sigma_{2}\in(E_{p_{0}}\otimes F_{2})_{0}$, il existe une solution s de Ps=0, tel qu’en p ₀ on ait s∼σ ₂ r ² et à l’infini s∼s _∞, où s _∞ est un 2-tenseur symétrique sans trace sur ∂M ₀.

Ce lemme permet la définition suivante.

Définition 11.2

On notera $S_{2}^{\infty}$ l’opérateur défini par le (2) du lemme 11.1, qui à un germe $\sigma_{2}\in (E_{p_{0}}\otimes F_{2})_{0}$ associe le 2-tenseur symétrique s _∞ sur ∂M ₀.

Avant de nous attaquer au lemme, nous montrons que l’application entre valeurs à l’infini de solutions de l’équation Ps=0, et valeurs en p ₀, est en un certain sens isométrique. Plus précisément, supposons données deux solutions s et t de l’équation Ps=0, avec les comportements asymptotiques « duaux » suivants :

• au point p ₀, on a s∼σ _k r ^−2−k et t∼τ _k r ^k ;

• à l’infini, on a $s\sim\sigma_{\infty}x^{\delta_{0}^{+}}$ et $t\sim \tau_{\infty}x^{\delta_{0}^{-}}$.

Puisque l’opérateur P est du type $\nabla^{*}\nabla+\mathcal {R}$, un calcul immédiat par intégration par parties fournit

et il en résulte la formule, si Ps=Pt=0,

$$ (2+2k) (\sigma_k,\tau_k) = \bigl( \delta_0^+-\delta_0^- \bigr) (\sigma_\infty, \tau_\infty). $$

(92)

Démonstration du lemme 11.1

Démontrons la première partie du lemme : considérons l’application

$$S_\infty^1 : \varGamma(T\partial M_0) \to T_{p_0}M_0\otimes F_1 , $$

qui à un champ de vecteurs X _∞ sur ∂M ₀ associe le germe X ₁ en p ₀ de la solution du problème

$$B\delta^*X=0, \quad X \sim\frac{X_1}{x} \ \text{quand} \ x\to0. $$

Soit une fonction f solution de l’équation

$$ (\Delta+6)f=0, \quad f\sim\frac{1}{r^2} \ \text{en} \ p_0, $$

(93)

et f est L ² à l’infini de M ₀. Comme vu dans la démonstration du lemme 10.1, on a alors $f=O(x^{\delta_{2}^{+}})$ pour un $\delta_{2}^{+}>4$. Appliquant la formule (92) à X et à df, on déduit que X ₁ est orthogonal à la composante ℝ de $T_{p_{0}}M_{0}\otimes F_{1}$. Ainsi, en réalité, au vu de la décomposition (90),

$$S_\infty^1 : \varGamma(T\partial M_0) \to S_+^2S_-^2\oplus S_+^2\oplus S_-^2 . $$

Supposons que cet opérateur $S_{\infty}^{1}$ ne soit pas surjectif. Par conséquent, il existe $Y_{1}\in S_{+}^{2}S_{-}^{2}\oplus S_{+}^{2}\oplus S_{-}^{2}$, tel que pour tout X _∞, on ait

$$ \bigl(Y_1,S_\infty^1(X_\infty)\bigr)=0. $$

(94)

D’après le lemme 10.1, il existe Y champ de vecteurs sur M ₀, solution de

$$B\delta^*Y=0, \quad Y\sim\frac{Y_1}{r^3} \text{ en }p_0, $$

et, à l’infini, Y∼Y _∞ x ⁴ avec Y _∞≠0. D’après (92) et (94), on déduit

$$(Y_\infty,X_\infty)=0 $$

pour tout X _∞, ce qui implique Y _∞=0. On obtient une contradiction. Donc $S_{\infty}^{1}$ est en réalité surjectif, ce qui démontre la première assertion du lemme.

Passons à présent à la seconde assertion, et considérons donc l’opérateur $P=\frac{1}{2}\nabla^{*}\nabla-\overset {\circ }{R}$. Par le lemme 10.1, nous avons un opérateur injectif $S_{0}^{\infty}:\operatorname {Sym}_{0}^{2}T_{p_{0}}M_{0}\to\varGamma(\operatorname {Sym}_{0}^{2} \partial M_{0})$, dont nous noterons l’image E ₀. Si $s_{\infty}\in E_{0}^{\perp}$, alors la solution s de Ps=0 telle que s∼s _∞, d’après la formule (92), est nulle en p ₀, donc s∼s ₂ r ² avec $s_{2}\in \operatorname {Sym}_{0}^{2}T_{p_{0}}M_{0}\otimes F_{2}$. On a ainsi défini une application

$$S_\infty^2:E_0^\perp\to \operatorname {Sym}_0^2T_{p_0}M_0\otimes F_2 . $$

Utilisons (91) pour décomposer le but de cette application comme

$$\operatorname {Sym}_0^2T_{p_0}M_0\otimes F_2 = \mathbb {R}\oplus R_1\oplus R_2, $$

avec

Commençons par observer que l’image de $S_{\infty}^{2}$ est orthogonale au facteur ℝ : cela se voit en intégrant la solution s contre δ ^∗ df, où f est la fonction construite par (93). Nous restreignons donc $S_{\infty}^{2}$ en une application

$$S_\infty^2:E_0^\perp\to R_1\oplus R_2 , $$

dont nous voulons montrer la surjectivité. Il résulte déjà de la première partie du lemme que l’image de $S_{\infty}^{2}$ contient R ₁. Supposons donc qu’existe s ₂∈R ₂, orthogonal à l’image de $S_{\infty}^{2}$. Par le lemme 10.1, il existe une solution s de Ps=0, telle qu’en p ₀,

$$s\sim\frac{s_2}{r^4}, $$

et à l’infini,

$$s\sim s_\infty x^3, \quad s_\infty\neq0. $$

Par (92), il faut que s _∞∈E ₀. Mais cela implique l’existence d’une solution t de Pt=0, tel qu’à l’infini t∼s _∞ x ³ et en p ₀ on ait seulement t=O(r ⁻²). Par continuation unique à nouveau [7], il faut que, près de l’infini, on ait s=t+δ ^∗ X. Le champ de vecteurs X peut être continué analytiquement le long de chemins, et donc près de p ₀ on obtient aussi l’existence de X tel que s=t+δ ^∗ X. Mais cela est incompatible avec s ₂∈R ₂, qui est justement l’orthogonal des valeurs induites par les champs de vecteurs.

Il en résulte que $S_{\infty}^{2}$ est surjective, et le lemme est démontré. □

12 Construction des métriques d’Einstein

Les tenseurs sans trace k _j de la proposition 2.1 ont une asymptotique à l’infini d’ordre 2,

$$k_j \sim\eta_j, $$

où $\eta_{j}\in E_{p_{0}}\otimes F_{2}$. Il est évident pour η ₂, η ₃, et il se vérifie par le calcul pour η ₁, qu’en réalité $\eta_{j}\in (E_{p_{0}}\otimes F_{2})_{0}$.

Lemme 12.1

Pour un infini conforme γ, soit λ _j (φ,γ) définies par (24). Alors

$$\frac{\partial\lambda_\ell}{\partial\gamma} \bigg|_{(1,\gamma_0)} \bigl(S_2^\infty (\eta_j) \bigr) = \delta_{j\ell}. $$

Démonstration

La variation $S_{2}^{\infty}(\eta_{j})$ de γ a été construite de sorte que la variation correspondante des termes quadratiques de g ₀(γ) en p ₀ soit égale aux termes quadratiques du tenseur k _j à l’infini de Eguchi-Hanson. Donc la solution h du problème (23) est modifiée par k _j , tel que $d_{\mathrm {eh}}\operatorname {Ric}(k_{j})=o_{j}$, et le lemme en résulte immédiatement. □

Par ailleurs, examinons l’influence du paramètre de jauge $\varphi\in \operatorname {Sp}_{1}/U_{1}$ sur les coefficients λ _j . Le résultat dépend de la partie $\mathbf {R}_{g_{0}}^{+}(p_{0})$ de l’opérateur de courbure en p ₀ agissant sur $\varOmega^{2}_{+}(p_{0})$. Supposons que $\det \mathbf {R}_{g_{0}}^{+}(p_{0})=0$, ce qui signifie que la condition (26) est satisfaite, après action éventuelle de la jauge. On peut donc supposer qu’au départ, dans la base standard (I ₁=dx ¹∧dx ²+dx ³∧dx ⁴,I ₂=dx ¹∧dx ³−dx ²∧dx ⁴,I ₃=dx ¹∧dx ⁴+dx ²∧dx ³) de $\varOmega^{2}_{+}(p_{0})$, l’opérateur de courbure a la forme diagonale

(95)

avec par exemple a ₃≠0 puisque $\operatorname {tr}(\mathbf {R}^{+})=\frac{1}{4}\operatorname {Scal}\neq0$. On dira que $\mathbf {R}_{g_{0}}^{+}(p_{0})$ est non dégénéré si on a aussi a ₂≠0. On peut représenter un élément de $\mathfrak {sp_{1}}/\mathfrak{u}_{1}$ comme

Sachant que l’action de $\operatorname {Sp}_{1}$ sur $\mathbf {R}_{g_{0}}^{+}(p_{0})$ est par conjugaison, et que (λ ₁,λ ₂,λ ₃) sont les coefficients de $\mathbf {R}_{g_{0}}^{+}(p_{0})(I_{1})$, on déduit immédiatement :

Lemme 12.2

Si $\xi\in\mathfrak{sp}_{1}/\mathfrak{u}_{1}$, alors

$$ \frac{\partial\lambda_1}{\partial\varphi} \bigg|_{(1,\gamma_0)}=0,\qquad \frac{\partial\lambda_j}{\partial\varphi} \bigg|_{(1,\gamma_0)}(\xi) = a_j\xi_j \quad \hbox{pour} \ j=2,3. $$

(96)

Soient γ(u ₁,u ₂) une famille d’infinis conformes tels que

$$ \gamma(0)=\gamma_0, \qquad\frac{\partial\gamma}{\partial u_j}\bigg|_{u=0} = S_2^\infty(\eta_j) . $$

(97)

On notera aussi

$$\gamma(u)=\gamma(u,0) . $$

On déduit immédiatement du développement (64), et des lemmes 12.1 et 12.2, la construction des métriques d’Einstein :

Théorème 12.3

Si (M ₀,g ₀), non dégénéré, satisfait la condition de courbure $\det \mathbf {R}_{g_{0}}^{+}(p_{0})=0$, alors :

• si $\mathbf {R}_{g_{0}}^{+}(p_{0})$ est non dégénéré (une seule valeur propre de $\det \mathbf {R}_{g_{0}}^{+}(p_{0})$ s’annule), alors pour t>0 suffisamment petit, il existe un réel u(t) et une jauge $\varphi (t)\in \operatorname {Sp}_{1}/U_{1}$, tels que $u(t)=O(t^{\frac{1}{2}-\delta})$ pour tout δ>0, et, pour j=1,2,3,

  $$\lambda_j \bigl(t,\varphi(t),\gamma\bigl(u(t)\bigr) \bigr)=0, $$

  c’est-à-dire g _{t,φ(t),γ(u(t))} est une métrique d’Einstein ;

• en général, pour t>0 suffisamment petit, il existe des réels u ₁(t),u ₂(t) et une jauge $\varphi(t)\in \operatorname {Sp}_{1}/U_{1}$, tels que $u_{j}(t)=O(t^{\frac{1}{2}-\delta})$ pour tout δ>0, et, pour j=1,2,3,

  $$\lambda_j \bigl(t,\varphi(t),\gamma\bigl(u_1(t),u_2(t) \bigr) \bigr)=0. $$

Remarque 12.4

La seconde partie du théorème est toujours vraie : le lien avec la première provient du fait suivant : dans le cas non dégénéré, on peut choisir γ(u ₁,u ₂) difféomorphe à γ(u ₁), ce qui est une manière détournée de changer la jauge à l’origine (on modifie la métrique g ₀ par une perturbation globale de la jauge au lieu de modifier le recollement) ; c’est une conséquence du (1) du lemme 11.1. C’est aussi pourquoi, dans la forme (95), le λ ₃ pourrait être compensé par une déformation de l’infini conforme par des difféomorphismes, équivalente au changement de jauge au recollement.

Remarque 12.5

Les métriques fabriquées dans la proposition 9.1 dépendent d’un paramètre υ∈ℝ³. Le théorème a été énoncé en utilisant les métriques construites pour υ=0, mais toute autre valeur (petite) de υ est possible. Si on fixe la famille γ(t) de déformations autorisées de l’infini conforme, on peut néanmoins s’attendre à un résultat d’unicité de la métrique d’Einstein, à infini conforme fixé. Mais il semble impossible de contrôler le noyau de la linéarisation $P_{g_{t}}$ après déformation, qui garde des petites valeurs propres issues du noyau de P _eh (voir section 13). Néanmoins, on verra en section 15 que génériquement, tel est bien le cas : les variables υ n’apportent pas de paramètre supplémentaire, et les métriques d’Einstein construites sont déterminées par leur infini conforme (théorème 15.1).

13 Petites valeurs propres de la linéarisation

Pour obtenir une meilleure approximation de la métrique d’Einstein, il faut raffiner substantiellement la construction faite jusqu’ici. La première étape consiste à remplacer les obstructions χ _t o _i , obtenues par troncation naïve des obstructions de Eguchi-Hanson, par de meilleures approximations des vecteurs propres associés aux petites valeurs propres de l’opérateur P _t sur M.

Sur Eguchi-Hanson, nous disposons donc d’un noyau de P, engendré par o ₁, o ₂ et o ₃, avec comportement asymptotique (27), que nous réécrivons

$$ o_j \sim\frac{\eta_j}{r^6}, $$

(98)

où les η _j sont des polynômes homogènes de degré 2, donc a priori $\eta_{j}\in(S_{+}^{2}S_{-}^{2})^{\otimes2}$. Il résulte de la formule (27), voir aussi la suite de la section 4, qu’en réalité on a

$$ \eta_j\in S_+^4\subset \bigl(S_+^2S_-^2 \bigr)^{\otimes2}. $$

(99)

Comme vu en section 10, il existe sur M ₀ des solutions $\bar{o}_{j}$ de l’équation $P\bar{o}_{j}=0$, qui soient L ² à l’infini et aient près de p ₀ le comportement

$$\bar{o}_j \sim\frac{\eta_j}{r^6}. $$

Compte tenu de ce comportement asymptotique, on a $B\bar{o}_{j}=O(r^{-3})$, donc on peut trouver un champ de vecteurs X _j =O(r ⁻¹), tel que $B\delta^{*}X_{j}=-B\bar{o}_{j}$. En remplaçant $\bar{o}_{j}$ par $\bar{o}_{j}+\delta^{*}X_{j}$, on peut ainsi supposer

$$B\bar{o}_j=0. $$

Nous définissons alors le recollement o _j,t sur M, par

$$ o_{j,t} = (1-\chi_t)t\bar{o}_j + \chi_t o_j, $$

(100)

où χ _t est la fonction de coupure définie par (40). Le facteur t est le facteur nécessaire pour faire coïncider les comportements asymptotiques de $\bar{o}_{j}$ en p ₀ et de o _j à l’infini après application de l’homothétie s _t , de rapport $\sqrt{t}$.

Par définition, $B_{g_{t}}o_{j,t}$ et P _t o _j,t ont leur support inclus dans EH^t. Les estimations suivantes améliorent d’un facteur $t^{\frac{1}{2}}$ les estimations (75) et (76) :

Lemme 13.1

On a sur EH^t les estimations, pour tout entier naturel k,

Démonstration

Les termes d’ordre r ⁻⁴ de o _j et $t\bar{o}_{j}$ coïncident, donc la différence satisfait $|o_{j}-t\bar{o}_{j}|_{\mathrm {eh}}\leq c \rho^{-6}$ sur $\mathrm {EH}^{t}_{>}$. Il en résulte qu’on peut améliorer (76) en

$$\bigl|B_{g_t}(\chi_to_{j,t})\bigr|_{\frac{g_t}{t}} \leq c t^{-2} \biggl( \frac{1_{\mathrm {EH}^t_>}}{\rho^7}+\frac{t}{\rho^3} \biggr). $$

La première estimation s’en déduit. L’amélioration de (75) est similaire. □

Ce lemme montre que la linéarisation P _t a des petites valeurs propres : en effet, quand t→0, on a o _j,t →o _j sur EH, et plus précisément

$$\|o_{j,t} \|_{L^2(g_t)}\to\|o_j\|_{L^2(\mathrm {eh})} $$

alors que

$$ \| P_to_{j,t} \|_{L^2(g_t)} = \bigl\| P_{\frac{g_t}{t}}t^{-1}o_{j,t} \bigr\|_{L^2(\frac{g_t}{t})} = O(1). $$

En revanche, la troncation χ _t o _j , utilisée auparavant, ne permet pas d’obtenir ces valeurs propres bornées.

L’application importante pour nous est l’amélioration suivante des estimations (72) et (73) :

Corollaire 13.2

On a les estimations

Démonstration

Comme dans (74), on utilise l’intégration par parties

$$(P_th,o_{j,t} )_{g_t}= \biggl(\frac{h}{t},P_{\frac{g_t}{t}}o_{j,t} \biggr)_{\frac{g_t}{t}}, $$

et la première estimation résulte alors immédiatement du lemme 13.1. Celui-ci nous fournit aussi, à la place de (77),

$$\|B_{g_t}o_{j,t}\|_{C^{k,\alpha}_{\delta+2}} \leq c t^{\frac{1}{2}+\frac{\delta}{4}} $$

qui améliore automatiquement d’un facteur $t^{\frac{1}{2}}$ l’estimation (73). □

Remarque 13.3

On déduit du corollaire que la proposition 9.1 reste valable en remplaçant χ _t o _j par o _j,t . Cela améliore l’estimation (64) en

$$\lambda_j(t)=t\lambda_j + O\bigl(t^{2-\frac{\delta_0}{2}} \bigr) . $$

Le poids $\frac{\delta_{0}}{2}$ restant vient de (84). Ce développement est insuffisant pour obtenir celui des solutions, qui requiert le terme en t ² de λ _j (t).

14 Asymptotique de la solution

La détermination de l’asymptotique de la solution quand t tend vers 0 se fait en raffinant la construction des solutions approchées. La solution approchée g _t a été construite en recollant g ₀ avec une modification h _t de la métrique de Eguchi-Hanson par un terme asymptotique aux termes quadratiques de g ₀ en p ₀. Une meilleure solution approchée sera obtenue, d’une part en raffinant h _t pour obtenir la coïncidence avec les termes d’ordre 4 de g ₀, d’autre part en modifiant g ₀ pour obtenir la coïncidence avec les termes en r ⁻⁴ de la métrique de Eguchi-Hanson.

Nous reprenons la section 3. On dispose sur EH^t d’une métrique h _t =eh+th, où h est solution du système (23). Pour pousser plus loin le développement d’une solution de $\operatorname {Ric}(g)=t\varLambda g \mod \mathcal {O}_{\mathrm {eh}}$, développons formellement

$$\operatorname {Ric}(\mathrm {eh}+u) = d_\mathrm {eh}\operatorname {Ric}(u) + Q(u) + R(u), $$

où Q(u) contient uniquement les termes quadratiques en u et R(u) les termes d’ordre au moins 3. Alors le terme t ² h ₂ de g sera obtenu en résolvant

$$ d_\mathrm {eh}\operatorname {Ric}(h_2) = \varLambda h - Q(h) \mod \mathcal {O}_\mathrm {eh}. $$

(101)

À l’infini, le terme h ₂ doit être d’ordre 4, et pour recoller avec la métrique g ₀ sur M ₀, on écrit en p ₀ le développement

$$g_0 = \mathrm {e}+ H + H_2 + O\bigl(r^6\bigr), $$

où H ₂ contient les termes d’ordre 4 de g ₀ seulement. Alors la condition à l’infini à considérer sur h ₂ est

$$ h_2 = H_2 + O \bigl(\rho^2\bigr) . $$

(102)

Le problème (101), (102) est à nouveau obstrué par les tenseurs o _j , et on résout à la place le système

$$ \begin{aligned} d_\mathrm {eh}\operatorname {Ric}(h_2) &= \varLambda h - Q(h) + \sum_1^3 \mu_j o_j , \\ h_2 &= H_2 + O \bigl(\rho^2 \bigr) , \end{aligned} $$

(103)

où les constantes μ _j font partie des inconnues.

Lemme 14.1

Le problème (103) a toujours une solution. Le tenseur

$$\hat {h}_t=\mathrm {eh}+th+t^2h_2 $$

est une métrique sur EH^t, satisfaisant

$$ \Biggl| \nabla^k \Biggl(\operatorname {Ric}_{\hat {h}_t}-t\varLambda \hat {h}_t-\sum_1^3 \bigl(t\lambda_j+t^2\mu_j \bigr)o_j\Biggr) \Biggr|_\mathrm {eh}\leq c_k t^3 \rho^{4-k}. $$

(104)

Les constantes μ _j sont une fonction du 2-jet de la courbure de g ₀ au point p ₀.

Démonstration

La résolution de l’équation se fait comme en section 3. L’estimation est similaire à celle du lemme 5.2 : on est juste allé une étape plus loin dans la résolution de l’équation d’Einstein, en compensant par h ₂ les termes quadratiques, donc il ne reste plus dans $\operatorname {Ric}_{\hat {h}_{t}}-t\varLambda \hat {h}_{t}$ que les obstructions et les termes d’ordre au moins 3, ce qui mène au lemme. □

Si on varie la jauge φ et l’infini conforme γ, on obtient une métrique $\hat {h}_{t,\varphi,\gamma}$ et des constantes λ _j (φ,γ) et μ _j (φ,γ). On a maintenant une métrique d’Einstein modulo obstructions à un ordre élevé par (104). Néanmoins, pour maintenir la qualité de l’approximation dans le recollement, il faut raffiner aussi g ₀(γ(t)) de la manière suivante. Écrivons, par (4),

$$\mathrm {eh}= \mathrm {e}+ \frac{\sigma}{\rho^6} + O\biggl(\frac{1}{ \rho^6}\biggr), $$

où σ est un terme homogène de degré 2. Comme dans la section 10, résolvons le problème

$$ \begin{aligned} P_{g_0}k &= 0, \\ B_{g_0}k &= 0, \\ k &\sim\frac{\sigma}{r^6} \quad \text{en }p_0, \end{aligned} $$

(105)

et k est L ² à l’infini de M ₀. Alors le tenseur

$$g_0 + t^2 k $$

est une métrique sur $M_{0}^{t}$. Bien sûr tout dépend ici de l’infini conforme γ ainsi que de la jauge φ et on notera explicitement cette dépendance k(φ,γ).

Nous pouvons maintenant définir une solution à un ordre élevé de l’équation d’Einstein modulo obstructions :

$$ \gimel _{t,\varphi,\gamma} = t \chi_t \hat {h}_{t,\varphi,\gamma} + (1-\chi_t) \bigl(g_0(\gamma)+t^2k(\varphi, \gamma) \bigr) . $$

(106)

Elle satisfait

Lemme 14.2

Sur EH^t on a les estimations

(107)

et sur $M_{0}^{t}$,

(108)

Démonstration

C’est une conséquence immédiate, d’une part de l’estimation (104), d’autre part du fait que les 2 métriques recollées, à savoir $\hat{h}_{t,\varphi,\gamma}$ et g ₀(γ)+t ² k(φ,γ) coïncident à un ordre élevé sur la transition $\mathrm {EH}^{t}_{>}$ :

$$\bigl|\hat{h}_{t,\varphi,\gamma} - \bigl(g_0(\gamma)+t^2k(\varphi,\gamma)\bigr) \bigr|_\mathrm {eh}\leq c\biggl( \frac{1}{\rho^6} + t^3 \rho^6 \biggr). $$

On remarquera que les deux termes de droite sont du même ordre de grandeur. L’estimation (107) s’en déduit immédiatement. L’autre estimation (108) sur la partie $M_{0}^{t}$ vient du fait que la métrique g ₀(γ)+t ² k(φ,γ) n’est plus d’Einstein qu’à l’ordre 1, et on doit donc tenir compte des termes quadratiques provenant de t ² k(φ,γ). □

Compte tenu, sur les 2-tenseurs, de l’égalité

$$\bigl|\nabla^k\cdot\bigr|_{\frac{g_0}{t}}=t^{1+\frac{k}{2}} \bigl| \nabla^k\cdot\bigr|_{g_0}, $$

la majoration (107) et le terme r ^4−k dans (108) donnent la même estimation sur la zone de transition $\mathrm {EH}^{t}_{>}$. Le terme $t^{4}x^{6}\tilde{r}^{-10-k}$ est provoqué par la correction t ² k(γ) de g ₀(γ) : il est global sur M ₀, mais d’ordre plus petit sur $\mathrm {EH}^{t}_{>}$ ; l’annulation x ⁶ près de ∂M ₀ vient de |k|=O(x ³).

Notons que sans la correction t ² k(γ), les termes d’ordre O(ρ ⁻⁴) ne se recollent pas, et provoquent une erreur $O(\rho^{-6})\sim O(t^{\frac{3}{2}})$ dans le tenseur de Ricci, ce qui serait insuffisant pour (107).

Par le lemme 14.2, on obtient

$$ \Biggl\| (\operatorname {Ric}-\varLambda) (\gimel _t)-\sum_1^3 \bigl(t\lambda_j+t^2 \mu_j \bigr)o_{j,t} \Biggr\|_{C^\alpha_{\delta_0+2,\delta_\infty;t}} = O \bigl(t^{\frac{3}{2}+\frac{\delta_0}{4}} \bigr) . $$

(109)

La méthode de résolution de l’équation d’Einstein employée à partir de la solution approchée g _t,φ,γ pour démontrer la proposition 9.1 s’applique aussi bien à partir de ℷ _t . On en déduit immédiatement l’existence et l’unicité d’une métrique $\hat{\gimel }_{t}$, par exemple en jauge de Bianchi par rapport à ℷ _t , et telle que

$$ \operatorname {Ric}\bigl(\hat{\gimel }_t\bigr)-\varLambda\hat{\gimel }_t = \sum_1^3 \hat{\lambda}_j(\varphi,\gamma) \pi_{\hat{\gimel }_t}(o_{j,t}). $$

(110)

Cette métrique satisfait

$$ \bigl\|\hat{\gimel }_t-\gimel _t\bigr\|_{C^{2,\alpha}_{\delta_0,\delta_\infty;t}} = O \bigl(t^{\frac{3}{2}+\frac{\delta_0}{4}} \bigr) . $$

(111)

En outre, vu les estimations du corollaire 13.2, on en déduit

$$ \hat{\lambda}_j(\varphi,\gamma) = t \lambda_j(\varphi,\gamma) + t^2 \mu_j( \varphi,\gamma) + O \bigl(t^{\frac{5}{2}} \bigr) . $$

(112)

Par le lemme 12.1, on peut maintenant annuler les coefficients $\hat{\lambda}_{j}$ des termes d’obstruction et raffiner ainsi le théorème 12.3 :

Théorème 14.3

Si (M ₀,g ₀), non dégénérée, satisfait la condition de courbure $\det \mathbf {R}^{+}_{g_{0}}(p_{0})=0$, avec jauge ajustée de sorte que les λ _j (γ ₀)=0, alors il existe une jauge $\varphi(t)\in \operatorname {Sp}_{1}/U_{1}$ et une famille d’infinis conformes γ(t) telle que γ(0)=γ ₀, et pour tout t>0 assez petit, la métrique $\hat{\gimel }_{t,\varphi(t),\gamma(t)}$ soit d’Einstein. Une telle famille γ(t) doit satisfaire

$$ \lambda_j \bigl(\varphi(t),\gamma(t) \bigr) = - t \mu_j \bigl(\varphi(0),\gamma_0 \bigr) + O \bigl(t^{\frac{3}{2}} \bigr). $$

(113)

Par exemple, dans le cas où $\mathbf {R}_{g_{0}}^{+}(p_{0})$ est non dégénéré, γ(t) peut être choisie dans la famille à un paramètre γ(u) utilisée pour le théorème 12.3, de sorte que

$$\dot{\gamma}(0)=-\mu_1(\gamma_0)S_2^\infty(\eta_1). $$

Notons à nouveau (remarque 12.5) qu’aucune unicité de la métrique d’Einstein produite n’est prouvée, et qu’en particulier elle semble à première vue dépendre du paramètre υ de la proposition 9.1.

La motivation pour obtenir une asymptotique en t beaucoup plus précise est l’analyse, dans le voisinage de γ ₀, des infinis conformes obtenus comme bords de métriques d’Einstein lisses. Notons $\mathcal {C}$ l’espace des métriques conformes sur ∂M ₀. Considérons l’hypersurface

$$ \mathcal {C}_0= \bigl\{ \det \mathbf {R}_{g_0}^+(p_0)=0 \bigr\} \subset \mathcal {C}. $$

(114)

D’un point de vue technique, pour travailler dans des variétés banachiques, il faut regarder l’infini conforme γ dans un espace de Hölder C ^k,α. Si $\mathbf {R}_{g_{0}}^{+}(p_{0})$ est non dégénéré, alors, d’après le lemme 12.1, $\mathcal {C}_{0}$ est une hypersurface lisse au point γ ₀. Le développement (113) a pour conséquence le résultat suivant :

Théorème 14.4

Soit $\gamma_{0}\in \mathcal {C}_{0}$. Si $\mathbf {R}_{g_{0}}^{+}(p_{0})$ est non dégénéré et μ ₁(γ ₀)≠0 (par exemple fixons μ ₁(γ ₀)>0), alors dans un petit voisinage de $\mathcal {C}_{0}=\{\lambda_{1}=0\}$, les infinis conformes des métriques d’Einstein produites par le théorème 14.3 sont exactement les métriques conformes vérifiant λ ₁<0. □

La même chose est valable si on varie le paramètre apparent υ.

Au vu de l’argument d’unicité (corollaire 9.3), sous les hypothèses du théorème, toutes les métriques d’Einstein suffisamment proches d’un recollement naïf $g_{t,\varphi,\gamma}^{0}$ doivent coïncider avec une métrique d’Einstein dans la famille que nous avons construite, et donc satisfaire λ ₁(γ)<0 dans le cas non dégénéré :

Corollaire 14.5

Sous les mêmes hypothèses, si une métrique AH d’Einstein g est suffisamment proche d’un recollement $g^{0}_{t,\varphi,\gamma}$ au sens du corollaire 9.3, alors son infini conforme doit satisfaire λ ₁<0. □

Cela suggère fortement que l’hypersurface $\mathcal {C}_{0}$ est un mur pour la résolution du problème de Dirichlet à l’infini sur M, c’est-à-dire que la résolution n’est possible que d’un seul côté de $\mathcal {C}_{0}$. Cela sera rendu précis en section 15.

Enfin, on peut se demander si le côté de $\mathcal {C}_{0}$ où l’on peut désingulariser ne dépend que du signe de $\det \mathbf {R}_{g_{0}}^{+}(p_{0})$, par exemple serait toujours $\det \mathbf {R}_{g_{0}}^{+}(p_{0})>0$ (comme le suggère l’exemple des métriques Ads-Taub-Bolt, voir après le théorème 15.1). Là encore, une compréhension fine des termes quadratiques de l’équation d’Einstein serait nécessaire pour trancher.

15 Transversalité

Dans cette section, nous donnons des arguments de transversalité visant à préciser l’espace des modules de métriques d’Einstein AH dans le voisinage de l’hypersurface $\mathcal {C}_{0}\subset \mathcal {C}$ définie par (114).

Soit $\gamma_{0}\in \mathcal {C}_{0}$, tel que μ ₁(γ ₀)≠0 (donc $\mathcal {C}_{0}$ est lisse en γ ₀), alors nous disposons d’une direction $\delta(\gamma_{0})=S_{2}^{\infty}(\eta_{1})$ dans $\mathcal {C}$ au point γ ₀, transverse à $\mathcal {C}_{0}$, telle qu’on puisse résoudre l’équation d’Einstein pour tout infini conforme

$$ \gamma(t) = \gamma_0 + t \delta(\gamma_0), \quad t>0 \ \text{petit}. $$

(115)

Cela nous permet de définir, dans un voisinage de γ ₀, une projection

$$ p:\mathcal {C}\to \mathcal {C}_0 $$

(116)

par p(γ ₀+tδ(γ ₀))=γ ₀.

Faisons brièvement quelques rappels sur la structure de l’espace des modules de métriques d’Einstein [2]. Notons $\mathcal {E}$ l’espace des modules des métriques d’Einstein AH sur M, modulo l’action des difféomorphismes de M induisant l’identité sur ∂M. Un détail technique, à nouveau, est qu’il faut considérer des infinis conformes de classe C ^k,α. Alors $\mathcal {E}$ est une variété banachique, et l’application qui à une métrique d’Einstein associe son infini conforme,

$$ \pi:\mathcal {E}\to \mathcal {C}, $$

(117)

est Fredholm d’indice 0.

Considérons un voisinage $\mathcal {V}$ de $\gamma_{0}\in \mathcal {C}_{0}$, et l’application

$$\tilde{\pi}:= p\circ\pi: \pi^{-1}(\mathcal {V}-\mathcal {C}_0) \to \mathcal {C}_0, $$

manifestement Fredholm, d’indice égal à 1. Par le théorème de Sard-Smale, $\tilde{\pi}$ admet un ensemble dense de valeurs régulières, et si γ ₀ est régulière, alors $\tilde{\pi}^{-1}(\gamma_{0})$ est une sous-variété de dimension 1 dans $\mathcal {E}$. Or nous disposons déjà dans la fibre $\tilde{\pi}^{-1}(\gamma_{0})$ de la famille de métriques d’Einstein $g_{t,\upsilon,\gamma_{0}}$ construite par le théorème 12.3 pour υ et t>0 assez petits. Il en résulte immédiatement que, quand on fait υ=0, la famille à un paramètre $g_{t,0,\gamma_{0}}$ décrit déjà toute la fibre $\tilde{\pi}^{-1}(\gamma_{0})$ (près de g ₀). Par conséquent, la famille $\{g_{t,\upsilon,\gamma_{0}}, 0<t<\frac{\eta}{2}, |\upsilon|<\epsilon\}$ est incluse dans la famille $\{g_{t,0,\gamma_{0}}, 0<t<\eta\}$. On a ainsi démontré que, génériquement, le paramètre υ ne fabrique pas de nouvelles métriques :

Théorème 15.1

Soit $\gamma_{0}\in \mathcal {C}_{0}$. Supposons comme dans le théorème 14.4 que μ ₁(γ ₀)>0. Si γ ₀ est une valeur régulière de $\tilde{\pi}$, alors la variation du paramètre υ dans les métriques d’Einstein $g_{t,\upsilon,\gamma_{0}}$ revient à varier seulement le paramètre t de la famille $g_{t,0,\gamma_{0}}$. Autrement dit, dans la famille de métriques d’Einstein construite, pour t et υ assez petits, la métrique $g_{t,\upsilon,\gamma_{0}}$ est entièrement déterminée par son infini conforme.

Le théorème a quelques conséquences sur la théorie du degré proposée par Anderson [3], que nous expliquons maintenant. Précisons bien que les considérations qui suivent sur le degré sont hypothétiques, et dépendent de la possibilité de construire un tel degré dans notre situation, ce qui reste à faire.

La définition du degré est simple : quand on se limite à un ouvert $\tilde{\mathcal {C}}\subset \mathcal {C}$, tel que $\pi|_{\pi^{-1}(\tilde{\mathcal {C}})}$ soit propre, alors le nombre de points, compté avec signe, d’une fibre de π en une valeur régulière de π, fournit le degré de π, un invariant de chaque composante connexe de $\tilde{\mathcal {C}}$. La principale difficulté dans la définition de ce degré consiste dans la propreté de l’application π.

Revenons à notre cas : le voisinage $\mathcal {V}$ de γ ₀ dans $\mathcal {C}$ ne peut pas être inclus dans $\tilde{\mathcal {C}}$, puisque nous avons justement construit une famille d’éléments de $\mathcal {E}$ qui ne converge pas dans $\mathcal {E}$, alors que leurs infinis conformes convergent vers γ ₀. Nécessairement donc, le degré ne peut être défini que sur une région

$$\tilde{\mathcal {C}}\subset \mathcal {C}- \mathcal {C}_0 . $$

Supposons à présent que le degré soit défini au moins sur la région $\tilde{\mathcal {C}}:=\mathcal {V}-\mathcal {C}_{0}$. Le théorème a pour conséquence que les métriques d’Einstein g _t,γ , dont les infinis conformes sont exactement d’un seul côté de $\mathcal {C}_{0}$, contribuent à une modification du degré par 1 à travers le mur $\mathcal {C}_{0}$. Pour établir complètement ce fait, il faudrait en outre démontrer que les seules métriques d’Einstein dégénérant vers g ₀ sont les métriques g _t,γ , c’est-à-dire sont proches, au sens du corollaire 9.3, du recollement d’une métrique d’Einstein orbifold avec la métrique d’Eguchi-Hanson.

L’exemple le plus simple est M=T ^∗ S ², désingularisation de ℝ⁴/ℤ₂, de bord S ³/ℤ₂. Une analyse simple de l’exemple de la famille de métriques AdS-Taub-Bolt [13] indique que l’une des métriques de Pedersen g ₀ se désingularise, et que la famille construite de désingularisations est du côté detR ⁺(p ₀)>0 de $\mathcal {C}_{0}$. De l’autre côté de $\mathcal {C}_{0}$, nous avons le quotient de l’espace hyperbolique réel par ℤ₂, qui satisfait detR ⁺(p ₀)<0, et on peut donc supposer que le degré serait nul pour detR ⁺(p ₀)<0 (du côté de la métrique ronde sur S ³/ℤ₂), et égal à 1 du côté detR ⁺(p ₀)>0. Cela va dans le même sens que la proposition d’Anderson [3, §7] selon laquelle la métrique ronde de S ³/ℤ₂ n’est pas le bord à l’infini d’une métrique d’Einstein.