Representation of conformal maps by rational functions

Abstract

The traditional view in numerical conformal mapping is that once the boundary correspondence function has been found, the map and its inverse can be evaluated by contour integrals. We propose that it is much simpler, and 10–1000 times faster, to represent the maps by rational functions computed by the AAA algorithm. To justify this claim, first we prove a theorem establishing root-exponential convergence of rational approximations near corners in a conformal map, generalizing a result of D. J. Newman in 1964. This leads to the new algorithm for approximating conformal maps of polygons. Then we turn to smooth domains and prove a sequence of four theorems establishing that in any conformal map of the unit circle onto a region with a long and slender part, there must be a singularity or loss of univalence exponentially close to the boundary, and polynomial approximations cannot be accurate unless of exponentially high degree. This motivates the application of the new algorithm to smooth domains, where it is again found to be highly effective.

1 Introduction

Traditionally in numerical conformal mapping, one first determines the boundary correspondence function, the one-to-one mapping between the boundaries of the domain and the image regions, and then one evaluates the map or its inverse in the interior by methods such as Cauchy integrals [7, 15, 19, 20, 40]. If the domains are smooth, the first step is often carried out by solving an integral equation. Most domains of interest in practice are not smooth, and the corners that appear so often bring in new challenges that traditionally would be addressed by the exploitation of the local structure of each singularity [3, 23, 29]. In the extreme case of the map of a disk or a half-plane onto a polygon, the problem is “all singularities,” and here one may make use of a numerical implementation of the Schwarz–Christoffel (henceforth SC) formula, for which the standard software is Driscoll’s SC Toolbox in MATLAB [10, 12, 28].

In this paper we propose a different approach to the second phase of computing a conformal map. Instead of evaluating Cauchy or SC integrals, we propose the use of rational functions to represent the maps, one rational function in the forward direction and another in the inverse direction. Instead of exploiting the structure of singularities, we ignore their presence and let the rational approximations do the work. This is not asymptotically optimal for very high accuracies, but in the practical regime, it is remarkable how efficient it can be. For a polygonal region with around six corners, we find that rational functions of degree 30 to 100 typically suffice for mapping to 7-digit accuracy, and the evaluation time is on the order of a microsecond per point mapped on a laptop. Mapping tens of thousands of points back and forth accordingly takes a fraction of a second.

Until recently, no fast method was available for constructing such rational approximations, but this situation has changed with the appearance of the AAA algorithm [26]. This algorithm represents rational functions stably by quotients of partial fractions rather than polynomials, with the necessary support points determined adaptively.¹ If Z and F are sets of, say, 5000 corresponding points on the boundaries of the domain and target regions, the command r = aaa(F,Z) in Chebfun [11] will typically construct a rational function mapping Z to F in less than a second on a laptop. A aaa code in MATLAB is listed in [26], and a Python implementation is available from the first author.

The mathematical basis of our method is a new result, proved in Sect. 2, that generalizes a theorem published by Donald Newman in 1964 [27]. Newman showed that the minimax error $E_n$ for approximation of $f(x) = |x|$ on $[-1,1]$ by type (n, n) rational functions decreases at the rate $\exp (-A\sqrt{n})$ for some $A>0$ as $n\rightarrow \infty$. The sharp constant is $A = \pi$, and more generally, for approximation on $[-1,1]$ of $f(x) = |x|^\alpha$ with $\alpha >0$, Stahl [35] showed that root-exponential convergence occurs at the rate

$$\begin{aligned} E_n = O(e^{-\pi \sqrt{\alpha n}}). \end{aligned}$$

(1)

This estimate is sharp unless $\alpha$ is an even integer, in which case f reduces to a polynomial. In the context of our conformal maps, the essential problem is that of approximating the complex function $x^\alpha$ on a one-sided complex neighborhood of $[-1,1]$ rather than the real function $|x|^\alpha$ on $[-1,1]$ alone. In Sect. 2, applying a different method from Newman’s, we prove that the convergence rate for this problem is also root-exponential. Section 3 then applies this result to conformal maps of polygons.

In Sect. 4 we turn to regions with analytic boundaries. We start from a theoretical perspective, showing in a sequence of four theorems that because of the “crowding phenomenon” of conformal mapping, the conformal map of a region with a smooth boundary necessarily has a singularity or loss of univalence exponentially close to the boundary if the region contains a part that is long and narrow in a certain sense. Under the same assumptions, polynomial approximations are proved to be inaccurate unless their degree is exponentially large. We believe these theorems are a significant contribution to the literature of crowding. In the context of the present paper, their role is to motivate Sect. 5, which applies our rational function method to conformal maps of domains with analytic boundaries. Section 6 examines the accuracy of our approximations.

One of the consequences of our rational approximations is that they eliminate much of the practical difference between conformal mapping methods in the “forward” and “inverse” directions. For example, the Schwarz–Christoffel formula maps from a half-plane or a disk to the problem domain, which traditionally introduces an asymmetry in the cost of evaluating the map in the two directions. Similarly, there have been computational consequences of the fact that integral equations from the problem domain to the disk are often linear, whereas in the direction from the disk to the problem domain theys are usually nonlinear. With the techniques introduced here, the directionality of the underlying representation becomes less important, since, once the boundary correspondence map has been computed, the initial representation is discarded in favor of rational functions in the two directions.

2 Rational approximation of $\varvec{x}^{\varvec{\alpha }}$

In this section we prove a result that is the basis of our algorithm, establishing that rational approximations can be highly efficient at representing a conformal map near a corner. The local behavior of a conformal map with straight sides at a corner of angle $\alpha \pi$ is of type $x^\alpha$ (or $x^{1/\alpha }$ in the inverse direction), as can be established from the Schwarz reflection principle [12].

Let H denote the closed upper half of the unit disk and $\Vert \cdot \Vert _H$ the supremum norm on H. In fact, the only property of H we shall use is that it is a bounded subset of the upper half-plane. Our proof is adapted from the argument for approximation of |x| on $[-1,1]$ given on pp. 211–212 of [38].

Theorem 1

Let $\alpha$ be any positive number. There exist a constant $A>0$ and type (n, n) rational approximations $r_n$ such that as $n\rightarrow \infty$,

$$\begin{aligned} \Vert x^\alpha - r_n \Vert _H^{} = O(e^{-A \sqrt{n}}). \end{aligned}$$

(2)

Proof

If $r_n(x)\approx x^\alpha$ with $\alpha \in (0,1]$, then $x^k r_n(x) \approx x^{k+\alpha }$, so without loss of generality we may assume $\alpha \in (0,1]$. Moreover, if $r_n(x)\approx x^\alpha$ with $\alpha \in (0,1/2]$, then $(r_n(x))^2 \approx x^{2\alpha }$, so without loss of generality we may further assume $\alpha \in (0,1/2]$.$\square$

We start from the identity

$$\begin{aligned} x^\alpha = C \int _0^\infty {x\, dt\over t^{1/\alpha } + x}, \quad C = {\sin (\alpha \pi )\over \alpha \pi }, \end{aligned}$$

(3)

valid for $x\not \in (-\infty ,0]$, which can be derived via the substitution $u = t/x^\alpha$ and the integral $\int _0^\infty du/(u^b + 1) = \pi \csc (\pi /b)/b$ for $b>1$ [18, eq. 3.241.2]. Since we wish to apply (3) for x in the closed upper half-plane, we rotate the integration contour to exclude zeros of the denominator, leaving the value of the integral unchanged since the integrand decreases faster than linearly as $|t|\rightarrow \infty$. Specifically, we make the change of variables $t = e^{\alpha \pi i/2 + s}$, $dt = e^{\alpha \pi i/2+ s} ds$, where s is real, which converts (3) to

$$\begin{aligned} x^\alpha = C \int _{-\infty }^\infty {x\, e^{\alpha \pi i/2 + s} ds\over e^{\pi i/2 + s/\alpha }+x}. \end{aligned}$$

(4)

Note that the integrand decays exponentially at the rate $e^{s(1-1/\alpha )}$ as $s\rightarrow +\infty$, and this is uniformly true for all values of $x\in H$ since H is bounded. As for $s \rightarrow -\infty$, here the integrand decays exponentially at the rate $e^s$ for each $x\ne 0$, uniformly for all x.

To get a rational approximation to $x^\alpha$, we now approximate (4) by the trapezoidal rule with node spacing $h>0$:

(5)

Here n is a positive even number, and there are n terms in the sum, so r(x) is a rational function of x of type (n, n). Its poles are on the negative imaginary axis, so r is analytic in the upper half-plane.

As reviewed in [39], the error $|r(x)-x^\alpha |$ in the trapezoidal rule approximation can be decomposed into two parts. One part is introduced by terminating the sum at $n<\infty$, on the order of $e^{-nh/2}$. (By “on the order,” we mean that the dominant exponential term is correct; there may be further lower-order algebraic factors). The other part is introduced by the finite step size $h>0$. According to Theorem 5.1 of [39], this will be of order $e^{-2\pi d/h}$, where d is the half-width of the strip of analyticity of the integrand around the real s-axis. To determine this half-width, we note that the denominator of (5) will be 0 when $e^{\pi i/2 + s/\alpha }$ is equal to $-x$, and for x in the upper half-plane, this can only happen when the argument of $e^{s/\alpha }$, namely the imaginary part of $s/\alpha$, is at least as large as $\pi /2$ in absolute value. The half-width of the strip of analyticity is consequently $d = \pi \alpha /2$, giving an error of $e^{-\alpha \pi ^2/h}$.

We now choose h to balance the errors $e^{-nh/2}$ and $e^{-\alpha \pi ^2/h}$. The balance occurs with $h = \pi \sqrt{2\alpha /n}$, giving a convergence rate

$$\begin{aligned} \Vert r_n(x) - x^\alpha \Vert _H^{} \lesssim \exp (-\pi \sqrt{\alpha n/2}). \end{aligned}$$

(6)

We use the inexact symbol “$\,\lesssim \,$” since we have only tracked the exponential term, not lower-order algebraic factors, but this is enough to establish (2) for any value $A<\pi \sqrt{\alpha /2}$.

The constants in our argument are not optimal, and one reason is that the approximation (5) is valid (nonuniformly) throughout the upper half-plane, not just in H. We do not know the optimal constants, which appear to be different from those given in (1) for approximation of $|x|^\alpha$ on $[-1,1]$. Our convergence rate bound slows down to zero as $\alpha \rightarrow 0$, but this is also the case in (1).

Note that the poles of the approximation (5) cluster exponentially near $x=0$, with exponentially decreasing residues, as we shall observe in our numerical experiments; see in particular Fig. 2.

Though a single straight-sided corner is the case we have analyzed, in practice the root-exponential approximation effect is more general. If there are k singular corners, the type (n, n) of the rational function required for a given accuracy increases only approximately in proportion to k, and whether the sides are straight or not is immaterial. For example, the standard branch of $z^{1/2}\log (z)$ is as easily approximated as that of $z^{1/2}$ for $z\approx 0$ in the upper half-plane. Application of aaa for these functions gives approximations accurate to 6 digits on $[-1,1]$ with $n = 36$ and 29, respectively.

3 Conformal maps of polygons

Fig. 1

Conformal map f of the unit disk onto an L-shaped region (top row) and the inverse map $f^{-1}$ (bottom row). The parameters for the map are computed by the SC Toolbox and then f and $f^{-1}$ are represented compactly to about eight digits of accuracy (except very near the vertices) by rational functions $r\approx f$ and $s\approx f^{-1}$ computed by the AAA algorithm. The white dots show the normalization of the map by an interior and a boundary point, and the small black dots in the interior show about 1000 points on a regular grid and their images. The large red dots show poles of the rational functions sized according to the absolute values of their residues

Let $\varDelta$ be the closed unit disk in the z-plane and P the closed region bounded by a polygon with k vertices $w_1,\dots , w_k$ in the w-plane. The SC formula represents a conformal map $f: \varDelta \rightarrow P$ in terms of an integral with fractional power singularities at the prevertices$z_j = f^{-1}(w_j)$ [12]. Determining the prevertices for a given P is a numerical problem known as the SC parameter problem.

We illustrate our method by applying it to five SC maps computed by the Schwarz–Christoffel Toolbox [10]. Our first example is a map of the unit disk onto an L-shaped region, shown in Fig. 1.² The Toolbox computes the forward and inverse maps with approximately twelve digits of accuracy almost everywhere in the domain, except that very close to some of the corners or their preimages, the accuracy falls to five or six digits (see Sect. 6).³ Figure 1 displays this conformal map and its inverse and illustrates the rational approximations that are the subject of this paper. The plots in the top row show the forward map f. First, the mapping parameters are computed with the SC Toolbox as above. Then 3000 equispaced points on the unit circle are collected in a vector Z. (We take the number of points to be 500k, i.e., 500 times the number of vertices; see Sect. 6.) The vector of images $F = f(Z)$ is computed with the SC Toolbox. We then execute the Chebfun commands

to determine forward and inverse rational functions r and s such that $F \approx r(Z)$ and $Z \approx s(F)$; these computations take less than a second. The poles of r and s are returned in the vectors rpol and spol, computed from the AAA barycentric representation by solving a generalized eigenvalue problem [26], and the corresponding residues are returned in rres and sres.

To make the plots, we next apply r to map a grid of points in $\varDelta$ to their images in P, which takes about a millisecond. As usual with conformal maps, there are exponential distortions involved (see the next section), leading to a very uneven distribution of image dots. The second row of the figure shows the inverse map $f^{-1}$, including a grid of points in P and their equally unevenly distributed (pre)images in $\varDelta$ computed with s, again requiring about a millisecond. The plots also show a white dot in the interior and another on the boundary of each region, together with their images, to complete the specification of the conformal mapping problem.

Fig. 2

Closeups of Fig. 1. The poles approach the singularities with exponentially decreasing spacing and residues, as one would expect based on Theorem 1

Most striking in Fig. 1 are the red dots representing poles of r (top left) and s (bottom left). These are sized to indicate the magnitude of each residue, with a logarithmic spacing from the smallest diameter for magnitude $10^{-3}$ or less to the largest for magnitude 1 or more. In the upper-left plot, we see chains of poles of r with diminishing residues approaching all six prevertices (two pairs of which are quite close together). This is a familiar effect in rational approximation [33, 36], and it occurs because all six points correspond to branch point singularities of f, with local behavior of type $(z-z_j)^{1/2}$ for the five salient corners and $(z-z_j)^{3/2}$ at the reentrant corner. The degree 58 marked in the title indicates that r is a rational function of type (58, 58), that is, with 58 poles (some of which are not in the picture). The lower-left plot, on the other hand, shows poles only approaching the reentrant corner for the inverse map. This is because the other corners have local behavior of type $(w-w_j)^2$, which is not singular.⁴ Figure 2 shows closeups from each of these figures.

The “speedup” numbers in the titles give estimates of how much faster AAA is for evaluating each map than the SC Toolbox. To compute these numbers, timings for mapping the grid of points are compared with timings for the corresponding SC Toolbox command. Throughout our explorations, we have found that the rational functions are typically 10–1000 times faster than the Toolbox. The speedup numbers in our plots are only approximate; they vary from one run to the next.

Fig. 3

A perturbed L-shaped region. All the corners are now singular, and r and s have poles near all six prevertices/vertices. However, some singularities are much stronger than others

Finally there are the errors listed in the titles. In the upper-right plot the first of these numbers, labeled ‘max’, is determined by sampling the boundary on a grid four times finer than the sample set and computing the maximum of $|f(z) - r(z)|$ at these points, with f calculated by the SC Toolbox. Since f and r are both analytic in $\varDelta$, the maximum modulus principle implies that this can be counted on as close to a true maximum error in the rational representation. These numbers are generally disappointing, but this reflects diminished accuracy only in extremely small regions close to the vertices, as we shall discuss in Sect. 6 (see in particular Fig. 11). Elsewhere, the accuracy is excellent, and this is reflected in the “rms” errors, which show root-mean-square errors in the grid of points. Note that the rms errors are much smaller than $1/\sqrt{1000}$ times the max errors, implying that none of the ${\approx } 1000$ grid points have errors even close to maximal.

Fig. 4

Conformal map of a 4-to-1 rectangle, an example we shall discuss further in the next section. Here $f^{-1}$ is an elliptic function, analytic in a neighborhood of P. On the unit circle, the pairs of prevertices are too close to distinguish by eye

The lower-right plot of Fig. 1, for the inverse map, is labeled in the same manner, now with the maximum error based on the maximum of $|f^{-1}(w) - s(w)|$, again on a boundary grid four times finer and with $f^{-1}$ computed by the SC Toolbox.

We mentioned that the five salient right angles of the L-shaped region are nonsingular. Figure 3 highlights this effect by repeating Fig. 1 with the vertices perturbed. Now all the corners are singular, and poles of s appear near all of them. At the same time, the widely varying numbers and sizes of the dots illustrate how much more important some singularities are than others. The rational function s has just three poles within a distance 1/2 of the singular vertex near $1+2 i$, for example, with residues of absolute value less than $10^{-3}$. By contrast there are 23 poles within the same distance of the reentrant corner near $1+i$, their distances decreasing from O(1) to $O(10^{-4})$ as the absolute values of the residues decrease from $O(10^{-1})$ to $O(10^{-7})$.

At the other extreme, Fig. 4 shows the conformal map onto a rectangle. Here the inverse map has no singular corners, and indeed it is a doubly periodic elliptic function (as follows from the Schwarz reflection principle). In this case, no poles approach the boundary of P, and the associated rational function has degree just 9. The two poles visible on these axes lie at about $1.5 i + 10^{-7}(4+4 i)$ and $-\,0.5 i + 10^{-7}(3+2 i)$, very close to the positions 1.5i and $-\,0.5 i$ of the innermost poles of the elliptic function. Their residues match the theoretical value $-\,2/\pi$ to about three digits. In this as in most rational approximations, one should bear in mind that r or s will match poles or residues of f or $f^{-1}$ only “as a means to the end” of approximating f or $f^{-1}$ itself at the prescribed sample points, so not too much should be read into the number of digits of agreement. For example, this elliptic function has infinitely many poles in the plane, and obviously s is not going to approximate all of them. One may also note in the upper-left image of Fig. 4, as in several of our other figures, that the AAA algorithm does not respect symmetry of approximation problems. One might have expected the poles of r to be real, or at least to fall in complex conjugate pairs, but the algorithm does not impose this condition. (As mentioned in [26], one could develop variant algorithms with this property).

Fig. 5

Conformal map of an isospectral drum from Gordon, Webb, and Wolpert [17]

Figure 5 shows one of the isospectral drums made famous by Gordon, Webb, and Wolpert [17]. Again it is clear from the pole distribution that there are particularly strong singularities at the reentrant corners.

Fig. 6

Map of a rectangle onto an infinite polygon, illustrating that rational approximations are not limited to bounded regions. The black dots in the second row were computed as a grid of points in the portion of the polygon with imaginary part ${\le }~3$, though the figure would look the same if such points could be included all the way out to $\infty$

These four examples involve maps of the unit disk to a polygon, but there are other possibilities. For example, variants of the SC formula are implemented in the SC Toolbox for mapping to a polygon from a half-plane, a rectangle, or an infinite strip [10, 12]. Moreover, the domains need not be bounded, and if they are unbounded, rational functions can still be used to represent the conformal maps. Figure 6 illustrates this with images for the map of a rectangle to an infinite polygon P consisting of another rectangle along one side of which a channel extending to $\infty$ has been attached at a $45^\circ$ angle. The polygon P is first prescribed; then a rectangle in the z-plane is found with the uniquely determined aspect ratio such that its four corners can map to the four right-angle corners of P.

4 Exponential distortions with analytic boundaries

We now turn to smooth domains, specifically, domains bounded by analytic Jordan curves. If f is a conformal map of the unit disk onto such a domain, then f can be analytically continued to a neighborhood of the closed unit disk. This implies that f can be approximated by degree n polynomials with exponential convergence, that is, errors diminishing at a rate $O( \rho ^{-n})$ as $n\rightarrow \infty$ for some $\rho > 1$. This might seem to suggest that approximation by rational functions should not be needed.

In fact, that conclusion would be mistaken, for the constant $\rho$ is likely to be exponentially close to 1. The aim of this section is to establish some theorems in this direction, whose root is the “crowding phenomenon” of conformal mapping [4, 9, 28, 37]. The crowding effect can be seen in all the plots of conformal maps we have presented, where in every case, a regular array of points in one domain maps to a set of points with exponentially varying densities in the other. In Fig. 4, for example, the distortion is extreme enough that as far as one can tell from the clusters of poles, four prevertices on the unit circle appear to be just two. Further examples will be given in Sect. 5.

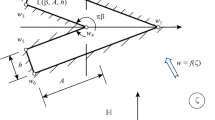
Let f be a conformal map of the unit disk D in the z-plane onto a region $\varOmega$ in the w-plane whose boundary is an analytic Jordan curve $\varGamma$. By the Osgood–Carathéodory theorem, f extends continuously to $\varGamma$ [20]. We say that $\varOmega$contains a finger of length$L>0$ if there is a rectangular channel of width 1 defined by a pair of parallel line segments of length L, disjoint from $\varOmega$, such that $\varOmega$ extends all the way through the channel with parts of $\varOmega$ lying outside both ends. Specifically, we consider a point $a\in \varOmega$ lying outside the channel at one end and the nonempty portion $\varGamma _{\mathrm{exit}}$ of $\varGamma$ lying outside the channel at the other end, which we call the “exit arc,” as shown in Fig. 7. We denote the ends of the channel by A and B. (If a part of $\varOmega$ extends beyond B and then bends around to cross B again and reenter the rectangle, it is still “beyond B” in a topological sense and this is how we interpret it and its portion of the boundary $\varGamma$ throughout the discussion below.)

Fig. 7

A region $\varOmega = f(D)$ with a finger of lengthL and a Brownian path $\gamma$ starting at a and ending when it hits the boundary $\varGamma$. The probability of a path getting all the way through the finger to first hit the boundary at a point beyond it shrinks exponentially with L at the rate $\exp (-\pi L)$. This provides one explanation of the exponential distortions characteristic of conformal maps, which render rational approximations much more efficient than polynomials

Let $\omega \in (0,1)$ denote the harmonic measure of $\varGamma _{\mathrm{exit}}$ at a with respect to $\varOmega$ [2, 16, 25]. This can be interpreted as the probability that a Brownian path in $\varOmega$ starting at a first hits $\varGamma$ somewhere along $\varGamma _{\mathrm{exit}}$, and it is equal to the value u(a) of the harmonic function u in $\varOmega$ that takes the boundary values 1 along $\varGamma _{\mathrm{exit}}$ and 0 elsewhere on $\varGamma$. Our first estimate relates the geometry of $\varOmega$ to the size of $\omega$. According to Garnett and Marshell [16, chap. IV], bounds of this kind go back to Ahlfors in 1930 [1], and in the conformal mapping literature, related results have been derived by authors including de Lillo, Dubiner, Pfaltzgraff, Pommerenke, Wegmann, and Zemach [8, 9, 30, 31, 40]; a survey is given in Sect. 3 of [8]. The most general treatments rely on the notions of extremal length and extremal distance from the theory of conformal invariants [2, 16], but our aim here is to state results as simple as possible that contain the key factor $e^{-\pi L}$. The following result is close to Theorem 6.1 of [16], which has a constant $C=16$ and certain other differences. The reason for writing the bound in terms of the quotient $C/2\pi$ is that it simplifies the formulas of the subsequent three theorems.

Theorem 2

Let $\varOmega$ contain a finger of length $L>1$, and let $a\in \varOmega$ be a point outside the finger on one end. The harmonic measure at a of the portion $\varGamma _{\mathrm{exit}}$ of $\varGamma$ beyond the other end satisfies

$$\begin{aligned} \omega < (C/2\pi )d e^{-\pi L}, \end{aligned}$$

(7)

where C is a constant independent of $\varOmega$ and L, and d is the length of the segment(s) $B\cap \varOmega$. Numerical computations indicate that a suitable value is $C \approx 14.7$.

Proof

We argue by a sequence of inequalities $\omega \le \omega _1 \le \omega _2 \le \omega _3 \le \omega _4$, followed by further inequalities to be explained, with a Schwarz–Christoffel conformal map at the end. The sequence is summarized in Fig. 8. In each image, the point marked on the left is a and the thickly marked part of the boundary on the right is $\varGamma _{\mathrm{exit}}$. From step to step, we sometimes adjust a or $\varGamma _{\mathrm{exit}}$.

Fig. 8

Sequence of steps for the proof of Theorem 2, as explained in the text. In each diagram $\omega _j$ denotes the harmonic measure at the point a on the left of the exit arc $\varGamma _{\mathrm{exit}}$ on the right with respect to the indicated domain

For the first step, from $\omega$ to $\omega _1$, we truncate any portions of the finger that protrude beyond B, so that $\varGamma _{\mathrm{exit}}$ is now a subset of B. By a principle of monotonicity of harmonic measure, this gives $\omega \le \omega _1$. Intuitively, any Brownian path that reaches the boundary arcs of the first image must have passed through one of the boundary arcs of the second; thus the latter event must be at least as likely. Note that the length of $\varGamma _{\mathrm{exit}}$ is now exactly d.

Second, we expand any arcs of $\varGamma$ lying between arcs of $\varGamma _{\mathrm{exit}}$ to the boundary segment B, giving $\omega _1\le \omega _2$ again by monotonicity. Intuitively, enlarging the domain means that more Brownian paths are available to reach $\varGamma _{\mathrm{exit}}$ before first hitting the boundary somewhere else.

Third, we expand $\varOmega$ to be the whole exterior of the three-sided open rectangle (a doubly-connected region in the plane), giving $\omega _2 \le \omega _3$ by monotonicity once more. From here on, the domain boundary consists of six segments, three on the inside of the rectangle and three on the outside. (Logically, this step could have been combined with the last one, but for clarity it seems helpful to describe them separately.)

Fourth, any path from a to the exit arc must have a point at which it first touches the entry segment A of the rectangle. Some such points will correspond to greater probabilities than others of eventually reaching $\varGamma _{\mathrm{exit}}$. We adjust a to be a point on A that is optimal in this respect, giving $\omega _3 \le \omega _4$.

We have now reached the problem of estimating the harmonic measure $\omega _4$ of a given segment or set of segments of total length d on the inside edge B of the closed end of an $L\times 1$ open-ended rectangle at a certain point a on the open end. Now at each point along B, there will be a harmonic measure density for the point a, a continuous function along B taking positive values in the interior of B and going to zero at the endpoints because of the corners. Let $\rho _4$ denote the maximum value of this density. Since $\varGamma _{\mathrm{exit}}$ has length d, we have $\omega _4 \le d \rho _4$.

We next note that the number $\rho _4$ depends only on L (which is fixed) and the point a along the entry segment A. Its maximal value for a given L will occur when a is at the center of A, and it will be attained at the midpoint of B, which we may call b. We denote the value of the harmonic measure density for this choice of a by $\rho _5$, implying $d\rho _4 \le d\rho _5$.

At this point we have a fully prescribed geometry, an open-ended $L\times 1$ rectangle for which we want the harmonic measure density $\rho _5$ of the midpoint b of the inner closed end at the midpoint a of the open end. This number is conformally invariant, so we can determine it by a Schwarz–Christoffel conformal map g of the unit disk to the exterior of the six-segment open rectangle boundary. Specifically, if $g(0) = a$ and $g(1) = b$, then $\rho _5 = (2\,\pi |g'(1)|)^{-1}$. As $L\rightarrow \infty$, it is well known that $\rho _5$ will decrease at a rate proportional to $e^{-\pi L}$ for a map with a channel of this kind (see any of the references listed above in connection with the crowding phenomenon, or for a beautiful analysis of a special case, chapter 10 of [5]). This establishes the theorem for some constant C, and we have obtained the estimate $C\approx 14.7$ by numerical computations with the Schwarz–Christoffel Toolbox [10].

Our next result asserts that if $\varOmega$ contains a slender finger, then $|f'(z)|$ must be exponentially large for some z on the unit circle.

Theorem 3

Let $\varOmega = f(D)$ contain a finger of length $L>1$, and let $a=f(0)$ be a point outside the finger on one end. Then there is a point z with $|z|=1$ for which $|f'(z)| > C^{-1} e^{\pi L}$, where C is the same constant as in Theorem 2.

Proof

Under the assumptions of Theorem 2, the arc length of $\varGamma _{\mathrm{exit}}$ is at least d and its harmonic measure at a is $<(C/2\pi )d e^{-\pi L}$. Dividing these quantities, we see that the average harmonic measure density along $\varGamma _{\mathrm{exit}}$ is $< (C/2\pi ) e^{-\pi L}$. Thus there are points along $\varGamma _{\mathrm{exit}}$ for which the harmonic measure density is $< (C/2\pi ) e^{-\pi L}$. If z is the preimage of such a point under f, then by conformal invariance, $|f'(z)| > C^{-1} e^{\pi L}$, as required.

Theorems 2 and 3 have identified the crucial exponential factor $e^{\pi L}$. We now apply this result to derive two consequences with implications for numerical approximation of conformal maps.

Define the radius of univalence of f, denoted by r, as the supremum of all radii of open disks about $z=0$ to which f can be continued to a univalent (i.e., one-to-one) analytic function. Our first consequence of Theorems 2 and 3 asserts that if f has a finger of length L, then r can be no bigger than $1 + O(e^{-\pi L})$. In typical cases, what is going on here is that if $\varOmega$ contains a finger, then f has singularities exponentially close to the unit circle. The precise situation is that f need not actually have singularities (after all, f can be approximated by polynomials), but at least it must lose univalence.

Theorem 4

Let $\varOmega = f(D)$ contain a finger of length $L>1$, let $a=f(0)$ be a point outside the finger on one end, and set $R = \sup _{w\in \varGamma } |w-f(0)|$. Then the radius of univalence of f satisfies

$$\begin{aligned} r < 1 + 4 R Ce^{-\pi L}, \end{aligned}$$

(8)

where C is the same constant as in Theorem 2, assuming $4R Ce^{-\pi L} < 1$.

Proof

Among the results of univalent function theory are certain distortion theorems [2, 16]. Let h be a univalent function in the unit disk with $h(0) = 0$ and $h'(0) = 1$. Then it is shown in Theorem I.4.5 of [16] that for any z with $|z|<1$,

$$\begin{aligned} |h'(z)| \le {(1+|z|) |h(z)|\over |z| (1-|z|)}. \end{aligned}$$

(9)

To apply this to our function f with radius of univalence r, define

$$\begin{aligned} h(z) = {f(rz) - f(0) \over r f'(0)}, \end{aligned}$$

(10)

which implies $h'(z) = f'(rz)/f'(0)$. Then applying (9) at a point z with $|z|=r^{-1}$, so that rz is on the unit circle, gives

$$\begin{aligned} \left| {f'(rz) \over f'(0)}\right| \le {(1+r^{-1}) |h(z)|\over r^{-1}-r^{-2}}, \end{aligned}$$

(11)

or by (10),

$$\begin{aligned} |f'(rz)| \le {(1+r^{-1}) |f(rz)-f(0)|\over 1-r^{-1}}. \end{aligned}$$

(12)

Since $r>1$ and $|f(rz)-f(0)|\le R$, this gives us

$$\begin{aligned} |f'(rz)| \le { 2R\over 1-r^{-1}}. \end{aligned}$$

(13)

Now assume that rz is one of the points for which Theorem 3 gives the bound $|f'(rz)| > M = C^{-1}e^{\pi L}$. Then (13) becomes $M < 2R/(1-r^{-1})$, which is equivalent to

$$\begin{aligned} r < {1\over 1 - 2R/M} \end{aligned}$$

(14)

since the assumptions $4R Ce^{-\pi L} < 1$ and $L>1$ imply that $2R/M \le 1/2$, so that $1-2R/M$ is positive. Since $(1-\varepsilon )^{-1}\le 1+2 \varepsilon$ whenever $\varepsilon \le 1/2$, (14) implies $r<1+4 R/M = 1+4 R Ce^{-\pi L}$ as required.

Our final consequence of Theorem 2 is that if a polynomial is a good approximation to the conformal map f, then its degree must be on the order of $e^{\pi L}$ or larger. For a finger of length 6, say, one must expect polynomial degrees in the millions. In the following statement, the “end segment B” refers to the same end of the rectangle illustrated in Fig. 7 and discussed in the proof of Theorem 2. Note that the definitions of R here and in the last theorem are slightly different. For simplicity, our statement assumes that $\varGamma _{\mathrm{exit}}$ consists of a single arc.

Theorem 5

Let $\varOmega = f(D)$ contain a finger of length $L>1$, let $a=f(0)$ be a point outside the finger on one end, and set $R = \sup _{w\in \varGamma } |w| \ge 1$. Assume the protrusion of $\varOmega$ beyond the other end segment B delimits just a single segment of B of length d. If p is a polynomial satisfying $\Vert f-p\Vert \le d/3$ on the unit disk, then the degree n of p satisfies

$$\begin{aligned} n > {e^{\pi L}\over 4 R C}, \end{aligned}$$

(15)

where C is the same constant as in Theorem 2.

Proof

The assumptions imply $\Vert p\Vert \le R + d/3$ on the unit disk, so by an inequality due to Bernstein [24, Cor. (6,4)], $\Vert p'(z)\Vert \le n (R+d/3)$. On the other hand, as we shall explain in the next paragraph, the assumptions together with Theorem 2 imply that for some z with $|z|=1$,

$$\begin{aligned} | p'(z)|\ge C^{-1} e^{\pi L}/ 3. \end{aligned}$$

(16)

Combining these bounds gives $n > C^{-1} e^{\pi L}/(3(R+d/3))$. With $d\le 1$, $R\ge 1$, and $L\ge 1$, this inequality implies (15).

To establish (16), let $w_1 = f(z_1)$ and $w_2 = f(z_2)$ be the endpoints of the segment of B indicated in the theorem statement, with $|w_2-w_1| = d$ and $|z_1|=|z_2|=1$. Since $\Vert f-p\Vert \le d/3$, we have $| p(z_2)- p(z_1)| \ge d/3$. To justify (16), it suffices to show $|\arg (z_2)-\arg (z_1)| \le d Ce^{-\pi L}$. Since $|\arg (z_2)-\arg (z_1)|$ is $2\,\pi$ times the harmonic measure at f(0) of the protrusion of $\varGamma$, this follows from Theorem 2.

5 Conformal maps of regions with analytic boundaries

Fig. 9

Maps of three smooth domains to the unit disk computed with the Kerzman–Stein integral equation, following Caldwell, Li, and Greenbaum [6, 21, 22]. Although the boundaries are analytic, these maps have singularities nearby, as explained by the theorems of the last section, and these are reflected in the poles of the adaptively determined rational approximations. Specifically, the distances of the closest poles to the unit disk in the plots of the second column are about 0.0003, 0.03, and 0.007, respectively

The prediction implicit in the last section is that even for regions with analytic boundaries, rational approximations of conformal maps will tend to have poles clustering nearby. This prediction is borne out by Figs. 9 and 10, which show conformal maps of five regions with analytic boundaries. Qualitatively speaking, these images look little different from those of section 3. The computations were done by a numerical implementation of the Kerzman–Stein integral equation in Chebfun using codes developed by Caldwell, Li, and Greenbaum [6, 21, 22], with a discretization by 800 points along the boundary. Unlike the Schwarz–Christoffel formula, the Kerzman–Stein equation constructs the mapping f in the direction from the problem domain to the unit disk. As before, one of the attractions of rational approximations is that they give representations of $f^{-1}$ as well as f.

The images in Fig. 9 show an ellipse with semiaxes 1 and 0.25, a rounded “snowflake” defined in polar coordinates by $r = 0.8 + 0.14\cos (6 \theta )$, and a shape with a smooth random boundary defined in Chebfun by setting $r(\theta )$ equal to 0.8+0.16*randnfun(0.6,[0 2*pi],’trig’) [14]. In each case the poles of the AAA rational approximation $r\approx f$ are shown in the left panel and those of $s\approx f^{-1}$ are shown in the right panel. The degrees of r and s are listed in the titles along with what we call the back-and-forth error, defined as the maximum of $|w_j - r(s(w_j))|$ over the grid of points $w_j$ plotted in the disk. For these computations we loosened the AAA tolerance from $10^{-7}$ to $10^{-6}$.

Fig. 10

Maps of two more smooth domains. The “bean” originates with Reichel in 1981 [32] and the “blade” with Ellacott in 1978 [13]. The poles of the rational approximations match only roughly the poles and branch points of the exact maps. The distances of the closest poles to the unit disk in the second column are about 0.05 and $1.4\times 10^{-6}$

As a further indication of the speed of rational representations of conformal maps, suppose that for the region in the bottom row of Fig. 9, instead of a grid of about $10^3$ points in the disk (the exact number is 1264), we increase the number to about $10^6$ and again compute $|w_j-r(s(w_j))|$, thus applying a degree 55 rational function and also a degree 44 rational function one million times each. On our laptop running MATLAB, the total time is 1.7 s. The maximum back-and-forth error is $1.7\times 10^{-6}$, and the rms back-and-forth error is $8.7\times 10^{-8}$.

Figure 10 shows two conformal maps of regions with smooth boundaries taken from the classical literature of numerical conformal mapping. The “bean” in the first row, defined by the boundary map

$$\begin{aligned} 0.45\cos \theta + 0.225\cos (2\theta )-0.225 + i [ 0.7875\sin \theta + 0.225\sin (2\theta )-0.045\sin (4\theta )] \end{aligned}$$

for $\theta \in [ 0,2\pi ]$, was introduced by Reichel in the technical report version of [32] and considered also by Papamichael et al. in [29]. The “blade” in the second row, defined by the boundary map

$$\begin{aligned} 2\cos \theta + i(\sin \theta + 2\cos ^3\theta ), \end{aligned}$$

was introduced by Ellacott [13] and considered also in [29, 32]. Both of these mapping problems were discussed in [29] as examples in which the structure of nearby poles and other singularities might be analyzed and exploited for numerical approximation, just the opposite of the point of view of the present paper. The exact bean map has poles at $\zeta _1 \approx -~0.650$ and $\zeta _2\approx 1.311$, but the rational approximation r does not approximate these closely. On the left we see five poles, not one, with clear asymmetry about the real axis; as the authors of [29] point out, the map additionally has square root branch points at $-~0.566 \pm 0.068 i$. As for $\zeta _2$, to the right of the bean, the approximation r shows three poles here, not a single pole. The pole near the real axis lies at $1.200 + 0.079 i$.

The example of the blade region likewise illustrates that exact singularities are only a rough guide to what may be effective for rational approximation. Here Papamichael, et al. show that the exact map has simple poles at $\pm ~2.885 \mp 1.584 i$, and these are matched to two digits of accuracy by poles of r at $2.908 - 1.557 i$ and $-~2.889 +1.571 i$. As with the bean region, on the other hand, the portion of the figure with a concave boundary segment is complicated by simple poles at $\pm ~0.455 \pm 1.902 i$ with square root branch points nearby. These are matched only roughly by poles of r at $0.475 + 1.813 i$ and $-~0.475 - 1.787 i$.

6 Accuracy

In the numerical experiments of Sects. 3 and 5, our rational approximations readily attain 7–8 digits of accuracy almost everywhere in the domains, but fall to 2–4 digits close to certain boundary points. Let us call this the “corner effect” (though domains with smooth boundaries are not immune). This seems disturbing, but as we shall now explain, it is actually a limitation not of our rational approximation method, but of the accuracy of the conformal mapping data we have been able to work with.

Fig. 11

Error contours $|f(z)-r(z)| = 10^{-8},10^{-7},10^{-6},10^{-5},10^{-4}$ for the conformal map of Fig. 1 of the unit disk onto an L-shaped region. On the left, mainly just the $10^{-8}$ contour is visible, indicating that the error is ${<}~10^{-8}$ in $90\%$ of the disk and ${<}~10^{-7}$ in most of the remainder. Very close to the vertices, however, the accuracy degrades, as shown by the closeup on the right near the prevertex that maps to $w = 0$. On this scale the $10^{-8}$ contour is not visible (apart from a small bubble on the left) and we see contours $10^{-7}$, $10^{-6}$, $10^{-5}$, and $10^{-4}$ as the singular point is approached. Thus, in a portion of the disk which has an area on the order of $10^{-6}$, the accuracy falls to 3–4 digits. This explains the max error value $2.6\times 10^{-3}$ in the upper right panel of Fig. 1

First we present a figure to illustrate the effect. Fig. 1 showed a map f of the unit disk onto an L-shaped region, and the upper-left image of that figure plotted the unit disk together with the poles of the rational approximation $r\approx f$. For the same problem, Fig. 11 plots contours of the error $|f(z)-r(z)|$. As explained in the caption, the contours confirm that the error is smaller than $10^{-7}$ almost everywhere in the disk but much worse near the prevertices.

The corner effect does not result from inherent limitations in the accuracy of rational approximations, since the root-exponential convergence is very fast. Our examples have shown that with ${\approx }~10$ poles near each singularity, rational functions are well capable of $10^{-3}$ accuracy, and there is no reason of approximation theory why this could not be improved to $10^{-6}$ with ${\approx }~40$ poles near each singularity.

The corner effect also does not result from limitations of the AAA algorithm. The algorithm does not produce an optimal approximant, but our experience shows that it reliably comes within one or two orders of magnitude of optimality on the discrete point set it works with.

Instead, the corner effect is a consequence of inaccurate boundary data. As we now explain, to achieve an approximation r with $\Vert r-f\Vert = O(\varepsilon )$ (the maximum norm on the domain) everywhere, it is necessary to sample the boundary map at distances $O(\varepsilon )$ from prevertices or vertices with an accuracy of $o(\varepsilon )$. (The “O” and “o” symbols here are heuristic, not precisely defined.) Partly because of the extreme ill-conditioning of conformal maps near corners, as well as in other contexts, and partly because of additional problems of accuracy of the SC Toolbox very near corners, this is hard to achieve when $\varepsilon$ is much less than $10^{-4}$.

Fig. 12

On the left, successful AAA approximation near a $z^{1/4}$ singularity. On the right, the values $z_j$ have been perturbed on the scale of $10^{-12}$, and the interpolant loses accuracy near the corner. Moreover, it now has poles inside the approximation domain, implying that even though the error is still very small almost everywhere in the domain, its maximum is $\infty$

Figure 12 illustrates the situation. The problem considered here is the map $w = f(z) = z^{1/4}$ of the right half-plane onto the wedge of angle $\pi /4$ about the positive real axis. In the left panel of the figure, this function has been approximated by the AAA algorithm with tolerance $10^{-7}$ based on data at 200 points $z_j$ fixed so that the images $f(z_j)$ are equispaced along the two sides of the wedge near $w=0$ out to a distance 0.1. Thus the points $z_j$ themselves lie in the imaginary interval $[-10^{-4} i, 10^{-4} i]$, and the two values closest to 0 are $\pm ~10^{-12} i$. The black dots in the figure are the data, and the blue curve is the AAA approximant. The behavior we see represents just what one would hope for. The curve closely matches the data and interpolates smoothly in-between.

This left panel of Fig. 12 reflects a rational approximation with a maximal error on the order of $10^{-4}$. To improve this to a level $O(\varepsilon )$ for some $\varepsilon \ll 10^{-4}$, it is clear that the mesh will have to be refined so that the data values near $w=0$ have spacing $O(\varepsilon )$. This means the corresponding z values will have minimal spacing $O(\varepsilon ^4)$. And here is where we see the difficulty in accuracy near corners. In 16-digit floating point arithmetic, spacings on the order of $\varepsilon ^4$ will not be accurately computable for $\varepsilon \ll 1$. To illustrate this effect, the right panel shows the same computation again, except that instead of data values $f(z_j)$, the values are taken to be $f({\tilde{z}}_j)$, where ${\tilde{z}}_j$ is $z_j$ plus a random complex perturbation of order $10^{-12}$. Now the rational approximation, while still excellent away from the vertex, has quite erroneous behavior nearby.

Based on these curves alone, one might guess that the approximation in the right panel of Fig. 12 was, say, ten times less accurate than for the one on the left. However, the loop in the curve is a hint that something more fundamental is going wrong. In fact, this rational function has poles in the approximation domain—three of them, as it happens, with real parts on the order of $10^{-8}$ and residues on the order of $10^{-7}$. From the point of view of the original problem, these poles are spurious; they have been introduced by the non-analytic perturbation of the fitting data. They will have negligible effect away from the vertex, but near the vertex, there is a portion of the approximation domain in which the error is infinite. One might not notice this in an application, but it can hardly be regarded as acceptable.

We believe that the inaccuracy of available boundary data, often due to the ill-conditioning of the conformal map, is usually what limits the accuracy of AAA approximants. If one could work with perfect data on grids clustered very finely near singularities, the rational approximants would have no trouble, but when the data are imperfect, one loses accuracy correspondingly. The SC Toolbox, unfortunately, seems to have additional difficulties near vertices that make the situation somewhat worse than what is inevitable due to ill-conditioning alone.

One might imagine that conformal maps of smooth domains, since there are no singularities on the boundary, would be exempt from these accuracy limitations. However, as we showed in Sect. 4, this is not the case since there are often singularities exponentially close to the boundary.

7 Conclusion

In this paper we established theorems concerning the power of rational functions in approximating conformal maps near singularities (Theorem 1) and the prevalence of singularities and weakness of polynomial approximations for such maps (Theorems 2–5). We then showed how effective AAA rational approximations are in realizing this potential to represent conformal maps far more efficiently than is usual. Their application is fast and easy to apply, capturing singularities to good accuracy without the need for any analysis. In a few seconds one typically gets a representation of both a conformal map f and its inverse $f^{-1}$ that can be applied to map points back and forth in microseconds on a laptop. The main complication, as with most computing with rational functions, it that it is advisable to monitor whether spurious poles have appeared in the region of approximation. If so, they can usually be removed by loosening the convergence tolerance, improving the accuracy of the data, or refining the grid.

Our approximations are rational functions of type (n, n), typically with $10\le n\le 100$. To get comparable accuracy with polynomial approximations, one would often need degrees in the millions.

Our discussion has concerned simply connected regions, but the same methods apply to conformal maps of multiply connected regions [3], and indeed, to analytic and meromorphic functions more generally.