Abstract
In this paper we develop the a priori analysis of a mixed finite element method for the coupling of fluid flow with porous media flow. Flows are governed by the Navier–Stokes and Darcy equations, respectively, and the corresponding transmission conditions are given by mass conservation, balance of normal forces, and the Beavers-Joseph-Saffman law. We consider the standard mixed formulation in the Navier–Stokes domain and the dual-mixed one in the Darcy region, which yields the introduction of the trace of the porous medium pressure as a suitable Lagrange multiplier. The finite element subspaces defining the discrete formulation employ Bernardi-Raugel and Raviart-Thomas elements for the velocities, piecewise constants for the pressures, and continuous piecewise linear elements for the Lagrange multiplier. We show stability, convergence, and a priori error estimates for the associated Galerkin scheme. Finally, several numerical results illustrating the good performance of the method and confirming the theoretical rates of convergence are reported.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The devising of suitable numerical methods for the coupling of fluid flow with porous media flow has become a very active research area during the last decades, mostly due to the relevance of this physical process for a variety of phenomena in medicine (filtration process of blood through vessel walls), geoscience (flow of a river and its riverbed) and industry (oil extraction process), to name a few.
One of the most studied models for this type of phenomena is the Stokes-Darcy coupled system, which consists in a set of equations where the Stokes model (for the free fluid flow) is coupled with the Darcy model (for the fluid flow in the porous medium) through a set of interface conditions, namely, continuity of the normal velocities (mass conservation), balance of normal forces, and the Beavers-Joseph-Saffman law. So far, several numerical methods have been developed to approximate the solution of the Stokes-Darcy coupled problem (see for instance [7, 13, 14, 18–20, 22, 26–28, 32, 36, 37, 39–41]), most of them based on appropriate combinations of stable elements for both media. In this direction, the first theoretical results go back to [39] and [20]. In [20] the authors introduce an iterative subdomain method employing the standard velocity-pressure formulation for the Stokes equation and the primal one in the Darcy domain, whereas in [39] the authors apply the velocity-pressure formulation in the free fluid domain and the dual-mixed velocity-pressure formulation in the porous medium, yielding the introduction of the trace of the porous medium pressure on the interface as an additional unknown. Next, in [26] and [28] new mixed finite element discretizations of the variational formulation from [39] have been introduced and analyzed. The stability of a specific Galerkin method, employing the Bernardi-Raugel and Raviart-Thomas elements for the free fluid and the fluid in the porous medium, respectively, is the main result in [26]. The results from [26] are improved in [28] where it is shown that the use of any pair of stable Stokes and Darcy elements implies the well-posedness of the Stokes-Darcy Galerkin scheme. In particular, this includes Hood-Taylor, Bernardi-Raugel, and MINI element for the Stokes region, and Raviart-Thomas of any order for the Darcy domain. The analysis in [28] hinges on the fact that the linear operator defining the continuous variational formulation is given by a compact perturbation of an invertible linear mapping.
The purpose of the present work is to contribute to the development of new numerical methods for the coupling of fluid flow with porous media flow by extending the approach in [26] to the Navier–Stokes/Darcy coupled problem. Up to the authors’ knowledge, the first works in developing numerical methods for the Navier–Stokes/Darcy coupled problem are [6, 31]. In [31] the authors introduce and analyze a DG discretization for the nonlinear coupled problem considering the usual nonsymmetric interior penalty Galerkin (NIPG), symmetric interior penalty Galerkin (SIPG), and incomplete interior penalty Galerkin (IIPG) bilinear forms for the discretization of the Laplacian in both media and the upwind Lesaint-Raviart discretization of the convective term in the free fluid domain. In [6] the authors extend the approach in [20] (see also [18]) and introduce an iterative subdomain method employing the velocity-pressure formulation for the Navier–Stokes equation and the primal one for the Darcy equation. They approximate the coupled nonlinear problem using conformal finite elements in both media and study the convergence properties of Newton- like iterative methods for solving this problem. We point out that, differently from [26, 39], the approach adopted in [6, 31] avoids the introduction of Lagrange multipliers to impose the continuity of the normal velocity of the fluid through the interface. Indeed, this condition is imposed weakly using the primal formulation of the Darcy problem for the sole pressure unknown.
According to the above discussion, in this paper we extend the analysis developed in [26] and study a conforming mixed finite element method for the Navier–Stokes/Darcy coupled problem. We consider the standard velocity-pressure formulation for the Navier–Stokes equation and the dual-mixed formulation for the Darcy equation, which yields the velocity and the pressure of the fluid in both media as the main unknowns of the coupled system. Since one of the interface conditions becomes essential, we proceed similarly to [26, 39] and incorporate the trace of the porous medium pressure as an additional unknown. As the coupled system is nonlinear (due to the convective term in the free fluid region), to analyze the continuous problem we first linearize it by considering the Oseen problem in the free fluid domain. The linearized problem is then analyzed by means of the classical Babuška-Brezzi theory, as it has been done for the Stokes-Darcy coupling in [26]. Then, we associate to the nonlinear coupling an equivalent fixed point problem based on the aforementioned linearization, and we establish existence and uniqueness of a fixed point using, respectively, Schauder’s and Banach’s fixed point theorems. Using similar arguments (but applying Brower’s fixed point theorem instead of Shauder’s for the existence result) we prove the well-posedness of the discrete problem for a specific choice of discrete spaces. More precisely, we consider Bernardi-Raugel elements for the velocity in the free fluid region, Raviart-Thomas elements of lowest order for the filtration velocity in the porous media, piecewise constants with null mean value for the pressures, and continuous piecewise linear elements for the Lagrange multiplier on the interface. It is important to remark that the interpolation properties of the Raviart-Thomas and Bernardi-Raugel operators, mainly those holding on the edges of the triangulations (see Eqs. (3.11), (4.2), and (4.7) in [26]), play a key role in the proof of one of the required discrete inf-sup conditions. We point out here that the extension of the present approach to arbitrary finite element subspaces, by using a classical result on projection methods for Fredholm operators of index zero as it has been done in [28] for the Stokes-Darcy coupling, is not straightforward since the operator defining the continuous variational formulation of the Navier–Stokes/Darcy system is nonlinear. This is subject of an ongoing work and remains as an open problem.
The rest of this paper is organized as follows. In Sect. 2 we introduce the continuous coupled problem, its weak formulation, the corresponding variational system and we prove its well-posedness. In Sect. 3 we define the Galerkin scheme, we prove its well-posedness and derive the corresponding Cea’s estimate and rate of convergence. Finally, several numerical examples illustrating the performance of the method and confirming the theoretical order of convergence are reported in Sect. 4.
2 The continuous problem
2.1 Statement of the model problem
For simplicity of exposition we set the problem in \(\mathbb {R}^2\). However, our study can be extended to the 3D case with few modifications that we will point out in the paper.
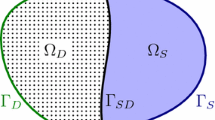
In order to describe the geometry, we let \(\Omega _{S}\) and \(\Omega _\mathrm {D}\) be two bounded and simply connected polygonal domains in \(\mathbb {R}^2\) such that \(\partial \Omega _{S}\,\cap \,\partial \Omega _\mathrm {D}\,=\, \Sigma \ne \emptyset \) and \(\Omega _{S}\,\cap \, \Omega _\mathrm {D}\,=\,\emptyset \). Then, let \(\Gamma _{S}\,:=\, \partial \Omega _{S}\backslash {\bar{\Sigma }}\), \(\Gamma _\mathrm {D}\,:=\,\partial \Omega _\mathrm {D}\backslash {\bar{\Sigma }}\), and denote by \(\mathbf n\) the unit normal vector on the boundaries, which is chosen pointing outward from \(\Omega _{S}\cup \Sigma \cup \Omega _\mathrm {D}\) and \(\Omega _{S}\) (and hence inward to \(\Omega _\mathrm {D}\) when seen on \(\Sigma \)). On \(\Sigma \) we also consider a unit tangent vector \(\mathbf t\) (see Fig. 1).
The free/porous-medium flow problem can be modelled by coupling the Navier–Stokes and the Darcy equations. More precisely, in the free fluid domain \(\Omega _{S}\), the motion of the fluid can be described by the incompressible Navier–Stokes equations:
where \(\mu >0\) is the dynamic viscosity of the fluid, \(\rho \) is its density, \(\mathbf {u}_{S}\) is the fluid velocity, \(p_{S}\) the pressure, \({\varvec{\sigma }}_{S}\) is the Cauchy stress tensor, \(\mathbf {I}\) is the \(2\times 2\) identity matrix, \(\mathbf {f}_{S}\) is a given external force, \(\mathbf {div}\,\) is the usual divergence operator \(\mathrm {div}\,\) acting row-wise on each tensor, and \(\mathbf e\) is the strain rate tensor:
where the superscript \(^t\) denotes transposition.
In the porous medium \(\Omega _\mathrm {D}\) we consider the following Darcy model:
where \(\mathbf {u}_\mathrm {D}\) is the Darcy velocity (specific discharge), \(p_\mathrm {D}\) is the pressure, and \(\mathbf {K}\in \mathbb {L}^\infty (\Omega _\mathrm {D})\) is a symmetric and uniformly positive definite tensor in \(\Omega _\mathrm {D}\) representing the intrinsic permeability \(\varvec{\kappa }\) of the porous medium divided by the dynamic viscosity \(\mu \) of the fluid. Throughout the paper we assume that there exists \(C > 0\) such that
for almost all \(x\in \Omega _\mathrm {D}\), and for all \(\varvec{\xi }\in \mathbb {R}^2\). Finally, \(\mathbf {f}_\mathrm {D}\) is a given external force that accounts for gravity, i.e. \(\mathbf {f}_\mathrm {D}= \rho \mathbf {g}\) where \(\rho \) is the density of the fluid and \(\mathbf {g}\) is the gravity acceleration.
The transmission conditions that couple the Navier–Stokes and the Darcy models through the interface \(\Sigma \) are given by
where \(\alpha _d\) is a dimensionless constant which depends only on the geometrical characteristics of the porous medium (see [8]).
The first condition in (3) is a consequence of the incompressibility of the fluid and of the conservation of mass across \(\Sigma \). The second transmission condition on \(\Sigma \) can be decomposed, at least formally, into its normal and tangential components as follows:
The first equation in (4) corresponds to the balance of normal forces [19, 31, 39], whereas the second one is known as the Beavers-Joseph-Saffman law, which establishes that the slip velocity along \(\Sigma \) is proportional to the shear stress along \(\Sigma \) (assuming also, based on experimental evidence, that \(\mathbf {u}_\mathrm {D}\cdot \mathbf {t}\) is negligible). We refer to [8, 35, 45] for further details on this interface condition.
To complete the definition of the Navier–Stokes/Darcy problem, we impose the boundary conditions
Remark 1
Other physically meaningful boundary conditions can be considered for the Navier–Stokes/Darcy problem as discussed, e.g., in [18]. For example one could impose natural boundary conditions to both subproblems on non-empty subsets of \(\Gamma _{S}\) and \(\Gamma _\mathrm {D}\). More precisely, one could replace (5) by the following alternative set of boundary conditions:
where \(\Gamma _{S}^d \cup \Gamma _{S}^n = \Gamma _{S}\), \(\Gamma _\mathrm {D}^d \cup \Gamma _\mathrm {D}^n = \Gamma _\mathrm {D}\), and \(\Gamma _{S}^d \cap \Sigma = \emptyset \), \(\Gamma _\mathrm {D}^n \cap \Sigma = \emptyset \).
The conforming FE discretization studied in this work can be applied also when (6) are used. However, in the latter case the analysis of the method requires introducing several technicalities in Sects. 2.3.1, 2.3.2, 3.1.1 and 3.1.2 that do not contribute to the main idea. Thus, for the sake of simplicity, in the rest of the paper we consider the boundary conditions (5).
2.2 The variational formulation
Let us first introduce some notation. Given \(\star \in \{{S},\mathrm {D}\}\), we denote
where, given two arbitrary tensors \(\varvec{\sigma }\) and \(\varvec{\tau }\), \(\,\,\varvec{\sigma } : \varvec{\tau }\,=\,\mathrm {tr}(\varvec{\sigma }^t\varvec{\tau })\,=\,\sum _{i,j=1}^2 \sigma _{ij}\tau _{ij}\).
We use the standard terminology for Lebesgue and Sobolev spaces. In addition, if \(\mathcal O\) is a domain, given and \(r\in \mathbb {R}\) and \(p\in [1,\infty ]\), we define \(\mathbf {H}^r(\mathcal {O})\,:=\, [H^r(\mathcal O)]^2\) and \(\mathbf L^p(\mathcal O):= [L^p(\mathcal O)]^2\). For \(r=0\) we write \(\mathbf L^2(\mathcal O)\) and \(L^2(\Gamma )\) instead of \(\mathbf H^0(\mathcal O)\) and \(H^0(\Gamma )\), respectively, where \(\Gamma \) is a closed Lipschitz curve. The corresponding norms are denoted by \(\Vert \cdot \Vert _{r,\mathcal O}\) (for \(H^r(\mathcal O)\) and \(\mathbf H^r(\mathcal O)\)), \(\Vert \cdot \Vert _{r,\Gamma }\) (for \(H^r(\Gamma )\)) and \(\Vert \cdot \Vert _{L^p(\mathcal O)}\) (if \(p\ne 2\)). Also, the Hilbert space
with norm \(\Vert \cdot \Vert _{\mathrm {div}\,,\mathcal O}\), is standard in the realm of mixed problems (see, e.g. [11]).
On the other hand, the symbol for the \(L^2(\Gamma )\) inner product
will also be employed for their respective extension as the duality product \(H^{-1/2}(\Gamma )\times H^{1/2}(\Gamma )\). In addition, given two Hilbert spaces \(H_1\) and \(H_2\), the product space \(H_1\times H_2\) will be endowed with the norm \(\Vert \cdot \Vert _{H_1\times H_2}=\Vert \cdot \Vert _{H_1}+\Vert \cdot \Vert _{H_2}\). Hereafter, given a non-negative integer k and a subset S of \(\mathbb {R}^2\), ¶\(_l(S)\) stands for the space of polynomials defined on S of degree \(\le l\). Finally, we employ \(\mathbf {0}\) as a generic null vector, and use C and c, with or without subscripts, bars, tildes or hats, to denote generic positive constants independent of the discretization parameters, which may take different values at different places.
The unknowns in the variational formulation of the Navier–Stokes/Darcy problem and the corresponding spaces will be:
where
In addition, analogously to [26] we need to define a further unknown on the coupling boundary:
Note that, in principle, the space for \(p_\mathrm {D}\) does not allow enough regularity for the trace \(\lambda \) to exist. However, the solution of (2) has the pressure in \(H^1(\Omega _\mathrm {D})\).
Next, for the derivation of the weak formulation of (1)–(3), (5) we write \(\Omega \,:=\,\Omega _{S}\cup \Sigma \cup \Omega _\mathrm {D}\), we define the space
and we group the unknowns and spaces as follows:
where \(p := p_{S}\chi _{\Omega _{S}}+p_\mathrm {D}\chi _{\Omega _\mathrm {D}}\), with \(\chi _{\Omega _\star }\) being the characteristic function:
for \(\star \in \{\mathrm {D},{S}\}\).
Hence, we proceed as in [26] (see also [39] for a previous similar approach) to find the mixed variational formulation: Find \((\mathbf {u},(p,\lambda ))=((\mathbf {u}_{S},\mathbf {u}_\mathrm {D}),(p,\lambda ))\,\in \,\mathbf {H}\times \mathbf {Q}\), such that
where \(\mathbf {a}:\mathbf {H}^1_{\Gamma _{S}}(\Omega _{S})\times (\mathbf {H}\times \mathbf {H})\rightarrow \mathbb {R}\) and \(\mathbf {b}:\mathbf {H}\times \mathbf {Q}\rightarrow \mathbb {R}\) are the forms defined by
with
and \(\mathbf {f}(\mathbf {v})\) is the linear functional \(\mathbf {f}: \mathbf {H}\rightarrow \mathbb {R}\) defined as
Let us observe that the forms \(A_{S}\), \(A_\mathrm {D}\), \(O_{S}\) and \(\mathbf {b}\) are continuous:
where \(C_{sob}\) is the continuity constant of the Sobolev embedding from \(H^1(\Omega _{S})\) into \(L^4(\Omega _{S})\). In addition, the continuity of the functional \(\mathbf {f}\) is straightforward:
We end this section by observing that owing to the well known Korn and Poincaré inequalities (see, e.g., [21]) and the fact that \(\mathbf {K}^{-1}\) is symmetric and positive definite, we easily obtain that there exist constants \(\alpha _{S},\,\alpha _\mathrm {D}>0\), depending only on \(\Omega _{S}\) and the tensor \(\mathbf {K}\), respectively, such that
for all \(\mathbf {v}:=(\mathbf {v}_{S},\mathbf {v}_\mathrm {D})\in \mathbf {H}\).
2.3 The Oseen-Darcy coupled problem
In this section we study the well-posedness of the linearized version of problem (8): Given \(\mathbf {w}_{S}\in \mathbf {H}_{\Gamma _{S}}^1(\Omega _{S})\), with \(\mathrm {div}\,\mathbf {w}_{S}=0\) in \(\Omega _{S}\), find \((\mathbf {u},(p,\lambda ))\,\in \,\mathbf {H}\times \mathbf {Q}\) such that
which corresponds to the variational formulation of the Oseen-Darcy coupled problem. Having studied the well-posedness of problem (12), in what follows we will be able to reformulate (8) as an equivalent fixed-point problem, and as a result, we will apply Shauder’s fixed point theorem to prove the existence of the solution of (8), and Banach’s fixed point theorem to establish its uniqueness.
Since the structure of problem (12) is similar to the one studied in [26], in the forthcoming analysis we proceed similarly to [26, Sect. 2] to prove its well-posedness, making use of the classical Babuška-Brezzi theory (see [10]). However, since the boundary conditions differ from the ones in [26], we need to adapt the analysis by using the techniques in [29], reason why we first introduce useful technical results and further notations.
2.3.1 Preliminaries
Here we follow [29] to recall some preliminary results concerning boundary conditions and extension operators. Given \(\mathbf {v}_\mathrm {D}\,\in \,{\mathbf {H}_{\Gamma _\mathrm {D}}(\mathrm{div};\Omega _\mathrm {D})}\), the boundary condition \(\mathbf {v}_\mathrm {D}\cdot \mathbf n\,=\,0\) on \(\Gamma _\mathrm {D}\) means
where \(\left<\cdot ,\cdot \right>_{\partial \Omega _\mathrm {D}}\) stands for the usual duality pairing between \(H^{-1/2}(\partial \Omega _\mathrm {D})\) and \(H^{1/2}(\partial \Omega _\mathrm {D})\) with respect to the \(L^2(\partial \Omega _\mathrm {D})\)-inner product, \(E_{0,\mathrm {D}} : H^{1/2}(\Gamma _\mathrm {D}) \rightarrow L^2(\partial \Omega _\mathrm {D})\) is the extension operator defined by
and
endowed with the norm \(\Vert \zeta \Vert _{1/2,00,\Gamma _\mathrm {D}}\,:=\,\Vert E_{0,\mathrm {D}}(\zeta )\Vert _{1/2,\partial \Omega _\mathrm {D}}\).
As a consequence, it is not difficult to prove (see e.g., Sect. 2 in [22]) that the restriction of \(\mathbf {v}_\mathrm {D}\cdot \mathbf n\) to \(\Sigma \) can be identified with an element of \(H^{-1/2}(\Sigma )\), namely
where \(E_\mathrm {D}: {H^{1/2}(\Sigma )}\rightarrow H^{1/2}(\partial \Omega _\mathrm {D})\) is any bounded extension operator. In particular, given \(\xi \,\in \,{H^{1/2}(\Sigma )}\), one could define \(E_\mathrm {D}(\xi ) \,:=\, z|_{\partial \Omega _\mathrm {D}}\), where \(z \,\in \, H^1(\Omega _\mathrm {D})\) is the unique solution of the boundary value problem: \(\,\,\Delta z\,=\,0{\quad \hbox {in}\quad }\Omega _\mathrm {D}, \quad z\,=\,\xi {\quad \hbox {on}\quad }\Sigma , \quad \nabla z\cdot \mathbf n\,=\, 0{\quad \hbox {on}\quad }\Gamma _\mathrm {D}\). In addition, one can show (see [22, Lemma 2.2]) that for all \(\psi \,\in \, H^{1/2}(\partial \Omega _\mathrm {D})\), there exist unique elements \(\psi _{\Sigma }\,\in \,{H^{1/2}(\Sigma )}\) and \(\psi _{\Gamma _\mathrm {D}}\,\in \, H^{1/2}_{00}(\Gamma _\mathrm {D})\) such that
and
Finally we observe that, since \(H^{1/2}(\partial \Omega _{S})\) is continuously embedded into \(L^4 (\partial \Omega _{S})\) and the trace operator is continuous, the following inequality holds:
for all \(\mathbf {v}_{S}\in \mathbf {H}^1_{\Gamma _{S}}(\Omega _{S})\), where \(C_{sob,\Sigma }\) is the continuity constant of the Sobolev embedding from \(H^{1/2}(\Sigma )\) into \(L^4(\Sigma )\).
2.3.2 Well-posedness of the Oseen-Darcy problem
We begin by proving the continuous inf-sup condition for \(\mathbf {b}\). To that end we adapt the proof of [26, Lemma 2.1] to the present case, using the results in [29, Lemma 3.3] to handle the mixed boundary conditions on \(\partial \Omega _\mathrm {D}\).
Lemma 1
There exists \(\beta > 0\) such that
Proof
Let \((q,\xi )\in \mathbf {Q}\). Since \(q\in L^2_0(\Omega )\), it is well known (see, e.g., Corollary 2.4 in Chapter I of [30]) that there exists \(\mathbf {z}\in \mathbf {H}^1_0(\Omega )\) such that \(\mathrm {div}\,\,\mathbf {z}= -\,q\) in \(\Omega \) and \(\,\,\Vert \mathbf {z}\Vert _{1,\Omega }\,\le \,c\,\Vert q\Vert _{0,\Omega }\). Setting \(\hat{\mathbf {v}} = (\hat{\mathbf {v}}_{S},\hat{\mathbf {v}}_\mathrm {D})\) with \(\hat{\mathbf {v}}_\star \,=\,\mathbf {z}|_{\Omega _\star }\) for \(\star \in \{{S},\mathrm {D}\}\), we find that \(\hat{\mathbf {v}}_{S}\cdot \mathbf n= \hat{\mathbf {v}}_\mathrm {D}\cdot \mathbf n\) on \(\Sigma \) and \(\Vert \hat{\mathbf {v}}\Vert _\mathbf {H}\,\le \, c\,\Vert q\Vert _{0,\Omega }\), and hence
On the other hand, given \(\phi \in H^{-1/2}(\Sigma )\), we define \(\eta \in H^{-1/2}(\partial \Omega _\mathrm {D})\) as
where \(\mu _\Sigma \) is given by the decomposition (15). It is not difficult to see that
and
We set \({\tilde{\mathbf {v}}}_\mathrm {D}\,:=\,\nabla z\) in \(\Omega _\mathrm {D}\), with \(z\in H^1(\Omega _\mathrm {D})\) being the unique solution of the boundary value problem:
Observe that \(\mathrm {div}\,{\tilde{\mathbf {v}}}_\mathrm {D}\,=\, \frac{1}{|\Omega _\mathrm {D}|} \left<\eta ,1\right>_{\partial \Omega _\mathrm {D}}\,\in \,\mathbb {P}_0(\Omega _\mathrm {D})\), \(\,{\tilde{\mathbf {v}}}_\mathrm {D}\cdot \mathbf n\,=\, \eta \) on \(\partial \Omega _\mathrm {D}\), and \(\,\Vert {\tilde{\mathbf {v}}}_\mathrm {D}\Vert _{\mathrm {div}\,,\Omega _\mathrm {D}}\,\le \,C\,\Vert \eta \Vert _{-1/2,\partial \Omega _\mathrm {D}} \,\le \,C\,\Vert \phi \Vert _{-1/2,\Sigma }\). In addition, owing to (14), (21) and (22), we find that
and
The latter means that \({\tilde{\mathbf {v}}}_\mathrm {D}\in {\mathbf {H}_{\Gamma _\mathrm {D}}(\mathrm{div};\Omega _\mathrm {D})}\). In this way, defining \({\tilde{\mathbf {v}}}:=(\mathbf {0},{\tilde{\mathbf {v}}}_\mathrm {D})\in \mathbf {H}\), we obtain
and using that \(\phi \in H^{-1/2}(\Gamma _2)\) is arbitrary, we get
Then, combining (19) and (24) we easily obtain that
which together with (19) implies (18) with \(\beta \) depending on \(c_1\), \(c_2\), and \(c_3\). \(\square \)
Now, let us consider the subspace
which corresponds to the kernel of the bilinear form \(\mathbf {b}\). According to the definition of \(\mathbf {b}\), we observe that \(\mathbf {v}\,=\,(\mathbf {v}_{S},\mathbf {v}_\mathrm {D})\in \mathbf {V}\) if and only if
and
Then, noting that \(L^2(\Omega )=L^2_0(\Omega )\oplus \mathbb {R}\), and taking \(\xi \in \mathbb {R}\) in the latter equation, we deduce that
which implies
Next, we establish the ellipticity of \(\mathbf {a}(\mathbf {w}_{S};\cdot ,\cdot )\) on \(\mathbf {V}\) for a suitable \(\mathbf {w}_{S}\in \mathbf {H}^1_{\Gamma _{S}}(\Omega _{S})\).
Lemma 2
Let \(\mathbf {w}_{S}\in \mathbf {H}^1_{\Gamma _{S}}(\Omega _{S})\), such that \(\mathrm {div}\,\mathbf {w}_{S}=0\) in \(\Omega _{S}\) and
Then, there exists \(\alpha > 0\), such that
Proof
Let \(\mathbf {v}:=(\mathbf {v}_{S},\mathbf {v}_\mathrm {D})\in \mathbf {V}\) and \(\mathbf {w}_{S}\in \mathbf {H}^1_{\Gamma _{S}}(\Omega _{S})\) satisfying (27) and \(\mathrm {div}\,\mathbf {w}_{S}=0\) in \(\Omega _{S}\). Integrating by parts, it is easy to see that
In turn, from (17), the continuity of the trace operator, and the Hölder inequality, we obtain
Therefore, combining (11), (27), (29), (30), and the fact that \(\mathrm {div}\,\mathbf {v}_\mathrm {D}=0\) in \(\Omega _\mathrm {D}\), we obtain
which yields the result setting \(\alpha = \frac{1}{2} \min (\mu \alpha _{S}, \alpha _\mathrm {D})\). \(\square \)
Remark 2
Condition (27) implies that the normal velocity of the fluid across the interface must be small enough. An analogous condition can be found also in [6] (more precisely, see equation (43), Theorem 2 and Remarks 2 and 4) to guarantee the well-posedness of the nonlinear interface equation associated with the Navier–Stokes/Darcy problem.
We are now in position to establish the well-posedness of (12).
Theorem 1
Let \(\mathbf {w}_{S}\in \mathbf {H}^1_{\Gamma _{S}}(\Omega _{S})\), such that \(\mathrm {div}\,\mathbf {w}_{S}=0\) in \(\Omega _{S}\) and
and let \(\mathbf {f}_{S}\in \mathbf {L}^2(\Omega _{S})\) and \(\mathbf {f}_\mathrm {D}\in \mathbf {L}^2(\Omega _\mathrm {D})\). Then, there exists a unique \((\mathbf {u},(\lambda ,p))\in \mathbf {H}\times \mathbf {Q}\) solution of (12). Moreover, there exists a constant \(C>0\), independent of the solution, such that
Proof
From Lemmas 1 and 2, and from a direct application of the classical Babuška-Brezzi theory, it follows that problem (12) is well posed and the estimate (32) holds. \(\square \)
2.4 Analysis of the continuous Navier–Stokes/Darcy problem
In this section we provide one of the more important contributions of this work, namely, the well-posedness of problem (8). This result will be attained by using a fixed-point strategy considering a similar approach as in [12, Sect. 3.2] (see also [3, 16]).
To begin, we first introduce the reduced version of problem (8) on the kernel of \(\mathbf {V}\) (see (25)), which consists in finding \(\mathbf {u}:=(\mathbf {u}_{S},\mathbf {u}_\mathrm {D})\in \mathbf {V}\) such that
The following equivalence property is standard (see [30]).
Lemma 3
If \((\mathbf {u},(p,\lambda ))=((\mathbf {u}_{S},\mathbf {u}_\mathrm {D}),(p,\lambda ))\in \mathbf {H}\times \mathbf {Q}\) is a solution of (8), then \(\mathbf {u}\in \mathbf {V}\) is also a solution of (33). Conversely, if \(\mathbf {u}=(\mathbf {u}_{S},\mathbf {u}_\mathrm {D})\in \mathbf {V}\) is a solution of (33), then there exists a unique \((p,\lambda )\in \mathbf {Q}\), such that \((\mathbf {u},(p,\lambda ))\in \mathbf {H}\times \mathbf {Q}\) is a solution of (8).
Remark 3
We recall that the existence of \((p,\lambda )\) in Lemma 3 is guaranteed thanks to the inf-sup condition (18).
Therefore, according to Lemma 3, in what follows we focus on analyzing the well-posedness of problem (33). To this aim, we introduce the set
and the mapping
with \(\mathbf {u}_{S}\) being the first component of the solution of the linearized version of (33): Find \(\mathbf {u}=(\mathbf {u}_{S},\mathbf {u}_\mathrm {D})\in \mathbf {V}\) such that
Let us notice that \(\mathbf {u}=(\mathbf {u}_{S},\mathbf {u}_\mathrm {D})\in \mathbf {V}\) is a solution of (33) if and only if \(\mathbb {T}(\mathbf {u}_{S})=\mathbf {u}_{S}\). According to this, in what follows we focus on providing sufficient conditions under which operator \(\mathbb {T}\) admits a fixed point. Let us also notice that (35) is nothing but the reduced version of problem (12), which thanks to the inf-sup condition (18), is equivalent to (35). In turn, assuming that
it is not difficult to see that \(\mathbb {T}\) is well defined. In fact, given \(\mathbf {w}_{S}\in \mathbf {X}\), from (36) we obtain that
which together with Lemma 2 implies that \(\mathbf {a}(\mathbf {w}_{S};\cdot ,\cdot )\) is elliptic on \(\mathbf {V}\). Hence, according to Lax-Milgram lemma, it follows that there exists a unique \(\mathbf {u}=(\mathbf {u}_{S},\mathbf {u}_\mathrm {D})\in \mathbf {V}\) solution to (35) satisfying
Moreover, from (38), we easily obtain
which implies that \(\mathbb {T}(\mathbf {w}_{S})\) is in \(\mathbf {X}\).
Let us now establish the following lemma providing an important estimate for the forthcoming analysis.
Lemma 4
Assume that the estimate (36) holds. Then,
Proof
Let \(\mathbf {w}_{S},{\tilde{\mathbf {w}}}_{S}\) in \(\mathbf {X}\), \(\mathbf {u}_{S}:=\mathbb {T}(\mathbf {w}_{S})\), \({\tilde{\mathbf {u}}}_{S}:=\mathbb {T}({\tilde{\mathbf {w}}}_{S})\) and \(\mathbf {u},{\tilde{\mathbf {u}}}\in \mathbf {V}\) the solutions of (35) with \(\mathbf {w}_{S}\) and \({\tilde{\mathbf {w}}}_{S}\), respectively. Observe that, according to assumption (36), the estimate (37) holds and \(\mathbf {a}(\mathbf {w}_{S},\cdot ,\cdot )\) is elliptic on \(\mathbf {V}\). In turn, from the definition of \(\mathbb {T}\) we observe that
which implies
In particular for \(\mathbf {v}=\mathbf {u}-{\tilde{\mathbf {u}}}\), adding and subtracting suitable terms, and utilizing inequality (31), it follows that
which together with the continuity of \(O_{S}\) (see (9)), implies
which yields the result. \(\square \)
The following lemma establishes the existence of a fixed point of \(\mathbb {T}\) in \(\mathbf {X}\) by means of the Schauder’s fixed point theorem written in the following form (see for instance [15, Theorem 9.12-1(b)]): Let W be a closed and convex subset of a Banach space X and let \(T:W\rightarrow W\) be a continuous mapping such that \(\overline{T(W)}\) is compact. Then T has at least one fixed point.
Lemma 5
Assume that the estimate (36) holds. Then \(\mathbb {T}\) has at least one fixed point in \(\mathbf {X}\).
Proof
We proceed analogously to the proof of Lemma 3.8 in [12]. In fact, since (36) holds, from (39) and the continuity of the Sobolev embedding from \(H^1\) into \(L^4\), it follows that
which implies the continuity of \(\mathbb {T}\). Next, given a bounded sequence \(\{\mathbf {z}_k\}_{k\in \mathbb {N}}\subseteq \mathbf {X}\), we let \(\{{\tilde{\mathbf {z}}}_k\}_{k\in \mathbb {N}}\) be a convergent subsequence of \(\{\mathbf {z}_k\}_{k\in \mathbb {N}}\), and \(\mathbf {z}\in \mathbf {H}^1(\Omega _{S})\) its limit. Then, due to the compactness of the Sobolev embedding from \(H^1\) into \(L^4\), from (39) we easily obtain that \(\mathbb {T}({\tilde{\mathbf {z}}}_k)\rightarrow \mathbb {T}(\mathbf {z})\) in \(\mathbf {H}^1(\Omega _{S})\), which implies that \(\overline{\mathbb {T}(\mathbf {X})}\) is compact. Therefore, the result is a straightforward application of the Schauder’s theorem. \(\square \)
Under a more restrictive assumption on the data, in what follows we prove that \(\mathbb {T}\) has exactly one fixed point by means of the Banach’s fixed point theorem in the following form: Let X be a Banach space, and let T a mapping of X into itself. Assume that there exists \(0<r<1\), such that \(\Vert T(u)-T(v)\Vert _X\le r\Vert u-v\Vert _X\) for all \(u,v\,\in X\), that is, T is a contraction mapping. Then there exists a unique \(u\in X\) such that \(T(u)=u\).
Lemma 6
Let \(\mathbf {f}_{S}\in \mathbf {L}^2(\Omega _{S})\) and \(\mathbf {f}_\mathrm {D}\in \mathbf {L}^2(\Omega _\mathrm {D})\) such that
with
Then, \(\mathbb {T}\) has a unique fixed point.
Proof
The result follows straightforwardly from (42), (43) and the fact that \(\mathbb {T}({\tilde{\mathbf {w}}}_{S})\) is in \(\mathbf {X}\). \(\square \)
Remark 4
Notice that condition (43) is analogous to the one usually imposed to guarantee the well-posedness of the Navier–Stokes equations (see, e.g., condition (10.1.9) in [42]). However, (43) is more restrictive since it takes into account also the terms arising from the Darcy problems due to the coupling.
Now, we are in position to establish the main result of this section, namely, the well-posedness of problem (8).
Theorem 2
Let \(\mathbf {f}_{S}\in \mathbf {L}^2(\Omega _{S})\) and \(\mathbf {f}_\mathrm {D}\in \mathbf {L}^2(\Omega _\mathrm {D})\). Assume that (36) holds. Then, problem (8) admits a solution \((\mathbf {u},(p,\lambda ))\in \mathbf {H}\times \mathbf {Q}\). In addition, if it is assumed that (43) holds, then the solution is unique. In any case, there exists a constant \(C>0\), independent of the solution, such that
Proof
The existence and uniqueness of solution of problem (8) follows straightforwardly by recalling the definition of operator \(\mathbb {T}\) and combining Lemmas 3, 5 and 6.
Next, owing to the inf-sup condition (18), the first equation of (8) and the continuity of \(A_{S}\), \(A_\mathrm {D}\) and \(O_{S}\), we have

Then, from the latter estimate and recalling that \(\mathbf {u}\in \mathbf {X}\) we obtain the estimate (44), which concludes the proof. \(\square \)
3 The discrete problem
Let \(\mathcal T_h^{S}\) and \(\mathcal T_h^\mathrm {D}\) be respective triangulations of the domains \(\Omega _{S}\) and \(\Omega _\mathrm {D}\) formed by shape-regular triangles of diameter \(h_T\) and denote by \(h_{S}\) and \(h_\mathrm {D}\) their corresponding mesh sizes. Assume that they match on \(\Sigma \) so that \(\mathcal {T}_h:=\mathcal T_h^{S}\,\cup \,\mathcal T_h^\mathrm {D}\) is a triangulation of \(\Omega :=\Omega _{S}\,\cup \,\Sigma \,\cup \,\Omega _\mathrm {D}\). Hereafter \(h:=\max \{h_{S},h_\mathrm {D}\}\).
For each \(T\in \mathcal T_h^\mathrm {D}\) we consider the local Raviart–Thomas space of the lowest order [43]:
In addition, for each \(T\in \mathcal {T}^{S}_h\) we denote by \(\mathrm{BR}(T)\) the local Bernardi-Raugel space (see [9, 30]):
where \(\{\eta _1,\eta _2,\eta _3\}\) are the baricentric coordinates of T, and \(\{\mathbf n_1,\mathbf n_2,\mathbf n_3\}\) are the unit outward normals to the opposite sides of the corresponding vertices of T. Hence, we define the following finite element subspaces:
The finite element subspaces for the velocities and pressure are, respectively,
Next, to introduce the finite element subspace of \(H^{1/2}(\Sigma )\), we denote by \(\Sigma _h\) the partition of \(\Sigma \) inherited from \(\mathcal T_h^{S}\) (or \(\mathcal T_h^\mathrm {D}\)) and we assume, without loss of generality, that the number of edges of \(\Sigma _h\) is even. Then, we let \(\Sigma _{2h}\) be the partition of \(\Sigma \) arising by joining pairs of adjacent edges of \(\Sigma _h\). Note that since \(\Sigma _h\) is inherited from the interior triangulations, it is automatically of bounded variation (i.e., the ratio of lengths of adjacent edges is bounded) and, therefore, so is \(\Sigma _{2h}\). If the number of edges of \(\Sigma _h\) is odd, we simply reduce it to the even case by joining any pair of two adjacent elements, and then construct \(\Sigma _{2h}\) from this reduced partition. Then, we define the following finite element subspace for \(\lambda \in H^{1/2}(\Sigma )\)
In this way, grouping the unknowns and spaces as follows:
where \(p_h := p_{h,{S}}\chi _{\Omega _{S}}+p_{h,\mathrm {D}}\chi _{\Omega _\mathrm {D}}\), the Galerkin approximation of (8) reads: Find \((\mathbf {u}_h, (p_h,\lambda _h))\in \mathbf {H}_h\times \mathbf {Q}_h\) such that
Here, \(\mathbf {a}_h:\mathbf {H}_{h,\Gamma _{S}}(\Omega _{S})\times (\mathbf {H}_h\times \mathbf {H}_h)\rightarrow \mathbb {R}\) is the discrete version of \(\mathbf {a}\) defined by
where \(O_{S}^h\) is the well-known skew-symmetric convection form (see [46]):
for all \(\mathbf {u}_{S},\mathbf {v}_{S},\mathbf {w}_{S}\in \mathbf {H}_h(\Omega _{S})\). Observe that integrating by parts, there holds
Moreover, using again the aforementioned Sobolev inequalities, it is easy to see that for all \(\mathbf {w}_{S},\,\mathbf {u}_{S},\,\mathbf {v}_{S}\in \mathbf {H}^1_{\Gamma _{S}}(\Omega _{S})\), there holds
In what follows, we proceed similarly to the continuous case to prove that problem (45) is well posed. We start by proving the solvability of the discrete version of (12).
3.1 The discrete Oseen-Darcy coupled problem
In this section we will apply the classical Babuška-Brezzi theory to prove the well-posedness of the problem: Given \(\mathbf {w}_{h,{S}}\in \mathbf {H}_{h,\Gamma _{S}}(\Omega _{S})\) and \(\mathbf {f}\in \mathbf {L}^2(\Omega _{S})\), find \((\mathbf {u}_h, (p_h,\lambda _h))\in \mathbf {H}_h\times \mathbf {Q}_h\) such that
We notice in advance that, similarly to the continuous case, the result follows by adapting the results in [26, Sect. 4] to our domain configuration, using the techniques in [29, Sect. 5]. To do that, we first need to introduce some notations and previous results.
3.1.1 Preliminaries
Let \(\Pi _{S}\,:\,\mathbf {H}^1_{\Gamma _{S}}(\Omega _{S}) \rightarrow \mathbf {H}_{h,\Gamma _{S}}(\Omega _{S})\) be the Bernardi-Raugel interpolation operator (see [9, 30]), which is linear and bounded with respect to the \(\mathbf {H}^1(\Omega _{S})\)-norm. We remark that, given \(\mathbf {v}\in \mathbf {H}^1_{\Gamma _{S}}(\Omega _{S})\), there holds
and hence
Equivalently, if \(\mathcal {Q}_{S}\) denotes the \(L^2(\Omega _{S})\)-orthogonal projection onto the restriction of \(L_h(\Omega )\) to \(\Omega _{S}\), then the relation (50) can be written as
Now, let \(\Pi _\mathrm {D}: \mathbf {H}^1(\Omega _\mathrm {D}) \rightarrow \mathbf {H}_h(\Omega _\mathrm {D})\) be the Raviart-Thomas interpolation operator, which thanks to [1, Theorem 3.1], can also be defined from the larger space \(\mathbf {H}^\delta (\Omega _\mathrm {D})\cap \mathbf {H}(\mathrm {div}\,;\Omega _\mathrm {D})\) onto \( \mathbf {H}_h(\Omega _\mathrm {D})\) for all \(\delta \in (0,1)\). In addition, as established by [24, Lemma 3.19], for all \({{\varvec{\tau }}}\in \mathbf {H}^\delta (\Omega _\mathrm {D})\cap \mathbf {H}(\mathrm {div}\,;\Omega _\mathrm {D})\), there holds
which implies
(see also [34, Theorem 3.16] for the global estimate). We also recall that, given \({{\varvec{\tau }}}\in \mathbf {H}^\delta (\Omega _\mathrm {D})\cap \mathbf {H}(\mathrm {div}\,;\Omega _\mathrm {D})\), there holds
and hence
Equivalently, if \(\mathcal {Q}_\mathrm {D}\) denotes the \(L^2(\Omega _\mathrm {D})\)-orthogonal projection onto the restriction of \(L_h(\Omega )\) to \(\Omega _\mathrm {D}\), then the relation (55) can be written as
Let us now observe that the set of discrete normal traces on \(\Sigma \) of \(\mathbf H_h(\Omega _\mathrm {D})\) is given by
In [41, Theorem A.1] it has been proved that there exists a discrete lifting
such that, for all \(\phi _h\in \Phi _h(\Sigma )\),
In addition, in [27, Lemma 5.2] it has been proved that there exists \(\widehat{\beta }_\Sigma \,>\, 0\), independent of h, such that the pair of subspaces \((\Phi _h(\Sigma ),\Lambda _h(\Sigma ))\) satisfies the discrete inf-sup condition:
3.1.2 The discrete inf-sup condition
In what follows, we adapt the results provided in [26, Sect. 4] to our domain configuration to prove that the bilinear form \(\mathbf {b}\) satisfies the corresponding discrete inf-sup condition. We start by establishing the following two preliminary lemmas.
Lemma 7
There exists \(\tilde{C}_1\,>\,0\), independent of h, such that
\(\forall \, (q_h,\xi _h)\,\in \,\mathbf {Q}_h\).
Proof
The proof can be readily obtained by combining the proof of [26, Lemma 4.1] and the lifting \(\mathbf {L}_h\) defined in (58). In fact, let \((q_h,\xi _h)\,\in \,\mathbf {Q}_h\). Given \(\phi _h\in \Phi _h(\Sigma )\), we define \({\bar{\mathbf {v}}}_{h,\mathrm {D}}=\mathbf {L}_h(\phi _h)\). From (59), it follows that
Hence, defining \({\bar{\mathbf {v}}}_h:=(\mathbf {0},{\bar{\mathbf {v}}}_{h,\mathrm {D}})\in \mathbf {H}_h\), we deduce that
which, noting that \(\phi _h\) is arbitrary in \(\Phi _h(\Sigma )\), yields
This inequality and (60) imply the result and complete the proof. \(\square \)
Lemma 8
There exist positive constants \(\tilde{C}_2\) and \(\tilde{C}_3\), independent of h, such that for all \((q_h,\xi _h)\in \mathbf {Q}_h\), there holds
Proof
In what follows we adapt the proof of [26], Lemma 4.2] to the present case. To do that, we let \((q_h,\xi _h)\in \mathbf {Q}_h\). Since \(q_h\in L^2_0(\Omega )\) there exists \(\mathbf {z}\in \mathbf {H}^1_0(\Omega )\) such that
Let \(\mathbf {z}_\star := \mathbf {z}|_{\Omega _\star }\) for \(\star \in \{{S},\mathrm {D}\}\). Then, since \(\mathbf {z}_{S}= \mathbf {z}_\mathrm {D}\) on \(\Sigma \), from (49), (54), and the fact that \(\mathcal {T}_h^{S}\) and \(\mathcal {T}_h^\mathrm {D}\) match on \(\Sigma \), it follows that
Let us now define \(\chi _h\,\in \,L^2(\partial \Omega _\mathrm {D})\,\subseteq \,H^{-1/2}(\partial \Omega _\mathrm {D})\) as
which clearly satisfies
with \(\psi _\Sigma \) being the element in \(H^{1/2}(\Sigma )\) satisfying (15), and
In addition, from (64), and the definition of \(\chi _h\), it is not difficult to see that
In this way, we let \(\varphi \in H^1(\Omega _\mathrm {D})\) be the unique weak solution of the problem:
and define
Recalling that \(\mathbf {z}\in \mathbf {H}^1_0(\Omega )\), we observe that \(\mathbf {z}_\mathrm {D}\in \mathbf {H}^1_{\Gamma _\mathrm {D}}(\Omega _\mathrm {D})\), and then
for all edge e on \(\Gamma _\mathrm {D}\), which implies that \(\mathbf {w}_{h,\mathrm {D}}\in \mathbf {H}_{h,\Gamma _\mathrm {D}}(\Omega _\mathrm {D})\). Then, we proceed analogously to the proof of [26, Lemma 4.2], set \(\mathbf {w}_h\,:=\,(\mathbf {w}_{h,{S}},\mathbf {w}_{h,\mathrm {D}})\in \mathbf {H}_h\), and use the properties of the interpolation operators in Sect. 3.1.1, to find that
and
from which
which completes the proof. \(\square \)
Now, we are in position to establish the discrete inf-sup condition of \(\mathbf {b}\).
Lemma 9
Assume that
where \(\tilde{C}_1,\,\tilde{C}_2,\,\tilde{C}_3,\,\) are the constants in Lemmas 7 and 8. Then there exists \(\tilde{\beta }>0\) , independent of h, such that
Proof
Setting
from Lemmas 7 and 8, we obtain
and
which combined yield
Together to (71), this implies the result. \(\square \)
Remark 5
Observe that the existence of a stable lifting \(\mathbf {L}_h\) satisfying (59) and the inf-sup condition (60) play an important role in the proof of the discrete inf-sup condition (61). In particular, as established in Sect. 3.1.1, the existence of a stable lifting \(\mathbf {L}_h\), satisfying (59), has been proved in [41, Theorem A.1] for the 2D case, where the only restriction on the grid is shape regularity (previously in [27], a similar result was proved under a quasi-uniformity condition on the mesh near the interface \(\Sigma \)). Now, concerning the existence of a discrete lifting \(\mathbf {L}_h\) in a three dimensional domain, recently in [2] the authors have extended the analogue of [41, Theorem A.1] to the 3D case, where again the only requirement on the mesh is shape regularity (see [2, Theorem 2.1]). However, in order to be able to prove the 3D version of the inf-sup condition (60), unlike the 2D case, the discrete subspace \(\Lambda _h\) must be defined on an independent triangulation \(\Sigma _{\tilde{h}}\) of the interface \(\Sigma \) formed by triangles of diameter \(\tilde{h}_K\). Then, setting \(\tilde{h}_\Sigma := \max \{\tilde{h}_K : K \in \Sigma _{\tilde{h}}\}\), and defining the set of normal traces of \(\mathbf H_h(\Omega _\mathrm {D})\) as in (57) (considering triangles instead of edges), with \(h_\Sigma := \max \{h_K : K \in \Sigma _h\}\), it can be proved (extending previous results on mixed methods with Lagrange multipliers originally provided in [5]) that there exists \(C_0 \in (0, 1)\) such that for each pair \((h_\Sigma ,\tilde{h}_\Sigma )\) verifying \(h_\Sigma \le C_0 \tilde{h}_\Sigma \), the 3D version of (60) is satisfied (see e.g., the second part of the proof of [25, Lemma 7.5]).
3.1.3 Well-posedness of the discrete Oseen-Darcy problem
Now we prove the well-posedness of problem (48). We begin by establishing the ellipticity of \(\mathbf {a}_h(\mathbf {w}_{S},\cdot ,\cdot )\) on the discrete kernel of \(\mathbf {b}\):
for a suitable \(\mathbf {w}_{S}\in \mathbf {H}_{h,\Gamma _{S}}(\Omega _{S})\).
Observe that, similarly to the continuous case, \(\mathbf {v}\in \mathbf {V}_h\) if and only if
and
which, in particular imply that
where \(L_h(\Omega _{S})\) is the set of functions of \(L_h(\Omega )\) restricted to \(\Omega _{S}\).
Remark 6
We recall here that if \(\mathbf {v}:=(\mathbf {v}_{S},\mathbf {v}_\mathrm {D})\in \mathbf {V}_h\), then \(\mathbf {v}_{S}\) is not necessarily divergence-free. This fact motivates the utilization of the skew-symmetric convective form \(O_{S}^h\).
In the next lemma we establish the ellipticity of \(\mathbf {a}_h(\mathbf {w}_{S},\cdot ,\cdot )\) on \(\mathbf {V}_h\).
Lemma 10
Let \(\mathbf {w}_{S}\in \mathbf {H}_{h,\Gamma _{S}}(\Omega _{S})\), such that
Then, there holds
with \(\alpha =\frac{1}{2}\min \{\mu \alpha _{S},\alpha _\mathrm {D}\}\).
Proof
Let \(\mathbf {w}_{S}\in \mathbf {H}_{h,\Gamma _{S}}(\Omega _{S})\) such that (74) holds. First, from identity (46), for all \(\mathbf {v}_{S}\in \mathbf {H}_{h,\Gamma _{S}}(\Omega _{S})\), we obtain
Then, the result follows analogously to the proof of Lemma 2. We omit further details. \(\square \)
We are now in a position to establish the well-posedness of (48).
Theorem 3
Let \(\mathbf {w}_{S}\in \mathbf {H}_{h,\Gamma _{S}}(\Omega _{S})\) satisfy (74) and assume that (71) holds. Then, for each \(\mathbf {f}_{S}\in \mathbf {L}^2(\Omega _{S})\) and \(\mathbf {f}_\mathrm {D}\in \mathbf {L}^2(\Omega _\mathrm {D})\), there exists a unique solution \((\mathbf {u}_h,(\lambda _h,p_h)) \in \mathbf {H}_h\times \mathbf {Q}_h\) to (48). Moreover, there exists a constant \(\tilde{C}>0\), independent of the solution, such that
Proof
It follows from Lemmas 9 and 10, and a straightforward application of the classical Babuška-Brezzi theory. \(\square \)
3.2 Well-posedness of the discrete Navier–Stokes/Darcy problem
In this section, we proceed analogously to Sect. 2.4 and prove the well-posedness of problem (45) by means of a fixed point argument. We begin by considering the reduced version of problem (8): Find \(\mathbf {u}_h:=(\mathbf {u}_{h,{S}},\mathbf {u}_{h,\mathrm {D}})\in \mathbf {V}_h\) such that
Since the discrete inf-sup condition holds (see Lemma 9), it is easy to see that problems (45) and (77) are equivalent. In fact, we have the following standard result (see [30]).
Lemma 11
Assume that (71) holds. If \((\mathbf {u}_h,(p_h,\lambda _h))\in \mathbf {H}_h\times \mathbf {Q}_h\) is a solution of (45), then \(\mathbf {u}_h=(\mathbf {u}_{h,{S}},\mathbf {u}_{h,\mathrm {D}})\in \mathbf {V}_h\) is also a solution of (77). Conversely, if \(\mathbf {u}_h=(\mathbf {u}_{h,{S}},\mathbf {u}_{h,\mathrm {D}})\) is a solution of (77), then there exists a unique \((p_h,\lambda _h)\in \mathbf {Q}_h\), such that \((\mathbf {u}_h,(p_h,\lambda _h))\in \mathbf {H}_h\times \mathbf {Q}_h\) is a solution of (45).
Now, similarly to the analysis of the continuous problem, we assume that
and define the set
and the mapping
where \(\mathbf {u}_{h,{S}}\) is the first component of the unique element \(\mathbf {u}_h=(\mathbf {u}_{h,{S}},\mathbf {u}_{h,\mathrm {D}})\) in \(\mathbf {X}_h\), such that
Assuming (78), and proceeding as in Sect. 2.4, we can easily obtain that the mapping \(\mathbb {T}_h\) is well defined and \(\mathbb {T}_h(\mathbf {X}_h)\subseteq \mathbf {X}_h\). In addition, it is clear that the analysis of existence of solution of problem (77), or equivalently (45), reduces to proving the existence of \(\mathbf {u}_{h,{S}}\in \mathbf {X}_h\), such that
In this way, in what follows we focus on analyzing the existence and uniqueness of such a fixed point.
Firstly, for the existence analysis we proceed differently from the continuous case, and simply verify that the hypotheses of the Brower’s fixed point theorem hold. This classical result is stated as follows: Let \(W_h\) be a nonempty compact convex subset of a finite-dimensional normed space, and let \(T :W_h \rightarrow W_h\) be a continuous mapping. Then T has at least one fixed point in \(W_h\). Secondly, analogously to the continuous case we assume a more restrictive assumption on the data and apply the Banach’s fixed point theorem to guarantee uniqueness.
The following result establishes the existence and uniqueness of the solution of the fixed point problem (81).
Lemma 12
Let \(\mathbf {f}_{S}\in \mathbf {L}^2(\Omega _{S})\) and \(\mathbf {f}_\mathrm {D}\in \mathbf {L}^2(\Omega )\), such that (78) holds. Then, \(\mathbb {T}_h\) has a unique fixed point in \(\mathbf {X}_h\). In addition, assuming further that
with
then the fixed point is unique.
Proof
Given \(\mathbf {w}_{S},\,{\tilde{\mathbf {w}}}_{S}\in \mathbf {X}_h\), analogously to the proof of Lemma 4, by assuming (78) one can readily obtain the estimate (see (41))
which together with the continuity of \(O_{S}^h\) (see (47)) yields
which implies the continuity of \(\mathbb {T}_h\). Then, the existence result follows from the Brower’s fixed point theorem. Moreover, from (83) and the fact \(\mathbb {T}_h({\tilde{\mathbf {w}}}_{S})\) belongs to \(\mathbf {X}_h\), it is easy to see that \(\mathbb {T}_h\) is a contraction mapping if and only if (82) holds, which owing to the Banach’s theorem implies the uniqueness result and concludes the proof. \(\square \)
Now, we are in position to establish the main result of this section, namely, existence and uniqueness of solution of problem (45).
Theorem 4
Let \(\mathbf {f}_{S}\in \mathbf {L}^2(\Omega _{S})\) and \(\mathbf {f}_\mathrm {D}\in \mathbf {L}^2(\Omega )\). Assume that (71) and (78) hold. Then, problem (45) admits a solution \((\mathbf {u}_h,(p_h,\lambda _h))\in \mathbf {H}_h\times \mathbf {Q}_h\). In addition, if assumption (82) holds then the solution is unique. In any of the cases, there exists a constant \(\tilde{C}>0\), independent of the solution, such that
Proof
By applying Lemmas 11 and 12, the proof follows analogously to the proof of Theorem 2. We omit further details. \(\square \)
3.3 Convergence of the Galerkin scheme
Our next goal is to provide the corresponding Cea’s estimate and rate of convergence of the Galerkin scheme (45). To this end and in order to simplify the subsequent analysis, we write \(\mathbf {e}_{\mathbf {u}_{S}}=\mathbf {u}_{S}-\mathbf {u}_{h,{S}}\), \(\mathbf {e}_{\mathbf {u}_\mathrm {D}}=\mathbf {u}_\mathrm {D}-\mathbf {u}_{h,\mathrm {D}}\), \(\mathrm {e}_p=p-p_h\), and \(\mathrm {e}_\lambda =\lambda -\lambda _h\), where \((\mathbf {u},(p,\lambda )):=((\mathbf {u}_{S},\mathbf {u}_\mathrm {D}),(p,\lambda ))\in \mathbf {H}\times \mathbf {Q}\) and \((\mathbf {u}_h,(p_h,\lambda _h)):=((\mathbf {u}_{h,{S}},\mathbf {u}_{h,\mathrm {D}}),(p,\lambda _h))\in \mathbf {H}_h\times \mathbf {Q}_h\) are the unique solutions of (8) and (45), respectively.
On the other hand, since the exact solution \(\mathbf {u}_{S}\in \mathbf {H}^1_{\Gamma _{S}}(\Omega _{S})\) satisfies \(\mathrm {div}\,\mathbf {u}_{S}=0\) in \(\Omega _{S}\), we have
Consequently, the following Galerkin orthogonality property holds:
for all \(\mathbf {v}:=(\mathbf {v}_{S},\mathbf {v}_\mathrm {D})\in \mathbf {H}_h,\) and \((q,\xi )\,\in \,\mathbf {Q}_h\).
The following theorem provides the corresponding Cea’s estimate.
Theorem 5
Let \(\mathbf {f}_{S}\in \mathbf {L}^2(\Omega _{S})\) and \(\mathbf {f}_\mathrm {D}\in \mathbf {L}^2(\Omega _\mathrm {D})\) such that
where \(\gamma \) and \({\tilde{\gamma }}\) are the constants in Lemmas 6 and 12, respectively. Assume that (71) holds. Let \((\mathbf {u},(p,\lambda )):=((\mathbf {u}_{S},\mathbf {u}_\mathrm {D}),(p,\lambda ))\,\in \,\mathbf {H}\times \mathbf {Q}\) and \((\mathbf {u}_h,(p_h,\lambda _h)):=((\mathbf {u}_{h,{S}},\mathbf {u}_{h,\mathrm {D}}), (p_h,\lambda _h))\,\in \,\mathbf {H}_h\times \mathbf {Q}_h\) be the unique solutions of the continuous and discrete problems (8) and (45), respectively. Then there exists \(C > 0\), independent of h and the continuous and discrete solutions, such that
Proof
Given \({\bar{\mathbf {v}}}=({\bar{\mathbf {v}}}_{h,{S}},{\bar{\mathbf {v}}}_{h,\mathrm {D}})\,\in \,\mathbf {V}_h\) and \((\bar{q}_h,{\bar{\xi }}_h) \in \mathbf {Q}_h\), as usual we decompose these errors into
where
Now, we recall that thanks to assumption (86), it follows that \(\mathbf {u}_{S}\in \mathbf {X}\) and \(\mathbf {u}_{h,{S}}\in \mathbf {X}_h\) (cf. (34) and (79)), which implies
and
In particular, from (91) we have
According to the above, and noting that for all \(\mathbf {v}_{S}\in \mathbf {H}_{h,\Gamma _{S}}(\Omega _{S})\), there holds
with
we add and subtract suitable terms in the first equation of (85) with \(\mathbf {v}=(\varvec{\eta }_{\mathbf {u}_\mathrm {D}},\varvec{\eta }_{\mathbf {u}_\mathrm {D}})\), and observe that \(\mathbf {b}((\varvec{\eta }_{\mathbf {u}_{S}},\varvec{\eta }_{\mathbf {u}_\mathrm {D}}),(\eta _p,\eta _\lambda ))=0\), to obtain
Hence, proceeding analogously to the proof of Lemma 2, and using the continuity of \(A_{S}\), \(A_\mathrm {D}\), \(O_{S}^h\) and \(\mathbf {b}\), we obtain
which together with (90) and assumption (86), implies that there exists \(C >0\), independent of h, such that
In this way, from (88), (94) and the triangle inequality, we obtain
Now, to estimate \(\mathrm {e}_p\) and \(\mathrm {e}_\lambda \) we observe that from the discrete inf-sup condition (72), the first equation of (85), and the first equation of (93), there holds
Then, owing to the continuity of \(A_{S}\), \(A_\mathrm {D}\), \(O_{S}^h\), \(\mathbf {b}\), inequalities (95) and (90), and assumption (86), we obtain
which together to the triangle inequality implies
with \(\tilde{c}>0\) independent of h.
Therefore, recalling that \({\bar{\mathbf {v}}}_h\in \mathbf {V}_h\) and \((\bar{q}_h,{\bar{\lambda }}_h)\in \mathbf {Q}_h\) are arbitrary, from (95) and (96) we obtain
We conclude the proof by recalling that the discrete inf-sup condition (72), and a classical result on mixed methods (see, for instance [24], Theorem 2.6]) ensure the existence of a constant \(c>0\), independent of h, such that
\(\square \)
Remark 7
An alternative proof for the Céa’s estimate (87), can be obtained by adapting the proof of [12], Theorem 4.4] (see also [3], Theorem 5.4] and [23], Theorem 4.2]) to our case, where the main tool is a Strang-type error estimate.
Now, in order to provide the theoretical rate of convergence of the Galerkin scheme (45), we recall the approximation properties of the subspaces involved (see, e.g. [4, 9, 11, 24, 44]). Note that each one of them is named after the unknown to which it is applied later on.
(AP \(\mathbf{^{\mathbf u_{S}}}_h\)) For each \(\mathbf {v}_{S}\,\in \,\mathbf H^2(\Omega _{S})\), there holds
(AP \(\mathbf{^{\mathbf u_\mathrm {D}}}_h\)) For each \(\mathbf {v}_\mathrm {D}\,\in \,\mathbf H^1(\Omega _\mathrm {D})\) with \(\mathrm {div}\,\,\mathbf {v}_\mathrm {D}\,\in \,H^1(\Omega _\mathrm {D})\), there holds
(AP \(\mathbf{^{p_h}}_h\)) For each \(q\,\in \,H^1(\Omega ) \,\cap \,L^2_0(\Omega )\), there exists \(q_h\,\in \,L_{h,0}(\Omega )\) such that
(AP \(\mathbf{^{\lambda }}_h\)) For each \(\xi \,\in \,H^{3/2}(\Sigma )\), there exists \(\xi _h\,\in \,\Lambda _h(\Sigma )\) such that
The following theorem provides the theoretical rate of convergence of the Galerkin scheme (45), under suitable regularity assumptions on the exact solution.
Theorem 6
Let \(\mathbf {f}_{S}\in \mathbf {L}^2(\Omega _{S})\) and \(\mathbf {f}_\mathrm {D}\in \mathbf {L}^2(\Omega _\mathrm {D})\), such that (86) holds. Assume that (71) holds. Let \((\mathbf {u},(p,\lambda ))\,\in \,\mathbf {H}\times \mathbf {Q}\) and \((\mathbf {u}_h,(p_h,\lambda _h))\,\in \,\mathbf {H}_h\times \mathbf {Q}_h\) be the unique solutions of the continuous and discrete problems (8) and (45), respectively, and assume that \(\mathbf {u}_{S}\,\in \,\mathbf {H}^2(\Omega _{S})\), \(\mathbf u_\mathrm {D}\,\in \,\mathbf H^1(\Omega _\mathrm {D})\), \(\mathrm {div}\,\,\mathbf u_\mathrm {D}\,\in \,H^1 (\Omega _\mathrm {D})\), \(p \,\in \,H^1(\Omega )\), and \(\lambda \,\in H^{3/2}(\Sigma )\). Then there exists \(C > 0\), independent of h and the continuous and discrete solutions, such that
Proof
It is suffices to apply Theorem 5 and the approximation properties of the discrete subespaces. We omit further details. \(\square \)
4 Numerical results
In this section we present some examples illustrating the performance of our mixed finite element scheme (45) on a set of quasi-uniform triangulations of the corresponding domains. Our implementation is based on a FreeFem++ code [33], in conjunction with the direct linear solver UMFPACK [17].
In order to solve the nonlinear problem, we propose the Newton-type strategy: Given \(\mathbf {u}^0=(\mathbf {u}_{S}^0,\mathbf {u}_\mathrm {D}^0)\in \mathbf {H}_h\), \(p^0\in L_{h,0}(\Omega )\) and \(\lambda ^0 \in \Lambda _h(\Sigma )\), for \(m\ge 1\), find \(\mathbf {u}^m=(\mathbf {u}_{S}^m,\mathbf {u}_\mathrm {D}^m)\in \mathbf {H}_h\), \(p^m\in L_{h,0}(\Omega )\) and \(\lambda ^m \in \Lambda _h(\Sigma )\), such that
for all \(\mathbf {v}=(\mathbf {v}_{S},\mathbf {v}_\mathrm {D})\in \mathbf {H}_h\), \(q\in L_{h,0}(\Omega )\) and \(\xi \in \Lambda _h(\Sigma )\).
In all the numerical experiments below, the iterations are terminated once the relative error of the entire coefficient vectors between two consecutive iterates is sufficiently small, that is,
where \(\Vert \cdot \Vert _{l^{2}}\) is the standard \(l^{2}\)-norm in \(\mathbb {R}^{N}\), with N denoting the total number of degrees of freedom defining the finite element subspaces \(\mathbf {H}_h\) and \(\mathbf {Q}_h\), and tol is a fixed tolerance chosen as \(tol = 1e-06\). For each example shown below we simply take \(\mathbf {u}^{0}=\mathbf {0}\) and \((p^{0},\lambda ^{0})=\mathbf {0}\) as initial guess.
We now introduce some additional notations. We denote by \(h_\Sigma := \max \{ h_e : e \in \Sigma _{2h}\}\). As in Sect. 3.3, the individual errors are denoted by \(\mathbf {e}_{\mathbf {u}_{S}}=\mathbf {u}_{S}-\mathbf {u}_{h,{S}}\), \(\mathbf {e}_{\mathbf {u}_\mathrm {D}}=\mathbf {u}_\mathrm {D}-\mathbf {u}_{h,\mathrm {D}}\), \(\mathrm {e}_{p_{S}}=p_{S}-p_{h,{S}}\), \(\mathrm {e}_{p_\mathrm {D}}=p_\mathrm {D}-p_{h,\mathrm {D}}\) and \(\mathrm {e}_\lambda =\lambda -\lambda _h\). Also, we let \(\mathbf {r}_{\mathbf {u}_{S}}\), \(\mathbf {r}_{\mathbf {u}_\mathrm {D}}\), \(\mathrm {r}_{p_{S}}\), \(\mathrm {r}_{p_\mathrm {D}}\) and \(\mathrm {r}_\lambda \) be the experimental rates of convergence given by
where \(h_\star \) and \(h'_\star \) (\(\star \in \{{S},\mathrm {D},\Sigma \}\)) denote two consecutive mesh sizes with their respective errors \(\mathbf {e}\), \(\mathbf {e}'\) (or \(\mathrm {e}\), \(\mathrm {e}'\)).
For each example below we consider the parameters \(\alpha _d=1\), \(\rho =1\), \(\varvec{\kappa }=\mathbf I\) and \(\mathbf {K}=\mathbf I\).
In our first example we illustrate the accuracy of our method considering a manufactured exact solution defined on \(\Omega =\Omega _{S}\cup \Sigma \cup \Omega _\mathrm {D}\), with \(\Omega _{S}\,:=\,(-1/2,1/2)\times (0,1/2)\) and \(\Omega _\mathrm {D}\,:=\,(-1/2,1/2)\times (-1/2,0)\). We consider the viscosity \(\mu =1\) and the terms on the right-hand side are adjusted so that the exact solution is given by the functions
with \(\star \in \{{S},\mathrm {D}\}\). Notice that, \(\mathbf {u}_{S}=\mathbf {u}_\mathrm {D}\) on \(\Sigma \). Notice also that the boundary conditions (4) are not satisfied and therefore the right-hand side of the resulting system must be modified accordingly.
In Table 1 we summarize the convergence history for a sequence of quasi-uniform triangulations. We observe that the rate of convergence O(h) predicted by Theorem 6 is attained in all the cases. Next, in Fig. 2 we display (to the left) the vector field of the approximate velocity \(\mathbf {u}_h\) and the magnitude of the error \(|\mathbf {u}-\mathbf {u}_h|\) (to the right) with \(N=443758\). Notice that our method preserves the direction of the velocities on \(\Sigma \) as expected. Also observe that the maximum value of the error in \(\Omega _{S}\) is of the order of \(3e-05\) whereas in \(\Omega _\mathrm {D}\) is of the order of \(3e-03\). In addition, in Fig. 3 we display (to the left) the approximate pressure and the magnitude of the error \(|p-p_h|\) (to the right) with \(N=443758\). Notice that the maximum value of \(|p-p_h|\) in \(\Omega _{S}\) is of the order of \(3e-02\), whereas in \(\Omega _\mathrm {D}\) is of the order of \(2e-05\). As noted from Figs. 2 and 3 (to the right), the approximation is not very accurate in those regions of high gradients. Nevertheless, this aspect could be easily fixed by applying an adaptive algorithm based on suitable a posteriori error estimates.
In our second example we focus on the performance of the iterative method (98) with respect to the viscosity \(\mu \). To do this we consider the domain \(\Omega =\Omega _{S}\cup \Sigma \cup \Omega _\mathrm {D}\), with \(\Omega _{S}\,:=\,(-1/2,3/2)\times (0,1/2)\) and \(\Omega _\mathrm {D}\,:=\,(-1/2,3/2)\times (-1/2,0)\). Then, the terms on the right-hand side are adjusted so that the exact solution is given by the functions:
where
and the constant c is such that \(\int _\Omega p=0\). Notice that \((\mathbf {u}_{S},p_{S})\) is the well known analytical solution for the Navier–Stokes problem obtained by Kovasznay in [38], which presents a boundary layer at \(\{-1/2\}\times (0,2)\). Notice also that in this example the boundary conditions (3) are not satisfied and the right-hand side of the resulting system must be modified accordingly.
In Table 2 we show the behaviour of the iterative method (98) as a function of the viscosity \(\mu \), considering different mesh sizes \(h:=\max \{h_{S},h_\mathrm {D}\}\), and a tolerance \(tol=1e{-06}\). Here we observe that the smaller the parameter \(\mu \) the higher the number of iterations as it occurs also in the Newton method for the sole Navier–Stokes equations. Numerical experiments for smaller values of \(\mu \) are not reported since the iterative methods need too many iterations to converge (more than 100). Next, the numerical results in Table 3 show the convergence history for a sequence of quasi-uniform triangulations, considering the viscosity \(\mu =0.1\). We see there that the rate of convergence O(h) provided by Theorem 6 is attained by the unknowns.
References
Agouzal, A., Thomas, J.-M.: An extension theorem for equilibrium finite elements spaces. Japan J. Indust. Appl. Math. 13(2), 257–266 (1996)
Ainsworth, M., Guzmán, J, Sayas, F.-J.: Discrete extension operators for mixed finite element spaces on locally refined meshes. Math. Comp. (2016). doi:10.1090/mcom/3074
Alvarez, M., Gatica, G.N., Ruiz-Baier, R.: An augmented mixed-primal finite element method for a coupled flow-transport problem. ESAIM Math. Model. Numer. Anal. 49(5), 1399–1427 (2015)
Aziz, A.K., Babuška, I.: Survey lectures on the mathematical foundations of the finite element method. In: The Mathematical Foundations of the Finite Element Method with Applications to Partial Differential Equations (Proc. Sympos., Univ. Maryland, Baltimore, Md., 1972), pp. 1–359. Academic Press, New York: With the collaboration of G. Fix and R. B, Kellogg (1972)
Babuška, I., Gatica, G.N.: On the mixed finite element method with Lagrange multipliers. Numer. Methods Partial Differ. Equ. 19(2), 192–210 (2003)
Badea, L., Discacciati, M., Quarteroni, A.: Numerical analysis of the Navier–Stokes/Darcy coupling. Numer. Math. 115(2), 195–227 (2010)
Badia, S., Codina, R.: Stokes, Maxwell and Darcy: a single finite element approximation for three model problems. Appl. Numer. Math. 62(4), 246–263 (2012)
Beavers, G.S., Joseph, D.D.: Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30, 197–207 (1967)
Bernardi, C., Raugel, G.: Analysis of some finite elements for the Stokes problem. Math. Comp. 44(169), 71–79 (1985)
Brezzi, F.: On the existence, uniqueness and approximation of saddle-point problems arising from Lagrange multipliers. Rev. Française Automat. Informat. Recherche Opérationnelle, sér. Rouge 8:129–151 (1974)
Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Method. Springer, New York (1991)
Camaño, J., Gatica, G.N., Oyarzúa, R., Tierra, G.: An augmented mixed finite element method for the Navier–Stokes equations with variable viscosity. SIAM J. Numer. Anal. 54(2), 1069–1092 (2016)
Cao, Y., Gunzburger, M., He, X., Wang, X.: Robin-Robin domain decomposition methods for the steady-state Stokes-Darcy system with the Beavers-Joseph interface condition. Numer. Math. 117(4), 601–629 (2011)
Chen, W., Gunzburger, M., Hua, F., Wang, X.: A parallel Robin-Robin domain decomposition method for the Stokes-Darcy system. SIAM J. Numer. Anal. 49(3), 1064–1084 (2011)
Ciarlet, P.: Linear and Nonlinear Functional Analysis with Applications. Society for Industrial and Applied Mathematics, Philadelphia (2013)
Colmenares, E., Gatica, G.N., Oyarzúa, R.: Fixed point strategies for mixed variational formulations of the stationary Boussinesq problem. C. R. Math. Acad. Sci. Paris 354(1), 57–62 (2016)
Davis, T.A.: Algorithm 832: UMFPACK V4.3-an unsymmetric-pattern multifrontal method. ACM Trans. Math Softw. 30(2), 196–199 (2004)
Discacciati, M.: Domain Decomposition Methods for the Coupling of Surface and Groundwater Flows. PhD thesis, École Polytechnique Fédérale de Lausanne, Switzerland (2004)
Discacciati, M.: Coupling free and porous-media flows: models and numerical approximation. Simulation of Flow in Porous Media. Applications in Energy and Environment, vol. 12 of Radon Series on Computational and Applied Mathematics, pp. 107–138. De Gruyter, Berlin and Boston (2013)
Discacciati, M., Miglio, E., Quarteroni, A.: Mathematical and numerical models for coupling surface and groundwater flows. Appl. Numer. Math. 43, 57–74 (2002)
Ern, A., Guermond, J.-L.: Theory and Practice of Finite Elements. Applied Mathematical Sciences, vol. 159. Springer, New York (2004)
Galvis, J., Sarkis, M.: Non-matching mortar discretization analysis for the coupling Stokes-Darcy equations. Electron. Trans. Numer. Anal. 26, 350–384 (2007)
Gatica, G., Ruiz-Baier, R., Tierra, G.: A mixed finite element method for Darcy’s equations with pressure dependent porosity. Math. Comp. 85(297), 1–33 (2016)
Gatica, G.N.: A Simple Introduction to the Mixed Finite Element Method. Springer, Berlin (2014)
Gatica, G.N., Hsiao, G.C., Meddahi, S.: A coupled mixed finite element method for the interaction problem between an electromagnetic field and an elastic body. SIAM J. Numer. Anal. 48(4), 1338–1368 (2010)
Gatica, G.N., Meddahi, S., Oyarzúa, R.: A conforming mixed finite-element method for the coupling of fluid flow with porous media flow. IMA J. Numer. Anal. 29(1), 86–108 (2009)
Gatica, G.N., Oyarzúa, R., Sayas, F.-J.: Analysis of fully-mixed finite element methods for the Stokes-Darcy coupled problem. Math. Comp. 80(276), 1911–1948 (2011)
Gatica, G.N., Oyarzúa, R., Sayas, F.-J.: Convergence of a family of Galerkin discretizations for the Stokes-Darcy coupled problem. Numer. Methods Part. Differ Equ. 27(3), 721–748 (2011)
Gatica, G.N., Oyarzúa, R., Sayas, F.-J.: A twofold saddle point approach for the coupling of fluid flow with nonlinear porous media flow. IMA J. Numer. Anal. 32(3), 845–887 (2012)
Girault, V., Raviart, P.A.: Finite Element Methods for Navier-Stokes Equations. Theory and Algorithms. Springer, Berlin (1986)
Girault, V., Rivière, B.: DG approximation of coupled Navier-Stokes and Darcy equations by Beaver-Joseph-Saffman interface condition. SIAM J. Numer. Anal. 47, 2052–2089 (2009)
Girault, V., Vassilev, D., Yotov, I.: Mortar multiscale finite element methods for Stokes-Darcy flows. Numer. Math. 127(1), 93–165 (2014)
Hecht, F.: New development in FreeFem++. J. Numer. Math. 20(3–4), 251–265 (2012)
Hiptmair, R.: Finite elements in computational electromagnetism. Acta Numer. 11, 237–339 (2002)
Jäger, W., Mikelić, A.: On the interface boundary condition of Beavers, Joseph and Saffman. SIAM J. Appl. Math. 60(4), 1111–1127 (2000)
Kanschat, G., Rivière, B.: A strongly conservative finite element method for the coupling of Stokes and Darcy flow. J. Comput. Phys. 229(17), 5933–5943 (2010)
Karper, T., Mardal, K.-A., Winther, R.: Unified finite element discretizations of coupled Darcy-Stokes flow. Numer. Methods Partial Differ. Equ. 25(2), 311–326 (2009)
Kovasznay, L.I.G.: Laminar flow behind a two-dimensional grid. Proc. Camb. Philos. Soc. 44, 58–62 (1948)
Layton, W.L., Schieweck, F., Yotov, I.: Coupling fluid flow with porous media flow. SIAM J. Numer. Anal. 40, 2195–2218 (2003)
Lipnikov, K., Vassilev, D., Yotov, I.: Discontinuous Galerkin and mimetic finite difference methods for coupled Stokes-Darcy flows on polygonal and polyhedral grids. Numer. Math. 126(2), 321–360 (2014)
Márquez, A., Meddahi, S., Sayas, F.-J.: Strong coupling of finite element methods for the Stokes-Darcy problem. IMA J. Numer. Anal. 35(2), 969–988 (2015)
Quarteroni, A., Valli, A.: Numerical Approximation of Partial Differential Equations. Springer, Berlin (1994)
Raviart, P.-A., Thomas, J.M.: A mixed finite element method for 2nd order elliptic problems. In: Mathematical Aspects of Finite Element Methods (Proc. Conf., Consiglio Naz. delle Ricerche (C.N.R.), Rome, 1975)
Roberts, J.E., Thomas, J.-M.: Mixed and hybrid methods. In: Handbook of Numerical Analysis, vol. II, pp 523–639. North-Holland, Amsterdam (1991)
Saffman, P.G.: On the boundary condition at the interface of a porous medium. Stud. Appl. Math. 1, 93–101 (1971)
Temam, R.: Navier–Stokes equations. Theory and Numerical Analysis. Studies in Mathematics and its Applications, vol. 2. North-Holland Publishing Co., Amsterdam-New York-Oxford (1977)
Author information
Authors and Affiliations
Corresponding author
Additional information
Marco Discacciati acknowledges funding from the European Union Seventh Framework Programme (FP7/2007-2013) under Grant Agreement No. 294229. Ricardo Oyarzúa acknowledges funding from CONICYT-Chile through project Fondecyt 11121347, project Anillo ACT1118 (ANANUM) and by Universidad del Bío-Bío through DIUBB project GI 151408/VC.
Rights and permissions
About this article
Cite this article
Discacciati, M., Oyarzúa, R. A conforming mixed finite element method for the Navier–Stokes/Darcy coupled problem. Numer. Math. 135, 571–606 (2017). https://doi.org/10.1007/s00211-016-0811-4
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-016-0811-4