Discontinuous Galerkin methods for solving a quasistatic contact problem

Abstract

We consider the numerical solution of a nonlinear evolutionary variational inequality, arising in the study of quasistatic contact problems. We study spatially semi-discrete and fully discrete schemes for the problem with several discontinuous Galerkin discretizations in space and finite difference discretization in time. Under appropriate regularity assumptions on the solution, a unified error analysis is established for the schemes, reaching the optimal convergence order for linear elements. Numerical results are presented on a two dimensional test problem to illustrate numerical convergence orders.

1 Introduction

Contact phenomena among deformable bodies or between deformable and rigid bodies abound in industry and daily life; they play an important role in structural and mechanical systems. Therefore, a considerable effort has been made in modeling and numerical simulations of contact processes. The well-known Signorini problem is an elastostatic problem describing the contact of a deformable body with a rigid frictionless foundation [16]. In early mathematical publications on contact problems, only static processes were studied. More recently, contact problems are studied involving viscoelastic and viscoplastic materials, leading to one type of time dependent models, known as quasistatic contact problems. These problems describe slowly evolving frictional contact processes among deformable bodies under various contact and friction conditions [15].

In this paper, we extend the ideas presented in [18] where discontinuous Galerkin (DG) methods for the Signorini problem were studied, to solve quasistatic contact problem. In the past two decades, DG methods have been widely used for solving many kinds of mathematical and physical problems due to the flexibility in constructing feasible local shape function spaces and the advantage to capture non-smooth or oscillatory solutions effectively. DG methods provide discontinuous approximations by using the Galerkin method element by element, and information is transferred between two neighboring elements through the use of numerical traces (numerical fluxes). One of the main advantages is the increase of locality in discretization, which is ideally suited for parallel computing. In addition, DG methods permit an easy treatment of nonhomogeneous boundary conditions, which greatly increases the robustness and accuracy of any boundary condition implementation. We refer to [10] and the references therein for a historical survey about DG methods.

In [12, 13], a DG formulation and algorithm for gradient plasticity problem, in the form of a quasistatic variational inequality of the second kind, was developed and analyzed. In [17], the ideas in [1] were extended to solving an obstacle problem and a simplified friction problem; a priori error estimates were established for these methods, which reach optimal order for linear elements. The discontinuous property makes DG methods easy to handle elements of arbitrary shapes and irregular meshes with hanging nodes, and flexible to construct local shape function spaces ($hp$-adaptivity). In [19], a posteriori error estimators of residual type were derived on DG methods for an obstacle problem, and an $h$-adaptive DG algorithm was proposed for solving the obstacle problem based on the a posteriori error analysis. In [18], ideas in [17] were extended to solve the Signorini problem through DG methods with linear elements and optimal order error estimate was derived. We will extend the ideas therein to solving the quasistatic contact problem with DG methods. A priori error analysis will be presented for these methods, which reaches optimal convergence order for linear elements.

The paper is organized as follows. In Sect. 2, we introduce the quasistatic contact problem and DG formulations for solving it; moreover, spatially semi-discrete approximation and fully discrete approximation are given. In Sect. 3, we first prove the consistency of the DG schemes, boundedness and stability of the bilinear forms, then we establish a priori error estimates for spatially semi-discrete approximation with these DG methods. Error analysis for fully discrete approximation is given in Sect. 4. In the final section, we present numerical results on a test problem, paying particular attention to numerical convergence orders with different choices of penalty constants in the DG schemes.

2 Quasistatic contact problem and DG formulations

2.1 Quasistatic contact problem and its weak formulation

The quasistatic contact problem is used to describe slowly evolving frictional contact process of a linearly elastic body occupying a Lipschitz domain $\Omega \subset \mathbb{R }^d$ ($d=2,3$). The boundary $\Gamma$ is divided into three parts $\overline{\Gamma _D}$, $\overline{\Gamma _F}$ and $\overline{\Gamma _C}$ with $\Gamma _D$, $\Gamma _F$ and $\Gamma _C$ relatively open and mutually disjoint such that $\mathrm{meas}\,(\Gamma _D)>0$. Let $t\in [0,T]$ be the time variable for some $T>0$. Denote by ${{\varvec{u}}}(\cdot ,t):\Omega \rightarrow \mathbb{R }^d$ a displacement variable. The linearized strain tensor

$$\begin{aligned} {\varvec{\varepsilon }}({{\varvec{u}}})=\frac{1}{2}\,(\nabla {{\varvec{u}}}+(\nabla {{\varvec{u}}})^T) \end{aligned}$$

and stress tensor ${\varvec{\sigma }}$ are second order symmetric tensors, which take values in $\mathbb{S }^d$, the space of second order symmetric tensors on $\mathbb{R }^d$ with the inner product ${\varvec{\sigma }}:{\varvec{\tau }}=\sum _{i,j=1}^d\sigma _{ij}\tau _{ij}$ and norm $|{\varvec{\tau }}| = ({\varvec{\tau }}:{\varvec{\tau }})^\frac{1}{2}$. Let ${\varvec{\nu }}$ be the unit outward normal vector on $\Gamma$. For a vector ${\varvec{v}}$, denote its normal component and tangential component by $v_{\nu }={\varvec{v}}\cdot {\varvec{\nu }}$ and ${\varvec{v}}_{\tau }={\varvec{v}}-v_{\nu }{\varvec{\nu }}$ on the boundary. Similarly for a tensor-valued function ${\varvec{\sigma }}:\Omega \rightarrow \mathbb{S }^d$, we define its normal component and tangential component by $\sigma _{\nu }=({\varvec{\sigma }}{\varvec{\nu }})\cdot {\varvec{\nu }}$ and ${\varvec{\sigma }}_{\tau } ={\varvec{\sigma }}{\varvec{\nu }}-\sigma _{\nu }{\varvec{\nu }}$, respectively. We have the decomposition formula

$$\begin{aligned} ({\varvec{\sigma }}{\varvec{\nu }})\cdot {\varvec{v}}=(\sigma _{\nu }{\varvec{\nu }}+ {\varvec{\sigma }}_{\tau })\cdot (v_\nu {\varvec{\nu }}+{\varvec{v}}_\tau ) =\sigma _{\nu } v_\nu +{\varvec{\sigma }}_{\tau }\cdot {\varvec{v}}_\tau . \end{aligned}$$

For a tensor-valued function ${\varvec{\sigma }}$, define its divergence by

$$\begin{aligned} \mathrm{div}\,{\varvec{\sigma }}=(\partial _j\sigma _{ij})_{1\le i\le d}. \end{aligned}$$

Then, for any symmetric tensor ${\varvec{\sigma }}$ and any vector field ${\varvec{v}}$, both being continuously differentiable over $\overline{\Omega }$, we have the following integration by parts formula

$$\begin{aligned} \int _\Omega \mathrm{div}\,{\varvec{\sigma }}\cdot {\varvec{v}}\,dx=\int _\Gamma {\varvec{\sigma }}{\varvec{\nu }}\cdot {\varvec{v}}\,ds -\int _\Omega {\varvec{\sigma }}:{\varvec{\varepsilon }}({\varvec{v}})\,dx. \end{aligned}$$

(2.1)

For the quasistatic contact problem, the displacement field ${{\varvec{u}}}:\Omega \times [0,T]\rightarrow \mathbb{R }^d$ and the stress field ${\varvec{\sigma }}:\Omega \times [0,T]\rightarrow \mathbb{S }^d$ satisfy the relations

$$\begin{aligned}&{\varvec{\sigma }}=\mathcal{C }{\varvec{\varepsilon }}({{\varvec{u}}}) \quad&\mathrm{in\ } \Omega \times (0,T),\end{aligned}$$

(2.2)

$$\begin{aligned}&-\mathrm{div}\,{\varvec{\sigma }}={{\varvec{f}}}_1 \quad&\mathrm{in\ }\Omega \times (0,T), \end{aligned}$$

(2.3)

$$\begin{aligned}&{{\varvec{u}}}=\mathbf{0}\quad&\mathrm{on\ }\Gamma _D\times (0,T), \end{aligned}$$

(2.4)

$$\begin{aligned}&{\varvec{\sigma }}{\varvec{\nu }}={{\varvec{f}}}_2 \quad&\mathrm{on\ }\Gamma _F\times (0,T), \end{aligned}$$

(2.5)

$$\begin{aligned}&{{\varvec{u}}}(0) = {{\varvec{u}}}_0 \quad&\mathrm{in\ }\Omega . \end{aligned}$$

(2.6)

Here, (2.2) is the constitutive relation of the elastic material, where $\mathcal{C } : \Omega \times \mathbb{S }^d\rightarrow \mathbb{S }^d$ denotes the fourth-order elasticity tensor of the material, and is assumed to be bounded, symmetric and positive definite in $\Omega$, i.e.

$$\begin{aligned} \left\{ \begin{aligned}&(a)\ \mathcal{C }_{ijkl}\in L^\infty (\Omega ), 1\le i,j,k,l\le d;\\&(b)\ \mathcal{C }{\varvec{\sigma }}:{\varvec{\tau }}= {\varvec{\sigma }}:\mathcal{C }{\varvec{\tau }}\ \forall \, {\varvec{\sigma }},{\varvec{\tau }}\in \mathbb{S }^d,\quad \mathrm{a.e.\ in}\ \Omega ;\\&(c)\ \exists \, m>0\ \mathrm{s.t.}\ \mathcal{C }{\varvec{\tau }}:{\varvec{\tau }}\ge m|{\varvec{\tau }}|^2,\ \forall {\varvec{\tau }}\in \mathbb{S }^d,\quad \mathrm{a.e.\ in}\ \Omega . \end{aligned}\right. \end{aligned}$$

(2.7)

If the elastic behavior of the material is homogeneous and isotropic, then the elasticity tensor is given by

$$\begin{aligned} \mathcal{C }{\varvec{\varepsilon }}=\lambda \,(\mathrm{tr}\,{\varvec{\varepsilon }}){{\varvec{I}}}+2\,\mu \,{\varvec{\varepsilon }}, \end{aligned}$$

(2.8)

where $\lambda >0$ and $\mu >0$ are Lamé coefficients. In the equilibrium equation (2.3), ${{\varvec{f}}}_1$ is the density of the volume forces. Boundary condition (2.4) means that the body is clamped on $\Gamma _D$ and so the displacement field vanishes there all the time. Surface traction of density ${{\varvec{f}}}_2$ acts on $\Gamma _F\times (0,T)$ in (2.5). On $\Gamma _C\times (0,T)$, we assume the contact is bilateral (no loss of contact during the process) and the friction is modeled with Tresca’s friction law (see, e.g., [15]):

$$\begin{aligned} \left. \begin{aligned}&u_\nu = 0,\ |{\varvec{\sigma }}_\tau |\le g, \\&|{\varvec{\sigma }}_\tau |< g \Rightarrow \dot{{{\varvec{u}}}}_\tau = \mathbf{0},\\&|{\varvec{\sigma }}_\tau |= g \Rightarrow \exists \lambda \ge 0\ \mathrm{s.t.}\ {\varvec{\sigma }}_\tau = -\lambda \dot{{{\varvec{u}}}}_\tau \end{aligned} \right\} \mathrm{on}\ \Gamma _C\times (0,T), \end{aligned}$$

(2.9)

where $g\ge 0$ represents the friction bound function. Note that

$$\begin{aligned} \dot{{{\varvec{u}}}} = \mathbf{0}\quad \mathrm{on}\,\Gamma _D \quad \mathrm{and} \quad \dot{u}_\nu = 0 \quad \mathrm{on}\, \Gamma _C \end{aligned}$$

(2.10)

from the boundary conditions (2.4) and (2.9).

To provide a variational formulation of the contact problem (2.2)–(2.9), we introduce a Hilbert space

$$\begin{aligned} V = \left\{ {\varvec{v}}\in [H^1(\Omega )]^d \mid {\varvec{v}}= \mathbf{0}\,\mathrm{a.e.\ on}\, \Gamma _D,\ v_\nu =0 \ \mathrm{a.e.\ on}\ \Gamma _C \right\} \end{aligned}$$

(2.11)

with the inner product and norm defined by

$$\begin{aligned} ({{\varvec{u}}},{\varvec{v}})_V = \int _\Omega {\varvec{\varepsilon }}({{\varvec{u}}}):{\varvec{\varepsilon }}({\varvec{v}})\,dx, \quad \Vert {\varvec{v}}\Vert _V = \sqrt{({\varvec{v}},{\varvec{v}})_V}. \end{aligned}$$

Since $\mathrm{meas}(\Gamma _D)>0$, Korn’s inequality holds [6], implying that $\Vert \cdot \Vert _V$ is a norm on $V$, equivalent to the standard $[H^1(\Omega )]^d$ norm on $V$. For the force densities, assume

$$\begin{aligned} {{\varvec{f}}}_1\in W^{1,\infty }(0,T;(L^2(\Omega ))^d),\quad {{\varvec{f}}}_2\in W^{1,\infty }(0,T; (L^2(\Gamma _F))^d), \end{aligned}$$

(2.12)

and for the friction bound function, assume

$$\begin{aligned} g\in L^\infty (\Gamma _C),\quad g\ge 0 \hbox { a.e.\ on}\, \Gamma _C. \end{aligned}$$

(2.13)

We define a bilinear form $a(\cdot ,\cdot )$ over $V$ by

$$\begin{aligned} a({{\varvec{u}}},{\varvec{v}})=\int _\Omega \mathcal{C }{\varvec{\varepsilon }}({{\varvec{u}}}):{\varvec{\varepsilon }}({\varvec{v}})\,dx \quad \quad \forall \,{{\varvec{u}}},{\varvec{v}}\in V, \end{aligned}$$

(2.14)

a functional $j: V\rightarrow \mathbb{R }^+$ by

$$\begin{aligned} j({\varvec{v}}) = \int _{\Gamma _C} g\Vert {\varvec{v}}_{\tau }\Vert \,ds \quad \forall \,{\varvec{v}}\in V, \end{aligned}$$

and ${\varvec{\ell }}(t)$, an element of $V$ given by

$$\begin{aligned}&\displaystyle ({\varvec{\ell }}(t),{\varvec{v}})_V=\int \limits _\Omega {{\varvec{f}}}_1(t)\cdot {\varvec{v}}\,dx +\int \limits _{\Gamma _F}{{\varvec{f}}}_2(t)\cdot {\varvec{v}}\,ds \quad \quad \forall \,{\varvec{v}}\in V. \end{aligned}$$

(2.15)

We know that ${\varvec{\ell }}(t)\in W^{1,\infty }(0,T;V)$ [15]. Assume the initial data satisfies

$$\begin{aligned} {{\varvec{u}}}_0 \in V,\quad a({{\varvec{u}}}_0,{\varvec{v}}) + j({\varvec{v}}) \ge ({\varvec{\ell }}(0),{\varvec{v}})_V \quad \forall \, v\in V. \end{aligned}$$

(2.16)

Following a standard argument [15], we can obtain the variational formulation of the quasistatic contact problem (2.2–2.9): Find ${{\varvec{u}}}: [0,T]\rightarrow V$ s.t. for $\mathrm{a.e.}\ t\in (0,T)$,

$$\begin{aligned} a({{\varvec{u}}}(t),{\varvec{v}}-\dot{{{\varvec{u}}}}(t)) + j({\varvec{v}}) - j(\dot{{{\varvec{u}}}}(t))&\ge ({\varvec{\ell }}(t),{\varvec{v}}-\dot{{{\varvec{u}}}}(t))_V\quad \forall \,{\varvec{v}}\in V, \end{aligned}$$

(2.17)

$$\begin{aligned} {{\varvec{u}}}(0)&= {{\varvec{u}}}_0. \end{aligned}$$

(2.18)

Under the assumptions (2.7), (2.12), (2.13) and (2.16), this problem has a unique solution ${{\varvec{u}}}\in W^{1,\infty }(0,T;V)$, moreover, the mapping $({\varvec{\ell }},{{\varvec{u}}}_0)\mapsto {{\varvec{u}}}$ is Lipschitz continuous from $W^{1,\infty }(0,T;V)\times V$ to $L^{\infty }(0,T;V)$ [15].

2.2 Notations and DG formulations

For brevity, in the following, we only consider the case $d=2$, although the discussion can be extended to the three dimensional case without problem. Given a bounded domain $D\subset \mathbb{R }^2$ and a positive integer $m, H^m(D)$ is the Sobolev space with the usual corresponding norm $\Vert \cdot \Vert _{m,D}$ and semi-norm $|\cdot |_{m,D}$. Let ${{\varvec{u}}}=(u_1,u_2)^T\in [H^m(D)]^2$ and define the corresponding norm by $\Vert {{\varvec{u}}}\Vert _{m,D}^2=\sum _{i=1,2}\Vert u_i\Vert _{m,D}^2$ and semi-norm by $|{{\varvec{u}}}|_{m,D}^2=\sum _{i=1,2}|u_i|_{m,D}^2$. Similarly, ${\varvec{\tau }}\in [L^2(\Omega )]^{2\times 2}_s$ is a matrix-valued function with each component $\tau _{ij}\in L^2(\Omega )$ and $\tau _{12} = \tau _{21}$. We assume $\Omega$ is a polygonal domain and consider a regular family of triangulations $\{\mathcal{T }_h\}_h$ of $\overline{\Omega }$ that is compatible with the boundary splitting: $\Gamma =\overline{\Gamma _D}\cup \overline{\Gamma _F}\cup \overline{\Gamma _C}$, i.e., if an element edge has a non-empty intersection with one of the sets $\Gamma _D, \Gamma _F$ and $\Gamma _C$, then the edge lies entirely in the corresponding closed set $\overline{\Gamma _D}$, $\overline{\Gamma _F}$, or $\overline{\Gamma _C}$. Let $h_K =\mathrm{diam}(K)$, $h = \max \{h_K: K\in \mathcal{T }_h\}$, and $h_e =\mathrm{length}(e)$. Denote by ${\mathcal{E }}_h$ the union of the boundaries of the elements $K$ of $\mathcal{T }_h, \mathcal{E }_h^i=\mathcal{E }_h \backslash \Gamma$ the set of all interior edges, and $\mathcal{E }_h^0=\mathcal{E }_h \backslash (\Gamma _F\cup \Gamma _C)$. We introduce the following finite element spaces:

$$\begin{aligned} \tilde{V}^h&= \left\{ {\varvec{v}}^h \in [L^2(\Omega )]^2: \;v^{h}_i |_K \in P_1(K)\ \forall \,K\in \mathcal{T }_h,\, i=1,2 \right\} ,\\ V^h&= \left\{ {\varvec{v}}^h\in \tilde{V}^h :\; v^{h}_\nu ({{\varvec{x}}})=0 \ \mathrm{for\,all\ nodes}\ {{\varvec{x}}}\in \overline{\Gamma _C} \right\} ,\\ W^h&= \left\{ {\varvec{\tau }}^h\in [L^2(\Omega )]^{2\times 2}_s:\, \tau ^{h}_{ij}|_K\in P_l(K)\ \forall \,K\in \mathcal{T }_h,\, i,j=1,2\right\} ,\quad l=0\ \mathrm{or }1. \end{aligned}$$

Here $P_l(K)$ stands for the set of all polynomials in $K$ with the total degree no more than $l\ge 0$. We know that $v^{h}_{\nu } = 0$ at all nodes on $\overline{\Gamma _C}$ guarantees $v^{h}_{\nu } = 0$ on $\Gamma _C$, consequently $\dot{v}^{h}_{\nu } = 0$ on $\Gamma _C$. For any vector-valued function ${\varvec{v}}$ and matrix-valued function ${\varvec{\tau }}, {\varvec{\varepsilon }}^h({\varvec{v}})$ and $\mathrm{div}^h {\varvec{\tau }}$ are defined by the relation ${\varvec{\varepsilon }}^h({\varvec{v}})={\varvec{\varepsilon }}({\varvec{v}})$ and $\mathrm{div}^h {\varvec{\tau }}=\mathrm{div}{\varvec{\tau }}$ on any element $K\in {\mathcal{T }}_h$.

Let $e$ be the common edge of two elements $K^+$ and $K^-$, and ${{\varvec{n}}}^{\alpha } = {{\varvec{n}}}|_{\partial K^{\alpha }}$ be the unit outward normal vector on $\partial K^{\alpha }$ with $\alpha =\pm$. For a scalar function $q$, let $q^{\alpha } = q|_{\partial K^{\alpha }}$ and similarly, for a vector-valued function ${\varvec{v}}$ and a matrix-valued function ${\varvec{\tau }}$, let ${\varvec{v}}^{\alpha }$ = ${\varvec{v}}|_{\partial K^{\alpha }}, {\varvec{\tau }}^{\alpha } = {\varvec{\tau }}|_{\partial K^{\alpha }}$. Then define the averages $\{\cdot \}$ and the jumps $[\cdot ]$, $[\![\cdot ]\!]$ on $e\in {\mathcal{E }}_h^i$ by

$$\begin{aligned}&\{q\} = \frac{1}{2}\,(q^+ + q^-),\quad \quad [q] = q^+ {{\varvec{n}}}^+ + q^- {{\varvec{n}}}^-,\\&\{{\varvec{v}}\} = \frac{1}{2}\,({\varvec{v}}^+ + {\varvec{v}}^-),\quad \quad [\![{\varvec{v}}]\!]= \frac{1}{2}\,({\varvec{v}}^+\otimes {{\varvec{n}}}^++{{\varvec{n}}}^+ \otimes {\varvec{v}}^++{\varvec{v}}^-\otimes {{\varvec{n}}}^-+{{\varvec{n}}}^-\otimes {\varvec{v}}^-),\\&\{{\varvec{\tau }}\} = \frac{1}{2}\,({\varvec{\tau }}^+ + {\varvec{\tau }}^-),\quad \quad [{\varvec{\tau }}] = {\varvec{\tau }}^+ {{\varvec{n}}}^+ + {\varvec{\tau }}^- {{\varvec{n}}}^-. \end{aligned}$$

Here ${{\varvec{u}}}\otimes {\varvec{v}}$ is a matrix with $u_iv_j$ as its $(i,j)$th element. If $e\in \mathcal{E }_h$ is an element edge on $\Gamma$, we set

$$\begin{aligned}&\{q\} = q,\quad \quad [q] = q{\varvec{\nu }},\\&\{{\varvec{v}}\} = {\varvec{v}},\quad \quad [\![{\varvec{v}}]\!]= \frac{1}{2}\,({\varvec{v}}\otimes {\varvec{\nu }}+{\varvec{\nu }}\otimes {\varvec{v}}),\\&\{{\varvec{\tau }}\} = {\varvec{\tau }},\quad \quad [{\varvec{\tau }}] = {\varvec{\tau }}{\varvec{\nu }}. \end{aligned}$$

For a vector-valued function ${\varvec{v}}$ and a matrix-valued function ${\varvec{\tau }}$, with a direct manipulation, we have

$$\begin{aligned} \sum _{K\in \mathcal{T }_{h}}\int _{\partial K}({\varvec{\tau }}{{\varvec{n}}})\cdot {\varvec{v}}\,ds =\sum _{e\in \mathcal{E }_{h}^{i}}\int _{e}[{\varvec{\tau }}]\cdot \{{\varvec{v}}\}\,ds+\sum _{e\in \mathcal{E }_{h}}\int _{e}\{{\varvec{\tau }}\}:[\![{\varvec{v}}]\!]\,ds. \end{aligned}$$

(2.19)

The lifting operators ${{\varvec{r}}}_0: \left( L^2(\mathcal E _h^0)\right) ^{2\times 2}_s\rightarrow W_h$, ${{\varvec{r}}}_e:\left( L^2(e)\right) ^{2\times 2}_s\rightarrow W_h$ are defined by

$$\begin{aligned} \int _\Omega {{\varvec{r}}}_0({\varvec{\phi }}):{\varvec{\tau }}\,dx&= -\int _\mathcal{E _h^0}{\varvec{\phi }}:\{{\varvec{\tau }}\}\,ds\quad \forall \,{\varvec{\tau }}\in W_h,\,{\varvec{\phi }}\in \left( L^2\left( \mathcal E _h^0\right) \right) ^{2\times 2}_s,\end{aligned}$$

(2.20)

$$\begin{aligned} \int _\Omega {{\varvec{r}}}_e({\varvec{\phi }}):{\varvec{\tau }}\,dx&= -\int _{e}{\varvec{\phi }}:\{{\varvec{\tau }}\}\,ds\quad \forall \,{\varvec{\tau }}\in W_h,\,{\varvec{\phi }}\in \left( L^2(e)\right) ^{2\times 2}_s. \end{aligned}$$

(2.21)

It is easy to check that the following identity and inequality hold

$$\begin{aligned} {{\varvec{r}}}_0({\varvec{\phi }})&= \sum _{e\in \mathcal{E }_h^0} {{\varvec{r}}}_e({\varvec{\phi }}|_e)\quad \forall \,{\varvec{\phi }}\in \left( L^2\left( \mathcal{E }_h^0\right) \right) ^{2\times 2}_s,\nonumber \\ \Vert {{\varvec{r}}}_0({\varvec{\phi }})\Vert ^2&= \Vert \sum _{e\in \mathcal{E }_h^0}{{\varvec{r}}}_e({\varvec{\phi }}|_e)\Vert ^2\le 3\sum _{e\in \mathcal{E }_h^0} \Vert {{\varvec{r}}}_e({\varvec{\phi }}|_e)\Vert ^2. \end{aligned}$$

(2.22)

We now present some DG formulations for the quasistatic contact problem (2.2)–(2.9). For this purpose, we multiply the Eqs. (2.2) and (2.3) by $\mathcal{C }^{-1}{\varvec{\tau }}$ and ${\varvec{v}}$, respectively, integrate on an arbitrary element $K$, and apply the integration by parts formula (2.1),

$$\begin{aligned} \int _K \mathcal{C }^{-1}{\varvec{\sigma }}:{\varvec{\tau }}\,dx&= -\int _K{{\varvec{u}}}\cdot \mathrm{div} {\varvec{\tau }}\,dx +\int _{\partial K}{{\varvec{u}}}\cdot ({\varvec{\tau }}{{\varvec{n}}})\,ds, \end{aligned}$$

(2.23)

$$\begin{aligned} \int _K{{\varvec{f}}}_1\cdot {\varvec{v}}\,dx&= \int _K{\varvec{\sigma }}:{\varvec{\varepsilon }}({\varvec{v}})\,dx -\int _{\partial K}({\varvec{\sigma }}{{\varvec{n}}})\cdot {\varvec{v}}\,ds. \end{aligned}$$

(2.24)

In above equations, we append superscript $h$ on ${\varvec{\sigma }}, {\varvec{\tau }}, {{\varvec{u}}}, {\varvec{v}}, \mathrm{div}$ and ${\varvec{\varepsilon }}$, add over all the elements, and use numerical trace $\widehat{{{\varvec{u}}}^h}$ and $\widehat{{\varvec{\sigma }}^h}$ to approximate ${{\varvec{u}}}$ and ${\varvec{\sigma }}$ over element edges to obtain

$$\begin{aligned} \int _{\Omega }\mathcal{C }^{-1}{\varvec{\sigma }}^h:{\varvec{\tau }}^h\,dx&= -\int _{\Omega }{{\varvec{u}}}^h\cdot \mathrm{div}^h {\varvec{\tau }}^h\,dx +\sum _{K\in \mathcal{T }_h}\int _{\partial K}\widehat{{{\varvec{u}}}^h}\cdot \left( {\varvec{\tau }}^h{{\varvec{n}}}_K\right) \,ds, \end{aligned}$$

(2.25)

$$\begin{aligned} \int _{\Omega }{{\varvec{f}}}_1\cdot {\varvec{v}}^h\,dx&= \int _{\Omega }{\varvec{\sigma }}^h: {\varvec{\varepsilon }}^h({\varvec{v}}^h)\,dx -\sum _{K\in \mathcal{T }_h}\int _{\partial K}\left( \widehat{{\varvec{\sigma }}^h}{{\varvec{n}}}_K\right) \cdot {\varvec{v}}^h\,ds, \end{aligned}$$

(2.26)

for all $({\varvec{\tau }}^h,{\varvec{v}}^h)\in W^h\times V^h$. The numerical traces $\widehat{{\varvec{\sigma }}^h}$ and $\widehat{{{\varvec{u}}}^h}$ will be selected to guarantee consistency and stability of the scheme.

To derive a new formulation which does not rely on ${\varvec{\sigma }}^h$ explicitly, using (2.1) and (2.19), we have from (2.25) and (2.26) that

$$\begin{aligned} \int _{\Omega }\mathcal{C }^{-1}{\varvec{\sigma }}^h:{\varvec{\tau }}^h\,dx&= \int _{\Omega }{\varvec{\varepsilon }}^h({{\varvec{u}}}^h):{\varvec{\tau }}^h\,dx +\int _{\mathcal{E }_h^i}\left\{ \widehat{{{\varvec{u}}}^h}-{{\varvec{u}}}^h\right\} \cdot [{\varvec{\tau }}^h]\,ds\nonumber \\&+\int _{\mathcal{E }_h}[\![\widehat{{{\varvec{u}}}^h}-{{\varvec{u}}}^h]\!]:\{{\varvec{\tau }}^h\}\,ds, \end{aligned}$$

(2.27)

$$\begin{aligned} \int _{\Omega }{{\varvec{f}}}_1\cdot {\varvec{v}}^h\,dx&= \int _{\Omega }{\varvec{\sigma }}^h: {\varvec{\varepsilon }}^h({\varvec{v}}^h)\,dx -\int _\mathcal{E _{h}^{i}}\left[ \widehat{{\varvec{\sigma }}^h}\right] \cdot \left\{ {\varvec{v}}^h\right\} \,ds\nonumber \\&-\int _\mathcal{E _{h}}[\![{\varvec{v}}^h]\!]: \left\{ \widehat{{\varvec{\sigma }}^h}\right\} \,ds. \end{aligned}$$

(2.28)

From now on, we assume the elasticity tensor $\mathcal{C }$ is constant. Then, we have $\mathcal{C } {\varvec{\varepsilon }}^h({\varvec{v}}^h)\in W^h$. Choosing ${\varvec{\tau }}^h=\mathcal{C } {\varvec{\varepsilon }}^h({\varvec{v}}^h)$ in (2.27), we get

$$\begin{aligned} \int _{\Omega }{\varvec{\sigma }}^h:{\varvec{\varepsilon }}^h({\varvec{v}}^h)\,dx&= \int _{\Omega }{\mathcal{C }} {\varvec{\varepsilon }}^h({{\varvec{u}}}^h):{\varvec{\varepsilon }}^h({\varvec{v}}^h)\, dx +\int _{\mathcal{E }_h^i}\left\{ {\widehat{{{{\varvec{u}}}}^{h}}}-{{\varvec{u}}}^h\right\} \cdot \left[ \mathcal{C } {\varvec{\varepsilon }}^h({\varvec{v}}^h)\right] \,ds\\&\,+\int _{\mathcal{E }_h}[\![{\widehat{{{\varvec{u}}}^h}}-{{\varvec{u}}}^h]\!]:\left\{ \mathcal{C } {\varvec{\varepsilon }}^h({\varvec{v}}^h)\right\} \,ds. \end{aligned}$$

Combination of this equation and (2.28) yields

$$\begin{aligned}&\int _{\Omega }\mathcal{C } {\varvec{\varepsilon }}^h({{\varvec{u}}}^h):{\varvec{\varepsilon }}^h({\varvec{v}}^h)\, dx + \int _{\mathcal{E }_h^i} \left\{ {\widehat{{{\varvec{u}}}^{h}}}-{{\varvec{u}}}^h\right\} \cdot \left[ \mathcal{C } {\varvec{\varepsilon }}^h({\varvec{v}}^h)\right] \,ds\nonumber \\&\quad +\int _{\mathcal{E }_h}[\![\widehat{{{\varvec{u}}}^h}-{{\varvec{u}}}^h]\!]:\left\{ \mathcal{C } {\varvec{\varepsilon }}^h({\varvec{v}}^h)\right\} \,ds\nonumber \\&\quad -\int _{\mathcal{E }_{h}^{i}}\left[ \widehat{{\varvec{\sigma }}^h}\right] \cdot \{{\varvec{v}}^h\}\,ds -\int _{\mathcal{E }_{h}}[\![{\varvec{v}}^h]\!]:\left\{ {\widehat{{\varvec{\sigma }}^{h}}}\right\} \,ds =\int _{\Omega }{{\varvec{f}}}_1\cdot {\varvec{v}}^h\,dx. \end{aligned}$$

(2.29)

We can get DG schemes from (2.29) by proper choices of numerical fluxes $\widehat{{\varvec{\sigma }}^h}$ and $\widehat{{{\varvec{u}}}^h}$, respecting three requirements: conservation, consistency, and stability. Conservation requires the numerical fluxes to be single-valued over all edges; consistency of the numerical fluxes needs $\widehat{{{\varvec{u}}}^h}({{\varvec{u}}})={{\varvec{u}}}|_{\mathcal{E }_h}$ and $\widehat{{\varvec{\sigma }}^h}({\varvec{\sigma }})={\varvec{\sigma }}|_{\mathcal{E }_h}$; stability is not easily ensured and it is usual to add a suitable penalty term (stability term) to guarantee it. We will introduce four consistent and stable DG methods. For all the following DG methods, we let $\widehat{{{\varvec{u}}}^h}$ and $\widehat{{\varvec{\sigma }}^h}$ satisfy the boundary condition (2.9), i.e.,

$$\begin{aligned} \left. \begin{aligned}&\widehat{u^h_\nu } = 0,\ |\widehat{{\varvec{\sigma }}^h_\tau }|\le g, \\&|\widehat{{\varvec{\sigma }}^h_\tau }|< g \Rightarrow \dot{\widehat{{{\varvec{u}}}^h_\tau }} = \mathbf{0},\\&|\widehat{{\varvec{\sigma }}^h_\tau }|= g \Rightarrow \exists \lambda \ge 0\ \mathrm{s.t.}\ \widehat{{\varvec{\sigma }}^h_\tau } = -\lambda \dot{\widehat{{{\varvec{u}}}^h_\tau }} \end{aligned} \right\} \mathrm{on}\ \Gamma _C\times (0,T). \end{aligned}$$

(2.30)

Choose

$$\begin{aligned} \left\{ \begin{aligned}&{\widehat{{{\varvec{u}}}^{h}}}=\left\{ {{\varvec{u}}}^h\right\} \quad \mathrm{on}\ \{\mathcal{E }_h\backslash \Gamma _D\}\times (0,T), \quad \quad {\widehat{{{\varvec{u}}}^{h}}}=\mathbf{0}\quad \mathrm{on}\ \Gamma _D\times (0,T),\\&{\widehat{{\varvec{\sigma }}^{h}}}=\{\mathcal{C } {\varvec{\varepsilon }}^h({{\varvec{u}}}^h)\}-\frac{\eta }{{\widetilde{h}}} [\![{{\varvec{u}}}^h]\!]\quad \mathrm{on}\ \mathcal{E }_h^0\times (0,T),\quad \quad {\widehat{{\varvec{\sigma }}^{h}}}{\varvec{\nu }}={{\varvec{f}}}_2\quad \mathrm{on}\ \Gamma _F\times (0,T), \end{aligned} \right. \end{aligned}$$

where $\eta$ is a positive, bounded, piecewise constant function on $\mathcal{E }_h^0$, and $\widetilde{h}$ is a piecewise constant function on $\mathcal{E }_h^0$ with $\widetilde{h}|_e=h_e$ for $e\in \mathcal{E }_h^0$. Denote $\eta _e=\eta |_e, e\in \mathcal{E }_h^0$. Then we obtain from (2.29) that

$$\begin{aligned} B_{1,h}^{(1)}({{\varvec{u}}}^h,{\varvec{v}}^h)=\int _{\Omega }{{\varvec{f}}}_1\cdot {\varvec{v}}^h\,dx +\int _{\Gamma _F}{{\varvec{f}}}_2\cdot {\varvec{v}}^h\,ds +\int _{\Gamma _C}{\widehat{{\varvec{\sigma }}^{h}}}{\varvec{\nu }}\cdot {\varvec{v}}^h\,ds, \end{aligned}$$

(2.31)

where

$$\begin{aligned} B_{1,h}^{(1)}({{\varvec{u}}}^h,{\varvec{v}}^h)&:= \int _{\Omega }\mathcal{C } {\varvec{\varepsilon }}^h({{\varvec{u}}}^h): {\varvec{\varepsilon }}^h({\varvec{v}}^h)\,dx -\int _{\mathcal{E }_h^0}[\![{{\varvec{u}}}^h]\!]: \{\mathcal{C }{\varvec{\varepsilon }}^h({\varvec{v}}^h)\}\,ds\nonumber \\&-\int _{\mathcal{E }_{h}^0}[\![{\varvec{v}}^h]\!]: \{\mathcal{C }{\varvec{\varepsilon }}^h({{\varvec{u}}}^h)\}\,ds +\int _{\mathcal{E }_{h}^0}\frac{\eta }{\widetilde{h}} [\![{{\varvec{u}}}^h]\!]:[\![{\varvec{v}}^h]\!]\,ds. \end{aligned}$$

(2.32)

Let ${\varvec{v}}^h = {{\varvec{w}}}^h - \dot{{{\varvec{u}}}}^h$ with ${{\varvec{w}}}^h\in V^h$. Using (2.30), we can derive from the Eq. (2.31) that (see also [15])

$$\begin{aligned} B_{1,h}^{(1)}({{\varvec{u}}}^h,{{\varvec{w}}}^h-\dot{{{\varvec{u}}}}^h) +j({{\varvec{w}}}^h) - j(\dot{{{\varvec{u}}}}^h)\ge ({\varvec{\ell }}(t),{{\varvec{w}}}^h-\dot{{{\varvec{u}}}}^h)_V \quad \forall \, {{\varvec{w}}}^h \in V^h. \qquad \end{aligned}$$

(2.33)

The penalty term in $B_{1,h}^{(1)}({{\varvec{u}}}^h,{\varvec{v}}^h)$ is $\int _\mathcal{E _{h}^0}\eta \widetilde{h}^{-1}[\![{{\varvec{u}}}^h ]\!]:[\![{\varvec{v}}^h]\!]\,ds$ and (2.33) is an interior penalty (IP) formulation [14]. With the lift operator ${{\varvec{r}}}_0$, we can rewrite $B_{1,h}^{(1)}$ as

$$\begin{aligned} B_{2,h}^{(1)}({{\varvec{u}}}^h,{\varvec{v}}^h)&:= \int _{\Omega }\mathcal{C } {\varvec{\varepsilon }}^h({{\varvec{u}}}^h):\left( {\varvec{\varepsilon }}^h({\varvec{v}}^h)+ {{\varvec{r}}}_0\left( [\![{\varvec{v}}^h]\!]\right) \right) \,dx\nonumber \\&+\int _{\Omega }{{\varvec{r}}}_0\left( [\![{{\varvec{u}}}^h]\!]\right) : \mathcal{C }{\varvec{\varepsilon }}^h({\varvec{v}}^h)\,dx+\int _{ \mathcal{E }_{h}^0}\frac{\eta }{\widetilde{h}} [\![{{\varvec{u}}}^h]\!]:[\![{\varvec{v}}^h]\!]\,ds. \end{aligned}$$

(2.34)

Notice that (2.32) and (2.34) are equivalent on $V^h$, implying that either one can be used to define the numerical solution ${{\varvec{u}}}^h$. In this paper, we give a priori error estimate for the first formula (2.32). Because (2.32) and (2.34) are equivalent on $V^h$, we will prove the stability for the second formula $B_{2,h}^{(1)}$ on $V^h$, which guarantees the stability for the first formulation $B_{1,h}^{(1)}$ on $V^h$. This comment is valid for the other DG methods to be introduced below.

Using the local lifting operator ${{\varvec{r}}}_e$, we can give the second example. Taking

$$\begin{aligned} \left\{ \begin{aligned}&{\widehat{{{\varvec{u}}}^{h}}}=\left\{ {{\varvec{u}}}^h\right\} \quad \mathrm{on}\ \{\mathcal{E }_h\backslash \Gamma _D\}\times (0,T), \quad \quad \widehat{{{\varvec{u}}}^h}=\mathbf{0}\quad \mathrm{on}\ \Gamma _D\times (0,T),\\&{\widehat{{\varvec{\sigma }}^{h}}}=\{\mathcal{C }{\varvec{\varepsilon }}^h({{\varvec{u}}}^h)\} +\left\{ \mathcal{C }{{\varvec{r}}}_0\left( [\![{{\varvec{u}}}^h]\!]\right) \right\} +\eta \left\{ \mathcal{C }{{\varvec{r}}}_e\left( [\![{{\varvec{u}}}^h]\!]\right) \right\} \quad \mathrm{on}\ \mathcal{E }_h^0\times (0,T),\\&{\widehat{{\varvec{\sigma }}^{h}}}{\varvec{\nu }}={{\varvec{f}}}_2\quad \mathrm{on}\ \Gamma _F\times (0,T) \end{aligned} \right. \end{aligned}$$

in (2.29), we get

$$\begin{aligned} B_{1,h}^{(2)}({{\varvec{u}}}^h,{\varvec{v}}^h)&:= \int _{\Omega }\mathcal{C } {\varvec{\varepsilon }}^h({{\varvec{u}}}^h):{\varvec{\varepsilon }}^h({\varvec{v}}^h)\,dx -\int _{\mathcal{E }_h^0}[\![{{\varvec{u}}}^h]\!]: \left\{ \mathcal{C }{\varvec{\varepsilon }}^h({\varvec{v}}^h)\right\} \,ds\\&-\int _{\mathcal{E }_{h}^0}[\![{\varvec{v}}^h]\!]: \left\{ \mathcal{C }{\varvec{\varepsilon }}^h({{\varvec{u}}}^h)\right\} \,ds +\int _{\Omega }{{\varvec{r}}}_0\left( [\![{\varvec{v}}^h]\!]\right) : \mathcal{C }{{\varvec{r}}}_0\left( [\![{{\varvec{u}}}^h]\!]\right) \,dx\\&+\sum _{e\in \mathcal{E }_h^0}\int _{\Omega }\eta \mathcal{C }{{\varvec{r}}}_e\left( [\![{{\varvec{u}}}^h]\!]\right) : {{\varvec{r}}}_e\left( [\![{\varvec{v}}^h]\!]\right) \,dx, \end{aligned}$$

or equivalently,

$$\begin{aligned} B_{2,h}^{(2)}({{\varvec{u}}}^h,{\varvec{v}}^h)&:= \int _{\Omega } \mathcal{C }\left( {\varvec{\varepsilon }}^h({{\varvec{u}}}^h) +{{\varvec{r}}}_0\left( [\![{{\varvec{u}}}^h]\!]\right) \right) :\left( {\varvec{\varepsilon }}^h({\varvec{v}}^h) +{{\varvec{r}}}_0\left( [\![{\varvec{v}}^h]\!]\right) \right) \,dx\\&+\sum _{e\in \mathcal{E }_h^0}\int _{\Omega }\eta \mathcal{C }{{\varvec{r}}}_e\left( [\![{{\varvec{u}}}^h]\!]\right) : {{\varvec{r}}}_e\left( [\![{\varvec{v}}^h]\!]\right) \,dx, \end{aligned}$$

which is an extension of the method of Brezzi et al. [7].

With the choice

$$\begin{aligned} \left\{ \begin{aligned} {\widehat{{{{\varvec{u}}}}^{h}}}=&\left\{ {{\varvec{u}}}^h\right\} \quad \mathrm{on}\ \left\{ \mathcal{E }_h\backslash \Gamma _D\right\} \times (0,T), \quad \quad {\widehat{{{\varvec{u}}}^{h}}}=\mathbf{0}\quad \mathrm{on}\, \Gamma _D\times (0,T),\\ {\widehat{{\varvec{\sigma }}^{h}}}=&\left\{ \mathcal{C }{\varvec{\varepsilon }}^h({{\varvec{u}}}^h)\right\} \!+\!\eta \left\{ \mathcal{C }{{\varvec{r}}}_e\left( [\![{{\varvec{u}}}^h]\!]\right) \right\} \mathrm{on}\ \mathcal{E }_h^0\times (0,T), {\widehat{{\varvec{\sigma }}^{h}}}{\varvec{\nu }}={{\varvec{f}}}_2\quad \mathrm{on}\ \Gamma _F\times (0,T), \end{aligned} \right. \end{aligned}$$

we obtain a DG formulation extended from the method of Bassi et al. [4],

$$\begin{aligned} B_{1,h}^{(3)}({{\varvec{u}}}^h,{\varvec{v}}^h)&:= \int _{\Omega }\mathcal{C } {\varvec{\varepsilon }}^h({{\varvec{u}}}^h):{\varvec{\varepsilon }}^h({\varvec{v}}^h)\,dx -\int _{\mathcal{E }_h^0}[\![{{\varvec{u}}}^h]\!]: \left\{ \mathcal{C }{\varvec{\varepsilon }}^h({\varvec{v}}^h)\right\} \,ds\\&-\int _{\mathcal{E }_{h}^0}[\![{\varvec{v}}^h]\!]: \left\{ \mathcal{C }{\varvec{\varepsilon }}^h({{\varvec{u}}}^h)\right\} \,ds +\sum _{e\in {\mathcal{E }}_h^0}\int _{\Omega }\eta {\mathcal{C }}{{\varvec{r}}}_e\left( [\![{{\varvec{u}}}^h]\!]\right) : {{\varvec{r}}}_e\left( [\![{\varvec{v}}^h]\!]\right) \,dx, \end{aligned}$$

or equivalently,

$$\begin{aligned} B_{2,h}^{(3)}({{\varvec{u}}}^h,{\varvec{v}}^h)&:= \int _{\Omega }\mathcal{C } {\varvec{\varepsilon }}^h({{\varvec{u}}}^h):\left( {\varvec{\varepsilon }}^h({\varvec{v}}^h)+{{\varvec{r}}}_0 \left( [\![{\varvec{v}}^h]\!]\right) \right) \,dx\nonumber \\&+\int _{\Omega }{{\varvec{r}}}_0\left( [\![{{\varvec{u}}}^h]\!]\right) :\mathcal{C }{\varvec{\varepsilon }}^h({\varvec{v}}^h)\,dx+\sum _{e\in \mathcal{E }_h^0}\int _{\Omega }\eta \mathcal{C }{{\varvec{r}}}_e\left( [\![{{\varvec{u}}}^h]\!]\right) :{{\varvec{r}}}_e\left( [\![{\varvec{v}}^h]\!]\right) \,dx. \end{aligned}$$

If we choose

$$\begin{aligned} \left\{ \begin{aligned} {\widehat{{{{\varvec{u}}}}_{h}}}=&\left\{ {{\varvec{u}}}^h\right\} \quad \mathrm{on}\ \{\mathcal{E }_h\backslash \Gamma _D\}\times (0,T), \quad \quad \widehat{{{{\varvec{u}}}}^{h}}=\mathbf{0}\quad \mathrm{on} \ \Gamma _D\times (0,T),\\ {\widehat{{\varvec{\sigma }}^{h}}}=&\left\{ \mathcal{C }{\varvec{\varepsilon }}^h({{\varvec{u}}}^h)\right\} +\left\{ \mathcal{C }{{\varvec{r}}}_0\left( [\![{{\varvec{u}}}^h]\!]\right) \right\} -\frac{\eta }{\widetilde{h}}[\![{{\varvec{u}}}^h]\!]\quad \mathrm{on}\ \mathcal{E }_h^0\times (0,T),\\ {\widehat{{\varvec{\sigma }}^{h}}}{\varvec{\nu }}=&{{\varvec{f}}}_2\quad \mathrm{on}\ \Gamma _F\times (0,T), \end{aligned} \right. \end{aligned}$$

then

$$\begin{aligned} B_{1,h}^{(4)}({{\varvec{u}}}^h,{\varvec{v}}^h)&:= \int _{\Omega }\mathcal{C }{\varvec{\varepsilon }}^h ({{\varvec{u}}}^h):{\varvec{\varepsilon }}^h({\varvec{v}}^h)\,dx -\int _{\mathcal{E }_h^0}[\![{{\varvec{u}}}^h]\!]: \left\{ \mathcal{C }{\varvec{\varepsilon }}^h({\varvec{v}}^h)\right\} \,ds\\&-\int _{\mathcal{E }_{h}^0}[\![{\varvec{v}}^h]\!]: \left\{ \mathcal{C }{\varvec{\varepsilon }}^h({{\varvec{u}}}^h)\right\} \,ds +\int _{\Omega } \mathcal{C }{{\varvec{r}}}_0\left( [\![{{\varvec{u}}}^h]\!]\right) : {{\varvec{r}}}_0\left( [\![{\varvec{v}}^h]\!]\right) \,dx\\&+\int _{\mathcal{E }_{h}^0}\frac{\eta }{{\widetilde{h}}}[\![{{\varvec{u}}}^h]\!]: [\![{\varvec{v}}^h]\!]\,ds, \end{aligned}$$

or equivalently,

$$\begin{aligned} B_{2,h}^{(4)}({{\varvec{u}}}^h,{\varvec{v}}^h)&:= \int _{\Omega }\mathcal{C } \left( {\varvec{\varepsilon }}^h({{\varvec{u}}}^h) +{{\varvec{r}}}_0\left( [\![{{\varvec{u}}}^h]\!]\right) \right) :\left( {\varvec{\varepsilon }}^h({\varvec{v}}^h) +{{\varvec{r}}}_0\left( [\![{\varvec{v}}^h]\!]\right) \right) \,dx\\&+\int _\mathcal{E _{h}^0} \frac{\eta }{\widetilde{h}} [\![{{\varvec{u}}}^h]\!]:[\![{\varvec{v}}^h]\!]\,ds, \end{aligned}$$

which is an extension of the local DG (LDG) method [11].

Spatially semi-discrete DG approximation. Let $B_h({{\varvec{u}}}^h,{\varvec{v}}^h)$ be one of the bilinear forms $B^{(j)}_{1,h}({{\varvec{u}}}^h,{\varvec{v}}^h)$ with $j=1,\ldots ,4$. Then a spatially semi-discrete DG approximation for the quasistatic contact problem (2.17) is: Find ${{\varvec{u}}}^h :[0,T]\rightarrow V^h$ such that

$$\begin{aligned} B_h\left( {{\varvec{u}}}^h(t),{\varvec{v}}^h-\dot{{{\varvec{u}}}}^{h}(t)\right) + j({\varvec{v}}^h) - j(\dot{{{\varvec{u}}}}^{h}(t))&\ge ({\varvec{\ell }}(t),{\varvec{v}}^h-\dot{{{\varvec{u}}}}^h(t))_V \qquad \forall \,{\varvec{v}}^h \in V^h,\end{aligned}$$

(2.35)

$$\begin{aligned} {{\varvec{u}}}^h(0)&= P^h_B{{\varvec{u}}}_{0}. \end{aligned}$$

(2.36)

Here $P^h_B$ is the $B_h$-projection from $V$ to $V^h$ defined by

$$\begin{aligned} B_h(P^h_B{{\varvec{u}}}_{0}-{{\varvec{u}}}_0,{\varvec{v}}^h) = 0 \qquad \forall {\varvec{v}}^h\in V^h. \end{aligned}$$

As we will see later, the bilinear form $B_h$ is bounded (Lemma 3.3) and coercive (Lemma 3.4) on $V^h$; so $P^h_B{{\varvec{u}}}_{0}$ exists and is unique.

Fully discrete approximation schemes. In addition to the finite element $V^h$, we need a partition of the time interval: $[0,T] =\bigcup _{n=1}^{N}[t_{n-1},t_n]$ with $0=t_0<t_1<\cdots <t_N=T$. Denote $k_n=t_n-t_{n-1}$ for the length of the sub-interval $[t_{n-1},t_n]$, and $k=\max _{n}k_n$. We allow an arbitrary partition. For the given function ${{\varvec{f}}}_1\in W^{1,\infty }(0,T;(L^2(\Omega ))^d)$, ${{\varvec{f}}}_2\in W^{1,\infty }(0,T; (L^2(\Gamma _F))^d)$ and the solution ${{\varvec{u}}}\in W^{1,\infty }(0,T;V)$, we use the notation ${{\varvec{u}}}_n = {{\varvec{u}}}(t_n)$ and ${\varvec{\ell }}_n = {\varvec{\ell }}(t_n)$, which are well-defined due to the Sobolev embedding $W^{1,\infty }(0,T;V) \hookrightarrow C(0,T;V)$. The symbol $\Delta {{\varvec{u}}}_n$ is used to denote the backward difference ${{\varvec{u}}}_n-{{\varvec{u}}}_{n-1}$, and $\delta _n {{\varvec{u}}}_n = \Delta {{\varvec{u}}}_n/k_n$ for the backward divided difference. No summation is implied over the repeated index $n$.

Let $B_h({{\varvec{u}}}^h,{\varvec{v}}^h)$ be one of the bilinear forms $B^{(j)}_{1,h}({{\varvec{u}}}^h,{\varvec{v}}^h)$ with $j=1,\ldots ,4$. Then a fully discrete approximation of (2.17) is: Find ${{\varvec{u}}}^{hk}=\{{{\varvec{u}}}^{hk}_n\}^N_{n=0}\subset V^h$ such that

$$\begin{aligned} B_h\left( {{\varvec{u}}}_n^{hk},{\varvec{v}}^h-\delta _n{{\varvec{u}}}_n^{hk}\right) + j({\varvec{v}}^h) - j\left( \delta _n{{\varvec{u}}}_n^{hk}\right)&\ge \left( {\varvec{\ell }}_{n},{\varvec{v}}^h-\delta _n{{\varvec{u}}}_n^{hk}\right) _V \qquad \forall \,{\varvec{v}}^h \in V^h,\end{aligned}$$

(2.37)

$$\begin{aligned} {{\varvec{u}}}^{hk}_0&= P^h_B{{\varvec{u}}}_{0}. \end{aligned}$$

(2.38)

In the following two sections, we will derive a priori error analysis for the spatially semi-discrete DG approximation and fully discrete approximation schemes, respectively.

3 Error estimates for the spatially semi-discrete approximation

As a preparation for error analysis, we first consider the consistency of the DG schemes, and the boundedness and stability of the bilinear forms.

3.1 Consistency, boundedness and stability

We notice that if the solution of (2.17) has the regularity ${{\varvec{u}}}\in L^{2}(0,T;[H^2(\Omega )]^2)$, then (2.2)–(2.5) and (2.9) are valid a.e., and on any interior edge $e$, $[\![{{\varvec{u}}}]\!]= \mathbf{0}, \{{{\varvec{u}}}\} = {{\varvec{u}}}, \{{\varvec{\varepsilon }}({{\varvec{u}}})\} = {\varvec{\varepsilon }}({{\varvec{u}}}), [{\varvec{\sigma }}] = \mathbf{0}, \{{\varvec{\sigma }}\} = {\varvec{\sigma }}$. For all DG methods introduced in the previous section, we first show the consistency of the DG schemes.

Lemma 3.1

(Consistency) Assume ${{\varvec{u}}}\in L^{2}(0,T;[H^2(\Omega )]^2)$ for the solution of (2.17). Then for the DG methods $B_h({{\varvec{w}}},{\varvec{v}})=B_{1,h}^{(j)}({{\varvec{w}}},{\varvec{v}})$ with $j=1,\ldots ,4$, we have

$$\begin{aligned} B_h({{\varvec{u}}},{\varvec{v}}^h-\dot{{{\varvec{u}}}}) + j({\varvec{v}}^h) - j(\dot{{{\varvec{u}}}}) \ge ({\varvec{\ell }}(t),{\varvec{v}}^h-\dot{{{\varvec{u}}}})\qquad \forall \,{\varvec{v}}^h\in V^h. \end{aligned}$$

(3.1)

Proof

Using (2.2), we obtain, for any ${\varvec{v}}^h\in V^h$,

$$\begin{aligned} B_h({{\varvec{u}}},{\varvec{v}}^h-\dot{{{\varvec{u}}}})&= \int _{\Omega } \mathcal{C }{\varvec{\varepsilon }}({{\varvec{u}}}):{\varvec{\varepsilon }}^h({\varvec{v}}^h-\dot{{{\varvec{u}}}}) \,dx -\int _\mathcal{E _{h}^0}[\![{\varvec{v}}^h-\dot{{{\varvec{u}}}}]\!]: \mathcal{C }{\varvec{\varepsilon }}({{\varvec{u}}})\,ds\\&= \sum _{K\in \mathcal{T }_h}\int _{K}{\varvec{\sigma }}:{\varvec{\varepsilon }}^h({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,dx -\int _{\mathcal{E }_h^0}[\![{\varvec{v}}^h-\dot{{{\varvec{u}}}}]\!]:{\varvec{\sigma }}\,ds. \end{aligned}$$

By (2.1), (2.19) and noting that $[{\varvec{\sigma }}]=\mathbf{0}$ on $\mathcal{E }_h^i$, we get

$$\begin{aligned}&\sum _{K\in \mathcal{T }_h}\int _{K}{\varvec{\sigma }}: {\varvec{\varepsilon }}^h({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,dx =\sum _{K\in \mathcal{T }_h}\int _{K}-\mathrm{div}{\varvec{\sigma }}\cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,dx \\&\quad +\sum _{K\in \mathcal{T }_h}\int _{\partial K} ({\varvec{\sigma }}{{\varvec{n}}}_K)\cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,ds=\sum _{K\in \mathcal{T }_h}\int _{K}{{\varvec{f}}}_1\cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,dx + \int _{\mathcal{E }_h}[\![{\varvec{v}}^h-\dot{{{\varvec{u}}}}]\!]:{\varvec{\sigma }}\,ds. \end{aligned}$$

Then

$$\begin{aligned} B_h({{\varvec{u}}},{\varvec{v}}^h-\dot{{{\varvec{u}}}})&= \int _{\Omega }{{\varvec{f}}}_1\cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,dx +\int _{\Gamma _F}{{\varvec{f}}}_2\cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,ds+\int _{\Gamma _C} ({\varvec{\sigma }}{\varvec{\nu }})\cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,ds\\&= ({\varvec{\ell }},{\varvec{v}}^h-\dot{{{\varvec{u}}}})_V+\int _{\Gamma _C} ({\varvec{\sigma }}_{\tau }\cdot {\varvec{v}}^{h}_{\tau } -{\varvec{\sigma }}_{\tau }\cdot \dot{{{\varvec{u}}}}_{\tau })\,ds\\&\ge ({\varvec{\ell }},{\varvec{v}}^h-\dot{{{\varvec{u}}}})_V - j({\varvec{v}}^{h}) + j(\dot{{{\varvec{u}}}}). \end{aligned}$$

The last inequality is obtained by (2.9). Hence, (3.1) holds. $\square$

To consider the boundedness and stability of the bilinear form $B_h$, as in [18], let $V(h) = V^h + V\cap [H^2(\Omega )]^2$, and for ${\varvec{v}}\in V(h)$, define seminorms as follows:

$$\begin{aligned} |{\varvec{v}}|^2_{K} := \int _K {\varvec{\varepsilon }}({\varvec{v}}):{\varvec{\varepsilon }}({\varvec{v}})\,dx, \quad \quad |{\varvec{v}}|^2_{h}: = \sum _{K\in \mathcal{T }_h} |{\varvec{v}}|^2_{K}, \quad \quad |{\varvec{v}}|^2_{*} := \sum _{e\in \mathcal{E }^0_h} h_e^{-1}\Vert [\![{\varvec{v}}]\!]\Vert ^2_{0,e}, \end{aligned}$$

where

$$\begin{aligned} \Vert [\![{\varvec{v}}]\!]\Vert ^2_{0,e}=\int _e[\![{\varvec{v}}]\!]: [\![{\varvec{v}}]\!]\,ds. \end{aligned}$$

Then define norms by

$$\begin{aligned} |||{\varvec{v}}|||^2_*: = |{\varvec{v}}|^2_{h} + |{\varvec{v}}|^2_{*}, \quad \quad |||{\varvec{v}}|||^2 : = |||{\varvec{v}}|||^2_*+ \sum _{K\in \mathcal{T }_h}h_K^2|{\varvec{v}}|^2_{2,K}. \end{aligned}$$

(3.2)

The norm $|||\cdot |||_*$ defined in (3.2) is equivalent to the usual DG-norm $(|\cdot |_{1,h}^2 + |\cdot |_{*}^2)^{1/2}$, thanks to Korn’s inequality (see [5] or [2, Proposition 4.6]). Here, $|\cdot |_{1,h}^2 \!=\! \sum _{K\in \mathcal{T }_h}\! | \cdot |_{1,K}^2$. In the following, we also need the norm $\Vert \cdot \Vert _{0,h}$ defined through the relation $\Vert \cdot \Vert _{0,h}^2 = \sum _{K\in \mathcal{T }_h} \Vert \cdot \Vert _{0,K}^2$.

Before presenting the boundedness and stability properties of the bilinear forms, we state a useful estimate for the lifting operator ${{\varvec{r}}}_e$, which is a trivial extension to vector-valued functions of Lemma 2 of [8]; see also [18].

Lemma 3.2

For any ${\varvec{v}}\in V(h)$ and $e\in \mathcal{E }_h^0$,

$$\begin{aligned} C_1 h_e^{-1}\Vert [\![{\varvec{v}}]\!]\Vert ^2_{0,e} \le \Vert {{\varvec{r}}}_e([\![{\varvec{v}}]\!])\Vert ^2_{0,h}\le C_2 h_e^{-1}\Vert [\![{\varvec{v}}]\!]\Vert ^2_{0,e}. \end{aligned}$$

(3.3)

From (3.3) and (2.22), we have

$$\begin{aligned} \Vert {{\varvec{r}}}_0([\![{\varvec{v}}]\!])\Vert ^2_{0,h}= \Vert \sum _{e\in \mathcal{E }_h^0}{{\varvec{r}}}_e([\![{\varvec{v}}]\!]) \Vert ^2_{0,h}\le 3 C_2 \sum _{e\in \mathcal{E }_h^0}h_e^{-1} \Vert [\![{\varvec{v}}]\!]\Vert ^2_{0,e}=3C_2|{\varvec{v}}|_*^2. \end{aligned}$$

For boundedness of the primal forms $B_h$, recalling (2.7) for the boundedness, symmetry and positive definiteness of $\mathcal{C }$, we know that the seminorm $|\cdot |_{a,h}$ defined by

$$\begin{aligned} |{\varvec{v}}|_{a,h}^2 = \sum _{K\in \mathcal{T }_h}a_K({\varvec{v}},{\varvec{v}}) = \sum _{K\in \mathcal{T }_h}\int _K \mathcal{C }{\varvec{\varepsilon }}({\varvec{v}}):{\varvec{\varepsilon }}({\varvec{v}})\,dx, \quad \quad {\varvec{v}}\in V(h), \end{aligned}$$

is equivalent to $|\cdot |_{h}$ on $V(h)$. Then we have the boundedness of $B_h$ as follows.

Lemma 3.3

(Boundedness) For $1\le j\le 4, B_h=B_{1,h}^{(j)}$ satisfies

$$\begin{aligned} B_h({{\varvec{w}}},{\varvec{v}})\lesssim |||{{\varvec{w}}}|||\,|||{\varvec{v}}|||\quad \quad \quad \forall \, {{\varvec{w}}},{\varvec{v}}\in V(h). \end{aligned}$$

(3.4)

Proof

We use the Cauchy-Schwarz inequality to bound them term by term,

$$\begin{aligned} \int _\Omega \mathcal{C }{\varvec{\varepsilon }}^h({{\varvec{w}}}):{\varvec{\varepsilon }}^h({\varvec{v}})\,dx&\lesssim |{{\varvec{w}}}|_{h}|{\varvec{v}}|_{h},\end{aligned}$$

(3.5)

$$\begin{aligned} \int _\Omega \mathcal{C }{{\varvec{r}}}_0([\![{{\varvec{w}}}]\!]) :{{\varvec{r}}}_0([\![{\varvec{v}}]\!])\,dx&\lesssim |{{\varvec{w}}}|_*|{\varvec{v}}|_*,\end{aligned}$$

(3.6)

$$\begin{aligned} \int _{\mathcal{E }_h^0}\eta \widetilde{h}^{-1}[\![{{\varvec{w}}}]\!]:[\![{\varvec{v}}]\!]\,ds&\le \max _{e\in \mathcal{E }_h^0} \eta _e |{{\varvec{w}}}|_*|{\varvec{v}}|_*,\end{aligned}$$

(3.7)

$$\begin{aligned} \sum _{e\in \mathcal{E }_h^0}\int _{\Omega }\eta \, {{\varvec{r}}}_e([\![{{\varvec{w}}}]\!]):{{\varvec{r}}}_e([\![{\varvec{v}}]\!])\,dx&\lesssim \max _{e\in \mathcal{E }_h^0} \eta _e |{{\varvec{w}}}|_*|{\varvec{v}}|_*. \end{aligned}$$

(3.8)

Here “$\lesssim \cdots$” stands for “$\le C\cdots$”, where $C$ is a positive generic constant independent of $h$ and $k$, which may take on different values at different places. Applying the trace inequality for a scalar function ([3, Exercise 10.3.2]) to each component of a vector function, we can get the trace inequality

$$\begin{aligned} \Vert {\varvec{\varepsilon }}^h({\varvec{v}})\Vert ^2_{0,e}\lesssim h_e^{-1}|{\varvec{v}}|^2_{1,K}+h_K|{\varvec{v}}|^2_{2,K}. \end{aligned}$$

Using this inequality, we have

$$\begin{aligned} \int _{\mathcal{E }_h^0}[\![{{\varvec{w}}}]\!]:\{\mathcal{C }{\varvec{\varepsilon }}^h({\varvec{v}})\}\,ds&\lesssim \left( \sum _{e\in \mathcal{E }_h^0}h_e^{-1}\Vert [\![{{\varvec{w}}}]\!]\Vert ^2_{0,e}\right) ^{1/2}\left( \sum _{e\in \mathcal{E }_h^0}h_e\Vert \{{\varvec{\varepsilon }}^h({\varvec{v}})\}\Vert ^2_{0,e}\right) ^{1/2}\nonumber \\&\lesssim |{{\varvec{w}}}|_* \left( \sum _{K\in \mathcal{T }_h} \left( |{\varvec{v}}|^2_{1,K}+h_K^2|{\varvec{v}}|^2_{2,K}\right) \right) ^{1/2} \le |{{\varvec{w}}}|_* |||{\varvec{v}}|||.\nonumber \\ \end{aligned}$$

(3.9)

The inequalities (3.5) and (3.9) are needed in the analysis of all bilinear forms. For the DG methods with the bilinear form $B_{1,h}^{(j)}, j=1, 4$, the inequality (3.7) is needed. The inequality (3.6) is needed by the formulas $B_{1,h}^{(j)}$ with $j=2, 4$. For the methods with the bilinear forms $B_{1,h}^{(j)}$, $j=2, 3$, the inequality (3.8) is needed. Proof for the boundedness of $B_h$ is completed. $\square$

For the stability, note that $|||{\varvec{v}}|||=|||{\varvec{v}}|||_*$ for any ${\varvec{v}}\in V^h$. Denote

$$\begin{aligned} \eta _0:=\min _{e\in \mathcal{E }_h^0} \eta _e. \end{aligned}$$

(3.10)

Since $B_{1,h}^{(j)}$ and $B_{2,h}^{(j)}$ coincide on $V^h$, once we have proved the stability for $B_{2,h}^{(j)}$ on $V^h$, the stability of $B_{1,h}^{(j)}$ on $V^h$ follows. We use the Cauchy-Schwarz inequality and Lemma 3.2 to get

$$\begin{aligned} B_{2,h}^{(1)}({\varvec{v}},{\varvec{v}})&= |{\varvec{v}}|_{a,h}^2 + 2\int _{\Omega } \mathcal{C }{\varvec{\varepsilon }}^h({\varvec{v}}):{{\varvec{r}}}_0([\![{\varvec{v}}]\!])\,dx +\int _{\mathcal{E }_h^0}\eta \widetilde{h}^{-1} [\![{\varvec{v}}]\!]:[\![{\varvec{v}}]\!]\, ds\\&\gtrsim |{\varvec{v}}|_{h}^2-\epsilon |{\varvec{v}}|_{h}^2-\frac{1}{\epsilon } \Vert {{\varvec{r}}}_0([\![{\varvec{v}}]\!])\Vert _{0,h}^2 +\eta _0 \sum _{e\in \mathcal{E }_h^0}h^{-1}_e\Vert [\![{\varvec{v}}]\!]\Vert ^2_{0,e}\\&\gtrsim (1-\epsilon )|{\varvec{v}}|_{h}^2+\left( \eta _0-\frac{3 C_2}{\epsilon }\right) |{\varvec{v}}|_*^2. \end{aligned}$$

Here $0<\epsilon <1$ is a constant and $C_2$ is the positive constant in (3.3). Therefore, stability is valid for the IP method when $\eta _0> 3C_2$. For other bilinear forms, we can similarly obtain

$$\begin{aligned} B_{2,h}^{(2)}({\varvec{v}},{\varvec{v}})&\gtrsim (1-\epsilon )|{\varvec{v}}|_{h}^2+\left( 3C_2\left( 1-\frac{1}{\epsilon }\right) +C_1\eta _0\right) |{\varvec{v}}|_*^2,\\ B_{2,h}^{(3)}({\varvec{v}},{\varvec{v}})&\gtrsim (1-\epsilon )|{\varvec{v}}|_{h}^2+\left( \eta _0C_1-\frac{3C_2}{\epsilon }\right) |{\varvec{v}}|_*^2,\\ B_{2,h}^{(4)}({\varvec{v}},{\varvec{v}})&\gtrsim (1-\epsilon )|{\varvec{v}}|_{h}^2+\left( \eta _0+3 C_2-\frac{3 C_2}{\epsilon }\right) |{\varvec{v}}|_*^2. \end{aligned}$$

For $B_{2,h}^{(2)}, \eta _0>3C_2(\epsilon ^{-1}-1)/C_1$ ensures stability holds, letting $\epsilon$ be close to 1, we see that $\eta _0>0$ is sufficient for the stability. It is easy to see that stability is valid for $B_{2,h}^{(3)}$ when $\eta _0>3C_2/C_1$. For $B_{2,h}^{(4)}$, it is clear that stability holds when $\eta _0>0$. For convenience, we define the following conditions on $\eta _0$ of (3.10):

$$\begin{aligned}&\eta _0>0\ \hbox {for the methods with }j=2,4,\hbox { and }\nonumber \\&\quad \eta _0 \hbox { is large enough for the methods with }j=1,3. \end{aligned}$$

(3.11)

We summarize the above argument in the next result.

Lemma 3.4

(Stability) Assume (3.11). Then for $1\le j\le 4$, $B_h=B_{1,h}^{(j)}$ and $B_{2,h}^{(j)}$ satisfy

$$\begin{aligned} B_h({\varvec{v}},{\varvec{v}})\gtrsim |||{\varvec{v}}|||^2_* \qquad \forall \, {\varvec{v}}\in V^h. \end{aligned}$$

(3.12)

From now on, we will assume the conditions (3.11) on $\eta$.

3.2 Error analysis

Denote by $\Pi ^h{{\varvec{u}}}\in V^h$ the usual continuous piecewise linear interpolant of the exact solution ${{\varvec{u}}}(t)\in [H^2(\Omega )]^2$, $t\in [0,T]$. Then $[\![{{\varvec{u}}}-\Pi ^h{{\varvec{u}}}]\!]=\mathbf{0}$ on the interelement boundaries. By the definition of norm (3.2), we have the approximation property

$$\begin{aligned} |||{{\varvec{u}}}-\Pi ^h{{\varvec{u}}}|||^2 = |{{\varvec{u}}}-\Pi ^h{{\varvec{u}}}|^2_{h}+ \sum _{K\in \mathcal{T }_h}h_K^2|{{\varvec{u}}}-\Pi ^h{{\varvec{u}}}|^2_{2,K} \lesssim h^{2}|{{\varvec{u}}}|^2_{2,\Omega }. \end{aligned}$$

(3.13)

To extend the analysis to nonconforming meshes, it is convenient to take an interpolant $\Pi ^h{{\varvec{u}}}$ which is discontinuous across the interelement boundaries. Then, we just require the local approximation property

$$\begin{aligned} |{{\varvec{u}}}-\Pi ^h{{\varvec{u}}}|_{1,K} \lesssim h_K|{{\varvec{u}}}|_{2,K}; \end{aligned}$$

hence, for the global approximation error, we have

$$\begin{aligned} |||{{\varvec{u}}}-\Pi ^h{{\varvec{u}}}|||\lesssim h |{{\varvec{u}}}|_{2,\Omega }. \end{aligned}$$

Similarly,

$$\begin{aligned} |||\dot{{{\varvec{u}}}}-\Pi ^h\dot{{{\varvec{u}}}}|||\lesssim h |\dot{{{\varvec{u}}}}|_{2,\Omega }. \end{aligned}$$

(3.14)

Next, we introduce another interpolation of ${{\varvec{u}}}$.

Lemma 3.5

Assume (3.11) and ${{\varvec{u}}}(t),\dot{{{\varvec{u}}}}(t)\in V\cap [H^2(\Omega )]^2$. Define ${{\varvec{u}}}^I(t)\in V^h$ by

$$\begin{aligned} B_h({{\varvec{u}}}^I(t)-{{\varvec{u}}}(t),{\varvec{v}}^h) = 0 \qquad \forall \, {\varvec{v}}^h\in V^h. \end{aligned}$$

(3.15)

Then

$$\begin{aligned} |||{{\varvec{u}}}^I(t)-{{\varvec{u}}}(t)|||\lesssim h, \quad \quad |||\dot{{{\varvec{u}}}}^I(t)-\dot{{{\varvec{u}}}}(t)|||\lesssim h. \end{aligned}$$

(3.16)

Proof

First we notice that because the bilinear form $B_h = B_{1,h}^{(j)}$ with $j=1,\ldots ,4$ is bounded and coercive on $V^h, {{\varvec{u}}}^I(t)$ is well defined. Letting ${\varvec{v}}^h = {{\varvec{u}}}^I(t) - \Pi ^h{{\varvec{u}}}(t)$ in (3.15), we get

$$\begin{aligned} B_h({{\varvec{u}}}^I(t)-{{\varvec{u}}}(t),{{\varvec{u}}}^I(t) - \Pi ^h{{\varvec{u}}}(t)) = 0. \end{aligned}$$

Notice that ${{\varvec{u}}}^I(t)-\Pi ^h{{\varvec{u}}}(t)\in V^h$. We obtain

$$\begin{aligned} |||{{\varvec{u}}}^I(t)-\Pi ^h{{\varvec{u}}}(t)|||^2&\lesssim B_h({{\varvec{u}}}^I(t)-\Pi ^h{{\varvec{u}}}(t),{{\varvec{u}}}^I(t)-\Pi ^h{{\varvec{u}}}(t))\\&= B_h({{\varvec{u}}}(t)-\Pi ^h{{\varvec{u}}}(t),{{\varvec{u}}}^I(t)-\Pi ^h{{\varvec{u}}}(t))\\&\lesssim |||{{\varvec{u}}}(t)-\Pi ^h{{\varvec{u}}}(t)||||||{{\varvec{u}}}^I(t)-\Pi ^h{{\varvec{u}}}(t)|||. \end{aligned}$$

Then

$$\begin{aligned} |||{{\varvec{u}}}^I(t)-\Pi ^h{{\varvec{u}}}(t)|||\lesssim |||{{\varvec{u}}}(t)-\Pi ^h{{\varvec{u}}}(t)|||\lesssim h. \end{aligned}$$

By the triangle inequality, we have

$$\begin{aligned} |||{{\varvec{u}}}^I(t)-{{\varvec{u}}}(t)|||\le |||{{\varvec{u}}}^I(t)-\Pi ^h{{\varvec{u}}}(t)|||+ |||\Pi ^h{{\varvec{u}}}(t)-{{\varvec{u}}}(t)|||\lesssim h, \end{aligned}$$

which completes the proof for the first inequality in (3.16). The second inequality can be obtained by differentiating (3.15) with respect to time,

$$\begin{aligned} B_h(\dot{{{\varvec{u}}}}^I(t)-\dot{{{\varvec{u}}}}(t),{\varvec{v}}^h) = 0 \qquad \forall \, {\varvec{v}}^h\in V^h, \end{aligned}$$

and by repeating the argument in proving the first inequality. $\square$

Note that ${{\varvec{u}}}^I(0) = P^h_B{{\varvec{u}}}_{0}$. Thus,

$$\begin{aligned} {{\varvec{u}}}^I(0) = {{\varvec{u}}}^{h}(0). \end{aligned}$$

(3.17)

Now we write the error as

$$\begin{aligned} {{\varvec{e}}}= {{\varvec{u}}}- {{\varvec{u}}}^h = ({{\varvec{u}}}- {{\varvec{u}}}^I) + ({{\varvec{u}}}^I - {{\varvec{u}}}^h). \end{aligned}$$

In the next result, we need some additional solution regularity assumption. We express the contact boundary $\overline{\Gamma _C}$ as the union of some line segments:

$$\begin{aligned} \overline{\Gamma _C}=\cup _{i=1}^{i_0}\Gamma _i. \end{aligned}$$

Theorem 3.6

Assume (3.11). Let ${{\varvec{u}}}$ and ${{\varvec{u}}}^h$ be the solutions of (2.17)–(2.18) and (2.35)–(2.36), respectively. Assume ${{\varvec{u}}}\in L^{2}(0,T;[H^2(\Omega )]^2)$, $\dot{{{\varvec{u}}}}\!\in \! L^{2}(0,T;[H^2(\Omega )]^2)$ and $\dot{{{\varvec{u}}}}|_{\Gamma _i}\in L^{2}(0,T;[H^2(\Gamma _i)]^2)$ for $1\le i\le i_0$. Then for the DG methods with $j=1,\ldots ,4$, we have

$$\begin{aligned} |||{{\varvec{u}}}(t)-{{\varvec{u}}}^h(t)|||\lesssim h \quad \quad \mathrm{for\,any}\ t\in [0,T]. \end{aligned}$$

(3.18)

Proof

Let ${\varvec{v}}^h = \dot{{{\varvec{u}}}}^h(t)$ in (3.1). Combining with (2.35), we obtain for all ${\varvec{v}}^h\in V^h$,

$$\begin{aligned} -B_h({{\varvec{u}}}^h,{\varvec{v}}^h-\dot{{{\varvec{u}}}}^h)&\le B_h({{\varvec{u}}},\dot{{{\varvec{u}}}}^h-\dot{{{\varvec{u}}}})+ j({\varvec{v}}^h) - j(\dot{{{\varvec{u}}}}) - ({\varvec{\ell }},{\varvec{v}}^h-\dot{{{\varvec{u}}}})_V \end{aligned}$$

(3.19)

Using (3.19) and (3.15), we have

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} B_h({{\varvec{u}}}^I(t)-{{\varvec{u}}}^h(t),{{\varvec{u}}}^I(t)-{{\varvec{u}}}^h(t))&= B_h({{\varvec{u}}}^I(t)-{{\varvec{u}}}^h(t),\dot{{{\varvec{u}}}}^I(t)-\dot{{{\varvec{u}}}}^h(t))\nonumber \\&\le T_1+T_2+T_3, \end{aligned}$$

(3.20)

where

$$\begin{aligned} T_1&= B_h({{\varvec{u}}}^I(t)-{{\varvec{u}}}^h(t),\dot{{{\varvec{u}}}}^I(t)-\dot{{{\varvec{u}}}}(t)),\\ T_2&= B_h({{\varvec{u}}}^I(t)-{{\varvec{u}}}^h(t),\dot{{{\varvec{u}}}}(t)-{\varvec{v}}^h),\\ T_3&= B_h({{\varvec{u}}}(t),{\varvec{v}}^h-\dot{{{\varvec{u}}}}(t))+ j({\varvec{v}}^h) - j(\dot{{{\varvec{u}}}}(t)) - ({\varvec{\ell }}(t),{\varvec{v}}^h-\dot{{{\varvec{u}}}}(t))_V. \end{aligned}$$

By the boundedness of the bilinear form $B_h$, we get

$$\begin{aligned} T_1&\lesssim |||{{\varvec{u}}}^I-{{\varvec{u}}}^h||||||\dot{{{\varvec{u}}}}^I-\dot{{{\varvec{u}}}}|||\lesssim |||{{\varvec{u}}}^I-{{\varvec{u}}}^h|||^2 + |||\dot{{{\varvec{u}}}}^I-\dot{{{\varvec{u}}}}|||^2,\end{aligned}$$

(3.21)

$$\begin{aligned} T_2&\lesssim |||{{\varvec{u}}}^I-{{\varvec{u}}}^h||||||\dot{{{\varvec{u}}}}-{\varvec{v}}^h|||\lesssim |||{{\varvec{u}}}^I-{{\varvec{u}}}^h|||^2 + |||\dot{{{\varvec{u}}}}-{\varvec{v}}^h|||^2, \end{aligned}$$

(3.22)

We turn to bound $T_3$. Note that on an interior edge, $[\![{{\varvec{u}}}]\!]=\mathbf{0}, \{{{\varvec{u}}}\}={{\varvec{u}}}$, $\{{\varvec{\sigma }}\}={\varvec{\sigma }}$, and on $\Gamma _D$, $[\![{{\varvec{u}}}]\!]=\mathbf{0}$. Then

$$\begin{aligned} B_h({{\varvec{u}}},{\varvec{v}}^h-\dot{{{\varvec{u}}}})&= \int _{\Omega }\mathcal{C }{\varvec{\varepsilon }}({{\varvec{u}}}): {\varvec{\varepsilon }}^h({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,dx -\int _{\mathcal{E }_h^0}\mathcal{C }{\varvec{\varepsilon }}({{\varvec{u}}}): [\![{\varvec{v}}^h-\dot{{{\varvec{u}}}}]\!]\,ds\\&= \sum _{K\in \mathcal{T }_h}\int _{K}{\varvec{\sigma }}: {\varvec{\varepsilon }}^h({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,dx -\int _{\mathcal{E }_h^0}[\![{\varvec{v}}^h-\dot{{{\varvec{u}}}}]\!]:{\varvec{\sigma }}\,ds \end{aligned}$$

Since $[{\varvec{\sigma }}]=\mathbf{0}$ on an interior edge and remembering (2.3), we have

$$\begin{aligned} \sum _{K\in \mathcal{T }_h}\int _{K}{\varvec{\sigma }}: {\varvec{\varepsilon }}^h({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,dx&= \sum _{K\in \mathcal{T }_h}\int _{K}-\mathrm{div}{\varvec{\sigma }}\cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,dx\nonumber \\&+\sum _{K\in \mathcal{T }_h}\int _{\partial K}({\varvec{\sigma }}{{\varvec{n}}}_K)\cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,ds\\&= \sum _{K\in \mathcal{T }_h}\int _{K}{{\varvec{f}}}_1\cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,dx +\int _{\mathcal{E }_h}[\![{\varvec{v}}^h-\dot{{{\varvec{u}}}}]\!]:{\varvec{\sigma }}\,ds. \end{aligned}$$

Then

$$\begin{aligned} B_h({{\varvec{u}}},{\varvec{v}}^h-\dot{{{\varvec{u}}}})&= \int _{\Omega }{{\varvec{f}}}_1 \cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,dx +\int _{\Gamma _F}{{\varvec{f}}}_2\cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,ds +\int _{\Gamma _C}({\varvec{\sigma }}{\varvec{\nu }})\cdot ({\varvec{v}}^h-\dot{{{\varvec{u}}}})\,ds\nonumber \\&= ({\varvec{\ell }}(t),{\varvec{v}}^h-\dot{{{\varvec{u}}}})_V +\int _{\Gamma _C}\left( {\varvec{\sigma }}_{\tau }\cdot {\varvec{v}}^{h}_{\tau }-{\varvec{\sigma }}_{\tau }\cdot \dot{{{\varvec{u}}}}_{\tau }\right) \,ds. \end{aligned}$$

(3.23)

Hence, we get

$$\begin{aligned} T_3&= \int _{\Gamma _C}{\varvec{\sigma }}_{\tau }\cdot \left( {\varvec{v}}^{h}_{\tau }-\dot{{{\varvec{u}}}}_{\tau }\right) \,ds + j({\varvec{v}}^h) - j(\dot{{{\varvec{u}}}}(t)) \nonumber \\&\le 2\int _{\Gamma _C} g \Vert {\varvec{v}}^{h}_{\tau }-\dot{{{\varvec{u}}}}_{\tau }\Vert \,ds \lesssim \Vert {\varvec{v}}^{h}-\dot{{{\varvec{u}}}}\Vert _{L^2(\Gamma _C)^2}. \end{aligned}$$

(3.24)

Then we obtain by (3.20), (3.21), (3.22) and (3.24),

$$\begin{aligned} \frac{d}{dt}B_h({{\varvec{u}}}^I(t)-{{\varvec{u}}}^h(t),{{\varvec{u}}}^I(t)-\!{{\varvec{u}}}^h(t))&\lesssim |||{{\varvec{u}}}^I(t)-{{\varvec{u}}}^h(t)|||^2 + |||\dot{{{\varvec{u}}}}^I(t)-\dot{{{\varvec{u}}}}(t)|||^2 \\&+ |||\dot{{{\varvec{u}}}}(t)-{\varvec{v}}^h(t)|||^2 \!+ \Vert {\varvec{v}}^{h}(t)-\dot{{{\varvec{u}}}}(t)\Vert _{L^2(\Gamma _C)^2}. \end{aligned}$$

Integrating the above inequality from 0 to $t$, applying Gronwall’s inequality, and using the stability of the bilinear form $B_h$, we obtain

$$\begin{aligned} |||{{\varvec{u}}}^I(t)-{{\varvec{u}}}^h(t)|||&\lesssim |||{{\varvec{u}}}^I(0)-{{\varvec{u}}}^h(0)|||+ |||\dot{{{\varvec{u}}}}^I-\dot{{{\varvec{u}}}}|||_{L^2(0,T;V(h))} \nonumber \\&+ |||\dot{{{\varvec{u}}}}-{\varvec{v}}^h|||_{L^2(0,T;V(h))} +\ \Vert {\varvec{v}}^{h}-\dot{{{\varvec{u}}}}\Vert _{L^2(0,T;L^2(\Gamma _C)^2)}^{1/2}\nonumber \\&= |||\dot{{{\varvec{u}}}}^I-\dot{{{\varvec{u}}}}|||_{L^2(0,T;V(h))} + |||\dot{{{\varvec{u}}}}-{\varvec{v}}^h|||_{L^2(0,T;V(h))}\nonumber \\&+\Vert {\varvec{v}}^{h}-\dot{{{\varvec{u}}}}\Vert _{L^2(0,T;L^2(\Gamma _C)^2)}^{1/2}, \end{aligned}$$

(3.25)

where in the last equality, the condition (3.17) was used.

Choosing ${\varvec{v}}^h(t) = \Pi ^h\dot{{{\varvec{u}}}}(t)$ in (3.25), we get

$$\begin{aligned} |||{{\varvec{u}}}^I(t)-{{\varvec{u}}}^h(t)|||&\lesssim |||\dot{{{\varvec{u}}}}^I-\dot{{{\varvec{u}}}}|||_{L^2(0,T;V(h))} + |||\dot{{{\varvec{u}}}}-\Pi ^h\dot{{{\varvec{u}}}}|||_{L^2(0,T;V(h))} \\&+ \Vert \Pi ^h\dot{{{\varvec{u}}}}-\dot{{{\varvec{u}}}}\Vert _{L^2(0,T;L^2(\Gamma _C)^2)}^{1/2}. \end{aligned}$$

By (3.14), (3.16) and using

$$\begin{aligned} \Vert \Pi ^h\dot{{{\varvec{u}}}}(t)-\dot{{{\varvec{u}}}}(t)\Vert _{L^2(\Gamma _C)^2} \lesssim h^2 \left( \sum _{i=1}^{i_0}\Vert \dot{{{\varvec{u}}}}(t)\Vert _{H^2(\Gamma _i)}^2\right) ^{1/2}, \end{aligned}$$

we obtain

$$\begin{aligned} |||{{\varvec{u}}}^I(t)-{{\varvec{u}}}^h(t)|||\lesssim h. \end{aligned}$$

Finally, by the triangle inequality

$$\begin{aligned} |||{{\varvec{u}}}(t)-{{\varvec{u}}}^h(t)|||\le |||{{\varvec{u}}}(t)-{{\varvec{u}}}^I(t)|||+ |||{{\varvec{u}}}^I(t)-{{\varvec{u}}}^h(t)|||, \end{aligned}$$

we get the error bound (3.18). $\square$

4 Error estimates for fully discrete approximation

In this section, we analyze the fully discrete schemes. First, we show the well-posedness of problem (2.37)–(2.38).

Theorem 4.1

Assume (3.11). The problem (2.37)–(2.38) admits a unique solution ${{\varvec{u}}}^{hk}$, which is stable in the sense that for given ${{\varvec{u}}}_{1,0}, {{\varvec{u}}}_{2,0}\in V$ and ${\varvec{\ell }}_1, {\varvec{\ell }}_2 \in W^{1,\infty }(0,T;V)$, the corresponding solutions ${{\varvec{u}}}^{hk}_{1,n}$ and ${{\varvec{u}}}^{hk}_{2,n}, 0\le n\le N$, satisfy the inequality

$$\begin{aligned} \max _{0\le n\le N}|||{{\varvec{u}}}^{hk}_{1,n}-{{\varvec{u}}}^{hk}_{2,n}|||\lesssim |||P^h_B{{\varvec{u}}}_{1,0}-P^h_B{{\varvec{u}}}_{2,0} |||+ \Vert {\varvec{\ell }}_1-{\varvec{\ell }}_2\Vert _{W^{1,\infty }(0,T;V)} . \end{aligned}$$

(4.1)

Proof

Because $j$ is positively homogeneous, the inequality (2.37) can be rewritten as

$$\begin{aligned}&B_h\left( \Delta {{\varvec{u}}}_n^{hk},{\varvec{v}}^h-\Delta {{\varvec{u}}}_n^{hk}\right) + j({\varvec{v}}^h) - j\left( \Delta {{\varvec{u}}}_n^{hk}\right) \\&\quad \ge \left( {\varvec{\ell }}_{n},{\varvec{v}}^h-\Delta {{\varvec{u}}}_n^{hk}\right) _V - B_h\left( {{\varvec{u}}}_{n-1}^{hk},{\varvec{v}}^h-\Delta {{\varvec{u}}}_n^{hk}\right) \qquad \forall \,{\varvec{v}}^h \in V^h. \end{aligned}$$

This inequality problem admits a unique solution $\Delta {{\varvec{u}}}_n^{hk}\in V^h$ by the boundedness and stability of the bilinear form $B_h$.

Then we turn to deduce the inequality (4.1). With $n=1,2,\ldots ,N$, we have

$$\begin{aligned} B_h\left( {{\varvec{u}}}_{1,n}^{hk},{\varvec{v}}^h-\delta _n{{\varvec{u}}}_{1,n}^{hk}\right) + j({\varvec{v}}^h) - j\left( \delta _n{{\varvec{u}}}_{1,n}^{hk}\right)&\ge \left( {\varvec{\ell }}_{1,n},{\varvec{v}}^h-\delta _n{{\varvec{u}}}_{1,n}^{hk}\right) _V \quad \forall \,{\varvec{v}}^h \in V^h,\end{aligned}$$

(4.2)

$$\begin{aligned} B_h\left( {{\varvec{u}}}_{2,n}^{hk},{\varvec{v}}^h-\delta _n{{\varvec{u}}}_{2,n}^{hk}\right) + j({\varvec{v}}^h) - j\left( \delta _n{{\varvec{u}}}_{2,n}^{hk}\right)&\ge \left( {\varvec{\ell }}_{2,n},{\varvec{v}}^h-\delta _n{{\varvec{u}}}_{2,n}^{hk}\right) _V \quad \forall \,{\varvec{v}}^h \in V^h,\nonumber \\ \end{aligned}$$

(4.3)

Denote ${{\varvec{e}}}_n={{\varvec{u}}}_{1,n}^{hk} - {{\varvec{u}}}_{2,n}^{hk}$. Taking ${\varvec{v}}^h = \delta _n{{\varvec{u}}}_{2,n}^{hk}$ in (4.2) and ${\varvec{v}}^h = \delta _n{{\varvec{u}}}_{1,n}^{hk}$ in (4.3), and adding the two inequalities, we obtain

$$\begin{aligned} A_n := B_h({{\varvec{e}}}_{n},\delta _n{{\varvec{e}}}_{n})\le ({\varvec{\ell }}_{1,n}-{\varvec{\ell }}_{2,n},\delta _n{{\varvec{e}}}_{n})_V. \end{aligned}$$

We can get the lower bound as

$$\begin{aligned} A_n&= \frac{1}{k_n} \big (B_h( {{\varvec{e}}}_{n},{{\varvec{e}}}_{n}) - B_h( {{\varvec{e}}}_{n},{{\varvec{e}}}_{n-1})\big ) \gtrsim \frac{1}{k_n} \big ( |||{{\varvec{e}}}_n |||^2 - |||{{\varvec{e}}}_n ||||||{{\varvec{e}}}_{n-1} |||\big )\nonumber \\&\gtrsim \frac{1}{k_n} \left( |||{{\varvec{e}}}_n |||^2 - \frac{1}{2}\left( |||{{\varvec{e}}}_n |||^2+|||{{\varvec{e}}}_{n-1} |||^2\right) \right) \gtrsim \frac{1}{2k_n}\left( |||{{\varvec{e}}}_{n} |||^2-|||{{\varvec{e}}}_{n-1} |||^2\right) .\nonumber \\ \end{aligned}$$

(4.4)

Then for $1\le n\le N$, we obtain

$$\begin{aligned} |||{{\varvec{e}}}_{n} |||^2-|||{{\varvec{e}}}_{n-1} |||^2 \lesssim ({\varvec{\ell }}_{1,n}-{\varvec{\ell }}_{2,n},{{\varvec{e}}}_{n}-{{\varvec{e}}}_{n-1})_V. \end{aligned}$$

A simple induction yields

$$\begin{aligned} |||{{\varvec{e}}}_{n} |||^2&\lesssim |||{{\varvec{e}}}_{0} |||^2 + \sum _{j=1}^n ({\varvec{\ell }}_{1,j}-{\varvec{\ell }}_{2,j},{{\varvec{e}}}_{j}-{{\varvec{e}}}_{j-1})_V\\&= |||{{\varvec{e}}}_{0} |||^2 + ({\varvec{\ell }}_{1,n}-{\varvec{\ell }}_{2,n},{{\varvec{e}}}_{n})_V - ({\varvec{\ell }}_{1,1}-{\varvec{\ell }}_{2,1},{{\varvec{e}}}_{0})_V\\&+ \sum _{j=1}^{n-1} (({\varvec{\ell }}_{1,j}-{\varvec{\ell }}_{1,j+1})-({\varvec{\ell }}_{2,j}-{\varvec{\ell }}_{2,j+1}),{{\varvec{e}}}_{j})_V. \end{aligned}$$

Let $M=\max _n |||{{\varvec{e}}}_{n} |||$. Then we obtain

$$\begin{aligned} |||{{\varvec{e}}}_{n} |||^2&\lesssim |||{{\varvec{e}}}_{0} |||^2 + \big (\Vert {\varvec{\ell }}_{1,n}-{\varvec{\ell }}_{2,n}\Vert _V + \Vert {\varvec{\ell }}_{1,1}-{\varvec{\ell }}_{2,1}\Vert _V\\&+ \sum _{j=1}^{n-1} \Vert ({\varvec{\ell }}_{1,j}-{\varvec{\ell }}_{1,j+1})-({\varvec{\ell }}_{2,j}-{\varvec{\ell }}_{2,j+1})\Vert _V\big )M. \end{aligned}$$

Therefore,

$$\begin{aligned} M^2&\lesssim |||{{\varvec{e}}}_{0} |||^2 + \big (\max _n\Vert {\varvec{\ell }}_{1,n}-{\varvec{\ell }}_{2,n}\Vert _V + \Vert {\varvec{\ell }}_{1,1}-{\varvec{\ell }}_{2,1}\Vert _V\\&+ \sum _{j=1}^{N-1} \Vert ({\varvec{\ell }}_{1,j}-{\varvec{\ell }}_{1,j+1}) -({\varvec{\ell }}_{2,j}-{\varvec{\ell }}_{2,j+1})\Vert _V\big )M\\&\lesssim |||{{\varvec{e}}}_{0} |||^2 + M \Vert {\varvec{\ell }}_1-{\varvec{\ell }}_2\Vert _{W^{1,\infty }(0,T;V)}. \end{aligned}$$

Applying the following inequality

$$\begin{aligned} x,a,b\ge 0\ \mathrm{and }\ x^2\le ax+b \Longrightarrow x\le a + b^{1/2}, \end{aligned}$$

we then obtain the stability inequality (4.1). $\square$

Now we show error estimates for the fully discrete scheme. Define ${{\varvec{e}}}_n={{\varvec{u}}}_{n} - {{\varvec{u}}}_{n}^{hk}$ for $n=1,2,\ldots ,N$. We have

$$\begin{aligned} {{\varvec{e}}}_n = \left( {{\varvec{u}}}_{n}- {{\varvec{u}}}_{n}^I\right) + \left( {{\varvec{u}}}_{n}^I - {{\varvec{u}}}_{n}^{hk}\right) := {\varvec{\eta }}_n+{{\varvec{e}}}_n^h, \end{aligned}$$

where ${{\varvec{u}}}_n^I = {{\varvec{u}}}^I(t)$. Denote

$$\begin{aligned} A_n^h = B_h\left( {{\varvec{e}}}_{n}^h,\delta _n{{\varvec{e}}}_{n}^h\right) . \end{aligned}$$

As (4.4), we have

$$\begin{aligned} A_n^h \gtrsim \frac{1}{2k_n}\left( |||{{\varvec{e}}}_{n}^h |||^2-|||{{\varvec{e}}}_{n-1}^h |||^2\right) . \end{aligned}$$

(4.5)

For an upper bound of $A_n^h$, write

$$\begin{aligned} A_n^h&= B_h\left( {{\varvec{u}}}_{n}^I-{{\varvec{u}}}_{n},\delta _n{{\varvec{u}}}_{n}^I-\delta _n{{\varvec{u}}}_{n}^{hk}\right) +B_h\left( {{\varvec{u}}}_{n},\delta _n{{\varvec{u}}}_{n}^I-\delta _n{{\varvec{u}}}_{n}^{hk}\right) \nonumber \\&-B_h\left( {{\varvec{u}}}_{n}^{hk},\delta _n{{\varvec{u}}}_{n}^I-{\varvec{v}}^{h}_n\right) -B_h\left( {{\varvec{u}}}_{n}^{hk},{\varvec{v}}^{h}_n-\delta _n{{\varvec{u}}}_{n}^{hk}\right) , \end{aligned}$$

(4.6)

where ${\varvec{v}}^h_n\in V^h$ is arbitrary. We take ${\varvec{v}}^h=\delta _n{{\varvec{u}}}_{n}^{hk}\in V^h$ in (3.1) at $t=t_{n}$ to get

$$\begin{aligned} B_h\left( {{\varvec{u}}}_{n},\delta _n{{\varvec{u}}}_{n}^{hk}-\dot{{{\varvec{u}}}}_{n}\right) + j\left( \delta _n{{\varvec{u}}}_{n}^{hk}\right) - j(\dot{{{\varvec{u}}}}_{n}) \ge \left( {\varvec{\ell }}_{n},\delta _n{{\varvec{u}}}_{n}^{hk}-\dot{{{\varvec{u}}}}_{n}\right) . \end{aligned}$$

Combining the above inequality with (2.37), we have

$$\begin{aligned} -B_h\left( {{\varvec{u}}}_n^{hk},{\varvec{v}}^h_n\!-\!\delta _n{{\varvec{u}}}_n^{hk}\right) \le j\left( {\varvec{v}}^h_n\right) \!-\! j\left( \dot{{{\varvec{u}}}}_{n}\right) \!-\! \left( {\varvec{\ell }}_{n},{\varvec{v}}^h_n\!-\!\dot{{{\varvec{u}}}}_{n}\right) \!+\! B_h\left( {{\varvec{u}}}_{n},\delta _n{{\varvec{u}}}_{n}^{hk}-\dot{{{\varvec{u}}}}_{n}\right) .\nonumber \\ \end{aligned}$$

(4.7)

In Eq. (4.6), inserting $B_h({{\varvec{u}}}_n^{I},\delta _n{{\varvec{u}}}_n^{I}-{\varvec{v}}^h_n)-B_h({{\varvec{u}}}_n^{I},\delta _n{{\varvec{u}}}_n^{I}-{\varvec{v}}^h_n)$ and applying (4.7), we get

$$\begin{aligned} A_n^h&\le \frac{1}{k_n}B_h\left( -{\varvec{\eta }}_n,{{\varvec{e}}}_{n}^h-{{\varvec{e}}}_{n-1}^{h}\right) +B_h\left( {\varvec{\eta }}_n,\delta _n{{\varvec{u}}}_{n}^I-{\varvec{v}}^{h}_n\right) \nonumber \\&+B_h\left( {{\varvec{e}}}_{n}^h,\delta _n{{\varvec{u}}}_{n}^I-{\varvec{v}}^{h}_n\right) + R_n\left( {{\varvec{u}}}_{n},{\varvec{v}}^h_n\right) , \end{aligned}$$

(4.8)

where

$$\begin{aligned} R_n\left( {{\varvec{u}}}_{n},{\varvec{v}}^h_n\right) = B_h\left( {{\varvec{u}}}_{n},{\varvec{v}}^{h}_n-\dot{{{\varvec{u}}}}_{n}\right) + j\left( {\varvec{v}}^h_n\right) - j(\dot{{{\varvec{u}}}}_{n}) - \left( {\varvec{\ell }}_{n},{\varvec{v}}^h_n-\dot{{{\varvec{u}}}}_{n}\right) . \end{aligned}$$

From the lower bound (4.5) and the upper bound (4.8), we obtain inequality

$$\begin{aligned} \frac{1}{2k_n}\left( |||{{\varvec{e}}}_{n}^h |||^2-|||{{\varvec{e}}}_{n-1}^h |||^2\right)&\lesssim \frac{1}{k_n}B_h\left( -{\varvec{\eta }}_n,{{\varvec{e}}}_{n}^h-{{\varvec{e}}}_{n-1}^{h}\right) +|||{\varvec{\eta }}_n||||||\delta _n{{\varvec{u}}}_{n}^I-{\varvec{v}}^{h}_n|||\nonumber \\&+ M |||\delta _n{{\varvec{u}}}_{n}^I-{\varvec{v}}^{h}_n|||+ \left| R_n\left( {{\varvec{u}}}_{n},{\varvec{v}}^h_n\right) \right| . \end{aligned}$$

(4.9)

Here, $M=\max _n |||{{\varvec{e}}}_{n}^h |||$. By an induction, we get

$$\begin{aligned} |||{{\varvec{e}}}_{n}^h |||^2&\lesssim 2 \sum _{j=1}^n B_h\left( -{\varvec{\eta }}_j,{{\varvec{e}}}_{j}^h-{{\varvec{e}}}_{j-1}^{h}\right) + \max _n|||{\varvec{\eta }}_n|||\sum _{j=1}^n k_j |||\delta _j{{\varvec{u}}}_{j}^I-{\varvec{v}}^{h}_j|||\nonumber \\&+ M \sum _{j=1}^n k_j|||\delta _j{{\varvec{u}}}_{j}^I-{\varvec{v}}^{h}_j|||+ \sum _{j=1}^n k_j \left| R_j\left( {{\varvec{u}}}_{j},{\varvec{v}}^h_j\right) \right| + |||{{\varvec{e}}}_{0}^h |||^2. \end{aligned}$$

Noticing that

$$\begin{aligned} \sum _{j=1}^n B_h\left( -{\varvec{\eta }}_j,{{\varvec{e}}}_{j}^h-{{\varvec{e}}}_{j-1}^{h}\right) = B_h\left( -{\varvec{\eta }}_n,{{\varvec{e}}}_{n}^h\right) + \sum _{j=1}^{n-1} B_h\left( {\varvec{\eta }}_{j+1}-{\varvec{\eta }}_j,{{\varvec{e}}}_{j}^h\right) \end{aligned}$$

and

$$\begin{aligned} \delta _j{{\varvec{u}}}_{j}^I = \frac{{{\varvec{u}}}_{j}^I - {{\varvec{u}}}_{j-1}^I}{k_j} = \frac{{{\varvec{u}}}_{j}^I - \left( {{\varvec{u}}}_{j}^I - k_j \dot{{{\varvec{u}}}}_{j}^I\right) }{k_j} = \dot{{{\varvec{u}}}}_{j}^I, \end{aligned}$$

we have

$$\begin{aligned} M^2&\lesssim M\left( \max _n |||{\varvec{\eta }}_n |||+ \sum _{j=1}^{N-1}|||{\varvec{\eta }}_{j+1}-{\varvec{\eta }}_j|||+\sum _{j=1}^N k_j|||\dot{{{\varvec{u}}}}_{j}^I-{\varvec{v}}^{h}_j|||\right) \nonumber \\&+\max _n|||{\varvec{\eta }}_n|||\sum _{j=1}^N k_j |||\dot{{{\varvec{u}}}}_{j}^I-{\varvec{v}}^{h}_j|||+ \sum _{j=1}^N k_j |R_j\left( {{\varvec{u}}}_{j},{\varvec{v}}^h_j\right) |. \end{aligned}$$

(4.10)

Using the relation

$$\begin{aligned} x,a,b\ge 0\ \mathrm{and }\ x^2\le ax+b \Longrightarrow x\le a + b^{1/2}, \end{aligned}$$

we obtain from (4.10) that

$$\begin{aligned}&\max _n |||u^I_n - u^{hk}_n|||\lesssim \max _n |||{\varvec{\eta }}_n |||+ \sum _{j=1}^{N-1}|||{\varvec{\eta }}_{j+1}-{\varvec{\eta }}_j |||+\sum _{j=1}^N k_j|||\dot{{{\varvec{u}}}}_{j}^I-{\varvec{v}}^{h}_j|||\nonumber \\&\quad +\left( \max _n|||{\varvec{\eta }}_n|||\sum _{j=1}^N k_j |||\dot{{{\varvec{u}}}}_{j}^I-{\varvec{v}}^{h}_j|||\right) ^{1/2} + \left( \sum _{j=1}^N k_j |R_j({{\varvec{u}}}_{j},{\varvec{v}}^h_j)|\right) ^{1/2}. \end{aligned}$$

(4.11)

By (3.16), we know that

$$\begin{aligned} |||{\varvec{\eta }}_n |||&= |||{{\varvec{u}}}^I_{n}-{{\varvec{u}}}_{n}|||\lesssim h. \end{aligned}$$

From Taylor’s theorem, we have

$$\begin{aligned} {\varvec{\eta }}_{j+1}-{\varvec{\eta }}_j&= \left( {{\varvec{u}}}^I_{j+1}-{{\varvec{u}}}^I_{j}\right) -({{\varvec{u}}}_{j+1}-{{\varvec{u}}}_{j}) = k_{j+1}\dot{{{\varvec{u}}}}^I_{j} - k_{j+1}\dot{{{\varvec{u}}}}_{j}\\&\quad - \int _{t_j}^{t_{j+1}} (t_{j+1}-t)\ddot{{{\varvec{u}}}}(t)\,dt. \end{aligned}$$

Then

$$\begin{aligned} \sum _{j=1}^{N-1}|||{\varvec{\eta }}_{j+1}-{\varvec{\eta }}_j |||&\le \sum _{j=1}^{N-1}k_{j+1} |||\dot{{{\varvec{u}}}}^I_{j} - \dot{{{\varvec{u}}}}_{j} |||+ \sum _{j=1}^{N-1}k_{j+1} |||\int _{t_j}^{t_{j+1}} \ddot{{{\varvec{u}}}}(t)\,dt |||\\&\lesssim h + k |||\ddot{{{\varvec{u}}}} |||_{L^1(0,T;V)}, \end{aligned}$$

where

$$\begin{aligned} |||\ddot{{{\varvec{u}}}} |||_{L^1(0,T;V)} = \int _0^T |||\ddot{{{\varvec{u}}}}(t) |||\,dt. \end{aligned}$$

Choose ${\varvec{v}}^{h}_j = \Pi ^h\dot{{{\varvec{u}}}}_{j}$, then $|||\dot{{{\varvec{u}}}}_{j}^I-\Pi ^h\dot{{{\varvec{u}}}}_{j}|||\lesssim h$. To estimate the term $|R_j({{\varvec{u}}}_{j},{\varvec{v}}^h_j)|$, doing similar argument for deriving (3.24), we obtain

$$\begin{aligned} R_j\left( {{\varvec{u}}}_{j},{\varvec{v}}^h_j\right) \lesssim \Vert \Pi ^h\dot{{{\varvec{u}}}}_{j}-\dot{{{\varvec{u}}}}_j\Vert _{L^2(\Gamma _C)^2} \lesssim h^2 \left( \sum _{i=1}^{i_0}\Vert \dot{{{\varvec{u}}}}_j\Vert _{H^2(\Gamma _i)}^2\right) ^{1/2}. \end{aligned}$$

Finally, we apply the triangle inequality

$$\begin{aligned} |||{{\varvec{u}}}_n-{{\varvec{u}}}^{hk}_n|||\le |||{{\varvec{u}}}_n-{{\varvec{u}}}^I_n|||+ |||{{\varvec{u}}}^I_n-{{\varvec{u}}}^{hk}_n|||\end{aligned}$$

to obtain

$$\begin{aligned} \max _n|||{{\varvec{u}}}_n-{{\varvec{u}}}^{hk}_n|||\lesssim h + k. \end{aligned}$$

(4.12)

Summarizing, we have shown the following results.

Theorem 4.2

Assume (3.11). Let ${{\varvec{u}}}$ and ${{\varvec{u}}}^{hk}$ be the solutions of (2.17)–(2.18) and (2.37)–(2.36), respectively. Assume ${{\varvec{u}}}\!\in \! L^{2}(0,T;[H^2(\Omega )]^2), \dot{{{\varvec{u}}}}\!\in \! L^{2} (0,T;[H^2(\Omega )]^2), \ddot{{{\varvec{u}}}}\in L^1(0,T;V)$ and $\dot{{{\varvec{u}}}}|_{\Gamma _i}\in L^{2}(0,T;[H^2(\Gamma _i)]^2)$ for $1\le i\le i_0$. Then the error bound (4.12) holds.

5 Numerical example

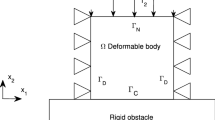
We report numerical results from a two dimensional test example discretized by the DG schemes in space and uniform finite difference scheme in time. We use Matlab to implement the numerical examples. The physical setting is shown in Fig. 1. The domain $\Omega = (0,1)\times (0,1)$ is the cross section of a linearized elastic body. On the boundary $\Gamma _D = \{1\}\times (0,1)$, the body is clamped and therefore the displacement field vanishes there. The traction ${{\varvec{f}}}_2$ acts on the boundary $\{0\}\times (0,1)$ whereas the boundary of $(0,1)\times \{1\}$ is traction free. Thus $\Gamma _F =\{\{0\}\times (0,1)\} \cup \{(0,1)\times \{1\}\}$. On the boundary $\Gamma _C = (0,1)\times \{0\}$, the body is in bilateral frictional contact with a rigid obstacle, and the friction is modeled with Tresca’s law. No volume force is assumed to act on the body $\Omega$.

Fig. 1

An elastic body in contact with a frictional rigid obstacle

We consider a homogeneous and isotropic elastic body. Let $E$ be the Young’s modulus and $\kappa$ be the Poisson’s ratio of the material. Then the Lamé coefficients are

$$\begin{aligned} \lambda = \frac{E\kappa }{(1+\kappa )(1-2\kappa )}, \quad \quad \mu =\frac{E}{2(1+\kappa )}. \end{aligned}$$

For computation, we use the following data

$$\begin{aligned}&E = 200 \ \mathrm{daN/mm}^2, \quad \kappa = 0.3, \quad {{\varvec{f}}}_1 = \mathbf{0}\ \mathrm{daN/mm}^2,\\&{{\varvec{f}}}_2(x_1,x_2,t) = (0.08(1.25-x_2)t,-0.01t)\ \mathrm{daN/mm}^2,\\&g=0.004 \ \mathrm{daN/mm}^2,\quad {{\varvec{u}}}_0 = \mathbf{0}\ m,\quad T=1 s. \end{aligned}$$

Here, the unit $\mathrm{daN/mm}^2$ denotes decanewtons per square millimeter.

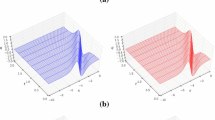
To observe the convergence behavior of the fully discrete scheme, we solve this problem on a family of uniform triangular meshes of the kind shown in Fig. 2. We start with $h=1/2$ and $k=1/2$ which are then decreased by half several times. To compute errors of numerical solutions, we adopt the numerical solution corresponding to $h=1/128$ and $k=1/128$ as “true” solution. The convergence behavior of the four DG schemes in the norm $|||\cdot |||$ is shown in Figs. 3, 4, 5, 6, respectively. To show the effect of the size of the penalty parameter $\eta$ on the convergence, we let $\eta _e=\eta$ be the same on every edge. In Figs. 3 and 4, the linear asymptotic convergence behavior is clearly observed for the method of Bassi et al. and that of Brezzi et al. with every penalty constant choice $\eta _e=1{,}10{,}100\ \mathrm{and}\ 1{,}000$, matching well the theoretical prediction (4.12). For $h$ not too large, the difference of numerical errors is invisible for the choices $\eta _e = 100$ and $\eta _e = 1{,}000$. The solid line for the variation of the meshsize $h$ is included for convenience in concluding linear convergence of the numerical solutions. It is seen from Fig. 5 that the LDG method does not work well with $\eta _e = 1, 10$ for the test problem. From Lemma 3.4, we know that a drawback of the IP method is that the penalty parameter can not be precisely quantified a priori, which must be chosen suitably large to guarantee stability. However, a large penalty parameter has a negative impact on accuracy. In Fig. 6, we only give the numerical error of the IP method for $\eta _e = 10{,}000\ \mathrm{and}\ 100{,}000$. We did the numerical test for the case $\eta _e = 1{,}10{,}100\ \mathrm{and}\ 1{,}000$, but the IP method fails to be convergent.

Fig. 2

A uniform triangulation of the domain

Fig. 3

Numerical errors of method of Bassi et al. [4] for several discretization parameters of $h$ and $k$ when $t=1s$

Fig. 4

Numerical errors of method of Brezzi et al. [7] for several discretization parameters of $h$ and $k$ when $t=1s$

Fig. 5

Numerical errors of LDG method [11] for several discretization parameters of $h$ and $k$ when $t=1s$

Fig. 6

Numerical errors of IP method [14] for several discretization parameters of $h$ and $k$ when $t=1s$

To compare the performance of the four DG methods, we pick up the best one error curve from each of Figs. 3, 4, 5, 6, and put them together into Fig. 7. In Fig. 8, we show the deformed mesh (amplified by 200) solved by LDG method with $\eta _e = 100$ for $h = 1/32$ when $t=1s$.

Fig. 7

Comparison of the numerical errors for the four DG methods

Fig. 8

Deformed mesh (amplified by 200) solved by LDG method for $h = 1/32$ with $t=1s$