Convergence of a semiclassical wavepacket based time-splitting for the Schrödinger equation

Abstract

We propose a new algorithm for solving the semiclassical time-dependent Schrödinger equation. The algorithm is based on semiclassical wavepackets. The focus of the analysis is only on the time discretization: convergence is proved to be quadratic in the time step and linear in the semiclassical parameter $\varepsilon$.

1 Introduction

We consider the semiclassical time-dependent Schrödinger equation

$$\begin{aligned} i \varepsilon ^{2}\partial _{t}\psi = H(\varepsilon ) \psi , \end{aligned}$$

(1)

where $\psi =\psi (x,t)$ is the wave function that depends on the spatial variables $x = (x_{1},\ldots ,x_{d})\in \mathbb R ^{d}$ and the time variable $t\in \mathbb R$. The Hamiltonian

$$\begin{aligned} H(\varepsilon ) = - \frac{\varepsilon ^{4}}{2}\Delta _{x}+V(x) \end{aligned}$$

involves the Laplace operator $\Delta _{x}$ and a smooth real potential $V$.

The main challenges in the numerical solution of (1) result from the dimension $d$ often being large and the existence of several time- and spatial-scales governed by the small parameter $\varepsilon$. In chemical applications, the dimension $d$ is $3N$, where $N$ is the number of nuclei in the molecule being considered. (It is $3N-3$ if the center of mass motion is removed.) One typically takes the mass of an electron to be 1 and the masses of the nuclei to be proportional to $\varepsilon ^{-4}$. If a molecule has various different nuclei, one has some freedom concerning the precise value, but that value lies in an interval determined by the heaviest and lightest nuclei in the molecule. For instance, the $\mathrm{H+H_{2} }$ reaction has $\varepsilon \approx 0.1528$. $\mathrm{CO_{2} }$ has $\varepsilon$ between 0.0764 and 0.0821. The standard model for $\mathrm{IBr }$ is one dimensional because both the center of mass and rotational motions have been separated. The relevant mass is then $\frac{m_\mathrm{I } m_\mathrm{Br }}{m_\mathrm{I }+m_\mathrm{Br }}$, which yields $\varepsilon \approx 0.0577$. In these physical problems, $\varepsilon$ has a clear meaning as the fourth root of a mass ratio, but mathematically we can regard Eq. (1) as a whole range of models indexed by the parameter $\varepsilon$. We recover full quantum dynamics when $\varepsilon =1$ and classical mechanics in the limit $\varepsilon \rightarrow 0$.

Here, we ignore the difficulties that arise from the possibly large dimension $d$ and focus on the challenges caused by a small $\varepsilon$ in the time-integration schemes. The preferred numerical integration scheme in quantum dynamics is the split operator technique [6] which, unlike Chebyshev or Lanczos schemes, does not suffer from a time step restriction, such as $\Delta t = O(\Delta x^{2})$ (see [12]). However, in the case of a semiclassical model (1), it is proved in [3] that the Lie–Trotter splitting requires a time-step of the order of $\varepsilon ^{2}$, and the error is of order $\Delta t/\varepsilon ^{2}$. For the Strang-splitting, convergence of order $(\Delta t)^{2}/\varepsilon ^{2}$ was observed in [2, 3] and proved in [4]. Our own numerical experiments with a fourth-order splitting in time, together with spectral discretizations in space show the same factor of $1/\varepsilon ^{2}$.

The small parameter $\varepsilon$ forces the choice of a small time-step (and for a Fourier based space discretization, a huge number of grid points) in order to have reliable results, even for a fourth-order scheme. Recent research has been done to control the error in such time-splitting spectral approximations [10]. We propose below a new splitting that is more appropriate for the semiclassical situation. We prove it has convergence of order $\varepsilon (\Delta t)^{2}$, which improves instead of deteriorating when $\varepsilon$ is reduced. While the submitted paper was in revision, the authors realized that new algorithms with this property are in development [1].

The new integration scheme is based on a spatial discretization via semiclassical wavepackets [7]. The wavepackets have already been useful in the time integration of the semiclassical time-dependent Schrödinger equation in many dimensions via a special Strang-splitting [5]. They are related to higher-order Gaussian beams which are known to allow computational meshes of size $O(\varepsilon )$, and have several appealing properties, see e.g., [8, 9, 14]. A family of wavepackets forms an orthonormal basis of $L^{2}$, which gives them several advantages. However, to the best knowledge of the authors, the previous known algorithms for the propagation in time wavepackets as for Gaussian beams feature also the $1/\varepsilon ^{2}$-dependence.

The main idea of the time-integration scheme in [5] was Strang-splitting between the kinetic and potential energy, together with the observation that the kinetic part and a quadratic part of the potential could be integrated exactly. This yielded a second splitting of the potential into a quadratic part and a remainder. The line of attack in [7] was slightly different: an approximate solution was built upon the integration of a system of ordinary differential equations for the parameters of the wavepackets. Then a second system of ordinary differential equations was used for determining the coefficients of the wavepackets. Our Algorithm 3 (called below semiclassical splitting) combines both of these two important ideas. The main achievement is to have the factor $\varepsilon$ instead of $1/\varepsilon ^{2}$ in the error estimate. The order of convergence in time could be further improved via a higher-order splitting together with a Magnus integrator, but that is not the subject of this paper.

Let us start with a short introduction to semiclassical wavepackets. They are an example of a spectral basis consisting of functions that are defined on unbounded domains. For simplicity, we describe only the case of dimension $d=1$, while the whole analysis can be carried out in general dimensions.

Given a set of parameters $q,p,Q,P$, a family of semiclassical wavepackets $\{\varphi _k^\varepsilon [q,p,Q,P], k=0,1,\ldots \}$ is an orthonormal basis of $L^{2}(\mathbb R )$ that is constructed in [7] from the Gaussian

$$\begin{aligned} \varphi _0^\varepsilon [q,p,Q,P](x) = (\pi )^{-\frac{1}{4}} (\varepsilon Q)^{-\frac{1}{2}}\exp \left( \frac{i}{2 \varepsilon ^{2}} PQ^{-1} (x-q)^{2}+ \frac{i}{\varepsilon ^{2}} p(x-q) \right) , \end{aligned}$$

via a raising operator. In the notation used here, $Q$ and $P$ correspond to $A$ and $iB$ of [7], respectively. Note that $Q$ and $P$ must obey the compatibility condition $\overline{Q}P-\overline{P}Q=2i$ (see [7]). Each state $\varphi _k(x) = \varphi _k^\varepsilon [q,p,Q,P](x)$ is concentrated in position near $q$ and in momentum near $p$ with uncertainties $\varepsilon |Q|\sqrt{k+\frac{1}{2}}$ and $\varepsilon |P|\sqrt{k+\frac{1}{2}}$, respectively. The recurrence relation

$$\begin{aligned} Q\sqrt{k+1}\varphi _{k+1}^{\varepsilon }(x) = \frac{\sqrt{2}}{\varepsilon } (x-q)\varphi _{k}^{\varepsilon }(x) - \overline{Q} \sqrt{k}\varphi _{k-1}^{\varepsilon }(x) \end{aligned}$$

holds for all values of $x$. We gather together the parameters of the semiclassical wavepackets and write $\Pi (t) = (q(t),p(t),Q(t),P(t))$, so that $\varphi _k[\Pi ](x) = \varphi _k^\varepsilon [q,p,Q,P](x)$.

We assume we have an initial condition $\psi (0)$ that is given as a linear combination of semiclassical wavepackets

$$\begin{aligned} \psi (0) = e^{iS(0)/\varepsilon ^{2}} \sum _{k=0}^{K-1} c_{k}(0,\varepsilon )\varphi _{k}[\Pi (0)]. \end{aligned}$$

If the initial condition is not given in terms of such wavepackets, but it is still well localized, then it can be approximated by such a finite sum. A discretization error arises then; the involved projection is costly, as long as no fast Hermite transform is known. However, typical initial values in chemical applications are in terms of eigenfunctions of harmonic oscillators (see [11, 13] for two examples among many). Hence, they are exactly such wavepackets or can be easily rewritten this way.

Note that we have an overall phase parameter $S(t)$ that will enlarge the parameter set. Hence, we shall also write $\varphi _{k}[\Pi ,S] = e^{iS/\varepsilon ^{2}} \varphi _{k}[\Pi ]$. Note that $K$ can be taken as large as we wish, just by inserting more trivial coefficients $c_{k}(0,\varepsilon ) = 0$. Theorem 2.10 in [7] establishes an upper bound for the semiclassical approximation: if the potential $V\in C^{M+2}(\mathbb R )$ satisfies $-C_{1}< V(x) < C_{2}e^{C_{3} x^{2}}$, there is an approximate solution $v(t)$ of the semiclassical time-dependent Schrödinger equation (1) such that for any $T>0$ we have:

$$\begin{aligned} \Vert \psi (t) - v(t)\Vert \le \mathcal{C}(T)\varepsilon ^{M},\quad {\text{ for } \text{ all } }\ t\in [0,T]. \end{aligned}$$

From now on, $\mathcal{C}$ will denote a generic constant, not depending on $\varepsilon$ or any involved time-step. We also only consider potentials $V$ that satisfy the above conditions. The approximate solution in Theorem 2.10 in [7] is defined as

$$\begin{aligned} v(t) = e^{iS(t)/\varepsilon ^{2}} \sum _{k=0}^{K-1} c_{k}(t,\varepsilon )\varphi _{k}[\Pi (t)], \end{aligned}$$

(2)

with the parameters $\Pi (t)$ and $S(t)$ given by the solution to the following system of ordinary differential equations

$$\begin{aligned} \begin{aligned} \dot{q}(t)&= p(t) \\ \dot{p}(t)&= -V^{\prime }(q(t)) \\ \dot{S}(t)&= \frac{1}{2} p(t)^{2} - V(q(t)) \\ \dot{Q}(t)&= P(t) \\ \dot{P}(t)&= - V^{\prime \prime }(q(t)) Q(t). \end{aligned} \end{aligned}$$

(3)

The coefficients $c_{k}(t,\varepsilon )$ obey a linear system of ordinary differential equations.

A similar result is valid in higher dimensions (see Theorem 3.6 of [7]). The dependence of $\mathcal{C}$ on the end-time $T$ is difficult to assess, and the system for the coefficients $c_{k}(t,\varepsilon )$ is difficult to solve, so an alternative numerical scheme is necessary.

This approximation result motivates us to look for an algorithm that does not deteriorate as $\varepsilon \rightarrow 0$. We note that our algorithm will separately handle the approximation for the parameters $\Pi (t)$ and $S(t)$ and the wave packet coefficients $c_{k}(t,\varepsilon )$. This observation is essential for the construction of the algorithm.

In the next section we present several splittings, ending with our proposed Algorithm 3 (called below semiclassical splitting). Numerical simulations show the desired behavior in $\varepsilon$ and time and emphasize the importance of the factor $\varepsilon$ instead of $1/\varepsilon ^{2}$. With the motivation of these numerical results we focus in the last section only on the analysis of the time-convergence.

2 Time-splittings

A starting point for an efficient time-integration is the scheme proposed in [5]: As in Strang-splitting, we decompose the Hamiltonian

$$\begin{aligned} H = T + U + W \end{aligned}$$

into its kinetic part $T = -\frac{\varepsilon ^{4}}{2}\Delta _{x}$ and its potential part $V(x) = U(q(t),x) + W(q(t),x)$, where $U(q(t),x)$ is the quadratic Taylor expansion of $V(x)$ around $q(t)$ and $W(q(t),x)$ is the corresponding remainder:

$$\begin{aligned} V(x) \!=\! U(q,x) \!+\! W(q,x) \!=\! V(q) \!+\! V^{\prime }(q)(x-q) \!+\! \frac{1}{2} V^{\prime \prime }(q)(x\!-\!q)^{2} \!+\! W(q,x). \end{aligned}$$

In the context of the wavepackets, the propagation with $U+W$ can be broken into two parts [5]. We call this algorithm the L-splitting for a time-step of length $\Delta t$:

Algorithm 1

(L-splitting) $H = \frac{1}{2} T + (U+W) +\frac{1}{2} T$

• 1. Propagate the solution for time $\frac{1}{2} \Delta t$, using only $T$.

• 2. Propagate the solution for time $\Delta t$, using only $U$.

• 3. Propagate the solution for time $\Delta t$, using only $W$.

• 4. Propagate the solution for time $\frac{1}{2} \Delta t$, using only $T$.

As shown in [5], the steps 1, 2, and 4 reduce to simple updates of the numerically propagated parameters $\tilde{\Pi }$ and $\tilde{S}$ (starting, of course from the given $\Pi (0)$ and $S(0)$). Step 3 keeps the parameters $\tilde{\Pi }$ and $\tilde{S}$ fixed and evolves the set of coefficients via the system of ordinary differential equations

$$\begin{aligned} i \varepsilon ^{2} \dot{\tilde{c}} = F\left[ \tilde{\Pi }\left( \frac{\Delta t}{2}\right) \right] \tilde{c},\quad {\text{ for } }\ t\in [0,\Delta t], \end{aligned}$$

(4)

with a $K\times K$ matrix $F[\tilde{\Pi }(\frac{\Delta t}{2})]$ whose entries are

$$\begin{aligned} F_{j,k}\left[ \tilde{\Pi }\left( \frac{\Delta t}{2}\right) \right] = \int \overline{\varphi _{j}\left[ \tilde{\Pi }\left( \frac{\Delta t}{2}\right) \right] (x)} W\left( \tilde{q}\left( \frac{\Delta t}{2}\right) ,x\right) \varphi _{k}\left[ \tilde{\Pi }\left( \frac{\Delta t}{2}\right) \right] (x)\,dx. \end{aligned}$$

As mentioned in the Introduction, the global convergence of this algorithm (measured by the $L^{2}$-error) is observed to be $(\Delta t)^{2}/\varepsilon ^{2}$, which can also be proved as in [4].

A splitting of $H=T+V$ that is of order 4 is the Y-splitting (see [15]). Denoting $\theta =1/(2-2^{1/3})$, we have:

Algorithm 2

(Y-splitting $H=T+V$)

• 1. Propagate the solution for time $\theta \frac{1}{2}\Delta t$, using only $T$.

• 2. Propagate the solution for time $\theta \Delta t$, using only $V$.

• 3. Propagate the solution for time $(1-\theta )\frac{1}{2}\Delta t$, using only $T$.

• 4. Propagate the solution for time $(1-2\theta )\Delta t$, using only $V$.

• 5. Propagate the solution for time $(1-\theta )\frac{1}{2}\Delta t$, using only $T$.

• 6. Propagate the solution for time $\theta \Delta t$, using only $V$.

• 7. Propagate the solution for time $\theta \frac{1}{2}\Delta t$, using only $T$.

If we use this also for our decomposition $H=T+U+W$ we get what we call YL-splitting: each of the steps 2, 4, and 6 above are decomposed in a step for $U$ and one for $W$.

We observed convergence of order $(\Delta t)^{4}/\varepsilon ^{2}$ in all tests based on this YL-splitting. Since the expensive propagation of the coefficients must be done three times (in the steps 3, 6, and 9) during each time step, the computational time is much greater than that for the L-splitting. We measure the error in the experiments via a numerical approximation of the $L^{2}$-norm based on $2^{16}$ equispaced points in the space domain; in order to emphasize that this is not the exact $L^{2}$-norm of the error, we denoted it by $\Vert \cdot \Vert _{wf}$ (see Fig. 1). The benchmark problem used in all numerical results presented here is based on the torsional potential $V(x)=1-\cos (x)$ with the initial value $\varphi _{0}[1,0,1,i]$ which is propagated from the initial time $t=0$ to the end time $T=2$ using $K=8$ wavepackets. Tests with different potentials (including $V(x)=x^4$) and various other initial values produced similar results. Equation (4) was solved via standard Padé approximation of the exponential matrix. We also used the Arnoldi method when computing with much larger $K$ without observing any significant difference concerning the results in this paper. The components of $\tilde{F}[(\frac{\Delta t}{2})]$ in (4) were computed via a very precise Gauss–Hermite quadrature which was adapted to the shape of the wavepackets. The computational setting is made such that the error due to the discretization in space has no significant effect. A larger number of basis functions does not make any difference until the end time $T=2$, which is already a long integration time, due to the $\varepsilon$-time scale. Other end times $T=4,6,8,10$ are possible¹ but require the use of more basis functions. Doing this may be questionable for the semiclassical approach, since the Ehrenfest-time is proportional to $\log (1/\varepsilon ^{2})$.

In each case, the reference solution used to estimate the error was the numerical solution computed with the time step $\Delta t_0=2^{-13}$.

Fig. 1

The error dependence on $\varepsilon$ in the propagation with YL-splitting and wavepackets. Although the method is of order 4 in time, the error scales as $1/\varepsilon ^{2}$ requiring small time-steps

Remark 1

Since the errors grow like $1/\varepsilon ^{2}$ as $\varepsilon \rightarrow 0$, the solution based on traditional second or fourth order splittings (Fourier or wavepacket based) should not be used as a reference solution for the semiclassical splitting, unless one can afford the sufficiently small time-steps and the large number of Fourier points. E.g., in the case of the harmonic oscillator, the exact solution is represented by a few wavepackets independently on the value of $\varepsilon$, while the sampling rate for the Fourier approximation has to be at least $2/\varepsilon ^{2}$ per dimension. This means for the space domain $[-\pi ,\pi ]$ about $2\times 10^{5}$ points when $\varepsilon =10^{-2}$ and $2\times 10^{6}$ points when $\varepsilon =10^{-3}$. Larger space domains could be necessary in order to avoid artificial boundary conditions, and hence they would require the use of even more computational points. The large number of space points makes one time-step of the traditional Fourier based split operator method computationally intensive. Furthermore the inherent time-step restriction $\Delta t \ll \varepsilon$ forces one to use many time-steps, yielding a long computational time even for efficient algorithms. In the case of other potentials, the solution based on wavepackets is no longer exact. However, if the solution remains localized in space (and this can be proved in the semiclassical situation), then a few wavepackets are sufficient for a good approximation, making the new numerical method competitive, even though we do not have such a marvelous tool as the FFT. This observation is even more important if we envisage higher dimensional applications.

The critical idea for our new algorithm comes from the observation that for small $\varepsilon$, the largest errors arise from the use of numerically computed parameters $\Pi$ and $S$, while the expensive part of the computation is finding the coefficients $c$. On the other hand, $\varepsilon$ is not present in the classical equations (3) for the parameters, but it appears only in the equation for the coefficients (4). Our algorithm combines the Strang-splitting for $H=(T+U)+W$ and the Y-splitting for $T+U$, i.e., it is a fourth order scheme for the approximation of the parameters $\Pi$ and $S$. We keep the expensive part of the computation (involving the remainder $W$) in the inner part of the Strang-splitting $H = \frac{1}{2} (T+U) + W + \frac{1}{2} (T+U)$ with a large time step $\Delta t$. We use a small time step $\delta t$ for the cheap propagation of the parameters. This small time step is chosen so that the desired overall convergence rate $\varepsilon (\Delta t)^{2}$ is achieved with a minimum value of $\Delta t/\delta t=N=N(\varepsilon ,\Delta t)$ small time steps per large time step. We call the resulting propagation algorithm semiclassical-splitting.

Algorithm 3

(Semiclassical-splitting) Define $N:=\mathtt {ceil}\left( 1+\frac{\sqrt{\Delta t}}{\varepsilon ^{3/4}}\right)$ and $\delta t:=\frac{\Delta t}{N}$, which hence satisfies $\delta t \le \min \{\varepsilon ^{3/4} \sqrt{\Delta t}, \Delta t \}$.

• 1. Propagate the solution for time $\frac{1}{2} \Delta t$ via $N$ steps of length $\delta t$ using the Y-splitting for $T+U$ (Algorithm 2).

• 2. Propagate the solution for time $\Delta t$, using only $W$, i.e., solve Eq. (4).

• 3. Propagate the solution for time $\frac{1}{2} \Delta t$ via $N$ steps of length $\delta t$ using the Y-splitting for $T+U$ (Algorithm 2).

Figures 2, 3, and 4 display the results of numerical experiments based on this semiclassical splitting. They confirm our theoretical considerations from Sect. 3, as long as the strong round off in $e^{-i\alpha /\varepsilon ^{2}}-e^{-i(\alpha +\mathrm{eps})/\varepsilon ^{2}}$ (with $\alpha \ne 0$ and eps = machine precision) in the measurement of the error can be avoided. The effect of this round off in the measurement of the error for $\Delta t$ and $\varepsilon$ simultaneously small is evident in Fig. 2; this effect is missing when measuring the error in the coefficients (see Fig. 3).

Fig. 2

The error dependence on $\varepsilon$ and on $\Delta t$ (semiclassical-splitting)

Fig. 3

The error dependence on $\varepsilon$ and on $\Delta t$ of the coefficients (semiclassical-splitting)

Fig. 4

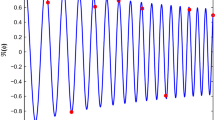
Left difference between the solution via Fourier method on $2^{16}$ grid points and the semiclassical-splitting with eight wavepackets: the $1/\varepsilon ^{2}$ factor in the error of the Fourier solution dominates. Right physical time in femtoseconds corresponding to the simulation parameter $\varepsilon$

The left part of Fig. 4 shows the $L^{2}$-norm of the difference between the solution via the Fourier method with $2^{16}$ grid points and the semiclassical-splitting with eight wavepackets. The semiclassical-splitting gives such a good approximation of the exact solution for small $\varepsilon$ that we see the $\varepsilon ^{-2}$-deterioration until the Fourier-based solution produces nonsense. In an intermediate range we see the $\varepsilon$-dependence of the error in the semiclassical splitting. We also see that for $\varepsilon >\frac{1}{4}$, the solution based on eight wavepackets is also poor. The right part of Fig. 4 shows the physical end time in femtoseconds for different values of the simulation parameter $\varepsilon$. Smaller $\varepsilon$ means a later physical time at the same computational end time $T$.

Finally, let us note that the convergence order can be improved to $\varepsilon (\Delta t)^{4}$ by replacing the Y-splitting with a higher order one and using a Magnus integrator for the step 2 in Algorithm 3. In Fig. 5 we plotted the error at different end times ($T=2$ and $T=5$) in the semiclassical-splitting with 8 (left) and 16 (right) wavepackets when the reference solution is computed via the Magnus method with 96 wavepackets: note that the $\varepsilon$-dependence of the approximation error dominates the second order error in time for large $\varepsilon$ and that a longer end time needs more basis functions in order to reach the same accuracy.

Fig. 5

The error dependence of the coefficients on $\varepsilon$ and $\Delta t$ in the semiclassical-splitting at end time $T=2$ (above) and $T=5$ (below); left with $K=8$, and right with $K=16$ basis functions; the reference solution is computed via 96 wavepackets and a Magnus time-integrator of fourth order

All time-steps in the steps 1 and 3 of the semiclassical-splitting, as well as in the steps 1, 2 and 4 of the L-splitting, are very cheap, since they consist of simple updates of the parameters $\Pi$ and $S$. A higher order splitting for those is indeed more expensive, but is negligible compared to the amount of work required for solving Eq. (4) via Pade-approximation or even a Krylov-method with a few steps. The internal parameter $\delta t$ depends (mildly) on $\varepsilon$, yielding more time-steps N in the steps 1 and 3 of the semiclassical-splitting, but this increase is still insignificant (for the same reason): the improvement in computing-time when using large time-steps $\Delta t$ is so important, that the extra work in the approximation of the parameters $\Pi$ and $S$ is not perceptible. A comparative look at Figs. 1 and 2 reveals that one may use a larger time step $\Delta t$ in the semiclassical algorithm than in the YL-splitting, while achieving the same error. The influences of the number of basis functions used and the detailed study of the method in many dimensions are the subjects of on-going and future investigations.

We now turn to the main topic of this paper, the analysis of the time-convergence of the semiclassical splitting.

3 Convergence results for the semiclassical-splitting algorithm

We first note that one cannot address the convergence of the proposed algorithms via the local error representation of exponential operator splitting methods as in Section 5 of [4]. This is because the parameters $\varepsilon ^{2}$ and $\Delta t$ enter the splitting in fundamentally different ways.

The overall error when using the semiclassical-splitting algorithm consists of an approximation error caused by using the representation with a finite number of moving wavepackets and a time-discretization error. Our main result is the following:

Theorem 1

Suppose the initial value is

$$\begin{aligned} \psi (0) = e^{iS(0)/\varepsilon ^{2}} \sum _{k=0}^{K_1-1} c_{k}(0,\varepsilon )\varphi _{k}[\Pi (0)], \end{aligned}$$

and that $K\ge K_1+3(N-1)$, where $N=1,2,$ or $3$. If the potential $V\in C^{5}(\mathbb R )$ and its derivatives satisfy $-C_{1}< V^{(s)}(x) < C_{2}e^{C_{3} x^{2}}$, for $s=0,1,\ldots ,5$, then there are constants $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$, such that

$$\begin{aligned} \Vert \psi (t) - \tilde{u}(t)\Vert \le \mathcal{C}_{1}\varepsilon ^N+ \mathcal{C}_{2}\varepsilon (\Delta t)^{2}, \end{aligned}$$

(5)

where $\tilde{u}$ is constructed via the semiclassical splitting Algorithm 3. The constants $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ do not depend on $\Delta t,\delta t$, or $\varepsilon$, but depend on the potential $V$ and its derivatives up to fifth order, on the $\sup$’s of $|Q|,|\dot{Q}|,|\ddot{Q}|,|q|,|\dot{q}|,|\ddot{q}|$ from (3) on $[0,T]$, on the number $K$ of wavepackets used in the approximation, and on the final integration time $T$.

Remark

If $V\in C^l(\mathbb R )$ with $l>5$, then the theorem is true with a larger $N$. More precisely, if $K\ge K_1+3(N-1)$, the first term on the right hand side of (5) still has the form $\mathcal{C}_{1}\varepsilon ^N$, but the restriction on $N$ becomes $N=1,2,\ldots ,l-2$, and $\mathcal{C}_{1}$ depends also on $V^{(s)}$ for $s\le l$.

Let us briefly outline the several steps that make up the proof of this theorem. We introduce an approximation $u$ to the solution of the time-dependent Schrödinger equation that is similar to (2). The parameters $\Pi$ and $S$ satisfy the system (3), and the coefficients $c_{k}$ are given by the solution to the linear system of ordinary differential equations

$$\begin{aligned} i\varepsilon ^{2}\dot{c} = F[\Pi (t)]c, \end{aligned}$$

(6)

where the $K\times K$ matrix $F[\Pi ]$ has entries

$$\begin{aligned} F_{j,k}[\Pi (t)] = \int \overline{\varphi _{j}[\Pi (t)](x)} W(q(t),x) \varphi _{k}[\Pi (t)](x)\,dx. \end{aligned}$$

Then, we prove that the approximation error $\Vert \psi (T) - u(T)\Vert$ is bounded by the Galerkin error, so that we can concentrate in the rest of the section only on $\Vert u(T) - \tilde{u}(T)\Vert$, or rather on showing that the error in one time-step $\Vert u(\Delta t) - \tilde{u}(\Delta t)\Vert$ is of order $\varepsilon (\Delta t)^{3}$. We introduce an intermediate function $u_{1}$ constructed via the parameters $\Pi (t)$ from the exact solution of (3) and coefficients $c^{1}$ from the linear system with constant matrix $F^{1} = F[\Pi ^{1}]$, where $\Pi ^{1} = \Pi (\frac{\Delta t}{2} )$. We then carefully investigate the quantities $\Vert u(\Delta t)-u_{1}(\Delta t)\Vert$ and $\Vert u_{1}(\Delta t)-\tilde{u}(\Delta t)\Vert$. A crucial observation is that the $\varepsilon$-dependence of the matrix entries $F_{j,k}$ can be written explicitly in several different ways that involve terms which contain $\varepsilon$-independent wavepackets. The fast decay at infinity of these wavepackets and the particular $\varepsilon$-dependence let us establish appropriate bounds on the matrix entries $F_{j,k}$, as well as on their time-derivatives. Also important is a bound on the error when using approximate wavepackets $\tilde{\varphi }_{k}$ instead of $\varphi _{k}$. The details of the proof follow; let us now start with the first step.

Our proof relies on the following elementary lemma that is Lemma 2.8 of [7]. We restate it here for completeness and to make the notation consistent with this paper.

Lemma 1

Suppose $H(\varepsilon )$ is a family of self-adjoint operators for $\varepsilon >0$. Suppose $\psi (t,\varepsilon )$ belongs to the domain of $H(\varepsilon )$, is continuously differentiable in $t$, and approximately solves the Schrödinger equation in the sense that

$$\begin{aligned} i \varepsilon ^2 \frac{\partial \psi }{\partial t}= H(\varepsilon ) \psi (t,\varepsilon ) + \zeta (t,\varepsilon ), \end{aligned}$$

where $\zeta (t,\varepsilon )$ satisfies

$$\begin{aligned} \Vert \zeta (t,\varepsilon )\Vert \le \mu (t,\varepsilon ). \end{aligned}$$

Then

$$\begin{aligned} \Vert e^{-itH(\varepsilon )/\varepsilon ^2}\psi (0,\varepsilon )- \psi (t,\varepsilon ) \Vert \le \varepsilon ^{-2} \int _0^t\mu (s,\varepsilon )\,ds. \end{aligned}$$

(7)

Proof

By the unitarity of the propagator $e^{-itH(\varepsilon )/\varepsilon ^2}$ and the fundamental theorem of calculus, the quantity on the left hand side of (7) can be estimated as

$$\begin{aligned}&\Vert e^{-itH(\varepsilon )/\varepsilon ^2} \psi (0,\varepsilon )- \psi (t,\varepsilon )\Vert \\&\quad =\Vert \psi (0,\varepsilon )- e^{itH(\varepsilon )/\varepsilon ^2}\psi (t,\varepsilon )\Vert \\&\quad =\left\| \int _0^t \frac{\partial }{\partial s} \left( \psi (0,\varepsilon )- e^{isH(\varepsilon )/\varepsilon ^2}\psi (s,\varepsilon )\right) \,ds\right\| \\&\quad =\left\| \int _0^t \left( -i\varepsilon ^{-2} e^{isH(\varepsilon )/\varepsilon ^2} H(\varepsilon ) \psi (s,\varepsilon )-e^{isH(\varepsilon )/\varepsilon ^2} \frac{\partial \psi }{\partial s}(s,\varepsilon )\right) \,ds\right\| \\&\quad =\left\| \int _0^t i\varepsilon ^{-2}e^{isH(\varepsilon )/\varepsilon ^2}\zeta (s,\varepsilon ) ds\,\right\| \\&\quad \le \varepsilon ^{-2} \int _0^t\mu (s,\varepsilon )\,ds. \end{aligned}$$

This proves the lemma. $\square$

Theorem 2

The approximation error is bounded by the Galerkin error:

$$\begin{aligned} \Vert \psi (T) - u(T)\Vert \le \frac{1}{\varepsilon ^{2}} \int _{0}^{T} \Vert P_{K}Wu - Wu\Vert \,dt. \end{aligned}$$

Under the hypotheses of Theorem 1 (or the remark after it), the integrand here is bounded by

$$\begin{aligned} \mathcal{C}_{K,Q,W}\varepsilon ^{N+2}. \end{aligned}$$

Proof

Corollary 2.6 of [7] ensures that each $\varphi _{k}[\Pi ,S]$ satisfies the time dependent Schrödinger equation with the Hamiltonian $T+U$. Using (6), we see that

$$\begin{aligned} i\varepsilon ^2\partial _{t} u = H(\varepsilon )u+P_{K}Wu-Wu, \end{aligned}$$

where $P_{k}$ denotes the $L^{2}$-orthogonal projection into the space spanned by the basis functions $\varphi _{0}[\Pi ],\ldots ,\varphi _{K-1}[\Pi ]$.

We shall apply Lemma 1, so we only have to find an upper bound for the Galerkin error

$$\begin{aligned} \Vert P_{K}Wu - Wu\Vert . \end{aligned}$$

We note that $\Vert P_{K}Wu - Wu\Vert$ is decreasing in $K$, so when $N=1$, it suffices to prove $\Vert P_{K_1}Wu - Wu\Vert =O(\varepsilon ^3)$. However, $\Vert P_{K}Wu - Wu\Vert \le \Vert Wu\Vert$, and since $W$ is locally cubic near $x=q$, estimate (2.68) of [7] immediately proves the result.

When $N=2$, it suffices to prove $\Vert P_{K_1+3}Wu - Wu\Vert =O(\varepsilon ^4)$. To show this, we first note that $\Vert (1-P_{K_1})u\Vert =O(\varepsilon )$ as in the proof of Theorem 2.10 of [7]. Next,

$$\begin{aligned} W(x,t) = V^{\prime \prime \prime }(q(t))(x-q(t))^{3/6} + V^{\prime \prime \prime \prime }(\xi (x,t))(x-q(t))^{4/24}. \end{aligned}$$

So, we have

$$\begin{aligned} \Vert (P_{K_1+3}-1) W u\Vert&\le \Vert (P_{K_1+3}-1) W P_{K_1} u\Vert \\&+ \Vert (P_{K_1+3}-1) W (1-P_{K_1}) u\Vert \\&\le \Vert (P_{K_1+3}-1) V^{\prime \prime \prime }(q) (x-a)^3 P_{K_1} u\Vert \\&+ \Vert (P_{K_1+3}-1) V^{\prime \prime \prime \prime }(\xi (x,t)) (x-q)^4 P_{K_1} u\Vert \\&+ \Vert (P_{K_1+3}-1) W (1-P_{K_1}) u\Vert . \end{aligned}$$

The first term on the right hand side is zero since $(P_{K_1+3}-1)(x-q)^3P_{K_1}=0$. The second term is $O(\varepsilon ^4)$ as in the proof of Theorem 2.10 of [7]. The third term is bounded by $\Vert W(1-P_{K_1})u\Vert$. This quantity is $O(\varepsilon ^4)$ because $W$ is locally cubic as in the $N=1$ case and $\Vert (1-P_{K_1})u\Vert =O(\varepsilon )$.

The $N=3$ case is similar, but with the next order Taylor series estimates. The $N\le l-2$ case is similar under the hypotheses of the remark, but with higher order Taylor series estimates.$\square$

The first term on the right hand side of estimate (5) in Theorem 1 arises from the estimate in Theorem 2. The rest of this paper concerns the second term on the right hand side of (5).

We concentrate on the local time-error when approximating $u(\Delta t)$; if we show that it can be bounded by $\varepsilon (\Delta t)^{3}$, then standard arguments and Theorem 2 prove Theorem 1.

The first step in Algorithm 3 produces approximations $\tilde{\Pi }(\frac{\Delta t}{2})$ of ${\Pi }(\frac{\Delta t}{2})$ and $\tilde{S}(\frac{\Delta t}{2})$ of ${S}(\frac{\Delta t}{2})$, both with errors $\mathcal{C}(\delta t)^{4}\frac{\Delta t}{2}$. Given these approximate parameters, the coefficients $\tilde{c}_{k}$ solve the system (6) with the constant matrix $\tilde{F}=F[\tilde{\Pi }(\frac{\Delta t}{2})]$ on right hand side, as in (4). They enter in the expression of the numerical solution at the end of the Strang-splitting

$$\begin{aligned} \tilde{u}(\Delta t) = e^{i\tilde{S}({\Delta t})/\varepsilon ^{2}} \sum _{k=0}^{K-1} \tilde{c}_{k}({\Delta t},\varepsilon ) \varphi _{k}[\tilde{\Pi }({\Delta t})]. \end{aligned}$$

In practice, they are computed via expensive (Padé or Arnoldi) iterations, but here we assume they are computed exactly.

In order to shorten the formulas, we denote $\varphi _{k}=\varphi _{k}[{\Pi }]$ and $\tilde{\varphi }_{k}=\varphi _{k}[\tilde{\Pi }]$.

To facilitate the proof, we introduce $u_{1}(t)$, constructed via the parameters $\Pi (t)$ from the exact solution of (3) and coefficients $c^{1}$ from the linear system with constant matrix $F^{1} = F[\Pi ^{1}]$, where $\Pi ^{1} = \Pi (\frac{\Delta t}{2} )$:

$$\begin{aligned} i \varepsilon ^{2}\dot{c^{1}} = F^{1}c^{1}, \quad {\text{ for } }\ t\in [0,\Delta t]. \end{aligned}$$

With this we construct

$$\begin{aligned} u_{1}(t) = e^{iS(t)/\varepsilon ^{2}} \sum _{k=0}^{K-1} c^{1}_{k}(t,\varepsilon ) \varphi _{k}[\Pi (t)], \end{aligned}$$

which has the parameters of $u$, but the coefficients $c^{1}$. The local error then decomposes as

$$\begin{aligned} \Vert u(\Delta t)-\tilde{u}(\Delta t)\Vert \le \Vert u(\Delta t)-u_{1}(\Delta t)\Vert + \Vert u_{1}(\Delta t)-\tilde{u}(\Delta t)\Vert . \end{aligned}$$

The next two theorems give upper bounds for these two last terms, ensuring the desired bound on the local error.

We now take a more careful look at the Galerkin matrix $F$. A crucial observation is that as in section 4.1 of [5], the change of variables $x=q+ \varepsilon y$ allows us to represent

$$\begin{aligned} F_{j,k} = \int \overline{\phi _{j}(y)} W(q+\varepsilon y) \phi _{k}(y)\, dy \end{aligned}$$

(8)

in terms of $\varepsilon$-independent, but orthogonal functions $\phi _{k}$, given by the recurrence relation

$$\begin{aligned} \phi _0(y)&= \pi ^{-1/4}|Q|^{-1/2}e^{-|Q|^{-2}|y|^2/2},\\ Q\sqrt{k_j+1}\phi _{k+1}(y)&= \sqrt{2}y\phi _k(y) - \overline{Q}\sqrt{k_j}\phi _{k-1}(y). \end{aligned}$$

By this change of variables, all of the dependence on $\varepsilon$ has been moved out of the wavepackets and put into the operator $W(q+\varepsilon y)$, which is

$$\begin{aligned}&W(q+\varepsilon y) \nonumber \\&\quad =V(q(t) + \varepsilon y) - V(q(t)) - V^{\prime }(q(t))\varepsilon y - \frac{1}{2} V^{\prime \prime }(q(t))\varepsilon ^{2}y^{2} \end{aligned}$$

(9)

$$\begin{aligned}&\quad = \frac{1}{6} V^{^{\prime \prime \prime }} (\zeta (y)) \varepsilon ^{3} y^{3} \nonumber \\&\quad = \int _{q(t)}^{q(t)+\varepsilon y} \frac{(q(t)+\varepsilon y-z)^2}{2} V^{\prime \prime \prime }(z)\, dz. \end{aligned}$$

(10)

Note that $Q$ is not present in the expression for $W$, while the functions $\phi _{k}$ are wavepackets that depend on $Q$ only: $\phi _{k} = \varphi _{k}^{\varepsilon =1}[0,0,Q,i(\overline{Q})^{-1}]$. We use this observation in the proofs of the following lemmas.

Lemma 2

Suppose $g$ and $Z$ are functions on $\mathbb{R }$ that satisfy $g\in L^2(\mathbb{R },dy)$ and $|Z(y)|\le P(y) e^{C \varepsilon ^2y^2/2}$, where $P$ is a non-negative polynomial. Then there exists a constant $\mathcal{C}$ depending only on $j$ and $Q$, such that

$$\begin{aligned} |\left\langle {\phi _{j}},\,{Zg}\right\rangle | = \left| \int \ \overline{\phi _j(y)} Z(y) g(y)\,dy \right| \le \mathcal{C}\Vert g\Vert , \end{aligned}$$

(11)

for all $\varepsilon <\frac{|Q|^{-1}}{\sqrt{2 C}}$ if $C>0$. If $C=0$, then the estimate is valid for $\varepsilon \in (0, D]$ for any fixed positive $D$.

Proof

Let us assume the more difficult situation $C>0$. By the Schwarz inequality, $|\langle \phi _j,Z g\rangle |\le \Vert Z\phi _j\Vert \Vert g\Vert$, so it suffices to prove that $\Vert Z \phi _j\Vert$ is finite. However,

$$\begin{aligned} \Vert Z\phi _j\Vert ^2 = \pi ^{-1/2}|Q|^{-1} \int _\mathbb R \ |Z(y)|^2 |p(y)|^2\ e^{-y^2/|Q|^2}\, dy, \end{aligned}$$

where $p$ is a polynomial. Under our assumptions, elementary estimates show that this integral is bounded by a constant, uniformly for $\varepsilon ^2<\frac{|Q|^{-2}}{2 C}. \square$

Lemma 3

The entries of the matrix $F[\Pi ]$ and their first two time-derivatives are bounded by constants times $\varepsilon ^{3}$:

$$\begin{aligned} |F_{j,k}(t)| \le \mathcal{C}_0\varepsilon ^{3},\quad | \dot{F}_{j,k}(t)| \le \mathcal{C}_1\varepsilon ^{3},\quad {\text{ and }}\quad |\ddot{F}_{j,k}(t)| \le \mathcal{C}_2\varepsilon ^{3}, \end{aligned}$$

where the constants $\mathcal{C}_l$ depend only on $j,k,Q,\dot{Q},\ddot{Q},\dot{q},\ddot{q}$, and bounds on the third, fourth, and fifth derivatives of $V$.

Proof

We use expression (10) to write

$$\begin{aligned} F_{j,k}(t) = \int _\mathbb R \overline{\phi _j(y)} \int _{q(t)}^{q(t)+\varepsilon y} \frac{(q(t)+\varepsilon y-z)^2}{2} V^{\prime \prime \prime }(z)\, dz \phi _k(y)\, dy. \end{aligned}$$

We then let $z=q(t)+\sigma \varepsilon y$ and rewrite the inner integral as

$$\begin{aligned} \int _0^1 \frac{(\varepsilon y(1-\sigma ))^2}{2} V^{\prime \prime \prime }(q(t)+\sigma \varepsilon y) \varepsilon y\, d\sigma . \end{aligned}$$

Next, we interchange the order of integration to obtain

$$\begin{aligned} F_{j,k}(t) = \varepsilon ^3 \int _0^1 \frac{(1-\sigma )^2}{2} \int _\mathbb R \overline{\phi _j(y)}\ y^3 V^{\prime \prime \prime }(q(t)+\sigma \varepsilon y) \phi _k(y)\, dy\, d\sigma . \end{aligned}$$

(12)

Lemma 2 with $Z(y) = y^3 V^{\prime \prime \prime }(q(t)+\sigma \varepsilon y)$ gives the result for $F_{j,k}$.

To study $\dot{F}_{j,k}$, we take the time derivative of expression (12). The only time dependent quantities here are $\phi _j,\phi _k$, and $V^{\prime \prime \prime }(q(t)+\sigma \varepsilon y)$. The time dependence in the $\phi$’s comes only from $Q(t)$ and its conjugate, while the time dependence in $V^{\prime \prime \prime }(q(t)+\sigma \varepsilon y)$ comes only from $q(t)$. The result for $\dot{F}_{j,k}$ then follows by several applications of Lemma 2.

The result for $\ddot{F}_{j,k}$ follows from the same arguments applied to the second time derivative of (12). $\square$

Corollary 1

$$\begin{aligned} \Vert F(t)\Vert \le \mathcal{C}\varepsilon ^{3},\quad \Vert \dot{F}(t)\Vert \le \mathcal{C}\varepsilon ^{3},\quad {\text{ and }}\quad \Vert \ddot{F}(t)\Vert \le \mathcal{C}\varepsilon ^{3}, \end{aligned}$$

where $\mathcal{C}$ has the same dependence as in Lemma 3 and depends additionally on $K$, but is independent of $\varepsilon$.

Lemma 4

The error caused by using the approximate parameters $\tilde{\Pi }$ in the wavepacket $\varphi _{k}$ satisfies

$$\begin{aligned} \Vert \varphi _{k}(\Delta t)-\tilde{\varphi }_{k}(\Delta t)\Vert \le \mathcal{C}\frac{(\delta t)^{4}}{\varepsilon ^{2}}\Delta t. \end{aligned}$$

Proof

Using a homotopy between $\Pi$ and $\tilde{\Pi }$, one can prove² via careful calculations that

$$\begin{aligned} \Vert \varphi _{k} - \tilde{\varphi _{k}}\Vert \le \mathcal{C}\frac{1}{\varepsilon ^{2}} (|q-\tilde{q}| + |p-\tilde{p}| + |Q-\tilde{Q}| + |P-\tilde{P}|). \end{aligned}$$

The fact that the Y-splitting with time step $\delta t$ for $\Pi$ on an interval of length $\Delta t$ is of fourth order then concludes this proof.

Let us briefly sketch the proof of the above inequality, which is the key to this lemma. We can construct a homotopy $\Pi [\theta ] = (q[\theta ], p[\theta ], Q[\theta ], P[\theta ])$ for $\theta \in [0,1]$ with the properties

$$\begin{aligned} p[\theta ]&= \tilde{p} + \theta (p-\tilde{p}), \quad q[\theta ] = \tilde{q} + \theta (q-\tilde{q}), \\ P[0]&= \tilde{P},\quad P[1] = P,\quad P^{\prime }[\theta ] = O(P-\tilde{P}), \\ Q[0]&= \tilde{Q},\quad Q[1] = Q,\quad Q^{\prime }[\theta ] = O(Q-\tilde{Q}), \end{aligned}$$

such that the compatibility conditions for $P[\theta ]$ and $Q[\theta ]$ are satisfied. These parameters then give a corresponding homotopy $\varphi _{0}^{\varepsilon }[\theta ] = \varphi _{0}^{\varepsilon }(\Pi [\theta ])$, for the raising and lowering operators and $\varphi _{k}^{\varepsilon }[\theta ]$ for every $k$. Using this homotopy, we have

$$\begin{aligned} \Vert \varphi _{k} - \tilde{\varphi _{k}}\Vert \le \int \limits _{0}^{1} \Vert \varphi _{k}^{\prime }[\theta ]\Vert d\theta \le \sup \limits _{\theta \in [0,1]} \Vert \varphi _{k}^{\prime }[\theta ]\Vert . \end{aligned}$$

An induction argument together with lengthy careful calculations gives an expression for $\varphi _{k}^{\prime }[\theta ]$ as a linear combination of slightly more basis functions. In the one-dimensional case this reads simply

$$\begin{aligned} \varphi _{k}^{\prime }[\theta ] = \frac{1}{\varepsilon ^{2}} \sum \limits _{m\le K+1} \alpha _{m}^{k}[\theta ] \varphi _{k}[\theta ], \quad {\text{ for } }\ k\le K, \end{aligned}$$

with the complex coefficients satisfying

$$\begin{aligned} \sup \limits _{\theta \in [0,1]} |\alpha _{m}^{k}[\theta ]| \le \mathcal{C}\frac{1}{\varepsilon ^{2}}( |q-\tilde{q}| + |p-\tilde{p}| + |Q-\tilde{Q}| + |P-\tilde{P}|), \end{aligned}$$

which completes the proof. In higher dimensions, the above sum extends over basis functions having $m_{j} < K_{j}+1$ for the $j$th coordinate. $\square$

Lemma 5

The error caused by using the approximate parameters $\tilde{\Pi }$ in the matrix $F$ satisfies

$$\begin{aligned} \Vert F^{1} -\tilde{F}\Vert \le \mathcal{C}(\delta t)^{4} \Delta t, \end{aligned}$$

with the constant $\mathcal{C}$ depending on $Q^{1},\tilde{Q}$, and $V$ and its derivatives up to third order.

Proof

The representation (8) of the entries of the matrix $F$ that depends only on $Q$ is again the key idea: it allows us to write $F^{1}_{j,k} - \tilde{F}_{j,k}$ as the sum of the following three terms

$$\begin{aligned} \left\langle {\phi ^{1}_{j}},\,{W^{1} (\phi ^{1}_{k}-\tilde{\phi }_{k})}\right\rangle + \left\langle {\phi ^{1}_{j} },\,{(W^{1}-\tilde{W} ) \tilde{\phi }_{k})}\right\rangle + \left\langle {\phi ^{1}_{j}-\tilde{\phi _{j}}},\,{\tilde{W}\tilde{\phi }_{k}}\right\rangle , \end{aligned}$$

where

$$\begin{aligned} W^{1}(y) = W(q^{1}+\varepsilon y) = \frac{1}{6} V^{^{\prime \prime \prime }}(q^{1}+\varepsilon \zeta ^{1}(y))\varepsilon ^{3} y^{3} \end{aligned}$$

and

$$\begin{aligned} \tilde{W}(y) = W(\tilde{q}+\varepsilon y) = \frac{1}{6} V^{^{\prime \prime \prime }}(\tilde{q}+\varepsilon \tilde{\zeta }(y)) \varepsilon ^{3} y^{3}. \end{aligned}$$

Note that $\phi ^{1}_{j} = \phi _{j}[Q]$ and $\tilde{\phi }_{j}=\phi _{j}[\tilde{Q}]$ do not depend on $q, p$, or $\varepsilon$. Lemma 2 now applies with $Z=W^{1}/\varepsilon ^{3}$ and $g= \phi ^{1}_{k} - \tilde{\phi }_{k}$ or $Z=\tilde{W}/\varepsilon ^{3}$ and $g = \phi ^{1}_{j} - \tilde{\phi _{j}}$ to estimate the first and the last term, respectively, by $\mathcal{C}\varepsilon ^{3} \Vert \phi ^{1}_{k} - \tilde{\phi }_{k}\Vert$ or $\mathcal{C}\varepsilon ^{3} \Vert \phi ^{1}_{j} - \tilde{\phi _{j}}\Vert$. As in the previous lemma, the last terms are both bounded by $\mathcal{C}\varepsilon (\delta t)^{4}\Delta t$ which is one order (in $\varepsilon$) smaller that the stated result. The largest error arises from the middle term. We bound it using (9) with the corresponding $q^{1}$ and $\tilde{q}$ and Lemma 2 again. This yields a bound of $\mathcal{C}(2+\varepsilon +\frac{1}{2}\varepsilon ^{2}) |q^{1}-\tilde{q}|$. Combining all these estimates, we get the upper bound for the quantity in the lemma:

$$\begin{aligned} \Vert F^{1}-\tilde{F}\Vert \le \mathcal{C}\left( \left( 2+\varepsilon +\frac{1}{2}\varepsilon ^{2}\right) |q-\tilde{q}|+ \varepsilon |Q-\tilde{Q}|\right) , \end{aligned}$$

which is bounded by $\mathcal{C}(\delta t)^{4} \Delta t$ as in the previous lemma. $\square$

Theorem 3

The difference between the approximate solution and the intermediate solution is

$$\begin{aligned} \Vert u(\Delta t) - u_{1}(\Delta t)\Vert \le \mathcal{C}\varepsilon (\Delta t)^{3}, \end{aligned}$$

where $\mathcal{C}$ depends on $K$ and $V$ and its derivatives up to 5th order, on $Q$ for $t$ between 0 and $T$, but is independent of $\varepsilon$ and $\Delta t$.

Proof

Denoting the (unitary) propagator for (6) by $\mathcal{U}(t,s)$, we can express the difference between the approximate solution and the intermediate solution as

$$\begin{aligned} \Vert \mathcal{U}(\Delta t,0)c(0) - e^{-i \frac{\Delta t}{\varepsilon ^{2}} F^{1}} c(0)\Vert = \Vert c(0) - \mathcal{U}(0,\Delta t)e^{-i\frac{\Delta t}{\varepsilon ^{2}}F^{1}}c(0) \Vert . \end{aligned}$$

We abbreviate $F(s):=F[\Pi (s)]$, and observe that since $F^{1} = F[\Pi (\frac{\Delta t}{2})]$, the expression in the second norm above is the integral from 0 to $\Delta t$ of

$$\begin{aligned} \mathcal{U}(0,s)\frac{1}{\varepsilon ^{2}}(F(s) - F^{1}) e^{-isF^{1}/\varepsilon ^{2}}c(0). \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert u(\Delta t) - u_{1}(\Delta t)\Vert&= \frac{1}{\varepsilon ^{2}} \left\| \int \limits _{0}^{\Delta t} \mathcal{U}(0,s)(F(s) - F^{1}) e^{-isF^{1}/\varepsilon ^{2}} c(0)\,ds \right\| . \end{aligned}$$

Standard arguments from the proof of the convergence order of the midpoint quadrature rule then shows that

$$\begin{aligned} \Vert u(\Delta t) - u_{1}(\Delta t)\Vert \le \frac{(\Delta t)^{3}}{\varepsilon ^{2}} \Vert R\Vert \end{aligned}$$

with the remainder $R$ involving the Peano kernel and a factor containing the second derivative with respect to $s$ of the integrand in the above formula. The first derivative of the integrand is

$$\begin{aligned}&\mathcal{U}(0,s) \frac{i}{\varepsilon ^{2}} F(s)(F(s) - F^{1})\ e^{- i s F^{1}/\varepsilon ^{2}} c(0) \\&\quad +\mathcal{U}(0,s) \dot{F}(s) e^{- i s F^{1}/\varepsilon ^{2}} c(0) \\&\quad +\mathcal{U}(0,s) (F(s) - F^{1}) \frac{-i}{\varepsilon ^{2}} F^{1} e^{- i s F^{1}/\varepsilon ^{2}} c(0) \end{aligned}$$

The second derivative has an even longer expression, but has the same character as the first one: every term containing the factor $1/\varepsilon ^{2}$ contains also a factor of $F^{1}$ or $F(s)$ or $\dot{F}(s)$, which are of order $\varepsilon ^{3}$, according to Corollary 1. Hence, the leading order terms are those involving only $\dot{F}(s)$ and $\ddot{F}(s)$, i.e., similar to the middle term in the first derivative. Those terms are themselves of order $\varepsilon ^{3}$, which shows that the remainder $R$ is bounded by $\mathcal{C}\varepsilon ^{3}. \square$

Theorem 4

The difference between the intermediate solution and the numerical solution is

$$\begin{aligned} \Vert u_{1}(\Delta t) - \tilde{u}(\Delta t)\Vert \le \mathcal{C}\frac{(\delta t)^{4}}{\varepsilon ^{2}}\Delta t. \end{aligned}$$

Proof

By the triangle inequality,

$$\begin{aligned}&\Vert u_{1}(t) - \tilde{u}(t)\Vert \\&\quad \le | e^{- i S(t)/\varepsilon ^2}- e^{- i \tilde{S}(t)/\varepsilon ^2} | + \left\| \sum _{k=0}^{K-1} {c}_{k}^{1}(t) \varphi _{k}(t) -\tilde{c}_{k}(t)\tilde{\varphi }_{k}(t) \right\| \\&\quad \le \mathcal{C}\frac{|S(t) - \tilde{S}(t)|}{\varepsilon ^{2}} + \left\| \sum _{k=0}^{K-1}c_{k}^{1}(t) \left( \varphi _{k}(t) -\tilde{\varphi }_{k}(t) \right) \right\| + \Vert \mathbf{c }^{1}(t)-\tilde{\mathbf{c }}(t)\Vert \\&\quad \le \mathcal{C}\frac{|S(t)-\tilde{S}(t)|}{\varepsilon ^{2}} + \sqrt{\sum _{k=0}^{K-1}\Vert \varphi _{k} - \tilde{\varphi }_{k}\Vert ^{2}} + \Vert \mathbf{c }^{1}(t)-\tilde{\mathbf{c }}(t)\Vert . \end{aligned}$$

We rewrite Eq. (4) as

$$\begin{aligned} i \varepsilon ^{2}\dot{\tilde{c}} = F_{1}\tilde{c} + (\tilde{F} - F_{1})\tilde{c},\quad {\text{ for } }\ t\in [0,\Delta t]. \end{aligned}$$

Lemma 1 and 5 give $\Vert \mathbf{c }(t)-\tilde{\mathbf{c }}(t)\Vert \le \mathcal{C}\frac{(\delta t)^{4}}{\varepsilon ^{2}}(\Delta t)^{2}$. Lemma 4 and the error in the splitting of (3) then yield the result. $\square$

Finally, Theorems 3, 4, and the triangle inequality give us an estimate of the local error:

$$\begin{aligned} \Vert u(\Delta t) - \tilde{u}(\Delta t)\Vert \le \mathcal{C}\frac{(\delta t)^{4}}{\varepsilon ^{2}}(\Delta t) + \mathcal{C}\varepsilon (\Delta t)^{3} \le \mathcal{C}\varepsilon (\Delta t)^{3} \end{aligned}$$

if we choose

$$\begin{aligned} \delta t \le \varepsilon ^{3/4} \sqrt{\Delta t}. \end{aligned}$$

This shows that the number $N$ of time-steps for solving (3) via a splitting is at least $N\ge \sqrt{\Delta t}\varepsilon ^{-3/4}$ for the semiclassical splitting Algorithm 3. With such a choice of $N$, standard arguments and Theorem 2 imply the result on the global error in our main Theorem 1.