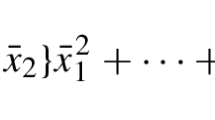Inequality conjectures on derivations of local k-th Hessain algebras associated to isolated hypersurface singularities

Abstract

Let (V, 0) be an isolated hypersurface singularity. We introduce a series of new derivation Lie algebras $L_{k}(V)$ associated to (V, 0). Its dimension is denoted as $\lambda _{k}(V)$. The $L_{k}(V)$ is a generalization of the Yau algebra L(V) and $L_{0}(V)=L(V)$. These numbers $\lambda _{k}(V)$ are new numerical analytic invariants of an isolated hypersurface singularity. In this article we compute $L_1(V)$ for fewnomial isolated singularities (Binomial, Trinomial) and obtain the formulas of $\lambda _{1}(V)$. We also formulate a sharp upper estimate conjecture for the $L_k(V)$ of weighted homogeneous isolated hypersurface singularities and we prove this conjecture for large class of singularities. Furthermore, we formulate another inequality conjecture and prove it for binomial and trinomial singularities.

1 Introduction

The algebra of germs of holomorphic functions at the origin of ${\mathbb {C}}^n$ is denoted as ${\mathcal {O}}_n$. Clearly, ${\mathcal {O}}_n$ can be naturally identified with the algebra of convergent power series in n indeterminates with complex coefficients. As a ring ${\mathcal {O}}_n$ has a unique maximal ideal m, the set of germs of holomorphic functions which vanish at the origin. Let ${\mathbb {C}}[x_1,\ldots , x_n]$ be the polynomial ring. For any $f\in {\mathbb {C}}[x_1,\ldots ,x_n]$, we denote by $V = V(f)$ the germ at the origin of ${\mathbb {C}}^n$ of hypersurface $\{f=0\}\subset {\mathbb {C}}^n$. In other words, if the origin is an isolated zero of the gradient of f, then V is a germ of isolated hypersurface singularity. According to Hilbert’s Nullstellensatz for an isolated singularity $V = V(f) = \{f=0\}$ the factor-algebra $A(V) = {\mathcal {O}}_n/(f, \frac{\partial f}{\partial x_1},\ldots , \frac{\partial f}{\partial x_n})$ is finite dimensional. This factor-algebra is called the moduli algebra of V and its dimension $\tau (V)$ is called Tyurina number. The Mather-Yau theorem stated that: Let $V_1$ and $V_2$ be two isolated hypersurface singularities and, $A(V_1)$ and $A(V_2)$ be the moduli algebra, then $(V_1,0)\cong (V_2,0)\Longleftrightarrow A(V_1)\cong A(V_2)$.

Recall that the order of the lowest nonvanishing term in the power series expansion of f at 0 is called the multiplicity (denoted by mult(f)) of the singularity (V, 0). A polynomial $f\in {\mathbb {C}}[x_1,\ldots , x_n]$ is said to be weighted homogeneous if there exist positive rational numbers $w_1,\cdots ,w_n$ (weights of $x_1,\ldots , x_n$) and d such that, $\sum a_iw_i = d$ for each monomial $\prod x_i^{a_i}$ appearing in f with nonzero coefficient. The number d is called weighted homogeneous degree (w-degree) of f with respect to weights $w_j$. The weight type of f is denoted as $(w_1,\ldots ,w_n; d)$. Without loss of generality, we can assume that w-deg$f=1$. According to ( [24, 30]) the weight types of 1 or 2-dimensional weighted homogeneous hypersurface singularities are topological invariants. The Milnor number of the isolated hypersurface singularity is defined by $\mu =\dim {{\mathcal {O}}_n }\big /(\frac{\partial f}{\partial x_1},\ldots , \frac{\partial f}{\partial x_n}).$ The Milnor number in case of weighted homogeneous hypersurface singularity is calculated by: $\mu =(\frac{1}{w_1}-1)(\frac{1}{w_2}-1)\ldots (\frac{1}{w_n}-1)$ [21]. In 1971, Saito was the first person who gave the necessary and sufficient numerical condition for V to be defined by a weighted homogeneous polynomial. His beautiful theorem says that f is a weighted homogeneous polynomial after a biholomorphic change of coordinates $\Longleftrightarrow$ $\mu =\tau$ [23].

An important class of weighted homogeneous isolated hypersurface singularity is fewnomial singularities which are defined by Elashvili and Khimshiashvili [9]. A weighted homogeneous polynomial $f(x_1,\ldots ,x_n)$ is called fewnomial if number of variables coincides with number of monomials ( [9, 19, 20, 33]). According to Ebeling and Takahashi [10], the fewnomial singularity, which is defined by a fewnomial polynomial, is also called an invertible singularity.

It is well-known that for any isolated hypersurface singularity $(V, 0)\subset ({\mathbb {C}}^n, 0)$ where $V=V(f)=\{f=0\}$, based on the Mather-Yau theorem [22], one considers the Lie algebra of derivations of moduli algebra $A(V) := {\mathcal {O}}_n/(f, \frac{\partial f}{\partial x_1},\ldots , \frac{\partial f}{\partial x_n})$, i.e., $L(V)=\text {Der}(A(V), A(V))$. It is known that L(V) is a finite dimensional solvable Lie algebra ([28, 29]). L(V) is called the Yau algebra of V in [31] and [20] in order to distinguish from Lie algebras of other types appearing in singularity theory ( [1, 2]). The Yau algerba plays an important role in singularities. Yau and his collabrators have been systematically studying the Lie algebras of isolated hypersurface singularities begin from eighties (see, e.g., [27]–[3, 5, 7, 12, 25, 26, 29, 32, 33]–[6, 11, 18]).

In the theory of isolated singularities, one always wants to find invariants associated to the isolated singularities. Hopefully with enough invariants found, one can distinguish between isolated singularities. However, not many invariants are known. In this paper we introduce the new series new derivation Lie algebra associated to the isolated hypersurface singularity (V, 0). For any isolated hypersurface singularity $(V, 0)\subset ({\mathbb {C}}^{n}, 0)$ defined by the holomorphic function $f(x_1,\ldots , x_n)$, let Hess(f) be the Hessian matrix $(f_{ij})$ of the second order partial derivatives of f and h(f) be the Hessian of f, i.e. the determinant of this matrix Hess(f). More generally, for each k satisfying $0 \le k \le n$ we denote by $h_k(f)$ the ideal in ${\mathcal {O}}_{n}$ generated by all $k \times k$-minors in the matrix Hess(f). In particular, the ideal $h_{n}(f) = (h(f))$ is a principal ideal. For each k as above, consider the graded k-th Hessian algebra of the polynomial f defined by

$$\begin{aligned} H_k(f) = {\mathcal {O}}_{n}/(f+J(f) + h_k(f)). \end{aligned}$$

In particular, $H_0(f)$ is exactly the well-known moduli algebra A(V).

It is easy to check that the isomorphism class of the local k-th Hessian algebra $H_k(f)$ is contact invariant of f, i.e. depends only on the isomorphism class of the germ (V, 0) [8]. The dimension of $L_k(V)$ is denoted by $\lambda _k(V)$ which is new numerical analytic invariant of an isolated hypersurface singularity.

Recall that in [13], we also generalized the Yau algebra and introduced a new series of k-th Yau algebras $L^k(V)$ which are defined to be the Lie algebras of derivations of the moduli algebras $A^k(V) = {\mathcal {O}}_n/(f, m^k J(f)), k\ge 0$, i.e., $L^k(V)=\text {Der}(A^k(V), A^k(V))$ and where m is the maximal ideal of ${\mathcal {O}}_n$. In particular, it is Yau algebra when $k=0$. The dimension of $L^k(V)$ is denoted by $\lambda ^k(V)$.

It is interesting to bound the Yau number with a number which depends on weight type. In [33], Yau and Zuo firstly proposed the sharp upper estimate conjecture that bound the Yau number $\lambda (V)$. They also proved that this conjecture holds in case of binomial isolated hypersurface singularities. Furthermore, in [12], this conjecture was verified for trinomial singularities (the definitions of fewnomial, binomial, and trinomial singularities can be found in [33]).

A natural interesting question is: whether one can give a sharp bound for the new introduced $\lambda _k(V)$ of an isolated hypersurface singularities (V, 0). We proposed the following sharp upper estimate conjecture.

Conjecture 1.1

For each $0\le k\le n$, assume that $\lambda _k(\{x_1^{a_1}+\ldots +x_n^{a_n}=0\})=h_k(a_1,\cdots , a_n)$. Let $(V, 0) = \{(x_1, x_2,\cdots , x_n) \in {\mathbb {C}}^n: f(x_1, x_2,\ldots , x_n) =0\}, (n\ge 2)$ be an isolated singularity defined by the weighted homogeneous polynomial $f(x_1, x_2,\ldots , x_n)$ of weight type $(w_1, w_2,\ldots , w_n; 1)$ and $mult(f)\ge 4$. Then $\lambda _k(V) \le h_k(1/w_1,\ldots , 1/w_n)$.

Remark 1.1

The inequality in Conjecture 1.1 holds true under the condition of $mult (f)=3$ and $k=0$ for binomial singularities [33] and trinomial singularities [12]. However, in this paper, we will give some examples which show that the inequality does not hold for $k=1$ and $mult(f)=3$ for binomial and trinomial singularities (see Remarks  3.2–3.8).

In [13] we also formulate a similar inequality conjecture as above for the $\lambda ^k(V)$ of weighted homogeneous isolated hypersurface singularities and we have also proven this conjecture for large class of singularities, i.e., for binomial and trinomial singularities. Another natural interesting question is: whether there is any relation between the numerical invariants $\lambda _k(V)$ and $\lambda ^k(V)$ of isolated hypersurface singularities (V, 0). We proposed the following an Inequality conjecture.

Conjecture 1.2

With the above notations, let (V, 0) be an isolated hypersurface singularity defined by $f \in {\mathcal {O}}_n,\; n\ge 2$, and $mult(f)\ge 3$. Then for each $i\ge 0$,

$$\begin{aligned} \cdots>\lambda ^{(i+1)}(V)> \lambda ^i(V) \cdots >\lambda ^0(V) \ge \lambda _l (V),\; l=1,2,\ldots ,n. \end{aligned}$$

In [6], we studied $L_n(V)$ (note that we use a different notation $L^*(V)$ in stead of $L_n(V)$ there) and obtained the following result.

Theorem 1.1

([6], Theorem D) Let f be a weighted homogeneous polynomial in ${\mathbb {C}}[x_1, x_2,\dots , x_n]$ $(2\le n \le 4)$ with respect to weight system $(w_1, w_2,\dots , w_n; 1)$ and with $mult(f) \ge 3$. Suppose that f defines an isolated singularity (V, 0), then

$$\begin{aligned} \lambda _n(V)= \lambda (V). \end{aligned}$$

Remark 1.2

It follows from Theorem 1.1 that $\lambda ^0(V)= \lambda _2(V)$ for binomial singularities and $\lambda ^0(V)= \lambda _3(V)$ for trinomial singularities.

The main purpose of this paper is to verify the Conjecture  1.1 and 1.2 for binomial and trinomial singularities. We obtain the following main results.

Main Theorem A

Let $(V, 0) = \{(x_1, x_2,\ldots , x_n) \in {\mathbb {C}}^n: x_1^{a_1}+\cdots +x_n^{a_n} =0\}, (n\ge 2;\; a_i\ge 3,\; 1\le i \le n).$ Then

$$\begin{aligned} \lambda _1(V)=h_1(a_1,\cdots , a_n)= \sum _{j=1}^{n}\frac{a_j-3}{a_j-2}\prod _{i=1}^{n}(a_i-2). \end{aligned}$$

Main Theorem B

Let (V, 0) be a binomial singularity defined by the weighted homogeneous polynomial $f(x_1, x_2)$ (see Corollary 2.1) with weight type $(w_1,w_2; 1)$ and $mult(f)\ge 4$. Then

$$\begin{aligned} \lambda _1(V)\le h_1\left( \frac{1}{w_1}, \frac{1}{w_2}\right) = \sum _{j=1}^{2}\frac{\frac{1}{w_j}-3}{\frac{1}{w_j}-2}\prod _{i=1}^{2}\left( \frac{1}{w_i}-2\right) . \end{aligned}$$

Main Theorem C

Let (V, 0) be a fewnomial singularity defined by the weighted homogeneous polynomial $f(x_1, x_2,x_3)$ (see Proposition  2.2) with weight type $(w_1,w_2,w_3; 1)$ and $mult(f)\ge 4$. Then

$$\begin{aligned} \lambda _1(V)\le h_1\left( \frac{1}{w_1},\frac{1}{w_2}, \frac{1}{w_3}\right) =\sum _{j=1}^{3}\frac{\frac{1}{w_j}-3}{\frac{1}{w_j}-2}\prod _{i=1}^{3}\left( \frac{1}{w_i}-2\right) . \end{aligned}$$

Main Theorem D

Let (V, 0) be a binomial singularity defined by the weighted homogeneous polynomial $f(x_1, x_2)$ (see Corollary 2.1) with weight type $(w_1,w_2; 1)$ and $mult(f)\ge 3$. Then

$$\begin{aligned} \lambda ^2> \lambda ^1> \lambda ^0=\lambda _2>\lambda _1. \end{aligned}$$

Main Theorem E

Let (V, 0) be a trinomial singularity defined by the weighted homogeneous polynomial $f(x_1, x_2,x_3)$ (see Proposition  2.2) with weight type $(w_1,w_2, w_3; 1)$ and $mult(f)\ge 3$. Then

$$\begin{aligned} \lambda ^2> \lambda ^1> \lambda ^0=\lambda _3>\lambda _1. \end{aligned}$$

Remark 1.3

In main Theorem E, the $\lambda _2(V)$ is extremely complicated to compute.

Main Theorem F

Let $(V_f, 0)\subset ({\mathbb {C}}^{n}, 0)$ and $(V_g, 0)\subset ({\mathbb {C}}^{m}, 0)$ be defined by weighted homogeneous polynomials $f(x_1, x_2, \cdots , x_n)=0$ of weight type $(w_1, w_2\cdots , w_n; 1)$ and $g(y_1, y_2, \cdots , y_m)=0$ of weight type $(w_{n+1}, w_{n+2},\cdots , w_{n+m}; 1)$ respectively. With the above notations. Then

$$\begin{aligned} L_1 (V_{f+g})=L_1(V_f)\otimes H_1(V_g)+H_1(V_f)\otimes L_1(V_g). \end{aligned}$$

(1.1)

We obtain the following result as an immediately corollary of Theorem F.

Corollary 1.1

Let $(V_f, 0)\subset ({\mathbb {C}}^{n}, 0)$ and $(V_g, 0)\subset ({\mathbb {C}}^{m}, 0)$ be defined by weighted homogeneous polynomials $f(x_1, x_2, \cdots , x_n)=0$ of weight type $(w_1, w_2\cdots , w_n; 1)$ and $g(y_1, y_2, \cdots , y_m)=0$ of weight type $(w_{n+1}, w_{n+2},\cdots , w_{n+m}; 1)$ respectively. With the above notations, let $\mu _1(V_f)$, $\mu _1(V_g)$ be dimensions of the 1-st Hessian algebras $H_1(V_f)$ and $H_1(V_g)$ respectively. Then

$$\begin{aligned} \lambda _1 (V_{f+g})=\mu _1(V_f)\lambda _1(V_g)+\mu _1(V_g)\lambda _1(V_f). \end{aligned}$$

(1.2)

2 Generalities on derivation Lie algebras of isolated singularities

In this section we shall briefly defined the basic definitions and important results which are helpful to solve the problem. The following basic concepts and results will be used to compute the derivation Lie algebras of isolated hypersurface singularities.

Let A, B be associative algebras over ${\mathbb { C}}$. The subalgebra of endomorphisms of A generated by the identity element and left and right multiplications by elements of A is called multiplication algebra M(A) of A. The centroid C(A) is defined as the set of endomorphisms of A which commute with all elements of M(A). Obviously, C(A) is a unital subalgebra of End(A). The following statement is a particular case of a general result from Proposition 1.2 of [4]. Let $S = A \otimes B$ be a tensor product of finite dimensional associative algebras with units. Then

$$\begin{aligned} \hbox {Der} S\cong (\hbox {Der}A)\otimes C(B) + C(A)\otimes (\hbox {Der}B). \end{aligned}$$

We will only use this result for commutative associative algebras with unit, in which case the centroid coincides with the algebra itself and one has following result for commutative associative algebras A, B:

Theorem 2.1

([4]) For commutative associative algebras A, B,

$$\begin{aligned} \hbox {Der} S\cong (\hbox {Der}A)\otimes B + A \otimes (\hbox {Der}B). \end{aligned}$$

(2.1)

We shall use this formula in the sequel.

Definition 2.1

Let J be an ideal in an analytic algebra S. Then $\hbox {Der}_JS\subseteq \hbox {Der}_{\mathbb {C}}S$ is Lie subalgebra of all $\sigma \in \hbox {Der}_{\mathbb {C}}S$ for which $\sigma (J)\subset J$.

We shall use the following well-known result to compute the derivations.

Theorem 2.2

([33]) Let J be an ideal in $R={\mathbb { C}}\{x_1,\cdots , x_n\}$. Then there is a natural isomorphism of Lie algebras

$$\begin{aligned} (\hbox {Der}_JR)/(J\cdot \hbox {Der}_{\mathbb { C}}R )\cong \hbox {Der}_{\mathbb { C}}(R/J). \end{aligned}$$

Recall that a derivation of commutative associative algebra A is defined as a linear endomorphism D of A satisfying the Leibniz rule: $D(ab) = D(a)b + aD(b)$. Thus for such an algebra A one can consider the Lie algebra of its derivations ${{ Der}}(A, A)$ with the bracket defined by the commutator of linear endomorphisms.

Definition 2.2

Let (V, 0) be an isolated hypersurface singularity. The series new derivation Lie algebra arising from the isolated hypersurface singularity (V, 0) is defined as $L_{k}(V):= {{ Der}}(H_{k}(f), H_{k}(f)), 0 \le k\le n$ (where $H_k(f) = {\mathcal {O}}_{n+1}/(f+J(f) + h_k(f))$ and $h_k(f)$ is the ideal in ${\mathcal {O}}_{n}$ generated by all $k \times k$-minors in the matrix Hess(f)). Its dimension is denoted as $\lambda _{k}(V)$. In particular, $H_0(f)$ is exactly the well-known moduli algebra A(V). Thus $L_{k}(V)$ is a generalization of Yau algebra L(V) and $L_{0}(V)=L(V)$. These numbers $\lambda _{k}(V)$ are new numerical analytic invariants of an isolated hypersurface singularity.

Definition 2.3

A polynomial $f\in {\mathbb {C}}[x_1,x_2,\ldots ,x_n]$ is called quasi-homogeneous (or weighted homogeneous) if there exist positive rational numbers $w_1, \ldots , w_n$ (called weights of indeterminates $x_j$) and d such that, for each monomial $\prod x_j^{k_j}$ appearing in f with non-zero coefficient, one has $\sum w_jk_j = d$. The number d is called the quasi-homogeneous degree (w-degree) of f with respect to weights $w_j$ and is denoted $\deg f$. The collection $(w;d) = (w_1, \cdots , w_n; d)$ is called the quasi-homogeneity type (qh-type) of f.

Definition 2.4

An isolated hypersurface singularity in ${\mathbb {C}}^n$ is fewnomial if it can be defined by a n-nomial in n variables and it is a weighted homogeneous fewnomial isolated singularity if it can be defined by a weighted homogeneous fewnomial. 3-nomial isolated hypersurface singularity is also called trinomial singularity.

Proposition 2.1

Let f be a weighted homogeneous fewnomial isolated singularity with mult$(f)\ge 3$. Then f analytically equivalent to a linear combination of the following three series:

Type A. $x_1^{a_1}+x_2^{a_2}+\cdots +x_{n-1}^{a_{n-1}}+x_n^{a_n}$, $n\ge 1$,

Type B. $x_1^{a_1}x_2+x_2^{a_2}x_3+\cdots +x_{n-1}^{a_{n-1}}x_n+x_n^{a_n}$, $n\ge 2$,

Type C. $x_1^{a_1}x_2+x_2^{a_2}x_3+\cdots +x_{n-1}^{a_{n-1}}x_n+x_n^{a_n}x_1$, $n\ge 2$.

Proposition 2.1 has an immediate corollary.

Corollary 2.1

Each binomial isolated singularity is analytically equivalent to one from the three series: A) $x_1^{a_1}+x_2^{a_2}$, B) $x_1^{a_1}x_2+x_2^{a_2}$, C) $x_1^{a_1}x_2+x_2^{a_2}x_1$.

Wolfgang and Atsushi [10] give the following classification of weighted homogeneous fewnomial singularities in case of three variables.

Proposition 2.2

[10] Let $f(x_1,x_2,x_3)$ be a weighted homogeneous fewnomial isolated singularity with mult$(f)\ge 3$. Then f is analytically equivalent to following five types:

Type 1. $x_1^{a_1}+x_2^{a_2}+ x_3^{a_3}$,

Type 2. $x_1^{a_1}x_2+x_2^{a_2}x_3+ x_3^{a_3}$,

Type 3. $x_1^{a_1}x_2+x_2^{a_2}x_3+x_3^{a_3}x_1$,

Type 4. $x_1^{a_1}+x_2^{a_2}+ x_3^{a_3}x_1$,

Type 5. $x_1^{a_1}x_2+x_2^{a_2}x_1+ x_3^{a_3}.$

3 Proof of main theorems

In order to prove the main theorems, we need to prove following propositions.

Proposition 3.1

Let (V, 0) be a weighted homogeneous fewnomial isolated singularity which is defined by $f=x_1^{a_1}+x_2^{a_2}+\cdots +x_n^{a_n}$ ($a_i\ge 3, i=1,2,\ldots ,n$) with weight type $(\frac{1}{a_1}, \frac{1}{a_2},\ldots ,\frac{1}{a_n}; 1)$. Then

$$\begin{aligned} \lambda _1(V)= \sum _{j=1}^{n}\frac{a_j-3}{a_j-2}\prod _{i=1}^{n}(a_i-2). \end{aligned}$$

Proof

The generalized moduli algebra

$$\begin{aligned} H_1(V)&={\mathbb {C}}\{x_1, x_2,x_3,\ldots ,x_n\}/({\tilde{J}}(f)) \end{aligned}$$

and where ${\tilde{J}}(f)$ is ideal of 2nd order partial derivative of f. It is note that $H_1(V)$ has dimension $\prod _{i=1}^{n}(a_i-2)$ and has a monomial basis of the form

$$\begin{aligned}&\{ x_1^{i_1}x_2^{i_2}\cdots x_n^{i_n}, 0\le i_1\le a_1-3, 0\le i_2\le a_2-3,\ldots , 0\le i_n\le a_n-3\}, \end{aligned}$$

with following relations:

$$\begin{aligned} x_1^{a_1-2}=0, x_2^{a_2-2}=0, x_3^{a_3-2}=0, \ldots , x_n^{a_n-2}=0. \end{aligned}$$

(3.1)

In order to compute a derivation D of $H_1(V)$ it suffices to indicate its values on the generators $x_1, x_2,\ldots , x_n$ which can be written in terms of the monomial basis. Without loss of generality, we write

$$\begin{aligned} Dx_j=\sum _{i_1=0}^{a_1-3}\sum _{ i_2=0}^{a_2-3}\ldots \sum _{ i_n=0}^{a_n-3} c_{i_1,i_2,\cdots ,i_n}^jx_1^{i_1}x_2^{i_2}\cdots x_n^{i_n}, \; j=1, 2,\ldots , n. \end{aligned}$$

Using the above relations (3.1) one easily finds the necessary and sufficient conditions defining a derivation of $H_1(V)$ as follows:

$$\begin{aligned}&c_{0,i_2,i_3,,\cdots , i_n}^1=0; 0\le i_2\le a_2-3, 0\le i_3\le a_3-3,\ldots , 0\le i_n\le a_n-3;\\&c_{i_1,0,i_3,,\cdots , i_n}^2=0; 0\le i_1\le a_1-3, 0\le i_3\le a_3-3,\ldots , 0\le i_n\le a_n-3;\\&c_{i_1,i_2,0,\cdots , i_n}^3=0; 0\le i_1\le a_1-3, 0\le i_2\le a_2-3,\ldots , 0\le i_n\le a_n-3; \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \vdots \\&c_{i_1,i_2,i_3,\ldots , i_{n-1}, 0}^n=0; 0\le i_1\le a_1-3, 0\le i_2\le a_2-3,\ldots , 0\le i_{n-1}\le a_{n-1}-3. \end{aligned}$$

Therefore we obtain the following description of Lie algebras in question:

$$\begin{aligned}&x_1^{i_1}x_2^{i_2}\cdots x_n^{i_n}\partial _1, \; 1\le i_1\le a_1-3, 0\le i_2\le a_2-3, 0\le i_3\le a_3-3,\ldots , 0\le i_n\le a_n-3;\\&x_1^{i_1}x_2^{i_2}\cdots x_n^{i_n}\partial _2, \; 0\le i_1\le a_1-3, 1\le i_2\le a_2-3, 0\le i_3\le a_3-3,\ldots , 0\le i_n\le a_n-3;\\&x_1^{i_1}x_2^{i_2}\cdots x_n^{i_n}\partial _3, \; 0\le i_1\le a_1-3, 0\le i_2\le a_2-3, 1\le i_3\le a_3-3, 0\le i_4\le a_4-3,\\&0\le i_5\le a_5-3, 0\le i_6\le a_6-3, \ldots , 0\le i_n\le a_n-3;\\&\vdots \\&x_1^{i_1}x_2^{i_2}\ldots x_n^{i_n}\partial _n, \; 0\le i_1\le a_1-3, 0\le i_2\le a_2-3, 0\le i_3\le a_3-3,\ldots , 1\le i_n\le a_n-3.\\ \end{aligned}$$

Therefore we have the following formula

$$\begin{aligned} \lambda _1(V)= \sum _{j=1}^{n}\frac{a_j-3}{a_j-2}\prod _{i=1}^{n}(a_i-2). \end{aligned}$$

$\square$

Remark 3.1

Let (V, 0) be a weighted homogeneous fewnomial isolated singularity of type A which is defined by $f=x_1^{a_1}+x_2^{a_2}$ ($a_1\ge 3,\;a_2\ge 3$) with weight type $(\frac{1}{a_1}, \frac{1}{a_2}; 1)$. Then it follows from Proposition 3.1 that

$$\begin{aligned} \lambda _1(V)=2a_1a_2-5(a_1+a_2)+12. \end{aligned}$$

Proposition 3.2

Let (V, 0) be a binomial isolated singularity of type B which is defined by $f=x_1^{a_1}+x_2^{a_2}x_1$ ($a_1\ge 3,\;a_2\ge 2$) with weight type $(\frac{1}{a_1}, \frac{a_1-1}{a_1a_2}; 1)$. Then

$$\begin{aligned} \lambda _1(V)= \left\{ \begin{array}{ll} 2a_1a_2-5(a_1+a_2)+15; &{}\quad a_1\ge 4, a_2\ge 3\\ a_2-2; &{}\quad a_1=3, a_2\ge 3\\ 0; &{}\quad a_1\ge 3, a_2=2. \end{array} \right. \end{aligned}$$

Furthermore, assuming that $mult(f)\ge 4$, we have

$$\begin{aligned} 2a_1a_2-5(a_1+a_2)+15\le \frac{2a_1^2a_2}{a_1-1}-5\left( \frac{a_1a_2}{a_1-1}+a_1\right) +12. \end{aligned}$$

Proof

It follows that the generalized moduli algebra

$$\begin{aligned} H_1(V)&={\mathbb {C}}\{x_1, x_2\}/\left( \frac{\partial ^2 f}{\partial x_1^{2}}, \frac{\partial ^2 f}{\partial x_1\partial x_2}, \frac{\partial ^2 f}{\partial x_2^{2}}\right) \end{aligned}$$

has dimension $a_1a_2-2(a_1+a_2)+5$ and has a monomial basis of the form

$$\begin{aligned} \{x_1^{i_1}x_2^{i_2}, 0\le i_1 \le a_1-3; 0\le i_2\le a_2-3; x_2^{a_2-2}\}, \end{aligned}$$

(3.2)

with the following relations:

$$\begin{aligned}&x_1^{a_1-2}=0, \end{aligned}$$

(3.3)

$$\begin{aligned}&x_2^{a_2-1}=0, \end{aligned}$$

(3.4)

$$\begin{aligned}&x_1x_2^{a_2-2}=0. \end{aligned}$$

(3.5)

In order to compute a derivation D of $H_1(V)$ it suffices to indicate its values on the generators $x_1, x_2$ which can be written in terms of the basis (3.2). Without loss of generality, we write

$$\begin{aligned} Dx_j=\sum _{i_1=0}^{a_1-3}\sum _{ i_2=0}^{a_2-3} c_{i_1,i_2}^jx_1^{i_1}x_2^{i_2}+c_{0,a_2-2}^jx_2^{a_2-2},\quad j=1, 2. \end{aligned}$$

Using the relations (3.3)–(3.5) one easily finds the necessary and sufficient conditions defining a derivation of $H_1(V)$ as follows:

$$\begin{aligned} c_{0,0}^1= & {} c_{0, 1}^1=\cdots =c_{0, a_2-3}^1=0; \end{aligned}$$

(3.6)

$$\begin{aligned} c_{0,0}^2= & {} c_{1, 0}^2=\cdots =c_{ a_1-4, 0}^2=0. \end{aligned}$$

(3.7)

Using (3.6) and (3.7) we obtain the following description of the Lie algebras in question. The following derivations form a basis of Der$H_1(V)$:

$$\begin{aligned}&x_1^{i_1}x_2^{i_2}\partial _1, 1\le i_1\le a_1-3, 0\le i_2\le a_2-3; x_1^{i_1}x_2^{i_2}\partial _2, 1\le i_1\le a_1-3, 1\le i_2\le a_2-3;\\&x_2^{i_2}\partial _2; \quad 1\le i_2\le a_2-2; x_1^{a_1-3}\partial _2. \end{aligned}$$

Therefore we have the following formula

$$\begin{aligned} \lambda _1(V)=2a_1a_2-5(a_1+a_2)+15. \end{aligned}$$

In case of $a_1=3, a_2\ge 3$ we have following basis:

$$\begin{aligned} x_2^{i_2}\partial _2,\quad 1\le i_2\le a_2-2. \end{aligned}$$

Therefore we have

$$\begin{aligned} \lambda _1(V)=a_2-2. \end{aligned}$$

It is follows from Proposition 3.1 we have

$$\begin{aligned} h_1(a_1,a_2)= 2a_1a_2-5(a_1+a_2)+12. \end{aligned}$$

After putting the weight type $(\frac{1}{a_1}, \frac{a_1-1}{a_1a_2}; 1)$ of binomial isolated singularity of type B we have

$$\begin{aligned} h_1(\frac{1}{w_1},\frac{1}{w_2})= \frac{2a_1^2a_2}{a_1-1}-5(a_1+\frac{a_1a_2}{a_1-1})+12. \end{aligned}$$

Finally we need to show that

$$\begin{aligned} 2a_1a_2-5(a_1+a_2)+15\le \frac{2a_1^2a_2}{a_1-1}-5(\frac{a_1a_2}{a_1-1}+a_1)+12. \end{aligned}$$

(3.8)

After solving 3.8 we have $(a_1-5)(a_2-3)+a_1a_2-12\ge 0$. $\square$

Remark 3.2

Note that, for $mult(f)=3$, the inequality in Proposition  3.2 does not hold true when $a_1\ge 5$ and $a_2=2$.

Proposition 3.3

Let (V, 0) be a binomial isolated singularity of type C which is defined by $f=x_1^{a_1}x_2+x_2^{a_2}x_1$ ($a_1\ge 2, a_2\ge 2$) with weight type $(\frac{a_2-1}{a_1a_2-1}, \frac{a_1-1}{a_1a_2-1}; 1)$. Then

$$\begin{aligned} \lambda _1(V)= \left\{ \begin{array}{ll} 2a_1a_2-5(a_1+a_2)+19; &{} \quad a_1\ge 5, a_2\ge 5\\ a_2+1; &{}\quad a_1=3, a_2\ge 3\\ 3a_2-2; &{}\quad a_1=4, a_2\ge 5\\ 9; &{}\quad a_1=4, a_2=4\\ 0; &{}\quad a_1=2, a_2\ge 2\\ \end{array} \right. \end{aligned}$$

Furthermore, assuming that $mult(f)\ge 4$, we have

$$\begin{aligned} 2a_1a_2-5(a_1+a_2)+19\le \frac{2(a_1a_2-1)^2}{(a_1-1)(a_2-1)}-5(a_1a_2-1)\left( \frac{a_1+a_2-2}{(a_1-1)(a_2-1)}\right) +12. \end{aligned}$$

Proof

It follows that the generalized moduli algebra

$$\begin{aligned} H_1(V)&={\mathbb { C}}\{x_1, x_2\}/\left( \frac{\partial ^2 f}{\partial x_1^{2}}, \frac{\partial ^2 f}{\partial x_1\partial x_2}, \frac{\partial ^2 f}{\partial x_2^{2}}\right) \end{aligned}$$

has dimension $a_1a_2-2(a_1+a_2)+7$ and has a monomial basis of the form

$$\begin{aligned} \{x_1^{i_1}x_2^{i_2}, 0\le i_1 \le a_1-3; 0\le i_2\le a_2-3; x_1^{a_1-2}; x_2^{i_2}, a_2-2\le i_2 \le a_2-1\}, \end{aligned}$$

(3.9)

with the following relations:

$$\begin{aligned}&\displaystyle a_1x_1^{a_1-1}+a_2x_2^{a_2-1}=0, \end{aligned}$$

(3.10)

$$\begin{aligned}&\displaystyle x_1^{a_1-2}x_2=0, \end{aligned}$$

(3.11)

$$\begin{aligned}&\displaystyle x_1x_2^{a_2-2}=0. \end{aligned}$$

(3.12)

In order to compute a derivation D of $H_1(V)$ it suffices to indicate its values on the generators $x_1, x_2$ which can be written in terms of the basis (3.9). Without loss of generality, we write

$$\begin{aligned} Dx_j=\sum _{i_1=0}^{a_1-3}\sum _{ i_2=0}^{a_2-3} c_{i_1,i_2}^jx_1^{i_1}x_2^{i_2}+c_{a_1-2,0}^jx_1^{a_1-2}+\sum _{ i_2=a_2-2}^{a_2-1} c_{0,i_2}^jx_2^{i_2},\quad j=1, 2. \end{aligned}$$

Using the relations (3.10)–(3.12) one easily finds the necessary and sufficient conditions defining a derivation of $H_1(V)$ as follows:

$$\begin{aligned}&\displaystyle c_{0,0}^1=c_{0, 1}^1=\cdots =c_{0, a_2-4}^1=0; \end{aligned}$$

(3.13)

$$\begin{aligned}&\displaystyle c_{0,0}^2=c_{1, 0}^2=\cdots =c_{ a_1-4, 0}^2=0; \end{aligned}$$

(3.14)

$$\begin{aligned}&\displaystyle -(a_1-1)a_2c_{1,0}^1+a_1a_2c_{0, 1}^2=0. \end{aligned}$$

(3.15)

Using (3.13)–(3.15) we obtain the following description of the Lie algebras in question. The following derivations form a basis of Der$H_1(V)$:

$$\begin{aligned}&x_1^{i_1}x_2^{i_2}\partial _1, 1\le i_1\le a_1-3, 1\le i_2\le a_2-3; x_1^{i_1}x_2^{i_2}\partial _2, \\&\quad 1 \le i_1\le a_1-3, 1\le i_2\le a_2-3;\\&x_2^{i_2}\partial _1; a_2-3\le i_2\le a_2-1; x_1\partial _1+\frac{a_1-1}{a_2-1}x_2\partial _2; x_1^{i_1}\partial _1,\\&\quad 2\le i_1 \le a_1-2; x_2^{i_2}\partial _2, 2\le i_2\le a_2-1;\\&x_1^{i_1}\partial _2, a_1-3\le i_1\le a_1-2. \end{aligned}$$

Therefore we have the following formula

$$\begin{aligned} \lambda _1(V)=2a_1a_2-5(a_1+a_2)+19. \end{aligned}$$

In case of $a_1=3, a_2\ge 3$ we have following basis:

$$\begin{aligned} x_2^{a_2-2}\partial _1+ \frac{3x_1}{a_2}\partial _2; x_2^{a_2-1}\partial _1; x_1\partial _1+ \frac{2x_2}{a_2-1}\partial _2; x_2^{i_2}\partial _2, 2\le i_2\le a_2-1. \end{aligned}$$

Therefore we have the following formula

$$\begin{aligned} \lambda _1 (V)=a_2+1. \end{aligned}$$

In case of $a_1=4, a_2\ge 5$ we have following basis:

$$\begin{aligned}&x_2^{i_2}\partial _1; a_2-3\le i_2\le a_2-1; x_1\partial _1+ \frac{3x_2}{a_2-1}\partial _2; x_1x_2^{i_2}\partial _1,\quad 1\le i_2\le a_2-3; \\&x_1^2\partial _1; x_2^{i_2}\partial _2, 2\le i_2\le a_2-1; x_1^{2}\partial _2; x_1x_2^{i_2}\partial _2,\quad 1\le i_2\le a_2-3. \end{aligned}$$

Therefore we have the following formula

$$\begin{aligned} \lambda _1 (V)=3a_2-2. \end{aligned}$$

In case of $a_1=4, a_2=4$ we have following basis:

$$\begin{aligned} x_2^{2}\partial _1; x_2^3\partial _1; x_1x_2\partial _1; x_1^{2}\partial _1; x_2^2\partial _2; x_2^3\partial _2; x_1x_2\partial _2; x_1^{2}\partial _2. \end{aligned}$$

Therefore we have the following formula

$$\begin{aligned} \lambda _1 (V)=9. \end{aligned}$$

It is follows from Proposition 3.1 and binomial isolated singularity of type C we have

$$\begin{aligned} h_1(\frac{1}{w_1},\frac{1}{w_2})= \frac{2(a_1a_2-1)^2}{(a_1-1)(a_2-1)}-5(\frac{a_1a_2-1}{a_2-1}+\frac{a_1a_2-1}{a_1-1})+12. \end{aligned}$$

Finally we need to show that

$$\begin{aligned} 2a_1a_2-5(a_1+a_2)+19\le \frac{2(a_1a_2-1)^2}{(a_1-1)(a_2-1)}-5(\frac{a_1a_2-1}{a_2-1}+\frac{a_1a_2-1}{a_1-1})+12.\nonumber \\ \end{aligned}$$

(3.16)

After solving (3.16) we have

$$\begin{aligned}&a_1a_2^2[(a_2-2)(a_1-3)-a_1(a_2-5)]+a_2^3+3a_1^2a_2+11a_2^2(a_1-1)+8a_1a_2(a_1-4)\\&\quad +2a_1^2(a_2-4)+a_1a_2(a_1-4)+17a_1+4(a_2-4)+(a_1-4)\ge 0. \end{aligned}$$

In case of $a_1=3, a_2\ge 4$, we need to prove that:

$$\begin{aligned} a_2+1\le \frac{2(3a_2-1)^2}{2(a_2-1)}-5(\frac{3a_2-1}{a_2-1}+\frac{3a_2-1}{2})+12. \end{aligned}$$

(3.17)

After solving 3.17 we have

$$\begin{aligned} a_2^2+8a_2-15\ge 0. \end{aligned}$$

In case of $a_1=4, a_2\ge 5$, we need to prove that:

$$\begin{aligned} 3a_2-2\le \frac{2(4a_2-1)^2}{3(a_2-1)}-5(\frac{4a_2-1}{a_2-1}+\frac{4a_2-1}{3})+12. \end{aligned}$$

(3.18)

After solving 3.18 we have

$$\begin{aligned} a_2(a_2-2)-10\ge 0. \end{aligned}$$

$\square$

Remark 3.3

For $mult(f)=3$, the inequality in Proposition 3.3 does not hold true when $a_1=2$ and $a_2\ge 3$.

Remark 3.4

Let (V, 0) be a fewnomial surface isolated singularity of type 1 (see Proposition 2.2) which is defined by $f=x_1^{a_1}+x_2^{a_2}+x_3^{a_3}$ ($a_1\ge 3, a_2\ge 3, a_3\ge 3$) with weight type $(\frac{1}{a_1}, \frac{1}{a_2}, \frac{1}{a_3}; 1)$. Then it follows from Proposition 3.1 that

$$\begin{aligned} \lambda _1(V)= 3a_1a_2a_3+16(a_1+a_2+a_3)-7(a_1a_2+a_1a_3+a_2a_3)-36. \end{aligned}$$

For the proofs of Propositions 3.4, 3.6 and 3.7, we skip the details due to space constraints.Interested readers can find all the detailed proofs in a longer version of this paper. http://archive.ymsc.tsinghua.edu.cn/pacm_download/89/11720-HYZ20.pdf.

Proposition 3.4

Let (V, 0) be a fewnomial surface isolated singularity of type 2 which is defined by $f=x_1^{a_1}x_2+x_2^{a_2}x_3+x_3^{a_3}$ ($a_1\ge 2, a_2\ge 2, a_3\ge 3$) with weight type $(\frac{1-a_3+a_2a_3}{a_1a_2a_3}, \frac{a_3-1}{a_2a_3}, \frac{1}{a_3}; 1)$. Then

$$\begin{aligned} \lambda _1(V)= \left\{ \begin{array}{ll} 3a_1a_2a_3-7(a_1a_2+a_1a_3+a_2a_3)+20(a_1+a_3) &{} \\ +16a_2-55; &{} a_1\ge 4, a_2\ge 4, a_3\ge 4\\ 2a_1a_3-a_1-3a_3-1; &{} a_1\ge 3, a_2=3, a_3\ge 4\\ 2a_2a_3-5a_2-a_3+5; &{} a_1=3, a_2\ge 4, a_3\ge 4\\ 2a_1a_2-3a_1-5a_2+10; &{} a_1\ge 3, a_2\ge 3, a_3=3\\ a_3-3; &{} a_1=2, a_2\ge 2, a_3\ge 3\\ a_1-3; &{} a_1\ge 3, a_2=2, a_3\ge 3. \end{array} \right. \end{aligned}$$

Furthermore, assuming that $mult(f)\ge 4$, we have

$$\begin{aligned}&3a_1a_2a_3-7(a_1a_2+a_1a_3+a_2a_3)+20(a_1+a_3)+16a_2-55\le \frac{3a_1a_2^{2}a_3^{3}}{(1-a_3+a_2a_3)(a_3-1)}\\&\quad -7\left( \frac{a_1a_2^{2}a_3^{2}}{(1-a_3+a_2a_3)(a_3-1)} +\frac{a_1a_2a_3^{2}}{1-a_3+a_2a_3}+\frac{a_2a_3^{2}}{a_3-1}\right) +16\left( \frac{a_1a_2a_3}{1-a_3+a_2a_3}\right. \\&\left. \quad + \frac{a_2a_3}{a_3-1}+a_3\right) -36. \end{aligned}$$

Remark 3.5

For $mult(f)=3$, the inequality in Proposition 3.4 is not true when $a_1=2$, $a_2\ge 3$ and $a_3\ge 3$.

Proposition 3.5

Let (V, 0) be a fewnomial surface isolated singularity of type 3 which is defined by $f=x_1^{a_1}x_2+x_2^{a_2}x_3+x_3^{a_3}x_1$ ($a_1\ge 2, a_2\ge 2, a_3\ge 2$) with weight type

$$\begin{aligned} \left( \frac{1-a_3+a_2a_3}{1+a_1a_2a_3}, \frac{1-a_1+a_1a_3}{1+a_1a_2a_3}, \frac{1-a_2+a_1a_2}{1+a_1a_2a_3}; 1\right) . \end{aligned}$$

Then

$$\begin{aligned} \lambda _1(V)= \left\{ \begin{array}{ll} 3a_1a_2a_3+20(a_1+a_2+a_3)-7(a_1a_2+a_1a_3+a_2a_3)&{}\\ -63; &{} a_1\ge 3, a_2\ge 3, a_3\ge 3\\ a_3-2; &{} a_1=2, a_2\ge 2, a_3\ge 2 \end{array} \right. \end{aligned}$$

Furthermore, assuming that $mult(f)\ge 4$, we have

$$\begin{aligned}&3a_1a_2a_3+20(a_1+a_2+a_3)-7(a_1a_2+a_1a_3+a_2a_3)-63\\&\quad \le \frac{3(1+a_1a_2a_3)^3}{(1-a_3+a_2a_3)(1-a_1+a_1a_3)(1-a_2+a_1a_2)}\\&\qquad +16\left( \frac{1+a_1a_2a_3}{1-a_3+a_2a_3}+ \frac{1+a_1a_2a_3}{1-a_1+a_1a_3} +\frac{1+a_1a_2a_3}{1-a_2+a_1a_2}\right) \\&\qquad -7\left( \frac{(1+a_1a_2a_3)^2}{(1-a_3+a_2a_3)(1-a_1+a_1a_3)} +\frac{(1+a_1a_2a_3)^2}{(1-a_1+a_1a_3)(1-a_2+a_1a_2)}\right. \\&\qquad \left. +\frac{(1+a_1a_2a_3)^2}{(1-a_3+a_2a_3)(1-a_2+a_1a_2)}\right) -36. \end{aligned}$$

Proof

It is easy to see that the moduli algebra

$$\begin{aligned} H_1(V)&={\mathbb {C}}\{x_1, x_2,x_3\}/\left( \frac{\partial ^2 f}{\partial x_1^{2}}, \frac{\partial ^2 f}{\partial x_1 \partial x_2} ,\frac{\partial ^2 f}{\partial x_1 \partial x_3},\frac{\partial ^2 f}{\partial x_2^{2}},\frac{\partial ^2 f}{\partial x_3^{2}},\frac{\partial ^2 f}{\partial x_2 \partial x_3}\right) \end{aligned}$$

has dimension $a_1a_2a_3-2(a_1a_2+a_1a_3+a_2a_3)+5(a_1+a_2+a_3)-14$ and has a monomial basis of the form

$$\begin{aligned}&\{ x_1^{i_1}x_2^{i_2}x_3^{i_3}, 0\le i_1\le a_1-3; 0\le i_2\le a_2-3; 0\le i_3\le a_3-3;x_1^{a_1-2} x_3^{i_3}, 0\le i_3\le a_3-3; \\&x_2^{i_2}x_3^{a_3-2}, 0\le i_2\le a_2-3; x_1^{i_1}x_2^{a_2-2}, 0\le i_1\le a_1-3\}, \end{aligned}$$

and in case of $a_1=2, a_2\ge 2, a_3\ge 2$ the monomial basis are $\{ x_3^{i_3}, 0\le i_3\le a_3-2\}$

with the following relations:

$$\begin{aligned}&x_1^{a_1-2}x_2=0, x_2^{a_2-2}x_3=0,x_3^{a_3-2}x_1=0, x_1^{a_1-1}=0, x_2^{a_2-1}=0, x_3^{a_3-1}=0. \end{aligned}$$

(3.19)

In order to compute a derivation D of $H_1(V)$ it suffices to indicate its values on the generators $x_1, x_2, x_3$ which can be written in terms of the basis. Thus we can write

$$\begin{aligned} Dx_j&= \sum _{i_1=0}^{a_1-3}\sum _{ i_2=0}^{a_2-3}\sum _{i_3=0}^{a_3-3} c_{i_1,i_2,i_3}^jx_1^{i_1}x_2^{i_2}x_3^{i_3}+\sum _{i_1=0}^{a_1-3} c_{i_1,a_2-2,0}^jx_1^{i_1}x_2^{a_2-2}+\sum _{i_3=0}^{a_3-3} c_{a_1-2,0,i_3}^jx_1^{a_1-2}x_3^{i_3}\\&\quad +\sum _{i_2=0}^{a_2-3} c_{0,i_2,a_3-2}^jx_2^{i_2}x_3^{a_3-2}, \; j=1, 2, 3. \end{aligned}$$

Using the relations (3.19) one easily finds the necessary and sufficient conditions defining a derivation of $H_1(V)$ as follows:

$$\begin{aligned}&c_{0,i_2,i_3}^1=0; 0\le i_2\le a_2-4, 0\le i_3\le a_3-3, c_{0,a_2-3,0}^1=0; \end{aligned}$$

(3.20)

$$\begin{aligned}&c_{i_1,0,i_3}^2=0; 0\le i_1\le a_1-3,0\le i_3\le a_3-4, c_{0,0,a_3-3}^2=0; \end{aligned}$$

(3.21)

$$\begin{aligned}&c_{i_1,i_2,0}^3=0; 0\le i_1\le a_1-4,0\le i_2\le a_2-3, c_{a_1-3,0,0}^3=0. \end{aligned}$$

(3.22)

Using (3.20)–(3.22) we obtain the following description of Lie algebras in question:

$$\begin{aligned}&x_1^{i_1}x_2^{i_2}x_3^{i_3}\partial _1, \; 1\le i_1\le a_1-3, 0\le i_2\le a_2-3, 0\le i_3\le a_3-3; x_2^{i_2} x_3^{a_3-2}\partial _1, \; 1\le i_2\le a_2-4,\\&x_2^{a_2-3}x_3^{i_3}\partial _1, \; 1\le i_3\le a_3-2; x_1^{i_1}x_2^{a_2-2}\partial _1, \; 1\le i_1\le a_1-3; x_1^{a_1-2}x_3^{i_3}\partial _1, \; 0\le i_3\le a_3-3;\\&x_1^{i_1}x_2^{i_2}x_3^{i_3}\partial _2, \; 0\le i_1\le a_1-3, 1\le i_2\le a_2-3, 0\le i_3\le a_3-3;x_1^{a_1-2} x_3^{i_3}\partial _2, \; 0\le i_3\le a_3-3; \\&x_1^{i_1}x_2^{a_2-2}\partial _2, \; 1\le i_1\le a_1-3; x_2^{a_2-2}\partial _2; x_1^{i_1}x_3^{a_3-3}\partial _2, \; 1\le i_1\le a_1-3,\\&x_1^{i_1}x_2^{i_2}x_3^{i_3}\partial _3, \; 0\le i_1\le a_1-3, 0\le i_2\le a_2-3, 1\le i_3\le a_3-3;\\&x_2^{a_2-2}\partial _3; x_1^{i_1}x_2^{a_2-2}\partial _3, \; 1\le i_1\le a_1-3;x_3^{a_3-2}\partial _2; x_3^{a_3-2}\partial _3; x_2^{a_2-2}\partial _1; \\&x_1^{a_1-3}x_2^{i_2}\partial _3, \; 1\le i_2\le a_2-3; x_1^{a_1-2}x_3^{i_3}\partial _3, \; 0\le i_3\le a_3-3; x_3^{a_3-2}\partial _1; \\&x_2^{i_2} x_3^{a_3-2}\partial _3, \; 1\le i_2\le a_2-3;x_2^{i_2}x_3^{a_3-2}\partial _2, \; 1\le i_2\le a_2-3. \end{aligned}$$

Therefore we have

$$\begin{aligned} \lambda _1(V)=3a_1a_2a_3+20(a_1+a_2+a_3)-7(a_1a_2+a_1a_3+a_2a_3)-63. \end{aligned}$$

In case of $a_1=2, a_2\ge 2, a_3\ge 2,$ we obtain the following basis:

$$\begin{aligned} x_3^{i_3}\partial _3, \; 1\le i_3\le a_3-2. \end{aligned}$$

Furthermore, we need to show that when $a_1\ge 3, a_2\ge 3, a_3\ge 3,$ then

$$\begin{aligned}&3a_1a_2a_3+20(a_1+a_2+a_3)-7(a_1a_2+a_1a_3+a_2a_3)-63\\&\quad \le \frac{3(1+a_1a_2a_3)^3}{(1-a_3+a_2a_3)(1-a_1+a_1a_3)(1-a_2+a_1a_2)}\\&\quad +16\left( \frac{1+a_1a_2a_3}{1-a_3+a_2a_3}+ \frac{1+a_1a_2a_3}{1-a_1+a_1a_3} \right. \\&\qquad \left. +\frac{1+a_1a_2a_3}{1-a_2+a_1a_2}\right) -7\left. (\frac{(1+a_1a_2a_3)^2}{(1-a_3+a_2a_3)(1-a_1+a_1a_3)}\right. \\&\left. \quad +\frac{(1+a_1a_2a_3)^2}{(1-a_1+a_1a_3)(1-a_2+a_1a_2)}\right. \\&\left. \quad +\frac{(1+a_1a_2a_3)^2}{(1-a_3+a_2a_3)(1-a_2+a_1a_2)}\right) -36. \end{aligned}$$

After simplification we get

$$\begin{aligned}&8(a_1a_2+a_2a_3+a_1a_3)+a_1(a_2-3)+a_2(a_3-3)+a_3(a_1-3)\\&\quad +6a_1^{2}[a_2(a_3-3)+a_3(a_2-3)]\\&\quad +6a_2^{2}[a_1(a_3-3)+a_3(a_1-3)]+ 6a_3^{2}[a_1(a_2-3)+a_2(a_1-3)]\\&\quad +6(a_1^{2}+a_2^2+a_3^2)+6(a_1^{3}a_2+a_2^{3}a_3\\&\quad +a_3^{3}a_1)+4a_1^{2}a_2^{2}a_3^{2}+8(a_1a_2^{2}a_3+a_1a_2a_3^{2})\\&\quad +4a_1^{2}a_2a_3+2a_1a_2a_3[3a_1-8]+a_1^{3}a_2a_3^{2}(a_3-3)(a_2-3)\\&\quad +a_1^{2}a_3^{2}(a_3-3)(a_1a_2-2)+2a_1^{2}a_2a_3^{2}(a_3+a_2-6)\\&\quad +6a_1a_2a_3^{3}(a_1-3)+a_1^{2}a_2^{3}a_{3}(a_{3}-3)(a_1-3)\\&\quad +a_1^{2}a_2^{2}(a_1-3)(a_2a_3-2)+2a_1^{3}a_{2}a_3(a_2-3)+2a_1^{2}a_2^{2}a_3(a_1-3+(a_3-3))\\&\quad +a_1a_2^{2}a_3^{3}(a_2-3)({a_1}-3)+a_2^{2}a_3^{2}(a_2-3)(a_1a_3-2)+14\ge 0. \end{aligned}$$

$\square$

Remark 3.6

For $mult(f)=3$, the inequality in Proposition 3.5 is not true when $a_1=2$, $a_2\ge 2$ and $a_3\ge 3$.

Proposition 3.6

Let (V, 0) be a fewnomial surface isolated singularity of type 4 which is defined by $f=x_1^{a_1}+x_2^{a_2}+x_3^{a_3}x_1$ ($a_1\ge 3, a_2\ge 3, a_3\ge 2$) with weight type $(\frac{1}{a_1}, \frac{1}{a_2}, \frac{a_1-1}{a_1a_3}; 1)$. Then

$$\begin{aligned} \lambda _1(V)= \left\{ \begin{array}{ll} 3a_1a_2a_3+16(a_1+a_3)+20a_2-7(a_1a_2+a_1a_3+a_2a_3)&{}\\ -45; &{} a_1\ge 4, a_2\ge 3, a_3\ge 3\\ 2a_2a_3-3a_2-5a_3+7; &{} a_1=3, a_2\ge 3, a_3\ge 2\\ a_2-3; &{} a_1\ge 4, a_2\ge 3, a_3=2 \end{array} \right. \end{aligned}$$

Furthermore, assuming that $mult(f)\ge 4$, we have

$$\begin{aligned}&3a_1a_2a_3+16(a_1+a_3)+20a_2-7(a_1a_2+a_1a_3+a_2a_3)-45\\&\quad \le \frac{3a_1^{2}a_2a_3}{a_1-1}+16\left( a_1+ a_2+\frac{a_1a_3}{a_1-1}\right) \\&\qquad -7(a_1a_2+\frac{a_1a_2a_3}{a_1-1}+\frac{a_1^{2}a_3}{a_1-1}) -36. \end{aligned}$$

Remark 3.7

For $mult(f)=3$, the inequality in Proposition 3.6 is not true when $a_1 \ge 5$, $a_2\ge 5$ and $a_3=2$.

Proposition 3.7

Let (V, 0) be a fewnomial surface isolated singularity of type 5 which is defined by $f=x_1^{a_1}x_2+x_2^{a_2}x_1+x_3^{a_3}$ ($a_1\ge 2, a_2\ge 2, a_3\ge 3$) with weight type $(\frac{a_2-1}{a_1a_2-1}, \frac{a_1-1}{a_1a_2-1}, \frac{1}{a_3}; 1)$. Then

$$\begin{aligned} \lambda _1(V)= \left\{ \begin{array}{ll} 3a_1a_2a_3+16(a_1+a_2)+26a_3-7(a_1a_2+a_1a_3+a_2a_3)&{}\\ -59; &{} a_1\ge 5, a_2\ge 5, a_3\ge 3\\ a_3-3; &{} a_1= 2, a_2\ge 2, a_3\ge 3\\ 2a_2a_3-5a_2+2a_3-5; &{} a_1= 3, a_2\ge 3, a_3\ge 3\\ 6a_2a_3-14a_2-8a_3+17; &{} a_1= 4, a_2\ge 4, a_3\ge 3 \end{array} \right. \end{aligned}$$

Furthermore, assuming that $mult(f)\ge 4$, we have

$$\begin{aligned}&3a_1a_2a_3+16(a_1+a_2)+26a_3-7(a_1a_2+a_1a_3+a_2a_3)-59 \\&\quad \le \frac{3a_3(a_1a_2-1)^2}{(a_2-1)(a_1-1)}+16(\frac{a_1a_2-1}{a_2-1}+\frac{a_1a_2-1}{a_1-1}\\&\qquad + {a_3})-7(\frac{(a_1a_2-1)^2}{(a_2-1)(a_1-1)}+ \frac{a_3(a_1a_2-1)}{a_1-1}+\frac{a_3(a_1a_2-1)}{a_2-1})-36. \end{aligned}$$

Remark 3.8

For $mult(f)=3$, the inequality in Proposition 3.7 is not true when $a_1=2$, $a_2\ge 3$ and $a_3\ge 3$.

Proof of Main Theorem A

It is an immediate corollary of Proposition 3.1. $\square$

Proof of Main Theorem B

Let $f\in {\mathbb {C}}\{x_1,x_2\}$ be a weighted homogeneous fewnomial isolated singularity. Then f can be divided into the following three types:

Type A. $x_1^{a_1}+x_2^{a_2}$,

Type B. $x_1^{a_1}x_2+x_2^{a_2}$,

Type C. $x_1^{a_1}x_2+x_2^{a_2}x_1$.

The Main Theorem B is an immediate corollary of Remark  3.1, Propositions 3.2, and Proposition 3.3. $\square$

Proof of Main Theorem C

Let $f\in {\mathbb {C}}\{x_1,x_2,x_3\}$ be a weighted homogeneous fewnomial isolated surface singularity. Then f can be divided into the following five types:

Type 1. $x_1^{a_1}+x_2^{a_2}+ x_3^{a_3}$,

Type 2. $x_1^{a_1}x_2+x_2^{a_2}x_3+ x_3^{a_3}$,

Type 3. $x_1^{a_1}x_2+x_2^{a_2}x_3+x_3^{a_3}x_1$,

Type 4. $x_1^{a_1}+x_2^{a_2}+ x_3^{a_3}x_1$,

Type 5. $x_1^{a_1}x_2+x_2^{a_2}x_1+ x_3^{a_3}$.

The Main Theorem C is an immediate corollary of Remark  3.4, Propositions 3.4, 3.5, 3.6, and 3.7. $\square$

Proof of Main Theorem D

It is easy to see, from Remarks 1.2, 3.1, Propositions  3.2–3.3, Propositions 4.1–4.3 in [33], Propositions  3.1–3.3 in [14], and Propositions 3.2–3.4 in [13], the inequality $\lambda ^2> \lambda ^1> \lambda ^0=\lambda _2>\lambda _1$ holds true. $\square$

Proof of Main Theorem E

It is easy to see, from Remarks 1.2, 3.4, Propositions  3.4–3.7, Proposition 4.1 in [33], Propositions 3.1, 3.2 in [12], Propositions 3.4, 3.5 in [14], Propositions 3.5-3.9 in [13], and Propositions 3.4–3.8 in [16], the inequality $\lambda ^2> \lambda ^1> \lambda ^0=\lambda _3>\lambda _1$ holds true. $\square$

Proof of Main Theorem F

In the following, we use the notations ${\mathcal {O}}_{n+m}:={\mathbb {C}}\{x_1,\ldots , x_n, y_1,\ldots , y_m\}$, ${\mathcal {O}}_{n}:={\mathbb {C}}\{x_1,\ldots , x_n\}$ and ${\mathcal {O}}_{m}:={\mathbb {C}}\{y_1,\ldots , y_m\}$.

$$\begin{aligned} L_1 (V_{f+g})= & {} Der {\mathcal {O}}_{n+m}\bigg /\bigg (\frac{\partial ^2 (f+g)}{\partial x_1^{2}},\ldots , \frac{\partial ^2 (f+g)}{\partial y_m^{2}}, \frac{\partial ^2 (f+g)}{\partial x_1 \partial x_2},\ldots , \frac{\partial ^2 (f+g)}{\partial x_1 \partial y_m}, \\&\ldots , \frac{\partial ^2 (f+g)}{\partial y_{m-1} \partial y_{m}} \bigg )\\= & {} Der {\mathcal {O}}_{n+m}\bigg /\bigg (\frac{\partial ^2 f}{\partial x_1^{2}},\ldots , \frac{\partial ^2 f}{\partial x_n^{2}}, \frac{\partial ^2 f}{\partial x_1 \partial x_2},\ldots , \frac{\partial ^2 f}{\partial x_1 \partial x_n},\ldots , \frac{\partial ^2 f}{\partial x_{n-1} \partial x_n}\\&\frac{\partial ^2 g}{\partial y_1^{2}},\ldots , \frac{\partial ^2 g}{\partial y_m^{2}}, \frac{\partial ^2 g}{\partial y_1 \partial y_2},\ldots , \frac{\partial ^2 g}{\partial y_1 \partial y_m}, \ldots , \frac{\partial ^2 g}{\partial y_{m-1} \partial y_m}\bigg )\\= & {} Der [ {\mathcal {O}}_{n}\bigg /\bigg ( \frac{\partial ^2 f}{\partial x_1^{2}},\ldots , \frac{\partial ^2 f}{\partial x_n^{2}}, \frac{\partial ^2 f}{\partial x_1 \partial x_2},\ldots , \frac{\partial ^2 f}{\partial x_1 \partial x_n},\ldots , \frac{\partial ^2 f}{\partial x_{n-1} \partial x_n} \bigg )\\&\otimes {\mathcal {O}}_{m}\bigg /\bigg ( \frac{\partial ^2 g}{\partial y_1^{2}},\ldots , \frac{\partial ^2 g}{\partial y_m^{2}}, \frac{\partial ^2 g}{\partial y_1 \partial y_2},\ldots , \frac{\partial ^2 g}{\partial y_1 \partial y_m}, \ldots , \frac{\partial ^2 g}{\partial y_{m-1} \partial y_m} \bigg ) ]\\= & {} Der [ {\mathcal {O}}_{n}\bigg /\bigg ( \frac{\partial ^2 f}{\partial x_1^{2}},\ldots , \frac{\partial ^2 f}{\partial x_n^{2}}, \frac{\partial ^2 f}{\partial x_1 \partial x_2},\ldots , \frac{\partial ^2 f}{\partial x_1 \partial x_n},\ldots , \frac{\partial ^2 f}{\partial x_{n-1} \partial x_n} \bigg )]\\&\otimes {\mathcal {O}}_{m}\bigg /\bigg ( \frac{\partial ^2 g}{\partial y_1^{2}},\ldots , \frac{\partial ^2 g}{\partial y_m^{2}}, \frac{\partial ^2 g}{\partial y_1 \partial y_2},\ldots , \frac{\partial ^2 g}{\partial y_1 \partial y_m}, \ldots , \frac{\partial ^2 g}{\partial y_{m-1} \partial y_m} \bigg ) \\&+ {\mathcal {O}}_{n}\bigg /\bigg ( \frac{\partial ^2 f}{\partial x_1^{2}},\ldots , \frac{\partial ^2 f}{\partial x_n^{2}}, \frac{\partial ^2 f}{\partial x_1 \partial x_2},\ldots , \frac{\partial ^2 f}{\partial x_1 \partial x_n},\ldots , \frac{\partial ^2 f}{\partial x_{n-1} \partial x_n} \bigg )\\&\otimes Der [ {\mathcal {O}}_{m}\bigg /\bigg ( \frac{\partial ^2 g}{\partial y_1^{2}},\ldots , \frac{\partial ^2 g}{\partial y_m^{2}}, \frac{\partial ^2 g}{\partial y_1 \partial y_2},\ldots , \frac{\partial ^2 g}{\partial y_1 \partial y_m}, \ldots , \frac{\partial ^2 g}{\partial y_{m-1} \partial y_m} \bigg ) ]\\= & {} L_1(V_f)\otimes H_1(V_g)+H_1(V_f)\otimes L_1(V_g). \end{aligned}$$

The first equality above comes from the fact that f, g are weighted homogeneous while the fourth equality follows from the Theorem 2.1. $\square$