Periods of double EPW-sextics

Abstract

We study the period map for double EPW-sextics, which are varieties making up a locally versal family of polarized hyperkähler fourfolds. Double EPW-sextics are parametrized by Lagrangian subspaces of the third wedge-product of a 6-dimensional complex vector space. We prove that Lagrangians in the indeterminacy locus of the period map contain a decomposable $3$-vector enjoying very special properties. In addition we prove a result about periods of double EPW-sextics which are either smooth or have isolated singular points with projectivized tangent cone isomorphic to the incidence variety in ${\mathbb P}^2\times ({\mathbb P}^2)^{\vee }$.

1 Introduction

Let $V$ be a $6$-dimensional complex vector space. Let $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) \subset \mathrm {Gr}(10,\bigwedge ^3 V)$ be the symplectic Grassmannian parametrizing subspaces which are Lagrangian for the symplectic form given by wedge-product. Given $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ we let

$$\begin{aligned} Y_A:=\left\{ [v]\in {\mathbb P}(V) \mid A\cap (v\wedge \bigwedge ^2 V)\not =\{0\}\right\} . \end{aligned}$$

(1.1)

Then $Y_A$ is a degeneracy locus and hence it is naturally a subscheme of ${\mathbb P}(V)$. For certain pathological choices of $A$ we have $Y_A={\mathbb P}(V)$: barring those cases $Y_A$ is a sextic hypersurface named EPW-sextic. An EPW-sextic comes equipped with a double cover [23]

$$\begin{aligned} f_A:X_A\rightarrow Y_A. \end{aligned}$$

(1.2)

The fourfold $X_A$ is what we call a double EPW-sextic. There is an open dense subset $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0\subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ parametrizing smooth double EPW-sextics—these fourfolds are hyperkähler (HK) deformations of the Hilbert square of a $K3$ surface (i.e. the blow-up of the diagonal in the symmetric product of a $K3$ surface); see [20]. By varying $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0$ one gets a locally versal family of HK varieties—one of the five known such families in dimensions greater than $2$; see [3, 5, 10–12] for the construction of the other families. The complement of $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0$ in $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ is the union of two prime divisors, $\varSigma$ and $\varDelta$; the former consists of those $A$ containing a non-zero decomposable tri-vector, the latter is defined in Sect. 2.2. If $A$ is generic in $\varSigma$ then $X_A$ is singular along a $K3$ surface (see Corollary 3.17), if $A$ is generic in $\varDelta$ then $X_A$ is singular at a single point whose tangent cone is isomorphic to the contraction of the zero-section of the cotangent sheaf of ${\mathbb P}^2$ (see Proposition 3.10 of [23]). By associating to $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0$ the Hodge structure on $H^2(X_A)$ one gets a regular map of quasi-projective varieties ${\fancyscript{P}}^0:\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0 \longrightarrow {\mathbb D}_{\varLambda }$ where ${\mathbb D}_{\varLambda }$ is a quasi-projective period domain, the quotient of a bounded symmetric domain of Type IV by the action of an arithmetic group (see [8] for a general discussion and Sect. 4.2 for the case at hand). Let ${\mathbb D}_{\varLambda }^{\text {BB}}$ be the Baily–Borel compactification of ${\mathbb D}_{\varLambda }$, and let

$$\begin{aligned} {\fancyscript{P}}:\mathbb {LG}\left( {\bigwedge ^{3}} V \right) \dashrightarrow {\mathbb D}_{\varLambda }^{\text {BB}} \end{aligned}$$

(1.3)

be the rational map defined by ${\fancyscript{P}}^0$. Then ${\fancyscript{P}}$ descends to the GIT-quotient of $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ for the natural action of $\textit{PGL}(V)$. More precisely: the action of $\textit{PGL}(V)$ on $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ is uniquely linearized and hence there is an unambiguous GIT quotient

$$\begin{aligned} \mathfrak {M}:=\mathbb {LG}\left( {\bigwedge ^{3}} V \right) /\!/\textit{PGL}(V). \end{aligned}$$

(1.4)

The map ${\fancyscript{P}}$ descends to a rational map

$$\begin{aligned} \mathfrak {p}:\mathfrak {M}\dashrightarrow {\mathbb D}_{\varLambda }^{\text {BB}} \end{aligned}$$

(1.5)

Let $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^\mathrm{st}$ and $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^\mathrm{ss}$ be the loci of (GIT) stable and semistable points of $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$. By Cor. 2.5.1 of [24] the open $\textit{PGL}(V)$-invariant subset $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0$ is contained in $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^\mathrm{st}$; we let

$$\begin{aligned} \mathfrak {M}^0:=\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0/\!/\textit{PGL}(V). \end{aligned}$$

(1.6)

The discussion above shows that ${\fancyscript{P}}$ is regular on $\mathfrak {M}^0$ and it maps it into ${\mathbb D}_{\varLambda }$. By Verbitsky’s global Torelli Theorem and Markman’s monodromy results the restriction of $\mathfrak {p}$ to $\mathfrak {M}^0$ is injective; see Theorem 1.3 and Lemma 9.2 of [17]. Since the domain and codomain of the period map have the same dimension it follows that $\mathfrak {p}$ is a birational map. In the present paper we will be mainly concerned with the following problem: what is the indeterminacy locus of $\mathfrak {p}$? In order to state our main results we will go through a few more definitions. Given $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ we let

$$\begin{aligned} \varTheta _A:=\left\{ W\in \mathrm {Gr}(3, V)\mid \bigwedge ^3 W\subset A\right\} . \end{aligned}$$

(1.7)

Thus $A\in \varSigma$ if and only if $\varTheta _A\not =\varnothing$. Suppose that $W\in \varTheta _A$; there is a natural degeneracy locus $C_{W,A}\subset {\mathbb P}(W)$ (see Subsect. 3.2 of [24]), which is either a sextic curve or (in pathological cases) ${\mathbb P}(W)$. Let

$$\begin{aligned} |{\fancyscript{O}}_{{\mathbb P}(W)}(6)|\dashrightarrow {\mathbb D}^{\text {BB}}_{\varPhi } \end{aligned}$$

(1.8)

be the compactified period map for $K3$ surfaces of degree $2$, where ${\mathbb D}^{\text {BB}}_{\varPhi }$ is the Baily–Borel compactification of the relevant period space; see [26].

Definition 1.1

• (1) Define $\mathfrak {M}^{\textit{ADE}}\subset \mathfrak {M}$ to be the subset of points represented by $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{\text {ss}}$ for which the following hold:

  • (1a) The orbit $\textit{PGL}(V)A$ is closed in $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{\text {ss}}$.

  • (1b) For all $W\in \varTheta _A$ the degeneracy locus $C_{W,A}$ is a sextic curve with simple singularities.

• (2) Define $\mathfrak {I}\subset \mathfrak {M}$ to be the subset of points represented by $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{\text {ss}}$ for which the following hold:

  • (2a) The orbit $\textit{PGL}(V)A$ is closed in $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{\text {ss}}$.

  • (2b) There exists $W\in \varTheta _A$ such that $C_{W,A}$ is either ${\mathbb P}(W)$ or a sextic curve in the indeterminacy locus of (1.8).

Then, $\mathfrak {M}^{\textit{ADE}}$ and $\mathfrak {I}$ are respectively open and closed subsets of $\mathfrak {M}$, and since every point of $\mathfrak {M}$ is represented by a single closed $\textit{PGL}(V)$-orbit, $\mathfrak {I}$ is in the complement of $\mathfrak {M}^{\textit{ADE}}$.

The family of double EPW-sextics is analogous to the family of varieties of lines on a smooth cubic fourfold, and the period map for double EPW-sextics is analogous to the period map for cubic fourfolds. Given these analogies the subset $\mathfrak {M}^{\textit{ADE}}$ is the analogue in our context of the moduli space of cubic fourfolds with simple singularities; see [14, 15]. Below is the main result of the present paper.

Theorem 1.2

The period map $\mathfrak {p}$ is regular away from $\mathfrak {I}$. Let $x\in (\mathfrak {M}{\setminus }\mathfrak {I})$; then $\mathfrak {p}(x)\in {\mathbb D}_{\varLambda }$ if and only if $x\in \mathfrak {M}^{\textit{ADE}}$.

In particular $\mathfrak {p}$ is regular on $\mathfrak {M}^{\textit{ADE}}$ and maps it into ${\mathbb D}_{\varLambda }$. This result is analogous to the result that the period map for cubic fourfolds extends regularly to the moduli space of cubic fourfolds with simple singularities, and maps it into the interior of the relevant Baily–Borel compactification; see [14, 15]. Theorem 1.2 is a first step towards an understanding of the rational map $\mathfrak {p}:\mathfrak {M}\dashrightarrow {\mathbb D}_{\varLambda }^{\text {BB}}$. Such an understanding will eventually include a characterization of the image of $(\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )$. (Notice that if $A\in (\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )$ then $A$ is a stable point (Cor. 2.5.1 of [24]) and moreover $[A]\in \mathfrak {M}^{\textit{ADE}}$ because $\varTheta _A$ is empty.)

In the present paper we give a preliminary result in that direction. Let $\mathfrak {N}:=\varSigma /\!/\textit{PGL}(V)$. The generic point of $\varSigma$ is $\textit{PGL}(V)$-stable by Cor. 2.5.1 of [24], hence $\mathfrak {N}$ is a prime divisor of $\mathfrak {M}$. In Sect. 4.3 we prove that the set of Hodge structures in ${\mathbb D}_{\varLambda }$ which have a $(1,1)$-root of negative square is the union of four prime divisors named ${\mathbb S}_2^{\star }$, ${\mathbb S}'_2$, ${\mathbb S}''_2$, ${\mathbb S}_4$.

Theorem 1.3

The restriction of the period map $\mathfrak {p}$ to $\mathfrak {M}{\setminus }\mathfrak {N}$ is an open embedding

$$\begin{aligned} \mathfrak {M}{\setminus }\mathfrak {N}\hookrightarrow {\mathbb D}_{\varLambda } {\setminus }\left( {\mathbb S}_2^{\star }\cup {\mathbb S}'_2\cup {\mathbb S}''_2\cup {\mathbb S}_4\right) . \end{aligned}$$

(1.9)

One should compare Theorem 1.3 with Question 9.1 of [4] and the sentence that follows it, keeping in mind that our divisors ${\mathbb S}_2^{\star }$, ${\mathbb S}'_2$, ${\mathbb S}''_2$ and ${\mathbb S}_4$ correspond to ${\fancyscript{D}}_8$, ${\fancyscript{D}}_2'$, ${\fancyscript{D}}_2''$ and ${\fancyscript{D}}_4$ respectively. The analogy with the period map for cubic fourfolds leads us to conjecture that the restriction of $\mathfrak {p}$ to $\mathfrak {M}{\setminus }\mathfrak {N}$ is an isomorphism onto the right hand side of (1.9).

Remark 1.4

The open subset $\mathfrak {M}{\setminus }\mathfrak {N}$ parametrizes double EPW-sextics which are either smooth or have isolated singular points with projectivized tangent cone isomorphic to the incidence variety in ${\mathbb P}^2\times ({\mathbb P}^2)^{\vee }$; see [23].

2 Preliminaries

In the present section we recall definition and properties of certain subsets of $\varSigma$, we define the prime divisor $\varDelta$ on $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$, and we prove a result, namely Proposition 2.1, which will be useful in analyzing the period map.

2.1 Geometrically significant subsets of $\varSigma$

Let

(2.1)

Given $d\ge 0$ we let be

(2.2)

Let $\varSigma [d]\subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ be the image of by the second projection. Notice that and $\varSigma =\varSigma [0]$. Proposition 3.1 of [22] gives

$$\begin{aligned} {{\mathrm{cod}}}\left( \varSigma [d],\mathbb {LG}\left( {\bigwedge ^{3}} V \right) \right) =(d^2+d+2)/2. \end{aligned}$$

(2.3)

Let

$$\begin{aligned} \varSigma _{+}:= \left\{ A\in \varSigma \mid {{\mathrm{Card}}}(\varTheta _A)>1\right\} . \end{aligned}$$

(2.4)

By Proposition 3.1 of [22], $\varSigma _{+}$ is a constructible subset of $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ and

$$\begin{aligned} {{\mathrm{cod}}}\left( \varSigma _{+},\mathbb {LG}\left( {\bigwedge ^{3}} V \right) \right) =2. \end{aligned}$$

(2.5)

We claim that

$$\begin{aligned} {{\mathrm{sing}}}\varSigma =\varSigma _{+}\cup \varSigma [1]. \end{aligned}$$

(2.6)

In fact $(\overline{\varSigma }_{+}{\setminus } \varSigma _{+})\subset \varSigma [1]$ by Equation (3.19) of [22] and hence (2.6) follows from Proposition 3.2 of [22]. We let

$$\begin{aligned} \varSigma _{\infty }:= \left\{ A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) \mid \dim \varTheta _A>0\right\} . \end{aligned}$$

(2.7)

Theorem 3.37 and Table 3 of [22] give

$$\begin{aligned} {{\mathrm{cod}}}\left( \varSigma _{\infty },\mathbb {LG}\left( {\bigwedge ^{3}} V \right) \right) =7. \end{aligned}$$

(2.8)

2.2 The divisor $\varDelta$

Let $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$. We let

$$\begin{aligned} Y_A[k]=\left\{ [v]\in {\mathbb P}(V)\mid \dim \left( A\cap \left( v\wedge \bigwedge ^2 V\right) \right) \ge k\right\} . \end{aligned}$$

(2.9)

Notice that $Y_A[0]={\mathbb P}(V)$ and $Y_A[1]=Y_A$. We set

$$\begin{aligned} Y_A(k):=Y_A[k]{\setminus } Y_A[k+1]. \end{aligned}$$

(2.10)

Let

$$\begin{aligned} \varDelta := \left\{ A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) \mid Y_A[3]\not =\varnothing \right\} . \end{aligned}$$

(2.11)

A dimension count gives that $\varDelta$ is a prime divisor in $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$; see [23]. Let

(2.12)

2.3 Lagrangians with positive dimensional $Y_A[3]$

The following result will be handy.

Proposition 2.1

Let $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ and suppose that $\dim Y_A[3]>0$. Then $A\in \varSigma _{\infty }\cup \varSigma [2]$.

Proof

By contradiction. Thus we assume that $\dim Y_A[3]>0$ and $A\notin \varSigma _{\infty }\cup \varSigma [2]$. By hypothesis there exists an irreducible component $C$ of $Y_A[3]$ of positive dimension. Let $[v]\in C$ be generic. We claim that one of the following holds:

• (a) There exist distinct $W_1,W_2\in \varTheta _A$ containing $v$.

• (b) There exists $W\in \varTheta _A$ containing $v$ such that

  $$\begin{aligned} \dim A\cap \left( \bigwedge ^2 W\wedge V\right) \cap \left( v\wedge \bigwedge ^2 V\right) \ge 2. \end{aligned}$$

  (2.13)

In fact assume first that $\dim (A\cap (v\wedge \bigwedge ^2 V))=3$ for $[v]$ in an open dense $C^0\subset C$. We may assume that $C^0$ is smooth; then we have an embedding defined by mapping $[v]\in C^0$ to $([v],A)$. Let $[v]\in C^0$; the differential of the projection at $([v],A)$ is not injective because it vanishes on ${{\mathrm{im}}}d\iota ([v])$. By Corollary 2.4 and Proposition 2.5 of [23] we get that one of Items (a), (b) above holds.

Now assume that $\dim (A\cap (v\wedge \bigwedge ^2 V))>3$ for generic $[v]\in C$ (and hence for all $[v]\in C$). Let notation be as in the proof of Proposition 2.5 of [23]; then $\mathbf{K}\cap \mathrm {Gr}(2,V_0)$ is a zero-dimensional (if it has positive dimension then $\dim \varTheta _A>0$ and hence $A\in \varSigma _{\infty }$ against our assumption) scheme of length $5$. It follows that either Item (a) holds (if $\mathbf{K}\cap \mathrm {Gr}(2,V_0)$ is not a single point) or Item (b) holds (if $\mathbf{K}\cap \mathrm {Gr}(2,V_0)$ is a single point $\mathbf{p}$ and hence the tangent space of $\mathbf{K}\cap \mathrm {Gr}(2,V_0)$ at $\mathbf{p}$ has dimension at least $1$).

Now we are ready to reach a contradiction. First suppose that Item (a) holds. Since $\varTheta _A$ is finite there exist distinct $W_1,W_2\in \varTheta _A$ such that $C\subset {\mathbb P}(W_1)\cap {\mathbb P}(W_2)$. Thus $\dim (W_1\cap W_2)=2$ and hence the line

$$\begin{aligned} \{W\in \mathrm {Gr}(3,V)\mid (W_1\cap W_2)\subset W\subset (W_1+W_2)\} \end{aligned}$$

(2.14)

is contained in $\varTheta _A$, that is a contradiction. Now suppose that Item (b) holds. Since $\varTheta _A$ is finite there exists $W\in \varTheta _A$ such that $C\subset {\mathbb P}(W)$ and

$$\begin{aligned} \forall [v]\in C\qquad \dim A\cap \left( \bigwedge ^2 W\wedge V\right) \cap \left( v\wedge \bigwedge ^2 V\right) \ge 2. \end{aligned}$$

(2.15)

Since $A\notin \varSigma [2]$ we have $\dim (A\cap (\bigwedge ^2 W\wedge V))=2$. Let $\{w_1,w_2,w_3\}$ be a basis of $W$; then

$$\begin{aligned} A\cap \left( \bigwedge ^2 W\wedge V\right) =\langle w_1\wedge w_2\wedge w_3,\, \beta \rangle . \end{aligned}$$

(2.16)

Let $\overline{\beta }$ be the image of $\beta$ under the quotient map $\left( \bigwedge ^2 W\wedge V\right) \rightarrow \left( \bigwedge ^2 W\wedge V\right) /\bigwedge ^3 W$. Then

$$\begin{aligned} \overline{\beta }\in \bigwedge ^2 W\wedge (V/W)\cong {{\mathrm{Hom}}}(W,V/W). \end{aligned}$$

(2.17)

(We choose a volume form on $W$ in order to define the isomorphism above.) By (2.15) the kernel of $\overline{\beta }$ (viewed as a map $W\rightarrow (V/W)$) contains all $v$ such that $[v]\in C$. Thus $\overline{\beta }$ has rank $1$. It follows that $\beta$ is decomposable; $\beta \in \bigwedge ^3 W'$ where $W'\in \varTheta _A$ and $\dim W\cap W'=2$. Then $\varTheta _A$ contains the line in $\mathrm {Gr}(3,V)$ joining $W$ and $W'$; that is a contradiction. $\square$

3 Singularities of EPW-sextics and their double covers

In this section we describe the singularities of a generic double EPW-sextic paramerized by $\varSigma$ and its hyperkähler resolution—the resulting picture is similar to that for the variety of lines of a (generic) cubic foufold containing a plane [29], except that in our case there is non-trivial monodromy of order $2$.

We start by giving local equations for an EPW-sextic. In good cases a local equation is given by the determinant of a variable quadratic form, this leads us to record some easy linear algebra facts that will be useful later on.

Next we associate to a couple a degeneracy locus $C_{W,A}\subset {\mathbb P}(W)$, which is generically a sextic curve. We consider and we describe $Y_A$ in a neighborhood of a point of ${\mathbb P}(W){\setminus } C_{W,A}$; this leads to a result about the intersection of a double EPW-sextic with two (generic) hyperplanes which suffices to extend the period map away from a subset of codimension $4$ (see Sect. 4.4).

Section 3.6 describes an arbitrary double EPW-sextic as the zero-locus of explicit equations. Let $A\in \varSigma$ be generic; in Sect. 3.7 we describe the double EPW-sextic $X_A$ and a hyperkähler resolution —this is the key result of the present section.

The last subsection compares the Beauville-Bogomolov quadratic form on for generic $A\in \varSigma$ and the intersection form on $H^2$ of the $K3$ surface which is the double cover of ${\mathbb P}(W)$ branched over $C_{W,A}$, where $W$ is the unique element of $\varTheta _A$ (unique because $A$ is generic in $\varSigma$).

3.1 Local equation of EPW-sextics

In order to give a local equation of $Y_A$ around $[v_0]\in {\mathbb P}(V)$ we choose a direct sum decomposition

$$\begin{aligned} V=[v_0]\oplus V_0. \end{aligned}$$

(3.1)

We identify $V_0$ with the open affine $({\mathbb P}(V){\setminus }{\mathbb P}(V_0))$ via the isomorphism

$$\begin{aligned} V_0&\overset{\sim }{\longrightarrow } {\mathbb P}(V){\setminus }{\mathbb P}(V_0)\nonumber \\ v&\longmapsto [v_0+v]. \end{aligned}$$

(3.2)

Thus $0\in V_0$ corresponds to $[v_0]$. Then

$$\begin{aligned} Y_A\cap V_0=V(f_0+f_1+\dots +f_6),\qquad f_i\in {{\mathrm{S}}}^i V_0^{\vee }. \end{aligned}$$

(3.3)

The following result collects statements contained in Corollary 2.5 and Proposition 2.9 of [22].

Proposition 3.1

Keep assumptions and hypotheses as above. Let $k:=\dim (A\cap (v_0\wedge \bigwedge ^2 V))$.

• (1) Suppose that no $W\in \varTheta _A$ contains $v_0$. Then the following hold:

  • (1a) $0=f_0=\dots = f_{k-1}$ and $f_k\not =0$.

  • (1b) Suppose that $k=2$ and hence $[v_0]\in Y_A(2)$. Then $Y_A(2)$ is smooth two-dimensional at $[v_0]$.

• (2) Suppose that there exists $W\in \varTheta _A$ containing $v_0$. Then $0=f_0=f_1$.

Next we recall how one describes $Y_A\cap V_0$ under the following assumption:

$$\begin{aligned} \bigwedge ^3 V_0 \cap A=\{0\}. \end{aligned}$$

(3.4)

Decomposition (3.1) determines a direct sum decomposition $\bigwedge ^3 V=(v_0\wedge \bigwedge ^2 V_0)\oplus \bigwedge ^3 V_0$. We will identify $\bigwedge ^2 V_0$ with $v_0\wedge \bigwedge ^2 V_0$ via multiplication by $v_0$. By (3.4) the subspace $A$ is the graph of a linear map . Choose a volume form ${{\mathrm{vol}}}_0:\bigwedge ^5 V_0\overset{\sim }{\longrightarrow } {\mathbb C}$ in order to identify $\bigwedge ^3 V_0$ with $\bigwedge ^2 V_0^{\vee }$. Then is symmetric because $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$. Explicitly

(3.5)

We let $q_A$ be the associated quadratic form on $\bigwedge ^2 V_0$. Notice that

$$\begin{aligned} \ker q_A=\left\{ \alpha \in \bigwedge ^2 V_0 \mid v_0\wedge \alpha \in A\cap (v_0\wedge \bigwedge ^2 V) \right\} \end{aligned}$$

(3.6)

is identified with $A\cap (v_0\wedge \bigwedge ^2 V)$. Let $v\in V_0$ and let $q_v$ be the Plücker quadratic form defined by

$$\begin{aligned} \bigwedge ^2 V_0&\overset{q_v}{\longrightarrow } {\mathbb C}\nonumber \\ \alpha&\longmapsto {{\mathrm{vol}}}_0( v\wedge \alpha \wedge \alpha ) \end{aligned}$$

(3.7)

Proposition 3.2

(Proposition 2.18 of [22]) Keep notation and hypotheses as above; in particular (3.4) holds. Then

$$\begin{aligned} Y_A\cap V_0=V(\det (q_A+q_v))\,. \end{aligned}$$

(3.8)

Next we will state a hypothesis which ensures the existence of a decomposition (3.1) such that (3.4) holds. First recall [21] that we have an isomorphism

$$\begin{aligned} \mathbb {LG}\left( {\bigwedge ^{3}} V \right)&\overset{\delta _V}{\overset{\sim }{\longrightarrow }}\mathbb {LG}\left( {\bigwedge ^{3}} V^{\vee }\right) \nonumber \\ A&\longmapsto A^{\bot }. \end{aligned}$$

(3.9)

Let $E\in \mathrm {Gr}(5,V)$; then

$$\begin{aligned} E\in Y_{\delta _V(A)} \text { if and only if } \left( \bigwedge ^3 E\right) \cap A\not =\{0\}. \end{aligned}$$

(3.10)

(The EPW-sextic $Y_{\delta _V(A)}$ is the dual of $Y_A$.) Thus there exists a decomposition (3.1) such that (3.4) holds if and only if $Y_{\delta _V(A)}\not ={\mathbb P}(V^{\vee })$. The proposition below follows at once from Claim 2.11 and Equation (2.82) of [22].

Proposition 3.3

Let $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ and suppose that $\dim \varTheta _A\le 2$. Then

$$\begin{aligned} Y_A\not ={\mathbb P}(V),\quad Y_{\delta _V(A)}\not ={\mathbb P}(V^{\vee }). \end{aligned}$$

In particular there exists a decomposition (3.1) such that (3.4) holds.

3.2 Determinant of a variable quadratic form

Let $U$ be a complex vector space of finite dimension $d$. We view ${{\mathrm{S}}}^2 U^{\vee }$ as the vector space of quadratic forms on $U$. Given $q\in {{\mathrm{S}}}^2 U^{\vee }$ we let be the associated symmetric map. Let $K:=\ker q$; then may be viewed as a (symmetric) map . The dual quadratic form $q^{\vee }$ is the quadratic form associated to the symmetric map ; thus $q^{\vee }\in {{\mathrm{S}}}^2 (U/K)$. We will denote by $\wedge ^i q$ the quadratic form induced by $q$ on $\bigwedge ^i U$.

Remark 3.4

If $0\not =\alpha =v_1\wedge \dots \wedge v_i$ is a decomposable vector of $\bigwedge ^i U$ then $\wedge ^i q(\alpha )$ is equal to the determinant of the Gram matrix of $q|_{\langle v_1,\dots , v_i\rangle }$ with respect to the basis $\{v_1,\dots , v_i\}$.

The following exercise in linear algebra will be handy.

Lemma 3.5

Suppose that $q\in {{\mathrm{S}}}^2 U^{\vee }$ is non-degenerate. Let $S\subset U$ be a subspace. Then

$$\begin{aligned} {{\mathrm{corank}}}(q|_S)={{\mathrm{corank}}}(q^{\vee }|_{S^{\bot }}). \end{aligned}$$

(3.11)

Let $q_{*}\in {{\mathrm{S}}}^2 U^{\vee }$. Then

$$\begin{aligned} \det (q_{*}+q)=\varPhi _0(q)+\varPhi _1(q)+\dots +\varPhi _d(q), \quad \varPhi _i\in {{\mathrm{S}}}^i ({{\mathrm{S}}}^2 U). \end{aligned}$$

(3.12)

Of course $\det (q_{*}+q)$ is well-defined up to multiplication by a non-zero scalar and hence so are the $\varPhi _i$. The result below follows from a straightforward computation.

Proposition 3.6

Let $q_{*}\in {{\mathrm{S}}}^2 U^{\vee }$ and set

$$\begin{aligned} K:=\ker q_{*}, k:=\dim K. \end{aligned}$$

(3.13)

Let $\varPhi _i$ be the polynomials appearing in (3.12). Then

• (1) $\varPhi _i=0$ for $i<k$, and

• (2) there exists $c\not =0$ such that $\varPhi _k(q)=c\det (q|_K)$.

Keep notation and hypotheses as in Proposition 3.6. Let ${\fancyscript{V}}_K\subset {{\mathrm{S}}}^2 U^{\vee }$ be the subspace of quadratic forms whose restriction to $K$ vanishes. Given $q\in {\fancyscript{V}}_K$ we have and hence it makes sense to consider the restriction of $q_{*}^{\vee }$ to .

Proposition 3.7

Keep notation and hypotheses as in Proposition 3.6. The restriction of $\varPhi _i$ to ${\fancyscript{V}}_K$ vanishes for $i<2k$. Moreover there exists $c\not =0$ such that

$$\begin{aligned} . \end{aligned}$$

(3.14)

Proof

Choose a basis $\{u_1,\dots ,u_d\}$ of $U$ such that $K=\langle u_1,\dots ,u_k\rangle$ and for $k<i\le d$. Let $M$ be the Gram matrix of $q$ in the chosen basis. Expanding $\det (q_{*}+tq)$ we get

$$\begin{aligned} \det (q_{*}+tq)\equiv (-1)^k t^{2k}\sum _{J}(\det M_{\mathbf{k},J})^2\pmod {t^{2k+1}} \end{aligned}$$

where $M_{\mathbf{k},J}$ is the $k\times k$ submatrix of $M$ determined by the first $k$ rows and the columns indexed by $J=(j_1,j_2,\dots , j_k)$. The claim follows from the equality

and Remark 3.4. $\square$

Now suppose that

(3.15)

We let $\overline{q}_{*}\in {{\mathrm{S}}}^2(U/\langle e\rangle )^{\vee }$ be the non-degenerate quadratic form induced by $q_{*}$ i.e.  $\overline{q}_{*}(\overline{v}):=q_{*}(v)$ for $\overline{v}\in U/\langle e\rangle$. Let $\varPhi _0,\dots ,\varPhi _d$ be as in (3.12). In particular $\varPhi _0=0$. Assume that

$$\begin{aligned} L\subset \ker \varPhi _1=\{q\mid q(e)=0\} \end{aligned}$$

(3.16)

is a vector subspace. Thus

$$\begin{aligned} \det (q_{*}+q)|_{L}=\varPhi _2|_{L}+\dots +\varPhi _d|_{L}. \end{aligned}$$

(3.17)

We will compute ${{\mathrm{rank}}}(\varPhi _2|_{L})$. Let $T\subset U$ be defined by

(3.18)

where $L$ and $e$ are as above. Geometrically, ${\mathbb P}(T)$ is the projective tangent space at $[e]$ of the intersection of the projective quadrics parametrized by ${\mathbb P}(L)$.

Proposition 3.8

Keep notation as above, and suppose that $L\subset {{\mathrm{S}}}^2 U^{\vee }$ is a vector subspace such that (3.16) holds, and let $T$ be given by (3.18). Then

$$\begin{aligned} {{\mathrm{rank}}}(\varPhi _2|{_L})={{\mathrm{cod}}}(T,U)-{{\mathrm{corank}}}(\overline{q}_{*}|_{T/\langle e\rangle }). \end{aligned}$$

(3.19)

(The last term on the right hand side makes sense because $T\supset \langle e\rangle$.)

Proof

Let

(3.20)

By Proposition 3.7 we have

$$\begin{aligned} {{\mathrm{rank}}}(\varPhi _2|_{L})={{\mathrm{rank}}}(\overline{q}^{\vee }_{*}|_{{{\mathrm{im}}}\alpha }). \end{aligned}$$

(3.21)

On the other hand Lemma 3.5 gives

$$\begin{aligned} {{\mathrm{rank}}}(\overline{q}_{*}^{\vee }|_{{{\mathrm{im}}}(\alpha )})=\dim {{\mathrm{im}}}(\alpha )- {{\mathrm{corank}}}(\overline{q}_{*}|_{{{\mathrm{im}}}(\alpha )^{\bot }}). \end{aligned}$$

(3.22)

By definition ${{\mathrm{im}}}(\alpha )^{\bot }=T/\langle e\rangle$. Since $\dim {{\mathrm{im}}}(\alpha )={{\mathrm{cod}}}(T, U)$ we get the proposition. $\square$

3.3 The subscheme $C_{W,A}$

Let [see (2.1)]. For the definition of the degeneracy locus $C_{W,A}\subset {\mathbb P}(W)$ we refer to Subsection 3.2 of [24]. Here we mention that $C_{W,A}$ is either a sextic curve or (in pathological cases) all of ${\mathbb P}(W)$. Moreover

$$\begin{aligned} {{\mathrm{supp}}}C_{W,A}=\left\{ [v]\in {\mathbb P}(W) \mid \dim (A\cap v\wedge \bigwedge ^2 V)\ge 2\right\} . \end{aligned}$$

(3.23)

(Notice that $(A\cap v\wedge \bigwedge ^2 V)\supset \bigwedge ^3 W$ for all $[v]\in {\mathbb P}(W)$.)

Definition 3.9

Let ${\fancyscript{B}}(W,A)\subset {\mathbb P}(W)$ be the set of $[w]$ such that one of the following holds:

• (1) There exists $W'\in (\varTheta _A{\setminus }\{W\})$ containing $w$.

• (2) $\dim (A\cap (w\wedge \bigwedge ^2 V) \cap (\bigwedge ^2 W\wedge V))\ge 2$.

The following result is obtained by pasting together Proposition 3.3.6 and Corollary 3.3.7 of [24].

Proposition 3.10

Let . Then the following hold:

• 1. $C_{W,A}$ is a smooth curve at $[v_0]$ if and only if $\dim (A\cap (v_0\wedge \bigwedge ^2 V))=2$ and $[v_0]\notin {\fancyscript{B}}(W,A)$.

• 2. $C_{W,A}={\mathbb P}(W)$ if and only if ${\fancyscript{B}}(W,A)={\mathbb P}(W)$.

3.4 Local structure of $Y_A$ along a singular plane

Let . Then ${\mathbb P}(W)\subset Y_A$. In this section we analyze the local structure of $Y_A$ at $[v_0] \in {\mathbb P}(W){\setminus } C_{W,A}$ under mild hypotheses on $A$. Let $[v_0 ]\in {\mathbb P}(W)$—for the moment being we do not require that $[v_0] \notin C_{W,A}$. Let $V_0\subset V$ be a subspace transversal to $[v_0 ]$. We identify $V_0$ with an open affine neighborhood of $[v_0 ]$ via (3.2); thus $0\in V_0$ corresponds to $[v_0 ]$. Let $f_i\in {{\mathrm{S}}}^i V_0^{\vee }$ for $i\in \{0,\dots ,6\}$ be the polynomials of (3.3). By Item (2) of Proposition 3.1 we have

$$\begin{aligned} Y_A\cap V_0=V(f_2+\dots +f_6). \end{aligned}$$

(3.24)

Suppose that $Y_A\not ={\mathbb P}(V)$. Then $[v_0 ]\in {{\mathrm{sing}}}Y_A$; since $[v_0 ]$ is an arbitrary point of ${\mathbb P}(W)$ we get ${\mathbb P}(W)\subset {{\mathrm{sing}}}Y_A$. It follows that ${{\mathrm{rank}}}f_2\le 3$.

Proposition 3.11

Let and suppose that $Y_{\delta _V(A)}\not ={\mathbb P}(V^{\vee })$. Let $[v_0 ]\in {\mathbb P}(W){\setminus } C_{W,A}$ and let $f_2$ be the quadratic term of the Taylor expansion of a local equation of $Y_A$ centered at $[v_0]$. Then

$$\begin{aligned} {{\mathrm{rank}}}f_2=4-\dim \left( A\cap \left( \bigwedge ^2 W\wedge V\right) \right) . \end{aligned}$$

(3.25)

Proof

By hypothesis there exists a subspace $V_0\subset V$ such that (3.1)–(3.4) hold. Let be the symmetric map whose graph is $A$ and $q_A$ be the associated quadratic form on $\bigwedge ^2 V_0$ (see Sect. 3.1). Let $Q_A:=V(q_A)\subset {\mathbb P}(\bigwedge ^ 2 V_0)$. By Proposition 3.2 we have

$$\begin{aligned} V(Y_A)|_{V_0}=V(\det (q_A+q_v)) \end{aligned}$$

(3.26)

where $q_v$ is as in (3.7). Let $W_0:=W\cap V_0$. Since $[v_0 ]\notin C_{W,A}$ we have $A\cap (v_0\wedge \bigwedge ^2 V)=\bigwedge ^ 3 W$. By (3.6) we get that ${{\mathrm{sing}}}Q_A=\{[\bigwedge ^ 2 W_0]\}$. Thus

$$\begin{aligned} \det (q_A+q_v)=\varPhi _2(v)+\varPhi _3(v)+\dots +\varPhi _6(v),\quad \varPhi _i\in {{\mathrm{S}}}^i V_0^{\vee } \end{aligned}$$

(3.27)

and the rank of $\varPhi _2$ is given by (3.19) with $q_{*}=q_A$ and $L=V_0$. Let us identify the subspace $T\subset \bigwedge ^ 2 V_0$ given by (3.18). Let $U_0\subset V_0$ be a subspace transversal to $W_0$; since the Plücker quadrics generate the ideal of the Grassmannian we have

$$\begin{aligned} T=\bigwedge ^ 2 W_0\oplus (W_0\wedge U_0). \end{aligned}$$

(3.28)

By Proposition 3.8 we get that

$$\begin{aligned} {{\mathrm{rank}}}\varPhi _2=3-\dim \ker (q_A|_{W_0\wedge U}). \end{aligned}$$

(3.29)

We claim that

$$\begin{aligned} \dim \ker (q_A|_{W_0\wedge U}) =\dim \left( A\cap \left( \bigwedge ^2 W\wedge V\right) \right) . \end{aligned}$$

(3.30)

In fact let $\alpha \in W_0\wedge U$. Then $\alpha \in \ker (q_A|_{W_0\wedge U})$ if and only if

(3.31)

Since $A\subset \left( \bigwedge ^ 3 W\right) ^{\bot }$ it follows from (3.5) that necessarily . Equation (3.5) gives a linear map

(3.32)

The direct sum decomposition

$$\begin{aligned} \bigwedge ^ 2 W\wedge U_0=[v_0 ]\wedge W_0\wedge U_0\oplus \bigwedge ^ 2 W_0\wedge U_0 \end{aligned}$$

(3.33)

shows that $\varphi$ is bijective. Since there is an obvious isomorphism $A\cap \left( \bigwedge ^ 2 W\wedge U_0\right) \cong (A\cap (\bigwedge ^2 W\wedge V))/\bigwedge ^3 W$ we get that (3.30) holds. $\square$

Remark 3.12

Suppose that $\dim (A\cap (\bigwedge ^2 W\wedge V))>4$. Then Eq. (3.25) does not make sense. On the other hand $C_{W,A}={\mathbb P}(W)$ by Proposition 3.10 hence there is no $[v_0 ]\in ({\mathbb P}(W){\setminus } C_{W,A})$.

3.5 Intersection of two generic hyperplanes on a double EPW-sextic

Lemma 3.13

Let $A_0\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma _{\infty }{\setminus }\varSigma [2]$. Then $Y_{A_0}[3]$ is finite and $C_{W,A_0}$ is a sextic curve for every $W\in \varTheta _{A_0}$.

Proof

$Y_{A_0}[3]$ is finite by Proposition 2.1. Let $W\in \varTheta _{A_0}$. Let us show that ${\fancyscript{B}}(W,A_0)\ne {\mathbb P}(W)$. Let $W'\in (\varTheta _{A_0}{\setminus }\{W\})$. Then $\dim (W\cap W')=1$ because otherwise $\bigwedge ^3 W$ and $\bigwedge ^3 W'$ span a line in $\mathrm {Gr}(3,V)$ which is contained in $\varTheta _{A_0}$ and that contradicts the assumption that $\varTheta _{A_0}$ is finite. This proves finiteness of the set of $[w]\in {\mathbb P}(W)$ such that Item (1) of Definition 3.9 holds. Since $\dim (\bigwedge ^2 W\wedge V)\le 2$ a similar argument gives finiteness of the set of $[w]\in {\mathbb P}(W)$ such that Item (2) of Definition 3.9 holds. This proves that ${\fancyscript{B}}(W,A_0)$ is finite, in particular ${\fancyscript{B}}(W,A_0)\ne {\mathbb P}(W)$. By Proposition 3.10 it follows that $C_{W,A_0}$ is a sextic curve. $\square$

Proposition 3.14

Let $A_0\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma _{\infty }{\setminus }\varSigma [2]$ and let $\mathbf{L}\subset {\mathbb P}(V)$ be a generic $3$-dimensional linear subspace. Let ${\fancyscript{U}}\subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma _{\infty }{\setminus }\varSigma [2]$ be a sufficiently small open set containing $A_0$. Let $A\in {\fancyscript{U}}$. Then the following hold:

• (a) The scheme-theoretic inverse image $f_{A}^{-1}\mathbf{L}$ is a reduced surface with DuVal singularities.

• (b) If in addition $A_0\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0$ then $f_{A}^{-1}\mathbf{L}$ is a smooth surface.

Proof

Let $\mathbf{L}\subset {\mathbb P}(V)$ be a generic $3$-dimensional linear subspace. Then

• (1) $\mathbf{L}\cap Y_{A_0}[3]=\varnothing$.

• (2) $\mathbf{L}\cap C_{W,A_0}=\varnothing$ for every $W\in \varTheta _{A_0}$.

In fact $Y_{A_0}[3]$ is finite by Lemma 3.13 and hence (1) holds. Since $\varTheta _{A_0}$ is finite and $C_{W,A_0}$ is a sextic curve for every $W\in \varTheta _{A_0}$, Item (2) holds as well. We will prove that $f_{A_0}^{-1}\mathbf{L}$ is reduced with DuVal singularities and that it is smooth if $A_0\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0$. The result will follow because being smooth, reduced or having DuVal singularities is an open property.

Write $\varTheta _{A_0}=\{W_1,\dots ,W_d\}$. By Item (2) above the intersection $\mathbf{L}\cap {\mathbb P}(W_i)$ is a single point $p_i$ for $i=1,\dots ,d$. Since $p_i\notin C_{W_i,A_0}$ the points $p_1,\dots ,p_d$ are pairwise distinct. By Proposition 3.1 we know that away from $\bigcup _{W\in \varTheta _{A_0}}{\mathbb P}(W)$ the locally closed sets $Y_A(1)$ and $Y_A(2)$ are smooth of dimensions $4$ and $2$ respectively. By Item (1) it follows that $f_{A_0}^{-1}\mathbf{L}$ is smooth away from

$$\begin{aligned} f_{A_0}^{-1}\{p_1,\dots ,p_d\}. \end{aligned}$$

(3.34)

It remains to show that $f_{A_0}^{-1}\mathbf{L}$ is DuVal at each point of (3.34). Since $p_i\in Y_{A_0}(1)$ the map $f_{A_0}$ is étale of degree $2$ over $p_i$; see (3.36). Thus $f_{A_0}^{-1}(p_i)=\{q_i^{+},q_i^{-}\}$ and $f_{A_0}$ defines an isomorphism between the germ $(X_{A_0},q_i^{\pm })$ (in the classical topology) and the germ $(Y_{A_0},p_i)$. By Proposition 3.11 we get that the tangent cone of $f_{A_0}^{-1}\mathbf{L}$ at $q_i^{\pm }$ is a quadric cone of rank $2$ or $3$; it follows that $f_{A_0}^{-1}\mathbf{L}$ has a singularity of type $A_n$ at $q_i^{\pm }$. $\square$

3.6 Local analytic description of double EPW-sextics

Throughout the present subsection we will assume that $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ and $Y_A\not ={\mathbb P}(V)$. Let $f_A:X_A\rightarrow Y_A$ be the double cover of (1.2). We let

$$\begin{aligned} H_A\in | f_A^{*}{\fancyscript{O}}_{Y_A}(1)|,\quad h_A:=f_A^{*}c_1({\fancyscript{O}}_{Y_A}(1)). \end{aligned}$$

(3.35)

If $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0$ then $X_A$ is hyperkähler and $h_A$ is an ample class of square $2$ for the Beauville-Bogomolov quadratic form. The following is an immediate consequence of the definition of $f_A$ (see [23]):

$$\begin{aligned} f_A \text { is a topological covering of degree } 2 \text { over } Y_A(1). \end{aligned}$$

(3.36)

Let $[v_0]\in Y_A$; we will give explicit equations for a neighborhood of $f_A^{-1}([v_0])$ in $X_A$. We will assume throughout the subsection that we are given a direct sum decomposition (3.1) such that (3.4) holds. We start by introducing some notation. Let $K:=\ker q_A$ and let $J\subset \bigwedge ^2 V_0$ be a maximal subspace over which $q_A$ is non-degenerate; we have a direct sum decomposition

$$\begin{aligned} \bigwedge ^2 V_0=J\oplus K. \end{aligned}$$

(3.37)

Choose a basis of $\bigwedge ^2 V_0$ adapted to Decomposition (3.37). Let $k:=\dim K$. The Gram matrices of $q_A$ and $q_v$ (for $v\in V_0$) relative to the chosen basis are given by

$$\begin{aligned} M(q_A)= \begin{pmatrix} N_{J} &{}\quad 0 \\ 0 &{}\quad 0_k \end{pmatrix}, \quad M(q_v)= \begin{pmatrix} Q_{J}(v) &{}\quad R_{J}(v)^t \\ R_{J}(v) &{}\quad P_{J}(v) \end{pmatrix}. \end{aligned}$$

(3.38)

(We let $0_k$ be the $k\times k$ zero matrix.) Notice that $N_{J}$ is invertible and $q_0=0$; thus there exists an open neighborhood $V_0'$ of $0$ in $V_0$ such that $(N_{J}+Q_{J}(v))^{-1}$ exists for $v\in V'_0$. We let

$$\begin{aligned} M_{J}(v):=P_{J}(v)-R_{J}(v)\cdot (N_{J}+Q_{J}(v))^{-1}\cdot R_{J}(v)^t, \qquad v\in V_0'\,. \end{aligned}$$

(3.39)

If $V_0'$ is sufficiently small in the classical topology we may write $N_{J}+Q_{J}(v)=S(v)\cdot S(v)^t$ for all $v\in V_0'$ where $S(v)$ is an invertible analytic function of $v$. Let $j:=\dim J$. The following product between functions of $v$ is easily checked:

$$\begin{aligned}&\begin{pmatrix} 1_j &{}\quad 0 \\ -R_J (S^{-1})^t &{}\quad 1_k \end{pmatrix} \begin{pmatrix} S^{-1} &{}\quad 0 \\ 0 &{}\quad 1_k \end{pmatrix} \begin{pmatrix} N_J+Q_{J}&{}\quad R_{J}^t \\ R_{J} &{}\quad P_{J} \end{pmatrix} \begin{pmatrix} (S^{-1})^t &{}\quad 0 \\ 0 &{}\quad 1_k \end{pmatrix} \begin{pmatrix} 1_j &{}\quad -S^{-1}R_J^t \\ 0 &{}\quad 1_k \end{pmatrix}\nonumber \\&\quad = \begin{pmatrix} 1_j &{}\quad 0 \\ 0 &{}\quad M_J \end{pmatrix} \end{aligned}$$

(3.40)

Let $\mathbf{X}_{J}\subset V_0'\times {\mathbb C}^{k}$ be the closed subscheme whose ideal is generated by the entries of the matrices

$$\begin{aligned} M_{J}(v)\cdot \xi ,\qquad \xi \cdot \xi ^t-M_{J}(v)^c, \end{aligned}$$

(3.41)

where $\xi \in {\mathbb C}^k$ is a column vector and $M_{J}(v)^c$ is the matrix of cofactors of $M_{J}(v)$. We identify $V'_0$ with an open neighborhood of $[v_0]\in {\mathbb P}(V)$ via (3.2). The first projection defines a map $\phi :\mathbf{X}_{J}\rightarrow V(\det M_{J})$. By (3.40) we have $V(\det M_{J})=V'_0\cap Y_A$.

Proposition 3.15

Keep notation and assumptions as above. There exists a commutative diagram

where the germs are in the analytic topology. Furthermore $\zeta$ is an isomorphism.

Proof

Let $[v]\in {\mathbb P}(V)$. There is a canonical identification between $v\wedge \bigwedge ^2 V$ and the fiber at $[v]$ of $\varOmega ^3_{{\mathbb P}(V)}(3)$; see Proposition 5.11 of [20]. Thus we have an injection $\varOmega ^3_{{\mathbb P}(V)}(3)\hookrightarrow \bigwedge ^3 V\otimes {\fancyscript{O}}_{{\mathbb P}(V)}$. Choose $B\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ transversal to $A$. The direct sum decomposition $\bigwedge ^3 V=A\oplus B$ gives rise to a commutative diagram with exact rows

(3.42)

(As suggested by our notation the map $\beta _A$ does not depend on the choice of $B$.) Suppose that $B$ is also transverse to $v_0\wedge \bigwedge ^2 V$. Then $\mu _{A,B}(0)$ is an isomorphism (recall that ${\mathbb P}(V){\setminus }{\mathbb P}(V_0)$ is identified with $V_0$ via (3.2), and $[v_0]$ corresponds to $0$), and hence there exists an open neighborhood ${\fancyscript{U}}$ of $0$ such that $\mu _{A,B}(v)$ is an isomorphism for all $v\in {\fancyscript{U}}$. The map $\lambda _A\circ \mu _{A,B}^{-1}$ is symmetric because $A$ is Lagrangian.

Choose a basis of $A$ and let $L(v)$ be the Gram matrix of $\lambda _A\circ \mu _{A,B}^{-1}(v)$ with respect to the chosen basis. Let $L(v)^c$ be the matrix of cofactors of $L(v)$. Claim 1.3 of [23] gives an embedding

$$\begin{aligned} f_A^{-1}({\fancyscript{U}}\cap Y_A)\hookrightarrow {\fancyscript{U}}\times {\mathbb A}^{10} \end{aligned}$$

(3.43)

with image the closed subscheme whose ideal is generated by the entries of the matrices $L(v)\cdot \xi$ and $\xi \cdot \xi ^t-L(v)^c$, where $\xi$ is a $10\times 1$-matrix whose entries are coordinates on ${\mathbb A}^{10}$. We will denote the above subscheme by $V(L(v)\cdot \xi ,\ \xi \cdot \xi ^t-L(v)^c)$. Under this embedding the restriction of $f_A$ to $f_A^{-1}({\fancyscript{U}}\cap Y_A)$ gets identified with the restriction of the projection ${\fancyscript{U}}\times {\mathbb A}^{10}\rightarrow {\fancyscript{U}}$.

Let $G:{\fancyscript{U}}\rightarrow {{\mathrm{GL}}}_{10}({\mathbb C})$ be an analytic map and, for $v\in {\fancyscript{U}}$, let $H(v):=G^t(v)\cdot L(v)\cdot G(v)$. The automorphism of ${\fancyscript{U}}\times {\mathbb A}^{10}$ given by $(v,\xi )\mapsto (v,G(v)^{-1}\xi )$ restricts to an isomorphism

$$\begin{aligned} V(L(v)\cdot \xi ,\ \xi \cdot \xi ^t-L(v)^c) \overset{\sim }{\longrightarrow } V(H(v)\cdot \xi ,\ \xi \cdot \xi ^t-H(v)^c). \end{aligned}$$

(3.44)

In other words we are free to replace $L(v)$ by an arbitrary congruent matrix function. Let

$$\begin{aligned} \bigwedge ^2 V_0&\overset{\phi _{v_0+v}}{\longrightarrow } (v_0+v)\wedge \bigwedge ^2 V \nonumber \\ \alpha&\longmapsto (v_0+v)\wedge \alpha \end{aligned}$$

(3.45)

A straightforward computation gives

(3.46)

Thus the Gram matrix $M(q_A+q_v)$ is congruent to $L(v)$ and hence we have an embedding (3.43) with image $V(M(q_A+q_v)\cdot \xi ,\ \xi \cdot \xi ^t-M(q_A+q_v)^c)$.

On the other hand (3.40) shows that $M(q_A+q_v)$ is congruent to the matrix

$$\begin{aligned} E(v):= \begin{pmatrix} 1_j &{}\quad 0 \\ 0 &{}\quad M_J(v) \end{pmatrix} \end{aligned}$$

(3.47)

Thus we have an embedding (3.43) with image $V(E(v)\cdot \xi ,\ \xi \cdot \xi ^t-E(v)^c)$. A straightforward computation shows that the latter subscheme is isomorphic to $\mathbf{X}_J\cap ({\fancyscript{U}}\times {\mathbb C}^k)$. $\square$

3.7 $X_A$ for generic $A$ in $\varSigma$

Let $A\in \varSigma {\setminus }\varSigma _{\infty }{\setminus }\varSigma [2]$, and let $W\in \varTheta _A$. Then ${\fancyscript{B}}(W,A)\not ={\mathbb P}(W)$ because, by Lemma 3.13, we know that $C_{W,A}\not ={\mathbb P}(W)$. By the same Lemma $Y_A[3]$ is finite. In particular $({\mathbb P}(W){\setminus } {\fancyscript{B}}(W,A){\setminus } Y_A[3])$ is not empty.

Proposition 3.16

Let $A\in \varSigma {\setminus }\varSigma _{\infty }{\setminus }\varSigma [2]$ and $W\in \varTheta _A$. Suppose in addition that $\dim (A\cap (\bigwedge ^2 W\wedge V))=1$. Let

$$\begin{aligned} x\in f_A^{-1}({\mathbb P}(W){\setminus } {\fancyscript{B}}(W,A){\setminus } Y_A[3]). \end{aligned}$$

(3.48)

The germ $(X_A,x)$ of $X_A$ at $x$ in the classical topology is isomorphic to $({\mathbb C}^2,0)\times A_1$ and ${{\mathrm{sing}}}X_A$ is equal to $f_A^{-1}{\mathbb P}(W)$ in a neighborhood of $x$.

Proof

Suppose first that $f_A(x)\notin C_{W,A}$. Then $f_A(x)\in Y_A(1)$ and hence $f_A$ is étale over $f_A(x)$, see (3.36). Thus the germ $(X_A,x)$ is isomorphic to the germ $(Y_A,f_A(x))$ and the statement of the proposition follows from Proposition 3.11 because by hypothesis the right hand side of (3.25) equals $3$. It remains to examine the case

$$\begin{aligned} f_A(x)\in C_{W,A}{\setminus } {\fancyscript{B}}(W,A){\setminus } Y_A[3]. \end{aligned}$$

(3.49)

Let $f_A(x)=[v_0 ]$. Since $A\notin \varSigma _{\infty }$ there exists a subspace $V_0\subset V$ transversal to $[v_0 ]$ and such that (3.4) holds—see Proposition 3.3. Thus we may apply Proposition 3.15. We will adopt the notation of that Proposition, in particular we will identify $V_0$ with ${\mathbb P}(V){\setminus }{\mathbb P}(V_0)$ via (3.2). Let $W_0:= W\cap V_0$; thus $\dim W_0=2$. Let $K\subset \bigwedge ^2 V_0$ be the subspace corresponding to $(v_0\wedge \bigwedge ^2 V)\cap A$ via the isomorphism $\bigwedge ^2 V_0\overset{\sim }{\rightarrow }(v_0\wedge \bigwedge ^2 V)$ given by multiplication by $v_0$. By (3.49) $\dim K=2$. Let us prove that there exists a basis $\{w_1,w_2,u_1,u_2,u_3\}$ of $V_0$ such that $w_1,w_2\in W_0$ and

$$\begin{aligned} K=\langle w_1\wedge w_2,\ w_1\wedge u_1+u_2\wedge u_3\rangle . \end{aligned}$$

(3.50)

In fact since $[v_0]\notin {\fancyscript{B}}(W,A)$ the following hold:

• (1) ${\mathbb P}(K)\cap \mathrm {Gr}(2,V_0)=\{\bigwedge ^2 W_0\}$.

• (2) ${\mathbb P}(K)$ is not tangent to $\mathrm {Gr}(2,V_0)$.

Now let $\{\alpha ,\beta \}$ be a basis of $K$ such that $\bigwedge ^ 2 W_0=\langle \alpha \rangle$. By (1) we have $\beta \wedge \beta \not =0$. Let $S:={{\mathrm{supp}}}(\beta \wedge \beta )$; thus $\dim S=4$. Let us prove that $W_0\not \subset S$. In fact suppose that $W_0\subset S$. Then $K\subset \bigwedge ^ 2 S$ and since $\mathrm {Gr}(2,S)$ is a quadric hypersurface in ${\mathbb P}(\bigwedge ^ 2 S)$ it follows that either ${\mathbb P}(K)$ intersects $\mathrm {Gr}(2,U)$ in two points or is tangent to it, that contradicts (1) or (2) above. We have proved that $W_0\not \subset S$.

Let $\{w_1,w_2\}$ be a basis of $W_0$ such that $w_1\in W_0\cap S$; it is clear that there exist $u_1,u_2,u_3\in S$ linearly independent such that $\beta =w_1\wedge u_1+u_2\wedge u_3$. This proves that (3.50) holds. Rescaling $u_1,u_3$ we may assume that

$$\begin{aligned} {{\mathrm{vol}}}_0 ( w_1\wedge w_2\wedge u_1\wedge u_2\wedge u_3)=1 \end{aligned}$$

(3.51)

where ${{\mathrm{vol}}}_0$ is our chosen volume form on $V_0$. Let

$$\begin{aligned} J:=\langle w_1\wedge u_1,\,w_1\wedge u_2,\, w_1\wedge u_3,\,w_2\wedge u_1,\,w_2\wedge u_2,\, w_2\wedge u_3,\,u_1\wedge u_2,\ u_1\wedge u_3\rangle . \end{aligned}$$

(3.52)

Thus $J$ is transversal to $K$ by (3.50) and hence we have Decomposition (3.37). Given $v\in V_0$ we write

$$\begin{aligned} v=s_1 w_1+s_2 w_2+t_1 u_1+t_2 u_2+ t_3 u_3. \end{aligned}$$

(3.53)

Thus $(s_1,s_2,t_1,t_2,t_3)$ are affine coordinates on $V_0$ and hence by (3.2) they are also coordinates on an open neighborhood of $[v_0 ]\in V_0$. Let $N=N_{J}$, $P=P_{J}$, $Q=Q_{J}$, $R=R_{J}$ be the matrix functions appearing in (3.38) . A straightforward computation gives

$$\begin{aligned} P(v)=\left( \begin{matrix} 0 &{}\quad t_1 \\ t_1 &{}\quad -2s_2 \end{matrix} \right) ,\quad R(v)= \left( \begin{matrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad t_3 &{}\quad -t_2 \\ -s_2 &{}\quad 0 &{}\quad 0 &{}\quad s_1 &{}\quad -t_3 &{}\quad t_2 &{}\quad 0 &{}\quad 0 \end{matrix} \right) . \end{aligned}$$

(3.54)

The $8\times 8$-matrix $(N+Q(v))$ is invertible for $(s,t)$ in a neighborhood of $0$; we set

$$\begin{aligned} (c_{ij})_{1\le i,j\le 8}=-(N+Q(v))^{-1} \end{aligned}$$

(3.55)

where $c_{ij}\in {\fancyscript{O}}_{V_0,0}$. A straightforward computation gives

$$\begin{aligned} P(v)-R(v)\cdot (N+Q(v))^{-1}\cdot R(v)^t= \left( \begin{matrix} c_{7,7}t_3^2-2 c_{7,8}t_2 t_3+c_{8,8} t_2^2 &{}\quad t_1+\delta \\ t_1+\delta &{}\quad -2s_2+\epsilon \end{matrix} \right) \end{aligned}$$

(3.56)

where $\delta ,\epsilon \in {\mathfrak m}^2_0$ (here ${\mathfrak m}_0\subset {\mathbb C}[s_1,s_2,t_1,t_2,t_3]$ is the maximal ideal of $(0,\dots ,0)$). Let us prove

$$\begin{aligned} \det \left( \begin{matrix} c_{7,7}(0) &{}\quad -c_{7,8}(0) \\ -c_{8,7}(0) &{}\quad c_{8,8}(0) \end{matrix} \right) \not =0. \end{aligned}$$

(3.57)

Since $Q(0)=0$ we have $c_{ij}(0)=-(\det N)^{-1}\cdot N^{ij}$ where $N^c=(N^{ij})_{1\le i,j\le 8}$ is the matrix of cofactors of $N$. Thus (3.57) is equivalent to

$$\begin{aligned} \det \left( \begin{matrix} N^{7,7} &{}\quad N^{7,8} \\ N^{8,7} &{}\quad N^{8,8} \end{matrix} \right) \not =0. \end{aligned}$$

(3.58)

The quadratic form $q_A|_{J}$ is non-degenerate and hence we have the dual quadratic form $(q_A|_{J})^{\vee }$ on $J^{\vee }$. Let $U:=\langle u_1,u_2,u_3\rangle$ where $u_1,u_2,u_3$ are as in (3.50). Applying Lemma 3.5 to $q_A|_{J}$ and the subspace $W_0\wedge U\subset J$ we get

$$\begin{aligned} {{\mathrm{corank}}}(q_A|_{W_0\wedge U})={{\mathrm{corank}}}((q_A|_{J})^{\vee }|_{(W_0\wedge U)^{\bot }}). \end{aligned}$$

(3.59)

By (3.30) $q_A|_{W_0\wedge U}$ is non-degenerate; it follows that $(q_A|_{J})^{\vee }|_{(W_0\wedge U)^{\bot }}$ is non-degenerate as well. The annihilator of $W_0\wedge U$ in $J^{\vee }$ is given by

$$\begin{aligned} (W_0\wedge U)^{\bot }= \langle u_1^{\vee }\wedge u_2^{\vee },\ u^{\vee }_1\wedge u_3^{\vee }\rangle \end{aligned}$$

(3.60)

and the Gram-matrix of $(q_A|_{J})^{\vee }|_{(W_0\wedge U)^{\bot }}$ with respect to the basis given by (3.60) is equal to $(\det N)^{-1}(N^{ij})_{7\le i,j\le 8}$. Hence (3.58) holds and this proves that (3.57) holds.

By (3.56) and (3.57) there exist new analytic coordinates $(x_1,x_2,y_1,y_2,y_3)$ on an open neighborhood ${\fancyscript{U}}$ of $0\in V_0$—with $(0,\dots ,0)$ corresponding to $0\in V_0$—such that

$$\begin{aligned} P(v)-R(v)\cdot (N+Q(v))^{-1}\cdot R(v)^t= \left( \begin{matrix} x_1^2+x_2^2 &{}\quad y_1 \\ y_1 &{}\quad y_2 \end{matrix} \right) . \end{aligned}$$

(3.61)

(Recall that $\delta ,\epsilon \in {\mathfrak m}^2_0$.) By Proposition 3.15 we get that

$$\begin{aligned} f_A^{-1}{\fancyscript{U}}=V\left( \xi _1^2-y_2,\ \xi _1\xi _2+y_1,\ \xi _2^2-x_1^2-x_2^2,\right) \subset {\fancyscript{U}}\times {\mathbb C}^2 \end{aligned}$$

(3.62)

where $(\xi _1,\xi _2)$ are coordinates on ${\mathbb C}^2$ and our point $x\in X_A$ has coordinates $(0,\dots ,0)$. (Notice that if $k=2$ the entries of the first matrix of (3.41) belong to the ideal generated by the entries of the second matrix of (3.41).) Let $B^3(0,r)\subset {\mathbb C}^3$ be a small open ball centered at the origin and let $(x_1,x_2,y_3)$ be coordinates on ${\mathbb C}^3$; there is an obvious isomorphism between an open neighborhood of $0\in f_A^{-1}{\fancyscript{U}}$ and

$$\begin{aligned} V(\xi _2^2-x_1^2-x_2^2)\subset B^3(0,r)\times {\mathbb C}^2 \end{aligned}$$

(3.63)

taking $(0,\dots ,0)$ to $(0,\dots ,0)$. This proves that $X_A$ is singular at $x$ with analytic germ as claimed. It follows that $f_A^{-1}({\mathbb P}(W){\setminus }{\fancyscript{B}}(W,A){\setminus } Y_A[3])\subset {{\mathrm{sing}}}Y_A$.

On the other hand an arbitrary point $x'$ in a sufficiently small neighborhood of $x$ is mapped to $Y_A(1)$ and if it does not belong to $f_A^{-1}{\mathbb P}(W)$ the map $f_A$ is étale at $x'$; by Proposition 3.1 $Y_A$ is smooth at $f(x')$ and therefore $X_A$ is smooth at $x'$. $\square$

Let $\varSigma ^\mathrm{sm}$ be the smooth locus of $\varSigma$.

Corollary 3.17

Let $A\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$ and let $W$ be the unique element in $\varTheta _A$ [unique by (2.6)]. Then

• (1) ${{\mathrm{sing}}}X_A=f_A^{-1}{\mathbb P}(W)$.

• (2) Let $x\in f_A^{-1}{\mathbb P}(W)$. The germ $(X_A,x)$ in the classical topology is isomorphic to $({\mathbb C}^2,0)\times A_1$.

• (3) $C_{W,A}$ is a smooth sextic curve in ${\mathbb P}(W)$.

• (4) The map

  $$\begin{aligned} \begin{aligned} f_A^{-1}{\mathbb P}(W)&\longrightarrow {\mathbb P}(W) \\ x&\longmapsto f_A(x) \end{aligned} \end{aligned}$$

  (3.64)

  is a double cover simply branched over $C_{W,A}$.

Proof

(1)–(2): By (2.6) $A\notin \varSigma _{\infty }\cup \varSigma [2]$, $\dim (A\cap (\bigwedge ^2 W\wedge V))=1$ and ${\fancyscript{B}}(W,A)=\varnothing$. Moreover $Y_A[3]$ is empty by definition. By Proposition 3.16 it follows that $f_A^{-1}{\mathbb P}(W)\subset {{\mathrm{sing}}}X_A$ and that the analytic germ at $x\in f_A^{-1}{\mathbb P}(W)$ is as stated. It remains to prove that $X_A$ is smooth at $x\in X_A{\setminus } f_A^{-1}{\mathbb P}(W)$. Since $A\notin \varDelta$ we have $f_A(x)\in Y_A(1)\cup Y_A(2)$. If $f_A(x)\in Y_A(1)$ then $f_A$ is étale over $f_A(x)$ (see (3.36)) and $Y_A$ is smooth at $f_A(x)$ by Proposition 3.1; it follows that $X_A$ is smooth at $x$. If $f_A(x)\in Y_A(2)$ then $X_A$ is smooth at $x$ by Lemma 3.3 of [23].

Item (3) is an immediate consequence of Proposition 3.10.

(4): Map (3.64) is an étale cover away from $C_{W,A}$ (see (3.36)), while $f_A^{-1}(y)$ is a single point for $y\in C_{W,A}$—see (3.62). Thus either $f_A^{-1}{\mathbb P}(W)$ is singular or else Map (3.64) is simply branched over $C_{W,A}$. Items (1), (2) show that $f_A^{-1}{\mathbb P}(W)$ is smooth; it follows that Item (4) holds. $\square$

Definition 3.18

Suppose that and that $C_{W,A}\not ={\mathbb P}(W)$. We let

$$\begin{aligned} S_{W,A}\longrightarrow {\mathbb P}(W) \end{aligned}$$

(3.65)

be the double cover ramified over $C_{W,A}$. If $\varTheta _A$ has a single element we let $S_A:=S_{W,A}$.

Remark 3.19

Let $A\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$ and let $W$ be the unique element of $\varTheta _A$. By Item (4) of Corollary 3.17 $f_A^{-1}{\mathbb P}(W)$ is identified with $S_A$ and the restriction of $f_A$ to $f_A^{-1}{\mathbb P}(W)$ is identified with the double cover $S_A\rightarrow {\mathbb P}(W)$. In particular $f_A^{-1}{\mathbb P}(W)$ is a polarized $K3$ surface of degree $2$.

3.8 Desingularization of $X_A$ for $A\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$

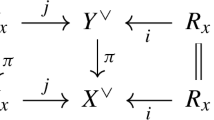
Let $A\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$ and $W$ be the unique element of $\varTheta _A$. Let

(3.66)

be the blow-up of ${{\mathrm{sing}}}X_{A}$. Then is smooth by Corollary 3.17. Below is the relevant picture

(3.67)

Let

(3.68)

(Recall (3.35) that $H_A\in |f_A^{*}{\fancyscript{O}}_{Y_A}(1)|$ and $h_A=f_A^{*}c_1({\fancyscript{O}}_{Y_A}(1))$.) Let

$$\begin{aligned} {\fancyscript{U}}\subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }{{\mathrm{sing}}}\varSigma {\setminus }\varDelta \end{aligned}$$

(3.69)

be an open (classical topology) contractible neighborhood of $A$. We may assume that there exists a tautological family of double EPW-sextics ${\fancyscript{X}}\rightarrow {\fancyscript{U}}$; see Subsection 3.1 of [23]. Let ${\fancyscript{H}}$ be the tautological divisor class on ${\fancyscript{X}}$; thus ${\fancyscript{H}}|_{X_A }\sim H_A$. The holomorphic line bundle ${\fancyscript{O}}_{{\fancyscript{U}}}(\varSigma )$ is trivial and hence there is a well-defined double cover $\phi :{\fancyscript{V}}\rightarrow {\fancyscript{U}}$ ramified over $\varSigma \cap {\fancyscript{U}}$. Let ${\fancyscript{X}}_2 :={\fancyscript{V}}\times _{{\fancyscript{U}}}{\fancyscript{X}}$ be the base change:

(3.70)

Given $A'\in \varSigma \cap {\fancyscript{U}}$ we will denote by the same symbol the unique point in ${\fancyscript{V}}$ lying over $A'$.

Proposition 3.20

Keep notation and assumptions as above. There is a simultaneous resolution of singularities fitting into a commutative diagram

(3.71)

Moreover $\pi$ is an isomorphism away from $g^{-1}(\phi ^{-1}(\varSigma \cap {\fancyscript{U}}))$ and

(3.72)

Proof

By Proposition 3.2 and Lemma 3.3 of [23] ${\fancyscript{X}}$ is smooth and the map $\rho$ of (3.70) is a submersion of smooth manifolds away from points $x\in {\fancyscript{X}}$ such that

$$\begin{aligned} \rho (x):=A'\in \varSigma \cap {\fancyscript{U}},\quad x\in S_{A'}. \end{aligned}$$

(3.73)

Let $(A',x)$ be as in (3.73). By Proposition 3.16 and smoothness of ${\fancyscript{X}}$ the map of analytic germs $({\fancyscript{X}},x)\rightarrow ({\fancyscript{U}},A')$ is isomorphic to

$$\begin{aligned} ({\mathbb C}^3_{\xi }\times {\mathbb C}^2_{\eta }\times {\mathbb C}^{53}_t,\mathbf{0})\longrightarrow & {} ({\mathbb C}^{54}_t,\mathbf{0}) \nonumber \\ (\xi ,\eta ,t)\longmapsto & {} (\xi _1^2+\xi _2^2+\xi _3^2,t_2,\ldots ,t_{54}) \end{aligned}$$

(3.74)

Thus (3.71) is obtained by the classical process of simultaneous resolution of ordinary double points of surfaces. More precisely let $\widehat{{\fancyscript{X}}}_2 \rightarrow {\fancyscript{X}}_2$ be the blow-up of ${{\mathrm{sing}}}{\fancyscript{X}}_2$. Then $\widehat{{\fancyscript{X}}}_2$ is smooth and the exceptional divisor is a fibration over ${{\mathrm{sing}}}{\fancyscript{X}}_2$ with fibers isomorphic to ${\mathbb P}^1\times {\mathbb P}^1$. Since ${{\mathrm{sing}}}{\fancyscript{X}}_2$ is simply connected, the exceptional divisor has two rulings by ${\mathbb P}^1$’s. It follows that there are two small resolutions of ${\fancyscript{X}}_2$ obtained by contracting the exceptional divisor along either one of the two rulings. Choose one small resolution and call it . Then (3.72) holds. $\square$

Corollary 3.21

Let $A\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$ and $A'\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0$. Then is a $HK$ variety deformation equivalent to $(X_{A'},H_{A'})$.

Proof

Since is a blow-up is projective. By Proposition 3.20, is a (smooth) deformation of $X_{A'}$; it follows that is a HK variety. $\square$

Definition 3.22

Let $A\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$. We let be the exceptional divisor of and set .

Given $A\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$ we have a smooth conic bundle¹

$$\begin{aligned} p:E_A \longrightarrow S_A. \end{aligned}$$

(3.75)

Claim 3.23

Let $(,)$ be the Beauville-Bogomolov quadratic form of . The following formulae hold:

(3.76)

(3.77)

Proof

We claim that

(3.78)

In fact the first equality follows from Fujiki’s relation

$$\begin{aligned} \int \limits _X \alpha ^4=3(\alpha ,\alpha )^2,\qquad \alpha \in H^2(X) \end{aligned}$$

(3.79)

valid for any deformation of the Hilbert square of a $K3$ (together with the fact that ) and third equality in (3.78) holds because $\dim S_A=2$. Equation (3.76) follows from (3.78). In order to prove (3.77) we notice that $K_{E_A}\cong {\fancyscript{O}}_E(E_A)$ by adjunction and hence

$$\begin{aligned} \int \limits _{p^{-1}(s)}\zeta _A=-2,\quad s\in S_A. \end{aligned}$$

(3.80)

Using (3.79), (3.76) and (3.80) one gets that

(3.81)

Equation (3.77) follows from the above equality. $\square$

3.9 Conic bundles in HK fourfolds

We have shown that if $A\in (\varSigma ^\mathrm{sm}{\setminus }\varDelta )$ then contains a divisor which is a smooth conic bundle over a $K3$ surface. In the present section we will discuss HK fourfolds containing a smooth conic bundle over a $K3$ surface. (Notice that if a divisor in a HK fourfold is a conic bundle over a smooth base then the base is a holomorphic symplectic surface.)

Proposition 3.24

Let $X$ be a hyperkähler fourfold. Suppose that $X$ contains a prime divisor $E$ which carries a conic fibration $p:E \longrightarrow S$ over a $K3$ surface $S$. Let $\zeta :=c_1({\fancyscript{O}}_X(E))$. Then:

• (1) $h^0({\fancyscript{O}}_X(E))=1$ and $h^p({\fancyscript{O}}_X(E))=0$ for $p>0$.

• (2) $q_X(\zeta )<0$ where $q_X$ is the Beauville-Bogomolov quadratic form of $X$.

Proof

By adjunction $K_E\cong {\fancyscript{O}}_E(E)$ and hence

$$\begin{aligned} \int \limits _{p^{-1}(s)}\zeta =-2,\quad s\in S. \end{aligned}$$

(3.82)

Thus $h^0({\fancyscript{O}}_E(E))=0$ and hence $h^0({\fancyscript{O}}_X(E))=1$. Let us prove that the homomorphism

$$\begin{aligned} H^q({\fancyscript{O}}_X)\longrightarrow H^q({\fancyscript{O}}_E) \end{aligned}$$

(3.83)

induced by restriction is an isomorphism for $q<4$. It is an isomorphism for $q=0$ because both $X$ and $E$ are connected. The spectral sequence with $E_2$ term $H^i(R^j(p|_E){\fancyscript{O}}_E)$ abutting to $H^q({\fancyscript{O}}_E)$ gives an isomorphism $H^q({\fancyscript{O}}_E)\cong H^q({\fancyscript{O}}_S)$. Since $S$ is a $K3$ surface it follows that $H^q({\fancyscript{O}}_E)=0$ for $q=1,3$. On the other hand $H^q({\fancyscript{O}}_X)=0$ for odd $q$ because $X$ is a HK manifold. Thus (3.83) is an isomorphism for $q=1,3$. It remains to prove that (3.83) is an isomorphism for $q=2$. By Serre duality it is equivalent to prove that the restriction homomorphism $H^0(\varOmega ^2_X)\rightarrow H^0(\varOmega ^2_E)$ is an isomorphism. Since $1= h^0(\varOmega ^2_X)=h^0(\varOmega ^2_E)$ it suffices to notice that a holomorphic symplectic form on $X$ cannot vanish on $E$ (the maximum dimension of an isotropic subspace for $\sigma |_{T_x X}$ is equal to $2$). This finishes the proof that (3.83) is an isomorphism for $q<4$.

The long exact cohomology sequence associated to

$$\begin{aligned} 0\longrightarrow {\fancyscript{O}}_X(-E)\longrightarrow {\fancyscript{O}}_X\longrightarrow {\fancyscript{O}}_E\longrightarrow 0 \end{aligned}$$

(3.84)

gives $h^q({\fancyscript{O}}_X(-E))=0$ for $q<4$. By Serre duality, Item (1) holds.

Let $c_X$ be the Fujiki constant of $X$; thus

$$\begin{aligned} \int \limits _X\alpha ^4= c_X q_X(\alpha )^2,\qquad \alpha \in H^2(X). \end{aligned}$$

(3.85)

Let $\iota :E\hookrightarrow X$ be the inclusion. Let $\sigma$ be a holomorphic symplectic form on $X$. We proved above that there exists a holomorphic symplectic form $\tau$ on $S$ such that $\iota ^{*}\sigma =p^{*}\tau$. Thus we have

$$\begin{aligned} \frac{c_X}{3} q_X(\zeta ) q_X(\sigma +\overline{\sigma })= \int \limits _X \zeta ^2\wedge (\sigma +\overline{\sigma })^2=\int \limits _E\iota ^{*}\zeta \wedge p^{*}(\tau +\overline{\tau })^2=-2\int \limits _S(\tau +\overline{\tau })^2. \end{aligned}$$

(3.86)

(The first equality follows from $(\zeta ,\sigma +\overline{\sigma })=0$, and we used (3.82) to get the last equality.) On the other hand $c_X>0$ and $q_X(\sigma +\overline{\sigma })>0$; thus $q_X(\zeta )<0$. $\square$

Let $X$ and $E$ be as in Proposition 3.24. Let ${{\mathrm{Def}}}_E(X)\subset {{\mathrm{Def}}}(X)$ be the germ representing deformations for which $E$ deforms and ${{\mathrm{Def}}}_{\zeta }\subset {{\mathrm{Def}}}(X)$ be the germ representing deformations that keep $\zeta$ of type $(1,1)$. We have an inclusion of germs

$$\begin{aligned} {{\mathrm{Def}}}_E(X)\hookrightarrow {{\mathrm{Def}}}_{\zeta }(X). \end{aligned}$$

(3.87)

Corollary 3.25

Let $X$ and $E$ be as in Proposition 3.24. The following hold:

• (1) Inclusion (3.87) is an isomorphism.

• (2) Let $C$ be a fiber of the conic vibration $p:E\rightarrow S$. Then

  $$\begin{aligned} \{\alpha \in H^2(X;{\mathbb C})\mid (\alpha ,\zeta )=0\}=\{\alpha \in H^2(X;{\mathbb C})\mid \int \limits _C\alpha =0\}. \end{aligned}$$

  (3.88)

• (3) The restriction map $H^2(X;{\mathbb C})\rightarrow H^2(E;{\mathbb C})$ is an isomorphism.

Proof

Item (1) follows from Item (1) of Proposition 3.24 and upper-semicontinuity of cohomology dimension. Let us prove Item (2). Let $X_t$ be a very generic small deformation of $X$ parametrized by a point of ${{\mathrm{Def}}}_{\zeta }\subset {{\mathrm{Def}}}(X)$ and $\zeta _t\in H^{1,1}_{{\mathbb Z}}(X_t)$ be the class deforming $\zeta$. A non-trivial rational Hodge sub-structure of $H^2(X_t)$ is equal to $\zeta _t^{\bot }$ or to ${\mathbb C}\zeta _t$. On the other hand (3.87) is an isomorphism; thus $X_t$ contains a deformation $E_t$ of $E$ and hence also a deformation $C_t$ of $C$. Clearly $\{\alpha \in H^2(X_t;{\mathbb C})\mid \int _{C_t}\alpha =0\}$ is a rational Hodge sub-structure of $H^2(X_t)$ containing $H^{2,0}(X_t)$ and non-trivial by (3.82); it follows that

$$\begin{aligned} \{\alpha \in H^2(X_t;{\mathbb C})\mid (\alpha ,\zeta _t)=0\}=\{\alpha \in H^2(X_t;{\mathbb C})\mid \int \limits _{C_t}\alpha =0\}. \end{aligned}$$

(3.89)

The kernel of the restriction map $H^2(X_t;{\mathbb C})\rightarrow H^2(E_t;{\mathbb C})$ is a rational Hodge sub-structure $V_t\subset H^2(X_t)$. By (3.82) we know that $\zeta _t\notin V_t$ and since (3.83) is an isomorphism for $q=2$ we know that $H^{2,0}(X_t)\not \subset V_t$; thus $V_t=0$. Parallel transport by the Gauss-Manin connection gives Items (2) and (3). $\square$

We recall that $\iota :E\hookrightarrow X$ is the inclusion. By Items (2) and (3) of Corollary 3.25 we have an isomorphism

$$\begin{aligned} \zeta ^{\bot }&\overset{\sim }{\longrightarrow } \left\{ \beta \in H^2(E;{\mathbb C})\mid \int \limits _C\beta =0\right\} \nonumber \\ \alpha&\longmapsto \iota ^{*}\alpha \end{aligned}$$

(3.90)

On the other hand $p^{*}:H^2(S;{\mathbb C})\rightarrow H^2(E;{\mathbb C})$ defines an isomorphism of $H^2(S;{\mathbb C})$ onto the right hand side of (3.90). Thus (3.90) gives an isomorphism

$$\begin{aligned} r:\zeta ^{\bot } \overset{\sim }{\longrightarrow } H^2(S;{\mathbb C}). \end{aligned}$$

(3.91)

Claim 3.26

Let $X$ and $E$ be as in Proposition 3.24 and let $r$ be as in (3.91). Suppose in addition that the Fujiki constant $c_X$ is equal to $3$ and that $q_X(\zeta )=-2$. Let $\alpha \in \zeta ^{\bot }$. Then

$$\begin{aligned} q_X(\alpha )=\int \limits _S r(\alpha )^2. \end{aligned}$$

(3.92)

Proof

Equality (3.82) gives

$$\begin{aligned} -2 q_X(\alpha )=\frac{c_X}{3} q_X(\zeta ) q_X(\alpha )=\int \limits _X \zeta ^2\wedge \alpha ^2=\int \limits _E\iota ^{*}\zeta \wedge (\iota ^{*}\alpha )^2=-2\int \limits _S r(\alpha )^2. \end{aligned}$$

(3.93)

$\square$

4 The period map and its indeterminacy locus

In the present section we prove Theorem 1.2.

We start with a discussion of the lattice structure on $H^2$ of a deformation of the Hilbert square of a $K3$ and the primitive sublattice with respect to a polarization of square $2$. Then we recall some facts on the period map. In Sect. 4.3 we define the Noether-Lefschetz divisors that enter into the statement of Theorem 1.3.

Our next result is that the period map is regular outside a subset of codimension (at least) $4$ in $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$. A key consequence is that the fiber of the graph of ${\fancyscript{P}}$ over a point of indeterminacy of ${\fancyscript{P}}$ has dimension at least $2$.

In Sect. 4.5 we prove that ${\fancyscript{P}}$ maps the intersection of $\varSigma$ with the regular locus of ${\fancyscript{P}}$ to a dense subset of ${\mathbb S}_2^{\star }$, one of the Noether-Lefschetz divisors defined in Sect. 4.3. The following subsection gives a precise connection between the Hodge structure of $X_A$, for $A$ generic in $\varSigma$, and the periods of the double cover $S_A\rightarrow {\mathbb P}(W)$ branched over $C_{W,A}$.

Lastly we prove Theorem 1.2 by putting together the results of the previous subsection and the fact that the fiber of the graph of ${\fancyscript{P}}$ over a point of indeterminacy of ${\fancyscript{P}}$ has dimension at least $2$.

4.1 Lattices

Let $L$ be an even lattice; we will denote by $(,)$ the bilinear symmetric form on $L$ and for $v\in L$ we let $v^2:=(v,v)$. For a ring $R$ we let $L_{R}:=L\otimes _{{\mathbb Z}} R$ and we let $(,)_{R}$ be the $R$-bilinear symmetric form on $L_R$ obtained from $(,)$ by extension of scalars.

Let $L^{\vee }:={{\mathrm{Hom}}}(L,{\mathbb Z})$. The bilinear form defines an embedding $L\hookrightarrow L^{\vee }$; the quotient $D(L):=L^{\vee }/L$ is the discriminant group of $L$. Let $0\ne v\in L$ be primitive i.e. $L/\langle v\rangle$ is torsion-free. The divisibility of $v$ is the positive generator of $(v,L)$ and is denoted by ${{\mathrm{div}}}(v)$; we let $v^{*}:=v/{{\mathrm{div}}}(v)\in D(L)$.

The group $O(L)$ of isometries of $L$ acts naturally on $D(L)$. The stable orthogonal group is equal to

(4.1)

We let $\mathbf{q}_L:D(L)\rightarrow {\mathbb Q}/2{\mathbb Z}$ and $\mathbf{b}_L:D(L)\times D(L)\rightarrow {\mathbb Q}/{\mathbb Z}$ be the discriminant quadratic form and symmetric bilinear form respectively; see [19]. The following criterion of Eichler will be handy.

Proposition 4.1

(Eichler’s Criterion, Proposition 3.3 of [7]) Let $L$ be an even lattice which contains $U^2$ (the direct sum of two hyperbolic planes). Let $v_1,v_2\in L$ be non-zero and primitive. There exists such that $g v_1=v_2$ if and only if $v_1^2=v_2^2$ and $v_1^{*}=v_2^{*}$.

Let us examine the lattices of interest to us. Let $U_1,U_2,U_3$ be three copies of the hyperbolic plane $U$, let $E_8(-1)$ be the unique unimodular negative definite even lattice of rank $8$ and let $(-2)$ the rank-$1$ lattice with generator of square $(-2)$. Let

(4.2)

If $X$ is a HK manifold deformation equivalent to the Hilbert square of a $K3$ surface, $H^2(X;{\mathbb Z})$, equipped with the Beauville-Bogomolov quadratic form, is isometric to ; see Remark 1 in Section 9 of [2].

A vector in of square $2$ has divisibility $1$; it follows from Proposition 4.1 that any two vectors in of square $2$ are -equivalent and hence the isomorphism class of $v^{\bot }$ for $v^2=2$ is independent of $v$. We choose $v_1\in U_1$ of square $2$ and let $\varLambda :=v_1^{\bot }$. Then

$$\begin{aligned} \varLambda \cong U^2\oplus E_8(-1)^2\oplus (-2)^2. \end{aligned}$$

(4.3)

Thus $\varLambda$ is isometric to the primitive $H^2(X;{\mathbb Z})_{pr}$ of a HK manifold $X$ as above with a polarization of square $2$.

We get an inclusion by associating with the unique which is the identity on ${\mathbb Z}v_1$ and restricts to $g$ on $v_1^{\bot }$ (such a lift exists because ).

The discriminant group and discriminant quadratic form of $\varLambda$ are described as follows. Let $e_1$ be a generator of $v_1^{\bot }\cap U_1$ and let $e_2$ be a generator of the last summand of (4.2):

$$\begin{aligned} {\mathbb Z}e_1=v_1^{\bot }\cap U_1,\qquad {\mathbb Z}e_2=(-2). \end{aligned}$$

(4.4)

Then $-2=e^2_1=e^2_2$, $(e_1,e_2)=0$ and $2={{\mathrm{div}}}_{\varLambda }(e_1)={{\mathrm{div}}}_{\varLambda }(e_2)$, where ${{\mathrm{div}}}_{\varLambda }(e_i)$ is the divisibility of $e_i$ as element of $\varLambda$ (notice that the divisibility of $e_1$ in is $1$, not $2$, while the divisibility of $e_2$ in is $2$, as in $\varLambda$). In particular $e_1/2$ and $e_2/2$ are order-$2$ elements of $D(\varLambda )$. We have an isomorphism

$$\begin{aligned} {\mathbb Z}/(2)\oplus {\mathbb Z}/(2)&\overset{\sim }{\longrightarrow } D(\varLambda ) \nonumber \\ ([x], [y])&\mapsto x(e_1/2)+y (e_2/2) \end{aligned}$$

(4.5)

and the formula

$$\begin{aligned} q_{\varLambda }(x(e_1/2)+y (e_2/2))\equiv -\frac{1}{2}x^2 -\frac{1}{2}y^2 \pmod {2{\mathbb Z}} \end{aligned}$$

(4.6)

In particular we get

(4.7)

4.2 Periods

Let $L$ be an even lattice of signature $(2,n)$. Let

$$\begin{aligned} \varOmega _L:= \{[\sigma ]\in {\mathbb P}(L_{\mathbb C})\mid (\sigma ,\sigma )_{\mathbb C}=0,\quad (\sigma ,\overline{\sigma })_{\mathbb C}>0\}. \end{aligned}$$

(4.8)

(Notice that the isomorphism class of $\varOmega _L$ depends on $n$ only.) Then $\varOmega _L$ is the union of two disjoint bounded symmetric domains of Type IV on which $O(L)$ acts. By Baily and Borel’s fundamental results, the quotient

(4.9)

is quasi-projective.

Remark 4.2

Suppose that $v_0\in L$ has square $2$. The reflection

$$\begin{aligned} L&\overset{R_{v_0}}{\longrightarrow } L \nonumber \\ v&\longmapsto v-(v,v_0) v_0 \end{aligned}$$

(4.10)

belongs to the stable orthogonal group. We claim that $R_{v_0}$ exchanges the two connected components of $\varOmega _L$. In fact let $M\subset L_{{\mathbb R}}$ be a positive definite subspace of maximal dimension (i.e. $2$) containing $v_0$. If $[\sigma ]\in \varOmega _L\cap (M_{{\mathbb C}})$ then $R_{v_0}([\sigma ])=[\overline{\sigma }]$; this proves our claim because conjugation interchanges the two connected components of $\varOmega _L$. It follows that if $L$ contains a vector of square $2$ then ${\mathbb D}_L$ is connected.

Now suppose that $X$ is a $HK$ manifold deformation equivalent to the Hilbert square of a $K3$ and that $h\in H^{1,1}_{{\mathbb Z}}(X)$ has square $2$. Since there is a single -orbit of square-$2$ vectors there exists an isometry

(4.11)

Such an isometry is a marking of $(X,h)$. If $H$ is a divisor on $X$ of square $2$, a marking of $(X,H)$ is a marking of $(X,c_1({\fancyscript{O}}_X(H)))$. Let be the ${\mathbb C}$-linear extension of $\psi$. Since $h$ is of type $(1,1)$, $\psi _{{\mathbb C}}(H^{2,0})\in v_1^{\bot }$. Moreover $\psi _{{\mathbb C}}(H^{2,0})\in \varOmega _{\varLambda }$ because of well-known properties of the Beauville-Bogomolov quadratic form. Any two markings of $(X,h)$ differ by the action of an element of . It follows that the equivalence class

$$\begin{aligned} \Pi (X,h):=[\psi _{{\mathbb C}}H^{2,0}]\in {\mathbb D}_{\varLambda } \end{aligned}$$

(4.12)

is well-defined i.e. independent of the marking; this is the period point of $(X,h)$.

The period map ${\fancyscript{P}}^0:\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0\rightarrow {\mathbb D}_{\varLambda }$ is defined by mapping $A$ to the period $\Pi (X_A,h_A)$ where $h_A=f_A^{*}c_1({\fancyscript{O}}_{Y_A}(1))$—see [8] for a proof that ${\fancyscript{P}}^0$ is a regular map of quasi-projective varieties.

Let $e_1,e_2\in \varLambda$ be as in Sect. 4.1, and let $\iota \in O(\varLambda )$ be the involution characterized by

$$\begin{aligned} \iota (e_1)=e_2,\quad \iota (e_2)=e_1,\quad \iota |_{\{e_1,e_2\}^{\bot }}={{\mathrm{Id}}}_{\{e_1,e_2\}^{\bot }}\,. \end{aligned}$$

(4.13)

Then . Since , the involution $\iota$ induces a non-trivial involution on ${\mathbb D}_{\varLambda }$ which extends to a regular involution

$$\begin{aligned} \overline{\iota }:{\mathbb D}_{\varLambda }^{\text {BB}}\rightarrow {\mathbb D}_{\varLambda }^{\text {BB}}. \end{aligned}$$

(4.14)

In fact $\overline{\iota }$ is the covering involution of the natural finite degree-$2$ map

$$\begin{aligned} {\mathbb D}_{\varLambda }^{\text {BB}}\longrightarrow (O(\varLambda )\backslash \varOmega _{\varLambda })^{\text {BB}}. \end{aligned}$$

(4.15)

The geometric counterpart of $\overline{\iota }$ is given by the involution $\delta :{\mathfrak M}\rightarrow {\mathfrak M}$ induced by the map defined in (3.9). In [21] we proved that

$$\begin{aligned} \overline{\iota }\circ \mathfrak {p}=\mathfrak {p}\circ \delta . \end{aligned}$$

(4.16)

4.3 Roots and Noether-Lefschetz divisors

Let $v_0\in \varLambda$ be primitive and let $v_0^2=-2d\not =0$; then $v_0$ is a root if the reflection

$$\begin{aligned} \varLambda _{{\mathbb Q}}&\overset{R}{\longrightarrow } \varLambda _{{\mathbb Q}} \nonumber \\ v&\longmapsto v+\frac{(v,v_0)v_0}{d} \end{aligned}$$

(4.17)

is integral, i.e. $R(\varLambda )\subset \varLambda$. We record the square of $v_0$ by stating that $v_0$ is a $(-2d)$-root. Notice that if $v_0^2=\pm 2$ then $v_0$ is a root. In particular $e_1$ and $e_2$ are $(-2)$-roots of $\varLambda$. Let

$$\begin{aligned} e_3\in U_2,\qquad e_3^2=-2. \end{aligned}$$

(4.18)

Notice that $e_3\in \varLambda$ and hence it is a $(-2)$-root of $\varLambda$. Since $(e_1+e_2)^2=-4$ and ${{\mathrm{div}}}(e_1+e_2)=2$ we get that $e_1+e_2$ is a $(-4)$-root of $\varLambda$.

Proposition 4.3

The set of negative roots of $\varLambda$ breaks up into $4$ orbits for the action of , namely the orbits of $e_1$, $e_2$, $e_3$ and $e_1+e_2$.

Proof

First let us prove that the orbits of $e_1$, $e_2$, $e_3$ and $(e_1+e_2)$ are pairwise disjoint. Since $-2=e_1^2=e_2^2=e_3^2$ and $(e_1+e_2)^2=-4$, the orbits of $e_1$, $e_2$ and $e_3$ are disjoint from that of $e_1+e_2$. We have ${{\mathrm{div}}}_{\varLambda }(e_3)=1$ and hence $e_3^{*}=0$. Since $e_1^{*}$, $e_2^{*}$ and $e_3^{*}$ are pairwise distinct elements of $D(\varLambda )$ it follows that the orbits of $e_1$, $e_2$, $e_3$ are pairwise disjoint. Now let $v_0\in \varLambda$ be a negative root. Since $D(\varLambda )$ is $2$-torsion, ${{\mathrm{div}}}(v_0)\in \{1,2\}$; it follows that $v_0$ is either a $(-2)$-root or a $(-4)$-root, and in the latter case ${{\mathrm{div}}}(v_0)=2$.

Suppose first that $v_0$ is a $(-2)$-root. If ${{\mathrm{div}}}_{\varLambda }(v_0)=1$ then $v_0^{*}=0$ and hence $v_0$ is in the orbit of $e_3$ by Proposition 4.1. If ${{\mathrm{div}}}_{\varLambda }(v_0)=2$ then $v^{*}\in \{e_1^{*},e_2^{*}\}$ because $q_{\varLambda }(e_1^{*}+ e_2^{*})\equiv -1\not \equiv -1/2\pmod {2{\mathbb Z}}$; it follows from Proposition 4.1 that $v_0$ belongs either to the -orbit of $e_1$ or to that of $e_2$.

Lastly suppose that $v_0$ is a $(-4)$-root. Since ${{\mathrm{div}}}(v_0)=2$ we have $q_{\varLambda }(v_0^{*})=-1$ and hence $v_0^{*}=e_1/2+e_2/2$; it follows from Proposition 4.1 that $v_0$ belongs to the -orbit of $(e_1+e_2)$. $\square$

Let $\kappa :\varOmega _{\varLambda }\rightarrow {\mathbb D}_{\varLambda }$ be the quotient map. Let

$$\begin{aligned}&{\mathbb S}_2':=\kappa ( e_1^{\bot }\cap \varOmega _{\varLambda }),\quad {\mathbb S}_2'':=\kappa ( e_2^{\bot }\cap \varOmega _{\varLambda }),\quad {\mathbb S}_2^{\star }:=\kappa (e_3^{\bot }\cap \varOmega _{\varLambda }),\nonumber \\&\quad {\mathbb S}_4:=\kappa ( (e_1+e_2)^{\bot }\cap \varOmega _{\varLambda }). \end{aligned}$$

(4.19)

The divisors defined above appear also in [4], as ${\fancyscript{D}}_2'$, ${\fancyscript{D}}_2''$, ${\fancyscript{D}}_8$ and ${\fancyscript{D}}_4$ respectively.

Remark 4.4

Let $i\in \{1,2,3\}$; then $e_i^{\bot }\,\cap \,\varOmega _{\varLambda }$ has two connected components—see Remark 4.2. Let $v_0\in U_3$ [we refer to (4.2)] of square $2$. Then $(v_0,e_i)=0$ for $i\in \{1,2,3\}$ and hence the reflection defined in (4.10) exchanges the two connected components of $e_i^{\bot }\cap \varOmega _{\varLambda }$ for $i=1,2,3$ and also the two connected components of $(e_1+e_2)^{\bot }\cap \varOmega _{\varLambda }$ . It follows that each of ${\mathbb S}_2'$, ${\mathbb S}_2''$, ${\mathbb S}_2^{\star }$ and ${\mathbb S}_4$ is a prime divisor in ${\mathbb D}_{\varLambda }$.

Let $\overline{\iota }$ be the involution given by (4.14); then

$$\begin{aligned} \overline{\iota }({\mathbb S}_2^\star ) = {\mathbb S}_2^\star ,\quad \overline{\iota }({\mathbb S}'_2) = {\mathbb S}''_{2},\quad \overline{\iota }({\mathbb S}''_2) = {\mathbb S}'_{2},\quad \overline{\iota }({\mathbb S}_4) = {\mathbb S}_4. \end{aligned}$$

(4.20)

We will describe the normalization of ${\mathbb S}_2^{\star }$ and we will show that it is a finite cover of the period space for $K3$ surfaces of degree $2$. Let $v_3$ be a generator of $e_3^{\bot }\cap U_2$. Let be the orthogonal to $e_3$,

(4.21)

and

$$\begin{aligned} \Gamma :=e_3^{\bot }\cap \varLambda ={\mathbb Z}e_1\oplus {\mathbb Z}v_3\oplus U_3\oplus E_8(-1)^2\oplus {\mathbb Z}e_2\cong (-2)\oplus (2)\oplus U\oplus E_8(-1)^2\oplus (-2).\nonumber \\ \end{aligned}$$

(4.22)

We have $\varOmega _{\Gamma }=e_3^{\bot }\cap \varOmega _{\varLambda }$. Viewing as the subgroup of fixing $e_3$ we get a natural map

$$\begin{aligned} \nu :{\mathbb D}^{\text {BB}}_{\Gamma }\longrightarrow \overline{\mathbb S}_2^{\star }. \end{aligned}$$

(4.23)

Claim 4.5

Map (4.23) is the normalization of ${\mathbb S}_2^{\star }$.

Proof

Since ${\mathbb D}_{\Gamma }^{\text {BB}}$ is normal and $\nu$ is finite, it sufffices to show that $\nu$ has degree $1$. Let $[\sigma ]\in e_3^{\bot }\cap \varOmega _{\varLambda }$ be generic. Let and $[\tau ]=g([\sigma ])$. We must show that there exists such that $[\tau ]=g'([\sigma ])$. Since $[\sigma ]$ is generic we have

$$\begin{aligned} \sigma ^{\bot }\cap \varLambda ={\mathbb Z}e_3. \end{aligned}$$

(4.24)

It follows that $g(e_3)=\pm e_3$. If $g(e_3)= e_3$ then and we are done. Suppose that $g(e_3)=- e_3$. Let $g':=(-1_{\varLambda })\circ g$. Since multiplication by $2$ kills $D(\varLambda )$ we have and hence ; in fact because $g'(e_3)=e_3$. On the other hand $[\tau ]=g'([\sigma ])$ because $-1_{\varLambda }$ acts trivially on $\varOmega _{\varLambda }$. $\square$

Our next task will be to define a finite map from ${\mathbb D}_{\Gamma }^{\text {BB}}$ to the Baily–Borel compactification of the period space for $K3$ surfaces with a polarization of degree $2$. Let

(4.25)

Then is isometric to the K3 lattice i.e. $H^2(K3;{\mathbb Z})$ equipped with the intersection form. Let

(4.26)

Then ${\mathbb D}_\varPhi$ is the period space for $K3$ surfaces with a polarization of degree $2$.

Claim 4.6

The lattice is the unique lattice contained in (with quadratic form equal to the restriction of the quadratic form on ) and containing as a sublattice of index $2$.

Proof

First it is clear that is contained in as a sublattice of index $2$. Now suppose that $L$ is a lattice contained in and containing as a sublattice of index $2$. Then $L$ must be generated by and an isotropic element of ; since there is a unique such element $L$ is unique. $\square$

By Claim 4.6 every isometry of induces an isometry of . It follows that we have well-defined injection . Since $\varOmega _\varLambda =\varOmega _\varPhi$ there is an induced finite map

$$\begin{aligned} \rho :{\mathbb D}^{\text {BB}}_\Gamma \longrightarrow {\mathbb D}^{\text {BB}}_\varPhi . \end{aligned}$$

(4.27)

Remark 4.7

Keep notation as above. Then $\deg \rho =2^{20}-1$.

4.4 First extension of the period map

Proposition 4.8

Let $A_0\in (\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma _{\infty }{\setminus }\varSigma [2])$. Then ${\fancyscript{P}}$ is regular at $A_0$ and ${\fancyscript{P}}(A_0)\in {\mathbb D}_{\varLambda }$.

Proof

Let ${\fancyscript{U}}$ and $\mathbf{L}$ be as in Proposition 3.14. Let $U\subset {\fancyscript{U}}$ be a subset containing $A_0$, open in the classical topology and contractible. Let $U^0:=U\cap \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0$. Let $\overline{A}\in U^0$; thus $X_{\overline{A}}$ is smooth.

By Lemma 3.13 we know that $f_{A}^{-1}\mathbf{L}$ is a smooth surface for every $A\in U^0$. Thus $\pi _1(U^0,\overline{A})$ acts by monodromy on $H^2(f_{\overline{A}}^{-1}\mathbf{L})$ and by Item (a) of Proposition 3.14 the image of the monodromy representation is a finite group.

On the other hand $H_{\overline{A}}$ is an ample divisor on $X_{\overline{A}}$; by the Lefschetz Hyperplane Theorem the homomorphism

$$\begin{aligned} H^2(X_{\overline{A}};{\mathbb Z})\longrightarrow H^2(f_{\overline{A}}^{-1}\mathbf{L};{\mathbb Z}) \end{aligned}$$

(4.28)

is injective. The image of (4.28) is a subgroup of $H^2(f_{\overline{A}}^{-1}\mathbf{L})$ invariant under the monodromy action of $\pi _1(U^0,\overline{A})$. By injectivity of (4.28) the monodromy action of $\pi _1(U^0,\overline{A})$ on $H^2(X_{\overline{A}})$ is finite as well, and hence the restriction of ${\fancyscript{P}}^0$ to $U^0$ extends to a holomorphic map $U\rightarrow {\mathbb D}_{\varLambda }$ by Griffith’s Removable Singularity Theorem (see p. 41 of [6]). Thus ${\fancyscript{P}}^0$ extends regularly in a neighborhood $A_0$ and it goes into ${\mathbb D}_{\varLambda }$. $\square$

Definition 4.9

Let $\widehat{\mathbb {LG}}\left( \bigwedge ^{3} V\right) \subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right) \times {\mathbb D}_{\varLambda }^{\text {BB}}$ be the closure of the graph of the restriction of ${\fancyscript{P}}$ to the set of its regular points and let

$$\begin{aligned} p:\widehat{\mathbb {LG}}\left( \bigwedge ^{3} V\right) \rightarrow \mathbb {LG}\left( {\bigwedge ^{3}} V \right) \end{aligned}$$

(4.29)

be the restriction of projection. Let $\widehat{\varSigma }\subset \widehat{\mathbb {LG}}\left( \bigwedge ^{3} V\right)$ be the proper transform of $\varSigma$.

Corollary 4.10

Keep notation as above. Let $A$ be in the indeterminacy locus of ${\fancyscript{P}}$ and let $p$ be as in (4.29). Then $p^{-1}(A)\cap \widehat{\varSigma }$ has dimension at least $2$.

Proof

Let ${{\mathrm{Ind}}}({\fancyscript{P}})$ be the indeterminacy locus of ${\fancyscript{P}}$. Since $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ is smooth the morphism $p$ identifies $\widehat{\mathbb {LG}}\left( \bigwedge ^{3} V\right)$ with the blow-up of ${{\mathrm{Ind}}}({\fancyscript{P}})$. Hence the exceptional set of $p$ is the support of a Cartier divisor $E$.

By Proposition 4.8 the indeterminacy locus of ${\fancyscript{P}}$ is contained in $\varSigma$ and thus $A\in \varSigma$. It follows that $p^{-1}(A)\cap \widehat{\varSigma }$ is not empty. Since $\widehat{\varSigma }$ is a prime divisor in $\widehat{\mathbb {LG}}\left( \bigwedge ^{3} V\right)$ and $E$ is a Cartier divisor every irreducible component of $E\cap \widehat{\varSigma }$ has codimension $2$ in $\widehat{\mathbb {LG}}\left( \bigwedge ^{3} V\right)$. On the other hand Proposition 4.8, (2.3) and (2.8) give that ${{\mathrm{cod}}}({{\mathrm{Ind}}}({\fancyscript{P}}),\mathbb {LG}\left( {\bigwedge ^{3}} V \right) )\ge 4$ and hence every component of a fiber of $E\cap \widehat{\varSigma }\rightarrow {{\mathrm{Ind}}}({\fancyscript{P}})$ has dimension at least $2$. Since $p^{-1}(A)\cap \widehat{\varSigma }$ is one such fiber we get the corollary. $\square$

4.5 The period map on $\varSigma ^\mathrm{sm}{\setminus }\varDelta$

Let $A_0\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$. By (2.6) and Cor. 2.5.1 of [24] $A_0$ belongs to the GIT-stable locus of $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$. By Luna’s étale slice Theorem [16] it follows that there exists an analytic $\textit{PGL}(V)$-slice at $A_0$, call it $Z_{A_0}$, such that the natural map

$$\begin{aligned} Z_{A_0}/{{\mathrm{Stab}}}(A_0)\rightarrow \mathfrak {M}\end{aligned}$$

(4.30)

is an isomorphism onto an open (classical topology) neighborhood of $[A_0]$. We may assume that $Z_{A_0}\subset {\fancyscript{U}}$ where ${\fancyscript{U}}$ is as in (3.69).

Let where $\phi :{\fancyscript{V}}\rightarrow {\fancyscript{U}}$ is as in (3.70). Then $\phi$ defines a double cover ramified over $\varSigma \cap Z_{A_0}$; if $A\in \varSigma \cap Z_{A_0}$ we will denote by the same letter the unique point in $\phi ^{-1}(A)$. By Proposition 3.20 points of parametrize deformations of $X_A$ for $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0$.

Since $\varSigma$ is smooth at $A_0$ also $\varSigma \cap Z_{A_0}$ is smooth at $A_0$. Thus is smooth at $A_0$. Shrinking $Z_{A_0}$ around $A_0$ if necessary we may assume that is contractible. Hence a marking $\psi$ of defines a marking of for all $A\in Z_{A_0}$; we will denote it by the same letter $\psi$. We have a local period map

(4.31)

Claim 4.11

The local period map of (4.31) defines an isomorphism of a sufficiently small open neighborhood of $A_0$ in onto an open subset of $\varOmega _{\varLambda }$.

Proof

Since is smooth and it suffices to prove that is injective. By Luna’s étale slice Theorem we have an isomorphism of germs

$$\begin{aligned} (Z_{A_0},A_0)\overset{\sim }{\longrightarrow }{{\mathrm{Def}}}(X_{A_0},H_{A_0}) \end{aligned}$$

(4.32)

induced by the local tautological family of double EPW-sextics parametrized by $Z_{A_0}$. By Corollary 3.17 the points of $Z_{A_0}\cap \varSigma$ parametrize deformations of $X_{A_0}$ which are locally trivial at points of $S_A$. Let be the inverse image of $\varSigma \cap Z_{A_0}$ with reduced structure. Let be the germ representing deformations that “leave $\zeta _{A_0}$ of type $(1,1)$”. The natural map of germs

(4.33)

is an inclusion because Map (4.32) is an isomorphism. Notice that by (3.76); since we have

(4.34)

Notice that $\zeta _{A_0}^{\bot }\cap \varOmega _{\varLambda }$ has codimension $1$ and is smooth because $(\zeta _{A_0},\zeta _{A_0})=-2$. By injectivity of the local period map we get injectivity of the period map restricted to :

(4.35)

Since domain and codomain have equal dimensions the above map is a local isomorphism. In particular is injective when restricted to the tangent space to at $A_0$. Thus it will suffice to exhibit a tangent vector such that . By Item (1) of Corollary 3.25 it suffices to prove that $E_{A_0}$ does not lift to $1$-st order in the direction $v$. Let $\varDelta$ be the unit complex disc and be an inclusion with . Let be obtained by base-change from . Let ${\mathbb P}^1$ be an arbitrary fiber of (3.75); then $N_{{\mathbb P}^1}{\fancyscript{X}}_{\varDelta } \cong {\fancyscript{O}}_{{\mathbb P}^1}(-1)\oplus {\fancyscript{O}}_{{\mathbb P}^1}(-1)$. It follows that $E_{A_0}$ does not lift to first order in the direction $v$. This finishes the proof that is injective. $\square$

Proposition 4.12

The restriction of $\mathfrak {p}$ to $(\varSigma ^\mathrm{sm}{\setminus }\varDelta )/\!/ \textit{PGL}(V)$ is a dominant map to ${\mathbb S}_2^{\star }$ with finite fibers. Let $A\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$ and let $\psi$ be a marking of ; then $\psi (\zeta _A)$ is a $(-2)$-root of $\varLambda$ and ${{\mathrm{div}}}(\psi (\zeta _A))=1$.

Proof

Let $A\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$. By Claim 4.11 we get that $[A]$ is an isolated point in the fiber $\mathfrak {p}^{-1}(\mathfrak {p}([A]))$. In particular

$$\begin{aligned} {{\mathrm{cod}}}(\mathfrak {p}((\varSigma ^\mathrm{sm}{\setminus }\varDelta )/\!/ {{\mathrm{PGL}}}(V)),{\mathbb D}_{\varLambda })=1. \end{aligned}$$

(4.36)

By (3.76) and (3.77) $\psi (\zeta _A)$ is a $(-2)$-root of $\varLambda$. By (4.34) and Proposition 4.3 we get

$$\begin{aligned} \mathfrak {p}((\varSigma ^\mathrm{sm}{\setminus }\varDelta )/\!/ {{\mathrm{PGL}}}(V))\subset {\mathbb S}_2^{\star }\cup {\mathbb S}'_2\cup {\mathbb S}''_2. \end{aligned}$$

(4.37)

By (4.36) and irreducibility of $\varSigma$ the left hand side of (4.37) is dense in one of ${\mathbb S}_2^{\star }$, ${\mathbb S}'_2$, ${\mathbb S}''_2$. Let $\delta _V$ be as in (3.9), let $\delta :\mathfrak {M}\rightarrow \mathfrak {M}$ be the induced involution, and let $\overline{\iota }:{\mathbb D}_{\varLambda }^{\text {BB}}\rightarrow {\mathbb D}_{\varLambda }^{\text {BB}}$ be the involution given by (4.14)). Then $\mathfrak {N}=(\varSigma /\!/ {{\mathrm{PGL}}}(V))$ is mapped to itself by $\delta$ and hence $\overline{\iota }$ maps $\mathfrak {p}(\mathfrak {N})$ to itself by (4.16). By (4.20) it follows that $\mathfrak {p}$ maps $(\varSigma ^\mathrm{sm}{\setminus }\varDelta )/\!/ \textit{PGL}(V)$ into ${\mathbb S}_2^{\star }$ and thus ${{\mathrm{div}}}(\psi (\zeta _A))=1$. $\square$

Remark 4.13

The restriction of $\mathfrak {p}$ to $\mathfrak {N}$ is, by Proposition 4.12, a map $\mathfrak {N}\dashrightarrow {\mathbb S}_2^{\star }$ of finite degree. Since $\mathfrak {p}$ is birational (by Global Torelli) and ${\mathbb D}_{\varLambda }^{\text {BB}}$ is normal it follows that $\mathfrak {p}|_{\mathfrak {N}}$ is a birational map $\mathfrak {N}\dashrightarrow {\mathbb S}_2^{\star }$.

Actually one can prove this without resorting to the general Global Torelli Theorem: the key elements are the computation of the degree of the map $\rho$ of (4.27) and the geometric interpretation of $\rho$ provided by commutativity of (4.51)—this argument is the analogue of the proof, given by Voisin [29], of the Global Torelli Theorem for cubic fourfolds containing a plane.

The following picture summarizes Proposition 4.12.

(4.38)

4.6 Periods of $K3$ surfaces of degree $2$

We recall results of Shah on the period map for double covers of ${\mathbb P}^2$ branched over a sextic curve. Set $\mathfrak {C}_6:=|{\fancyscript{O}}_{{\mathbb P}^2}(6)|/\!/ \textit{PGL}_3$ and let $\varPhi$ be the lattice given by (4.26). There is a period map

$$\begin{aligned} \mathfrak {s}:\mathfrak {C}_6 \dashrightarrow {\mathbb D}_{\varPhi }^{\text {BB}} \end{aligned}$$

(4.39)

whose restriction to the open set parametrizing smooth sextics is defined as follows. Let $C$ be a smooth plane sextic and let $f:S\rightarrow {\mathbb P}^2$ be the double cover branched over $C$. Then (4.39) maps the orbit of $C$ to the period point of the polarized $K3$ surface $(S,f^{*}{\fancyscript{O}}_{{\mathbb P}^2}(1))$. Shah [26] determined the “boundary”and the indeterminacy locus of the above map. In order to state Shah’ results we recall a definition.

Definition 4.14

A curve $C\subset {\mathbb P}^2$ has a simple singularity at $p\in C$ if and only if the following hold:

• (i) $C$ is reduced in a neighborhood of $p$.

• (ii) ${{\mathrm{mult}}}_p(C)\le 3$ and if equality holds $C$ does not have a consecutive triple point at $p$.²

Remark 4.15

Let $C\subset {\mathbb P}^2$ be a sextic curve. Then $C$ has simple singularities if and only if the double cover $S\rightarrow {\mathbb P}^2$ branched over $C$ is a normal surface with DuVal singularities or equivalently the minimal desingularization of $S$ is a $K3$ surface (with A-D-E curves lying over the singularities of $S$); see Theorem 7.1 of [1].

Let $C\subset {\mathbb P}^2$ be a sextic curve with simple singularities. Then $C$ is $\textit{PGL}_3$-stable by [26]. We let

$$\begin{aligned} \mathfrak {C}^{\textit{ADE}}_6:=\{C\in |{\fancyscript{O}}_{{\mathbb P}^2}(6)| \mid \text {C has simple singularities}\}/\!/ \textit{PGL}_3. \end{aligned}$$

(4.40)

Let $C$ be a plane sextic. If $C$ has simple singularities the period map (4.39) is regular at $C$ and takes value in ${\mathbb D}_{\varPhi }$—see Remark 4.15. More generally Shah [26] proved that (4.39) is regular at $C$ if and only if $C$ is $\textit{PGL}_3$-semistable and the unique closed orbit in $\overline{\textit{PGL}_3 C}\cap |{\fancyscript{O}}_{{\mathbb P}^2}(6)|^{\text {ss}}$ is not that of triple (smooth) conics.

Definition 4.16

Let $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{\textit{ADE}}\subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ be the set of $A$ such that $C_{W,A}$ is a curve with simple singularities for every $W\in \varTheta _A$. Let $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{ILS}\subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ be the set of $A$ such that the period map (4.39) is regular at $C_{W,A}$ for every $W\in \varTheta _A$.

Notice that both $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{\textit{ADE}}$ and $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{ILS}$ are open. We have inclusions

$$\begin{aligned} (\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )\subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{\textit{ADE}}\subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{ILS}. \end{aligned}$$

(4.41)

The reason for the superscript $ILS$ is the following: a curve $C\in |{\fancyscript{O}}_{{\mathbb P}(W)}(6)|$ is in the regular locus of the period map (1.8) if and only if the double cover of ${\mathbb P}(W)$ branched over $C$ has Insignificant Limit Singularities in the terminology of Mumford; see [27].

Definition 4.17

Let $\varSigma ^{ILS}:=\varSigma \cap \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{ILS}$. Let be the inverse image of $\varSigma ^{ILS}$ by the forgetful map , and set

$$\begin{aligned} \widehat{\varSigma }^{ILS}:=(p|_{\widehat{\varSigma }})^{-1}(\varSigma ^{ILS})\subset \widehat{\varSigma }, \end{aligned}$$

(4.42)

where $p:\widehat{\mathbb {LG}\left( {\bigwedge ^{3}} V \right) }\rightarrow \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ and $\widehat{\varSigma }$ are as in Definition 4.9.

4.7 The period map on $\varSigma$ and periods of $K3$ surfaces

Let

(4.43)

be the forgetful map. Let $A\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$; then $\varTheta _A$ is a singleton by (2.6) and if $W$ is the unique element of $\varTheta _A$ then $C_{W,A}$ is a smooth sextic by Item (3) of Corollary 3.17. It follows that $(\varSigma ^\mathrm{sm}{\setminus }\varDelta )\subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{ILS}$ and $\tau$ defines an isomorphism $\tau ^{-1}(\varSigma ^\mathrm{sm}{\setminus }\varDelta )\rightarrow \varSigma ^\mathrm{sm}{\setminus }\varDelta$. Thus we may regard $\varSigma ^\mathrm{sm}{\setminus }\varDelta$ as an (open dense) subset of :

(4.44)

By definition of we have a regular map

(4.45)

where $D_{W,A}$ is the pull-back to $S_{W,A}$ of ${\fancyscript{O}}_{{\mathbb P}(W)}(1)$ and $\Pi (S_{W,A},D_{W,A})$ is the (extended) period point of $(S_{W,A},D_{W,A})$. Recall that we have defined a finite map $\rho :{\mathbb D}^{\text {BB}}_{\Gamma }\rightarrow {\mathbb D}^{\text {BB}}_{\varPhi }$ [see (4.27)] and that there is a natural map $\nu :{\mathbb D}^{\text {BB}}_{\Gamma }\rightarrow \overline{\mathbb S}_2^{\star }$ which is the normalization of $\overline{\mathbb S}_2^{\star }$; see (4.23).

Proposition 4.18

There exists a regular map

(4.46)

such that $\rho \circ Q=q$. Moreover the composition $\nu \circ (Q|_{(\varSigma ^\mathrm{sm}{\setminus }\varDelta )})$ is equal to the restriction of the period map ${\fancyscript{P}}$ to $\varSigma ^\mathrm{sm}{\setminus }\varDelta$.

Proof

By Proposition 4.12 the restriction of the period map to $\varSigma ^\mathrm{sm}{\setminus }\varDelta$ is a dominant map to $\overline{\mathbb S}_2^{\star }$ and therefore it lifts to the normalization of $\overline{\mathbb S}_2^{\star }$:

(4.47)

We claim that

$$\begin{aligned} \rho \circ Q_0=q|_{\varSigma ^\mathrm{sm}{\setminus }\varDelta }. \end{aligned}$$

(4.48)

In fact let $A\in \varSigma ^\mathrm{sm}{\setminus }\varDelta$. Let $r:\zeta _A^{\bot }\rightarrow H^2(S_A;{\mathbb C})$ be the isomorphism given by (3.91). Let us prove that

(4.49)

In fact $r$ is a homomorphism of lattices by Claim 3.26. Since $H^2(S_A;{\mathbb Z})$ and have the same rank it follows that is of finite index in $H^2(S_A;{\mathbb Z})$; let $d$ be the the index. By the last clause of Proposition 4.12 the lattice is isometric to —see (4.21). Hence we have

(4.50)

Equation (4.49) follows at once.

Next let be a marking of . By the last clause of Proposition 4.12 we know that $\psi (\zeta _A)$ is a $(-2)$-root of $\varLambda$ of divisibility $1$. By Proposition 4.3 there exists such that $g\circ \psi (\zeta _A)=e_3$. Let $\phi :=g\circ \psi$. Then $\phi$ is a new marking of and $\phi (\zeta _A)=e_3$. It follows that . Let be the ${\mathbb Q}$-linear extension of $\phi$. By (4.49) $H^2(S_A;{\mathbb Z})$ is an overlattice of and hence it may be emebedded canonically into ; thus $\phi _{\mathbb Q}(H^2(S_A;{\mathbb Z}))$ makes sense. By (4.49) $\phi _{\mathbb Q}(H^2(S_A;{\mathbb Z}))$ is an overlattice of and that has index $2$ in $\phi _{\mathbb Q}(H^2(S_A;{\mathbb Z}))$. By Claim 4.6 it follows that . Equation (4.48) follows at once from this. By (4.48) we have a commutative diagram

(4.51)

where $\iota$ is the inclusion map (4.44). Let ${\fancyscript{Z}}$ be the closure of ${{\mathrm{im}}}(\iota ,Q_0)$. Then ${\fancyscript{Z}}$ is an irreducible component of because $\iota$ is an open inclusion. The natural projection is a finite birational map and hence it is an isomorphism because is smooth. We define the map as the composition of the inverse and the projection ${\fancyscript{Z}}\rightarrow {\mathbb D}_{\Gamma }^{\text {BB}}$. The properties of $Q$ stated in the proposition hold by commutativity of (4.51). $\square$

Corollary 4.19

The image of the map is equal to $\widehat{\varSigma }^{ILS}$.

Proof

Let $p:\widehat{\mathbb {LG}\left( {\bigwedge ^{3}} V \right) }\rightarrow \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ be as in Definition 4.9. Since ${\fancyscript{P}}$ is regular on $\varSigma ^\mathrm{sm}{\setminus } \varDelta$, the map $p^{-1}(\varSigma ^\mathrm{sm}{\setminus } \varDelta )\rightarrow \varSigma ^\mathrm{sm}{\setminus } \varDelta$ is an isomorphism and $p^{-1}(\varSigma ^\mathrm{sm}{\setminus } \varDelta )$ is an open dense subset of $\widehat{\varSigma }^{ILS}$ (recall that $\varSigma$ is irreducible and hence so is $\widehat{\varSigma }$). By the second clause of Proposition 4.18 we have

$$\begin{aligned} (\tau ,\nu \circ Q)(\varSigma ^\mathrm{sm}{\setminus } \varDelta )= p^{-1}(\varSigma ^\mathrm{sm}{\setminus } \varDelta ). \end{aligned}$$

(4.52)

Since $\widehat{\varSigma }$ is closed in $\widehat{\mathbb {LG}}\left( \bigwedge ^{3} V\right) \times {\mathbb D}_{\varLambda }^{\text {BB}}$ it follows that ${{\mathrm{im}}}(\tau ,\nu \circ Q)\subset \widehat{\varSigma }$. Thus we have a commutative diagram

(4.53)

and in particular ${{\mathrm{im}}}(\tau ,\nu \circ Q)\subset \widehat{\varSigma }^{ILS}$. The right hand side of (4.52) is dense in $\widehat{\varSigma }^{ILS}$; thus in order to finish the proof it suffices to show that ${{\mathrm{im}}}(\tau ,\nu \circ Q)$ is closed in $\widehat{\varSigma }^{ILS}$. The equality $(p|_{\widehat{\varSigma }^{ILS}})\circ (\tau ,\nu \circ Q)=\tau$ and properness of $\tau$ give that $(\tau ,\nu \circ Q)$ is proper (see Ch. II, Cor. 4.8, Item (e) of [9]) and hence closed; thus ${{\mathrm{im}}}(\tau ,\nu \circ Q)$ is closed in $\widehat{\varSigma }^{ILS}$. $\square$

4.8 Extension of the period map away from $\mathfrak {I}$

Proposition 4.20

Let $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{ILS}$. If $\dim \varTheta _A\le 1$ the period map ${\fancyscript{P}}$ is regular at $A$ and moreover ${\fancyscript{P}}(A)\in {\mathbb D}_\varLambda$ if and only if $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^{\textit{ADE}}$.

Proof

If $A\notin \varSigma$ then ${\fancyscript{P}}$ is regular at $A$ by Proposition 4.8. Now assume that $A\in \varSigma ^{ILS}$ and suppose that ${\fancyscript{P}}$ is not regular at $A$; we will reach a contradiction. Let $p:\widehat{\mathbb {LG}}\left( \bigwedge ^{3} V\right) \rightarrow \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ be as in Definition 4.9. Then $p^{-1}(A)\cap \widehat{\varSigma }$ is a subset of $\{A\}\times {\mathbb D}^{\text {BB}}_{\varLambda }$ and hence we may identify it with its projection in ${\mathbb D}^{\text {BB}}_{\varLambda }$. This subset is equal to $\nu \circ Q(\tau ^{-1}(A))$ by Corollary 4.19 and Commutative Diagram (4.53). On the other hand $\tau ^{-1}(A)=\varTheta _A$ and hence $\dim \tau ^{-1}(A)\le 1$ by hypothesis; it follows that $\dim p^{-1}(A)\le 1$ and this contradicts Corollary 4.10. This proves that ${\fancyscript{P}}$ is regular at $A$. The last clause of the proposition follows from Corollary 4.19. $\square$

Proof of Theorem 1.2

Let $x\in (\mathfrak {M}{\setminus }\mathfrak {I})$. There exists a GIT-semistable $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ representing $x$ with ${{\mathrm{PGL}}}(V)$-orbit closed in the semistable locus $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^\mathrm{ss}$, and such an $A$ is determined up to the action of ${{\mathrm{PGL}}}(V)$. By Luna’s étale slice Theorem [16] it suffices to prove that the period map ${\fancyscript{P}}$ is regular at $A$.

If $A\notin \varSigma$ then ${\fancyscript{P}}$ is regular at $A$ and ${\fancyscript{P}}(A)\in {\mathbb D}_{\varLambda }$ by Proposition 4.8. Now suppose that $A\in \varSigma$. Then $A\in \varSigma ^{ILS}$ because $x\notin \mathfrak {I}$. By Proposition 4.20 in order to prove that ${\fancyscript{P}}$ is regular at $A$ it will suffice to show that $\dim \varTheta _A\le 1$.

Suppose that $\dim \varTheta _A\ge 2$. Theorem 3.26 and Theorem 3.36 of [22] give that $A$ belongs to certain subsets of $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$, namely ${\mathbb X}_{{\fancyscript{A}}_{+}},{\mathbb X}_{{\fancyscript{A}}^{\vee }_{+}},\dots ,{\mathbb X}_{+}$ (notice the misprint in the statement of Theorem 3.36; ${\mathbb X}_{{\fancyscript{D}}}$ is to be replaced by ${\mathbb X}_{{\fancyscript{D}},+}$). Thus, unless

$$\begin{aligned} A\in {\mathbb X}_{{\fancyscript{Y}}}\cup {\mathbb X}_{{\fancyscript{W}}}\cup {\mathbb X}_{h}\cup {\mathbb X}_{k}, \end{aligned}$$

(4.54)

(notice that ${\mathbb X}_{+} \subset {\mathbb X}_{{\fancyscript{W}}}$) the Lagrangian $A$ belongs to one of the standard unstable strata listed in Table 2 of [24], and hence is ${{\mathrm{PGL}}}(V)$-unstable. This is a contradiction because $A$ is semistable, and hence we conclude that (4.54) holds.

If $A\in {\mathbb X}_{{\fancyscript{Y}}}$ then $A$ is ${{\mathrm{PGL}}}(V)$-equivalent to $A_{+}$ by Proposition 4.4.7 of [24]. Thus $A\in {{\mathrm{PGL}}}_6 A_{+}$ because $A$ has minimal ${{\mathrm{PGL}}}(V)$-orbit, and therefore $A\in {\mathbb X}_{{\fancyscript{W}}}$. Hence we may assume that $A\in {\mathbb X}_{{\fancyscript{W}}}\cup {\mathbb X}_{h}\cup {\mathbb X}_{k}$. If $A\in {\mathbb X}_{{\fancyscript{W}}}$ then $A\notin \varSigma ^{ILS}$ by Claim 4.4.5 of [24], if $A\in {\mathbb X}_{h}$ then $A\notin \varSigma ^{ILS}$ by (4.5.6) of [24], if $A\in {\mathbb X}_{k}$ then $A\notin \varSigma ^{ILS}$ by (4.5.5) of [24]; this is a contradiction. This shows that $\dim \varTheta _A\le 1$ and hence $\mathfrak {p}$ is regular at $x$. By the last clause of Proposition 4.20, $\mathfrak {p}(x)\in {\mathbb D}_{\varLambda }$ if and only if $x\in \mathfrak {M}^{\textit{ADE}}$. $\square$

5 On the image of the period map

We will prove Theorem 1.3. We start by describing periods of $X_A$ for $A\in \varDelta {\setminus }\varSigma$, and by describing families of (quasi)polarized HK fourfolds $(X,H)$ whose periods fill out dense subsets of ${\mathbb S}''_2$ and of ${\mathbb S}_4$. In each of these families $H$ is either not ample, or is ample but the map $X\dashrightarrow |H|^{\vee }$ is not of degree $2$ onto its image.

Next we prove that $\mathfrak {p}(\mathfrak {M}{\setminus }\mathfrak {N})$ does not intersect ${\mathbb S}^{\star }_2\cup {\mathbb S}'_2\cup {\mathbb S}''_2\cup {\mathbb S}_4$; the point is that the results mentioned above, together with Global Torelli, prove that an element of ${\mathbb S}^{\star }_2\cup {\mathbb S}'_2\cup {\mathbb S}''_2\cup {\mathbb S}_4$ cannot be the period of a smooth double EPW-sextic.

In the last subsection we prove that $\mathfrak {p}$ defines an open embedding of $\mathfrak {M}{\setminus }\mathfrak {N}$ into ${\mathbb D}_{\varLambda }$.

5.1 Double EPW-sextics parametrized by $\varDelta$ and their periods

Let $S$ be a $K3$ surface. We recall [2] the description of $H^2(S^{[2]})$ and the Beauville-Bogomolov form $q_{S^{[2]}}$. Let $\mu :H^2(S)\rightarrow H^2(S^{[2]})$ be the composition of the symmetrization map $H^2(S)\rightarrow H^2(S^{(2)})$ and the pull-back map $H^2(S^{(2)})\rightarrow H^2(S^{[2]})$. There is a direct sum decomposition

$$\begin{aligned} H^2(S^{[2]})=\mu (H^2(S;{\mathbb Z}))\oplus {\mathbb Z}\xi \end{aligned}$$

(5.1)

where $2\xi$ is represented by the locus parametrizing non-reduced subschemes. Moreover $\mu$ is an isometric embedding, Decomposition (5.1) is orthogonal, and $q_{S^{[2]}}(\xi )=-2$, provided $H^2(S)$ and $H^2(S^{[2]})$ are equipped with the intersection form and Beauville-Bogomolov quadratic form $q_{S^{[2]}}$ respectively.

Now let $A\in \varDelta {\setminus }\varSigma$ be generic. By Theorem 4.15 of [23] there exist a projective $K3$ surface $S_A$ of genus $6$ and a small contraction $S_A^{[2]}\rightarrow X_A$. Moreover the period point ${\fancyscript{P}}(A)$ may be identified with the Hodge structure of $S_A^{[2]}$ as follows. The surface $S_A$ comes equipped with an ample divisor $D_A$ of genus $6$ i.e. $D_A\cdot D_A=10$, let $d_A$ be the Poincaré dual of $D_A$. Then ${\fancyscript{P}}(A)$ is identified with the Hodge structure on $(\mu (D_A)-2\xi )^{\bot }$, where $\xi$ is as above.

We recall that $\delta _V:\mathbb {LG}\left( {\bigwedge ^{3}} V \right) \overset{\sim }{\longrightarrow }\mathbb {LG}\left( {\bigwedge ^{3}} V^{\vee }\right)$ is defined by $\delta _V(A):=A^{\bot }$; see (3.9).

Proposition 5.1

Neither ${\fancyscript{P}}(\varDelta {\setminus }\varSigma )$ nor ${\fancyscript{P}}(\delta _V(\varDelta ){\setminus }\varSigma )$ is contained in ${\mathbb S}_2^{\star }\cup {\mathbb S}'_2\cup {\mathbb S}''_2\cup {\mathbb S}_4$.

Proof

Let $A\in \varDelta {\setminus }\varSigma$ be very general, and let $(S_A,D_A)$ be as above. By Proposition 4.14 of [23], $(S_A,D_A)$ is a very general polarized $K3$ surface of genus $6$, and hence we may assume that $H^{1,1}_{{\mathbb Z}}(S_A)={\mathbb Z}d_A$. It follows that

$$\begin{aligned} H^{1,1}_{{\mathbb Z}}(S_A^{[2]})\cap (\mu (d_A)-2\xi )^{\bot }={\mathbb Z}(2\mu (d_A)-5\xi ). \end{aligned}$$

(5.2)

Now suppose that ${\fancyscript{P}}(A)\in ({\mathbb S}_2^{\star }\cup {\mathbb S}'_2\cup {\mathbb S}''_2\cup {\mathbb S}_4)$. By definition there exists $\alpha \in H^{1,1}_{{\mathbb Z}}(S_A^{[2]})\cap (\mu (d_A)-2\xi )^{\bot }$ of square $(-2)$ or $(-4)$; since $q_{S^{[2]}_A}(2\mu (d_A)-5\xi )=-10$ that contradicts (5.2). This proves that ${\fancyscript{P}}(\varDelta {\setminus }\varSigma )$ is not contained in ${\mathbb S}_2^{\star }\cup {\mathbb S}'_2\cup {\mathbb S}''_2\cup {\mathbb S}_4$.

Next suppose that ${\fancyscript{P}}(\delta _V(\varDelta ){\setminus }\varSigma )$ is contained in ${\mathbb S}_2^{\star }\cup {\mathbb S}'_2\cup {\mathbb S}''_2\cup {\mathbb S}_4$. Let $\overline{\iota }:{\mathbb D}_{\varLambda }^{\text {BB}}\rightarrow {\mathbb D}_{\varLambda }^{\text {BB}}$ be the involution defined by $\iota$; see (4.14). By (4.20), $\overline{\iota }$ maps ${\mathbb S}_2^{\star }\cup {\mathbb S}'_2\cup {\mathbb S}''_2\cup {\mathbb S}_4$ to itself; since $\mathfrak {p}\circ \delta _V=\overline{\iota }\circ \mathfrak {p}$ [see (4.16)] it follows that ${\fancyscript{P}}(\varDelta {\setminus }\varSigma )$ is contained in ${\mathbb S}_2^{\star }\cup {\mathbb S}'_2\cup {\mathbb S}''_2\cup {\mathbb S}_4$. This contradicts the result proved above, hence ${\fancyscript{P}}(\delta _V(\varDelta ){\setminus }\varSigma )$ is not contained in ${\mathbb S}_2^{\star }\cup {\mathbb S}'_2\cup {\mathbb S}''_2\cup {\mathbb S}_4$. $\square$

5.2 Quasi-polarized fourfolds whose periods are in ${\mathbb S}''_2$ or ${\mathbb S}'_2$

Let $U$ be a $3$-dimensional complex vector space and $\pi :S\rightarrow {\mathbb P}(U)$ a double cover branched over a smooth sextic curve; thus $S$ is a $K3$ surface. Let $D\in |\pi ^{*}{\fancyscript{O}}_S(1)|$ and $d\in H^{1,1}_{{\mathbb Z}}(S;{\mathbb Z})$ be its Poincaré dual. Since $S^{[2]}$ is simply connected there is a unique class $\mu (D)\in {{\mathrm{Pic}}}(S^{[2]})$ whose first Chern class is equal to $\mu (d)$.

One easily checks the following facts. There is a natural isomorphism

$$\begin{aligned} {\mathbb P}({{\mathrm{S}}}^2 U^{\vee }) \overset{\sim }{\longrightarrow } |\mu (D)| \end{aligned}$$

(5.3)

and the composition of the natural maps

$$\begin{aligned} S^{[2]}\longrightarrow S^{(2)}\longrightarrow {\mathbb P}(U)^{(2)}\longrightarrow {\mathbb P}({{\mathrm{S}}}^2 U) \end{aligned}$$

(5.4)

is identified with the natural map $f:S^{[2]}\rightarrow |\mu (D)|^{\vee }$. The image of $f$ is the chordal variety ${\fancyscript{V}}_2$ of the Veronese surface $\{[u^2] \mid 0\not =u\in U\}$, and the map $S^{[2]}\rightarrow {\fancyscript{V}}_2$ is finite of degree $4$.

Since $\mu (d)$ has square $2$ we have a well-defined period point $\Pi (S^{[2]},\mu (d))\in {\mathbb D}_{\varLambda }$. The class $\xi \in H^{1,1}_{{\mathbb Z}}(S^{[2]})$ is a $(-2)$-root of divisibility $2$ and it is orthogonal to $\mu (d)$; it follows that $\Pi (S^{[2]},\mu (d))\in ({\mathbb S}'_2\cup {\mathbb S}''_2)$. Actually $\Pi (S^{[2]},\mu (d))\in {\mathbb S}''_2$ because the divisibility of $\xi$ as an element of $H^2(S^{[2]};{\mathbb Z})$ is equal to $2$ (and not only as element of $\mu (d)^{\bot }$). The periods $\Pi (S^{[2]},\mu (d))$ with $S$ as above fill-out an open dense subset of ${\mathbb S}''_2$.

Let us also describe polarized HK fourfolds whose periods fill out a dense subset of ${\mathbb S}'_2$, although this is not needed for what follows. Let $\pi :S\rightarrow {\mathbb P}(U)$ and let $D$, $d$ be as above. Let $v\in H^{*}(S;{\mathbb Z})$ be the Mukai vector $v:=(0,d,0)$ and let ${\fancyscript{M}}_v(S)$ be the corresponding moduli space of $D$-semistable sheaves on $S$ with Mukai vector $v$. The generic sheaf parametrized by ${\fancyscript{M}}_v(S)$ is isomorphic to $\iota _{*}\eta$ where $\iota :C\hookrightarrow S$ is the inclusion of a smooth $C\in |D|$ and $\eta$ is an invertible sheaf on $C$ of degree $1$. Then ${\fancyscript{M}}_v(S)$ is a hyperkähler variety deformation equivalent to $K3^{[2]}$. Moreover $H^2({\fancyscript{M}}_v(S))$ with its Hodge structure and B-B form is identified with $v^{\bot }$ with the Hodge structure it inherits from the Hodge structure of $H^{*}(S)$ and the quadratic form given by the Mukai pairing; see [28]. Let $h\in H^2({\fancyscript{M}}_v(S))$ correspond to $\pm (1,0,-1)$. Then $h$ has square $2$ and, as is easily checked, the period point of $({\fancyscript{M}}_v(S),h)$ belongs to ${\mathbb S}'_2$; more precisely $\Pi ({\fancyscript{M}}_v(S),h)=\overline{\iota }(\Pi (S^{[2]},\mu (d)))$.

5.3 Polarized fourfolds whose periods are in ${\mathbb S}_4$

Let $S\subset {\mathbb P}^3$ be a smooth quartic surface, let $D\in |{\fancyscript{O}}_S(1)|$ and let $d$ be the Poincaré dual of $D$. We have a natural map

$$\begin{aligned} S^{[2]}&\overset{f}{\longrightarrow } \mathrm {Gr}(1,{\mathbb P}^3)\subset {\mathbb P}^5 \nonumber \\ Z&\longmapsto \langle Z\rangle \end{aligned}$$

(5.5)

where $\langle Z\rangle$ is the unique line containing the length-$2$ scheme $Z$. Let $H\in |f^{*}{\fancyscript{O}}_{{\mathbb P}^5}(1)|$ and $h$ be its Poincaré dual. One checks easily that $h=(\mu (d)-\xi )$, in particular $q_{S^{[2]}}(h)=2$. Moreover pull-back gives an identification of $f$ with the natural map $S^{[2]}\rightarrow | H|^{\vee }$. We have

$$\begin{aligned} (h,\mu (d)-2\xi )_{S^{[2]}}=0,\qquad q_{S^{[2]}}(\mu (d)-2\xi )=-4,\qquad (h^{\bot },\mu (d)-2\xi )_{S^{[2]}}=2{\mathbb Z}. \end{aligned}$$

(5.6)

Thus $(\mu (d)-2\xi )$ is a $(-4)$-root of $h^{\bot }$ and hence $\Pi (S^{[2]},h)\in {\mathbb S}_4$ by Proposition 4.3. The generic point of ${\mathbb S}_4$ is equal to $\Pi (S^{[2]},h)$ for some $(S,d)$ as above because ${\mathbb S}_4$ is irreducible (see Remark 4.4), of dimension $19$ i.e. the dimension of the set of periods $\Pi (S^{[2]},h)$ for $(S,d)$ as above.

5.4 Proof that ${\fancyscript{P}}(\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )\cap {\mathbb S}_2^{\star }$ is empty

Suppose that ${\fancyscript{P}}(\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )\cap {\mathbb S}_2^{\star }$ is nonempty. Since ${\mathbb S}_2^{\star }$ is a ${\mathbb Q}$-Cartier divisor of ${\mathbb D}_{\varLambda }$ it follows that ${\fancyscript{P}}^{-1}({\mathbb S}_2^{\star })\cap (\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )$ has pure codimension $1$; let $C$ be one of its irreducible components. Then $C\not =\varDelta$ by Proposition 5.1 and hence $C^0:=C{\setminus }\varDelta$ is a codimension-$1$ ${{\mathrm{PGL}}}(V)$-invariant closed subset of $(\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )$.

Since $C^0$ has pure codimension $1$ and is contained in the stable locus of $\mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ (see Cor. 2.5.1 of [24]) the quotient $C^0/\!/{{\mathrm{PGL}}}(V)$ has codimension $1$ in $\mathfrak {M}$. If $A\in (C^0{\setminus }\varDelta )$ then $X_A$ is smooth and hence the local period map ${{\mathrm{Def}}}(X_A,H_A)\rightarrow \varOmega _{\varLambda }$ is a (local) isomorphism (local Torelli for HK manifolds); it follows that the restriction of $\mathfrak {p}$ to $C^0/\!/{{\mathrm{PGL}}}(V)$ has finite fibers and hence ${\fancyscript{P}}(C^0)$ is dense in ${\mathbb S}_2^{\star }$.

Now consider the period map $\mathfrak {p}:(\mathfrak {M}{\setminus }\mathfrak {I})\rightarrow {\mathbb D}^{\text {BB}}_{\varLambda }$; it is birational by Verbitsky’s Global Torelli and Markman’s monodromy results (see Theorem 1.3 and Lemma 9.2 of [17]). We have proved that there are (at least) two distinct components in $\mathfrak {p}^{-1}(\overline{\mathbb S}_2^{\star })$ which are mapped dominantly to $\overline{\mathbb S}_2^{\star }$ by $\mathfrak {p}$, namely $(\varSigma /\!/{{\mathrm{PGL}}}(V)){\setminus }\mathfrak {I}$ and the closure of $C^0/\!/{{\mathrm{PGL}}}(V)$; that is a contradiction because ${\mathbb D}^{\text {BB}}_{\varLambda }$ is normal. $\square$

5.5 Proof that ${\fancyscript{P}}(\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )\cap ({\mathbb S}'_2\cup {\mathbb S}''_2)$ is empty

First we will prove that ${\fancyscript{P}}(\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )\cap {\mathbb S}''_2$ is empty. Suppose that there exists $A\in (\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )$ such that ${\fancyscript{P}}(A)\in {\mathbb S}''_2$. Since ${\mathbb S}''_2$ is a ${\mathbb Q}$-Cartier divisor of ${\mathbb D}_{\varLambda }$ it follows that ${\fancyscript{P}}^{-1}({\mathbb S}''_2)\cap (\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )$ has pure codimension $1$; let $C$ be one of its irreducible components.

By Proposition 5.1 $C^0:=C{\setminus }\varDelta$ is a codimension-$1$ subset of $\mathbb {LG}\left( {\bigwedge ^{3}} V \right) ^0$ and hence ${\fancyscript{P}}(C^0)$ contains an open dense subset of ${\mathbb S}''_2$. By Sect. 5.2, there exist $A\in C^0$ and a double cover $\pi :S\rightarrow {\mathbb P}(U)$ (notation as in Sect. 5.2) with ${{\mathrm{Pic}}}(S)={\mathbb Z}\mu (D)$ such that ${\fancyscript{P}}(A)=\Pi (S^{[2]},\mu (d))$.

There exists a birational map $\varphi :S^{[2]}\dashrightarrow X_A$ by Verbitsky’s Global Torelli Theorem. Now $\varphi ^{*}h_A$ is a $(1,1)$-class of square $2$; since ${{\mathrm{Pic}}}(S)=D$ it follows easily that $\varphi ^{*}h_A=\pm \mu (d)$, and hence $\varphi ^{*}H_A=\mu (D)$. But that is a contradiction because the map $f_A:X_A\rightarrow |H_A|^{\vee }$ is $2$-to-$1$ onto its image while the map $f:S^{[2]}\rightarrow |\mu (D)|^{\vee }$ has degree $4$ onto its image. This proves that ${\fancyscript{P}}(\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )\cap {\mathbb S}''_2$ is empty.

It remains to prove that ${\fancyscript{P}}(\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )\cap {\mathbb S}'_2$ is empty. Suppose the contrary. Let $\varSigma (V^{\vee })$ be the locus of $A\in \mathbb {LG}\left( {\bigwedge ^{3}} V^{\vee }\right)$ containing a non-zero decomposable tri-vector. Since $\delta _{V}(\varSigma )=\varSigma (V^{\vee })$ we get that ${\fancyscript{P}}(\mathbb {LG}\left( {\bigwedge ^{3}} V^{\vee }\right) {\setminus }\varSigma (V^{\vee }))\cap {\mathbb S}''_2$ is nonempty by (4.16) and (4.20); that contradicts the result we proved above. $\square$

5.6 Proof that ${\fancyscript{P}}(\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )\cap {\mathbb S}_4$ is empty

Suppose that ${\fancyscript{P}}(\mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varSigma )\cap {\mathbb S}_4$ is nonempty. Arguing as in Sect. 5.5 we get that there exists a closed ${{\mathrm{PGL}}}(V)$-invariant codimension-$1$ subvariety $C^0\subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right) {\setminus }\varDelta {\setminus }\varSigma$ such that ${\fancyscript{P}}(C^0)\subset {\mathbb S}_4$. Thus ${\fancyscript{P}}(C^0)$ contains an open dense subset of ${\mathbb S}_4$ and therefore if $A\in C^0$ is very generic $h^{1,1}_{{\mathbb Z}}(X_A)=2$.

By Sect. 5.3 there exists a quartic surface $S$ such that $\Pi (S^{[2]},h)=\Pi (X_A,h_A)$ (notation as in Sect. 5.3); since $h^{1,1}_{{\mathbb Z}}(X_A)=2$ the Néron-Severi group of $S$ is generated by the (hyper)plane class.

There exists a birational map $\varphi :S^{[2]}\dashrightarrow X_A$ by Verbitsky’s Global Torelli Theorem. Since the map $f_A:X_A\rightarrow |H_A|^{\vee }$ is of degree $2$ onto its image, and since $\varphi$ defines an isomorphism between the complement of a codimension-$2$ subsets of $S^{[2]}$ and the complement of a codimension-$2$ subsets of $X_A$ (because both are varieties with trivial canonical bundle), the following hold:

• 1. $q_{S^{[2]}}(\varphi ^{*}h_A)=2$,

• 2. $|\varphi ^{*}H_A|$ has no base divisor,

• 3. $S^{[2]}\dashrightarrow |\varphi ^{*}H_A|^{\vee }$ is of degree $2$ onto its image.

We will get a contradiction by showing that there exists no divisor of square $2$ on $S^{[2]}$ such that Items (1), (2) and (3) hold. Notice that if $H$ is the divisor on $S^{[2]}$ defined above then Items (1) and (2) hold but not Item (3) (the degree of the map is equal to $6$). This does not finish the proof because the set of square-$2$ elements of $H^{1,1}_{{\mathbb Z}}(S^{[2]})$ is infinite.

Lemma 5.2

There exists $n\in {\mathbb Z}$ such that

$$\begin{aligned} \varphi ^{*}h_A=x\mu (d)+y\xi ,\qquad y+x\sqrt{2}=(-1+\sqrt{2})(3+2\sqrt{2})^n. \end{aligned}$$

(5.7)

Proof

Since $h^{1,1}_{{\mathbb Z}}(S^{[2]})=2$, $H^{1,1}_{{\mathbb Z}}(S^{[2]})$ is generated by $\mu (d)$ and $\xi$. Let

$$\begin{aligned} \begin{aligned} H^{1,1}_{{\mathbb Z}}(S^{[2]})&\overset{\psi }{\longrightarrow } {\mathbb Z}[\sqrt{2}] \\ x\mu (d)+y\xi&\mapsto y+x\sqrt{2}. \end{aligned} \end{aligned}$$

(5.8)

Then

$$\begin{aligned} (\alpha ,\beta )=-{{\mathrm{Tr}}}(\psi (\alpha )\cdot \overline{\psi (\beta )}). \end{aligned}$$

(5.9)

Since $\varphi ^{*}h_A$ is an element of square $2$ we need to solve a (negative) Pell equation. Solving Pell’s equation $N(y+x\sqrt{2})=1$ (see for example Proposition 17.5.2 of [13]) and noting that $N(-1+\sqrt{2})=-1$ we get that there exists $n\in {\mathbb Z}$ such that

$$\begin{aligned} \varphi ^{*}h_A=x\mu (d)+y\xi ,\qquad y+x\sqrt{2}=\pm (-1+\sqrt{2})(3+2\sqrt{2})^n. \end{aligned}$$

(5.10)

Next notice that $S$ does not contains lines because $h^{1,1}_{{\mathbb Z}}(S)=1$; it follows that the map $S^{[2]}\rightarrow \mathrm {Gr}(1,{\mathbb P}^3)$ is finite and therefore $H$ is ample. Since $|\varphi ^{*}H_A|$ is not empty and $\varphi ^{*}H_A$ is not equivalent to $0$ we get that

$$\begin{aligned} 0<(\varphi ^{*}h_A,h)_{S^{[2]}}=-{{\mathrm{Tr}}}\left( \pm (-1+\sqrt{2})(3+2\sqrt{2})^n(-1-\sqrt{2})\right) . \end{aligned}$$

(5.11)

It follows that the $\pm$ is actually $+$. $\square$

Next we consider the analogue of nodal classes on $K3$ surfaces. For $n\in {\mathbb Z}$ we define $\alpha _n\in H^{1,1}_{{\mathbb Z}}(S^{[2]})$ by requiring that

$$\begin{aligned} \psi (\alpha _n)=-(3-2\sqrt{2})^n. \end{aligned}$$

(5.12)

Thus $q_{S^{[2]}}(\alpha _n)=-2$ for all $n$.

Lemma 5.3

If $n> 0$ then $2\alpha _n$ is effective. If $n\le 0$ then $-2\alpha _n$ is effective.

Proof

By Theorem 1.11 of [18] either $2\alpha _n$ or $-2\alpha _n$ is effective (because $q_{S^{[2]}}(\alpha _n)=-2$). Since $(\mu (d)-\xi )$ is ample we decide which of $\pm 2\alpha _n$ is effective by requiring that the product with $(\mu (d)-\xi )$ is positive. Thus the result follows from (5.9). $\square$

Proposition 5.4

Suppose that $\varphi ^{*}h_A$ is given by (5.7) with $n\not =0$. Then there exists an effective $\beta \in H^{1,1}_{{\mathbb Z}}(S^{[2]})$ such that $(\varphi ^{*}h_A,\beta )_{S^{[2]}}<0$.

Proof

Identify $H^{1,1}_{{\mathbb Z}}(S^{[2]})$ with ${\mathbb Z}[\sqrt{2}]$ via (5.8) and let $g:H^{1,1}_{{\mathbb Z}}(S^{[2]}) \rightarrow H^{1,1}_{{\mathbb Z}}(S^{[2]})$ correspond to multiplication by $(3-2\sqrt{2})$. Since $N(3-2\sqrt{2})=1$ the map $g$ is an isometry. Notice that $\alpha _k=g^k(-\xi )$ and by Lemma 5.2 we have $\varphi ^{*}h_A=g^{-n}(\mu (d)-\xi )$. Now suppose that $n>0$. Then $-2\alpha _{-n+1}$ is effective by Lemma 5.3 and

$$\begin{aligned}&(\varphi ^{*}h_A,-2\alpha _{-n+1})_{S^{[2]}}=(g^{-n}(\mu (d)-\xi ),2g^{-n+1}(\xi ))_{S^{[2]}}\nonumber \\&\quad =(\mu (d)-\xi ,2g(\xi ))_{S^{[2]}}=(\mu (d)-\xi ,-4\mu (d)+6\xi )_{S^{[2]}}=-4<0. \end{aligned}$$

(5.13)

Lastly suppose that $n<0$. Then $2\alpha _{-n}$ is effective by Lemma 5.3 and

$$\begin{aligned} (\varphi ^{*}h_A,2\alpha _{-n})_{S^{[2]}}=(g^{-n}(\mu (d)-\xi ),2g^{-n}(-\xi ))_{S^{[2]}}=(\mu (d)-\xi ,-2\xi )_{S^{[2]}} =-4<0. \end{aligned}$$

(5.14)

$\square$

Now we are ready to prove that Items (1), (2) and (3) can not hold and hence reach a contradiction. By Lemma 5.2 we know that $\varphi ^{*}h_A$ is given by (5.7) for some $n\in {\mathbb Z}$. We have already noticed that Items (1), (2) and (3) cannot hold if $n=0$ . Suppose that $n\not =0$. By Proposition 5.4 there exists an effective $\beta \in H^{1,1}_{{\mathbb Z}}(S^{[2]})$ such that

$$\begin{aligned} (\varphi ^{*}h_A,\beta )_{S^{[2]}}<0. \end{aligned}$$

(5.15)

Let $B$ be an effective divisor representing $\beta$ and $C\in | \varphi ^{*}h_A |$. Then $C\cap B$ does not have codimension $2$ i.e. there exists at least one prime divisor $B_i$ which is both in the support of $B$ and in the support of $C$. In fact suppose the contrary. Let $c\in H^2(S^{[2]})$ be the Poincaré dual of $C$ and $\sigma$ be a symplectic form on $S^{[2]}$; then

$$\begin{aligned} 0\le \int \limits _{B\cap C}\sigma \wedge \overline{\sigma }=(\beta ,c)_{S^{[2]}}(\sigma ,\overline{\sigma })_{S^{[2]}} \end{aligned}$$

(5.16)

and since $(\sigma ,\overline{\sigma })_{S^{[2]}}>0$ we get that $(\beta ,c)\ge 0$ i.e. $(\varphi ^{*}h_A,\beta )_{S^{[2]}}\ge 0$, contradicting (5.15). The conclusion is that there exists a prime divisor $B_i$ which is in the support of $B$ and of any $C\in | \varphi ^{*}h_A |$. Thus $B_i$ is a base divisor of the linear system $| \varphi ^{*}h_A |$; this shows that Item (2) does not hold. $\square$

5.7 Proof that $\mathfrak {p}$ restricted to $\mathfrak {M}{\setminus }\mathfrak {N}$ is an open embedding

Let $\mathfrak {T}:=\varDelta /\!/{{\mathrm{PGL}}}(V)$. Let $\delta :\mathfrak {M}\rightarrow \mathfrak {M}$ be the duality involution defined by (3.9). By [20], pp. 36–38, we have

$$\begin{aligned} {{\mathrm{cod}}}(\mathfrak {T}\cap \delta (\mathfrak {T}),\mathfrak {M})\ge 2. \end{aligned}$$

(5.17)

Claim 5.5

The restriction of $\mathfrak {p}$ to $\mathfrak {M}{\setminus }\mathfrak {N}{\setminus }(\mathfrak {T}\cap \delta (\mathfrak {T}))$ is open.

Proof

It suffices to prove that the restriction of $\mathfrak {p}$ to $\mathfrak {M}{\setminus }\mathfrak {N}{\setminus }(\mathfrak {T}\cap \delta (\mathfrak {T}))$ is open in the classical topology.

Suppose first that $[A]\in \mathfrak {M}{\setminus }\mathfrak {N}{\setminus }\mathfrak {T}$ i.e. $X_A$ is smooth. Then $A$ is stable by Corollary 2.5.1 of [24]. Let $Z_A\subset \mathbb {LG}\left( {\bigwedge ^{3}} V \right)$ be an analytic ${{\mathrm{PGL}}}(V)$-slice at $A$; see [16]. We may and will assume that $Z_A$ is contractible; hence a marking of $(X_A,H_A)$ defines a lift of ${\fancyscript{P}}|_{Z_A}$ to a regular map . The family of double EPW-sextics parametrized by $Z_A$ is a representative of the universal deformation space of the polarized fourfold $(X_A,H_A)$ and hence is a local isomorphism $(Z_A,A)\rightarrow (\varOmega _{\varLambda },{\fancyscript{P}}(A))$ (injectivity and surjectivity of the local period map for compact hyperkähler manifolds).

Now suppose that $[A]\in \mathfrak {T}$. By hypothesis $\delta ([A])\notin \mathfrak {T}$, and since $\delta (\mathfrak {N})=\mathfrak {N}$ it follows that $\delta ([A])\in \mathfrak {M}{\setminus }\mathfrak {N}{\setminus }\mathfrak {T}$; hence $\mathfrak {p}$ is open at $[A]$ by openness at $\delta ([A])$ (which we have just proved) and (4.16). $\square$

Next we notice that ${\mathbb D}_{\varLambda }$ is ${\mathbb Q}$-factorial. In fact by Lemma 7.2 in Ch. 7 of [25] there exists a torsion-free subgroup of finite index. Thus the natural map $\pi :\varOmega _{\varLambda }/G\rightarrow {\mathbb D}_{\varLambda }$ is a finite map of quasi-projective varieties, and $\varOmega _{\varLambda }/G$ is smooth: it follows that ${\mathbb D}_{\varLambda }$ is ${\mathbb Q}$-factorial. The restriction of $\mathfrak {p}$ to $\mathfrak {M}{\setminus }\mathfrak {N}$ is a birational map $\mathfrak {M}{\setminus }\mathfrak {N}\rightarrow {\mathbb D}_{\varLambda }$, and hence its exceptional set is either empty or of pure codimension $1$ because ${\mathbb D}_{\varLambda }$ is ${\mathbb Q}$-factorial. By Claim 5.5 there are no components of codimension $1$ in the the exceptional set, hence it is empty. This proves that $\mathfrak {p}$ defines an open embedding $\mathfrak {M}{\setminus }\mathfrak {N}\hookrightarrow {\mathbb D}_{\varLambda }$.