1 Introduction

Transmission lines represent one of the six major components of the power system. Transmission lines operate at high voltages and their parameters must meet certain limit requirements in order to ensure safe and reliable operation [1]. Energy technologies for transmission of electric energy, the transmission loss and economy of transmission lines represent the key issues to take into account. Considering the technical characteristics of present high-voltage transmission lines, significant losses of energy occur in transmission over longer distances [2]. In the future, the existing generation capacity will be replaced by a new one. This means that the new power plants will be located in a different layout and farther from load centers. This will lead to the transformation of the generation infrastructure of power plants [3]. The high voltage transmission lines will cooperate with renewable resources to a larger extent. Currently, natural conditions are changing and the further increase of the temperature is predicted. This means, there will probably be less cold winters, but hotter summers [2]. It also changes the consumption of electrical energy; in winters people will need less heating, but in the summer the electrical energy will be used to drive air conditioners in order to cool buildings. Experience from countries where a large part of consumption of electrical energy is used to drive air conditioners shows that not all the problems associated are resolved through innovations in the electric power systems, for example Smart Grid. The creation of complex distribution systems enabling transmission of electrical energy over long distances but also within the overall social structures of individual territories is effective, because we do not need to build local energy resources, but on the other hand it contains two major problems. Equally, it is energy transmission losses as well as a significant increase in the risk of running electric power systems in the face of cyber, hacker, or terrorist attacks. At the same time, transmission systems are vulnerable to extreme atmospheric phenomena, which can destabilize the electric power system in case of disturbance and cause power failure for huge territories or huge areas on the continent. On the other side, resistance of the transmission lines influences their energy losses, subsequently influencing the economy of their operation, too, and therefore the operating efficiency of the entire electric power system [3].

Moreover, the load of the transmission lines is expected to be increased because there is certain development in the solar, wind and other renewable resources. Subsequently, the load of the transmission lines should be increased for cross-border trading. For that reason, high-voltage transmission lines will face new challenges [4].

One of the important operating problems of the transmission lines is operating temperature, which affects their technical and economic properties [5]. The electric current flowing through the conductor causes the increase in its operating temperature. The power losses in insulation of insulated conductors or the power losses due to corona around of bare conductors cause the rise of operating temperature, too. The heat is transferred from the conductor to the environment by heat transfer conduction, especially at the insulated conductors and by convection at the bare conductors. While the maximum of the surface temperature is relatively small, the share of the heat induced by radiation is also relatively small compared to convection and conduction [6,7,8]. The resulting operating temperature of conductor is given by the balance between produced heat, heat stored in the conductor and heat transferred to the environment [9].

In many cases, it is necessary to determine the operating temperature of bare transmission line conductors more accurately in a continuously changing environment in order to avoid violations of safety distances or possible damage to the materials due to high operating temperatures [10]. Ampacity (current-carrying capacity or ampere capacity) is the significant parameter of the design and operation of transmission line. This value represents the maximum allowable operating current at continuously permissible (or allowable) temperature under the weather conditions like environment temperature, speed and direction of the wind and solar irradiance that can flow through the transmission line without disturbing electrical and mechanical conductor properties [11]. However, transmission lines mostly operate in a complex environment (weather conditions), which corresponds to a forced convective heat transfer situation.[12, 13]. Several factors, such as wind and solar irradiance, affect the heat transfer of transmission lines [14,15,16]. For example in article, [17] have described measuring of the magnetic field around overhead transmission lines. The method utilized for calculation of operating temperature obtained from ideal weather conditions is not able to accurately and comprehensively reflect the influence of real weather conditions on the transient response rise of operating temperature of the conductor [18].

The environment temperature and other weather conditions affect the operating temperature of the conductors of transmission line and it is necessary to consider the actual weather conditions in individual territories of the world. Weather conditions change significantly during day and they are recorded, processed [19], predicted, modeled and verified [20,21,22] by various methodologies. There is a difference between the obtained (measured) and the real values of weather conditions and this difference cannot be ignored. The measured operating temperature cannot completely represent the actual maximum of operating temperature for long-distance transmission lines that run across multiple regions with different weather conditions given the limited location and quantity of measuring devices for operating temperature [18]. Since weather conditions significantly affect the operating temperature, it is necessary to calculate with the uncertainty of such parameters [23, 24].

The overhead conductors are the most important part of transmission lines and the most widely used conductors lines are ACSR conductors (aluminum conductor steel reinforced or AlFe) [12, 13]. The operating temperature of a conductor is dependent on weather conditions (environment temperature, speed and direction of the wind and solar irradiance) and especially the value of the flowing current. The length of the conductor may vary according to its operating temperature, which can affect the sag and mechanical stress of the conductor [25]. In this regard, the methods of research of operating temperature of the transmission lines have undergone a significant development. These methods need to properly relate to the changes of different parameters and variables of a transmission line with time. Producers report the maximum operating temperature of ACSR conductors ranged between 90 and 110 °C [12, 13]. The research of the weather conditions and research of parameters of the conductor (operating temperature, sag, clearance, tension and vibration), as well as monitoring parameters of the conductor, are described by several authors [26,27,28,29,30,31,32]. A useful description is to be found in articles [28, 29] which refer to the identification of critical spans for the optimum placement of climatic conditions sensors to measure weather conditions and conductor parameters.

The first part of the STNEN 50 341-1 standard [33]: Overhead electrical lines exceeding the voltage AC 45 kV determine the maximum operating temperature of the conductor, while it is advised to select no less than 70 °C [12, 13]. This standard describes the maximum allowable current according specified maximum operating temperature for following weather conditions: high environment temperature (35 °C), high solar irradiance (1000 W m−2), low wind speed (0.5 m s−1), angle of attack of the wind (45°), absorption and emissivity coefficient (0.5) [34]. Based on long-term measurements of weather conditions (environment temperature, wind speed and direction and solar irradiance) around transmission lines, it is obvious that for most of the year these weather conditions do not reach the values according to this standard [12, 13].

The terminology according to ENTSO-E: Dynamic line rating for overhead lines—V6 is used in the case of transmission line design operating temperature [35]. Transmission line design operating temperature is a maximum temperature that conductor in any span may reach without any fear that the safety measures will be violated. It should be noted that design operating temperature may be lower than the maximum operating temperature which can be reached by finished (stranded) conductor. The main difference between static and dynamic line rating is that “static current” is calculated based on rather conventional atmospheric conditions while dynamic line rating takes into account real atmospheric conditions which most of the time offer better cooling and thus allow higher “dynamic” current, contributing to improve safety [43,44,45,46]. The aim of dynamic line rating is to safely utilize existing transmission lines transmission capacity based on real conditions in which power lines operate [12, 13]. There are many articles [36,37,38,39,40,41,42,43,44,45,46] dealing with the models of transmission line design operating temperature.

Several industrial standards refer to the calculation of design temperature of overhead transmission lines (or overhead conductors). The most frequently used methods are described in the IEEE Standard for calculating the current–temperature relationship of bare overhead conductors [47] and CIGRE Technical Brochure 207 [48]. The enhanced version of standard CIGRE Technical Brochure 207 [48] is CIGRE Technical Brochure 601 [49]. Several research studies [21, 38, 42, 50, 51] illustrate the comparison of IEEE and CIGRE standards for calculating the design temperature of overhead transmission lines (or overhead conductors). The operating temperature calculation method obtained from ideal natural convection conditions is not able to accurately and comprehensively reflect the influence of ambient meteorological environment on the transient temperature rise response of the conductor [12, 13, 18].

The CIGRE Technical Brochure 207 [48] describes the operating temperature of the transmission line conductors at low current densities (less than 1.5 A mm−2) and low temperatures (less than 100 °C). The CIGRE Technical Brochure 601 [49] describes the calculation for the thermal rating of transmission lines, including those transmission lines operated at high current densities and high operating temperatures. The CIGRE Technical Brochure 601 [49] describes the variations in weather conditions or loading current with time along with higher loading currents and higher operating temperatures of conductors of the transmission line. Also, these methods for calculating the operating temperature consider transient state. The following standards are also used: CIGRE Technical Brochure 498—Guide for application of direct real-time monitoring systems [52], CIGRE Technical Brochure 345—alternating current (AC) resistance of helically stranded conductors [53], CIGRE Technical Brochure 324—Sag-Tension calculation methods for overhead lines [54], CIGRE Technical Brochure 299—guide for the selection of weather parameters for bare overhead conductor ratings [55], and CIGRE Technical Brochure 244—conductors for the uprating of overhead line [56]. CIGRE Technical Brochure 601 [49] considers the steady-state. (Parameters of the conductor and weather conditions are relatively constant over time.)

Neither CIGRE Technical Brochure 207 [48] nor CIGRE Technical Brochure 601 [49] describes the calculation of the operating temperature considering corona discharge. This article presents the calculation methods of the operating temperature of the overhead transmission line conductor while considering the losses due to corona. The advantage of this proposed method is the improvement in calculation accuracy of the operating conductor temperature under real conditions.

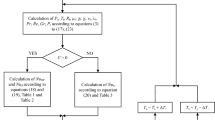
2 Methods for calculating the operating temperature

The first method calculates the operating temperature ϑP using the differential equation [6,7,8] for perpetual balance of heat energy. When current I flows through the conductor in time dt, it produces the Joule heat dQ´. The losses in the insulated conductors or losses in air due to corona discharges in bare conductors produce heat dQ´´. Part of the heat consumed by the heating of the conductor is marked as dQ1 and part of the heat transferred to environment is identified as dQ2.

When current I flows through the conductor with resistance RACϑ, then the heat dQ´ developed in time dt is defined by the following equation.

$$ {\rm d}Q^{\prime} = R_{{\rm AC}\vartheta } I^{2} {\rm d}t = R_{{\rm AC}0} I^{2} \left( {1 + \alpha_{\rm R} \Delta \vartheta_{0} } \right) {\rm d}t = R_{\rm AC0} I^{2} \left( {1 + \alpha_{\rm R} \left( {\Delta \vartheta + \Delta \vartheta_{\rm W} } \right)} \right) {\rm d}t $$
(1)

where Q′ is the produced Joule heat (J), RACϑ is the AC conductor resistance (including skin effects) at operating temperature, RAC0 is the AC conductor resistance (including skin effects) at reference temperature (Ω), I is the current (A), t is the time (s), Δϑ0 is the difference of reference temperature (°C), αR is the temperature coefficient of resistance (°C−1), Δϑ is the operating difference of the temperature (°C) and ΔϑW is the initial difference of the temperature of conductor (°C).

Heat generated by losses in air due to corona discharge in bare conductors dQ´´ is expressed by this equation.

$$ {\rm d}Q^{\prime\prime} = G_{\rm c} U_{\rm f}^{2} {\rm d}t $$
(2)

where Q″ is the heat generated by losses in air due to corona discharge in bare conductors (J), Gc is the conductance by corona (S or Ω−1) and Uf is the voltage among phase and ground (V).

Part of the heat dQ1 is stored in the conductor and its temperature will change by about d(Δϑ).

$$ {\rm d}Q_{1} = m c d\left( {\Delta \vartheta } \right) = V \rho_{\rm m} c d\left( {\Delta \vartheta } \right) = S l \rho_{\rm m} c d\left( {\Delta \vartheta } \right) = S l c_{V} d\left( {\Delta \vartheta } \right) $$
(3)

Part of the heat dQ2 transferred to environment in time dt.

$$ {\rm d}Q_{2} = h_{\rm E} S_{\rm P} \Delta \vartheta {\rm d}t = h_{\rm E} o l \Delta \vartheta {\rm d}t $$
(4)

For the volumetric specific heat, cV equation can be defined like this

$$ c_{V} = c \rho_{\rm m} $$
(5)

where Q1 is the heat transferred to environment (J), Q2 is the heat transferred to environment (J), m is the mass (kg), c is the specific heat (J kg−1 °C−1), V is the volume of the conductor (m3), ρm is the density (kg m−3), S stands for the cross-sectional area (m2), hE is the overall heat transfer coefficient for the outer conductor surface (W m−2 °C−1), Sp is the outer conductor surface (m2), o is the circle perimeter of conductor (m), l is the length of conductor (m) and cV is the volumetric specific heat (J m−3 °C−1).

The perpetual balance of heat energy by differential equation is determined below:

$$ {\rm d}Q^{\prime} + {\rm d}Q^{\prime\prime} = {\rm d}Q_{\rm 1} + {\rm d}Q_{\rm 2} $$
(6)

After substituting the previous Eqs. (1)–(4) into Eq. (6), we obtain a new differential equation:

$$ R_{\rm AC0} I^{2} \left( {1 + \alpha_{\rm R} \Delta \vartheta_{0} } \right) {\rm d}t + G_{\rm c} U_{\rm f}^{2} {\rm d}t = S \rho_{\rm m} c l d\left( {\Delta \vartheta } \right) + h_{\rm E} o l \Delta \vartheta {\rm d}t $$
(7)
$$ R_{\rm AC0} I^{2} \left( {1 + \alpha_{\rm R} \left( {\Delta \vartheta + \Delta \vartheta_{\rm W} } \right)} \right) {\rm d}t + G_{\rm c} U_{\rm f}^{2} {\rm d}t = S \rho_{\rm m} c l d\left( {\Delta \vartheta } \right) + h_{\rm E} o l \Delta \vartheta {\rm d}t $$
(8)
$$ {\rm d}t = \frac{{\frac{{S \rho_{\rm m} c l d\left( {\Delta \vartheta } \right)}}{{h_{\rm E} o l - R_{\rm AC0} I^{2} \alpha_{\rm R} }}}}{{\frac{{R_{\rm AC0} I^{2} \left( {1 + \alpha_{\rm R} \Delta \vartheta_{\rm W} } \right) + G_{\rm c} U_{\rm f}^{2} }}{{h_{\rm E} o l - R_{\rm AC0} I^{2} \alpha_{\rm R} }} - \Delta \vartheta }} $$
(9)

For these conditions, we solve the integral between boundaries ΔϑE and ΔϑP. After a few steps, one obtains this new equation

$$ \Delta \vartheta_{\rm P} = \frac{{R_{\rm AC0} I^{2} \left( {1 + \alpha_{\rm R} \Delta \vartheta_{\rm W} } \right) + G_{\rm c} U_{\rm f}^{2} }}{{h_{\rm E} o l - R_{\rm AC0} I^{2} \alpha_{\rm R} }} \left( {1 - e^{{ - \frac{t}{\tau }}} } \right) + \Delta \vartheta_{\rm E} e^{{ - \frac{t}{\tau }}} $$
(10)

In the previous equations, τ is the thermal time constant (s) and its equation can be defined the following way

$$ \tau = \frac{{S \rho_{\rm m} c l}}{{h_{\rm E} o l - R_{\rm AC0} I^{2} \alpha_{\rm R} }} = \frac{{S l c_{V} }}{{h_{\rm E} o l - R_{\rm AC0} I^{2} \alpha_{\rm R} }} $$
(11)

Increase of the temperature of conductor ΔϑP is the difference between operating temperature ϑP and environment temperature ϑE.

$$ \Delta \vartheta_{\rm P} = \vartheta_{\rm P} - \vartheta_{\rm E} $$
(12)

Initial increase of the temperature of conductor ΔϑE is the difference between initial temperature of conductor ϑW and environment temperature ϑE.

$$ \Delta \vartheta_{\rm E} = \vartheta_{\rm W} - \vartheta_{\rm E} $$
(13)

Initial difference of the temperature of conductor ΔϑW is the difference between initial temperature of conductor ϑW and reference temperature ϑ0.

$$ \Delta \vartheta_{\rm W} = \vartheta_{\rm W} - \vartheta_{\rm 0} $$
(14)

Operating difference of the temperature of conductor Δϑ is the difference between operating temperature ϑP and initial temperature of conductor ϑW.

$$ \Delta \vartheta = \vartheta_{\rm P} - \vartheta_{\rm W} $$
(15)

In the previous equations, ΔϑP is the increase of the temperature of conductor (°C), ϑP is the operating temperature (°C), ϑE is the environment temperature (°C), ΔϑE is the initial increase of the temperature of conductor (°C), ϑW is the initial temperature of conductor (°C), ΔϑW is the initial difference of the temperature of conductor (°C), ϑ0 is the reference temperature (°C) and Δϑ is the operating difference of the temperature of conductor (°C). With these calculations, we obtain this solution of the differential equation

$$ \vartheta_{\rm P} = \frac{{R_{\rm AC0} I^{2} \left( {1 + \frac{{\vartheta_{\rm W} - \vartheta_{0} }}{{\vartheta_{\rm f} + \vartheta_{0} }}} \right) + G_{\rm c} U_{\rm f}^{2} }}{{h_{\rm E} o l - R_{\rm AC0} I^{2} \alpha_{\rm R} }} \left( {1 - e^{{ - \frac{t}{\tau }}} } \right) + \left( {\vartheta_{\rm W} - \vartheta_{\rm E} } \right) e^{{ - \frac{t}{\tau }}} + \vartheta_{\rm E} $$
(16)

The second method is called the CIGRE method which is described in CIGRE Technical Brochure 601 [49] and CIGRE Technical Brochure 207 [48]. This method defines thermal conditions of the conductor as steady state. The general heat equation for a homogeneous and isotropic solid can be expressed in polar coordinates r, φ and z in the form

$$ \frac{{\partial \vartheta_{\rm P} }}{\partial t} = \frac{{\lambda_{\rm W} }}{{\rho_{\rm m} c}} \left( {\frac{{\partial^{2} \vartheta_{\rm P} }}{{\partial r^{2} }} + \frac{1}{r} \frac{{\partial \vartheta_{\rm P} }}{\partial r} + \frac{1}{{r^{2} }} \frac{{\partial^{2} \vartheta_{\rm P} }}{{\partial \phi^{2} }} + \frac{{\partial^{2} \vartheta_{\rm P} }}{{\partial z^{2} }}} \right) + \frac{{q\left( {\vartheta_{\rm P} , \phi , z, r, t} \right)}}{{\rho_{\rm m} c}} $$
(17)

For the second method, the resistance RACϑ is calculated at average temperature ϑAV

$$ R_{{\rm AC}\vartheta } = R_{\rm AC0} \left( {1 + \alpha_{\rm R} \left( {\vartheta_{\rm AV} - \vartheta_{0} } \right)} \right) $$
(18)

For the second method, the specific heat c varies significantly and can be assumed to rise linearly with temperature and it is calculated at average temperature ϑAV with the help of the temperature coefficient of specific heat β

$$ c = c_{0} \left( {1 + \beta \left( {\vartheta_{\rm AV} - \vartheta_{0} } \right)} \right) $$
(19)

where r is the radius (m), φ is the polar angle (°), z is the dimension of the conductor (m), λW is the thermal conductivity (W m−1 °C−1), ϑAV is the average temperature (°C) and β is the temperature coefficient of specific heat (°C−1). The steady state is the situation when the heat supplied to conductor is balanced by heat dissipation.

$$ S l c \rho_{\rm m} \frac{{d\vartheta_{\rm P} }}{{\rm d}t} = P_{\rm J} + P_{\rm M} + P_{\rm S} + P_{\rm c} + P_{\rm r} $$
(20)

where PJ is the Joule heat gain (W) PM is the magnetic heat gain (W), PS is the solar heat gain (W), Pc is convection heat loss and Pr radiation heat loss (W). The solar heat gain PS depends basically on the solar irradiance ST, whatever the current I (A) and operating temperature ϑP (°C). The convection heat loss Pc varies with the surface temperature ϑsur, environment temperature ϑE and in forced convection with the wind speed and direction. In other words, the changes in the operating temperature ϑP of the conductor are induced by the changes in the current I in the conductor and by the changes in the weather conditions: wind speed V (m s−1), angle of attack of the wind Δ (°), environment temperature ϑE (°C) and solar irradiance ST (W m−2). The radiation heat loss Pr is very nonlinear with the surface temperature ϑsur and depends on the environment temperature ϑE. The temperature of the air in contact with the surface of the conductor (so-called the film temperature) ϑf is defined by this equation:

$$ \vartheta_{\rm f} = \frac{{\vartheta_{\rm sur} + \vartheta_{\rm E} }}{2} $$
(21)

The average temperature of the conductor ϑAV is defined by this equation

$$ \vartheta_{\rm AV} = \frac{{\vartheta_{\rm core} + \vartheta_{\rm sur} }}{2} $$
(22)

where ϑsur is the average temperature of the conductor surface (°C), ϑcore is the core temperature of the conductor (°C).

The thermal differential equation can be solved by taking small increments of temperature rise of conductor dϑP and calculating each component: the power input, the power loss and heat capacity for the mean temperature rise.

$$ {\rm d}t_{\rm i} = \frac{{S l \rho_{\rm m} c \left( {\vartheta_{\rm Pi} } \right) d\vartheta_{\rm P} }}{{P_{\rm J} \left( {\vartheta_{\rm Pi} } \right) + P_{\rm M} \left( {\vartheta_{\rm Pi} } \right) + P_{\rm S} \left( {\vartheta_{\rm Pi} } \right) + P_{\rm c} \left( {\vartheta_{\rm Pi} } \right) + P_{\rm r} \left( {\vartheta_{\rm Pi} } \right)}} $$
(23)

Previous equations for the increase of the temperature of conductor ΔϑP and the initial increase of the temperature of conductor ΔϑE can be used for the second method.

The asymptotic increase of the temperature of conductor Δϑm is the difference between asymptotic value of temperature ϑm and environment temperature ϑE.

$$ \Delta \vartheta_{\rm m} = \vartheta_{\rm m} - \vartheta_{\rm E} $$
(24)

where Δϑm is the asymptotic increase of the temperature of conductor (°C) and ϑm is the asymptotic value of temperature (°C).

The heat balance can be solved by numerical integration, but by a certain degree of approximation it is possible to obtain a closed form for solution. In particular, if the radiative heat can be linearized, or the loss is small relative to the forced convection heat loss, and solar and magnetic heat gains are assumed to be constant, the solution for differential equation can be adjusted in the following way

$$ t = \frac{{ - S l c \rho_{\rm m} \left( {\Delta \vartheta_{\rm m} - \Delta \vartheta_{\rm E} } \right)}}{{p_{\rm T} }} \left( {\beta \left( {\Delta \vartheta_{\rm P} - \Delta \vartheta_{\rm E} } \right) + \left( {1 + \beta \Delta \vartheta_{\rm m} } \right) \left( {\ln \left( {\frac{{\Delta \vartheta_{\rm m} - \Delta \vartheta_{\rm P} }}{{\Delta \vartheta_{\rm m} - \Delta \vartheta_{\rm E} }}} \right)} \right)} \right) $$
(25)

where pT is the difference in the heat gain per unit of length of the conductor (W m−1) for step change in current I (A). For the first and second method, it is necessary to calculate the heat transfer coefficient hc and the overall heat transfer coefficient for the outer surface of conductors hE.

According to CIGRE Technical Brochure 601 [49] and CIGRE Technical Brochure 207 [48], the equation can be written for convection heat loss pc per unit of length of the conductor

$$ p_{\rm c} = \pi \lambda_{\rm f} \left( {\vartheta_{\rm sur} - \vartheta_{\rm E} } \right) \left( {f_{\rm x} N_{{\rm u}\,{\rm nat}} + p_{\rm x} N_{{\rm u}\,{\rm for}} k_{\rm air} } \right) $$
(26)

where ϑsur is the average temperature of the conductor surface (°C), Nu nat is the Nusselt number of natural convective heat transfer (dimensionless) and Nu for is the Nusselt number of forced convective heat transfer (dimensionless), respectively. Nu nat and Nu for are different when the fluid sweeps across various parts of the conductor surface, kair is the constant for the air thermal conductivity (dimensionless) and must be corrected by constant fx (dimensionless) and constant px (dimensionless). In this equation difference between temperature of surface ϑsur and environment temperature ϑE is used [18, 49, 57]. In the next step, the equation can be written for convective heat transfer coefficient hc

$$ h_{\rm c} = \frac{{p_{\rm c} }}{{\pi D \left( {\vartheta_{\rm sur} - \vartheta_{\rm E} } \right)}} = \lambda_{\rm f} \frac{{\pi \left( {\vartheta_{\rm sur} - \vartheta_{\rm E} } \right) \left( {f_{\rm x} N_{{\rm u}\,{\rm nat}} + p_{\rm x} N_{{\rm u}\,{\rm for}} k_{\rm air} } \right)}}{{\pi D \left( {\vartheta_{\rm sur} - \vartheta_{\rm E} } \right)}} = \lambda_{\rm f} \frac{{f_{\rm x} N_{{\rm u}\,{\rm nat}} + p_{\rm x} N_{{\rm u}\,{\rm for}} k_{\rm air} }}{D} $$
(27)

where hc is the convective heat transfer coefficient (W m−2 °C−1), D is the outer diameter of the conductor (m) and λf is the thermal conductivity of the air (W m−1 °C−1). According to Stefan–Boltzmann law, the radiation heat loss pr of the conductor surface is related to the temperature difference between the conductor surface ϑsur and the surrounding environment ϑE

$$ p_{\rm r} = \pi D \sigma_{\rm B} \varepsilon_{\rm S} \left( {\left( {\vartheta_{\rm sur} + 273} \right)^{4} - \left( {\vartheta_{\rm E} + 273} \right)^{4} } \right) $$
(28)

where pr is the radiation heat loss (W m−1), εS is the emissivity coefficient of conductor surface (dimensionless) and σB is the Stefan-Boltzmann constant (W m−2 °C−1), σB = 5.6697 × 10 W m−2 °C−1. For solar heat, pS per unit of length of the conductor can be defined by the following equation

$$ p_{\rm S} = \alpha_{\rm S} S_{\rm T} D $$
(29)

where pS solar heat (W m−1), αS is the absorptivity of the conductor surface (dimensionless) and ST is the solar irradiance (W m−2). For differential equation, it is necessary to calculate the heat transfer to environment hE (W m−2 °C−1). Subsequently, the equation can be written for the heat loss transfer to environment pE and this equation is defined using the convection heat loss pc, radiation heat loss pr and solar heat gain pS [49]. The values pE, pc, pr, pS are calculated per unit of length of the conductor.

$$ p_{\rm E} = p_{\rm c} + p_{\rm r} - p_{\rm S} $$
(30)

where pE is the heat loss transfer to environment (W m−1). For overall heat transfer coefficient for the outer surface of conductors hE, the equation can be written using the values of the heat loss divert to environment pE

$$ h_{\rm E} = \frac{{p_{\rm E} }}{{\pi D \left( {\vartheta_{\rm sur} - \vartheta_{\rm E} } \right)}} = \frac{{p_{\rm c} + p_{\rm r} - p_{\rm S} }}{{\pi D \left( {\vartheta_{\rm sur} - \vartheta_{\rm E} } \right)}} = h_{\rm c} + \frac{{p_{\rm r} - p_{\rm S} }}{{\pi D \left( {\vartheta_{\rm sur} - \vartheta_{\rm E} } \right)}} $$
(31)

3 Comparison of the operating temperature calculated by a differential equation with CIGRE technical brochure 601 on ACSR conductor

There are similar studies [41, 51] comparing the operating temperature calculated by the CIGRE Technical Brochure 601 or standard IEEE with the measured operating temperature of conductors in laboratory conditions. For the following calculation, we ascertain properties of the ACSR conductor 143-AL1/25-ST1A [58,59,60] and these necessary technical properties are shown in Table 1.

Table 1 Technical specification of analyzed ACSR conductor
Full size table

For comparison of the operating temperature, ϑP calculations were selected with the help of the first method [6,7,8] and second method [49] described in the previous section. The calculations of operating temperature ϑP were performed for an ACSR conductor 143-AL1/25-ST1A. This was not a new conductor, but rather a conductor with moderate soiling. For this conductor, the value of absorptivity coefficient was set to 0.35 and the value of emissivity coefficient was set to 0.5. These coefficients correspond approximately to the theoretical presumptions described in CIGRE Technical Brochure 601 [49] and the values of these coefficients range from 0.2 for new overhead conductors to 0.9 for weathered overhead conductors in industrial environments [16]. The used voltage between phase and ground Uf equals 63,508.53 V and the used voltage between phases U equals 110,000 V. The calculations by first method are calculated for two cases with or without conductance by corona Gc. In these graphs, we can see the calculated operating temperature ϑP in dependence on the time t. The presented results of the operating temperature ϑP are compared with second method (the CIGRE method). The following graphs are made for two different values of current I and the graphs on their left- and right-hand sides correspond to the current I values of 197.8 A and 395.6 A. For time t, range from 0 to 6000 s has been used. Once time t reaches 6000 s, in the next 300 s the operating temperature ϑP increases to less than 0.0025 °C for a current I equal to 197.8 A and less than 0.025 °C for a current I equal to 395.6 A. The initial temperature of conductor ϑW is equal to environment temperature ϑE. Figures 1, 2 and 3 present the operating temperature ϑP at wind speed 0.2 m s−1 with 45° angle of attack, solar irradiance 770 W m−2, and height above sea level of 216 m.

Fig. 1
figure 1

Calculated operating temperatures ϑP by the first method without conductance by corona Gc

Full size image
Fig. 2
figure 2

Calculated operating temperatures ϑP by the first method with conductance by corona Gc

Full size image
Fig. 3
figure 3

Calculated operating temperatures ϑP by the second method

Full size image

For example, we can compare these methods for environment temperature ϑE equals 25 °C and initial temperature of conductor ϑW equals 25 °C according to Figs. 1, 2 and 3. For the current I equals 395.6 A the operating temperature ϑP according to first method without conductance by corona Gc equals 74.2 °C, according to first method with conductance by corona Gc equals 75.7 °C and according to second method equals 74.5 °C. For the current I equals 197.8 A the operating temperature ϑP according to first method without conductance by corona Gc equals 35.7 °C, according to first method with conductance by corona Gc equals 37.1 °C and according to second method equals 36 °C.

The next section focuses on comparing the calculations of values of the operating temperature ϑP for each 3 min during 3 days, realized for the analyzed transmission line with ACSR conductor 143-AL1/25-ST1A. The analyzed transmission line (voltage level 110,000 V, length 50 km) was located between two electric power stations in the Slovak Republic (height above sea level of 216 m and 254 m). The calculations of operating temperature ϑP were performed in 2019 on three summer days. Different weather conditions (environment temperature ϑE, solar irradiance ST, wind speed V and angle of attack of the wind Δ) affected the conductors of transmission line during the transmission of electrical energy. Two different measuring devices were installed in one of the electric stations (216 m a.s.l.) and recorded the RMS (Root Mean Square) value of the AC current flowing through the analyzed transmission line, solar irradiance, environment temperature, wind speed and direction. Measured data were obtained within a recording interval of 3 min. The used voltage between phase and ground Uf equals 63,508.53 V and used voltage between phases U equals 110,000 V. For comparison, the operating temperature ϑP is calculated with the help of the first and second methods. The first method considers operating temperature ϑP according to the solution of the differential Eq. (16) with or without conductance by corona Gc. Figure 4 shows the input values of current I, which flows through the conductor. Figures 4 and 5 show the input values of the solar irradiance ST, environment temperature ϑE, wind speed V and angle of attack of the wind Δ. Figure 6 shows the calculations of the operating temperature ϑP, and Fig. 7 shows enlarged detail for maximum and minimum operating temperature ϑP. Figure 8 shows calculations of relative difference between used methods.

Fig. 4
figure 4

Input values of current I, environment temperature ϑE and solar irradiance ST

Full size image
Fig. 5
figure 5

Input values of wind speed V and angle of attack of the wind Δ

Full size image
Fig. 6
figure 6

Calculated operating temperatures ϑP for ACSR conductor 143-AL1/25-ST1A

Full size image
Fig. 7
figure 7

Details of maximum and minimum of the operating temperature ϑP for ACSR conductor 143-AL1/25-ST1A

Full size image
Fig. 8
figure 8

Calculated relative difference between used methods

Full size image

The maximum and minimum of calculated operating temperature ϑP can be found in Fig. 7. The maximum of operating temperature ϑP according to the first method without conductance by corona Gc equals 70.5 °C, according to the first method with conductance by corona Gc it equals 71.9 °C, and according to the second method it equals 70.7 °C. The minimum of operating temperature ϑP according to the first method without conductance by corona Gc equals 23.8 °C, according to the first method with conductance by corona Gc it equals 24.6 °C, and according to the second method it equals 24.1 °C.

In most cases, the value of the relative difference becomes higher when the value of the operating temperature ϑP decreases. The value of the relative difference between the first method without conductance by corona Gc and the second method is within the range of − 0.18 to 1.22%. The value of the relative difference between the first method with conductance by corona Gc and the second method is within the range of 0.96% to 3.42%. The value of the relative difference between the first method with conductance by corona Gc and the first method without conductance by corona Gc is within the range of 1.72–4.37%.

The proposed calculations of operating temperature ϑP can be easily expanded when considering different cases of current I in dependence on the time t. These calculations can be recalculated in relation to specific weather conditions that occur in summer or winter season. At the same time, the calculations of operating temperature ϑP can be used for long-distance transmission lines that run across multiple territories. The ascertaining of operating temperature ϑP is important for the design of the transmission line and the analysis can be used in a wide range of transmission lines with different materials of conductors, voltage ratings and other properties.

4 Conclusion

With an increasing demand for electrical energy, it is necessary to transfer that produced electrical energy to the end consumers. Important parameters of conductors of the transmission line are their operating temperature ϑP as well as the ampacity and these two parameters are interconnected.

The main contribution of the article is the proposed calculation method of the operating temperature of the overhead transmission line conductor in real operating conditions (external weather influences, current loading and corona effect). The originality of this newly developed method lies in considering corona effect. Additionally, this method (the first method) was compared with the CIGRE method (the second method), taking into account the actual weather conditions.

In the first step, the calculations of the operating temperature ϑP were performed for two different values of current I flowing through analyzed ACSR conductor 143-AL1/25-ST1A using the first and the second methods. These calculations were realized for several values of environment temperature ϑE and simultaneously for initial temperature of conductor ϑW. In the next part of this article, the calculations according to these methods of the operating temperature ϑP were performed for the real transmission line in a row three summer days. The mathematical description of influence of the weather conditions on power line conductors is stated in CIGRE Technical Brochure 207 [48] and CIGRE Technical Brochure 601 [49]. A good measuring system of the weather conditions and current I surrounding overhead transmission line provides very important information to calculate the conductor operating temperature ϑP. Data of the weather conditions and current I flowing through the overhead wire (recorded every 3 min during 3 days) were known.

The second method [67, 68] describes the calculation of the operating temperature ϑP without considering the conductance by corona Gc. Thus, the first method without conductance by corona Gc can be compared to the second method. In this case, the average value of relative difference equals 0.55%. Both methods give very similar results with only slight differences due to the different way of solving the heat balance. The first method [6,7,8] can assess the conductance by corona Gc. This gives room for comparison of the first method with conductance by corona Gc to the first method without conductance by corona Gc. This comparison revealed that the average value of relative difference equals 2.4%. Furthermore, the comparison of the method with conductance by corona Gc to the second method showed that the average value of relative difference equals 1.84%.

The obtained results confirm that the first method and second method are applicable for an approximate calculation of the operating temperature ϑP. However, no significant influence of the losses due to corona on the operating temperature was identified.

For the transmission of electrical energy with considering the technical parameters of the actual transmission lines, significant part of the energy is lost in the high voltage transmission lines over longer distances [2]. In our case, the relative power losses with considering the losses due to corona are 8.80%. The relative power losses without considering the losses due to corona are 8.55%. On this basis, there is a presumption use of these calculations to ensure safe and reliable operation of the transmission lines supposed by changing the parameters of transmission line due to increase in the operating temperature ϑP. The corona causes additional losses of electric power, and therefore, it is necessary to reduce it with the help of the homogenizing high-voltage transmission lines. All of these issues create an extremely complex tissue of relation to achieving the proper operation of the transmission line in the electric power industry. Ultimately, there is a need for a new comprehensive approach to the transmission lines as one important part of the entire electric power system.