1 Introduction

With the increase in power demand and generation, simultaneously economic and safe operation of power systems has become a current and important issue. In order to operate the power systems in an economical way, it is necessary to use the existing infrastructure and capacity in the most efficient and optimal way. Minimization of power loss (Ploss) is one of the priorities of the power system operators in terms of achieving both technical and economic benefit. Optimal distribution of reactive power generation in a power system by tuning the control variables to minimize specific objective function and satisfy the numerous constraints is known as optimal reactive power dispatch (ORPD). According to grid code, it is not enough to minimize only the considered objective function such as the minimization of Ploss or total voltage deviation (TVD), but also all equality and inequality constraints must be satisfied simultaneously. Therefore, ORPD is a complex, nonlinear and non-convex problem.

It is seen from the literature survey that researchers have used deterministic approaches such as linear programming [1], nonlinear programming [2], quadratic programming [3] and interior point [4] for solving ORPD in early years. By the reason of the nonlinearity, non-differential, multi-modal, non-convex characteristics of the ORPD, the majority of the deterministic methods may be very sensitive to the starting point and converge to a local optimum point [5]. Instead of these methods, population-based algorithms and their hybrid or improved/modified versions, such as genetic algorithm (GA) [6], differential evolution (DE) [7], biogeography-based optimization (BBO) [8], seeker optimization algorithm (SOA) [9], gravitational search algorithm (GSA) and its variants [10, 11], particle swarm optimization (PSO) with an aging leader and challengers (ALC-PSO) [12], hybrid PSO and imperialist competitive algorithm (ICA) (PSO–ICA) [13], hybrid modified ICA and invasive weed optimization (IWO) (MICA–IWO) [14], hybrid PSO and GSA (PSOGSA) [15], multi-objective chaotic improved PSO (MOCIPSO) [16], firefly algorithm (FA) [17], gray wolf optimization (GWO) [18], moth-flame optimization (MFO) [19], water cycle algorithm (WCA) and gaussian bare-bones WCA (NGBWCA) [20], chaotic parallel vector evaluated interactive honeybee mating optimization (CPVEIHBMO) [21], ant lion optimization (ALO) [22], modified ALO (MALO) [23], exchange market algorithm (EMA) [24], have been proposed for solving the ORPD. However, one of the disadvantages of some of the above-mentioned algorithms is that they have various algorithmic parameters, which influence the solution significantly and require to be identified carefully. The crossover and mutation probability values for GA, acceleration and inertia weight parameters for PSO, gravitational and α constants for GSA, differentiation (or mutation) and crossover constants for DE, reflection, expansion and contraction coefficients for FA are just a few examples. These parameters affect the convergence speed and balance between exploration and exploitation. Since the performance of these algorithms is closely associated with these parameters, it is important and necessary to adjust them to their ideal values [25].

In 2014, the Symbiotic Organisms Search algorithm (SOS) has introduced a population-based meta-heuristic algorithm that does not require any user-defined algorithmic parameters [26]. SOS algorithm’s underlying logic is symbiotic interaction behavior of organisms to survive in the ecosystem. SOS has been tested for unconstrained and constrained benchmark functions and yields better results than well-known algorithms [26].

While setting the optimal value of these algorithmic parameters is sometimes a challenging process, they fulfill an important mission of balancing the global and local search capabilities of algorithms in search space. The absence of such an algorithmic parameter in the SOS algorithm makes it difficult to maintain the global and local search balance of the algorithm [25]. Unfortunately, SOS algorithm seems to be able to trap into local optima points and converge late, especially in solving highly nonlinear and non-convex problems with much boundary conditions. This is also the case for the ORPD problem as the number of bus and control parameters increases. Therefore, the mentioned frailties of the SOS algorithm needs to be eliminated. For this reason, studies are being done to improve the SOS algorithm and applied to various optimization problems. The quasi-oppositional SOS algorithm is developed and applied to load frequency control by Guha et al. [27]. The modified SOS algorithm is introduced and implemented on economic dispatch problem with valve-point effects by Secui [28]. The adaptive SOS algorithm is created by updating the benefit factor terms in SOS throughout the iteration and tested on structural design optimization problems by Tejani et al. [29]. Saha et al. proposed chaotic SOS (CSOS) algorithm by replacing the parasitism phase that one of the phases of SOS with a chaotic local search for unconstrained benchmark test functions and siting and sizing problem of distributed generators in radial distribution system in [25]. Chaotic local search (CLS) was used in CSOS [25], but CLS was applied only to the best organism. Although the algorithm’s local search capability is enhanced by this way, it limits global search capabilities. Therefore, CSOS, like the SOS algorithm, unable to get rid of local optima points in solving more complex and non-convex optimization problems.

It is a frequently used method to obtain new algorithms by hybridizing existing algorithms with other algorithms or by adding extra features. Due to the positive impact of algorithms on local and global searching performance and easy implementation, chaos maps are an often-preferred healing method by researchers. In many heuristic algorithms, the “rand” operator is defined to increase the randomness of the solution candidates and the search capability in the solution space. The logistic map, one of the variance of chaos, known for their ergodicity, randomness and non-repeatability, have been found to improve algorithms search capability and convergence speed compared to rand operators. Along with the modification in the algorithm stages, it is important to improve the constraint handling mechanisms integrated with the algorithms. The most common classical method for constraint handling is the static penalty function (SPF) method, which involves penalty coefficients that must be defined by the user. The main problem with SPF method is that it requires many trial and error process to find the ideal value of the penalty coefficients. As a solution to this situation, the researchers define higher values than necessary for the penalty coefficients, but this causes the algorithms to be fell into local optima points. On the other hand, global competitive ranking (GCR), developed by Runarsson and Yao [30], quickly finds the nearest candidate solution to the global optimum point by making a balanced search in both the feasible and the infeasible region. By using algorithms such as SOS, CSOS or the other algorithms using SPF method it is very difficult and time consuming to find both minimum and feasible solutions to more complex and more constrained optimization problems like ORPD. The GCR provides substantial improvements in algorithmic speed by finding the feasible solution very quickly without requiring any trial and error process. It also appears to improve the standard deviation values encountered in mentioned algorithms. inspired by these ideas, a new A-CSOS algorithm is developed by merging the logistic map and GCR constraint handling mechanism with SOS to eliminate the weakness of the SOS as mentioned earlier and enhance the exploration and exploitation skills of the SOS even further.

The main contributions of this paper are: developing a new A-CSOS algorithm, hybridizing the logistic map and global competitive ranking with SOS, eliminating the drawbacks in more complex and con-convex problems of the SOS such as being trapped into local optima and premature convergence, implementing the proposed A-CSOS and SOS on the ORPD problem. In order to analyze the performance of the A-CSOS and SOS, both algorithm are applied to the ORPD problem in IEEE 57-, 118-, 300-bus standard test systems. Since both Ploss and TVD minimization are studied as objective functions for each power systems, and some of control variables are considered the mix of discrete and continuous or fully continuous, the results of the proposed algorithm are evaluated in 10 different cases under six different scenarios in this study. Moreover, the proposed algorithm is not only compared with the SOS but also compared with other state-of-art algorithms. It is clear that the proposed A-CSOS yields up to 15.3% and 44.1% better results than many of the latest studies in literature and SOS. Therefore, A-CSOS algorithm is a promising method for ORPD and other constrained optimization problems.

The rest of this paper is organized as follows. ORPD problem is explained in Sect. 2. Description of the A-CSOS algorithm is given in Sect. 3. Implementation steps of A-CSOS for ORPD problem is described in Sect. 4. The studied scenarios and obtained results are presented in Sect. 5, conclusions are given in Sect. 6.

2 The ORPD problem formulation

Since ORPD is a nonlinear, non-convex and constrained optimization problem composed of a specific objective function to be optimized while satisfying numerous constraints, it is necessary to express mathematically each objective functions and constraints. In this work, two different objective functions including Ploss and TVD minimization are concerned separately for ORPD problem. Mathematical explanation of these objective functions and constraints are explained in the next sub-sections.

2.1 Objective functions

2.1.1 Minimization of Ploss

ORPD solution is mainly to minimize Ploss in the existing branches while fulfilling all constraints. Minimization of active power loss can be mathematically stated by Eq. (1).

$$ f_{1} \left( {x,u} \right) = \mathop \sum \limits_{l = 1}^{{N_{L} }} \left[ {G_{l} \left( {V_{i}^{2} + V_{j}^{2} - 2V_{i} V_{j} \cos \delta_{ij} } \right)} \right] $$
(1)

where NL is the number of branch, Gl is the conductance of branch-l connecting buses i and j; Vi and Vj are voltage magnitudes at buses i and j, respectively; and δij is the phase difference between buses i and j, respectively.

2.1.2 Minimization of TVD

The second objective function used in this study is TVD that aims to minimize absolute deviations of all the present load bus voltages from the referenced magnitude. Thus, voltage profile can be enhanced by this way. The mathematical expression of TVD minimization problem is described as follows:

$$ f_{2} \left( {x,u} \right) = \mathop \sum \limits_{k = 1}^{{N_{\text{PQ}} }} \left| {V_{k} - V_{k}^{\text{ref}} } \right| \left( {{\text{where}}\;V_{k}^{\text{ref}} = 1\;{\text{p}}.{\text{u}}.} \right) $$
(2)

where NPQ is the number of PQ bus, Vk is the voltage of PQ bus-k, \( V_{k}^{\text{ref}} \) is desired voltage at bus-k.

Each objective function is related to the state/dependent and control/independent variables denoted by x and u, respectively. The dependent variable vector is composed of the voltages of PQ-bus (\( V_{L} \)), Mvar output of generators \( (Q_{G} ) \) and MVA loading of branches (\( S_{L} \)), while independent variable vector is composed of the voltages of PV bus (\( V_{G} \)), the tap ratios of transformers (\( T_{N} \)) and Mvar output of shunt compensators \( \left( {Q_{C} } \right) \).

$$ x = \left[ {V_{{L_{1} }} , \ldots ,V_{{L_{{N_{\text{PQ}} }} }} , Q_{{G_{1} }} , \ldots ,Q_{{G_{{N_{\text{PV}} }} }} ,S_{{L_{1} }} , \ldots ,S_{{L_{{N_{L} }} }} } \right] $$
(3)
$$ u = \left[ {V_{{G_{1} }} , \ldots ,V_{{G_{{N_{\text{PV}} }} }} , T_{1} , \ldots ,T_{{N_{T} }} , Q_{{C_{1} }} , \ldots ,Q_{{C_{{N_{c} }} }} } \right] $$
(4)

where NPV is the number of PV bus, NT is the number of transformers, and NC is the number of shunt compensators.

2.2 Constraints

2.2.1 Equality constraints

The equality constraints “g(x, u)” for ORPD problem are described using power balance formulas expressed by Eqs. (5)–(6) [11].

$$ P_{{G_{i} }} - P_{{L_{i} }} = V_{i} \mathop \sum \limits_{{j \in N_{i} }} V_{j} \left[ {G_{ij} \cos \theta_{ij} + B_{ij} \sin \theta_{ij} } \right] $$
(5)
$$ Q_{{G_{i} }} - Q_{{L_{i} }} = V_{i} \mathop \sum \limits_{{j \in N_{i} }} V_{j} \left[ {G_{ij} \sin \theta_{ij} - B_{ij} \cos \theta_{ij} } \right] $$
(6)

where Ni is the number of buses connected to bus-i, PGi and QGi are the MW and Mvar generation, respectively; PLi and QLi are the MW and Mvar demand; Gij and Bij are the conductance and susceptance, respectively.

2.2.2 Inequality constraints

The lower and upper limit values of the essential parameters for the grid are defined in the grid codes so that the grid can be safely operated by transmission system operators (TSOs) and distribution system operators (DSOs). In addition, the existing equipment in the grid has its own operating limits. The limits in this context including the limits of PV and PQ bus voltages, Mvar output of generators and shunt VAR compensators, transformers’ taps, transmission line loading capacities constitute the inequality constraints denoted by h(x, u) and expressed below, respectively.

$$ V_{Gi}^{ \rm{min} } \le V_{Gi} \le V_{Gi}^{ \rm{max} } , \quad i \in N_{G} $$
(7)
$$ V_{Li}^{\rm{min} } \le V_{Li} \le V_{Li}^{\rm{max} } , \quad i \in N_{\text{PQ}} $$
(8)
$$ Q_{Gi}^{\rm{min} } \le Q_{Gi} \le Q_{Gi}^{\rm{max} } , \quad i \in N_{G} $$
(9)
$$ Q_{Ci}^{\rm{min} } \le Q_{Ci} \le Q_{Ci}^{\rm{max} } ,\quad i \in N_{C} $$
(10)
$$ T_{i}^{\rm{min} } \le T_{i} \le T_{i}^{\rm{max} } , \quad i \in N_{T} $$
(11)
$$ \left| {S_{Li} } \right| \le S_{Li}^{\rm{max} } ,\quad i \in N_{L} $$
(12)

The superscripts min and max used in Eqs. (7–12) mean the corresponding lower and upper limits, respectively.

3 The proposed technique

3.1 Symbiotic organisms search algorithm

The SOS algorithm is one of the new meta-heuristic population-based algorithm introduced in 2014 [26]. This algorithm simulates symbiotic reciprocations between different organisms living in an ecosystem.

The fundamental relations between different species in universe are mutualism, commensalism, and parasitism. These interactions are modeled in SOS by their mathematical expressions given in the following sub-headings.

3.1.1 Mutualism

The mutualism phase simulates to the reciprocal action between two different organisms where both of them get benefited from this relation. \( X_{i\_org} \) and \( X_{j\_org} , \) which enter into mutualist relation and denote to ith and jth organism in the ecosystem, may benefit from each other at equal or different rates. Two new, but temporary organisms, \( X_{i\_temp} \) and \( X_{j\_temp} \) are produced after performing mutualism relation. It replaces the better one by comparing the newly produced organisms with originals. The mutualism process mathematically can be described by Eqs. (13) and (14) [26].

$$ X_{i\_temp} = X_{i\_org} + rand\left( {0,1} \right)\left( {X_{\text{best}} - mVector \times bF_{1} } \right) $$
(13)
$$ X_{j\_temp} = X_{j\_org} + rand\left( {0,1} \right)\left( {X_{\text{best}} - mVector \times bF_{2} } \right) $$
(14)

In above equations, Xbest is an organism with the highest degree of adaption and gives the best solution so far in the ecosystem; rand(0, 1) is a random number between 0 and 1; mVector, bF1, and bF2 are calculated using Eqs. (15)–(17).

$$ mVector = \frac{{X_{i\_org} + X_{j\_org} }}{2} $$
(15)
$$ bF_{1} = round\left( {1 + rand\left( {0,1} \right)} \right) $$
(16)
$$ bF_{2} = round\left( {1 + rand\left( {0,1} \right)} \right) $$
(17)

where bF1 and bF2 are the beneficial factors which show the rate of profit from each other. As can be understood from Eqs. 16 and 17, bF1 and bF2 can take a value of four possible combinations. If bF1 and bF2 take equal values, it means that both organisms benefit equally in mutualist relation to each other, otherwise an organism will benefit more from this relation than the other.

3.1.2 Commensalism

Unlike the mutualism phase, only one organism gets to benefit from this dependency between two different organisms. The other is not affected significantly. Similarly, \( X_{i\_org} \) is an organism that corresponds to organism-i in the ecosystem and \( X_{j\_org} \) is an arbitrary selected organism that interacts with \( X_{i\_org} \). In this phase, \( X_{i\_org} \) attempts to acquire benefit from \( X_{j\_org} \), while \( X_{j\_org} \) is not affected negatively or positively. The new temporary obtained organism after performing commensalism process \( X_{i\_temp} \) is formulated by Eq. (18).

$$ X_{i\_temp} = X_{i\_org} + rand\left( { - 1,1} \right)\left( {X_{\text{best}} - X_{j\_org} } \right) $$
(18)

3.1.3 Parasitism

In the parasitism phase, one organism takes advantage from this relationship while the other is damaged. \( X_{i\_org} \) is an organism that represents the parasite vector which is the duplicating form of \( X_{i\_org} \) and \( X_{j\_org} \) is a randomly selected organism that hosting the parasite vector and interacting with \( X_{i\_org} \). In this phase, \( X_{j\_org} \) is modified by interacting with parasite vector. The infected and parasite vector’s fitness value are calculated separately. The infected vector must have a better fitness value than the parasite vector to maintain its position. Otherwise, the parasite vector kills and replaces the infected vector.

3.2 Adaptive chaotic symbiotic organisms search algorithm

The most important feature that makes the SOS algorithm attractive is that not necessitate any user-defined algorithmic parameters. This requirement affects negatively both the performance of the other algorithms and causes a lot of time loss. However, the SOS algorithm has some adverse properties need to be solved. The most important of these is that it is easily lodged in local optimum points, especially in the solution of complex non-convex problems.

Various modifications have been made in the literature to overcome these deficiencies in the SOS algorithm. In this context, the chaotic local search feature has been added to the SOS in CSOS [25], but limited local search capability has been developed since chaos is only applied to the best organism and the parasitism phase is removed. In addition, this can lead to an unbalanced search in the global and local search space and trap into local optima because it increases the orientation toward the best organism. It is important to develop both the local and global exploring capabilities of the SOS so that it can be overcome by all sorts of challenging problems. In addition, some characteristics such as the convergence speed of the SOS algorithm can still be improved.

Another important issue is that for constrained optimization problems, an integrated constraint handling strategy that works in an efficient and compatible manner with the algorithm is required. Constraint handling mechanisms support the performance of algorithms. If this is ignored, the algorithm is inherently capable, but cannot be exploited enough without the algorithm due to the constraint handling methodology.

In order to remove the problems mentioned above, two important contributions have been integrated to the SOS algorithm: the logistic map that is one of the chaos functions, and the global competitive ranking that is one of the adaptive penalty strategies. Finally, a new algorithm named A-CSOS is obtained. The changes made on the SOS algorithm can be categorized as chaos adaptation to mutualism phase, chaos adaptation to commensalism phase, and Global Competitive Ranking (GCR) constraint handling integration. It should be noted that in this study chaos is applied not only to the best organism but also to all the organisms in the ecosystem in order to be able to make a more effective search in the local and global search space. The details of modifications are explained in the following sub-headings.

3.2.1 Increasing randomness of mutualism with logistic map

Chaos maps are known to significantly improve the exploration and exploitation capabilities of the algorithms. In some of the studies in which chaos is integrated, chaos is only used during the generation of initial population phase, while in others it is adapted to some stages of the algorithm. Although various chaos functions are proposed depending on the problem in the studies, logistic map is the most known of these.

The rand expression in Eqs. (13)–(14) affects the organism’s range of motion and local search abilities. Therefore, logistic map is implemented on random statements of \( X_{i\_temp} \) and \( X_{j\_temp} \) formulas in mutualism phase and the equations of mutualism phase are modified as follows:

$$ X_{i\_temp} = X_{i\_org} + c_{i}^{t} \left( {X_{best} - mVector \times bF_{1} } \right) $$
(19)
$$ X_{j\_temp} = X_{j\_org} + c_{j}^{t} \left( {X_{best} - mVector \times bF_{2} } \right) $$
(20)
$$ c_{i,k}^{t} = \mu \times c_{i,k - 1}^{t} \times \left( {1 - c_{i,k - 1}^{t} } \right)\quad {\text{where}}\; 0 < \mu \le 4 $$
(21)

where \( c_{i,k}^{t} \) denotes the kth chaotic variable of ith organism in the tth iteration. μ is called control parameter and \( c_{i,k}^{t} \in \left( {0,1} \right). \) The value of μ affects the behavior of the steady-state solution of this map. For μ ∈ (0, 1), \( c_{i,k}^{t} \) tends to zero; for μ ∈ [1, 3), a fixed point; for μ ∈ [3, 3.57), periodic; and finally for μ ∈ [3.57, 4), chaotic. Therefore, the output \( c_{i,k}^{t} \) is aperiodic, non-convergent and very sensitive to the initial value of \( c_{i,0}^{t} \), which is not equal to {0, 0.25, 0.5, 0.75, 1}. Although μ can also set close to 4, μ = 4 assures that the equation is chaotic [31].

3.2.2 Increasing randomness of commensalism with logistic map

The rand(− 1, 1) expression in Eq. (18) affects the exploration and exploitation performance of the SOS algorithm. Therefore, logistic map is implemented on rand(– 1, 1) statement of \( X_{i\_temp} \) formula in commensalism phase. The new commensalism phase equation after the modification can be rewritten as follow:

$$ X_{i\_temp} = X_{i\_org} + \left( {2c_{i}^{t} - 1} \right) \times \left( {X_{\text{best}} - X_{j\_org} } \right) $$
(22)

3.2.3 Global competitive ranking-based constraint handling methodology

To satisfy equality and inequality constraints, a constrained problem converts into an unconstrained problem by adding a penalty value to the objective function. This method is known as static penalty function (SPF). The general formula of SPF integrated with ORPD can be expressed as follows:

$$ F\left( {X_{i} } \right) = f_{n} \left( {X_{i} } \right) + \tau_{v} \mathop \sum \limits_{i = 1}^{{N_{\text{PQ}} }} \left( {V_{Li} - V_{Li}^{ \lim } } \right)^{2} + \tau_{q} \mathop \sum \limits_{i = 1}^{{N_{G} }} \left( {Q_{Gi} - Q_{Gi}^{ \lim } } \right)^{2} $$
(23)

In Eq. (23), \( f_{n} \) is described as the objective function either Ploss or TVD value. τv and τq are expressed as static penalty factors for voltage and reactive power constraints, respectively; \( V_{Li}^{ \lim } \) and \( Q_{Gi}^{ \lim } \) are the limit values of PQ bus voltage and generator reactive power output, respectively.

The main handicap of the SPF method is that it requires a time-consuming trial-and-error process to adjust the penalty coefficients affecting solution accuracy. This situation also overshadows the algorithmic parameterless nature of the SOS algorithm. Therefore, instead of the SPF method, GCR mechanism that more accurately and quickly converges to the global optimum point by correctly interpreting the information it receives from the SOS algorithm is proposed.

GCR is a sorting-based adaptive penalty method developed by Runarsson and Yao [30]. GCR is an advanced version of stochastic ranking (SR) [32]. Unlike SR, a solution candidate is sorted by analogizing it with not the only adjacent neighborhood but also all other members of the population. Another difference between SR and GCR is that fitness evolution is made according to both objective function and constraint violation at the rate of Pf in GCR. The fitness level of each individual in the GCR method can be evaluated as follows [30]:

$$ F(X_{i} ) = P_{f} \frac{{rank\left( {f\left( {X_{i} } \right)} \right) - 1}}{{N_{\text{pop}} - 1}} + \left( {1 - P_{f} } \right)\frac{{rank\left( {\mathop \sum \nolimits_{j = 1}^{m} v_{j} \left( {X_{i} } \right)} \right) - 1}}{{N_{\text{pop}} - 1}} $$
(24)
$$ v_{j} \left( {X_{i} } \right) = \hbox{max} \left\{ {0,g_{j} \left( {X_{i} } \right)} \right\} $$
(25)

In Eq. (24), \( F(X_{i} ) \) is the actual fitness value of organism-i, \( rank\left( {f\left( {X_{i} } \right)} \right) \) represents the actual rank of ith organism in the population considering objective function value; \( rank\left( {\mathop \sum \nolimits_{j = 1}^{m} v_{j} \left( {X_{i} } \right)} \right) \) represents the actual rank of ith organism in the population considering the sum of its constraint violations, Npop is the number of individuals, Pf symbolize the probability that fitness is calculated based on the rank of objective function. It is recommended that the value of Pf be between 0 and 0.5 to find both a feasible and a minimum solution.

4 Implementation of the A-CSOS algorithm for ORPD problem

Creating the ecosystem is the first phase of the A-CSOS algorithm. An ecosystem comprises a number of organisms. Each organism represents a candidate solution in search space. The ecosystem, in other words control variable vector including generator set voltages, reactive power outputs of shunt VAR compensators and tap settings of transformers is created randomly considering their limits. Moreover, basic parameters like the number of organisms, maximum number of iteration, maximum and minimum limits of related variables are also defined in this phase. The bus, generator and branch data of each test system are prepared.

Secondly, each organism is exposed to Newton–Raphson power flow using the Matpower and then objective function and the sum of constraint violation values are calculated from the obtained results. In accordance with GCR method, organisms in the ecosystem are separately ranked according to their objective function and sum of the constraint violation value. The fitness function value of each organism is calculated by using Eq. (24).

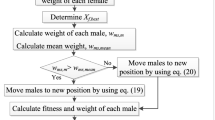
Thirdly, mutualism, commensalism and parasitism relationship are established between Xi and randomly selected organism Xj until the predefined maximum iteration is achieved. Nevertheless, unlike the mathematical expressions of mutualism and commensalism phases of conventional SOS, Eqs. (19–22) are used that is highlighted in Fig. 1.

Fig. 1
figure 1

Flowchart of A-CSOS algorithm-based reactive power dispatch

Full size image

5 Results and discussion

A-CSOS and SOS algorithms are implemented on ORPD problem for IEEE 57-, 118- and 300-bus standard power systems. Two different objective functions are studied including Ploss and TVD minimization for each test case for understanding performance of the A-CSOS. Algorithms are implemented using the MATLAB R2013a and applied on a 2.60 GHz Intel Core i5 with 4 GB RAM notebook. Due to a fair evolution of the simulation results, Matpower software [33] is selected for power flow analysis. For each case, above-mentioned boundary conditions are also checked in Matpower. The maximum number of iteration is 100 for IEEE 57-, 118-bus simulation analysis, and 200 for IEEE 300-bus simulation analysis. The numbers of organism in the simulations are taken as 30 for IEEE 57-bus, 50 for IEEE 118-bus, 75 for IEEE 300-bus power system. The algorithm is tested with 100 runs of each test case. The best, mean and standard deviations of each objective functions after 100 runs are given in the related sub-sections.

However, it is useful to first investigate the effect on the results of the value of benefit factors, since these values are taken into account in the other results given in the following headings. The beneficial factors can be taken two different values, 1 or 2. Beneficial factor is critical because it determines the direction of motion of organisms and express the benefit degree of organisms to each other. A deep analysis of the best results for all scenarios revealed that bF1 and bF2 parameters are equal to 1. The statistical results of analyses carried out for IEEE-57 bus system are presented in Table 1.

Table 1 The effect of bF1 and bF2 on the simulation results
Full size table

As can be seen in Table 1, the worst solution for all cases has been obtained when both bF1 and bF2 are equal to 2. On the other hand, the algorithm when both bF1 and bF2 are equal to 1 is much better in terms of best, mean and standard deviation values for all test scenarios. The results confirm that adjusting the benefit factors of the SOS strengthened the ability of the SOS and the algorithm become more stable and promising. Therefore, both bF1 and bF2 have been taken as 1 for the results given in the paper.

5.1 Test System 1: IEEE 57-bus power system

The IEEE 57-bus power system has 25 control variables including seven PV bus voltages, fifteen transformers’ tap ratios and three shunt VAR compensators. Test system data are adapted from [28]. The permissible voltage limits at load and generator buses are 0.95–1.05 p.u. and 0.95–1.1 p.u., respectively. The permissible limits of transformer tap ratios are 0.9–1.1 p.u. The permissible Mvar limits of shunt capacitor linked to bus-18, -25 and -53, respectively are set to 0–10 Mvar, 0–5.9 Mvar, and 0–6.3 Mvar. The proposed algorithm and studied SOS algorithm are applied to IEEE 57-bus test system for minimization of Ploss as Scenario 1 and minimization of TVD as Scenario 2. Transformer taps and VAR compensators are considered continuous in Scenario 1.1 and 2.1, and discrete with the 0.01 p.u stepwise in Scenario 1.2 and 2.2.

Comparison of the best results of proposed A-CSOS with SOS algorithm and the best results of other state-of-the-art optimization techniques such as self-adaptive differential evolution (L-SaDE) [9], SOA [9], comprehensive learning particle swarm optimizer (CLPSO) [9], ABC [23], FA [23], BAT [23], ALO [23], MALO [23], MFO [19], hybrid PSO–ICA [13], modified ICA and IWO (MICA–IWO) [14], MOCIPSO [16], OGSA [11] for Scenario 1 and 2 are given in Tables 2 and 3, respectively.

Table 2 Comparison of the results for Scenario 1
Full size table
Table 3 Comparison of the results for Scenario 2
Full size table

Table 4 demonstrates the best solutions for each scenario and optimal values of variables. After applying the A-CSOS algorithm to IEEE 57-bus test system, Ploss is reduced to a minimum value of 23.8193 MW (Scenario 1.1) and 23.8284 MW (Scenario 1.2) from the initial case Ploss of 27.8638 MW. It is clear that approximately the same and the best results are obtained via A-CSOS and SOS algorithms for each scenario. The result of A-CSOS is 0.4336 MW (1.79%) better than the MFO [19] that is the best result of above-mentioned algorithms considering continuous variables.

Table 4 Optimal value of control variables for best result of Ploss and TVD optimization on Test System 1
Full size table

According to the result of Scenario 1.2, A-CSOS yields 0.0716 MW better than MALO [23], which is the best result of given algorithms. As can be seen in Figs. 2 and 3, all dependent variables are within permissible limits after Scenario 1 and Scenario 2 optimizations, respectively.

Fig. 2
figure 2

Dependent variable profiles after Scenario 1 (Ploss optimization). a Bus voltage profiles. b Mvar output of generators

Full size image
Fig. 3
figure 3

Dependent variable profiles after Scenario 2 (TVD optimization). a Bus voltage profiles. b Mvar output of generators

Full size image

While the results obtained from A-CSOS and SOS algorithms in Scenario 1 are close to each other, there is an important difference between the results of the two algorithms obtained under Scenario 2. According to Scenario 2.1 results shown in Table 3, the proposed algorithm is 4.44% better than SOS and 5.22% better than OGSA [11] algorithm with the lowest value among the algorithms shown in Table 3. In the Scenario 2.2 analysis, the A-CSOS algorithm yielded a 4.18% better result than the SOS, and 15.32% better than the MALO [23], which regarded the control variables as discrete.

To illustrate the convergence profile of A-CSOS and SOS algorithms, Ploss and TVD value changes over 100 iterations are demonstrated in Figs. 4 and 5, respectively.

Fig. 4
figure 4

The convergence profiles for Scenario 1

Full size image
Fig. 5
figure 5

The convergence profiles for Scenario 2

Full size image

There is a great difference between the convergence speed of A-CSOS and SOS. As Fig. 4 shows, A-CSOS converges to the minimum optimal solution about the fifteenth iteration while SOS needs twenty-five more iterations to converge.

It is observed in Fig. 5 that A-CSOS converges faster as compared to SOS and the results are very promising in all scenarios. The obtained best solution is achieved about the twentieth iteration. It is also noted that logistic map has been very effective to generate organism from the first iteration. Hence, it can be concluded that both the chaos and adaptive penalty approaches are a significant positive contribution to convergence speed.

5.2 Test System 2: IEEE 118-bus power system

Considering that today’s power systems are more complex, it is important to proof the performance of the A-CSOS algorithm in larger power systems. For this reason, Ploss and TVD minimization for IEEE 118-bus power system are studied as Scenario 3 and Scenario 4, respectively. As in analyses on Test System 1, the mentioned variables are considered as discrete in Scenarios 3.2 and 4.2. Seventy-seven control parameters have to be adjusted for the solution of the ORPD problem in IEEE 118-bus test system consisting of fifty-four generators, nine transformers, and fourteen shunt VAR compensators. The bus, generator, and line data are adapted from [33]. The lower and upper permissible voltages at PQ and PV buses are 0.94 and 1.06 p.u., respectively. The permissible tap ratio limits set to 0.9–1.1 p.u.

The comparison of the best result of A-CSOS with SOS and the most recent ORPD studies for Scenario 3 are given in Table 5. The optimal control variable settings for the best result of Scenario 3 are demonstrated in Table 6.

Table 5 Comparison of the results for Scenario 3
Full size table
Table 6 Optimal value of control variables for best result of Ploss optimization on Test System 2
Full size table

It is clear from Tables 5 and 6 that, in contrast to Scenario 1, where the number of bus is increased and the power system is more complex, the superiority of the proposed algorithm over the SOS is more obvious.

In addition, as the number of buses increases, it becomes difficult to find a feasible and minimum solution for the SOS. The active power loss is reduced to 118.4089 MW and 119.4842 MW from the initial case Ploss of 132.8629 MW via A-CSOS for Scenario 3.1 and 3.2, respectively. Moreover, A-CSOS algorithm is 4.45% and 1.86% better than standard SOS and GWO [18], which is the best result of declared state-of-art algorithms in Scenario 3.1. The obtained best result of the proposed algorithm in Scenario 3.2 is 6.63% lesser than SOS.

The comparison of the best result of A-CSOS with SOS and the other state-of-the-art algorithms for Scenario 4 is given in Table 7. Table 7 shows that for Scenario 4.1 and Scenario 4.2, the A-CSOS algorithm provides 34.74% and 40.52% better TVD values than SOS. Compared with the most recent ORPD studies in the literature, the result obtained with A-CSOS is also 5.55% better than NGBWCA [15] that the best result of above-mentioned algorithms for Scenario 4.

Table 7 Comparison of the results for Scenario 4
Full size table

The control variable settings of best results for Scenario 4 are demonstrated in Table 8. Figures 6 and 7 show that the related dependent variables are within the boundaries after Scenario 3 and Scenario 4 optimizations.

Table 8 Optimal value of control variables for best result of TVD optimization on Test System 2
Full size table
Fig. 6
figure 6

Dependent variable profiles after Scenario 3 (Ploss optimization). a Bus voltage profiles. b Mvar output of generators

Full size image
Fig. 7
figure 7

Dependent variable profiles after Scenario 4 (TVD optimization). a Bus voltage profiles. b Mvar output of generators

Full size image

It is observed that Scenario 3.2 and Scenario 4.2 analyses defined as discrete variables are more difficult than the algorithms defined as the continuous variables. Nevertheless, it has been proven that the performance of A-CSOS algorithm in discrete variable ORPD problem is superior to SOS and other algorithms.

Objective function values obtained from the proposed method and SOS over 100 iterations for Scenario 3 and 4 are presented in Figs. 8 and 9. It is appeared from these figures that the SOS algorithm is trapped into local optimum points in the early stage, while the A-CSOS algorithm finds faster and better values due to increase global and local search capability for both scenarios.

Fig. 8
figure 8

The convergence profiles of A-CSOS and SOS for Scenario 3

Full size image
Fig. 9
figure 9

The convergence profiles of A-CSOS and SOS for Scenario 4

Full size image

5.3 Test System 3: IEEE 300-bus power system

To evaluated the performance of the proposed algorithm in more complex test systems, the A-CSOS algorithm is implemented on IEEE 300-bus power system as Test System 3. The IEEE 300-bus power system has 145 control variables including sixty-nine continuous variables related to PV bus voltage magnitudes, sixty-two discrete variables related to tunable tap ratios of tap changing transformers with 0.01 p.u. stepwise, forty-five fixed tap transformer, and fourteen discrete variables related to shunt VAR compensators with 1 Mvar stepwise.

Test system data and initial values of the control variables are adapted from [33]. The permissible maximum and minimum bus voltages are 1.1 p.u. and 0.9 p.u., respectively. The maximum and minimum tap ratios of transformers are the same as the bus voltage limits and are 1.1 and 0.9 p.u.

The A-CSOS and SOS algorithm are applied to IEEE 300-bus test system for minimization of Ploss as Scenario 5 and minimization of TVD as Scenario 6. The active power loss was 408.3155 MW for initial case, and the reactive power outputs of some generators (e.g., Gen-3, -23, -40, -56) and voltage magnitudes of some buses (e.g., Bus-17, -96, -97, -128, -149) exceeded the related limit values.

Table 9 presents the best values obtained after applying the A-CSOS and SOS algorithm on Test System 3 within the scope of Scenario 5 and Scenario 6 analyses.

Table 9 Comparison of the results for Scenario 5 and Scenario 6 on Test System 3
Full size table

Moreover, analogizing the best result of A-CSOS with ALO [22], differential evolutionary PSO (DEEPSO) [34] and mean–variance mapping optimization (MVMO) [34] algorithms is given in Table 9. It should be noted that the DEEPSO and MVMO algorithms were the two best algorithms in the Competition on Application of Modern Heuristic Optimization Algorithms for Solving Optimal Power Flow Problems held in 2014 [34].

According to results, Ploss is decreased to a minimum value of 367.1255 MW from the initial Ploss of 408.3155 MW via A-CSOS, which is the best value in reported results. The tap settings of transformers and Mvar output of shunt VAR compensators for the best result of A-CSOS and SOS algorithms are demonstrated in Figs. 10 and 11, respectively.

Fig. 10
figure 10

Tap settings for the best results in Scenario 5

Full size image
Fig. 11
figure 11

Shunt compensator settings for the best results in Scenario 5

Full size image

After Scenario 6 optimization, where TVD minimization is performed, the TVD value of 5.4286 p.u. initially decreased to 2.7113 p.u. The tap ratios of transformers and the output of shunt compensators for the best result in Scenario 6 are demonstrated in Figs. 12 and 13, respectively.

Fig. 12
figure 12

Tap settings for the best results in Scenario 6

Full size image
Fig. 13
figure 13

Shunt compensator settings for the best results in Scenario 6

Full size image

The dependent variable characteristics after Ploss and TVD optimization are demonstrated in Fig. 14. It can be seen that both objective functions are minimized as well as the related numerous dependent variables are all within the permissible limit values after optimization.

Fig. 14
figure 14

Dependent variable profiles after Ploss and TVD optimization based on A-CSOS algorithm. a Bus voltage profiles. b Mvar output of generators

Full size image

The convergence profile of A-CSOS algorithm for Scenario 5 and Scenario 6 is given in Figs. 15 and 16, respectively.

Fig. 15
figure 15

The convergence profile for Scenario 5

Full size image
Fig. 16
figure 16

The convergence profile for Scenario 6

Full size image

When the convergence characteristics of the two algorithms are examined, it is clear that the effect of the features added to the SOS algorithm is more apparent in large power systems and the convergence performance of the A-CSOS algorithm is much better than the SOS algorithm.

6 Conclusion

In this paper, a new chaos and global competitive ranking-based symbiotic organisms search (A-CSOS) algorithm is suggested to deal with ORPD that is one of the highly nonlinear and non-convex optimization problem. The most important property of SOS algorithm is not to need any particular algorithmic parameters. SOS algorithm is hybridized with chaos theory and self-adaptive penalty approach for designing A-CSOS.

As has been explained broadly in previous chapters, although chaos was integrated to SOS algorithm in literature, only the local search capability was slightly increased, but global search capability of the SOS was impaired. On the other hand, SOS was tended to trap into local minimum points for the reason that the chaos was only applied to the best organism and the parasitism phase was removed. These problems seem to be more apparent especially in complex, nonlinear and non-convex optimization problems such as ORPD.

The effectiveness and efficiency of the proposed A-CSOS algorithm is demonstrated on IEEE 57-, 118-, and 300-bus test power systems for minimizing Ploss and TVD. Simulation results reveal that A-CSOS is provided up to 7.67% Ploss improvement and 44.06% TVD improvement considering the SOS. Moreover, it is clear that the proposed A-CSOS yields up to 1.85% better Ploss value and 15.32% better TVD value than the best result of reported algorithms to the related test cases. According to statistical data of the results given in each scenarios, A-CSOS is considerably better than SOS, statistically. As the problem gets more complicated, the superiority of the A-CSOS over SOS becomes more apparent. Therefore, the performance of A-CSOS is considerably better than basic SOS. Any reduction of power loss is not only providing energy efficiency but also saving considerable money.

The results proved that global search capability and convergence speed of SOS have been considerably improved by utilizing chaos and self-adaptive penalty strategies. While the chaos helps the optimizer to find near global minimum solution in a very short time, GCR eliminates the trial and error process needed to find the ideal penalty coefficients and helps the optimizer to direct the organisms to the optimal feasible region.

Therefore, A-CSOS is an excellent candidate to be implemented on ORPD and other constrained nonlinear optimization problems for the future researches. Further investigation on the performance of A-CSOS using other chaotic maps and adaptive penalty techniques may prove fruitful. Proposed method can be hybridized with other optimization algorithms for improving or investigating performance of the hybrid algorithms.