An adaptive sliding-mode control technique for three-phase UPS system with auto-tuning of switching gain

Abstract

This paper presents an adaptive sliding-mode control (ASMC) technique for a three-phase UPS system with an auto-tuning mechanism of the switching gain. First, a sliding-mode control (SMC) scheme for the three-phase UPS inverter is designed to guarantee the robustness against the system uncertainties and external disturbances. Then, through addition of an adaptive control term, the ASMC algorithm is developed to optimize the switching gain without the prior information of the unknown and bounded uncertainties. It is shown that the upper bounds of the uncertainties are not required to be known in the SMC design. Also, the chattering problem in the reaching mode is considerably alleviated and the excessive use of electric power can be reduced by avoiding overestimation of the switching gain. Both the stability and robustness of the proposed ASMC method are proven by using the Lyapunov theory. In addition, a simple sliding-mode observer is used to estimate the load current without any additional current sensors. Therefore, the proposed ASMC system can accomplish the superior control performance (such as faster voltage recovery under a sudden load change, smaller steady-state error under parameter deviations, and lower THD under nonlinear load) compared to the conventional SMC scheme. Finally, the performance verifications of the proposed algorithm are carried out through the comparative simulation and experimental results on a prototype 1-kVA three-phase UPS inverter using TMS320F28335 DSP.

1 Introduction

Due to increasing importance of the power quality issues, the uninterruptible power supply (UPS) system is becoming more popular as a backup power supply for various applications, such as computer server systems, communication systems, and medical equipments [1–3]. The most important role of the UPS control system is to maintain the sinusoidal output voltage with low total harmonic distortion (THD) under any kind of load conditions. Particularly, for the high-power rectifier loads with a high crest-factor (i.e., nonlinear loads), keeping the low THD values is a key issue in recent years. In accordance with the standards of IEEE 519-1992, the THD component of the output voltage in the UPS system should be less than 5% in general applications such as office and communications equipment, measuring instruments, and household appliances. Meanwhile, it is recommended that the THD value should be less than 3% in special applications such as airport equipment, life support systems, and safety devices [4].

Generally, the performance of the UPS system is influenced by the output filters of the inverter which are tuned to absorb the specified harmonic frequency components. That means, the LC output filters are widely used to provide high quality voltages with low THD. However, these LC filters create complications in the dynamic equations of the UPS inverter. As a result, the control design and stability analysis of the UPS system become more complex. To deal with these problems, many kinds of control strategies [5–12] have been developed by researchers. In [5, 6], hybrid PID control schemes with multiple loops are suggested. These both methods ensure a good performance and an easy implementation. However, for selecting the proper control gains, which guarantee the stable system performance, not a few trials are required. In [7, 8], a deadbeat control (DB) technique has been successfully applied to the UPS system. Although this method certifies the fast dynamic response and high accuracy, the deep dependence on system parameters is its main drawback. Next, a model predictive control (MPC) with a load current observer is proposed in [9]. This scheme has good aspects such as the small steady-state error and the reduced number of the current sensors by load current observer. But, the THD level in output voltage is high. In [10], a repetitive control (RC) is presented for the UPS system. This strategy shows a low voltage distortion level under various load conditions, but it has a problem of slow dynamic responses. Two iterative learning control (ILC) strategies are described in [11], which can achieve a high-performance control. However, the design procedure is complicated. In [12], a feedback linearization control (FLC) scheme is proposed and this technique is possible to accomplish the low THD and fast dynamic response. But, the method does not consider parameter uncertainties.

Looking at sliding-mode control (SMC) technique, it has emerged as a common robust control approach because of its robustness to system uncertainties and insensitivity to external disturbances [13–15]. Actually, the basic concepts of the SMC method are to use the switching gain for driving the system trajectory toward the specific sliding surface and prevent the system trajectory from leaving the sliding surface chosen by the control system designer. Once the system trajectory intersects the sliding surface, then it stays on it afterward. In a classical sliding-mode control strategy, the prior information about the upper bounds of the uncertainties and disturbances is essential to guarantee the reachability of the sliding-mode. However, in the practical applications, it is very difficult to know the exact upper bounds of the uncertainties and disturbances. Also, the large switching gains may lead to extremely strong robustness against the system uncertainties and disturbances, but the practical limitations discard this choice. In order to overcome this drawback, several control strategies have been investigated. As a result, an adaptive sliding-mode control (ASMC) method is one of the most effective approaches because of its good property of combining the robustness of a variable-structure control scheme with the good tracking capability of an adaptive control scheme [16–19].

The aim of this paper is to develop an ASMC technique for the three-phase UPS system with an LC filter. In the first stage, the conventional SMC system for three-phase UPS inverter is designed. Then, the ASMC scheme is developed by adding an adaptive control law. In this paper, the adaptive control law automatically tunes the switching gain of the SMC technique, so the proposed control system does not need any prior information for the upper bounds of the system uncertainties and disturbances. Likewise, the chattering problem in the reaching mode can be remarkably attenuated and the excessive use of electric power can be reduced. With the help of Lyapunov theory, the reachability and stability of the sliding mode dynamics are analytically proven. Also, a simple sliding-mode observer is employed to exactly estimate the unknown load currents without any additional current sensors. To verify the feasibility of the proposed ASMC method, simulations are carried out with MATLAB/Simulink software and experiments are performed with a prototype 1-kVA three-phase UPS inverter system using TMS320F28335 DSP. Moreover, the upgraded performances of the proposed ASMC algorithm are justified by faster voltage recovery under a sudden load change, smaller steady-state error under parameter deviations, and lower THD under a nonlinear load in comparison with the conventional SMC method.

2 Formulation of three-phase UPS system

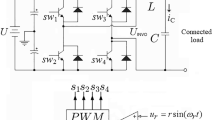
The three-phase UPS inverter system with an LC output filter is illustrated in Fig. 1. It is composed of a DC-link ($V_{dc})$, a three-phase IGBT inverter, filter capacitors ($C_{f})$, filter inductors ($L_{f})$, and a three-phase load. The LC output filter is employed to filter out the harmonic components of the inverter outputs. Applying KVL and KCL to the LC output filter, the three-phase UPS inverter system can be modeled by the following differential equations [9]:

$$\begin{aligned} C_f \frac{\mathrm{d} \mathbf{V}_L }{\mathrm{d}t}=\mathbf{I}_i -\mathbf{I}_L,\quad L_f \frac{\mathrm{d} \mathbf{I}_i }{\mathrm{d}t}=\mathbf{V}_i -\mathbf{V}_L \end{aligned}$$

(1)

where V $_{i}$ = [$v_{iA} v_{iB} v_{iC}]^\mathrm{T}$ is a line to neutral inverter voltage vector, V $_{L}$ = [$v_{LA} v_{LB} v_{LC}]^\mathrm{T}$ is a line to neutral load voltage vector, I $_{i}$ = [$i_{iA} i_{iB} i_{iC}]^\mathrm{T}$ is a phase inverter current vector, and I $_{L}$ = [$i_{LA} i_{LB} i_{LC}]^\mathrm{T}$ is a phase load current vector.

Fig. 1

Circuit diagram of a three-phase UPS inverter system with an LC filter

The differential equations (1) in the abc-axis stationary reference frame can be transformed to those in the dq-axis synchronously rotating reference frame [12]:

$$\begin{aligned} \dot{v}_{Ld}&= \omega v_{Lq} +\left( {h_1 +\Delta h_1 } \right) i_{id} -\left( {h_1 +\Delta h_1 } \right) i_{Ld} \nonumber \\ \dot{v}_{Lq}&= -\omega v_{Ld} +\left( {h_1 +\Delta h_1 } \right) i_{iq} -\left( {h_1 +\Delta h_1 } \right) i_{Lq} \nonumber \\ \dot{i}_{id}&= -\left( {h_2 +\Delta h_2 } \right) v_{Ld} +\omega i_{Lq} +\left( {h_2 +\Delta h_2 } \right) v_{id} \nonumber \\ \dot{i}_{iq}&= -\left( {h_2 +\Delta h_2 } \right) v_{Lq} -\omega i_{Ld} +\left( {h_2 +\Delta h_2 } \right) v_{iq} \end{aligned}$$

(2)

where $\omega$ is the source angular frequency ($\omega$=2$\pi$f), $f$ is the fundamental frequency, $h_{1}$ and $h_{2}$ are the parameters determined by the filter capacitance ($C_{f})$ and inductance ($L_{f})$, i.e., $h_{1}$ = 1/$C_{f}$, $h_{2}$ = 1/$L_{f}$, and $\Delta h_{1}$ and $\Delta h_{2}$ are the parameter deviations of $h_{1}$ and $h_{2}$, respectively. Notice that the dq-axis load voltages ($v_{Ld}$ and $v_{Lq})$ and the dq-axis inverter currents ($i_{id}$ and $i_{iq})$ are state variables, the dq-axis inverter voltages ($v_{id}$ and $v_{iq})$ are the control outputs, and the dq-axis load currents ($i_{Ld}$ and $i_{Lq})$ are considered as the unknown external disturbances.

3 Sliding-mode controller design and stability analysis

In this section, a conventional SMC law [20] is systematically designed for the three-phase UPS system. The conventional SMC design includes the following two procedures: the design of a sliding surface function and the construction of a control law. First, the errors of the state variables can be defined as $e_{vd}=v_{Ld}-v_{dr}$, $e_{vq}=v_{Lq}-v_{qr}$, $e_{id}=i_{id}-i_{dr}$, $e_{iq}=i_{iq}-i_{qr }$where $v_{dr}$, $v_{qr}$ are the constant reference values of $v_{Ld}$ and $v_{Lq}$, and $i_{qr}$ and $i_{dr}$ are the reference values of $i_{id}$ and $i_{iq}$, respectively. The detailed expressions for the $i_{dr}$ and $i_{qr}$ are given by

$$\begin{aligned} i_{dr}&= i_{Ld} -\frac{1}{h_1 +\Delta h_1 }\omega v_{qr} \approx i_{Ld} -\frac{1}{h_1 }\omega v_{qr} \nonumber \\ i_{qr}&= i_{Lq} +\frac{1}{h_1 +\Delta h_1 }\omega v_{dr} \approx i_{Lq} -\frac{1}{h_1 }\omega v_{dr} \end{aligned}$$

(3)

where ${\vert }\Delta h_{1}{\vert }$ is assumed to be sufficiently small and $h_{1}+\Delta h_{1}$ can be set as $\alpha$. Then, the error state-space model can be expressed as

$$\begin{aligned} \dot{e}=Ae+B\left[ {u+u_d } \right] \end{aligned}$$

(4)

where

$$\begin{aligned} A&= \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 0&{} \omega &{} {h_1 }&{} 0 \\ {-\omega }&{} 0&{} 0&{} {h_1 } \\ 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0 \\ \end{array} }} \right] , B=\left[ {{\begin{array}{l@{\quad }l} 0&{} 0 \\ 0&{} 0 \\ {h_2 }&{} 0 \\ 0&{} {h_2 } \\ \end{array} }} \right] , e=\left[ {{\begin{array}{l} {e_{vd} } \\ {e_{vq} } \\ {e_{id} } \\ {e_{iq} } \\ \end{array} }} \right] , \\ u&= \left[ {{\begin{array}{l} {v_{id} } \\ {v_{iq} } \\ \end{array} }} \right] ,\\ u_d&= \left[ {{\begin{array}{l} {d_d } \\ {d_q } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {-v_{Ld} +\frac{1}{h_2 }\omega i_{Lq} -\frac{\Delta h_2 }{h_2 }v_{Ld} +\frac{\Delta h_2 }{h_2 }v_{id} } \\ {-v_{Lq} -\frac{1}{h_2 }\omega i_{Ld} -\frac{\Delta h_2 }{h_2 }v_{Lq} +\frac{\Delta h_2 }{h_2 }v_{iq} } \\ \end{array} }} \right] \end{aligned}$$

and ${\vert }\Delta h_{2}{\vert }\le \rho _{k}\cdot h_{2}$, $\rho _{k}$ is unknown, and $0 \le \rho _{k} < 1$.

In the closed-loop control system (4), $A \in R^{4 \times 4}$ and $B \in R^{4\times 2 }$ are constant matrices. Then, assuming that the following linear matrix inequality (LMI) condition [20] is feasible

$$\begin{aligned} Y > 0 , \Phi ^{T}\left( {AY+YA^{T}} \right) \Phi < 0 \end{aligned}$$

(5)

where $Y\in R^{4\times 4}$ is a determined positive definite matrix, and $\Phi \in R^{4\times 2}$ is a full-rank matrix such that $\Phi ^{T}B$ = 0 and $\Phi \Phi ^{T}= I$. Then the sliding surface function $S$ is defined by the following equation:

$$\begin{aligned} S=\Gamma e=\left( {B^{T}PB} \right) ^{-1}B^{T}Pe=0 \end{aligned}$$

(6)

where $P=Y^{-1}$, $\Gamma$ = [$\Gamma _{1} \Gamma _{2}$]$^{\mathrm{T}}$ and $S$ = [$\Gamma _{1}e \Gamma _{2}e$]$^{\mathrm{T}}$ = [$S_{1} S_{2}$]$^{\mathrm{T}}$.

Next, the second procedure is to determine the control law. Let us choose the control output variables $v_{id}$ and $v_{iq}$ as

$$\begin{aligned} v_{id}&= v_{db} +v_{df} \nonumber \\ v_{iq}&= v_{qb} +v_{qf} \end{aligned}$$

(7)

where $v_{db}$ and $v_{qb}$ are the switching feedback control law, and $v_{df}$ and $v_{qf}$ are the sliding-mode compensator given as

$$\begin{aligned} v_{df}&= v_{Ld} -\frac{1}{h_2 }\omega i_{Lq} \nonumber \\ v_{qf}&= v_{Lq} +\frac{1}{h_2 }\omega i_{Ld} \end{aligned}$$

(8)

The control outputs, which force the system to $S$ = 0, are defined by the following switching feedback control law:

$$\begin{aligned} v_{db}&= -D_d e-\rho _d^*\left( t \right) \hbox {sgn}\left( {S_1 } \right) \nonumber \\ v_{qb}&= -D_q e-\rho _q^*\left( t \right) \hbox {sgn}\left( {S_2 } \right) \end{aligned}$$

(9)

where $\Gamma$A = [$D_{d} D_{q}]^\mathrm{T}$ and

$$\begin{aligned} \rho _{d}^{*} \left( t \right)&= \varepsilon _d +\rho ^{*}\left[ {2\left| {v_{Ld} } \right| +\frac{\omega \left| {i_{Lq} } \right| }{h_2 }+\left| {D_d e} \right| } \right] \nonumber \\ \rho _{q}^{*} \left( t \right)&= \varepsilon _q +\rho ^{*}\left[ {2\left| {v_{Lq} } \right| +\frac{\omega \left| {i_{Ld} } \right| }{h_2 }+\left| {D_q e} \right| } \right] \end{aligned}$$

(10)

with $\rho ^{*} = \rho _{k}$/($1 - \rho _{k}), \varepsilon _{d} >$ 0, and $\varepsilon _{q} >$ 0.

Generally, the stability analysis of the sliding-mode control system can be divided into two steps: the first step is the analysis of the sliding-mode dynamics to approach to zero in a finite time, and the second step is the analysis of the reachability condition to guarantee that the sliding motion is reached from an initial time.

First, to analyze the sliding-mode dynamics, an associated vector $z$ is defined as follows:

$$\begin{aligned} z=\left( {\Phi ^{T}Y\Phi } \right) ^{-1}\Phi ^{T}e \end{aligned}$$

(11)

where $z\in R^{2}$. Then, the time derivative of $z$ is calculated as

$$\begin{aligned} \dot{z}=\left( {\Phi ^{T}Y\Phi } \right) ^{-1}\Phi ^{T}AY\Phi {z}. \end{aligned}$$

(12)

Let us define a Lyapunov function for (5) as

$$\begin{aligned} V\left( z \right) =z^{T}\left( {\Phi ^{T}Y\Phi } \right) z. \end{aligned}$$

(13)

And the time derivative of the Lyapunov function $V(z)$ can be obtained by

$$\begin{aligned} \dot{V}\left( z \right) =2z^{T}\Phi ^{T}AY\Phi {z}\le 0. \end{aligned}$$

(14)

Thus, the sliding surface (6) is asymptotically stable if there exists a positive definite matrix $Y\in R^{4\times 4}$.

Second, the reachability condition $S^{T}\dot{S}$ is satisfied for all $S\ne$ 0 [18] as follows:

$$\begin{aligned} S^{T}\dot{S}&= S^{T}\left( {\Gamma Ae+u+u_d } \right) \nonumber \\&= S_1 \left( {D_d e+v_{id} +d_d } \right) +S_2 \left( {D_q e+v_{iq} +d_q } \right) \nonumber \\&\le \left| {S_1 } \right| \left( {\rho _k \left| {v_{Ld} } \right| +\rho _k \left| {v_{id} } \right| -\rho _d } \right) \nonumber \\&+ \left| {S_2 } \right| \left( {\rho _k \left| {v_{Lq} } \right| +\rho _k \left| {v_{iq} } \right| -\rho _q } \right) \nonumber \\&\le \left| {S_1 } \right| \left( {\rho _k \left| {v_{Ld} } \right| +\rho _k \left[ {\begin{array}{l} \left| {v_{Ld} } \right| +{\omega \left| {i_{Lq} } \right| }/{h_2 } \\ +\left| {D_d e} \right| +\rho _d \\ \end{array}} \right] -\rho _d } \right) \nonumber \\&+ \left| {S_2 } \right| \left( {\rho _k \left| {v_{Lq} } \right| +\rho _k \left[ {\begin{array}{l} \left| {v_{Lq} } \right| +{\omega \left| {i_{Ld} } \right| }/{h_2 } \nonumber \\ +\left| {D_q e} \right| +\rho _q \\ \end{array}} \right] -\rho _q } \right) \\&\le -\left( {1-\rho _k } \right) \varepsilon _d \left| {S_1 } \right| -\left( {1-\rho _k } \right) \varepsilon _q \left| {S_2 } \right| \end{aligned}$$

(15)

Therefore, according to (13), (14), and (15), the global state-space model (4) with a SMC law is asymptotically stable in spite of the system uncertainties and external disturbances. However, the performance of the conventional SMC law depends on the switching gain ($\rho ^{*})$. Note that too small a value $\rho ^{*}$ can cause a slow transient response, and too large a value of $\rho ^{*}$ is able to induce the chattering problem in the steady-state response and the excessive use of electric power. Therefore, $\rho ^{*}$ is a critical control parameter which can efficiently affect the control performance. To calculate the proper $\rho ^{*}$, the information of the upper bounds of the system uncertainties is needed. Unfortunately, this information is very hard to achieve in practice. In next section, an adaptive algorithm will be included into the SMC law in order to auto-calculate the value of $\rho ^{*}$.

4 Adaptive sliding-mode controller design and stability analysis

The main advantage of the SMC method is its robustness to the system uncertainties such as parameter deviations and external disturbances. In order to select a sliding-mode switching gain, it is necessary to know the upper bounds of the system uncertainties. However, the parameter deviations of the system are difficult to measure, and the exact value of the external load disturbances is also difficult to identify in real practical applications. In this section, an adaptive SMC law is proposed to auto-tune the appropriate switching gain without measurements of the system uncertainties. Equivalent to the switching gain $\rho _{d}^{*}$ and $\rho _{q}^{*}$ expressed in (10), the adaptive tuning algorithm for the bounds of $\rho _{d}$ and $\rho _{q}$ is modified to be

$$\begin{aligned} \rho _d \left( t \right)&= \varepsilon _d +\hat{{\rho }}\left[ {2\left| {v_{Ld} } \right| +\frac{\omega \left| {i_{Lq} } \right| }{h_2 }+\left| {D_d e} \right| } \right] \nonumber \\ \rho _q \left( t \right)&= \varepsilon _q +\hat{{\rho }}\left[ {2\left| {v_{Lq} } \right| +\frac{\omega \left| {i_{Ld} } \right| }{h_2 }+\left| {D_q e} \right| } \right] \end{aligned}$$

(16)

where $\hat{{\rho }}$ is the tuned value of $\rho$ by an adaptive tuning law. As stated in the previous section, the small values of $\rho _\mathrm{d}$ and $\rho _\mathrm{q}$ are more suitable for steady-state operating condition. However, in terms of control activities, too small values of $\rho _\mathrm{d}$ and $\rho _\mathrm{q}$ can lead to slow transient responses. Therefore, the values of $\rho _\mathrm{d}$ and $\rho _\mathrm{q}$ should satisfy both of the two stated sides, i.e., steady-state and transient responses.

Note that the adaptive tuning law should use the estimated $\hat{{\rho }}$ because its exact value is unknown. Now let the adaptive tuning law be:

$$\begin{aligned} \dot{\hat{{\rho }}}=\frac{1}{\lambda }\left[ {\begin{array}{l} \left| {S_1 } \right| \cdot \left( {2\left| {v_{Ld} } \right| +\frac{\omega \left| {i_{Lq} } \right| }{h_2 }+\left| {D_d e} \right| } \right) +\\ \left| {S_2 } \right| \cdot \left( {2\left| {v_{Lq} } \right| +\frac{\omega \left| {i_{Ld} } \right| }{h_2 }+\left| {D_q e} \right| } \right) \\ \end{array}} \right] \end{aligned}$$

(17)

where $\lambda$ is the positive adaptive gain. The adaptation speed of $\hat{{\rho }}$ can be modulated by $\lambda$ [17]. Employing a fast adaptation law leads to an improved tracking performance, but at the same time it can result in a poor robustness that can adversely affect the stability of the control system. To be more specific, there typically exists a balance between stability and adaptation margins. Thus, the adaptive gain $\lambda$ should be selected by carefully observing the balance between the transient response and system stability. Then, the control output variables $v_{id}$ and $v_{iq}$ are

$$\begin{aligned} v_{id}&= v_{Ld} -\frac{1}{h_2 }\omega i_{Lq} -D_d e-\rho _d \left( t \right) \hbox {sgn}\left( {S_1 } \right) \nonumber \\ v_{iq}&= v_{Lq} +\frac{1}{h_2 }\omega i_{Ld} -D_q e-\rho _q \left( t \right) \hbox {sgn}\left( {S_2 } \right) . \end{aligned}$$

(18)

Figure 2 shows the block diagram of the proposed ASMC scheme. In the following, the validity of the modified control law (16) and (17) is confirmed by using Lyapunov theory. Consider a Lyapunov function as [19]

$$\begin{aligned} V\left( {S,\tilde{\rho }} \right) =\frac{1}{2}S^{T}S+\frac{\zeta }{2}\tilde{\rho }^{2} \end{aligned}$$

(19)

where $\tilde{\rho }=\rho ^*-\hat{{\rho }}, \zeta =\left( {1-\rho _k } \right) \lambda$. By taking the time derivative of $V\left( {\sigma ,\tilde{\rho }} \right)$ and using (14), $\dot{V}\left( {\sigma ,\tilde{\rho }} \right)$ can be expressed as

$$\begin{aligned} \dot{V}\left( {S,\tilde{\rho }} \right)&= S^{T}\dot{S}-\zeta \tilde{\rho }\dot{\hat{{\rho }}}=\sigma ^{T}\left( {\Gamma Ae+u+u_d } \right) -\zeta \tilde{\rho }\dot{\hat{{\rho }}} \nonumber \\&= S_1 \left( {D_d e+v_{id} +d_d } \right) +S_2 \left( {D_q e+v_{iq} +d_q } \right) \nonumber \\&-\zeta \tilde{\rho }\dot{\hat{{\rho }}} \nonumber \\&\le \left| {S_1 } \right| \left( {\rho _k \left[ {2\left| {v_{Ld} } \right| +\frac{1}{h_2 }\omega \left| {i_{Lq} } \right| +\left| {D_d e} \right| } \right] }\right. \nonumber \\&\left. {-\left[ {1-\rho _k } \right] \rho _d } \right) + \nonumber \\&\left| {S_2 } \right| \left( {\rho _k \left[ {2\left| {v_{Lq} } \right| +\frac{1}{h_2 }\omega \left| {i_{Ld} } \right| +\left| {D_q e} \right| } \right] }\right. \nonumber \\&\left. {-\left[ {1-\rho _k } \right] \rho _q } \right) -\zeta \tilde{\rho }\dot{\hat{{\rho }}}\nonumber \\&\le -\left[ {1-\rho _k } \right] \left( {\varepsilon _d \left| {S_1 } \right| +\varepsilon _q \left| {S_2 } \right| } \right) -\zeta \tilde{\rho }\dot{\hat{{\rho }}} \nonumber \\&+\left[ {1-\rho _k } \right] \cdot \tilde{\rho }\cdot \left| {S_1 }\right| \cdot \nonumber \\&\left[ {2\left| {v_{Ld} } \right| +\frac{1}{h_2 }\omega \left| {i_{Lq} } \right| +\left| {D_d e} \right| } \right] \nonumber \\&+ \left[ {1-\rho _k } \right] \cdot \tilde{\rho }\cdot \left| {S_2 }\right| \cdot \nonumber \\&\left[ {2\left| {v_{Lq} } \right| +\frac{1}{h_2 }\omega \left| {i_{Ld} } \right| +\left| {D_q e} \right| } \right] \nonumber \\&\le -\left[ {1-\rho _k } \right] \left( {\varepsilon _d \left| {S_1 }\right| +\varepsilon _q \left| {S_2 } \right| } \right) \end{aligned}$$

(20)

Hence, the convergence of $S$ and $\tilde{\rho }$ is proven by the Lyapunov stability criterion. Thus, the convergence of the estimated value $\hat{{\rho }}$ and the reachability condition can be guaranteed. Consequentially, the proposed ASMC technique offers two advantageous characteristics which are: (i) the knowledge on the upper bounds of the system uncertainties is not needed and (ii) the proposed ASMC method is designed to automatically calculate the switching gain according to the operating condition so that the chattering problem in the reaching mode is remarkably alleviated. As a result, the excessive use of electric power is also reduced.

Fig. 2

Block diagram of the proposed adaptive sliding-mode control scheme

5 Observer-based adaptive sliding-mode control law

In this section, a conventional sliding-mode load current observer [20] is utilized for the purpose of estimating the load currents $i_{Ld}$ and $i_{Lq}$. The estimated load currents would be used instead of the load current data measured by current sensors. The use of an observer is motivated by the fact that the sensors can create a sudden breakdown and can provide inaccurate information due to noises. Thus, avoiding the current sensors also makes the overall system more reliable and reduces the system cost.

In order to accurately estimate the load currents $i_{Ld}$ and $i_{Lq}$, the following sliding-mode observer (SMO) is used:

$$\begin{aligned} \dot{\hat{{v}}}_{Ld}&= \omega v_{Lq} +h_1 i_{id} +l_d \hbox {sgn}\left( {v_{Ld} -\hat{{v}}_{Ld} } \right) \nonumber \\ \dot{\hat{{v}}}_{Lq}&= -\omega v_{Ld} +h_1 i_{iq} +l_q \hbox {sgn}\left( {v_{Lq} -\hat{{v}}_{Lq} } \right) \end{aligned}$$

(21)

where $l_{d} >$ 0, $l_{q} >$ 0. By referring to the standard SMO methods [20], it is easy to see that $i_{Ld} \approx -\frac{l_d }{h_1 }\hbox {sgn}(v_{Ld} -\hat{{v}}_{Ld} ) , i_{Lq} \approx -\frac{l_q }{h_1 }\hbox {sgn}(v_{Lq} -\hat{{v}}_{Lq} )$ in the steady-state.

The estimated load currents $\hat{{i}}_{Ld} , \hat{{i}}_{Lq}$ can be reconstructed as:

$$\begin{aligned} \dot{\hat{{i}}}_{Ld}&= -\frac{1}{1+\delta _d s}\frac{l_d }{h_1 }\hbox {sgn}\left( {v_{Ld} -\hat{{v}}_{Ld} } \right) \nonumber \\ \dot{\hat{{i}}}_{Lq}&= -\frac{1}{1+\delta _q s}\frac{l_q }{h_1 }\hbox {sgn}\left( {v_{Lq} -\hat{{v}}_{Lq} } \right) \end{aligned}$$

(22)

where $s$ is the Laplace variable, and 0 $< \delta _{d} \ll$ 1, 0 $< \delta _{q} \ll$ 1 are sufficiently small filter time constants.

If the estimated load currents $\hat{{i}}_{Ld} , \hat{{i}}_{Lq}$ are used instead of $i_{Ld}, i_{Lq}$, then the dq-axis load currents error can be estimated as follows:

$$\begin{aligned} \hat{{e}}_{id}&= i_{id} -\hat{{i}}_{Ld} +\frac{1}{h_1 }\omega v_{qr} \nonumber \\ \hat{{e}}_{iq}&= i_{iq} -\hat{{i}}_{Lq} -\frac{1}{h_1 }\omega v_{dr} \end{aligned}$$

(23)

Finally, the observer-based control law $v_{id}$ and $v_{iq}$, which involves an ASMC law and a load current observer, can be rewritten as

$$\begin{aligned} v_{id}&= v_{Ld} -\frac{1}{h_2 }\omega \hat{{i}}_{Lq} -D_d \hat{{e}}-\hat{{\rho }}_d \left( t \right) \hbox {sgn}\left( {\hat{{S}}_1 } \right) \nonumber \\ v_{iq}&= v_{Lq} +\frac{1}{h_2 }\omega \hat{{i}}_{Ld} -D_q \hat{{e}}-\hat{{\rho }}_q \left( t \right) \hbox {sgn}\left( {\hat{{S}}_2 } \right) \nonumber \\ \hat{{\rho }}_d \left( t \right)&= \varepsilon _d +\hat{{\rho }}\left[ {2\left| {v_{Ld} } \right| +\frac{1}{h_2 }\omega \left| {\hat{{i}}_{Lq} } \right| +\left| {D_d \hat{{e}}} \right| } \right] \nonumber \\ \hat{{\rho }}_q \left( t \right)&= \varepsilon _q +\hat{{\rho }}\left[ {2\left| {v_{Lq} } \right| +\frac{1}{h_2 }\omega \left| {\hat{{i}}_{Ld} } \right| +\left| {D_q \hat{{e}}} \right| } \right] \end{aligned}$$

(24)

where $\hat{{e}} = \left[ {e_{vd} ,e_{vq} , \hat{{e}}_{id} , \hat{{e}}_{iq} } \right] ^{T}, \hat{{S}}_1 =\Gamma _1 \hat{{e}}, \hat{{S}}_2 =\Gamma _2 \hat{{e}}$, and

$$\begin{aligned} \dot{\hat{{\rho }}}=\frac{1}{\lambda }\left[ {\begin{array}{l} \left| {\hat{{S}}_1 } \right| \cdot \left( {2\left| {v_{Ld} } \right| +\frac{1}{h_2 }\omega \left| {\hat{{i}}_{Lq} } \right| +\left| {D_d \hat{{e}}} \right| } \right) + \\ \left| {\hat{{S}}_2 } \right| \cdot \left( {2\left| {v_{Lq} } \right| +\frac{1}{h_2 }\omega \left| {\hat{{i}}_{Ld} } \right| +\left| {D_q \hat{{e}}} \right| } \right) \\ \end{array}} \right] . \end{aligned}$$

(25)

6 Performance verifications

In order to evaluate the system performance of the proposed ASMC strategy, both simulations and experiments have been carried out on a prototype 1-kVA three-phase UPS system using TMS320F28335 DSP. Figure 3 shows the overall configuration of a three-phase UPS inverter system and Table 1 summarizes its whole system parameters. In order to obtain a better filter performance, both $L_{f}$ and $C_{f}$ with larger values can be used. However, these large values increase the system cost and volume, and in particular a large current flows into the capacitor even at no load condition. Thus, there is a trade-off when choosing the values of $L_{f}$ and $C_{f}$. Note that as listed in Table 1, an LC output filter of each phase is designed with $L_{f}$ = 10 mH and $C_{f}$ = 6.25 $\upmu$F, and its cut-off frequency is calculated as 600 Hz.

Fig. 3

Overall configuration of a three-phase UPS inverter system

Table 1 System parameters

In this paper, the MATLAB/Simulink package is used for simulating the UPS inverter system, and experiments are performed on a prototype of 1-kVA three-phase UPS inverter system with Texas Instruments DSP TMS320F28335. The LV-25P voltage sensor and LTS 6-NP current sensor manufactured by LEM are utilized to capture the feedback information signals. The both voltage and current signals are first measured, and then digitized using A/D converters.

To highlight the performance of the proposed control system, a comparison is presented between the proposed ASMC scheme and the conventional SMC scheme as discussed earlier. Note that the adaptive control law suggested in this paper can prevent an overestimation of the switching gain. For the both control laws, the values of the parameters are designed as $\varepsilon _{d}=\varepsilon _{q}$ = 0.1, $\lambda$ = 0.2, $\delta _{d}$ = $\delta _{q} = 1\times 10^{-4}, l_{d} = 6\times 10^{5}, l_{q} = 4\times 10^{5}$ because these parameters can achieve the good control performance during verification process and fulfill the requirement of stability. The proposed ASMC method is designed to minimize the switching gain without affecting the fast transient response. Similarly, depending on the various load conditions, the switching gain of the ASMC scheme can be changed appropriately. Thus, the initial value of $\hat{{\rho }}$ is set to be zero. Also, the controller matrix $\Gamma A$ is selected as follows:

$$\begin{aligned} \Gamma A=\left[ {{\begin{array}{l} {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {-0.0007}&{}\quad {0.8405}&{} \quad {356.7148}&{} \quad {0.2980} \\ \end{array} }} \\ {{\begin{array}{llll} {-1.8395}&{} \quad {-0.0057}&{} \quad {-2.4332}&{} \quad {780.7159} \\ \end{array} }} \nonumber \\ \end{array} }} \right] ^{\mathrm{T}}.\nonumber \\ \end{aligned}$$

(26)

On the other hand, the parameter $\rho ^{*}$of the conventional SMC method is selected to be 2 to guarantee the global stability, and this value is also set to reveal the performance of the SMC under an overestimated switching gain. This is due to the fact that there could be no conspicuous differences for the comparative simulation and experimental results between the conventional SMC and the proposed ASMC if the switching gain of the SMC acquires appropriate values.

In this paper, three conditions (i.e., a resistive load with a step change, a resistive load with parameter deviations, and a nonlinear load) are provided to confirm the system performance via simulations and experiments. In the first condition, a load step change (no load to full load) is employed to show the fast transient response. In the second condition, the parameter deviations of the LC output filter are given. It is known that the capacitance value of the output filter is mainly affected by the changes in temperature around the capacitor and the dielectric aging because the dielectric properties may change. Also, the filter inductance is influenced by the temperature rise in the inductor and the saturation in the magnetic core [23]. In practical applications, the most common tolerance variations for filter capacitors and inductors are within $\pm 10~\%$ when used as a filter. In this paper, it is assumed that the parameter values of the LC output filter are reduced by 30 % i.e., $L_{f} = (100-30~\%)\times 10$ = 7 mH and $C_{f}$ = (100–30 %)$\times$6.25 = 4.375 $\upmu$F in order to certainly verify the robustness against system uncertainties. In the third condition, the nonlinear load is constructed with a three-phase diode rectifier and a 500-$\Omega$ resistance ($R_{non})$.

6.1 Simulation results

Figures 4 and 5 illustrate the simulation results of the proposed ASMC method and the conventional SMC method under three different conditions, respectively. Each figure shows the waveforms of load voltages (V $_{L})$, load currents (I $_{L})$, load voltage error (V $_{L\;\; \mathrm{error}})$, and estimated load currents (${\hat{\mathbf{I}}}_L )$. First, Figs. 4a and 5a show the output voltage transient response under a resistive load condition with a step change (no load to full load) at instant of 0.055 s. Second, Figs. 4b and 5b show the waveforms under a resistive load condition with parameter deviations. Next, Figs. 4c and 5c show the simulation results under a nonlinear load condition with a three-phase diode rectifier. According to Fig. 4a, the proposed ASMC method shows that the voltage dip depth is about 50 V during transient-state when the load changes with a step. In Figs. 4b, c, the voltage error V $_{L \;\; \mathrm{error}}$ during steady-state is under 3V. In addition, the THDs are lower than 0.5 % under three conditions as shown in Fig. 4. On the other hand, Fig. 5a shows that the voltage dip depth of the SMC scheme is about 63 V during transient-state. In Figs. 5b, c, during steady-state the load voltage error V $_{L \;\; \mathrm{error}}$ is within 10 V and the THD of the output voltage is about 2.7 % under the nonlinear load. Based on Figs. 4 and 5, Table 2 provides the transient and THD performances of the simulation results under the three different conditions.

Fig. 4

Simulation results of a three-phase UPS system with the proposed ASMC method under various load conditions. a Resistive load with a step change (no load to full load). b Resistive load with parameter deviations ($-$30 % of $L_{f}$ and $C_{f})$. c Nonlinear load

Fig. 5

Simulation results of a three-phase UPS system with the conventional SMC method under various load conditions. a Resistive load with a step change (no load to full load). b Resistive load with parameter deviations ($-$30 % of $L_{f}$ and $C_{f})$. c Nonlinear load

Table 2 Transient and THD performance of simulation results

Figure 6 shows the trajectories of the adaptive switching gain $\hat{{\rho }}$ for the proposed ASMC technique under three load conditions. It can be observed that the adaptive control law approximates a suitable switching gain and prevents its overestimation under various conditions.

Fig. 6

Trajectories of an adaptive switching gain under three conditions

6.2 Experimental results

Experimental results are provided to further demonstrate the effectiveness of the proposed ASMC method. Figures 7 and 8 show the experimental results under the same conditions as Figs. 4 and 5, respectively. Since the digital oscilloscope used has only four channels, each figure illustrates the following waveforms: phase-$A$ load voltage (V $_{LA})$, phase-$A$ load current (I $_{LA})$, phase-$A$ load voltage error (V $_{LA \;\; \mathrm{error}})$, and estimated phase-$A$ load current (${\hat{\mathbf{I}}}_{LA} )$. In Figs. 7a and 8a, when the load suddenly changes with a step, the load voltage dip depths of the proposed ASME method and the conventional SMC method are observed as about 25 and 53 V, respectively. Also, it is observed from Figs. 7c and 8c that the THDs of both control schemes are recorded as 2 and 4 %, respectively, under the nonlinear load condition. Table 3 summarizes the transient and THD performances of the experimental results depicted in Figs. 7 and 8.

Fig. 7

Experimental results of a three-phase UPS system with the proposed ASMC method under various load conditions. a Resistive load with a step change (no load to full load). b Resistive load with parameter deviations ($-$30 % of $L_{f}$ and $C_{f})$. c Nonlinear load

Fig. 8

Experimental results of a three-phase UPS system with the conventional SMC method under various load conditions. a Resistive load with a step change (no load to full load). b Resistive load with parameter deviations ($-$30 % of $L_{f}$ and $C_{f})$. c Nonlinear load

Table 3 Transient and THD performance of experimental results

In these results, the proposed ASMC scheme demonstrates the better performances such as more rapid voltage recovery and lower THDs compared with the conventional SMC method. It can be concluded that the adaptive control law of the proposed control technique appropriately tunes the switching gain against the system uncertainties and disturbances.

7 Conclusion

This paper presented an adaptive sliding-mode control (ASMC) technique for a three-phase UPS system with an LC filter. In this paper, the proposed adaptive control law can appropriately adjust the switching gain without the knowledge of the system uncertainties and external disturbances. Also, the reachability and stability of the sliding mode dynamics were established mathematically. Finally, the proposed ASMC scheme justified a better voltage regulation capability (i.e., faster voltage recovery under a sudden load change, smaller steady-state error under parameter deviations, and lower THD under a nonlinear load) than the conventional SMC scheme, via simulations and experiments on a prototype 1-kVA three-phase UPS system.