Channeling the final say in politics: a simple mechanism

Abstract

We examine public project provision and redistribution in a model of legislative bargaining and provide a foundation of how to channel the say. We consider a large and heterogeneous legislature and show that socially optimal outcomes are obtained by a mechanism based on the majority rule that involves two proposal-making rounds, with the minority moving first and the majority moving second.

1 Introduction

Can we design legislative bargaining for public project provision and redistribution such that outcomes maximize aggregate utility? In this paper, we answer this inquiry affirmatively by introducing a simple dynamic proposal-making procedure and showing that any equilibrium outcome of the underlying game is socially optimal.

To elaborate, we analyze an environment that consists of a large legislature of risk-neutral legislators (or members), which decides by majority rule whether or not to carry out a costly public project—henceforth simply called project.¹ Individual utilities are heterogeneous, with some legislators benefiting from the project—henceforth called winners—and the others losing—henceforth called losers—relative to per-capita costs.² We proceed on the assumption that losers account for a majority of the legislature, but our results also hold when winners account for a majority. We further consider that there are small but positive deadweight costs of redistribution. A (utilitarian) socially optimal allocation will thus require the absence of transfers. It will also prescribe project provision if and only if aggregate benefits exceed production costs. Whether a project is socially efficient or not, as well as the identity of winners and losers and their share in the legislature, is common knowledge, but the exact valuations of the project are privately known to each of the legislators.

If all legislators are losers (or all are winners), the question whether to carry out the project or not is trivial. Otherwise, voting with the majority rule can lead to inefficiencies, as the majority will impose its will on the entire legislature, no matter whether total benefits associated with the project are positive or negative. Since transfers are distortionary, a socially optimal solution cannot be achieved by simply using transfers and voting in one round, say between a proposal and the status quo (i.e., no project and no transfers).

In our setup, a proposal will consist of a decision about project implementation and a budget-neutral transfer scheme, which has to satisfy the condition that proposal makers—whom we call agenda-setters—have to obtain the lowest (negative) transfer among all legislators. Imposing the latter condition helps, albeit it is not sufficient, to motivate the agenda-setters to waive the use of socially inefficient transfers in their proposal. The set of all possible proposals (i.e., the set of alternatives) is thus very large, and the procedures to choose one proposal are also numerous and can yield very different outcomes. Both in theory and in practice, the complexity of the choice problem is typically reduced by having some agenda-setters pick a few policies from the set of alternatives in a first stage, and, in a second stage, by letting all members of the legislature decide over the selected policies through voting. This is our approach. Specifically, we consider a dynamic mechanism that works as follows: two proposals have to be made sequentially (by the corresponding agenda-setters) and the final decision about which of the two proposals to implement has to be taken according to the majority rule.

Our main result is that this mechanism channels the final say toward utilitarian welfare optimality if the two agenda-setters are chosen appropriately. When it is socially efficient to carry out the project, optimality is attained when the first agenda-setter is a winner and the second agenda-setter is a loser whose project valuation is not too low. This suffices to ensure that the second agenda-setter will always prefer to accept implementation of the project if by doing so, he can eliminate all transfers made in the first agenda-setter’s proposal. By contrast, when it is not socially efficient to carry out the project, optimality is attained with the same proposal-making order—namely, the minority (of winners) goes first, followed by the majority (of losers)—provided that the second agenda-setter has a valuation of the project that is sufficiently low. This guarantees that the second agenda-setter will always find it in his best interest to pay some transfers and build a minimal winning coalition that can defeat the first agenda-setter’s proposal, thereby avoiding project implementation altogether. In anticipation, the first agenda-setter will propose to maintain the status quo. In the case of homogeneous winners and losers, it is enough for optimality that any member of the minority makes a first proposal and any member of the majority makes a counter-proposal.

Because the agenda-setters’ valuations and the order in which they make their proposals is crucial for optimality, we outline how our mechanism can be extended by including an agenda-setter selection stage prior to proposal-making and voting. This extended mechanism elicits some information about the project, so that it can be used subsequently by the chosen agenda-setters to reach the socially optimal outcome. This relaxes the information requirements that are necessary for the correct functioning of the mechanism.

We consider that none of the parameters that define the project is contractible—i.e., none of them can be enforced in court—even if they are public. While our main focus is on legislative bargaining, we therefore also contribute to the literature on incomplete social contracts introduced by Aghion and Bolton (2003) and further developed by Gersbach (2009). If we interpret agents as citizens and a transfer scheme as the result of tax scheme and a subsidy scheme, our results suggest in particular that minorities in a direct democracy should have the right to take the initiative with a first proposal on a public project. This feature has not received much scholarly attention to date. It is important to stress that since at the constitutional level all individuals are identical, they unanimously prefer a procedure that maximizes aggregate expected welfare such as the one we consider in this paper.³

Finally, in the last part of the paper, we discuss some model choices and equilibrium features that are critical for our results beyond the agenda-setters’ selection. We also analyze the performance of our mechanism when the level of the public project can be chosen from a continuous set and when deadweight costs of redistribution are large.

The paper is organized as follows. In Sect. 2 we discuss various literature areas related to our model in greater detail. In Sect. 3 we analyze an example of a legislature with a few members and homogeneous project valuations, which conveys the main insights of our results. Section 4 presents the formal model of legislative bargaining and the main underlying assumptions, and then describes our mechanism. Section 5 contains the main finding of the paper, which is that when the minority proposes and the majority counter-proposes, the final say yields the social optimum. In Sect. 6 we discuss how to select agenda-setters to ensure social optimality. Section 7 addresses some critical features of our mechanism. In Sect. 8 we discuss two extensions of our baseline setup. Section 9 concludes. The Appendix contains the proofs.

2 Relation to the literature

Our model and results are connected to the well-developed literature on legislative bargaining pioneered by Baron and Ferejohn (1989) and further developed by Banks and Duggan (2000), Diermeier and Merlo (2000), Dutta et al. (2001), Eraslan (2002), Eraslan and Merlo (2002), Battaglini and Coate (2007) and Baron (2019), among many others.⁴ Our paper is complementary to this literature insofar that we identify a set of rules that can channel the say toward socially desirable outcomes in (large) legislatures. The procedure we suggest can be seen as a simple, yet modified version of a dynamic legislative bargaining game within a large legislature. Unlike the above standard models, the only decisive vote is held between the original proposal and the amendment, and the proposal-making order (to be determined by some recognition rule) is not random but inversely related to the size of the agenda-setters’ groups. Both features are critical for utilitarian welfare optimality in our setting: The possibility that the status quo can be automatically superseded by the first proposal provides the first agenda-setter with power to set a new default point. If he is a member of the minority, this power is balanced out by the power of the majority group to make an amendment and to vote on it against the new default point. Importantly, the right order of proposal-making can be guaranteed—when it matters for social optimality—if we extend our baseline mechanism to include a properly designed agenda-setter selection stage. This stage therefore implements the desired recognition rule.⁵

Our approach is also in the spirit of the incomplete social contract literature, since some of the parameters of the project are known (or can be elicited) but are not contractible. Typically, applying the majority rule in such environments cannot avoid inefficiencies in public good provision when there are costs of redistribution. We show that there is a set of rules—two rounds of proposal-making and certain conditions on the agenda-setter’s selection and transfers—that can achieve the social optimum in our setting together with the majority rule. Our procedure thus avoids cycling and prevents the majority from exploiting the minority.

We also contribute to the literature on mechanism design in the framework of public good provision (see, e.g., Jackson and Moulin 1992; Bierbrauer and Hellwig 2016; Shao and Zhou 2016; Kuzmics and Steg 2017; Kushnir and Liu 2019) by showing that a (democratic) mechanism based on voting with the majority rule can implement the utilitarian welfare optimum (in any perfect Bayesian equilibrium) if some coarse information is learned by the agenda-setters: namely, the identity of winners and losers (but not the intensity of individual preferences) and whether or not the project is socially efficient. Without this information, it is known that impossibility results apply to Bayesian mechanisms (see Green and Laffont 1978; Börgers 2015). We will say that a mechanism is democratic if it is based on voting with the majority rule and participation (and taxation) can be enforced by some political institution.

Finally, our setup features a public policy with concentrated benefits and costs spread over the entire population. Such fiscal commons problems and the associated excessive spending have been the focus of a large literature developed by Buchanan and Tullock (1962) and first formalized by Weingast et al. (1981). A variety of institutional provisions has been suggested that might help to mitigate the fiscal commons problem—see Schaltegger and Feld (2009) for an overview. We complement this literature by a set of rules that simultaneously induces optimal public project provision and avoids excessive taxation to finance distortionary transfers.

3 An example of a legislature with a few members

In this section, we provide an example that illustrates the functioning of the mechanism we consider in the paper. There is a legislature composed of $2q+1$ members, who are indexed by $i\in N=\{1,\ldots ,2q+1\}$, with $q\ge 3$ being an integer.⁶ The legislature has to decide whether or not to carry out a certain (public) project. If the project is not implemented, legislator i’s utility is normalized to 0.⁷ If the project is implemented, legislator i derives utility $V_i$. We assume that $V_1=\cdots =V_q=V>0$ and $V_{q+1}=\cdots =V_{2q+1}=-1$, and hence legislators 1 to q are winners and legislators $q+1$ to $2q+1$ are losers from the implementation of the project. Because the individual project valuations are homogeneous for winners and for losers, we assume that they are common knowledge (but not contractible). Note that winners are the minority and losers the majority of the population. For simplicity, we also assume that implementing the project is costless. Clearly, from a utilitarian perspective, it is socially efficient to carry out the project if and only if $V\ge (q+1)/q$. Assuming small deadweight costs of redistribution, the utilitarian welfare criterion also prescribes no transfers.

We consider a procedure (or mechanism) where legislator 1 (a winner, denoted by $AS_w$) and legislator $2q+1$ (a loser, denoted by $AS_l$) each make a proposal sequentially, which are publicly observable as soon as they are made. Members 1 and $2q+1$ are henceforth called agenda-setters. A proposal $\pi =(g_{\pi },s_{\pi })$ consists of (i) a decision whether to implement the project ($g_{\pi }=1$) or not ($g_{\pi }=0$), and (ii) a vector of transfers $s_{\pi }=(s_{\pi }(1), s_{\pi }(2),\ldots ,s_{\pi }(2q),s_{\pi }(2q+1))\in \mathbb {R}_- \times \mathbb {R}^{2q-1} \times \mathbb {R}_-$, where⁸

$$\begin{aligned}&s_{\pi } (1)+\cdots + s_{\pi } (2q+1)=0 \text{, } \text{ and } \end{aligned}$$

(1)

$$\begin{aligned}&s_{\pi }(AS_w)=s_{\pi } (AS_l) \le s_{\pi } (i) \text{ for } \text{ all } i\in N. \end{aligned}$$

(2)

Conditions (1) and (2) ensure that $s_{\pi }$ is budget-neutral and that some legislators—including the agenda-setters—have to finance the positive transfers to the remaining legislators. Transfers are added to each legislator’s utility derived from the project, and hence agenda-setters will aim at the lowest value of transfers to the net receivers and at as many contributors as possible. Condition (2) thus prompts the agenda-setters to internalize that transfers are distortionary. We let $u_i(\pi )$ denote the utility that legislator i derives if some proposal $\pi$ is approved. After the two proposals are made, all members of the legislature vote for the proposal they prefer. The decision is taken by the majority rule. Because $AS_l$ has the option to replicate $AS_w$’s proposal, we can consider that $AS_l$’s proposal will win the vote, i.e., his proposal will be voted by at least $q+1$ legislators. It suffices to assume that in case of indifference, legislators will prefer to vote for the counter-proposal and that $AS_l$ prefers his alternative to win the vote all else being equal. We distinguish two cases.

First, assume that $V< (q+2)/(q-1)$. It can be verified that for the project to be prescribed by $AS_l$’s (winning) counter-proposal, $AS_w$ needs to first make a proposal $\pi _w$ such that $g_{\pi _w}=1$. We claim that $AS_l$’s best response to $\pi _w$ will nonetheless never prescribe implementation of the project. Indeed, let $\pi _l$ be a counter-proposal by $AS_l$ with $g_{\pi _l}=1$ such that it is preferred to $\pi _w$ by a certain (minimal winning) majority of legislators that includes $AS_l$ and excludes $AS_w$.⁹ Then consider another counter-proposal by $AS_l$, which we denote by ${{\hat{\pi }}}_l$, such that $g_{{{\hat{\pi }}}_l}=0$ and prescribes the following transfers:

$$\begin{aligned} s_{{{\hat{\pi }}}_l}(i)= {\left\{ \begin{array}{ll} s_{\pi _l}(i)-V\cdot (q-1)/(q+2) &{} \text{ if } i=1,q+1,\ldots ,2q+1,\\ s_{\pi _l}(i)+V &{} \text{ if } i=2,\ldots ,q. \end{array}\right. } \end{aligned}$$

Then, for $i=2,\ldots ,q$,

$$\begin{aligned} u_i ({{\hat{\pi }}}_l)&=s_{\pi _l}(i)+V = u_i (\pi _l), \end{aligned}$$

(3)

while for $i=q+1,\ldots ,2q+1$,

$$\begin{aligned} u_i ({{\hat{\pi }}}_l)&=s_{\pi _l}(i)-V\cdot (q-1)/(q+2) > s_{\pi _l}(i) -1= u_i (\pi _l). \end{aligned}$$

(4)

That is, ${{\hat{\pi }}}_l$ is preferred by $AS_l$ to $\pi _l$. Moreover, since there is a majority of legislators (not including $AS_w$) that prefers $\pi _l$ to $\pi _w$, (3) and (4) imply that there must also be a majority of legislators that prefers $\hat{\pi }_l$ to $\pi _w$. This ensures that ${{\hat{\pi }}}_l$ will defeat $\pi _w$ in the voting round. As a consequence, $AS_l$ can always avoid implementation of the project (yet ${{\hat{\pi }}}_l$ is not necessarily the best option for $AS_l$). In anticipation, $AS_w$ will then make a first proposal that induces $AS_l$ to renounce the project and prescribe no transfers at all. It suffices for $AS_w$ to propose the status quo (i.e., no project and no transfers). This constitutes the second-best for $AS_w$.

Second, assume that $V\ge (q+2)/(q-1)$. Then consider that $AS_w$ makes some proposal $\pi _w^*$, with $g_{\pi _w^*}=1$ and

$$\begin{aligned} s_{\pi _w^*}(i)= {\left\{ \begin{array}{ll} -(V+1) \cdot q/ 2&{} \text{ if } i=1,2q+1,\\ 0 &{} \text{ if } i=2,\ldots ,q,\\ V+1 &{} \text{ if } i=q+1,\ldots ,2q. \end{array}\right. } \end{aligned}$$

Note that

$$\begin{aligned} u_2(\pi _w^*)=\cdots =u_{2q}(\pi _w^*)=V. \end{aligned}$$

(5)

The second agenda-setter, $AS_l$, has now two possibilities for choosing his counter-proposal, which will have to defeat $\pi _w^*$ (in equilibrium). On the one hand, he can propose ${\pi _l^{*}}$ with $g_{\pi _l^{*}}=1$ and $s_{\pi _l^{*}}(i)=0$ for $i=1,\ldots ,2q+1$. In such case,

$$\begin{aligned} u_{AS_w} ({\pi _l^{*}})&=V> V -(V+1) \cdot q/ 2= u_{AS_w}(\pi _w^*),\\ u_{AS_l} ({\pi _l^{*}})&= -1 > -1-(V+1) \cdot q/ 2 = u_{AS_l} (\pi _w^*), \end{aligned}$$

and for $i=2,\ldots ,q$,

$$\begin{aligned} u_i ({\pi _l^{*}})&=V = u_i(\pi _w^*). \end{aligned}$$

Accordingly, ${\pi _l^{*}}$ will defeat $\pi _w^*$ in the voting round. We point out that ${\pi _l^{*}}$ is the best proposal for $AS_l$ among those that prescribe the implementation of the project because it prescribes no transfers. On the other hand, $AS_l$ can propose that the project should not be implemented. For a proposal forbidding the implementation of the project to defeat $\pi _w^*$ in the voting round, $AS_l$ needs to build a (minimal winning) majority by paying transfers adequately. Assuming that the agenda-setters prefer implementing the project in case of indifference, it can be verified that the “cheapest” majority is made up of $AS_l$ and $AS_w$ plus $q-1$ other legislators. By (5) it is immaterial which one of all legislators who are not agenda-setters, so we assume without loss of generality that legislators 2 to q are chosen. Let ${\pi _l^{**}}$ be one such proposal. That is, consider that $g_{\pi _l^{**}}=0$ and let

$$\begin{aligned} s_{\pi _l^{**}}(i)= {\left\{ \begin{array}{ll} -V \cdot (q-1)/(q+2) &{} \text{ if } i=1,q+1,\ldots ,2q+1,\\ V &{} \text{ if } i=2,\ldots ,q. \end{array}\right. } \end{aligned}$$

Then note that

$$\begin{aligned} u_{AS_w} ({\pi _l^{**}})&=-V \cdot (q-1)/(q+2)> V -(V+1) \cdot q/ 2 = u_{AS_w}(\pi _w^*),\\ u_{AS_l} ({\pi _l^{**}})&= -V \cdot (q-1)/(q+2) >-1 -(V+1) \cdot q/ 2= u_{AS_l} (\pi _w^*), \end{aligned}$$

and for $i=2,\ldots ,q$,

$$\begin{aligned} u_i ({\pi _l^{**}})&=V = u_i(\pi _w^*). \end{aligned}$$

This means that ${\pi _l^{**}}$ will defeat $\pi _w^*$ in the voting round.¹⁰ Finally,

$$\begin{aligned} u_{AS_l} ({\pi _l^{*}})&=-1\ge -V \cdot (q-1)/(q+2) = u_{AS_l}({\pi _l^{**}}) , \end{aligned}$$

and hence $AS_l$ will nevertheless prefer to propose ${\pi _l^{*}}$ to ${\pi _l^{**}}$. This means that the project will be implemented but, unlike in $\pi _w^*$, no transfers will occur in the winning proposal ${\pi _l^{*}}$. Now recall that the project should be implemented according to our welfare measure if and only if $V\ge (q+1)/q$. By contrast, according to our analysis, the suggested procedure will implement the project if and only if $V\ge (q+2)/(q-1)$. Moreover, there will be no transfers in the winning proposal no matter the exact value of V. This means that the socially optimal solution is implemented except when $V\in ((q+1)/q,(q+2)/(q-1))$. This inefficiency can arise because with an odd, finite number of legislators, a majority of legislators represents strictly more than 50% of the legislature and the set of agenda-setters has positive measure. As the number of legislators grows, however, both phenomena vanish and the upper bound and the lower bound of $((q+1)/q,(q+2)/(q-1))$ converge to each other, and hence the socially optimal solution is always implemented.

Two final remarks are in order. First, we have assumed that the first agenda-setter was a winner and the second agenda-setter was a loser. This proposal-making order is critical for utilitarian welfare optimality. Second, our analysis has also relied on the fact that agenda-setters know whether or not it is socially efficient to carry out the project and can target transfers depending on whether the recipient is a loser or a winner. These and other issues are addressed in Sect. 5.

4 Model

4.1 Setup

We consider a (large) legislature facing a problem of public project provision and financing, which must be resolved by voting with the majority rule. Individuals are indexed by either i or j and are uniformly arranged on the unit interval. We normalize the utility that each legislator obtains under the status quo—i.e., no project and no transfers—to zero. The provision of a project yields benefits $v_i$ for legislator $i\in \left[ 0,1\right]$ and involves per-capita costs $k\ge 0$. We refer to legislators for which $v_i>k$ as winners and to legislators for which $v_i<k$ as losers. We assume that there are $p\in (0,1)$ and $V_w,V_l \in \mathbb {R}$, with $V_w>k>V_l$, such that¹¹

$$\begin{aligned} v_i ={\left\{ \begin{array}{ll} V_w+x_i &{} \text {if }i\in [0,p],\\ V_l+x_i &{} \text {if }i\in (p,1]. \end{array}\right. } \end{aligned}$$

(6)

For each $i\in [0,1]$, $x_i$ is drawn i.i.d. from a uniform distribution on $[-\delta ,\delta ]$, with $\delta \ge 0$ and $V_w- \delta> k > V_l+\delta$.¹² With a continuum of legislators, the average utility that a legislator derives from the project is $pV_w+(1-p)V_l$.¹³ Without loss of generality, we have assumed in (6) that winners are located on the interval $\left[ 0,p\right]$ and losers on the interval $\left( p,1\right]$. The variable $x_i$ is any private information representing idiosyncratic elements that are particular to legislator i and affect the intensity (but not the direction) of his preferences regarding the project. Parameter $\delta$ determines the amplitude of such idiosyncratic shocks.

Because only the legislators’ relative net valuations of the project are relevant in our framework, we can assume without loss of generality that $k=0$ and $V_l=-1$, and then let $V:=V_w$. Moreover, by symmetry we can focus on the case $p<1/2$.¹⁴ When the project beneficiaries account for less than half of the population, the set of winners constitutes the minority, while the set of losers constitutes the majority. To sum up, the set of all possible projects is

$$\begin{aligned} {\mathcal {P}}:=\left\{ (p,V,\delta )\in \left( 0,1/2\right) \times \mathbb {R}_{++} \times \mathbb {R}_{+} \mid \delta <\min \{1,V\}\right\} . \end{aligned}$$

For the subsequent analysis, we consider an arbitrary project from the set $\mathcal {P}$. We assume that the project parameters are common knowledge—we discuss this assumption in Sect. 7.

A proposal, denoted by $\pi$, comprises a decision $g_{\pi }$ on the project and a budget-neutral transfer scheme $s_{\pi }$. The variable $g_{\pi }\in \{0,1\}$ indicates whether the project is suggested ($g_{\pi }=1$) or not ($g_{\pi }=0$). The transfer scheme $s_{\pi }$ is a Lebesgue-integrable function on the unit interval, i.e., $s_{\pi }\in L^1[0,1]$, that is budget-balanced.^15,16 That is to say, $\int _0 ^1 s_{\pi }(i)di=0$, where $s_{\pi }(i)\in \mathbb {R}$ denotes the transfer given to individual $i\in [0,1]$ under proposal $\pi$. We also consider that agenda-setters (i.e., proposal makers) cannot obtain positive transfers and that, in fact, no legislator can be assigned a lower (negative) transfer than them. One possibility is that the transfer scheme results from the combination of two nonnegative schemes—say, subsidies and uniform taxes—and that agenda-setters (denoted generically by AS) cannot receive subsidies.¹⁷ To sum up, the set of admissible proposals is

$$\begin{aligned} \Pi := \left\{ \pi = (g_{\pi },s_{\pi })\in \{0,1\}\times L^1[0,1]\left| \begin{aligned} \int _0^1 s_{\pi }(i)di =0 \text{ and } s_{\pi }(AS) \le s_{\pi }(j) \forall j \in [0,1] \end{aligned} \right. \right\} . \end{aligned}$$

To a legislator $i\in \left[ 0,1\right]$, adoption of a proposal $\pi \in \Pi$ yields a net utility given by

$$\begin{aligned} u_i(\pi ):= g_{\pi } \cdot v_i+s_{\pi }(i). \end{aligned}$$

We further assume that there are (arbitrarily low) welfare-reducing deadweight costs of redistribution.¹⁸ Such costs can be interpreted in a narrow sense, i.e., as resources used for collecting and transferring funds. In a broader sense, they may represent distortions, say when individuals reduce labor supply because income is taxed.¹⁹ The importance of these costs for efficiency is discussed in Sect. 8.2.

For any given realization of parameters $(p,V,\delta )\in \mathcal {P}$, a social planner who wishes to maximize utilitarian welfare will thus carry out the project if and only if

$$\begin{aligned} V\ge \frac{1-p}{p}. \end{aligned}$$

Moreover, the social planner will never implement any transfers as this would reduce welfare. These characteristics define the socially optimal proposal, which we denote by $\pi ^{soc}\in \Pi$.²⁰ Such a solution prescribes that when the project is carried out, losers will not be compensated, regardless of the extent of their loss. This may be objectionable. Nevertheless, compensation schemes could complement our procedure, say through separate taxation of income.

4.2 A procedure with two proposal-making rounds

We consider a two-round proposal-making procedure that specifies the following sequence of events:

• (1) A first agenda-setter ($AS^1$) makes a first proposal $\pi ^1 \in \Pi$.

• (2) A second agenda-setter ($AS^2$) makes a second proposal (or counter-proposal) $\pi ^2\in \Pi$.

• (3) All members of the legislature cast their vote for either $\pi ^1$ or $\pi ^2$, and no abstention occurs.²¹ The proposal that receives more votes is adopted. Ties between proposals are broken in favor of the counter-proposal by design of the procedure.

We defer to Sect. 6 the discussion about how the agenda-setters are selected. For now, it suffices to take them as given.

4.3 Equilibrium concept and information assumptions

We assume that the project parameters are common knowledge, as is whether any given legislator is a winner or a loser. Nevertheless, none of these features is contractible, i.e., they cannot be enforced in court. If parameters were contractible, complete social contracts guaranteeing socially optimal solutions could be drafted easily. We also recall the exact project valuations are private to each legislator. In Sect. 7 we discuss how critical these assumptions are. Then, an equilibrium in our setup is any perfect Bayesian equilibrium where legislators vote as if they were pivotal, and hence they always vote for the proposal they prefer the most.²² This refinement is standard in voting games and rules out implausible equilibria. Accordingly, an equilibrium consists of a proposal made by the first agenda-setter, a counter-proposal made by the second agenda-setter, and a voting decision for each possible pair of proposal/counter-proposal taken by all legislators, plus beliefs at all decision nodes.

5 An efficient mechanism

There are three types of inefficiency that may arise in the process of choosing a proposal:

• 1. Socially inefficient projects may be implemented.

• 2. Socially efficient projects may not be implemented.

• 3. Socially harmful transfers may be implemented.

The main result of this paper—see Theorem 1—shows that the procedure outlined in Sect. 4.2, which we call Efficient Channeling of the Say (ECS), can avoid all three types of inefficiency at the same time if the agenda-setters are selected appropriately. To see this, it will come in handy to introduce some further notation. First, for each project $(p,V,\delta )\in \mathcal {P}$, define

$$\begin{aligned} {\hat{p}} = {\hat{p}} (p,V,\delta ) := \frac{1}{V+1}. \end{aligned}$$

Note that ${\hat{p}}$ only depends on V. Clearly, implementing project $(p,V,\delta )$ is socially efficient if and only if $p\ge {\hat{p}}$. Second, for each project $(p,V,\delta )\in \mathcal {P}$, define

$$\begin{aligned} {\underline{v}} = {\underline{v}} (p,V,\delta ):=&\max \left\{ -1-\delta ,-\frac{p}{1-p} \cdot \frac{1-{\hat{p}}}{{\hat{p}}} -\frac{p}{1-p} \cdot \delta \right\} \\ =&{\left\{ \begin{array}{ll} -1-\delta &{} \text{ if } p\ge {\hat{p}} \cdot \frac{1+\delta }{1+2\delta {\hat{p}}},\\ -\frac{p}{1-p} \cdot \frac{1-{\hat{p}}}{{\hat{p}}} -\frac{p}{1-p} \cdot \delta &{} \text{ if } p< {\hat{p}} \cdot \frac{1+\delta }{1+2\delta {\hat{p}}}. \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned}&\overline{v} = \overline{v} (p,V,\delta ):= \min \left\{ -1+\delta ,1-\delta -2 \cdot \frac{p}{{\hat{p}}}\right\} \\&\quad = {\left\{ \begin{array}{ll} -1+\delta &{} \text{ if } p< {\hat{p}} \cdot (1-\delta ),\\ 1-\delta -2 \cdot \frac{p}{{\hat{p}}} &{} \text{ if } p\ge {\hat{p}} \cdot (1-\delta ). \end{array}\right. } \end{aligned}$$

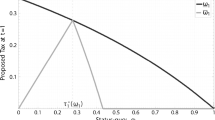
Figure 1 illustrates the shape of these two functions.

Fig. 1

The bounds ${\underline{v}}$ (in blue) and $\overline{v}$ (in red) as functions of $p\in (0,1)$ for a given ${\hat{p}} \in (0,1/2)$

We are now in a position to state our main result regarding ECS. (The proof is in the Appendix.)

Theorem 1

Suppose that the first agenda-setter is a member of the minority ($AS_w$, a winner) and the second agenda-setter is a member of the majority ($AS_l$, a loser). Then, in any equilibrium, the outcome for project $(p,V,\delta )\in \mathcal {P}$ under ECS is $\pi ^{soc}$, provided that $AS_l$’s project valuation $v_{AS_l}$ is at most $\overline{v}$ when $p<{\hat{p}}$ and at least ${\underline{v}}$ when $p\ge {\hat{p}}$.

According to the above theorem, ${\underline{v}}$ and $\overline{v}$, respectively, determine a lower bound and upper bound for a loser’s project valuation, which guarantee that ECS yields the socially optimal outcome. On the one hand, consider the case when $p<{\hat{p}}$, with ${\hat{p}}$ fixed. Then it must be that $v_{AS_l}\le \overline{v}$. As depicted by Fig. 1, this always holds if we further have that

$$\begin{aligned} p<{\hat{p}} \cdot (1-\delta ). \end{aligned}$$

(7)

The above inequality follows from $p<{\hat{p}}$ when $\delta =0$, in which case all losers have the same project valuation. When the inequality in (7) does not hold, the closer p is to ${\hat{p}}$, the less likely it is that a random loser has a valuation that lies below the upper bound ${\overline{v}}$. Yet, there always is a positive measure of losers who have a valuation that lies below $\overline{v}$. On the other hand, consider the case when $p \ge {\hat{p}}$, with ${\hat{p}}$ fixed. Then it must be that $v_{AS_l}\ge {\underline{v}}$. As depicted by Fig. 1, this always holds if we further have that

$$\begin{aligned} p \ge {\hat{p}} \cdot \frac{1+\delta }{1+2\delta {\hat{p}}} . \end{aligned}$$

(8)

The above inequality follows from $p\ge {\hat{p}}$ when $\delta =0$.²³ When the inequality in (8) does not hold, the closer p is to ${\hat{p}}$, the less likely it is that a random loser has a valuation that lies above the lower bound ${\underline{v}}$. Yet, similarly to the above case, there always is a positive measure of losers who have a valuation that lies above ${\underline{v}}$.

Theorem 1 has identified sufficient conditions for ECS to yield the efficient outcome for society. When the project is socially efficient, ECS attains social optimality as long as the first agenda-setter is a winner and the second agenda-setter is a loser whose project valuation is not too low. This is because such a loser will always prefer to accept implementation of the project if by doing so he can eliminate all transfers made in the first agenda-setter’s proposal. When the project is not socially efficient, by contrast, optimality is attained by ECS with the same proposal-making order, provided that the second agenda-setter has a valuation of the project that is sufficiently low. This is because a loser with such a valuation will always find it in his best interest to pay some transfers and build a minimal winning coalition that can defeat the first agenda-setter’s proposal, thereby avoiding the project implementation of the project altogether. In the particular case where $\delta =0$ and project valuations are thus the same for all winners and for all losers, it suffices that the first agenda-setter is a winner (i.e., a member of the minority) and the second agenda-setter is a loser (i.e., a member of the majority). The same is also true for $\delta >0$ if $p \notin ( {\hat{p}} (1-\delta ), {\hat{p}} (1+\delta )/(1+2\delta {\hat{p}}) )$. The forces driving the above theorem are best illustrated by Fig. 1 and the following corollary:

Corollary 1

Let $v^1$ be the project valuation of the first agenda-setter and $v^2$ be the project valuation of the second agenda-setter. Then the following properties hold in any equilibrium outcome under ECS for a given project $(p,V,\delta )\in \mathcal {P}$:

(i):

If $v^1>0$ and $v^2 \le \overline{v}$, the project is not implemented and no transfers occur,

(ii):

If $v^1>0$ and $v^2 \ge {\underline{v}}$, the project is implemented and no transfers occur.

It is thus crucial for social optimality that the right order of proposal-making takes place (and that the agenda-setters’ project valuations are appropriate). How to ensure this is discussed next.

6 The Agenda-setters’ selection

In this section, we outline a way to select agenda-setters that guarantees that the conditions of Theorem 1 regarding the agenda-setters’ project valuations are met in all cases where they matter for social optimality.²⁴ Indeed, assume now that the following procedure—called Stage 0—takes place before ECS starts:

• Stage 0.1: Each legislator i bids $b_i\ge 0$ to become the first agenda-setter ($AS^1$). A legislator is selected by fair randomization among the legislators with the highest bid, all of whom are paid back their bid. All other legislators who bid less pay their bid. The identity of $AS^1$ and his bid are made public.

• Stage 0.2: Each legislator decides whether or not to apply for being the second agenda-setter ($AS^2$).

• Stage 0.3: All legislators vote for one eligible candidate among those who applied in Stage 0.2. The candidate with the most votes becomes the second agenda-setter, with ties being broken by fair randomization. If no legislator is eligible, the first agenda-setter is also the second agenda-setter. If at least one legislator is eligible and the first agenda-setter bid was zero in Stage 0.1, the second agenda-setter also becomes the first agenda-setter. The identity of $AS^2$ as well as the number of votes supporting him are made public.

This procedure determines the identity of the first and the second agenda-setters.²⁵ The entire mechanism—selection stage of agenda-setters followed by ECS—is called Extended Efficient Channeling of the Say (EECS). For its analysis, it will be useful to define the willingness-to-pay of legislator $i\in [0,1]$ as the absolute difference in utility obtained from implementing project $(p,V,\delta )\in \mathcal {P}$ and from not implementing it, namely

$$\begin{aligned} w_i=w_i(p,V,\delta ):= \vert v_i \vert . \end{aligned}$$

For legislator $i\in [0,1]$, $w_i$ denotes how much he should be willing to pay to avoid that his least preferred option—implementing the project or maintaining the status quo—is chosen. For losers, the maximum willingness-to-pay is $1+\delta$, while for winners the maximum willingness-to-pay is $V+\delta$. When $p\ge {\hat{p}}$, we obtain

$$\begin{aligned} \frac{1}{2}>p\ge {\hat{p}} = \frac{1}{V+1}, \end{aligned}$$

which implies

$$\begin{aligned} V+\delta > 1+\delta . \end{aligned}$$

(9)

That is, when the project is socially efficient, a winner with the highest project valuation has a willingness-to-pay that is higher than any loser’s willingness-to-pay (and not lower than any other winner’s willingness-to-pay). This follows from the fact that losers are a majority (i.e., $p<1/2$), and together the two features are crucial for the functioning of the extended mechanism.²⁶

To solve the game underlying EECS, we focus on perfect Bayesian equilibria where all legislators eliminate weakly dominated strategies iteratively and legislators with the same project valuation play the same pure strategy regarding agenda-setting (type-symmetric). Moreover, we consider monotonicity in the bidding behavior (relative to the willingness-to-pay) and assume that legislators can coordinate their votes on a preferred agenda-setter.²⁷ We recall that the legislators’ exact valuations are private information. This implies that all losers expect the same transfers on and off the equilibrium path of ECS, since agenda-setters cannot observe other members’ valuations and cannot therefore make transfers targeted at losers with specific project valuations. The same property holds also for all winners.²⁸

To investigate the equilibrium outcome of the dynamic game underlying EECS, we need the following properties of ECS in the case of arbitrary agenda-setters. They can be easily derived using the logic of the proof of Theorem 1.

Corollary 2

Let $v^1$ be the project valuation of the first agenda-setter and $v^2$ be the project valuation of the second agenda-setter. Then the following properties hold in any equilibrium outcome under ECS for a given project $(p,V,\delta )\in \mathcal {P}$:

(i):

If $v^1,v^2<0$, the project is not implemented and no transfers occur.

(ii):

If $v^1,v^2>0$, the project is implemented and no transfers occur.

To see how EECS can yield the socially optimal outcome, it will be useful to use $\pi ^{0,*}$ to denote the status quo (i.e., no project and no transfers) and $\pi ^{1,*}$ to denote project implementation and no transfers. Except for possible transfers, $\pi ^{0,*}$ is the best outcome for a loser and $\pi ^{1,*}$ is the best outcome for a winner. With a continuum of legislators, we can assume that there will always be a winner with project valuation equal to $V+\delta$ and a loser with project valuation equal to $-1-\delta$.²⁹

For our analysis of EECS, we distinguish whether the project is socially efficient or not. We stress that the social (un)desirability of the project is common knowledge, and this information can be used by legislators in any stage of EECS. We proceed in three steps.

Step 1

We start by noting that no transfers will be implemented in any equilibrium of EECS.³⁰ Indeed, suppose that this is not the case, i.e., that some transfers occur in the winning proposal. It is straightforward that one agenda-setter must be a winner and the other a loser, since the outcome will be either $\pi ^{0,*}$ or $\pi ^{1,*}$ if this is not the case—see Corollary 2. Both these proposals entail no transfers. Then, because the legislators’ exact valuations are private and transfers are budget-neutral, there are two possibilities if the winning proposal entails transfers: Either all winners (losers) expect a positive (negative) transfer, or all losers (winners) expect a positive (negative) transfer. In the former case, in which all winners expect a positive transfer, none of them wants to act as an agenda-setter. The reason is that renouncing agenda-setting will lead to a positive expected transfer instead of a certain negative transfer as an agenda-setter. Indeed, recall that we are assuming equilibria to be type-symmetric and monotonic.³¹ Then, given that there is an equilibrium where some winner applies for agenda-setting, there will always be other winners with this same valuation who will apply, and hence an individual deviation from applying for agenda-setting to not doing so will not change the equilibrium path.³² This implies that the (expected) outcome after the deviation will remain the same, and hence the deviation will indeed be profitable. The case where any loser expects a positive transfer and any winner a negative transfer is analogous.

Step 2

Let us assume next that $p<{\hat{p}}$, i.e., it is not socially efficient to implement project $(p,V,\delta )\in \mathcal {P}$. Then consider a loser with valuation $-1-\delta$ deciding whether or not to apply for being the second agenda-setter in Stage 0.2. Because $-1-\delta \le {\overline{v}}$, the outcome will be $\pi ^{0,*}$ if such a loser becomes the second agenda-setter—see Theorem 1 and part (i) of Corollary 2. If he decides not to apply for being the second agenda-setter (and so no other loser does), there are three options at most: (a) the first agenda-setter is a winner, so that the outcome will be $\pi ^{1,*}$—see part (ii) of Corollary 2; (b) the first agenda-setter is a loser and no winner is eligible for being the second agenda-setter, so that $\pi ^{0,*}$ will be the outcome—see part (i) of Corollary 2; and (c) the first agenda-setter is a loser and the second agenda-setter is a winner, in which case the outcome will be either $\pi ^{0,*}$ or $\pi ^{1,*}$, but no transfers will occur in equilibrium.

From Cases (a)–(c), it follows that any loser with valuation $-1-\delta$ will choose to apply for being the second agenda-setter in Stage 0.2, as not doing so is weakly dominated. This guarantees that $\pi ^{0,*}$ will be implemented. As for the losers with higher project valuations, because being an agenda-setter implies foregoing possible positive transfers, by applying for being the second agenda-setter (and becoming it), they cannot expect to obtain a higher utility than under $\pi ^{0,*}$. Accordingly, they will not apply for being the second agenda-setter. We stress that given that more than one loser with valuation $-1-\delta$ may be eligible, all losers are able to coordinate their votes on one of them. This ensures that one loser with valuation $-1-\delta$ will be chosen as the second agenda-setter in Stage 0.3. Recall that $p<1/2$, so that losers form the majority, which means that they can determine who the second agenda-setter will be if they can coordinate their votes. That is, the outcome under EECS when $p<{\hat{p}}$ will be $\pi ^{0,*}$.

Step 3

Now, let us assume that $p\ge {\hat{p}}$, i.e., it is socially efficient to implement project $(p,V,\delta )\in \mathcal {P}$. By Theorem 1 and part (ii) of Corollary 2, if a winner with valuation $V+\delta$ becomes the first agenda-setter, the outcome will be $\pi ^{1,*}$ (and his bid will be paid back to him). If such a winner does not bid a positive amount for becoming the first agenda-setter, no other winner will and the outcome will be either $\pi ^{0,*}$ or $\pi ^{1,*}$. In particular, no transfers will be implemented. Hence, for a winner with valuation $V+\delta$, bidding zero is weakly dominated by bidding (some amount). As for any winner with a project valuation lower than $V+\delta$, he cannot expect to obtain a higher utility than under $\pi ^{1,*}$ if he makes a bid (and is chosen as the first agenda-setter). The reason is that agenda-setting implies foregoing any positive transfers. Hence, no winner with a valuation lower than $V+\delta$ will make any positive bid in Stage 0.1. We claim that all winners with valuation $V+\delta$ will bid just the minimum possible amount above $1+\delta$, which is strictly lower than their project valuation, and that one of them will win. It suffices to assume that the possible bids are discrete. This follows from (9) and the fact that bids are paid back only to those individuals bidding the winning-bid amount (including the first agenda-setter), and from the fact that for a loser bidding above his willingness-to-pay is strictly dominated, given that no positive transfers will occur in equilibrium. As a conclusion, the outcome under EECS when $p\ge {\hat{p}}$ will be $\pi ^{1,*}$ no matter who becomes the second agenda-setter.

To sum up, we obtain the following result:

Theorem 2

The outcome for project $(p,V,\delta )\in \mathcal {P}$ under EECS is $\pi ^{soc}$ in any equilibrium.

Finally, it is worth noting that there are some circumstances in democracies where beneficiaries and losers from public projects can be ascertained easily, and majorities and minorities can be identified. In such cases, the agenda-setter selection stage embedded in EECS may be omitted. In the case of a direct democracy, if a project benefits either only older or only younger people, for instance, winners and losers can be identified by their age. Similarly, policies that are targeted at specific groups (such as families with two or more children) or sectors (such as the agricultural sector) will typically permit a verifiable winner/loser division of the population.

7 Other critical features

Beyond the selection of agenda-setters, some other features of our procedure require some scrutiny. We discuss them in this section.

Transfers to agenda-setters

We have derived our results under the assumption that transfers to agenda-setters have to be the lowest of all transfers to legislators, and in particular, never be positive since transfer schemes are budget-neutral. This prompts the agenda-setters to internalize that transfers are distortionary. Yet, this feature alone does not suffice for efficiency nor does it guarantee in principle that no transfers will occur in the final proposal—the agenda-setters’ project valuations must be chosen appropriately. As already discussed, one possibility is that transfers are the combination of taxes and subsidies.³³ In this case, the restriction on the transfers to the agenda-setters results from imposing uniform taxation and requiring that agenda-setters cannot receive subsidies (or that such subsidies have to be fixed exogenously).

In practice, the latter rule could be applied or manifest itself in several ways. In the US Congress, for instance, when a group of senators introduces a bill, the agenda-setters could be banned from adding earmarks benefiting their constituency to this bill. Earmarks are a common practice in US legislative decision-making (see, e.g., Lazarus and Steigerwalt 2009; Doyle 2011). Since 2006, there have been notable congressional efforts aimed at reforming earmarks, including some attempts to ban them altogether.³⁴ Our paper suggests that it might suffice to ban earmarks for the group of Congress members who introduce or support a bill, or, more generally, that such earmarks would be exogenously-established. In the EU, to consider another example, it would suffice that transfers are fixed for those countries that intervene directly in the proposal-making procedure. Finally, in direct democracy settings, the rule on agenda-setters would imply that an interest group could not take the initiative for a public vote on a project prescribing the extent of subsidies to the group of citizens represented by this same interest group: such initiatives would be declared unconstitutional.

Information assumptions

For Theorem 1, we made two main informational assumptions: first, the project parameters are common knowledge (but cannot be enforced in court), and in particular, it is common knowledge whether the project is socially efficient or not; second, agenda-setters are able to distinguish between losers and winners, yet they do not know the other legislators’ exact project valuations.

As for the agenda-setters selection stage, it requires less statistical information about the project and the corresponding legislators’ valuations. Indeed, it only relies on the assumption that agents know whether p is lower or larger than ${\hat{p}}$, like in the mechanism examined by Jackson and Moulin (1992), as well as the support of the distribution from which valuations are drawn. In particular, it can be verified that this stage does not rely on the exact value of p, not even on whether such parameter is lower or bigger than one half. The latter is an important feature, since it determines whether losers or winners are the majority. As a matter of fact, the process of selecting the agenda-setters itself provides information about p through Stage 0.3. This information can subsequently be used in ECS. It is only required that the two agenda-setters learn this information. Note that Stage 0.3 would also enable the identification of winners and losers (yet not their exact valuations) by agenda-setters if votes were public—as in roll call votes—, or at least they were revealed to the agenda-setters.³⁵

Off-equilibrium threats

Another important feature of ECS is that it induces threats of large transfers along the equilibrium path. This is reminiscent of proposals that only serve the purpose of trying to influence the final outcome. We mention one example: In 2005, the Parliament of Catalonia approved a project to change its constitution, which then had to be amended by the Spanish Parliament and ratified in a referendum by the vote of all Catalan citizens.³⁶ To gain leverage, the initial proposal was deliberately designed as too far-fetched.

Large decision bodies

Although the focus of our analysis is on large decision bodies—whether they are legislatures, the entire electorate, or committees—, the main forces driving our results also operate for a finite number of agents, yet potentially not in all cases. This has been illustrated by the example of Sect. 3. Proceeding with a continuum of legislators instead of a large finite number has simplified the analysis since the law of large numbers (for a continuum of random variables) operates.

8 Extensions

In this section, we discuss two extensions of our baseline setup, for which we analyze the performance of ECS (and hence of EECS). To illustrate our results, it suffices to focus on the case where $\delta =0$, i.e., to assume homogeneous winners and losers. More specifically, we examine the case where the decision on the public project is not binary and the case where deadweight costs of redistribution may be significant.³⁷

8.1 Divisible projects

Assume now that instead of simply proposing a choice between implementing the project or not, agenda-setters can suggest the level $\rho$ of the project, where $\rho$ varies continuously in [0, 1].³⁸ The associated per-capita costs are normalized to zero for all levels of the project provided. Each member of the legislature $i\in [0,1]$ values project $\rho$ either with $V_w (\rho )$ if $i\in [0,p]$ or with $V_l(\rho )$ if $i\in (p,1]$, where $V_w (0)=0$, $V_w (1)=V$, $V_l (0)=0$, and $V_l (1)=-1$. We further assume that $V_l (\rho )< 0 <V_w (\rho )$ for each $\rho \in [0,1]$, that $V_w(\rho )$ and $-V_l(\rho )$ are increasing functions of $\rho \in [0,1]$, and that $-V_l(\rho )/ (V_w(\rho )-V_l(\rho ))$ is a non-increasing function of $\rho \in (0,1]$. This latter assumption implies that if $pV_w(\rho )+(1-p)V_l(\rho ) \ge 0$ for some $\rho \in [0,1]$, then $pV_w(\rho ^{\prime })+(1-p)V_l(\rho ^{\prime }) \ge 0$ for all $\rho ^{\prime } \in (\rho ,1]$. Note that the set of winners, namely [0, p], and the set of losers, namely (p, 1], remain invariant for all positive levels of public good provision.

The following result demonstrates that in this modified setting where legislators have quasi-linear utilities, the outcome under ECS is always (weakly) welfare-improving—according to our notion of social utility—with respect to the status quo.

Proposition 1

If the decision on the project is not binary, the outcome in any equilibrium under ECS—proposal by a winner, counter-proposal by a loser—yields a level of project provision that is the maximal $\rho \in [0,1]$ for which $p V_w(\rho ) + (1-p) V_l(\rho ) \ge 0$. Moreover, no transfers occur in equilibrium.

In particular, if $p V_w(\rho ) + (1-p) V_l(\rho ) < 0$ for all $\rho \in (0,1]$, i.e., if there is no positive level of public good provision that is socially welfare-improving, the outcome of the two-round procedure in equilibrium is the status quo.

8.2 Arbitrary deadweight costs of redistribution

Throughout the paper, we have assumed that deadweight costs of redistribution exist but are arbitrarily low.³⁹ In this section, we assume that such costs, captured by $\varepsilon$, are strictly positive. That is, for each dollar transferred to one legislator, $1+\varepsilon$ dollars need to be collected via taxes.⁴⁰ It turns out that for large deadweight costs of redistribution, the performance of ECS remains attractive, but some inefficiencies cannot in principal be avoided for particular projects although they remain limited. This is captured in the following result:

Proposition 2

If $\varepsilon \in \left( 0,\frac{1}{3}\right)$, under ECS—proposal by a winner, counter-proposal by a loser—we obtain that given a project $(p,V,\delta )\in {\mathcal {P}}$, the outcome in any equilibrium is $\pi ^{soc}$ if $p\notin \left[ \frac{{\hat{p}}}{1+\varepsilon },\frac{{\hat{p}}+\varepsilon }{1+\varepsilon }\right]$.

Proposition 2 only gives sufficient conditions guaranteeing that ECS yields the first-best outcome. When $\varepsilon$ approximates to zero, in particular, we recover the result in Theorem 1 as a limit result in the case of homogeneous valuations. To assess the performance of ECS when $\varepsilon \in \left( 0,\frac{1}{3}\right)$, we do two simple exercises. First, let V (and hence ${\hat{p}}$) be given, and assume that p is drawn from a uniform distribution on the interval [0, 1]. Then, the probability that the procedure yields the socially optimal solution is at least $\frac{1}{1+\varepsilon } \ge \frac{3}{4}$. Second, let now $p\in (0,1)$ be fixed, and assume that V is chosen randomly, so that ${\hat{p}}$ is drawn from a certain probability distribution $G(\cdot )$. Then the probability that the procedure yields the socially optimal solution is $1-\left[ G(p(1+\varepsilon )) - G(p(1+\varepsilon )-\varepsilon ) \right] .$ When $G(\cdot )$ is uniformly distributed on [0, 1], this probability is at least $1-\varepsilon \ge \frac{2}{3}$.

9 Conclusion

In this paper, we have identified a mechanism for legislative bargaining that guarantees utilitarian welfare optimality: only welfare-enhancing projects are selected and wasteful transfers are avoided in equilibrium. The procedure is simple and imposes few exogenous constraints: in a nutshell, a member of the minority makes a first proposal, followed by a counter-proposal made by a member of the majority. We have also outlined how to extend our mechanism by including an initial stage of agenda-setter selection that guarantees optimality and elicits relevant information that can later be used to achieve socially efficient decisions. This broadens the informational environments in which the entire mechanism could deliver. In either variant of our mechanism—with or without agenda-setter selection—transfers are critical on and off the equilibrium path for achieving optimality, although they are not part of the optimal outcome. While the core message of the paper is clearly normative, our insights are also relevant from a purely positive perspective, since the suggested mechanism can serve as a benchmark to which current real-world procedures can be compared.

Our results might also have implications for the design of democratic institutions: Social optimality may be attained, provided that the order in proposal-making is inversely related to the size of the groups supporting either alternative. Although this procedural feature of proposal-making has been overlooked in the literature up to now, rules that enable minorities (but also majorities) to take the lead in proposal-making exist in direct and parliamentary democracies. Our insights suggest that when designing such procedures, one should bear in mind whether they guarantee the right proposal-making order or not. One possibility is to add a stage prior to proposal-making, in which agenda-setters would be selected as in EECS. Alternatively, wherever possible, one could impose stricter rules discriminating in favor of minorities, by granting them the right to move first in the proposal-making process. Due to its simplicity, either variant of our mechanism could be introduced on a experimental basis within concrete collective decision-making environments.

Appendix

In this appendix, we do three things. First, we discuss some properties of equilibria in our framework, which will make our analysis easier without entailing any loss of generality. Second, we prove an auxiliary result—see Lemma 1. This auxiliary result will also facilitate the analysis throughout. The reason is that counter-proposals that are not seconded by at least half of the society will be ruled out in equilibrium. Finally, we provide the proof of Theorem 1.

Accordingly, let us first consider three tie-breaking rules. To define them, let $\pi '\in \Pi$ be a proposal by the first agenda-setter and $\pi ''\in \Pi$ a proposal by the second agenda-setter. It will come in handy to use the indicator function $I(\pi ',\pi '')$, which adopts a value of 0 if the first proposal, $\pi '$, is implemented and a value of 1 if the counter-proposal, $\pi ''$, is implemented.

Tie-breaking Rule 1

If $u_j(\pi ')=u_j(\pi '')$, individual j will vote for the counter-proposal $\pi ''$.

Tie-breaking Rule 2

If the second agenda-setter, $AS_2$, is indifferent between a proposal ${{\tilde{\pi }}}\in \Pi$ involving $g_{{\tilde{\pi }}}=1$ and a proposal ${\hat{\pi }} \in \Pi$ involving $g_{{\hat{\pi }}}=0$, i.e., $u_{AS_2} ({\tilde{\pi }}) = u_{AS_2} ({\hat{\pi }})$, he will always suggest ${\tilde{\pi }}$ over ${{\hat{\pi }}}$.

Tie-breaking Rule 3

If, given the first proposal $\pi '$, the second agenda-setter is indifferent between the voting outcome when making a proposal ${\tilde{\pi }} \in \Pi$ with $I(\pi ',{\tilde{\pi }})=1$ and the voting outcome when making a proposal ${\hat{\pi }} \in \Pi$ with $I(\pi ',{\hat{\pi }})=0$, he will always suggest ${\tilde{\pi }}$ over ${\hat{\pi }}$.

Several remarks are in order, which will make it clear that we are not reducing the set of equilibria by considering the above tie-breaking rules. This is important because it allows us to interpret Theorem 1 as an implementation of the utilitarian social welfare function.

First, Tie-breaking Rule 1 guarantees that the counter-proposal is adopted if at least half of the legislature is not worse off than it would be with the first proposal. Under sincere voting, the second agenda-setter can always engineer that legislators who are indifferent between the two proposals vote for the counter-proposal $\pi ''$. It suffices to modify the latter proposal with an additional, infinitesimally small transfer to a certain share of legislators that includes all those who are indifferent between the two proposals. Due to Tie-breaking Rule 1, we can then write

$$\begin{aligned} I(\pi ',\pi '')={\left\{ \begin{array}{ll} 1 &{}\text {if } u_j(\pi '')\ge u_j(\pi ') \text { holds for at least half of the society,} \\ 0 &{}\text {otherwise,} \end{array}\right. } \end{aligned}$$

where, recall, $\pi '$ and $\pi ''$ denote the proposal by the first agenda-setter and the counter-proposal by the second agenda-setter, respectively.

Second, Tie-breaking Rule 2 ensures that the second agenda-setter will choose to implement the project in case of indifference. We could dispense with Tie-breaking Rule 2 if the second agenda-setter obtains an arbitrarily small utility gain from being active (changing the status quo), compared to being passive (keeping the status quo). Tie-breaking Rule 2 is actually only used in the proof of Theorem 1 in the case of a particular combination of project parameters.⁴¹ Hence, except for this very particular parameter constellation, we can interpret Tie-breaking Rule 2 as a feature of the equilibria of the game rather than as a tie-breaking rule per se.

Third and last, Tie-breaking Rule 3 simply ensures that the second agenda-setter does not make proposals that are bound to be rejected. Since the second agenda-setter can always repeat the first proposal, Tie-breaking Rule 3 does not constrain the set of equilibrium outcomes. Tie-breaking Rule 3 follows immediately if the second agenda-setter obtains a very small disutility whenever his proposal is defeated.

Building on the above tie-breaking rules, we can prove the following result:

Lemma 1

If a counter-proposal $\pi ''\in \Pi$ is a best response to proposal $\pi '\in \Pi$, then

$$I(\pi ',\pi '')=1.$$

Proof

Given an arbitrary proposal $\pi '\in \Pi$, the second agenda-setter can always match the first agenda-setter’s proposal, i.e., choose $\pi ''_C:=\pi '$. Since $u_j(\pi ''_C)=u_j(\pi ')$ for all $j\in \left[ 0,1\right]$, it holds by Tie-breaking Rule 1 that $I(\pi ',\pi ''_C)=1$. Moreover, due to Tie-breaking Rule 3, the second agenda-setter will prefer making proposal $\pi ''_C$ to any proposal $\pi ''\ne \pi ''_C$ such that $I(\pi ',\pi '')=0$. As a consequence, either the second agenda-setter will choose $\pi ''_C$ or he will choose a proposal $\pi ''\ne \pi ''_C$ such that $I(\pi ',\pi ''_C)=1$ and $u_k(\pi '')\ge u_k(\pi ''_C)=u_k(\pi ')$, where k denotes the second agenda-setter.⁴²

As a consequence of Lemma 1, the best response for the second agenda-setter, k, can be described by the correspondence

$$\begin{aligned} R(\pi ') \quad = \mathop {{\mathrm{argmax}}}\limits _{ \pi ''\in \Pi , I(\pi ',\pi '')=1 } \left\{ u_k(\pi '') \vert u_k(\pi '') \ge u_k(\pi ')\right\} . \end{aligned}$$

We will work for simplicity with equivalence classes. That is, two transfer schemes will be equivalent if they are equal almost everywhere. Unless specified otherwise, this allows us to consider the best response to be a function rather than a correspondence.

The remainder of this appendix is devoted to the proof of Theorem 1.

Proof of Theorem 1:

Recall that we are assuming $p<1/2$. Let $v_{AS_w}$ be the project valuation of the first agenda-setter ($AS_w=0$, a winner) and $v_{AS_l}$ be the project valuation of the second agenda-setter ($AS_l=1$, a loser). Recall that for each project $(p,V,\delta )$, we can define

$$\begin{aligned} {\hat{p}} = \frac{1}{V+1}, \end{aligned}$$

(10)

and that such a project is socially efficient if and only if $p\ge {\hat{p}}$.

For the proof of the theorem, we distinguish two main cases, depending on the values of p and ${\hat{p}}$.

Case 1: $p<\hat{p}$

Let $\pi _w \in \Pi$ be the proposal made in equilibrium by $AS_w$. We distinguish two subcases, depending on the value of $g_{\pi _w}$.

Case 1.A: $g_{\pi _w}=1$

Accordingly, we assume that $AS_w$ has proposed the implementation of the project. We claim that $AS_l$’s best response to $\pi _w$ can never be a counter-proposal prescribing implementation of the project. Indeed, if $AS_l$’s best response suggests the implementation of the project, there must exist an admissible proposal $\pi _l\in \Pi$, with $g_{\pi _l}=1$, and a set $Q_1$, with measure $q_1=1/2$, such that⁴³

$$\begin{aligned} u_{i}(\pi _l)\ge u_{i}(\pi _w) \text{ for } \text{ all } i\in Q_1 \cup \{AS_l\}. \end{aligned}$$

The above condition is equivalent to

$$\begin{aligned} s_{\pi _l}(i)\ge s_{\pi _w}(i) \text{ for } \text{ all } i\in Q_1 \cup \{AS_l\}. \end{aligned}$$

(11)

Then define

$$\begin{aligned} Q_1^w:= \left\{ i\in Q_1\mid i\in \left( 0,p\right] \right\} \text{ and } Q_1^l:= \left\{ i\in Q_1\mid i\in \left( p,1\right) \right\} . \end{aligned}$$

Set $Q_1^w$ comprises all winners from $Q_1$ and set $Q_1^l$ all losers from $Q_1$. Observe that, by definition,

$$\begin{aligned} q_1^{w}\le p. \end{aligned}$$

(12)

Now, starting from $\pi _l$, it will be helpful to define an auxiliary proposal ${{\tilde{\pi }}}_l$ to be considered by the second agenda-setter, $AS_l$. Specifically, let ${{\tilde{\pi }}}_l$ be a proposal that comprises $g_{{{\tilde{\pi }}}_l}=0$ and the following transfer scheme:

$$\begin{aligned} s_{{{\tilde{\pi }}}_l}(i)={\left\{ \begin{array}{ll} s_{\pi _l}(i) + V + \delta &{}\text { for } i\in Q_1^w,\\ s_{\pi _l}(i) -1+ \delta &{}\text { for } i\in Q_1^l ,\\ s_{\pi _l}(i) +1-\delta - 2q_1^w \cdot (V+1) &{}\text { for all other } i \in (0,1) ,\\ s_{\pi _l}(i) +\min \{-1+ \delta , 1-\delta - 2q_1^w \cdot (V+1) \} &{}\text { for } i\in \{AS_w,AS_l\} . \end{array}\right. } \end{aligned}$$

We stress that to construct $\pi _l$, $AS_l$ does not need to know the exact valuations of legislators, but only to be able to target individuals in set $Q_1$ and distinguish winners from losers in this set. It readily follows that

$$\begin{aligned} \int _{0}^{1} s_{{{\tilde{\pi }}}_l}(i) \mathrm{d}i = \int _{0}^{1} s_{\pi _l}(i) \mathrm{d}i = 0 \end{aligned}$$

and

$$\begin{aligned} s_{{{\tilde{\pi }}}_l}(AS_w)= & {} s_{{{\tilde{\pi }}}_l} (AS_l) \le s_{{{\tilde{\pi }}}_l}(i) \text{, } \forall i\in [0,1]\\\Leftrightarrow & {} s_{\pi _l}(AS_w)= s_{\pi _l}(AS_l) \le s_{\pi _l}(i) \text{, } \quad \forall i\in [0,1]. \end{aligned}$$

We thus obtain that $\pi _l\in \Pi$ implies ${{\tilde{\pi }}}_l\in \Pi$, i.e., ${{\tilde{\pi }}}_l$ is an admissible proposal.

We claim—and show in the following—that $u_i({{\tilde{\pi }}}_l)\ge u_i(\pi _w)$ for all $i \in Q_1$, and hence ${{\tilde{\pi }}}_l$ would defeat $\pi _w$ in the voting round. On the one hand, consider $i\in Q_1^w$. Because i is a winner, his valuation $v_i$ of the project is at most $V+\delta$. Accordingly,

$$\begin{aligned} u_i({{\tilde{\pi }}}_l)-u_i(\pi _w) = (s_{\pi _l}(i) - s_{\pi _w}(i) )+ (V+\delta -v_i)\ge s_{\pi _l}(i) - s_{\pi _w}(i) \ge 0, \end{aligned}$$

where the second inequality holds by Eq. (11). On the other hand, consider $i\in Q_1^l$. Because i is a loser, his valuation $v_i$ of the project is at most $-1+\delta$. Accordingly,

$$\begin{aligned} u_i({{\tilde{\pi }}}_l)-u_i(\pi _w) = (s_{\pi _l}(i) - s_{\pi _w}(i) )+ (-1+\delta -v_i)\ge s_{\pi _l}(i) - s_{\pi _w}(i) \ge 0, \end{aligned}$$

where the second inequality holds again by Eq. (11). This completes our claim.

Finally, it remains to show that $AS_l$ will prefer the implementation of ${{\tilde{\pi }}}_l$ to that of $\pi _l$. Indeed, note that

$$\begin{aligned} u_{AS_l}({{\tilde{\pi }}}_l)&= s_{\pi _l}(AS_l) +\min \{-1+ \delta , 1-\delta - 2q_1^w \cdot (V+1) \} \\&\ge v_{AS_l}+ s_{\pi _l}(AS_l) = u_{AS_l}(\pi _l), \end{aligned}$$

is equivalent to

$$\begin{aligned} v_{AS_l} \le \min \left\{ -1+ \delta , 1 -\delta -2q_1^w \cdot (V+1) \right\} . \end{aligned}$$

Since a loser’s valuation of the project is at most $-1+\delta$, a sufficient condition for $AS_l$ to prefer the implementation of ${{\tilde{\pi }}}_l$ over implementation of $\pi _l$ is that

$$\begin{aligned} v_{AS_l}\le 1-\delta -2q_1^w \cdot (V+1). \end{aligned}$$

Then note that

$$\begin{aligned} 1-\delta - 2q_1^w \cdot (V+1)\ge 1- \delta - 2 p \cdot (V+1) =1 -\delta -2 \cdot \frac{p}{{\hat{p}}} > -1-\delta , \end{aligned}$$

where the first inequality is due to $q_1^{w}\le p$, see (12), the equality follows from Equation (10), and the last inequality holds because $p< {\hat{p}}$. This completes the proof of our claim, and in turn the proof of Case 1.A.

Case 1.B: $g_{\pi _w}=0$

Accordingly, we assume that $AS_w$ has proposed not to implement the project. We claim that as in Case 1.A, the best response to $\pi _w$ can never be a counter-proposal prescribing implementation of the project. Assume this is not the case, and let $\pi _l\in \Pi$, with $g_{\pi _l}=1$, be $AS_l$’s best response to $\pi _w$. Then consider $\tilde{\pi }_l$ such that $g_{\tilde{\pi }_l}=0$ and $s_{\tilde{\pi }_l}=s_{\pi _l}$. Clearly, $\tilde{\pi }_l\in \Pi$, i.e., $\tilde{\pi }_l$ is an admissible proposal. Moreover, for all $i\in (p,1]$, i.e., for all losers including $AS_l$, we have

$$\begin{aligned} u_i(\tilde{\pi }_l)= s_{\tilde{\pi }_l}(i)>-1+ s_{\tilde{\pi }_l}(i)=-1+ s_{\pi _l}(i)=u_i(\pi _l). \end{aligned}$$

Our claim then follows from the facts that $1-p>1/2$ and $AS_l \in (p,1]$.

To sum up, from Cases 1.A and 1.B, we have shown that when $p < \hat{p}$, the second agenda-setter ($AS_l$, a loser) will never propose the implementation of the project if his valuation is not too high. In anticipation (and knowing the identity of the agenda-setter), the first agenda-setter ($AS_w$, a winner) will make a proposal $\pi _w$ that will trigger the following response by $AS_l$: no project and no transfers. This is the best possible outcome for $AS_w$ provided that the project is not implemented, and it coincides with the socially optimal outcome $\pi ^{soc}$. Note that one such proposal, $\pi _w$, exists: It suffices that $\pi _w$ itself prescribes no project implementation and no transfers. This completes the proof of Case 1.

Case 2: $p \ge \hat{p}$

Consider the proposal $\pi _w^*$ defined such that $g_{\pi _w^*}=1$ and

$$\begin{aligned} s_{\pi _w^*}(i)={\left\{ \begin{array}{ll} 0 &{}\text {for } i\in \left( 0,p\right] , \\ V+1 &{}\text {for } i\in \left( p,\frac{1}{2}+p \right] , \\ -\frac{1/2}{1/2-p} \cdot \left( V+1 \right) &{} \text{ for } \text{ all } \text{ other } i. \end{array}\right. } \end{aligned}$$

We point out that $\pi _w^*$ is well-defined, because $0< p<\frac{1}{2}$, and it is moreover admissible, i.e., $\pi _w^* \in \Pi$. Note also that to construct proposal $\pi _w^*$, $AS_w$ only needs to know the parameters of the project $(p,V,\delta )$ and then be able to distinguish losers from winners (but does not need to know their exact project valuations). There are two possibilities for $AS_l$ to build his counter-proposal: he can suggest to implement the project or he can suggest not to implement it. On the one hand, let $\pi ^1_l\in \Pi$ be such that $g_{\pi ^1_l}=1$ and $s_{\pi ^1_l}(j)=0$ for all $j\in [0,1]$. For all $i\in (0,p]$,

$$\begin{aligned} u_i(\pi ^1_l)= v_i = u_i(\pi _w^*) . \end{aligned}$$

In turn, for all $i\in \left( 1/2+p ,1 \right) \cup \{AS_l\}$,

$$\begin{aligned} u_i(\pi ^1_l)=v_i > v_i -\frac{\frac{1}{2}}{\frac{1}{2}-p} \cdot \left( V+1 \right) = u_i(\pi _w^*) , \end{aligned}$$

where the inequality holds since $p<1/2$. Accordingly, because $p+(1/2-p)=1/2$, proposal $\pi ^1_l$ would win a vote against $\pi _w^*$ (i.e., the former would be supported by a majority of the legislature members). In addition, $\pi ^1_l$ is more preferred by $AS_l$ to $\pi _w^*$. What is more, $\pi ^1_l$ is the best proposal for $AS_l$ among those that prescribe implementation of the project, since it prescribes no transfers at all. On the other hand, suppose that $AS_l$ is considering to make a proposal $\pi ^0_l$ such that $g_{\pi ^0_l}=0$. Note that for all $i\in (0,p]$ and all $j\in (p,\frac{1}{2}+p)$,

$$\begin{aligned} \mathbb {E} [u_j(\pi ^*_w)]= V = \mathbb {E} [ u_i(\pi ^*_w)]. \end{aligned}$$

In fact, $u_j(\pi ^*_w)$ and $u_i(\pi ^*_w)$ are i.i.d. according to a uniform distribution in $[V-\delta ,V+\delta ]$, and in particular, all such utilities are strictly positive (since $\delta <V$). Now, in order for $\pi ^0_l$ to defeat $\pi ^*_w$ in the voting round, the “cheapest” majority that $AS_l$ needs to construct (to have his proposal win the vote) must include some legislators from $(0,p]\cup \left( p,\frac{1}{2}+p \right]$, who have to receive a positive transfer. However, this transfer can neither be targeted at each legislator nor be based on his idiosyncratic project valuation. The reason, we recall, is that the exact valuation of any legislator is private information: It is only public knowledge whether they are losers or winners. Accordingly, suppose that a set of legislators M, with $M\subseteq \left( 0,\frac{1}{2}+p \right]$, is given a transfer $s\in [V-\delta ,V+\delta ]$ under $\pi ^0_l$, with all other legislators being net contributors. Note that for $AS_l$ to consider transfers that are higher than $V+\delta$ is strictly dominated, as such transfers will not change the decision of their recipients as whether to vote for $\pi ^*_w$ or for $\pi ^0_l$—compared to case where the transfer is $V+\delta$—, and they will moreover have to be financed by the net contributors, in particular by $AS_l$ himself. Similarly, for $AS_l$ to consider transfers that are lower than $V-\delta$ is also strictly dominated. That is, assume that beyond the fact that $g_{\pi ^0_l}=0$, we have

$$\begin{aligned} s_{\pi _l^0}(i)={\left\{ \begin{array}{ll} s &{}\text {for } i\in M, \\ -\frac{m}{1-m} \cdot s&{}\text{ for } \text{ all } \text{ other } i. \end{array}\right. } \end{aligned}$$

Trivially, $\pi ^0_l \in \Pi$, i.e., $\pi ^0_l$ is admissible. On occasion, it will be more convenient to make the dependence of $\pi ^0_l$ on s and M explicit, in which case we will write $\pi ^0_l(s,M)$. First, for all $i\in M$,

$$\begin{aligned} u_i(\pi ^0_l)-u_i(\pi ^*_w)=s-u_i(\pi ^*_w), \end{aligned}$$

and, hence,

$$\begin{aligned} Prob [u_i(\pi ^0_l)-u_i(\pi ^*_w)\ge 0]=U (s), \end{aligned}$$

where $U(\cdot )$ denotes the CDF of a uniform distribution in $[V-\delta ,V+\delta ]$. Second, for all $i\in \left( 0,1/2+p \right) \setminus M$, it can be readily verified that

$$\begin{aligned} u_i(\pi ^0_l)= & {} -\frac{m}{1-m} \cdot s<0< V-\delta \\\le & {} {\left\{ \begin{array}{ll} v_i = u_i(\pi ^*_w)&{} \text{ if } i\in (0,p] \setminus M,\\ v_i+V+1 = u_i(\pi ^*_w) &{} \text{ if } i\in \left( p,\frac{1}{2}+p \right] \setminus M. \end{array}\right. } \end{aligned}$$

Third, if we assume momentarily that

$$\begin{aligned} m\le \frac{1}{2}, \end{aligned}$$

(13)

we obtain that for all $i\notin \left( 0,1/2+p \right)$, and in particular for the second agenda-setter $AS_l$,

$$\begin{aligned} u_i(\pi ^0_l)&=-\frac{m}{1-m} \cdot s \ge - s \ge -(V+\delta ) \ge v_i-\frac{1/2}{1/2-p} \cdot \left( V+1 \right) =u_i(\pi ^*_w), \end{aligned}$$

(14)

where the first inequality holds because $m\le 1/2$, the second inequality holds since $s\le V+\delta$, the third inequality holds because $\delta < 1$ and $0<p<1/2$, and due to the fact that i is a loser, and hence $v_i\le -1+\delta <0$. All in all, by the law of large numbers (for a continuum of random variables), the share of legislators that (weakly) prefer $\pi ^0_l$ to $\pi ^*_w$ if (13) holds is

$$\begin{aligned} U (s)\cdot m + \frac{1}{2}-p = \frac{s-V+\delta }{2\delta }\cdot m +\frac{1}{2}-p . \end{aligned}$$

(15)

If (13) does not hold, i.e., if m is larger than 1 / 2, expression (15) determines an upper bound for such a share in the case of $\pi ^0_l(s,M)$, since the chain of inequalities in (14) may not hold anymore for some $i\notin \left( 0,1/2+p \right)$. We will revisit this case below. If (13) does hold, by setting the share in expression (15) equal to 1 / 2 (the measure of a minimal winning coalition), we obtain

$$\begin{aligned} m (s) = \frac{2\delta \cdot p}{s-V+\delta }. \end{aligned}$$

(16)

We point out that the share in expression (15) has to be generally equal or higher than 1 / 2, but that this restriction must be binding. This follows because (15) is increasing in s and m, while the utility $AS_l$ obtains from $\pi ^0_l$ is decreasing in such variables. Then define

$$\begin{aligned} f(s):=u_{AS_l}(\pi ^0_l) = - \frac{m(s)}{1-m(s)} \cdot s. \end{aligned}$$

By means of some standard algebra, it can be verified that

$$\begin{aligned} sgn\{f'(s)\}=sgn\left\{ -m'(s)s-m(s)(1-m(s))\right\} =sgn\{V-\delta +2\delta p\} >0, \end{aligned}$$

where the inequality holds because $\delta <V$.

It is then immediate to verify that in order to maximize $AS_l$’s utility from $\pi ^0_l$ (and, hence, in order to maximize f(s) for $s\in [V-\delta ,V+\delta ]$), it must be

$$\begin{aligned} s=V+\delta , \end{aligned}$$

and, hence, by Eq. (16), we also obtain

$$\begin{aligned} m=p. \end{aligned}$$

Since by assumption we have $p<1/2$, any pair $(V+\delta ,M)$, with $m=p$, solves the following maximization problem:

$$\begin{aligned}&\max \quad h(s):=u_{AS_l} (\pi ^l_0(s,M)) \nonumber \\&\text{ s.t. } s\in [V-\delta ,V+\delta ], M\subseteq (0,1/2+p), \text{ and } \text{ Eqs. } (13) \text { and }(16) \text { hold}. \end{aligned}$$

(17)

It remains to show that setting m above 1 / 2 will never be optimal for $AS_l$. To prove this claim, we start by noting that for $s\in [V-\delta ,V+\delta ]$ and M, with $1/2 \le m \le 1/2+p$, the share of legislators that (weakly) prefer $\pi ^0_l$ to $\pi ^*_w$ representing a (minimal winning) majority imposes the following condition:

$$\begin{aligned} \frac{s-V+\delta }{2\delta }\cdot m +\left( \frac{1}{2}-p\right) \cdot U(\eta (s,m))=\frac{1}{2}, \end{aligned}$$

(18)

where

$$\begin{aligned} \eta (s,m)=\frac{1-p}{1/2-p} \cdot (V+1)-\frac{m}{1-m} \cdot s. \end{aligned}$$

(19)

As with the case where (13) holds, one can check that (18) must indeed hold, i.e., that the condition imposing the share of legislators preferring $\pi ^0_l$ to $\pi ^*_w$ be at least 1 / 2 must be binding. Equation (19) follows from noting that for all $i\notin \left( 0,1/2+p \right)$,

$$\begin{aligned}&-\frac{m}{1-m} \cdot s \ge v_i-\frac{1/2}{1/2-p} \cdot \left( V+1 \right) =u_i(\pi ^*_w) \\&\quad \Leftrightarrow v_i+(V+1) \le \frac{1-p}{1/2-p} \cdot (V+1)-\frac{m}{1-m} \cdot s, \end{aligned}$$

with $v_i+(V+1)$ distributed according to $U(\cdot )$. Clearly, $\eta (s,m)$ is decreasing in both s and m, while

$$\begin{aligned} U(\eta (s,m))= {\left\{ \begin{array}{ll} 1 &{} \text{ if } \eta (s,m) \ge V+\delta , \\ \frac{\eta (s,m) -V+\delta }{2\delta } &{} \text{ if } V-\delta< \eta (s,m) < V+\delta , \\ 0 &{} \text{ if } \eta (s,m) \le V-\delta . \end{array}\right. } \end{aligned}$$

In particular, $U(\eta (s,m))$ is non-increasing in both variables s and m. Then, conditional on $m\ge 1/2$, $AS_l$ solves the following maximization problem:

$$\begin{aligned}&\max \quad h(s)=- \frac{m(s)}{1-m(s)} \cdot s \nonumber \\&\text{ s.t. } s\in [V-\delta ,V+\delta ], M\subseteq (0,1/2+p), \text{ and } \text{ Eq. }\,(18)~\text {holds} \end{aligned}$$

(20)

This is a complicated optimization problem. However, one can show that even if a local maximum $s^*\in [V-\delta ,V+\delta ]$ exists for the optimization problem defined in (20) where

$$\begin{aligned} V-\delta< \eta (s^*,m(s^*)) < V+\delta , \end{aligned}$$

(21)

this will not be the global maximum. On the one hand, assuming (21), it follows from (19) that

$$\begin{aligned} h(s^*)= \eta (s^*,m(s^*)) -\frac{1-p}{1/2-p} \cdot (V+1). \end{aligned}$$

On the other hand, we have shown above that the (local) maximum $(s^{**},m(s^{**}))=(V+\delta ,p)$ obtained when (13) holds leads to

$$\begin{aligned} h(s^{**})= - \frac{p}{1-p}\cdot (V+\delta ). \end{aligned}$$

Then note that

$$\begin{aligned} - \frac{p}{1-p}\cdot (V+\delta )&> (V+\delta ) -\frac{1-p}{1/2-p} \cdot (V+1) \\&> \eta (s^*,m(s^*)) -\frac{1-p}{1/2-p} \cdot (V+1), \end{aligned}$$

where the last inequality is due to (21). In turn, the first inequality holds since $\delta <1$ and $0<p<1/2$, which implies

$$\begin{aligned} \frac{1-p}{1/2-p} \cdot (V+1)> \frac{1-p}{1/2-p} \cdot (V+\delta ) > \frac{1}{1-p}\cdot (V+\delta ). \end{aligned}$$

For the sake of understanding, we note that the second inequality in the above chain of inequalities is equivalent to

$$\begin{aligned} \frac{1}{2}-p(1-p)>0. \end{aligned}$$

That is,

$$\begin{aligned} h(s^{**})=- \frac{p}{1-p}\cdot (V+\delta ) > \eta (s^*,m(s^*)) -\frac{1-p}{1/2-p} \cdot (V+1) = h(s^*), \end{aligned}$$

and hence choosing $s^{**}$ is preferred to choosing $s^*$ by $AS_l$. Finally, we note that the cases where $s^*$ is such that either $\eta (s^*,m(s^*))\le V-\delta$ or $\eta (s^*,m(s^*))\ge V+\delta$, with $m(s^*)\ge 1/2$ in both cases, follow the same logic underlying the optimization problem (17). This implies, in particular, that in both cases we must have $s^*=V+\delta$. Since the objective function is strictly decreasing in both s and m, $s^{**}$ will also be preferred to $s^{*}$ if either $\eta (s^*,m(s^*))\le V-\delta$ or $\eta (s^*,m(s^*))\ge V+\delta$. This follows because

$$\begin{aligned} m(s^*)\ge \frac{1}{2}>p = m(s^{**}). \end{aligned}$$

All in all, (13) must hold in the best response by $AS_l$, and, hence, $\pi ^0_l$ with $s=V+\delta$ and $m=p$ is the best proposal for $AS_l$ among those that do not prescribe implementation of the project. Setting $s=V+\delta$ and $m=p$ yields

$$\begin{aligned} u_{AS_l}(\pi ^0_l) = - \frac{p}{1-p} \cdot (V + \delta ) = -\frac{p}{1-p} \cdot \frac{1-{\hat{p}}}{{\hat{p}}} -\frac{p}{1-p} \cdot \delta , \end{aligned}$$

where the second equality follows from Equation (10). Finally,

$$\begin{aligned} u_{AS_l} (\pi ^1_l)=v_{AS_l} \ge -\frac{p}{1-p} \cdot \frac{1-{\hat{p}}}{{\hat{p}}} -\frac{p}{1-p} \cdot \delta = u_{AS_l}(\pi ^0_l), \end{aligned}$$

which holds if and only if the second agenda-setter’s valuation is at least

$$\begin{aligned} -\frac{p}{1-p} \cdot \frac{1-{\hat{p}}}{{\hat{p}}} -\frac{p}{1-p} \cdot \delta . \end{aligned}$$

In such case, $AS_l$ will prefer to propose $\pi ^1_l$ over $\pi ^0_l$. That is, $AS_l$ will prefer to accept the implementation of the project and eliminate all transfers in response to $\pi ^*_w$, which again coincides with the socially optimal outcome $\pi ^{soc}$. This completes the proof of Case 2, because it shows that the winning proposal will be $\pi ^{soc}$, the best possible outcome for the first agenda-setter (a winner). We stress that there could be other equilibria, in which the first agenda-setter makes a proposal different from $\pi ^*_w$, but they must necessarily lead to (the equivalence class of) $\pi ^{soc}$ being the winning proposal, too. The reason is that $\pi ^{soc}$ yields the best possible outcome for the first agenda-setter, $AS_w$. $\square$