Price caps, oligopoly, and entry

Abstract

We extend the analysis of price caps in oligopoly markets to allow for sunk entry costs and endogenous entry. In the case of deterministic demand and constant marginal cost, reducing a price cap yields increased total output, consumer welfare, and total welfare, results consistent with those for oligopoly markets with a fixed number of firms. With deterministic demand and increasing marginal cost, these comparative static results may be fully reversed, and a welfare-improving cap may not exist. Recent results in the literature show that for a fixed number of firms, if demand is stochastic and marginal cost is constant, then lowering a price cap may either increase or decrease output and welfare (locally); however, a welfare-improving price cap does exist. In contrast to these recent results, we show that a welfare-improving cap may not exist if entry is endogenous. However, within this stochastic demand environment we show that certain restrictions on the curvature of demand are sufficient to ensure the existence of a welfare-improving cap when entry is endogenous.

1 Introduction

Price ceilings or caps are relevant in many areas, including: electricity markets, pharmaceuticals, interest on loans and credit, telecommunications services, taxi services, and housing in urban areas. Price caps are common in pharmaceutical markets outside the USA such as in India, where legislation passed in 2013 that significantly expanded the number of drugs facing price cap regulation.¹ Regulators have imposed price caps in a number of US regional wholesale electricity markets, including ERCOT (Texas), New England, and PJM. A key goal for price caps in wholesale electricity markets is to limit the exercise of market power. The principle that a price cap can limit market power is well understood in the case of a monopolist with constant marginal cost in a perfect-information environment. A price cap increases marginal revenue in those situations where it is binding and incentivizes the monopolist to increase output. Total output, consumer surplus, and total welfare increase as the cap decreases toward marginal cost.

Recent papers by Earle et al. (2007) (hereafter, EST) and Grimm and Zottl (2010) (hereafter, GZ) examine the effectiveness of price caps in oligopoly markets with constant marginal cost. EST show that while the classic monopoly results for price caps carry over to Cournot oligopoly when demand is certain, these results do not hold under demand uncertainty.² In particular, they show that when firms make output decisions prior to the realization of demand, total output, welfare, and consumer surplus may be locally increasing in the price cap. This result would seem to raise into question the effectiveness of price caps as a welfare-enhancing policy tool. However, GZ demonstrate that, within the framework of Cournot oligopoly with uncertain demand analyzed by Earle et al., there exists an interval of prices such that any price cap in this interval increases both total market output and welfare compared to the no-cap case. Thus, while the standard comparative statics results of price caps may not hold with uncertain demand, there always exists a welfare-improving price cap.

Importantly, prior analyses of oligopoly markets with price caps assume that the number of firms is held fixed. Yet an important practical concern with the use of price caps is that a binding cap may decrease the profitability of an industry, deter potential market entrants, and thereby reduce competition. Once entry incentives are taken into account, the efficacy of price caps for limiting the exercise of market power and improving welfare is less clear. In this paper, we explore the welfare impact of price caps, taking firm entry decisions into consideration. We modify the analyses of EST and GZ by introducing an initial market entry period prior to a second period of product market competition. Market entry requires a firm to incur a sunk cost. The inclusion of a sunk entry cost introduces economies of scale into the analysis. This would seem to be a natural formulation, since an oligopolistic market structure in a homogeneous product market may well be present because of economies of scale.³

Given the prominent use of price caps as a regulatory tool in settings with multiple suppliers, an analysis that fails to consider their impact on market entry decisions may be missing a vital component. We show that when entry is endogenous, demand is deterministic, and marginal cost is constant, the standard comparative statics results continue to hold. In this case, a price cap may result in fewer firms, but the incentive provided by the cap to increase output overwhelms the incentive to withhold output due to a decrease in competition. It follows that, regardless of the number of firms that enter the market, output increases as the cap is lowered. Welfare gains are realized on two fronts. First, the cap increases total output. Second, the cap may deter entry, and in doing so, reduce the total cost associated with entry.

We also consider the case of increasing marginal costs of production. When coupled with our sunk entry cost assumption, increasing marginal cost yields a U-shaped average cost curve for each active firm. The standard comparative statics results hold for a range of caps when the number of firms is fixed; a lower cap within this range yields greater output and higher welfare. However, these comparative statics results need not hold when entry is endogenous. In fact, we show that if marginal cost rises sufficiently rapidly relative to the demand price elasticity, then the standard comparative statics results may be fully reversed; welfare and output may monotonically decrease as the cap is lowered. In contrast to results for a fixed number of firms, it may be the case that any price cap reduces total output and welfare (i.e., there does not exist a welfare-improving cap). We also provide sufficient conditions for the existence of a welfare-improving cap. These conditions restrict the curvature of demand and marginal cost.

We then show that a welfare-improving price cap may not exist when demand is uncertain and entry is endogenous (with firms facing constant marginal cost). Thus, the results of GZ do not generalize to the case of endogenous entry. On the other hand, we provide sufficient conditions for existence of a welfare-improving price cap. These conditions restrict the curvature of inverse demand, which in turn influences the extent of the business-stealing effect⁴ when an additional firm enters the market. We also consider a version of the model with disposal; firms do not have to sell the entire quantity they produced, but instead may choose the amount to sell after demand uncertainty has been resolved. We show that the sufficient condition for existence of a welfare-improving price cap for the no-disposal model carries over to the model with disposal. Our results for the model with disposal are complementary to results in Lemus and Moreno (2013) on the impact of a price cap on a monopolist’s capacity investment. They show that a price cap influences welfare through two separate channels: an investment effect and an effect on output choices made after realization of a demand shock. Our formulation with disposal allows for welfare to operate through these two channels as well as a third channel, firm entry decisions.

In order to highlight the role of discrete entry decisions in our analysis, we examine an environment in which the number of firms, n, is continuous. This may be interpreted as an environment in which the size of firms may be easily adjusted. For the continuous-n case, we provide a sufficient condition under which a welfare-improving cap exists with either deterministic demand or stochastic demand, allowing for convex costs and free disposal. As in the discrete-n/stochastic demand case, the sufficient condition restricts the curvature of demand and implies the presence of the business-stealing effect. The condition is not sufficient to ensure the existence of a welfare-improving cap when n is discrete, thus highlighting the relevance of the integer constraint in our model.

Our results imply that policy makers should be aware of the potential impact of price caps on firm entry decisions. We also bring to light three important considerations for assessing the impact of price caps, which are not apparent in model with a fixed number of firms. First, our results suggest that industries characterized by a weak business-stealing effect are less likely to benefit from the imposition of a price cap than industries where this effect is strong. Second, our results indicate that industries in which firms face sharply rising marginal cost curves are less likely to benefit from a price cap, than industries where marginal cost is less steep. Third, our results suggest that industries in which the size of firms can be easily adjusted are more likely to benefit from price cap regulation.

Our model of endogenous entry builds on results and insights from Mankiw and Whinston (1986) and Amir and Lambson (2000). Mankiw and Whinston show that when total output is increasing in the number of firms but per-firm output is decreasing in the number of firms (the term for the latter is the business-stealing effect), the socially optimal number of firms will be less than the free-entry number of firms when the number of firms, n, is continuous. For discrete n, the free-entry number of firms may be less than the socially optimal number of firms, but never by more than one. Intuitively, when a firm chooses to enter, it does not take into account decreases in per-firm output and profit of the other active firms. Thus, the social gain from entry may be less than the private gain to the entrant. Amir and Lambson provide a taxonomy of the effects of entry on output in Cournot markets. In particular, they provide a general condition under which equilibrium total output is increasing in the number of firms. Our results rely heavily on their approach and results.

2 The model

We assume an arbitrarily large number, $N \in \mathbb {N}$, of symmetric potential market entrants, and formulate a two-period game. The N potential entrants are ordered in a queue and make sequential entry decisions in period one. Each firm’s entry decision is observed by the other firms. There is a cost of entry $K >0$, which is sunk if a firm enters. If a firm does not enter, it receives a payoff of zero.⁵

The n market entrants produce a homogeneous good in period two. Each firm faces a strictly increasing, convex cost function, $C: \mathbb {R}_+ \rightarrow \mathbb {R}_+$. Output decisions are made simultaneously. The inverse demand function is given by $P(Q, \theta )$ which depends on total output, Q, and a random variable, $\theta$. The random variable, $\theta$, is continuously distributed according to CDF F with corresponding density f. The support of $\theta$ is compact and given by $\varTheta \equiv [\underline{\theta }, \overline{\theta }] \subset \mathbb {R}$. Each firm knows the distribution of $\theta$ but must make its output decision prior to its realization. A regulator may impose a price cap, denoted $\overline{p}$. The following assumption is in effect throughout the paper.

Assumption 1

• (a) P is continuous in Q and $\theta$, strictly decreasing in Q for fixed $\theta$, and strictly increasing in $\theta$ for fixed Q.

• (b) $\displaystyle \lim _{Q \rightarrow \infty } \{QP(Q, \overline{\theta }) - C(Q)\} < 0$

• (c) $\displaystyle \max _{Q \in \mathbb {R}_{+}} \{QE[P(Q, \theta )] -C(Q)\} > K$

Assumption (1a) matches the assumptions imposed by EST; GZ additionally assume differentiability of inverse demand in Q and $\theta$. Assumption (1b) ensures that a profit-maximizing quantity exists for period two decisions.

EST assume that $E[P(0, \theta )]$ is greater than marginal cost, which is assumed to be constant in their analysis. Their assumption ensures that “production is gainful”; that is, given a fixed number, $n > 0$, of market participants, there exist price caps such that equilibrium market output will be strictly positive. Our Assumption (1c) is a “profitable entry” condition, which guarantees that there exist price caps such that at least one firm enters the market and that equilibrium output will be strictly positive. We let $\mathbb {P}$ denote the set of price caps which induce at least one market entrant. That is

$$\begin{aligned} \mathbb {P} = \left\{ \overline{p} > 0 \mid \max _{Q \in \mathbb {R}_{+}} \left\{ QE[\min \{P(Q, \theta ), \overline{p} \}] -C(Q)\right\} \ge K \right\} \end{aligned}$$

Assumption 1 implies $\mathbb {P} \ne \emptyset$. In this paper, we are only concerned with price caps $\overline{p} \in \mathbb {P}$. We restrict attention to subgame perfect pure strategy equilibria and focus on period two subgame equilibria that are symmetric with respect to the set of market entrants. For a given price cap and a fixed number of firms, there may exist multiple period two subgame equilibria. As is common in the oligopoly literature, we focus on extremal equilibria—the equilibria with the smallest and largest total output levels—and comparisons between extremal equilibria. So when there is a change in the price cap, we compare equilibrium outcomes before and after the change, taking into account the change (if any) in the equilibrium number of firms, while supposing that subgame equilibria involve either maximal output or minimal output.

One other point to note: Imposing a price cap may require demand rationing. When rationing occurs, we assume rationing is efficient; i.e., rationed units are allocated to buyers with the highest willingness to pay. This is consistent with prior analyses of oligopoly with price caps.⁶

We denote by $Q_{n}^{*}(\overline{p})$ ($q_n^*(\overline{p})$), period two subgame extremal equilibrium total (per-firm) output⁷ when n firms enter and the price cap is $\overline{p}$. We let $\pi _n^*(\overline{p})$ denote each firm’s expected period two profit in this equilibrium. We also let $Q_n^{\infty } = Q_n^*(\infty )$ be the period two equilibrium total output when n firms enter with no price cap, and define $q_n^{\infty }$ and $\pi _n^{\infty }$ analogously. Firms are risk neutral and make output decisions to maximize expected profit. That is, each firm i takes the total output of its rivals, y, as given and chooses q to maximize

$$\begin{aligned} \pi (q, y, \overline{p}) = E[q \min \{P(q + y, \theta ), \overline{p} \} - C(q) ] \end{aligned}$$

After being placed in the queue, firms have an incentive to enter as long as their expected period two equilibrium profit is at least as large as the cost of entry. We assume that firms whose expected second period profits are exactly equal to the cost of entry will choose to enter. For a fixed price cap, $\overline{p}$, subgame perfection in the entry period (along with the indifference assumption) implies that the equilibrium number of firms, $n^*$, is the largest positive integer less than (or equal to) N such that $\pi ^*_{n^*}(\overline{p}) \ge K$. Clearly, $n^*$ exists and is unique. Moreover, for any $\overline{p} \in \mathbb {P}$ we also have $n^* \ge 1$.

3 Deterministic demand

We begin our analysis by considering a deterministic inverse demand function. That is, the distribution of $\theta$ places unit mass at some particular $\tilde{\theta } \in \varTheta$. In this section, we suppress the second argument in the inverse demand function and simply write P(Q). We study both the case of constant marginal cost and strictly increasing marginal cost.

3.1 Constant marginal cost

Suppose marginal cost is constant : $C(q) = cq$, where $c \ge 0$. For a given number, $n \in \mathbb {N}$, of market participants EST prove the existence of a period two subgame equilibrium that is symmetric for the n firms. Our main result in this section demonstrates that the classic results on price caps continue to hold when entry is endogenous; all proofs are in the “Appendix.”

Proposition 1

Restrict attention to $\overline{p} \in \mathbb {P}$. In an extremal equilibrium, the number of firms is non-decreasing in the cap, while total output, total welfare, and consumer surplus are non-increasing in the price cap.

Proposition 1 is similar to Theorem 1 in EST. However, our model takes into account the effects of price caps on firm entry decisions. As we show in the proof of Proposition 1, firm entry decisions are potentially an important consideration as equilibrium output is non-decreasing in the number of firms (for a fixed cap). This fact, along with the fact that a lower price cap may deter entry, suggest that a reduction in the cap could have the effect of lowering the number of firms and reducing total output. Our result shows that with constant marginal cost and non-stochastic demand, even if entry is reduced, the incentive for increased production with a cap dominates the possible reduction in output due to less entry. There are two sources of welfare gains. First, total output is decreasing in the price cap, so a lower price cap yields either constant or reduced deadweight loss. Second, a lower price cap may reduce the number of firms, and thereby decrease the total sunk costs of entry.

In a recent contribution, Amir et al. (2014) show that if demand is log-convex then, in the absence of a price cap, the free-entry number of firms may be strictly less than the socially optimal number of firms. In such instances, one may be particularly concerned that a price cap that deters entry may lead to a reduction in welfare. It is worth pointing out, however, that Proposition 1 applies even in this setting. Intuitively, the incentive provided by the cap to expand output will dominate any potential reduction in output caused by entry deterrence. The following example, which is based on Example 1 in Amir et al., illustrates this point.

Example 1

Consider the following inverse demand and costs:

$$\begin{aligned} P(Q) = \frac{1}{(Q + 1)^5}; \quad c = 0, \quad K = .02592 \end{aligned}$$

With no cap, 2 firms enter, total equilibrium output is $.\overline{6}$, and the equilibrium price is approximately .07776. Equilibrium per-firm profit is exactly equal to the cost of entry, and equilibrium welfare is .16576. Note that the socially optimal number of firms without a cap is 3. Any cap, $\overline{p} \in (.02302, .07776)$ results in exactly 1 entrant, and total output satisfies: $P(Q^*(\overline{p})) = \overline{p}$; so, $Q^*(\overline{p}) = \frac{1}{\overline{p}^5} - 1$. Any cap in the interval (.02302, .07776) results in higher total output and welfare than in the absence of a cap. For instance, a cap equal to .07 results in total output of approximately .70208 and welfare of approximately .19429. As the cap decreases within this interval, it is easy to see that total output and welfare both (strictly) increase monotonically.

Assumption 1 allows for a very general demand function, and because of this, there may be multiple equilibria. Proposition 1 provides results for extremal equilibria of period two subgames for cases with multiple equilibria. With an additional restriction on the class of demand functions, the equilibrium is unique and we achieve a stronger result on the impact of changes in the price cap.

Proposition 2

Suppose P is log-concave in output. Then, for any $\overline{p} \in \mathbb {P}$, there exists a unique symmetric subgame equilibrium in the period 2 subgame. Moreover, equilibrium output, welfare, and consumer surplus are strictly decreasing in the cap for all $\overline{p} < P(Q^{\infty })$ and $\overline{p} \in \mathbb {P}$.

The intuition behind Proposition 2 is straightforward. When inverse demand is log-concave, there is a unique symmetric period two subgame equilibrium for each n and $\overline{p}$. If $\overline{p}$ is less than the equilibrium price when there is no cap, then $\overline{p}$ must bind in the subgame equilibrium. With no cap, Amir and Lambson (2000) show that the subgame equilibrium price is non-increasing in n. Any price cap below the no-cap free-entry equilibrium price must bind in equilibrium, since the number of firms that enter will be no greater than the number of firms that enter in the absence of a cap. A lower price cap therefore yields strictly greater total output.

A consequence of our results is that the welfare-maximizing price cap is the lowest cap that induces exactly one firm to enter. Imposing such a cap both increases output and reduces entry costs. Since marginal cost is constant, the total industry cost of producing a given level of total output does not depend on the number of market entrants.

3.2 Increasing marginal cost

The assumption that marginal cost is constant is not innocuous. In this section, we consider a variation of the deterministic demand model in which firms have symmetric, strictly increasing marginal costs of production. This assumption on marginal cost, coupled with a sunk cost of entry, implies that firms have U-shaped average cost. We assume that the cost function, $C: \mathbb {R}_+ \rightarrow \mathbb {R}_+$, is twice continuously differentiable with $C(0) = 0$, $C'(x) > 0$ and $C''(x) > 0$ for all $x \in \mathbb {R}_+$.

Reynolds and Rietzke (2015) show that when the number of firms is fixed, there exists a range of caps under which extremal equilibrium output and associated welfare are monotonically non-increasing in the cap.⁸ This range of caps consists of all price caps above the n-firm competitive equilibrium price. Intuitively, price caps above this threshold are high enough that marginal cost in equilibrium is strictly below the price cap for each firm. A slight decrease in the price cap means the incentive to increase output created by a lower cap outweighs the fact that marginal cost has increased (since the cap still lies above marginal cost).⁹

We now provide an example, which demonstrates that the results for the fixed-n model do not carry over to our model with endogenous entry. In fact, our example shows that the comparative statics results for a change in the price cap may be fully reversed with endogenous entry, and a welfare-improving cap may not exist.

Example 2

Consider the following inverse demand and cost function:

$$\begin{aligned} P(Q) = aQ^{1/\eta }, \quad C(q) = \frac{\gamma }{(1+\gamma )}q^\frac{(1+\gamma )}{\gamma } \quad \end{aligned}$$

These functions yield iso-elastic demand and competitive, single-firm supply functions with price elasticities $\eta$ and $\gamma$, respectively. Suppose that $a = \sqrt{96}$, $\eta =-2$, $\gamma =1$, and $K=7.5$. Then, absent a price cap, two firms enter, each firm produces 3 units of output and the equilibrium price is 4. Each firm earns product market payoff of 7.5 and zero total profit, since product market payoff is equal to the sunk entry cost. For price caps between minimum average total cost $ATC^m$ of 3.87 and 4, one firm enters and total output and welfare are strictly less than output and welfare in the no-cap case.

Duopoly firms exert market power and the equilibrium price exceeds marginal cost in Example 2. However, profits are completely dissipated through entry. Imposing a price cap in this circumstance does indeed limit market power. However, a price cap also reduces entry, results in rationing of buyers, and yields lower total output, total welfare and consumer surplus than the no-cap equilibrium. A welfare-improving price cap does not exist for this example. In fact, total output and welfare are increasing in the price cap for $\overline{p} \in [ ATC^m,P(Q^{\infty }))$. A welfare improvement could be achieved by a policy that combines an entry subsidy—to encourage entry—with a price cap—to incentivize increased output.

It is worth pointing out that the integer constraint on n plays a role in the example. In a subgame with n firms, a cap set below the n-firm competitive price results in demand rationing. If the $n^{\infty } - 1$ firm competitive price is greater than the $n^{\infty }$ firm Cournot price (as is the case for the parameters given), then a binding cap that deters entry must therefore lead to rationing. If n is continuous, then a sufficiently high cap (which results in a small reduction in the number of firms) need not lead to rationing. This issue is explored further in Sect. 5.

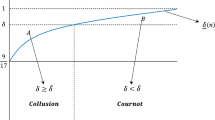
Proposition 3 below provides sufficient conditions for existence of a welfare-improving price cap. The key condition is that the equilibrium price in the no-cap case exceeds the competitive equilibrium price in the event that one less firm enters the market. This condition rules out outcomes such as that of Example 2 in which a binding price cap reduces the number of firms and yields a discrete reduction in output. In what follows, we let $n^\infty$ denote the equilibrium number of firms when there is no price cap and let $p^c_{n}$ denote the competitive equilibrium price when n firms enter.

Proposition 3

Suppose that $P(\cdot )$ is log-concave in output. If $P(Q^{\infty })>p^c_{n^{\infty } - 1}$, then a welfare-improving price cap exists.

Proposition 3 is based on two conditions. The first is that demand is log-concave in output. Log-concavity of demand implies that, in the absence of a price cap, there is a unique symmetric subgame equilibrium in stage 2. As a result, in a subgame with n firms, a cap set below the n-firm Cournot price must bind in equilibrium. The second condition is that the $n^{\infty } - 1$-firm competitive price is strictly less than the $n^{\infty }$-firm Cournot price. Consider a cap $\overline{p} \in (p^c_{n^{\infty } - 1}, P(Q^{\infty }))$, which is also sufficiently high so as to deter no more than 1 entrant. Log-concave demand implies that such a cap must bind in equilibrium. Hence, total output must be higher than in the absence of a cap. As in the case of constant MC, welfare gains are realized on two fronts: greater production, which increases consumer surplus, and entry cost savings associated with fewer market participants. Still, the welfare impact of the price cap is not immediately obvious since the cap may decrease the number of market entrants; with a convex cost function, total production costs for a given level of output are higher with fewer market entrants. We are able to show, however, that for high enough caps, the two sources of welfare gains are large enough to offset the increase in production costs.

The condition in Proposition 3 that equilibrium price with no cap and $n^{\infty }$ firms exceeds the competitive price with $n^{\infty }-1$ firms depends on the relative steepness of demand and supply curves. This condition is satisfied for the parametric demand and (competitive) supply functions in Example 2 if the elasticity of supply exceeds a threshold level that is increasing in the (absolute value of) elasticity of demand. Specifically, elasticities must satisfy:

$$\begin{aligned} \gamma > \frac{\ln \left( \frac{n}{n-1}\right) }{\ln \left( \frac{\eta n}{\eta n+1}\right) } \end{aligned}$$

in order to satisfy this condition.

4 Stochastic demand

We now investigate the impact of price caps when demand is stochastic. In this section, we assume marginal cost is constant, so $C(q) = cq$. For the fixed n model with stochastic demand, GZ demonstrate that there exists a range of price caps which strictly increase output and welfare as compared to the case with no cap. Their result is driven by the following observation. Fix an extremal symmetric equilibrium of the game with n firms and no price cap. Let $\overline{\rho }^{\infty } = P(Q^{\infty }_n, \overline{\theta })$ denote the lowest price cap that does not affect prices; i.e., $\overline{\rho }^{\infty }$ is the maximum price in the no-cap equilibrium. And let $\overline{\text {MR}}_n$ be a firm’s maximum marginal revenue in this equilibrium; that is:

$$\begin{aligned} \overline{\text {MR}}_n = \max _{\theta \in {\varTheta }}\left\{ P(Q^{\infty }_n, \theta ) + \frac{Q^{\infty }_n}{n}P_1(Q^{\infty }_n, \theta )\right\} \end{aligned}$$

If firms choose their equilibrium outputs and a cap is set between $\overline{\text {MR}}_n$ and $\overline{\rho }^{\infty }$ then the cap will bind for an interval of high demand shocks; for these shocks marginal revenue will exceed what marginal revenue would have been in the absence of a cap, and for other shocks marginal revenue is unchanged. Firms therefore have an incentive to increase output relative to the no-cap case for caps between $\overline{\text {MR}}_n$ and $\overline{\rho }^{\infty }$.¹⁰ EST provide a quite different result for price caps when demand is stochastic. They show that decreasing a price cap can decrease both total output and welfare. This is a comparative static result, holding locally, in contrast to Grimm and Zottl’s result on the existence of welfare-improving price caps. We begin this section by providing an example, which demonstrates that a welfare-improving price cap may not exist when entry is endogenous.

Example 3

Consider the following inverse demand, costs, and distribution for $\theta$:

$$\begin{aligned} P(Q, \theta ) = \theta + \exp (-Q), \quad K = \exp (-2), \quad c=\frac{1}{2}, \quad \theta \sim U[0,1] \end{aligned}$$

With no cap, each firm has a dominant strategy in the period 2 subgame to choose an output of 1. This leads to 2 market entrants, each earning second period profit exactly equal to the cost of entry. Total welfare is approximately 0.59, and $\overline{\rho }^{\infty } =1 + \exp (-2)$. Imposing a cap $\overline{p} < \overline{\rho }^{\infty }$ will reduce entry by at least one firm. So, consider the subgame with one firm and price cap below $\overline{\rho }^\infty$. With one market entrant, output must exceed $\overline{Q} \equiv 2 - \ln (2) \approx 1.3$ to achieve a welfare improvement. Applying Theorem 4 in GZ, the optimal price cap in the period 2 subgame with one firm satisfies:

$$\begin{aligned} \overline{p}^* = 1 + \exp (-Q^*(\overline{p}^*))(1 - Q^*(\overline{p}^*)) \end{aligned}$$

Imposing such a cap yields total output of $Q^*(\overline{p}^*) \approx 1.22$ and welfare of approximately .57.

Example 3 demonstrates that when demand is stochastic and entry is endogenous, a welfare-improving price cap may not exist. There are two key features of the example. First, when demand is stochastic, a price cap creates a weaker incentive for the monopolist to expand output than when demand is certain. As explained in Earle et al. (p. 95), when demand is uncertain the monopolist maximizes a weighted average of profit when the cap is non-binding (low demand realizations) and profit when the cap is binding (high demand realizations). These two scenarios provide conflicting incentives for the firm. The first effect is that a higher price cap creates an incentive to expand output, as the benefits of increasing quantity increase when the cap is binding (and are not affected when the cap is not binding). The second effect is that a higher price cap decreases the probability that the cap will bind, and this reduces the incentive to increase quantity. For example 3, the second effect dominates the first for caps $\overline{p} \in (\overline{p}^*, \overline{\rho }^\infty )$; in this range, equilibrium output increases as the cap decreases. For caps, $\overline{p} \in (c, \overline{p}^*)$, the first effect dominates the second; in this range, equilibrium output decreases as the cap decreases. The second key feature of this example is that the particular inverse demand and marginal cost imply that, when there is no price cap, firms have a dominant strategy to choose an output of exactly one unit; the business-stealing effect is absent, and total output increases linearly in the number of firms.¹¹ With no business-stealing effect and a binding entry constraint, it follows from Mankiw and Whinston that the free-entry number of firms is equal to the socially optimal number of firms. The optimal cap for this example does not stimulate enough output from the monopolist to account for the welfare lost due to reduced entry.

Example 3 suggests that a zero or weak business-stealing effect is one source of failure of existence of welfare-improving price caps. Our main result for this section provides sufficient conditions on demand that ensure the existence of a welfare-improving cap. Our sufficient conditions ensure that the business-stealing effect is relatively strong, so that reduced entry does not have a large effect on total output. Before proceeding, we introduce some key terms for the model. Let $\theta ^b(Q, \overline{p})$ be defined as:

$$\begin{aligned} \theta ^b(Q, \overline{p}) \equiv \max \left\{ \min \left\{ \left( \theta | \theta + p(Q) = \overline{p}\right) , \overline{\theta }\right\} , \underline{\theta }\right\} \end{aligned}$$

$\theta ^b(Q, \overline{p})$ is the critical demand scenario where, when total production is Q, and the cap is $\overline{p}$, the cap binds for any $\theta > \theta ^b(Q, \overline{p})$. This demand scenario is bounded below by $\underline{\theta }$ and above by $\overline{\theta }$. The second-stage expected profit to some firm i is then given by:

$$\begin{aligned} \int _{\underline{\theta }}^{\theta ^b(Q, \overline{p})} \! qP(Q, \theta )\, {\text {d}}F(\theta ) + \int _{\theta ^b(Q, \overline{p})}^{\overline{\theta }}\! q \overline{p} \, {\text {d}}F(\theta ) - cq \end{aligned}$$

GZ show that for any n, at an interior solution, equilibrium total output satisfies the first-order condition:

$$\begin{aligned} \int _{\underline{\theta }}^{\theta ^b(Q^*, \overline{p})} \! \left( P(Q^*, \theta ) + \frac{Q^*}{n}P_1(Q^*, \theta ))\right) \, {\text {d}}F(\theta ) + \int _{\theta ^b(Q, \overline{p})}^{\overline{\theta }}\! \overline{p} \, {\text {d}}F(\theta ) - c =0 \end{aligned}$$

Now consider the following additional structure on the model

Assumption 2

• (a) $f(\theta ) > 0$ and continuous for all $\theta \in \varTheta$

• (b) For all $\theta$, P is twice continuously differentiable in Q, with $P_1(\cdot , \theta ) < 0$ and $P_{11}(\cdot , \theta ) \le 0$.

• (c) P is additively or multiplicatively separable in Q and $\theta$: $P(Q, \theta ) = \theta + p(Q)$ or $P(Q, \theta ) = \theta h(Q)$.¹²

• (d) For the case of the additive demand shock: $\underline{\theta } + p(0) = 0$.¹³ For the case of the multiplicative demand shock, restrict attention to positive shocks: $\underline{\theta } > 0$.

Assumption 2 places fairly strong restrictions on the form of inverse demand, but no restrictions other than a positive and continuous density on the form of demand uncertainty.¹⁴ We are now ready to state our main results for this section. We first state a useful lemma, which pertains to the game with no price cap. In what follows, we let $W_n$ denote equilibrium expected welfare in the game with no cap when n firms enter.

Lemma 1

Consider the game with no price cap. Suppose Assumption 2 is satisfied and $\pi ^{\infty } = K$, then the socially optimal number of firms is strictly less than the free-entry number of firms. Moreover, $W_{n^{\infty } - 1} > W_{n^{\infty }}$.

Proposition 4

Under Assumptions 1 and 2, there exists a unique symmetric equilibrium. Moreover, there exists a price cap that strictly increases equilibrium welfare.

Concavity of $P(\cdot , \theta )$ implies a relatively strong business-stealing effect. When the business-stealing effect is present and n is continuous, Mankiw and Whinston show the free-entry number of firms is strictly greater than the socially optimal number of firms. This result does not, in general, carry over to the case where n is constrained to be an integer. When n is integer-constrained, the free-entry number of firms may be less than or equal to the socially optimal number of firms.¹⁵ Lemma 1 complements the results of Mankiw and Whinston by providing sufficient conditions, in the case where n is an integer, under which the free-entry number of firms is strictly greater than the socially optimal number of firms. The role of the integer constraint is explored in more detail in Sect. 5.

Proposition 4 establishes the existence of a welfare-improving price cap, but which caps can be guaranteed to increase welfare? To convey the intuition, first suppose the entry constraint is not binding in the absence of a cap (i.e., $\pi ^{\infty } > K$). In this case, there is an interval of prices below $\overline{\rho }^{\infty }$ and above $\overline{\text {MR}}_{n}$ such that a price cap chosen from this interval will yield the same number of firms. Any cap in this interval will result in higher total output and welfare; this follows directly from Theorem 1 in GZ. Next, suppose the entry constraint is binding in the absence of a cap (i.e., $\pi ^{\infty } = K$). In this case, the set of welfare-improving price caps consists of all caps that (a) reduce entry by one firm; and (b) are greater than $\overline{\text {MR}}_{n - 1}$ (the proof of Proposition 4 shows that the set of caps satisfying (a) and (b) is indeed non-empty). The imposition of a such a price cap has two welfare-enhancing effects. First, the cap deters entry, due to the result established in Lemma 1, reducing the number of entrants by one is welfare enhancing. Second, by Theorem 1 in GZ, the cap increases total output and welfare relative to what output and welfare would be in the new entry scenario (i.e., with one less firm) in the absence of a cap.¹⁶

4.1 Free disposal

We now examine a variation of the game examined in Sect. 4. As in the previous versions of the model, at the start of the game the regulator may impose a price cap. The game then proceeds in three periods. In the first period, firms sequentially decide whether to enter or not (again, with each firm’s entry decision observed by all firms). Entry entails a sunk cost $K > 0$. In the second period, before $\theta$ is realized, firms simultaneously choose production, with $x_i$ designating the production choice of firm i; $x_i$ is produced at constant marginal cost $c > 0$. In the third period, firms observe $\theta$ and simultaneously choose how much to sell, with firm i choosing sales quantity $q_i \in [0,x_i ]$; unsold output may be disposed of at zero cost.¹⁷ The effect of price caps in this model with a fixed number of firms has been analyzed by EST, GZ, and Lemus and Moreno.

The free-disposal model may also be interpreted as one in which the firms that enter make long-run capacity investment decisions prior to observing the level of demand, and then make output decisions after observing demand. Under this interpretation, c is the marginal cost of capacity investment, and the marginal cost of output is constant and normalized to zero.¹⁸ We use this description of the model with disposal for the remainder of the paper (i.e., we will refer to $x_i$ and $q_i$ as the capacity choice and output choice, respectively, of firm i).

Our results for free disposal parallel the results above for the no-disposal model. We first extend Example 3 to allow free disposal and show that a welfare-improving cap does not exist. We then show that under Assumptions 1 and 2, a welfare-improving price cap always exists in the model with disposal and endogenous entry.

Example 4

Maintain the same setup as in Example 3. In the absence of a price cap, each firm has a dominant strategy to choose capacity of 1 in the period 2 subgame. In the period 3 subgame, the capacity constraint binds for each $\theta \in [0, 1]$. Two firms enter, each earning third-period profit equal to the cost of entry. This yields total welfare of approximately 0.59; this market behaves exactly as in Example 3 with no cap. Any binding price cap will reduce entry by at least one firm. So, consider the subgame with one firm and price cap $\overline{p} < \overline{\rho }^{\infty }$. When total capacity is X, stage 2 expected equilibrium welfare in the model with disposal is always (weakly) less than equilibrium welfare in the no-disposal model with total output, $Q = X$, since disposal may result in lower output for some demand realizations. Thus, in order to achieve a welfare improvement, total capacity under the cap must exceed the threshold, $\overline{Q} \approx 1.3$, found in Example 3. Applying Theorem 4 in GZ, the cap that maximizes capacity satisfies:

$$\begin{aligned} \overline{p}^* = 1 + \exp (-X^*(\overline{p}^*))(1 - X^*(\overline{p}^*)) \end{aligned}$$

Imposing such a cap yields $X^* \approx 1.23$ Since $X^*< \overline{Q}$, no welfare-improving price cap exists.

Before stating the main result for the model with free disposal, we introduce some of the key expressions. Under Assumptions 1 and 2, GZ show that there exists a unique symmetric equilibrium level of capacity in the second-stage subgame, and a unique symmetric equilibrium level of output in the third-stage subgame. In the third period, each firm solves:

$$\begin{aligned} \max _{q_i} \left\{ q_i\min \{P(q_i + y, \theta ), \overline{p}\}\right\} \quad \text {such that} \quad q_i \le x_i \end{aligned}$$

where y is the total output of the other $n-1$ firms. Let $X \equiv \sum _{i=1}^{n}{x_i}$ denote the total level of capacity. For any n, X and $\overline{p}$, define

$$\begin{aligned} \tilde{\theta }_n(X, \overline{p}) = \max \left\{ \min \left\{ \left( \theta | P(X, \theta ) + \frac{X}{n}P_1(X,\theta ) = 0\right) , \theta ^b(X, \overline{p})\right\} , \underline{\theta }\right\} \end{aligned}$$

$\tilde{\theta }_n(\cdot )$ is the critical demand scenario above which firm output is equal to capacity in equilibrium. At this critical demand scenario, the price cap may or may not be binding. For an additive demand shock, Assumption 2d ensures that $\tilde{\theta }_n(X, \overline{p}) > \underline{\theta }$ whenever $X > 0$. We let $\pi _n^0(\theta , \overline{p})$ denote the equilibrium third-period revenue to a firm in those demand scenarios where the capacity constraint is non-binding. Equilibrium expected firm profit in stage two is given by:

$$\begin{aligned} \pi _n^*(\overline{p})= & {} \int _{\underline{\theta }}^{\tilde{\theta }_n(X^*, \overline{p})}\! \pi _n^{0}(\theta , \overline{p})\, \text {d}F(\theta ) + \int ^{\theta ^b(X^*,\overline{p})}_{\tilde{\theta }_n(X^*, \overline{p})}\!x^{*}P(X^*, \theta )\, \text {d}F(\theta ) \\&+ \int _{\theta ^{b}(X^*, \overline{p})}^{\overline{\theta }}\! x^*\overline{p}\, \text {d}F(\theta ) - cx^* \end{aligned}$$

GZ show that, for a fixed number of firms, and any cap that induces positive production, equilibrium capacity satisfies the first-order condition:

$$\begin{aligned} \int _{\tilde{\theta }_n(X^*, \overline{p})}^{\theta ^{b(X^*, \overline{p})}}\!\left[ P(X^*, \theta ) + \frac{X^*}{n}p_1(X^*, \theta ) \right] \, \text {d}F(\theta ) + \int _{\tilde{\theta }_n(X^*, \overline{p})}^{\overline{\theta }} \overline{p}\, \text {d}F(\theta ) - c = 0 \end{aligned}$$

We are now ready to state the main results for this section. In what follows, we let $W_n$ denote equilibrium welfare in the game with no cap when n firms enter.

Lemma 2

Consider the game with no price cap. Suppose Assumption 2 is satisfied and $\pi ^{\infty } = K$, then the socially optimal number of firms is strictly less than the free-entry number of firms. Moreover, $W_{n^{\infty } - 1} > W_{n^{\infty }}$.

Proposition 5

In the model with disposal, under Assumptions 1 and 2 there exists a price cap that strictly improves welfare.

To understand which price caps are welfare improving, we refer the reader to the discussion following Proposition 4. In that discussion, we describe the set of welfare-improving price caps in the setting without free disposal; however, in the setting with disposal, the set of welfare-improving caps will be qualitatively similar.

GZ show that, for a fixed number of firms, a high price cap increases welfare by creating stronger incentives for capacity investment in the second stage, and reducing the incentive for output withholding in the third-stage market game. Our Proposition 5 extends their welfare result to the case of free entry. It is worthwhile comparing these results to Grimm and Zoettl (2013), who consider the effects of a different form of price regulation, and also allows considering the case of free entry. The authors study an environment in which a regulator can impose marginal-cost pricing (i.e., the competitive outcome) in the market game, at each demand scenario (so long as this outcome is feasible, given firms’ capacities). It is shown that the welfare implications of this form of regulation are not clear, even for a fixed number of firms, when capacities are chosen strategically. The reason is that competitive pricing in the market game leads firms to reduce their capacity investments. The authors thus highlight a tension between reducing the incentive to withhold output in the market game and providing a strong incentive for capacity investment that may arise from price regulation. This tension is further complicated by entry effects, as marginal-cost pricing will reduce entry, as compared to the unregulated outcome.

The tension between providing incentives for capacity investment, and reducing the incentive to withhold output in the market game also arises in our model—where the regulator commits to a price cap before demand uncertainty is resolved. This fact is highlighted by Lemus and Moreno, who show that, because of the tension between output/capacity decisions, the optimal price cap (with a fixed number of firms) will be well above marginal cost; low price caps provide stronger incentives to reduce output withholding, but decrease the incentive to invest in capacity. Our results demonstrate that a high enough price cap can provide an incentive for both increased capacity and increased output in the market game, even when taking potential entry effects into account.

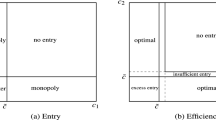
5 Continuous n

Thus far in the analysis, firms were taken to be indivisible, discrete entities. In this section, we modify the model and allow firms to be perfectly divisible, allowing n to take on any value $n \in [1, N]$.¹⁹ Our next result identifies sufficient conditions under which a welfare-improving cap exists when n is continuous. This result allows for either deterministic or stochastic demand, and either constant or increasing marginal costs. The sufficient conditions identified in this section to ensure the existence of a welfare-improving cap are a strict generalization of the conditions identified in Sect. 4. After we discuss our result, we provide an example, which shows that the conditions identified in this section are not sufficient to ensure the existence of a welfare-improving cap when n is integer-constrained.

Proposition 6

In addition to Assumption 1, suppose that P and C are twice continuously differentiable with $P_1 <0$, $P_2 > 0$, $C'>0$, and $C'' \ge 0$. Also suppose $P(0, \underline{\theta }) = 0$, and $\frac{\partial ^2}{\partial Q \partial \theta }\left[ QP(Q, \theta )\right] \ge 0$.²⁰ If the number of firms is continuous and

$$\begin{aligned} P_1(Q, \theta ) + QP_{11}(Q, \theta ) \le 0 \end{aligned}$$

then there exists a price cap that strictly improves welfare:

• (i) in the model with deterministic demand

• (ii) in the model with stochastic demand

• (iii) in the model with free disposal

The key condition for Proposition 6 is: $P_1 + QP_{11} \le 0$, which implies the presence of the business-stealing effect. When n is continuous, the presence of the business-stealing effect implies that the free-entry equilibrium number of firms is strictly greater than the socially optimal (second best) number of firms (see Mankiw and Whinston 1986). We demonstrate that a high enough cap produces two sources of welfare gains. First, is the “entry-deterrence effect”; the cap deters entry, which is welfare enhancing due to the presence of the business-stealing effect. Second, is the “marginal-revenue effect” described by Grimm and Zottl (2010); a high enough cap increases marginal revenue for high demand realizations and reduces incentives for output withholding.

Proposition 6 also brings to light the relevance of the integer constraint on n in assessing the welfare impact of price caps when entry is endogenous. When n is constrained to be an integer, a price cap that deters entry will cause a discrete jump in output and welfare as compared to the no-cap case. Moreover, even in the presence of the business-stealing effect, the free-entry number of firms may be less than or equal to the socially optimal number of firms. As a result, a reduction in the number of firms may result in a downward jump in welfare,²¹ and the entry-deterrence effect and the marginal-revenue effect may work in opposite directions. Further complicating matters, when marginal cost is strictly increasing, any binding cap that deters entry may result in demand rationing, as exemplified by Example 2. Assessing the net welfare impact of a cap becomes very much dependent on the parameters on the model, and a result of the sort provided in Proposition 6 does not obtain.

In contrast, when the equilibrium number of firms changes smoothly with changes in the cap, the presence of the business-stealing effect implies that a small reduction in the number of firms results in an increase in overall welfare. For high enough caps, the entry-deterrence effect and the marginal-revenue effect work in the same direction to improve welfare.²² Moreover, with convex costs, a small reduction in the number of firms, say by $\epsilon$, leaves the $n^{\infty } - \epsilon$ competitive price below the $n^{\infty }$-firm Cournot price. As a result, high caps do not result in rationing.

We conclude this section by presenting an example, which demonstrates that the hypotheses of Proposition 6 are not sufficient to ensure the existence of a welfare-improving cap when n is discrete. Our example satisfies the critical assumptions of Proposition 6, namely the presence of the business-stealing effect (implied by $P_{1} + QP_{11} \le 0$), but does not satisfy the hypotheses of Propositions 4 and 5. We show that a welfare-improving cap exists when n is continuous, but does not exist when n is integer-constrained.

Example 5

Consider the following inverse demand, costs and distribution for $\theta$:

$$\begin{aligned} P(Q, \theta )= & {} \theta - \log (Q), \quad K = \frac{1}{4}e^{-3/2}, \quad C(q)=2q, \quad \theta = 0 \quad \text {with prob} =0.99; \\ \theta= & {} 100 \quad \text {with prob} =0.01 \end{aligned}$$

This inverse demand function satisfies the hypothesis of Proposition 6. With no cap, 2 firms enter, total equilibrium output is $\exp \big (-\frac{3}{2}\big ) \approx .2231$ and per-firm profit is exactly equal to the cost of entry. Total welfare is approximately .2231, and $\overline{\rho }^{\infty } = 101.5$.

With discrete n, imposing a price cap less than 101.5 results in at most 1 entrant. For caps less than $\overline{\rho }^{\infty }$, output is maximized as $\overline{p} \uparrow \overline{\rho }^{\infty }$. A cap set just below $\overline{\rho }^{\infty }$ yields total output of approximately .1360; welfare is approximately .2156, which is less than welfare with no cap. Thus, no welfare-improving cap exists when n is discrete. If n is continuous, then a cap set at 101.4 will result in approximately 1.992 entrants, yielding total output of approximately .2236 and welfare of about .2238; slightly higher than welfare with no cap.

6 Conclusion

This paper analyzes the welfare impact of price caps, taking into account the possibility that a price cap may reduce the number of firms that enter a market. The vehicle for the analysis is a two-period oligopoly model in which product market competition in quantity choices follows endogenous entry with a sunk cost of entry. First, we analyze the impact of price caps when there is no uncertainty about demand when firms make their output decisions. Consistent with models with a fixed number of firms, when marginal cost is constant, we show that output, welfare, and consumer surplus all increase as the price cap is lowered. If marginal cost is increasing, these comparative statics results may be fully reversed and a welfare-improving cap may not exist. We provide sufficient conditions, however, under which a welfare-improving cap exists. Next, we analyze the impact of price caps when demand is stochastic and firms must make output decisions prior to the realization of demand. We show that the existence of a welfare-improving price cap cannot be guaranteed. Our results point to an important role for entry of firms in response to price caps. It is precisely because a price cap can reduce entry that a welfare-improving cap may fail to exist when marginal cost is increasing and/or demand is stochastic.

For the case of stochastic demand, we provide sufficient conditions on demand for which a range of welfare-improving price caps exists. The sufficient conditions restrict the curvature of the inverse demand function, which in turn influences the welfare impact of entry. Indeed, these demand conditions are sufficient for the result so weaker conditions on demand, perhaps coupled with restrictions on the distribution of demand shocks, may also yield existence of a welfare-improving price cap. We extend this result on welfare-improving price caps to an environment with free disposal. Finally, we identify sufficient conditions under which a welfare-improving cap exists when the number of firms is continuous, allowing for both deterministic and stochastic demand and either constant or increasing marginal cost. The condition identified is not sufficient to ensure the existence of a welfare-improving cap when the number of firms is integer-constrained, highlighting the role played by the integer constraint in our model.

Appendix

1.1 Proof of Proposition 1

Before we prove the proposition, we state and prove two useful lemmas.

Lemma A1

For fixed $\overline{p}$, extremal subgame equilibrium total output, $Q_n^*(\overline{p})$ is non-decreasing in the number of firms, n and extremal subgame equilibrium profit $\pi _n^*(\overline{p})$ is non-increasing in n.

Proof

Assumption (1c) implies there exists $M > 0$ such that a firm’s best response is bounded by M. We express a firm’s problem as choosing total output, Q, given total rivals’ output, y. Define a payoff function,

$$\begin{aligned} \tilde{\pi }(Q, y, \overline{p}) = (Q-y)[\min \{P(Q), \overline{p}\} - c], \end{aligned}$$

and a lattice, $\varPhi \equiv \{(Q,y): 0 \le y \le (n-1)M, y \le Q \le y+M \}.$

First we show that $\tilde{\pi }$ has increasing differences (ID) in (Q, y) on $\varPhi$. Let $Q_1 \ge Q_2$ and $y_1 \ge y_2$ such that the points $(Q_1 , y_1), (Q_1 , y_2), (Q_2 , y_1), (Q_2 , y_2)$ are all in $\varPhi$. Since $y_1 \ge y_2$ and $P(Q_2) \ge P(Q_1)$, we have,

$$\begin{aligned} (y_2 -y_1 )\min \{P(Q_1 ),\overline{p} \} \ge (y_2 -y_1 ) \min \{ P(Q_2 ),\overline{p} \}. \end{aligned}$$

(1)

Add $(Q_1 - Q_1 )\min \{P(Q_1 ),\overline{p} \}=0$ and $(Q_2 - Q_2 )\min \{P(Q_2 ),\overline{p} \}=0$ to the left- and right-hand sides of (1), respectively, to yield,

$$\begin{aligned} \begin{array}{lcl} (Q_1 -y_1 )\min \{P(Q_1 ),\overline{p} \} - (Q_1 - y_2 )\min \{P(Q_1 ),\overline{p} \} \ge \\ (Q_2 -y_1 ) \min \{ P(Q_2 ),\overline{p}\} -(Q_2- y_2 )\min \{ P(Q_2 ),\overline{p} \} . \end{array} \end{aligned}$$

(2)

Subtracting $c(y_1 - y_2 )$ from both sides of (2) yields,

$$\begin{aligned} \tilde{\pi } (Q_1,y_1,\overline{p})-\tilde{\pi } (Q_1,y_2,\overline{p}) \ge \tilde{\pi } (Q_2,y_1,\overline{p})-\tilde{\pi } (Q_2,y_2,\overline{p}), \end{aligned}$$

which establishes that $\tilde{\pi }$ has increasing differences in (Q, y) on $\varPhi$.

Note that the choice set $\varPhi$ is ascending in y and $\tilde{\pi }$ is continuous in Q and satisfies ID in (Q, y). Then, as shown in Topkis (1978), the maximal and minimal selections of $\arg \max _Q\{(Q-y)[\min \{P(Q),\overline{p}\}-c]: y \le Q \le y+M \}$ are non-decreasing in y. The remainder of the proof follows almost directly from the proofs of Theorems 2.1 and 2.2 in Amir and Lambson. A symmetric equilibrium exists for the subgame; extremal total output is non-decreasing in n, and extremal profit per firm is non-increasing in n for symmetric equilibria. It is worth pointing out, however, that asymmetric subgame equilibria may exist in our formulation, in contrast to Amir and Lambson, since with a price cap, $\tilde{\pi }$ does not have strict increasing differences in (Q, y).

Lemma A2

For fixed n, extremal subgame equilibrium profit $\pi _n^*(\overline{p})$ is non-decreasing in the price cap $\overline{p}$.

Proof

Fix $n \in \mathbb {N}$. Let $\overline{p}_1 > \overline{p}_2$ and let $q_i$ ($Q_i$) denote an extremal equilibrium output per-firm (total) output in the subgame with n firms and cap $\overline{p}_i$. Note that Theorem 1 in EST implies $q_2 \ge q_1$. Then,

$$\begin{aligned} \pi _n^*(\overline{p}_1)= & {} q_1(\min \{P(Q_1), \overline{p}_1\} - c)\\\ge & {} q_2(\min \{P(q_2 + (n-1)q_1), \overline{p}_1\} - c)\\\ge & {} q_2(\min \{P(q_2 + (n-1)q_2), \overline{p}_2\} - c) = \pi _n^*(\overline{p}_2) \end{aligned}$$

The first inequality follows from the definition of $q_1$. The second inequality holds since $q_2 \ge q_1$ (and P is strictly decreasing) and since $\overline{p}_1 > \overline{p}_2$.

We now prove the proposition. We let $Q^*_n(\overline{p})$ ($q^*_n(\overline{p})$) denote extremal equilibrium total (per-firm) output in the subgame with n firms and cap, $\overline{p}$. It is straightforward to show that the equilibrium where firms play the minimal (maximal) output level corresponds to the equilibrium in which firms earn maximal (minimal) equilibrium profit. Moreover, the maximal (minimal) equilibrium number of firms corresponds to the equilibrium in which firms receive maximal (minimal) equilibrium profit in the subsequent market competition subgame. The fact that the extremal equilibrium number of firms is non-deceasing in the cap is then immediate from Lemmas A1 and A2.

Then, let $\overline{p}_1 > \overline{p}_2$. Let $n_i$ be the equilibrium number of firms under $\overline{p}_i$, $i \in \{1, 2\}$; we must have $n_1 \ge n_2$. Let $\hat{Q}_i = P^{-1}(\overline{p}_i)$. We must have $Q^*_{n_i}(\overline{p}_i) \ge \hat{Q}_i$, otherwise any one firm could increase output slightly and increase profit. Moreover, since $\overline{p}_1 > \overline{p}_2$ Assumption (1a) implies that $\hat{Q}_2 > \hat{Q}_1$.

Part (i) We will show that $Q^*_{n_2}(\overline{p}_2) \ge Q^*_{n_1}(\overline{p}_1)$. EST prove in their Theorem 1 that the desired result holds if $n_1 = n_2$. So the remainder of part (i) deals with the case $n_1 > n_2$. The arguments for the equilibrium with the smallest subgame outputs are different from those for the equilibrium with the largest subgame outputs. We provide the argument for the smallest subgame outputs first, followed by the argument for the largest subgame outputs. It is straightforward to show that the equilibrium where firms play the minimal (maximal) output level corresponds to the maximal (minimal) equilibrium profit.

We will proceed by contradiction. So, suppose $Q^*_{n_2}(\overline{p}_2) < Q^*_{n_1}(\overline{p}_1)$. Immediately this implies $Q^*_{n_1}(\overline{p}_1) > Q^*_{n_2}(\overline{p}_2) \ge \hat{Q}_2 > \hat{Q}_1$. Now, consider the subgame with price cap $\overline{p}_2$ and $n_1$ active firms; let q be any nonnegative output. We will show that $q^*_{n_1}(\overline{p}_1)$ is an equilibrium output level in the game with $n_1$ firms and cap $\overline{p}_2$.

$$\begin{aligned} \pi _{n_1}(q^*_{n_1}(\overline{p}_1), (n_1-1)q^*_{n_1}(\overline{p}_1), \overline{p}_2)= & {} q^*_{n_1}(\overline{p}_1)(\min \{P(Q^*_{n_1}(\overline{p}_1) ), \overline{p}_2\} -c) \\= & {} q^*_{n_1}(\overline{p}_1)(\min \{P(Q^*_{n_1}(\overline{p}_1) ), \overline{p}_1\} -c) \\\ge & {} q(\min \{P(q + (n_1 -1)q^*_{n_1}(\overline{p}_1) ), \overline{p}_1\} -c) \\\ge & {} q(\min \{P(q + (n_1 -1)q^*_{n_1}(\overline{p}_1) ), \overline{p}_2\} -c) \\= & {} \pi _{n_1}(q, (n_1-1)q^*_{n_1}(\overline{p}_1), \overline{p}_2) \end{aligned}$$

The first equality follows from the definition of subgame payoffs. The second equality follows from the fact that neither price cap binds when total output is $Q^*_{n_1}(\overline{p}_1)$. The first inequality follows by definition of $q^*_{n_1}(\overline{p}_1)$. The second inequality holds since $\overline{p}_1 > \overline{p}_2$. This establishes that $Q^*_{n_1}(\overline{p}_1)$ is an equilibrium total quantity in the subgame with cap $\overline{p}_2$ and $n_1$ firms. In addition we know that (1) $Q^*_{n_1}(\overline{p}_2)$ is the extremal (minimum) equilibrium total output in this subgame, and (2) $Q^*_{n_1}(\overline{p}_2) \ge Q^*_{n_1}(\overline{p}_1)$ by Theorem 1 in EST. Taking these results together yields $Q^*_{n_1}(\overline{p}_2) = Q^*_{n_1}(\overline{p}_1)$ (i.e., $Q^*_{n_1}(\overline{p_2})$ is the minimal equilibrium output level in the game with $n_1$ firms and cap $\overline{p}_1$).

Now since $Q^*_{n_1}(\overline{p}_2) = Q^*_{n_1}(\overline{p}_1)$ and $Q^*_{n_1}(\overline{p}_1) > \hat{Q}_2 > \hat{Q}_1$ this means that the extremal (maximal) equilibrium payoff for the subgame with $n_1$ firms and price cap $\overline{p}_2$ satisfies the following:

$$\begin{aligned} \pi ^*_{n_1}(\overline{p}_2)= & {} q^*_{n_1}(\overline{p}_1)\left[ \min \{P(Q^{*}_{n_1}(\overline{p}_1)), \overline{p}_2\} - c\right] \\= & {} q^*_{n_1}(\overline{p}_1)\left[ \min \{P(Q^{*}_{n_1}(\overline{p}_1)), \overline{p}_1\} - c\right] \\= & {} \pi ^*_{n_1}(\overline{p}_1) \ge K \end{aligned}$$

But this contradicts the fact that $n_2$ is the extremal equilibrium number of entering firms when the price cap is $\overline{p}_2$; the extremal (maximal) subgame equilibrium payoff for $n_1$ firms and price cap $\overline{p}_2$ must be less than K since $n_1 > n_2$. So we have the result, $Q^*_{n_2}(\overline{p}_2) \ge Q^*_{n_1}(\overline{p}_1)$.

The argument above explicitly relies on the fact that the equilibrium under consideration is the smallest equilibrium output level. We now provide an alternative proof of this result for the largest equilibrium output level. As before, let $\overline{p}_1 > \overline{p}_2$. Let $Q^*_n(\overline{p})$ be the maximal equilibrium output when the cap is $\overline{p}$ and n firms are active. We aim to show that $Q^*_{n_2}(\overline{p}_2) \ge Q^*_{n_1}(\overline{p}_1)$. We will proceed by contradiction. So, assume that $Q^*_{n_2}(\overline{p}_2) < Q^*_{n_1}(\overline{p}_1)$. Immediately it follows $\hat{Q}_1 < \hat{Q}_2 \le Q^*_{n_2}(\overline{p}_2) < Q^*_{n_1}(\overline{p}_1)$.

Claim

$Q_{n_1}^{*}(\overline{p}_2)$ is an equilibrium output level in the subgame with $n_1$ firms and price cap $\overline{p}_1$.

Proof of Claim

We proceed by contradiction. So, suppose $Q^{*}_{n_1}(\overline{p}_2)$ is not an equilibrium in the subgame with cap $\overline{p}_1$ and $n_1$ firms. By Theorem 1 in EST it must be that $Q^*_{n_1}(\overline{p}_2) > Q^*_{n_1}(\overline{p}_1)$. Let $y^*_n(\overline{p}) = (n - 1)q^{*}_n(\overline{p})$ denote the equilibrium output of the other $n-1$ in the subgame with n firms and cap, $\overline{p}$. Let $b(y, \overline{p})$ be the maximal selection from $\arg \max _{Q \ge y}\{\tilde{\pi }(Q, y, \overline{p})\}$, where $\tilde{\pi }$ is as defined in the proof of Lemma A1.

Since $Q^*_{n_1}(\overline{p}_2)$ is not an equilibrium in the subgame with cap $\overline{p}_1$ and $n_1$ firms, but is a feasible choice when $y = y^*_{n_1}(\overline{p}_2)$ we have:

$$\begin{aligned} \tilde{\pi }( Q^{*}_{n_1}(\overline{p}_2), y^{*}_{n_1}(\overline{p}_2), \overline{p}_1) <\tilde{\pi }( b(y^*_{n_1}(\overline{p}_2), \overline{p}_1), y^*_{n_1}(\overline{p}_2), \overline{p}_1) \end{aligned}$$

(3)

The inequality $Q^{*}_{n_1}(\overline{p}_1) < Q^{*}_{n_1}(\overline{p}_2)$ implies $y^{*}_{n_1}(\overline{p}_1) < y^{*}_{n_1}(\overline{p}_2)$. It is shown in the proof of Lemma A1 that $b(\cdot , \overline{p})$ is non-decreasing. Hence, $b(y^{*}_{n_1}(\overline{p}_1) , \overline{p}_1) \le b(y^{*}_{n_1}(\overline{p}_2), \overline{p}_1)$. But by definition of $Q^{*}_{n_1}(\overline{p}_1)$ we must have $b(y^{*}_{n_1}(\overline{p}_1) , \overline{p}_1) = Q^{*}_{n_1}(\overline{p}_1)$. Hence:

$$\begin{aligned} Q^{*}_{n_1}(\overline{p}_1) = b(y^{*}_{n_1}(\overline{p}_1) , \overline{p}_1) \le b(y^{*}_{n_1}(\overline{p}_2), \overline{p}_1) \end{aligned}$$

(4)

Recall that $\hat{Q}_1 < \hat{Q}_2 < Q^*_{n_1}(\overline{p}_1) < Q^*_{n_1}(\overline{p}_2)$. Equation (4) therefore implies $\hat{Q}_1 < \hat{Q}_2 < b(y^{*}_{n_1}(\overline{p}_2), \overline{p}_1)$. But then (3) implies,

$$\begin{aligned} \tilde{\pi }( Q^{*}_{n_1}(\overline{p}_2), y^{*}_{n_1}(\overline{p}_2), \overline{p}_2) <\tilde{\pi }( b(y^*_{n_1}(\overline{p}_2), \overline{p}_1), y^*_{n_1}(\overline{p}_2), \overline{p}_2) \end{aligned}$$

since neither cap binds under either output level. The above equation contradicts the definition of $Q^{*}_{n_1}(\overline{p}_2)$. Hence, the claim is established.

The Claim establishes that $Q_{n_1}^{*}(\overline{p}_2)$ is an equilibrium total output for the subgame with $n_1$ firms and cap $\overline{p}_1$. This output cannot exceed maximal equilibrium output for this subgame, so $Q_{n_1}^{*}(\overline{p}_2) \le Q_{n_1}^{*}(\overline{p}_1)$. By Theorem 1 in EST, we must have $Q_{n_1}^{*}(\overline{p}_2) \ge Q_{n_1}^{*}(\overline{p}_1)$. Combining these two inequalities yields, $Q_{n_1}^{*}(\overline{p}_2) = Q_{n_1}^{*}(\overline{p}_1)$. As in the proof for the minimal equilibrium output level, we can use this equality to show that $n_1$ firms would have an incentive to enter when the cap is $\overline{p}_2$, contradicting the condition $n_1 > n_2$.

Part (ii) We now show that equilibrium welfare is non-increasing in the cap. Let $W(\overline{p})$ be total welfare in the equilibrium with the lowest output when the price cap is $\overline{p}$. Let $Q_i^{*} = Q_{n_i}^{*}(\overline{p}_i)$, $i \in \{1, 2\}$. Now note:

$$\begin{aligned} W(\overline{p}_2)= & {} \int _{0}^{Q^*_2} \! [P(z) -c ]\, \text {d}z - n_{2}K \\\ge & {} \int _{0}^{Q^*_2} \! [P(z) -c] \, \text {d}z - n_{1}K\\\ge & {} \int _{0}^{Q^*_1} \! [P(z) -c] \, \text {d}z - n_{1}K\\= & {} W(\overline{p}_1) \end{aligned}$$

The first inequality follows since $n_1 \ge n_2$. The second inequality follows from the fact that $Q_2^* \ge Q_1^*$ and that $P(Q_2^*) \ge c$ (otherwise any firm could increase its period two profit by reducing output).

Part (iii) We now show that equilibrium consumer surplus is non-increasing in the cap. Let $CS(Q, \overline{p})$ denote consumer surplus when total production is Q and the price cap is $\overline{p}$.

$$\begin{aligned} CS(Q, \overline{p}) = \int _{0}^{Q} \! [ P(z) - \min \{P(Q), \overline{p}\} ]\, \text {d}z \end{aligned}$$

Note that $CS(Q, \overline{p})$ is increasing in Q and is decreasing in $\overline{p}$. Since $Q_{n_2}^*(\overline{p}_2) \ge Q_{n_1}^*(\overline{p}_1)$ and $\overline{p}_2 < \overline{p}_1$, immediately we have that $CS(Q_{n_2}^*(\overline{p}_2), \overline{p}_2) \ge CS(Q_{n_1}^*(\overline{p}_1),\overline{p}_1)$.

1.2 Proof of Proposition 2

Let $\overline{p} < P(Q^{\infty })$ such that $\overline{p} \in \mathbb {P}$. Let $n^*$ denote the equilibrium number of firms under this cap. Let $Q^{\infty }_{n^*}$ ($q^{\infty }_{n^{*}}$) denote equilibrium total (per-firm) output in the subgame with no cap and $n^*$ firms. And let $y^{\infty }_{n^*} = (n^{*} - 1)q^{\infty }_{n^*}$. Let $\hat{Q}$ satisfy: $P(\hat{Q}) = \overline{p}$ and let $\hat{q} = \frac{\hat{Q}}{n^*}$. Let $Q^*$ ($q^*$) be a symmetric equilibrium total (per-firm) output candidate under the cap, and let $y^* = (n^* - 1)q^*$. Let $\pi _L(q, y) = \log (q(P(q + y) - c))$. Note that for all (q, y) such that $P(q + y) > c$, $\pi _L(\cdot , y)$ is concave. We first claim $q^* = \hat{q}$. By way of contradiction, suppose $q^* \ne \hat{q}$. In particular, it must be that $q^* > \hat{q}$. Lemma A1 implies $\hat{Q} > Q^{\infty } \ge Q^{\infty }_{n^*}$, which means $\hat{q} > q^{\infty }_{n^*}$. It must hold that $P(q^* + y^{\infty }_{n^{*}}) > c$; then since $q^* > \hat{q} > q^{\infty }_{n^*}$ concavity of $\pi _L(\cdot , y^{\infty }_{n^*})$ implies $\pi (\hat{q}, y^{\infty }_{n^*}) \ge \pi (q^*, y^{\infty }_{n^*})$.

Log-concavity of P implies $\pi (q, y)$ has the dual strong single-crossing property in (q; y) (see proof of Theorem 2.1 in Amir (1996)). As $q^* > \hat{q}$ and $y^* > y^{\infty }_{n^*}$ it follows that $\pi (\hat{q}, y^{\infty }_{n^*}) \ge \pi (q^*, y^{\infty }_{n^*}) \implies \pi (\hat{q}, y^*) > \pi (q^*, y^*)$. Equivalently, since $P(q^* + y^*) < \overline{p}$ and $P(\hat{q} + y^*) < \overline{p}$, this means:

$$\begin{aligned} \hat{q}[\min \{P(\hat{q} + y^*), \overline{p}\} - c] > q^*[\min \{P(q^* + y^*), \overline{p}\} - c] \end{aligned}$$

This contradicts the hypothesis that $q^*$ is an equilibrium (per-firm) output level. Hence, under any relevant cap, equilibrium output satisfies $P(Q^{*}(\overline{p})) = \overline{p}$. This implies that there is a single symmetric equilibrium, and since P is strictly decreasing, $Q^*(\overline{p})$ is strictly decreasing in the cap. The fact that welfare and consumer surplus are strictly decreasing in the cap follows along the same lines as in the proof of Proposition 1 parts (ii) and (iii). $\square$

1.2.1 Proof of Proposition 3

We consider two cases. Case (i): suppose $\pi ^{\infty } > K$. Let $\hat{\pi }(q, n) \equiv qP(nq) - C(q)$. $\hat{\pi }(\cdot , n)$ is continuous, and strictly decreasing for $q > q^{\infty }$ if $n = n^{\infty }$. Let $q^c_{n^{\infty }}$ denote the per-firm competitive equilibrium output level in the subgame with $n^{\infty }$ firms. Consider any $q^c_{n^{\infty }} > q' > q^{\infty }$ such that $\pi ^{\infty } > \pi (q', n^{\infty }) \ge K$ and set $\overline{p} = P(q'n^{\infty }) > p^c_{n^{\infty }}$. Given the cap $\overline{p}$, if $n = n^{\infty }$ firms enter in stage one then symmetric subgame equilibrium output per firm in stage two is $q'$; this holds by log-concavity of $P(\cdot )$, following an argument similar to that made in the proof of Proposition 2. Since $\hat{\pi }(q', n^{\infty }) \ge K$, $n^{\infty }$ firms enter in stage one. By Proposition 3 in Reynolds and Rietzke (2015), welfare is strictly higher with cap $\overline{p}$ than with no cap.

Case (ii): suppose $\pi ^{\infty } = K$. In this case, Assumption (1c) implies $n^{\infty } \ge 2$. Any cap $\overline{p} < P(Q^{\infty })$ results in fewer than $n^{\infty }$ entrants in stage one. Suppose $n^{\infty } - 1$ firms enter in the first stage and consider a cap satisfying

$$\begin{aligned} P(Q^{\infty }) - \epsilon < \overline{p} < P(Q^{\infty }) \end{aligned}$$

where $\epsilon > 0$. For $0 < \epsilon < P(Q^{\infty }) - p^c_{n^{\infty } - 1}$, log-concavity of $P(\cdot )$ implies that, when $n = n^{\infty } - 1$ firms enter, the symmetric subgame equilibrium per-firm output level satisfies $P(q'n) = \overline{p}$. We claim that it is profitable for n firms to enter in the first stage under $\overline{p}$ for $\epsilon$ sufficiently small. To demonstrate the claim, define: $q^m = \arg \min _{q}\{ATC(q)\}$ where $ATC(q) = \frac{C(q) + K}{q}$. We consider two subcases.

Subcase (a): $q' \ge q^m$. We know that $C'(q') \le \overline{p} = P(q'n)$, and $C'(q') \ge ATC(q')$ since $q' \ge q^m$. So, $P(q'n) = \overline{p} \ge ATC(q')$ and firms earn nonnegative profit if $n = n^{\infty } - 1$ firms enter.

Subcase (b): $q' < q^m$. Strict convexity of $C(\cdot )$ implies strict convexity of $ATC(\cdot )$. We know that $(n^{\infty } - 1)q' > n^{\infty }q^{\infty } = Q^{\infty }$, and hence:

$$\begin{aligned} q' > \frac{n^{\infty }}{n^{\infty } - 1}q^{\infty } \end{aligned}$$

(5)

Define $\delta \equiv \frac{ATC(q^{\infty }) - ATC^m}{q^m - q^{\infty }} > 0$. Strict convexity of $ATC(\cdot )$ yields $\delta < \frac{ATC(q^{\infty }) - ATC(q')}{q' - q^{\infty }}$, which implies $ATC(q') < ATC(q^{\infty }) - \delta (q' - q^{\infty })$. But Eq. (5) then implies: $ATC(q') < ATC(q^{\infty }) - \delta \big (\frac{q^{\infty }}{n^{\infty } - 1}\big )$. Let $n = n^{\infty } - 1$, and choose $\overline{p}$ such that $\epsilon < \min \left\{ \frac{1}{n}\delta q^{\infty }, P(Q^{\infty }) - p^c_n\right\}$. We have:

$$\begin{aligned} \hat{\pi }(q', n) - K&= q'\overline{p} - q'ATC(q') \\&> q'P(Q^{\infty }) - \epsilon q' - q'ATC(q^{\infty }) + q'\delta \frac{1}{n}\delta q^{\infty }\\&= q'\left[ \frac{1}{n}\delta q^{\infty } - \epsilon \right] \\&> 0 \end{aligned}$$

The last equality follows since $\pi ^{\infty } = K$. Hence, for $\epsilon$ sufficiently small, it is indeed profitable for $n = n^{\infty } - 1$ firms to enter in the first stage. To establish the proposition, the final step is to show that welfare is higher with price cap $\overline{p} \in (P(Q^{\infty }) - \epsilon , P(Q^{\infty }))$ than with no cap.

Using $n \equiv n^{\infty } - 1$, let $W(\overline{p}) = B(nq') - TC_n$ denote equilibrium welfare under the cap, where $B(x) \equiv \int _0^{x}P(z)dz$, and $TC_n \equiv n(C(q') + K)$. Analogously, define $W^{\infty } = B(Q^{\infty }) - TC^{\infty }$ as equilibrium welfare with no cap. To establish the proposition, we must show $W(\overline{p}) > W^{\infty }$.

By hypothesis, $\pi ^{\infty } = K$; we have established that $\pi ^*(\overline{p}) = \hat{\pi }(q', n) \ge K$. It follows that $n(\pi ^*(\overline{p}) - K) \ge (n + 1)(\pi ^{\infty } - K) = 0$, equivalently, letting $Q' = nq'$: $Q'P(Q') - Q^{\infty }P(Q^{\infty }) \ge TC_n - TC^{\infty }$. This implies:

$$\begin{aligned} W(\overline{p}) - W^{\infty } \ge B(Q') - B(Q^{\infty }) - \left[ Q'P(Q') - Q^{\infty }P(Q^{\infty })\right] \end{aligned}$$

Adding and subtracting $Q^{\infty }P(Q')$ from the RHS of the inequality above gives:

$$\begin{aligned} W(\overline{p}) - W^{\infty }\ge & {} \int _{Q^{\infty }}^{Q'}P(z)\text {d}z -P(Q')(Q' - Q^{\infty }) + Q^{\infty }(P(Q^{\infty }) - P(Q'))\\> & {} \int _{Q^{\infty }}^{Q'}P(Q')\text {d}z -P(Q')(Q' - Q^{\infty }) + Q^{\infty }[P(Q^{\infty }) - P(Q')]\\= & {} Q^{\infty }[P(Q^{\infty }) - P(Q')]\\> & {} 0 \end{aligned}$$

$\square$

1.3 Proof of Lemma 1

We will prove Lemma 1 for the case of the additive demand shock. The proof for the multiplicative demand shock is similar. Just for the moment, it will be useful to suppose that n is a continuous variable. Letting $E[\theta ] = \mu$, in a subgame with no cap and n firms, the symmetric equilibrium condition is given by:

$$\begin{aligned} \mu - c + p(Q_{n}) + \frac{Q_n}{n}p'(Q_{n}) = 0 \end{aligned}$$

(6)

Using (6) and the implicit function theorem, it is straightforward to show that concavity of p implies $\frac{\partial Q_n}{\partial n} > 0$ and $\frac{\partial q_n}{\partial n} < 0$. Let $W_n$ denote equilibrium welfare when n firms enter. Using an argument identical to that used in the proof of Proposition 1 in Mankiw and Whinston, it is straightforward to show that $\frac{\partial W_n}{\partial n} < 0$ for all $n \ge n^{\infty }_c$, where $n^{\infty }_c$ is the free-entry number of firms when n is continuous. When n is integer-constrained, equilibrium output and welfare are not smooth functions of n, as in the case where n is continuous, but are particular points along these corresponding smooth functions. From this observation, it follows that when n is integer-constrained, total equilibrium output is strictly increasing in n, per-firm equilibrium output is strictly decreasing in n, and $W_n$ is strictly decreasing in n for $n \ge n^{\infty }_c$. But note that when the integer-constrained entry condition binds (i.e., $\pi _{n^{\infty }}^{\infty } = K$), it follows that $n^{\infty } = n^{\infty }_c$ Thus, $W_n$ is strictly decreasing in n for $n \ge n^{\infty }$. To establish both statements made in the lemma, it therefore suffices to show $W_{n^{\infty } -1} > W_{n^{\infty }}$.

Assumption 1(c) coupled with the hypothesis of this Lemma that $\pi ^{\infty } =K$ implies that $n^{\infty } \ge 2$. So we let $n \ge 2$ in the remainder of this proof. To establish the result, we show that $\pi _n^{\infty } = K \implies W_{n-1} > W_n$. Define $\Delta Q \equiv Q_n - Q_{n-1}$. We claim that $\Delta Q \le \frac{1}{n}q_n$. By way of contradiction, suppose $\Delta Q > \frac{1}{n}q_n$; equivalently, $Q_{n-1} < g$ where $g \equiv Q_n - \frac{1}{n}q_n$. Since $g > Q_{n-1}$ Eq. (6) implies that:

$$\begin{aligned} 0> \mu - c + p(g) + \frac{g}{n-1}p'(g) \end{aligned}$$

(7)

Concavity of p implies:

$$\begin{aligned} p(g) \ge p(Q_n) - \left( \frac{1}{n}q_n\right) p'(g) \end{aligned}$$

(8)

Together, (7) and (8) imply $0 > \mu - c + p(Q_n) + q_np'(g)$. But then $Q_n > g$ implies $0 > \mu - c + p(Q_n) + q_np'(Q_n)$, which contradicts (6). So we must have $0 \le \Delta Q_n \le \frac{1}{n}q_n$. Then, since $\pi _n^{\infty } = K$, it follows:

$$\begin{aligned} W_{n-1} - W_n = -\left[ (\mu - c)\Delta Q + \int _{Q_{n-1}}^{Q_n} \! p(s)\, \text {d}s\right] + \pi _n^{\infty } \end{aligned}$$

$T(s; x) = p'(x)s + p(x) - p'(x)x$ is the equation of the line tangent to $p(\cdot )$ at output x. As $p(\cdot )$ is concave and decreasing, for all $s \in [Q_{n-1}, Q_n]$, $p(s) \le T(s, Q_n)$. This means

$$\begin{aligned} \int _{Q_{n-1}}^{Q_n} \! p(s)\, \text {d}s \le \int _{Q_{n-1}}^{Q_n} \! T(s; Q_n)\, \text {d}s = \Delta Q p(Q_n) - \frac{1}{2}(\Delta Q)^{2}p'(Q_n) \end{aligned}$$

It follows that:

$$\begin{aligned} W_{n-1} - W_n \ge \frac{1}{2}p'(Q_n)(\Delta Q_n)^2 - \left( p(Q_n) + \mu - c\right) \Delta Q + \pi _n^{\infty } \end{aligned}$$

Using (6), it follows that $\pi _n^{\infty } = - p'(Q_n)(q_n)^2$. Combining this with the fact that $\Delta Q \le \frac{1}{n}q_n$, $p' < 0$ and $n \ge 2$ yields:

$$\begin{aligned} W_{n-1} - W_n\ge & {} \frac{1}{2}p'(Q_n)(\Delta Q)^2 + p'(Q_n)q_n\Delta Q - p'(Q_n)(q_n)^2 \\\ge & {} \frac{1}{2}p'(Q_n)(\frac{1}{n}q_n)^2 + p'(Q_m)\frac{1}{n}(q_n)^2 - p'(Q_n)(q_n)^2 \\= & {} p'(Q_n)q_n^2 \left( \frac{1}{2n^2} + \frac{1}{n} - 1 \right) > 0 \end{aligned}$$

which establishes the lemma.

1.4 Proof of Proposition 4

We will prove Proposition 4 for the case of the additive demand shock. The proof for the multiplicative demand shock is similar. We first establish the following lemma.

Lemma A3

For a fixed cap, $\overline{p} > c$, and a fixed number of firms, n, there exists a unique symmetric subgame equilibrium. For a fixed cap, $\overline{p} >c$ (possibly non-binding), in equilibrium: total output, $Q^*_n(\overline{p})$, is strictly increasing in n, per-firm output, $q^*_n(\overline{p})$, is strictly decreasing in n, and profit, $\pi ^*_n(\overline{p})$, is strictly decreasing in n. Finally, for fixed n, equilibrium profit, $\pi ^*_n(\overline{p})$, is strictly decreasing in the price cap for caps $c < \overline{p} < \overline{\rho }^{\infty }$.

Proof

See proof of Lemma A6, which is stated and proved in the proof of Proposition 6(ii). The assumptions made on demand in this section are a special case of the assumptions considered in the proof of Lemma A6. Although these proofs take n to be continuous, and exploit the fact that output and profit are continuous functions of n, we may think of output and profit in the integer-n case as particular points along these smooth functions.

We now prove the proposition. Concavity of $p(\cdot )$ implies that, for a fixed number of firms, equilibrium output is continuous in the price cap. Therefore, equilibrium expected profit is continuous in the cap. If $\pi ^{\infty } > K$, then by the continuity of period two profit in $\overline{p}$, there is an interval of price caps below $\overline{\rho }^{\infty }$ such that the equilibrium number of entrants remains at $n^{\infty }$. For any fixed number of firms, n, GZ establish that any price cap $\overline{p} \in [\overline{\text {MR}}_n, \overline{\rho }^{\infty }_n)$ both increases output and total welfare. Thus, a price cap in the intersection of $[\overline{\text {MR}}_{n^{\infty }}, \overline{\rho }^{\infty })$ and the set of price caps for which $n^{\infty }$ firms enter will leave the equilibrium number of firms unchanged and will increase both output and welfare.

If $\pi ^{\infty } = K$, then there exists a range of price caps, $\overline{p} \in (\overline{\rho }^{\infty }- \epsilon , \overline{\rho }^{\infty })$ such that the equilibrium number of firms decreases by exactly one; this follows since equilibrium profit is strictly decreasing in n and strictly increasing in $\overline{p}$ (by Lemma A3) and since equilibrium profit is continuous in the cap for fixed n. Also, if $\pi ^{\infty } = K$ then Assumption (1c) implies $n^{\infty } \ge 2$. By Lemma 1 welfare is higher in the game with no cap and $n^{\infty } -1$ firms than with no cap and $n^{\infty }$ firms. Moreover, GZ’s result implies that any cap $\overline{p} \in (\overline{\text {MR}}_{n^{\infty }-1}, \overline{\rho }_{n^{\infty }-1}^{\infty })$ results in a welfare improvement in the subgame with $n^{\infty } -1$ firms, compared to the subgame with $n^{\infty }-1$ firms and no cap. So, to establish the existence of a welfare-improving price cap in the game with endogenous entry, it suffices to show:

$$\begin{aligned} (\overline{\text {MR}}_{n^{\infty }-1}, \overline{\rho }_{n^{\infty }-1}^{\infty }) \cap (\overline{\rho }^{\infty } - \epsilon , \overline{\rho }^{\infty }) \ne \emptyset \end{aligned}$$

(9)

Given any $n \ge 2$ Lemma A3 implies $\overline{\rho }_{n-1}^{\infty } > \overline{\rho }_n^{\infty }$. Thus, to establish (9) we need only show that $\overline{\text {MR}}_{n-1} < \overline{\rho }_{n}^{\infty }$ for any $n \ge 2$. See that that $\overline{\rho }_{n}^{\infty } = \overline{\theta } + p(Q^{\infty }_n)$. Moreover, by assumptions placed on demand: $\overline{\text {MR}}_{n} = \overline{\theta } + p(Q_{n}^{\infty }) + \frac{Q^{\infty }_{n}}{n }p'(Q^{\infty }_{n})$. Since $p'< 0$ clearly $\overline{\text {MR}}_n < \overline{\rho }_n^{\infty }$. Finally, using (6) it follows that $\overline{\text {MR}}_n = \overline{\text {MR}}_{n-1} = \overline{\theta } + c - \mu$, which implies $\overline{\text {MR}}_{n-1} = \overline{\text {MR}}_{n} < \overline{\rho }_n^{\infty }$. $\square$

1.5 Proof of Lemma 2

We will prove Lemma 2 for the case of the additive demand shock. The proof for the case of the multiplicative shock is similar.

Just for the moment, it will be useful to suppose that n is a continuous variable. Let $W_n$ denote equilibrium welfare when n firms enter. For continuous n, it is shown under more general conditions in the proof of Lemma A8 that $\frac{\partial W_n}{\partial n} < 0$ for all $n \ge n^{\infty }_c$, where $n^{\infty }_c$ is the free-entry number of firms when n is continuous. Using an identical argument as made in the proof of Lemma 1, it therefore suffices to show that if $\pi _n^{\infty } = K$ for some $n \ge 2$ then $W_{n-1} > W_{n}$.

Let $n\ge 2$ be given such that $\pi _n^{\infty } = K$. In the subgame with $m \in \{n, n-1\}$ firms, let $Q_m(\theta )$ denote total third-stage equilibrium output at demand realization $\theta$, and let $X_m$ denote total equilibrium capacity. For each $\theta \in \varTheta$, let $\Delta Q(\theta ) \equiv Q_n(\theta ) - Q_{n-1}(\theta )$. We will show that for each $\theta$, $\Delta Q(\theta ) \le \frac{1}{n}q_n(\theta )$. For those demand realizations where the capacity constraint is non-binding (i.e., $\theta < \tilde{\theta }_m(X_m)$) third-stage equilibrium total output, $Q^0_m(\theta )$ satisfies the first-order condition:

$$\begin{aligned} \theta + p(Q^0_m(\theta )) + \frac{Q^0_m(\theta )}{m}p'(Q^0_m(\theta )) = 0 \end{aligned}$$

(10)

It follows that

$$\begin{aligned}Q_m(\theta ) = {\left\{ \begin{array}{ll} Q^0_m(\theta ) &{} \text {if}\,\, \theta < \tilde{\theta }_m(X_m)\\ X_m &{} \text {if}\,\, \theta \ge \tilde{\theta }_m(X_m) \end{array}\right. } \end{aligned}$$

Equilibrium total capacity satisfies the first-order condition:

$$\begin{aligned} \int _{\tilde{\theta }_m(X_m)}^{\overline{\theta }}\! \left[ \theta + p(X_m) + \frac{X_m}{m}p'(X_m) \right] \,\text {d}F(\theta ) = c \end{aligned}$$

(11)

With our assumptions on demand, it holds that $\tilde{\theta }_m(X_m) = - p(X_m) - \frac{X_m}{m}p'(X_m)$. Using this fact, (11) may be written:

$$\begin{aligned} \int _{\tilde{\theta }_m(X_m)}^{\overline{\theta }} \left[ \theta - \tilde{\theta }_m(X_m)\right] \, \text {d}F(\theta ) = c \end{aligned}$$

(12)

For any $z < \overline{\theta }$ the function $G(z) = \int _{z}^{\overline{\theta }} [\theta - z]\, dF(\theta )$ is strictly decreasing in z. Equation (12) then implies $\tilde{\theta }_{m'}(X_{m'}) = \tilde{\theta }_{m}(X_{m}) \equiv \tilde{\theta }$ for any $m'$ and m. Using Eq. (10), for $\theta < \tilde{\theta }$, the proof that $\Delta Q(\theta ) \le \frac{1}{n}q_n(\theta )$ follows along exactly the same lines as in the proof of Lemma 1. For $\theta \ge \tilde{\theta }$, we may use the definition of $\tilde{\theta }$ and write:

$$\begin{aligned} \tilde{\theta } + p(X_m) + \frac{X_m}{m}p'(X_m) = 0 \end{aligned}$$

(13)

Using Eq. (13), the proof that $\Delta Q(\theta ) \le \frac{1}{n}q_n(\theta )$ for $\theta \ge \tilde{\theta }$ is identical to the argument given in the proof Lemma 1. Thus, for each $\theta$ $\Delta Q(\theta ) \le \frac{1}{n}q_n(\theta )$. Now, note that

$$\begin{aligned} W_n= & {} \int _{\underline{\theta }}^{\tilde{\theta }} \! \left[ \int _{0}^{{Q}^0_n(\theta )} \! [\theta + p(s) \,] \text {d}s \right] \, \text {d}F(\theta ) + \int _{\tilde{\theta }}^{\overline{\theta }} \! \left[ \int _{0}^{X_n} \! [\theta + p(s) ] \, \text {d}s \right] \, \text {d}F(\theta ) \\&- cX_n - n\pi ^\infty _n \end{aligned}$$

and

$$\begin{aligned} W_{n-1} - W_n= & {} -\int _{\underline{\theta }}^{\tilde{\theta }} \! \left[ \int _{{Q}^0_{n-1}(\theta )}^{{Q}^0_n(\theta )} \! [\theta + p(s) \,] \text {d}s \right] \, \text {d}F(\theta ) \\&- \int _{\tilde{\theta }}^{\overline{\theta }} \! \left[ \int _{X_{n-1}}^{X_n} \! [\theta + p(s) ] \, \text {d}s \right] \, \text {d}F(\theta ) + (\Delta X)c + \pi ^\infty _n \end{aligned}$$

Concavity of p implies that for each $\theta \in [\underline{\theta }, \tilde{\theta }]$

$$\begin{aligned} \int _{{Q}^0_{n-1}(\theta )}^{{Q}^0_n(\theta )} \! [\theta + p(s) \,] \text {d}s\le & {} \Delta {Q}^0(\theta )(\theta + p({Q}^0_n(\theta )))\\&- \frac{1}{2}\left( \Delta {Q}^0(\theta )\right) ^2p('{Q}^0_n(\theta )) \equiv A(\theta ) \end{aligned}$$

where $\Delta Q^0(\theta ) \equiv Q^0_n(\theta ) - Q^0_{n-1}(\theta )$. Moreover, for each $\theta \in [\tilde{\theta }, \overline{\theta }]$

$$\begin{aligned} \int _{X_{n-1}}^{X_n} \! [\theta + p(s) \,] \text {d}s \le \Delta X(\theta + p(X_n)) - \frac{1}{2}\left( \Delta X\right) ^2p'(X_n) \equiv B(\theta ) \end{aligned}$$

where $\Delta X \equiv X_n - X_{n-1}$. Using (10) and (12), we may write:

$$\begin{aligned} \pi ^\infty _n= & {} \left( -\int _{\underline{\theta }}^{\tilde{\theta }} \! ({q}^0_n(\theta ))^2p'({Q}^0_n(\theta )) \, \text {d}F(\theta )\right) + \left( - \int _{\tilde{\theta }}^{\overline{\theta }} \! (x_n)^2p'(X_n) \, \text {d}F(\theta )\right) \\ {}\equiv & {} \pi _n^A + \pi _n^B \end{aligned}$$

Hence, it follows that

$$\begin{aligned} W_{n-1} - W_{n} \ge -\int _{\underline{\theta }}^{\tilde{\theta }} \! A(\theta ) \, \text {d}F(\theta ) - \int _{\tilde{\theta }}^{\overline{\theta }} \! B(\theta ) \, \text {d}F(\theta ) + (\Delta X)c + \pi _n^A + \pi _n^B \end{aligned}$$

Using (10), and the fact that $\Delta {Q}(\theta ) \le \frac{1}{n}{q}_n(\theta )$:

$$\begin{aligned} -\int _{\underline{\theta }}^{\tilde{\theta }} \! A(\theta ) \, \text {d}F(\theta ) + \pi _n^A \ge \int _{\underline{\theta }}^{\tilde{\theta }} \! ({q}^0_n(\theta ))^2p'({Q}^0_n(\theta )\left( \frac{1}{n} + \frac{1}{2n^2} - 1\right) \, \text {d}F(\theta ) > 0 \end{aligned}$$

Now also see that

$$\begin{aligned}&-\int _{\tilde{\theta }}^{\overline{\theta }} \! B(\theta ) \, \text {d}F(\theta ) + (\Delta X)c + \pi _n^B\\&\quad = -\Delta X \left[ \int _{\tilde{\theta }}^{\overline{\theta }} \! (\theta + p(X_n)) \, \text {d}F(\theta ) - c \right] \\&\qquad + \int _{\tilde{\theta }}^{\overline{\theta }} \! \left[ \frac{1}{2}(\Delta X)^2p'(X_n) - (x^\infty _n)^2p'(X^\infty _n) \right] \, \text {d}F(\theta ) \end{aligned}$$

From (12) and the definition of $\tilde{\theta }$, it follows that

$$\begin{aligned} \int _{\tilde{\theta }}^{\overline{\theta }} \! (\theta + p(X_n)) \, \text {d}F(\theta ) - c = \int _{\tilde{\theta }}^{\overline{\theta }} \! -x_np'(X_n) \, \text {d}F(\theta ) \end{aligned}$$

Combined with the fact that $\Delta X \le \frac{1}{n}x_n$ allows us to write:

$$\begin{aligned} -\int _{\tilde{\theta }}^{\overline{\theta }} \! B(\theta ) \, \text {d}F(\theta ) + (\Delta X)c + \pi _n^B \ge (x^\infty _n)^2 p'(X_n)\int _{\tilde{\theta }}^{\overline{\theta }} \! \left( \frac{1}{n} + \frac{1}{2n^2} - 1 \right) \, \text {d}F(\theta ) > 0 \end{aligned}$$

It follows immediately that $W_{n-1} - W_n > 0$. $\square$

1.6 Proof of Proposition 5

We will prove Proposition 5 for the case of the additive demand shock. The proof for the case of the multiplicative shock is similar. We first establish the following lemma.

Lemma A4

For a fixed cap, $\overline{p} > c$ and fixed n there exists a unique symmetric equilibrium in the capacity choice subgame. For a fixed cap, $\overline{p} > c$ (possibly non-binding) in equilibrium: total capacity, $X^*_n(\overline{p})$, is non-decreasing in n, per-firm capacity, $x^*_n(\overline{p})$, is strictly decreasing in n, and profit, $\pi ^*_n(\overline{p})$, is strictly decreasing in n. Finally, for fixed n, second-stage expected equilibrium profit, $\pi ^*_n(\overline{p})$, is strictly increasing in the cap for any $c < \overline{p} <\overline{\rho }^\infty$.

Proof

See proof of Lemma A7, which is stated and proved in the proof of Proposition 6(iii). Note that concave demand is a special case of the environment considered in the proof of Lemma A7. Although the proof of Lemma A7 takes n to be continuous, and exploits the fact that output and profit are continuous functions of n, we may think of output and profit in the integer-n case as particular points along these smooth functions.

We now prove the proposition. Concavity of $p(\cdot )$ implies that, for a fixed number of firms, equilibrium capacity and equilibrium 3rd-stage output decisions are continuous in the cap. Therefore, equilibrium expected profit is continuous in the price cap. If $\pi ^{\infty } > K$, then by the continuity of period two profit in $\overline{p}$, there is an interval of price caps below $\overline{\rho }^{\infty }_{n^{\infty }}$ such that the equilibrium number of entrants remains at $n^{\infty }$. For any fixed number of firms, n, Theorem 3 in GZ implies that any price cap $\overline{p} \in [\overline{\text {MR}}_n, \overline{\rho }^{\infty }_n)$ both increases output and total welfare. Thus, a price cap in the intersection of $[\overline{\text {MR}}_{n^{\infty }}, \overline{\rho }^{\infty })$ and the set of price caps for which $n^{\infty }$ firms enter will leave the equilibrium number of firms unchanged and will increase both output and welfare.

If $\pi ^{\infty } = K$, then there exists a range of price caps, $\overline{p} \in (\overline{\rho }^{\infty } - \epsilon , \overline{\rho }^{\infty })$ such that the equilibrium number of firms decreases by exactly one (this follows from Lemma A4 and continuity of equilibrium profit in the cap for fixed n). Also, if $\pi ^{\infty } = K$, then Assumption (1c) implies $n^{\infty } \ge 2$. By Lemma 2 welfare is higher in the game with no cap and $n^{\infty } -1$ firms than with no cap and $n^{\infty }$ firms. Moreover, Theorem 3 in GZ implies that any price cap $\overline{p} \in (\overline{\text {MR}}_{n^{\infty }-1}, \overline{\rho }_{n^{\infty }-1})$ results in a welfare improvement in the subgame with $n^{\infty } -1$ firms, compared to the subgame with $n^{\infty }-1$ firms and no cap. So, to establish the existence of a welfare-improving price cap in the game with endogenous entry, it suffices to show:

$$\begin{aligned} (\overline{\text {MR}}_{n^{\infty }-1}, \overline{\rho }^{\infty }_{n^{\infty }-1}) \cap (\overline{\rho }^{\infty } - \epsilon , \overline{\rho }^\infty ) \ne \emptyset \end{aligned}$$

(14)

Given any $n \ge 2$ Lemma A4 implies $\overline{\rho }^\infty _{n-1} \ge \overline{\rho }^\infty _{n}$. To establish (14), it therefore suffices to show $\overline{\text {MR}}_{n-1} < \overline{\rho }^\infty _n$ for any $n \ge 2$. In the proof of Lemma 2, it is shown that, in the absence of a cap, equilibrium capacity satisfies $\tilde{\theta }_m(X_m^{\infty }) = \tilde{\theta }_{m'}(X_{m'}^{\infty }) \equiv \tilde{\theta }$ for any m and $m'$. By assumptions placed on demand, and the definition of $\tilde{\theta }$:

$$\begin{aligned} \overline{\text {MR}}_{n} = \overline{\theta } + p(X^\infty _n) + \frac{X^\infty _n}{n}p'(X^\infty _n) = \theta - \tilde{\theta } = \overline{\text {MR}}_{n-1} \end{aligned}$$

Note that $\overline{\rho }^\infty _n = \overline{\theta } + p(X^\infty _n)$. Then, $p' < 0 \implies \overline{\text {MR}}_{n} < \overline{\rho }^\infty _n \implies \overline{\text {MR}}_{n-1} < \overline{\rho }^\infty _n$ , which establishes the existence of a welfare-improving cap. $\square$

1.7 Proof of Proposition 6

We will show each part of Proposition 6 separately. First, some preliminaries. For the case of deterministic demand/constant MC, the existence of a welfare-improving cap follows from Proposition 1. Thus, for deterministic demand we focus on the case of convex costs. Second, for the case of stochastic demand we assume $P(0, \underline{\theta }) = 0$. It is clear that under this condition the cap will not bind for low enough realizations of $\theta$. This means that for any level of production, and any cap, $\theta ^b(Q, \overline{p}) > \underline{\theta }$. Moreover, when $\theta ^b(Q, \overline{p}) < \overline{\theta }$ it holds that $\theta ^b_1(Q, \theta ) > 0$ and $\theta ^b_2(Q, \theta ) > 0$. We also point out that for this proof:

$$\begin{aligned} P_1(Q, \theta ) + QP_{11}(Q, \theta ) \le 0 \end{aligned}$$

(15)

Finally, in this section, the equilibrium number of firms, $n^*$, satisfies:

$$\begin{aligned} \pi ^*_{n^*}(\overline{p}) = K \end{aligned}$$

1.8 Proof of Proposition 6(i)

We begin with the following lemma.

Lemma A5

For any fixed cap and fixed n there is a unique symmetric subgame equilibrium. Let $p^c_n$ denote the n-firm competitive price. For any cap $\overline{p} \in [p^c_n, \overline{\rho }^{\infty }_n)$ equilibrium output satisfies $P(Q^*_n(\overline{p})) = \overline{p}$. For $\overline{p} < p^c_n$ equilibrium output satisfies: $C'(\frac{Q^*}{n}) = \overline{p}.$

Fix $n \ge 1$ and let $\overline{p} \in (p^c_n, \overline{\rho }^{\infty }_n)$. Let $\hat{Q}$ be the unique solution to $P(\hat{Q}) = \overline{p}$. Let $Q^*$ be a symmetric equilibrium total (per-firm) output candidate. We will show that $Q^* = \hat{Q}$. If $Q^* < \hat{Q}$ then the cap is binding, and moreover, $Q^* < \hat{Q} < Q^c_n$ where $Q^c_n$ is the n firm competitive output level. We must have $\overline{p} > p^c = C'\big (\frac{Q^c_n}{n}\big ) > C'\big (\frac{Q^*}{n}\big )$. It follows that any one firm could increase output slightly and increase profit. Thus, $Q^* < \hat{Q}$ cannot be a symmetric total output level. Now suppose $Q^* > \hat{Q}$. Total output with no cap satisfies the first-order condition:

$$\begin{aligned} P(Q^{\infty }_n) + \frac{Q^{\infty }_n}{n}P'(Q^{\infty }_n) - C'\bigg (\frac{Q^{\infty }_n}{n}\bigg ) = 0 \end{aligned}$$

(16)

Condition (15) implies that the LHS of (16) is strictly decreasing in total output. Hence for $Q^* > \hat{Q} > Q^{\infty }_n$:

$$\begin{aligned} \pi _1\bigg (\frac{Q^*}{n}, \frac{n-1}{n}Q^*, \overline{p}\bigg ) = P(Q^*) + \frac{Q^*}{n}P'(Q^*) - C'\bigg (\frac{Q^*}{n}\bigg ) < 0 \end{aligned}$$

Any individual firm could increase profit by decreasing output slightly. It follows that $Q^*_n(\overline{p}) = \hat{Q}$. Finally, the result concerning a cap $\overline{p} < p^c$ is implied by Lemma A6 in Reynolds and Rietzke (2015). This establishes the lemma. $\square$

We now prove part (i). We will first show that the equilibrium number of firms is differentiable and strictly increasing in the cap, for caps close to $P(Q^{\infty })$. Let $\hat{Q}$ satisfy $P(\hat{Q}(\overline{p})) = \overline{p}$, and let $\overline{\rho }^{\infty } \equiv P(Q^{\infty })$. Define:

$$\begin{aligned} \hat{\pi }(n, \overline{p}) = \frac{\hat{Q}(\overline{p})}{n}\overline{p} - C\bigg (\frac{\hat{Q}(\overline{p})}{n}\bigg ) \end{aligned}$$

Using the fact that $\hat{Q}(\overline{\rho }^{\infty }) = Q^{\infty }$, see that:

$$\begin{aligned} \hat{\pi }_1(n, \overline{p})|_{n^{\infty }, \overline{\rho }^{\infty }} = \frac{q^{\infty }}{n^{\infty }}\left[ C'(q^{\infty }) - \overline{\rho }^{\infty }\right] < 0 \end{aligned}$$

Moreover, note that $\hat{Q}'(\overline{p}) = \frac{1}{P'(\hat{Q}(\overline{p}))}$, and hence:

$$\begin{aligned} \hat{\pi }_2(n, \overline{p})|_{n^{\infty },\overline{\rho }^{\infty }} = \frac{1}{P'(Q^{\infty })n^{\infty }}\left[ P(Q^{\infty }) + Q^{\infty }P'(Q^{\infty }) - C'(q^{\infty })\right] > 0 \end{aligned}$$

The term in square brackets is strictly negative from (16) and since $n^{\infty } > 1$. Let ${n}(\overline{p})$ satisfy $\hat{\pi }({n}(\overline{p}), \overline{p}) = K$. Note that ${n}(\overline{\rho }^{\infty }) = n^{\infty }$. The implicit function theorem implies that for $\overline{p}$ close to $\overline{\rho }^{\infty }$, ${n}(\overline{p})$ is differentiable and ${n}'(\overline{p}) > 0$. We will show that for high enough caps, the equilibrium number of firms is in fact given by ${n}(\cdot )$.

If $p^c_{{n}(\overline{p})} < \overline{p} < \overline{\rho }^{\infty }_{{n}(\overline{p})}$ then Lemma A5 implies that equilibrium total output is $\hat{Q}(\overline{p})$; equilibrium profit in this subgame is given by $\hat{\pi }(n(\overline{p}), \overline{p})$. Using (16), it is straightforward to show that $\overline{\rho }^{\infty }_n$ is strictly decreasing in n. Since $p^c_{n^{\infty }} < \overline{\rho }^{\infty }$, and ${n}(\cdot )$ is strictly increasing and continuous then $p^c_{{n}(\overline{p})} < \overline{p} < \overline{\rho }^{\infty }_{{n}(\overline{p})}$ for caps close enough to $\overline{\rho }^{\infty }$. Thus, for high enough caps, equilibrium output is $\hat{Q}(\overline{p})$ and the equilibrium number of firms satisfies $\hat{\pi }(n(\overline{p}), \overline{p}) = K$. For sufficiently high caps welfare is:

$$\begin{aligned} W(\overline{p}) = \int _{0}^{\hat{Q}(\overline{p})}\! P(z)\,\text {d}z - n(\overline{p})C\left( \frac{\hat{Q}(\overline{p})}{n(\overline{p})}\right) - n(\overline{p})K \end{aligned}$$

Using the fact that $\pi ^{\infty } = K$ it may be verified that:

$$\begin{aligned} W'(\overline{p})|_{\overline{p} = \overline{\rho }^{\infty }} =\left[ P(Q^{\infty }) - C'(q^{\infty })\right] \left[ \hat{Q}'(\overline{\rho }^{\infty }) - q^{\infty }n'(\overline{\rho }^{\infty })\right] < 0 \end{aligned}$$

Hence, there is an interval of caps, $(\overline{\rho }^{\infty } - \epsilon , \overline{\rho }^{\infty })$ such that any cap in this interval strictly increases welfare. $\square$

1.8.1 Proof of Proposition 6(ii)

We begin by establishing the following lemma.

Lemma A6

For a fixed cap, $\overline{p}$, and a fixed number of firms, n, there exists a unique symmetric equilibrium. Moreover, for any fixed cap $\overline{p} > c$ (possibly non-binding), $\frac{\partial Q^*_n(\overline{p})}{\partial n} > 0$, $\frac{\partial q^*_n(\overline{p})}{\partial n} < 0$, and $\frac{\partial \pi ^*_n(\overline{p})}{\partial n} < 0$. Finally, for fixed n $\frac{\partial \pi ^*_n(\overline{p})}{\partial \overline{p}} > 0$ for caps $\overline{p} < \overline{\rho }^\infty _n$.²³

For fixed $\overline{p}$ and n, existence of a symmetric equilibrium follows from Lemma 1 in GZ.²⁴ To show uniqueness, note that symmetric equilibrium total output must satisfy the first-order condition:

$$\begin{aligned} \varGamma _n(Q, \overline{p})= & {} \int _{\underline{\theta }}^{\theta ^b(Q, \overline{p})}\, \left[ P(Q, \theta ) + \frac{Q}{n}P_1(Q, \theta )\right] \text {d}F(\theta )\nonumber \\&+ \int _{\theta ^b(Q, \overline{p})}^{\overline{\theta }}\, \overline{p}\, \text {d}F(\theta ) - C'\bigg (\frac{Q}{n}\bigg ) = 0 \end{aligned}$$

(17)

Differentiating $\varGamma _n(Q, \overline{p})$ with respect to Q we obtain:

$$\begin{aligned} \frac{\partial \varGamma _n(Q, \overline{p}) }{\partial Q}= & {} \theta ^b_1(Q, \overline{p})\frac{Q}{n}P_1(Q, \theta ^b)f(\theta ^b)\\&+ \frac{1}{n}\int _{\underline{\theta }}^{\theta ^b}\left[ P_1(Q, \theta )(1 + n) + QP_{11}(Q, \theta )\right] \text {d}F(\theta ) - C''\bigg (\frac{Q}{n}\bigg )\frac{1}{n} \end{aligned}$$

The first term above is non-positive and is strictly negative if $\theta ^b < \overline{\theta }$. Moreover, (15) implies the second term is strictly negative. Thus, $\frac{\partial \varGamma _n(Q, \overline{p}) }{\partial Q}< 0$; by the implicit function theorem, equilibrium total output is differentiable in n and $\overline{p}$. It is also readily verified that $\frac{\partial \varGamma _n(Q, \overline{p})}{\partial n} > 0$. Together with the fact that $\varGamma$ is strictly decreasing in Q, this implies that $\frac{\partial Q^*_n(\overline{p})}{\partial n} > 0$. Writing (17) in terms of per-firm outputs and using similar arguments, it can be shown that $\frac{\partial q^*_n(\overline{p})}{\partial n} < 0$.

We now show that $\frac{\partial \pi ^*_n(\overline{p})}{\partial n} < 0$. Fix $\overline{p}$ and let $Q_n$ ($q_n$) denote total (per-firm) equilibrium output under the cap in a subgame with n firms. Also let $y_n = (n-1)q_n$ denote the total output of all firms except some firm i. Since $\frac{\partial Q_n}{\partial n} > 0$ and $\frac{q_n}{\partial n} < 0$, clearly it must be the case that $\frac{\partial y_n}{\partial n} > 0$. Let $\pi (q, y, \overline{p})$ denote the profit to some firm i if i chooses output q and the other firms choose total output y. Note that for all n: $\pi _n^*(\overline{p}) = \pi (q_n, y_n, \overline{p})$. Hence

$$\begin{aligned} \frac{\partial \pi _n^*(\overline{p})}{\partial n} = \pi _1(q_n, y_n, \overline{p})\frac{\partial q_n}{\partial n} + \pi _2(q_n, y_n, \overline{p})\frac{\partial y_n}{\partial n} = \pi _2(q_n, y_n, \overline{p})\frac{\partial y_n}{\partial n} \end{aligned}$$

$\pi _1(q_n, y_n, \overline{p}) = 0$ is the equilibrium first-order condition for firm i. Thus, to demonstrate $\frac{\partial \pi ^*_n(\overline{p})}{\partial n} < 0$, it suffices to show that $\pi _2(q_n, y_n, \overline{p}) < 0$. To see this, note that:

$$\begin{aligned} \pi _2(q_n, y_n, \overline{p}) = \int _{\underline{\theta }}^{\theta ^b(Q_n, \overline{p})} q_nP_1(Q_n, \theta )\,\text {d}F(\theta ) < 0 \end{aligned}$$

Finally, we will show that, for fixed n, $\frac{\partial \pi ^{*}_n(\overline{p})}{\partial \overline{p}} > 0$, for caps below $\overline{\rho }^{\infty }_n$. Fix n and let $\overline{p} < \overline{\rho }^{\infty }_n$ be given. Let $Q(\overline{p})$ ($q(\overline{p})$) denote total (per-firm) equilibrium output in this subgame with n firms and cap $\overline{p}$. As demonstrated by EST, when demand is stochastic, equilibrium output may be either increasing or decreasing in the cap, so we must consider either possibility. As already argued, $Q(\cdot )$ is differentiable; first suppose $Q'(\overline{p}) \le 0$. Note that:

$$\begin{aligned} \frac{\partial \pi ^*_n(\overline{p})}{\partial \overline{p}}= & {} \frac{Q'(\overline{p})}{n}\left[ \int _{\underline{\theta }}^{\theta ^b}\, \left[ P(Q(\overline{p}), \theta ) + Q(\overline{p})P_1(Q(\overline{p}), \theta )\right] \text {d}F(\theta )\right. \\&\left. + \int _{\theta ^b}^{\overline{\theta }}\! \overline{p}\, \text {d}F(\theta ) - C'(q(\overline{p}))\right] + \int _{\theta ^b}^{\overline{\theta }}\! q(\overline{p})\, \text {d}F(\theta ) \end{aligned}$$

Equation (17) implies the term in square brackets is non-positive. But $\overline{p} < \overline{\rho }^{\infty }_n \implies \theta ^b(Q(\overline{p}, \overline{p}) < \overline{\theta }$, and so the second term is strictly positive. Hence, $Q'(\overline{p}) \le 0 \implies \frac{\partial \pi ^*_n(\overline{p})}{\partial \overline{p}} > 0$. Next, suppose $Q'(\overline{p}) > 0$. Using (17), expected equilibrium profit can be written:

$$\begin{aligned} \pi ^*_n(\overline{p}) = - \int _{\underline{\theta }}^{\theta ^b} q(\overline{p})^2P_1(Q, \theta )\text {d}F(\theta ) + q(\overline{p})C'(q(\overline{p})) - C(q(\overline{p})) \end{aligned}$$

It follows:

$$\begin{aligned} \frac{\partial \pi ^*(\overline{p})}{\partial \overline{p}}= & {} - P_1(Q, \theta ^b)q^2\left[ \theta ^b_1(\cdot )Q'(\overline{p}) + \theta ^b_2(\cdot )\right] f(\theta ^b) \\&- \frac{q}{n}Q'(\overline{p})\int _{\underline{\theta }}^{\theta ^b}\!\left[ 2P_1(\cdot ) + QP_{11}(\cdot )\right] \,\text {d}F(\theta ) + qC''(q)q'(\overline{p}) \end{aligned}$$

Note that $\overline{p} < \overline{\rho }^{\infty }_n \implies \theta ^b_1 > 0$ and $\theta ^b_2 > 0$. Moreover, condition (15) implies that the integral in the expression above is non-positive. Hence, $Q'(\overline{p}) > 0$ implies the RHS of the expression above is strictly positive. So, we have the result; for fixed n $\frac{\partial \pi ^*(\overline{p})}{\partial \overline{p}} > 0$ for all $\overline{p} < \overline{\rho }^{\infty }_n$. This establishes the lemma. $\square$

We now establish the proposition. Consider the game with no price cap. Let $Q^{\infty }_n$ ($q^{\infty }_n$) denote total (per-firm) equilibrium output in the subgame with n firms and no cap. Lemma A6 implies $\frac{\partial Q^{\infty }}{\partial n} >0$, $\frac{\partial q^{\infty }}{\partial n} < 0$, and $\frac{\partial \pi ^{\infty }}{\partial n} < 0$.

Let $W^\infty (n)$ denote (expected) equilibrium welfare with no cap, when n firms enter. Using nearly identical arguments as those used in the proof of Proposition 1 in Mankiw and Whinston, it can be shown that the free-entry equilibrium number of firms, $n^\infty$, is strictly greater than the welfare-maximizing (second best) number of firms. Moreover, it may also be shown that $\frac{\partial W^\infty (n)}{\partial n}|_{n = n^\infty } < 0$. Thus, $\exists$ $n_1 < n^\infty$ s.t. $n \in [n_1, n^\infty ) \implies W^\infty (n) > W^\infty (n^\infty )$.

Now consider the imposition of a price cap, $\overline{p} \in \mathbb {P}$, and let $n(\overline{p})$ denote the equilibrium number of firms under the cap. First, we claim that $n(\cdot )$ is continuous and $n(\overline{p}) < n^{\infty }$ for any $\overline{p} < \overline{\rho }^{\infty }$. To see these facts, note that $n(\overline{p})$ satisfies the equilibrium entry condition: $\pi ^*_{n(\overline{p})}(\overline{p}) = K$. Lemma A6 implies that for any cap $\frac{\partial \pi ^*_n(\overline{p})}{\partial n} < 0$; The implicit function theorem then implies that $n(\overline{p})$ is a differentiable (and hence continuous) function of the cap. Moreover, in the subgame with n firms, Lemma A6 implies $\frac{\partial \pi ^*_n(\overline{p})}{\partial \overline{p}} > 0$ for any cap $\overline{p} < \overline{\rho }^{\infty }_n$. This implies $n'(\overline{p}) > 0$ for any cap that binds in the subgame with $n(\overline{p})$ firms. But since $\frac{\partial Q^{\infty }_n}{\partial n} > 0$, a cap that binds in the subgame with $n^{\infty }$ firms will also bind in a subgame with $n(\overline{p})< n^{\infty }$ firms, which means $n'(\overline{p}) > 0$ for all $\overline{p} < \overline{\rho }^{\infty }$ and $\overline{p} \in \mathbb {P}$. Finally, since $n(\overline{\rho }^{\infty }) = n^{\infty }$, $\overline{p} < \overline{\rho }^{\infty } \implies n(\overline{p}) < n^{\infty }$. Now, let

$$\begin{aligned} \overline{\text {MR}}(n) = \max _{\theta \in \varTheta }\left\{ P(Q^\infty _n, \theta ) + \frac{Q^\infty _n}{n}P_1(Q^\infty _n, \theta )\right\} \end{aligned}$$

(18)

Since P is twice continuously differentiable in Q and $\theta$, and $Q^{\infty }_n$, is differentiable in n then the maximand in (18) is continuous in n and $\theta$. The theorem of the maximum implies $\overline{\text {MR}}(\cdot )$ is continuous. In the proof of their Proposition 1, GZ show that for any n: $\overline{\text {MR}}(n) < \overline{\rho }^{\infty }_{n}$. In particular, this means that $\overline{\text {MR}}(n(\overline{\rho }^{\infty })) < \overline{\rho }^{\infty }$. As $\overline{\text {MR}}(\cdot )$ is continuous, and $n(\cdot )$ is continuous, for high enough caps we have $\overline{\text {MR}}(n(\overline{p})) < \overline{p}$

Now choose $\overline{p} < \overline{\rho }^{\infty }$ sufficiently high such that $n(\overline{p}) \in [n_1, n^\infty )$ and $\overline{\text {MR}}(n(\overline{p})) < \overline{p}$. Then, $n(\overline{p}) \in [n_1, n^\infty )$ implies that, in the game with no cap, welfare is strictly higher with $n(\overline{p})$ firms than in the subgame with $n^{\infty }$ firms. But since $\overline{\text {MR}}(n(\overline{p})) < \overline{p}$, Theorem 1 in GZ²⁵ implies that welfare in the subgame with $n(\overline{p})$ firms is higher under the cap than with no cap. This establishes the existence of a welfare-improving cap. $\square$

1.9 Proof of Proposition 6(iii)

We first establish two lemmas and then prove the proposition.

Lemma A7

For any cap $\overline{p}$, and n, there exists a unique symmetric equilibrium. For any fixed cap (possibly non-binding), $\frac{\partial X_n(\overline{p})}{\partial n} \ge 0$, $\frac{\partial x_n(\overline{p})}{\partial n} < 0$, and $\frac{\partial \pi _n(\overline{p})}{\partial n} < 0$. Finally, for fixed n $\frac{\partial \pi ^*_n(\overline{p})}{\partial \overline{p}} > 0$ for caps $\overline{p} < \overline{\rho }^\infty _n$.²⁶

Equilibrium capacity satisfies the first-order condition:

$$\begin{aligned} \varGamma _n(X) = \int _{\tilde{\theta }_n(X, \overline{p})}^{\theta ^b(X, \overline{p})}\! \left[ P(X, \theta ) + \frac{X}{n}P_1(X, \theta )\right] \text {d}F(\theta ) + \int _{\theta ^b(X, \overline{p})}^{\overline{\theta }}\! \overline{p}\text {d}F(\theta ) - C'\bigg (\frac{X}{n}\bigg ) = 0 \end{aligned}$$

(19)

Note that:

$$\begin{aligned} \frac{\partial \varGamma _n(X)}{\partial X}= & {} \theta ^b_1(X, \overline{p})\frac{X}{n}P_1(X, \theta ^b)f(\theta ^b)\\&+ \int _{\tilde{\theta }_n}^{\theta ^b}\! \left[ P_1(X, \theta )\bigg (1 + \frac{1}{n}\bigg ) + \frac{X}{n}P_{11}(X, \theta )\right] \text {d}F(\theta ) - \frac{1}{n}C''\bigg (\frac{X}{n}\bigg ) \end{aligned}$$

Each of the three terms above is non-positive. We claim that in fact the RHS of the expression above is strictly negative. If the cap is binding, then $\underline{\theta } < \theta ^b < \overline{\theta }$; in this case $\theta ^b_1 > 0$ and the first term in the expression above is strictly negative. If the cap is non-binding, then $\theta ^b = \overline{\theta } > \tilde{\theta }$; (15) then implies that the second term above is strictly negative. Hence $\frac{\partial \varGamma _n(X)}{\partial X} < 0$. Thus, there exists a unique solution to (19). Moreover, by the implicit function theorem equilibrium capacity, $X^*_n(\overline{p})$, is differentiable in n and $\overline{p}$. Now note that

$$\begin{aligned} \frac{\partial \varGamma _n(X)}{\partial n} = -\int _{\tilde{\theta }_n}^{\theta ^b}\! \frac{X}{n^2}P_1(X, \theta )\, \text {d}F(\theta ) + \frac{X}{n^2}C''\bigg (\frac{X}{n}\bigg ) \ge 0\end{aligned}$$

This inequality holds strictly whenever $\tilde{\theta }_n < \theta ^b$ (as would be the case if the cap is non-binding) or when $C'' > 0$. Hence, $\frac{\partial X_n}{\partial n} \ge 0$. Using (19), and replacing total capacity, X, with per-firm capacity, $x = \frac{X}{n}$, similar arguments can be applied to show $\frac{\partial x_n}{\partial n} < 0$. Now see that equilibrium profit is given by:

$$\begin{aligned} \pi _n(\overline{p}) = \int _{\underline{\theta }}^{\tilde{\theta }}\! \pi ^0_n(\theta , \overline{p})\, \text {d}F(\theta ) + \int _{\tilde{\theta }}^{\theta ^b}\! P(X_n, \theta )x_n\, \text {d}F(\theta ) + \int _{\theta ^b}^{\overline{\theta }}\! \overline{p}x_n\,\text {d}F(\theta ) - C(x_n) \end{aligned}$$

And so:

$$\begin{aligned} \frac{\partial \pi ^*_n(\overline{p})}{\partial n} =&\int _{\underline{\theta }}^{\tilde{\theta }}\! \frac{\partial \pi ^0_n(\theta , \overline{p})}{\partial n}\, \text {d}F(\theta ) +\frac{\partial x_n}{\partial n}\left[ \int _{\tilde{\theta }}^{\theta ^b} P(X_n, \theta )\, \text {d}F(\theta ) + \int _{\theta ^b}^{\overline{\theta }}\! \overline{p}\,\text {d}F(\theta ) - C'(x_n)\right] \\&+ \frac{\partial X_n}{\partial n}x_n\int _{\tilde{\theta }}^{\theta ^b}\! P_1(X_n, \theta )\, \text {d}F(\theta ) < 0 \end{aligned}$$

To see why this strict inequality holds, first note that the second and third terms above are non-positive. Also note that for $\theta$ close to $\underline{\theta }$, the cap is non-binding. Using the equilibrium characterized in Lemma A5 for convex costs and deterministic demand, it can be shown that $\pi ^0_n$ is non-increasing in n for all $\theta \in [\underline{\theta }, \tilde{\theta }]$. But, for $\theta$ sufficiently close to $\underline{\theta }$, neither the cap nor the capacity constraint will bind. For these realizations, standard techniques can be used to show that $\frac{\partial \pi ^0_n(\theta , \overline{p})}{\partial n} < 0$. Hence, the first term is strictly negative.

Finally, we show $\frac{\partial \pi ^*_n(\overline{p})}{\partial \overline{p}} > 0$ for caps $\overline{p} < p^{\infty }_n$. Fix n and let $X(\overline{p})$ denote equilibrium total capacity for some cap $\overline{p} < p^{\infty }_n$. Note that we have already shown that $X(\cdot )$ is differentiable in the cap. Theorem 6 in EST implies that $X(\cdot )$ may either be increasing or decreasing. Thus, we must consider both possibilities. First suppose $X'(\overline{p}) \le 0$. See that:

$$\begin{aligned} \frac{\partial \pi ^*_n(\overline{p})}{\partial \overline{p}} =&\int _{\underline{\theta }}^{\tilde{\theta }}\! \frac{\partial \pi ^0_n(\theta , \overline{p})}{\partial \overline{p}}\, \text {d}F(\theta )\\&+\frac{X'(\overline{p})}{n}\left[ \int _{\tilde{\theta }}^{\theta ^b}\! \left[ P(X, \theta ) + XP_1(X, \theta )\right] \, \text {d}F(\theta ) + \int _{\theta ^b}^{\overline{\theta }}\! \overline{p}\,\text {d}F(\theta ) - C'(x)\right] \\&+ \int _{\theta ^b}^{\overline{\theta }}\! x\, \text {d}F(\theta ) \end{aligned}$$

Using the equilibrium constructed in Lemma A5, it can be shown that $\frac{\partial \pi ^0(\theta , \overline{p})}{\partial \overline{p}} \ge 0$. Moreover, Eq. (19) implies that the term in square brackets is non-positive, which means the second term above is nonnegative. But $\overline{p} < \overline{\rho }^{\infty }_n \implies \theta ^b(X(\overline{p}), \overline{p}) < \overline{\theta }$, and hence the third term is strictly positive. Thus, $X'(\overline{p}) \le 0 \implies \frac{\partial \pi ^*_n(\overline{p})}{\partial \overline{p}} > 0$.

Next, suppose $X'(\overline{p}) > 0$. Using (19), equilibrium profit may be written:

$$\begin{aligned} \pi ^*_n(\overline{p}) \!= \!\int _{\underline{\theta }}^{\tilde{\theta }(X, \overline{p})}\! \pi ^0(\theta , \overline{p})\, \text {d}F(\theta ) -x^{2} \int _{\tilde{\theta }(X, \overline{p})}^{\theta ^b(X, \overline{p})}\! P_1(X, \theta )\, \text {d}F(\theta ) \!+\! xC'(x) \!-\! C(x) \end{aligned}$$

Using this expression for profit, one finds:

$$\begin{aligned} \frac{\partial \pi ^*_n(\overline{p})}{\partial \overline{p}} =&\int _{\underline{\theta }}^{\tilde{\theta }}\! \frac{\partial \pi ^0_n(\theta , \overline{p})}{\partial \overline{p}}\, \text {d}F(\theta ) - \left[ \theta ^b_1(\cdot )X'(\overline{p}) + \theta ^b_2(\cdot )\right] x^2P_1(X, \theta ^b)f(\theta ^b)\\&- x\frac{X'(\overline{p})}{n}\left[ \int _{\tilde{\theta }}^{\theta ^b}\! \left[ 2P_1(X, \theta ) + XP_{11}(X, \theta )\right] \, \text {d}F(\theta )\right] + xC''(x)x'(\overline{p}) \end{aligned}$$

For a cap $\overline{p} < p^{\infty }_n$ it holds that $\theta ^b_1 > 0$ and $\theta ^b_2 > 0$. Moreover, condition (15) implies that the term in large square brackets is non-positive. It follows that the RHS of the expression above is strictly positive. Thus, we have the result; $\frac{\partial \pi ^*_n(\overline{p})}{\partial \overline{p}}> 0$ for all caps $\overline{p} < p^{\infty }_n$, and the lemma is established.

Lemma A8

Let $n^W$ denote the welfare-maximizing (second best) number of firms and $n^\infty$ the free-entry number of firms with no cap. Then, $n^W < n^\infty$ and $n \ge n^{\infty } \implies \frac{\partial W_n}{\partial n} < 0.$

If n firms enter equilibrium welfare is given by:

$$\begin{aligned} W_n= & {} \int _{\underline{\theta }}^{\tilde{\theta }_n(X_n)}{\left[ \int _{0}^{Q_n^0(\theta )}P(z, \theta )\text {d}z\right] \text {d}F(\theta )} \\&+ \int ^{\overline{\theta }}_{\tilde{\theta }_n(X_n)}{\left[ \int _{0}^{X_n}P(z, \theta )\text {d}z\right] \text {d}F(\theta )} - nC(x_n) - nK \end{aligned}$$

Differentiating $W_n$ with respect to n, and using the definition of $\pi ^{\infty }_n$, we obtain:

$$\begin{aligned} \frac{\partial W_n}{\partial n}= & {} \pi _n^\infty - K + \int _{\underline{\theta }}^{\tilde{\theta }_n(X_n)}{n\frac{\partial q_n^0(\theta )}{\partial n}P(Q_n^0(\theta ),\theta ) \text {d}F(\theta )} \\&+\,n\frac{\partial x_n}{\partial n}\left[ \int ^{\overline{\theta }}_{\tilde{\theta }_n(X_n)}{P(X_n, \theta ) \text {d}F(\theta )} - C'(x_n)\right] \end{aligned}$$

By definition of $n^{\infty }$, it follows that $n \ge n^{\infty } \implies \pi ^{\infty }_{n} \le K$, and hence:

$$\begin{aligned} \frac{\partial W_n}{\partial n}\le & {} \int _{\underline{\theta }}^{\tilde{\theta }_n(X_{n})}{n\frac{\partial q_{n}^0(\theta )}{\partial n}P(Q_{n}(\theta ),\theta ) \text {d}F(\theta )} \\&+\,n\frac{\partial x_{n}}{\partial n}\left[ \int ^{\overline{\theta }}_{\tilde{\theta }_n(X_n)}{P(X_{n}, \theta ) \text {d}F(\theta )} - C'(x_n)\right] < 0 \end{aligned}$$

To see why this strict inequality holds, first note that standard techniques can be used to show that: $\frac{\partial q_n^0(\theta )}{\partial n} < 0$. Moreover, by Lemma A7 $\frac{\partial x_n}{\partial n} < 0$. Finally, using the first-order condition in (19), with $\theta ^b = \overline{\theta }$, it can be verified that the term in square brackets must be strictly positive. Thus, $\frac{\partial W_n}{\partial n} < 0$ for all $n \ge n^{\infty }$, and hence $n^W < n^{\infty }$. This establishes the lemma. $\square$

We now prove the proposition. Lemma A8 implies $\frac{\partial W_n}{\partial n}|_{n = n^\infty } < 0$. Moreover, GZ show that for any n: $\overline{\text {MR}}(n) < \overline{\rho }^{\infty }_n$ and that for fixed n any cap $\overline{p} \in [\overline{\text {MR}}(n) ,\overline{\rho }^{\infty }_n)$ increases welfare, where

$$\begin{aligned} \overline{\text {MR}}(n) = \max _\theta \left\{ P(X_n^{\infty }, \theta ) + \frac{X_n^{\infty }}{n}P_1(X_n^{\infty }, \theta )\right\} \end{aligned}$$

The remainder of the proof follows exactly along the same lines as the proof of Proposition 6(ii). $\square$